Журнал вычислительной математики и математической физики, 2020, T. 60, № 5, стр. 864-872

1. ВВЕДЕНИЕ

При исследовании, вообще говоря, нестационарного движения жидких сред с поверхностью раздела $\Gamma $ в неоднородном поле температур разность потоков тепла на ней, в общем случае, не равна нулю [1], [2]

где $\unicode{230} = - \partial \sigma {\text{/}}\partial \theta $, $\omega = \partial (\sigma (\theta ) + \unicode{230} (\theta )){\text{/}}\partial \theta $, $\sigma (\theta )$ — коэффициент поверхностного натяжения. В равенстве (1.1) ${{k}_{j}}$, ${{\theta }_{j}}$ — коэффициенты теплопроводностей и температуры жидкостей, $j = 1,2$; $\theta = {{\theta }_{1}} = {{\theta }_{2}}$, ${\mathbf{u}} = {{{\mathbf{u}}}_{1}} = {{{\mathbf{u}}}_{2}}$ – общие значения температур и векторов скоростей на поверхности раздела $\Gamma $, n – нормаль к $\Gamma $, направленная во вторую жидкость. Условие (1.1) можно назвать энергетическим условием на поверхности раздела двух жидкостей $\Gamma $ [3]. Оно означает, что скачок теплового потока в направлении нормали к $\Gamma $ компенсируется изменением внутренней энергии этой поверхности. В свою очередь, это изменение связано как с изменением температуры, так и площади границы раздела.

Для многих жидких сред зависимость $\sigma (\theta )$ хорошо аппроксимируется линейной функцией

с положительными постоянными ${{\sigma }_{0}}$, $\unicode{230} $, ${{\theta }_{0}}$. В этом случае энергетическое равенство (1.1) упрощается

Порядок отношения правой части равенства (1.3) к первому члену левой ее части оценивается параметром ${\text{E}} = \unicode{230} \theta {\text{*/}}{{\mu }_{2}}{{k}_{2}}$(для второго надо положить ${{\mu }_{1}}{{k}_{1}}$, ${{\mu }_{j}}$ – динамические вязкости), определяющим влияние межфазной энергии на динамику движения жидкостей внутри слоев; $\theta {\text{*}}$ – характерная температура на границе раздела. Эти параметры для обычных жидкостей при комнатной температуре малы [2], [4], [5]. Так, в экспериментах в системе воздух – этиловый спирт при $\theta {\text{*}} = 15^\circ {\text{C}}$ имеем ${\text{E}} \sim 5 \times {{10}^{{ - 4}}}$. Поэтому часто правую часть в (1.1) опускают и говорят о равенствах потока тепла через границу раздела. Однако для маловязких жидкостей эти слагаемые надо учитывать. Расчеты [5], проведенные для движения пузырьков в различных жидкостях, показали, что значение ${\text{E}} = O(1)$ достигаeтся при достаточно высоких температурах – вязкость быстро уменьшается с ростом температуры. Кроме того, этот факт имеет место и для некоторых криогенных жидкостей, например для жидкого ${\text{C}}{{{\text{O}}}_{2}}$. Максимальные значения ${\text{E}}$ достигаются вблизи критических точек. Так, для воды ${\text{E}} \sim 0.02$ при $\theta = 303.15$ К; ${\text{E}} \sim 0.6$ при $\theta = 573.15$ К; ${\text{E}} \sim 0.7$ при $\theta = 623.15$ К (критическая точка для воды ${{\theta }_{{{\text{кр}}}}} = 647.30$ К).

В книге [2] на простых примерах двухслойных систем, когда основное состояние либо покой, либо однонаправленное стационарное течение, показано влияние теплоты, поглощаемой или выделяющейся при локальных изменениях площади межфазной поверхности, на формирование напряжений Марангони и слаболинейных волновых режимов на границе раздела жидкостей, вязкость которых достаточно мала. В [6] изучено влияние изменения межфазной поверхностной энергии на характер и тип неустойчивостей основного однонаправленного течения, когда для возмущений использовано условие (1.3). Показано, что существенное отличие от классического случая (правая часть в (1.3) равна нулю) в поведении возмущений наблюдается в области коротких волн. Именно, в задаче с полным условием кризис течения вызывается тепловой колебательной модой и сопровождается формированием поперечных бегущих волн, которые распространяются в противоположном основному течению направлении. В задаче с классическим условием неустойчивость проявляется в виде поперечных стоячих волн. Учет дополнительного слагаемого в энергетическом условии позволил получить результат, качественно совпадающий с экспериментальными данными для системы FC-72 – азот.

В упомянутых выше задачах основное стационарное двухслойное течение не зависело от изменения межфазной энергии. В настоящей работе исследуется такая зависимость для двумерного двухслойного стационарного течения с полем скоростей типа Хименца.

2. ПОСТАНОВКА ЗАДАЧИ

Рассматривается плоское двухслойное стационарное течение вязких теплопроводных жидкостей в слоях, ограниченных твердыми стенками $y = 0$, $y = h$ с общей поверхностью раздела $y = l < h$ в отсутствие массовых сил.

Межфазная поверхность предполагается плоской, для этого достаточно потребовать, чтобы капиллярное число ${\text{Ca}} = {{\mu }_{1}}{{\chi }_{1}}{\text{/}}{{\sigma }_{0}}l \ll 1$ (см. [7]), $\chi $ – коэффициент температуропроводности. Поле скоростей и температур системы уравнений вязкой теплопроводной жидкости в слоях будем искать в виде

причем $0 < y < l$ при $j = 1$, $l < y < h$ при $j = 2$ и ${{\operatorname{div} }_{\Gamma }}{\mathbf{u}} = {{w}_{1}}(l)$. Такое представление поля скоростей соответствует известному решению Хименца [8]. Подстановка (2.1) в уравнения движения и переноса тепла и их анализ на совместность приводят к следующим следствиям: функции ${{w}_{j}}(y)$, ${{v}_{j}}(y)$, ${{a}_{j}}(y)$ и ${{b}_{j}}(y)$ есть решения нелинейных систем уравнений где ${{\nu }_{j}}$ – кинематические вязкости, ${{\rho }_{j}} = {{\mu }_{j}}{\text{/}}{{\nu }_{j}}$ – плотности, ${{f}_{j}}$ – постоянные. Давления в жидкостях распределены по законам так, что значения ${{f}_{j}}$ характеризуют градиенты давлений вдоль оси $x$.

Будем считать, что на твердой стенке $y = 0$ (подложке) задано распределение температуры ${{\theta }_{1}}(x,0) = {{a}_{{10}}}{{x}^{2}} + {{b}_{{10}}}$ с постоянными ${{a}_{{10}}}$, ${{b}_{{10}}}$. При ${{a}_{{10}}} > 0$ температура имеет в точке $x = 0$ минимальное значение, а при ${{a}_{{10}}} < 0$ – максимальное. Верхняя стенка теплоизолирована: ${{\theta }_{{2y}}}(x,h) = 0$. Таким образом, на твердых стенках для искомых функций заданы условия

На границе раздела $y = l$ выполнены соотношения

Первые четыре условия в (2.5) есть следствия непрерывности поля скоростей и температур на границе раздела, а пятое – динамическое условие. Последние два условия получены с учетом зависимости коэффициента поверхностного натяжения (1.2) и соотношения (1.3).

Замечание 1. Поставленная задача является обратной, поскольку наряду с функциями ${{w}_{j}}$, ${{v}_{j}}$, ${{a}_{j}}$, ${{b}_{j}}$ постоянные ${{f}_{j}}$(градиенты давлений вдоль слоев) также неизвестны. Сами давления по известным ${{v}_{j}}$ и ${{f}_{j}}$ определяются по формулам (2.3).

Исключим вертикальные скорости ${{v}_{j}}(y)$ из уравнений неразрывности с учетом условий прилипания на стенках (2.4)

Тогда основной будет следующая обратная сопряженная краевая задача:

Граничные условия для нее следуют из (2.4), (2.5) и представлений (2.6)

Задача для функций ${{b}_{j}}(y)$ отделяется и они находятся после решения задачи для функций ${{w}_{j}}(y),\;{{a}_{j}}(y)$ и не влияют на поле скоростей в слоях.

Введем безразмерные функции и параметры

где ${{{\text{P}}}_{j}}$ – числа Прандтля, ${\text{M}}$ – число Марангони, $\theta {\text{*}} = {\text{|}}{{a}_{{10}}}{\text{|}}{{l}^{2}}$ – характерная температура вдоль поверхности раздела, так что ${\text{M}}$, ${\text{E}}$ могут быть как положительными, так и отрицательными числами. Тогда в безразмерных переменных нелинейная сопряженная краевая задача примет вид где $\gamma = l{\text{/}}h < 1$, $\mu = {{\mu }_{1}}{\text{/}}{{\mu }_{2}}$, $\chi = {{\chi }_{1}}{\text{/}}{{\chi }_{2}}$, $k = {{k}_{1}}{\text{/}}{{k}_{2}}$. К граничным условиям (2.11) необходимо добавить интегральные условия переопределения которые позволяют найти неизвестные постоянные (градиенты давлений вдоль слоев) ${{F}_{j}}$, $j = 1,2$.

3. РЕШЕНИЕ МОДЕЛЬНОЙ ЗАДАЧИ – ПОЛЗУЩИЕ ТЕЧЕНИЯ

Известно, что при малых числах Рейнольдса уравнения импульса и энергии упрощаются за счет отбрасывания конвективного ускорения. Такие движения принято называть ползущими. Ползущие течения имеют место во многих конструктивных элементах машин, механизмов, оборудования и приборов, если поперечные размеры каналов или скорости течения малы или вязкость протекающей жидкости велика. В нашем случае роль числа Рейнольдса играет число Марангони, которое может быть является малым как за счет физических параметров жидкости, так и толщины канала [9], [10].

Поэтому предположим что $\left| {\text{M}} \right| \ll 1$ и ищем решение задачи (2.10)–(2.12) в виде ${{W}_{j}} = W_{j}^{0} + {\text{M}}W_{j}^{1} + ...$, ${{F}_{j}} = F_{j}^{0} + {\text{M}}F_{j}^{1} + ...$, ${{A}_{j}} = A_{j}^{0} + {\text{M}}A_{j}^{1} + ...$, тогда решение для нулевого приближения имеет вид [11]

причем и ${{C}_{2}}$ есть решение квадратного уравнения с дискриминантом Значит, при имеется два решения (для ${{a}_{{10}}} > 0$ это всегда так), при ${\text{E}} = {\text{E*}}$ – одно, а при ${\text{E}} < {{{\text{E}}}^{ * }}$ решений нет. Последние два случая реализуются только для ${{a}_{{10}}} < 0$, когда температура на нижней стенке имеет максимум в точке $x = 0$. Выражения для безразмерных вертикальных скоростей определятся по формуле (2.6) и будут иметь вид

Замечание 2. Простые вычисления показывают, что при ${\text{E}} = 0$ единственное решение задачи (1.10)–(1.16), при малых числах Марангони, таково

и оно существенно отличается от решения (3.1)–(3.4).

4. МЕТОД ЧИСЛЕННОГО РЕШЕНИЯ И РЕЗУЛЬТАТЫ РАСЧЕТОВ

Для решения общей нелинейной задачи (2.10)–(2.12) применяется тау-метод, являющийся модификацией метода Галеркина [12]. Произведем замену переменных: $\xi {\text{'}} = \xi {\text{/}}\gamma $ для $j = 1$ и $\xi {\text{'}} = (1 - \xi ){\text{/}}(1 - \gamma )$ для $j = 2$. Тогда задача (2.10)–(2.12) перепишется в виде (штрихи опущены)

Приближенное решение задачи(4.1)–(4.4) ищется в виде сумм: где ${{R}_{k}}(z) = {{P}_{k}}(2z - 1)$ – смещенные полиномы Лежандра [13], $z \in [0,1]$, ${{P}_{k}}(z)$ – обычные полиномы Лежандра. Из интегральных условий (4.4), учитывая ортогональность полиномов ${{R}_{k}}(z)$ на отрезке $[0,1]$получаем $W_{1}^{0} = W_{2}^{0} = 0$. Остальные коэффициенты $W_{j}^{k},\;A_{j}^{k},\;B_{j}^{k}$ и постоянные ${{F}_{{1n}}},\;{{F}_{{2n}}}$ находятся из системы галeркинских приближений и преобразованных граничных условий (4.3) В частности, неизвестные постоянные ${{F}_{{1n}}},\;{{F}_{{2n}}}$ определяются по известным ${{W}_{{jn}}}$ и ${{A}_{{jn}}}$, из уравнений $\int_0^1 {{{L}_{j}}({{W}_{{jn}}},{{F}_{{jn}}}){{R}_{0}}(\xi )d\xi = 0} $, $j = 1,2$. При выводе системы (4.7) было учтено, что ${{R}_{k}}(1) = 1$, ${{R}_{k}}(0) = {{( - 1)}^{k}}$. Таким образом, уравнения (4.6), (4.7) образуют замкнутую систему алгебраических нелинейных уравнений на коэффициенты $W_{j}^{k},\;A_{j}^{k}$ и постоянные ${{F}_{{jn}}},\;j = 1,2$.

Для решения нелинейной системы уравнений (4.6), (4.7) применялся метод Ньютона. В качестве нулевых приближений для неизвестных коэффициентов $W_{j}^{k}$, $A_{j}^{k}$, $B_{j}^{k}$ и постоянных ${{F}_{{1n}}}$, ${{F}_{{2n}}}$ взяты значения, удовлетворяющие условиям (4.7) и равенствам

Интегральные равенства (4.8) следуют из уравнений (4.1), (4.2), учитывая граничные условия (4.3) и вид решений (4.5).

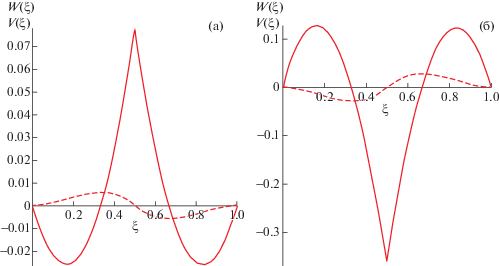
Расчеты проводились для следующих значений определяющих параметров, соответствующих системе вода ($j = 1$) – водяной пар ($j = 2$) на линии насыщения при температуре ${{300}^{{^{ \circ }}}}{\text{C}}$ [14]: ${\text{E}} = 0.6$, ${\text{M}} = 11.5$, $h = 1 \times {{10}^{{ - 6}}}$ м, $l = 0.5 \times {{10}^{{ - 6}}}$ м и $n = 15$ (далее нижний индекс $n$ будет опущен). Было получено два различных значения безразмерных постоянных ${{F}_{1}}$, ${{F}_{2}}$: $\{ F_{1}^{1} = - 0.434,\;F_{2}^{1} = - 1.506\} $, $\{ F_{1}^{2} = 2.446,\;F_{2}^{2} = 7.366\} $ (верхний индекс означает номер решения). При этом разность значений, полученных при $n = 15$ и $n = 16$, составляет порядка ${{10}^{{ - 15}}}$ и ${{10}^{{ - 10}}}$ для ${{F}^{1}}$ и ${{F}^{2}}$ соответственно, что говорит о хорошей сходимости $\tau $ – метода при решении данной краевой задачи. На фиг. 1 приведены профили безразмерных функций ${{W}_{j}}(\xi )$ и поперечных скоростей ${{V}_{j}}(\xi )$ для значений ${{F}^{1}}$ и ${{F}^{2}}$ соответственно. Здесь и далее функции $W(\xi )$ и $V(\xi )$ совпадают с функциями ${{W}_{j}}(\xi )$ и ${{V}_{j}}(\xi )$, $j = 1,2$ соответственно на своих областях определения. Стоит также отметить, что с уменьшением числа Марангони найденные значения $F_{1}^{1},\;F_{2}^{1}$ и $F_{1}^{2},\;F_{2}^{2}$ стремятся к параметрам модельной задачи $F_{1}^{{01}} = - 0.515$, $F_{2}^{{01}} = - 1.743$ и $F_{1}^{{02}} = 72.615$, $F_{2}^{{02}} = 245.712$ соответственно (см. (3.3)). Так, при ${\text{M}} = 0.001$ получим ${\text{|}}F_{j}^{{01}} - F_{j}^{1}{\text{|}} \approx {\text{1}}{{{\text{0}}}^{{ - 15}}}$ и ${\text{|}}F_{j}^{{02}} - F_{j}^{2}{\text{|}} \approx {{10}^{{ - 10}}}$, $j = 1,2$.

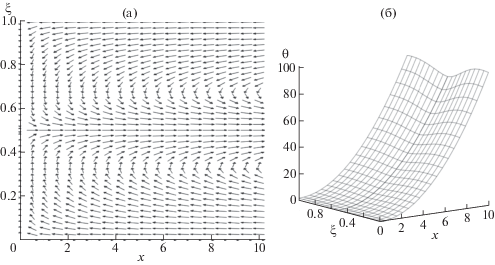
На фиг. 2, 3 изображены поля скоростей и температур в слоях для ${{F}^{1}}$ и ${{F}^{2}}$ соответственно. В обоих случаях возникают зоны возвратного течения: в первом случае – вблизи поверхности раздела (фиг. 2), а во втором – вблизи твердых стенок (фиг. 3). Помимо градиента поверхностного натяжения, имеется еще один механизм движения, возникающий при нагреве нижней стенки – градиент давления в слоях. Вычисления показывают, что градиент давления в первом слое по модулю существенно превосходит градиент поверхностного натяжения и действует в противоположном направлении. Поэтому в обоих случаях течение вблизи поверхности раздела направлено в сторону роста температуры, то есть в сторону, противоположную направлению действия термокапиллярных сил.

Для случая, когда отсутствует влияние изменения внутренней межфазной энергии (${\text{E}} = 0$) имеется одно решение ${{F}_{1}} = - 0.438$, ${{F}_{2}} = - 1.518$. Это решение с уменьшением числа Марангони стремится к единственному решению модельной задачи (3.6) $F_{1}^{0} = - 0.519$, $F_{2}^{0} = - 1.756$, и при ${\text{M}} = 0.001$ получим ${\text{|}}F_{j}^{0} - {{F}_{j}}{\text{|}} \approx {{10}^{{ - 15}}}$, $j = 1,2$.

Стоит также сказать о влиянии безразмерных параметров на возникающие течения: с ростом безразмерных параметров ${\text{M}}$ и ${\text{E}}$ значения безразмерной функции $W(\xi )$ и поперечной скорости $V(\xi )$ уменьшаются. С увеличением толщины второго слоя (уменьшение $\gamma $) безразмерный градиент давления во второй жидкости убывает по модулю, а в первой практически не изменяется. Так, при $E = 0,\;\gamma = 0.2$ (толщина второго слоя в 4 раза больше первого) ${{F}_{1}} = - 0.431$, ${{F}_{2}} = - 0.081$. На интенсивность течений безразмерный параметр $\gamma $ не влияет.