Журнал вычислительной математики и математической физики, 2020, T. 60, № 6, стр. 1013-1026
К численному решению обратной многочастотной задачи скалярной акустики
А. Б. Бакушинский 1, *, А. С. Леонов 2, **
1 Ин-т системного анализа ФИЦ ИУ РАН
117312 Москва, пр-т 60-летия Октября, 9, Россия
2 Национальный исследовательский ядерный ун-т “МИФИ”
115409 Москва, Каширское ш., 31, Россия
* E-mail: asleonov@mephi.ru
** E-mail: bakush@isa.ru
Поступила в редакцию 05.06.2019
После доработки 25.11.2019
Принята к публикации 11.02.2020
Аннотация
В работе предлагается новый алгоритм решения трехмерной скалярной обратной задачи акустического зондирования неоднородной среды по комплексной амплитуде волнового поля, измеряемого вне области неоднородности. Для схемы регистрации данных “в плоском слое” обратная задача сводится с помощью преобразования Фурье к решению совокупности одномерных интегральных уравнений Фредгольма I рода, к последующему вычислению комплексной амплитуды волнового поля в области неоднородности и далее к нахождению искомого поля скоростей звука в этой области. Алгоритм позволяет решать обратную задачу на персональном компьютере средней производительности (без распараллеливания) для достаточно мелких трехмерных сеток за несколько минут. Проведено численное исследование точности предлагаемого алгоритма для решения модельных обратных задач на одной частоте и нескольких частотах одновременно, исследованы вопросы устойчивости алгоритма по отношению к возмущениям данных. Библ. 24. Фиг. 10.
1. ВВЕДЕНИЕ
Пусть скалярная функция $p({\mathbf{x}},t)$ определяет акустическое волновое поле, зависящее от координат ${\mathbf{x}} \in {{\mathbb{R}}^{3}}$ и времени $t \geqslant 0$. Поле создается в бесконечной среде источниками, локализованными в известной области $S$. Среда характеризуется локальной фазовой скоростью звука $c({\mathbf{x}})$ и имеет постоянную плотность. При этом известно, что $c({\mathbf{x}}) = {{c}_{0}} = {\text{const}}$ вне заданной области $X$, удовлетворяющей условию $X \cap S = \emptyset $. В самой области $X$ функция $c({\mathbf{x}})$ может быть переменной, и это интерпретируется как нахождение там акустических неоднородностей. В этом случае для гармонического источника вида $f({\mathbf{x}},\omega ){{e}^{{i\omega t}}}$ с известной частотой $\omega $ поле $p({\mathbf{x}},t)$ в рамках приближения линейной акустики может быть найдено в форме $p({\mathbf{x}},t) = u({\mathbf{x}},\omega ){{e}^{{i\omega t}}}$, где комплексная амплитуда $u({\mathbf{x}},\omega )$ удовлетворяет уравнению
(1)
$\Delta u({\mathbf{x}},\omega ) + k_{0}^{2}u({\mathbf{x}},\omega ) = f({\mathbf{x}},\omega ) + {{\omega }^{2}}\xi ({\mathbf{x}})u({\mathbf{x}},\omega ),\quad {\mathbf{x}} \in {{\mathbb{R}}^{3}},$Нас интересует следующая обратная задача для уравнения (1): зная комплексную амплитуду поля $u({\mathbf{x}},\omega )$ в области $Y,Y \cap X = \emptyset $, $Y \cap S = \emptyset $, для некоторого набора частот $\omega $ найти коэффициент $\xi (x)$, т.е. функцию $c({\mathbf{x}})$, определяющую акустические неоднородности в области $X$. Вводя функцию Грина для уравнения Гельмгольца (1) в ${{\mathbb{R}}^{3}}$: $G(\rho ,\omega ) = - \tfrac{{exp\left( {i\omega \rho {\text{/}}{{c}_{0}}} \right)}}{{4\pi \rho }}$, можно при определенных предположениях о гладкости функций $u({\mathbf{x}},\omega )$, $f({\mathbf{x}},\omega )$, $c({\mathbf{x}})$ (см., например, [1]) свести обратную задачу к нелинейной относительно неизвестных $u({\mathbf{x}}{\text{'}},\omega )$, $\xi ({\mathbf{x}}{\text{'}})$, ${\mathbf{x}}{\text{'}} \in X$, системе интегральных уравнений:
(2)
$\begin{gathered} u({\mathbf{x}},\omega ) = {{u}_{0}}({\mathbf{x}},\omega ) + {{\omega }^{2}}\int\limits_X G (\left| {{\mathbf{x}} - {\mathbf{x}}{\text{'}}} \right|,\omega )\xi ({\mathbf{x}}{\text{'}})u({\mathbf{x}}{\text{'}},\omega )d{\mathbf{x}}{\text{'}},\quad {\mathbf{x}} \in X, \\ {{\omega }^{2}}\int\limits_X G (\left| {{\mathbf{x}} - {\mathbf{x}}{\text{'}}} \right|,\omega )\xi ({\mathbf{x}}{\text{'}})u({\mathbf{x}}{\text{'}},\omega )d{\mathbf{x}}{\text{'}} = W({\mathbf{x}},\omega ),\quad {\mathbf{x}} \in Y. \\ \end{gathered} $Задача (2) достаточно хорошо исследована теоретически: изучены вопросы существования и единственности ее решения (см., например, [2]–[4] и др.).
Во многих работах рассмотрены различные численные методы решения задачи (2) в двумерной и трехмерной постановках. Так, в [1] система (2) сводится к нелинейному операторному уравнению, которое затем решается специальным итерационным методом. При этом явно не учитывается, что это уравнение является некорректно поставленной задачей и итерационный метод не регуляризируется. Тем не менее метод работает для модельных “рассеивателей средней силы” [1, с. 101–105]. В работе [4] для решения системы уравнений (2) в трехмерном аксиально-симметричном случае использован регуляризованный метод Гаусса–Ньютона. В работе [5] для аналогичной задачи были применены специальный градиентный метод и метод Флетчера–Ривса. Другие градиентные методы были использованы в [6], [7].
Отметим, что имеются и альтернативные подходы в решении обратной задачи акустического зондирования, не связанные с системой (2). В частности, оригинальный метод граничного управления, позволяющий решать трехмерные задачи типа (2), был предложен и развит в работах [8], [9]. В [10] для решения двумерной обратной задачи рассеяния был применен известный метод Р.Г. Новикова [11], а в последующей работе [12] проведен сравнительный анализ разновидности этого метода и некоторых других функционально-аналитических методов решения двумерных обратных задач акустического рассеяния. Весьма многообещающими при обработке реальных экспериментальных данных оказались методы М.В. Клибанова, суммированные в монографии [13], а также методы из монографии [14]. Большой интерес представляют также недавние работы [15], [16].
Все упомянутые методы решения обратной задачи акустического зондирования требуют в трехмерной постановке значительных вычислительных ресурсов. В связи с этим отметим статьи [17], [18], в которых исходная обратная коэффициентная задача для волнового уравнения, из которой собственно и получается уравнение (1), сводится к трехмерному интегральному уравнению Фредгольма I рода с правой частью, содержащей специальные интегралы от регистрируемого поля. Предложенный метод решения этого уравнения оказался очень эффективным численно, и позволяет решать трехмерные обратные задачи для достаточно мелких сеток на персональном компьютере (ПК) даже без распараллеливания. Этот метод оказывается также очень полезным и для задачи (2), и это будет продемонстрировано ниже.
В данной статье мы придерживаемся следующей схемы решения нелинейной системы (2), сводящей последнюю к решению линейных интегральных уравнений:
1) решаем второе уравнение, записанное в виде
(3)
${{\omega }^{2}}\int\limits_X G \left( {\left| {{\mathbf{x}} - {\mathbf{x}}{\text{'}}} \right|,\omega } \right){v}({\mathbf{x}}{\text{'}},\omega )d{\mathbf{x}}{\text{'}} = W({\mathbf{x}},\omega ),\quad {\mathbf{x}} \in Y,$2) вычисляем функцию $u({\mathbf{x}},\omega )$, ${\mathbf{x}} \in X$, из первого равенства системы (2), записанного в форме
(4)
$u({\mathbf{x}},\omega ) = {{u}_{0}}({\mathbf{x}},\omega ) + {{\omega }^{2}}\int\limits_X G \left( {\left| {{\mathbf{x}} - {\mathbf{x}}{\text{'}}} \right|,\omega } \right){v}({\mathbf{x}}{\text{'}},\omega )d{\mathbf{x}}{\text{'}},\quad {\mathbf{x}} \in X;$3) находим функцию $\xi ({\mathbf{x}})$ из уравнения ${v}({\mathbf{x}},\omega ) = \xi ({\mathbf{x}})u({\mathbf{x}},\omega )$, ${\mathbf{x}} \in X$.
Близкая схема использовалась, например, в работе [19]. Однако там для решения некорректной задачи – трехмерного уравнения, аналогичного (3), не использовались методы регуляризации, а решение обратной задачи искалось на достаточно узком классе функций с “кусочно-постоянным током”. В итоге для решения такой трехмерной обратной задачи на сравнительно мелких сетках также требуются значительные вычислительные ресурсы.
Ниже мы покажем, что при некоторых, не очень обременительных, специальных предположениях о множестве регистрации данных $Y$ и о множестве $X$, где ищется решение обратной задачи, схема 1 )–3) эффективно реализуется численно и позволяет решать соответствующую трехмерную обратную задачу на достаточно мелких сетках даже на персональном компьютере средней производительности за несколько минут (без распараллеливания). Предлагаемый алгоритм решения обратной задачи и его численное исследование являются основными результатами этой работы.
2. СХЕМА РЕГИСТРАЦИИ ДАННЫХ ОБРАТНОЙ ЗАДАЧИ И РЕДУКЦИЯ ЗАДАЧИ
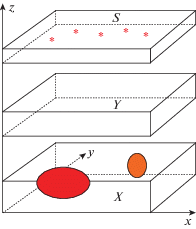
Будем рассматривать конкретную схему регистрации данных, т.е. функции $u({\mathbf{x}},\omega )$, “в плоском слое” $Y$ для декартовых координат ${\mathbf{x}} = (x,y,z)$. Эта схема была ранее использована в [17], [18] для решения обратной задачи с другими данными. На фиг. 1 схематично изображена соответствующая геометрическая схема: область неоднородностей поля скоростей $X$, область $S$, в которой расположены источники, и область регистрации рассеянного поля $Y$. Эти области имеют вид плоских слоев, по переменным $x$, $y$, перпендикулярных оси $Oz$. Звездочками показано возможное положение источников зондирующего поля. Таким образом,
Фиг. 1.
Геометрическая схема регистрации данных обратной задачи: $X$ – область рассеивателей волнового поля, $Y$ – область регистрации данных $u({\mathbf{x}},\omega )$, звездочки – положения источников поля.
Будем использовать двумерное преобразования Фурье ${{F}_{r}}[{\kern 1pt} \cdot {\kern 1pt} ]$ по переменным $r = (x,y)$, которое для функции $a(r,z,\omega ) = a(x,y,z,\omega )$ задается в виде
(5)
$\tilde {V}(z{\text{'}},\omega ,\Omega ) = {{F}_{r}}[\xi (r,z{\text{'}})F_{\Omega }^{{ - 1}}[\tilde {U}(z{\text{'}},\omega ,\Omega )](r)](\Omega ),\quad z{\text{'}} \in [{{z}_{1}},{{z}_{2}}],$3. АЛГОРИТМ РЕШЕНИЯ ПРЯМОЙ ЗАДАЧИ
Рассматриваемая нами прямая задача заключается в нахождении из системы (5) функции $\tilde {W}(z,\omega ,\Omega )$, $z \in [{{z}_{3}},{{z}_{4}}]$, по известной финитной функции $\xi (r,z{\text{'}})$ и заданной функции источников ${{\tilde {U}}_{0}}(z,a,\Omega )$. Для решения этой задачи используем следующий
Алгоритм 1
Шаг 1. Вычисляем преобразования Фурье ${{\tilde {U}}_{0}}(z,\omega ,\Omega )$, $\tilde {G}(z - z{\text{'}},\omega ,\Omega )$ (алгоритмически – применяя быстрое дискретное преобразование Фурье (БПФ)).
Шаг 2. Для каждого из параметров $\omega $, $\Omega $ (матрично) реализуем итерационный процесс решения первых двух уравнений из (5):
(6)
$\begin{gathered} {{{\tilde {U}}}_{{n + 1}}}(z,\omega ,\Omega ) = {{{\tilde {U}}}_{0}}(z,\omega ,\Omega ) + {{\omega }^{2}}\int\limits_{{{z}_{1}}}^{{{z}_{2}}} {\tilde {G}} (z - z{\text{'}},\omega ,\Omega ){{F}_{r}}[\xi (r,z{\text{'}})F_{\Omega }^{{ - 1}}[{{{\tilde {U}}}_{n}}(z{\text{'}},\omega ,\Omega )](r)](\Omega )dz{\text{'}}, \\ z \in [{{z}_{1}},{{z}_{2}}];\quad n = 0,1,2,\; \ldots , \\ \end{gathered} $Шаг 3. Останавливаем процесс по некоторому правилу на итерации номер $\nu $ и получаем приближенное решение ${{\tilde {U}}_{\nu }}(z,\omega ,\Omega )$.
Шаг 4. Последовательно вычисляем величины
(7)
$\begin{gathered} {{{\tilde {V}}}_{\nu }}(z{\text{'}},\omega ,\Omega ) = {{F}_{r}}[\xi (r,z{\text{'}}{\kern 1pt} )F_{\Omega }^{{ - 1}}[{{{\tilde {U}}}_{\nu }}(z{\text{'}},\omega ,\Omega )](r)](\Omega ),\quad z{\text{'}} \in [{{z}_{1}},{{z}_{2}}], \\ {{{\tilde {W}}}_{\nu }}(z,\omega ,\Omega ) = {{\omega }^{2}}\int\limits_{{{z}_{1}}}^{{{z}_{2}}} {\tilde {G}} (z - z{\text{'}},\omega ,\Omega ){{{\tilde {V}}}_{\nu }}(z{\text{'}},\omega ,\Omega )dz{\text{'}},\quad z \in [{{z}_{3}},{{z}_{4}}], \\ \end{gathered} $Мы не будем здесь проводить теоретический анализ сходимости алгоритма 1, так как формально он не используется нами при решении обратной задачи. Он нужен лишь для генерации ее модельных данных. Отметим лишь, что, как следует из общей теории решения интегральных уравнений II рода (см., например, [21]), алгоритм будет быстро сходиться, по крайней мере, для “малых” $\omega $. Ниже будут продемонстрированы численные примеры, подтверждающие это положение.
4. ОБРАТНАЯ ЗАДАЧА
Она состоит в нахождении из системы (5) по заданной величине $\tilde {W}(z,\omega ,\Omega )$, $z \in [{{z}_{3}},{{z}_{4}}]$, функции $\xi (r,z{\text{'}})$, $z{\text{'}} \in [{{z}_{1}},{{z}_{2}}]$. Для этого мы применим
Алгоритм 2
Шаг 1. При заданной функции $\tilde {W}(z,\omega ,\Omega )$ решаем для всех рассматриваемых параметров $\omega $, $\Omega $ одномерные уравнения I рода
(8)
${{\omega }^{2}}\int\limits_{{{z}_{1}}}^{{{z}_{2}}} {\tilde {G}} (z - z{\text{'}},\omega ,\Omega )\tilde {V}(z{\text{'}},\omega ,\Omega )dz{\text{'}} = \tilde {W}(z,\omega ,\Omega ),\quad z \in [{{z}_{3}},{{z}_{4}}],\quad \Rightarrow \quad \tilde {V}(z{\text{'}},\omega ,\Omega ),$Шаг 2. По найденной функции $\tilde {V}(z{\text{'}},\omega ,\Omega )$ вычисляем величину
(9)
$\tilde {U}(z,\omega ,\Omega ) = {{\tilde {U}}_{0}}(z,\omega ,\Omega ) + {{\omega }^{2}}\int\limits_{{{z}_{1}}}^{{{z}_{2}}} {\tilde {G}} (z - z{\text{'}},\omega ,\Omega )\tilde {V}(z{\text{'}},\omega ,\Omega )dz{\text{'}},\quad z \in [{{z}_{1}},{{z}_{2}}],$Шаг 3. Находим $\xi (r,z{\text{'}})$ из уравнения $u(r,z{\text{'}},\omega )\xi (r,z{\text{'}}) = V(r,z{\text{'}},\omega )$. Это можно сделать, используя метод наименьших квадратов (МНК по величине $\omega $) или просто вычисляя решение в виде $\xi (r,z{\text{'}}) = V(r,z{\text{'}},\omega ){\text{/}}u(r,z{\text{'}},\omega )$. В последнем случае результат будет, вообще говоря, зависеть от $\omega $.
Сделаем некоторые замечания об алгоритме 2.
1. Для реализации ш.1 необходимо детализировать предположения о функциях $V$, $W$. Мы используем включения $V({\mathbf{x}},\omega ) \in {{L}_{2}}(\mathbb{R}_{{xyz}}^{3})$, $W({\mathbf{x}},\omega ) \in {{L}_{2}}(\mathbb{R}_{{xyz}}^{3})$ для каждой рассматриваемой частоты $\omega $. Первое из них вытекает из финитности функции $\xi $, а второе постулируется. В этом случае для уравнений (8) применимы многие методы решения линейных некорректно поставленных задач (например, [4], [5], [22], [23], [24] и др.).
2. Уравнение (3) (и порождаемые им уравнения (8)) могут иметь не единственное решение для используемого конечного набора частот $\omega $. Поэтому для реализации ш.1 алгоритма мы применяем РА, ориентированные на поиск нормальных решений (тихоновская регуляризация, метод TSVD). В случае единственности решения для (3) оно будет совпадать с вычисленным единственным нормальным решением [17], [18].
3. Уравнения (8) можно решать отдельно для каждой фиксированной частоты $\omega $, а можно решать их и как систему уравнений в совокупности для всех используемых частот. Соответственно в последнем случае ш.3 алгоритма реализуется по МНК.
5. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ
Везде далее полагается, что уравнения (5) записаны в безразмерном виде с ${{c}_{0}} = 1$, так что ${{k}_{0}} = \omega $. Мы будем также считать, что модельные источники задаются в форме
где ${{{\mathbf{x}}}_{m}}$ – координаты точечных $\delta $-образных источников. ТогдаДля численного исследования предлагаемых алгоритмов рассмотрены прямые и обратные модельные задачи с функциями $\xi (x,y,z)$ вида
Величина ${{A}_{0}}$ определяет “контраст”
Исходные уравнения (3), (4) аппроксимировались конечно-разностным методом на равномерных сетках в областях
Все задачи решались с различными источниками. В данной работе мы не ставим своей целью оптимизацию их положения и числа. Отметим лишь, что для решенных задач с источниками, расположенными в точках
5.1. Получение модельных данных для решения обратной задачи с помощью алгоритма 1
Приведем типичные результаты численного исследования итерационного процесса (6) для получения данных обратной задачи. На фиг. 2 показаны в сравнении скорости сходимости процесса (6) для различных величин $\omega = {{k}_{0}}$. Принято обозначение ${{u}_{n}} = {{\tilde {U}}_{n}}(z,\omega ,\Omega )$.
Останов итераций производился, когда для номера итерации $\nu $ выполнялось условие
Данные обратной задачи, вообще говоря, задавались с некоторой ошибкой, которая интерпретируется как ошибка измерения. В наших расчетах это моделировалось наложением на функцию ${{W}_{\nu }}(x,y,z,\omega )$ аддитивной нормально распределенной псевдослучайной помехи с нулевым средним так, что получаемая в итоге приближенная функция $W_{\nu }^{{(\delta )}}(x,y,z,\omega )$ удовлетворяла бы условию
5.2. Реализация алгоритма 2
Первый шаг алгоритма 2 – решение уравнений I рода (8) методами регуляризации – обсуждался в работах [17], [18] в связи с решением другой обратной задачи, формально схожей с рассматриваемой и отличающейся от нее только видом ядра и правой части. В этих работах отмечено, что используемая дискретизация приводит уравнения (8) к набору систем линейных алгебраических уравнений (СЛАУ) вида ${{A}^{{(m)}}}{{\tilde {V}}^{{(m)}}} = {{\tilde {W}}^{{(m)}}}$, в нашем случае, с матрицами ${{A}^{{(m)}}} = [{{\mu }_{{kl}}}\tilde {G}({{z}_{k}} - z_{l}^{{\text{'}}},\omega ,{{\Omega }^{{(m)}}})]$ размера $M \times {{M}_{1}}$ и правыми частями ${{\tilde {W}}^{{(m)}}} = [\tilde {W}_{\nu }^{{(\delta )}}({{z}_{k}},\omega ,{{\Omega }^{{(m)}}})]$ – вектор-столбцами высоты $M$. Здесь ${{\Omega }^{{(m)}}}$ – точки двумерной сетки величин $\Omega $, занумерованных одним индексом $m$, а ${{\mu }_{{kl}}}$ – квадратурные коэффициенты для вычисления интегралов в (8). Указанные СЛАУ решались с помощью различных вариантов метода регуляризации А.Н. Тихонова [22], [23] и с помощью метода TSVD [24]. Обоснование применения этих методов дано в [17], [18]. Наилучшие результаты в расчетах получились для метода TSVD. Их мы и будем приводить в дальнейшем.
Шаг 2 алгоритма 2 не вызывает сложностей для дискретизованной задачи, т.к. сводится к матричному умножению дискретных величин $\tilde {G}$, $\tilde {V}$ и сложению результата с дискретным аналогом функции ${{\tilde {U}}_{0}}$. Дальнейшие вычисления этого шага проводятся в помощью БПФ. Наконец, шаг 3 в случае решения обратной задачи для одной частоты $\omega $ (или раздельного ее решения для нескольких частот) реализуется делением $\xi (r,z{\text{'}}) = V(r,z{\text{'}},\omega ){\text{/}}u(r,z{\text{'}},\omega )$, а в случае совместного решения для нескольких частот – применением МНК по переменной $\omega $. Далее, при необходимости нетрудно пересчитать функцию $\xi ({\mathbf{x}})$ в $c({\mathbf{x}})$. В приводимых ниже примерах мы для краткости этого не делаем, представляя на рисунках непосредственно величину $\xi ({\mathbf{x}})$.
5.3. Решение обратной задачи с данными в “толстом слое”
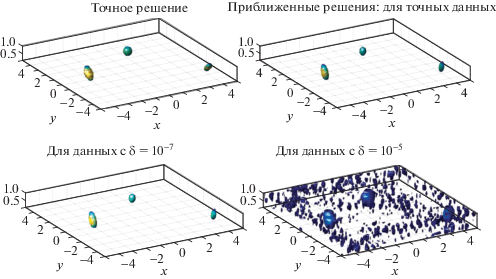
Этому посвящена первая серия численных экспериментов. Данные задаются в слое $Y = [ - 10,10] \times [ - 10,10] \times [6.01,6.5]$ на одной частоте ($\omega = {{k}_{0}} = 2$). Используются сетки размеров $N = 128$, $M = {{M}_{1}} = 71$. Фигура 4 позволяет качественно сравнить точное ${{\xi }_{{{\text{exact}}}}}(x,y,z)$ и приближенные решения ${{\xi }_{{{\text{appr}}}}}(x,y,z)$ обратной задачи в различных сечениях по $z$. Точное решение показано в первой строке фигуры. Во второй строке приведено приближенное решение обратной задачи для точных данных. В третьей и четвертой строках изображены решения для возмущенных данных с $\delta = {{10}^{{ - 7}}}$ и $\delta = {{10}^{{ - 5}}}$ соответственно. Фигура демонстрирует достаточно высокую чувствительность решений к возмущениям данных: решениe для более зашумленных данных оказывается более искаженным.
Фиг. 4.
Качественное сравнение точного (а) и приближенных решений обратной задачи: (б) для точных данных (в “толстом слое”); (в) для возмущенных данных с $\delta = {{10}^{{ - 7}}}$; (г) для возмущенных данных с $\delta = {{10}^{{ - 5}}}$.

Более детальная информация о точности решения обратной задачи, т.е. о величине относительной точности
Фиг. 5.
Относительная точность ${{\Delta }_{{{{L}_{2}}}}}(z)$ приближенного решения (в норме пространства ${{L}_{2}}(\mathbb{R}_{{xy}}^{2})$ в сечении решения для различных $z$. Линия 1 – величина ${{\Delta }_{{{{L}_{2}}}}}(z)$ для невозмущенных данных задачи, линия 2 – для приближенных данных с $\delta = {{10}^{{ - 7}}}$, линия 3 – для приближенных данных с $\delta = {{10}^{{ - 5}}}$.

Следующая фиг. 6 показывает качественно влияние возмущения данных задачи на определение положения и геометрии неоднородностей. Видно, что положения могут быть достаточно уверенно определены в случае $\delta = {{10}^{{ - 7}}}$, а при использовании подходящей фильтрации шумов и для $\delta = {{10}^{{ - 5}}}$.
Фиг. 6.
Качественное сравнение влияния возмущения данных на положение восстанавливаемой неоднородности $\xi ({\mathbf{x}})$ (${{k}_{0}} = 2$).
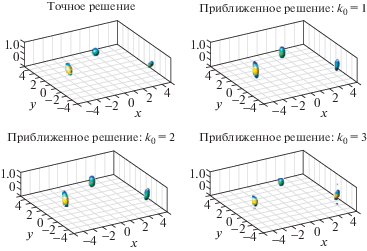
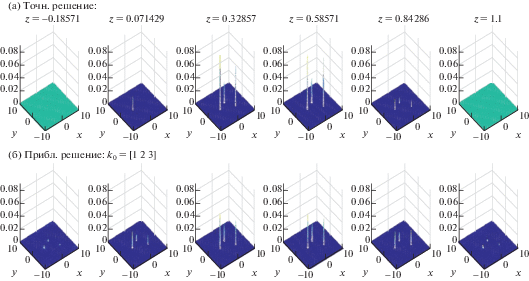
Теперь приведем решения обратной задачи отдельно для различных частот $\omega = {{k}_{0}} = [1,2,3]$. При этом будем использовать точные данные задачи, чтобы более рельефно выделять влияние частоты на результаты. Фигура 7 показывает, как восстанавливаются положения и геометрия неоднородностей при решении обратной задачи раздельно для каждой из частот исследования.
Фиг. 7.
Качественное сравнение положений и геометрии восстанавливаемой неоднородности $\xi ({\mathbf{x}})$ для различных ${{k}_{0}}$, ${{k}_{0}} = [1,2,3]$ (невозмущенные данные).
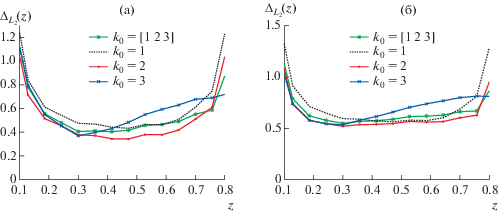
Можно решить обратную задачу, рассматривая равенства (8) и (9) как системы уравнений для нескольких частот. На фиг. 8 представлены результаты решения обратной задачи сразу для трех частот: $\omega = {{k}_{0}} = [1,2,3]$ с нахождением итоговой функции $\xi (r,z{\text{'}})$ из уравнения $u(r,z{\text{'}},\omega )\xi (r,z{\text{'}}) = V(r,z{\text{'}},\omega )$ по МНК. Более детально это продемонстрировано на фиг. 9а, где дано сравнение точности получаемых решений для каждой из частот раздельно и для одновременного решения обратной задачи на трех частотах. Отметим, что в последнем случае результат оказался несколько хуже, чем, например, для ${{k}_{0}} = 2$ при раздельном решении обратной задачи для каждой частоты (см. фиг. 9). Это можно объяснить. Алгоритм 2 при отдельном его применении для разных частот дает различную точность приближенных решений. Поэтому точность совместного решения обратной задачи на нескольких частотах сразу (с получением окончательного результата по методу наименьших квадратов) вполне может оказаться хуже, чем на некоторых конкретных частотах из используемого набора. Например, на фиг. 9а видно, что точность решения для ${{k}_{0}} = 2$ в целом лучше, чем точность совместного решения.
Фиг. 8.
Качественное сравнение точного решения $\xi ({\mathbf{x}})$ и приближенного решения обратной задачи одновременно на трех частотах (для точных данных).
Фиг. 9.
(а) – относительная точность ${{\Delta }_{{{{L}_{2}}}}}(z)$ приближенных решений с данными в “толстом слое” для различных ${{k}_{0}}$ в отдельности и для совместного решения для всех ${{k}_{0}}$ сразу (невозмущенные данные). (б) – аналогичная точность приближенных решений, полученных по невозмущенным данным “в тонком слое”.
5.4. Решение обратной задачи для данных “в тонком слое”
В этих экспериментах для дискретизации использовались равномерные сетки в областях
6. НЕКОТОРЫЕ СВОЙСТВА АЛГОРИТМА 2
Все вычисления проводились в системе МАТЛАБ на ПК с процессором Intel (R) Core (TM) i7-7700 CPU 3.60 GHz, ОЗУ 16Гб (без распараллеливания). Алгоритм 2 решения обратной задачи оказался достаточно “быстрым”. Приведем данные соответствующих численных экспериментов для решения обратной задачи на одной частоте $\omega = 2$. Величины $M$, ${{M}_{1}}$ определяют скорость решения одномерного интегрального уравнения (8) при фиксированном $\Omega $. Соответствующее время решения ${{t}_{0}}(M,{{M}_{1}})$ практически мало меняется при переходе от одного уравнения к другому. Это время управляется требуемой разрешающей способностью алгоритма по переменной $z$. Для полного времени решения обратной задачи на указанных сетках фактически справедлива оценка $t(N,M,{{M}_{1}}) \approx {{t}_{0}}(M,{{M}_{1}}){{N}^{2}}$, и число $N$ управляется здесь требуемой разрешающей способностью по осям $x$, $y$. Приведем на фиг. 10 эту зависимость $t(N) = t(N,M,{{M}_{1}})$, полученную для фиксированных $M = 51$, ${{M}_{1}} = 51$.
Отметим, что решаемая обратная задача весьма чувствительна к ошибкам входных данных. При ее решении с двойной точностью, внесение в правую часть уравнения (8) случайных ошибок с амплитудой порядка ${{10}^{{ - 5}}}$ приводит к чрезмерному искажению приближенного решения при использовании и метода TSVD, и метода регуляризации. Это связано с весьма “быстрым” убыванием сингулярных чисел матриц ${{A}^{{(m)}}}$ для СЛАУ, решаемых на ш. 1 алгоритма 2, и это является специфической особенностью решаемой обратной задачи. Аналогичное свойство обратной коэффициентной задачи для волнового уравнения отмечалось ранее в работах [12], [13]. Соответствующие оценки погрешности при различных априорных предположениях на точное решение можно найти в [2], [3].
7. ВЫВОДЫ
Из численных экспериментов, проведенных в работе, можно сделать следующие выводы.
1. Трехмерная обратная коэффициентная задача для уравнения колебаний, возникающая при моделировании акустического зондирования, может быть решена численно с помощью предлагаемого алгоритма для достаточно мелких сеток за время порядка нескольких минут на ПК (даже без распараллеливания). Для этого следует, например, использовать схему регистрации данных обратной задачи “в плоском слое”.
2. Рассматриваемая обратная задача сама по себе весьма чувствительна к возмущениям данных: для получения детального приближенного решения требуются данные, измеренные с большой точностью. Эта особенность задачи не зависит от используемого алгоритма ее решения.
3. Предлагаемый алгоритм позволяет достаточно надежно определять положения небольших локальных неоднородностей акустической среды при данных с малыми ошибками. Данные могут задаваться даже в “тонком слое”.
4. Алгоритм 2 при отдельном его применении для разных частот дает различную точность приближенных решений. Поэтому точность совместного решения обратной задачи на нескольких частотах сразу (по МНК) может оказаться несколько хуже, чем на некоторых конкретных частотах из используемого набора.
Авторы благодарны О.Д. Румянцевой и А.С. Шурупу за полезные замечания.
Список литературы
Горюнов А.А., Сасковец А.В. Обратные задачи рассеяния в акустике. М.: Изд-во МГУ, 1989.
Colton D., Kress R. Inverse Acoustic and Electromagnetic Scattering Theory. 2nd ed. Appl. Math. Sci. 93. Berlin: Springer, 1998.
Ramm A.G. Multidimensional Inverse Scattering Problems. Pitman Monogr. Surv. Pure Appl. Math. 51. Harlow: Longman Scientific & Technical, 1992.
Bakushinsky A., Goncharsky A. Ill-Posed Problems: Theory and Applications. Dordrecht: Kluwer Academic Publishers, 1994.
Bakushinsky A.B., Kokurin M.Yu. Iterative methods for approximate solution of inverse problems. Mathematics and Its Applications. Dordrecht: Kluwer Academic Publishers, 2004.
Гончарский А.В., Романов С.Ю. О двух подходах к решению коэффициентных обратных задач для волновых уравнений // Ж. вычисл. матем. и матем. физ. 2012. Т. 52. № 2. С. 263–269.
Гончарский А.В., Романов С.Ю. Суперкомпьютерные технологии в разработке методов решения обратных задач в УЗИ-томографии // Вычисл. методы и программирование: новые вычисл. технологии. 2012. Т. 13. № 1. С. 235–238.
Belishev M.I. Recent progress in the boundary control method // Inverse Problems. 2007. V. 23. № 5. P. 1–67.
Пестов Л.Н., Болгова В.М., Данилин А.Н. Численная реконструкция трехмерной скорости звука методом граничного управления // Вестн. Югорского государственного университета. 2011. Вып. 3. С. 92–98.
Буров В.А., Алексеенко Н.В., Румянцева О.Д. Многочастотное обобщение алгоритма Новикова для решения обратной двумерной задачи рассеяния // Акустический ж. 2009. Т. 55. № 6. С. 784–798.
Новиков P.Г. Восстановление двумерного оператора Шредингера по амплитуде рассеяния при фиксированной энергии // Функцион. анализ и его прил. 1986. Т. 20. № 3. С. 90–91.
Буров В.А., Вечерин С.Н., Морозов С.А., Румянцева О.Д. Моделирование точного решения обратной задачи акустического рассеяния функциональными методами // Акустический ж. 2010. Т. 56. № 4. С. 516–536.
Beilina L., Klibanov M.V. Approximate Global Convergence and Adaptivity for Coefficient Inverse Problems. New York: Springer, 2012.
Kabanikhin S.I., Satybaev A.D., Shishlenin M.A. Direct Methods of Solving Multidimensional Inverse Hyperbolic Problems. Utrecht: VSP, 2004.
Klibanov M.V., Kolesov A.E. Convexification of a 3-D coefficient inverse scattering problem // Computers and Mathematics with Applications. 2019. V. 77. P. 1681–1702.
Klibanov M.V., Kolesov A.E., Nguyen Dinh-Liem. Convexification method for an inverse scattering problem and its performance for experimental backscatter data for buried targets // SIAM J. Imaging Sciences. 2019. V. 12. № 1. P. 576–603.
Bakushinsky A.B., Leonov A.S. Fast numerical method of solving 3D coefficient inverse problem for wave equation with integral data // J. of Inverse and Ill-Posed Problems. 2018. V. 26. Issue 4. P. 477–492.
Бакушинский А.Б., Леонов А.С. Экономичный численный метод решения коэффициентной обратной задачи для волнового уравнения в трехмерном пространстве // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 4. С. 561–574.
Евстигнеев Р.О., Медведик М.Ю., Смирнов Ю.Г., Цупак А.А. Обратная задача восстановления неоднородностей тела для ранней диагностики заболеваний с помощью микроволновой томографии // Известия высших учебных заведений. Поволжский регион. Физико-математические науки. 2017. Т. 44. № 4. С. 3–17.
Владимиров В.С. Обобщенные функции в математической физике. М.: Наука, 1976.
Красносельский М.А., Вайникко Г.М., Забрейко П.П., Рутицкий Я.Б., Стеценко В.Я. Приближенное решение операторных уравнений. М.: Наука, 1969.
Тихонов А.Н., Гончарский А.В., Степанов В.В., Ягола А.Г. Численные методы решения некорректных задач. М.: Наука, 1990.
Леонов А.С. Решение некорректно поставленных обратных задач: Очерк теории, практические алгоритмы и демонстрации в МАТЛАБ. Изд. 2. М: Либроком, 2013.
Engl H.W., Hanke M., Neubauer A. Regularization of Inverse Problems. Dordrecht: Kluwer Academic Publishers, 1996.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики