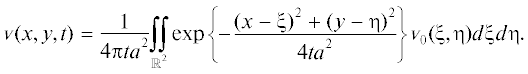Журнал вычислительной математики и математической физики, 2020, T. 60, № 6, стр. 985-1012
Экстраоптимальные методы решения некорректно поставленных задач: обзор теории и примеры
А. С. Леонов *
Национальный исследовательский ядерный ун-т (МИФИ)
115409 Москва, Каширское ш., 31, Россия
* E-mail: asleonov@mephi.ru
Поступила в редакцию 24.10.2019
После доработки 24.10.2019
Принята к публикации 11.02.2020
Аннотация
В статье дан обзор одного нового направления в методах решения некорректно поставленных задач – теории регуляризующих алгоритмов с экстраоптимальным качеством приближенных решений. Отличительной особенностью этих методов является не только оптимальность по порядку точности получаемых приближенных решений, но и дополнительная оптимальность их по некоторому функционалу качества, задаваемому пользователем. Такими функционалами могут служить, например, апостериорная оценка качества (точности) получаемых приближенных решений, апостериорные оценки различных линейных функционалов от этих решений, оценки их математической энтропии и многомерных вариаций выбранных типов. Изучается взаимосвязь экстраоптимальных регуляризующих алгоритмов и регуляризующих алгоритмов, оптимальных по порядку качества. Рассматриваются вопросы практического получения апостериорных оценок качества приближенных решений и численные алгоритмы нахождения этих оценок. Изложение иллюстрируется результатами численных экспериментов. Библ. 51. Фиг. 6.
1. ВВЕДЕНИЕ
В статье дается обзор одного нового направления в методах решения некорректно поставленных задач – теории регуляризующих алгоритмов (РА) с экстраоптимальным качеством приближенных решений. Начиная с классических работ А.Н. Тихонова, М.М. Лаврентьева и В.К. Иванова 60-х годов ХХ века, к настоящему времени усилиями их учеников и последователей создано много различных типов РА для решения некорректных задач в разнообразных постановках. По этой тематике опубликовано около 100 монографий и трудно поддающееся учету число статей. Отметим среди них лишь некоторые, см. [1]–[21], в определенном смысле, подводящие итоги исследований. Таким образом, в распоряжении ученого или инженера, решающего прикладную некорректную задачу, имеется богатый инструментарий. Можно использовать различные по типу и свойствам регуляризующие алгоритмы: вариационные, итерационные, спектральные и т.д.
Важной особенностью многих из этих методов является оптимальность точности получаемых приближенных решений или, в более общем смысле, указанном ниже, оптимальность их по некоторому функционалу качества, задаваемому пользователем. Исследование оптимальности точности РА составляет большой раздел теории некорректно поставленных задач, и в его развитие внесли вклад многие ученые (см., например, [1]–[21]). Обычно удается установить не собственно оптимальность РА, а лишь оптимальность его приближенных решений по порядку точности (или по порядку выбранного качества). Поэтому представляется естественным при выборе рабочего РА для решения конкретной задачи использовать именно оптимальные по порядку точности (качества) алгоритмы. Именно так и поступают многие исследователи. Обзор элементов этой теории дан в разд. 2. Естественным кажется и стремление использовать те оптимальные по порядку РА, которые имеют и некоторые дополнительные свойства оптимальности по другим своим характеристикам – экстраоптимальные РА. Теория таких РА развита относительно недавно (см. [22]–[28]) и связана в первую очередь с такой важной характеристикой регуляризующего алгоритма, как апостериорная оценка точности (качества) его приближенных решений. В теории некорректно поставленных задач хорошо известно, что получение априорных оценок точности приближений требует существенных знаний (предположений) об искомом точном решении задачи. Эти предположения не всегда можно проверить, и часто они не выполнены на практике. Кроме того, получаемые априорные оценки зачастую содержат некоторые константы, вычисление которых затруднительно. Поэтому получить априорную оценку точности приближенного решения практической некорректной задачи в виде числа, как правило, невозможно.
Именно по этой причине в последние годы развита теория апостериорных оценок точности решений некорректных задач (см. [22]–[35]). Эти оценки эффективно вычислимы и удобны для практических приложений. Одно из направлений в методах получения таких оценок будет рассмотрено ниже в разд. 3. Если оказывается, что используемый РА имеет не только оптимальный порядок точности (качества) приближенных решений, но обладает также и оптимальной по порядку апостериорной оценкой их точности (качества), то такой РА в дальнейшем и будет называться экстраоптимальным РА. При этом установлено, что многие хорошо известные РА имеют свойство экстраоптимальности по различным функционалам качества. Примеры таких функционалов приведены в разд. 4. Оказывается также, что не каждый РА, оптимальный по порядку, будет экстраоптимальным. Примеры даны в разд. 5.
Для практических нужд чрезвычайно важно, чтобы алгоритмы вычисления апостериорных оценок точности (качества) были быстродействующими. Соответствующий анализ имеющихся методов вычисления апостериорных оценок точности различных некорректных задач приведен в разд. 6. В связи с этим отметим появившийся совсем недавно весьма эффективный численный алгоритм получения апостериорных оценок точности для линейных некорректных задач в гильбертовых пространствах [36], [37].
Заключает данный обзор раздел, посвященный численным экспериментам по применению экстраоптимальных РА к решению некоторых обратных задач.
2. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ, ПРИМЕРЫ ЕЕ КОНКРЕТИЗАЦИИ И МЕТОДОВ РЕШЕНИЯ
Ниже будут рассмотрены некорректно поставленные экстремальные задачи [18], [4] и сводящиеся к ним различные операторные уравнения. Общая теория этих задач в топологических пространствах рассмотрена, например, в [12], [20], [38]. В этой работе мы для краткости ограничимся рассмотрением экстремальных задач и их приложений в банаховых пространствах.
Пусть $Z$ – банахово пространство с элементами $z$ и с топологией $\tau $. Обычно это топология сильной или слабой сходимости, но в некоторых примерах тип топологии будет специально уточнен. Предположим, что на множестве $\mathcal{D} \subset Z$, $\mathcal{D} \ne \emptyset $, определен ограниченный снизу функционал $J(z)$. Рассмотрим следующую экстремальную задачу: найти все элементы $z* \in \mathcal{D}$, для которых
Будем предполагать, что множество $Z{\text{*}}$ таких элементов $z{\text{*}}$ не пусто. Множество $Z{\text{*}}$ зачастую содержит более одного элемента. Поэтому возникает проблема выбора из $Z{\text{*}}$ некоторого элемента, обладающего дополнительными оптимальными свойствами. Для этого введем некоторый вспомогательный функционал $\Omega (z)$, определенный на множестве $\mathcal{D}$ и ограниченный там снизу. Без ограничения общности можно считать, что $\Omega * = inf\{ \Omega (z):z \in \mathcal{D}\} \geqslant 0$.Будем рассматривать так называемые $\Omega $-оптимальные решения задачи (2.1), т.е. элементы $\bar {z} \in Z{\text{*}}$, для которых
Обозначим через $\bar {Z}$ совокупность всех $\Omega $-оптимальных решений. В дальнейшем считаем, что $\Omega (\bar {Z}) > \Omega {\text{*}}$. Последнее неравенство означает, “нетривиальность” решения задачи (2.1), т.е. невозможность ее сведения к минимизации только функционала $\Omega $ на множестве $\mathcal{D}$ без использования функционала $J$.Предположим теперь, что точный функционал $J$ неизвестен, а вместо него в нашем распоряжении имеются некоторые “приближенные” функционалы. Будем говорить, что функционал ${{J}_{\eta }}(z)$, определенный на $\mathcal{D}$ и ограниченный там снизу, является приближенным для функционала $J(z)$, если он удовлетворяет условию аппроксимации
(2.3)
$\left| {J(z) - {{J}_{\eta }}(z)} \right| \leqslant \Psi (\eta ,\Omega (z))\quad \forall z \in \mathcal{D}.$Свойства функционалов $J(z),\;{{J}_{\eta }}(z),\;\Omega (z)$ и меры аппроксимации $\Psi (\eta ,\Omega )$ будут указаны ниже. Эти свойства, среди прочего, гарантируют, что $\bar {Z} \ne \emptyset $ [20].
Основная задача. Требуется по данным $({{J}_{\eta }},\eta ,\Psi )$ найти $\tau $-устойчивое в $Z$ приближение ${{z}_{\eta }} \in \mathcal{D}$ к множеству $\bar {Z}$ при $\eta \to 0$. Если решение $\bar {z}$ единственно, то это означает сходимость ${{z}_{a}}\;\mathop \to \limits^\tau \;\bar {z}$. В случае нормированного пространства $Z$ с сильной топологией это соответствует сходимости
(2.4)
$\mathop {\lim }\limits_{\eta \to 0} \inf \left\{ {\left\| {{{z}_{\eta }} - \bar {z}} \right\|:\bar {z} \in \bar {Z}} \right\} = 0.$Приведем типичные примеры экстремальных задач типа (2.1), (2.2), возникающих в приложениях. Другие примеры даны, например, в [1]–[21] и других публикациях.
Пример 2.1. Решение линейных операторных уравнений I рода в гильбертовых пространствах вариационным методом.
Пусть $Z$, $U$ – гильбертовы пространства, $A:Z \to U$ – линейный ограниченный оператор, а $\Omega [z] = \mathop {\left\| {Lz} \right\|}\nolimits_Z $. Здесь $L:Z \to Z$ – линейный замкнутый оператор с областью определения $D(L)$, которая плотна в $Z$. Предположим также, что $\mathop {\left\| {Lz} \right\|}\nolimits_Z \geqslant k\mathop {\left\| z \right\|}\nolimits_Z $ для всех $z \in D(L)$ ($k = {\text{const}} > 0$). Будем решать на множестве $\mathcal{D} = D(L)$ операторное уравнение
с некоторой правой частью $u \in U$. Для этого мы используем вариационный метод, т.е. вместо (2.5) рассмотрим задачу (2.1) с $J[z] = \mathop {\left\| {Az - u} \right\|}\nolimits_U $. Предположим, что решения $z* \in \mathcal{D}$ последней задачи существуют и образуют множество $Z{\text{*}}$. Тогда величинаПример 2.2. Решение нелинейных операторных уравнений в банаховом пространстве вариационным методом.
В этом примере считаем, что $Z$ и $U$ – это банаховы пространства; $F(z)$ есть оператор (в общем случае, нелинейный), который определен на заданном множестве ограничений $\mathcal{D}$, $\mathcal{D} \subset Z$, и непрерывен из $\mathcal{D}$ в $U$. Будем решать на множестве $\mathcal{D}$ операторное уравнение
с помощью минимизации на $\mathcal{D}$ функционала $J[z] = \mathop {\left\| {F(z) - u} \right\|}\nolimits_U $, т.е путем решения задачи (2.1). Если множество решений $Z{\text{*}}$ уравнения (2.6) не пусто, можно искать $\Omega $-оптимальные решения уравнения из задачи (2.2). Снова считаем, что для этого в нашем распоряжении имеются приближенные данные ${\text{\{ }}{{F}_{h}},{{u}_{\delta }}{\text{\} }}$ задачи (2.6). Здесь ${{F}_{h}}:\mathcal{D} \to U$ – непрерывный оператор, а ${{u}_{\delta }} \in U$. Выполнены условия аппроксимацииВ дальнейшем мы считаем выполненными следующие
Основные предположения [12], [20], [38]
(А) Функционалы $J[z]$, ${{J}_{\eta }}[z]$ и $\Omega [z]$ ограничены снизу и $\tau $-полунепрерывны снизу на множестве $\mathcal{D}$. Без ограничения общности, считаем, что $J[z] \geqslant 0$, ${{J}_{\eta }}[z] \geqslant 0$c и $\Omega [z] \geqslant 0$ $\forall z \in \mathcal{D}$.
(Б) Каждое непустое множество ${{\Omega }_{C}} = \left\{ {z \in \mathcal{D}:\Omega [z] \leqslant C} \right\}$, $C = {\text{const}}$, $\tau $-компактно в $Z$.
(В) Функция $\Psi (\eta ,t) = \Psi ({{\eta }_{1}},\; \ldots ,\;{{\eta }_{m}},t)$ непрерывна в области ${\text{\{ }}\eta \in \mathbb{R}_{ + }^{m}{\text{\} }} \times {\text{\{ }}t \geqslant 0{\text{\} }}$, т.е. для всех ${{\eta }_{1}},\; \ldots ,\;{{\eta }_{m}}$, $t \geqslant 0$. Кроме того, функция $\Psi (\eta ,t)$ возрастает по переменной $t$ для каждого фиксированного $\eta \in \mathbb{R}_{ + }^{m}$, $\left\| \eta \right\| > 0$, и $\Psi (0,t) = 0$, $\forall t \geqslant 0$. Наконец, $\Psi (\eta ,t) > 0$ для всех $(\eta ,t)$, если $\left\| \eta \right\| > 0$ и $t > 0$. Примеры таких функций $\Psi (\eta ,t)$ для различных нелинейных некорректных задач даны в [20].
(Г) Задача (2.1) имеет единственное нетривиальное решение $\bar {z} = z{\text{*}}$.
Последнее условие используется главным образом для получения оценок качества приближенных решений. По мере необходимости некоторые из приведенных условий будут уточняться.
Основную задачу можно решить, используя РА различных видов (см. [1], [3], [6], [7], [18]–[20] и др.). Тогда приближенное решение можно записать в виде ${{z}_{\eta }} = {{P}_{\eta }}({{J}_{\eta }},\eta ,\Psi ) \in \mathcal{D}$, где ${\text{\{ }}{{P}_{\eta }}{\text{\} }}$ – некоторое параметрическое семейство регуляризующих операторов, действующих на приближенные данные задачи. Это семейство явно зависит от оценок ошибок данных $\eta $. Если для алгоритма ${{P}_{\eta }}$ гарантировано выполнение условий регулярности приближенных решений ${{z}_{\eta }}$:
(2.7)
$\overline {\mathop {\lim }\limits_{\eta \to 0} } \,\Omega [{{z}_{\eta }}] \leqslant {\text{const}},\quad \mathop {lim}\limits_{\eta \to 0} {{J}_{\eta }}[{{z}_{\eta }}] \leqslant J{\text{*,}}$Хотя операторы ${{P}_{\eta }}$ можно вводить различными способами, но предпочтение часто отдается вариационным РА. Кратко опишем наиболее популярные вариационные РА для решения экстремальных задач.
Пример 2.3. Тихоновская регуляризация с выбором параметра по обобщенному принципу невязки (ОПН) в применении к выпуклой оптимизации.
В этом примере используем теорию из [20] и будем применять вместо предположения (Г) обеспечивающее его выполнение более сильное предположение
(Г1) Функционалы $J[z]$, ${{J}_{\eta }}[z]$ выпуклы на выпуклом множестве $\mathcal{D}$; функционал $\Omega [z]$ – строго выпуклый на $\mathcal{D}$; решение $\bar {z}$ нетривиально.
Введем вспомогательную выпуклую функцию $f(x) \geqslant 0$, считая, что $f(x) \in {{C}^{l}}[0,\infty )$ $l \geqslant 1$, ${{f}^{{(n)}}}(x) \geqslant 0$ для $n = 1,\; \ldots ,\;l - 1$ и ${{f}^{{(l)}}}(x) \geqslant {{\kappa }_{0}} = {\text{const}} > 0$. На практике наиболее часто используется $f(x) = {{x}^{l}}$. Введем далее выпуклый функционал ${{I}_{\eta }}[z] = f({{J}_{\eta }}[z])$ и определим для каждого числа $\alpha > 0$ функционал Тихонова
Из предположений (А), (Б) и (Г1) следует, что экстремальная задача(2.9)
${{M}^{\alpha }}[z_{\eta }^{\alpha }] = inf{\text{\{ }}{{M}^{\alpha }}[z]:z \in \mathcal{D}{\text{\} }}$(2.10)
$\beta (\alpha ) = {{J}_{\eta }}[z_{\eta }^{\alpha }],\quad \pi (\alpha ) = {{C}_{0}}\Psi (\eta ,\Omega [z_{\eta }^{\alpha }]) + {{\lambda }_{\eta }},\quad \rho (\alpha ) = \beta (\alpha ) - \pi (\alpha ).$(2.11)
${{J}_{\eta }}[{{z}_{\eta }}] = {{\lambda }_{\eta }} + {{C}_{0}}\Psi (\eta ,\Omega [{{z}_{\eta }}]).$Алгоритм ОПН можно существенно упростить при решении линейных операторных уравнений в гильбертовых пространствах (см. пример 2.1). В этом случае можно положить $\Omega [z] = \left\| {Lz} \right\|_{Z}^{2}$ и ${{I}_{\eta }}[z] = \left\| {{{A}_{h}}z - {{u}_{\delta }}} \right\|_{U}^{2}$. Хорошо известно (см., например, [6], [18], [20]), что
(2.12)
$z_{\eta }^{\alpha } = {{(\alpha L{\text{*}}L + A_{h}^{ * }{{A}_{h}})}^{{ - 1}}}A_{h}^{ * }{{u}_{\delta }}.$Отметим важную особенность обобщенного принципа невязки. Если априорно известно, что уравнение (2.5) разрешимо, то число ${{\lambda }_{\eta }}$ можно исключить в соотношениях (2.10), (2.11).
Алгоритм ОПН можно применять и для решения нелинейных операторных уравнений из примера 2.2, если задача (2.9) имеет единственное решение для каждого $\alpha > 0$. Если экстремали $z_{\eta }^{\alpha }$ функционала Тихонова не единственны, то необходимо применять специальные варианты ОПН (см., например, [20] и др.).
Пример 2.4. Обобщенный метод невязки (ОМН) для решения экстремальных задач в банаховых пространствах.
Этот метод решения задачи (2.1) состоит в нахождении элементов ${{z}_{\eta }} = {{z}_{\eta }}({{J}_{\eta }},\Psi ,\eta )$, для которых выполнено соотношение:
(2.13)
$\Omega [{{z}_{\eta }}] = inf\{ \Omega [z]:z \in \mathcal{D},\;{{J}_{\eta }}[z] \leqslant C\Psi (\eta ,\Omega [z]) + {{\lambda }_{\eta }}\} .$3. АПОСТЕРИОРНЫЕ ОЦЕНКИ КАЧЕСТВА ПРИБЛИЖЕННЫХ РЕШЕНИЙ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ И ИХ СВОЙСТВА
Следуя [28], [38], формализуем вопрос о “качестве” приближений, получаемых с помощью РА поиска $\Omega $-оптимальных решений. Введем для этого меру качества $Q({{z}_{\eta }},\bar {z})$ приближенного решения ${{z}_{\eta }}$ относительно точного решения $\bar {z}$. Здесь $Q({{z}_{1}},{{z}_{2}})$ – функционал, определенный для всех ${{z}_{1}},{{z}_{2}} \in \mathcal{D}$.
Величина $Q({{z}_{\eta }},\bar {z})$ при неизвестном $\bar {z}$ может быть только оценена (априорно или апостериорно). Нас интересуют апостериорные оценки качества приближенных решений рассматриваемого РА по функционалу качества $Q$, т.е. оценки для $Q({{z}_{\eta }},\bar {z})$, получаемые после решения основной задачи. Оценки могут быть получены по следующей схеме.
В результате применения РА вычислим для данных $({{J}_{\eta }},\eta ,\Psi )$ приближенное решение ${{z}_{\eta }}$, а также устойчивую оценку ${{\mu }_{\eta }}$ для точной нижней грани (2.1). Далее, найдем величины ${{\Delta }_{\eta }} = {{\mu }_{\eta }} + \Psi (\eta ,C\Omega ({{z}_{\eta }}))$, ${{R}_{\eta }} = C\Omega ({{z}_{\eta }})$, где $C > 1$ – заданная константа. Введем множество ${{\mathcal{Z}}_{\eta }} = \{ z \in \mathcal{D}:{{J}_{\eta }}(z) \leqslant {{\Delta }_{\eta }},\;\Omega (z) \leqslant {{R}_{\eta }}\} $ и предположим, что $\bar {z},{{z}_{\eta }} \in {{\mathcal{Z}}_{\eta }}$. Тогда
(3.1)
$Q({{z}_{\eta }},\bar {z}) \leqslant sup\{ Q({{z}_{\eta }},z):z \in {{\mathcal{Z}}_{\eta }}\} \;\mathop = \limits^{{\text{def}}} \;{{E}_{Q}}(\eta ).$Определение 3.1. Назовем функцию ${{E}_{Q}}(\eta )$ апостериорной оценкой качества приближенного решения ${{z}_{\eta }}$ (по функционалу $Q$).
В дальнейшем при изучении апостериорных оценок качества мы считаем выполненными предположения (А)–(Г), а также следующие дополнительные предположения.
(Д) Используемый регуляризующий алгоритм дает: 1) оценку ${{\mu }_{\eta }}$ величины $J{\text{*}}$, обладающую свойствами: ${{\mu }_{\eta }} \geqslant J{\text{*}}$ при любом $0 < \eta \leqslant {{\eta }_{0}}$ и ${{\mu }_{\eta }} \to J{\text{*}}$ при $\eta \to 0$; 2) приближенные решения ${{z}_{\eta }}$, удовлетворяющие условиям
(3.2)
${{J}_{\eta }}({{z}_{\eta }}) \leqslant {{\mu }_{\eta }} + \Psi (\eta ,\Omega ({{z}_{\eta }}))$(Е) функционал $Q({{z}_{1}},{{z}_{2}})$ определен для всех ${{z}_{1}},{{z}_{2}} \in \mathcal{D}$ и $\tau $-непрерывен по совокупности переменных; кроме того, $Q(z,{{z}_{0}}) \geqslant Q({{z}_{0}},{{z}_{0}}) \geqslant 0$ $\forall z,{{z}_{0}} \in \mathcal{D}$, и выполнено неравенство (аналог неравенства треугольника): $Q({{z}_{1}},{{z}_{2}}) \leqslant Q({{z}_{0}},{{z}_{1}}) + Q({{z}_{0}},{{z}_{2}})$ $\forall {{z}_{0}},{{z}_{1}},{{z}_{2}} \in \mathcal{D}$.
Предположения (А)–(Д) вместе с условиями аппроксимации обеспечивают выполнение условий регулярности приближенных решений (2.7). В свою очередь (см., например, [20]), из условия регулярности вытекают сходимости ${{z}_{\eta }}\;\mathop \to \limits^\tau \;\bar {z}$, $\Omega ({{z}_{\eta }}) \to \Omega (\bar {z})$ при $\eta \to 0$, а поэтому и сходимости ${{\Delta }_{\eta }} \to J{\text{*}}$, ${{R}_{\eta }} \to C\Omega (\bar {z})$. Если в условии (Д) считать, что $\bar {C} > \Omega (\bar {z})$, то гарантируется лишь сходимость ${{z}_{\eta }}\;\mathop \to \limits^\tau \;\tilde {z}$ [38].
Иногда в дальнейшем для краткости формулировок будем вместо фраз типа “выполнено при $0 < \eta \leqslant {{\eta }_{0}}$, где ${{\eta }_{0}}$ – некоторая константа” писать “при достаточно малых $\eta $”.
Возможность получения апостериорной оценки (3.1) связана с выполнением включений ${{z}_{\eta }} \in {{\mathcal{Z}}_{\eta }}$, $\bar {z} \in {{\mathcal{Z}}_{\eta }}$. Первое включение гарантировано неравенством $\Omega ({{z}_{\eta }}) \leqslant C\Omega ({{z}_{\eta }}) = {{R}_{\eta }}$, справедливым при $C > 1$, и вытекающим из него и из (3.2) неравенством
Второе включение гарантируется следующим утверждением [25], [28].
Теорема 3.1. При выполнении условий (А)–(Д) включение $\bar {z} \in {{\mathcal{Z}}_{\eta }}$ справедливо, по крайней мере, для достаточно малых $\eta $.
Таким образом, апостериорная оценка качества (3.1): $Q({{z}_{\eta }},\bar {z}) \leqslant {{E}_{Q}}(\eta )$ справедлива, по крайней мере, при достаточно малых $\eta $.
3.1. Состоятельность оценки качества приближенного решения экстремальной задачи
Будем говорить, что оценка качества (3.1) приближенного решения ${{z}_{\eta }}$ состоятельна, если $li{{m}_{{\eta \to 0}}}{{E}_{Q}}(\eta ) = Q(\bar {z},\bar {z})$. Следующая теорема (см. [28], [38]) дает достаточные условия состоятельности.
Теорема 3.2. При выполнении предположений (А)–(Е): 1) точная верхняя грань (3.1) достигается; 2) справедлива сходимость $li{{m}_{{\eta \to 0}}}{{E}_{Q}}(\eta ) = Q(\bar {z},\bar {z})$.
Из теоремы 3.2 ясно, что оценка качества (3.1) может быть найдена численными методами оптимизации функционалов, рассмотренными, например, в [4], [5], [21], [43] и др.
3.2. Оптимальность качества регуляризующих алгоритмов для экстремальных задач
В работах [1], [3], [6], [7], [12], [14], [17], [20], [24], [25], [26], [38] и ряде других развита теория РА, оптимальных по порядку точности решения обратных задач. В данном разделе эти результаты обобщаются и даются основные положения теории оптимальности качества приближенных решений экстремальных задач (см. [38]).
Вернемся к задаче (2.1), предполагая выполненными условия (А)–(Е). Особо подчеркнем выполнение условия единственности решение $z* = \bar {z}$ экстремальной задачи (2.1). Кроме того, в этом разделе мы будем использовать конкретную устойчивую оценку величины $J{\text{*}}$ из (2.1): ${{\mu }_{\eta }} = inf\{ {{J}_{\eta }}(z) + \Psi (\eta ,\Omega (z)):z \in \mathcal{D}\} $. Как показано в [20, гл. 2, § 3], она обладает требуемыми свойствами (E,1).
Введем специальное множество элементов ${{M}_{R}} = {\text{\{ }}z \in \mathcal{D}:\Omega (z) \leqslant R{\text{\} }}$, где $R \geqslant \Omega (\bar {z})$. Из предположения (Б) следует $\tau $-компактность множества ${{M}_{R}}$.
Будем рассматривать экстремальные задачи типа (2.1) с различными точными функционалами. Эти функционалы $\bar {J}(z)$ должны удовлетворять двум требованиям:
1) для каждого $\bar {J}(z)$ экстремальная задача $arginf\left\{ {\bar {J}(z):z \in \mathcal{D}} \right\}$ имеет единственное решение $\bar {z}(\bar {J}) \in {{M}_{R}}$;
2) приближенный функционал ${{J}_{\eta }}(z)$ для задачи (2.1) аппроксимирует все функционалы $\bar {J}(z)$ на множестве ${{M}_{R}}$:
Найдем приближенное решение ${{z}_{\eta }}$ задачи (2.1) с помощью некоторого метода ${{P}_{\eta }}$: ${{z}_{\eta }} = {{P}_{\eta }}({{J}_{\eta }},\eta ,\Psi )$. Зададим следующую характеристику качества метода ${{P}_{\eta }}$:
Теорема 3.3. Пусть выполнены условия (А)–(Е). Если ${{z}_{\eta }} = {{P}_{\eta }}({{J}_{\eta }},\eta ,\Psi )\;\mathop \to \limits^\tau \;\bar {z} = \bar {z}(J)$ при $\eta \to 0$, то ${{\Delta }_{Q}}(\eta ,{{P}_{\eta }};{{J}_{\eta }},\eta ,\Psi ;{{M}_{R}}) \to Q(\bar {z},\bar {z})$.
Смысл теоремы 3.3 состоит в следующем: если метод ${{P}_{\eta }}$ – это РА, то его характеристика качества ${{\Delta }_{Q}}(\eta ,{{P}_{\eta }})$ по функционалу $Q$ состоятельна: ${{\Delta }_{Q}}(\eta ,{{P}_{\eta }}) \to Q(\bar {z},\bar {z})$ при $\eta \to 0$.
Определение 3.2. Пусть $\mathcal{P} = {\text{\{ }}P{\text{\} }}$ – класс всех возможных методов $P$ решения задачи (2.1). При фиксированном множестве ${{M}_{R}}$, оптимальным качеством решения $\bar {z}$ этой задачи назовем число
Подчеркнем, что константа ${{k}_{0}}$ в определении 3.2 не зависит от $\eta $, ${{J}_{\eta }}$ и $R$.
3.3. Экстраоптимальное качество регуляризующих алгоритмов
Будем считать выполненными все предположения разд. 3.2, полагая, кроме того, что $R > C\Omega (\bar {z})$.
Теорема 3.4. При сделанных предположениях для каждого $\eta $, $0 < \left\| {\eta {\kern 1pt} } \right\| \leqslant \mathop {\bar {\eta }}\nolimits_0 = {\text{const}}$, оценочная функция ${{E}_{Q}}(\eta )$ имеет оптимальный порядок качества:
Определение 3.3. Будем говорить, что регуляризующий алгоритм ${{z}_{\eta }} = {{P}_{\eta }}({{J}_{\eta }},\eta ,\Psi )$ имеет экстраоптимальное качество $Q$ (на ${{M}_{R}}$), если апостериорная оценка его качества – функция ${{E}_{Q}}(\eta )$ вида (3.1) – является оптимальной по порядку при $\eta \to 0$, т.е. найдется определяемая этим алгоритмом константа ${{k}_{1}} > 0$ такая, что
В свете этого определения теорему 3.4 можно интерпретировать следующим образом. Если экстремальная задача (2.1) удовлетворяет условиям (А)–(Г), а функционал качества $Q$ – условию (Е), то для всякого РА, для которого выполнены условия (Д), теорема 3.4 гарантирует оптимальный порядок качества приближенных решений. Согласно определению 3.3, это означает экстраоптимальность качества такого РА (по функционалу $Q$).
Пример 3.1. Экстраоптимальность качества метода регуляризации Тихонова с апостериорным выбором параметра по обобщенному принципу невязки.
Уточним постановку задачи для этого примера. Будем считать, что $Z$ – рефлексивное банахово пространство, $\tau $ – топология слабой сходимости в $Z$, а функционалы $J(z)$, ${{J}_{\delta }}(z)$ – выпуклые и сильно полунепрерывные снизу на выпуклом замкнутом множестве $\mathcal{D} \subset Z$. Функционал $\Omega (z) \geqslant 0$ предполагается строго выпуклым и сильно полунепрерывным снизу на $\mathcal{D}$. Эти предположения обеспечивают выполнение условий (А), (Б) (см. [20, с. 62–64], [12, с. 92–93]). Кроме того, считаем, что выполнены условия аппроксимации (В). Предполагая, что экстремальная задача (2.1) имеет единственное нетривиальное решение $\bar {z} = \bar {z}(J)$ (условие (Г)), будем его искать по приближенным данным $({{J}_{\eta }},\eta ,\Psi )$ с помощью метода регуляризации Тихонова со сглаживающим функционалом вида
При сформулированных условиях функционал (3.3) будет иметь для каждого $\alpha > 0$ единственную экстремаль ${{z}^{\alpha }}$, реализующую его минимум на $\mathcal{D}$. В этом случае, как показано в [12], [20], при достаточно малых $\left\| \eta \right\| > 0$ можно выбрать параметр $\alpha = {{\alpha }_{\eta }}$ по одному из вариантов обобщенного принципа невязки, а именно: из условия ${{J}_{\eta }}({{z}^{{{{\alpha }_{\eta }}}}}) = {{\mu }_{\eta }} + \Psi (\eta ,\Omega ({{z}^{{{{\alpha }_{\eta }}}}}))$. Зададим приближенное решение задачи (2.1) в виде ${{z}_{\delta }} = {{z}^{{{{\alpha }_{\delta }}}}}$. В [12], [20] показано выполнение для таких приближенных решений условий (Д). Тогда из теоремы 3.4 следует, что метод регуляризации Тихонова с выбором $\alpha $ по обобщенному принципу невязки имеет экстраоптимальное качество, если рассматриваемый функционал качества $Q$ удовлетворяет условию (Е).Аналогичный результат справедлив и для обобщенного метода невязки и некоторых других алгоритмов из [12], [20], которые также будут иметь экстраоптимальное качество.
Отметим следствие неравенства (3.1) и приведенных выше определений: на множестве ${{M}_{R}}$ любой РА с экстраоптимальным качеством по функционалу $Q$ (определение 3.3) имеет качество, оптимальное по порядку (определение 3.2), так как
Обратное, вообще говоря, неверно: не всякий оптимальный по порядку качества регуляризующий алгоритм будет иметь экстраоптимальное качество. Примеры приведены ниже в разд. 5.4. ПРИМЕРЫ АПОСТЕРИОРНЫХ ОЦЕНОК КАЧЕСТВА РЕШЕНИЙ ОБРАТНЫХ ЗАДАЧ
В этом разделе будут рассмотрены типичные функционалы, используемые для оценки качества приближенных решений некорректных обратных задач.
4.1. Глобальные и локальные апостериорные оценки точности
Уточним постановку задачи из разд. 2. Пусть $Z$ – банахово пространство с топологией сильной сходимости, а $U$ – нормированное пространство; элементы в этих пространствах обозначим как $z$ и $u$ соответственно. Пусть, далее, $\mathcal{D} \ne \emptyset $ – заданное множество в $Z$, $F:Z \to U$ – некоторый оператор, возможно, нелинейный. Предположим, что операторное уравнение $F(z) = u$ имеет для данной правой части $u \in U$ единственное квазирешение $\bar {z} \in \mathcal{D}$, т.е.
(4.1)
$\mathop {\left\| {F(\bar {z}) - u} \right\|}\nolimits_U = inf\left\{ {\mathop {\left\| {F(z) - u} \right\|}\nolimits_U :z \in \mathcal{D}} \right\} = \mu \geqslant 0.$Введем теперь функционал $Q({{z}_{\delta }},\bar {z}) = \left\| {{{z}_{\eta }} - \bar {z}} \right\|$, т.е. рассмотрим точность приближенного решения как его “качество”. Для функционала $Q$ очевидно выполнены условия (Е). Поэтому можно апостериорно оценить точность найденного приближенного квазирешения по схеме из разд. 3. Для этого вычислим величины
(4.2)
$\left\| {{{z}_{\eta }} - \bar {z}} \right\| \leqslant sup\left\{ {\left\| {{{z}_{\eta }} - z} \right\|:z \in {{Z}_{\eta }}} \right\}\;\mathop = \limits^{{\text{def}}} \;\varepsilon (\eta ),$Пусть теперь в $Z$ задана топология слабой сходимости и выполнены условия (А)–(Г). Зададим линейный непрерывный функционал $f = \left\langle {f,z} \right\rangle $, определенный на множестве $\mathcal{D}$. Наша задача заключается в приближенном нахождении величины $\left\langle {f,\bar {z}} \right\rangle $ по данным $\left( {{{F}_{h}},{{u}_{\delta }},h,\delta ,\psi } \right)$. Это можно сделать, решив обратную задачу $F(z) = u$ с помощью некоторого РА и затем вычислив по ее приближенному решению ${{z}_{\eta }} \in \mathcal{D}$ величину $\left\langle {f,{{z}_{\eta }}} \right\rangle $. Для оценки точности такого приближения можно использовать функционал качества $Q({{z}_{\eta }},\bar {z}) = \left| {\left\langle {f,{{z}_{\eta }} - \bar {z}} \right\rangle } \right|$, обладающий всеми свойствами (Е). Сама апостериорная оценка качества (3.1) принимает вид
Пусть $Z = Z(T)$ – нормированное пространство функций $z(s)$, определенных в замкнутой области $T \subset {{\mathbb{R}}^{N}}$. Рассмотрим непрерывные функционалы $\left\langle {{{f}_{s}},z} \right\rangle $, которые зависят от точки $s \in T$. Следующие функционалы часто используются при локальных апостериорных оценках точности приближенных решений ${{z}_{\eta }}$.
(а) Поточечная оценка точности приближенных решений:
(б) Оценка точности вычисления среднего значения решения обратной задачи в некоторой окрестности $B(s)$, $B(s) \subset T$, точки $s \in T{\backslash }\partial T$:
(в) Оценка точности взвешенного среднего значения:
Для апостериорных оценок точности из п.п. (а)–(в) справедливы все свойства и утверждения из разд. 3.
4.2. Другие функционалы качества
Можно указать широкий класс функционалов качества, для которых условия (Е) заведомо выполнены. Пусть $f(z)$ есть $\tau $-непрерывный на множестве $\mathcal{D}$ функционал. Будем говорить, что он характеризует качество приближенного решения ${{z}_{\eta }} \in \mathcal{D}$ задачи (2.1), если $Q({{z}_{\eta }},\bar {z}) = \left| {f({{z}_{\eta }}) - f(\bar {z})} \right|$. Для определенного таким образом функционала $Q({{z}_{1}},{{z}_{2}})$ свойства (Е) очевидны. Приведем теперь конкретные примеры.
Пусть $T$ – выпуклая ограниченная область в ${{\mathbb{R}}^{N}}$. Зададим в пространстве ${{L}_{2}}(T)$ функций $z = z(x)$, $x \in T$, множество ${{\mathcal{D}}_{0}}$, на котором определен функционал $J(z)$, и рассмотрим экстремальную задачу: найти элемент, реализующий точную нижнюю грань $inf\{ J(z):z \in {{\mathcal{D}}_{0}}\} $. Предположим, что эта задача имеет единственное решение $\bar {z} \in {{\mathcal{D}}_{0}}$ (условие (Г)) и оно обладает дополнительной гладкостью: $\bar {z}(x)$ принадлежит пространству Соболева $W_{2}^{2}(T)$. Тогда рассматриваемая экстремальная задача сводится к задаче (2.1) с $Z = W_{2}^{2}(T)$ и $\mathcal{D} = {{\mathcal{D}}_{0}} \cap W_{2}^{2}(T)$. Положим теперь $\Omega (z) = \mathop {\left\| z \right\|}\nolimits_{W_{2}^{2}(T)} $ и будем решать экстремальную задачу (2.1), предполагая, что $\tau $ – топология слабой сходимости в $Z = W_{2}^{2}(T)$, что выполнены условия (А)–(В), и используя приближенные данные $({{J}_{\eta }},\eta ,\Psi )$. Применим для этих целей какой-либо метод, дающий приближенное решение ${{z}_{\eta }} \in \mathcal{D}$ со свойствами (Д).
BV-вариация как характеристика качества приближенного решения. Пусть $N \geqslant 2$. Для оценки качества полученного приближенного решения используем функционал BV-вариации (см., например, [39]). Если $z(x) \in W_{2}^{2}(T)$, то в силу вложения $W_{2}^{2}(T) \subset W_{1}^{1}(T)$, он представим в виде $BV(z) = \int_T {\left| {\operatorname{grad} z(x)} \right|} {\kern 1pt} dx$ [39].
Пусть $z(x) \in W_{2}^{2}(T)$, $\{ {{z}_{n}}(x)\} \subset W_{2}^{2}(T)$. Так как пространство $W_{2}^{2}(T)$ компактно вложено в пространство $W_{2}^{1}(T)$ при $N \geqslant 2$ и справедлива оценка
то из слабой сходимости ${{z}_{n}}(x) \rightharpoonup z(x)$ ($n \to \infty $) в $W_{2}^{2}(T)$ следует сильная сходимость ${{z}_{n}}(x) \to z(x)$ в $W_{2}^{1}(T)$, и оценка (4.3) доказывает $\tau $-непрерывность функционала $BV$-вариации. Из сказанного ясно, что можно характеризовать качество приближений ${{z}_{\eta }}$ с помощью функционала $Q({{z}_{\eta }},\bar {z}) = \left| {BV({{z}_{\eta }}) - BV(\bar {z})} \right|$, и при этом будут справедливы все утверждения разд. 3.Функционал энтропии как характеристика качества приближенного решения. Изменим приведенную выше постановку задачи, считая, что $N = 2$ и ${{\mathcal{D}}_{0}} = \{ z(x) \in {{L}_{2}}(T):z(x) \geqslant {{\varepsilon }_{0}} = {\text{const}} > 0\} $. Тогда на ${{\mathcal{D}}_{0}}$ определен функционал энтропии
широко используемый в приложениях (см., например, [40]). Из компактности вложения $W_{2}^{2}(T) \subset C(T)$ следует, что этот функционал будет $\tau $-непрерывен на $\mathcal{D} = {{\mathcal{D}}_{0}} \cap W_{2}^{2}(T)$. Поэтому его можно использовать для оценки качества приближенного решения задачи (2.1), вводя $Q({{z}_{\delta }},\bar {z}) = \left| {E({{z}_{\delta }}) - E(\bar {z})} \right|$. При этом снова сохраняют силу результаты разд. 3.
5. О СВЯЗИ ОПТИМАЛЬНЫХ И ЭКСТРАОПТИМАЛЬНЫХ ПО ПОРЯДКУ ТОЧНОСТИ РА
Основная причина, по которой оптимальный по порядку качества РА может оказаться не экстраоптимальным, – это нарушение неравенства (3.2) в условии (Д). Продемонстрируем это двумя примерами апостериорной оценки качества – глобальной и локальной точности алгоритмов.
5.1. Глобальные оценки точности
Пример 5.1. Задача, для которой тихоновский алгоритм с оптимальным выбором параметра регуляризации не будет экстраоптимальным.
Предположим, что $Z = \mathcal{D} = U = {{l}_{2}}$ и $z = {{({{z}_{1}},{{z}_{2}},\; \ldots )}^{{\text{т}}}} \in Z$. Рассмотрим уравнение (2.5) с оператором, действующим в ${{l}_{2}}$ и определяемым бесконечной диагональной матрицей $A = \operatorname{diag} (1,q,{{q}^{2}},\; \ldots ,\;{{q}^{n}},\; \ldots )$, $0 < q = {\text{const}} < 1$. Правая часть уравнения задана как $u = {{(1,0,0,\; \ldots )}^{{\text{т}}}} \in U$. Тогда уравнение имеет единственное решение $\bar {z} = {{(1,0,0,\; \ldots )}^{{\text{т}}}} \in Z$. Приближенные данные задачи определим в виде $\left\{ {{{A}_{n}},{{u}_{n}},{{h}_{n}},{{\delta }_{n}}} \right\}$. Здесь ${{A}_{n}} = \operatorname{diag} (1,q,{{q}^{2}},\; \ldots ,\;{{q}^{n}},0,0,\; \ldots .)$, ${{u}_{n}} = {{(1,0,0,\; \ldots ,\;{{q}^{{3n}}},0,0,\; \ldots )}^{{\text{т}}}}$, причем число ${{q}^{{3n}}}$ стоит на $(n + 1)$-й позиции. Погрешности данных определяются как ${{\delta }_{n}} = {{q}^{{3n}}}$, ${{h}_{n}} = {{q}^{{n + 1}}} + {{q}^{{n + 2}}} + \ldots = \tfrac{{{{q}^{{n + 1}}}}}{{1 - q}}$. Применим для нахождения приближенного решения этой обратной задачи метод регуляризации Тихонова (2.8) с $\Omega [z] = \mathop {\left\| z \right\|}\nolimits^2 $ и $f(x) = {{x}^{2}}$. Тогда из (2.12) получим
Изучим теперь для приближенного решения ${{z}_{\eta }} = {{z}^{{{{\alpha }_{{{\text{opt}}}}}}}} = {{z}^{{{{\alpha }_{n}}}}}$ глобальную апостериорную оценку точности: $\varepsilon (\eta ) = sup\left\{ {\left\| {z - {{z}_{\eta }}} \right\|:\left\| z \right\| \leqslant {{R}_{\eta }},\;\left\| {{{A}_{n}}z - {{u}_{n}}} \right\| \leqslant {{\Delta }_{\eta }}} \right\}$, где ${{R}_{\eta }} = C\left\| {{{z}^{{{{\alpha }_{n}}}}}} \right\|$, ${{\Delta }_{\eta }} = C\left\| {{{A}_{n}}{{z}^{{{{\alpha }_{n}}}}} - {{u}_{n}}} \right\|$. Так как $\left\| {{{z}^{{{{\alpha }_{n}}}}}} \right\| \to \left\| {\bar {z}} \right\| = 1$, то при достаточно больших $n$ выполнены неравенства ${{R}_{\eta }} = C\left\| {{{z}^{{{{\alpha }_{n}}}}}} \right\| \geqslant {{C}_{1}} = {\text{const}} > 1$, ${{\Delta }_{\eta }} \geqslant {{c}_{4}}{{q}^{{2n}}}$, ${{c}_{4}} = {\text{const}} > 0$, и верна оценка
(5.1)
$\begin{gathered} {{\varepsilon }^{2}}(\eta ) \geqslant sup\left\{ {{{{\left\| {z - {{z}_{\eta }}} \right\|}}^{2}}:\Omega [z] \leqslant {{C}_{1}},\;\left\| {{{A}_{n}}z - {{u}_{n}}} \right\| \leqslant {{c}_{4}}{{q}^{{2n}}}} \right\} \geqslant \\ \geqslant \;sup\left\{ {{{{(x - {{x}_{n}})}}^{2}} + {{{(y - {{y}_{n}})}}^{2}}:{{x}^{2}} + {{y}^{2}} \leqslant C_{1}^{2},\;{{{(x - 1)}}^{2}} + {{{({{q}^{n}}y - {{q}^{{3n}}})}}^{2}} \leqslant c_{4}^{2}{{q}^{{4n}}}} \right\} \geqslant \\ \geqslant \;{{(x{\text{*}} - {{x}_{n}})}^{2}} + {{(y{\text{*}} - {{y}_{n}})}^{2}}, \\ \end{gathered} $Таким образом, апостериорная оценка точности (4.2) в данном примере не будет оптимальной по порядку, и рассматриваемый РА для данной задачи не является экстраоптимальным. Однако при этом он будет оптимальным по точности.
5.2. Локальные оценки точности
Пусть $Z(T)$ – нормированное пространство функций $z(s)$, определенных в замкнутой области $T \subset {{\mathbb{R}}^{N}}$. Пусть, далее, $\mathcal{D} \ne \emptyset $, $\mathcal{D} \subset C(T)$, – заданное множество в $Z(T)$, наделенное топологией равномерной сходимости $\tau $, $U$ – нормированное пространство с элементами $u$, а $A:\mathcal{D} \to U$ – линейный ограниченный оператор. Будем решать уравнение $Az = u$ с точным оператором и приближенной правой частью, используя некоторый РА, и пусть ${{z}_{\delta }}(s)$ – приближение для точного решения $\bar {z}(s) \in \mathcal{D}$. Нас интересует конкретная локальная оценка качества метода – поточечная апостериорная оценка точности приближения, т.е. величина ${{E}_{s}}(\delta )$ из неравенства
Теорема 5.1. Для того, чтобы регуляризующий алгоритм решения линейной задачи (2.5) с точно заданным оператором $A$ был поточечно экстраоптимальным в точках $s \in {{T}_{0}}$, необходимо и достаточно существование такой константы ${{k}_{1}} > 0$, не зависящей от $s$, что
(5.2)
$\frac{{{{\omega }_{s}}({{\Delta }_{\delta }},{{R}_{\delta }})}}{{{{\omega }_{s}}(2\delta ,R)}} \leqslant {{k}_{1}}\quad \forall s \in {{T}_{0}},\quad \forall \delta :0 < \delta \leqslant {{\delta }_{0}} = {\text{const}}.$Пример 5.2. Задача, для которой тихоновский алгоритм, будучи оптимальным по порядку в некоторой точке, не будет экстраоптимальным в этой точке.
Предположим, что $Z = U = \left\{ {z(s) \in {{L}_{2}}[0,1]:z{\text{'}}(0) = z{\text{'}}(1) = 0} \right\}$. Зададим в этом подпространстве гильбертова пространства ${{L}_{2}}[0,1]$ ортонормированный базис $\mathop {\{ {{\varphi }_{k}}\} }\nolimits_{k = 0}^\infty = \mathop {\{ {{\gamma }_{k}}cos\pi ks\} }\nolimits_{k = 0}^\infty $, где ${{\gamma }_{k}}$ – нормирующие коэффициенты. Тогда для элементов $z \in Z$, $u \in U$ справедливы разложения
Введем линейный самосопряженный оператор $A:Z \to U$ по формуле $Az = \sum\nolimits_{k = 0}^\infty {{{q}^{k}}} {{z}_{k}}{{\varphi }_{k}}(x)$, $0 < q = {\text{const}} < 1$, и определим $\mathcal{D} = \{ z = A{v}:\forall {v} \in Z,\;\left\| {v} \right\| \leqslant r = C{{\left\| A \right\|}^{{ - 1}}}\} $ $\mathcal{D} = \{ z = A{v}:\forall {v} \in Z,\;\left\| {v} \right\| \leqslant r = C{{\left\| A \right\|}^{{ - 1}}}\} $, $C > 1$. Можно убедиться, что $\mathcal{D} \subset C[0,1]$. Рассмотрим операторное уравнение (2.5) с таким оператором $A$ и правой частью $u = {{\varphi }_{0}}(x) = 1$. Оно имеет единственное непрерывное решение $\bar {z} = {{\varphi }_{0}}(s) = 1$. Зададим приближенную правую часть уравнения (2.5): ${{u}_{n}} = {{\varphi }_{0}}(x) - {{q}^{n}}{{\varphi }_{n}}(x)$, так что ${{\delta }_{n}} = {{q}^{n}}$. Применим для нахождения приближенного решения задачи (2.5) метод регуляризации Тихонова с $\Omega [z] = \mathop {\left\| z \right\|}\nolimits_{{{L}_{2}}}^2 $. Для такого $\Omega [z]$ выполнены условия (А), (Б) с топологией равномерной сходимости. Из (2.12) получим
(5.3)
${{z}^{\alpha }} = \mathop {\left( {\alpha E + A{\text{*}}A} \right)}\nolimits^{ - 1} A{\text{*}}{{u}_{n}} = z_{0}^{\alpha }{{\varphi }_{0}}(s) + z_{n}^{\alpha }{{\varphi }_{n}}(s),\quad z_{0}^{\alpha } = \frac{1}{{1 + \alpha }},\quad z_{n}^{\alpha } = \frac{{ - {{q}^{{2n}}}}}{{\alpha + {{q}^{{2n}}}}}.$(5.4)
${{\left\| {A{{z}^{{{{\alpha }_{n}}}}} - {{u}_{n}}} \right\|}_{{{{L}_{2}}}}}{{\Delta }_{{{{\delta }_{n}}}}} \asymp {{q}^{{n/2}}} = \sqrt {{{\delta }_{n}}} .$6. ЧИСЛЕННЫЕ АЛГОРИТМЫ АПОСТЕРИОРНОГО ОЦЕНИВАНИЯ
В этом разделе будут представлены численные алгоритмы апостериорного оценивания точности приближенных решений обратных задач (2.6) и (2.5). Выбор функционалов качества типа точности не случаен: именно они чаще всего интересны пользователям при решении обратных задач.
6.1. Алгоритмы глобальной апостериорной оценки точности
Сначала рассмотрим численные алгоритмы глобальной апостериорной оценки точности приближенных решений задач вида (2.6) с общим нелинейным оператором ${{F}_{h}}$ и регуляризатором общего вида $\Omega $, т.е. алгоритмы нахождения величины
(6.1)
$\varepsilon (\eta ) = sup\left\{ {\left\| {{{z}_{\eta }} - z} \right\|:z \in \mathcal{D},\;\Omega [z] \leqslant {{R}_{\eta }},\;\left\| {{{F}_{h}}(z) - {{u}_{\delta }}} \right\| \leqslant {{\Delta }_{\eta }}} \right\}$Лемма 6.1. Предположим, что при данном $\eta $, $0 < \left\| \eta \right\| \leqslant {{\eta }_{0}}$, справедливо включение $\bar {z} \in {{Z}_{{\Omega \eta }}}$ и приближенное решение ${{z}_{\eta }}$ получено с помощью нетривиального регуляризующего алгоритма, т.е. ${{z}_{\eta }} = {{P}_{\eta }}({{F}_{h}},{{u}_{\delta }},h,\delta ) \ne \bar {z}$. Тогда все решения $\tilde {z}$ задачи (6.1) находятся среди решений следующих экстремальных задач:
(6.2)
$\arg \sup \left\{ {{{{\left\| {z - {{z}_{\eta }}} \right\|}}^{2}}:\Omega [z] = {{R}_{\eta }},\;{{{\left\| {{{F}_{h}}(z) - {{u}_{\delta }}} \right\|}}^{2}} = \Delta _{\eta }^{2}} \right\},$(6.3)
$\arg \sup \left\{ {{{{\left\| {z - {{z}_{\eta }}} \right\|}}^{2}}:\Omega [z] < {{R}_{\eta }},\;{{{\left\| {{{F}_{h}}(z) - {{u}_{\delta }}} \right\|}}^{2}} = \Delta _{\eta }^{2}} \right\},$(6.4)
$\arg \sup \left\{ {{{{\left\| {z - {{z}_{\eta }}} \right\|}}^{2}}:\Omega [z] = {{R}_{\eta }},\;{{{\left\| {{{F}_{h}}(z) - {{u}_{\delta }}} \right\|}}^{2}} < \Delta _{\eta }^{2}} \right\}.$Из леммы 6.1 следует, что $\tilde {z} \ne {{z}_{\eta }}$ в случае, когда уравнение (2.6) решается с помощью нетривиального алгоритма ${{P}_{\eta }}$ и $\bar {z} \in {{Z}_{{\Omega \eta }}}$. Справедлива также
Лемма 6.2. Если приближенное решение ${{z}_{\eta }}$ получено с помощью нетривиального регуляризующего алгоритма и выполнены условия (Д), то, по крайней мере, для достаточно малых $\eta $ все решения экстремальной задачи (6.1) находятся среди решений задачи (6.3).
Приведем необходимые условия локальных максимумов в задаче (6.1). Для этого уточним постановку задачи. Предположим, что $Z$ и $U$ – гильбертовы пространства и $\mathcal{D} = H$, где $H$ – вложенное в $Z$ банахово пространство, на котором определены дифференцируемые по Фреше в $Z$ оператор ${{F}_{h}}$ и функционал $\Omega [z]$. Обозначим как $F_{h}^{'}(z)$, $\Omega {\text{'}}{\kern 1pt} [z]$ производные Фреше величин ${{F}_{h}}(z)$, $\Omega [z]$. В [24], [25] доказана
Теорема 6.1. Предположим, что выполняются условия леммы 6.1 и пусть $\tilde {z}$ – произвольное решение задачи (6.1). Если справедливы неравенства $(F_{h}^{'}(\tilde {z})){\text{*}}({{F}_{h}}(\tilde {z}) - {{u}_{\delta }}) \ne 0$ и $\Omega {\text{'}}{\kern 1pt} [\tilde {z}] \ne 0$, то возможны следующие варианты:
а) или $\tilde {z}$ есть решение задачи (6.2) и существуют такие числа $\alpha ,\beta > 0$, что обеспечены равенства:
б) или $\tilde {z}$ есть решение задачи (6.2) и существует такое число $\beta > 0$, что выполнены равенства:
в) или $\tilde {z}$ есть решение задачи (6.3) и существует такое число $\alpha > 0$, что справедливы соотношения:
г) или $\tilde {z}$ есть решение задачи (6.4) и существует такое число $\beta > 0$, что выполнены соотношения:
Замечание 6.1. Пусть удовлетворяются условия леммы 6.2 и функционал $\Omega [z]$ непрерывно дифференцируем по Фреше в некоторой окрестности точки $\bar {z}$, причем $\Omega {\text{'}}{\kern 1pt} [\bar {z}] \ne 0$. Тогда можно доказать (см. [24], [25]), что при достаточно малых $\eta $ выполняются неравенства из условий теоремы 33 и, кроме того, неравенство $\Omega [\tilde {z}] < {{R}_{\eta }}$. Это означает, что при сделанных предположениях в теореме реализуется только вариант из пункта в).
Сформулируем алгоритм вычисления глобальной апостериорной оценки (6.1) по данным $\{ {{F}_{h}},{{u}_{\delta }},\Omega ,{{z}_{\eta }},{{R}_{\eta }},{{\Delta }_{\eta }}\} $, считая справедливой теорему 6.1.
Алгоритм 1
Предварительный шаг. Задание множества допустимых значений параметров $\alpha $, $\beta $, которые будут использованы в алгоритме.
Шаг 1. Решение задачи (6.2) с помощью необходимых условий из п. а) теоремы 6.1:
А) нахождение решений ${{z}^{{\alpha \beta }}}$ уравнения $z - \alpha (F_{h}^{'}[z]){\text{*}}({{F}_{h}}(z) - {{u}_{\delta }}) - \beta \Omega {\text{'}}{\kern 1pt} [z] = {{z}_{\eta }}$ для допустимых значений параметров $\alpha > 0$, $\beta > 0$; Б) выбор множества ${{\mathcal{A}}_{1}} = {\text{\{ }}(\alpha *,\beta *){\text{\} }}$ тех параметров, для которых равенства $\Omega [{{z}^{{\alpha \beta }}}] = {{R}_{\eta }}$, $\left\| {{{F}_{h}}({{z}^{{\alpha \beta }}}) - {{u}_{\delta }}} \right\| = {{\Delta }_{\eta }}$ выполнены с заданной (относительной) точностью $\nu > 0$:
В) нахождение числа ${{M}_{1}} = max\left\{ {\left\| {{{z}^{{\alpha *\beta *}}} - {{z}_{\eta }}} \right\|:(\alpha *,\beta *) \in {{\mathcal{A}}_{1}}} \right\}$; если множество ${{\mathcal{A}}_{1}}$ пусто, то считаем ${{M}_{1}} = 0$.
Шаг 2. Решение задачи (6.2) с помощью необходимых условий из п. б) теоремы 6.1:
А) нахождение решений ${{z}^{\beta }}$ уравнения $\beta \Omega {\text{'}}{\kern 1pt} [z] + (F_{h}^{'}(z)){\text{*}}({{F}_{h}}(z) - {{u}_{\delta }}) = 0$ для допустимых значений $\beta > 0$; Б) выбор множества ${{\mathcal{A}}_{2}} = {\text{\{ }}\beta *{\text{\} }}$ тех значений параметра, для которых равенства $\Omega [{{z}^{{\beta *}}}] = {{R}_{\eta }}$, $\left\| {{{F}_{h}}({{z}^{{\beta *}}}) - {{u}_{\delta }}} \right\| = {{\Delta }_{\eta }}$ выполнены с заданной точностью $\nu $; В) нахождение числа ${{M}_{2}} = max\left\{ {\left\| {{{z}^{{\beta *}}} - {{z}_{\eta }}} \right\|:\beta * \in {{\mathcal{A}}_{2}}} \right\}$; если ${{\mathcal{A}}_{2}} = $, то считаем ${{M}_{2}} = 0$.
Шаг 3. Решение задачи (6.3) с помощью необходимых условий из п. в) теоремы 6.1: А) нахождение решений ${{z}^{\alpha }}$ уравнения $z - \alpha (F_{h}^{\prime }(z)){\text{*}}({{F}_{h}}(z) - {{u}_{\delta }}) = {{z}_{\eta }}$ для допустимых значений параметра $\alpha > 0$; Б) выбор множества ${{\mathcal{A}}_{3}} = {\text{\{ }}\alpha *{\text{\} }}$ тех значений параметра, для которых с заданной точностью $\varepsilon $ выполнено равенство $\left\| {{{F}_{h}}({{z}^{{\alpha *}}}) - {{u}_{\delta }}} \right\| = {{\Delta }_{\eta }}$ и $\Omega [{{z}^{{\alpha *}}}] < {{R}_{\eta }}$; В) нахождение числа ${{M}_{3}} = max\left\{ {\left\| {{{z}^{{\alpha *}}} - {{z}_{\eta }}} \right\|:\alpha * \in {{\mathcal{A}}_{3}}} \right\}$; если ${{\mathcal{A}}_{3}} = $, то ${{M}_{3}} = 0$.
Шаг 4. Решение задачи (6.4) с помощью необходимых условий из п. г) теоремы 6.1:
А) нахождение решений ${{z}^{\beta }}$ уравнения $z - \beta \Omega {\text{'}}{\kern 1pt} [z] = {{z}_{\eta }}$ для допустимых значений $\beta > 0$; Б) выбор множества ${{\mathcal{A}}_{4}} = {\text{\{ }}\beta *{\text{\} }}$ тех значений параметра, для которых с точностью $\nu $ выполнено равенство $\Omega [{{z}^{{\beta *}}}] = {{R}_{\eta }}$ и $\left\| {{{F}_{h}}({{z}^{{\beta *}}}) - {{u}_{\delta }}} \right\| < {{\Delta }_{\eta }}$; В) нахождение числа ${{M}_{4}} = max\left\{ {\left\| {{{z}^{{\beta *}}} - {{z}_{\eta }}} \right\|:\beta * \in {{A}_{4}}} \right\}$; если ${{\mathcal{A}}_{4}} = $, то ${{M}_{4}} = 0$.
Шаг 5. Нахождение элементов ${{z}_{1}}$, ${{z}_{2}}$, для которых нарушаются условия теоремы 6.1, т.е. решение уравнений $(F_{h}^{'}(z)){\text{*}}({{F}_{h}}(z) - {{u}_{\delta }}) = 0$, $\Omega {\text{'}}{\kern 1pt} [{{z}_{2}}] = 0$ и проверка ограничений $\Omega [{{z}_{{1,2}}}] \leqslant {{R}_{\eta }}$, $\left\| {{{F}_{h}}({{z}_{{1,2}}}) - {{u}_{\delta }}} \right\| \leqslant {{\Delta }_{\eta }}$; нахождение числа ${{M}_{0}} = max\left\{ {\left\| {{{z}_{1}} - {{z}_{\eta }}} \right\|,\left\| {{{z}_{2}} - {{z}_{\eta }}} \right\|} \right\}$. Если такие элементы ${{z}_{1}}$, ${{z}_{2}}$ не существуют, то считается, что ${{M}_{0}} = 0$.
Шаг 6. Вычисление точной верхней грани (6.1): $\varepsilon (\eta ) = max{\text{\{ }}{{M}_{1}},{{M}_{2}},{{M}_{3}},{{M}_{4}},{{M}_{0}}{\text{\} }}$.
Справедливость последнего равенства следует из теоремы 6.1. Итак, предлагаемый алгоритм дает искомую апостериорную оценку точности приближенного решения ${{z}_{\eta }}$.
Замечание 6.2. 1) В п. 1 алгоритма допустимые параметры ($\alpha $, $\beta $) при практических расчетах обычно берутся на сетках вида $\alpha = {\text{\{ }}{{\alpha }_{0}}q_{1}^{i},\;i = 0,1,\; \ldots ,\;m{\text{\} }}$, $\beta = {\text{\{ }}{{\beta }_{0}}q_{2}^{j},j = 0,1,\; \ldots ,\;n{\text{\} }}$, где ${{\alpha }_{0}},{{\beta }_{0}} > 0$, $0 < {{q}_{1}}$, ${{q}_{2}} < 1$, $m,n \in \mathbb{N}$ – заданные константы. Иногда максимальные значения параметров ${{\alpha }_{0}}$, ${{\beta }_{0}}$ удается оценить по схеме из [20, с. 154], [12, с. 308].
2) Уравнения, решаемые в пунктах А) алгоритма, – это операторные (вообще говоря, нелинейные) уравнения II рода, так что при некоторых параметрах $\alpha ,\beta > 0$ они могут не иметь единственного решения.
3) Если верны условия из замечания 6.1, то при $0 < \left\| \eta \right\| \leqslant {{\eta }_{0}}$ можно выполнять только шаги 3 и 6 алгоритма. Если уравнение (2.5) линейное, то в пункте А) шага 3 нужно решать линейные операторные уравнения II рода $(E - \alpha A_{h}^{ * }{{A}_{h}})z = {{z}_{\eta }} - \alpha A_{h}^{ * }{{u}_{\delta }}$.
6.2. Алгоритмы локальной апостериорной оценки точности
Следуя [26], [27], изучим задачу вычисления величины
(6.5)
${{E}_{f}}(\eta ) = sup\left\{ {\left| {\left\langle {f,{{z}_{\eta }} - z} \right\rangle } \right|:z \in {{\mathcal{Z}}_{\eta }}} \right\}.$Лемма 6.3. Пусть $f[z]$ – некоторый функционал, ограниченный на некотором множестве $\mathcal{Z}$, $\mathcal{Z} \subset Z$, и $f* = sup\left\{ {\left| {f[z]} \right|:z \in \mathcal{Z}} \right\}$. Пусть далее, ${{f}^{{( + )}}} = sup{\text{\{ }}f[z]:z \in \mathcal{Z}{\text{\} }}$ и ${{f}^{{( - )}}} = sup{\text{\{ }} - f[z]:z \in \mathcal{Z}{\text{\} }}$. Тогда $f{\kern 1pt} {\text{*}} = max\{ {{f}^{{( + )}}},{{f}^{{( - )}}}\} $.
В силу предположение (Б) семейство элементов ${{\Omega }_{{{{R}_{\eta }}}}} = {\text{\{ }}z \in \mathcal{D}:\Omega [z] \leqslant {{R}_{\eta }}{\text{\} }}$ $\tau $-секвенциально компактно. Поэтому при фиксированном $\eta $ $\tau $-непрерывный функционал $f[z] = \left\langle {f,z - {{z}_{\eta }}} \right\rangle $ ограничен на ${{\Omega }_{{{{R}_{\eta }}}}}$, а значит, и на ${{\mathcal{Z}}_{\eta }}$. Тогда из леммы 6.3, примененной к задаче (6.5), получается равенство
где(6.7)
$E_{f}^{{( + )}}(\eta ) = sup\left\{ {\left\langle {f,z - {{z}_{\eta }}} \right\rangle :\forall z \in {{\mathcal{Z}}_{\eta }}} \right\} = inf\left\{ {\left\langle {f,{{z}_{\eta }} - z} \right\rangle :\forall z \in \mathcal{D},\;\left\| {{{F}_{h}}(z) - {{u}_{\delta }}} \right\| \leqslant {{\Delta }_{\eta }},\;\Omega [z] \leqslant {{R}_{\eta }}} \right\},$(6.8)
$E_{f}^{{( - )}}(\eta ) = sup\left\{ {\left\langle {f,{{z}_{\eta }} - z} \right\rangle :\forall z \in {{Z}_{\eta }}} \right\} = inf\left\{ {\left\langle {f,z - {{z}_{\eta }}} \right\rangle :\forall z \in \mathcal{D},\;\left\| {{{F}_{h}}(z) - {{u}_{\delta }}} \right\| \leqslant {{\Delta }_{\eta }},\;\Omega [z] \leqslant {{R}_{\eta }}} \right\}.$Алгоритм 2
Шаг 1. Вычислить число $E_{f}^{{( + )}}(\eta )$, решая задачу (6.7) минимизации линейного функционала $\left\langle {f,{{z}_{\eta }} - z} \right\rangle $.
Шаг 2. Вычислить число $E_{f}^{{( - )}}(\eta )$, решая задачу (6.8) минимизации линейного функционала $\left\langle {f,z - {{z}_{\eta }}} \right\rangle $.
Шаг 3. Найти величину ${{E}_{f}}(\eta )$ по формуле (6.6).
Применив алгоритм 2, можно найти локальную апостериорную оценку (6.5).
Из условия (Б) следует, что точные грани в задачах (6.7), (6.8) минимизации $\tau $-непрерывных функционалов достигаются на некоторых элементах.
Если $\mathcal{D} = Z$, оператор ${{F}_{h}}$ линеен, а функционал $\Omega [z]$ выпуклый, то задачи на минимум (6.7), (6.8) – это задачи выпуклого программирования. Для их решения имеется развитое программное обеспечение.
6.3. Методы апостериорного оценивания для линейных задач
В случае решения линейных операторных уравнений в гильбертовом пространстве алгоритмы вычисления апостериорных оценок (6.1), (6.5) можно упростить (см. [36], [37]). Уточним постановку задачи, считая, что выполнены следующие предположения:
1) $Z$, $U$ – гильбертовы пространства со скалярными произведениями $\mathop {\left( { \cdot , \cdot } \right)}\nolimits_Z $, $\mathop {\left( { \cdot , \cdot } \right)}\nolimits_U $ и нормами $\mathop {\left\| {\, \cdot \,} \right\|}\nolimits_Z $, $\mathop {\left\| {\, \cdot \,} \right\|}\nolimits_U $; там, где это не вызывает сомнений, индексы у скалярных произведений и норм будем опускать;
2) функционал $\Omega $ имеет специальный вид $\Omega [z] = \left\| {Lz} \right\|$, где $L:Z \to Z$ – линейный замкнутый оператор с областью определения $D(L)$, которая плотна в $Z$; считается также, что $\left\| {Lz} \right\| \geqslant k\left\| z \right\|$, $\forall z \in D(L)$, где $k = {\text{const}} > 0$, и поэтому оператор $L$ имеет нулевое ядро: $N(L) = 0$;
3) $\mathcal{D} = D(L)$ и точное решение удовлетворяет условиям $\bar {z} \in D(L)$, $\bar {z} \ne 0$;
4) линейные и ограниченные операторы $A,{{A}_{h}}:Z \to U$ удовлетворяют условию аппроксимации: $\left\| {{{A}_{h}}z - Az} \right\| \leqslant h\left\| {Lz} \right\|$, $\forall z \in D(L)$; кроме того, $N(A) = 0$;
5) приближенные решения ${{z}_{\eta }} \in D(L)$, получаемые с помощью используемого РА для приближенного решения задачи $Az = u$: а) обеспечивают сходимости ${{z}_{\eta }}\xrightarrow{Z}\bar {z}$, $\left\| {L{{z}_{\eta }}} \right\| \to \left\| {L\bar {z}} \right\|$ при $\eta \to 0$; б) удовлетворяют условию $\left\| {{{A}_{h}}{{z}_{\eta }} - {{u}_{\delta }}} \right\| > 0$, $\left\| {L{{z}_{\eta }}} \right\| > 0$ при рассматриваемых $\eta $.
Отметим, что из предположений 2) следует, что можно ввести новое гильбертово пространство $H$, вложенное в $Z$, со скалярным произведением $\mathop {\left( {z,{v}} \right)}\nolimits_H = \mathop {\left( {Lz,L{v}} \right)}\nolimits_Z $, и порождаемой им нормой $\mathop {\left\| z \right\|}\nolimits_H $ (см., например, [14]).
Задачи (6.1), (6.5) принимают тогда вид
(6.9)
$\begin{gathered} \varepsilon (\eta ) = sup\left\{ {\left\| {z - {{z}_{\eta }}} \right\|:z \in D(L),\;\left\| {{{A}_{h}}z - {{u}_{\delta }}} \right\| \leqslant C\left\| {{{A}_{h}}{{z}_{\eta }} - {{u}_{\delta }}} \right\|,\;\left\| {Lz} \right\| \leqslant C\left\| {L{{z}_{\eta }}} \right\|} \right\} = \\ = sup\left\{ {\left\| {z - {{z}_{\eta }}} \right\|:z \in H,\;\left\| {{{A}_{h}}z - {{u}_{\delta }}} \right\| \leqslant C\left\| {{{A}_{h}}{{z}_{\eta }} - {{u}_{\delta }}} \right\|,\;\mathop {\left\| z \right\|}\nolimits_H \leqslant C\mathop {\left\| {{{z}_{\eta }}} \right\|}\nolimits_H } \right\}, \\ \end{gathered} $(6.10)
$\begin{gathered} {{E}_{f}}(\eta ) = sup\left\{ {\left| {\left\langle {f,z - {{z}_{\eta }}} \right\rangle } \right|:z \in D(L),\;\left\| {{{A}_{h}}z - {{u}_{\delta }}} \right\| \leqslant C\left\| {{{A}_{h}}{{z}_{\eta }} - {{u}_{\delta }}} \right\|,\;\left\| {Lz} \right\| \leqslant C\left\| {L{{z}_{\eta }}} \right\|} \right\} = \\ = sup\left\{ {\left| {\left\langle {f,z - {{z}_{\eta }}} \right\rangle } \right|:z \in H,\;\left\| {{{A}_{h}}z - {{u}_{\delta }}} \right\| \leqslant C\left\| {{{A}_{h}}{{z}_{\eta }} - {{u}_{\delta }}} \right\|,\;\mathop {\left\| z \right\|}\nolimits_H \leqslant C\mathop {\left\| {{{z}_{\eta }}} \right\|}\nolimits_H } \right\}. \\ \end{gathered} $Теорема 6.2. Выполнены равенства
(6.11)
${{\varepsilon }^{2}}(\eta ) = \mathop {sup}\limits_{w \in H} \left\{ {g_{\eta }^{2}(w):\left\| w \right\|_{Z}^{2} = 1} \right\},\quad E_{f}^{2}(\eta ) = \mathop {sup}\limits_{w \in H} \left\{ {{{g}_{\eta }}{{{(w)}}^{2}}{{{\left\langle {f,w} \right\rangle }}^{2}}:\left\| w \right\|_{Z}^{2} = 1} \right\}.$(6.12)
$\begin{gathered} \rho _{m}^{2}(\eta ) = \mathop {sup}\limits_{w \in H} \left\{ {{{\xi }_{m}}[{{{(t_{\eta }^{{(A)}}(w))}}^{2}},{{{(t_{\eta }^{{(L)}}(w))}}^{2}}]:\mathop {\left\| w \right\|}\nolimits_Z^2 = 1} \right\}, \\ \sigma _{m}^{2}(\eta ) = \mathop {sup}\limits_{w \in H} \left\{ {{{{\left\langle {f,w} \right\rangle }}^{2}}{{\xi }_{m}}[{{{(t_{\eta }^{{(A)}}(w))}}^{2}},{{{(t_{\eta }^{{(L)}}(w))}}^{2}}]:\mathop {\left\| w \right\|}\nolimits_Z^2 = 1} \right\}, \\ \end{gathered} $Теорема 6.3. Пусть выполнено дополнительное условие $N({{A}_{h}}) = 0$. Тогда целевые функционалы
Заметим, что ограничение в задачах (6.12) определяется непрерывно дифференцируемой в $H$ функцией $\left\| w \right\|_{Z}^{2}$. Поэтому теорема 6.3 обосновывает возможность применения известных градиентных методов оптимизации (см., например, [4], [43] и др.) и их реализаций из пакетов MATLAB, SciLab, Python для нахождения величин ${{\rho }_{m}}(\eta )$, ${{\sigma }_{m}}(\eta )$ из (6.12).
7. АПОСТЕРИОРНАЯ ОЦЕНКА ТОЧНОСТИ ПРИ КОНЕЧНОМЕРНОЙ АППРОКСИМАЦИИ ЗАДАЧИ
В этом разделе мы следуем работе [24]. Пусть определена последовательность конечномерных пространств ${{Z}_{n}}$ размерности $n$ и последовательность конечномерных множеств ${{\mathcal{D}}_{n}}$ (${{\mathcal{D}}_{n}} \subset {{Z}_{n}}$), причем:
Применим для решения задачи (2.6) некоторый РА. Пусть для данных $({{F}_{h}},{{u}_{\delta }},h,\delta )$ он дает приближенное решение ${{z}_{\eta }} \in \mathcal{D}$, точность которого оценивается как в формуле (6.1) функцией $\varepsilon (\eta )$. Предположим, что имеется конечномерный вариант этого РА и он позволяет построить по величинам $({{F}_{n}},{{u}_{n}},{{h}_{n}},{{\delta }_{n}})$ элемент ${{z}_{{\eta n}}} \in {{\mathcal{D}}_{n}}$ такой, что ${{z}_{{\eta n}}} \to {{z}_{\eta }}$ в $Z$ при $n \to \infty $. Для апостериорной оценки точности конечномерного приближенного решения ${{z}_{{\eta n}}}$ будем использовать экстремальную задачу: найти такой элемент ${{\tilde {z}}_{{\eta n}}} \in {{\mathcal{D}}_{n}}$, для которого
(7.1)
$\left\| {{{{\tilde {z}}}_{{\eta n}}} - {{z}_{{\eta n}}}} \right\| = sup\left\{ {\left\| {z - {{z}_{{\eta n}}}} \right\|:z \in {{\mathcal{D}}_{n}},{{\Omega }_{n}}[z] \leqslant C{{\Omega }_{n}}[{{z}_{{\eta n}}}],\;\left\| {{{F}_{n}}z - {{u}_{n}}} \right\| \leqslant C\left\| {{{F}_{n}}{{z}_{{\eta n}}} - {{u}_{n}}} \right\|} \right\}\;\mathop = \limits^{{\text{def}}} \;{{\varepsilon }_{n}}(\eta ).$Теорема 7.1. Если множество ${{Z}_{{\Omega \eta }}} = {\text{\{ }}z \in \mathcal{D}:\Omega [z] \leqslant {{R}_{\eta }},\left\| {{{F}_{h}}z - {{u}_{\delta }}} \right\| \leqslant {{\Delta }_{\eta }}{\text{\} }}$ при каждом $\eta $, $0 < \left\| {\eta {\kern 1pt} } \right\| \leqslant {{\eta }_{0}}$ имеет непустую внутренность: $\operatorname{int} {{Z}_{{\Omega \eta }}} \ne \emptyset $, то для этих $\eta $ справедливо соотношение: $li{{m}_{{n \to \infty }}}{{\varepsilon }_{n}}(\eta ) = \varepsilon (\eta )$.
Условие теоремы 7.1 справедливо при достаточно малых $\eta $, например, если выполнены условия (Д). Вид конечномерной апостериорной оценки точности приближенного решения ${{z}_{{\eta n}}}$ в сравнении с конечномерным аналогом ${{\mathcal{P}}_{n}}\bar {z}$ точного решения $\bar {z}$ дает
Теорема 7.2. Если $\bar {z} \in {\text{int}}\,{{Z}_{{\Omega \eta }}}$ для всех $\eta $, $0 < \left\| \eta \right\| \leqslant {{\eta }_{0}}$, то $\left\| {{{\mathcal{P}}_{n}}\bar {z} - {{z}_{{\eta n}}}} \right\| \leqslant {{\varepsilon }_{n}}(\eta )$.
8. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ПО ПРИМЕНЕНИЮ ЭКСТРАОПТИМАЛЬНЫХ РА С АПОСТЕРИОРНЫМ ОЦЕНИВАНИЕМ
8.1. Применение алгоритма 1 для вычисления глобальных оценок точности
Пример 8.1. Обратная ретроспективная задача теплопроводности (диффузии).
Прямая задача имеет вид: найти классическое решение ${v}(x,y,t)$, $(x,y) \in {{\mathbb{R}}^{2}}$, $t \geqslant 0$, задачи Коши
(8.2)
$u(x,y) = \frac{1}{{4\pi (t - \tau ){{a}^{2}}}}\iint\limits_{{{\mathbb{R}}^{2}}} {exp\left\{ { - \frac{{{{{(x - \xi )}}^{2}} + {{{(y - \eta )}}^{2}}}}{{4(t - \tau ){{a}^{2}}}}} \right\}\bar {z}(\xi ,\eta )d\xi d\eta }\;\mathop = \limits^{{\text{def}}} \;A\bar {z},$Пусть функция $u(x,y)$ из уравнения (8.2) известна с относительной ошибкой $\delta $, т.е. задана функция ${{u}_{\delta }}(x,y)$, для которой $\mathop {\left\| {u(x,y) - {{u}_{\delta }}(x,y)} \right\|}\nolimits_{{{L}_{2}}({{R}^{2}})} \leqslant \delta \mathop {\left\| {{{u}_{\delta }}(x,y)} \right\|}\nolimits_{{{L}_{2}}({{R}^{2}})} $. Как в примере 2.3, применим для решения уравнения (8.2) с данными ${\text{\{ }}A,{{u}_{\delta }},\delta {\text{\} }}$ метод регуляризации Тихонова в пространстве $W_{2}^{2}({{\mathbb{R}}^{2}})$ с нахождением параметра регуляризации по принципу невязки. Используем стабилизирующий функционал $\Omega [z] = \mathop {\left\| z \right\|}\nolimits_{W_{2}^{2}}^2 = \mathop {\left\| z \right\|}\nolimits_{{{L}_{2}}}^2 + \mathop {\left\| {{{\Delta }_{2}}z} \right\|}\nolimits_{{{L}_{2}}}^2 $. В разд. 3 3 указано, что такой алгоритм будет экстраоптимальным. Он сводится к нахождению решений $z = z_{\delta }^{\alpha }$ операторного уравнения II рода
вычислению корня $\alpha (\delta ) > 0$ уравнения $B(\alpha ) \equiv \left\| {Az_{\delta }^{\alpha } - {{u}_{\delta }}} \right\| = \bar {C}\delta \left\| {{{u}_{\delta }}} \right\|$, $\bar {C} = {\text{const}} \geqslant 1$, и вычислению приближенного решения ${{z}_{\delta }} = z_{\delta }^{{\alpha (\delta )}}$.Согласно теории из разд. 3, пп. 4.1, 6.1, глобальная апостериорная оценка точности приближенного решения ${{z}_{\delta }}$ получается так. Вычислим величины ${{R}_{\delta }} = C\mathop {\left\| {{{z}_{\delta }}} \right\|}\nolimits_{W_{2}^{2}}^2 $, ${{\Delta }_{\delta }} = C\left\| {A{{z}_{\delta }} - {{u}_{\delta }}} \right\|$ и применим алгоритм 33 к вычислению функции
(8.4)
${{\varepsilon }_{1}}(\delta ) = sup\left\{ {\mathop {\left\| {z - {{z}_{\delta }}} \right\|}\nolimits_{{{L}_{2}}} :z \in W_{2}^{2},\;\mathop {\left\| z \right\|}\nolimits_{W_{2}^{2}}^2 \leqslant {{R}_{\delta }},\;\left\| {Az - {{u}_{\delta }}} \right\| \leqslant {{\Delta }_{\delta }}} \right\},$С вычислительной точки зрения, уравнение (8.3) удобно решать в спектральной форме (как в [18], [19]). Для этого введем двумерное преобразование Фурье $F[z](\omega )$ функции $z({{x}_{1}},{{x}_{2}})$, ${{x}_{1}} = x$, ${{x}_{2}} = y$, в котором $\omega = ({{\omega }_{1}},{{\omega }_{2}})$. Решение уравнения (8.3) с оператором типа свертки $A$ записывается в виде (см. [19]) $z_{\delta }^{\alpha }({{x}_{1}},{{x}_{2}}) = {{F}^{{ - 1}}}\{ F[z_{\delta }^{\alpha }](\omega )\} ({{x}_{1}},{{x}_{2}})$, где
(8.5)
$F[z_{\delta }^{\alpha }](\omega ) = \frac{{F{\text{*}}[K](\omega )F[{{u}_{\delta }}](\omega )}}{{\alpha {{r}^{2}}(\omega ) + {{{\left| {F[K](\omega )} \right|}}^{2}}}},$В алгоритме 1 апостериорной оценки точности при решении задачи (8.4) используются решения ${{z}^{{\mu \nu }}}$ одного и того же операторного уравнения $(E - \mu A{\text{*}}A - \nu \Omega {\text{'}})z = {{z}_{\delta }} - \mu A{\text{*}}{{u}_{\delta }}$, а также функции ${{\gamma }^{2}}(\mu ,\nu ) = \Omega [{{z}^{{\mu \nu }}}]$, ${{\beta }^{2}}(\mu ,\nu ) = \mathop {\left\| {A{{z}^{{\mu \nu }}} - {{u}_{\delta }}} \right\|}\nolimits_{{{L}_{2}}}^2 $, для допустимых значений параметров $\mu ,\nu \geqslant 0$, $\mu + \nu > 0$. Решая это уравнение с помощью преобразования Фурье и учитывая, что $F[\Omega {\text{'}}{\kern 1pt} [z]](\omega ) = {{r}^{2}}(\omega )F[z](\omega )$, получим формулу ${{z}^{{\mu \nu }}} = {{F}^{{ - 1}}}{\text{\{ }}F[{{z}^{{\mu \nu }}}](\omega ){\text{\} }}$, где
Если носитель решения $\bar {z}(x,y)$ лежит в прямоугольнике $\Pi = [ - {{L}_{x}},{{L}_{x}}] \times [ - {{L}_{y}},{{L}_{y}}]$, то можно записать приближенное решение и алгоритм апостериорной оценки его точности в дискретной форме, применяя стандартную процедуру конечномерной аппроксимации, которая подробно описана, например, в [19]. Она использует равномерные сетки ${\text{\{ }}({{x}_{i}},{{y}_{i}}){\text{\} }} = {\text{\{ }}({{\xi }_{i}},{{\eta }_{j}}){\text{\} }} = $ $ = \left\{ {\left( {\left( {i - \tfrac{N}{2}} \right){{\Delta }_{x}},\left( {j - \tfrac{N}{2}} \right){{\Delta }_{y}}} \right)} \right\}$, $i,j = 0,1,\; \ldots ,\;N - 1$, с шагами ${{\Delta }_{x}}$, ${{\Delta }_{y}}$, заданные в $\Pi $; $N$ – четное. При этом в приведенных формулах функции двух переменных $K$, $z$, ${{u}_{\delta }}$ заменяются на матрицы $\hat {K} = [K({{x}_{i}},{{y}_{j}}){{\Delta }_{x}}{{\Delta }_{y}}]$, $\hat {z} = [z({{\xi }_{i}},{{\eta }_{j}})]$, $\hat {u} = [u({{x}_{i}},{{y}_{j}})]$; $i,j = 0,1,\; \ldots ,\;N - 1$, а преобразования Фурье $F[K](\omega )$, $F[z](\omega )$, $F[{{u}_{\delta }}](\omega )$ заменяются на двумерные дискретные преобразования Фурье $\hat {F}(\hat {K})$, $\hat {F}(\hat {z})$, $\hat {F}(\hat {u})$. Множители $\tfrac{1}{{2\pi }}$ заменяются на $\tfrac{1}{N}$.
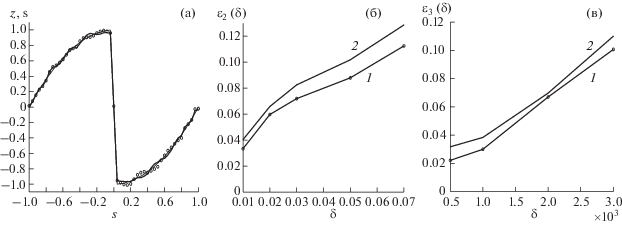
Конкретизируем задачу и возьмем безразмерные параметры уравнения (8.2) такие же, как в [46]: $a = 0.2$, $t = 0.075$, $\tau = 0.05$, ${{L}_{x}} = {{L}_{y}} = 0.5$. Эти величины соответствуют обезразмеренным реальным физическим параметрам ретроспективной обратной задачи диффузии некоторого загрязнителя в водоемах. Для точного модельного решения, показанного на фиг. 1а, приближенные решения ${{z}_{\delta }}(x,y)$ вычислялись для возмущенных данных обратной задачи ${{u}_{\delta }}(x,y)$ с различными уровнями ошибок $\delta $. Точности полученных приближений оценивались путем решения задачи (8.4). Вычисленная зависимость относительной апостериорной точности приближения от $\delta $, т.е функция ${{\varepsilon }_{1}}(\delta ) = {{\mathop {\left\| {\tilde {z}(x,y) - {{z}_{\delta }}(x,y)} \right\|}\nolimits_{{{L}_{2}}({{R}^{2}})} } \mathord{\left/ {\vphantom {{\mathop {\left\| {\tilde {z}(x,y) - {{z}_{\delta }}(x,y)} \right\|}\nolimits_{{{L}_{2}}({{R}^{2}})} } {\mathop {\left\| {{{z}_{\delta }}(x,y)} \right\|}\nolimits_{{{L}_{2}}({{R}^{2}})} }}} \right. \kern-0em} {\mathop {\left\| {{{z}_{\delta }}(x,y)} \right\|}\nolimits_{{{L}_{2}}({{R}^{2}})} }}$, показана на фиг. 1б. Для сравнения там же приведена истинная зависимость относительной ошибки приближенного решения ${{\Delta }_{{{{L}_{2}}}}}(\delta ) = {{\mathop {\left\| {\bar {z}(x,y) - {{z}_{\delta }}(x,y)} \right\|}\nolimits_{{{L}_{2}}({{R}^{2}})} } \mathord{\left/ {\vphantom {{\mathop {\left\| {\bar {z}(x,y) - {{z}_{\delta }}(x,y)} \right\|}\nolimits_{{{L}_{2}}({{R}^{2}})} } {\mathop {\left\| {{{z}_{\delta }}(x,y)} \right\|}\nolimits_{{{L}_{2}}({{R}^{2}})} }}} \right. \kern-0em} {\mathop {\left\| {{{z}_{\delta }}(x,y)} \right\|}\nolimits_{{{L}_{2}}({{R}^{2}})} }}$ от $\delta $. На фиг. 1в показано также решение ${{\tilde {z}}_{\delta }}$ задачи (8.4) при $\delta = 0.03$. Для использованной в расчетах сетки с $N = 256$ погрешность конечномерной аппроксимации оператора $A$ оказалась не существенной при рассмотренных $\delta $.
Фиг. 1.
Пример 8.1. (а) Точное решение; (б) модельная оценка точности ${{\Delta }_{{{{L}_{2}}}}}(\eta )$ – кривая 1 и апостериорная оценка точности ${{\varepsilon }_{1}}(\delta )$ – кривая 2; (в) решение задачи (8.4) для $\delta = 0.03$.

Пример 8.2. Решение линейного интегрального уравнения Фредгольма I рода на классе функций с ограниченной вариацией.
Рассмотрим линейное интегральное уравнение Фредгольма I рода
(8.6)
$Az = \int\limits_{ - 1}^1 {\,\frac{{z(s)dx}}{{1 + 100{{{(s - x)}}^{2}}}}} = u(x),\quad x \in [ - 1,1],$(8.7)
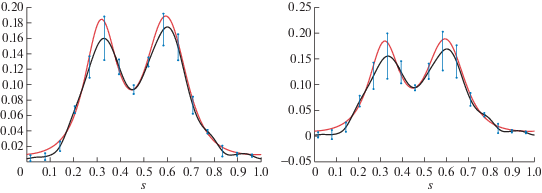
${{\varepsilon }_{2}}(\delta ) = sup\left\{ {\mathop {\left\| {z - {{z}_{\delta }}} \right\|}\nolimits_{{{L}_{2}}} :z \in V[ - 1,1],\;\Omega [z] \leqslant {{R}_{\delta }},\;\left\| {Az - {{u}_{\delta }}} \right\| \leqslant {{\Delta }_{\delta }}} \right\},$Фиг. 2.
(а) Пример 8.2: $\bar {z}$ – тонкая линия, ${{z}_{\delta }}$ – жирная линия, $\mathop {\tilde {z}}\nolimits_\delta $ – кружки. (б) Пример 8.2: модельная оценка точности ${{\Delta }_{{{{L}_{2}}}}}(\delta )$ – кривая 1 и апостериорная оценка точности ${{\varepsilon }_{2}}(\delta )$ – кривая 2. (в) Пример 8.3: модельная оценка точности ${{\Delta }_{{{{L}_{2}}}}}(\delta )$ – кривая 1 и апостериорная оценка точности ${{\varepsilon }_{3}}(\delta )$ – кривая 2.
В этом примере конечномерные операторные уравнения из алгоритма 1 (шаги 1, 2, 4) являются нелинейными. Не останавливаясь на деталях, отметим, что они решались итерационным методом.
Пример 8.3. Решение нелинейной обратной задачи с помощью тихоновской регуляризации второго порядка.
В заключение рассмотрим широко известную модельную нелинейную обратную задачу [47]: зная функции $u(x) \in {{C}^{2}}[0,1]$, $f(x) \in C[0,1]$, найти коэффициент $a(x) \in {{C}^{1}}[0,1]$, $a(x) > 0$, в краевой задаче
Дискретизируем дифференциальное уравнение на равномерной сетке по $x \in [0,1]$ с числом узлов $n = 80$. Тогда прямая задача: по заданной функции $a(x)$ найти классическое решение $u(x)$ краевой задачи (8.8) с известной функцией $f(x)$ – решается в дискретном ее варианте методом прогонки. В результате по сеточной функции $\hat {a}$ можно найти сеточный аналог $\hat {u}$ функции $u(x)$. Обозначим эту процедуру как $\hat {u} = {{F}_{n}}[\hat {a}]$. Для решения обратной задачи применим метод регуляризации Тихонова 2-го порядка с выбором параметра регуляризации по обобщенному принципу невязки. Это сводится к нахождению экстремалей сглаживающего функционала ${{M}^{\alpha }}[\hat {a}] = \alpha \mathop {\left\| {\hat {a}} \right\|}\nolimits_{\mathop {\hat {W}}\nolimits_2^2 }^2 + \mathop {\left\| {{{F}_{n}}(\hat {a}) - \mathop {\hat {u}}\nolimits_\delta } \right\|}\nolimits^2 $, где $\mathop {\left\| {\, \cdot \,} \right\|}\nolimits_{\mathop {\hat {W}}\nolimits_2^2 } $ – конечномерный аналог нормы в $W_{2}^{2}$. Полученное приближенное решение $\mathop {\hat {a}}\nolimits_n^{\alpha (\delta )} $ используем для апостериорной оценки его точности, решая соответствующую задачу вида (6.1). Расчеты сделаны для модельных данных: $a(x) = {{x}^{2}}{{(1 - x)}^{2}} + 0.01$, $u(x) = {{x}^{4}}{{(1 - x)}^{4}}$, а функция $f(x)$ вычислена по ним из (8.8). При этом обратная задача решалась для различных уровней возмущения $\delta $ величины $u(x)$, а $f(x)$ считалась заданной точно. Полученная зависимость ${{\varepsilon }_{3}}(\delta )$ апостериорной оценки точности приближений $a_{n}^{{\alpha (\delta )}}$ в пространстве ${{L}_{2}}$ от $\delta $ представлена на фиг. 2в. Минимизация функционала ${{M}^{\alpha }}[\hat {a}]$ и решение условной экстремальной задачи (6.1) проводилась с помощью стандартных модулей пакета МАТЛАБ.8.2. Применение алгоритма 2 для вычисления локальных оценок точности
Пример 8.4. Апостериорная оценка поточечной точности гладкого решения.
Снова рассмотрим линейное интегральное уравнение (8.6), но уже с точным решением $\bar {z}(s) = {{(1 - {{s}^{2}})}^{2}} \in W_{2}^{1}[ - 1,1]$. Считаем $Z = U = {{L}_{2}}[ - 1,1]$, $\mathcal{D} = W_{2}^{1}[ - 1,1]$ и будем использовать регуляризатор $\Omega [z] = \mathop {\left\| z \right\|}\nolimits_{W_{2}^{1}[ - 1,1]}^2 $. Вычислим по решению $\bar {z}(s)$ правую часть уравнения $u(x)$ и наложим на нее аддитивную нормально распределенную помеху с нулевым средним так, чтобы приближенная правая часть ${{u}_{\delta }}$ имела относительную ошибку ${{\mathop {\left\| {{{u}_{\delta }} - u} \right\|}\nolimits_{{{L}_{2}}[ - 1,1]} } \mathord{\left/ {\vphantom {{\mathop {\left\| {{{u}_{\delta }} - u} \right\|}\nolimits_{{{L}_{2}}[ - 1,1]} } {\mathop {\left\| u \right\|}\nolimits_{{{L}_{2}}[ - 1,1]} }}} \right. \kern-0em} {\mathop {\left\| u \right\|}\nolimits_{{{L}_{2}}[ - 1,1]} }} = \delta $. После дискретизации задачи на равномерных сетках $\left\{ {{{x}_{i}} = {{s}_{i}} = - 1 + 2(i - 1){\text{/}}(N - 1),\,i = 1,\; \ldots ,\;N} \right\}$ с шагом $\hat {h} = 2{\text{/}}(N - 1)$ по $x$, $s$ для $N = 201$ и аппроксимации оператора $A$ по формуле трапеций, решим полученную систему линейных уравнений с приближенными (сеточными) данными
Оценим поточечную ошибку полученного конечномерного приближенного решения $\mathop {\hat {z}}\nolimits_\eta = \mathop {\{ {{{\hat {z}}}_{\eta }}({{s}_{j}})\} }\nolimits_{j = 1}^N $, используя алгоритм 2 для избранных точек сетки с номерами из некоторого множества $\mathcal{M} \subset {\text{\{ }}1,2,\; \ldots ,\;N{\text{\} }}$.
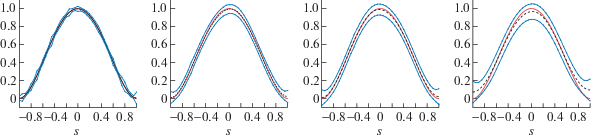
На фиг. 3 изображены точное решение задачи (8.6), приближенные решения для различных значений $\delta $ и полученные в избранных точках сетки ($\dim \mathcal{M} = 41$) апостериорные оценки точности в виде коридоров ошибок $[{{\hat {z}}_{\eta }}({{s}_{i}}) - {{\hat {E}}_{{{{s}_{i}}}}}(\eta ),{{\hat {z}}_{\eta }}({{s}_{i}}) + {{\hat {E}}_{{{{s}_{i}}}}}(\eta )]$ для всех $i \in \mathcal{M}$.
Фиг. 3.
Пример 8.4. Слева направо – результаты для $\delta = 0.01,0.03,0.05,0.07$: точное решение $\bar {z}(s) = {{(1 - {{s}^{2}})}^{2}}$ задачи (8.6) (жирная линия), приближенное решение (пунктир) и коридор ошибок в избранных точках (линии с точками).
Пример 8.5. Оценка точности разрывного решения.
Теперь будем предполагать, что уравнение (8.6) имеет разрывное точное решение $\bar {z}(s) = \operatorname{sign} (s)(1 - \left| s \right|) \in V[ - 1,1]$. Как в примере 8.2, используем для нахождения приближенного решения метод регуляризации Тихонова с функционалом $\Omega [z] = \mathop {\left\| z \right\|}\nolimits_{V[ - 1,1]} = \left| {z( - 1)} \right| + $ $ + \;\left| {z(1)} \right| + \vee _{{ - 1}}^{1}(z)$. Тогда $\bar {z}(s)$ будет единственным в существенном $\Omega $-оптимальным решением задачи (см. [20, гл. 4]). Применим ту же сеточную аппроксимацию, что и в примере 8.4, и заменим функционал $\Omega [z]$ на его сглаженный конечномерный аналог
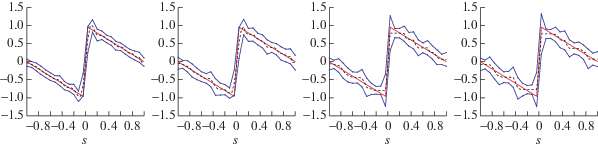
Результаты оценки точности показаны на фиг. 4. Видно, что для рассмотренных $\delta $ точное решение попадает в найденный коридор ошибок около приближенного решения.
Фиг. 4.
Пример 8.5. Слева направо – результаты для $\delta = 0.01$, 0.03, 0.05, 0.07: точное решение $\bar {z}(s) = \operatorname{sign} (s)(1 - \left| s \right|)$ (жирная линия), приближенное решение (пунктир) и коридор ошибок в избранных точках (линии с точками).
Пример 8.6. Двумерная обратная задача.
Теперь рассмотрим хорошо известную задачу продолжения трехмерного потенциального поля ${v}({{x}_{1}},{{x}_{2}},{{x}_{3}})$, создаваемого источниками, которые лежат в полупространстве ${{x}_{3}} < 0$ (см. [18] и др.). В этой задаче требуется по функции $u({{x}_{1}},{{x}_{2}}) = {v}({{x}_{1}},{{x}_{2}},\nu )$ на плоскости ${{x}_{3}} = \nu $ найти функцию $\bar {z}({{x}_{1}},{{x}_{2}}) = {v}({{x}_{1}},{{x}_{2}},\zeta )$ на плоскости ${{x}_{3}} = \zeta $ при условии $0 < \zeta < \nu $. Функции $\bar {z}({{x}_{1}},{{x}_{2}})$ и $u({{x}_{1}},{{x}_{2}})$ связаны равенством $A\bar {z} = u$. Здесь
(8.9)
$A\bar {z} = \frac{{\nu - \zeta }}{{2\pi }}\int {\int\limits_{ - \infty }^{ + \infty } {\frac{{\bar {z}({{s}_{1}},{{s}_{2}})d{{s}_{1}}d{{s}_{2}}}}{{{{{[{{{({{x}_{1}} - {{s}_{1}})}}^{2}} + {{{({{x}_{2}} - {{s}_{2}})}}^{2}} + {{{(\nu - \zeta )}}^{2}}]}}^{{3/2}}}}}\;\mathop = \limits^{{\text{def}}} \;{{T}_{{\nu - \zeta }}}\bar {z}.} } $(8.10)
$\bar {z} = {{T}_{\zeta }}\bar {w} = \frac{\zeta }{{2\pi }}\int {\int\limits_{ - \infty }^{ + \infty } {\frac{{\bar {w}({{\xi }_{1}},{{\xi }_{2}})d{{\xi }_{1}}d{{\xi }_{2}}}}{{{{{[{{{({{s}_{1}} - {{\xi }_{1}})}}^{2}} + {{{({{s}_{2}} - {{\xi }_{2}})}}^{2}} + {{\zeta }^{2}}]}}^{{3/2}}}}},} } $Пусть правая часть $u({{x}_{1}},{{x}_{2}})$ уравнения $A\bar {z} = u$ известна с ошибкой $\delta $, т.е. задана функция ${{u}_{\delta }}$ такая, что $\mathop {\left\| {{{u}_{\delta }} - u} \right\|}\nolimits_{{{L}_{2}}({{\mathbb{R}}^{2}})} \leqslant \delta $. Как в примере 8.1, используем для решения этого уравнения с данными ${\text{\{ }}A,{{u}_{\delta }},\delta {\text{\} }}$ метод регуляризации Тихонова в форме (8.3) с выбором параметра регуляризации $\alpha = \alpha (\delta )$ по принципу невязки [14]. В итоге приближенное решение имеет вид ${{z}_{\delta }} = z_{\delta }^{{\alpha (\delta )}}(s)$.
Метод регуляризации снова применим в спектральной форме, так что приближенное решение находится из (8.5) с $K = K({{x}_{1}},{{x}_{2}}) = \tfrac{{\nu - \zeta }}{{2\pi }}{{[{{({{x}_{1}})}^{2}} + {{({{x}_{2}})}^{2}} + {{(\nu - \zeta )}^{2}}]}^{{ - 3/2}}}$ и с $r(\omega ) = \sqrt {1 + {{{(\omega _{1}^{2} + \omega _{2}^{2})}}^{2}}} $, $F{\text{*}}[{\kern 1pt} \cdot {\kern 1pt} ](\omega )$.
Используя теорему Планшереля, можно, как и в примере 8.1, выписать функционалы $\mathop {\left\| {Az - {{u}_{\delta }}} \right\|}\nolimits_{{{L}_{2}}} $ и $\Omega [z]$, используемые при выборе параметра регуляризации и в алгоритме 2 вычисления апостериорной оценки ${{E}_{s}}(\eta )$.
Аналогично примеру 8.1 проведем и дискретизацию задачи, используя двумерную равномерную сетку $\hat {x} = {{\hat {x}}_{1}} \times {{\hat {x}}_{2}} = {\text{\{ }}({{x}_{{1i}}},{{x}_{{2j}}}){\text{\} }}$, $i,j = 0,1,\; \ldots ,\;N - 1$, с шагами $\Delta {{x}_{1}}$, $\Delta {{x}_{2}}$, заданную в области $\Pi = [0,{{a}_{1}}] \times [0,{{a}_{2}}]$ при “достаточно больших” ${{a}_{{1,2}}} > 0$.
Такой подход был применен для решения уравнения $A\bar {z} = u$ при $\zeta = 0.15$, $\nu = 0.25$ с точным решением $\bar {z}({{x}_{1}},{{x}_{2}})$, вычисляемым по формуле (8.10) для функции источника $\bar {w}({{\xi }_{1}},{{\xi }_{2}})\;{\text{ = }}\;{\text{20}}\chi ({{T}_{1}}) + \chi ({{T}_{2}})$ $\bar {w}({{\xi }_{1}},{{\xi }_{2}})\;{\text{ = }}\;{\text{20}}\chi ({{T}_{1}}) + \chi ({{T}_{2}})$. Здесь множества ${{T}_{1}}$, ${{T}_{2}}$ задаются как ${{T}_{1}} = {\text{\{ }}({{x}_{1}},{{x}_{2}}):{{({{x}_{1}} - 0.32)}^{2}} + {{({{x}_{2}} - 0.32)}^{2}} < 0.0004{\text{\} }}$ ${{T}_{1}} = {\text{\{ }}({{x}_{1}},{{x}_{2}}):{{({{x}_{1}} - 0.32)}^{2}} + {{({{x}_{2}} - 0.32)}^{2}} < 0.0004{\text{\} }}$, ${{T}_{2}} = {\text{\{ }}({{x}_{1}},{{x}_{2}}):{{({{x}_{1}} - 0.6)}^{2}} + ({{x}_{1}} - 0.6)({{x}_{2}} - 0.6) + {{({{x}_{2}} - 0.6)}^{2}} < 0.01{\text{\} }}$ ${{T}_{2}} = {\text{\{ }}({{x}_{1}},{{x}_{2}}):{{({{x}_{1}} - 0.6)}^{2}} + ({{x}_{1}} - 0.6)({{x}_{2}} - 0.6) + {{({{x}_{2}} - 0.6)}^{2}} < 0.01{\text{\} }}$, а $\chi ( \cdot )$ есть характеристическая функция множества. Вид точного решения в области $\Pi = [0,\;1] \times [0,\;1]$ представлен на фиг. 5 слева. По этому решению с помощью вытекающей из (8.9) формулы $u = {{F}^{{ - 1}}}{\text{\{ }}F[K](\omega )F[\bar {z}](\omega ){\text{\} }}$ вычислялась функция $u({{x}_{1}},{{x}_{2}})$ – модельная точная правая часть уравнения $A\bar {z} = u$. Расчеты велись на “мелких” сетках $\hat {x} = \hat {\omega }$ с $N = 512$. Затем функция $u({{x}_{1}},{{x}_{2}})$ возмущалась нормально распределенной случайной ошибкой так, что полученная приближенная правая часть уравнения ${{u}_{\delta }}({{x}_{1}},{{x}_{2}})$ удовлетворяла неравенству ${{\left\| {u - {{u}_{\delta }}} \right\|}_{{{{L}_{2}}(\Pi )}}}\left\| {{{u}_{\delta }}} \right\|_{{{{L}_{2}}(\Pi )}}^{{ - 1}} \leqslant \bar {\delta }$, где число $\bar {\delta }$ есть уровень относительной ошибки приближенных данных ${{u}_{\delta }}({{x}_{1}},{{x}_{2}})$ задачи. Обратная задача нахождения функции $\bar {z}({{x}_{1}},{{x}_{2}})$ по функции ${{u}_{\delta }}({{x}_{1}},{{x}_{2}})$ решалась на относительно “грубых” сетках $\hat {x} = \hat {\omega }$ с $N = 128$ для различных уровней погрешности данных $\bar {\delta }$. При этом погрешность конечномерного приближения оператора была пренебрежимой по сравнению с ошибками правой части уравнения. Затем производилось поточечное оценивание точности полученного приближенного решения с использованием алгоритма 2.
Фиг. 5.
Пример 8.6. Слева: точное решение двумерной обратной задачи с оператором (8.9) и линия, на которой оценивается точность. Справа: сужение на отрезок $\mathfrak{L}$ точного решения (жирная линия), соответствующее приближенное решение (тонкая линия) и коридор ошибок в избранных точках для $\bar {\delta } = 0.01$.
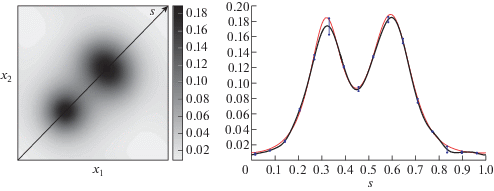
Оценки вычислялись для точек (${{x}_{1}}$, ${{x}_{2}}$), лежащих на отрезке прямой $\mathcal{L}$, который отмечен на фиг. 5 (слева) жирной линией. Результаты решения обратной задачи и оценки его точности на отрезке $\mathcal{L}$ отображены на фиг. 5 (справа) и фиг. 6. Здесь тонкой линией изображено сужение точного решения $\bar {z}({{x}_{1}},{{x}_{2}})$ на отрезок $\mathcal{L}$, а жирной линией – аналогичное сужение ${{\hat {z}}_{\eta }}(s)$, $s \in \mathcal{L}$, полученного приближенного решения. Координаты точек $s$ отнесены к длине отрезка $s \in \mathcal{L}$. Вертикальные отрезки с точками изображают “коридор ошибок” $[{{\hat {z}}_{\eta }}({{s}_{i}}) - {{\hat {E}}_{{{{s}_{i}}}}}(\eta ),{{\hat {z}}_{\eta }}({{s}_{i}}) + {{\hat {E}}_{{{{s}_{i}}}}}(\eta )]$ для избранных точек ${{s}_{i}} \in \mathcal{L}$.
8.3. Применение алгоритма апостериорного оценивания для линейных задач
Приведем результаты апробации методов апостериорной оценки точности из разд. 6.3, основанных на вычислении величин ${{\rho }_{n}}(\eta )$ и ${{\sigma }_{n}}(\eta )$, для типичной обратной задачи – примера 8.6. Уравнение $Az = u$ с оператором (8.9) решалось по той же схеме для $\zeta = 0.15$, $\nu = 0.25$ в области $\Pi = [0,1] \times [0,1]$. Точное решение $z = \bar {z}({{x}_{1}},{{x}_{2}})$ вычислялось по формуле (8.10) для функции источника $w = \bar {w}({{\xi }_{1}},{{\xi }_{2}}) = \chi ({{T}_{1}}) + 2\chi ({{T}_{2}})$. Здесь множества ${{T}_{1}}$, ${{T}_{2}}$ задаются как ${{T}_{1}} = {\text{\{ }}({{x}_{1}},{{x}_{2}}):{{({{x}_{1}} - 0.32)}^{2}}$ + + ${{({{x}_{2}} - 0.32)}^{2}} < 0.01{\text{\} }}$, ${{T}_{2}} = {\text{\{ }}({{x}_{1}},{{x}_{2}}):{{({{x}_{1}} - 0.6)}^{2}}$ – $({{x}_{1}} - 0.6)({{x}_{2}} - 0.6)$ + ${{({{x}_{2}} - 0.6)}^{2}} < 0.01{\text{\} }}$, а $\chi ( \cdot )$ есть характеристическая функция множества. По этому решению, как в примере 8.6, по формуле $u = {{F}^{{ - 1}}}{\text{\{ }}F[K](\omega )F[\bar {z}](\omega ){\text{\} }}$ вычислялась функция $u({{x}_{1}},{{x}_{2}})$ – модельная точная правая часть уравнения $A\bar {z} = u$. Расчеты велись на сетках $\hat {x} = \hat {\omega }$ с $N = 512$. Функция $u({{x}_{1}},{{x}_{2}})$ возмущалась нормально распределенной случайной ошибкой так, что полученная приближенная правая часть уравнения ${{u}_{\delta }}({{x}_{1}},{{x}_{2}})$ удовлетворяла неравенству ${{\left\| {u - {{u}_{\delta }}} \right\|}_{{{{L}_{2}}(\Pi )}}}\left\| {{{u}_{\delta }}} \right\|_{{{{L}_{2}}(\Pi )}}^{{ - 1}} \leqslant \tilde {\delta }$, где число $\tilde {\delta }$ есть уровень относительной ошибки приближенных данных ${{u}_{\delta }}({{x}_{1}},{{x}_{2}})$ задачи. Обратная задача приближенного нахождения функции $\bar {z}({{x}_{1}},{{x}_{2}})$ по функции ${{u}_{\delta }}({{x}_{1}},{{x}_{2}})$ решалась с помощью метода регуляризации на сетках $\hat {x} = \hat {\omega }$ с $N = 128$ для различных уровней погрешности данных $\tilde {\delta }$. Затем по предложенной в разд. 6.3 методике вычислялась глобальная апостериорная оценка точности ${{\rho }_{n}}(\tilde {\delta })$. Вычислялась также апостериорная оценка точности приближенного нахождения среднего значения решения обратной задачи в области ${{T}_{1}}$, т.е. локальная апостериорная оценка ${{\sigma }_{n}}(\tilde {\delta })$ для функционала $\left\langle {f,z} \right\rangle = \tfrac{1}{{\operatorname{mes} ({{T}_{1}})}}\int_{{{T}_{1}}} z (s)ds$. В расчетах и, в частности, при максимизации в задачах (6.12), использовались стандартные функции пакета SciLab.
Поскольку расчеты зависят от конкретных реализаций случайных ошибок данных, в табл. 1 приводятся результаты, усредненные по 40 реализациям этих ошибок.
Таблица 1
| $\tilde {\delta }$ | 0.001 | 0.005 | 0.01 | 0.03 | 0.05 | 0.07 |
|---|---|---|---|---|---|---|
| $\Delta $ | 0.0063 | 0.0201 | 0.0325 | 0.0690 | 0.0972 | 0.1262 |
| $\mathop {\bar {\rho }}\nolimits_n $ | 0.0064 | 0.0202 | 0.0331 | 0.0715 | 0.1018 | 0.1404 |
| ${{\Delta }_{f}}$ | 0.0034 | 0.0103 | 0.0181 | 0.0404 | 0.0533 | 0.0554 |
| $\mathop {\bar {\sigma }}\nolimits_n $ | 0.0034 | 0.0103 | 0.0182 | 0.0405 | 0.0535 | 0.0557 |
В первой строке даны значения уровней $\tilde {\delta }$ относительной погрешности данных задачи. Во второй строке представлены величины истинных относительных ошибок приближенных решений, вычисляемые по известному модельному решению как $\Delta = \tfrac{{{{{\left\| {\bar {z} - {{z}_{\delta }}} \right\|}}_{{{{L}_{2}}(\Pi )}}}}}{{{{{\left\| {\bar {z}} \right\|}}_{{{{L}_{2}}(\Pi )}}}}}$. В третьей строке показаны относительные глобальные апостериорные оценки точности приближенных решений: $\mathop {\bar {\rho }}\nolimits_n = \tfrac{{{{\rho }_{n}}(\tilde {\delta })}}{{{{{\left\| {\bar {z}} \right\|}}_{{{{L}_{2}}(\Pi )}}}}}$, полученные с помощью метода из разд. 6.3. В четвертой и пятой строках представлены истинные относительные ошибки ${{\Delta }_{f}} = \tfrac{{\left| {\left\langle {f,{{z}_{\delta }} - \bar {z}} \right\rangle } \right|}}{{\left| {\left\langle {f,\bar {z}} \right\rangle } \right|}}$ вычисления функционала и соответствующие относительные локальные апостериорные оценки ошибки $\mathop {\bar {\sigma }}\nolimits_n = \tfrac{{{{\sigma }_{n}}(\tilde {\delta })}}{{\left| {\left\langle {f,\bar {z}} \right\rangle } \right|}}$. Можно видеть, что глобальные апостериорные оценки весьма близки к истинным точностям полученных приближений, особенно для данных с малым уровнем возмущения $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta } $. Локальные апостериорные оценки оказались еще более близкими к истинным точностям, причем для всех рассмотренных уровней погрешности данных. Аналогичные результаты получались и для других модельных задач.
Отметим, что метод апостериорной оценки точности в линейных обратных задачах из разд. 6.3 является гораздо более быстродействующим (в среднем, в 3–5 раз, в зависимости от решаемой задачи), чем более общие алгоритмы 1, 2. Например, для рассматриваемой модельной задачи оценка $\mathop {\bar {\rho }}\nolimits_n $ получалась в 5 раз быстрее.
В заключение укажем, что рассмотренные в статье экстраоптимальные методы решения некорректных задач и апостериорные оценки качества (точности) их приближенных решений неоднократно использовались при решении практических задач и показали высокую эффективность. В этой связи упомянем, например, работы [48]–[51].
Список литературы
Бакушинский А.Б., Гончарский А.В. Итеративные методы решения некорректных задач. М.: Наука, 1989.
Бакушинский А.Б., Кокурин М.Ю. Итерационные методы решения некорректных операторных уравнений с гладкими операторами. М.: Едиториал УРСС, 2002.
Вайникко Г.М., Веретенников А.Ю. Итерационные процедуры в некорректных задачах. М.: Наука, 1986.
Васильев Ф.П. Методы оптимизации. Кн. 1, 2. М.: Изд. МЦНМО, 2011.
Васин В.В., Агеев А.Л. Некорректные задачи с априорной информацией. Екатеринбург: Наука, 1993.
Иванов В.К., Васин В.В., Танана В.П. Теория линейных некорректных задач и ее приложения. М.: Наука, 1978. 206 с.
Engl H.W., Hanke M., NeubauerA. Regularization of Inverse Problems. Dordrecht: Kluwer Academic Publ., 1996.
Kabanikhin S.I., Satybaev A.D., Shishlenin M.A. Direct Methods of Solving Multidimensional Inverse Hyperbolic Problems. Utrecht, VSP, 2004.
Кабанихин С.И. Обратные и некорректные задачи. Новосибирск: Сибирское научное издательство, 2009.
Korolev Yu.M., Yagola A.G. On inverse problems in partially ordered spaces with a priori information // J. Inverse and III-posed Problems. 2012. V. 20. Issue 4. P. 567–573.
Лаврентьев М.М., Романов В.Г., Шишатский С.П. Некорректные задачи математической физики и анализа. М.: Наука, 1980.
Леонов А.С. Решение некорректно поставленных обратных задач. Очерк теории, практические алгоритмы и демонстрации в МАТЛАБ. М.: Либроком, 2010.
Лисковец О.А. Вариационные методы решения неустойчивых задач. Минск: Наука и техн., 1981.
Морозов В.А. Регулярные методы решения некорректно поставленных задач. М.: Наука, 1987.
Осипов Ю.С., Васильев Ф.П., Потапов М.М. Основы метода динамической регуляризации. М.: Изд-во МГУ, 1999.
Prilepko A.I., Orlovsky D.G., Vasin I.A. Methods for solving inverse problems in mathematical physics. New York–Basel: Marcel Dekker inc., 2000.
Танана В.П. Методы решения операторных уравнений. М.: Наука, 1981.
Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979.
Тихонов А.Н., Гончарский А.В., Степанов В.В., Ягола А.Г. Численные методы решения некорректных задач. М.: Наука, 1990.
Тихонов А.Н., Леонов А.С., Ягола А.Г. Нелинейные некорректные задачи. М.: КУРС, 2017.
Ягола А.Г., Степанова И.Э., Титаренко В.Н., Ван Я. Обратные задачи и методы их решения. Приложения к геофизике. М.: Бином, 2014.
Леонов А.С. Об апостериорных оценках точности решения линейных некорректно поставленных задач и экстраоптимальных регуляризующих алгоритмах // Вычисл. методы и программирование. 2010. Т. 11. № 1. С. 14–24.
Леонов А.С. Экстраоптимальные апостериорные оценки точности решения некорректных задач продолжения потенциальных геофизических полей // Физика Земли. 2011. № 6. С. 69–78.
Леонов А.С. Апостериорные оценки точности решения некорректно поставленных обратных задач и экстраоптимальные регуляризующие алгоритмы их решения // Сиб. журн. выч. матем. 2012. Т. 15. № 1. С. 85–102.
Leonov A.S. Extra-optimal methods for solving ill-posed problems // J. Inverse and III-posed Problems. 2012. V. 20. Issue 5–6. P. 637–665.
Leonov A.S. Locally extra-optimal regularizing algorithms // J. Inverse and III-posed Problems. 2014. V. 22. Issue 5. P. 713–737.
Леонов А.С. Локально экстраоптимальные регуляризующие алгоритмы и апостериорные оценки точности для некорректных задач с разрывными решениями // Журн. вычисл. матем. и матем. физ. 2016. Т. 56. № 1. С. 3–15.
Леонов А.С. Регуляризующие алгоритмы с оптимальным и экстраоптимальным качеством // Сиб. журн. вычисл. матем. 2016. Т. 19. № 4. С. 371–383.
Гапоненко Ю.Л., Винокуров В.А. Апостериорные оценки решения некорректных обратных задач // Докл. АН СССР. 1982. Т. 263. № 2. С. 277–280.
Ягола А.Г., Дорофеев К.Ю. Метод расширяющихся компактов решения некорректных задач при условии истокопредставимости // Вестн. Моск. ун-та. Сер. 3. Физика. Астрономия. 1999. № 2. С. 64–66.
Дорофеев К.Ю., Титаренко В.Н., Ягола А.Г. Алгоритмы построения апостериорных оценок погрешностей для некорректных задач // Ж. вычисл. матем. и матем. физ. 2003. Т. 43. № 1. С. 12–25.
Ягола А.Г., Николаева Н.Н., Титаренко В.Н. Оценка погрешности решения уравнения Абеля на множествах монотонных и выпуклых функций // Сиб. журн. вычисл. матем. 2003. Т. 6. № 2. С. 171–180.
Titarenko V.N., Yagola A.G. The problems of linear and quadratic programming for ill-posed problems on some compact sets // J. Inverse and Ill-posed Problems. 2003. V. 11. № 3. P. 311–328.
Бакушинский А.Б. Апостериорные оценки точности для приближенных решений нерегулярных операторных уравнений // Докл. АН. 2011. Т. 437. № 4. P. 439–440.
Bakushinsky A.B., Smirnova A., Liu Hui. A posteriori error analysis for unstable models // J. Inverse and III-posed Problems. 2012. V. 20. Issue 4. P. 411–428.
Леонов А.С. Новый алгоритм апостериорной оценки точности приближенных решений линейных некорректных задач // Ж. вычисл. матем. и матем. физ. 2019. Т. 59. № 2. С. 193–200.
Leonov A.S., Yanfei Wang, Yagola A.G. Piecewise uniform regularization for the inverse problem of microtomography with a-posteriori error estimate // Inverse Problems in Science and Engineering. 2018. https://doi.org/10.1080/17415977.2018.1561676
Леонов А.С. Методы решения некорректных экстремальных задач, обладающие оптимальным и экстраоптимальным качеством // Матем. заметки. 2019. Т. 105. № 3. С. 406–420.
Guisti E. Minimal surfaces and functions of bounded variation. Boston, Basel, Stuttgart: Birkhauser, 1984.
Wernecke S.J., D’Addario L.R. Maximum entropy image reconstruction // IEEE Trans. Comput. 1977. C. 26. P. 351–364.
Леонов А.С. Поточечно экстраоптимальные регуляризующие алгоритмы // Вычисл. методы и программирование. 2013. Т. 14. С. 215–228.
Иванов В.К., Королюк Т.И. Об оценке погрешностей при решении линейных некорректно поставленных задач // Журн. вычисл. матем. и матем. физ. 1969. Т. 9. № 1. С. 30–41.
Фиакко А., Мак-Кормик Г. Нелинейное программирование. Методы последовательной безусловной минимизации. М.: Мир, 1972.
Хилл Э. Функциональный анализ и полугруппы. М.: Изд-во иностр. лит., 1951.
Леонов А.С. Численная реализация специальных регуляризующих алгоритмов для решения одного класса некорректных задач с истокообразно представимыми решениями // Сиб. журн. вычисл. матем. 2001. Т. 4. № 3. С. 269–280.
Леонов А.С. Об устранении насыщения точности регуляризующих алгоритмов // Сиб. журн. вычисл. матем. 2008. Т. 11. № 2. С. 167–186.
Chavent G. Non Linear Least Squares For Inverse Problems. Scientific Computation. NY: Springer, 2009.
Leonov A.S., Sorokin V.N. Upper bound of errors in solving the inverse problem of identifying a voice source // Acoustical Physics. 2017. V. 63. № 5. P. 532–545.
Leonov A.S., Sharov A.N., Yagola A.G. A posteriori error estimates for numerical solutions to inverse problems of elastography // Inverse Problems in Science and Engineering. 2017. V. 25. Issue 1. P. 114–128.
Leonov A.S., Sharov A.N., Yagola A.G. Solution of the inverse elastography problem for parametric classes of inclusions with a posteriori error estimate // J. Inverse Ill-Posed Probl. 2018. V. 26. Issue 4. P. 493–499.
Sorokin V.N., Leonov A.S. Multisource Speech Analysis for Speaker Recognition // Pattern recognition and image analysis. 2019. V. 29. № 1. P. 181–193.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики