1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 60, № 6, 2020

Журнал вычислительной математики и математической физики, 2020, T. 60, № 6, стр. 1053-1065

Применение нейронных сетей в нелинейных обратных задачах геофизики

Е. А. Оборнев 1, И. Е. Оборнев 2, Е. А. Родионов 1, М. И. Шимелевич 1, *

1 Российский государственный геологоразведочный университет
117485 Москва, ул. Миклухо-Маклая, 23, Россия

2 МГУ, Институт ядерной физики
119991 Москва, Ленинские горы, Россия

* E-mail: shimelevich-m@yandex.ru

Поступила в редакцию 20.01.2020
После доработки 20.01.2020
Принята к публикации 11.02.2020

Полный текст (PDF)

Аннотация

Нейронные сети широко используются при решении различного рода задач интерпретации и обработки геофизических данных. В настоящей работе рассматриваются вопросы применения аппроксимационного нейросетевого метода для решения обратных, в том числе многокритериальных задач геофизики, которые сводятся к нелинейному операторному уравнению I рода (соответственно к системе операторных уравнений). Аппроксимационный нейросетевой метод заключается в построении приближенного обратного оператора задачи с помощью нейросетевых аппроксимационных конструкций (MLP сетей) на основе заранее построенного множества опорных решений прямых и обратных задач. Приводится обзор применения aппроксимационного нейросетевого метода при решении обратных нелинейных задач геофизики. Рассматриваются методы оценки практической неоднозначности (погрешности) приближенных решений многокритериальных обратных задач. Приводятся результаты авторов по решению аппроксимационным нейросетевом методом обратной двухкритериальной 2D задачи гравиметрии в комплексе с магнитометрией. Библ. 50. Фиг. 1. Табл. 2.

Ключевые слова: обратная задача, аппроксимация, априорные и апостериорные оценки, нейронные сети, комплексирование, многокритериальная обратная задача, большая размерность.

ВВЕДЕНИЕ

Одно из важнейших практических приложений нейронных сетей (НС) связано с их аппроксимационными и интерполяционными свойствами, что делает их эффективным инструментом задач вычислительной математики. Начиная с 90-х годов прошлого столетия, нейронные сети начинают применяться при решении обратных коэффициентных задач математической физики и, в частности, задач геофизики. В этих методах неизвестный обратный оператор задачи представляется в виде аппроксимационной конструкции (нейронной сети) с неопределенными коэффициентами, которые вычисляются в процессе обучения нейросети на предварительно построенном обучающем множестве опорных решений прямых (а значит, и обратных) задач (так называемом “банке решений”). С помощью построенного таким образом обратного нейросетевого оператора (НС аппроксиматора) может быть получено интерполяционное решение обратной задачи для произвольных входных данных, не принадлежащих обучающему множеству, сравнительно быстро (обычно за первые секунды). Данный метод называют аппроксимационным нейросетевым (АНС) методом. Здесь уместна аналогия АНС метода инверсии на множестве опорных решений с механизмами обработки изображений головным мозгом человека: считается, что полученное за единицу времени на сетчатке неполное изображение окружающей среды, состоящее из конечного числа элементов (в рассматриваемом случае – известных решений обратной задачи), мозг обрабатывает (нейросеть интерполирует и экстраполирует) и выдает некоторое “полное” изображение (ответ нейросети).

Нейронные сети широко используются при решении различного рода задач интерпретации и обработки геофизических данных. В настоящей работе мы ограничиваемся рассмотрением НС методов применительно к проблеме решения нелинейных обратных задач геофизики, в том числе многокритериальных, которые сводятся к нелинейному операторному уравнению I рода (соответственно к системе операторных уравнений). Дается краткое описание НС методов поиска приближенных решений операторных уравнений с оценкой практической неоднозначности (погрешности) получаемых решений; приводится обзор применения этих методов в литературе. В заключение предоставляются новые результаты авторов, связанные с применением АНС метода для решения обратной двухкритериальной 2D задачи гравиметрии в комплексе с магнитометрией, которые ранее не рассматривались в известных авторам публикациях.

1. НЕЛИНЕЙНЫЕ ОБРАТНЫЕ ЗАДАЧИ ГЕОФИЗИКИ

Многие обратные задачи геофизики сводятся к решению нелинейного операторного уравнения I рода вида [1], [2]:

(1.1)
${Ag = f,\quad g \in {{G}_{1}}}\; \subset G,\quad f \in F,$
где $G[\Omega ]$ – нормированное пространство искомых характеристик среды $g$, определенных в исследуемой области $\Omega $, $F[{{\Omega }_{1}}]$ – нормированное пространство данных (характеристик $f$ геофизического поля), определенных на границе ${{\Omega }_{1}}$ области $\Omega $; $A$ – заданный непрерывный оператор прямой задачи, действующий из $G$ в $F$; ${{G}_{1}}[\Omega ]$ – множество допустимых решений обратной задачи, определяемое с учетом естественных априорных ограничений. При условии непрерывной взаимно-однозначности оператора $A$ (т.е., когда доказана единственность решения уравнения (1.1) при точных данных) и компактности множества ${{G}_{1}}$ задача решения уравнения (1.1) относится к классу условно-корректных обратных задач, которые являются реальной математической моделью для большинства задач геофизики. К нелинейному уравнению вида (1.1) сводятся следующие основные обратные задачи геофизики:

• структурные обратные задачи потенциальных полей гравиметрии и магнитометрии, в которых требуется определить геометрию поверхности рудных тел или границ пластов при известных фиксированных значениях плотности и намагниченности [3], [4], на основе характеристик соответствующего поля, заданных в области ${{\Omega }_{1}}$. Вопросы единственности решения обратных задач гравиметрии и магнитометрии рассмотрены в [4]–[6] и ряде других работ;

• коэффициентные обратные задачи электромагнитных полей, используемых в электроразведке, где искомой величиной является удельная электропроводность среды (в более общих случаях – магнитная и диэлектрическая проницаемости) [7]–[9] при заданных в области ${{\Omega }_{1}}$ характеристиках электромагнитного поля. Вопросы единственности решения обратных задач электроразведки рассмотрены в [10];

• коэффициентные обратные задачи сейсмических упругих полей и их различных приближений, используемых в сейсморазведке [2], [7], [11], [12], в которых искомыми являются скоростные характеристики сред при заданных в области ${{\Omega }_{1}}$ характеристиках сейсмического поля. Некоторые вопросы единственности решения обратных задач сейсморазведки рассмотрены в [2], [9].

Операторами прямых задач являются дифференциальные операторы решения соответствующих краевых (начально-краевых) задач, или эквивалентные им интегральные операторы, рассмотренные в указанных выше работах.

Для приближенных решений условно-корректной задачи (1.1) могут быть определены априорные и апостериорные оценки погрешности решения, которые являются функциями погрешности $\delta $ правой части. Среди априорных оценок наиболее распространенными являются оценки, основанные на использовании модуля непрерывности обратного оператора [2]:

(1.2)
$\beta (\eta ) = \max \left\{ {{{{\left\| {g{\text{'}} - g} \right\|}}_{G}}\,{\text{:}}\,g,\;g{\text{'}} \in {{G}_{1}},\;{{{\left\| {Ag{\text{'}} - Ag} \right\|}}_{F}} \leqslant \eta } \right\}.$
Если ${{g}_{T}}$ – точное решение (1.1) при точной правой части ${{f}_{T}} = A{{g}_{T}}$, а ${{g}_{\delta }}$ – приближенное решение ${{\left\| {A{{g}_{\delta }} - f} \right\|}_{F}} \leqslant \delta $, полученное для приближенной правой части $f$, заданной с погрешностью $\delta $, ${{\left\| {f - {{f}_{T}}} \right\|}_{F}} \leqslant \delta $, то справедливо неравенство [2]:
${{\left\| {{{g}_{\delta }} - g_{T}^{{}}} \right\|}_{G}} \leqslant \beta (2\delta ).$
Для оценки погрешности фиксированного приближенного решения ${{g}_{\delta }}$, найденного с невязкой $ \leqslant \delta $ при фиксированной правой части $f \in F$ уравнения (1.1), может быть использована следующая величина [13]:
${{\beta }_{1}}(\delta ) = \max \left\{ {{{{\left\| {g{\text{'}} - {{g}_{\delta }}} \right\|}}_{G}}\,{\text{:}}\,g{\text{'}} \in {{G}_{1}},\;{{{\left\| {Ag{\text{'}} - f} \right\|}}_{F}} \leqslant \delta } \right\}.$
В некоторых случаях полезно использовать апостериорную оценку $\beta _{1}^{*}(\delta )$, не зависящую от найденного решения ${{g}_{\delta }}$ (диаметр множества $\delta $-эквивалентных решений):
(1.3)
$\beta _{1}^{*}(\delta ) = \max \left\{ {{{{\left\| {g{\text{'}} - {{g}_{\delta }}} \right\|}}_{G}}\,{\text{:}}\,g{\text{'}},\;{{g}_{\delta }} \in {{G}_{1}},\;{{{\left\| {Ag{\text{'}} - f} \right\|}}_{F}} \leqslant \delta ,\;{{{\left\| {A{{g}_{\delta }} - f} \right\|}}_{F}} \leqslant \delta } \right\}.$
Для рассмотренных оценок выполняются неравенства
${{\left\| {{{g}_{\delta }} - g_{T}^{{}}} \right\|}_{G}} \leqslant {{\beta }_{1}}(\delta ) \leqslant \beta _{1}^{*}(\delta ) \leqslant \beta (2\delta ).$
Если величина погрешности $\delta $ правой части неизвестна (что, как правило, имеет место, в задачах геофизики), то могут быть получены априорные и апостериорные оценки (характеристики) практической неоднозначности ${{\beta }_{1}}({{\delta }_{f}})$, $\beta _{1}^{*}({{\delta }_{f}})$, $\beta (2{{\delta }_{f}})$ решений ${{g}_{{\delta f}}}$, получаемых с некоторой фактической невязкой ${{\delta }_{f}}$ [14].

Для условно-корректной обратной задачи, помимо рассмотренных выше скалярных оценок неоднозначности, могут быть получены также локальные оценки неоднозначности для выделенных подобластей ${{\Omega }_{i}} \subset \Omega $ исследуемой области, которые более детально и дифференцированно оценивают степень неоднозначности решений обратной задачи с учетом глубины и других особенностей расположения рассматриваемой подобласти ${{\Omega }_{i}}$ [14].

1.1. Многокритериальные обратные задачи

В геофизической практике в большинстве случаев проводится комплексная интерпретация измеренных данных с использованием различных типов геофизических полей (критериев инверсии). Комплексирование (совместная инверсия) может проводиться в пределах одного метода, или с использованием полей различной физической природы [8], [15], [16]. Например, двухкритериальная обратная задача в пределах одного геофизического метода возникает при определении удельной электропроводности среды с использованием различных типов $TM$, $TE$ мод 2D электромагнитного (магнитотеллурического) поля [8], [17], при этом для каждого типа поля доказана единственность решения обратной задачи. Схожая обратная задача рассмотрена в работе [18], где в качестве различных критериев используются электромагнитные поля с учетом и без учета токов смещения. Двухкритериальные обратные задачи с использованием гравитационного и магнитного полей рассмотрены в работе [19], электромагнитного и сейсмического полей – в работе [20]. Обзор различных подходов к комплексной инверсии геофизических данных представлен в работе [21].

Рассмотрим задачу, когда требуется определить две характеристики ${{g}_{1}}$, ${{g}_{2}}$ среды на основе двух типов характеристик ${{f}_{1}}$, ${{f}_{2}}$ геофизических полей одинаковой или различной физической природы – задача двухкритериальной инверсии. Эта задача определяется системой двух операторных уравнений относительно ${{g}_{1}}$, ${{g}_{2}}$:

(1.5)
$\begin{array}{*{20}{c}} {{{A}_{1}}{{g}_{1}} = {{f}_{1}},\quad {{g}_{1}} \in {{G}_{1}} \subset G,\quad \quad \quad \;\;\;} \\ {{{A}_{2}}{{g}_{2}} = {{f}_{2}},\quad {{g}_{2}} \in {{G}_{2}} \subset G,\quad {{f}_{1}},{{f}_{2}} \in F,} \end{array}\quad $
где ${{A}_{1}}$, ${{A}_{2}}$ – заданные непрерывные операторы прямых задач. При этом обычно предполагается, что для каждого критерия обратная задача имеет единственное решение [8], и поэтому с учетом компактности ${{G}_{1}}$, ${{G}_{2}}$ является условно-корректной. Для простоты изложения предполагается, что решения ${{g}_{1}}$, ${{g}_{2}}$ принадлежат одному и тому же функциональному пространству, то же самое касается элементов ${{f}_{1}}$, ${{f}_{2}}$ пространства данных.

Часто физические характеристики сред являются зависимыми и при заданном значении одной характеристики другая может принимать только определенные значения [11]. Взаимозависимость характеристик среды ${{g}_{1}}$, ${{g}_{2}}$ во многих практических случаях может быть выражена с помощью некоторых функционалов ${{u}_{i}}({{g}_{1}},{{g}_{2}})$ в виде неравенств:

(1.6)
${{u}_{i}}({{g}_{1}},{{g}_{2}}) \leqslant 0,\quad i = 1,\; \ldots ,\;{{I}_{g}}.$
Например, на основе экспериментальных или теоретических данных могут задаваться интервалы изменения характеристики ${{g}_{1}}$ в зависимости от значений характеристики ${{g}_{2}}$ [11]. В случае зависимости характеристик ${{g}_{1}}$, ${{g}_{2}}$ двухкритериальная задача сводится к решению системы (1.5) при дополнительных условиях (1.6).

В частном случае, когда обратная задача состоит в определении одной характеристики среды ${{g}_{{}}}$ (при этом условия (1.6) приобретают вид: ${{g}_{1}} = {{g}_{2}} = g$) на основе двух критериев ${{f}_{1}}$, ${{f}_{2}}$ различной или одинаковой физической природы, получаем двухкритериальную задачу, которая сводится к более простой системе уравнений:

(1.7)
$\begin{array}{*{20}{c}} {{{A}_{1}}g = {{f}_{1}},\quad \quad \quad \quad \quad \quad \quad \quad \,} \\ {{{A}_{2}}g = {{f}_{2}},\quad g \in {{G}_{1}} \subset G,\quad {{f}_{1}},{{f}_{2}} \in F.} \end{array}$

Задача типа (1.7) рассматривалась в работах [8], [17], [18].

Исследуем вопрос оценки погрешности решений двухкритериальной задачи (1.7). Пусть ${{f}_{1}}$, ${{f}_{2}}$ – правые части двухкритериальной задачи (1.7) заданы с погрешностями ${{\delta }_{1}}$, ${{\delta }_{2}}$ соответственно, а ${{g}_{T}}$ – точное решение (1.7) при ${{\delta }_{1}},{{\delta }_{2}} = 0$. Обозначим через ${{g}_{{1\delta }}}$, $\left\| {{{A}_{1}}{{g}_{{1\delta }}} - {{f}_{1}}} \right\| \leqslant {{\delta }_{1}}$ – некоторое приближенное решение первого уравнения системы (1.7), полученное независимо от второго уравнения. Апостериорная оценка $\beta _{1}^{*}(\delta )$ погрешности решения ${{g}_{{\delta 1}}}$ типа (1.3) определяется величиной:

(1.8)
$\beta _{1}^{*}({{\delta }_{1}}) = \max \left\{ {{{{\left\| {g{\text{'}} - {{g}_{{1\delta }}}} \right\|}}_{G}}\,{\text{:}}\,g{\text{'}},\;{{g}_{{1\delta }}} \in {{G}_{1}},\;{{{\left\| {{{A}_{1}}g{\text{'}} - {{f}_{1}}} \right\|}}_{F}} \leqslant {{\delta }_{1}},\;{{{\left\| {{{A}_{1}}{{g}_{{1\delta }}} - {{f}_{1}}} \right\|}}_{F}} \leqslant {{\delta }_{1}}} \right\}.$

Предположим теперь, что существует некоторое приближенное решение $g_{\delta }^{'}$, удовлетворяющее обоим уравнениям системы (1.7): ${{\left\| {{{A}_{k}}g_{\delta }^{'} - {{f}_{k}}} \right\|}_{F}} \leqslant {{\delta }_{k}}$, $k = 1,2$. Оценку погрешности решения $g_{\delta }^{'}$ определим величиной:

(1.9)
$\beta _{{12}}^{*}({{\delta }_{1}},{{\delta }_{2}}) = \max \left\{ {{{{\left\| {g{\text{'}} - g_{\delta }^{'}} \right\|}}_{G}}{\kern 1pt} \,:\,g{\text{'}},\;g_{\delta }^{'} \in {{G}_{1}},\;{{{\left\| {{{A}_{k}}g{\text{'}} - {{f}_{k}}} \right\|}}_{F}} \leqslant {{\delta }_{k}},\;{{{\left\| {{{A}_{k}}g_{\delta }^{'} - {{f}_{k}}} \right\|}}_{F}} \leqslant {{\delta }_{k}},\;k = 1,2} \right\}.$
Задачи (1.8), (1.9) отличаются допустимыми множествами, на которых ищется максимум функционала, при этом допустимое множество задачи (1.9), ввиду дополнительных ограничений, является подмножеством допустимого множества задачи (1.8). Так как максимум по подмножеству не может превышать максимума по всему множеству, то справедливо неравенство:
(1.10)
$\beta _{{12}}^{*}({{\delta }_{1}},{{\delta }_{2}}) \leqslant \beta _{1}^{*}({{\delta }_{1}}).$
Аналогичное неравенство справедливо и для оценки $\beta _{2}^{*}({{\delta }_{2}})$ погрешности приближенного решения второго уравнения системы (1.7) ${{g}_{{2\delta }}}$, $\left\| {{{A}_{1}}{{g}_{{2\delta }}} - {{f}_{2}}} \right\| \leqslant {{\delta }_{2}}$, полученного независимо от первого:

(1.11)
$\beta _{{12}}^{*}({{\delta }_{1}},{{\delta }_{2}}) \leqslant \beta _{2}^{*}({{\delta }_{2}}).$

Таким образом, мы получаем, что для задач вида (1.7) апостериорная оценка погрешности типа (1.3) при добавлении критерия убывает (не строго). Аналогичный результат может быть получен и для априорных оценок погрешности решений двухкритериальных задач, основанных на модуле непрерывности обратного оператора (1.2), а также для локальных оценок неоднозначности [17]. Можно показать также, что данная закономерность двухкритериальных задач, при определенных условиях, сохраняется для более общих двухкритериальных задач типа (1.5), (1.6).

Представленные выше результаты верны для любого конечного числа критериев.

2. АППРОКСИМАЦИОННЫЙ НЕЙРОСЕТЕВОЙ МЕТОД РЕШЕНИЯ НЕЛИНЕЙНЫХ ОПЕРАТОРНЫХ УРАВНЕНИЙ

В конечно-параметрических классах сред обратная задача (1.1) сводится к решению операторного уравнения на компактном множестве ${{S}_{N}} \subset {{R}^{N}}$ [22]:

(2.1)
${{A}_{1}}s = \;{e,\quad }s \in {{S}_{N}} \subset {{R}^{N}},\quad e \in F,$
где ${{A}_{1}}$: ${{R}^{N}} \to F$ – непрерывный оператор прямой задачи в заданном конечно-параметрическом классе сред; ${{S}_{N}}$ – ограниченное замкнутое множество конечномерного пространства, например, замкнутый куб: $[{{s}_{{\min }}} \leqslant {{s}^{n}} \leqslant {{s}_{{\min }}} + {{D}_{s}}]$, $n = 1,\; \ldots ,\;N$; $e \equiv e({{\tilde {e}}^{1}},\; \ldots ,\;{{\tilde {e}}^{M}})$ – элемент пространства данных $F$, построенный с помощью аппроксимационно-интерполяционных процедур, примененных к конечному набору входных (измеренных) данных ${{\tilde {e}}^{1}},\; \ldots ,\;{{\tilde {e}}^{M}}$, $M \geqslant N$, определенных на некоторой сетке в области ${{\Omega }_{1}}$. Погрешность построенного таким способом элемента данных рассматривается как составная часть суммарной погрешности правой части. При выполнении определенных требований к параметризации единственность решения конечномерной обратной задачи при переходе от (1.1) к (2.1) сохраняется и задача (2.1) остается условно-корректной [14], [22]. Обратная задача (2.1), будучи условно-корректной на заданном конечно-параметрическом множестве ${{S}_{N}}$, на практике при больших $N$ обычно является плохо обусловленной и практически неустойчивой, что приводит к большой практической неоднозначности численных решений. Для обеспечения численной устойчивости решений предварительно решается задача определения максимальной размерности $N = {{N}_{{{\text{opt}}}}}(\varepsilon )$ проводимой параметризации при условии, что численная оценка модуля непрерывности обратного оператора задачи (2.1) не превышает заданной желаемой величины $\varepsilon $ при заданном уровне погрешности данных $\delta $: $\beta ({{N}_{{{\text{opt}}}}},2\delta ) \leqslant \varepsilon $ (задача эффективной (оптимальной) параметризации среды) [14], [17].

2.1. Аппроксимационный метод решения нелинейных операторных уравнений

Каким бы численным методом не решалась обратная задача (2.1), ее приближенное решение $\tilde {s} = (\tilde {s}_{{}}^{1},\; \ldots ,\;\tilde {s}_{{}}^{N})$ является некоторой векторной функцией $M$ переменных от входных данных ${{\tilde {e}}^{1}},\; \ldots ,\;{{\tilde {e}}^{M}}$:

$\tilde {s}_{{}}^{n} = \psi _{{}}^{n}({{\tilde {e}}^{{_{1}}}},\; \ldots ,\;{{\tilde {e}}^{{_{M}}}}),\quad n = 1, \ldots ,\;N.$
Векторная функция ${\mathbf{\Psi }} = (\psi _{{}}^{1},\; \ldots ,\;\psi _{{}}^{N})$ представляет собой последовательность вычислительных процедур решения задачи инверсии (каким-либо из существующих методов) и любому заданному набору входных данных $\tilde {e} = ({{\tilde {e}}^{1}},\; \ldots ,\;{{\tilde {e}}^{M}})$ ставит в соответствие искомый приближенный вектор $\tilde {s} = (\tilde {s}_{{}}^{1},\; \ldots ,\;\tilde {s}_{{}}^{N})$ параметров, выполняя таким образом роль приближенного обратного оператора для уравнения (2.1).

Предположим, что имеется заранее рассчитанное множество ${{{\text{B}}}_{{bs}}}\left\{ {{{s}_{q}},{{e}_{q}}} \right\}$, ${{e}_{q}} = {{A}_{1}}{{s}_{q}}$, $q = 1,\; \ldots ,\;{{Q}_{{bs}}}$ опорных решений прямых (а значит, и обратных) задач для уравнения (2.1). Суть аппроксимационного подхода к решению уравнения (2.1) на основе имеющегося множества опорных решений ${{{\text{B}}}_{{bs}}}$ состоит в том, что строится задаваемая в аналитическом виде и простая в вычислительном плане непрерывная векторная функция ${\mathbf{\Psi }}(\hat {a},x_{{}}^{1},\; \ldots ,\;x_{{}}^{M}) = (\psi _{a}^{1},\; \ldots ,\;\psi _{a}^{N})$ от $M$ переменных $x_{{}}^{1},\; \ldots ,\;x_{{}}^{M}$ (аппроксиматор инверсии), которая позволяет получать приближенные решения уравнения (2.1) для любой правой части $e \in {{R}^{M}}$ в явном виде. Задача определения матрицы $\hat {a}$ коэффициентов функции-аппроксиматора сводится к аппроксимационно-интерполяционной проблеме (основной задаче теории аппроксимации [23]). Так как в опорных точках множества ${{{\text{B}}}_{{bs}}}$ значения функции ${\mathbf{\Psi }}(\hat {a},{{e}_{q}})$ известны, то в них должны выполняться равенства ${\mathbf{\Psi }}(\hat {a},{{e}_{q}}) = s_{q}^{{}}$, ${{s}_{q}},{{e}_{q}} \in {{{\text{B}}}_{{bs}}}$, $q = 1,\; \ldots ,\;{{Q}_{{bs}}}$, на основе которых формулируется экстремальная задача обучения аппроксиматора, решение которой определяет матрицу $\hat {a}$ коэффициентов [14], [24]:

(2.2)
$\sum\limits_{q = 1}^{{{Q}_{{bs}}}} {{{{\left( {\left\| {\Psi (\hat {a},{{e}_{q}}) - {{s}_{q}}} \right\|} \right)}}^{2}}} \to \mathop {\min }\limits_{\hat {a}} ,\quad {{s}_{q}},{{e}_{q}} \in {{{\text{B}}}_{{bs}}}.$

Обученный аппроксиматор инверсии ${\mathbf{\Psi }}$ с вычисленными коэффициентами принимается за приближенный обратный оператор $A_{1}^{{ - 1}} \approx {\mathbf{\Psi }}$ для уравнения (2.1), с помощью которого решение обратной задачи может быть получено для произвольных входных данных, не принадлежащих обучающему множеству, сравнительно быстро (обычно за первые секунды) без задания первого приближения. Решение, получаемое с помощью аппроксиматора ${\mathbf{\Psi }}$ по формуле $\tilde {s} = {\mathbf{\Psi }}(e)$ является интерполяционным; его ошибка ${{\varepsilon }_{\Psi }}$ за счет погрешности обратного оператора (собственная ошибка аппроксиматора) отлична от нуля даже при точной правой части (2.1) и определяется величиной [14]:

${{\varepsilon }_{\Psi }} = \mathop {\max }\limits_s {{\left\| {{\mathbf{\Psi }}({{A}_{1}}s) - s} \right\|}_{{{{R}^{N}}}}}{\kern 1pt} ,\quad s \in {{S}_{N}}.$
Для численного расчета собственной ошибки аппроксиматора ${{\varepsilon }_{\Psi }}$ создается независимое тестирующее (экзаменационное) множество известных решений.

Аппроксимационный метод решения обратной задачи не минимизирует в явном виде невязку для заданной фиксированной правой части уравнения (2.1). В частности, невязка интерполяционного решения может оказаться больше погрешности данных. Уменьшение невязки интерполяционного решения может быть достигнуто за счет улучшения интерполяционных свойств, используемых для построения аппроксиматора конструкций, увеличения числа опорных точек множества опорных решений, а также путем проведения уточняющих итераций на основе аппроксимационно-итерационного метода [14], [17], [24]. Помимо собственной ошибки аппроксиматора, приближенное решение содержит ошибку, обусловленную погрешностью входных данных. Если ${{\delta }_{f}}$ – фактическая невязка приближенного решения ${{s}_{1}} = {\mathbf{\Psi }}(e)$, то для него может быть определена апостериорная оценка практической неоднозначности, не зависящая от применяемого численного метода инверсии. Приближенный обратный оператор задачи, определяемый аппроксиматором инверсии ${\mathbf{\Psi }}$, является непрерывным, поэтому решения (2.1), получаемые с его помощью, являются устойчивыми по отношению к изменению входных данных.

Рассмотренный аппроксимационный метод обобщается на многокритериальные задачи, при этом матрица $\hat {a}$ коэффициентов многокритериального аппроксиматора ${\mathbf{\Psi }}$ определяется на основе объединенного обучающего множества опорных решений, составленного из отдельных множеств, соответствующих различным критериям [17].

2.2. Аппроксимационный метод с использованием нейронных сетей

В аппроксимационном нейросетевом (АНС) методе в качестве координатных функций $\psi _{{}}^{n}$ аппроксиматора используются аппроксимационные конструкции, называемые нейронными сетями типа многослойного персептрона (MLP сети) [25], [26]. Использование многослойного персептрона в задачах общей теории аппроксимации функций в своей основе опирается на известные теоремы Колмогорова, Вейерштрасса-Стоуна, Цыбенко. Эффективность применения MLP сетей на практике при решении нелинейных операторных уравнений обусловлена тем, что они являются мощным инструментом аппроксимации (а также интерполяции и экстраполяции) сложных нелинейных многомерных зависимостей [26], которыми определяются обратные операторы для задач типа (2.1). Алгоритмы обучения MLP сетей в задачах построения сложных нелинейных зависимостей различной природы подробно рассмотрены в работе [26]. Целевой функционал (2.2) задачи обучения задан в аналитическом виде и легко дифференцируется, поэтому для решения задачи минимизации функционала применяется наиболее распространенный на практике метод стохастического градиента [25], [26], [27], который является модификацией классического градиентного метода. Производные функционала рассчитываются на основе алгоритма обратного распространения ошибки (BPE – Back Propagation Error) [25], [26], [28]. Целевой функционал обучения в общем случае является многоэкстремальным. Строгое обоснование методов решения многоэкстремальных задач в большинстве случаев затруднительно, поэтому стандартные методы оптимизации для решения задачи обучения комбинируют с неформальными, эвристическими подходами [26], [27]. Алгоритм обучения НС аппроксиматора с использованием MLP сетей применительно к обратным задачам геофизики рассмотрен в работе [24].

Резюмируя вышеизложенное, отмечаем, что аппроксимационный нейросетевой метод обращения нелинейных операторных уравнений вида (2.1) в заданном классе решений включает в себя следующие основные этапы:

• построение множества опорных решений прямых и обратных задач (обучающего множества) с помощью прямого оператора задачи;

• построение приближенного обратного оператора задачи (НС аппроксиматора инверсии) с помощью нейросетевых аппроксимационно-интерполяционных конструкций на основе имеющегося множества опорных решений (обучение НС аппроксиматора);

• тестирование НС аппроксиматора инверсии на независимом множестве известных решений обратной задачи и определение собственной ошибки аппроксиматора;

• инверсия предложенных входных данных с помощью НС аппроксиматора и при необходимости проведение уточняющих итераций;

• расчет оценок степени неоднозначности (погрешности) получаемых приближенных решений, не зависящих от применяемого метода инверсии.

3. ПРИМЕНЕНИЕ НЕЙРОСЕТЕВЫХ МЕТОДОВ ПРИ РЕШЕНИИ ОБРАТНЫХ ЗАДАЧ ГЕОФИЗИКИ

Общая концепция возможности применения НС технологий в задачах обработки и интерпретации геофизических данных изложена в пионерской работе А. Райча [29]. В работе рассмотрены основные виды нейросетевой архитектуры: персептрон (Роземблатта), самоорганизующиеся сети (Кохонена), сети ассоциативной памяти (Хопфилда) и др. Рассматривается теория основных алгоритмов обучения данных видов сетей. В заключение А. Райч замечает, что рост вычислительной мощности современных компьютеров позволяет ставить задачи численного моделирования для очень большой геометрии, которые требуют параллельной работы на суперкомпьютерных кластерах. Автор ставит несколько перспективных вопросов: как можно использовать накопленные обширные предыдущие знания в решении интерпретационных задач с новыми данными? Как экстраполировать старые данные, используя наши знания в новой ситуации? Как можно в машинные хранилища информации включать огромные множества данных, выделяя их по внешнему виду? А. Райч дает прогноз, что нейросетевая парадигма предлагает нам прекрасный симулятор для реализации этих процедур, что подтверждается современным уровнем развития нейросетевых технологий в геофизике.

В последующие годы появилось много примеров применения НС технологий для решения различных задач обработки геофизической информации: распознавания образов, классификации, построения различного рода зависимостей и др. Остановимся более подробно на работах, в которых применяются в основном аппроксимационные MLP сети для решения нелинейных обратных задач геофизики в классической постановке, сводящихся к решению операторного уравнения вида (1.1) с заданным обратимым оператором прямой задачи. Наиболее широко такие работы представлены в задачах геоэлектрики, гравиметрии, магнитометрии и сейсморазведки.

Геоэлектрика. Обратные задачи геоэлектрики относятся к типу коэффициентных обратных задач для системы уравнений Максвелла. Примеры решения обратной коэффициентной 1D задачи геоэлектрики с использованием нейросетей представлены в работах [30], [31]. В этих работах нейронные MLP сети используются для решения малопараметрических обратных задач геоэлектрики в рамках слоистой модели. Первые результаты применения нейронных сетей для решения обратных задач геоэлектрики в горизонтально-неоднородных средах были представлены в работах [32], [33]. В этих работах было показано, что с помощью нейронных сетей могут быть получены приближенные решения обратных задач геоэлектрики в горизонтально-неоднородных средах с числом искомых параметров $N\sim {\text{10}}{\kern 1pt} \div {\kern 1pt} {\text{15}}$.

Адаптация общих методов построения НС аппроксиматоров инверсии к особенностям решаемой задачи и разработка усовершенствованных модификаций АНС метода с использованием алгоритмов Монте-Карло позволили авторам настоящей работы обобщить АНС метод на случай 2D, 3D сред, геоэлектрические свойства которых определяются числом параметров $N\sim {\text{1}}{{{\text{0}}}^{2}}{\kern 1pt} \div {\kern 1pt} {\text{1}}{{{\text{0}}}^{3}}$ [14], [34]. При этом вычисляются априорные и апостериорные оценки степени практической неоднозначности решений обратных задач, не зависящие от численного метода инверсии [14], [24], [35]. В работах [17], [36] представлен аппроксимационно-итерационный нейросетевой метод решения обратной задачи, который позволяет проводить дополнительные итерации решения обратной задачи с помощью АНС метода после найденного первого приближения. Для уменьшения размерности задачи обучения сети производится предварительное сжатие данных и определение оптимальных размерностей входного и выходного векторов нейросети с учетом специфики решаемой задачи. Принципиальная возможность использования сжатых данных для решения обратной задачи геоэлектрики, как задача частичной инверсии на основе неполных данных с помощью локальных НС аппроксиматоров инверсии, была рассмотрена в работе [34] и численно реализована в работах [14], [24], [37]. Полученные в этих работах результаты позволили существенно понизить размерность задачи обучения (на 2 порядка и более) и одновременно уменьшить собственную ошибку получаемых НС-аппроксиматоров инверсии, что в целом повышает эффективность АHC метода.

Гравиметрия, магнитометрия. Основной класс обратных нелинейных задач гравиметрии и магнитометрии связан со структурными задачами, которые заключаются в определении границ звездного тела с известной избыточной плотностью на основе измеренных характеристик соответствующих потенциальных полей.

В статье [38] используется АНС метод решения задачи определения геометрических параметров подземной структуры. В ядре алгоритма решается нелинейная структурная задача гравиметрии определения формы 2D звездного тела при различных задаваемых значениях избыточной плотности. Метод использовался при построении карты гравитационных аномалий в Мексиканском заливе для антиклинальной структуры. В работе [39] с помощью АНС метода решается обратная структурная 3D задача гравиметрии для простых тел: сфера, бесконечно протяженный горизонтальный цилиндр и полубесконечный вертикальный цилиндр. Искомыми являются два геометрических параметра: радиус тела и глубина залегания центра с известными значениями избыточной плотности. В качестве обучающей выборки используются модельные данные решения прямой задачи гравиметрии. Строится НС аппроксиматор инверсии с параметрами MLP сети: 20 нейронов, три входных и два выходных параметра. Метод апробирован на нефтяном битуме Dehloran, Иран.

В статье [40] решается обратная структурная 3D задача гравиметрии определения геометрии границ трехслойной среды с известными значениями избыточной плотности слоев. Представлен НС метод, в котором универсальный аппроксиматор инверсии в заданном классе сред не конструируется. Для решения обратной задачи строится “псевдонейросеть”, которая заново обучается на каждом шаге итерации с учетом приближения, полученного на предыдущем шаге. Для каждой новой модели из рассматриваемого класса сред строится своя последовательность нейросетей. Используется трехслойная MLP сеть, у которой число нейронов во входном слое равно числу нейронов в выходном слое и равно числу измерений гравитационного поля. Число определяемых параметров: 50 в случае одной границы, 20 в случае двух, или трех границ. Нейросетевая 3D инверсия выполнена на данных наблюдений гравитационной аномалии Окинавской впадины. В работе [41] АНС метод применяется для решения обратной структурной 3D задачи гравиметрии определения параметров сферы, бесконечного горизонтального цилиндра и полубесконечного вертикального цилиндра. Искомыми являются три параметра: тип формы, характеристика размера и глубина залегания тела. Метод применяется для инверсии полевых данных на территории Ирана. В работе [42] применяется АНС метод для оценки глубины источника с простой геометрией. В статье [43] АНС метод применяется для решения обратной структурной 3D задачи магнитометрии определения границ слоев в скважине. Сеть трехслойная (количество нейронов 8, 10, 16). При построении сети входной вектор формируется на основе выбранных характерных значений поля (пониженные значения поля, разница между ними и др.). Применение сети к реальным данным (поля Дармиана, Иран) показывает приемлемую точность в предсказании глубин залегания слоев.

Сейсморазведка. Определение скоростных характеристик среды в общем случае является коэффициентной обратной задачей для уравнения упругих полей. На практике используются различные приближения этой задачи: акустическое, геометрической сейсмики и некоторые другие [9]. С помощью нейронных сетей в сейсмике в основном решаются задачи классификации, распознавания образов, построения нелинейных зависимостей и обработки данных, нелинейные классические обратные задачи решаются редко. В ранних работах [44] АНС метод применялся для решения обратной коэффициентной 1D задачи для волнового уравнения, которая заключается в определении скоростных характеристик слоистой среды (8 слоев). Для обучения использовалось 450 модельных примеров. Удовлетворительный результат инверсии получается в 80% случаев. В работе [45] АНС метод применяется для решения обратной 1D задачи сейсмики в акустическом приближении. Искомой величиной является упругий импеданс, который зависит от скоростей волн, плотности среды, являясь обобщением акустического импеданса для ненулевых углов падения [46], эффективно используется в задачах интерпретации сейсмических данных. Прямая задача решается на основе приближенных формул для упругого импеданса. Сейсмические трассы и трассы упругого импеданса моделируются как временные ряды. Инверсия сейсмических данных проводится на основе нейронной сети, содержащей сверточный и рекуррентный слои. В работе [47] приводится пример решения АНС методом обратной коэффициентной 1D задачи определения скоростей среды для волнового уравнения.

Замечание. Последнее время в геофизике активно используются так называемые глубокие нейронные сети (технология “Deep Learning”). В работе [48] для решения коэффициентной обратной 2D задачи геоэлектрики технология “Deep Learning” используется на основе сверточной нейронной сети с распространенной архитектурой U-Net. Другой пример использования этой технологии представлен в работе [49] для решения обратной 2D задачи сейсмики. При использовании технологий глубоких нейронных сетей в упомянутых работах обратная задача решается в предположении, что решение принадлежит одному из нескольких гипотетических классов сред. В процессе инверсии на основе данных, полученных в процессе наблюдения, определяется класс сред (т.е. решается задача классификации) и уточняются параметры модели из найденного класса. На данной стадии развития технологии глубоких сетей пока удается решать достаточно простые задачи геофизики, однако, по мнению упомянутых авторов, следует ожидать значительного прогресса в применении этих методов.

3.1. Пример решения двухкритериальной 2D задачи

Приведем результаты по решению АНС методом нелинейной обратной двухкритериальной 2D задачи на основе данных гравиметрии и магнитометрии с целью показать принципиальную возможность применения MLP нейронных сетей для задач такого типа.

Решалась двухкритериальная обратная 2D задача (1.7) определения геометрии границ слоев при заданных на границе ${{\Omega }_{1}}$ исследуемой области $\Omega $ гравитационном и магнитном полях и фиксированных значениях плотности и намагниченности слоев. Однокритериальные задачи имеют единственное решение при точных данных [4], [5], [6]. Рассматривается класс сред $GM1[\Omega ]$: четырехслойная 2D среда с тремя изменяющимися криволинейными границами, которые аппроксимируются кусочно-постоянными функциями с заданным шагом по горизонтали, нижняя граница самого нижнего 4-го слоя отнесена на бесконечность. Искомыми параметрами задачи являются значения ординат нижних границ трех слоев (общее число искомых параметров $N = 45$). Априорная информация о возможных изменениях границ слоев представлена в табл. 1. Входными данными обратной задачи являются значения гравитационного и магнитного полей, определенные на пространственной сетке в точках границы ${{\Omega }_{1}}$. Общая размерность входных данных обратной задачи составляет 76 значений для каждого метода и 152 для двухкритериальной задачи. Перед проведением численной инверсии проводился априорный анализ оценки практической неоднозначности решений обратной задачи в рассматриваемом классе сред на основе расчетных значений модуля непрерывности обратного оператора. В пространстве решений ${{R}^{N}}$ использовалась норма вида

$\left\| x \right\|_{{{{l}_{1}}}}^{N} = \frac{1}{{N \cdot {{D}_{s}}}}\sum\limits_{n = 1}^N {\left| {{{x}_{n}}} \right|} ;$
в пространстве данных $F$ – норма ${{L}_{{2,b}}}$ с весом $b$. Расчеты априорных и апостериорных оценок неоднозначности (погрешности) решений обратной задачи проводились на основе методов, представленных в работе [35]. Операторы численного решения прямых задач строились на основе конечно-разностной аппроксимации краевых задач для потенциального поля на сетке прямой задачи ${{\theta }_{{{{N}_{0}}}}}$ размерности ${{N}_{0}}$ [50].

Таблица 1.  

Средние собственные ошибки НС для аппроксиматоров ${{{\mathbf{\Psi }}}_{{G1}}}$, ${{{\mathbf{\Psi }}}_{{M1}}}$, ${{{\mathbf{\Psi }}}_{{GM1}}}$ по слоям на тестирующих выборках. Большим номерам соответствуют более глубокие слои

№ границы слоя 1 2 3
Интервалы изменения ординат границ слоев мин-макс, км 1–1.5 1.8–2.0 2.2–2.3
${{{\mathbf{\Psi }}}_{{G1}}}$, % 4.62 11.80 25.69
${{{\mathbf{\Psi }}}_{{M1}}}$, % 5.26 11.48 22.59
${{{\mathbf{\Psi }}}_{{GM1}}}$, % 2.46 8.13 11.42

Для рассматриваемого класса $GM1$ сред были построены НС аппроксиматоры инверсии ${{{\mathbf{\Psi }}}_{{G1}}}$, ${{{\mathbf{\Psi }}}_{{M1}}}$, ${{{\mathbf{\Psi }}}_{{GM1}}}$ для гравитационного, магнитного полей и их объединения. Использовалась нейронная сеть типа пятислойного персептрона с числом нейронов в трех скрытых слоях, равным 32, 16 и 8. Число опорных решений обучающего множества включало по 30 000 примеров для задачи гравиметрии и магнитометрии. Выборка для каждой однокритериальной задачи делилась на три части: тренировочную (основную обучающую) – 21 000 примеров, тестирующую (в процессе обучения) – 8000 примеров и независимую экзаменационную – 1000 примеров (для определения собственной ошибки аппроксиматора). Двухкритериальная задача решалась на объединенной выборке общим объемом 60 000 примеров.

В табл. 1 приведены средние по слоям собственные ошибки НС аппроксиматоров ${{{\mathbf{\Psi }}}_{{G1}}}$, ${{{\mathbf{\Psi }}}_{{M1}}}$, ${{{\mathbf{\Psi }}}_{{GM1}}}$ по соответствующим экзаменационным выборкам. Из таблицы видно, что собственные ошибки аппроксиматоров растут с увеличением глубины слоя.

На фиг. 1 приведен результат двухкритериальной инверсии синтезированных данных, рассчитанных для фиксированного модельного примера из класса $GM1$. Штриховой линией обозначены истинные значения, сплошной линией – решение, полученное с помощью НС аппроксиматора ${{{\mathbf{\Psi }}}_{{GM1}}}$. В табл. 2 представлены средние по слоям ошибки инверсии для этой модели и апостериорные локальные (послойные) оценки неоднозначности найденных параметров границ при достигнутых фактических невязках, которые получились равными: для метода гравиметрии ${{\delta }_{G}} = 4.04$%, для магнитометрии ${{\delta }_{M}} = 4.62$% и для двухкритериальной инверсии ${{\delta }_{G}} = 0.81$%, ${{\delta }_{M}} = 1.89$% (в среднем ${{\overline \delta }_{{GM}}} = 1.35$%).

Фиг. 1.

Результаты двухкритериальной инверсии модельных данных. Штриховой линией обозначены истинные значения, сплошной – результат инверсии.

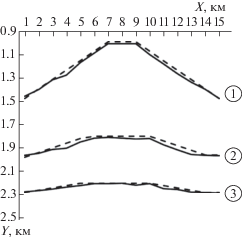
Таблица 2.  

Средние по слою ошибки НС инверсии (числитель дроби) и локальные (по слоям) апостериорные оценки $\beta _{1}^{i}(\delta )$ неоднозначности приближенных решений (знаменатель дроби) при полученных фактических невязках для модельного примера

№ слоя, i 1 2 3
Гравиметрия $\beta _{1}^{i}({{\delta }_{G}})$, % 7.80/11.52 24.60/30.04 38.40/65.98
Магнитометрия $\beta _{1}^{i}({{\delta }_{M}})$, % 8.00/6.44 24.70/14.85 35.90/39.17
Комплекс $\beta _{1}^{i}({{\delta }_{G}},{{\delta }_{M}})$, % 3.60/1.71 11.60/7.56 11.20/10.15

Из данных в табл. 2 видно, что фактические ошибки инверсии и апостериорные оценки погрешности возрастают с глубиной залегания слоя. Апостериорные оценки показывают, насколько по норме пространства решений могут отклоняться другие $\delta $-эквивалентные решения от найденного. При комплексировании критериев фактические ошибки и апостериорные оценки для каждого слоя уменьшаются. Например, для третьего слоя фактическая ошибка инверсии при комплексировании уменьшается примерно в 3.5–3.8 раза по сравнению с отдельными инверсиями, а апостериорная оценка уменьшается в 3.9–6.8 раза.

Подводя итог по данному разделу, отметим, что АНС метод без существенных изменений может применяться для решения многокритериальных задач. При этом оценки неоднозначности (погрешности) решения обратной задачи уменьшаются при комплексировании критериев.

ЗАКЛЮЧЕНИЕ

Приведенные в работе результаты позволяют сделать вывод о том, что за последние годы наблюдается заметный прогресс в области применения нейросетевых технологий при решении классических, в том числе многокритериальных, обратных задач геофизики. Накопленный опыт позволяет:

• строить универсальные НС аппроксиматоры инверсии, способные устойчиво решать нелинейные обратные задачи в конечно-параметрических классах сред с числом искомых параметров 2D, 3D сред порядка ∼103 за первые секунды – фактически в режиме реального времени, с приемлемой для практики точностью;

• вычислять оценки практической неоднозначности (погрешности) решений, получаемых с помощью нейросетевых технологий, присущие самому НС методу инверсии, а также универсальные оценки, не зависящие от применяемого метода.

Авторы выражают признательность А.С. Долгалю за полезные советы и обсуждения в ходе выполнения работы.

Список литературы

  1. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979. 288 с.

  2. Лаврентьев М.М., Романов В.Г., Шишатский С.П. Некорректные задачи математической физики и анализа. М.: Наука, 1980. 286 с.

  3. Страхов В.Н. Об интегральных и функциональных уравнениях некоторых обратных задач теории логарифмического потенциала и их значении для интерпретации гравитационных и магнитных аномалий // Изв. АН СССР. Сер. Физика Земли. 1976. № 3. С. 54–66.

  4. Гравиразведка. Справочник геофизика. М.: Недра, 1981. 397 с.

  5. Новиков П.С. Об единственности обратной задачи потенциала // Докл. АН СССР. 1938. Т. 18. № 3. С. 165–168.

  6. Страхов В.Н. Об условиях однозначного определения границ раздела двухмерных слоистых сред по данным гравитационных наблюдений // Докл. АН УССР. 1975. № 12. С. 1086–1091.

  7. Романов В.Г., Кабанихин С.И. Обратные задачи геоэлектрики. М.: Наука, 1991. 304 с.

  8. Дмитриев В.И. Обратные задачи геофизики. Монография. М.: МАКС Пресс, 2012. 340 с.

  9. Жданов М.С. Теория обратных задач и регуляризации в геофизике. М.: Научный мир, 2007. 712 с.

  10. Дмитриев В.И. О единственности решения трехмерной обратной задачи электромагнитного зондирования // Прикл. матем. и информатика, серия Труды факультета ВМК МГУ. М.: МГУ, 2018. Т. 57. С. 5–20.

  11. Гурвич И.И., Боганик Г.Н. Сейсмическая разведка. М.: Недра, 1980. 551 с.

  12. Сейсморазведка. Справочник геофизика. М.: Недра, 1981. 464 с.

  13. Тихонов А.Н., Гончарский А.В., Степанов В.В., Ягола А.Г. Численные методы решения некорректных задач. М.: Наука, 1990. 232 с.

  14. Шимелевич М.И., Оборнев Е.А., Оборнев И.Е., Родионов Е.А. Аппроксимационный нейросетевой метод решения многомерных нелинейных обратных задач геофизики // Физика Земли. 2017. № 4. С. 100–109.

  15. Никитин А.А., Хмелевской В.К. Комплексирование геофизических методов. М.: ВНИИгеосистем, 2012. 346 с.

  16. Haber E., Oldenburg D. Joint inversion: a structural approach // Inverse Problems. 1997. V. 13. P. 63–77.

  17. Шимелевич М.И. Методы повышения устойчивости инверсии данных геоэлектрики на основе нейросетевого моделирования // Геофизика. 2013. № 4. С. 49–55.

  18. Бухаров А.В., Кабанихин С.И., Шишленин М.А. Совмещенная постановка обратной задачи электромагнитного зондирования // Тезисы IV междунар. конференции “Функциональные пространства. Дифференц. операторы. Общая топология. Проблемы матем. образования”. М.: РУДН, 2013. С. 394–395.

  19. Gallardo L.A., Perez M.A., Treviño E.G. A versatile algorithm for joint 3D inversion of gravity and magnetic data // Geophysics. 2003. V. 68. № 3. P. 949–959.

  20. Gallardo L.A., Meju M.A. Joint two-dimensional DC resistivity and seismic travel time inversion with cross-gradients constraints // J. Geophys. Res. 2004. V. 109. B03311.

  21. Спичак В.В. Современные подходы к комплексной инверсии геофизических данных // Геофизика. 2009. № 5. С. 10–19.

  22. Гончарский А.В., Черепащук А.М., Ягола А.Г. Обратные задачи астрофизики. М.: Изд-во знание, Сер. Матем. и кибернетика. 1987. № 2. 32 с.

  23. Ахиезер Н.И. Лекции по теории аппроксимации. М.: Наука, 1965. 408 с.

  24. Шимелевич М.И., Оборнев Е.А., Оборнев И.Е., Родионов Е.А. Алгоритм решения обратной задачи геоэлектрики на основе нейросетевой аппроксимации // Сиб. журн. вычисл. матем. 2018. Т. 21. № 4. С. 451–468; Num. Anal. Appl. 2018. 11:4. P. 359–371.

  25. Галушкин А.И. Синтез многослойных систем распознавания образов. М.: Энергия, 1974. 368 с.

  26. Хайкин С. Нейронные сети. Полный курс. Изд-во Вильямс, 2006. 1104 с.

  27. Воронцов К.В. Лекции по искусственным нейронным сетям. 2009. Режим доступа: http://www.ccas.ru/voron/download/NeuralNets.pdf, свободный.

  28. Werbos P.J. Beyond regression: New tools for prediction and analysis in the behavioral sciences. Ph.D. thesis, Harvard University, Cambridge, MA, 1974.

  29. Raiche A. A pattern recognition approach to geophysical inversion using neural nets // Geophysics J. Int. 1991. V. 105. P. 629–648.

  30. Hidalgo H., Gómez-Treviño E., Swiniarski R. Neural network approximation of a inverse functional // Proc. IEEE Internat. Conference on Neural Networks. 1994. V. 5. P. 3387–3392.

  31. Poulton M., Sternberg B., Glass C. Neural network pattern recognition of subsurface EM images // J. Appl. Geophysics. 1992. V. 29. № 1. P. 21–36.

  32. Спичак В.В., Попова И.В. Применение нейросетевого подхода для реконструкции параметров трехмерной геоэлектрической структуры // Изв. РАН. Сер. Физика Земли. 1998. № 1. С. 39–45.

  33. Shimelevitch M., Obornev E. The method of neuron network in inverse problems MTZ // Abstracts of the 14-th workshop on Electromagnetic Induction in the Earth, Sinaia. Romania, 1998. P. 159.

  34. Шимелевич М.И., Оборнев Е.А. Аппроксимационный метод решения обратной задачи МТЗ с использованием нейронных сетей // Физика Земли. 2009. № 12. С. 22–38.

  35. Шимелевич М.И., Оборнев Е.А., Оборнев И.Е., Родионов Е.А. Численные методы оценки степени практической устойчивости обратных задач геоэлектрики // Физика Земли. 2013. № 3. С. 58–64.

  36. Шимелевич М.И., Оборнев Е.А., Оборнев И.Е., Родионов Е.А. Модифицированный нейросетевой метод решения обратной задачи МТЗ // Изв. вузов, Геология и разведка. 2013. № 3. С. 46–52.

  37. Dolenko S., Guzhva A., Obornev E., Persiantsev I., Shimelevich M. Comparison of adaptive algorithms for significant feature selection in neural network based solution of the inverse problem of electrical prospecting // Proc. ICANN 2009. Part II. Berlin, Heidelberg: Springer-Verlag, 2009. P. 397–405.

  38. Osman O., Albora A.M., Ucan O.N. Forward modeling with forced neural networks for gravity anomaly profile // Math Geol. 2007. V. 39. P. 593–605.

  39. Abedi M., Afshar A., Ardcstaiii V.E., Norouzi G.H., Lucas C. Application of various methods for 2D inverse modeling of residual gravity anomalies // Acta Geophys. 2010. V. 582. P. 317–336.

  40. Chen X., Du Y., Liu Z. et al. Inversion of Density Interfaces Using the Pseudo-Backpropagation Neural Network Method // Pure Appl. Geophys. 2018. V. 175. P. 4427–4447. https://doi.org/10.1007/s00024-018-1889-7

  41. Eshaghzadeh A., Hajian A. 2D inverse modeling of residual gravity anomalies from Simple geometric shapes using Modular Feed-forward Neural Network // Annals of Geophysics. 2018. V. 61. № 1. SE115.

  42. Al-Garni M.A. Inversion of residual gravity anomalies using neural network // Arab. J. Geosci. 2013. V. 6. P. 1509–1516.

  43. Alimoradi A., Angorani S., Ebrahimzadeh M., Shariat Panahi M. Magnetic inverse modelling of a dike using the artificial neural network approach // Near Surface Geophysics. 2011. V. 9. P. 339–347.

  44. Roth G., Tarantola A. Neural networks and inversion of seismic data // J. Geophys. Res. 1994. V. 99. P. 6753–6768.

  45. Alfarraj M., AlRegib G. Semisupervised sequence modeling for elastic impedance inversion // Interpretation. 2019. V. 7. I. 3. P. SE237–SE249.

  46. Connolly P. Elastic impedance: The Leading Edge. 1999. V. 18. P. 438–452.

  47. Kailai Xu, Eric Darve. The neural network approach to inverse problems in differential equations // 2019. arXiv:1901.07758 [math.NA]. 2019.

  48. Bin Liu, Qian Guo, Shucai Li, Benchao Liu, Yuxiao Ren, Yonghao Pang, Lanbo Liu, Peng Jiang. Deep Learning Inversion of Electrical Resistivity Data // arXiv:1904.05265. 2019.

  49. Shucai Li, Bin Liu, Yuxiao Ren, Yangkang Chen, Senlin Yang, Yunhai Wang, Peng Jiang. Deep learning Inversion of Seismic Data // IEEE Transactions on Image Processing. 2019. P. 1–15.

  50. Долгаль А.С. Компьютерные технологии обработки и интерпретации данных гравиметрической и магнитной съемок в горной местности. Абакан. ООО “Фирма-МАРТ”, 2002. 188 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал