Журнал вычислительной математики и математической физики, 2020, T. 60, № 6, стр. 1045-1052

ВВЕДЕНИЕ

Многослойные оптические покрытия относятся к ключевым компонентам современных оптических и оптоэлектронных технологий. Оптические покрытия для лазерной, медицинской, космической и других областей имеют десятки и сотни тонких слоев, наносимых на оптические элементы в вакуумных напылительных установках [1]. Расчет таких покрытий представляет собой сложную многопараметрическую обратную задачу, которая, однако, эффективно решается разработанными к настоящему времени методами [2]. На сегодняшний день основной проблемой в технологическом и математическом планах является повышение надежности контроля процесса напыления покрытий.

Основными параметрами, контролируемыми в процессе напыления, являются толщины слоев покрытия. При этом в процессе напыления приходится решать обратные задачи определения толщин уже напыленных слоев и толщины текущего напыляемого слоя. Алгоритмы решения данных обратных задач зависят от типа измерений, производимых для контроля процесса напыления. Наиболее широко разрабатываемым в настоящее время является так называемый прямой широкополосный контроль, основанный на измерениях спектра коэффициента пропускания покрытия в процессе его напыления [3]. Данный тип контроля был впервые использован еще четыре десятилетия назад [4]–[6], но интерес к нему особенно усилился в последние годы в связи с возросшей точностью измерения спектров сигналов внутри напылительной камеры и с возросшими вычислительными возможностями обработки больших объемов спектральных данных в режиме on-line.

Важнейшим фактором для выбора широкополосного контроля процесса напыления является наличие связанного с этим методом эффекта самокомпенсации ошибок напыления. Возможность проявления данного эффекта была отмечена еще в упомянутых выше первых работах [4]–[6], а затем его наличие было статистически подтверждено в работе [7]. Однако детальное математическое исследование эффекта самокомпенсации ошибок при широкополосном оптическом контроле началось только в самые последние годы. Толчком к этому исследованию послужило обнаружение чрезвычайно сильного эффекта самокомпенсации при создании поляризаторов лазерного излучения для сверхмощных лазерных пучков [8]. Первой математической работой по исследованию механизма эффекта самокомпенсации была статья [9], в которой было дано математическое описание процесса корреляции ошибок в толщинах напыляемых слоев при их прямом оптическом контроле. Процесс корреляции был описан с помощью специальной прямоугольной матрицы, элементы которой вычисляются по заданной теоретической конструкции покрытия и основным параметрам широкополосного оптического контроля. Эффект самокомпенсации был объяснен в терминах сингулярных чисел этой матрицы и расширенной матрицы, получаемой из нее добавлением матрицы Гессе функционала, оценивающего качество теоретического покрытия [9].

В дальнейших работах [10], [11] был введен специальный параметр, оценивающий степень корреляции ошибок при широкополосном оптическом контроле, и проведено статистическое исследование распределения значений данного параметра. Целью настоящей работы является обобщение полученных ранее результатов, а также приведение их к виду, позволяющему проводить практические производственные оценки ожидаемого при напылении эффекта самокомпенсации ошибок.

1. ПРОЦЕСС КОРРЕЛЯЦИИ ОШИБОК И ЭФФЕКТ ИХ САМОКОМПЕНСАЦИИ

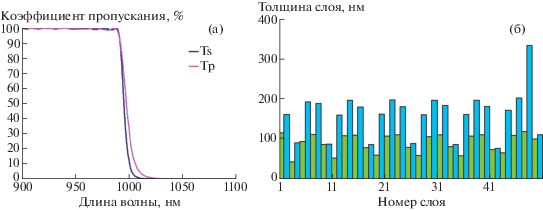
Для иллюстрации обсуждаемых в данном разделе результатов мы используем так называемый неполяризующий фильтр для угла падения светa 45°. При наклонном падении света следует различать спектральные характеристики покрытия для волн двух различных поляризаций: s- и p-поляризованных волн. Методы расчета спектральных характеристик хорошо известны [12]. На фиг. 1а представлены коэффициенты пропускания фильтра T_s и T_p для s- и p-поляризованных волн. На фиг. 1б показаны толщины слоев фильтра, в котором все нечетные слои имеют показатель преломления 2.35, а все четные слои – 1.45. Показатель преломления подложки, на которую нанесен фильтр, равен 1.52. Расчет данного фильтра произведен с помощью программного комплекса OptiLayer [13].

В работе [14] на основе вычислительных экспериментов по симуляции процесса напыления было показано, что в случае широкополосного оптического контроля проявляется чрезвычайно сильный эффект самокомпенсации ошибок в толщинах слоев напыляемого фильтра. Сущность этого эффекта состоит в том, что, несмотря на большой уровень ошибок в каждом из слоев покрытия, его характеристики мало отличаются от изображенных на фиг. 1а. Мы продолжим обсуждение данного эффекта ниже после рассмотрения самого метода оптического контроля и связанного с ним процесса корреляции ошибок в толщинах слоев.

В работе [14] предполагалось, что оптический контроль проводится в диапазоне длин волн от 400 до 900 нм с шагом 1 нм. При этом внутри напылительной камеры через равные промежутки времени (3 с в вычислительных экспериментах данной работы) измеряется коэффициент пропускания T_meas(λ_j) на сетке длин волн {λ_j} (501 точка в обсуждаемых экспериментах). Коэффициент пропускания измеряется при нормальном падении света на напыляемое покрытие. В процессе вычислительных экспериментов симулируются различные ошибки, присущие как самому процессу напыления, так и процессу измерения коэффициента пропускания T_meas(λ) [14].

Для описания метода широкополосного оптического контроля рассмотрим процесс напыления j-го слоя покрытия. Пусть d – толщина растущего j-го слоя. Измеряемый в процессе напыления коэффициент пропускания покрытия T_j(d) может быть записан в следующем виде:

где $d_{1}^{a},\; \ldots ,\;d_{{j - 1}}^{a}$ – толщины уже напыленных слоев, а δT_meas – ошибка измерений.

В (1) и далее для сокращения записи мы будем опускать обозначения очевидной зависимости T от длины волны λ.

Пусть ${{T}_{j}}(d_{1}^{t},\; \ldots ,\;d_{j}^{t})$ – коэффициент пропускания системы из первых j слоев теоретической конструкции покрытия. Толщины уже напыленных слоев отличаются от значений $d_{i}^{t}$ в силу различных ошибок процесса напыления. При широкополосном контроле процесс напыления j-го слоя прерывается в соответствии с условием достижения минимума функционалом невязки

Суммирование здесь ведется по всей сетке длин волн, на которой измеряется коэффициент пропускания.

Из условия (2) очевидно, что ошибка в толщине j-го слоя, т.е. отличие фактически напыленной толщины слоя $d_{j}^{a}$, от теоретически планировавшейся толщины слоя $d_{j}^{t}$ связана не только с ошибкой измерения, но определяется еще и всеми допущенными ранее ошибками $\delta {{d}_{i}} = d_{i}^{a} - d_{i}^{t}$, $i = 1,\; \ldots ,\;j - 1$. Таким образом, имеет место корреляция ошибок в толщинах слоев, связанная с самим процессом контроля.

Корреляция ошибок в толщинах слоев может приводить к негативному кумулятивному эффекту роста этих ошибок с увеличением числа слоев [15]. Но наряду с этим может проявляться и положительный эффект самокомпенсации этих ошибок. Пусть $\delta {{d}_{1}},\; \ldots ,\;\delta {{d}_{m}}$ – коррелированные ошибки в толщинах всех слоев покрытия (m – общее число этих слоев). Эффект самокомпенсации проявляется в том, что вызванные этими ошибками вариации спектральных характеристик покрытия оказываются существенно меньшими, чем в случае, когда ошибки в толщинах слоев являются независимыми нормально распределенными случайными величинами со среднеквадратичными отклонениями, равными |δd_j| (см. [14]).

Математическое описание процесса корреляции ошибок было дано в работе [9]. Для представления основного результата этой работы введем в рассмотрение вектор ошибок в толщинах слоев покрытия $\Delta = {{\{ \delta {{d}_{1}},\; \ldots ,\;\delta {{d}_{m}}\} }^{{\text{т}}}}$. При рассмотрении условий корреляции ошибок (2) для каждого из слоев покрытия, начиная с j = 2, появляются матрицы

в которых $\partial {{T}_{j}}{\text{/}}\partial {{d}_{i}}$ – частные производные парциальных коэффициентов пропускания для подсистем из первых j слоев по толщинам уже напыленных слоев.

Пусть $\lambda _{i}^{j}$ и $P_{j}^{i}$ – собственные значения и собственные векторы матриц C_j, а $p_{1}^{{ij}},\; \ldots ,\;p_{j}^{{ij}}$ – элементы собственных векторов $P_{j}^{i}$. С их помощью для всех i от 1 до j и всех  j от 2 до m вводятся векторы-строки

которые затем образуют прямоугольную матрицу W размерности k × m, где m – число слоев покрытия, а $k = (m - 1)(m + 2){\text{/}}2$. В соответствии с результатами работы [9] (см. также [11]) корреляция ошибок процесса напыления, описываемая условиями (2), приводит к малости нормы вектора WΔ.

Пусть

есть сингулярное разложение прямоугольной матрицы W. При этом U и V – ортогональные матрицы размерности k × k и m × m соответственно, а Σ – прямоугольная матрица k × m, на диагонали которой стоят сингулярные значения матрицы W.

Используя сингулярное разложение (5), квадрат нормы вектора WΔ можно представить в виде

где σ_i – сингулярные числа матрицы W, а V_i – столбцы матрицы V.

В соответствии с результатами [9], [11] корреляция ошибок в толщинах слоев покрытия, т.е. корреляция компонент вектора Δ, приводит к тому, что величина нормы вектора WΔ оказывается малой. Для формализации понятия малости этой нормы в [11] был введен параметр α, вычисляемый в виде

где Δ⁰ – нормированный вектор ошибок Δ, а $\left\langle {{{{\left\| {W{{\Delta }^{r}}} \right\|}}^{2}}} \right\rangle $ – среднее значение квадрата нормы WΔ^r на сфере $\left\| {{{\Delta }^{r}}} \right\| = 1$ для векторов единичной длины и случайного направления. Данное среднее значение явно выражается через сингулярные числа матрицы W [11]:

В [11] было предложено считать, что процесс корреляции ошибок тем сильнее, чем меньше α. При этом на примере рассматриваемого нами 50-слойного фильтра было показано, что в случае случайных векторов ошибок вероятность получения значения α, меньшего, чем 0.1, составляет всего 0.000333. В силу этого было предложено говорить о сильной корреляции ошибок в случае, если нормированному вектору ошибок Δ соответствует значение α, меньшее 0.1.

Условия проводимых с помощью программного обеспечения OptiLayer [13] вычислительных экспериментов по напылению 50-слойного фильтра детально описаны в [14]. На фиг. 2 представлена гистограмма значений α, построенная по 100 векторам ошибок, полученным в ходе подобных экспериментов.

При этом полученное в 100 экспериментах минимальное значение α равно 0.0145, среднее – 0.0336, а максимальное – 0.0731. Как мы видим, во всех экспериментах наблюдается сильная корреляция ошибок.

Перейдем теперь к рассмотрению собственно эффекта самокомпенсации ошибок. Пусть MF – функционал, оценивающий качество решения обратной задачи проектирования оптического покрытия [2]. В случае рассматриваемого нами неполяризующего фильтра он имеет вид

где T_s, T_p – зависящие от длины волны коэффициенты пропускания фильтра для s- и p-поляризованных волн при угле падения света 45°, $\hat {T}$ – одинаковый для обоих коэффициентов целевой коэффициент пропускания, равный 100% в области от 900 до 990 нм и 0 в области от 1010 до 1100 нм, L – число точек сетки длин волн. Шаг сетки по длинам волн в обеих областях – 1 нм.

При проектировании оптических покрытий принято оценивать качество решения задачи проектирования с помощью функционалов типа (9), поскольку подобная оценка имеет очевидный смысл, а именно, представляет собой среднеквадратичное отклонение в процентах фактических характеристик покрытия от целевых характеристик на заданной сетке длин волн. Однако при практическом решении задач удобнее минимизировать функционал F = MF². Пусть A – матрица Гессе этого функционала:

Пусть λ_j – собственные значения этой матрицы, а Q_j – ее собственные векторы. На решении задачи проектирования функционал F достигает минимума и соответственно его приращение в случае наличия ошибок в толщинах слоев может быть записано в виде

В работе [9] было показано, что в случае поляризатора лазерного излучения сильный эффект самокомпенсации ошибок достигался благодаря наличию двух факторов. Во-первых, число существенно отличных от нуля собственных значений матрицы Гессе намного меньше, чем размерность m пространства решений задачи проектирования. Во-вторых, процесс корреляции ошибок приводит к тому, что вектор ошибок Δ оказывается “почти ортогональным” собственным векторам Q_i, соответствующим этим собственным значениям. Точно такая же картина наблюдается и в случае рассматриваемого нами неполяризующего фильтра.

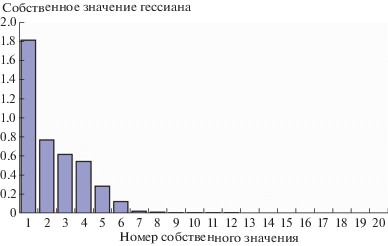
На фиг. 3 представлены собственные значения матрицы Гессе для функционала F, равного квадрату функционала MF из оценки (9). Как видно, собственные значения быстро убывают, и в дальнейшем мы будем рассматривать только первые шесть из них.

В табл. 1 приведены среднеквадратичные значения скалярных произведений нормированных векторов ошибок $\Delta {\text{'}} = {\Delta \mathord{\left/ {\vphantom {\Delta {\left\| \Delta \right\|}}} \right. \kern-0em} {\left\| \Delta \right\|}}$ с первыми шестью собственными векторами Q_i. Эти среднеквадратичные значения рассчитаны по всем 100 векторам ошибок, полученным в ходе описанных выше вычислительных экспериментов по симуляции процесса напыления. Как следует из этой таблицы, значения скалярных произведений (Δ', Q_i) действительно малы, т.е. векторы ошибок Δ оказываются почти ортогональными собственным векторам матрицы Гессе, соответствующим ее главным собственным значениям.

2. ОЦЕНКА СИЛЫ ЭФФЕКТА САМОКОМПЕНСАЦИИ ОШИБОК

Несмотря на корреляцию ошибок в толщинах слоев, векторы ошибок Δ имеют одновременно и случайный характер, поскольку определяются множеством случайных факторов [14]. Поэтому очевидно, что оценка силы эффекта самокомпенсации ошибок должна иметь статистическую форму. При этом естественно сравнивать влияние коррелированности ошибок на качество решения задачи проектирования с влиянием некоррелированных ошибок.

Для оценки влияния ошибок на решение задачи проектирования будем использовать функционал MF типа (9), поскольку, как уже отмечалось выше, такие функционалы имеют ясный физический смысл и широко используются на практике [2]. Пусть Δ – вектор коррелированных ошибок, а δMF(Δ) – приращение функционала MF, соответствующее этому вектору ошибок. Некоррелированные ошибки в толщинах слоев покрытий в наибольшей степени соответствуют процессам производства с такими широко используемыми методами контроля, как контроль по времени напыления и контроль по кварцевому датчику [3]. Принято считать, что при использовании этих методов наилучшая точность контроля толщин слоев составляет порядка 1% от планируемых толщин слоев. Мы воспользуемся этой оценкой для задания некоррелированных ошибок в толщинах слоев.

На фиг. 4 представлены гистограммы значений функционала MF, рассчитанные по 10 000 случайных векторов ошибок, генерировавшихся двумя способами. В первом случае (синие ромбы) ошибки в толщинах слоев задавались гауссовым распределением с нулевым математическим ожиданием и среднеквадратичными отклонениями, равными 1% от толщин соответствующих слоев (см. фиг. 1б). Вторая гистограмма (розовые квадраты) построена для векторов ошибок со случайными направлениями и нормой 9.717 нм. Эта величина соответствует норме вектора ошибок, вычисленного для случая, когда ошибки толщин слоев составляют 1% от теоретических толщин.

Как видно, характер обеих гистограмм на фиг. 4 очень близок, среднеквадратичные значения MF составляют примерно 2.686 и 2.751. Поэтому при задании некоррелированных ошибок достаточно рассматривать случайные векторы на сфере с радиусом, равным одной сотой нормы вектора толщины покрытия.

Обозначим через $\left\langle {\delta MF} \right\rangle $ среднеквадратичное отклонение функционала MF в случае некоррелированных ошибок. Оценку силы эффекта самокомпенсации для конкретного вектора коррелированных ошибок Δ будем производить с помощью величины

где величина в числителе рассчитана как среднее по всем векторам ошибок со случайными направлениями и нормой ошибки, соответствующей средней ошибке толщин слоев в 1%. Как указывалось выше, эта величина характерна для современных процессов напыления и алгоритмов широкополосного мониторинга.

На фиг. 5a представлены гистограммы значений S для 100 коррелированных векторов ошибок, полученных в ходе вычислительных экспериментов по симуляции процесса напыления (см. разд. 2). Как видно из этого рисунка, для всех коррелированных векторов ошибок величины S больше 1. При этом среднее значение S составляет 5.75.

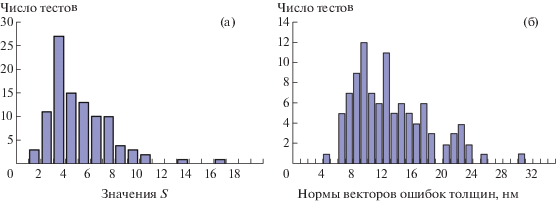
Наряду с эффектом самокомпенсации ошибок, корреляция ошибок в толщинах слоев вызывает еще и негативный эффект роста этих ошибок. Несомненно, что с наличием этого эффекта связан значительный разброс норм векторов ошибок на гистограмме, представленной на фиг. 5б. Этот вывод подтверждается исследованием наличия корреляции между значениями параметра корреляции α (фиг. 2) и значениями норм векторов ошибок. Коэффициент корреляции значений 1/α и нормы вектора ошибок в наших экспериментах составляет 0.53.

Следует заметить, что в то же время не наблюдается заметной корреляции между значениями 1/α и S, в нашем случае коэффициент корреляции для этих величин равен 0.07.

В целом представленные на фиг. 5 результаты свидетельствуют о наличии сильного эффекта самокомпенсации ошибок в рассматриваемом нами случае. Среднее значение S (5.751) намного превышает 1 несмотря на то, что среднеквадратичное значение нормы вектора ошибок составляет 14.1 нм, т.е. заметно превышает значение нормы некоррелированных ошибок, для которых рассчитывалась величина $\left\langle {\delta MF} \right\rangle $ в формуле (12).

ЗАКЛЮЧЕНИЕ

В работе развит подход к исследованию корреляции ошибок в толщинах слоев оптических покрытий и связанному с ней эффекту самокомпенсации этих ошибок при широкополосном оптическом контроле процесса напыления. Введена новая форма оценки силы эффекта самокомпенсации, основанная на наиболее адекватном с точки зрения практики сравнении с влиянием некоррелированных ошибок. Показано, что практическое исследование наличия эффекта самокомпенсации может адекватно проводиться на основе двух параметров, характеризующих степень коррелированности ошибок и силу эффекта самокомпенсации. Эти параметры находятся на основе вычислительных экспериментов по симуляции процесса напыления покрытий. Получаемые при таком подходе результаты в полной мере соответствуют полученным ранее результатам по исследованию эффекта самокомпенсации ошибок на основе сингулярного разложения специальных прямоугольных матриц, описывающих процесс корреляции ошибок при широкополосном оптическом контроле. В то же время исследование эффекта самокомпенсации на основе серии вычислительных экспериментов по симуляции процесса напыления более доступно для практического применения благодаря достаточно широкому наличию соответствующих программных средств.