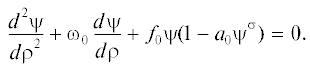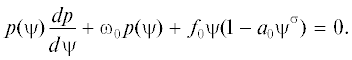Журнал вычислительной математики и математической физики, 2020, T. 60, № 8, стр. 1315-1328

Параметризации решений уравнения Эмдена–Фаулера и модель Томаса–Ферми сжатого атома

С. В. Пикулин^*

ВЦ ФИЦ ИУ РАН
119234 Москва, ул. Вавилова, 40, Россия

Поступила в редакцию 15.02.2020
После доработки 15.02.2020
Принята к публикации 09.04.2020

DOI: 10.31857/S004446692008013X

Аннотация

Для нелинейного уравнения Эмдена–Фаулера рассмотрены сингулярная задача Коши и сингулярная двухточечная краевая задача на полупрямой $r \in [0, + \infty )$ и на отрезке $r \in [0,R]$ с краевым условием первого рода в начале координат и условием третьего рода в правом конце промежутка. Данная постановка краевой задачи при специальных значениях параметров отвечает модели Томаса–Ферми распределения плотности заряда внутри сферически симметричного тяжелого охлажденного атома, заключенного в ограниченном объеме либо занимающего все доступное пространство, где величина $R$ соответствует границе сжатого атома и обращается в бесконечность для несжатого атома. Для краевой задачи на полупрямой получено новое параметрическое представление решения, охватывающее полный промежуток изменения аргумента, т.е. числовой луч $r \in [0, + \infty )$, с параметром $t$, пробегающим единичный отрезок. Для входящих в данное представление аналитических функций дан алгоритм явного вычисления коэффициентов Тейлора при $t = 0$. В приложении к задаче Томаса–Ферми о свободном атоме предъявлены соответствующие тейлоровские разложения, и продемонстрирован экспоненциальный характер их сходимости на единичном отрезке $t \in [0,1]$ с более высокой скоростью сходимости, чем у построенного ранее аналогичного представления. Дан эффективный аналитико-численный метод, позволяющий вычислить решение задачи Томаса–Ферми на полупрямой с любой наперед заданной точностью не только в окрестности $r = + \infty $, но также и в любой точке луча $r \in [0, + \infty )$. Получена новая формула для критического значения производной при постановке задачи Коши в начале координат, соответствующего решению задачи на полупрямой. В численном эксперименте показано, что полученная формула является более эффективной по сравнению с известной формулой Майораны. Для решения задачи Коши с положительным значением производной в начале координат получена параметризация решения, обеспечивающая выполнение краевых условий сингулярной краевой задачи на отрезке $r \in [0,R]$ при подходящем $R > 0$. Построен эффективный аналитико-численный метод решения такой задачи Коши и проведена его численная реализация. Библ. 23. Фиг. 4. Табл. 1.

Ключевые слова: уравнение Эмдена–Фаулера, сингулярная задача Коши, параметрическое представление, задача Томаса–Ферми, модель сжатого атома, уравнение Абеля II рода, модифицированный тест Пенлеве.

1. ВВЕДЕНИЕ

1.1. Задача Томаса–Ферми и уравнение Эмдена–Фаулера

Согласно известной модели Томаса–Ферми (см. [1], [2]) распределение кулоновского потенциала и плотности электронов внутри охлажденного ионизированного тяжелого атома или иона может быть описано с помощью коэффициента экранирования $\Psi (r)$, удовлетворяющего уравнению

(1.1)

$\frac{{{{d}^{2}}\Psi }}{{d{{r}^{2}}}} - \frac{1}{{\sqrt r }}{{\Psi }^{{3/2}}}(r) = 0,\quad r \in (0,R),\quad R \in (0, + \infty ].$

В данной модели рассматриваются как уединенные частицы (атомы и ионы), так и сжатые в ограниченном объеме, например, помещенные внутрь кристаллической решетки. Случай уединенной частицы отвечает краевым условиям

(1.2)

$\mathop {lim}\limits_{r \to + 0} \Psi (r) = Z,$

(1.3)

$\mathop {lim}\limits_{r \to R} \Psi (r) = 0,$

для уравнения (1.1), где физически $R > 0$ – размер, $Z > 0$ – заряд ядра, причем $R = + \infty $ в модели атома и $R \in (0, + \infty )$ в модели положительно заряженного иона. В случае сжатой частицы постановка задачи для уравнения (1.1) включает условие (1.2) в начале координат и условие третьего рода

(1.4)

$\Psi (R) - R\frac{{d\Psi }}{{dr}}(R) = 0$

в правом конце $r = R$ промежутка интегрирования. Отметим, что при $R = + \infty $ условие (1.3), понимаемое в смысле предела при $r \to \infty $, и условие (1.4) совпадают, так как решение $\Psi (r)$ задачи (1.1)–(1.3) при $R = + \infty $ удовлетворяет соотношениям (см. [3]):

(1.5)

$\Psi (r) = O({{r}^{{ - 3}}}),\quad \frac{{d\Psi }}{{dr}} = O({{r}^{{ - 4}}}),\quad r \to \infty .$

Уравнение (1.1) является частным примером следующего уравнения Эмдена–Фаулера (см. [4, гл. VII]):

(1.6)

$\frac{{{{d}^{2}}y}}{{d{{r}^{2}}}} - {{a}_{0}}{{r}^{\nu }}{{y}^{{1 + \sigma }}}(r) = 0,\quad {{a}_{0}} \ne 0,\quad \sigma \ne 0,\quad r > 0,$

при $\nu = - 1{\text{/}}2$, $\sigma = 1{\text{/}}2$, ${{a}_{0}} = 1$. Помимо атомной теории (см. [5, § 70]), сингулярное нелинейное уравнение (1.6) возникает также в задачах астрофизики ([6], [7]), теории погранслоя (см. [8], [9]) и в других приложениях.

Разработке методов решения различных задач для уравнений (1.1), (1.6) посвящена обширная литература (см., например, работы [10]–[14], а также [15] и цитированные там источники).

1.2. Сингулярная задача Коши и двухточечные краевые задачи для уравнения Эмдена–Фаулера

Для уравнения

(1.7)

$\frac{{{{d}^{2}}y}}{{d{{r}^{2}}}} - {{r}^{\nu }}{{y}^{{1 + \sigma }}}(r) = 0,\quad r \in (0,R),\quad \nu > - 1,\quad \sigma > 0,$

вида (1.6) при ${{a}_{0}} = 1$ с условиями, заданными в начале координат

(1.8)

$\mathop {lim}\limits_{r \to + 0} y(r) = Z,\quad Z \in (0, + \infty ),$

(1.9)

$\frac{{dy}}{{dr}}(0) = b,\quad b = {\text{const}} \in \mathbb{R},$

сингулярная задача Коши (1.7)–(1.9) имеет в окрестности нуля единственное решение для любого $b \in \mathbb{R}$ согласно теореме Каратеодори (см. [16, гл. 2, § 1]). При этом существует некоторый критический наклон $b = B < 0$ графика в нуле, приводящий к решению двухточечной краевой задачи для уравнения (1.7) на полупрямой с условиями первого рода (1.8) и

(1.10)

$\mathop {lim}\limits_{r \to + \infty } y(r) = 0.$

При $b < B$ траектория решения задачи (1.7)–(1.9) пересекает горизонтальную ось в некоторой конечной точке $r = R \in (0, + \infty )$, где выполняется условие типа (1.3):

(1.11)

$y(R) = 0.$

При $b > B$ решение $y(r)$ неограниченно растет с ростом $r$ и при некотором конечном $r = R$ удовлетворяет условию

(1.12)

$y(R) - R\frac{{dy}}{{dr}}(R) = 0,\quad R \in (0, + \infty ).$

Решаемая проблема заключается, во-первых, в вычислении критического значения $B$ и, во-вторых, в построении таких аналитических представлений решений уравнения (1.7), подчиненных условиям (1.8) и (1.10), (1.11) или (1.12), которые допускают эффективную численную реализацию.

В статье [15] дана формула критического наклона $B$ при условии рациональности показателя $\nu > - 1$ в уравнения (1.7). Частным случаем этого результата является известная формула Майораны (см. [17]). Кроме того, в [15] построено параметрическое представление семейства решений двухточечной краевой задачи (1.7), (1.8), (1.11) при $R \in (0, + \infty ]$, или, иначе говоря, семейства решений задачи Коши (1.7)–(1.9) при $b \in ( - \infty ,B]$.

В настоящей работе получены аналогичные параметрическое представление решения задачи Коши (1.7)–(1.9) при $b = B$, т.е. краевой задачи на полупрямой (см. теорему 1), а также представление решения задачи при $b > 0$, где в концах отрезка параметризации решение $y(r)$ удовлетворяет краевым условиям (1.8) и (1.12) (см. теорему 2). Отметим, что условие первого рода (1.10) является предельным случаем условия третьего рода (1.12) при обращении $R$ в бесконечность. Задача Коши при отрицательных значениях $b$ из промежутка $(B,0]$ в данной работе не рассмотрена.

Построенная параметризация решения задачи Коши при $b > 0$ не дает, строго говоря, метода решения краевой задачи (1.7), (1.8), (1.12) при заданном $R$, поскольку значение $b$ в этом случае не задано. Однако в приложениях требуемое значение $b$ может быть известно: например, в модели Томаса–Ферми $b$ имеет физический смысл энергии взаимодействия (см. [5]). Соответствующая величина $R$ в этом случае находится как значение параметризующей функции $r(t)$ в конце отрезка параметризации.

Для критического значения $B$ получена новая формула на основе суммирования сходящегося с экспоненциальной скоростью числового ряда, имеющего явно вычисляемые коэффициенты. Для задачи Томаса–Ферми начальный отрезок соответствующего ряда вычислен явно, и продемонстрирована его более быстрая сходимость по сравнению с аналогичным рядом в формуле Майораны.

1.3. Параметрические представления решения задачи на полуоси

Предполагая в дальнейшем, что входящие в уравнения (1.6), (1.7) показатели $\sigma $ и $\nu $ удовлетворяют условиям

(1.13)

$\nu \ne - 2,\quad \nu + \sigma \ne - 2,$

введем следующие обозначения:

(1.14)

$\beta : = \frac{{\nu + 2}}{\sigma } \ne 0,\quad {{f}_{0}}: = \beta (\beta + 1) \ne 0,\quad {{\omega }_{0}}: = - (2\beta + 1),\quad K: = \frac{1}{{\sigma \beta }} = \frac{1}{{\nu + 2}}.$

Известно (см. [15, теорема 1]), что при $\sigma > 0$ и при рациональном $\nu > - 1$, т.е.

$\nu = :\frac{N}{M},\quad N \in \mathbb{Z},\quad M \in \mathbb{N},$

справедливо следующее параметрическое представление решения задачи (1.7), (1.8), (1.10) на полупрямой $r \in [0, + \infty )$:

(1.15)

$r(t) = \frac{{\mathop {{{f}_{0}}}\nolimits^K }}{{\mathcal{H}(1)}}{{Z}^{{ - 1/\beta }}}{{t}^{{1/\alpha }}}{{(1 - t)}^{M}}\mathcal{H}(t),\quad y(t) = {{\mathcal{H}}^{\beta }}(1)Z{{t}^{{ - \beta /\alpha }}}{{\mathcal{H}}^{{ - \beta }}}(t),\quad t \in (0,1],$

где величины $\beta ,\;{{f}_{0}},\;K > 0$ заданы формулами (1.14),

(1.16)

$\alpha : = - \frac{{{{\omega }_{0}} + \sqrt {\omega _{0}^{2} + 4\sigma {{f}_{0}}} }}{2} < 0,$

положительная функция $\mathcal{H}(t)$ сохраняет аналитичность на всем отрезке параметризации $t \in [0,1]$, включая обе его концевые точки. В работе [15] построены формулы вычисления коэффициентов ряда Тейлора функции $\mathcal{H}(t)$ при $t = 0$ в конечном виде.

В случае задачи Томаса–Ферми (1.1)–(1.3) при $R = + \infty $, т.е. задачи (1.7), (1.8), (1.10) при $ - \nu = \sigma = 1{\text{/}}2$ ряд Тейлора функции $\mathcal{H}(t)$ в представлении (1.15) демонстрирует в численном эксперименте экспоненциально быструю сходимость на всем отрезке параметризации $t \in [0,1]$ с радиусом сходимости $ \approx {\kern 1pt} 1.2$ (см. [15, теорема 7]).

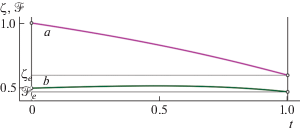
В настоящей работе построено (см. теорему 1) аналогичное (1.15) новое параметрическое представление решения задачи (1.7), (1.8), (1.10), где в качестве параметра выбрана другая переменная, пробегающая также единичный отрезок. В применении к задаче Томаса–Ферми эта новая параметризация демонстрирует еще более быструю экспоненциальную сходимость с эмпирическим (т.е. найденным численно) радиусом сходимости $ \approx {\kern 1pt} 1.5$ (см. фиг. 3, табл. 1).

Фиг. 1.

Графики решений задачи (1.1), (1.2), (1.4), $Z = 1$: линия a – при $R = + \infty $, $y_{r}^{'}(0) = B \approx - 1.588$ (модель свободного атома Томаса–Ферми); линия b – при $R \approx 0.83$, $y_{r}^{'}(0) = {{10}^{{ - 3}}}$ (модель сжатого атома Томаса–Ферми).

Фиг. 2.

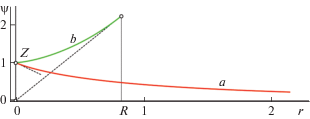
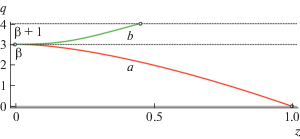
Графики функции $q(z)$: линия a – сепаратриса седла $z = 1$, $q = 0$; линия b – траектория, ведущая из точки (2.10) в некоторую точку на прямой (2.12).

Фиг. 3.

Абсолютные величины тейлоровских коэффициентов в полулогарифмической шкале: линия a – для функции $\mathcal{H}(t)$ из представления (1.15); линия b – для функции $\mathcal{F}(t)$ из представления (4.3).

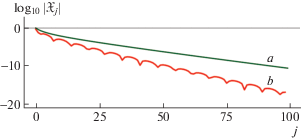
Таблица 1.

Коэффициенты тейлоровских разложений (4.7)

j	${{\zeta }_{j}}$	${{F}_{j}}$	${{\mathcal{F}}_{j}}$
0	1.0	0.0	0.5
1	–2.9533364544E–01	–3.83210945E–01	5.83945274E–02
2	–7.4161080174E–02	–1.80565206E–01	–2.43726822E–02
3	–2.6019524330E–02	–9.64937461E–02	–3.05254965E–02
4	–8.4242415553E–03	–5.12759165E–02	–2.04407837E–02
5	–1.4015234843E–03	–2.57139891E–02	–1.03946693E–02
6	1.1159354471E–03	–1.15211011E–02	–3.81327351E–03
7	1.6545126696E–03	–4.08944635E–03	–3.90582397E–04
8	1.4088585127E–03	–5.88964617E–04	9.57424468E–04
9	9.5001385209E–04	7.53253283E–04	1.19040694E–03
10	5.2745463992E–04	1.02089432E–03	9.50353629E–04
11	2.2419700374E–04	8.40391994E–04	5.96439141E–04
12	4.3457487590E–05	5.42688574E–04	2.92825462E–04
13	–4.2859665627E–05	2.78053388E–04	8.94672998E–05
14	–6.8780919226E–05	9.51891916E–05	–1.98371089E–05
15	–6.2863370748E–05	–7.31107997E–06	–6.16857848E–05
16	–4.4757016704E–05	–5.00969534E–05	–6.41907493E–05
17	–2.5773970513E–05	–5.65613698E–05	–4.90885115E–05
18	–1.1017091429E–05	–4.55747799E–05	–3.00754398E–05
19	–1.7074035119E–06	–2.95541670E–05	–1.40631083E–05
20	2.9176323006E–06	–1.51661066E–05	–3.34673631E–06
21	4.3165669692E–06	–4.97748979E–06	2.35322605E–06
22	3.9144385311E–06	8.65727547E–07	4.38542273E–06
23	2.7856075925E–06	3.33263893E–06	4.24937609E–06
24	1.5928187835E–06	3.66554426E–06	3.15143830E–06
25	6.5536267050E–07	2.93804847E–06	1.87554200E–06
26	6.0034153292E–08	1.89433614E–06	8.25219758E–07
27	–2.3391715372E–07	9.52644429E–07	1.33005016E–07
28	–3.1674809848E–07	2.82731613E–07	–2.25248222E–07
29	–2.8056606611E–07	–1.00591374E–07	–3.40629629E–07
30	–1.9673292863E–07	–2.58088731E–07	–3.13795121E–07
31	–1.1014089154E–07	–2.71590941E–07	–2.26005912E–07
32	–4.2691342596E–08	–2.13630271E–07	–1.30160788E–07
33	–2.8554025466E–10	–1.35365078E–07	–5.32640063E–08
34	2.0147810733E–08	–6.58699421E–08	–3.67867890E–09
35	2.5232707912E–08	–1.69394478E–08	2.10625465E–08
36	2.1741548744E–08	1.06142554E–08	2.80083528E–08
37	1.4936555241E–08	2.14120854E–08	2.47391569E–08
38	8.1273068843E–09	2.15975946E–08	1.73087461E–08
39	2.9121558037E–09	1.66123077E–08	9.61597008E–09
40	–3.0828748875E–10	1.02915883E–08	3.60709248E–09

Неформально говоря, параметризация (1.15) отвечает представлению о нейтральном атоме как о предельном случае положительного иона с нулевой ионизацией, а новое представление (3.16) – как о предельном случае сжатого атома при отсутствии сжатия.

Использованный метод состоит в редукции исходного уравнения Эмдена–Фаулера (1.6) к такому уравнению первого порядка, которое является регулярным на всем отрезке изменения независимой переменной; эта редукция проведена в п. 2.3. Возможность описанного перехода обусловлена свойством частичного прохождения модифицированного теста Пенлеве в узловой особой точке уравнения Абеля II рода (см. [18]), получаемого из уравнения (1.6) в результате обычной процедуры понижения порядка. Описанный метод применялся в работах [15], [19], а также для построения автомодельных решений типа бегущей волны нелинейного параболического уравнения Колмогорова–Петровского–Пискунова (см. [20]).

2. ПОНИЖЕНИЕ ПОРЯДКА УРАВНЕНИЯ ЭМДЕНА–ФАУЛЕРА

В п. 2.1 данного раздела дано обобщение известной (см. [17], [18], [21], [22]) процедуры редукции уравнения (1.6) к уравнению первого порядка, сохраняющему регулярность вдоль всего исследуемого отрезка изменения независимой переменной при условии рациональности показателя $\nu $. На основе проведенного в п. 2.2 анализа краевых условий (1.8), (1.12) для уравнения Эмдена–Фаулера в п. 2.3 описана используемая далее модификация этой процедуры.

2.1. Редукция уравнения Эмдена–Фаулера к уравнению Абеля II рода

Предполагая справедливость условий (1.13) и пользуясь обозначениями (1.14), применим к уравнению (1.6) подстановку (см. [4, гл. VII]):

(2.1)

$\psi : = \mathop {{{f}_{0}}}\nolimits^{ - 1/\sigma } {{r}^{\beta }}y(r),\quad \rho : = lnr,$

тогда уравнение (1.6) принимает следующий вид:

(2.2)

Определяя новую переменную $p = p(\psi )$ в виде

(2.3)

$p(\psi ): = \frac{{d\psi }}{{d\rho }},$

понижаем порядок уравнения (2.2) и получаем уравнение Абеля II рода

(2.4)

Следуя работам [15], [18], введем в рассмотрение параметр $\tilde {N} \ne 0$ и переменные $q,z$, связанные с $p,\psi $ равенствами

(2.5)

$p = :\psi q,\quad \psi = :{{z}^{{\tilde {N}/\sigma }}},$

тогда относительно $q(z)$ уравнение (2.4) принимает вид

(2.6)

$\frac{\sigma }{{2\tilde {N}}}z\frac{{d{{q}^{2}}}}{{dz}} + {{q}^{2}}(z) + {{\omega }_{0}}q(z) + {{f}_{0}}(1 - {{a}_{0}}{{z}^{{\tilde {N}}}}) = 0.$

Подставим $q(z)$ в левую часть уравнения (2.6) в виде

(2.7)

$q(z) = :\beta (1 - {{z}^{M}}\mathcal{Q}(z)),\quad M: = K\tilde {N},$

где $K$ задано последним равенством (1.14). С учетом (1.14) и соотношения ${{\beta }^{2}} + {{\omega }_{0}}\beta + {{f}_{0}} = 0$ получаем

$\begin{gathered} \frac{\sigma }{{2\tilde {N}}}z\frac{{d{{q}^{2}}}}{{dz}} + {{q}^{2}}(z) + {{\omega }_{0}}q(z) + {{f}_{0}}(1 - {{a}_{0}}{{z}^{{\tilde {N}}}}) = - \frac{{\sigma \beta }}{{\tilde {N}}}zq({{z}^{M}}\frac{{d\mathcal{Q}}}{{dz}} + M{{z}^{{M - 1}}}\mathcal{Q}(z)) + {{\beta }^{2}}(1 - 2{{z}^{M}}\mathcal{Q}(z) + \\ + \;{{z}^{{2M}}}{{\mathcal{Q}}^{2}}(z)) + {{\omega }_{0}}\beta (1 - {{z}^{M}}\mathcal{Q}(z)) + {{f}_{0}}(1 - {{a}_{0}}{{z}^{{\tilde {N}}}}) = - \frac{1}{M}{{z}^{{M + 1}}}q\frac{{d\mathcal{Q}}}{{dz}} + {{\beta }^{2}}{{z}^{{2M}}}{{\mathcal{Q}}^{2}} + (\beta - q){{z}^{M}}\mathcal{Q} - {{a}_{0}}{{f}_{0}}{{z}^{{\tilde {N}}}} = \\ = \;\beta {{z}^{{M + 1}}}\left( { - \frac{q}{{\beta M}}\frac{{d\mathcal{Q}}}{{dz}} + (\beta + 1){{z}^{{M - 1}}}{{\mathcal{Q}}^{2}} - {{a}_{0}}(\beta + 1){{z}^{{\tilde {N} - M - 1}}}} \right), \\ \end{gathered} $

тем самым, уравнение (2.6) принимает вид

(2.8)

$\frac{{d\mathcal{Q}}}{{dz}} = K\tilde {N}(\beta + 1)\frac{{{{z}^{{K\tilde {N} - 1}}}{{\mathcal{Q}}^{2}}(z) - {{a}_{0}}{{z}^{{(1 - K)\tilde {N} - 1}}}}}{{1 - {{z}^{{K\tilde {N}}}}\mathcal{Q}(z)}}.$

Наличие произвольного параметра $\tilde {N}$ в уравнениях (2.6) и (2.8) связано с тем, что эти уравнения сохраняют свой вид при степенных заменах переменной $z$. Если $K$ является рациональным и лежит в единичном интервале, т.е.

(2.9)

$ - 1 < \nu = :\frac{N}{M} \in \mathbb{Q},\quad N \in \mathbb{Z},\quad M \in \mathbb{N},\quad K = \frac{M}{{M + 2N}} \in (0,1) \cap \mathbb{Q},\quad \tilde {N} = M + 2N,$

то за счет выбора $\tilde {N}$ равным знаменателю $K$, т.е. $(M + 2N)$, получаем, что правая часть уравнения (2.8) содержит только целые степени $z$ и, более того, аналитическим образом зависит от переменных $z,\;\mathcal{Q}$ в окрестности $z = 0$. Тем самым для уравнения (2.8) при указанных условиях справедлива теорема Коши (см. [23, гл. I, § 3]) о существовании единственного аналитического решения $\mathcal{Q}(z)$ в окрестности точки $z = 0$, $\mathcal{Q} = C$ для любого $C \in \mathbb{C}$. В этом случае все решения уравнения (2.6), проходящие через точку $z = 0$, $\mathcal{Q} = \beta $, имеют вид (2.7) c аналитической функцией $\mathcal{Q}(z)$. Все такие решения являются аналитическими функциями при $z = 0$ в силу того, что $M \in \mathbb{N}$ (см. [15, гл. I, § 3]).

Отметим, что редукция уравнения (1.6) к уравнению (2.8) была ранее известна (см. [21], [22]) в частном случае $ - \nu = \sigma \in (0,1)$ при $\tilde {N} = (2 - \sigma )(1 + {{\sigma }^{2}}{\text{/}}{{(1 - \sigma )}^{2}})$. При $ - \nu = \sigma = 1{\text{/}}2$ уравнение (2.8) с параметрами $K = 2{\text{/}}3$, $\tilde {N} = 3$, $\beta = 3$ было выведено Э. Майораной (см. [17]). В работах [15], [18] указанная редукция проведена при $\sigma > 0$ и $ - 1 < \nu \in \mathbb{Q}$, а в данной работе – при любых $\sigma ,\nu $, удовлетворяющих условиям (1.13).

Отметим, что функция $\mathcal{H}(t)$ в представлении (1.15) выражается через решение $\mathcal{Q}(z)$ соответствующего уравнения (2.8) (см. [15, п. 2.1.1]).

2.2. Краевые условия типа сжатого атома в терминах переменной $q$

Известно (см., например, [15, п. 1.5], [20, предложение 1]), что краевое условие (1.8) для уравнения (1.7) при $\sigma > 0$, $\nu > - 1$ влечет равенства

(2.10)

$z = 0,\quad q = \beta $

при всяком $Z \in (0, + \infty )$.

Известно также (см., например, [4]), что при $R = + \infty $ условие (1.12) приводит в пределе при $r \to + \infty ,y \to 0$ к равенствам

(2.11)

$z = 1,\quad q = 0.$

Отметим, что точка (2.11) является седловой для уравнения (2.6), а соответствующая траектория этого уравнения – сепаратрисой седла (см. фиг. 2, линия a).

Легко видеть, что условие (1.12), достигаемое при $y \ne 0$ (при конечных значениях $R$), выражается равенством

(2.12)

$q = \beta + 1.$

В самом деле, из первого равенства (2.5) и из (2.3) находим $q = d(ln\psi ){\text{/}}d\rho $, и с учетом (2.1) имеем

$y(R) - R\frac{{dy}}{{dr}}(R) = \left[ {\left( {1 - \frac{{dlny}}{{dlnr}}} \right)y} \right](R) = \left[ {\left( {1 + \beta - \frac{{dln\psi }}{{d\rho }}} \right)y} \right](R).$

Таким образом, траектории решения уравнения (2.6) на плоскости $(z,q)$, отвечающие решениям задачи (1.7)–(1.12), при различных $R,\;Z$ имеют один конец в точке (2.10), а второй конец – либо в точке (2.11), либо на прямой (2.12) (см. фиг. 2).

2.3. Модифицированная схема редукции

Преобразуем уравнение (2.6) таким образом, чтобы независимая переменная оказалась связана с $q$ взаимно однозначным образом. Введем в рассмотрение новую переменную $w$ с помощью следующей подстановки, аналогичной (2.7):

(2.13)

$q = :\beta (1 - \epsilon {{w}^{M}}),\quad \epsilon = \pm 1,\quad M = K\tilde {N} = \frac{{\tilde {N}}}{{\sigma \beta }},$

где параметр знака $\epsilon $ выбирается в зависимости от поведения $q$ в окрестности точки (2.10) в исследуемой задаче: $\epsilon = 1$ при $q < \beta $ либо $\epsilon = - 1$ при $q > \beta $.

Подставляя (2.13) в правую часть уравнения (2.6), находим

$\begin{gathered} \frac{\sigma }{{2\tilde {N}}}z\frac{{d{{q}^{2}}}}{{dz}} + {{q}^{2}}(z) + {{\omega }_{0}}q(z) + {{f}_{0}}(1 - {{a}_{0}}{{z}^{{\tilde {N}}}}) - \epsilon zq{{w}^{{M - 1}}}\frac{{dw}}{{dz}} + {{\beta }^{2}}(1 - 2\epsilon {{w}^{M}} + {{w}^{{2M}}}) + \\ + \;{{\omega }_{0}}\beta (1 - \epsilon {{w}^{M}}) + {{f}_{0}}(1 - {{a}_{0}}{{z}^{{\tilde {N}}}}) = \beta ( - \epsilon z(1 - \epsilon {{w}^{m}}){{w}^{{M - 1}}}\frac{{dw}}{{dz}} + \epsilon {{w}^{M}} + \beta {{w}^{{2M}}} - {{a}_{0}}(\beta + 1){{z}^{{\tilde {N}}}}), \\ \end{gathered} $

откуда получаем уравнение

(2.14)

$\frac{{dw}}{{dz}} = \frac{{\beta {{w}^{{2M}}} + \epsilon {{w}^{M}} - {{a}_{0}}(\beta + 1){{z}^{{\widetilde N}}}}}{{z(\epsilon - {{w}^{M}}){{w}^{{M - 1}}}}}.$

Переходя в уравнении (2.14) к $w$ как независимой переменной и вводя новую переменную $\zeta $ по формуле

(2.15)

$z = :\zeta w,$

находим

$\zeta + w\frac{{d\zeta }}{{dw}} = \frac{{\zeta (\epsilon - {{w}^{M}}){{w}^{M}}}}{{\beta {{w}^{{2M}}} + \epsilon {{w}^{M}} - {{a}_{0}}(\beta + 1){{\zeta }^{{\tilde {N}}}}{{w}^{{\tilde {N}}}}}},$

далее, перенося слагаемое $\zeta $ в правую часть и сокращая полученную дробь на ${{w}^{M}}$, получаем

(2.16)

$w\frac{{d\zeta }}{{dw}} = \zeta \frac{{ - (\beta + 1){{w}^{M}} + {{a}_{0}}(\beta + 1){{w}^{{\tilde {N} - M}}}{{\zeta }^{{\tilde {N}}}}}}{{\beta {{w}^{M}} + \epsilon - {{a}_{0}}(\beta + 1){{w}^{{\tilde {N} - M}}}{{\zeta }^{{\tilde {N}}}}}},\quad \frac{{d\zeta }}{{dw}} = (\beta + 1)\zeta \frac{{ - {{w}^{{K\tilde {N} - 1}}} + {{a}_{0}}{{w}^{{(1 - K)\tilde {N} - 1}}}{{\zeta }^{{\tilde {N}}}}}}{{\epsilon + \beta {{w}^{{K\tilde {N}}}} - {{a}_{0}}(\beta + 1){{w}^{{(1 - K)\tilde {N}}}}{{\zeta }^{{\tilde {N}}}}}}.$

Отметим, что если выполнены условия (2.9), то правая часть уравнения (2.16) подобно уравнению (2.8) содержит только целые неотрицательные степени переменных $\zeta ,w$ и удовлетворяет условиям теоремы Коши при $\zeta = 0$.

3. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЭМДЕНА–ФАУЛЕРА

В этом разделе получены параметрические представления решений сингулярной задачи Коши (1.7)–(1.9) при $b > 0$, удовлетворяющих в концах отрезка параметризации краевым условиям (1.8) и (1.12), а также параметризация решения сингулярной краевой задачи на полупрямой. Предполагается, что для показателя $\nu $ в уравнении (1.7) выполнены условия рациональности (2.9).

3.1. Задача на полупрямой

Рассмотрим задачу (1.7), (1.8), (1.10) на луче $r \in (0, + \infty )$. Известно (см. [4]), что при любом $Z \in (0, + \infty )$ эта задача имеет единственное решение, которое представляет собой положительную монотонно убывающую аналитическую функцию, имеющую на бесконечности асимптотику

(3.1)

$y(r) \sim \mathop {{{f}_{0}}}\nolimits^{1/\sigma } {{r}^{{ - \beta }}},\quad r \to + \infty ,$

где константы ${{f}_{0}} > 0,\;\beta > 0$ заданы равенствами (1.14). Согласно (2.1) имеем $\psi \sim 1$ при $r \to \infty $.

Проводя анализ фазовой диаграммы, можно показать (см., например, [15], [20]), что решение $y(r)$ задачи (1.7), (1.8), (1.10) в результате подстановок (2.1), (2.3), (2.5) приводит к траектории уравнения (2.6), выходящей из его седловой точки (2.10) в виде сепаратрисы с отрицательным наклоном к оси $z$ и входящей в точку (2.11), при этом решение $q(z)$ является монотонно убывающей аналитической функцией на полуинтервале $z \in (0,1]$. Если, кроме того, выполнено условие рациональности (2.9), то функция $q(z)$ аналитична при $z = 0$ и имеет разложение в ряд Тейлора по степеням $z$ (см. [15]) в виде

(3.2)

$q(z) = \beta (1 - C{{z}^{M}} + {{g}_{{\tilde {N}}}}{{z}^{{\tilde {N}}}} + {{g}_{{\tilde {N} + 1}}}{{z}^{{\tilde {N} + 1}}} + \cdots ),\quad C > 0,$

где число $C$ связано с производной в начале координат $y_{r}^{'}(0)$ решения исходной задачи (1.7)–(1.12) следующей формулой (см. [15, теорема 6]):

(3.3)

$\frac{{dy}}{{dr}}(0) = - \frac{{\beta C}}{{\mathop {{{f}_{0}}}\nolimits^K }}{{Z}^{{1 + 1/\beta }}}.$

Переходя с помощью подстановок (2.13), (2.15) при $\epsilon = 1$ к переменным $\zeta $, $w$, получаем относительно $\zeta = \zeta (w)$ задачу Коши для уравнения (2.16) на отрезке $w \in [0,1]$ с условиями

(3.4)

$\zeta (1) = 1,\quad \frac{{d\zeta }}{{dw}}(1) > 0,$

где значение производной при $w = 1$ задается требованием аналитичности решения $\zeta (w)$, соответствующего сепаратрисе седла $w = 1$, $\zeta = 1$.

Вводя новую переменную

(3.5)

$t: = 1 - w,$

получаем из (2.16), (3.4) следующую задачу относительно $\zeta (t)$:

(3.6)

$\frac{{d\zeta }}{{dt}} = (\beta + 1)\zeta (t)\frac{{{{{(1 - t)}}^{{M - 1}}} - {{{(1 - t)}}^{{\tilde {N} - M - 1}}}{{\zeta }^{{\tilde {N}}}}(t)}}{{1 + \beta {{{(1 - t)}}^{M}} - (\beta + 1){{{(1 - t)}}^{{\tilde {N} - M}}}{{\zeta }^{{\tilde {N}}}}(t)}},\quad t \in [0,1],$

(3.7)

$\zeta (0) = 1,\quad \frac{{d\zeta }}{{dt}}(0) = \gamma : = \frac{1}{\alpha } + 1 < 0,$

где $\alpha $ задано формулой (1.16), начальное значение $\gamma $ удовлетворяет требованию равенства членов нулевого порядка по $t$ в уравнении (3.6) относительно аналитической функции $\zeta (t)$:

$\gamma = (\beta + 1)\frac{{1 - M - (\tilde {N}\gamma - (\tilde {N} - M - 1))}}{{ - \beta M - (\beta + 1)(\tilde {N}\gamma - (\tilde {N} - M))}} \equiv \frac{{ - 2(\beta + 1)M - (\beta + 1)\tilde {N}(\gamma - 1)}}{{{{\omega }_{0}}M - (\beta + 1)\tilde {N}(\gamma - 1)}},$

$\gamma - 1 = \frac{{ - 1}}{{{{\omega }_{0}} - \sigma \beta (\beta + 1)(\gamma - 1)}},\quad - {\kern 1pt} \sigma {{f}_{0}}{{(\gamma - 1)}^{2}} + {{\omega }_{0}}(\gamma - 1) + 1 = 0.$

Ряд Тейлора функции $\zeta (t)$ в точке $t = 0$ можно найти из уравнения (3.6) методом неопределенных коэффициентов по аналогии с рядом Тейлора для решения $\mathcal{Q}(z)$ уравнения (2.8) при $z = 1$ (см. [15, п. 2.1.2]).

Из подстановок (2.3), (2.5), (2.7), (2.15) находим

$\rho = \mathop \smallint \limits^\psi \frac{{d\psi }}{{p(\psi )}} = \mathop \smallint \limits^\psi \frac{{d\ln \psi }}{{q(\psi )}} = \frac{{\tilde {N}}}{\sigma }\mathop \smallint \limits^z \frac{{d\ln z}}{{q(z)}} = \frac{{\tilde {N}}}{{\sigma \beta }}\left( {\mathop \smallint \limits^w \frac{{d\ln w}}{{1 - {{w}^{M}}}} + \mathop \smallint \limits^w \frac{{d\ln \zeta (w)}}{{1 - {{w}^{M}}}}} \right) = :{{J}_{1}}(w) + {{J}_{2}}(w),$

где с учетом последнего равенства (2.13) получаем

(3.8)

${{J}_{1}} = M\mathop \smallint \limits^w \frac{{d\ln w}}{{1 - {{w}^{M}}}} = \mathop \smallint \limits^w \left( {\frac{1}{{{{w}^{M}}}} + \frac{1}{{1 - {{w}^{M}}}}} \right)d{{w}^{M}} = \ln \frac{{{{w}^{M}}}}{{1 - {{w}^{M}}}} + {{c}_{1}},\quad {{c}_{1}} = {\text{const}},$

(3.9)

${{J}_{2}} = M\mathop \smallint \limits^w \frac{{d\ln \zeta (w)}}{{1 - {{w}^{M}}}} = M\mathop \smallint \limits^w \frac{{\zeta {\kern 1pt} '(w){\text{/}}\zeta (w)}}{{(1 - w)(1 + w + \cdots + {{w}^{{M - 1}}})}}dw.$

Исходя из условий (3.4) и подстановки (3.5), находим $(\zeta _{w}^{'}{\text{/}}\zeta ) = - \gamma $ при $w = 1$, следовательно, подынтегральное выражение в правой части равенства (3.9) имеет при $w = 1$ полюс с вычетом $(\gamma {\text{/}}M)$. Таким образом, имеем

(3.10)

${{J}_{2}} = \gamma \mathop \smallint \limits^w \frac{{dw}}{{w - 1}} + \mathop \smallint \limits^w \frac{{h(w)}}{{1 + w + \cdots + {{w}^{{M - 1}}}}}dw,$

где функция

$h(w): = \frac{{M\zeta {\text{'}}(w){\text{/}}\zeta (w) + \gamma (1 + w + \cdots + {{w}^{{M - 1}}})}}{{1 - w}},$

является аналитической при $w = 1$, точнее, имеет устранимую особенность в этой точке (полюс первого порядка с нулевым вычетом).

Переходя к переменной $t$ с помощью замены (3.5) и вводя в рассмотрение многочлен

(3.11)

$P(t): = 1 + (1 - t) + \cdots + {{(1 - t)}^{{M - 1}}} = \frac{{1 - {{{(1 - t)}}^{M}}}}{t} \geqslant P(1) = 1,\quad t \in [0,1],$

на основании подстановок (2.1), (2.5), (2.15) и равенств (2.13), (3.8)–(3.10) получаем

(3.12)

$\begin{gathered} r(t) = exp\rho = {{C}_{1}}{{t}^{{\gamma - 1}}}{{(1 - t)}^{M}}\mathcal{F}(t),\quad {{C}_{1}} = {\text{const}} > 0, \\ y(t) = \mathop {{{f}_{0}}}\nolimits^{1/\sigma } {{r}^{{ - \beta }}}{{(\zeta w)}^{{\widetilde N/\sigma }}} = {{C}_{2}}{{t}^{{(1 - \gamma )\beta }}}{{\mathcal{F}}^{{ - \beta }}}(t){{\zeta }^{{\widetilde N/\sigma }}}(t),\quad {{C}_{2}} = \mathop {{{f}_{0}}}\nolimits^{1/\sigma } \mathop {{{C}_{1}}}\nolimits^{ - \beta } , \\ \end{gathered} $

где

(3.13)

$\mathcal{F}(t) = \frac{{expF(t)}}{{P(t)}},\quad F(t): = \int\limits_0^t {f(t)dt} ,\quad f(t): = \frac{{(M\zeta {\text{'}}(t){\text{/}}\zeta (t) - \gamma P(t)){{t}^{{ - 1}}}}}{{P(t)}}.$

Отметим, что коэффициенты ряда Тейлора для функций $f(t),\;F(t),\;\mathcal{F}(t)$ выражаются в конечном виде через соответствующие коэффициенты $\zeta (t)$ (аналогичные формулы см., например, [15, п. 2.12]).

Вводя обозначения

(3.14)

${{\zeta }_{e}}: = {{\left. {\zeta (t)} \right|}_{{t = 1}}},\quad {{\mathcal{F}}_{e}}: = {{\left. {\mathcal{F}(t)} \right|}_{{t = 1}}},$

находим константу ${{C}_{1}}$ в представлении (3.12) из краевого условия (1.8), т.е. $y = Z$ при $t = 1$:

$Z = \mathop {{{f}_{0}}}\nolimits^{1/\sigma } \mathop {{{C}_{1}}}\nolimits^{ - \beta } \mathcal{F}_{e}^{{ - \beta }}\zeta _{e}^{{\tilde {N}/\sigma }},\quad {{C}_{1}} = {{Z}^{{ - 1/\beta }}}\mathop {{{f}_{0}}}\nolimits^K \frac{{\zeta _{e}^{M}}}{{{{\mathcal{F}}_{e}}}}.$

Найдем производную решения $y(r)$ в начале координат $r = 0$. Сопоставляя (3.2), (2.15) и (2.13) при $\varepsilon = 1$, находим $C = 1{\text{/}}{{\zeta }^{M}}$ при $z = w = 0$, откуда по формуле (3.3) получаем

(3.15)

$\frac{{dy}}{{dr}}(0) = B{{Z}^{{1 + 1/\beta }}},\quad B = - \frac{\beta }{{f_{0}^{K}\zeta _{e}^{M}}} < 0.$

На основании изложенного приходим к следующему результату.

Теорема 1. Для решения задачи (1.7), (1.8), (1.10) при рациональном $\nu $ вида (2.9) справедливо следующее параметрическое представление:

(3.16)

$r(t) = {{Z}^{{ - 1/\beta }}}\mathop {{{f}_{0}}}\nolimits^K \frac{{\zeta _{e}^{M}}}{{{{\mathcal{F}}_{e}}}}{{t}^{{1/\alpha }}}{{(1 - t)}^{M}}\mathcal{F}(t),\quad y(t) = Z\frac{{\mathcal{F}_{e}^{\beta }}}{{\zeta _{e}^{{\tilde {N}/\sigma }}}}{{t}^{{ - \beta /\alpha }}}\frac{{{{\zeta }^{{\tilde {N}/\sigma }}}(t)}}{{{{\mathcal{F}}^{\beta }}(t)}},$

где функции $\zeta (t),\;\mathcal{F}(t)$ являются положительными и аналитическими на отрезке $[0,1]$, причем $\zeta (t)$ удовлетворяет уравнению (3.6) и условиям (3.7), а $\mathcal{F}(t)$ выражается через $\zeta (t)$ по формулам (3.11), (3.13), константы $\beta ,$ ${{f}_{0}},$ $M,$ $\tilde {N},$ $K,$ $\alpha ,$ ${{\zeta }_{e}},$ ${{\mathcal{F}}_{e}}$ находятся по формулам (1.14), (2.9), (1.16), (3.14). Производная решения в нуле ${{y}_{r}}(0)$ вычисляется по формуле (3.15).

3.2. Задача на отрезке

Рассмотрим задачу (1.7)–(1.12), (2.9) при $R \in (0, + \infty )$. В качестве входных данных вместо пары $(Z,R)$ будем рассматривать данные Коши – пару $(Z,b)$, где наклон $b: = y_{r}^{'}(0)$ графика решения в начале координат превышает критическое значение (3.15): $b > B{{Z}^{{1 + 1/\beta }}}$.

Построим параметрическое представление решения $y(r)$ этой задачи, ограничившись рассмотрением случая $b > 0$, когда соответствующая этому решению траектория уравнения (2.6) взаимно однозначным образом проектируется на отрезок вертикальной оси $q \in [\beta ,\beta + 1]$, соединяя точку (2.10) и некоторую точку на прямой (2.12) (см. фиг. 2, линия b).

Воспользуемся подстановкой (2.13) при $\epsilon = - 1,$ ${{a}_{0}} = 1$,

(3.17)

$q = :\beta (1 + {{w}^{M}}),$

приведя уравнение (2.6) к виду (2.16):

(3.18)

$\frac{{d\zeta }}{{dw}} = (\beta + 1)\zeta (w)\frac{{ - {{w}^{{M - 1}}} + {{w}^{{\tilde {N} - M - 1}}}{{\zeta }^{{\tilde {N}}}}(w)}}{{ - 1 + \beta {{w}^{M}} - (\beta + 1){{w}^{{\tilde {N} - M}}}{{\zeta }^{{\tilde {N}}}}(w)}},\quad w \in [0,{{\beta }^{{ - 1/M}}}],\quad \zeta (0) = {{\zeta }_{0}},$

где начальное значение ${{\zeta }_{0}}$ функции $\zeta (w)$ при $w = 0$ находится из формулы (3.3) с учетом равенства $C = - 1{\text{/}}\zeta _{0}^{M}$, следующего из разложения (3.2) и подстановки (3.17):

(3.19)

$b = \frac{\beta }{{\mathop {{{f}_{0}}}\nolimits^K \mathop {{{\zeta }_{0}}}\nolimits^M }}{{Z}^{{1 + 1/\beta }}},\quad {{\zeta }_{0}} = \frac{{{{\beta }^{{1/M}}}}}{{\mathop {{{f}_{0}}}\nolimits^{1/\tilde {N}} {{b}^{{1/M}}}}}{{Z}^{{(\beta + 1)/(\beta M)}}}.$

Из подстановок (2.3), (2.5), (3.17), (2.15) находим

$\rho = \mathop \smallint \limits^\psi \frac{{d\psi }}{{p(\psi )}} = \mathop \smallint \limits^\psi \frac{{d\ln \psi }}{{q(\psi )}} = \frac{{\tilde {N}}}{\sigma }\mathop \smallint \limits^z \frac{{d\ln z}}{{q(z)}} = \frac{{\tilde {N}}}{{\sigma \beta }}\left( {\mathop \smallint \limits^w \frac{{d\ln w}}{{1 + {{w}^{M}}}} + \mathop \smallint \limits^w \frac{{d\ln \zeta (w)}}{{1 + {{w}^{M}}}}} \right) = :{{I}_{1}}(w) + {{I}_{2}}(w),$

где с учетом последнего равенства (2.13) имеем

(3.20)

${{I}_{1}} = M\mathop \smallint \limits^w \frac{{d\ln w}}{{1 + {{w}^{M}}}} = \mathop \smallint \limits^w \left( {\frac{1}{{{{w}^{M}}}} - \frac{1}{{1 + {{w}^{M}}}}} \right)d{{w}^{M}} = \ln \frac{{{{w}^{M}}}}{{1 + {{w}^{M}}}} + {{c}_{2}},\quad {{c}_{2}} = {\text{const}},$

(3.21)

${{I}_{2}} = M\mathop \smallint \limits^w \frac{{d\ln \zeta (w)}}{{1 + {{w}^{M}}}} = M\mathop \smallint \limits^w \frac{{\zeta {\kern 1pt} '(w)}}{{(1 + {{w}^{M}})\zeta (w)}}dw.$

Из подстановок (2.1), (2.5), (2.15) и равенств (3.20), (3.21) получаем

(3.22)

$\begin{gathered} r(t) = exp\rho = {{C}_{3}}{{w}^{M}}\mathcal{G}(t),\quad {{C}_{3}} = {\text{const}} > 0, \\ y(t) = \mathop {{{f}_{0}}}\nolimits^{1/\sigma } {{r}^{{ - \beta }}}{{(\zeta w)}^{{\tilde {N}/\sigma }}} = \mathop {{{f}_{0}}}\nolimits^{1/\sigma } \mathop {{{C}_{3}}}\nolimits^{ - \beta } {{\mathcal{G}}^{{ - \beta }}}(w){{\zeta }^{{\tilde {N}/\sigma }}}(w), \\ \end{gathered} $

где функция

(3.23)

$\mathcal{G}(w) = \frac{1}{{1 + {{w}^{M}}}}exp\left\{ {M\int\limits_0^w {\frac{{\zeta {\text{'}}(w)}}{{(1 + {{w}^{M}})\zeta (w)}}dw} } \right\}$

является аналитической на отрезке $w \in [0,{{\beta }^{{ - 1/M}}}]$. Константа ${{C}_{3}}$ находится из условия $y = Z$ при $r = w = 0$ с учетом равенств (3.19):

(3.24)

$Z = \mathop {{{f}_{0}}}\nolimits^{1/\sigma } \mathop {{{C}_{3}}}\nolimits^{ - \beta } \zeta _{0}^{{\tilde {N}/\sigma }},\quad {{C}_{3}} = Z\frac{\beta }{b}.$

Получаем следующий результат.

Теорема 2. Для решения $y(r)$ задачи (1.7)–(1.12), (2.9), производная которого в нуле равна

$b = \frac{{dy}}{{dr}}(0) > 0,$

справедливо следующее параметрическое представление с параметром $w$:

(3.25)

$r(w) = Z\frac{\beta }{b}{{w}^{M}}\mathcal{G}(w),\quad y(w) = Z{{\mathcal{G}}^{{ - \beta }}}(w){{\left( {\frac{{\zeta (w)}}{{{{\zeta }_{0}}}}} \right)}^{{\tilde {N}/\sigma }}},\quad w \in [0,{{w}_{1}}],\quad {{w}_{1}}: = {{\beta }^{{ - 1/M}}},$

где функции $\zeta (w),\;\mathcal{G}(w)$ являются положительными и аналитическими на отрезке $[0,{{w}_{1}}]$, причем $\zeta (w)$ есть решение задачи Коши (3.18), (3.19), а $\mathcal{G}(w)$ выражается через $\zeta (w)$ по формуле (3.23), константы $\beta ,\;{{f}_{0}},\;M,\;\tilde {N}$ находятся по формулам (1.14), (2.9).

Коэффициенты Тейлора функции $\zeta (w)$ при $w = 0$ (и в любой точке отрезка $[0,{{w}_{1}}]$, где известно значение функции) получаются методом неопределенных коэффициентов из уравнения (3.18). Тейлоровское разложение функции $\mathcal{G}(w)$ находится из соответствующего разложения функции $\zeta (w)$ при помощи арифметики степенных рядов.

4. ЗАДАЧА ТОМАСА–ФЕРМИ

Для уравнения (1.1) введенные выше константы (1.14), (1.16), (2.9), (3.7) имеют следующие числовые значения:

(4.1)

$\nu = - \frac{1}{2},\quad \sigma = \frac{1}{2},\quad M = 2,\quad \tilde {N} = 3,\quad K = \frac{2}{3},\quad \beta = 3,\quad {{\omega }_{0}} = - 7,\quad {{f}_{0}} = 12,$

(4.2)

$\alpha = \frac{{7 - \sqrt {73} }}{2} \approx - 0.772,\quad \gamma = \frac{1}{\alpha } + 1 = \frac{{5 - \sqrt {73} }}{{12}} \approx - 0.295.$

4.1. Задача на полупрямой

Применим теорему 1 к решению задачи (1.1)–(1.3) при $R = + \infty $, отвечающей модели свободного атома Томаса–Ферми. Представление (3.16) с учетом равенств (4.1) в этом случае принимает вид

(4.3)

$r(t) = {{Z}^{{ - 1/3}}}\mathop {12}\nolimits^{2/3} \frac{{\mathop {{{\zeta }_{e}}}\nolimits^2 }}{{{{\mathcal{F}}_{e}}}}{{t}^{{1/\alpha }}}{{(1 - t)}^{2}}\mathcal{F}(t),\quad y(t) = Z\frac{{\mathop {{{\mathcal{F}}_{e}}}\nolimits^3 }}{{\mathop {{{\zeta }_{e}}}\nolimits^6 }}{{t}^{{ - 3/\alpha }}}\frac{{{{\zeta }^{6}}(t)}}{{{{\mathcal{F}}^{3}}(t)}},$

где аналитическая функция $\zeta (t)$ является решением задачи (3.6), (3.7) на отрезке $t \in [0,1]$:

(4.4)

$\frac{{d\zeta }}{{dt}} = 4\zeta (t)\frac{{1 - t - {{\zeta }^{3}}(t)}}{{1 + 3{{{(1 - t)}}^{2}} - 4(1 - t){{\zeta }^{3}}(t)}},\quad \zeta (0) = 1,\quad \frac{{d\zeta }}{{dt}}(0) = \gamma ,$

аналитическая функция $\mathcal{F}(t)$ выражается через $\zeta (t)$ по формулам

(4.5)

$\mathcal{F}(t) = \frac{{expF(t)}}{{2 - t}},\quad F(t): = \int\limits_0^t {f(t)dt} ,\quad f(t): = \frac{{(2\zeta {\text{'}}(t){\text{/}}\zeta (t) - (2 - t)\gamma ){{t}^{{ - 1}}}}}{{2 - t}},$

числа $\alpha ,\gamma $ принимают значения (4.2), а константы ${{\zeta }_{e}},\;{{\mathcal{F}}_{e}}$ определены равенствами (3.14).

Производная решения $y(r)$ в нуле вычисляется по формуле (3.15):

(4.6)

$\frac{{dy}}{{dr}}(0) = B{{Z}^{{4/3}}},\quad B = - \frac{3}{{\mathop {12}\nolimits^{2/3} \mathop {{{\zeta }_{e}}}\nolimits^2 }}.$

В табл. 1 даны значения нескольких коэффициентов тейлоровских разложений при $t = 0$ функций, используемых в представлении (4.3):

(4.7)

$\zeta (t) = :\sum\limits_{j = 0}^\infty \,{{\zeta }_{j}}{{t}^{j}},\quad F(t) = :\sum\limits_{j = 0}^\infty \,{{F}_{j}}{{t}^{j}},\quad \mathcal{F}(t) = :\sum\limits_{j = 0}^\infty \,{{\mathcal{F}}_{j}}{{t}^{j}},$

где коэффициенты ${{\zeta }_{j}}$ найдены методом неопределенных коэффициентов из данных задачи (4.4), а коэффициенты ${{F}_{j}},\;{{\mathcal{F}}_{j}}$ получены из ${{\zeta }_{j}}$ в соответствии с формулами (4.5). На фиг. 3 дана зависимость от порядкового номера абсолютных величин тейлоровских коэффициентов функций $\mathcal{F}(t),\;\mathcal{H}(t)$, входящих в параметрические представления соответственно (4.3) и (1.15). Приведенные графики демонстрируют экспоненциальный характер сходимости обоих представлений на единичном отрезке с преимуществом по скорости сходимости у нового представления (4.3). Графики функций $\zeta (t),\;\mathcal{F}(t)$ приведены на фиг. 4.

Фиг. 4.

Графики функций, входящих в параметризацию (4.3): линия a – график функции $\zeta (t)$; линия b – график функции $\mathcal{F}(t)$.

4.2. Задача на отрезке

Рассмотрим задачу (1.1), (1.2), (1.4) при $R \in (0, + \infty )$, отвечающую модели сжатого атома Томаса–Ферми. Накладывая дополнительно условие положительности производной $\Psi _{r}^{'}(0)$ решения в нуле, применим теорему 2 к решению этой задачи. Представление (3.25) с учетом равенств (4.1) принимает следующий вид:

(4.8)

$r(w) = Z\frac{3}{b}{{w}^{2}}\mathcal{G}(w),\quad y(w) = Z{{\mathcal{G}}^{{ - 3}}}(w){{\left( {\frac{{\zeta (w)}}{{{{\zeta }_{0}}}}} \right)}^{6}},\quad w \in [0,{{w}_{1}}],\quad {{w}_{1}}: = \frac{1}{{\sqrt 3 }},$

где $\zeta (w)$ является решением задачи Коши (3.18), (3.19):

(4.9)

$\begin{gathered} \frac{{d\zeta }}{{dw}} = 4\zeta (w)\frac{{{{\zeta }^{3}}(w) - w}}{{ - 1 + 3{{w}^{2}} - 4w{{\zeta }^{3}}(w)}},\quad w \in [0,{{w}_{1}}],\quad {{w}_{1}} = \frac{1}{{\sqrt 3 }}, \\ \zeta (0) = {{\zeta }_{0}} = \frac{{\sqrt 3 {{Z}^{{2/3}}}}}{{\mathop {12}\nolimits^{1/3} \sqrt b }}, \\ \end{gathered} $

функция $\mathcal{G}(w)$ имеет вид

(4.10)

$\mathcal{G}(w) = \frac{1}{{1 + {{w}^{2}}}}exp\left\{ {2\int\limits_0^w {\frac{{\zeta {\text{'}}(w)}}{{(1 + {{w}^{2}})\zeta (w)}}dw} } \right\}.$

На фиг. 1, линия b, приведен график решения задачи (1.1), (1.2), (1.4), полученного в численном эксперименте с использованием формул (4.8)–(4.10).

Список литературы

Fermi E. Un metodo statistico per la determinazione di alcune prioprieta dell’atomo // Rend. Accad. Naz. Lincei 6. 1927. P. 602–607.
Thomas L.H. The calculations of atomic fields // Proc. Cambridge Philos. Soc. 1927. № 23. P. 542–598.
Sommerfeld A. Integrazione asintotica dell’equazione differenziale di Fermi–Thomas // Rend. R. Accademia dei Lincei 15. 1932. P. 293–308.
Беллман Р. Теория устойчивости решений дифференциальных уравнений. М.: Изд-во иностр. лит., 1954.
Ландау Л.Д., Лившиц Е.М. Теоретическая физика. Квантовая механика (нерелятивистская теория). М.: Наука, 1989.
Lane J.H. On the theoretical temperature of the Sun under the hypothesis of a gaseous mass maintaining its volume by its internal heat and depending on the laws of gases known to terrestrial experiment // The American Journal of Science and Arts. 1870. V. 2. P. 57–74.
Emden R. Gaskugeln: Anwendungen der mechanischen W armetheorie auf kosmologische und meteorologische Probleme. Leipzig, Berlin: Teubner, 1907.
Nachman A., Callegari A. A nonlinear singular boundary value problem in the theory of pseudoplastic fluids // SIAM J. Appl. Math. 1980. V. 38. № 2. P. 275–281.
Олейник O.A., Самохин B.H. Математические методы в теории пограничного слоя. М.: Физматгиз, 1997.
Laurenzi B.J. An analytic solution to the Thomas–Fermi equation // Jour. Math. Phys. 1990. V. 31. № 10. P. 2535–2537.
Wazwaz A. The variational iteration method for solving linear and nonlinear ODEs and scientific models with variable coefficients // Cent. Eur. J. eng. 2019. V. 135. P. 186–205.
Parand K., Delkhosh M. Accurate solution of the Thomas–Fermi equation using the fractional order of rational chebyshev functions // J. Comput. Appl. Mathem. 2017. V. 317. P. 624–642.
Zhang X., Boyd J.P. Revisiting the Thomas–Fermi equation: Accelerating rational chebyshev series through coordinate transformations // Appl. Numer. Mathem. 2019. V. 135. P. 186–205.
Ahmad S.U.I., Faisal F., Shoaib M., Raja M.A.Z. A new heuristic computational solver for nonlinear singular Thomas–Fermi system using evolutionary optimized cubic splines // Eur. Phys. J. Plus. 2020. V. 135. N. 55. P. 1–29.
Пикулин С.В. О задаче Томаса–Ферми и о решениях уравнения Эмдена–Фаулера // Ж. вычисл. матем. и матем. физ. 2019. Т. 59. № 8. С. 1358–1380.
Коддингтон Э.А., Левинсон Н. Теория обыкновенных дифференциальных уравнений. М.: Изд-во иностр. лит., 1958.
Esposito S. Majorana solution of the Fermi–Thomas equation // Am. J. Phys. 2002. V. 70. № 8. P. 852–856.
Пикулин С.В. О поведении решений уравнения Абеля II рода специального вида вблизи узловой особой точки // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 12. С. 2074–2095.
Pikulin S.V. Analytical-numerical method for calculating the Thomas–Fermi potential // Russ. J. Math. Phys. 2019. V. 26. № 4. P. 544–552.
Пикулин С.В. О решениях типа бегущей волны уравнения Колмогорова–Петровского–Пискунова // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 2. С. 244–252.
Lampariello G. Su una classe notevole di equazioni differenziali del 2 o ordine non lineari (i, ii) // Atti Accad. Lincei. 1934. V. 6 (2.3). P. 284–290, 386–393.
Rosu Haret C., Mancas Stefan C. Generalized Thomas–Fermi equations as the Lampariello class of Emden–Fowler equations // Physica A: Statistical Mechanics and its Applications. 2017. V. 471. P. 212–218.
Голубев В.В. Курс аналитической теории дифференциальных уравнений. М.: Гостехтеориздат, 1950.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал