Журнал вычислительной математики и математической физики, 2020, T. 60, № 8, стр. 1304-1314

1. ВВЕДЕНИЕ

Дифференциальные уравнения с запаздыванием по времени часто возникают в качестве математических моделей [1]–[5]. Главной особенностью таких уравнений является то, что соответствующее фазовое пространство является бесконечномерным [6]. Из-за этой особенности уравнения с запаздыванием обладают более сложной (по сравнению с обыкновенными дифференциальными уравнениями) динамикой [7]–[9].

Уравнения с двумя запаздываниями, во-первых, являются естественным обобщением уравнений с одним запаздыванием, а во-вторых, выступают в качестве математических моделей процессов в медицине [10], математической биологии [11], [12], лазерной физике [13], [14] и других отраслях знаний.

В работе описываются новые динамические эффекты, возникающие при добавлении в систему второго запаздывания. Рассмотрим уравнение с одним запаздыванием

и уравнение с двумя запаздываниями Здесь $x(t)$ – скалярная функция, $a$ и $b$ – некоторые постоянные. Достаточно гладкая функция $f$ имеет в нуле порядок малости выше первого, т.е. $f(0) = f{\text{'}}(0) = 0$.

Основное предположение состоит в том, что запаздывание $T$ в обоих уравнениях достаточно велико, т.е.

Относительно второго запаздывания ${{T}_{1}}$ будем предполагать, что оно также велико и пропорционально $T$: Параметр ${{k}_{1}}$ может быть, вообще говоря, любым, потребуем только, чтобы при ${{k}_{0}} = 1$ значение ${{k}_{1}}$ было положительным. Таким образом, всегда ${{T}_{1}} > T$.

Важный частный случай возникает при ${{k}_{0}} = 1$. В этом случае отношение ${{T}_{1}}{{T}^{{ - 1}}} = 1 + {{\varepsilon }^{\alpha }}{{k}_{1}}$, т.е. запаздывания близки друг к другу. При этом, как будет показано в работе, малой величиной ${{\varepsilon }^{\alpha }}{{k}_{1}}$ нельзя пренебрегать, и поведение решений задачи с двумя близкими запаздываниями сложнее, чем задачи с одним запаздыванием.

Поставим задачу исследовать поведение решений в некоторой малой (но не зависящей от $\varepsilon $) окрестности нулевого состояния равновесия фазового пространства (${{C}_{{[ - T,0]}}}$ для задачи с одним запаздыванием и ${{C}_{{[ - {{T}_{1}},0]}}}$ для задачи с двумя запаздываниями) и построить равномерные по всем $t \geqslant 0$ приближения установившихся режимов в этой окрестности при достаточно малых $\varepsilon $.

Как будет показано ниже, важную роль играют алгебраические свойства числа ${{k}_{0}}$. Принципиально различными будут случаи рационального и иррационального ${{k}_{0}}$. Отметим, что некоторые частные случаи были изложены ранее в работах [15], [16]. Результаты относительно уравнения с одним запаздыванием см. в работах [17], [18].

Для упрощения вычислений далее будем предполагать, что функция $f$ зависит только от первого аргумента. Представим $f(x)$ в окрестности нуля в виде ряда Тейлора

Сделаем замену времени $t \to tT$ в исходных уравнениях, после чего получим их в более удобной для исследований форме. Уравнение с одним запаздыванием имеет вид

Уравнение с двумя запаздываниями преобразуется к виду Теперь перед нами стоит задача описать поведение и асимптотику решений уравнений (1.1) и (1.2) в окрестности нуля фазового пространства ${{C}_{{[ - 1,0]}}}$ и ${{C}_{{[ - {{k}_{0}} - \varepsilon {{k}_{1}},0]}}}$ соответственно.

Обратим внимание, что уравнения (1.1) и (1.2) являются сингулярно возмущенными. Если в них формально положить $\varepsilon = 0$, то получим разностные уравнения

соответственно. Их динамика существенно беднее, чем у (1.1) и (1.2) [19].

Далее будут выделены области параметров, когда динамика тривиальна, т.е. все решения стремятся к состоянию равновесия, и когда динамика становится нелокальной, т.е. в окрестности состояния равновесия нет устойчивых режимов. В оставшихся – критических – случаях, как будет показано, неограниченно большое количество корней характеристического уравнения находится сколь угодно близко к мнимой оси (при достаточно малых $\varepsilon $), поэтому будем говорить, что возникающие критические случаи имеют бесконечную размерность. Для исследования решений (1.1) и (1.2) в бесконечномерных критических случаях будет развит так называемый метод квазинормальных форм, описанный в [17], [18]. Главная его идея состоит в том, что исходное сингулярно возмущенное уравнение в бесконечномерном критическом случае сводится к специальной нелинейной задаче – аналогу (укороченной) нормальной формы Пуанкаре, – решения которой определяют главные части асимптотического разложения решений (1.1) и (1.2). Такие задачи мы будем называть квазинормальными формами. Важным является то, что квазинормальная форма не зависит от малого параметра либо зависит от него регулярно, а следовательно, может быть исследована численно. Как будет показано, квазинормальные формы (1.1) и (1.2), как правило, имеют вид нелинейных параболических уравнений.

В разд. 2 мы приведем результаты работ [17], [18] относительно локальной динамики (1.1). В разд. 3 опишем линейный анализ для уравнения (1.2), определим область устойчивости нуля, выделим и классифицируем критические случаи. Будет показано, что все они имеют бесконечную размерность. В разд. 4 в критических случаях построим квазинормальные формы (1.2) и опишем особенности локальной динамики при $\varepsilon \to 0$.

2. УРАВНЕНИЕ С ОДНИМ ЗАПАЗДЫВАНИЕМ

Приведем здесь кратко основные результаты относительно локальной динамики уравнения (1.1) из работ [17], [18].

Характеристическое уравнение линеаризованной в нуле задачи (1.1) имеет вид

Расположение его корней, а следовательно, устойчивость нулевого решения и локальная динамика (1.1), при каждом фиксированном значении $a$ и малых $\varepsilon $ описывается следующей теоремой.

Теорема 1. Пусть $\left| a \right| < 1$, тогда при достаточно малых $\varepsilon $ все корни (2.1) имеют отрицательные вещественные части и отделены от мнимой оси. Нулевое решение (1.1) асимптотически устойчиво, динамика в его окрестности тривиальна: все решения из некоторой малой, но не зависящей от $\varepsilon $ окрестности стремятся к нулю.

Пусть $\left| a \right| > 1$, тогда при достаточно малых $\varepsilon $ существует корень (2.1) с положительной, отделенной от нуля вещественной частью. Нулевое решение (1.1) неустойчиво, и в его малой, но не зависящей от $\varepsilon $ окрестности не существует устойчивых решений.

Из этой теоремы следует, что в дополнительном рассмотрении нуждаются случаи, когда параметр $a$ близок к $ \pm 1$. Пусть

Случай, когда надкритичность имеет другой порядок малости, т.е. $a = - (1 + {{\varepsilon }^{p}}{{a}_{1}})$, изучен в [18], здесь на нем останавливаться не будем. Тогда характеристическое уравнение (2.1) имеет бесконечное количество корней, стремящихся к мнимой оси при $\varepsilon \to 0$. Таким образом, рассматриваемый критический случай имеет бесконечную размерность.

Рассмотрим параболическое уравнение

с антипериодическими краевыми условиями Здесь, вообще говоря, $\tau \geqslant 0$, $r \in [0,\;1]$. Однако краевые условия (2.3) позволяют продлевать решения на все $r \in \mathbb{R}$.

Задача (2.2), (2.3) является квазинормальной формой для (1.1) в рассматриваемом случае. Его решения позволяют найти приближения для решений (1.1).

Теорема 2. Пусть краевая задача (2.2), (2.3) имеет классическое периодическое по $\tau $ решение ${{u}_{ * }}(\tau ,r)$. Тогда уравнение (1.1) имеет асимптотическое по невязке решение с точностью до $O({{\varepsilon }^{4}})$ равномерно по $t \in [0, + \infty )$:

Таким образом, решения (1.1) определяются в главном решениями задачи (2.2), (2.3), которая не зависит от малого параметра. Как следует из теоремы 2, при уменьшении $\varepsilon $ к нулю монотонно уменьшается амплитуда колебаний.

В случае, когда значение $a$ близко к +1, т.е. $a = 1 + {{\varepsilon }^{2}}{{a}_{1}}$, роль задачи (2.2), (2.3) играет параболическая краевая задача

Все ее решения стремятся либо в бесконечность, либо к пространственно-однородному состоянию равновесия $u(\tau ,r) \equiv {\text{const}}$.

3. ЛИНЕЙНЫЙ АНАЛИЗ

1. Поведение решений (1.2) в малой окрестности нулевого состояния равновесия определяется линеаризованной в нуле задачей (см. [6])

В свою очередь динамика этого линейного уравнения определяется расположением корней характеристического квазиполинома В случае (см. [6]), когда все корни этого уравнения при достаточно малых $\varepsilon $ имеют отрицательные вещественные части и отделены от мнимой оси (т.е. все вещественные части меньше некоторого отрицательного числа), тогда состояние равновесия устойчиво, и все решения из некоторой его малой (но не зависящей от $\varepsilon $) окрестности стремятся к нулю. Если при каждом достаточно малом $\varepsilon $ существует хотя бы один корень с вещественной частью, большей некоторого положительного числа, то изучаемое состояние равновесия неустойчиво, в его некоторой малой (но не зависящей от $\varepsilon $) окрестности нет устойчивых режимов. Оставшиеся случаи являются критическими, в них необходимо проводить дополнительные исследования.

Исследуем расположение корней (3.1). Прежде всего отметим, что при малых $\left| a \right|$ и $\left| b \right|$ уравнение (3.1) имеет только корни в левой комплексной полуплоскости. Справедлива

Лемма 1. Пусть $\left| a \right| + \left| b \right| < 1$, тогда найдется такое $M > 0$, что все корни (3.1) при достаточно малых $\varepsilon $ удовлетворяют $Re\lambda < - M$.

Доказательство. Предположим противное. Пусть при $\left| a \right| + \left| b \right| < 1$ существует корень $\lambda (\varepsilon )$ уравнения (3.1) такой, что для каждого $q > 0$ значение $Re\lambda (\varepsilon ) > - q$ при достаточно малых $\varepsilon $. Тогда оценим модули левой и правой частей в (3.1) для $\lambda = \lambda (\varepsilon )$:

Устремляя $q$ к нулю, получаем $1 \leqslant \left| a \right| + \left| b \right|$, что противоречит сделанному ранее предположению. Таким образом, лемма доказана.

Это утверждение является достаточным условием устойчивости нулевого состояния равновесия (1.2). Для иррационального ${{k}_{0}}$, как будет показано далее, это условие является и необходимым, а для рационального ${{k}_{0}}$ оно будет уточнено.

Итак, при малых $\left| a \right|$ и $\left| b \right|$ (и достаточно малых $\varepsilon $) все корни уравнения (3.1) имеют отрицательные вещественные части. Будем увеличивать абсолютные значения $a$ и $b$ до тех пор, пока это свойство впервые не нарушится.

Определим такие значения $a$ и $b$, при которых у уравнения (3.1) какой-либо корень попадает на мнимую ось. Подставляя $\lambda = i\omega $ в (3.1) и приравнивая вещественные и мнимые части, получаем

2. Дальнейшие исследования и результаты будут существенно зависеть от алгебраических свойств числа ${{k}_{0}}$. Рассмотрим сначала случай иррационального ${{k}_{0}}$.

Теорема 3. Пусть ${{k}_{0}}$ иррационально. Тогда при $\left| a \right| + \left| b \right| < 1$ и достаточно малых $\varepsilon $ нулевое состояние равновесия (1.2) устойчиво, все решения (1.2) из некоторой малой (но не зависящей от $\varepsilon $ окрестности) стремятся к нулю. При $\left| a \right| + \left| b \right| > 1$ и достаточно малых $\varepsilon $ нулевое решение (1.2) неустойчиво, и в его некоторой не зависящей от $\varepsilon $ окрестности не существует устойчивых режимов.

Доказательство. Ситуация $\left| a \right| + \left| b \right| < 1$ была рассмотрена ранее в лемме 1: все корни характеристического уравнения имеют отрицательные вещественные части, следовательно, состояние равновесия устойчиво.

Покажем теперь, что при $\left| a \right| + \left| b \right| = 1$ уравнение (3.1) имеет сколь угодно близкие к мнимой оси корни. Рассмотрим “главную часть” системы (3.2)

При $a,b > 0$ очевидно $\omega = 0$ удовлетворяет этой системе. При других знаках параметров эта система не может быть выполнена точно, но для любого $\delta > 0$ можно указать такое $\omega $ (не зависящее от $\varepsilon $), что $\left| {acos\omega - \left| a \right|} \right| + \left| {bcos{{k}_{0}}\omega - \left| b \right|} \right| < \delta $. Такое $\omega $ будет соответствовать корню (3.1) вида ${{\lambda }_{ * }} = i\omega + O(\delta ) + o(1)$.

Теперь пусть $\left| a \right| + \left| b \right| > 1$, тогда найдутся такие ${{a}_{0}}$, ${{b}_{0}}$ и $\rho > 0$, что $a = {{a}_{0}}{{e}^{\rho }}$, $b = {{b}_{0}}{{e}^{{{{k}_{0}}\rho }}}$ и $\left| {{{a}_{0}}} \right| + \left| {{{b}_{0}}} \right| = 1$. Тогда по теореме о неявной функции следует, что у уравнения (3.1) существует корень ${{\lambda }_{\rho }} = {{\lambda }_{ * }} + \rho + o(1)$, действительная часть которого равна $\rho + O(\delta ) + o(1)$ и при малых $\delta $ и $\varepsilon $ больше нуля. Следовательно, состояние равновесия неустойчиво. Что и требовалось доказать.

3. Далее будем считать, что ${{k}_{0}}$ рационально, т.е.

где $m$ и $n$ – натуральные, взаимно простые числа.

Потеря устойчивости состоянием равновесия произойдет, когда система (3.2) впервые (при возрастании $\left| a \right|$ и $\left| b \right|$) станет разрешима при достаточно малых $\varepsilon $. Сформулируем это условие более аккуратно. Рассмотрим систему уравнений относительно $\Omega $ и ${{\omega }_{0}}$

Эта система получается из (3.2) после замены и отбрасывания малых величин. Здесь через ${{\theta }_{0}} = {{\theta }_{0}}(\varepsilon )$ обозначено такое значение из $[0,\;2\pi n)$, что ${{\omega }_{0}}{{\varepsilon }^{{ - 1}}} + {{\theta }_{0}}$ кратно $2\pi n$. Функция ${{\theta }_{0}}(\varepsilon )$ является ограниченной и кусочно-непрерывной, она принимает каждое свое значение бесконечное количество раз при $\varepsilon \to 0$.

Обозначим через $S$ связное множество на плоскости параметров $(a,b)$, содержащее точку $(0,0)$, такое, что (3.3) неразрешима при значениях параметров из этой области.

Лемма 2. Множество $S$ открытое.

Доказательство. Заметим, что если существует решение системы (3.3), то ${{\omega }_{0}} \in \left[ { - \left| a \right| - \left| b \right|,\;\left| a \right| + \left| b \right|} \right]$ (это следует из второго уравнения), а $\Omega $ можно считать из отрезка $[0,\;2\pi n]$.

Введем функцию

Рассмотрим точку $({{a}_{0}},{{b}_{0}}) \in S$. Так как в ней нет решений (3.3), то $g({{\omega }_{0}},\Omega ,{{a}_{0}},{{b}_{0}}) > 0$ при всех значениях ${{\omega }_{0}}$ и $\Omega $. Обозначим через ${{g}_{0}}({{a}_{0}},{{b}_{0}})$ минимум $g({{\omega }_{0}},\Omega ,{{a}_{0}},{{b}_{0}})$ при всех ${{\omega }_{0}} \in [ - 2(\left| {{{a}_{0}}} \right| + \left| {{{b}_{0}}} \right|),$ $2(\left| {{{a}_{0}}} \right|,\left| {{{b}_{0}}} \right|)]$ и $\Omega \in [0,\;2\pi n]$. Он существует и строго положителен. Следовательно, при достаточно близких значениях $(a,b)$ к $({{a}_{0}},{{b}_{0}})$ также $g(a,b) > 0$. Значит, при $(a,b)$, близких к $({{a}_{0}},{{b}_{0}})$, не существует корней (3.3) в квадрате $({{\omega }_{0}},\Omega ) \in \left[ { - 2\left( {\left| {{{a}_{0}}} \right| + \left| {{{b}_{0}}} \right|} \right),\;2(\left| {{{a}_{0}}} \right|,\left| {{{b}_{0}}} \right|)} \right] \times [0,\;2\pi n]$. Но как мы отмечали выше, если корни (3.3) существуют, то ${{\omega }_{0}} \in \left[ { - \left| a \right| - \left| b \right|,\;\left| a \right| + \left| b \right|} \right] \subset \left[ { - 2\left( {\left| {{{a}_{0}}} \right| + \left| {{{b}_{0}}} \right|} \right),\;2\left( {\left| {{{a}_{0}}} \right|,\left| {{{b}_{0}}} \right|} \right)} \right]$ при $(a,b)$ достаточно близких к $({{a}_{0}},{{b}_{0}})$. Отсюда получаем, что при таких $(a,b)$ система (3.3) корней не имеет, т.е. $(a,b) \in S$, и $S$ открытое.

Границу области $S$ обозначим через $\Gamma $. Таким образом, при $(a,b) \in \Gamma $ существует решение системы (3.3) $(\Omega ,{{\omega }_{0}})$. Отметим, что в этой точке обязательно должно нарушаться условие теоремы о неявной функции (так как сколь угодно близко есть точки множества $S$), т.е. соответствующий якобиан равен нулю:

Кроме того, если система (3.3) имеет решение $(\Omega ,{{\omega }_{0}})$ при $(a,b) \in \Gamma $, то все ее решения имеют вид $( \pm \Omega + 2\pi np,\; \pm {{\omega }_{0}})$ ($p \in \mathbb{Z}$).

Множество $S$ является областью устойчивости нуля при достаточно малых значениях $\varepsilon $. Справедлива следующая теорема.

Теорема 4. Пусть ${{k}_{0}} = m{\text{/}}n$ ($m$ и $n$ натуральные и взаимно простые). Тогда при $(a,b) \in S$ и достаточно малых $\varepsilon $ все решения (1.2) из некоторой малой (но не зависящей от $\varepsilon $) окрестности нулевого решения стремятся к нулю.

При $(a,b) \notin \bar {S}$ и всех достаточно малых $\varepsilon $ в некоторой малой (и не зависящей от $\varepsilon $) окрестности нуля нет устойчивых решений.

При $(a,b) \in \Gamma $ существует бесконечное количество корней (3.1), вещественная часть которых стремится к мнимой оси:

Доказательство. Из леммы 1 следует, что при $\left| a \right| + \left| b \right| < 1$ все корни характеристического уравнения (3.1) имеют отрицательные вещественные части, т.е. нулевое состояние равновесия устойчиво. Пока $(a,b) \in S$ система (3.3) неразрешима, следовательно, не имеет решений при малых $\varepsilon $ и система (3.2), а значит, все корни (3.1) при малых $\varepsilon $ будут иметь отрицательные вещественные части. Следовательно, нулевое состояние равновесия устойчиво при $(a,b) \in S$.

Также из непрерывной зависимости следует, что при $(a,b) \in \Gamma $ и малых $\varepsilon $ у (3.1) нет корней с положительной вещественной частью.

Пусть $(a,b) \notin S$. Тогда можно представить $a$ и $b$ в виде

Пусть $\Omega $ и ${{\omega }_{0}}$ – решение системы (3.3) при $a = {{a}_{0}}$, $b = {{b}_{0}}$. Докажем, что при любом $p \in \mathbb{Z}$

удовлетворяет (3.1).

Подставим (3.6) в (3.1). После упрощений получим

В этом уравнении присутствует не непрерывно зависящая от $\varepsilon $ функция ${{\theta }_{0}}$, поэтому теорема о неявной функции к нему не применима непосредственно. Заметим, что ${{\theta }_{0}}$ принимает лишь значения из отрезка $[0,\;2\pi n]$ (мы расширим для доказательства область значений). Выберем произвольно число $y \in [0,\;2\pi n]$ и рассмотрим уравнение (3.7) при ${{\theta }_{0}} = y$. Считаем $y$ параметром. При каждом его значении уравнение (3.7) имеет при $\varepsilon = 0$ корень $\mu = 0$, для которого уже можно применить теорему о неявной функции. Из нее следует, что существует такое решение ${{\mu }_{0}}(\varepsilon ,y)$, которое стремится к нулю при $\varepsilon \to 0$. Заметим, что ${{\mu }_{0}}(\varepsilon ,y)$ зависит от $y$ непрерывно, следовательно, ${{\mu }_{0}}(\varepsilon ,y)$ стремится к нулю равномерно по $y \in [0,2\pi n]$ при $\varepsilon \to 0$.

Теперь вернемся к уравнению (3.7). Его решением, очевидно, будет $\mu (\varepsilon ) = {{\mu }_{0}}(\varepsilon ,{{\theta }_{0}}(\varepsilon ))$. Из вышесказанного следует, что $\mu (\varepsilon ) \to 0$ при $\varepsilon \to 0$, т.е. $\mu (\varepsilon ) = o(1)$. Следовательно, формула (3.6) действительно приближает корень (3.1), вещественная часть которого близка к неотрицательному числу $\rho $ при $\varepsilon \to 0$. Отсюда получаем, что при $(a,b) \notin \bar {S}$ у характеристического уравнения (3.1) при малых $\varepsilon $ есть корень с положительной вещественной частью, т.е. состояние равновесия уравнения (1.2) неустойчиво.

При $(a,b) \in \Gamma $ имеем $\rho = 0$, при этом нет корней с положительной вещественной частью и, как мы показали, есть корни вида (3.5), находящиеся сколь угодно близко к мнимой оси.

Из этой теоремы следует, что в дополнительном изучении нуждается случай, когда $(a,b)$ близко к кривой $\Gamma $. Множество $S$ (а значит, и кривая $\Gamma $) может выглядеть по-разному. На фиг. 1 приведен вид кривой $\Gamma $ и множества $S$ (внутри кривой) при некоторых значениях ${{k}_{0}}$ и ${{k}_{1}}$. В общем виде описать его представляется проблематичным. Можно лишь утверждать, что оно содержит в себе квадрат $\left| a \right| + \left| b \right| < 1$ (это следует из леммы 1). Легко видеть, что система (3.3) имеет решение $\Omega = {{\omega }_{0}} = 0$ при $a + b = 1$. Также есть решение ${{\omega }_{0}} = 0$, $\Omega = \pi n$ при ${{( - 1)}^{n}}a + {{( - 1)}^{m}}b = 1$. Таким образом, в двух четвертях плоскости $(a,b)$ кривая $\Gamma $ проходит по сторонам квадрата $\left| a \right| + \left| b \right| = 1$. На фиг. 1 сплошной линией обозначены точки кривой $\Gamma $, в которых ${{\omega }_{0}} = 0$, а штриховой – в которых ${{\omega }_{0}} \ne 0$.

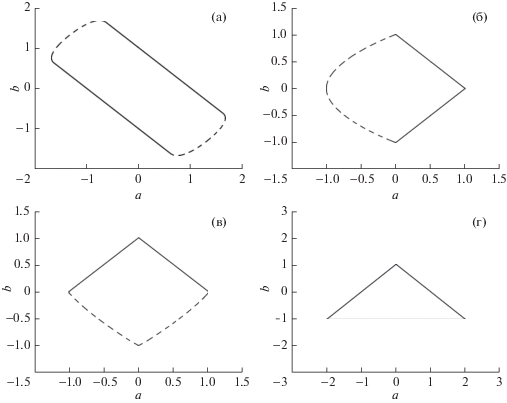
Далее приведем анализ динамики уравнения (1.2) при условии, что $(a,b)$ близко к кривой $\Gamma $.

4. НЕЛИНЕЙНЫЙ АНАЛИЗ

1. Опишем особенности динамики (1.2) при условии, что ${{k}_{0}} = \tfrac{m}{n}$, где $m,n \in \mathbb{N}$ и взаимно просты. Как показано выше (см. теорему 4), при условии, что точка $(a,\;b)$ принадлежит множеству $S$, локальная динамика тривиальная, а при условии, что она лежит вне этой области – нелокальная. Таким образом, необходимо исследовать ситуацию, когда система находится в близком к критическому случаю. Пусть

При $a = {{a}_{0}}$, $b = {{b}_{0}}$ система уравнений (3.3) имеет решение $(\Omega ,{{\omega }_{0}})$, где $\omega \in [0,\;2\pi n)$, ${{\omega }_{0}} \geqslant 0$. Введем обозначения

Из равенства (3.4) следует, что $D$ вещественное ($ImD = 0$). А из того, что при уменьшении $a$ и $b$ внутрь области $S$ корней уравнения (3.3) нет, следует, что

Рассмотрим отдельно две следующие ситуации. Сначала изучим наиболее простой случай, когда ${{\omega }_{0}} = \Omega = 0$. Как несложно видеть, он реализуется, например, при ${{a}_{0}} + {{b}_{0}} = 1$. Второй случай – это ситуация ${{\omega }_{0}} \ne 0$ или $\Omega \ne 0$.

Далее, в каждом случае мы сведем задачу к квазинормальной форме и с ее помощью получим асимптотику решений (1.2).

2. Случай ${{\omega }_{0}} = \Omega = 0$ является наиболее простым. Он реализуется при ${{a}_{0}} + {{b}_{0}} = 1$ (и $({{a}_{0}},{{b}_{0}}) \in \Gamma $) и является аналогом ситуации, когда $a$ близко к $1$ в уравнении с одним запаздыванием. Значения $D$ и $d$ при этом принимают вид

Роль квазинормальной формы в этом случае играет задача параболического типа для $\tau \geqslant 0$, $r \in [0,\;1]$

с краевыми условиями Отметим, что этот результат принципиально не отличается от аналогичного для уравнения с одним запаздыванием.

Из неравенства (4.2) следует, что построенная краевая задача (4.3), (4.4) является параболической. Она может иметь устойчивыми лишь пространственно однородные состояния равновесия. В силу этого динамика исходного уравнения (1.2) описывается следующим образом.

Теорема 5. Пусть ${{a}_{0}} + {{b}_{0}} = 1$, $({{a}_{0}},{{b}_{0}}) \in \Gamma $. Если ${{a}_{1}} + {{b}_{1}} > 0$, то при малых $\varepsilon $ нулевое решение уравнения (1.2) неустойчиво, а в его окрестности существует асимптотически устойчивое близкое к постоянному решение вида

Если ${{a}_{1}} + {{b}_{1}} < 0$, то при малых $\varepsilon $ нулевое решение уравнения (1.2) асимптотически устойчиво, а ${{x}_{ * }}$ неустойчиво.

3. Пусть теперь $\Omega \ne 0$ или ${{\omega }_{0}} \ne 0$. Обозначим через ${{\theta }_{0}} = {{\theta }_{0}}(\varepsilon )$ число из $[0;\;2\pi n)$ такое, что ${{\omega }_{0}}{{\varepsilon }^{{ - 1}}} + {{\theta }_{0}}(\varepsilon )$ кратно $2\pi n$. Отметим, что если ${{\omega }_{0}} = 0$, то ${{\theta }_{0}} \equiv 0$.

Сделаем в исходном уравнении (1.2) замену

$\tau = {{\varepsilon }^{2}}t$, ${{t}_{0}} = ({{\omega }_{0}}{{\varepsilon }^{{ - 1}}} + ({{\theta }_{0}} + \Omega )(1 - \varepsilon D + {{\varepsilon }^{2}}{{D}^{2}}))t$. Время $r$ определяется как $r = n(1 - \varepsilon D + {{\varepsilon }^{2}}{{D}^{2}})t$. Относительно функций $u(\tau ,r)$, ${{u}_{2}}(\tau ,{{t}_{0}},r)$ и ${{u}_{3}}(\tau ,{{t}_{0}},r)$ предполагаем, что они являются периодическими по $r$ с периодом 1, а по ${{t}_{0}}$ – периодическими с периодом $2\pi $.

Приравнивая коэффициенты при одинаковых степенях $\varepsilon $ в получившемся равенстве, на втором шаге получаем

а на третьем шаге, в качестве условия разрешимости получившегося уравнения относительно ${{u}_{3}}$ в классе периодических функций, получаем квазинормальную форму с краевыми условиями Здесь, как и ранее, $\tau \geqslant 0$, $r \in [0,\;1]$.

Система (4.7), (4.8) представляет собой, в силу неравенства (4.2), комплексное параболическое уравнение типа Гинзбурга–Ландау. Сформулируем аккуратно результаты о соответствии решений квазинормальной формы и исходного уравнения. Сначала опишем наиболее простой случай, когда ${{\omega }_{0}} = 0$.

Теорема 6. Пусть $\Omega \ne 0$, ${{\omega }_{0}} = 0$. Пусть краевая задача (4.7), (4.8) имеет классическое периодическое решение ${{u}_{ * }}(\tau ,r)$. Тогда при достаточно малых $\varepsilon $ уравнение (1.2) имеет асимптотическое по невязке c точностью до $O({{\varepsilon }^{3}})$ равномерно по всем $t \geqslant 0$ решение

где $r = n(1 - \varepsilon D + {{\varepsilon }^{2}}{{D}^{2}})t$.

Доказательство. Для доказательства этой теоремы нам достаточно подставить (4.9) в (1.2) и найти невязку. При этом при вычислении выражений $x(t - 1)$ и $x(t - m{\text{/}}n - \varepsilon {{k}_{1}})$ разложим экспоненту и ${{u}_{ * }}$, используя периодичность по $r$, в ряд Тейлора до величин порядка $O({{\varepsilon }^{3}})$. Остаточный член будет мал равномерно по $t \geqslant 0$ в силу того, что ${{u}_{ * }}(\tau ,r)$ периодическая и бесконечно дифференцируемая при всех $\tau > 0$ и $r \in [0,\;1]$ (см., например, [20]), а значит, ее производные непрерывны, периодичны, а следовательно, ограничены.

В случае, когда ${{\omega }_{0}} > 0$, коэффициенты задачи (4.7) зависят через ${{\theta }_{0}}$ от $\varepsilon $.

Теорема 7. Пусть ${{\omega }_{0}} > 0$. Пусть последовательность ${{\varepsilon }_{l}} \to 0$ такова, что ${{\theta }_{0}}({{\varepsilon }_{l}}) \equiv \xi $. Пусть (4.7), (4.8) при ${{\theta }_{0}} = \xi $ имеет классическое периодическое по $\tau $ решение ${{u}_{ * }}(\tau ,r)$. Тогда исходное уравнение имеет асимптотическое по невязке на последовательности ${{\varepsilon }_{l}}$ с точностью до $O(\varepsilon _{l}^{3})$ равномерно по $t \geqslant 0$ решение вида

где ${{t}_{0}}$ определено выше.

Доказательство этой теоремы полностью аналогично доказательству теоремы 6.

Новым, по сравнению со случаем одного запаздывания, здесь является то, что коэффициенты (4.7), (4.8) зависят от малого параметра. При $\varepsilon \to 0$ выражение ${{\theta }_{0}}(\varepsilon )$ принимает каждое значение из промежутка $[0;\;2\pi )$ бесконечное количество раз, а следовательно, вид решений (4.7), (4.8) и их устойчивость могут меняться бесконечное количество раз. Из этого следует вывод о возможности бесконечного процесса прямых и обратных бифуркаций в (1.2) при $\varepsilon \to 0$.

Замечание 1. Полученные асимптотические приближения можно уточнить. Для этого достаточно ряд (4.5) оборвать после ${{u}_{2}}$ (которое задается формулой (4.6)), тогда получим асимптотическое по невязке решение с точностью до $O({{\varepsilon }^{3}})$. Если дополнительно использовать и ${{u}_{3}}$ (про которое известно, что оно существует), то получим невязку порядка $O({{\varepsilon }^{4}})$.

Если в дополнительно к условиям теоремы потребовать грубость периодического решения ${{u}_{ * }}(\tau ,r)$, то асимптотическое приближение можно построить с любой точностью.

Замечание 2. Требование периодичности можно заменить требованием ограниченности решения вместе со своими производными вплоть до третьего порядка. Однако тогда становится затруднительным уточнение асимптотики решения.

Замечание 3. Отметим, что из теорем 6 и 7 нельзя сделать вывод о существовании у (1.2) точного решения с приведенной асимптотикой. Можно лишь утверждать, что если ${{u}_{ * }}$ неустойчиво, то из существования точного решения следует его неустойчивость. Поэтому при изучении динамики интерес представляют только устойчивые решения квазинормальных форм.

Отметим еще, что при $\omega \ne 0$ мы получаем высокочастотные колебания с частотой порядка ${{\omega }_{0}}{{\varepsilon }^{{ - 1}}}$, а при ${{\omega }_{0}} = 0$ частота колебаний имеет порядок $O(1)$.

5. ЗАКЛЮЧЕНИЕ

Проведено исследование локальной динамики сингулярно возмущенных уравнений с двумя запаздываниями в случае, когда оба запаздывания асимптотически велики и при этом одинаковы по порядку (пропорциональны).

Были выделены критические случаи, показано, что все они имеют бесконечную размерность, т.е. неограниченно большое число корней характеристического уравнения находится сколь угодно близко к мнимой оси. Для изучения поведения решений в близких к критическим случаях были построены специальные нелинейные уравнения – квазинормальные формы. Показано, что роль таких уравнений играют параболические системы с периодическими или антипериодическими краевыми условиями. Решения этих уравнений определяют главные слагаемые в асимптотике решений исходной задачи. Квазинормальные формы могут быть легко решены численно, в отличие от исходных сингулярно возмущенных задач, численное решение которых требует высокой точности (а значит, трудоемко) либо узкоспециализированных алгоритмов.

Интересным фактом является зависимость результатов от алгебраических свойств числа ${{k}_{0}}$. Существенно отличаются случаи иррационального и рационального ${{k}_{0}}$.

Новым, по сравнению с задачей с одним запаздыванием, является то, что в задаче с двумя запаздываниями квазинормальная форма может зависеть от малого параметра через функцию $\theta (\varepsilon )$. Это позволяет сделать вывод о бесконечной цепочке прямых и обратных бифуркаций в исходной задаче при $\varepsilon \to 0$. В том числе это справедливо и для случая “близких” запаздываний ${{k}_{0}} = 1$.