Журнал вычислительной математики и математической физики, 2022, T. 62, № 9, стр. 1532-1550

Тестирование бикомпактных схем для одномерных уравнений Максвелла в слоистых средах

А. А. Белов^1, 2, *, Ж. О. Домбровская^1, **

¹ МГУ им. М.В. Ломоносова
119991 Москва, Ленинские горы, 1, стр. 2, Россия

² РУДН
117198 Москва, ул. Миклухо-Маклая, 6, Россия

^* E-mail: aa.belov@physics.msu.ru
^** E-mail: dombrovskaya@physics.msu.ru

Поступила в редакцию 26.01.2021
После доработки 11.02.2022
Принята к публикации 11.03.2022

EDN: GBONRH
DOI: 10.31857/S0044466922070031

Полный текст (PDF)

Аннотация

Проведено тестирование бикомпактных схем для системы одномерных уравнений Максвелла в стационарном и нестационарном случаях. Выполнены расчеты ряда представительных тестовых задач с обобщенными точными решениями. Некоторые из этих задач рассмотрены впервые. Проведено сравнение с наиболее популярными известными подходами: методом конечных разностей во временной области и методом конечных элементов. Эти расчеты убедительно показывают преимущества бикомпактных схем в задачах со слоистыми средами. Библ. 22. Фиг. 18.

Ключевые слова: уравнения Максвелла, бикомпактные схемы, слоистые среды, условия сопряжения, дисперсия вещества.

1. ВВЕДЕНИЕ

1. Задачи для системы уравнений Максвелла встречаются во многих физических и технических приложениях. Примерами являются расчеты элементов радиотехнических цепей и микросхем, распространение излучения по волноводам, оптика диэлектрических и плазмонных наноструктур. Многие реальные задачи рассматриваются в нестационарной постановке. В этом случае электромагнитное поле является не монохроматическим, а содержит набор различных частот.

2. Если задача рассматривается в однородной среде, либо показатель преломления плавно меняется с координатой, то поведение электромагнитного поля определяется уравнениями Максвелла. Если в задаче присутствуют границы раздела, на которых показатель преломления меняется скачком, то дополнительно учитывают условия сопряжения. Они связывают тангенциальные компоненты полей по обе стороны от границы раздела. Решение таких задач является обобщенным: на границе раздела поля испытывают излом или даже скачок. Это представляет серьезную трудность для численного расчета.

Подавляющее большинство конечно-разностных подходов (например, методы конечных разностей, конечных объемов и конечных элементов во временной области, см. [1]–[3]) основано на предположении о достаточной гладкости решения. Поэтому при наличии границ раздела сходимость резко ухудшается либо может вовсе отсутствовать. Фактически задачи в слоистых средах выходят за рамки применимости этого класса методов.

Вторая трудность заключается в том, что показатель преломления может зависеть не только от координат, но и от частоты электромагнитного поля. Такую среду называют диспергирующей. Во временнóм представлении это приводит к тому, что текущий вектор электрической индукции ${\mathbf{D}}$ зависит от вектора напряженности ${\mathbf{E}}$ не только в текущий момент времени, но и в предыдущие моменты. Система уравнений Максвелла становится интегродифференциальной. Такие задачи намного более трудны, чем чисто дифференциальные.

Указанные трудности удалось преодолеть в предложенных недавно бикомпактных схемах (см. [4]–[6]). На данный момент они построены только для одномерного случая. Обоснование этих методов дано в [7].

3. Одновременно с разработкой новых методов возникает проблема их апробации. Для этого проводят расчеты некоторых тестовых задач. Хороший тест должен удовлетворять следующим требованиям. Во-первых, для него должно быть известно точное решение. Особенно ценны решения, выражающиеся в элементарных функциях, поскольку вычисление специальных функций зачастую представляет отдельную проблему. Во-вторых, решение должно содержать характерные особенности, присущие реальным задачам, – разрывы решения либо его производной на границах раздела сред.

Отметим, что в литературе нередко рассматриваются слишком простые задачи, например, задача о распространении импульса в однородном пространстве. Это не позволяет выявить поведение метода в сложных реальных задачах.

4. Как правило, при апробации нового метода устанавливают факт близости численного решения к точному на фиксированной сетке. Однако такое тестирование нельзя считать исчерпывающим. Необходимо проводить серию расчетов на наборе сеток, в которых от сетки к сетке шаг уменьшается. Такие сетки называют сгущающимися. На каждой сетке следует вычислять погрешность как разность численного и точного решений в некоторой норме и исследовать зависимость погрешности от шага сетки. Это позволяет не только установить сам факт сходимости, но и определить фактический порядок точности. Тест считается успешно пройденным, если фактическая скорость сходимости соответствует теоретической.

Данная работа посвящена апробации бикомпактных схем. Выполнены расчеты ряда представительных тестовых задач с обобщенными точными решениями. Некоторые из этих задач рассмотрены впервые. Проведено сравнение с наиболее популярными известными подходами: методом конечных разностей во временной области (finite-difference time domain, FDTD) и методом конечных элементов (finite element method, FEM). Эти расчеты убедительно показывают преимущества бикомпактных схем в задачах со слоистыми средами.

2. ОДНОМЕРНЫЕ ЗАДАЧИ

Важное место занимают задачи электродинамики плоско-параллельных структур. Примерами являются излучение плоских проводников и их взаимодействие с близко расположенными слоями диэлектриков (см. [8]), проектирование печатных плат (см. [9]), рассеяние падающего излучения набором диэлектрических либо металлических плоскопараллельных пластин (см. [10]) и формирование в них связанных оптических состояний и ряд других задач. В них электромагнитное поле зависит только от одной пространственной координаты. Приведем постановку задач, рассматриваемых в данной работе.

2.1. Стационарный случай

1. Рассмотрим слоистую структуру, состоящую из $Q$ изотропных плоскопараллельных пластин общей толщиной $a$. Ориентируем координатную ось $z$ перпендикулярно пластинам; оси $x$ и $y$ ориентированы в плоскости пластин. Обозначим координаты границ слоев через $0 = {{\xi }_{0}} < {{\xi }_{1}} < \ldots < {{\xi }_{Q}} = a$. При $z < 0$ и $z > a$ расположены полубесконечные диэлектрические среды. Будем считать последние однородными и изотропными.

Пластины могут быть как диэлектриками, так и проводниками и полупроводниками. Обозначим через ${{\varepsilon }_{q}}$ диэлектрическую проницаемость, ${{\mu }_{q}}$ – магнитную восприимчивость, ${{\sigma }_{q}}$ – проводимость $q$-й пластины (для диэлектрических пластин ${{\sigma }_{q}} = 0$).

2. В проводящих пластинах текут внешние токи с объемной плотностью ${{{\mathbf{J}}}_{q}} = \{ {{J}_{q}},0,0\} $, направленные вдоль оси $x$. Будем считать, что величины ${{J}_{q}}$ зависят только от $z$. По границам раздела между $q$-й и $(q - 1)$-й пластинами текут поверхностные токи с поверхностными плотностями ${{{\mathbf{J}}}_{q}} = \{ {{j}_{q}},0,0\} $, которые также имеют только $x$-компоненту.

Указанные токи излучают волны в обоих направлениях оси $z$, причем в этих волнах электрическое поле ${\mathbf{E}}$ направлено по оси $x$, магнитное поле ${\mathbf{H}}$ – по оси $y$. Кроме того, пусть на структуру из $z = - \infty $ и $z = + \infty $ нормально падают линейно поляризованные плоские волны с частотой $\omega $ и таким же направлением векторов ${\mathbf{E}}$ и ${\mathbf{H}}$.

3. Из-за омического нагрева пластины могут становиться оптически неоднородными, т.е. их показатель преломления может зависеть от координаты. Будем считать, что величины ${{\varepsilon }_{q}}$, ${{\mu }_{q}}$, ${{\sigma }_{q}}$ зависят от $z$ и не зависят от $x$ и $y$. Тогда и амплитуды полей зависят только от $z$.

Описанную задачу будем называть одномерной.

4. Пусть все объемные и поверхностные токи зависят от времени как $ \sim {\kern 1pt} {{e}^{{ - i\omega t}}}$, где $\omega $ – частота колебаний. Тогда поля ${{E}_{x}}$ и ${{H}_{y}}$ также зависят от времени как $ \sim {\kern 1pt} {{e}^{{ - i\omega t}}}$. Такую задачу называют монохроматической или стационарной.

5. Приведем математическую формулировку одномерной стационарной задачи.

Основными уравнениями электродинамики являются уравнения Максвелла. Традиционно в литературе рассматривают их дифференциальную форму. Однако по причинам, указанным далее, мы будем пользоваться интегральной формой этих уравнений. Она имеет следующий вид:

(1)

$\int\limits_\Gamma \,{{{\mathbf{H}}}_{q}}d{\mathbf{l}} = \frac{{4\pi }}{c}\int\limits_S \,({{{\mathbf{J}}}_{q}} + {{\sigma }_{q}}{{{\mathbf{E}}}_{q}})d{\mathbf{s}} - \frac{{i\omega }}{c}\int\limits_S \,{{{\mathbf{D}}}_{q}}d{\mathbf{s}},\quad {{{\mathbf{D}}}_{q}} = {{\varepsilon }_{q}}{{{\mathbf{E}}}_{q}},\quad 1 \leqslant q \leqslant Q;$

(2)

$\int\limits_\Gamma \,{{{\mathbf{E}}}_{q}}d{\mathbf{l}} = \frac{{i\omega }}{c}\int\limits_S \,{{{\mathbf{B}}}_{q}}d{\mathbf{s}},\quad {{{\mathbf{B}}}_{q}} = {{\mu }_{q}}{{{\mathbf{H}}}_{q}},\quad 1 \leqslant q \leqslant Q.$

Здесь $S$ – произвольная поверхность, ограниченная контуром $\Gamma $. Используется система единиц СГС.

На внешних границах поставим условия излучения

(3)

$\frac{{\partial {{{\mathbf{E}}}_{1}}}}{{\partial z}} + ik{{{\mathbf{E}}}_{1}} = 2ik{{{\mathbf{E}}}^{0}},\quad z = 0;\quad \frac{{\partial {{{\mathbf{E}}}_{Q}}}}{{\partial z}} - ik{{{\mathbf{E}}}_{Q}} = 2ik{{{\mathbf{E}}}^{a}}{{e}^{{ - ika}}},\quad z = a.$

Здесь ${{{\mathbf{E}}}^{0}}$, ${{{\mathbf{E}}}^{a}}$ – заданные амплитуды волн, падающих справа и слева.

На границах раздела поставим условия сопряжения

(4)

$\begin{gathered} {{{\mathbf{e}}}_{z}} \times ({{{\mathbf{E}}}_{q}} - {{{\mathbf{E}}}_{{q - 1}}}) = 0,\quad {{{\mathbf{e}}}_{z}}({{{\mathbf{D}}}_{q}} - {{{\mathbf{D}}}_{{q - 1}}}) = 0, \\ {{{\mathbf{e}}}_{z}} \times ({{{\mathbf{H}}}_{q}} - {{{\mathbf{H}}}_{{q - 1}}}) = \frac{{4\pi }}{c}{{{\mathbf{J}}}_{q}},\quad {{{\mathbf{e}}}_{z}}({{{\mathbf{B}}}_{q}} - {{{\mathbf{B}}}_{{q - 1}}}) = 0. \\ \end{gathered} $

2.2. Нестационарный случай

В этом случае электромагнитное поле содержит не одну частоту, а набор различных частот.

В постановке (1)–(4) следует заменить множитель $( - i\omega )$ на производную ${{\partial }_{t}}$. Пусть объемные ${{J}_{q}}(z,t)$ и поверхностные ${{j}_{q}}(z,t)$ токи являются финитными функциями времени. Слева и справа на рассеиватель падают волновые пакеты ${{{\mathbf{E}}}^{0}}(t - z{\text{/}}c)\exp ( - i{{\omega }^{0}}t + i{{k}^{0}}z)$, ${{{\mathbf{E}}}^{a}}(t + z{\text{/}}c)\exp ( - i{{\omega }^{0}}t - i{{k}^{0}}z)$ с несущей частотой ${{\omega }^{0}}$ и заданными огибающими ${{E}^{{0,a}}}$. Будем считать огибающие финитными функциями, а поля в начальный момент времени – нулевыми. Таким образом, постановка нестационарной задачи имеет следующий вид:

(5)

$\int\limits_\Gamma \,{{{\mathbf{H}}}_{q}}d{\mathbf{l}} = \frac{{4\pi }}{c}\int\limits_S \,{{{\mathbf{J}}}_{q}}d{\mathbf{s}} + \frac{1}{c}\frac{\partial }{{\partial t}}\int\limits_S \,{{{\mathbf{D}}}_{q}}d{\mathbf{s}},\quad 1 \leqslant q \leqslant Q;$

(6)

$\int\limits_\Gamma \,{{{\mathbf{E}}}_{q}}d{\mathbf{l}} = - \frac{1}{c}\frac{\partial }{{\partial t}}\int\limits_S \,{{{\mathbf{B}}}_{q}}d{\mathbf{s}},\quad 1 \leqslant q \leqslant Q;$

(7)

$\begin{array}{*{20}{c}} {\frac{\partial }{{\partial z}}{{{\mathbf{E}}}_{1}} - \frac{1}{c}\frac{\partial }{{\partial t}}{{{\mathbf{E}}}_{1}} = 2ik{{{\mathbf{E}}}^{0}}(t - z{\text{/}}c)\exp ( - i{{\omega }^{0}}t + i{{k}^{0}}z),\quad z = 0;} \\ {\frac{\partial }{{\partial z}}{{{\mathbf{E}}}_{Q}} + \frac{1}{c}\frac{\partial }{{\partial t}}{{{\mathbf{E}}}_{Q}} = 2ik{{{\mathbf{E}}}^{a}}(t + z{\text{/}}c)\exp ( - i{{\omega }^{0}}t - i{{k}^{0}}z),\quad z = a;} \end{array}$

(8)

(9)

${{{\mathbf{E}}}_{q}} = 0,\quad {{{\mathbf{H}}}_{q}} = 0,\quad t = 0,\quad 1 \leqslant q \leqslant Q,\quad t = 0.$

3. БИКОМПАКТНЫЕ СХЕМЫ

1. Задачи в слоистых средах представляют особенную трудность для численного расчета. Из-за наличия изломов и разрывов решения схемы, использующие дифференцирование через границу раздела, страдают от катастрофического падения точности. Поэтому для таких задач требуются двухточечные консервативные схемы. Такие схемы называются бикомпактными.

Прообразом бикомпактных схем является классическая двухточечная схема Годунова (см. [11]), разработанная для задачи о распаде разрыва. Калиткин и Корякин впервые сформулировали идею бикомпактности и построили бикомпактную схему для уравнения теплопроводности в слоистой среде в одномерном и двумерном случаях (см. [12], [13]). Позднее Калиткин и Корякин построили бикомпактную схему для уравнения колебаний (см. [14]).

2. Общий подход к построению бикомпактных схем заключается в следующем (см. [14]). Введем сетку так, чтобы границы слоев были узлами. Такие сетки называются специальными (см. [15]). Запишем закон сохранения в интегральной форме и аппроксимируем интегралы квадратурами. При этом используем двухточечный шаблон, в котором задействованы 2 соседних узла сетки. Во всех внутренних узлах сетки запишем условия сопряжения для сеточных функций, а в граничных узлах – граничные условия. Подчеркнем, что реализация условий сопряжения и граничных условий должна быть одноточечной либо двухточечной.

В силу аддитивности интегралов и соответствующих квадратур, а также благодаря явному учету условий сопряжения из выполнения законов сохранения в отдельных ячейках сетки следует выполнение тех же законов сохранения во всей расчетной области. Поэтому описанные схемы являются консервативными по Тихонову–Самарскому (см. [16]). Именно консервативность обеспечивает сходимость к правильному обобщенному решению (см. [17]).

3. Для задач электродинамики исходными законами сохранения являются закон Гаусса для электрической индукции, закон Гаусса для магнитной индукции, закон Фарадея, теорема о циркуляции магнитной индукции. Они приводят к уравнениям Максвелла в интегральной форме. Именно поэтому мы ее используем.

Напомним, что условия сопряжения (4) являются следствием интегральных уравнений Максвелла. Чтобы это показать, рассматривают такой контур $\Gamma $, чтобы часть его находилась по одну сторону от границы раздела, часть – по другую, а сам контур стягивают в точку, лежащую на границе раздела. Таким образом, схемы, в которых эти условия не учитываются, не могут быть консервативными.

4. Бикомпактная схема для уравнений (1)–(4) была предложена в [4]–[6]. Введем специальную сетку $0 = {{z}_{0}} < {{z}_{1}} < \ldots < {{z}_{N}} = a$, ${{z}_{{n + 1}}} - {{z}_{n}} = \Delta {{z}_{n}}$. Поля могут испытывать разрыв, поэтому в каждом внутреннем узле нужно определить левое и правое предельные значения решения. Поэтому для каждого шага $\Delta {{z}_{{n - 1/2}}}$, $1 \leqslant n \leqslant N$, введем значения полей ${{E}_{{2n - 2}}}$, ${{H}_{{2n - 2}}}$, относящиеся к левой границе ${{z}_{{n - 1}}}$, и значения полей ${{E}_{{2n - 1}}}$, ${{H}_{{2n - 1}}}$, относящиеся к правой границе ${{z}_{n}}$.

Разностная схема для задачи (1)–(4) имеет следующий вид:

(10)

$\sqrt {{{\varepsilon }_{0}}} {{E}_{0}} + \sqrt {{{\mu }_{0}}} {{H}_{0}} = \sqrt {{{\varepsilon }_{0}}} {{E}^{0}},$

(11)

${{H}_{{2n}}} - {{H}_{{2n - 2}}} - \frac{{i\omega }}{{2c}}{{A}_{{n - 1/2}}}\Delta {{z}_{{n - 1/2}}}({{E}_{{2n}}} + {{E}_{{2n - 2}}}) = \frac{{4\pi }}{c}({{J}_{{n - 1/2}}}\Delta {{z}_{{n - 1/2}}} - {{j}_{n}}),$

(12)

${{E}_{{2n}}} - {{E}_{{2n - 2}}} - \frac{{i\omega }}{{2c}}{{\mu }_{{n - 1/2}}}\Delta {{z}_{{n - 1/2}}}({{H}_{{2n - 1}}} + {{H}_{{2n - 2}}}) = \frac{{4\pi i\omega }}{{2{{c}^{2}}}}{{\mu }_{{n - 1/2}}}\Delta {{z}_{{n - 1/2}}}{{j}_{n}},$

(13)

${{H}_{{2N - 1}}} - {{H}_{{2N - 2}}} - \frac{{i\omega }}{{2c}}{{A}_{{N - 1/2}}}\Delta {{z}_{{N - 1/2}}}({{E}_{{2N - 1}}} + {{E}_{{2N - 2}}}) = \frac{{4\pi }}{c}{{J}_{{N - 1/2}}}\Delta {{z}_{{N - 1/2}}},$

(14)

${{E}_{{2N - 1}}} - {{E}_{{2N - 2}}} - \frac{{i\omega }}{{2c}}{{\mu }_{{N - 1/2}}}\Delta {{z}_{{N - 1/2}}}({{H}_{{2N - 1}}} + {{H}_{{2N - 2}}}) = 0,$

(15)

$\sqrt {{{\varepsilon }_{N}}} {{E}_{{2N - 1}}} - \sqrt {{{\mu }_{N}}} {{H}_{{2N - 1}}} = \sqrt {{{\varepsilon }_{N}}} {{E}^{a}}.$

Здесь $A = - i\omega {\text{/}}c + 4\pi \sigma {\text{/}}c$. Индекс у $\varepsilon $, $\mu $, $\sigma $, $J$ соответствует номеру узла, в котором вычислена соответствующая величина; например, ${{\varepsilon }_{{n - 1/2}}} \equiv {{\varepsilon }_{q}}({{z}_{{n - 1/2}}})$, где ${{z}_{{n - 1/2}}} = 0.5({{z}_{{n - 1}}} + {{z}_{n}})$. Поверхностные токи ${{j}_{n}} = j({{z}_{n}})$ относятся ко внутренним узлам. В уравнениях (11), (12) индекс $n$ пробегает значения от 1 до $N - 1$. Таким образом, система (10)–(15) содержит $2N + 2$ уравнения.

5. Для нестационарных задач в [4]–[6] был предложен метод спектрального разложения. Кратко напомним его суть.

При распространении волнового пакета в линейной диспергирующей среде для разных спектральных компонент решения реализуются разные значения $\varepsilon $, $\mu $, $\sigma $. Разложим пакет на монохроматические компоненты, решим стационарную задачу для каждой из них и просуммируем полученные решения. Спектральное разложение исходного пакета есть прямое преобразование Фурье, суммирование полученных решений – обратное преобразование Фурье. Оба преобразования выполняются с помощью численных квадратур. Описанный алгоритм назовем нестационарной бикомпактной схемой.

Таким образом, нестационарная задача сводится к набору стационарных задач. Данный подход имеет простой физический смысл. Он позволяет учитывать произвольный закон дисперсии, включая таблично заданный.

4. СТАЦИОНАРНЫЕ ТЕСТЫ

Для апробации бикомпактных схем мы провели расчеты ряда тестовых задач, у которых точное решение выражается в конечном виде через элементарные функции. Для простоты рассматривались диэлектрические (непроводящие) среды. Наличие ненулевой проводимости не вносит принципиальных трудностей. В приведенных ниже модельных задачах все размерные величины нормированы (т.е. являются относительными).

4.1. Однородная среда

1. Рассмотрим простейшую задачу – распространение плоской монохроматической волны через однородную диэлектрическую среду. Пусть $\varepsilon $, $\mu $ постоянны, и объемные и поверхностные токи отсутствуют $J = 0$, $j = 0$. Пусть слева на выделенную область $0\;\leqslant \;z\;\leqslant \;a$ падает плоская монохроматическая волна.

2. Решение удобно строить с помощью перехода к волновому уравнению. Запишем одномерную систему уравнений Максвелла в дифференциальной форме

(16)

$\frac{{\partial {{E}_{x}}}}{{\partial z}} = \frac{{i\mu \omega }}{c}{{H}_{y}},\quad \frac{{\partial {{H}_{y}}}}{{\partial z}} = \frac{{i\varepsilon \omega }}{c}{{E}_{z}},\quad 0\;\leqslant \;z\;\leqslant \;a;$

(17)

$\frac{{\partial {{E}_{x}}}}{{\partial z}} + i\tilde {k}{{E}_{x}} = 2i\tilde {k}{{E}^{0}},\quad z = 0;\quad \quad \frac{{\partial {{E}_{x}}}}{{\partial z}} - i\tilde {k}{{E}_{x}} = 0,\quad z = a.$

Здесь $\tilde {k} = \omega \sqrt {\varepsilon \mu } {\text{/}}c$ – волновое число в среде. В записи граничных условий используется именно это значение, поскольку за пределами отрезка $[0,a]$ волна распространяется не в вакууме, а в той же самой среде.

Исключим из (16) ${{H}_{y}}$. Для этого продифференцируем первое из уравнений по $z$, выразим из него $\partial {{H}_{y}}{\text{/}}\partial z$ и подставим во второе уравнение. Получим

(18)

$\frac{{{{\partial }^{2}}{{E}_{x}}}}{{\partial {{z}^{2}}}} + {{\tilde {k}}^{2}}{{E}_{x}} = 0.$

Общее решение (18) есть

(19)

${{E}_{x}} = {{C}_{1}}\exp (i\tilde {k}z) + {{C}_{2}}\exp ( - i\tilde {k}z).$

С учетом граничных условий (17) имеем ${{C}_{1}} = {{E}^{0}}$, ${{C}_{2}} = 0$. Решение ${{H}_{y}}$ найдем с помощью первого из уравнений (16). Таким образом, окончательное решение имеет вид

(20)

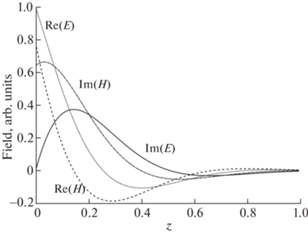
${{E}_{x}} = {{E}^{0}}{{e}^{{i\tilde {k}z}}},\quad {{H}_{y}} = {{E}^{0}}\sqrt {\frac{\varepsilon }{\mu }} {{e}^{{i\tilde {k}z}}}.$

Оно известно из учебников.

3. Приведем результаты численных расчетов по предложенной стационарной схеме. Положим ${{E}^{0}} = 1$, $\omega = \pi {\text{/}}2$, $c = 1$, $a = 1$. Рассмотрим сначала среду с поглощением: $\varepsilon = 1 + 5i$, $\mu = 5$. Такую задачу можно трактовать как жесткую: при $z = a$ амплитуды полей уменьшатся в $\exp (i\tilde {k}a) \approx 150$ раз по сравнению с таковыми при $z = 0$. Решение этой задачи представлено на фиг. 1.

Фиг. 1.

Решение задачи о среде с поглощением.

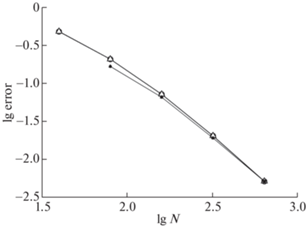
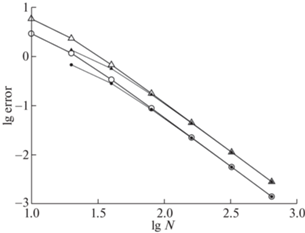
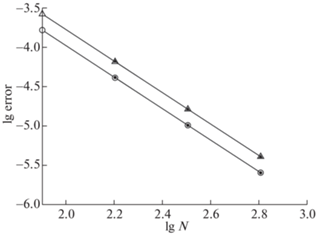
Расчеты проводились на наборе сгущающихся сеток. Погрешность расчета определялась двумя способами: во-первых, как разность численного решения и точного, во-вторых, с помощью апостериорной оценки по методу Ричардсона. Нормы ${{L}_{2}}$ полученных погрешностей для полей ${{E}_{x}}$ и ${{H}_{y}}$ приведены на фиг. 2 в двойном логарифмическом масштабе. Видно, что для обоих полей погрешность убывает. Линии погрешности являются прямыми с наклоном $ - $2. Поэтому фактический порядок точности равен 2, что совпадает с теорией. Видно также, что оценка точности по методу Ричардсона практически совпадает с погрешностью, определенной непосредственно по разности численного решения и точного.

Фиг. 2.

Погрешность решения в задаче о среде с поглощением: $\bigcirc $ – ${{E}_{x}}$, $\vartriangle $ – ${{H}_{y}}$, светлые маркеры – разность численного и точного решений, темные маркеры – оценки по методу Ричардсона.

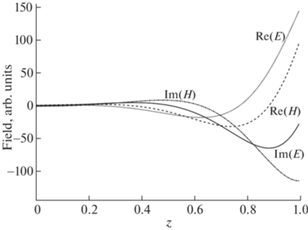
4. Аналогичные расчеты проводились для активной среды: $\varepsilon = 1 - 5i$, $\mu = 5$. В этом случае амплитуды полей при $z = 1$ оказываются в $ \approx {\kern 1pt} 150$ раз больше, чем при $z = 0$. Такая задача является плохо обусловленной по левому граничному условию. Вид решения показан на фиг. 3, а полученные погрешности – на фиг. 4. В этом случае справедливы те же выводы, что и в предыдущем. Начальные участки графиков погрешности искривлены, но по мере сгущения сеток погрешность начинает убывать в соответствии с теоретическим вторым порядком точности.

Фиг. 3.

Решение задачи об активной среде.

Фиг. 4.

Погрешность решения в задаче об активной среде. Обозначения те же, что на фиг. 2.

4.2. Граница раздела диэлектриков

1. Пусть расчетная область состоит из двух однородных недиспергирующих сред с границей в точке $z = b$. Пусть слева от нее материальные параметры равны ${{\varepsilon }_{1}}$, ${{\mu }_{1}}$, а справа – ${{\varepsilon }_{2}}$, ${{\mu }_{2}}$. Пусть волна падает слева ${{E}^{0}} = 1$, ${{E}^{a}} = 0$, а токи отсутствуют ${{J}_{{1,2}}} = 0$, ${{j}_{1}} = 0$. Постановка задачи в форме одномерных дифференциальных уравнений Максвелла имеет следующий вид:

(21)

$\frac{{\partial {{E}_{x}}}}{{\partial z}} = \frac{{i{{\mu }_{1}}\omega }}{c}{{H}_{y}},\quad \frac{{\partial {{H}_{y}}}}{{\partial z}} = \frac{{i{{\varepsilon }_{1}}\omega }}{c}{{E}_{x}},\quad 0\;\leqslant \;z\;\leqslant \;b;$

(22)

$\frac{{\partial {{E}_{x}}}}{{\partial z}} = \frac{{i{{\mu }_{2}}\omega }}{c}{{H}_{y}},\quad \frac{{\partial {{H}_{y}}}}{{\partial z}} = \frac{{i{{\varepsilon }_{2}}\omega }}{c}{{E}_{x}},\quad b\;\leqslant \;z\;\leqslant \;a;$

(23)

$\frac{{\partial {{E}_{x}}}}{{\partial z}} + \frac{{i\omega }}{c}{{E}_{x}} = 2i\tilde {k}{{E}^{0}},\quad z = 0;\quad \frac{{\partial {{E}_{x}}}}{{\partial z}} - \frac{{i\omega }}{c}{{E}_{x}} = 0,\quad z = a.$

(24)

${{\left. {{{E}_{x}}} \right|}_{{z = b - 0}}} = {{\left. {{{E}_{x}}} \right|}_{{z = b + 0}}},\quad {{\left. {{{H}_{y}}} \right|}_{{z = b - 0}}} = {{\left. {{{H}_{y}}} \right|}_{{z = b + 0}}}.$

2. Получим точное решение этой задачи. От (21) и (22) перейдем к уравнениям типа (18) для областей $0\;\leqslant \;z\;\leqslant \;b$ и $b\;\leqslant \;z\;\leqslant \;a$. Общее решение имеет вид

(25)

${{E}_{x}} = {{C}_{1}}{{e}^{{i{{{\tilde {k}}}_{1}}z}}} + {{C}_{2}}{{e}^{{ - i{{{\tilde {k}}}_{1}}z}}},\quad {{H}_{y}} = \sqrt {\frac{{{{\varepsilon }_{1}}}}{{{{\mu }_{1}}}}} ({{C}_{1}}{{e}^{{i{{{\tilde {k}}}_{1}}z}}} - {{C}_{2}}{{e}^{{ - i{{{\tilde {k}}}_{1}}z}}}),\quad 0\;\leqslant \;z\;\leqslant \;b;$

(26)

${{E}_{x}} = {{C}_{3}}{{e}^{{i{{{\tilde {k}}}_{2}}z}}} + {{C}_{4}}{{e}^{{ - i{{{\tilde {k}}}_{2}}z}}},\quad {{H}_{y}} = \sqrt {\frac{{{{\varepsilon }_{2}}}}{{{{\mu }_{2}}}}} ({{C}_{3}}{{e}^{{i{{{\tilde {k}}}_{2}}z}}} - {{C}_{4}}{{e}^{{ - i{{{\tilde {k}}}_{2}}z}}}),\quad b\;\leqslant \;z\;\leqslant \;a.$

Из граничных условий (23) следует, что

(27)

${{C}_{1}} = {{E}^{0}} = 1,\quad {{C}_{4}} = 0.$

Подстановка в условия сопряжения дает

(28)

${{C}_{2}} = {{E}^{0}}\frac{{\sqrt {{{\varepsilon }_{1}}{\text{/}}{{\mu }_{1}}} - \sqrt {{{\varepsilon }_{2}}{\text{/}}{{\mu }_{2}}} }}{{\sqrt {{{\varepsilon }_{1}}{\text{/}}{{\mu }_{1}}} + \sqrt {{{\varepsilon }_{2}}{\text{/}}{{\mu }_{2}}} }}{{e}^{{i{{{\tilde {k}}}_{1}}b}}},\quad {{C}_{3}} = {{E}^{0}}\frac{{2\sqrt {{{\varepsilon }_{1}}{\text{/}}{{\mu }_{1}}} }}{{\sqrt {{{\varepsilon }_{1}}{\text{/}}{{\mu }_{1}}} + \sqrt {{{\varepsilon }_{2}}{\text{/}}{{\mu }_{2}}} }}{{e}^{{i({{{\tilde {k}}}_{1}} - {{{\tilde {k}}}_{2}})b}}}.$

Выражения (28) являются частным случаем общеизвестных формул Френеля.

3. Положим $c = 1$, $\omega = \pi $, $a = 1$, $b = 0.5$. Пусть для левой среды ${{\varepsilon }_{1}} = {{\mu }_{1}} = 1$, а для правой – ${{\varepsilon }_{2}} = 10$, ${{\mu }_{2}} = 2$. На фиг. 5 представлен вид решения: при $z = b$ возникает слабый разрыв у $\operatorname{Im} E$ и $\operatorname{Im} H$, а $\operatorname{Re} E$ и $\operatorname{Re} H$ непрерывны.

Фиг. 5.

Решение задачи о диэлектрической границе раздела. Вертикальная прямая – граница раздела.

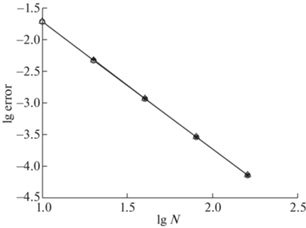
Приведем результаты расчета по стационарной бикомпактной схеме. Выберем специальную сетку, у которой узел попадает в точку $z = b$. Очевидно, все последующие сетки, полученные последовательным уменьшением шага вдвое, также являются специальными. На фиг. 6 показана зависимость погрешности в норме ${{L}_{2}}$ от числа шагов сетки. Масштаб графика двойной логарифмический. Видно, что погрешности, полученные сравнением численного решения с точным, практически совпадают с оценками по методу Ричардсона. Эти кривые стремятся к прямым линиям с наклоном $ - 2$, соответствующим теоретическому порядку точности. Напомним, что именно это обеспечивает применимость метода Ричардсона.

Фиг. 6.

Погрешность решения в задаче о диэлектрической границе раздела. Обозначения те же, что на фиг. 2.

4. Сравним предлагаемую схему с методом конечных элементов на примере пакета FreeFEM++ (см. [18]). Расчеты проводились с использованием следующих элементов: лагранжевы элементы L1 1-го порядка, пузырьковые (B, bubble) элементы 1-го порядка (см. [19]), разрывные (NC, non-conforming) элементы 1-го порядка (см. [20]), лагранжевы элементы L2 2-го порядка. Для простоты мы задавали граничные условия для обоих полей $E$, $H$ по значению точного решения на левой границе

(29)

${{\left. {{{E}_{x}}} \right|}_{{z = 0}}} = E_{x}^{{{\text{ex}}}}(0),\quad {{\left. {{{H}_{y}}} \right|}_{{z = 0}}} = H_{y}^{{{\text{ex}}}}(0).$

Такая постановка соответствует, например, [21], [22].

Расчет проводился на сгущающихся специальных сетках, и на каждой вычислялись погрешности $\delta E$, $\delta H$ относительно точного решения. Чтобы не загромождать график, мы проводили дополнительное усреднение погрешностей по компонентам полей

(30)

$\delta = \frac{1}{2}(\delta E + \delta H).$

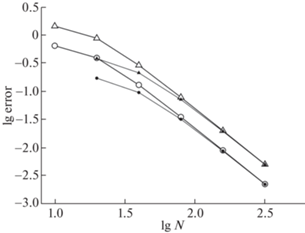
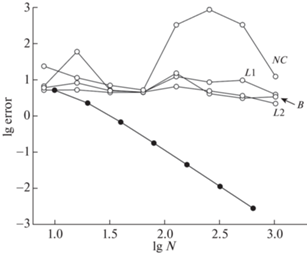
Величины (30) для перечисленных видов конечных элементов приведены на фиг. 7. Масштаб графика двойной логарифмический. Видно, что элементы L2 обеспечивают 2-й порядок точности, причем кривая погрешности является плавной. Для элементов L1 порядок точности в среднем близок ко 2-му, но кривая оказывается дерганой, т.е. отсутствует на ней прямолинейный участок теоретической сходимости. Это затрудняет контроль точности по Ричардсону и ухудшает надежность расчета. Элементы B и NC обеспечивают только первый порядок точности и значительно уступают по точности элементам L1 и L2.

Фиг. 7.

Усредненные погрешности (30) в задаче о диэлектрической границе раздела: $ \bullet $ – бикомпактная схема, $\bigcirc $ – метод конечных элементов в пакете FreeFEM++. Типы элементов указаны у кривых.

На фиг. 7 приведена также усредненная погрешность бикомпактной схемы. Видно, что эта схема дает несколько худшую точность, чем элементы L2, и практически не уступает в точности элементам L1. При этом трудоемкость бикомпактной схемы такова же, как у элементов L1, и существенно меньше, чем у элементов L2.

5. Таким образом, предложенная схема уверенно справляется с задачами, в которых решение испытывает слабый разрыв. При этом она практически не уступает методу конечных элементов.

4.3. Граница раздела с токами

1. Пусть в предыдущей задаче отсутствуют падающие волны ${{E}^{0}} = {{E}^{a}} = 0$ и объемные токи ${{J}_{{1,2}}} = 0$, но по границе раздела течет поверхностный ток, излучающий волны в положительном и отрицательном направлении оси $z$. Такая модель описывает переизлучение тонкого металлического напыления на границе рассеивателя. Эта задача особенно трудна, поскольку у $\operatorname{Re} H$ возникает сильный разрыв, а у $\operatorname{Im} E$ и $\operatorname{Im} H$ – слабый. В литературе такая задача не рассматривалась.

Постановка задачи включает уравнения (21), (22), граничные условия (23); условия сопряжения на границе раздела $z = b$ формулируются следующим образом:

(31)

${{\left. {{{E}_{x}}} \right|}_{{z = b - 0}}} = {{\left. {{{E}_{x}}} \right|}_{{z = b + 0}}},\quad {{\left. {{{H}_{y}}} \right|}_{{z = b + 0}}} - {{\left. {{{H}_{y}}} \right|}_{{z = b - 0}}} = \frac{{4\pi }}{c}{{j}_{1}}.$

2. Выведем точное решение этой задачи. Перейдем от уравнений Максвелла к уравнениям типа (18) для областей $0\;\leqslant \;z\;\leqslant \;b$ и $b\;\leqslant \;z\;\leqslant \;a$. Общее решение этих уравнений имеет вид (25), (26). Волны, приходящие из бесконечности, отсутствуют, поэтому граничные условия дают

(32)

${{C}_{1}} = {{C}_{4}} = 0.$

Подставим эти решения в условия сопряжения (31) и найдем ${{C}_{2}}$, ${{C}_{3}}$:

(33)

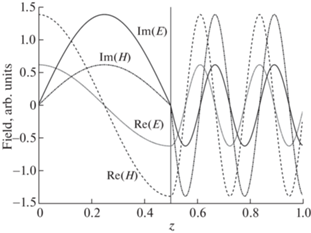
${{C}_{2}} = \frac{{4\pi }}{c}{{j}_{1}}\frac{{{{e}^{{ - i{{{\tilde {k}}}_{1}}b}}}}}{{\sqrt {{{\varepsilon }_{1}}{\text{/}}{{\mu }_{1}}} + \sqrt {{{\varepsilon }_{2}}{\text{/}}{{\mu }_{2}}} }},\quad {{C}_{3}} = \frac{{4\pi }}{c}{{j}_{1}}\frac{{{{e}^{{ - i{{{\tilde {k}}}_{2}}b}}}}}{{\sqrt {{{\varepsilon }_{1}}{\text{/}}{{\mu }_{1}}} + \sqrt {{{\varepsilon }_{2}}{\text{/}}{{\mu }_{2}}} }}.$

Полученное решение приведено на фиг. 8. Оно является новым.

Фиг. 8.

Решение задачи о границе раздела с поверхностным током. Вертикальная прямая – граница раздела.

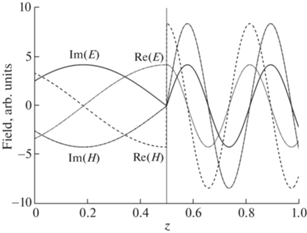
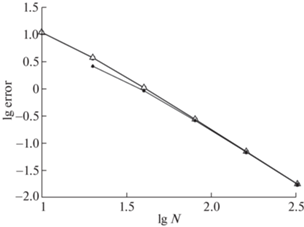
3. В расчетах положим $j = 1$, а все остальные параметры выберем такими же, как в предыдущей задаче. Выберем специальную сетку указанным выше способом. На фиг. 9 показана зависимость погрешности в норме ${{L}_{2}}$ от числа шагов сетки в двойном логарифмическом масштабе. Видно, что значения погрешности, вычисленные по методу Ричардсона, практически совпадают с погрешностями относительно точного решения. Скорость убывания погрешности соответствует теоретическому второму порядку точности.

Фиг. 9.

Погрешность решения в задаче о границе раздела с поверхностным током. Обозначения те же, что на фиг. 2.

4. Был проведен расчет этой задачи в пакете FreeFEM++. Граничные условия задавались аналогично (29). Использовались те же 4 типа конечных элементов.

В пакете FreeFEM++ не предусмотрено задание точечных источников, поэтому для имитации поверхностного тока вводился объемный ток следующего вида:

(34)

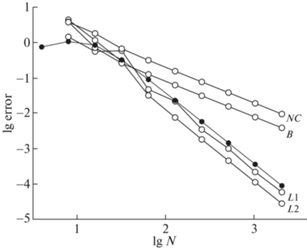
$J = \frac{{2\pi }}{c}\delta (z - a{\text{/}}2) \approx \frac{{4\pi }}{{cd}}\left( \begin{gathered} \frac{{x - {{x}_{l}}}}{{a{\text{/}}2 - {{x}_{l}}}},\quad {{x}_{l}} < x < a{\text{/}}2; \hfill \\ \frac{{x - l{\text{/}}2}}{{{{x}_{r}} - a{\text{/}}2}},\quad a{\text{/}}2 < x < {{x}_{r}}; \hfill \\ 0,\quad 0 < x < {{x}_{l}},\quad {{x}_{r}} < x < a. \hfill \\ \end{gathered} \right.$

Здесь $d \ll a$, ${{x}_{l}} = a{\text{/}}2 - d{\text{/}}2$, ${{x}_{r}} = a{\text{/}}2 + d{\text{/}}2$. Ток (34) является кусочно-линейной функцией координаты. Он отличен от нуля вне отрезка $[{{x}_{l}},{{x}_{r}}]$, нарастает на отрезке $[{{x}_{l}},a{\text{/}}2]$ и убывает на отрезке $[a{\text{/}}2,{{x}_{r}}]$. При этом выполняется условие нормировки

(35)

$\int\limits_0^a \,Jdz = \frac{{2\pi }}{c}.$

Погрешности, полученные в пакете FreeFEM++ в данной задаче, приведены на фиг. 10 в двойном логарифмическом масштабе. Здесь выбрано $\delta {{ = 10}^{{ - 3}}}$. Видно, что для всех рассмотренных типов конечных элементов погрешность велика: она составляет $ \sim {\kern 1pt} {{10}^{1}}$. При сгущении сеток погрешность не убывает, т.е. сходимость отсутствует. Аналогичные результаты имели место и при других значениях $d{{ = 10}^{{ - 1}}}$, ${{10}^{{ - 2}}}$, ${{10}^{{ - 5}}}$.

Фиг. 10.

Усредненные погрешности (30) в задаче о границе раздела с поверхностным током. Обозначения те же, что на фиг. 7.

На фиг. 10 приведена также усредненная погрешность бикомпактной схемы. Видно, что она убывает в соответствии с теоретическим 2-м порядком сходимости. Точность бикомпактной схемы кардинально превосходит пакет FreeFEM++.

5. Таким образом, предлагаемая бикомпактная схема на специальных сетках позволяет проводить расчеты решений с сильными разрывами. Это свидетельствует об исключительно высокой надежности данного метода. Пакет FreeFEM++, основанный на методе конечных элементов, не позволил решить эту задачу, что убедительно показывает преимущества предлагаемой схемы.

4.4. Плотность энергии электромагнитного поля

Рассмотрим плотность энергии электромагнитного поля

(36)

$\mathcal{E} = \frac{1}{{8\pi }}(\varepsilon {\kern 1pt} {\text{|}}{{E}_{x}}{\kern 1pt} {{{\text{|}}}^{2}} + \mu {\text{|}}{{H}_{y}}{\kern 1pt} {{{\text{|}}}^{2}}).$

Если среда прозрачная (т.е. поглощение отсутствует), то энергия сохраняется при распространении волны.

В задачах п. 4.2, 4.3 мы вычисляли $\mathcal{E}$ в каждом узле сетки. Затем вычислялась L₂-норма разности численного ${{\mathcal{E}}_{n}}$ и точного ${{\mathcal{E}}^{{{\text{ex}}}}}$ значений этой величины

(37)

$\delta \mathcal{E} = {{\left\| {{{\mathcal{E}}^{{{\text{ex}}}}}({{z}_{n}}) - {{\mathcal{E}}_{n}}} \right\|}_{{{{L}_{2}}}}}.$

Величину $\delta \mathcal{E}$ можно интерпретировать как средний дисбаланс энергии электромагнитного поля. Расчеты велись со сгущением сеток, и средний дисбаланс вычислялся на каждой сетке. На фиг. 11 приведена зависимость $\delta \mathcal{E}$ от числа узлов сетки для обеих задач 4.2, 4.3. Масштаб графика двойной логарифмический. Видно, что в задаче 4.2 дисбаланс составляет $\delta \mathcal{E} \sim 3 \times {{10}^{{ - 17}}}{\kern 1pt} - {\kern 1pt} 3 \times {{10}^{{ - 15}}}$, а в задаче 4.3 – $\delta \mathcal{E} \sim 3 \times {{10}^{{ - 15}}}{\kern 1pt} - {\kern 1pt} 3 \times {{10}^{{ - 13}}}$. С увеличением $N$ дисбаланс возрастает, причем средний наклон кривых равен 1/2. Это соответствует закону возрастания $\delta \mathcal{E} \sim {{N}^{{1/2}}}$. Такие значения дисбаланса и характер его роста соответствуют ошибкам компьютерного округления.

Фиг. 11.

Дисбаланс энергии (37) для бикомпактной схемы. Сплошная линия – задача п. 4.2, пунктир – задача п. 4.3.

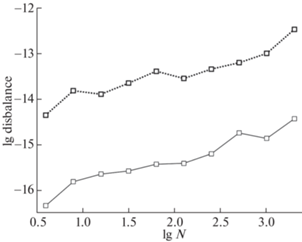
Таким образом, независимо от величины шага сетки предложенная бикомпактная схема передает закон сохранения энергии электромагнитной волны с точностью ошибок округления. Это является дополнительным преимуществом данной схемы.

5. НЕСТАЦИОНАРНЫЕ ТЕСТЫ

В нестационарном случае были проведены расчеты тех же трех тестовых задач: распространение излучения в однородной среде (в том числе диспергирующей), распространение излучения через границу раздела, излучение поверхностных токов). Для определенности в задачах этого раздела падающий импульс считается гауссовым

(38)

$\mathcal{E}(t) = \exp \left( { - \frac{{{{t}^{2}}}}{{2{{W}^{2}}}} - i{{\omega }^{0}}t} \right),\quad {{\omega }^{0}} = \frac{{3\pi }}{2}\pi ,\quad W = \frac{\pi }{4}.$

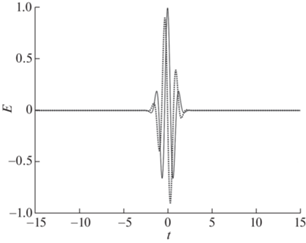
Напомним, что все величины считаются обезразмеренными. Ширина импульса составляет $ \approx {\kern 1pt} \pi $ на половине высоты и $ \approx {\kern 1pt} 3\pi $ по основанию. Временная развертка импульса представлена на фиг. 12, а его спектр – на фиг. 13.

Фиг. 12.

Временная развертка падающего импульса. Сплошная линия – $\operatorname{Re} E$, пунктир – $\operatorname{Im} E$.

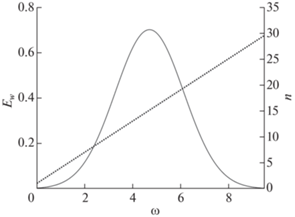
Фиг. 13.

Спектр падающего импульса (сплошная линия) и зависимость показателя преломления от частоты в задаче о диспергирующей среде (пунктир).

5.1. Однородная среда

1. Рассмотрим первую задачу из разд. 4 в нестационарной постановке. Пусть в однородной среде с материальными параметрами $\varepsilon = 1 + 5i$, $\mu = 1$ распространяется импульс (38).

2. Построим точное решение этой задачи. Разложим падающий импульс $\mathcal{E}(t)$ в интеграл Фурье

(39)

${{E}_{\omega }} = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } \mathcal{E}(t){{e}^{{i\omega t}}}dt.$

Решим задачу (1)–(4) для (3): ${{E}^{0}} = {{E}_{\omega }}$, ${{E}^{a}} = 0$. Это решение имеет вид (20). Выполним обратное преобразование Фурье

(40)

$\begin{gathered} {{E}_{x}}(z,t) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } {{E}_{\omega }}{{e}^{{i\tilde {k}z}}}{{e}^{{ - i\omega t}}}d\omega = \mathcal{E}\left( {t - \sqrt {\varepsilon \mu } \frac{z}{c}} \right),\quad \tilde {k} = \frac{{\omega \sqrt {\varepsilon \mu } }}{c}, \\ {{H}_{y}}(z,t) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } \,\sqrt {\frac{\varepsilon }{\mu }} {{E}_{\omega }}{{e}^{{i\tilde {k}z}}}{{e}^{{ - i\omega t}}}d\omega = \sqrt {\frac{\varepsilon }{\mu }} \mathcal{E}\left( {t - \sqrt {\varepsilon \mu } \frac{z}{c}} \right). \\ \end{gathered} $

Это решение известно из учебников.

3. Расчет проводился по нестационарной бикомпактной схеме. Полученные погрешности приведены на фиг. 14. Видно, что, во-первых, погрешности, найденные сравнением с точным решением, совпадают с оценками по Ричардсону, и, во-вторых, фактически порядок точности равен 2 и совпадает с теоретическим.

Фиг. 14.

Погрешность решения в нестационарной задаче о среде с поглощением. Обозначения те же, что на фиг. 2.

5.2. Диспергирующая среда

1. Рассмотрим предыдущую задачу в усложненной постановке. Пусть теперь среда является диспергирующей, т.е. величины $\varepsilon (\omega )$ и $\mu (\omega )$ зависят от частоты.

2. Точное решение по-прежнему выражается квадратурой (40), однако класс $\varepsilon (\omega )$ и $\mu (\omega )$, при которых ее удается вычислить в элементарных функциях, весьма узок.

Положим $\varepsilon (\omega ) = \mu (\omega ) = {{A}_{1}}\omega + {{A}_{0}}$. Тогда обе квадратуры в (40) берутся через интеграл Пуассона

(41)

$\begin{gathered} {{E}_{x}}(z,t) = \frac{W}{{\sqrt {2a} }}\exp \left( {\frac{{{{b}^{2}}}}{{4a}} - c} \right),\quad {{H}_{y}}(z,t) = {{E}_{x}}(z,t), \\ a = \frac{{{{W}^{2}}}}{2} - i\frac{{{{A}_{1}}}}{c}z,\quad b = {{\omega }^{0}}{{W}^{2}} + i\left( {\frac{{{{A}_{0}}z}}{c} - t} \right),\quad c = \frac{1}{2}{{({{\omega }^{0}}W)}^{2}}. \\ \end{gathered} $

Этот случай представляет большую ценность, поскольку обе компоненты решения выражаются явно. По-видимому, это решение является новым.

В конкретном расчете были выбраны значения ${{A}_{1}} = 3$, ${{A}_{0}} = 1$. Соответствующая зависимость $n(\omega ) = \sqrt {\varepsilon (\omega )\mu (\omega )} $ показателя преломления от частоты приведена на фиг. 13 (правая ось ординат). Видно, что на отрезке частот, содержащихся в импульсе (38), показатель преломления изменяется почти в 30 раз: от $n = 1$ до $n \approx 30$. Поэтому данный тест достаточно представителен.

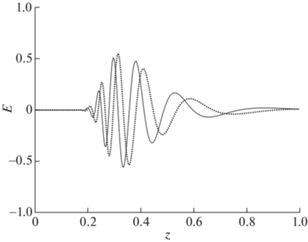
3. Проанализируем характер решения. На фиг. 15 показана зависимость ${{E}_{x}}$ и ${{H}_{y}}$ от $z$ при фиксированном $t$. Видно, что высокочастотные компоненты, для которых $n(\omega )$ велико, распространяются медленно, а низкочастотные их заметно обгоняют. В результате импульс расплывается, причем несимметрично.

Фиг. 15.

Пространственная развертка решения в задаче о диспергирующей среде. Обозначения те же, что на фиг. 12.

За время $T$ область локализации импульса увеличивается на $cT(1{\text{/}}\min n - 1{\text{/}}\max n)$, это наибольший из пространственных масштабов задачи. Наименьший масштаб есть длина волны самой высокочастотной компоненты $\min \lambda = 2\pi c{\text{/}}\max (\omega n)$. Поэтому отношение наибольшего пространственного масштаба к наименьшему в данной задаче равно

(42)

$\frac{{cT(1{\text{/}}\min n - 1{\text{/}}\max n)}}{{2\pi c{\text{/}}\max (\omega n)}} \approx 46T.$

Видно, что, увеличивая $T$, разномасштабность (42) можно сделать сколь угодно большой. Поэтому задачу следует относить к жестким. Это является дополнительным преимуществом предложенного точного решения, поскольку оно оказывается хорошим тестом для алгоритмов адаптивного выбора шага по пространству и времени. Особенность этого теста заключается в том, что область, где нужно сгущать пространственную сетку, перемещается с течением времени, и ее положение заранее неизвестно. На данный момент такие алгоритмы еще не построены.

В проведенных расчетах полное время равнялось $T = 30$, и величина (42) достигала $ \sim {\kern 1pt} 1400$. Это достаточно высокая жесткость. Расчет проводился с постоянным шагом по пространству и времени. Поэтому требовались достаточно подробные сетки.

4. На фиг. 16 показаны полученные погрешности. Видно, что при сгущении сеток погрешности убывают в соответствии со вторым порядком точности, и оценки по методу Ричардсона хорошо согласуются с погрешностями, определенными непосредственно сравнением численного решения с точным. Этот тест убедительно подтверждает правильность предложенного метода учета дисперсии.

Фиг. 16.

Погрешность решения в задаче о диспергирующей среде. Обозначения те же, что на фиг. 2.

5. Отметим еще два случая, когда хотя бы часть решения удается выразить явно. Во-первых, пусть $\mu = 1$, и $\varepsilon (\omega )$ представимо в виде отношения квадратов некоторых полиномов

(43)

$\begin{gathered} \varepsilon (\omega ) = {{\left( {\frac{{{{P}_{1}}(\omega )}}{{{{P}_{2}}(\omega )}}} \right)}^{2}}, \\ {{P}_{1}}(\omega ) = {{A}_{n}}{{\omega }^{n}} + {{A}_{{n - 1}}}{{\omega }^{{n - 1}}} + \ldots + {{A}_{0}}, \\ {{P}_{2}}(\omega ) = {{B}_{m}}{{\omega }^{m}} + {{B}_{{m - 1}}}{{\omega }^{{m - 1}}} + \ldots + {{B}_{0}}. \\ \end{gathered} $

Тогда интеграл для ${{H}_{y}}(z,t)$ берется через вычеты в нулях полинома ${{P}_{2}}$. Однако вычислить квадратуру для ${{E}_{x}}(z,t)$ не удается. Такой тест менее информативен, чем описанный выше. Тем не менее диэлектрическую проницаемость многих реальных материалов можно описать равенством (43). Поэтому данный случай также представляет значительную ценность.

Во-вторых, гауссова огибающая является моделью. Вместо нее можно использовать огибающую следующего вида:

(44)

$\mathcal{E}(t) = \frac{A}{{B + {{t}^{{2k}}}}},$

где $k$ – натуральное число. Качественное поведение (44) аналогично (38). В этом случае квадратуры (40) можно вычислить через вычеты при произвольном законе дисперсии $\varepsilon (\omega )$, $\mu (\omega )$.

Насколько нам известно, в литературе эти случаи не описаны.

5.3. Граница раздела диэлектриков

1. Рассмотрим эту задачу в нестационарной постановке: пусть слева на границу раздела падает импульс вида (38).

2. Разложим падающий импульс в интеграл Фурье и для каждой спектральной амплитуды ${{E}_{\omega }}$ решим стационарную задачу (1)–(4). Точное решение последней имеет вид (25)–(28), где ${{E}^{0}} = {{E}_{\omega }}$. Обратное преобразование Фурье дает точное решение нестационарной задачи: при $z < b$ решение состоит из падающей и отраженной волн

(45)

$\begin{gathered} {{E}_{x}} = \mathcal{E}\left( {\sqrt {{{\varepsilon }_{1}}{{\mu }_{1}}} \frac{z}{c} - t} \right) + {{C}_{2}}\mathcal{E}\left( {\frac{{2b - z}}{c}\sqrt {{{\varepsilon }_{1}}{{\mu }_{1}}} - t} \right), \\ {{H}_{y}} = \sqrt {\frac{{{{\varepsilon }_{1}}}}{{{{\mu }_{1}}}}} \mathcal{E}\left( {\sqrt {{{\varepsilon }_{1}}{{\mu }_{1}}} \frac{z}{c} - t} \right) - \sqrt {\frac{{{{\varepsilon }_{1}}}}{{{{\mu }_{1}}}}} {{C}_{2}}\mathcal{E}\left( {\frac{{2b - z}}{c}\sqrt {{{\varepsilon }_{1}}{{\mu }_{1}}} - t} \right); \\ \end{gathered} $

а при $z > b$ – из прошедшей

(46)

$\begin{gathered} {{E}_{x}} = {{C}_{3}}\mathcal{E}\left( {\frac{b}{c} + \sqrt {{{\varepsilon }_{2}}{{\mu }_{2}}} \frac{{z - b}}{c} - t} \right), \\ {{H}_{y}} = {{C}_{3}}\sqrt {\frac{{{{\varepsilon }_{2}}}}{{{{\mu }_{2}}}}} \mathcal{E}\left( {\frac{b}{c} + \sqrt {{{\varepsilon }_{2}}{{\mu }_{2}}} \frac{{z - b}}{c} - t} \right). \\ \end{gathered} $

Найти это решение в литературе не удалось. По-видимому, оно является новым.

3. Выберем такие же материальные параметры, как в п. 4: ${{\varepsilon }_{1}} = {{\mu }_{1}}$, ${{\varepsilon }_{2}} = 10$, ${{\mu }_{2}} = 2$. Расчет проводился по нестационарной схеме, соответствующие погрешности приведены на фиг. 17. Видно, что, во-первых, погрешности, найденные сравнением с точным решением, совпадают с оценками по Ричардсону, и, во-вторых, фактический порядок точности равен 2 и совпадает с теоретическим.

Фиг. 17.

Погрешность решения в нестационарной задаче о границе раздела диэлектриков. Сплошные линии – расчет по бикомпактной схеме, пунктир – по методу FDTD, другие обозначения те же, что на фиг. 2.

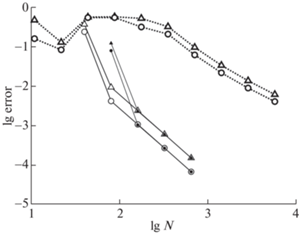
4. Для сравнения проводился расчет нестационарной задачи по схеме “с перешагиванием” метода FDTD. Граница раздела расположена в целом узле (напомним, что в этом методе к целым узлам относится поле ${{E}_{x}}$, а к полуцелым – поле ${{H}_{y}}$). Соответствующие погрешности приведены на фиг. 17. Видно, что они существенно хуже, чем у бикомпактной схемы, а порядок точности только 1-й (вместо теоретического 2-го).

Причина снижения порядка точности у метода FDTD заключается в том, что схема “с перешагиванием” некомпактна: шаблон занимает 1.5 шага по пространству и по времени. Поэтому, как бы ни была расположена граница раздела (в целом узле или в полуцелом), обеспечить достаточную гладкость решения внутри шаблона не удается. Это приводит к большой немонотонности решения (т.е. появлению сильных нефизичных осцилляций). Величина этих осцилляций составляет $O(h + \tau )$. Это и приводит к падению точности вблизи границ раздела.

5.4. Граница раздела с токами

1. В нестационарном случае зададим поверхностный ток на границе раздела в виде (38).

2. Построим точное решение этой задачи. Разложим поверхностный ток в интеграл Фурье и обозначим фурье-образ ${{j}_{1}}$ через ${{j}_{\omega }}$. Решим стационарную задачу (1)–(4) при ${{E}^{0}} = {{E}^{a}} = 0$ и ${{j}_{1}} = {{j}_{\omega }}$. Ее точное решение имеет вид (25), (26), (32), (33).

Выполним обратное преобразование Фурье и получим точное решение нестационарной задачи. При $z < b$ оно имеет вид

(47)

$\begin{gathered} {{E}_{x}}(z,t) = \frac{{4\pi }}{c}\frac{1}{{\sqrt {{{\varepsilon }_{1}}{\text{/}}{{\mu }_{1}}} + \sqrt {{{\varepsilon }_{2}}{\text{/}}{{\mu }_{2}}} }}{{j}_{1}}\left( {\frac{{b - z}}{c}\sqrt {{{\varepsilon }_{1}}{{\mu }_{1}}} - t} \right), \\ {{H}_{y}}(z,t) = - \sqrt {\frac{{{{\varepsilon }_{2}}}}{{{{\mu }_{2}}}}} {{E}_{x}}(z,t). \\ \end{gathered} $

При $z > b$ нужно поменять местами индексы 1 и 2 и изменить знак разности $(b - z) \to (z - b)$:

(48)

$\begin{gathered} {{E}_{x}}(z,t) = \frac{{4\pi }}{c}\frac{1}{{\sqrt {{{\varepsilon }_{1}}{\text{/}}{{\mu }_{1}}} + \sqrt {{{\varepsilon }_{2}}{\text{/}}{{\mu }_{2}}} }}{{j}_{1}}([z - b]\sqrt {{{\varepsilon }_{2}}{{\mu }_{2}}} {\text{/}}c - t), \\ H(z,t) = - \sqrt {\frac{{{{\varepsilon }_{2}}}}{{{{\mu }_{2}}}}} {{E}_{x}}(z,t). \\ \end{gathered} $

Решение (47), (48) является новым.

3. Погрешности расчета по нестационарной бикомпактной схеме приведены на фиг. 18. Видно, что, начиная со второй сетки ($N \approx 80$), погрешность убывает в соответствии со вторым порядком точности. Величины погрешностей, вычисленные по методу Ричардсона, практически совпадают с погрешностями, вычисленными по разности численного и точного решений.

Фиг. 18.

Погрешность решения в нестационарной задаче о границе раздела с поверхностными токами. Обозначения те же, что на фиг. 17.

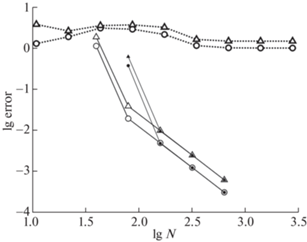
4. Для сравнения был проведен расчет нестационарной задачи по явной схеме “с перешагиванием” метода FDTD. При этом расчет велся по однородной схеме, т.е. без явного выделения особенности. Соответствующие погрешности даны на фиг. 18. Видно, что этот метод вообще не может обеспечить сходимость: при уменьшении шага погрешность не убывает.

5. Таким образом, приведенные примеры расчетов убедительно показывают преимущества предложенного метода по сравнению с известными подходами.

Авторы искренне благодарны Н.Н. Калиткину за ценные замечания и обсуждения и А.Н. Боголюбову за внимание к работе.

Список литературы

Inan U.S., Marshall R.A. Numerical electromagnetics. The FDTD method. Cambridge University Press, Cambridge, 2011.
Sullivan D.M. Electromagnetic simulation using the FDTD method. IEEE Press. 2000.
Taflove A., Johnson S.G., Oskooi A. Advances in FDTD Computational Electromagnetics: Photonics and Nanotechnology. Artech House, London. 2013.
Белов А.А., Домбровская Ж.О. Бикомпактная разностная схема для уравнений Максвелла в слоистых средах // Докл. АН. 2020. Т. 492. С. 15–19.
Белов А.А., Домбровская Ж.О. Прецизионные методы расчета нестационарных задач интегральной фотоники // Изв. РАН. Сер. физ. 2022. Т. 86. № 2. С. 259–265.
Belov A.A., Dombrovskaya Zh.O., Bogolyubov A.N. A bicompact scheme and spectral decomposition method for difference solution of maxwell’s equations in layered media // Comput. and Math. with Appl. 2021. T. 96C. C. 178–187.
Белов А.А., Домбровская Ж.О. Прецизионные методы решения одномерных уравнений Максвелла в слоистых средах // Ж. вычисл. матем. и матем. физ. 2022. Т. 62. № 1. С. 51–65.
Харвей А.Ф. Техника сверхвысоких частот. М.: Сов. радио. 1965.
Ушаков Н.Н. Технология элементов вычислительных машин. М.: Высш. школа, 1976.
Егоров А.А., Ловецкий К.П., Севастьянов Л.А., Хохлов А.А. Многослойные оптические покрытия. М.: Изд. РУДН, 2014.
Годунов С.К. Разностный метод численного расчета разрывных решений уравнений гидродинамики // Матем. сб. 1959. Т. 47 (89). № 3. С. 271–306.
Калиткин Н.Н., Корякин П.В. Бикомпактные схемы и слоистые среды // Докл. АН. 2008. Т. 419. № 6. С. 744–748.
Калиткин Н.Н., Корякин П.В. Одномерные и двумерные бикомпактные схемы в слоистых средах // Матем. моделирование. 2009. Т. 21. № 8. С. 44–62.
Калиткин Н.Н., Корякин П.В. Численные методы. Т. 2. Методы математической физики. М.: Академия, 2013.
Толстых А.И. Компактные разностные схемы и их применение в задачах аэрогидродинамики. М.: Наука, 1990.
Тихонов А.Н., Самарский А.А. О сходимости разностных схем в классе разрывных коэффициентов // Докл. АН. 1959. Т. 8. № 3. С. 529–532.
Самарский А.А. Теория разностных схем. М.: Наука, 1989.
Hecht F. New development in freefem++ // J. of Numeric. Math. 2012. V. 20. № 3–4. P. 251–266.
Yvonnet J., Villon P., Chinesta F. Bubble and hermite natural element approximations // Lect. Not. on Comput. Sci. and Engineer. 2007. C. 283–298.
Droniou J., Eymard R., Thierry G., Guichard C., Herbin R. The gradient discretisation method // Chapter Non-conforming finite element methods. C. 285–305. 07 2018.
Тихонравов А.В. Амплитудно-фазовые свойства спектральных коэффициентов слоистых сред // Ж. вычисл. матем. и матем. физ. 1985. Т. 25. № 3. С. 442–450.
Furman Sh.A., Tikhonravov A.V. Basics of optics of multilayer systems. Gifsur-Yvette. 1992.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал