Журнал вычислительной математики и математической физики, 2023, T. 63, № 8, стр. 1395-1412

1. ВВЕДЕНИЕ

Начиная с классической работы Гейла и Шепли [1], область задач о стабильных марьяжах и их обобщений привлекала внимание многочисленных исследователей, и в этой области был собран богатый урожай интересных результатов, как теоретического, так и прикладного характера.

В задаче о стабильном марьяже (или, более определенно, о стабильном матчинге в двудольном графе) рассматривается двудольный граф $G = (V,E)$, в котором для каждой вершины ${v}$ задан линейный порядок ${{ < }_{{v}}}$, указывающий предпочтения на множестве ребер ${{\delta }_{G}}({v})$, инцидентных ${v}$. Пусть $I$ и $J$ – вершинные доли в $G$. В [1] и других работах вершины в $I$ и $J$ понимались как лица разных полов (“мужчины” и “женщины” соответственно), а ребра как возможные союзы (или “браки”) между ними: если для вершины $m \in I$ (“man”) и инцидентных ей ребер $e = mw$ и $e{\kern 1pt} ' = mw{\kern 1pt} '$ выполняется $e{{ < }_{m}}e{\kern 1pt} '$, это означает, что $m$ предпочитает союз с $w$ союзу с $w{\kern 1pt} '$. И аналогично для $w \in J$ (“woman”) относительно порядка ${{ < }_{w}}$.

Матчинг в $G$ – это подмножество ребер $M \subseteq E$, где никакие два ребра не имеют общей вершины; таким образом, можно считать, что M описывает множество “моногамных браков”. Матчинг M называется стабильным, если для любого ребра $e = mw \in E - M$ по крайней мере одна из вершин $m$ и $w$ имеет инцидентное ребро в $M$ (определяющее выбранного “партнера”), и это ребро является более предпочтительным для данной вершины, чем $e$. Стабильный матчинг существует для любого двудольного $G = (V,E)$ с произвольными линейными порядками ${{ < }_{{v}}}$ на ${{\delta }_{G}}({v})$, ${v} \in V$, что первоначально было доказано Гейлом и Шепли [1] для полных двудольных графов с долями одного размера, и обобщено последующими авторами на произвольные двудольные графы.

Впоследствии развитие в области стабильности, касающейся графов, шло по нескольким направлениям. В одном из них понятие стабильности переносилось на матчинги в произвольных графах (здесь следует особо выделить основополагающие работы Ирвинга [2] и Тана [3] о “стабильных расселениях по комнатам” (stable roommates)). В другом направлении изучались вопросы стабильности при рассмотрении вариантов весовых функций на ребрах и вершинах графа (отметим, как одну из наиболее общих, задачу о “стабильном распределении” (stable allocation problem), которая была введена и изучена Бейу и Балински [4]).

В то же время целый ряд глубоких результатов был получен в пределах собственной теории стабильных матчингов для двудольных графов, и цель данной работы – сделать обзор избранных, наиболее значительных на наш взгляд, известных результатов в этой теории. Они в большой степени связаны между собой и охватывают комбинаторные, полиэдральные, алгоритмические и др. аспекты. Ряд задач, освещаемых в обзоре, состоит в описании структурных свойств множества $\mathcal{M}(G)$ стабильных матчингов в $(G, < )$.

Наше изложение организовано следующим образом.

Раздел 2 содержит описание базовых утверждений и конструкций. Он начинается с напоминания классических результатов, восходящих к работе Гейла и Шепли о существовании стабильного матчинга и о методе “отложенных принятий” для его построения. Затем объясняется, что в множестве $\mathcal{M}(G)$ стабильных матчингов произвольного двудольного графа $G$ все матчинги покрывают одно и то же множество вершин (предложение 2), и описываются операции на парах стабильных матчингов, позволяющих определить частичный порядок $ \prec $ на множестве $\mathcal{M}(G)$, представляющий его в виде дистрибутивной решетки (предложение 3).

Раздел 3 посвящен обсуждению ключевого понятия ротации в стабильном матчинге. Оно было введено Ирвингом [2] в связи с задачей на произвольном графе (stable roommates problem), но оказалось очень полезным и для исследования структуры множества стабильных матчингов двудольного графа $G$. В графе $G$ со стабильным матчингом $M$ мы понимаем под ротацией определенный цикл в $G$, чередующийся относительно $M$. К числу основных из известных утверждений, обсуждаемых в этом разделе, относятся такие: (а) трансформация вдоль ротации преобразует стабильный матчинг в стабильный (предложение 4); (б) ротационные трансформации соответствуют отношениям немедленного предшествования в решетке $(\mathcal{M}(G), \prec )$ (предложение 6); (в) во всех максимальных цепях решетки $(\mathcal{M}(G), \prec )$ множество ротаций одно и то же, обозначаемое ${{\mathcal{R}}_{G}}$ (предложение 7).

В разделе 4 продолжаются обсуждения, связанные с ротациями. Здесь вводится частичный порядок $ \lessdot $ на множестве ${{\mathcal{R}}_{G}}$ и приводится альтернативное представление для множества стабильных матчингов $\mathcal{M}(G)$, установленное Ирвингом и Лейтером [5], а именно: стабильные матчинги в $G$ взаимно-однозначно соответствуют идеалам (или анти-цепям) посета $({{\mathcal{R}}_{G}}, \lessdot )$ (предложение 8).

В разделе 5 рассматривается усиленный, “стоимостной”, вариант задачи о стабильном матчинге. Здесь множество ребер двудольного графа $G = (V,E, < )$ снабжаются вещественной весовой функцией $c:E \to \mathbb{R}$, и требуется найти стабильный матчинг $M$, минимизирующий общий вес $\sum \,(c(e)\,:e \in E)$. В частном случае, когда для ребра $e = mw$ вес $c(e)$ равняется сумме его рангов в порядках ${{ < }_{m}}$ и ${{ < }_{w}}$, получаем задачу об эгалитарном стабильном матчинге (в котором стороны $I$ и $J$ “уравниваются”), поставленную в [6]. Для произвольных весов $c$ задача минимизации (или максимизации) решается эффективным комбинаторным алгоритмом, разработанном в [7]. Это является следствием того, что: во-первых, стабильные матчинги представляются идеалами посета ротаций $({{\mathcal{R}}_{G}}, \lessdot )$, в котором число элементов ${\text{|}}{{\mathcal{R}}_{G}}{\kern 1pt} {\text{|}}$ не превосходит числа ребер ${\text{|}}E{\kern 1pt} {\text{|}}$; во-вторых, вес стабильного матчинга выражается, с точностью до константы, как вес соответствующего идеала (при назначении подходящих весов ротаций); и, в-третьих, задача о нахождении идеала (или “замкнутого множества”) минимального веса в произвольном конечном посете сводится к задаче о минимальном разрезе ориентированного графа, как показано Пикаром [8].

Раздел 6 посвящен полиэдральным аспектам. Здесь описывается многогранник стабильных матчингов ${{\mathcal{P}}_{{{\text{st}}}}}(G)$ через систему линейных неравенств (близкую к той, что указана Ванде Вейтом [9]). Также, следуя полиэдральной конструкции Тео и Сетурамана [10], показывается, что для произвольного набора стабильных матчингов ${{M}_{1}}, \ldots ,{{M}_{\ell }}$ и любого $k \leqslant \ell $, выбирая для каждой покрытой вершины в доле $I$ ребро, имеющее порядок $k$ среди этих матчингов, мы снова получаем стабильный матчинг. В частности, когда $\ell $ нечетно и $k = (\ell + 1){\text{/}}2$, определяется т.н. медианный стабильный матчинг для заданных ${{M}_{1}}, \ldots ,{{M}_{\ell }}$.

В заключительном разд. 7 формулируется результат, полученный в [7], о труднорешаемости ($\# P$-полноте) задачи определения числа стабильных матчингов в двудольном графе. Это отвечает на вопрос Кнута [11] об алгоритмической сложности вычисления такого числа.

Для полноты изложения мы, как правило, сопровождаем представленные утверждения доказательствами, часто альтернативными и более короткими по сравнению с оригинальными доказательствами в работах авторов. Отметим, что везде, где мы даем ссылки на работы [5, 7] и некоторые другие, соответствующие результаты в этих работах были получены для случая полного двудольного графа ${{K}_{{n,n}}}$ (с произвольными порядками $ < $), но эти результаты распространяются и на случай произвольного двудольного графа $G$.

2. ОПРЕДЕЛЕНИЯ И БАЗОВЫЕ ФАКТЫ

На протяжении всего изложения мы рассматриваем двудольный граф $G = (V,E)$ с разбиением множества вершин $V$ на подмножества $I$ и $J$ (где каждое ребро соединяет вершины из разных подмножеств). Иногда мы будем считать граф $G$ ориентированным, с ребрами, направленными от $I$ к $J$. Ребро, соединяющее вершины $m \in I$ (“man”) и $w \in J$ (“woman”), обозначается через $mw$. Множество ребер, инцидентных вершине $v \in V$, обозначается $\delta (v) = {{\delta }_{G}}(v)$. Каждая вершина $v$ снабжена линейным порядком ${{ < }_{v}}$, задающим предпочтения на множестве $\delta (v)$. А именно для ребер $e,e{\kern 1pt} ' \in \delta (v)$, если $e{{ < }_{v}}e{\kern 1pt} '$, то ребро $e$ считается более предпочтительным для $v$, чем ребро $e{\kern 1pt} '$; иногда нам также будет удобно говорить, что $e$ расположено раньше или левее, чем $e{\kern 1pt} '$ (а $e{\kern 1pt} '$ позднее, или правее, чем $e$). Если вершина $v$ ясна из контекста, можно писать $e < e{\kern 1pt} '$. Обычно мы включаем порядки $ < $, а также разбиение V на доли $I,\;J$ в описание графа, применяя обозначение $G = (V,E, < )$ или $G = (I \sqcup J,E, < )$.

Матчинг $M$ в $G$ называется стабильным, если он не допускает блокирующих ребер. Здесь ребро $e = mw \in E - M$ считается блокирующим для $M$, если вершина $m$ либо не покрывается $M$, либо ребро $e{\kern 1pt} '$ в $M$, инцидентное $m$, менее предпочтительно: $e{{ < }_{m}}e{\kern 1pt} '$, и аналогичное верно для вершины $w$.

Ниже в этом разделе мы приводим две группы базовых свойств стабильных матчингов в $G$.

I. В основании теории стабильных матчингов лежит эффективный алгоритм построения стабильного матчинга Гейла и Шепли [1] (в изложении для полного двудольного графа с долями $I,\;J$ одинакового размера $n$: $G \simeq {{K}_{{n,n}}}$). Рекурсивное изложение этого алгоритма, который часто называют “алгоритмом отложенных принятий” (АОП), дано МакВайти и Вилсоном в работе [6] (где также описан алгоритм последовательного конструирования множества всех стабильных матчингов для $G \simeq {{K}_{{n,n}}}$). Короткое неконструктивное доказательство существования стабильного матчинга в двудольном случае можно найти в [12, Sec. 18.5g].

В АОП роли сторон $I$ и $J$ неравнозначны: одна сторона “предлагает”, а другая “принимает или отвергает” предложения. (Напомним, что на каждом шаге АОП произвольно выбирается не включенный в текущий марьяж “man” $m \in I$, который делает предложение “woman” $w \in J$ согласно наилучшему ребру $mw$ из еще не использованных им ребер в $\delta (m)$; это предложение сразу отвергается, если $w$ уже имеет лучшее предложение от $m{\kern 1pt} ' \in I$ (т.е. $m{\kern 1pt} 'w{{ < }_{w}}mw$), и принимается в ином случае, отвергая предыдущее предложение, если таковое имеется.) Результаты естественно расширяются и для произвольного двудольного графа $G$. Это приводит к следующему важному свойству.

Предложение 1 (см. [1, 6]). В случае, когда $I$ предлагает, а $J$ принимает/отвергает, АОП находит (за линейное время $O(\left| V \right| + \left| E \right|)$) канонический стабильный матчинг, в котором выбор ребер для вершин в $I$ наилучший, а для вершин в $J$ наихудший по всем стабильным матчингам.

Мы обозначаем этот матчинг ${{M}^{{{\text{min}}}}} = {{M}^{{{\text{min}}}}}(G)$. По симметрии, если АОП применяется в варианте, когда $J$ предлагает, то алгоритм строит стабильный матчинг, для которого выборы ребер для $J$ наилучшие, а для $I$ наихудшие; обозначим его ${{M}^{{{\text{max}}}}} = {{M}^{{{\text{max}}}}}(G)$. Уточним смысл терминов “наилучший-наихудший”, рассматривая любой другой стабильный матчинг $L$ для $G$. А именно, если ребра $e \in {{M}^{{{\text{min}}}}}$ и $e{\kern 1pt} ' \in L$ имеют общую вершину $m \in I$, то $e{{ \leqslant }_{m}}e{\kern 1pt} '$, а если общую вершину $w \in J$, то $e{\kern 1pt} '{{ \leqslant }_{w}}e$. Здесь мы опираемся на инвариантность множества вершин, покрытых стабильным матчингом (что тривиально в случае полного двудольного графа ${{K}_{{n,n}}}$, где стабильный матчинг является совершенным, т.е. покрывающим все вершины). А именно, справедливо следующее свойство, установленное в [13].

Предложение 2. Для двудольного $G = (V,E, < )$ все стабильные матчинги покрывают одно и то же множество вершин.

Чтобы показать это свойство, примем следующие определения и обозначения (которые понадобятся и в дальнейшем).

Путь в ориентированном графе – это последовательность $P = ({{v}_{0}},{{e}_{1}},{{v}_{1}}, \ldots ,{{e}_{k}},{{v}_{k}})$, где ${{e}_{i}}$ – ребро, соединяющее вершины ${{v}_{{i - 1}}}$ и ${{v}_{i}}$. Для пути $P$ мы можем также применять сокращенную запись через вершины: ${{v}_{0}}{{v}_{1}} \cdots {{v}_{k}}$, или ребра: ${{e}_{1}}{{e}_{2}} \cdots {{e}_{k}}$. Ребро ${{e}_{i}}$ в $P$ называется прямым (forward), если ${{e}_{i}} = {{v}_{{i - 1}}}{{v}_{i}}$, и обратным (backward), если ${{e}_{i}} = {{v}_{i}}{{v}_{{i - 1}}}$. (Мы обозначаем ребро, выходящее из $u$ и входящее в $v$, как $uv$, вместо $(u,v)$.) Путь называется ориентированным, если все его ребра прямые, и называется простым, если все его вершины различные. Путь из вершины $u$ в вершину $v$ может быть назван $u$–$v$ путем. Для подмножества ребер $A \subseteq E$ множество вершин, покрытых $A$, обозначается ${{V}_{A}}$. Для подмножеств $X,\;Y$ множества $S$ мы пишем $X - Y$ вместо $X{{\backslash }}Y$ ($ = \{ s \in X:s \notin Y\} $) и обозначаем $X\Delta Y$ симметрическую разность $(X - Y) \cup (Y - X)$.

Пусть теперь $M,\;L$ – два стабильных матчинга в двудольном $G$. Рассмотрим подграф ${{\Delta }_{{M,L}}}$ в $G$, индуцированный множеством ребер $M\Delta L$. Заметим, что

Действительно, пусть для определенности $e{\kern 1pt} ' \in M$. Тогда $e,e{\kern 1pt} '{\kern 1pt} ' \in L$. Если бы было $e{\kern 1pt} '{{ < }_{v}}e{\kern 1pt} '{\kern 1pt} '$, то ребро $e{\kern 1pt} '$ было бы блокирующим для $L$.

Перейдем теперь к доказательству предложения 2. Предположим, что ${{V}_{M}} \ne {{V}_{L}}$. Тогда, по крайней мере, одна из компонент в ${{\Delta }_{{M,L}}}$ является простым путем $P = ({{v}_{0}},{{e}_{1}},{{v}_{1}}, \ldots ,{{e}_{k}},{{v}_{k}})$. В этом пути ребра из $M$ и $L$ чередуются, и из стабильности $M,\;L$ следует $k \geqslant 2$. Без ограничения общности можно считать, что ${{e}_{1}} \in M$. Тогда ${{v}_{0}} \notin {{V}_{L}}$, и так как ребро ${{e}_{1}}$ не является блокирующим для $L$, то должно выполняться ${{e}_{1}}{{ > }_{{{{v}_{1}}}}}{{e}_{2}}$.

Ввиду этого, последовательно применяя (2.1) к тройкам соседних ребер в $P$, получаем, что ${{e}_{{k - 1}}}{{ > }_{{{{v}_{{k - 1}}}}}}{{e}_{k}}$. Но тогда при нечетном $k$ ребро ${{e}_{k}}$ является блокирующим для $L$ (так как ${{e}_{{k - 1}}} \in L$, ${{e}_{k}} \notin L$ и ${{v}_{k}} \notin {{V}_{L}}$), а при четном $k$ ребро ${{e}_{k}}$ является блокирующим для $M$ (так как ${{e}_{{k - 1}}} \in M$, ${{e}_{k}} \notin M$ и ${{v}_{k}} \notin {{V}_{M}}$); противоречие.

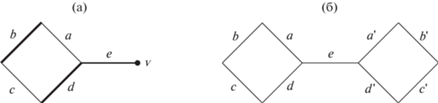
Будем обозначать множество вершин в $G$, покрытых стабильным матчингом, через $\tilde {V}$. Очевидно, при удалении вершин в $V - \tilde {V}$ каждый стабильный матчинг для $G$ остается стабильным и для результирующего графа $\tilde {G}$. Однако в $\tilde {G}$ могут появиться новые стабильные матчинги (и, следовательно, включение $\mathcal{M}(G) \subseteq \mathcal{M}(\tilde {G})$ может быть строгим), как показывает простой пример в левом фрагменте на фиг. 1. Здесь отношения предпочтений устроены так: $a < b$, $b < c$, $c < d$, $d < e < a$, и можно проверить, что имеется единственный стабильный матчинг, а именно, $M = \{ b,d\} $. Тогда вершина $v$ не покрыта $M$, однако при ее удалении (вместе с ребром $e$) появляется новый стабильный матчинг $\{ a,c\} $.

Таким образом, при исследовании множества стабильных матчингов для $G$ мы, вообще говоря, не можем выкидывать из рассмотрения непокрытые вершины, оставляя только подграф $\tilde {G} = (\tilde {V} = (\tilde {I} \sqcup \tilde {J}),\tilde {E})$ (где доли $\tilde {I}: = I \cap \tilde {V}$ и $\tilde {J}: = J \cap \tilde {V}$ имеют одинаковый размер, и все стабильные матчинги совершенные). По похожим причинам в случае отсутствия непокрытых вершин удаление ребра, не входящего ни в один стабильный матчинг, может повлечь появление нового стабильного матчинга. На фиг. 1а изображено расширение предыдущего графа с аналогичными предпочтениями для новых ребер, а именно, $a{\kern 1pt} ' < b{\kern 1pt} '$, $b{\kern 1pt} ' < c{\kern 1pt} '$, $c{\kern 1pt} ' < d{\kern 1pt} '$ и $d{\kern 1pt} ' < e < a{\kern 1pt} '$. Здесь имеются три стабильных матчинга, а именно: $\{ a,c,b{\kern 1pt} ',d{\kern 1pt} '{\kern 1pt} \} $, $\{ b,d,a{\kern 1pt} ',c{\kern 1pt} '{\kern 1pt} \} $ и $\{ b,d,b{\kern 1pt} ',d{\kern 1pt} '{\kern 1pt} \} $, однако, при удалении непокрытого ребра $e$ появляется четвертый стабильный матчинг $\{ a,c,a{\kern 1pt} ',c{\kern 1pt} '{\kern 1pt} \} $, для которого ранее имелось блокирующее ребро $e$.)

II. Далее рассмотрим упорядоченную пару $(M,L)$ стабильных матчингов в $G$. Из предложения 2 следует, что граф ${{\Delta }_{{M,L}}}$, индуцированный $M\Delta L$, распадается на некоторое множество $\mathcal{C} = \mathcal{C}(M,L)$ непересекающихся чередующихся циклов. Считая $G$ ориентированным от $I$ к $J$, будем полагать каждый цикл $C = ({{v}_{0}},{{e}_{1}},{{v}_{1}}, \ldots ,{{e}_{k}},{{v}_{k}} = {{v}_{0}}) \in \mathcal{C}$ направленным согласно ориентации ребер в $L$, т.е. прямые ребра в $C$ принадлежат $L$, а обратные принадлежат $M$. Ввиду (2.1), все предпочтения вдоль $C$ “направлены в одну сторону”, а именно:

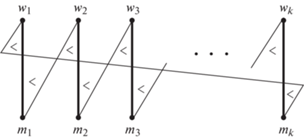
В этом случае скажем, что цикл $C$ повышающий, или правый, относительно $M$. Иначе $C$ считается понижающим, или левым. Обозначим через ${{\mathcal{C}}^{ + }}(M,L)$ и ${{\mathcal{C}}^{ - }}(M,L)$ множества правых и левых циклов для $(M,L)$ соответственно. Если матчинг $M{\kern 1pt} '$ получается из M заменой ребер вдоль цикла C, будем писать $M\;\xrightarrow{C}\;M{\kern 1pt} '$ или $M{\kern 1pt} ' = {\text{Repl}}(M,C)$, и аналогично, будем писать $L\;\xrightarrow{C}\;L{\kern 1pt} '$ или $L{\kern 1pt} ' = {\text{Repl}}(L,C)$ для замены вдоль $C$ в $L$. Заметим, что если цикл $C$ правый относительно $M$, то по сравнению с $M$ матчинг $M{\kern 1pt} '$ является менее предпочтительным для всех вершин в $I \cap C$ (“men”) и более предпочтительным для всех вершин в $J \cap C$ (“women”), а для $L$ и $L{\kern 1pt} '$ поведение противоположное. (Иначе говоря, при замене вдоль повышающего цикла мы как бы удаляемся от ${{M}^{{{\text{min}}}}}$ и приближаемся к ${{M}^{{{\text{max}}}}}$.) Повышающий цикл показан на фиг. 2.

Можно было бы ожидать, что матчинг $M{\kern 1pt} ' = {\text{Repl}}(M,C)$ должен быть стабильным. Однако это может быть неверным. Например, рассмотрим граф как в правом фрагменте на фиг. 1 (с указанными выше предпочтениями) и возьмем стабильные матчинги $M = \{ b,d,a{\kern 1pt} ',c{\kern 1pt} '{\kern 1pt} \} $ и $L = \{ a,c,b{\kern 1pt} ',d{\kern 1pt} '{\kern 1pt} \} $. Тогда ребра $a,\;b,\;c,\;d$ порождают цикл $C$ в ${{\Delta }_{{M,L}}}$, но матчинг $M{\kern 1pt} ' = \{ a,c,a{\kern 1pt} ',c{\kern 1pt} '{\kern 1pt} \} $, получающийся в результате замены ребер в $M$ вдоль $C$, не является стабильным.

Тем не менее стабильность сохраняется при замене сразу во всех циклах в ${{\mathcal{C}}^{ + }}(M,L)$ или в ${{\mathcal{C}}^{ - }}(M,L)$. В этих случаях будем писать $M{\kern 1pt} ' = {\text{Repl}}(M,{{\mathcal{C}}^{ + }}(M,L))$ и $M{\kern 1pt} ' = {\text{Repl}}(M,{{\mathcal{C}}^{ - }}(M,L))$ соответственно.

Лемма 1 (см. [11]). Если $M,\;L$ – стабильные матчинги, то $M{\kern 1pt} ' = {\text{Repl}}(M,{{\mathcal{C}}^{ + }}(M,L))$ – тоже стабильный матчинг. Аналогично для ${\text{Repl}}(M,{{\mathcal{C}}^{ - }}(M,L))$.

Доказательство. Очевидно, $M{\kern 1pt} '$ является матчингом. Предположим, $M{\kern 1pt} '$ имеет блокирующее ребро $e = mw$ (где $m \in I$). Легко видеть, что это в принципе возможно, только если одна из вершин $m,\;w$ принадлежит правому циклу, а другая – левому циклу в $\mathcal{C}(M,L)$. Без ограничения общности можно считать, что $m$ принадлежит циклу $C \in {{\mathcal{C}}^{ + }}(M,L)$, а $w$ – циклу $C{\kern 1pt} ' \in {{\mathcal{C}}^{ - }}(M,L)$. Пусть вершина $m$ инцидентна ребрам $a \in M$ и $b \in L$ в $C$, а $w$ инцидентна ребрам $c \in M$ и $d \in L$ в $C{\kern 1pt} '$. Тогда $a{{ < }_{m}}b$ и $c{{ < }_{w}}d$ (учитывая $m \in I$ и $w \in J$). При преобразовании $M \mapsto M{\kern 1pt} '$ в матчинг $M{\kern 1pt} '$ попадают ребра $b$ и $c$, и должно выполняться $e{{ < }_{m}}b$ и $e{{ < }_{w}}c$ (так как по предположению $e$ блокирует $M{\kern 1pt} '$). Но тогда получаем $e < d$ (ввиду $c < d$), и, следовательно, $e$ блокирует $L$; противоречие.

Это позволяет определить решетку на стабильных матчингах в $G$. Заметим, что для $M,L \in \mathcal{M}(G)$ заменить в $M$ ребра вдоль всех повышающих циклов для $M$ – это все равно, что сделать в $L$ замены вдоль всех повышающих циклов для $L$, т.е. ${\text{Repl}}(M,{{\mathcal{C}}^{ + }}(M,L)) = $ $ = {\text{Repl}}(L,{{\mathcal{C}}^{ + }}(L,M))$. Аналогично ${\text{Repl}}(M,{{\mathcal{C}}^{ - }}(M,L)) = {\text{Repl}}(L,{{\mathcal{C}}^{ - }}(L,M))$. Ввиду Предложения 1, в $\mathcal{C}(M,L)$ нет понижающих циклов при $M = {{M}^{{{\text{min}}}}}$, и нет повышающих циклов при $M = {{M}^{{{\text{max}}}}}$.

Предложение 3 (см. [11]). Для различных $M,L \in \mathcal{M}(G)$ положим $M \prec L$, если для каждой пары ребер $e \in M$ и $e{\kern 1pt} ' \in L$, инцидентных вершине в $\tilde {I}$ ($ = I \cap \tilde {V}$) выполняется $e \leqslant e{\kern 1pt} '$ (давая противоположные соотношения для вершин в $\tilde {J}$). Тогда $ \prec $ определяет дистрибутивную решетку на $\mathcal{M}(G)$ с минимальным элементом ${{M}^{{{\text{min}}}}}(G)$ и максимальным элементом ${{M}^{{{\text{max}}}}}(G)$, в которой для $M,L \in \mathcal{M}(G)$ точной нижней гранью $M \wedge L$ является ${\text{Repl}}(M,{{\mathcal{C}}^{ - }}(M,L)) = {\text{Repl}}(L,{{\mathcal{C}}^{ - }}(L,M))$, а точной верхней гранью $M \vee L$ – ${\text{Repl}}(M,\mathcal{C}(M,L)) = {\text{Repl}}(L,{{\mathcal{C}}^{ + }}(L,M))$.

3. РОТАЦИИ

Благодаря решеточности множества $\mathcal{M}(G)$, можно, имея два или более стабильных матчингов, конструировать новые, делая переназначения в соответствующих циклах для пар матчингов, как указано в лемме 1. Другой метод, связанный с понятием ротации, позволяет порождать новые стабильные матчинги, исходя из одиночных элементов в $\mathcal{M}(G)$. Это понятие было введено Ирвингом и Лейтером [5] для задачи о стабильном марьяже, основываясь на концепции “цикла типа все или ничего” (all-or-nothing cycle) из работы Ирвинга [2], посвященной задаче о стабильных матчингах в общем графе (“stable roommates problem”). Впоследствии понятие ротации было распространено и на другие задачи о стабильности, такие как задачи о стабильных b-матчингах, распределениях (allocations) и др. (см., например, [14]. Отметим также недавнюю работу [15], где устанавливается связь между выпуклой оболочкой стабильных распределений при отсутствии ограничений на ребрах и порядковым многогранником посета ротаций.) Заметим, что хотя в [5] рассматривался случай полного двудольного графа $G \simeq {{K}_{{n,n}}}$, конструкции и результаты без особого труда переносятся на произвольный случай, и как выше, мы далее будем рассматривать произвольный двудольный граф $G = (V = I \sqcup J,{\kern 1pt} E, < )$.

Пусть $M$ – стабильный матчинг в $G$.

Определение 1. Скажем, что ребро $a = mw \in E - M$ (где $m \in I$) допустимое, если в $M$ есть ребро $e$, инцидентное $m$, и это ребро более предпочтительное, чем $a$ (т.е. $e{{ < }_{m}}a$), и при этом либо вершина $w$ непокрытая, либо $M$ имеет ребро $e{\kern 1pt} '$, инцидентное $w$, и это ребро менее предпочтительное, чем $a$ (т.е. $a{{ < }_{w}}e{\kern 1pt} '$). Если для вершины $m \in I$ множество допустимых ребер в $\delta (m)$ непустое, то самое первое (наиболее предпочтительное) из них назовем активным. Обозначим через $A$ множество активных ребер для $M$. Подграф в $G$, индуцированный множеством ребер $M \cup A$, обозначим $\Gamma = \Gamma (M)$ и назовем активным графом.

Учитывая то, что из каждой вершины в $I$ исходит не более одного активного ребра (в то время как в вершину в $J$ может входить несколько активных ребер), всякий цикл в $\Gamma $ должен быть чередующимся относительно $M$ и $A$. Кроме того, каждая компонента $K$ в $\Gamma $ либо является деревом, либо содержит ровно один цикл. (Действительно, в противном случае в $K$ имелась бы пара циклов и соединяющий их простой $u$–$v$ путь $P$, все вершины которого, кроме $u,\;v$, не принадлежат циклам.) Концевые ребра этого пути должны принадлежать $A$, и, по крайней мере, одна из вершин $u,\;v$ должна находиться в $I$. Эта вершина имеет два инцидентных ребра в $A$ (одно на $P$, другое на цикле); противоречие. При наличии цикла мы называем компоненту $K$ цикло-содержащей, а сам цикл обозначаем через ${{C}_{K}}$ и называем ротацией для $M$. (Заметим, что в [5] ротацией называется не сам цикл, а его пересечение с $M$.) Ребра в ${{C}_{K}}$, принадлежащие $M$, назовем матчинговыми, а остальные – активными. При замене ребер вдоль ротации $C$ возникает матчинг, который по сравнению с $M$ менее предпочтителен для вершин в $I \cap C$ и более предпочтительный для вершин в $J \cap C$. (Для операции замены вдоль $C$ в [5] применяется термин “rotation elimination”.) Когда $C$ – цикл в $\Gamma (M)$, мы также можем говорить, что матчинг $M$ допускает ротацию $C$.

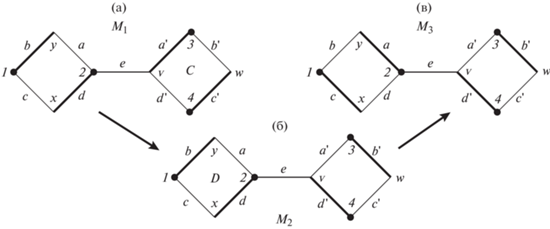
Пример. На фиг. 3 изображены три стабильных матчинга ${{M}_{1}},\;{{M}_{2}},\;{{M}_{3}}$ (выделенных жирной линией) в графе $G = (V,E, < )$ как на фиг. 1б. Здесь доля $I$ составлена вершинами $1,\;2,\;3,\;4$, а доля $J$ – вершинами $x,\;y,\;v,\;w$, и предпочтения заданы как и раньше, а именно:

Для матчинга ${{M}_{1}}$ все нематчинговые ребра $a,\;c,\;e,\;b{\kern 1pt} ',\;d{\kern 1pt} '$ являются допустимыми, но из них активными оказываются только $c,\;e,\;b{\kern 1pt} ',\;d{\kern 1pt} '$ (так как $e{{ < }_{2}}a$). Поэтому подграф $\Gamma ({{M}_{1}})$ порожден ${{M}_{1}} \cup \{ c,e,b{\kern 1pt} ',d{\kern 1pt} '{\kern 1pt} \} $, имеет ровно одну компоненту, и она является цикло-содержащей с циклом $C = a{\kern 1pt} 'b{\kern 1pt} 'c{\kern 1pt} 'd{\kern 1pt} '$. При замене вдоль ротации $C$ получаем матчинг ${{M}_{2}}$ (являющийся стабильным согласно предложению 4 ниже). Для ${{M}_{2}}$ допустимыми ребрами в $E - {{M}_{2}}$ являются только $a$ и $c$ (а $e,\;a{\kern 1pt} ',\;c{\kern 1pt} '$ – не допустимые, ввиду $d{\kern 1pt} '{{ < }_{v}}e,a{\kern 1pt} '$ и $b{\kern 1pt} '{{ < }_{w}}c{\kern 1pt} '$, учитывая $b{\kern 1pt} ',d{\kern 1pt} ' \in {{M}_{2}}$ и $v,w \in J$). Поэтому активными ребрами являются $a$ и $c$, и граф $\Gamma ({{M}_{2}})$ состоит из трех компонент, порожденных $\{ a,b,c,d\} $, $\{ b{\kern 1pt} '\} $ и $\{ d{\kern 1pt} '\} $. Первая из них образует цикл $D = abcd$. Наконец, при замене вдоль ротации $D$ получаем стабильный матчинг ${{M}_{3}}$. Для него ни одно из ребер в $E - {{M}_{3}}$ не является допустимым, и $\Gamma ({{M}_{3}})$ составлено просто ребрами в ${{M}_{3}}$. Можно видеть, что ${{M}_{1}} = {{M}^{{{\text{min}}}}}$ и ${{M}_{3}} = {{M}^{{{\text{max}}}}}$.

Следующие два утверждения демонстрируют важные свойства $\Gamma (M)$.

Предложение 4 (см. [5]). Для любого цикла (ротации) $C$ в $\Gamma (M)$ матчинг $M{\kern 1pt} ' = {\text{Repl}}(M,C)$ является стабильным.

Доказательство. Оба $M$ и $M{\kern 1pt} '$ покрывают одно и то же множество вершин $\tilde {V}$. Предположим, что $M{\kern 1pt} '$ допускает блокирующее ребро $e = mw \in E - M{\kern 1pt} '$. Заметим, что $e \notin M$ (учитывая то, что ребра в $C \cap M$ не могут быть блокирующими для $M{\kern 1pt} '$). Возможны два случая.

Случай 1: $w \in \tilde {V}$. Тогда вершина $w$ принадлежит ребрам $a \in M{\kern 1pt} '$ и $b \in M$, и мы имеем $e{{ < }_{w}}a$ (ввиду блокирования) и $a{{ \leqslant }_{w}}b$ (так как в случае $a \ne b$ ребро $a$ лежит в $C$ и является допустимым). Следовательно, $e{{ < }_{w}}b$. Тогда $m \in \tilde {V}$ (иначе $e$ было бы блокирующим для $M$).

Пусть вершина $m$ принадлежит ребрам $c \in M{\kern 1pt} '$ и $d \in M$. Тогда $e{{ < }_{m}}c$, и должно выполняться $d{{ < }_{m}}e$ (иначе $e$ было бы блокирующим для $M$, учитывая $e{{ < }_{w}}b$). Следовательно, $e$ является допустимым для $M$ и более предпочтительным, чем ребро $c$, которое принадлежит $A$; противоречие.

Случай 2: $w \notin \tilde {V}$. Тогда $m \in \tilde {V}$. Пусть $m$ принадлежит ребрам $c \in M{\kern 1pt} '$ и $d \in M$. Так как $e$ является блокирующим для $M{\kern 1pt} '$, но не для $M$, имеем $d{{ < }_{m}}e{{ < }_{m}}c$. Но тогда ребро $e$ допустимое и более предпочтительное, чем активное ребро $c$; противоречие.

Говоря далее о чередующихся (относительно $M$ и $A$) путях и циклах в $\Gamma (M)$, мы считаем, что в них выбрано такое направление, чтобы ребра из $A$ были прямыми, а ребра из $M$ обратными.

Предложение 5. Пусть $e$ – ребро в $M$, принадлежащее древесной компоненте $K$ в $\Gamma (M)$. Тогда для любого стабильного матчинга $L \in \mathcal{M}(G)$ либо $e \in L$, либо $e$ содержится в понижающем цикле в $\mathcal{C}(M,L)$.

Доказательство. Предположим, ребро $e = mw \in M$ из древесной компоненты $K$ находится в повышающем цикле $C \in {{\mathcal{C}}^{ + }}(M,L)$ для некоторого $L \in \mathcal{M}(G)$. Пусть $C$ имеет вид ${{e}_{1}}{{e}_{2}} \cdots {{e}_{k}}$ (применяя обозначение через ребра и учитывая направленность $C$), и пусть $e: = {{e}_{1}} \in M$. Возьмем максимальный чередующийся путь $P = {{p}_{1}}{{p}_{2}} \cdots {{p}_{r}}$ (через ребра) в $\Gamma (M)$, начиная с ${{p}_{1}} = e$. Можно считать, что никакое ребро в $P \cap M$, кроме ${{p}_{1}}$, не лежит в повышающем цикле в $\mathcal{C}(M,L)$ (в противном случае возьмем его в качестве $e$). Ребра ${{e}_{1}}$ и ${{e}_{2}} = mw{\kern 1pt} '$ инцидентны вершине $m \in I$, и поскольку $C$ повышающий, ${{e}_{1}}{{ < }_{m}}{{e}_{2}}$ и ${{e}_{2}}{{ < }_{{w'}}}{{e}_{3}}$. Кроме того, ${{e}_{1}},{{e}_{3}} \in M$ и ${{e}_{2}} \in L$. Следовательно, ${{e}_{2}}$ – допустимое ребро для $M$, и в $\delta (m)$ есть активное ребро $a = m{v}$, для которого ${{e}_{1}}{{ < }_{m}}a{{ \leqslant }_{m}}{{e}_{2}}$. Это $a$ совпадает с ребром ${{p}_{2}}$ в $P$. Кроме того, $a \ne {{e}_{2}}$ (иначе ${{e}_{3}} \in P$ и ${{e}_{3}} \in C \cap M$, вопреки условию на ${{p}_{1}} = e$).

Мы утверждаем, что ребро $a = {{p}_{2}}$ – блокирующее для $L$. Это следует из $a{{ < }_{m}}{{e}_{2}} \in L$, если $r = 2$ (в этом случае концевая вершина $v$ в $P$ является непокрытой), а также если $r \geqslant 3$ и ${{p}_{3}} \in L$ (так как ${{p}_{3}} \in M$ и $a{{ < }_{v}}{{p}_{3}}$). Наконец, пусть ${{p}_{3}} \notin L$. Тогда ${{p}_{3}}$ принадлежит понижающему циклу $C{\kern 1pt} ' \in {{\mathcal{C}}^{ - }}(M,L)$. Для ребра $b$ в $C{\kern 1pt} '$, инцидентного $v$ и отличного от ${{p}_{3}}$, выполняется $b \in L$ и ${{p}_{3}}{{ < }_{v}}b$ (учитывая $v \in J$ и то, что $C{\kern 1pt} '$ понижающий). Тогда из $a{{ < }_{v}}{{p}_{3}}{{ < }_{v}}b$ и $a{{ < }_{m}}{{e}_{2}} \in L$ следует, что $a$ блокирует $L$; противоречие.

Ясно, что для матчинга $M{\kern 1pt} ' = {\text{Repl}}(M,C)$, полученного заменой вдоль ротации $C$ в $\Gamma (M)$, выполняется $M \prec M{\kern 1pt} '$, где $ \prec $ – частичный порядок в решетке на $\mathcal{M}(G)$ (см. предложение 3). Как было установлено в [5] (при $G \simeq {{K}_{{n,n}}}$), начиная с ${{M}^{{{\text{min}}}}}$ и используя ротации, можно исчерпать все $\mathcal{M}(G)$.

Определение 2. Назовем трассой последовательность стабильных матчингов $\tau = ({{M}_{0}},{{M}_{1}}, \ldots ,{{M}_{N}})$ в $G$ такую, что ${{M}_{0}} = {{M}^{{{\text{min}}}}}$, ${{M}_{N}} = {{M}^{{{\text{max}}}}}$, и каждое ${{M}_{i}}$ ($1 \leqslant i \leqslant N$) получается из ${{M}_{{i - 1}}}$ заменой вдоль одной ротации ${{C}_{i}}$ в $\Gamma ({{M}_{{i - 1}}})$. Последовательность ротаций ${{C}_{1}}, \ldots ,{{C}_{N}}$ обозначим через $\mathcal{R}(\tau )$.

Предложение 6. Трассы покрывают всю решетку $(\mathcal{M}(G), \prec )$.

Доказательство. Достаточно показать, что если матчинги $M,L \in \mathcal{M}$ удовлетворяют $M \prec L$, то найдется ротация $C$ для $M$ такая, что для $M{\kern 1pt} ' = {\text{Repl}}(M,C)$ справедливо $M{\kern 1pt} ' \preccurlyeq L$. Чтобы построить такую ротацию, возьмем вершину $m \in \tilde {I}$, для которой инцидентные ребра $e = mw \in M$ и $f = mv \in L$ различны. Тогда $e{{ < }_{m}}f$ (ввиду $M \prec L$), и ребро $f$ допустимое для $M$ (так как имеется ребро $b \in M$, инцидентное $v$, и для него выполняется $f{{ < }_{v}}b$, ввиду $M \prec L$ и $w \in \tilde {J}$). Поэтому в $\delta (m)$ есть активное ребро $a = mw{\kern 1pt} '$, и выполняется $a{{ \leqslant }_{m}}f$. Заметим, что $w{\kern 1pt} ' \in \tilde {V}$ (иначе должно быть $a \notin L$; тогда $a \ne f$, и $a$ блокирует $L$).

Следовательно, имеется ребро $e{\kern 1pt} ' = m{\kern 1pt} 'w{\kern 1pt} ' \in M$, а также ребро $f{\kern 1pt} ' \in L$, инцидентное $m{\kern 1pt} '$. Мы утверждаем, что $f{\kern 1pt} ' \ne e{\kern 1pt} '$. Действительно, в случае $f{\kern 1pt} ' = e{\kern 1pt} '$, мы имели бы $a{{ < }_{{w{\kern 1pt} '}}}f{\kern 1pt} '$ и $a{{ < }_{m}}f$, и, следовательно, $a$ блокировало бы $L$.

Теперь из $f{\kern 1pt} ' \ne e{\kern 1pt} '$ получаем $e{\kern 1pt} '{{ < }_{{m{\kern 1pt} '}}}f{\kern 1pt} '$, аналогично $e{{ < }_{m}}f$ в начальной ситуации. Продолжая построение, мы получаем “неограниченный” чередующийся путь $P$ в $\Gamma (M)$ с последовательностью ребер $e = {{e}_{1}} = {{m}_{1}}{{w}_{1}}$, $a = {{a}_{1}} = {{m}_{2}}{{w}_{1}}$, $e{\kern 1pt} ' = {{e}_{2}} = {{m}_{2}}{{w}_{2}}$, ${{a}_{2}} = {{m}_{2}}{{w}_{3}}, \ldots $, и для каждого $i$ имеется ребро ${{f}_{i}} \in L$, инцидентное ${{m}_{i}}$ и отличное от ${{e}_{i}}$. Тогда ${{e}_{i}}{{ < }_{{{{m}_{i}}}}}{{a}_{i}}{{ \leqslant }_{{{{m}_{i}}}}}{{f}_{i}}$, и $P$ содержит искомую ротацию $C$.

Назовем рангом матчинга $M$ сумму $\rho (M)$ порядковых номеров его ребер $mw$ в множествах $\delta (m)$ (упорядоченных согласно ${{ < }_{m}}$), где $m \in I$. Очевидно, $\rho (M) \leqslant {\text{|}}E{\kern 1pt} {\text{|}}$, и если $M \prec L$, то $\rho (M) < \rho (L)$. Поэтому

Из предложений 4–6 мы также получаем

Следствие 1. (i) Граф $\Gamma ({{M}^{{{\text{max}}}}}(G))$ является лесом (и ротации для ${{M}^{{{\text{max}}}}}(G)$ отсутствуют).

(ii) Ребра минимального стабильного матчинга $M = {{M}^{{{\text{min}}}}}(G)$, находящиеся в древесных компонентах активного графа $\Gamma (M)$, принадлежат всем стабильным матчингам в $\mathcal{M}(G)$.

(iii) $G$ имеет единственный стабильный матчинг тогда и только тогда, когда $\Gamma ({{M}^{{{\text{min}}}}})$ является лесом.

Следующее утверждение, установленное в [5], несмотря на относительную простоту доказательства, является наиболее существенным в области ротаций.

Предложение 7. Множество ротаций $\mathcal{R}(\tau )$ для всех трасс $\tau $ в $(\mathcal{M}(G), \prec )$ одно и то же.

Доказательство. Для $M \in \mathcal{M}(G)$ определим $\mathcal{T}(M)$ как множество отрезков трасс (“подтрасс”), начинающихся с $M$ и оканчивающихся в ${{M}^{{{\text{max}}}}}$. Для такой подтрассы $\tau \in \mathcal{T}(M)$ соответствующее множество ротаций обозначим через $\mathcal{R}(\tau )$ и скажем, что матчинг $M$ особый, если в $\mathcal{T}(M)$ имеются подтрассы $\tau $ и $\tau {\kern 1pt} '$ с $\mathcal{R}(\tau ) \ne \mathcal{R}(\tau {\kern 1pt} ')$. Надо доказать, что ${{M}^{{{\text{min}}}}}$ не является особым.

Предположим, что это не так, и рассмотрим особый матчинг $M$ максимальной высоты, т.е. такой, что матчинг $L$ не является особым, если $M \prec L$. Пусть $\mathcal{C}(M)$ – множество ротаций в $\Gamma (M)$; тогда для любой подтрассы $\tau = (M = {{M}_{0}},{{M}_{1}},{{M}_{2}}, \ldots ,{{M}_{k}} = {{M}^{{{\text{max}}}}})$ матчинг ${{M}_{1}}$ получается из $M$ заменой вдоль некоторой ротации $C \in \mathcal{C}(M)$. Ввиду максимальности $M$, найдутся ротации $C{\kern 1pt} ',C{\kern 1pt} '{\kern 1pt} ' \in \mathcal{C}(M)$ такие, что матчинги $M{\kern 1pt} ' = {\text{Repl}}(M,C{\kern 1pt} ')$ и $M{\kern 1pt} '{\kern 1pt} ' = {\text{Repl}}(M,C{\kern 1pt} '{\kern 1pt} ')$ неособые, и множества ротаций $\mathcal{R}(\tau {\kern 1pt} ')$ и $\mathcal{R}(\tau {\kern 1pt} '{\kern 1pt} ')$ различны для подтрасс $\tau {\kern 1pt} ',\tau {\kern 1pt} '{\kern 1pt} ' \in \mathcal{T}(M)$ таких, что $\tau {\kern 1pt} '$ проходит через $M{\kern 1pt} '$, а $\tau {\kern 1pt} '{\kern 1pt} '$ проходит через $M{\kern 1pt} '{\kern 1pt} '$.

Теперь заметим, что поскольку ротации $C{\kern 1pt} '$ и $C{\kern 1pt} '{\kern 1pt} '$ не пересекаются, то $C{\kern 1pt} '$ является ротацией в $\Gamma (M{\kern 1pt} '{\kern 1pt} ')$, а $C{\kern 1pt} '{\kern 1pt} '$ – ротацией в $\Gamma (M{\kern 1pt} ')$. Поэтому в $\mathcal{T}(M)$ есть подтрассы $\tau {\kern 1pt} ',\;\tau {\kern 1pt} '{\kern 1pt} '$ такие, что $\tau {\kern 1pt} '$ начинается с $M,M{\kern 1pt} ',{\text{Repl}}(M{\kern 1pt} ',C{\kern 1pt} '{\kern 1pt} ')$, и $\tau {\kern 1pt} '{\kern 1pt} '$ начинается с $M,M{\kern 1pt} '{\kern 1pt} ',{\text{Repl}}(M{\kern 1pt} '{\kern 1pt} ',C{\kern 1pt} ')$, а после матчинга ${\text{Repl}}(M{\kern 1pt} ',C{\kern 1pt} '{\kern 1pt} ') = {\text{Repl}}(M{\kern 1pt} '{\kern 1pt} ',C{\kern 1pt} ')$ подтрассы $\tau {\kern 1pt} '$ и $\tau {\kern 1pt} '{\kern 1pt} '$ совпадают. Но тогда $\mathcal{R}(\tau {\kern 1pt} ') = \mathcal{R}(\tau {\kern 1pt} '{\kern 1pt} ')$; противоречие.

Это множество ротаций $\mathcal{R}(\tau )$, не зависящее от трасс $\tau \in \mathcal{T}({{M}^{{{\text{min}}}}})$, обозначим через ${{\mathcal{R}}_{G}}$. Вви-ду (3.1), получаем

Следствие 2. Число ротаций в ${{\mathcal{R}}_{G}}$ не превосходит ${\text{|}}E{\kern 1pt} {\text{|}}$.

Приведем еще одно полезное свойство:

Действительно, если $e = mw$ – матчинговое ребро в ротации $C$, где $m \in I$, то при трансформации в $C$ новым матчинговым ребром в $\delta (m)$ становится активное ребро $a = mv$ в $C$; при этом выполняется $e{{ < }_{m}}a$. При дальнейшем движении вдоль трассы матчинговые ребра в $\delta (m)$ могут перемещаться только “вправо” (по аналогичным причинам), и возврата к ребру $e$ не происходит.

В заключение этого раздела скажем о компонентах графа объединения стабильных матчингов ${{\Sigma }_{G}}$. Для этого обозначим через ${{M}^{0}}$ множество ребер минимального матчинга ${{M}^{{{\text{min}}}}}$, принадлежащих древесным компонентам в $\Gamma ({{M}^{{{\text{min}}}}})$, и обозначим через ${{U}_{G}}$ подграф в $G$, являющийся объединением всех ротаций в ${{\mathcal{R}}_{G}}$. Как указано в следствии 1(ii), ${{M}^{0}}$ принадлежит всем матчингам в $\mathcal{M}(G)$ (поскольку активный граф $\Gamma ({{M}^{{{\text{min}}}}})$ не имеет понижающих циклов, и учитывая предложение 5); отсюда получаем, что каждое ребро в ${{M}^{0}}$ образует компоненту в ${{\Sigma }_{G}}$. В то же время очевидно, что каждая ротация целиком лежит в ${{\Sigma }_{G}}$, и поэтому ${{U}_{G}} \subseteq {{\Sigma }_{G}}$. Более того, так как каждый стабильный матчинг получается из ${{M}^{{{\text{min}}}}}$ в результате последовательности ротационных трансформаций, то справедливо

Следствие 3. ${{\Sigma }_{G}}$ является объединением ${{U}_{G}} = \cup \{ C \in {{\mathcal{R}}_{G}}\} $ и ${{M}^{{{\text{min}}}}}$. Каждое ребро в ${{M}^{0}}$ и каждая компонента в ${{U}_{G}}$ является компонентой в ${{\Sigma }_{G}}$.

Таким образом, ${{\Sigma }_{G}}$ строится эффективно (за время $O(\left| V \right|\left| E \right|)$, ввиду сказанного в следующем разделе). А также каждое ребро в ${{M}^{0}}$ и каждая компонента в ${{U}_{G}}$ является компонентой в ${{\Sigma }_{G}}$. В связи с этим можно спросить, есть ли в ${{\Sigma }_{G}}$ другие компоненты? Если да, то ими могут быть только ребра в ${{M}^{{{\text{min}}}}}$, которые находятся в цикло-содержащих компонентах $K$ графа $\Gamma ({{M}^{{{\text{min}}}}})$, но при этом не входят в объединение ротаций ${{U}_{K}}$. Вопрос о существовании таких компонент открытый для нас.

4. ИДЕАЛЫ ПОСЕТА РОТАЦИЙ И СТАБИЛЬНЫЕ МАТЧИНГИ

Как было сказано выше, естественный частичный порядок $ \prec $ на стабильных матчингах превращает множество $\mathcal{M}(G)$ в дистрибутивную решетку (см. предложение 3). Известно, что любая дистрибутивная решетка изоморфна решетке идеалов некоторого посета (и наоборот). Для решетки $(\mathcal{M}(G), \prec )$ Ирвинг и Лейтер [5] указали явную конструкцию. (Хотя [5] и последующая работа [7] имеют дело с полным двудольным графом ${{K}_{{n,n}}}$, полученные там результаты без большого труда распространяются на произвольный двудольный граф $G$.) А именно, опираясь на ключевой факт о постоянстве множества ротаций, ассоциированных с трассами (см. предложение 7), а также на определенный способ задания структуры посета на множестве ротаций ${{\mathcal{R}}_{G}}$, было показано соответствие между стабильными матчингами и идеалами в таком посете. Это представление для $\mathcal{M}(G)$ имеет важные применения, в частности, позволяет эффективно решать задачи линейной оптимизации для $\mathcal{M}(G)$ и установить труднорешаемость задачи вычисления числа ${\text{|}}\mathcal{M}(G){\kern 1pt} {\text{|}}$, о чем будет сказано в разд. 6 и 7.

Начнем с построения упомянутого посета на ${{\mathcal{R}}_{G}}$. Напомним, что для трассы τ = $ = ({{M}_{0}},{{M}_{1}}, \ldots ,{{M}_{N}})$ мы обозначаем через $\mathcal{R}(\tau )$ последовательность ротаций ${{C}_{1}}, \ldots ,{{C}_{N}}$, где ${{M}_{i}}$ получается из ${{M}_{{i - 1}}}$ заменой вдоль ${{C}_{i}}$.

Определение 3. Для ротаций $C,D \in {{\mathcal{R}}_{G}}$ скажем, что $C$ предшествует $D$, и обозначим это как $C \lessdot D$, если для каждой трассы $\tau $ в $(\mathcal{M}(G), \prec )$ ротация $C$ встречается в последовательности $\mathcal{R}(\tau )$ раньше, чем $D$. Иными словами, трансформация матчинга в $D$ не может произойти ранее, чем трансформация в $C$.

Это бинарное отношение антисимметричное и транзитивное и дает частичный порядок на ${{\mathcal{R}}_{G}}$.

Чтобы объяснить связь с матчингами, рассмотрим $M \in \mathcal{M}(G)$. Пусть $\tau = ({{M}_{0}},{{M}_{1}}, \ldots ,{{M}_{N}})$ – трасса, содержащая $M$, скажем, $M = {{M}_{i}}$, и пусть $\mathcal{R}(\tau ) = ({{C}_{1}}, \ldots ,{{C}_{N}})$. Тогда $M$ получается из ${{M}_{0}} = {{M}^{{{\text{min}}}}}$ последовательностью трансформаций относительно ротаций ${{C}_{1}}, \ldots ,{{C}_{i}}$. Из предложения 7 легко следует, что

В соответствии с определением $ \lessdot $ отношение ${{C}_{j}} \lessdot {{C}_{k}}$ может выполняться, только если $j < k$. Более того, ${{\mathcal{R}}_{M}}$ образует замкнутое множество, или идеал, в посете $({{\mathcal{R}}_{G}}, \lessdot )$ (т.е. из $C \lessdot D$ и $D \in {{\mathcal{R}}_{M}}$ следует $C \in {{\mathcal{R}}_{M}}$). Это дает инъективное отображение $\beta $ множества $\mathcal{M}(G)$ в множество идеалов в $({{\mathcal{R}}_{G}}, \lessdot )$. В действительности, $\beta $ является биекцией, как показано в [5, Th. 4.1].

Предложение 8. Отображение 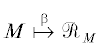устанавливает изоморфизм между решеткой стабильных матчингов $(\mathcal{M}(G), \prec )$ и решеткой $\mathcal{I}(G)$ идеалов в $({{\mathcal{R}}_{G}}, \lessdot )$.

Доказательство. Рассмотрим стабильные матчинги $M$ и $L$, и пусть $E{\kern 1pt} '$ и $E{\kern 1pt} '{\kern 1pt} '$ – множества ребер, принадлежащих циклам в ${{\mathcal{C}}^{ + }}(M,L)$ и ${{\mathcal{C}}^{ - }}(M,L)$ соответственно. Очевидно, подграфы, порожденные этими множествами, не пересекаются. Из доказательства предложения 6 следует, что $E{\kern 1pt} '$ является объединением множества $R{\kern 1pt} '$ ротаций, требуемых для получения $M \vee L$ из $M$ (или, эквивалентно, $L$ из $M \wedge L$), а $E{\kern 1pt} '{\kern 1pt} '$ – объединением множества $R{\kern 1pt} '{\kern 1pt} '$ ротаций, требуемых для получения $M \vee L$ из $L$ (эквивалентно, $M$ из $M \wedge L$). Следовательно, ротации $R{\kern 1pt} '$ и $R{\kern 1pt} '{\kern 1pt} '$ “перестановочны”: чтобы получить матчинг $M \vee L$ из $M \wedge L$, можно применять сначала $R{\kern 1pt} '$, а затем $R{\kern 1pt} '{\kern 1pt} '$, или наоборот. Это дает $\beta (M) \cap \beta (L) = \beta (M \wedge L)$ и $\beta (M) \cup \beta (L) = \beta (M \vee L)$ (т.е. $\beta $ определяет гомоморфизм решеток). Теперь утверждение легко следует из того факта, что для ротаций $C,D \in {{\mathcal{R}}_{G}}$ не выполняется $C \lessdot D$ тогда и только тогда, когда найдется стабильный матчинг $M$ такой, что .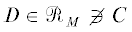

Как следствие, $\mathcal{M}(G)$ биективно множеству $\mathcal{A}(G)$ анти-цепей в $({{\mathcal{R}}_{G}}, \lessdot )$. (Напомним, что а-нти‑цепь в посете $(P, < )$ – это множество $A$ попарно несравнимых элементов. Оно определяет идеал $\{ p \in P:p \leqslant a \exists a \in A\} $, и определяется идеалом, будучи множеством его максимальных элементов.)

Мы завершаем этот раздел, объясняя, как эффективно проверять отношение $ \lessdot $. Заметим, что $C,\;D$ не связаны этим отношением, если они являются ротациями для одного и того же стабильного матчинга $M$ (и, следовательно, трансформации в $C$ и $D$ могут производиться в произвольном порядке); в этом случае $C$ и $D$ лежат в разных компонентах в $\Gamma (M)$, и поэтому ${{V}_{C}} \cap {{V}_{D}} = \emptyset $. С другой стороны, если $C$ и $D$ имеют общую вершину $v$, то они сравнимы по $ \lessdot $.

Действительно, для $C$ и $D$ матчинговые ребра, инцидентные $v$, различные, и порядок следования $C$ и $D$ для любой трассы один и тот же и определяется порядком ${{ < }_{v}}$ для этих ребер (см. объяснение свойства (3.2)). Вообще, множество ротаций ${{\mathcal{R}}^{{v}}}$, содержащих фиксированную вершину $v$, упорядочено по $ \lessdot $, скажем, ${{\mathcal{R}}^{v}} = ({{C}_{1}} \lessdot {{C}_{2}} \lessdot \cdots \lessdot {{C}_{k}})$, и этот порядок легко определяется, так как он согласуется с порядком в ${{ < }_{v}}$, если $v \in I$, и обратным порядком, если $v \in J$.

Есть еще одна локальная причина того, что две ротации $C,\;D$ должны быть сравнимы по $ \lessdot $. А именно, предположим, что

Тогда $C \lessdot D$. Действительно, ввиду $a{{ < }_{w}}b{{ < }_{w}}e$, после трансформации в $C$ ребро $b$ становится недопустимым. С другой стороны, если бы $D$ предшествовало $C$ в какой-то трассе, то именно $b$ было бы активным ребром в $\delta (m{\kern 1pt} ')$ и вошло бы в ротацию.

Пример в разд. 3 именно таков: здесь после замены вдоль ротации $C$ ребро $e = 2v$ становится недопустимым, ввиду $d{\kern 1pt} '{{ < }_{v}}e{{ < }_{v}}a{\kern 1pt} '$ и $d,d{\kern 1pt} ' \in {{M}_{2}}$ (при этом $e$ – первое после $d$ ребро в $\delta (2)$). В этом примере посет состоит из двух ротаций $C,\;D$ при соотношении $C \lessdot D$, и есть ровно три идеала: $\emptyset $, $\{ C\} $ и $\{ C,D\} $, отвечающие стабильным матчингам ${{M}_{1}} = {{M}^{{{\text{min}}}}}$, ${{M}_{2}}$ и ${{M}_{3}} = {{M}^{{{\text{max}}}}}$ (а $\{ D\} $ – не идеал).

Заметим, что для нахождения множества ротаций ${{\mathcal{R}}_{G}}$ достаточно определить ${{M}^{{{\text{min}}}}}$ и затем построить произвольную трассу, делая трансформации на ротациях в текущих матчингах. (Это выполняется естественным алгоритмом за время $O(\left| V \right|\left| E \right|)$. В [16] предложен алгоритм формирования ${{\mathcal{R}}_{G}}$ за время $O({\text{|}}V{\kern 1pt} {{{\text{|}}}^{2}})$.)

В свою очередь в [7, Sec. 5] был установлен важный фокт, что для эффективного описания порядка $ \lessdot $, действительно достаточно рассмотреть пересечения ротаций и учесть (4.2). А именно, образуем ориентированный граф $H = ({{\mathcal{R}}_{G}},\mathcal{E})$, ребрами которого являются пары ротаций $(C,D)$ такие, что либо ${{V}_{C}} \cap {{V}_{D}} \ne \emptyset $ и $C \lessdot D$, либо выполняется (4.2) (этот граф легко строится за время $O({\text{|}}V{\text{|}}\,{\text{|}}E{\text{|}})$; с некоторой изобретательностью время можно уменьшить до $O({\text{|}}E{\kern 1pt} {\text{|}}{\kern 1pt} )$). Можно показать, что

Граф $H$ ациклический, и если какая-либо вершина $D$ в $H$ достижима ориентированным путем из $C$, то выполняется $C \lessdot D$. Верно и обратное.

Предложение 9. Если $C \lessdot D$, то в $H$ имеется ориентированный путь из $C$ в $D$. Следовательно, отношение достижимости для вершин в $H$ совпадает с отношением $ \lessdot $.

Доказательство. Пусть $\mathcal{I}{\kern 1pt} '$ – множество идеалов в посете для $H$; тогда $\mathcal{I}{\kern 1pt} ' \supseteq \mathcal{I}(G)$. Надо доказать, что $\mathcal{I}{\kern 1pt} ' \supseteq \mathcal{I}(G)$. Предположим, это не так, т.е. имеется $X \in \mathcal{I}{\kern 1pt} '$, не являющийся идеалом в $({{\mathcal{R}}_{G}}, \lessdot )$. Пусть при этом $X$ выбрано так, чтобы число элементов ${\text{|}}X{\text{|}}$ было максимальным. Также выберем идеал $R \in \mathcal{I}(G)$ такой, что $R \subset X$, и при этом ${\text{|}}R{\text{|}}$ максимально. Согласно предложению 8, $R = {{\mathcal{R}}_{M}}$ для некоторого стабильного матчинга $M$. Возьмем допустимую ротацию $C$ для $M$. Ввиду максимальности $R$, элемент $C$ должен быть вне $X$. Тогда $R{\kern 1pt} ': = R \cup \{ C\} $ – идеал в $({{\mathcal{R}}_{G}}, \lessdot )$ (соответствующий матчингу $M{\kern 1pt} '$, получаемому из $M$ заменой вдоль $C$). Также $X{\kern 1pt} ': = X \cup \{ C\} \in \mathcal{I}{\kern 1pt} '$.

Ввиду максимальности $X$, имеем $X{\kern 1pt} ' \in \mathcal{I}(G)$. Поскольку $X{\kern 1pt} ' \supset R{\kern 1pt} '$, и оба $X{\kern 1pt} ',\;R{\kern 1pt} '$ – идеалы в $({{\mathcal{R}}_{G}}, \lessdot )$, множество $X{\kern 1pt} '\; - R{\kern 1pt} '$ содержит элемент (ротацию) $D$ такой, что $R{\kern 1pt} '{\kern 1pt} ': = R{\kern 1pt} '\; \cup \{ D\} \in \mathcal{I}(G)$. В то же время $X{\kern 1pt} '{\kern 1pt} ': = R \cup \{ D\} $ не является идеалом в $({{\mathcal{R}}_{G}}, \lessdot )$; иначе, ввиду $R \subset X{\kern 1pt} '{\kern 1pt} ' \subseteq X$, мы получили бы противоречие с максимальностью $R$ (если $X{\kern 1pt} '{\kern 1pt} ' \ne X$) или с условием на $X$ (если $X{\kern 1pt} '{\kern 1pt} ' = X$).

Итак, мы пришли к ситуации, когда $R,R{\kern 1pt} ',R{\kern 1pt} '{\kern 1pt} ' \in \mathcal{I}(G)$, $R{\kern 1pt} ' = R \cup \{ C\} $, $R{\kern 1pt} '{\kern 1pt} ' = R{\kern 1pt} '\; \cup \{ D\} $, но $R \cup \{ D\} \notin \mathcal{I}(G)$. Тогда ротация $D$ недопустима для матчинга $M$, но становится допустимой сразу после того, как в $M$ производится замена вдоль ротации $C$. Это в точности означает, что граф $H$ содержит ребро $(C,D)$; ср. (4.3). Но такое ребро идет из ${{\mathcal{R}}_{G}} - X$ в $X$, вопреки тому, что $X$ принадлежит $\mathcal{I}{\kern 1pt} '$.

Можно показать, что ребра $(C,D)$ графа $H$ как в (4.3) определяют отношения непосредственного предшествования в посете $({{\mathcal{R}}_{G}}, \lessdot )$, а именно, выполнение $C \lessdot D$ и отсутствие ротации $C{\kern 1pt} '$ между $C$ и $D$ (т.е. $C \lessdot C{\kern 1pt} ' \lessdot D$).

Замечание 1. Пусть нам даны стабильные матчинги $M$ и $M{\kern 1pt} '$ в двудольном $G$ такие, что $M \prec M{\kern 1pt} '$, и пусть $[M,M{\kern 1pt} ']$ обозначает множество (“интервал”) стабильных матчингов $L$, для которых $M \preccurlyeq L \preccurlyeq M{\kern 1pt} '$. (Как специальные случаи можно рассматривать $M = {{M}^{{{\text{min}}}}}$ или $M{\kern 1pt} ' = {{M}^{{{\text{max}}}}}$.) Нас интересует возможность “очистки” графа $G$ путем удаления части его ребер с тем, чтобы для полученного графа $G{\kern 1pt} '$ множество стабильных матчингов в точности совпадало с интервалом $[M,M{\kern 1pt} ']$ для $G$. Чтобы попытаться ответить на данный вопрос, возьмем произвольную трассу $\tau $, проходящую через оба $M,\;M{\kern 1pt} '$, и рассмотрим множество ротаций, используемых на участке трассы от $M$ до $M{\kern 1pt} '$, т.е. ${{\mathcal{R}}_{{M,M{\kern 1pt} '}}}$, см. (4.1). (Трасса $\tau $ и множество ${{\mathcal{R}}_{{M,M{\kern 1pt} '}}}$ строятся эффективно; ср. доказательство предложения 6.) Тогда интервал $[M,M{\kern 1pt} ']$ состоит ровно из тех $L \in \mathcal{M}(G)$, которые получаются из $M$ применением последовательности ротаций из множества ${{\mathcal{R}}_{{M,M{\kern 1pt} '}}}$. Поэтому искомый граф $G{\kern 1pt} '$ должен включать $M$ и объединение всех ротаций из ${{\mathcal{R}}_{{M,M{\kern 1pt} '}}}$. Однако он также должен учитывать структуру графа $H$ (см. (4.3)), чтобы избежать появления “лишних” матчингов, использующих ротации из ${{\mathcal{R}}_{{M,M{\kern 1pt} '}}}$. Следовательно, нужно добавить ребра как в (4.2) (вида $m{\kern 1pt} '{\kern 1pt} w$), чтобы гарантировать сохранение указанного там отношения $C \lessdot D$ для соответствующих ротаций $C,D$ в ${{\mathcal{R}}_{{M,M{\kern 1pt} '}}}$. Гипотеза: подграф $G{\kern 1pt} '$ существует и получается из $G$ удалением всех остальных ребер.

5. ОПТИМАЛЬНЫЕ СТАБИЛЬНЫЕ МАТЧИНГИ

В этом разделе мы рассматриваем ситуацию, когда двудольный граф $G = (V,E, < )$ дополнительно снабжен вещественной функцией весов (или стоимостей) ребер $c:E \to \mathbb{R}$. Нас интересует задача о стабильном матчинге минимального веса:

(Ввиду того, что все стабильные матчинги в $G$ имеют одинаковый размер, добавление константы к функции $c$ фактически не меняет задачи; поэтому можно считать функцию $c$ неотрицательной. При замене $c$ на $ - c$ получаем задачу максимизации веса $c(M)$.)

В важном частном случае этой задачи, известном как задача об оптимальном стабильном матчинге (см. [6]), вес $c(e)$ ребра $e = mw$ определяется как

где ${{r}_{I}}(e)$ – порядковый номер ребра $e$ в упорядоченном (согласно ${{ < }_{m}}$) списке $\delta (m)$, и, аналогично, ${{r}_{J}}(e)$ – номер в списке $\delta (w)$. (Такая постановка широко обсуждалась в литературе, в частности, в [11, 17]. Здесь интересуются матчингом, который “наиболее благоприятен по суммарным (или средним) предпочтениям для всех персон” (в то время как “алгоритм отложенных принятий” (АОП) дает наилучшее решение только для одного множества из $I$ и $J$).) В [7] задача с весовой функцией как в (5.2) также называется задачей об эгалитарном стабильном матчинге.

Задача (5.1) может быть сформулирована как задача линейного программирования с $0, \pm 1$-матрицей размера $({\text{|}}V{\text{|}}{\kern 1pt} \; + \;{\text{|}}E{\kern 1pt} {\text{|}})\; \times \;{\text{|}}E{\kern 1pt} {\text{|}}$ (о чем будет сказано в следующем разделе), поэтому она может быть решена универсальным сильно полиномиальным алгоритмом (усиленной версией метода эллипсоидов в [18]). Однако изложенное в предыдущем разделе представление $\mathcal{M}(G)$ в виде множества идеалов в посете ротаций $({{\mathcal{R}}_{G}}, \lessdot )$ дает возможность решать (5.1) намного более экономным и наглядным методом. Это было предложено Ирвингом–Лейтером–Гасфилдом в [7], и ниже мы описываем этот метод (применительно к рассматриваемому нами произвольному двудольному графу $G$).

Для заданной функции весов $c$ и произвольной ротации $R = {{e}_{1}}{{a}_{1}}{{e}_{2}}{{a}_{2}} \cdots {{e}_{k}}{{a}_{k}}$ в ${{\mathcal{R}}_{G}}$, где ребра ${{e}_{i}}$ матчинговые, а ребра ${{a}_{i}}$ активные, определим вес $R$ как

При трансформации относительно ротации $R$ к весу текущего матчинга прибавляются веса активных ребер и из него вычитаются веса матчинговых ребер в $R$. Поэтому вес любого стабильного матчинга $M$ выражается как

где ${{\mathcal{R}}_{M}}$ – идеал в $({{\mathcal{R}}_{G}}, \lessdot )$, соответствующий $M$ (т.е. множество ротаций, возникающих на участке (любой) трассы от ${{M}^{{{\text{min}}}}}$ до $M$).

Таким образом, (5.1) эквивалентно задаче нахождения идеала минимального веса. В общем случае задача такого рода выглядит следующим образом:

(Напомним, что множество $X$ считается замкнутым, если нет ребер, идущих из ${{V}_{Q}} - X$ в $X$. В частности, замкнутыми множествами являются $\emptyset $ и ${{V}_{Q}}$. Без ограничения общности можно считать граф $Q$ ациклическим, так как любой ориентированный цикл не может разделяться замкнутым множеством, и его можно стянуть в одну вершину суммарного веса.)

Решение задачи (5.4), предложенное Пикаром [8], состоит в ее сведении к задаче о минимальном разрезе в ориентированном графе $\hat {Q} = (\hat {V},\hat {E})$ с пропускными способностями ребер $h(e)$, $e \in \hat {E}$, определяемыми следующим образом.

Положим ${{V}^{ + }}: = \{ v \in {{V}_{Q}}:\zeta (v) > 0\} $ и ${{V}^{ - }}: = \{ v \in {{V}_{Q}}:\zeta (v) < 0\} $. Граф $\hat {Q}$ получается из $Q$ добавлением двух вершин: “источника” $s$ и “стока” $t$, а также множества ребер ${{E}^{ + }}$ из $s$ в $v$ для всех $v \in {{V}^{ + }}$ и множества ребер ${{E}^{ - }}$ из $u$ в $t$ для всех $u \in {{V}^{ - }}$. Пропускные способности ребер $e \in \hat {E}$ задаются так:

Для подмножества $S \subseteq \hat {V}$ такого, что 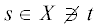, обозначим через $\delta (S)$ множество ребер в $\hat {Q}$, идущих из $S$ в $\hat {V} - S$, называемое $s$–$t$ разрезом; величина $h(\delta (S)): = \sum \,(h(e):e \in \delta (S))$ считается пропускной способностью этого разреза.

Лемма 2 (см. [8]). Подмножество $X \subseteq {{V}_{Q}}$ является замкнутым множеством минимального веса в $(Q,\zeta )$ тогда и только тогда, когда $\delta (({{V}_{Q}} - X) \cup \{ s\} )$ является $s$–$t$ разрезом минимальной пропускной способности в $(\hat {Q},h)$.

Доказательство. Заметим, что $X \subseteq {{V}_{Q}}$ – замкнутое множество тогда и только тогда, когда разрез $E' = \delta (({{V}_{Q}} - X) \cup \{ s\} )$ не содержит ребер бесконечной пропускной способности; эквивалентно, $E{\kern 1pt} '$ содержится в ${{E}^{ + }} \cup {{E}^{ - }}$. Для такого разреза, состоящего из ребер вида $sv$ для $v \in X$ и ребер вида $ut$ для $u \in {{V}_{Q}} - X$, пропускная способность выглядит так:

Следовательно, вес замкнутого множества отличается от пропускной способности соответствующего разреза на постоянную величину $ - \zeta ({{V}^{ - }})$, откуда получаем требуемое утверждение.

Таким образом, задача (5.1) сводится к задаче о минимильном двухполюсном разрезе в сети с $N = O({\text{|}}E{\kern 1pt} {\text{|}}{\kern 1pt} )$ вершинами и $A = O({\text{|}}E{\kern 1pt} {\text{|}}{\kern 1pt} )$ ребрами. (Учитывая то, что вместо всего посета $({{\mathcal{R}}_{G}}, \lessdot )$ достаточно рассматривать его порождающий граф $H$, имеющий $O({\text{|}}E{\kern 1pt} {\text{|}}{\kern 1pt} )$ ребер, см. предложение 9. Применяя быстрые алгоритмы для задачи о максимальном потоке и минимальном разрезе (см., например, обзор в [12, Sec. 10.8]), можно получить временную оценку $O(NA\log N) \simeq $ $ \simeq O({\text{|}}V{\kern 1pt} {{{\text{|}}}^{4}}\log {\text{|}}V{\kern 1pt} {\text{|}}{\kern 1pt} )$. В [7] приведена имплементация, решающая (5.1) за время $O({\text{|}}V{\kern 1pt} {{{\text{|}}}^{4}})$.)

Замечание 2. В [19] доказывалась труднорешаемость некоторых вариантов задачи о замкнутых множествах. Используя один из них, а также тот факт, что любой транзитивно замкнутый граф реализуется как посет ротаций (о чем будет сказано в разд. 7), можно показать NP-трудность следующего усиления задачи (5.1): для двудольного $G = (V,E, < )$, функций $c,g:E \to {{\mathbb{R}}_{ + }}$ и числа $K \in {{\mathbb{R}}_{ + }}$ найти стабильный матчинг $M \in \mathcal{M}(G)$, минимизирующий $c(M)$ при условии $g(M) \geqslant K$. (Здесь $g(M)$ можно интерпретировать как прибыль, а $c(M)$ как затраты при организации союзов (или контрактов) в $M$.)

6. ПОЛИЭДРАЛЬНЫЕ АСПЕКТЫ И МЕДИАННЫЕ СТАБИЛЬНЫЕ МАТЧИНГИ

Как мы упоминали ранее, для двудольного графа $G = (V = I \sqcup J,E, < )$ имеется полиэдральная характеризация многогранника стабильных матчингов ${{\mathcal{P}}_{{{\text{st}}}}}(G)$, задаваемая линейным от ${\text{|}}V{\kern 1pt} {\text{|}},\;{\text{|}}E{\kern 1pt} {\text{|}}$ числом неравенств. Здесь ${{\mathcal{P}}_{{{\text{st}}}}}(G)$ – выпуклая оболочка множества характеристических векторов ${{\chi }^{M}}$ стабильных матчингов $M$ в пространстве ${{\mathbb{R}}^{E}}$. Первоначальное описание ${{\mathcal{P}}_{{{\text{st}}}}}(G)$ (в случае $G \simeq {{K}_{{n,n}}}$) было дано в работе Ванде Вейта [9] (и повторено в работе [20]). Ниже мы приводим описание (несколько отличающееся по виду, но близкое к тому, что в [9]) и доказательство, основываясь на изложении в [12], Sec. 18.5g.

Для ребер $e,f \in E$ будем писать $f \prec e$, если они имеют общую вершину $v$, и выполняется $f{{ < }_{v}}e$ (т.е. $f$ предпочтительнее, чем $e$). Для $e \in E$ обозначим $\gamma (e)$ множество ребер $f$ таких, что $f \preccurlyeq e$ (в частности, $e \in \gamma (e)$).

Напомним, что многогранник матчингов в двудольном случае описывается системой линейных неравенств

В случае стабильных матчингов добавляется еще один тип неравенств:

Предложение 10. Система (6.1)–(6.3) описывает в точности множество векторов $x \in {{\mathbb{R}}^{E}}$, принадлежащих ${{\mathcal{P}}_{{{\text{st}}}}}(G)$.

Доказательство. Легко видеть, что для любого стабильного матчинга $M$ вектор $x = {{\chi }^{M}}$ удовлетворяет (6.1)–(6.3). Поэтому достаточно доказать, что если $x$ – вершина многогранника $\mathcal{P}{\kern 1pt} '$, определяемого (6.1)–(6.3), то вектор $x$ целочисленный.

Положим ${{E}^{ + }}: = \{ e \in E:x(e) > 0\} $ и обозначим ${{V}^{ + }}$ множество вершин в $G$, покрытых ${{E}^{ + }}$. Для $v \in {{V}^{ + }}$ обозначим через ${{e}_{v}}$ наилучшее ребро в $\delta (v) \cap {{E}^{ + }}$ относительно порядка ${{ < }_{v}}$. Справедливо следующее свойство:

Действительно, полагая $e: = {{e}_{{v}}}$, имеем

Здесь все неравенства должны обращаться в равенства. Это дает $\sum \,(x(f):f{{ > }_{u}}e) = 0$ и $x(\delta (u)) = 1$, откуда следует (6.4).

Образуем множества $M: = \{ e \in {{E}^{ + }}:e = {{e}_{v}}$ для $v \in I\} $ и $L: = \{ e \in {{E}^{ + }}:e = {{e}_{v}}$ для $v \in J\} $. Для любой вершины $v \in I \cap {{V}^{ + }}$ наилучшее ребро в $\delta (v) \cap {{E}^{ + }}$ принадлежит $M$, а наихудшее ребро, и только оно, принадлежит $L$ (ввиду (6.4)); для вершин в $J \cap {{V}^{ + }}$ поведение обратное. Отсюда можно заключить, что оба $M$ и $L$ являются матчингами. Каждое ребро $e \in M \cap L$ образует компоненту в подграфе $({{V}^{ + }},{{E}^{ + }})$; это дает $x(e) = 1$ (ввиду (6.2), (6.3)). В частности, $x$ целочисленный, если $M = L$.

Пусть теперь $M \ne L$. Очевидно, для любого ребра $e$ в $M{\kern 1pt} ': = M - L$ или в $L{\kern 1pt} ': = L - M$ выполняется $0 < x(e) < 1$. Поэтому можно выбрать достаточно малое число $\varepsilon > 0$ так, чтобы вектора $x{\kern 1pt} ': = x + \varepsilon {{\chi }^{{M{\kern 1pt} '}}} - \varepsilon {{\chi }^{{L{\kern 1pt} '}}}$ удовлетворяли (6.1) и (6.2). Проверим, что оба $x{\kern 1pt} '$ и $x{\kern 1pt} '{\kern 1pt} '$ удовлетворяют также и (6.3).

Для этого рассмотрим ребро $e = mw$ с $x(e) < 1$ и предположим, что $x{\kern 1pt} '(\gamma (e)) < x(\gamma (e))$. Это возможно только если $a{{ \leqslant }_{w}}e{{ < }_{w}}b$, где $\{ a\} = L \cap \delta (w)$ и $\{ b\} = M \cap \delta (w)$. При этом должно выполняться либо (i) $m \notin {{V}^{ + }}$, либо (ii) $m \in {{V}^{ + }}$, и $e$ более предпочтительное, чем ребро в $M \cap \delta (m)$ (иначе такое ребро давало бы положительный вклад в $x{\kern 1pt} '(\gamma (e))$, откуда $x{\kern 1pt} '(\gamma (e)) = x(\gamma (e))$). Но в этих случаях из равенства $x(\delta (w) = 1$ (ввиду (6.4)) и неравенства $x(b) > 0$ следует

что невозможно. Аналогично, (6.3) верно для $x{\kern 1pt} '{\kern 1pt} '$.

Таким образом, $x{\kern 1pt} ',x{\kern 1pt} '{\kern 1pt} ' \in \mathcal{P}{\kern 1pt} '$. Но $x{\kern 1pt} ' \ne x{\kern 1pt} '{\kern 1pt} '$ и $(x{\kern 1pt} '\; + x{\kern 1pt} '{\kern 1pt} '){\text{/}}2 = x$. Это противоречит тому, что $x$ – вершина в $\mathcal{P}{\kern 1pt} '$.

Имеется еще одно полезное свойство, показанное в [21]; мы приводим его в несколько иной, но эквивалентной, форме.

Лемма 3. Пусть $x \in {{\mathcal{P}}_{{{\text{st}}}}}(G)$, и пусть $e = mw$ – ребро в $G$, для которого $x(e) > 0$. Тогда $x(\delta (m)) = x(\delta (w)) = x(\gamma (e)) = 1$.

Доказательство. Представим $x$ как ${{\alpha }_{1}}{{\chi }^{{{{M}_{1}}}}} + \cdots + {{\alpha }_{k}}{{\chi }^{{{{M}_{k}}}}}$, где ${{M}_{i}}$ – стабильный матчинг, ${{\alpha }_{i}} > 0$, и ${{\alpha }_{1}} + \cdots + {{\alpha }_{k}} = 1$. Обозначим ${{x}_{i}}: = {{\chi }^{{{{M}_{i}}}}}$. Ввиду $x(e) > 0$, ребро $e$ принадлежит некоторому ${{M}_{i}}$. Тогда ${{x}_{i}}(\delta (m)) = {{x}_{i}}(\delta (w)) = {{x}_{i}}(\gamma (e)) = 1$. Аналогичные равенства имеют место и для матчинга ${{M}_{j}}$, не содержащего $e$. Действительно, так как ${{M}_{i}}$ и ${{M}_{j}}$ покрывают одно и то же множество вершин (ввиду предложения 2), в ${{M}_{j}}$ есть ребро $e{\kern 1pt} '$, инцидентное $m$, и ребро $e{\kern 1pt} '{\kern 1pt} '$, инцидентное $w$. Более того, рассматривая пару ${{M}_{i}},\;{{M}_{j}}$ и применяя (2.1), получаем либо $e{\kern 1pt} '{{ < }_{m}}e{{ < }_{w}}e{\kern 1pt} '{\kern 1pt} '$, либо $e{\kern 1pt} '{{ > }_{m}}e{{ > }_{w}}e{\kern 1pt} '{\kern 1pt} '$. В обоих случаях в $\gamma (e)$ попадает ровно одно ребро из $e{\kern 1pt} ',\;e{\kern 1pt} '{\kern 1pt} '$; поэтому ${{x}_{j}}(\gamma (e)) = 1$. Теперь утверждение следует из ${{\alpha }_{1}} + \cdots + {{\alpha }_{k}} = 1$.

Эта лемма помогает получить интересный результат Тео и Сетурамана.

Предложение 11 (cм. [10]). Пусть ${{M}_{1}}, \ldots ,{{M}_{\ell }}$ – стабильные матчинги в $G$. Для каждого $m \in \tilde {I}$ обозначим ${{E}_{m}}$ список (с возможными повторениями) ребер в $\delta (m)$, принадлежащих этим матчингам и упорядоченных согласно ${{ < }_{m}}$, и пусть ${{e}_{m}}(i)$ обозначает $i$-й элемент в ${{E}_{m}}$, $i = 1, \ldots ,\ell $. Аналогично, для каждого $w \in \tilde {J}$ пусть ${{e}_{w}}(j)$ обозначает $j$-й элемент в списке ${{E}_{w}}$ ребер в $\delta (w)$, принадлежащих данным матчингам и упорядоченных согласно ${{ < }_{w}}$, $j = 1, \ldots ,\ell $. Тогда для любого $k \in \{ 1, \ldots ,\ell \} $ множество ребер $A(k): = \{ {{e}_{m}}(k):m \in \tilde {I}\} $ совпадает с множеством $B(\ell - k + 1): = \{ {{e}_{w}}(\ell - k + 1):w \in \tilde {J}\} $ и образует стабильный матчинг в $G$.

Доказательство. Положим ${{x}_{i}}: = \frac{1}{\ell }{{\chi }^{{{{M}_{i}}}}}$. Тогда $x = {{x}_{1}} + \cdots + {{x}_{\ell }}$ лежит в многограннике ${{\mathcal{P}}_{{{\text{st}}}}}(G)$ (является т.н. “дробным стабильным матчингом”).

Вначале предположим для простоты, что все ребра в ${{M}_{1}}, \ldots ,{{M}_{\ell }}$ различны. Тогда для $m \in \tilde {I}$ список ${{E}_{m}}$ состоит из $\ell $ различных ребер, и ребро ${{e}_{m}}(k)$ является $k$-м элементом в ${{E}_{m}}$. Из Леммы 3, примененной к $x$ и $e = {{e}_{m}}(k)$ следует, что множество $\gamma (e)$ состоит из $\ell $ элементов. Тогда $e$ является в точности $(\ell - k + 1)$-м элементом в списке ${{E}_{w}}$ (по предположению состоящем из $\ell $ различных ребер), и тем самым ${{e}_{m}}(k) = {{e}_{w}}(\ell - k + 1)$.

Таким образом, $A(k) = B(\ell - k + 1)$, откуда следует, что $A(k)$ является матчингом в $G$. Чтобы показать стабильность $A(k)$ рассмотрим произвольное ребро $e = mw \notin A(k)$ в $G$. Надо проверить, что $e$ не блокирует $A(k)$, или, эквивалентно, что $A(k) \cap \gamma (e) \ne \emptyset $.

По крайней мере один из концов $e$, скажем, $m$, принадлежит $\tilde {V}$ (и покрывается $A(k)$); иначе для $x$ и $e$ мы имели бы $x(\gamma (e)) = 0$ вопреки (6.3). Если $w \notin \tilde {V}$, то $x(\delta (w)) = 0$, и из неравенства $x(\gamma (e)) \geqslant 1$ следует, что для всех ребер $f \in {{E}_{m}}$ (включая $f = {{e}_{m}}(k)$) выполняется $f{{ < }_{m}}e$. Это дает требуемое $A(k) \cap \gamma (e) \ne \emptyset $.

Пусть теперь $w \in \tilde {V}$. Ввиду $x(\gamma (e)) \geqslant 1$, число ребер $f$ в ${{E}_{m}} \cup {{E}_{w}}$, для которых $f \preccurlyeq e$, не меньше $\ell $. Тогда должно выполняться по крайней мере одно из ${{e}_{m}}(k){{ \leqslant }_{m}}e$ и ${{e}_{w}}(\ell - k + 1){{ \leqslant }_{w}}e$, откуда опять следует $A(k) \cap \gamma (e) \ne \emptyset $.

В том случае, когда в ${{M}_{1}}, \ldots ,{{M}_{\ell }}$ есть общие ребра, можно рассмотреть мультиграф, получаемый из $G$ заменой каждого ребра $e = mw$ с $x(e) > 0$ на $\ell x(e) = :r$ параллельных ребер ${{e}^{1}}, \ldots ,{{e}^{r}}$. При этом продолжение порядка ${{ < }_{m}}$ на эти ребра назначается противоположным продолжению порядка ${{ < }_{w}}$, скажем, ${{e}^{1}}{{ < }_{m}} \cdots {{ < }_{m}}{{e}^{r}}$ и ${{e}^{1}}{{ > }_{w}} \cdots {{ > }_{w}}{{e}^{r}}$. Требуемое утверждение для этого общего случая получается повторением (с незначительными уточнениями) рассуждений для случая непересекающихся матчингов выше.

Следствие 4. Если $\ell $ нечетно, то для $k: = (\ell + 1){\text{/}}2$ множество, состоящее из $k$-х по порядку элементов в списках ребер ${{E}_{v}}$, инцидентных $v$ и принадлежащих ${{M}_{1}}, \ldots ,{{M}_{\ell }}$, для всех вершин $v \in \tilde {V}$, является стабильным матчингом.

Такой матчинг называют медианным для ${{M}_{1}}, \ldots ,{{M}_{\ell }}$. В [10] был поставлен вопрос о возможности эффективного нахождения медианного стабильного матчинга среди всех стабильных матчингов в $G$ (или “почти медианного”, когда число стабильных матчингов четное). Нам это представляется маловероятным в свете того, что задача вычисления числа ${\text{|}}\mathcal{M}(G){\text{|}}$ является труднорешаемой, о чем будет сказано ниже.

7. О ПОДСЧЕТЕ ЧИСЛА СТАБИЛЬНЫХ МАТЧИНГОВ

Кнут [11] указал примеры, когда число стабильных матчингов двудольного графа экспоненциально велико по сравнению с размером графа, и задал вопрос о сложности точного вычисления этого числа. Ответ был дан Ирвингом и Лейтером [5], которые показали труднорешаемость такой задачи (рассматривая графы вида ${{K}_{{n,n}}}$). Ниже мы кратко поясним идею их доказательства.

Напомним некоторые понятия (отсылая за точными определениями к [22] или [23, разд. 7.3]). Не вдаваясь в полную логическую строгость, можно понимать, что описание той или иной перечислительной задачи (enumeration problem) $\mathcal{P}$ состоит из бесконечного семейства $\mathcal{S}$ конечных множеств, и для каждого $S \in \mathcal{S}$ имеется семейство $\mathcal{F}(\mathcal{S})$ подмножеств в $S$ (“объектов”). В задаче $\mathcal{P}$ требуется для заданного $S \in \mathcal{S}$ определить число ${\text{|}}\mathcal{F}(S){\kern 1pt} {\text{|}}$. Говорят, что $\mathcal{P}$ является $\# P$-задачей (или $KP$-задачей, в терминологии некоторых авторов), если распознавание объекта проводится за полиномиальное время, т.е. имеется алгоритм, который для любых $S \in \mathcal{S}$ и $X \subseteq S$ за время, полиномиальное от ${\text{|}}S{\text{|}}$, определяет, принадлежит или нет данное множество $X$ семейству $\mathcal{F}(S)$. Говорят, что $\# P$-задача $\mathcal{P} = \{ \mathcal{F}(S),S \in \mathcal{S}\} $ является $\# P$-полной (или универсальной в классе $\# P$), если любая другая $\# P$-задача $\mathcal{P}{\kern 1pt} ' = \{ \mathcal{F}{\kern 1pt} '(S{\kern 1pt} '),S{\kern 1pt} ' \in \mathcal{S}{\kern 1pt} '\} $ сводится к ней за полиномиальное время (т.е. есть отображение $\omega :\mathcal{S}{\kern 1pt} ' \to \mathcal{S}$ такое, что для каждого $S{\kern 1pt} ' \in \mathcal{S}$ число ${\text{|}}\mathcal{F}{\kern 1pt} '(S{\kern 1pt} '){\kern 1pt} {\text{|}}$ определяется из ${\text{|}}\mathcal{F}(\omega (S{\kern 1pt} ')){\kern 1pt} {\text{|}}$ за время, полиномиальное от ${\text{|}}S{\kern 1pt} '{\text{|}}$).

В рассматриваемой нами задаче роль cемейства $\mathcal{S}$ играет совокупность реберных множеств $E$ двудольных графов $G = (V,E, < )$, а роль семейства $\mathcal{F}(S)$, $S \in \mathcal{S}$, – соответствующее множество стабильных матчингов в $G$. Задача определения ${\text{|}}\mathcal{M}(G){\kern 1pt} {\text{|}}$ – это действительно $\# P$-задача, так как для любого подмножества $M \subseteq E$ можно определить, является ли $M$ стабильным матчингом, за время $O({\text{|}}E{\kern 1pt} {\text{|}})$.

Заметим, что $\# P$-аналог любой $NP$-полной задачи является “труднорешаемым” (поскольку в последней задаче требуется “всего лишь” определить, является ли непустым соответствующее семейство объектов $\mathcal{F}(S)$ (например, содержит ли заданный граф хотя бы один гамильтонов цикл), а в первой нужно найти количество объектов). Однако есть $P$-задачи, чьи перечислительные аналоги являются $\# P$-полными. Именно таковой и является задача определения ${\text{|}}\mathcal{M}(G){\text{|}}$. Это вытекает из следующих двух результатов.

Предложение 12. Задача определения числа анти-цепей в конечном посете является $\# P$-полной.

Предложение 13. Пусть $(P, < {\kern 1pt} ')$ – посет на $n$ элементах. Существует и может быть построен за время полиномиальное от $n$ двудольный граф $G = (V,E, < )$ такой, что его ротационный посет $({{\mathcal{R}}_{G}}, \lessdot )$ изоморфен $(P, < {\kern 1pt} ')$. Следовательно (ввиду предложения 8), число ${\text{|}}\mathcal{M}(G){\text{|}}$ стабильных матчингов в $G$ равно числу анти-цепей (или числу идеалов) в посете $(P, < {\kern 1pt} ')$.

Предложение 12 было установлено Прованом и Боллом [24]. Предложение 13 было доказано в [5, Sec. 5] путем явной конструкции требуемого графа $G$ для заданного посета $(P, < {\kern 1pt} ')$.

Автор благодарит рецензента за анализ начальной версии статьи и сделанные замечания.