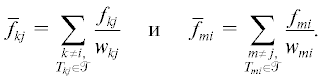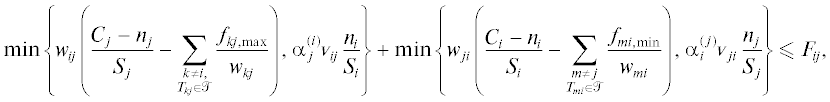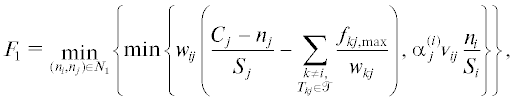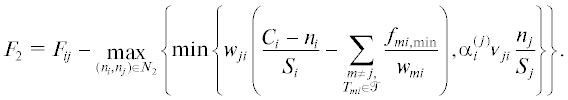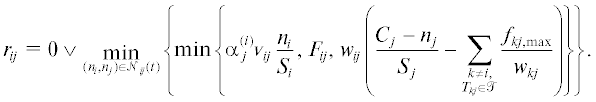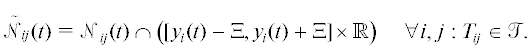Журнал вычислительной математики и математической физики, 2023, T. 63, № 8, стр. 1381-1394

Методы построения оценок множеств достижимости в задаче моделирования потоков людей

М. В. Зайцева^1, *, П. А. Точилин^1, **

¹ МГУ им. М.В. Ломоносова, ВМК
119991 Москва, Ленинские горы, Россия

^* E-mail: zaimarko@gmail.com
^** E-mail: tochilin@cs.msu.ru

Поступила в редакцию 23.01.2023
После доработки 23.01.2023
Принята к публикации 30.03.2023

EDN: ZXXNGL
DOI: 10.31857/S0044466923070190

Аннотация

Работа посвящена математическому моделированию потоков людей в помещении. За основу взята модификация дискретной макромодели CTM, построенная на гарантированных оценках. Для описанной модели предложено два способа приближенного вычисления множества достижимости – количества людей в каждой комнате в последующий момент времени. Строятся интервальные оценки и оценки в форме совокупностей двумерных проекций. Предложенные алгоритмы проиллюстрированы численными примерами. Библ. 14. Фиг. 3.

Ключевые слова: моделирование потоков людей, линейное программирование, множество достижимости, нелинейная динамика.

1. ВВЕДЕНИЕ

В математическом моделировании потоков людей можно выделить два основных подхода: микромоделирование и макромоделирование. В первом случае необходимо учитывать положение и скорость каждого элемента системы, во втором используются их усредненные характеристики.

Настоящая работа посвящена математическому моделированию движения групп людей в помещении на основе известной макромодели CTM (Cell Transmission Model) (см. [1], [2]), которая часто используется при математическом моделировании транспортных потоков и является дискретным аналогом гидродинамической модели LWR (Lighthill, Whitham, Richards) (см. [3]). Подробное описание и возможный метод калибровки для моделирования движения групп людей были предложены в [4]. Существуют и другие ее модификации, например, PedCTM (Pedestrian Cell Transmission Model) (см. [5]). Наряду с дискретными моделями рассматривают также непрерывные модели движения групп людей, построенные как обобщение одномерных транспортных моделей (см. [6]).

Недостатками указанных методов являются предположения об известном поведении людей или известной плотности их распределения в помещении. Поэтому предлагается использовать модификацию из [4] модели CTM, основанную на гарантированных оценках количества людей в комнатах. Однако построение этих оценок также является непростой задачей. Данная работа посвящена двум методам аппроксимации множества достижимости в последующий момент времени на основе интервальных оценок и оценок двумерных проекций. В дальнейшем такие краткосрочные численные прогнозы могут быть полезны при выборе стратегии управления и при оценке ее качества. Особенно актуальны задачи оптимизации эвакуации людей из помещений (см. [7]), а также перераспределения потоков людей в общественном транспорте (см. [5], [8]). Построение оценок распределений людей в будущие моменты времени является важным элементом решения указанных задач.

В настоящей статье предложены два метода численного прогноза в модели движения групп людей, описаны алгоритмы построения оценок множества достижимости, а также представлены численные результаты двух подходов.

2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

2.1. Схема помещения

План помещения или его части представим в виде ориентированного графа $\Gamma = \{ \mathcal{R},\mathcal{T}\} $, где множество вершин $\mathcal{R} = \{ {{R}_{1}}, \ldots ,{{R}_{N}}\} $ обозначает $N$ комнат (это могут быть не только отдельные комнаты, но и части больших холлов и коридоров), множество ребер $\mathcal{T}$ – переходы между ними. Множество $\mathcal{T}$ состоит из элементов ${{T}_{{ij}}},$ $i,j \in \{ 1, \ldots ,N\} $, ${{T}_{{ij}}}$ обозначает переход между комнатами ${{R}_{i}}$ и ${{R}_{j}}$, если он существует.

Каждой комнате ${{R}_{i}}$ сопоставлены следующие характеристики:

• ${{S}_{i}}$ – площадь $i$-й комнаты;

• ${{C}_{i}}$ – максимальная вместимость (наибольшее количество человек, которое может одновременно находиться в $i$-й комнате);

• ${{n}_{i}}(t)$ – количество людей в комнате $i$ в момент времени $t$.

Замечание 1. В рассматриваемой модели время $t$ – дискретное.

Замечание 2. Величина ${{n}_{i}}(t)$ является усредненной по небольшому интервалу времени, поэтому функция ${{n}_{i}}(t)$ не обязательно является целочисленной, однако условие ${{n}_{i}}(t) \in [0,{{C}_{i}}]$ выполнено всегда.

Для комнаты ${{R}_{i}}$, связанной переходами с комнатами ${{R}_{{{{j}_{1}}}}}, \ldots ,{{R}_{{{{j}_{k}}}}}$, дополнительно вводится ${{\alpha }^{{(i)}}}(t) = \left( {\alpha _{0}^{{(i)}}(t),\alpha _{{{{j}_{1}}}}^{{(i)}}(t), \ldots ,\alpha _{{{{j}_{k}}}}^{{(i)}}(t)} \right)$ – набор коэффициентов расщепления, где $k$ – количество соседних комнат, в которые можно перейти из $i$-й. При этом $\alpha _{s}^{{(i)}}(t)\; \geqslant \;0$, $s = 0,{{j}_{1}}, \ldots ,{{j}_{k}}$, и $\alpha _{0}^{{(i)}}(t) + \alpha _{{{{j}_{1}}}}^{{(i)}}(t) + \; \cdots \; + \alpha _{{{{j}_{k}}}}^{{(i)}}(t) = 1$ $\forall t$. Коэффициент расщепления $\alpha _{j}^{{(i)}}(t)$ определяет долю людей, находящихся в комнате ${{R}_{i}}$ в момент времени $t$, которые собираются перейти в комнату ${{R}_{j}}$. Коэффициент $\alpha _{0}^{{(i)}}(t)$ задает долю людей, которые собираются остаться в комнате ${{R}_{i}}$.

Каждому переходу ${{T}_{{ij}}}$ сопоставлена тройка $({{v}_{{ij}}},{{F}_{{ij}}},{{w}_{{ij}}})$, где ${{v}_{{ij}}}\; \geqslant \;0$, ${{F}_{{ij}}}\; \geqslant \;0$, ${{w}_{{ij}}}\; \geqslant \;0$ – коэффициенты, подобные коэффициентам фундаментальной диаграммы (см. [3]), определяющие зависимость потока людей ${{f}_{{ij}}}(t)$ от плотности ${{\rho }_{{ij}}}(t)$: ${{f}_{{ij}}}(t) = {{f}_{{ij}}}({{\rho }_{{ij}}}(t))$, ${{v}_{{ij}}}$ характеризует скорость свободного движения, ${{w}_{{ij}}}$ – скорость распространения затора, ${{F}_{{ij}}}$ – максимальную пропускную способность перехода между комнатами.

Коэффициенты ${{v}_{{ij}}}$, ${{F}_{{ij}}}$, ${{w}_{{ij}}}$ в рассматриваемой задаче будем считать известными и постоянными. Оценку на их численные значения для каждого случая можно получить, например, с помощью способа, предложенного в [4], опирающегося на молекулярную модель взаимодействия из [9].

2.2. Пересчет числа людей в комнатах

Рассмотрим моменты времени $t = {{t}_{0}},{{t}_{0}} + \Delta t, \ldots $ и уравнения пересчета количеств людей ${{n}_{i}}$ в комнатах:

(1)

${{n}_{i}}(t + \Delta t) = {{n}_{i}}(t) + \Delta t\left( {\sum\limits_{{{T}_{{ji}}} \in \mathcal{T}} {{f}_{{ji}}}(t) - \sum\limits_{{{T}_{{ij}}} \in \mathcal{T}} {{f}_{{ij}}}(t)} \right)\quad \forall i = 1, \ldots ,N,$

где ${{f}_{{ij}}}(t)$ – поток людей на соединении ${{T}_{{ij}}}$ в момент времени $t$, где шаг $\Delta t > 0$ фиксирован, является решением задачи оптимизации

(2)

$\sum\limits_{{{T}_{{ij}}} \in \mathcal{T}} {{{f}_{{ij}}}} (t) \to \mathop {\max }\limits_{\{ {{f}_{{ij}}}\} } ,$

(3)

$0\;\leqslant \;{{f}_{{ij}}}(t)\;\leqslant \;{{F}_{{ij}}} - {{f}_{{ji}}}(t)\quad \forall i,j:{{T}_{{ij}}} \in \mathcal{T},$

(4)

${{f}_{{ij}}}(t)\;\leqslant \;\alpha _{j}^{{(i)}}(t){{v}_{{ij}}}\frac{{{{n}_{i}}(t)}}{{{{S}_{i}}}}\quad \forall i,j:{{T}_{{ij}}} \in \mathcal{T},$

(5)

$\sum\limits_{{{T}_{{ij}}} \in \mathcal{T}} \frac{{{{f}_{{ij}}}(t)}}{{{{w}_{{ij}}}}}\;\leqslant \;\left( {\frac{{{{C}_{j}} - {{n}_{j}}(t)}}{{{{S}_{j}}}}} \right)\quad \forall j.$

Неравенство (3) характеризует влияние противонаправленных потоков ${{f}_{{ij}}}$ и ${{f}_{{ji}}}$ друг на друга, (4) определяет количество желающих перейти из комнаты $i$ в комнату $j$, неравенство (5) является ограничением на суммарный входящий поток в $j$-ю комнату. Максимизация потоков (2) соответствует тому принципу, что люди всегда будут занимать с максимально возможной скоростью все доступное им свободное место, если это соответствует желаемому направлению их движения.

Замечание 3. В случае соединения ${{T}_{{ij}}}$ с возможным двусторонним движением будем считать, что ${{F}_{{ij}}} = {{F}_{{ji}}}$.

2.3. Решение задачи оптимизации

С учетом ограничений на противонаправленный поток (3) и суммарный входящий поток (5) задача линейного программирования (2)–(5) должна быть рассмотрена сразу для всех комнат одновременно, т.е. в общем случае ее нельзя разбить на несколько подзадач, относящихся к отдельным комнатам. Это значительно усложняет вычисления, а также существенно отличает рассматриваемую математическую модель от аналогичной транспортной модели, где потоки на перекрестках можно рассчитывать независимо.

Кроме того, решение может не быть единственным – это соответствует неопределенности в распределении потоков. Если в какой-либо комнате имеет место давка (неравенство (5) превращается в равенство), то, вообще говоря, существует бесконечное количество вариантов того, как при этом распределятся входящие в эту комнату потоки. Одним из выходов в этой ситуации является предположение о том, что входящие потоки должны быть пропорциональны спросу на свободное место в комнате со стороны соседних комнат (т.е. поток пропорционален размеру толпы на входе) или максимальным пропускным способностям (аналогично подходу из [10] для транспортной модели). Это приводит к необходимости вводить дополнительные параметры – коэффициенты приоритетов – и усложнять задачу оптимизации. В настоящей работе мы не будем использовать такой подход, а будем интерпретировать неоднозначность в определении потоков как неопределенность.

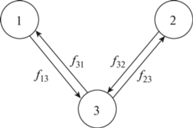
Пример. Рассмотрим три комнаты, причем комнаты с номерами $1$ и $2$ соединены с комнатой $3$, но не соединены между собой (фиг. 1).

Фиг. 1.

Схема помещения из примера.

Пусть ${{S}_{i}} = S$, ${{C}_{i}} = C$, $i = 1,2,3$, для каждого перехода ${{T}_{{ij}}}$: ${{v}_{{ij}}} = v$, ${{F}_{{ij}}} = F$, ${{w}_{{ij}}} = w$, и в некоторый момент $t$: $\alpha _{3}^{{(1)}}(t) = \alpha _{3}^{{(2)}} = 1$, $\alpha _{1}^{{(3)}}(t) = \alpha _{2}^{{(3)}}(t) = 1{\text{/}}2$, ${{n}_{1}}(t) = {{n}_{2}}(t) = {{n}_{3}}(t) = C{\text{/}}2$. Пусть также $v > 2w$. Требуется определить потоки ${{f}_{{13}}}(t)$, ${{f}_{{23}}}(t)$, ${{f}_{{31}}}(t)$, ${{f}_{{32}}}(t)$.

Решая задачу оптимизации (2)–(5), получим, что ${{f}_{{13}}} + {{f}_{{23}}} + {{f}_{{31}}} + {{f}_{{32}}} \to \max $ при условиях

(6)

${{f}_{{13}}} + {{f}_{{31}}}\;\leqslant \;F,\quad {{f}_{{23}}} + {{f}_{{32}}}\;\leqslant \;F,\quad {{f}_{{13}}} + {{f}_{{23}}}\;\leqslant \;\frac{{wC}}{{2S}},\quad {{f}_{{31}}}\;\leqslant \;\frac{{wC}}{{2S}},\quad {{f}_{{32}}}\;\leqslant \;\frac{{wC}}{{2S}}.$

Пусть $2F\;\leqslant \;wC{\text{/}}(2S)$. Тогда последние три неравенства в (6) являются следствием первых двух, а значит, максимальный суммарный поток равен $2F$, и максимум достигается в любой точке $({{f}_{{13}}},{{f}_{{31}}},{{f}_{{23}}},{{f}_{{32}}})$, для которой ${{f}_{{13}}} \in [0,F]$, ${{f}_{{23}}} \in [0,F]$, ${{f}_{{13}}} + {{f}_{{31}}} = F$, ${{f}_{{23}}} + {{f}_{{32}}} = F$.

Пусть теперь $wC{\text{/}}S\;\leqslant \;F$. Тогда, наоборот, первые два неравенства (6) с учетом неотрицательности потоков являются следствием из последних трех, а потому максимальный суммарный поток равен $3wC{\text{/}}(2S)$, и максимум достигается в любой точке $({{f}_{{13}}},{{f}_{{31}}},{{f}_{{23}}},{{f}_{{32}}})$, для которой ${{f}_{{13}}}\; \geqslant \;0$, ${{f}_{{23}}}\; \geqslant \;0$, ${{f}_{{13}}} + {{f}_{{23}}} = wC{\text{/}}(2S)$, ${{f}_{{31}}} = wC{\text{/}}(2S)$, ${{f}_{{32}}} = wC{\text{/}}(2S)$. Видим, что в двух разобранных случаях решение задачи оптимизации является неединственным.

Вне зависимости от предположений о распределении потоков в конфликтных ситуациях будем считать, что в каждый момент времени количество людей в той или иной комнате точно не известно. Можно построить оценку, используя особенности рассматриваемой математической модели, а также поступающие результаты измерений – неточную информацию о текущем количестве людей в некоторых комнатах, например, в результате обработки изображений с камер видеонаблюдения.

3. ОЦЕНИВАНИЕ МНОЖЕСТВА ДОСТИЖИМОСТИ

Предполагается, что задано некоторое начальное множество $\mathcal{X}({{t}_{0}})$ возможных значений переменных ${{n}_{i}}({{t}_{0}})$, $i = 1, \ldots ,N$. Множеством достижимости $\tilde {X}(t)$ (см. [11]) в некоторый момент времени $t\; \geqslant \;{{t}_{0}}$ называется множество, содержащее все векторы $\bar {n}(t) \in {{\mathbb{R}}^{N}}$, которые могут быть получены в качестве решений задач (1)–(5) для некоторого начального условия $\bar {n}({{t}_{0}}) \in \mathcal{X}({{t}_{0}})$. Поиск точного множества достижимости $\tilde {X}(t)$ для нелинейной системы является сложной задачей, поэтому будем искать $\mathcal{X}(t)$ – внешнюю оценку множества достижимости в некоторый момент времени $t\; \geqslant \;{{t}_{0}}$. На основании этой оценки можно будет судить о сложившейся ситуации, предсказывать места возможного возникновения давки и, в частности, анализировать качество предлагаемой стратегии управления. Далее будут описаны два разных вида таких множеств, задающих внешние оценки.

Основной идеей, использованной в указанных ниже алгоритмах, является разделение большой задачи линейного программирования (2)–(5) на множество более простых подзадач, относящихся к парам связанных между собой комнат, что позволяет легко интерпретировать получающиеся при решении соотношения геометрически.

3.1. Интервальные оценки

Предположим, что задано начальное множество $\mathcal{X}({{t}_{0}})$ возможных значений ${{n}_{i}}({{t}_{0}})$ во всех комнатах, являющееся декартовым произведением интервалов:

$\mathcal{X}({{t}_{0}}) = \{ [{{n}_{{i, - }}}({{t}_{0}}),{{n}_{{i, + }}}({{t}_{0}})],\;i = 1, \ldots ,N\} ,$

где $0\;\leqslant \;{{n}_{{i, - }}}({{t}_{0}})\;\leqslant \;{{n}_{{i, + }}}({{t}_{0}})\;\leqslant \;{{C}_{i}}$ – заданные величины. Необходимо найти внешнюю оценку множества $\mathcal{X}(t)$ в некоторый момент времени $t > {{t}_{0}}$ также в виде декартового произведения интервалов:

$\mathcal{X}(t) = \{ [{{n}_{{i, - }}}(t),\;{{n}_{{i, + }}}(t)],\;i = 1, \ldots ,N\} .$

Для любой траектории системы (1), для которой ${{n}_{i}}({{t}_{0}}) \in [{{n}_{{i, - }}}({{t}_{0}}),{{n}_{{i, + }}}({{t}_{0}})]$, $i = 1, \ldots ,N$, обязательно должно быть выполнено условие ${{n}_{i}}(t) \in [{{n}_{{i, - }}}(t),{{n}_{{i, + }}}(t)]$, $i = 1,\; \ldots ,\;N$ (подробнее о применении интервальных оценок для множества достижимости см. [12], [13]).

Фиксируем произвольный момент времени $t\; \geqslant \;{{t}_{0}}$, и будем считать, что множество $\mathcal{X}(t)$ уже найдено. Найдем множество $\mathcal{X}(t + \Delta t)$ в следующий момент времени. Для этого сперва необходимо вычислить потоки ${{f}_{{ij}}}(t)$ или же множество их значений $\{ {{f}_{{ij}}}(t)\} $, учитывая неединственность решения задачи и неопределенность в состоянии системы. Далее опишем алгоритм построения множеств возможных значений ${{f}_{{ij}}}(t)$.

1. Будем использовать вспомогательные переменные ${{\sigma }_{{ij}}}$ для всех $i$, $j$: ${{T}_{{ij}}} \in \mathcal{T}$. Изначально положим ${{\sigma }_{{ij}}} = 0$ $\forall i,j$. Переменная ${{\sigma }_{{ij}}}$ имеет смысл минимального суммарного входящего потока в комнату $j$ из комнат $k \ne i$, ${{T}_{{kj}}} \in \mathcal{T}$.

Для каждой пары $i,j$, ${{T}_{{ij}}} \in \mathcal{T}$, необходимо определить множество ${{\mathcal{F}}_{{ij}}} \subset \mathbb{R}_{ + }^{2}$, содержащее все возможные пары величин ${{f}_{{ij}}}$ и ${{f}_{{ji}}}$. Далее всюду предполагается, что для любой пары индексов $i$, $j$ множества ${{\mathcal{F}}_{{ij}}}$ и ${{\mathcal{F}}_{{ji}}}$ отличаются друг от друга лишь перестановкой компонент входящих в них векторов.

Изначально положим

(7)

${{\mathcal{F}}_{{ij}}} = \left\{ {({{f}_{{ij}}},{{f}_{{ji}}}):0\;\leqslant \;{{f}_{{ij}}}\;\leqslant \;{{F}_{{ij}}} - {{f}_{{ji}}},\;0\;\leqslant \;{{f}_{{ji}}}\;\leqslant \;{{F}_{{ji}}} - {{f}_{{ij}}}} \right\}.$

Зафиксируем некоторое значение параметра $\Theta \in \mathbb{N}$, а также положим $\theta = 1$. Параметр $\theta $ будет соответствовать номеру итерации основного цикла алгоритма, а $\Theta $ – максимальное количество таких итераций.

2. Необходимо уточнить множества ${{\mathcal{F}}_{{ij}}}$ так, чтобы были выполнены неравенства² ² (4), (5) с учетом вспомогательной переменной ${{\sigma }_{{ij}}}$:

(8)

${{f}_{{ij}}}\;\leqslant \;\alpha _{j}^{{(i)}}{{v}_{{ij}}}\frac{{{{n}_{i}}}}{{{{S}_{i}}}},\quad {{f}_{{ji}}}\;\leqslant \;\alpha _{i}^{{(j)}}{{v}_{{ji}}}\frac{{{{n}_{j}}}}{{{{S}_{j}}}},$

(9)

${{f}_{{ij}}}\;\leqslant \;{{w}_{{ij}}}\left( {\frac{{{{C}_{j}} - {{n}_{j}}}}{{{{S}_{j}}}}} \right) - {{\sigma }_{{ij}}},\quad {{f}_{{ji}}}\;\leqslant \;{{w}_{{ji}}}\left( {\frac{{{{C}_{i}} - {{n}_{i}}}}{{{{S}_{i}}}}} \right) - {{\sigma }_{{ji}}},$

для каких-либо значений $({{n}_{i}},{{n}_{j}}) \in \left[ {{{n}_{{i, - }}},{{n}_{{i, + }}}} \right] \times \left[ {{{n}_{{j, - }}},{{n}_{{j, + }}}} \right]$.

Сначала отдельно рассмотрим пару неравенств

${{f}_{{ij}}}\;\leqslant \;\alpha _{j}^{{(i)}}{{v}_{{ij}}}\frac{{{{n}_{i}}}}{{{{S}_{i}}}},\quad {{f}_{{ji}}}\;\leqslant \;{{w}_{{ji}}}\left( {\frac{{{{C}_{i}} - {{n}_{i}}}}{{{{S}_{i}}}}} \right) - {{\sigma }_{{ji}}}.$

При каждом фиксированном значении ${{n}_{i}}$ они определяют на плоскости $\left( {{{f}_{{ij}}},{{f}_{{ji}}}} \right)$, где ${{f}_{{ij}}}\; \geqslant \;0$, ${{f}_{{ji}}}\; \geqslant \;0$ – некоторый прямоугольник. Так как точное значение ${{n}_{i}}$ неизвестно, то построим объединение всех таких прямоугольников при ${{n}_{i}} \in [{{n}_{{i, - }}},{{n}_{{i, + }}}]$. Верхняя правая вершина таких прямоугольников будет находиться на прямой

$\frac{{{{f}_{{ij}}}{{S}_{i}}}}{{\alpha _{j}^{{(i)}}{{v}_{{ij}}}}} = {{C}_{i}} - \frac{{({{f}_{{ji}}} + {{\sigma }_{{ji}}}){{S}_{i}}}}{{{{w}_{{ji}}}}} \Leftrightarrow {{f}_{{ji}}} + \frac{{{{w}_{{ji}}}}}{{\alpha _{j}^{{(i)}}{{v}_{{ij}}}}}{{f}_{{ij}}} = \frac{{{{w}_{{ji}}}{{C}_{i}}}}{{{{S}_{i}}}} - {{\sigma }_{{ji}}}.$

Таким образом, искомое объединение прямоугольников ${{\hat {\mathcal{F}}}_{{ij}}}$ задается неравенствами

$\left\{ {\left( {{{f}_{{ij}}},{{f}_{{ji}}}} \right):{{f}_{{ij}}}\;\leqslant \;\alpha _{j}^{{(i)}}{{v}_{{ij}}}\frac{{{{n}_{{i, + }}}}}{{{{S}_{i}}}},\;{{f}_{{ji}}}\;\leqslant \;{{w}_{{ji}}}\left( {\frac{{{{C}_{i}} - {{n}_{{i, - }}}}}{{{{S}_{i}}}}} \right) - {{\sigma }_{{ji}}},\;{{f}_{{ji}}} + \frac{{{{w}_{{ji}}}}}{{\alpha _{j}^{{(i)}}{{v}_{{ij}}}}}{{f}_{{ij}}}\;\leqslant \;\frac{{{{w}_{{ji}}}{{C}_{i}}}}{{{{S}_{i}}}} - {{\sigma }_{{ji}}}} \right\}.$

Тогда уточненное множество ${{\mathcal{F}}_{{ij}}}$ можно представить в виде пересечения трех множеств

${{\mathcal{F}}_{{ij}}}: = {{\mathcal{F}}_{{ij}}} \cap {{\hat {\mathcal{F}}}_{{ij}}} \cap {{\hat {\mathcal{F}}}_{{ji}}}$

(формула для множества ${{\hat {\mathcal{F}}}_{{ij}}}$ отличается от ${{\hat {\mathcal{F}}}_{{ji}}}$ перестановкой индексов).

3. Предположим, что вычисления из предыдущего пункта проделаны для фиксированного $j$ и всех $k$ таких, что ${{T}_{{kj}}} \in \mathcal{T}$, т.е. известны множества ${{\mathcal{F}}_{{kj}}}$.

Множество ${{\mathcal{F}}_{{ij}}}$ может быть избыточным, так как содержит малые величины ${{f}_{{ij}}}$, ${{f}_{{ji}}}$, которые заведомо не являются решением задачи максимизации (2). Поэтому определим нижние границы на эти величины, учитывая, что движущиеся люди всегда по максимуму заполняют все доступное им свободное место. Допустимые значения потоков ${{f}_{{ij}}}$ и ${{f}_{{ji}}}$ задаются неравенствами

(10)

$0\;\leqslant \;{{f}_{{ij}}}\;\leqslant \;{{w}_{{ij}}}\left( {\frac{{{{C}_{j}} - {{n}_{j}}}}{{{{S}_{j}}}} - \sum\limits_{\substack{ k \ne i, \\ {{T}_{{kj}}} \in \mathcal{T} } } \frac{{{{f}_{{kj}}}}}{{{{w}_{{kj}}}}}} \right),\quad 0\;\leqslant \;{{f}_{{ji}}}\;\leqslant \;{{w}_{{ji}}}\left( {\frac{{{{C}_{i}} - {{n}_{i}}}}{{{{S}_{i}}}} - \sum\limits_{\substack{ m \ne j, \\ {{T}_{{mi}}} \in \mathcal{T} } } \frac{{{{f}_{{mi}}}}}{{{{w}_{{mi}}}}}} \right),$

(11)

${{f}_{{ij}}} + {{f}_{{ji}}}\;\leqslant \;{{F}_{{ij}}},\quad {{f}_{{ij}}}\;\leqslant \;\alpha _{j}^{{(i)}}{{v}_{{ij}}}\frac{{{{n}_{i}}}}{{{{S}_{i}}}},\quad {{f}_{{ji}}}\;\leqslant \;\alpha _{i}^{{(j)}}{{v}_{{ji}}}\frac{{{{n}_{j}}}}{{{{S}_{j}}}}.$

(a) Пусть в переходе между комнатами $i$ и $j$ допустимо движение в противоположных направлениях. Предположим, что нам известны величины ${{n}_{i}}$, ${{n}_{j}}$, ${{\bar {f}}_{{kj}}}$, ${{\bar {f}}_{{mi}}}$, где

Рассмотрим задачу линейного программирования ${{f}_{{ij}}} + {{f}_{{ji}}} \to \max $ при условиях (10), (11). Если неравенство

(12)

$\min \left\{ {\alpha _{j}^{{(i)}}{{v}_{{ij}}}\frac{{{{n}_{i}}}}{{{{S}_{i}}}},\;{{w}_{{ij}}}\left( {\frac{{{{C}_{j}} - {{n}_{j}}}}{{{{S}_{j}}}} - {{{\bar {f}}}_{{kj}}}} \right)} \right\} + \min \left\{ {\alpha _{i}^{{(j)}}{{v}_{{ji}}}\frac{{{{n}_{j}}}}{{{{S}_{j}}}},\;{{w}_{{ji}}}\left( {\frac{{{{C}_{i}} - {{n}_{i}}}}{{{{S}_{i}}}} - {{{\bar {f}}}_{{mi}}}} \right)} \right\}\;\leqslant \;{{F}_{{ij}}}$

выполнено, то решение этой задачи единственно. Найдем первую компоненту максимизатора

$f_{{ij}}^{*}\left( {{{n}_{i}},{{n}_{j}},{{{\bar {f}}}_{{kj}}},{{{\bar {f}}}_{{mi}}}} \right) = \min \left\{ {\alpha _{j}^{{(i)}}{{v}_{{ij}}}\frac{{{{n}_{i}}}}{{{{S}_{i}}}},\;{{w}_{{ij}}}\left( {\frac{{{{C}_{j}} - {{n}_{j}}}}{{{{S}_{j}}}} - {{{\bar {f}}}_{{kj}}}} \right)} \right\}.$

Если же указанное выше неравенство не выполнено, то решения задачи образуют отрезок прямой ${{f}_{{ij}}} + {{f}_{{ji}}} = {{F}_{{ij}}}$. В качестве компоненты максимизатора $f_{{ij}}^{*}\left( {{{n}_{i}},{{n}_{j}},{{{\bar {f}}}_{{kj}}},{{{\bar {f}}}_{{mi}}}} \right)$ возьмем ту точку этого отрезка, которая соответствует наименьшему значению ${{f}_{{ij}}}$:

$f_{{ij}}^{*}\left( {{{n}_{i}},{{n}_{j}},{{{\bar {f}}}_{{kj}}},{{{\bar {f}}}_{{mi}}}} \right) = {{F}_{{ij}}} - \min \left\{ {\alpha _{i}^{{(j)}}{{v}_{{ji}}}\frac{{{{n}_{j}}}}{{{{S}_{j}}}},\;{{w}_{{ji}}}\left( {\frac{{{{C}_{i}} - {{n}_{i}}}}{{{{S}_{i}}}} - {{{\bar {f}}}_{{mi}}}} \right)} \right\}.$

Теперь учтем, что параметры ${{n}_{i}}$, ${{n}_{j}}$, ${{\bar {f}}_{{kj}}}$, ${{\bar {f}}_{{mi}}}$ являются компонентами неопределенности. Следовательно, для потока ${{f}_{{ij}}}$ справедлива оценка

$\begin{gathered} {{f}_{{ij}}}\; \geqslant \;{{r}_{{ij}}} = \max \left\{ {0,\min \left\{ {f_{{ij}}^{*}\left( {{{n}_{i}},{{n}_{j}},{{{\bar {f}}}_{{kj}}},{{{\bar {f}}}_{{mi}}}} \right):{{n}_{i}}\mathop \in \limits_{} } \right.} \right.\;[{{n}_{{i, - }}},{{n}_{{i, + }}}],\;{{n}_{j}} \in [{{n}_{{j, - }}},{{n}_{{j, + }}}], \\ {{f}_{{kj}}} \in {{\Pr }_{1}}{{\mathcal{F}}_{{kj}}},\;{{f}_{{mi}}}\left. {\left. {\mathop \in \limits_{} {{{\Pr }}_{1}}{{\mathcal{F}}_{{mi}}},\;\forall k \ne i,\;m \ne j} \right\}} \right\}, \\ \end{gathered} $

где ${{\Pr }_{1}}{{\mathcal{F}}_{{kj}}} = \left\{ {{{f}_{{kj}}}} \right\}$. Используя геометрическую интерпретацию указанной выше задачи линейного программирования, легко установить, что минимум $f_{{ij}}^{*}$ будет достигаться при ${{n}_{j}} = {{n}_{{j, + }}}$, ${{n}_{i}}\;\; = \;\;{{n}_{{i, - }}}$, ${{f}_{{kj}}}\;\; = \;\;{{f}_{{kj,\max }}}$, ${{f}_{{mi}}}\;\; = \;\;{{f}_{{mi,\min }}}$. Здесь ${{f}_{{kj,\max }}}\;\; = \;\;\max \left\{ {{{f}_{{kj}}}:({{f}_{{kj}}},{{f}_{{jk}}}) \in {{\mathcal{F}}_{{kj}}}} \right\},\;{{f}_{{mi,\min }}}\;\; = $ $ = \min \left\{ {{{f}_{{mi}}}:({{f}_{{mi}}},{{f}_{{im}}}) \in {{\mathcal{F}}_{{mi}}}} \right\}$.

Аналогичную оценку можно выписать и для потока ${{f}_{{ji}}}$. Величина ${{r}_{{ij}}}$ имеет смысл гарантированного ресурса свободного места в ячейке $j$, который может быть использован людьми, идущими из ячейки $i$.

(б) Рассмотрим частный случай, когда в переходе между комнатами $i$ и $j$ движение является односторонним (из $i$-й комнаты в $j$-ю). Тогда ${{r}_{{ji}}} = 0$, а для ${{r}_{{ij}}}$ можно получить более простую формулу:

${{r}_{{ij}}} = 0 \vee \min \left\{ {\alpha _{j}^{{(i)}}{{v}_{{ij}}}\frac{{{{n}_{{i, - }}}}}{{{{S}_{i}}}},\;{{F}_{{ij}}},\;{{w}_{{ij}}}\left( {\left( {\frac{{{{C}_{j}} - {{n}_{{j, + }}}}}{{{{S}_{j}}}}} \right) - \sum\limits_{\substack{ k \ne i, \\ {{T}_{{kj}}} \in \mathcal{T} } } \frac{{{{f}_{{kj,\max }}}}}{{{{w}_{{kj}}}}}} \right)} \right\}.$

Если ${{r}_{{ij}}} > 0$, то модифицируем множество ${{\mathcal{F}}_{{ij}}}: = {{\mathcal{F}}_{{ij}}} \cap \left\{ {\left( {{{f}_{{ij}}},{{f}_{{ji}}}} \right):{{f}_{{ij}}}\; \geqslant \;{{r}_{{ij}}}} \right\}$.

Указанные модификации множеств ${{\mathcal{F}}_{{ij}}}$ проведем для всех возможных пар индексов $i,j$.

4. Если в п. 3 было изменено множество ${{\mathcal{F}}_{{kj}}}$ для некоторых значений индексов $k$, $j$ (т.е. увеличена нижняя граница возможного потока ${{f}_{{kj}}}$), то пересчитаем значение ${{\sigma }_{{ij}}}$ для фиксированного $j$ и разных $i \ne k$. А именно,

(13)

${{\sigma }_{{ij}}} = {{w}_{{ij}}}\sum\limits_{\substack{ k \ne i, \\ {{T}_{{kj}}} \in \mathcal{T} } } \frac{{{{f}_{{kj,\min }}}}}{{{{w}_{{kj}}}}} > 0.$

5. Если в п. 4 были изменены значения ${{\sigma }_{{ij}}}$ хотя бы для одной пары индексов $i$, $j$, и при этом $\theta < \Theta $, то значение $\theta $ увеличивается на 1, и алгоритм снова переходит к п. 2. Иначе алгоритм завершает работу, на выходе – совокупность множеств ${{\mathcal{F}}_{{ij}}}$.

Для полученных множеств справедливы следующие утверждения.

Теорема 1. Пусть $f_{{ij}}^{*}$ – какое-либо решение задачи оптимизации (2)–(5) в момент времени $t$ при условии, что истинное состояние системы находится в некоторой точке множества $\mathcal{X}(t)$. Тогда $f_{{ij}}^{*} \in {{\mathcal{F}}_{{ij}}}$ $\forall i,j$.

Теорема 2. Пусть комнаты с номерами $i$, $j$ являются частью системы связанных комнат с односторонним движением без разветвлений, т.е.

$\alpha _{j}^{{(i)}} = 1,\quad \alpha _{i}^{{(j)}} = 0,\quad \alpha _{j}^{{(k)}} = 0\quad \forall k \ne i.$

Тогда множество ${{\mathcal{F}}_{{ij}}}$ совпадет со множеством допустимых потоков ${{f}_{{ij}}}$, рассчитанным на основании интервальных оценок при моделировании транспортного потока (см. [14]):

(14)

${{f}_{{ij}}} \in \left[ {\max \left\{ {0,\;\min \left\{ {{{v}_{{ij}}}\frac{{{{n}_{{i, - }}}}}{{{{S}_{i}}}},\;{{F}_{{ij}}},\;{{w}_{{ij}}}\frac{{{{C}_{j}} - {{n}_{{j, + }}}}}{{{{S}_{j}}}}} \right\}} \right\},\;\min \left\{ {{{v}_{{ij}}}\frac{{{{n}_{{i, + }}}}}{{{{S}_{i}}}},\;{{F}_{{ij}}},\;{{w}_{{ij}}}\frac{{{{C}_{j}} - {{n}_{{j, - }}}}}{{{{S}_{j}}}}} \right\}} \right].$

Доказательство. Найдем допустимые значения ${{f}_{{ij}}}$, ${{f}_{{ji}}}$ с помощью приведенного алгоритма. В пунктах 1 и 2 получаем

${{f}_{{ji}}} = 0,\quad 0\;\leqslant \;{{f}_{{ij}}}\;\leqslant \;\min \left\{ {{{F}_{{ij}}},\;\alpha _{j}^{{(i)}}{{v}_{{ij}}}\frac{{{{n}_{{i, + }}}}}{{{{S}_{i}}}},\;{{w}_{{ij}}}\frac{{{{C}_{j}} - {{n}_{{j, - }}}}}{{{{S}_{j}}}}} \right\},\quad {{\sigma }_{{ij}}} = 0.$

Далее, в п. 3 алгоритма

${{r}_{{ij}}} = \max \left\{ {0,\;\min \left\{ {\alpha _{j}^{{(i)}}{{v}_{{ij}}}\frac{{{{n}_{{i, - }}}}}{{{{S}_{i}}}},\;{{F}_{{ij}}},\;{{w}_{{ij}}}\left( {\frac{{{{C}_{j}} - {{n}_{{j, + }}}}}{{{{S}_{j}}}}} \right)} \right\}} \right\},\quad {{f}_{{ij}}}\; \geqslant \;{{r}_{{ij}}}.$

В п. $4$ получим ${{\sigma }_{{ij}}} = 0$, а потому на дальнейших итерациях работы алгоритма (при $\theta > 1$) уточнение верхней оценки для ${{f}_{{ij}}}$ не проводится. Объединяя полученные неравенства и учитывая $\alpha _{j}^{{(i)}} = 1$, получим (14). Теорема доказана.

В итоге на основании оценки потоков можно аппроксимировать множества достижимости

$\mathcal{X}(t + \Delta t) = \left\{ {[{{n}_{{i, - }}}(t + \Delta t),{{n}_{{i, + }}}(t + \Delta t)],\;i = 1, \ldots ,N} \right\},$

${{n}_{{i, - }}}(t + \Delta t) = \max \left\{ {0,\;{{n}_{{i, - }}}(t) + \Delta t\sum\limits_{{{T}_{{ij}}} \in \mathcal{T}} {\min } \left\{ {{{f}_{{ji}}} - {{f}_{{ij}}}:\left( {{{f}_{{ij}}},{{f}_{{ji}}}} \right) \in {{\mathcal{F}}_{{ij}}}} \right\}} \right\},$

${{n}_{{i, + }}}(t + \Delta t) = \min \left\{ {{{C}_{i}},\;{{n}_{{i, + }}}(t) + \Delta t\sum\limits_{{{T}_{{ij}}} \in \mathcal{T}} {\max } \left\{ {{{f}_{{ji}}} - {{f}_{{ij}}}:\left( {{{f}_{{ij}}},{{f}_{{ji}}}} \right) \in {{\mathcal{F}}_{{ij}}}} \right\}} \right\}.$

Замечание 4. Рассмотрим частный случай, когда ${{w}_{{ij}}} = w$ $\forall i,j$, и для некоторого номера $i$ выполнено следующее неравенство:

$\sum\limits_{j:{{T}_{{ji}}} \in \mathcal{T}} {\min } \left\{ {\alpha _{i}^{{(j)}}{{v}_{{ji}}}\frac{{{{n}_{{j, - }}}}}{{{{S}_{j}}}},\;{{F}_{{ji}}} - {{f}_{{ji,\max }}}} \right\}\; \geqslant \;w\frac{{{{C}_{i}} - {{n}_{{i, - }}}}}{{{{S}_{i}}}}.$

Тогда для реальных потоков неравенство (5) обязательно должно обратиться в равенство (это условие затора на входах в комнату с номером $i$). Значит, суммарный входящий поток будет не меньше, чем $w({{C}_{i}} - {{n}_{{i, - }}}{\text{)/}}{{S}_{i}}$, т.е.

${{n}_{{i, - }}}(t + \Delta t): = \max \left\{ {{{n}_{{i, - }}}(t + \Delta t),\;{{n}_{{i, - }}}(t) + \Delta t\left( {w\frac{{{{C}_{i}} - {{n}_{{i, - }}}}}{{{{S}_{i}}}} - \sum\limits_{{{T}_{{ij}}} \in \mathcal{T}} {{f}_{{ij,\max }}}} \right)} \right\},$

где в правой части ${{n}_{{i, - }}}(t + \Delta t)$ – ранее полученная оценка. Эта формула в отдельных случаях позволяет улучшить оценку снизу на величину ${{n}_{i}}$.

3.2. Оценки двумерных проекций

Из приведенных выше уравнений видно, что потоки ${{f}_{{ij}}}$ и ${{f}_{{ji}}}$ одновременно зависят от двух фазовых переменных: ${{n}_{i}}$ и ${{n}_{j}}$. В случае интервальных оценок эти переменные аппроксимируются с помощью двух независимых отрезков – одномерных проекций множества достижимости. Однако, если их заменить на двумерные, можно получить более качественные оценки.

Теперь рассмотрим оценки множества достижимости вида

$\mathcal{X}(t) = \left\{ {{{\mathcal{N}}_{{ij}}}(t),\;i,j = 1, \ldots ,N:{{T}_{{ij}}} \in \mathcal{T}} \right\},$

где ${{\mathcal{N}}_{{ij}}}(t) \subset \left[ {0,{{C}_{i}}} \right] \times \left[ {0,{{C}_{j}}} \right]$ – некоторое компактное множество, содержащее возможные значения пары переменных $({{n}_{i}}(t),{{n}_{j}}(t))$. Будем далее считать, что множество ${{\mathcal{N}}_{{ij}}}(t)$ является выпуклым многоугольником, задаваемым совокупностью своих вершин ${{g}^{{(ij,1)}}}(t), \ldots ,{{g}^{{(ij,m)}}}(t)$, где $m = m(t,i,j) \in \mathbb{N}$.

Далее приведем алгоритм построения оценки возможных значений потоков ${{f}_{{ij}}}(t)$ при условии, что в некоторый произвольный момент времени $t\; \geqslant \;{{t}_{0}}$ заданы множества ${{\mathcal{N}}_{{ij}}}(t)$ указанного выше вида.

1. Как и в случае интервальных оценок, будем использовать вспомогательные переменные ${{\sigma }_{{ij}}}$ для всех $i$, $j$, ${{T}_{{ij}}} \in \mathcal{T}$. Изначально положим ${{\sigma }_{{ij}}} = 0$ $\forall i,j$.

Для каждой пары $i,j$, ${{T}_{{ij}}} \in \mathcal{T}$, необходимо определить множество ${{\mathcal{F}}_{{ij}}} \subset \mathbb{R}_{ + }^{2}$, содержащее все возможные пары величин ${{f}_{{ij}}}$ и ${{f}_{{ji}}}$. Множества ${{\mathcal{F}}_{{ij}}}$ и ${{\mathcal{F}}_{{ji}}}$ отличаются друг от друга лишь перестановкой компонент входящих в них векторов.

Изначально определим множества ${{\mathcal{F}}_{{ij}}}$ аналогично формуле (7).

Зафиксируем некоторое значение параметра $\Theta \in \mathbb{N}$, а также положим $\theta = 1$.

2. Необходимо уточнить множества ${{\mathcal{F}}_{{ij}}}$ так, чтобы были выполнены неравенства (8), (9) для какой-либо пары значений $({{n}_{i}},{{n}_{j}}) \in {{\mathcal{N}}_{{ij}}}(t)$. Пусть

(15)

$\begin{gathered} {{{\hat {\mathcal{F}}}}_{{ij}}} = \bigcup\limits_{({{n}_{i}},{{n}_{j}}) \in {{\mathcal{N}}_{{ij}}}(t)} \left\{ {{{{\left( {{{f}_{{ij}}},{{f}_{{ji}}}} \right)}}^{T}}:0\;\leqslant \;{{f}_{{ij}}}\;\leqslant \;\min \left\{ {\alpha _{j}^{{(i)}}{{v}_{{ij}}}\frac{{{{n}_{i}}}}{{{{S}_{i}}}},\;{{w}_{{ij}}}\left( {\frac{{{{C}_{j}} - {{n}_{j}}}}{{{{S}_{j}}}}} \right) - {{\sigma }_{{ij}}}} \right\}} \right., \\ 0\;\leqslant \;{{f}_{{ji}}}\;\leqslant \;\min \left. {\left\{ {\alpha _{i}^{{(j)}}{{v}_{{ji}}}\frac{{{{n}_{j}}}}{{{{S}_{j}}}},\;{{w}_{{ji}}}\left( {\frac{{{{C}_{i}} - {{n}_{i}}}}{{{{S}_{i}}}}} \right) - {{\sigma }_{{ji}}}} \right\}} \right\}. \\ \end{gathered} $

Тогда уточненное множество ${{\mathcal{F}}_{{ij}}}$ можно представить в виде ${{\mathcal{F}}_{{ij}}}: = {{\mathcal{F}}_{{ij}}} \cap {{\hat {\mathcal{F}}}_{{ij}}} \cap {{\hat {\mathcal{F}}}_{{ji}}}.$ Покажем, как можно построить выпуклые многоугольники, оценивающие сверху множества ${{\hat {\mathcal{F}}}_{{ij}}}$. Введем обозначения для двух вспомогательных прямых на плоскости:

${{H}_{1}} = \left\{ {{{{({{n}_{i}},{{n}_{j}})}}^{T}}:\alpha _{j}^{{(i)}}{{v}_{{ij}}}\frac{{{{n}_{i}}}}{{{{S}_{i}}}} = {{w}_{{ij}}}\left( {\frac{{{{C}_{j}} - {{n}_{j}}}}{{{{S}_{j}}}}} \right) - {{\sigma }_{{ij}}}} \right\},$

${{H}_{2}} = \left\{ {{{{({{n}_{i}},{{n}_{j}})}}^{T}}:\alpha _{i}^{{(j)}}{{v}_{{ji}}}\frac{{{{n}_{j}}}}{{{{S}_{j}}}} = {{w}_{{ji}}}\left( {\frac{{{{C}_{i}} - {{n}_{i}}}}{{{{S}_{i}}}}} \right) - {{\sigma }_{{ji}}}} \right\}.$

Эти прямые разбивают ${{\mathcal{N}}_{{ij}}}(t)$ на несколько многоугольных частей (не более четырех), в каждой из которых оба минимума из (15) раскрываются однозначно. Вершины $k$-й такой части обозначим через ${{z}^{{(k),1}}}, \ldots ,{{z}^{{(k),{{s}_{k}}}}}$. Рассмотрим опорную функцию³ ³ ко множеству ${{\mathcal{F}}_{{ij}}}$ в направлении $l \in {{\mathbb{R}}^{2}}$:

(16)

$\begin{gathered} \rho \left( {l\,|\,{{{\hat {\mathcal{F}}}}_{{ij}}}} \right) = \mathop {\sup }\limits_{({{n}_{i}},{{n}_{j}}) \in {{\mathcal{N}}_{{ij}}}(t)} \left\{ {\max \left\{ {0,{{l}_{1}}\min \left\{ {\alpha _{j}^{{(i)}}{{v}_{{ij}}}\frac{{{{n}_{i}}}}{{{{S}_{i}}}},{{w}_{{ij}}}\frac{{{{C}_{j}} - {{n}_{j}}}}{{{{S}_{j}}}} - {{\sigma }_{{ij}}}} \right\}} \right\}} \right. + \\ + \;\max \left. {\left\{ {0,{{l}_{2}}\min \left\{ {\alpha _{i}^{{(j)}}{{v}_{{ji}}}\frac{{{{n}_{j}}}}{{{{S}_{j}}}},{{w}_{{ji}}}\frac{{{{C}_{i}} - {{n}_{i}}}}{{{{S}_{i}}}} - {{\sigma }_{{ji}}}} \right\}} \right\}} \right\}. \\ \end{gathered} $

Здесь нужно учесть, что если какая-то из упомянутых выше четырех частей множества ${{\mathcal{N}}_{{ij}}}(t)$ пуста, то соответствующий максимум по ее вершинам отсутствует. Таким образом, ${{\hat {\mathcal{F}}}_{{ij}}}$ представляет собой многоугольник, являющийся выпуклой оболочкой точек

${{(0,0)}^{T}},\quad {{\left( {\alpha _{j}^{{(i)}}{{v}_{{ij}}}\frac{{z_{1}^{{(1),s}}}}{{{{S}_{i}}}},\;\alpha _{i}^{{(j)}}{{v}_{{ji}}}\frac{{z_{2}^{{(1),s}}}}{{{{S}_{j}}}}} \right)}^{T}},\quad {{\left( {\alpha _{j}^{{(i)}}{{v}_{{ij}}}\frac{{z_{1}^{{(2),s}}}}{{{{S}_{i}}}},\;{{w}_{{ji}}}\frac{{{{C}_{i}} - z_{1}^{{(2),s}}}}{{{{S}_{i}}}} - {{\sigma }_{{ji}}}} \right)}^{T}},$

${{\left( {{{w}_{{ij}}}\frac{{{{C}_{j}} - z_{2}^{{(3),s}}}}{{{{S}_{j}}}} - {{\sigma }_{{ij}}},\;\alpha _{i}^{{(j)}}{{v}_{{ji}}}\frac{{z_{2}^{{(3),s}}}}{{{{S}_{j}}}}} \right)}^{T}},\quad {{\left( {{{w}_{{ij}}}\frac{{{{C}_{j}} - z_{2}^{{(4),s}}}}{{{{S}_{j}}}} - {{\sigma }_{{ij}}},\;{{w}_{{ji}}}\frac{{{{C}_{i}} - z_{1}^{{(4),s}}}}{{{{S}_{i}}}} - {{\sigma }_{{ji}}}} \right)}^{T}},$

${{\left( {0,\;\mathop {\max }\limits_s \left\{ {\alpha _{i}^{{(j)}}{{v}_{{ji}}}\frac{{z_{2}^{{(1),s}}}}{{{{S}_{j}}}},\;{{w}_{{ji}}}\frac{{{{C}_{i}} - z_{1}^{{(2),s}}}}{{{{S}_{i}}}} - {{\sigma }_{{ji}}},\;\alpha _{i}^{{(j)}}{{v}_{{ji}}}\frac{{z_{2}^{{(3),s}}}}{{{{S}_{j}}}},\;{{w}_{{ji}}}\frac{{{{C}_{i}} - z_{1}^{{(4),s}}}}{{{{S}_{i}}}} - {{\sigma }_{{ji}}}} \right\}} \right)}^{T}},$

${{\left( {\mathop {\max }\limits_s \left\{ {\alpha _{j}^{{(i)}}{{v}_{{ij}}}\frac{{z_{1}^{{(1),s}}}}{{{{S}_{i}}}},\;\alpha _{j}^{{(i)}}{{v}_{{ij}}}\frac{{z_{1}^{{(2),s}}}}{{{{S}_{i}}}},\;{{w}_{{ij}}}\frac{{{{C}_{j}} - z_{2}^{{(3),s}}}}{{{{S}_{j}}}} - {{\sigma }_{{ij}}},\;{{w}_{{ij}}}\frac{{{{C}_{j}} - z_{2}^{{(4),s}}}}{{{{S}_{j}}}} - {{\sigma }_{{ij}}}} \right\},\;0} \right)}^{T}},$

где $s$ – вершины соответствующего многоугольника с номером $k = 1,2,3,4$.

3. Предположим, что известны множества ${{\mathcal{F}}_{{kj}}}$. Уточним множество ${{\mathcal{F}}_{{ij}}}$ аналогично тому, как это было сделано в случае с интервальными оценками.

(a) Пусть в переходе между комнатами $i$ и $j$ допустимо движение в двух противоположных направлениях. Определим величины

${{f}_{{kj,\max }}} = \max \left\{ {{{f}_{{kj}}}:{{{\left( {{{f}_{{kj}}},{{f}_{{jk}}}} \right)}}^{T}} \in {{\mathcal{F}}_{{kj}}}} \right\},\quad {{f}_{{mi,\min }}} = \min \left\{ {{{f}_{{mi}}}:{{{\left( {{{f}_{{mi}}},{{f}_{{im}}}} \right)}}^{T}} \in {{\mathcal{F}}_{{mi}}}} \right\}.$

Рассмотрим разные варианты раскрытия минимумов в левой части (12) и найдем минимальные значения величины $f_{{ij}}^{*}$. Пусть ${{N}_{1}}$ – это та часть множества ${{\mathcal{N}}_{{ij}}}(t)$, для которой выполнено неравенство

и ${{N}_{2}} = {{\mathcal{N}}_{{ij}}}(t){{\backslash }}{{N}_{1}}$. Подсчитаем следующие величины:

Теперь определим величину

${{r}_{{ij}}} = 0 \vee \min \left\{ {{{F}_{1}},{{F}_{2}}} \right\}.$

Как и в предыдущем разделе, эта величина имеет смысл максимального гарантированного ресурса свободного места в комнате $j$, который будет использован людьми из комнаты $i$.

(б) Рассмотрим частный случай, когда в переходе между комнатами $i$ и $j$ движение является односторонним, из $i$-й в $j$-ю. Тогда ${{r}_{{ji}}} = 0$,

Если ${{r}_{{ij}}} > 0$, то модифицируем множество ${{\mathcal{F}}_{{ij}}}: = {{\mathcal{F}}_{{ij}}} \cap \left\{ {({{f}_{{ij}}},{{f}_{{ji}}}):{{f}_{{ij}}}\; \geqslant \;{{r}_{{ij}}}} \right\}.$ Аналогичные модификации ${{\mathcal{F}}_{{ij}}}$ проведем для всех возможных пар $i$, $j$.

4. Если в п. 3 было изменено множество ${{\mathcal{F}}_{{kj}}}$ для некоторых значений индексов $k$, $j$, то пересчитаем значение ${{\sigma }_{{ij}}}$ для фиксированного $j$ и разных $i \ne k$ по формуле (13).

На основании оценки потоков можно аппроксимировать множества достижимости в момент времени $t + \Delta t$. При этом для потоков между двумя соседними комнатами $i$ и $j$ будем использовать оценку в виде многоугольника ${{\mathcal{F}}_{{ij}}}$, а для внешних (относительно $i$-й и $j$-й комнат) – интервальную оценку. В итоге получаем

$\mathcal{X}(t + \Delta t) = \{ {{\mathcal{N}}_{{ij}}}(t + \Delta t),\;i,j = 1, \ldots ,N:{{T}_{{ij}}} \in \mathcal{T}\} ,$

${{\mathcal{N}}_{{ij}}}(t + \Delta t) = \left( {{{\mathcal{N}}_{{ij}}}(t) + \Delta t\left( {C{{\mathcal{F}}_{{ij}}} + {{f}_{{ij,{\text{ext}}}}}(t)} \right)} \right) \cap \left( {[0,{{C}_{i}}] \times [0,{{C}_{j}}]} \right),\quad C = \left( {\begin{array}{*{20}{c}} { - 1}&1 \\ 1&{ - 1} \end{array}} \right),$

${{f}_{{ij,{\text{ext}}}}}(t) = \left[ {{{f}_{{ji,{\text{ext}}, - }}},{{f}_{{ji,{\text{ext}}, + }}}} \right] \times \left[ {{{f}_{{ij,{\text{ext}}, - }}},{{f}_{{ij,{\text{ext}}, + }}}} \right],$

${{f}_{{ji,{\text{ext}}, - }}} = \sum\limits_{k \ne j:{{T}_{{ki}}} \in \mathcal{T}} {\mathop {\min }\limits_{{{{({{f}_{{ki}}},{{f}_{{ik}}})}}^{T}} \in {{\mathcal{F}}_{{ki}}}} \{ {{f}_{{ki}}} - {{f}_{{ik}}}\} } ,\quad {{f}_{{ji,{\text{ext}}, + }}} = \sum\limits_{k \ne j:{{T}_{{ki}}} \in \mathcal{T}} \mathop {\max }\limits_{{{{({{f}_{{ki}}},{{f}_{{ik}}})}}^{T}} \in {{\mathcal{F}}_{{ki}}}} \{ {{f}_{{ki}}} - {{f}_{{ik}}}\} .$

Так как линейная комбинация выпуклых многоугольников является выпуклым многоугольником, то множество ${{\mathcal{N}}_{{ij}}}(t + \Delta t)$ – выпуклый многоугольник. Его вершины можно найти из приведенных выше формул, зная вершины ${{\mathcal{N}}_{{ij}}}(t)$ и ${{\mathcal{F}}_{{ij}}}$.

Замечание 5. Полученные оценки можно улучшить за счет сопоставления между собой полученных множеств, соответствующих соседним парам комнат (т.е. множеств вида ${{\mathcal{N}}_{{ij}}}(t + \Delta t)$ и ${{\mathcal{N}}_{{ik}}}(t + \Delta t)$). Для каждой пары $i$, $j$ положим

${{\mathcal{N}}_{{ij}}}(t + \Delta t): = {{\mathcal{N}}_{{ij}}}(t + \Delta t) \cap ([{{n}_{{ij,{\text{ext}}, - }}},{{n}_{{ij,{\text{ext}}, + }}}] \times [{{n}_{{ji,{\text{ext}}, - }}},{{n}_{{ji,{\text{ext}}, + }}}]),$

${{n}_{{ij,{\text{ext}}, - }}} = \mathop {\max }\limits_{k \ne j,{{T}_{{ik}}} \in \mathcal{T}} \min \left\{ {{{n}_{i}}:({{n}_{i}},{{n}_{k}}) \in {{\mathcal{N}}_{{ik}}}(t + \Delta t)} \right\},$

${{n}_{{ij,{\text{ext}}, + }}} = \mathop {\min }\limits_{k \ne j,{{T}_{{ik}}} \in \mathcal{T}} \max \left\{ {{{n}_{i}}:({{n}_{i}},{{n}_{k}}) \in {{\mathcal{N}}_{{ik}}}(t + \Delta t)} \right\}.$

Данную процедуру можно проводить до тех пор, пока на каждой итерации хотя бы одна из оценок ${{\mathcal{N}}_{{ij}}}(t + \Delta t)$ изменяется (уточняется).

3.3. Количество вершин в многоугольных оценках ${{\mathcal{N}}_{{ij}}}(t)$

В описанном алгоритме построения оценок множества достижимости в форме выпуклых многоугольников может иметь место эффект увеличения с течением времени количеств вершин, задающих многоугольники ${{\mathcal{N}}_{{ij}}}(t)$. Это может привести к значительному росту вычислительной сложности при больших значениях $t > {{t}_{0}}$. Для решения этой проблемы можно на отдельных шагах алгоритма после подсчета очередного набора оценок ${{\mathcal{N}}_{{ij}}}(t + \Delta t)$ дополнительно огрублять их, уменьшая количество используемых вершин.

Пусть $\nu \in \mathbb{N}$ – фиксированное число, задающее максимально допустимое количество вершин многоугольника, ${{g}^{{(ij,1)}}},\; \ldots ,\;{{g}^{{(ij,m)}}}$ – вершины многоугольника ${{\mathcal{N}}_{{ij}}}(t + \Delta t)$. Пусть $m > \nu $, опишем алгоритм удаления вершины (индексы $ij$ опущены для краткости).

1. Для каждой стороны $\left[ {{{g}^{{(k)}}},{{g}^{{(k + 1)}}}} \right]$ (индексацию следует брать по модулю $m$) вычисляется ${{\tilde {g}}^{k}}$ – точка пересечения лучей $\left[ {{{g}^{{(k - 1)}}},{{g}^{{(k)}}}} \right]$ и $\left[ {{{g}^{{(k + 2)}}},{{g}^{{(k + 1)}}}} \right]$.

2. Для всех треугольников c вершинами вида ${{\tilde {g}}^{k}},{{g}^{{(k)}}},{{g}^{{(k + 1)}}}$ вычисляются площади.

3. Находим сторону $\left[ {{{{\bar {g}}}^{{(k)}}},{{{\bar {g}}}^{{(k + 1)}}}} \right]$, на которой располагается треугольник наименьшей площади.

4. Пару вершин ${{\bar {g}}^{{(k)}}},{{\bar {g}}^{{(k + 1)}}}$ в многоугольной оценке заменяем на найденную точку ${{\tilde {g}}^{k}}$.

Указанный алгоритм применяется до тех пор, пока количество вершин не станет равным заданному числу $\nu $. На выходе получаем многоугольник ${{\tilde {\mathcal{N}}}_{{ij}}}(t + \Delta t)$ c $m = \nu $ вершинами. Легко видеть, что ${{\mathcal{N}}_{{ij}}}(t + \Delta t) \subseteq {{\tilde {\mathcal{N}}}_{{ij}}}(t + \Delta t)$.

4. УЧЕТ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Рассмотрим теперь ситуацию, когда в некоторый момент времени $t$ появляется неточная информация (оценка) о количестве людей в комнате $i$. Например, это могут быть результаты обработки изображений, полученных с видеокамер. С точки зрения рассматриваемой математической модели можно использовать уравнение измерения

(17)

${{y}_{i}}(t) = {{n}_{i}}(t) + {{\xi }_{i}}(t).$

Здесь ${{\xi }_{i}}(t)$ – помеха измерения, относительно которой известны ограничения $\left| {{{\xi }_{i}}(t)} \right|\leqslant \Xi $, где константа $\Xi $ считается заданной и не зависит от номера комнаты или момента времени. Таким образом, ${{n}_{i}}(t) \in \left[ {{{y}_{i}}(t) - \Xi ,{{y}_{i}}(t) + \Xi } \right]$.

Поступившие результаты измерений могут быть использованы для уточнения текущей оценки величины ${{n}_{i}}(t)$. В случае с интервальными оценками такое уточнение выглядит следующим образом:

${{\tilde {n}}_{i}}(t) \in \left[ {{{{\tilde {n}}}_{{i, - }}}(t),{{{\tilde {n}}}_{{i, + }}}(t)} \right] = \left[ {{{n}_{{i, - }}}(t),{{n}_{{i, + }}}(t)} \right] \cap \left[ {{{y}_{i}}(t) - \Xi ,{{y}_{i}}(t) + \Xi } \right].$

Будем считать, что результаты измерений не противоречат математической модели, и потому полученное пересечение отрезков не пусто.

В случае с оценками двумерных проекций множества достижимости результаты измерений могут быть использованы следующим образом:

Заметим, что в отдельных случаях результаты измерения количества людей в комнате с номером $i$ могут быть также использованы для уточнения оценок величин ${{n}_{j}}(t)$, соответствующих соседним комнатам. Например, если используются интервальные оценки и известны оценки ${{\mathcal{F}}_{{ij}}}$ потоков, то

${{\tilde {n}}_{{j, - }}}(t) = \max \left\{ {{{n}_{{j, - }}}(t),\;{{n}_{{j, - }}}(t - \Delta t) + \Delta t\sum\limits_{{{T}_{{jk}}} \in \mathcal{T},k \ne i} {\min } \{ {{f}_{{kj}}} - {{f}_{{jk}}}:({{f}_{{jk}}},{{f}_{{kj}}}) \in {{\mathcal{F}}_{{jk}}}\} + {{s}_{{ij, - }}}} \right\},$

${{\tilde {n}}_{{j, + }}}(t) = \min \left\{ {{{n}_{{j, + }}}(t),\,{{n}_{{j, + }}}(t - \Delta t) + \Delta t\sum\limits_{{{T}_{{jk}}} \in \mathcal{T},k \ne i} {\max } \left\{ {{{f}_{{kj}}} - {{f}_{{jk}}}:({{f}_{{jk}}},{{f}_{{kj}}}) \in {{\mathcal{F}}_{{jk}}}} \right\} + {{s}_{{ij, + }}}} \right\},$

${{s}_{{ij, - }}} = {{\tilde {n}}_{{i, - }}}(t) - {{n}_{{i, + }}}(t - \Delta t) + \Delta t\sum\limits_{{{T}_{{ik}}} \in \mathcal{T},k \ne j} {\min } \left\{ {{{f}_{{ki}}} - {{f}_{{ik}}}:\left( {{{f}_{{ik}}},{{f}_{{ki}}}} \right) \in {{\mathcal{F}}_{{ik}}}} \right\},$

${{s}_{{ij, + }}} = {{\tilde {n}}_{{i, + }}}(t) - {{n}_{{i, - }}}(t - \Delta t) + \Delta t\sum\limits_{{{T}_{{ik}}} \in \mathcal{T},k \ne j} {\max } \{ {{f}_{{ki}}} - {{f}_{{ik}}}:({{f}_{{ik}}},{{f}_{{ki}}}) \in {{\mathcal{F}}_{{ik}}}\} .$

5. РЕЗУЛЬТАТЫ РАБОТЫ ПРОГРАММЫ

Для численной иллюстрации двух алгоритмов возьмем ранее приведенный пример, граф которого изображен на фиг. 1. Пусть $n = 10$, $S = 15$, $C = 20$, $v = 1.2$, $w = 0.5$, $F = 3$, параметры $\alpha _{3}^{{(1)}} = \alpha _{3}^{{(2)}} = 1$, $\alpha _{1}^{{(3)}} = \alpha _{2}^{{(3)}} = 1{\text{/}}2$ считаем не зависящими от времени.

Построим оценку множества достижимости $\mathcal{X}(t)$ двумя способами с шагом $\Delta t = 4$ из начального состояния в момент времени ${{t}_{0}} = 0$, при котором точно известно начальное количество людей в каждой комнате ${{n}_{{i, - }}} = {{n}_{{i, + }}} = 10$, $i = 1,2,3$. Далее достаточно рассмотреть ситуацию в переходе ${{T}_{{13}}}$ (${{T}_{{31}}}$), в соседнем переходе ${{T}_{{23}}}$ ситуация будет в точности повторяться из-за симметричности схемы помещения и начальных условий.

Пересчитывая количества людей в комнатах ${{n}_{i}}(t)$ с помощью интервальных оценок потоков, получаем набор отрезков $\left\{ {\left[ {{{n}_{{i, - }}}(t),{{n}_{{i, + }}}(t)} \right]} \right\}$, $t > 0$. Для удобного сравнения двух подходов изобразим декартово произведение отрезков $\left\{ {\left[ {{{n}_{{1, - }}}(t),{{n}_{{1, + }}}(t)} \right]} \right\}$ и $\left\{ {\left[ {{{n}_{{3, - }}}(t),{{n}_{{3, + }}}(t)} \right]} \right\}$ на плоскости $({{n}_{1}},{{n}_{3}})$ (фиг. 2a).

Фиг. 2.

Эволюция проекции оценки множества достижимости на плоскость $({{n}_{1}},{{n}_{3}})$: (a) – интервальные оценки, (б) – двумерные проекции.

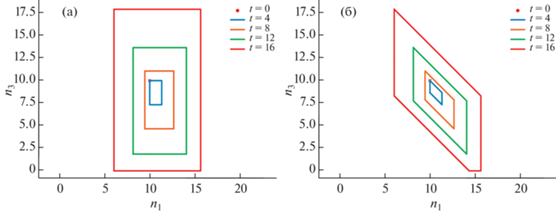
Уточним множества возможных потоков до пересчета ${{n}_{{i, - }}}$, ${{n}_{{i, + }}}$ в момент времени $t = 4$. Так как выполняется $wC{\text{/}}S\leqslant F$, в результате работы первого алгоритма получаем оценку ${{\mathcal{F}}_{{13}}} = \left\{ {({{f}_{{13}}},{{f}_{{31}}}):0\;\leqslant \;{{f}_{{13}}}\;\leqslant \;1{\text{/}}3,\;{{f}_{{31}}} = 1{\text{/}}3} \right\}$ (множество ${{\mathcal{F}}_{{31}}}$ отличается от ${{\mathcal{F}}_{{13}}}$ перестановкой компонент). Далее, так как $\min \left\{ {{{f}_{{31}}} - {{f}_{{13}}}} \right\} = \max \left\{ {{{f}_{{13}}} - {{f}_{{31}}}} \right\} = 0$, ${{n}_{{1, - }}}$ не уменьшается, а ${{n}_{{3, + }}}$ не увеличивается. Это соответствует тому, что при рассматриваемых параметрах модели из третьей комнаты в первую переходит больше человек, чем в противоположном направлении. В следующие моменты времени такая ситуация не наблюдается, так как значение ${{n}_{i}}$ известно неточно, поэтому нижняя граница ${{n}_{{1, - }}}$ начнет уменьшаться, а верхняя ${{n}_{{3, + }}}$ увеличиваться.

Применение двумерных проекций в данном случае позволяет одновременно учитывать увеличение и уменьшение значения потоков в двух комнатах. Это можно интерпретировать следующим образом: при пересчете значений ${{n}_{i}}$ мы сразу же учитываем то, что если, например, увеличилось ${{n}_{1}}$, то при этом обязательно должно уменьшиться ${{n}_{3}}$, оно в данном случае никак не может остаться неизменным, так как в комнату 1 нет других входящих переходов, кроме ${{T}_{{31}}}$. Таким образом, получается более сложная оценка в виде выпуклого многоугольника ${{\mathcal{N}}_{{13}}}$ (фиг. 2б). Заметим, что одномерные проекции $\left[ {{{n}_{{1, - }}},{{n}_{{1, + }}}} \right]$ и $\left[ {{{n}_{{3, - }}},{{n}_{{3, + }}}} \right]$ множества ${{\mathcal{N}}_{{13}}}$ совпадают с интервальной оценкой, построенной с помощью первого метода.

Наиболее ощутимое различие между двумя подходами можно заметить в случае учета результатов измерений. Пусть в момент времени $t = 12$ поступило измерение ${{y}_{3}}(t) = 5$, $\Xi = 1$. Очевидно, что в случае интервальных оценок такая ситуация уточняет только значения $\left[ {{{{\tilde {n}}}_{{3, - }}},{{{\tilde {n}}}_{{3, + }}}} \right] = [4,\;6]$, на текущую оценку количества людей в соседних комнатах она никак не повлияет (фиг. 3a): $\left[ {{{{\tilde {n}}}_{{1, - }}},{{{\tilde {n}}}_{{1, + }}}} \right] = [8.17,\;14.07]$.

Фиг. 3.

Учет результата измерения ${{y}_{3}}(t)$ в момент времени $t = 12$: (a) – интервальные оценки, (б) – двумерные проекции.

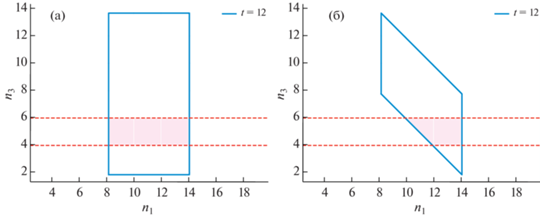
Напротив, в случае двумерных оценок уточнение может затрагивать значения в соседней комнате. Для данного примера проекция множества 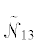улучшается по сравнению с интервальными оценками, построенными с помощью первого метода (фиг. 3б): $\left[ {{{{\tilde {n}}}_{{1, - }}},{{{\tilde {n}}}_{{1, + }}}} \right] = [9.93,\;14.07]$.

6. ЗАКЛЮЧЕНИЕ

Рассмотрена задача оценивания числа людей в каждой комнате для модифицированной модели CTM, описывающей перемещение потоков людей внутри помещения. Предложено два способа оценки множеств достижимости задачи: с помощью одномерных интервальных оценок и двумерных проекций. Работа двух алгоритмов проиллюстрирована численными примерами, показано преимущество второго способа оценивания.

Список литературы

Daganzo C.F. The cell transmission model: a dynamic representation of highway traffic consistent with the hydrodynamic theory // Transp. Res. B. 1994. V. 28B. № 4. P. 269–287.
Daganzo C.F. The cell transmission model, part II: network traffic // Transp. Res. B. 1995. V. 29B. № 2. P. 79–93.
Piccoli B., Garavello M. Traffic flow on networks. American institute of mathematical sciences. Springfield, 2006.
Зайцева М.В., Точилин П.А. Управление потоками людей в здании во время эвакуации // Вестник Московского ун-та. Сер. 15. Вычисл. матем. и кибернетика. 2020. № 4. С. 3–17.
Hänseler F.S., Bierlaire M., Farooq B., Mühlematter T. A macroscopic loading model for time-varying pedestrian flows in public walking areas // Transp. Res. B. 2014. V. 69. P. 60–80.
Kachroo P., Al-nasur S.J., Wadoo S.A., Shende A. Pedestrian dynamics. Feedback control of crowd evacuation. Springer, 2008.
Акопов А.С., Бекларян Л.А. Агентная модель поведения толпы при чрезвычайных ситуациях // Автомат. и телемех. 2015. Вып. 10. С. 131–143.
Samson B.P.V., Aldanese IV C.R., Chan D.M.C., San Pascual J.J.S., Sido M.V.A.P. Crowd dynamics and control in high-volume metro rail stations // Proced. Comput. Sci. 2007. V. 108. P. 195–204.
Helbing D., Farcas I., Vicsek T. Simulating dynamical features of escape panic // Nature. 2000. V. 407. P. 487–490.
Tampere C.M.J., Corthout R., Catrysse D., Immers L.H. A generic class of first order node models for dynamic macroscopic simulation of traffic flows // Trans. Rep. B. 2011. № 45. P. 289–309.
Kurzhanski A.B., Varaiya P. Dynamics and control of trajectory tubes. Birkhäuser, 2014.
Корнушенко Е.К. Интервальные покоординатные оценки для множества достижимых состояний линейной стационарной системы // Автомат. и телемех. 1980. Вып. 5. С. 12–22.
Tang W., Wang Z., Wang Y., Raissi T., Shen Y. Interval estimation methods for discrete-time linear time-invariant systems // IEEE Trans. Automat. Control. 2019. V. 64. № 11. P. 4717–4724.
Куржанский А.Б., Куржанский А.А., Варайя П. Роль макромоделирования в активном управлении транспортной сетью // Тр. МФТИ. 2010. Т. 2. № 4. С. 100–118.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал