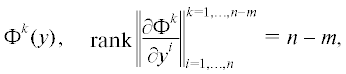Журнал вычислительной математики и математической физики, 2023, T. 63, № 9, стр. 1575-1586

ВВЕДЕНИЕ

Под агрегированием сложных математических моделей, например, моделей большой размерности, обычно понимается сопоставление исходной модели некоторой упрощенной модели (агрегированной модели), оперирующей укрупненными характеристиками, обычно имеющей меньшую размерность, и функционирующей в определенном смысле в силу функционирования исходной модели. Информация об агрегированной модели может быть использована для изучения исходной модели. В частности, агрегированию может сопутствовать декомпозиция модели на совокупность более простых моделей, одна из которых как раз является агрегированной моделью.

Хорошо известным примером агрегирования является случай управляемых динамических систем (см. [1, 2])

Здесь рассматриваются произвольные системы дифференциальных уравнений с частными производными первого порядка где символ $p$ обозначает частные производные $y$ по $t$. Как известно, такую систему путем введения дополнительных переменных можно привести к специальному виду в параметрической форме, разрешенной относительно всех производных (см. [3]), Для таких систем открывается возможность применения методов агрегирования и декомпозиции теории динамических систем с управлением, используя некоторую аналогию данных объектов.

Здесь следует отметить родственное направление исследований факторизации (декомпозиции) дифференциальных уравнений с позиций теории групп. Это направление известно под названием групповой анализ дифференциальных уравнений – раздел математики, изучающий свойства симметрий дифференциальных уравнений относительно различных преобразований зависимых и независимых переменных; включает в себя методы и прикладные аспекты дифференциальной геометрии, теории групп и алгебр Ли, вариационного исчисления и является, в свою очередь, эффективным инструментом исследования в теории ОДУ, ДУЧП и математической физике. Считается, что Л.В. Овсянников положил начало этому научному направлению (см. [4]), хотя по существу он возродил исследования Софуса Ли XIX в. Л.В. Овсянников ввел понятие инвариантного решения, которое сопутствует некоторой факторизации (агрегированию) систем уравнений, что позволяет снижать размерность задач, в частности, уравнений газовой динамики. Известными учениками Л.В. Овсянникова являются Н.Х. Ибрагимов (см. [5]) и Ю.Н. Павловский, который, кстати, первоначально использовал именно методы группового анализа для изучения агрегирования управляемых динамических систем (см. [1, 2]).

Кроме того, существует школа А.В. Виноградова, который также под влиянием идей Софуса Ли начал систематическое исследование оснований геометрической теории дифференциальных уравнений в частных производных (см. [6, 7]).

Подчеркнем, что применение группового анализа для дифференциальных уравнений основано на использовании симметрий, нахождение которых сводится к решению также дифференциальных (определяющих) уравнений, которые могут быть весьма сложными. Между тем применение подхода настоящей работы сводится к исследованию на совместность стандартного типа дифференциальных уравнений с одинаковой главной частью (см. [8, 9]).

1. АГРЕГИРОВАНИЕ (ФАКТОРИЗАЦИЯ) ДИНАМИЧЕСКИХ СИСТЕМ С УПРАВЛЕНИЕМ

Рассматриваются динамические системы с управлением вида (1). Предполагается, что функции ${{g}^{i}}$, $\partial {{f}^{i}}{\text{/}}\partial {{y}^{j}}$, $\partial {{g}^{i}}{\text{/}}\partial {{u}^{\alpha }}$ являются гладкими. Обычно $y$ называют фазовыми переменными (состояниями), $u$ – управлениями (внешними воздействиями). Множество $M$, называемое фазовым пространством, – область, $U$ – область. Управления могут быть кусочно-непрерывными функциями $u(t)$, $t \in [{{t}_{0}},{{t}_{1}}]$. В этом случае они называются допустимыми. Решением или фазовой траекторией системы (1) называется непрерывная кусочно-гладкая функция $y(t)$, $t \in [{{t}_{0}},{{t}_{1}}]$, для которой существует такое допустимое управление $u(t)$, $t \in [{{t}_{0}},{{t}_{1}}]$, что функции $y(t)$, $u(t)$ удовлетворяют соотношениям (1).

Под декомпозицией управляемой системы (1) в этом разделе понимается приведение этой системы с помощью замены фазовых переменных $y \mapsto z = \varphi (t,y)$ к виду

Представление (3), (4) характеризуется тем, что уравнения (3) образуют замкнутую систему. Поэтому любое решение $z(t)$ системы (3), (4) может быть получено следующим образом. Сначала нужно найти решение ${{z}^{1}}(t), \ldots ,{{z}^{m}}(t)$ системы (3) (соответствующее некоторому допустимому управлению $u(t)$), а затем, после подстановки ${{z}^{1}}(t), \ldots ,{{z}^{m}}(t)$ в систему (4), которая становится замкнутой системой, найти оставшиеся функции ${{z}^{{m + 1}}}(t), \ldots ,{{z}^{n}}(t)$. Таким образом, декомпозиция (3), (4) позволяет свести процесс нахождения решения системы к нахождению решений для двух систем, фазовые пространства которых имеют размерности, меньшие, чем $n$.

Если существует такое представление, то говорят также, что система (1) допускает агрегирование или факторизацию порядка $n - m$. При этом среди функций

осуществляющих соответствующую замену фазовых координат $y \mapsto z = \varphi (t,y)$, первые $m$ функций называются агрегатами, а система (3) – агрегированной системой. Функционирование агрегированной системы происходит в силу функционирования исходной системы в следующем смысле: если $y(t)$ – решение системы (1), то ${{z}^{k}}(t) = {{\varphi }^{k}}(y(t))$, $k = 1, \ldots ,m$, – решение системы (3). Заметим также, что с точки зрения теории категорий систему (3) можно трактовать как фактор-объект (фактор-систему) объекта (1) в категории систем (1) с морфизмами, являющимися отображениями фазовых пространств и переводящими решения в решения.

Для изучения возможностей такой декомпозиции в теории динамических систем применяется так называемый метод полных семейств векторных полей (см. [1, 2, 8]). Согласно этому методу, отыскиваются условия, которым должны удовлетворять полные семейства векторных полей, для которых агрегаты (5) являются интегралами. Этот метод будем применять и для декомпозиции дифференциальных уравнений с частными производными в следующем разделе, где он будет подробно описан.

2. ДЕКОМПОЗИЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

Рассматривается система дифференциальных уравнений с частными производными первого порядка

содержащая $t = ({{t}^{1}} \ldots ,{{t}^{m}})$, $y = ({{y}^{1}}, \ldots .{{y}^{n}})$ и производные от функций ${{y}^{i}}$ первого порядка, причем используется обозначение $p = ( \ldots ,{{\partial }_{k}}{{y}^{i}}, \ldots ),$ где ${{\partial }_{k}}{{y}^{i}} = \partial {{y}^{i}}{\text{/}}\partial {{x}^{k}}$. В дальнейшем предполагаем для простоты, что функции ${{\Delta }_{\nu }}$, а также все встречающиеся функции (в том числе решения) гладкие. Под гладкостью понимаем бесконечную дифференцируемость. Считаем, что система (6) максимального ранга и матрица Якоби размера $(l \times mn)$ производных от функций ${{\Delta }_{\nu }}$ по $p$ имеет ранг $l$ всюду, где $\Delta (t,y,p) = 0$. При этом условии соотношения (6) задают гдадкое многообразие ${{\mathcal{S}}_{\Delta }}$ в пространстве переменных $(t,y,p)$ или, иначе говоря, пространстве 1-струй функций $y(t)$. Относительно системы (6) будем считать также, что она локально разрешима. Согласно [10], система локально разрешима в точке $({{x}_{0}},{{y}_{0}},{{p}_{0}}) \in {{\mathcal{S}}_{\Delta }}$, если существует гладкое решение $y = f(t)$, определенное для $t$ из некоторой окрестности точки ${{t}_{0}}$, имеющее предписанные начальные условия ${{y}_{0}} = f({{t}_{0}}),$ ${{p}_{0}} = (\partial f{\text{/}}\partial t{{)}_{{t = {{t}_{0}}}}}$. Система называется локально разрешимой, если она локально разрешима в каждой точке многообразия ${{\mathcal{S}}_{\Delta }}$.

Уравнения (6) задают многообразие ${{\mathcal{S}}_{\Delta }}$ в неявном виде. Это многообразие можно (в силу невырожденности) представить и в параметрическом виде (в некоторой локальной карте) путем разрешения (6) относительно максимального числа производных, причем если остальные (параметрические) производные обозначить через $u$ как параметрические переменные типа ${{\partial }_{\delta }}{{y}^{\beta }} = {{u}^{\gamma }}$, то получим локальное представление ${{\mathcal{S}}_{\Delta }}$ в параметрической форме, разрешенной относительно всех производных (см. [3]):

где $I,\;L,\;U$ – некоторые области. Такое представление произвольной системы дифференциальных уравнений с частными производными известно как специальный вид (см. [3]). В (7) остальные (параметрические) производные обозначены через $u$ как параметрические переменные.

Пример 1. Рассмотрим систему

Полагая $\partial {{y}^{2}}{\text{/}}\partial {{x}_{1}} = u$, запишем данную систему в виде (7)

Далее будем рассматривать системы уравнений в специальном виде и в карте (8). Условие локальной разрешимости в данном случае означает, что для любой точки ${{t}_{o}} \in I,$ ${{y}_{0}} \in M,$ ${{u}_{0}} \in U$ существует окрестность $V \subset L$ точки ${{t}_{0}}$, в которой определено такое гладкое решение $y(t)$, что $y({{t}_{0}}) = {{y}_{0}}$, $u({{t}_{0}}) = {{u}_{0}}$.

Сравнивая (7) и (1), можно заметить некоторую аналогию этих систем. Действительно, каждое решение $y(t)$ управляемой системы (1) получается после подстановки в правую часть управлений $u(t)$ из некоторого класса допустимых функций. С другой стороны, решения $y(t)$ системы (7) соответствуют некоторому выбору параметрической функции $u(t)$ также из некоторого класса. Однако есть существенное различие в классах допустимых “управлений”. Для управляемых систем классы допустимых управлений достаточно известны и широки: от класса кусочно-непрерывных функций до класса измеримых функций. Для систем (7) заранее задать класс допустимых “управлений” затруднительно, ибо далеко не каждый выбор функций $u(t)$ приводит к решению $y(t)$. Препятствием является, в частности, возможность несовместности полученной системы после подстановки $u(t)$. Тем не менее идеология теории управлений может быть полезна.

Далее рассматриваются дифференциальные уравнения с частными производными специального вида, причем для простоты изложения и не ограничивая общности, “автономные”, т.е. с правыми частями, не завиcящими от аргументов $t$:

Речь пойдет о декомпозиции системы (13) с помощью замены зависимых переменных $y$, точнее о возможности преобразования системы с помощью замены переменных к виду

Если такое представление возможно, то будем говорить также, как в разд. 1, что систе-ма (13) допускает агрегирование по зависимым переменным порядка $n - m$, причем первые $m$ функций в замене переменных (14)

называются агрегатами. Далее рассматривается применение метода полных семейств для исследования возможности декомпозиции (15), (16) для систем (13). Этот метод впервые применен Ю.Н. Павловским для агрегирования динамических систем (см. [1, 2]). Полным семейством векторных полей или операторов называется семейство полей (по повторяющемуся индексу здесь и далее производится суммирование), если:

1)

т.е. векторы ${{Z}_{a}}(y)$, $a = 1, \ldots ,p$, линейно независимы в каждой точке $y \in M$ или, как еще говорят, линейно несвязаны в области $M$;

2)

т.е. все коммутаторы $[{{Z}_{a}},{{Z}_{c}}]$ семейства выражаются линейно с переменными коэффициентами $h_{{ac}}^{d}(y)$ через остальные поля семейства.

Гладкая функция $\Phi (y)$, $y \in M$, называется интегралом поля ${{Z}_{a}}$ или корнем оператора ${{Z}_{a}}$, если

Теорема 1 (см. [10]). Полное семейство (18), $p < n$, имеет в окрестности каждой точки $m = n - p$ функционально независимых интегралов (полный набор)

причем любой интеграл $\Phi (y)$ функционально выражается через полный набор

Теорема 2 (см. [10]). Пусть в области $M$ заданы независимые функции (20). Тогда в окрестности каждой точки $M$ найдется полное семейство (18), $p - n - m$, для которого функции (20) составляют полный набор интегралов.

Доказательство. Рассмотрим систему однородных линейных алгебраических уравнений

относительно компонент векторного поля $\xi = {{\xi }^{i}}\partial {\text{/}}\partial {{y}^{i}}$. Для любой точки $y$ найдется окрестность, в которой некоторый минор $m$-го порядка матрицы системы уравнений (21) отличен от нуля. Фундаментальная система решений в этой окрестности определяет линейно несвязанное семейство векторных полей (18), для которого функции (20) являются интегралами. Любое поле $\xi = {{\xi }^{i}}\partial {\text{/}}\partial {{y}^{i}}$, удовлетворяющее (21), должно линейно выражаться через поля (18). В частности, так как коммутаторы $[{{\xi }_{a}},{{\xi }_{b}}]$ в силу свойства удовлетворяют (21), то справедливо свойство 2 семейства (18). Следовательно, построенное семейство (18) является полным. Функции (20) составляют максимальный набор независимых интегралов семейства (18), ибо в противном случае получилось бы противоречие с теоремой 1.

Переходим к условиям существования декомпозиции (15), (16). Введем в рассмотрение операторы полного дифференцирования системы (13) по переменным ${{t}^{l}}$ (здесь отсутствует явное дифференцирование $\partial {\text{/}}\partial {{t}^{l}}$ по ${{t}^{l}}$ в силу вышеупомянутой “автономности”):

Замена зависимых переменных (14) в системе (13) осуществляется следующим образом: нужно подействовать операторами (23) на функции (14) и варазить функционально полученные функции через (14) Функции являются новыми правыми частями системы, при этом декомпозиция (15), (16) возникает, когда первые $m$ функций (25) функционально выражаются только через агрегаты (17), т.е. Непосредственное применение этого условия не дает конструктивного метода нахождения агрегатов и проверки возможности декомпозиции. Поэтому применяется опосредственный подход, когда сначала с помощью решения некоторых систем дифференциальных уравнений отыскиваются полные семейства векторных полей, для которых агрегаты являются интегралами, а затем находятся агрегаты, т.е. интегралы этих семейств. При этом совместность упомянутых систем дифференциальных уравнений определяет возможность декомпозиции.

Теорема 3. Система (13) тогда и только тогда локально приводится к виду (15), (16) с помощью замены переменных (14), когда существует такое полное семейство (18), $p = n - m < n$, что

причем агрегаты (17) составляют полный набор интегралов семейства (18).

Доказательство. Необходимость. Для агрегатов (17) по теореме 2 существует полное семейство (18), интегралами которого являются агрегаты. Подействуем коммутаторами $[{{X}_{l}},{{Z}_{a}}]$ на эти функции, используя свойство коммутатора (22). Получим

Здесь использовано то обстоятельство, что функции ${{X}_{l}}({{\varphi }^{i}}(y)$, согласно (27), функционально выражаются через полный набор интегралов семейства (18) и поэтому также являются интегралами этого семейства. В доказательстве теоремы 2 отмечено, что условие (29) влечет (28).

Достаточность. Для семейства (18) возьмем полный набор интегралов ${{\varphi }^{i}}(y)$, $i = 1, \ldots ,m = n - p$, и рассмотрим опять выражения (29). Из (29) вытекает, что функции ${{X}_{l}}({{\varphi }^{i}}(y)$ являются интегралами семейства (18) и по теореме 1 функционально выражаются через полный набор интегралов и, следовательно, ${{\varphi }^{i}}(y)$ являются агрегатами для системы (13).

Выражения (29) можно трактовать как систему дифференциальных уравнений

относительно неизвестных компонент семейства (18). В (30) выражения ${{\xi }_{u}}(b_{a}^{i})$, ${{Z}_{a}}({{f}^{i}})$ представляют собой действия полей ${{\xi }_{u}}$, ${{Z}_{a}}$ на функции $b_{a}^{i}(y)$, ${{f}^{i}}(y,u)$ как операторов. После решения этой системы нужно найти полный набор интегралов ${{\varphi }^{i}}(y)$, $i = 1, \ldots ,m = n - p$, полного семейства (18), что, согласно [11], сводится к решению некоторых систем обыкновенных дифференциальных уравнений. Для нахождения правых частей фактор-системы следует функции ${{f}^{i}}(y,u)\frac{{\partial {{\varphi }^{k}}}}{{\partial {{y}^{i}}}}$ выразить функционально через функции ${{\varphi }^{i}}(y)$, $i = 1, \ldots ,m = n - p$, т.е. представить их в виде Построенные функции ${{h}^{k}}$ и определяют искомую фактор-систему

Система (30) содержит, помимо $b_{a}^{i}(y)$, еще неизвестные параметрические переменные $\mu _{{la}}^{b}(y,u)$. Последнее обстоятельство усложняет дело. Кроме того, нужно добавить условие полноты $[{{Z}_{b}},{{Z}_{a}}] = \kappa _{{ba}}^{c}(y){{Z}_{c}}$ семейства (18), которое тоже представляет собой систему дифференциальных уравнений, причем с неизвестными параметрическими переменными $\kappa _{{ba}}^{c}(y)$. Рассмотрим метод исключения параметрических переменных; осуществляется с помощью использования якобиевых семейств (для динамических систем эта процедура предложена автором в [8]). Сначала докажем одно утверждение, которое связывает полные семейства и их интегралы. Для того чтобы исключить функции $\mu _{{ua}}^{c}$ из (30), следует задаться некоторым свойством, которым должны обладать агрегаты (17). Это свойство заключается в определенном расположении базисного минора в якобиевой матрице $\left\| {\partial {{\varphi }^{k}}{\text{/}}\partial {{y}^{i}}} \right\|$.

Теорема 4. Пусть (18) – полное семейство векторных полей, (20) – полный набор интегралов этого семейства, а $I$ – некоторое подмножество из $p$ элементов множества индексов $\{ 1, \ldots ,n\} $, $\bar {I} = \{ 1, \ldots ,n\} {{\backslash }}I$. Тогда следующие условия эквивалентны:

Доказательство. Пусть выполняется условие (а). Рассмотрим семейство полей ${{\eta }_{b}},\;b \in I$, которое получается из исходного семейства линейным невырожденным преобразованием: ${{\eta }_{b}} = \mu _{b}^{a}(y){{\xi }_{a}}$, $b \in I$. Здесь функции $\mu _{b}^{a}$ составляют матрицу, обратную к матрице $\left\| {\xi _{a}^{i}} \right\|_{{a = 1, \ldots ,p}}^{{i \in I}}$. Построенное семейство полей будет иметь следующий вид:

где $\eta _{b}^{c}$ – некоторые функции. Ясно, что функции ${{\varphi }^{k}}$ являются интегралами и полей ${{\eta }_{b}}$, т.е. Отсюда вытекает, что выполняется условие (б).

Пусть теперь выполняется условие (б). Рассмотрим систему линейных однородных уравнений относительно неизвестного векторного поля $\xi = {{\xi }^{i}}(y)\partial {\text{/}}\partial {{y}^{i}}$:

Очевидно, что поля ${{\xi }_{a}},\;a = 1, \ldots ,p$, образуют фундаментальную систему решений этой системы уравнений. С другой стороны, нетрудно видеть, что существует фундаментальная система решений вида (31). Два семейства (18) и (31) должны быть связаны линейным невырожденным преобразованием. Отсюда вытекает справедливость условия (а).

Для того чтобы исключить функции $h_{{ua}}^{c}$ из (30), следует задаться некоторым свойством, которым должны обладать агрегаты (17). Это свойство заключается в определенном расположении базисного минора в якобиевой матрице $\left\| {\partial {{\varphi }^{k}}{\text{/}}\partial {{y}^{i}}} \right\|$. Предположим, что для искомых агрегатов (17)

Справедлива

Теорема 5. Для того чтобы система (1) допускала (локальную) факторизацию порядка $p = n - m$, характеризующуюся свойством (32), необходимо и достаточно, чтобы была совместна система дифференциальных уравнений относительно неизвестных функций $b_{a}^{l}(y)$:

где

Доказательство. Необходимость. Если система (1) допускает факторизацию со свойством (32), то, согласно доказательству теоремы 4, существует семейство вида (35). Семейство (35) должно удовлетворять соотношениям (28). Запишем эти соотношения покомпонентно:

Из (36) имеем $h_{a}^{i} = - {{Z}_{a}}({{f}^{i}})$. Подставляя $h_{a}^{i}$ в (37), получим (33). Равенства (34) представляют собой условие полноты семейства (35). Действительно, согласно доказательству теоремы 1, семейство вида (35) является полным тогда и только тогда, когда оно якобиево, т.е. $[{{Z}_{a}},{{Z}_{c}}] = 0$, $a,c = 1, \ldots ,p$, что равносильно равенствам (34).

Достаточность. Если совместна система (33), (34), то семейство полей (35) является полным. Далее, полагая $h_{a}^{i} = - {{Z}_{a}}({{f}^{i}})$, из (33) получим (36), (37), откуда вытекает (28). Следовательно, система (1) допускает факторизацию порядка $p$. Свойство (32) вытекает из вида семейства (35) и теоремы 4. Теорема 5 доказана.

Уравнения (33) представляют собой систему уравнений относительно $b_{a}^{l}$ без параметрических переменных.

При ином расположении базисного минора в матрице $\left\| {\partial {{\varphi }^{k}}{\text{/}}\partial {{y}^{i}}} \right\|$ условия факторизации (33), (34) преобразуются очевидным образом. Итак, задача решения системы дифференциальных уравнений (30) с параметрическими переменными сведена к задаче решения нескольких систем дифференциальных уравнений вида (33) без параметрических переменных. Решение систе-мы (33), т.е. набор компонент семейства полей (35), следует подставить для проверки в уравнения (34), представляющие собой условия полноты семейства (35). Лишь те решения системы (33), которые одновременно являются и решениями системы (34), определяют семейство, порождающее факторизацию порядка $p$.

Система такого вида является частным случаем так называемых уравнений в частных производных с одинаковой главной частью

Функции $a_{k}^{j},\;b_{k}^{i}$ – гладкие в области $V \times U$, где $V \subset {{R}^{m}}$, $U \subset {{R}^{n}}$.

Замечание 1. Системы (38) для $r = 1$ рассматривались в [12]. Другой частный случай систем вида

также хорошо известен (см., например, [10]). Для проверки совместности следует рассмотреть равенство смешанных производных: в силу (39). Если эти уравнения тождественно удовлетворяются, то система (38) вполне интегрируема. В противном случае получаем систему конечных уравнений, устанавливающих условия на $y$, как функций от $x$. Если каждое из этих уравнений продифференцировать по ${{x}^{i}}$ и заменить производные $\partial {{y}^{i}}{\text{/}}\partial {{x}^{i}}$ их значениями из (39), то полученные уравнения либо будут следствиями полученных уравнений, либо составят новую систему. Продолжая этот процесс, получим ряд систем, которые должны быть совместны, если уравнения (39) имеют решения. В противном случае решений у (39) нет. Данные рассуждения и выводы можно применять также и тогда, когда заданы какие-либо дополнительные функциональные соотношения между переменными $y$ и $x$:

В [8, 9] автором получен алгоритм проверки совместности и нахождения решений систем уравнений систем (38), точнее в [7] были исследованы частные случаи систем типа (151), которые возникают при рассмотрении агрегирования управляемых динамических систем, а в [8] уже рассмотрен общий случай.

Наконец, рассмотрим один весьма общий случай систем, когда можно проверить совместность системы (33), (34), не решая предварительно систему (33). Но сначала следует рассмотреть важный частный случай декомпозиции, когда правые части агрегированной системы равны нулю. Он связан с понятием первого интеграла систем дифференциальных уравнений.

ЗАКЛЮЧЕНИЕ

Рассмотрена возможность применения методов теории управления в теории уравнений с частными производными. При этом использована специальная форма представления любой системы уравнений с частными производными. Эта форма дает возможность трактовать параметрические переменные как некоторые управления, порождающие все решения. Такая трактовка позволяет в определенном смысле использовать идеологию теории управления, но, главное, позволяет ввести аналогичные математические объекты, которые показали свою эффективность для решения задач управления. Здесь показана эффективность этих методов для исследования проблемы декомпозиции систем уравнений с частными производными. Следующая проблема – исследование симметрий – для следующих работ.