Журнал вычислительной математики и математической физики, 2023, T. 63, № 9, стр. 1565-1574
Влияние демпфирования податливой поверхности на невязкую неустойчивость несжимаемого пограничного слоя над ней
1 ВЦ ФИЦ ИУ РАН
119991 Москва, ул. Вавилова, 40, Россия
* E-mail: isavenkov@mail.ru
Поступила в редакцию 02.11.2022
После доработки 14.05.2023
Принята к публикации 29.05.2023
- EDN: SGZLHK
- DOI: 10.31857/S0044466923090144
Аннотация
В рамках асимптотической теории свободного взаимодействия изучена неустойчивость несжимаемого пограничного слоя над податливой пластиной по отношению к невязким возмущениям в пределе высоких чисел Рейнольдса. Показано, что неустойчивые невязкие возмущения могут существовать только при учете инерционности и/или демпфирования пластины. Выявлена двоякая роль демпфирования: при одних условиях она приводит к подавлению неустойчивости, при других – к ее возникновению. Библ. 18. Фиг. 6.
ВВЕДЕНИЕ
Податливые поверхности стали объектом довольно пристального внимания с ранних экспериментов (см. [1]), в которых было показано, что значительное затягивание процесса ламинарно-турбулентного перехода может быть достигнуто путем замены жесткой поверхности на деформируемую. Последовавшие исследования в рамках линейной теории устойчивости (см., например, [2–5]) показали, что инкременты нарастания неустойчивых волн в пограничном слое на податливой поверхности действительно могут быть меньше, чем на жесткой поверхности.
Несмотря на прогресс, достигнутый к настоящему времени (см. [6–9] и ссылки в них), остается немало вопросов из-за сложности уравнений, описывающих взаимодействие течения с податливой поверхностью. Первая сложность вызвана тем, что характерные числа Рейнольдса, при которых происходит ламинарно-турбулентный переход, довольно высоки, так что в уравнениях движения появляется малый параметр при старшей производной. Вторая сложность связана с большим числом параметров, характеризующим свойства податливой поверхности, к числу которых относятся ее инерционность, демпфирование, упругость, продольное натяжение и изгибная жесткость, так что трудно выявить характерные закономерности при таком обилии параметров.
Первую сложность можно преодолеть, используя концепцию свободно взаимодействующего пограничного слоя (см. [10–12]), справедливую при высоких числах Рейнольдса. Чтобы обойти вторую сложность, можно зафиксировать все параметры податливой поверхности (или пренебречь некоторыми из них), кроме одного, и смотреть, как течение реагирует на изменение этого параметра. В рамках такого подхода в ряде работ и изучалась неустойчивость несжимаемого пограничного слоя на базе концепции свободного взаимодействия (см. [13–17]). Настоящая работа является дальнейшим развитием [17].
1. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим двумерное обтекание податливой пластины равномерным потоком несжимаемой жидкости плотности $\rho _{\infty }^{*}$ и вязкости $\mu _{\infty }^{*}$ со скоростью $U_{\infty }^{*}$. Введем ортогональную систему координат, поместив ее начало на некотором расстоянии $L{\kern 1pt} *$ от передней кромки и направив ось $х{\kern 1pt} *$ вниз по потоку. Введем малый параметр $\varepsilon = {{R}^{{ - 1{\text{/}}8}}}$, считая число Рейнольдса $R = \rho _{\infty }^{*}U_{\infty }^{*}L{\kern 1pt} *{\text{/}}\mu _{\infty }^{*}$ очень большим. Здесь и далее звездочками вверху обозначаются размерные величины.
Пусть на пластину локально воздействует внешнее давление $\Delta p{\kern 1pt} *\sim {{\delta }^{2}}\rho _{\infty }^{*}U_{\infty }^{{*2}}$ на участке $\Delta x{\kern 1pt} *\sim {{\varepsilon }^{4}}{\text{/}}\delta {\kern 1pt} L{\kern 1pt} *$ с характерным временем $\Delta t{\kern 1pt} *\sim {{\varepsilon }^{4}}{\text{/}}{{\delta }^{2}}L{\kern 1pt} *{\text{/}}U_{\infty }^{*}$, вызывая локальные деформации стенки высотой $\Delta y{\kern 1pt} *\sim {{\varepsilon }^{4}}\delta {\kern 1pt} L{\kern 1pt} *$, где малый параметр $\delta $ таков, что $\varepsilon \ll \delta \ll 1$. Тогда возмущенное движение можно описать с помощью концепции свободного взаимодействия (см. [10–12]), развитой применительно к локально-невязким возмущениям (см., например, [18]). Согласно этой теории, вся область течения разбивается на следующие четыре характерные области.
1.1. Основная толща пограничного слоя
В основной толще пограничного слоя, т.е. на расстояниях $y{\kern 1pt} * = {{R}^{{ - 1/2}}}L{\kern 1pt} *{\kern 1pt} {{Y}_{m}}$ от стенки $({{Y}_{m}} = O(1))$, течение в пограничном слое будет лишь слабовозмущенным:
(1.1)
$\frac{{u{\kern 1pt} *}}{{U_{\infty }^{*}}} = {{U}_{0}} + \delta {{u}_{{1m}}} + \ldots ,\quad \frac{{{v}{\kern 1pt} *}}{{U_{\infty }^{*}}} = {{\delta }^{2}}{{{v}}_{{1m}}} + \ldots ,\quad \frac{{p{\kern 1pt} {\text{*}} - p_{\infty }^{*}}}{{\rho _{\infty }^{*}U{{{_{\infty }^{*}}}^{2}}}} = {{\delta }^{2}}{{p}_{{1m}}} + \ldots ,$Время t и продольная координата x будут “сквозными” для всех областей взаимодействия, тогда как поперечная координата меняется при переходе между ними.
После подстановки (1.1) в уравнения Навье–Стокса и тривиального интегрирования имеем
(1.2)
${{u}_{{1m}}} = {{A}_{1}}(t,x)\frac{{d{{U}_{0}}}}{{d{{Y}_{m}}}},\quad {{v}_{{1m}}} = - \frac{{\partial {{A}_{1}}}}{{\partial x}}{{U}_{0}}({{Y}_{m}}),\quad {{p}_{{1m}}} = {{p}_{{1m}}}(t,x),$1.2. Нелинейный слой
В силу предельного поведения, ${{U}_{0}} = {{\lambda }_{1}}{{Y}_{m}} + \ldots $ $({{\lambda }_{1}} = \operatorname{const} )$ при ${{Y}_{m}} \to 0$, разложения (1.1) нарушаются вблизи стенки: при ${{Y}_{m}} = O(\delta )$ первые два слагаемых в разложении для $u{\kern 1pt} *$ становятся величинами одного порядка. Поэтому в нижнем подслое с ${{Y}_{a}} = {{\delta }^{{ - 1}}}{{Y}_{m}} = {{\delta }^{{ - 1}}}{{\varepsilon }^{{ - 4}}}y{\kern 1pt} *{\text{/}}L{\kern 1pt} *\sim 1$ возмущения становятся нелинейными, а ряды (1.1) трансформируются в
(1.3)
$\frac{{u{\kern 1pt} *}}{{U_{\infty }^{*}}} = \delta {\kern 1pt} {{u}_{{1a}}} + ...,\quad \frac{{v{\kern 1pt} *}}{{U_{\infty }^{*}}} = {{\delta }^{3}}{{v}_{{1a}}} + \ldots ,\quad \frac{{p{\kern 1pt} {\text{*}} - p_{\infty }^{*}}}{{\rho _{\infty }^{*}U_{\infty }^{{*2}}}} = {{\delta }^{2}}{{p}_{{1a}}} + \ldots ,$(1.4)
$\frac{{\partial {\kern 1pt} {{u}_{{1a}}}}}{{\partial x}} + \frac{{\partial {{v}_{{1a}}}}}{{\partial {{Y}_{a}}}} = 0,\quad \frac{{\partial {\kern 1pt} {{p}_{{1a}}}}}{{\partial {{Y}_{a}}}} = 0,\quad \frac{{\partial {{u}_{{1a}}}}}{{\partial t}} + {{u}_{{1a}}}\frac{{\partial {{u}_{{1a}}}}}{{\partial x}} + {{v}_{{1a}}}\frac{{\partial {{u}_{{1a}}}}}{{\partial {{Y}_{a}}}} = - \frac{{\partial {{p}_{{1a}}}}}{{\partial x}},$Сращивание разложений (1.1) и (1.3) с учетом решения (1.2) ведет к предельному условию
(1.5)
${{u}_{{1a}}} - {{\lambda }_{1}}{{Y}_{a}} \to {{\lambda }_{1}}{{A}_{1}}(t,x)\quad {\text{при}}\quad {{Y}_{a}} \to \infty .$Если предположить, что пограничный слой был изначально невозмущенным, то можно выписать точное решение системы (1.4), удовлетворяющее граничному условию (1.5):
(1.6)
${{u}_{{1a}}} = {{\lambda }_{1}}{{Y}_{a}} + {{\lambda }_{1}}{{A}_{1}}(t,x),\quad {{v}_{{1a}}} = - \frac{{\partial {{A}_{1}}}}{{\partial t}} - {{\lambda }_{1}}{{Y}_{a}}\frac{{\partial {{A}_{1}}}}{{\partial x}} - {{\lambda }_{1}}{{A}_{1}}\frac{{\partial {{A}_{1}}}}{{\partial x}} - \frac{1}{{{{\lambda }_{1}}}}\frac{{\partial {{p}_{{1a}}}}}{{\partial x}}.$Учитывая условие непротекания на стенке
(1.7)
$\frac{{\partial ({{A}_{1}} + {{F}_{1}})}}{{\partial t}} + {{\lambda }_{1}}({{A}_{1}} + {{F}_{1}})\frac{{\partial ({{A}_{1}} + {{F}_{1}})}}{{\partial x}} = - \frac{1}{{{{\lambda }_{1}}}}\frac{{\partial {{p}_{{1a}}}}}{{\partial x}},$1.3. Вязкий подслой
Нетрудно видеть, что решение (1.6) не удовлетворяет условиям прилипания на стенке (должно быть ${{u}_{{1a}}} = 0$ при ${{Y}_{a}} = 0$), из-за чего требуется ввести вязкий подслой со своими асимптотическими разложениями следующего вида:
(1.8)
$\begin{gathered} \frac{{\partial {{u}_{{1l}}}}}{{\partial x}} + \frac{{\partial {{v}_{{1l}}}}}{{\partial {{Y}_{l}}}} = 0,\quad \frac{{\partial {{p}_{{1l}}}}}{{\partial {{Y}_{l}}}} = 0, \\ \frac{{\partial {\kern 1pt} {{u}_{{1l}}}}}{{\partial t}} + {{u}_{{1l}}}\frac{{\partial {\kern 1pt} {{u}_{{1l}}}}}{{\partial x}} + {{v}_{{1l}}}\frac{{\partial {{u}_{{1l}}}}}{{\partial {{Y}_{l}}}} = - \frac{{\partial {{p}_{{1l}}}}}{{\partial x}} + \frac{{{{\partial }^{2}}u_{{1l}}^{{}}}}{{\partial Y_{l}^{2}}}. \\ \end{gathered} $Сращивание разложений (1.3) и (1.8) дает
1.4. Внешняя область
В этой области течения, примыкающей сверху к пограничному слою, введем следующие асимптотические разложения:
(1.9)
$\frac{{u{\kern 1pt} *}}{{U_{\infty }^{*}}} = 1 + {{\delta }^{2}}{{u}_{{1u}}} + \ldots ,\quad \frac{{v{\kern 1pt} *}}{{U_{\infty }^{*}}} = {{\delta }^{2}}{{v}_{{1u}}} + \ldots ,\quad \frac{{p{\kern 1pt} * - p_{\infty }^{*}}}{{\rho _{\infty }^{*}U_{\infty }^{{*2}}}} = {{\delta }^{2}}{{p}_{{1u}}} + \ldots ,$Подстановка разложений (1.9) в уравнения Навье–Стокса ведет к уравнению Лапласа для давления
(1.10)
${{{{\partial }^{2}}{{p}_{{1u}}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{p}_{{1u}}}} {\partial {{x}^{2}}}}} \right. \kern-0em} {\partial {{x}^{2}}}} + {{{{\partial }^{2}}{{p}_{{1u}}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{p}_{{1u}}}} {\partial Y_{u}^{2}}}} \right. \kern-0em} {\partial Y_{u}^{2}}} = 0$(1.11)
${{u}_{{1u}}} = - {{p}_{{1u}}},\quad \partial {{v}_{{1u}}}{\text{/}}\partial x = {{ - \partial {{p}_{{1u}}}} \mathord{\left/ {\vphantom {{ - \partial {{p}_{{1u}}}} {\partial {{Y}_{u}}}}} \right. \kern-0em} {\partial {{Y}_{u}}}}.$1.5. Податливая поверхность
Будем считать, что податливая поверхность описывается моделью Крамера (см. [1]), тогда уравнение движения такой поверхности принимает следующий вид:
(1.13)
$p{\kern 1pt} * - p_{0}^{*} = - {\kern 1pt} K{\kern 1pt} *{\kern 1pt} F{\kern 1pt} {\text{*}} + T{\kern 1pt} {\text{*}}\frac{{{{\partial }^{2}}F{\kern 1pt} *}}{{\partial x_{{}}^{{*2}}}} - B{\kern 1pt} {\text{*}}\frac{{{{\partial }^{4}}F{\kern 1pt} *}}{{\partial x_{{}}^{{*4}}}} - \rho _{s}^{*}h_{s}^{*}\frac{{{{\partial }^{2}}F{\kern 1pt} *}}{{\partial t_{{}}^{{*2}}}} - d{\kern 1pt} {\text{*}}\frac{{\partial F{\kern 1pt} *}}{{\partial t{\kern 1pt} *}},$(1.14)
${{\gamma }_{1}}\frac{{{{\partial }^{2}}{{F}_{1}}}}{{\partial {{t}^{2}}}} + {{d}_{1}}\frac{{\partial {{F}_{1}}}}{{\partial t}} - {{\alpha }_{1}}\frac{{{{\partial }^{2}}{{F}_{1}}}}{{\partial {{x}^{2}}}} + {{\beta }_{1}}\frac{{{{\partial }^{4}}{{F}_{1}}}}{{\partial {{x}^{4}}}} + {{K}_{1}}{{F}_{1}} = - {{p}_{{1a}}}(t,x) + {{p}_{0}}(t,x),$Таким образом, мы получили три уравнения: (1.7), (1.12) и (1.14) для трех неизвестных функций ${{F}_{1}}$, ${{A}_{1}}$ и ${{p}_{{1a}}}$. Сделаем еще аффинное преобразование
(1.15)
$\begin{gathered} \gamma \frac{{{{\partial }^{2}}F}}{{\partial {{T}^{2}}}} - \alpha \frac{{{{\partial }^{2}}F}}{{\partial {{X}^{2}}}} + \beta \frac{{{{\partial }^{4}}F}}{{\partial {{X}^{4}}}} + KF = - \left( {P(T,X) - {{P}_{0}}(T,X)} \right), \\ \frac{{\partial (A + F)}}{{\partial T}} + (A + F)\frac{{\partial (A + F)}}{{\partial X}} = - \frac{{\partial P}}{{\partial X}},\quad P(T,X) = \frac{1}{\pi }\int\limits_{ - \infty }^\infty {\frac{{\partial A(T,\xi ){\text{/}}\partial \xi }}{{X - \xi }}} d\xi , \\ \end{gathered} $2. ДИСПЕРСИОННОЕ СООТНОШЕНИЕ
Изучим собственные малые колебания течения, линеаризовав систему (1.15) по малому амплитудному параметру ${{\delta }_{1}} \to 0$ и положив внешнее давление ${{P}_{0}} = 0$:
(2.1)
$\left( {F,P,A} \right) = {{\delta }_{1}}{\kern 1pt} \left( {F{\kern 1pt} ',P{\kern 1pt} ',A{\kern 1pt} '} \right).$(2.2)
$\left( {{{\omega }_{0}} - {{k}^{2}}} \right)\left( {\gamma \omega _{0}^{2} + id{{\omega }_{0}} - \Lambda } \right) + k{{\omega }_{0}} = 0.$2.1. Безынерционная пластина
Начнем исследование неустойчивости с более простого случая, когда $\gamma = 0$, что соответствует безынерционной пластине. В этом случае уравнение (2.2) вырождается в квадратное уравнение
(2.3)
$\left( {{{\omega }_{0}} - {{k}^{2}}} \right)\left( {id{{\omega }_{0}} - \Lambda } \right) + k{{\omega }_{0}} = 0,$(2.4)
${{\omega }_{{0, \pm }}} = \frac{{ik - i\Lambda + {{k}^{2}} \pm i\sqrt {{{{\left( {i{{k}^{2}} - k + \Lambda } \right)}}^{2}} - 4i\Lambda {{k}^{2}}} }}{2},$Нетрудно получить следующие асимптотики корней (2.4):
– для $\beta \ne 0$:
(2.5)
${{\omega }_{{0, + }}} = {{k}^{2}} + \frac{1}{\beta }{{k}^{{ - 1}}} + \frac{{i - \alpha }}{{{{\beta }^{2}}}}{{k}^{{ - 3}}} + \ldots ,\quad {{\omega }_{{0, - }}} = - i\beta {{k}^{4}} + \ldots \quad {\text{при}}\quad k \to \infty ;$– для $\beta = 0$:
(2.6)
${{\omega }_{{0, + }}} = {{k}^{2}} + \frac{{\alpha + i}}{{{{\alpha }^{2}} + 1}}k + \ldots ,\quad {{\omega }_{{0, - }}} = - i\alpha {{k}^{2}} + \ldots \quad {\text{при}}\quad k \to \infty .$($\sigma = \operatorname{Im} {{\omega }_{{0, + }}} \sim \frac{1}{{{{\beta }^{2}}}}{{k}^{{ - 3}}}$ или $\sigma = \operatorname{Im} {{\omega }_{{0, + }}} \sim \frac{1}{{{{\alpha }^{2}} + 1}}k$) положителен в пределе больших k, а значит, этот корень неустойчив при всех k (как было отмечено ранее, все корни или целиком неустойчивы, или целиком устойчивы, поскольку нейтральных решений не существует). По этой же причине “минусовой” корень всегда устойчив (ведь $\operatorname{Im} {{\omega }_{{0, - }}} \sim - \beta {{k}^{4}} < 0$ или $\operatorname{Im} {{\omega }_{{0, - }}} \sim - \alpha {{k}^{2}}$ в пределе больших k).
Таким образом, можно сразу сделать вывод общего характера: наличие демпфирования безынерционной пластины всегда ведет к появлению неустойчивости, причем единственный неустойчивый корень неустойчив во всем диапазоне волновых чисел k.
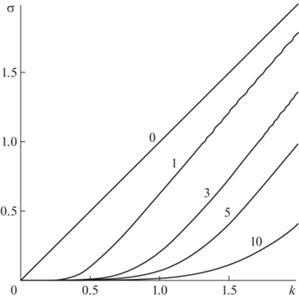
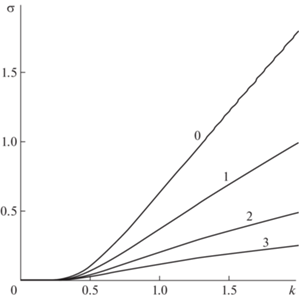
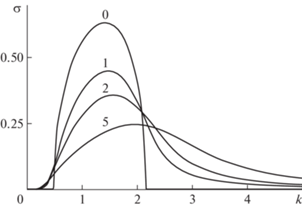
Далее, асимптотика (2.6) говорит о том, что инкремент нарастания $\sigma \sim \frac{1}{{{{\alpha }^{2}} + 1}}k$ может стать сколь угодно большим с увеличением k, если пренебречь изгибной жесткостью пластины ($\beta = 0$). Сказанное иллюстрируют зависимости инкремента нарастания $\sigma $ от k при $\alpha = \beta = 0$ для ряда значений K, приведенные на фиг. 1. Видно, что $\sigma $ довольно быстро выходит на свою линейную асимптотику (2.6). Учет продольного натяжения ($\alpha \ne 0$) может только уменьшить скорость этого роста, но не подавить линейную зависимость (см. фиг. 2 для ряда значений α при $K = 1,\;\beta = 0$). И только наличие изгибной жесткости радикально меняет ситуацию, уводя $\sigma $ на алгебраическое затухание $ \sim {\kern 1pt} \frac{1}{{{{\beta }^{2}}}}{{k}^{{ - 3}}}$ в пределе больших k, согласно асимптотике (2.5). Насколько сильно подавляется неустойчивость уже при малых $\beta $, можно проследить по фиг. 3 для ряда значений $\beta $ (при $K = 1,\;\alpha = 0$).
2.2. Общий случай
Рассмотрим общий случай инерционной пластины, когда $\gamma \ne 0$. Путем аффинного преобразования
(2.7)
$\begin{gathered} {{\omega }_{0}} \to {{\gamma }^{{ - 2{\text{/}}3}}}{{\omega }_{0}},\quad k \to {{\gamma }^{{ - 1{\text{/}}3}}}k,\quad d \to {{\gamma }^{{1{\text{/}}3}}}d,\quad \Lambda \to {{\gamma }^{{ - 1{\text{/}}3}}}\Lambda , \\ K \to {{\gamma }^{{ - 1{\text{/}}3}}}K,\quad \alpha \to {{\gamma }^{{1{\text{/}}3}}}\alpha ,\quad \beta \to \gamma \beta \\ \end{gathered} $(2.8)
$\left( {{{\omega }_{0}} - {{k}^{2}}} \right)\left( {\omega _{0}^{2} + id{{\omega }_{0}} - \Lambda } \right) + k{{\omega }_{0}} = 0.$Начнем изучение (2.8) с предельного случая волновых чисел k, стремящихся к бесконечности. В таком случае нетрудно получить следующие асимптотики дисперсионного соотношения (2.8).
Для первого корня:
– при $\beta \ne 1$:
(2.9)
${{\omega }_{{0,1}}} = {{k}^{2}} - \frac{1}{{1 - \beta }}k + \frac{{id - \alpha }}{{{{{(1 - \beta )}}^{2}}}}{{k}^{{ - 3}}} + \ldots \quad {\text{при}}\quad k \to \infty ;$– при $\beta = 1$:
(2.10)
${{\omega }_{{0,1}}} = {{k}^{2}} + i\frac{1}{{\sqrt 2 }}{{k}^{{1/2}}} + \frac{{\alpha - id}}{2} + \ldots \quad {\text{при}}\quad k \to \infty .$Для второго и третьего корней:
– при $\beta \ne 0$:
(2.11)
${{\omega }_{{0,2,3}}} = \pm {{\beta }^{{1/2}}}{{k}^{2}} \pm \frac{\alpha }{{2{{\beta }^{{1/2}}}}} - \frac{1}{2}id + \ldots \quad {\text{при}}\quad k \to \infty ;$– при $\beta = 0$:
(2.12)
${{\omega }_{{0,2,3}}} = \pm {{\alpha }^{{1/2}}}k - \frac{1}{2}id + \ldots \quad {\text{при}}\quad k \to \infty .$Как видно из (2.11) и (2.12), инкремент нарастания $\sigma = \operatorname{Im} {{\omega }_{{0,2,3}}}\sim - 1{\text{/}}2d < 0$ в пределе $k \to \infty $, значит, и второй, и третий корень устойчивы при больших k и будут оставаться таковыми при всех k (как мы ранее заметили, корни могут быть только целиком устойчивыми или целиком неустойчивыми).
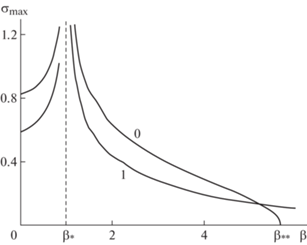
Первый же корень, напротив, всегда неустойчив (при всех $k \ne 0$, $K$, $\alpha $, $\beta $ и $d \ne 0$), причем согласно (2.9) он затухает алгебраически: $\sigma = \operatorname{Im} {{\omega }_{{0,1}}}\sim \frac{d}{{{{{(1 - \beta )}}^{2}}}}{{k}^{{ - 3}}}$ в пределе $k \to \infty $ при $\beta \ne 1$. Но самое интересное с точки зрения неустойчивости происходит при $\beta = 1$, когда этот корень согласно (2.10) неограниченно растет: $\sigma = \operatorname{Im} {{\omega }_{{0,1}}}\sim \frac{1}{{\sqrt 2 }}{{k}^{{1/2}}}$ в пределе $k \to \infty $. Собственно, этот эффект был обнаружен ранее в работе [17], в которой не учитывалось демпфирование пластины. Учет демпфирования в настоящей работе показывает, что хотя демпфирование и несколько подавляет этот рост (на постоянную величину $ - 1{\text{/}}2d$), но оно не в силах справиться с ним. Сказанное иллюстрирует фиг. 4, на которой представлены зависимости ${{\sigma }_{{\max }}}(\beta ) = \max \sigma ( - \infty < k < \infty )$ при $K = 1$ и $\alpha = 0$ для значений $d = 0$, 1 (отмечены соответствующими цифрами рядом).
Отметим еще одну характерную особенность, прослеживающуюся по фиг. 4. Как было выяснено в [17], в случае бездемпферной пластины $(d = 0)$ существует пороговое значение 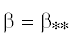 (зависящее от $K$ и $\alpha $), при превышении которого неустойчивость пропадает (
(зависящее от $K$ и $\alpha $), при превышении которого неустойчивость пропадает (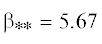 для $K = 1$ и $\alpha = 0$ на фиг. 4). При учете демпфирования $(d \ne 0)$ такое пороговое значение
для $K = 1$ и $\alpha = 0$ на фиг. 4). При учете демпфирования $(d \ne 0)$ такое пороговое значение 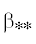 не может существовать, поскольку тогда первый корень неустойчив всегда; и на фиг. 4 видно, что ${{\sigma }_{{\max }}}(\beta ;d = 1)$ плавно затухает при $\beta \to \infty $, никак не “ощущая” переход через пороговое значение
не может существовать, поскольку тогда первый корень неустойчив всегда; и на фиг. 4 видно, что ${{\sigma }_{{\max }}}(\beta ;d = 1)$ плавно затухает при $\beta \to \infty $, никак не “ощущая” переход через пороговое значение 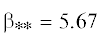 , при котором ${{\sigma }_{{\max }}}(\beta ;d = 0)$ резко падает до нуля. Таким образом, хотя демпфирование при умеренных $\beta $ подавляет неустойчивость, при достижении порогового значения ${{\beta }_{{*{\kern 1pt} *}}}$ и выше оно оказывает противоположный эффект, приводя к появлению неустойчивости (хотя
и слабой).
, при котором ${{\sigma }_{{\max }}}(\beta ;d = 0)$ резко падает до нуля. Таким образом, хотя демпфирование при умеренных $\beta $ подавляет неустойчивость, при достижении порогового значения ${{\beta }_{{*{\kern 1pt} *}}}$ и выше оно оказывает противоположный эффект, приводя к появлению неустойчивости (хотя
и слабой).
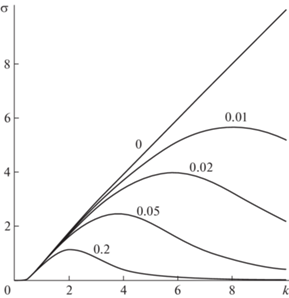
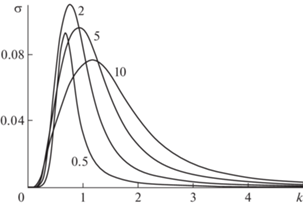
Характер влияния демпфирования на неустойчивость при увеличении d можно проследить по типичным фиг. 5 и фиг. 6, на которых отображена зависимость инкремента нарастания $\sigma (k)$ при $K = 1$ и $\alpha = 0$ для ряда значений d (отмечены соответствующими цифрами рядом). Как показывают расчеты, в “допороговом”
случае (см. фиг. 5 для 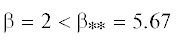 ) максимальный инкремент нарастания ${{\sigma }_{{\max }}}$ монотонно снижается с ростом d (т.е., чем больше демпфирование, тем больше оно подавляет неустойчивость), тогда
как в “запороговом” случае (см. фиг. 6 для
) максимальный инкремент нарастания ${{\sigma }_{{\max }}}$ монотонно снижается с ростом d (т.е., чем больше демпфирование, тем больше оно подавляет неустойчивость), тогда
как в “запороговом” случае (см. фиг. 6 для 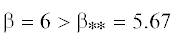 ) максимальный инкремент нарастания ${{\sigma }_{{\max }}}$ сначала растет, а затем падает (т.е. демпфирование сначала приводит к появлению и
росту неустойчивости, а затем начинает давить ее).
) максимальный инкремент нарастания ${{\sigma }_{{\max }}}$ сначала растет, а затем падает (т.е. демпфирование сначала приводит к появлению и
росту неустойчивости, а затем начинает давить ее).
3. ВЫВОДЫ
1. Итак, в рамках теории свободного взаимодействия показано, что в пределе высоких чисел Рейнольдса невязкая неустойчивость может существовать только за счет инерционности или демпфирования пластины (если инерционность и демпфирование пренебрежимо малы, то течение будет устойчивым по отношению к невязким возмущениям).
2. Если при наличии демпфирования инерционность и изгибная жесткость пренебрежимо малы, то это приводит к катастрофической потере неустойчивости: инкремент нарастания возмущений неограниченно растет в коротковолновом пределе $(k \to \infty )$.
3. При наличии инерционности существует критическое значение изгибной жесткости $\beta = \beta _{*}^{{}} = 1$, при которой инкремент нарастания возмущений неограниченно растет в коротковолновом пределе. Демпфирование не может справиться с этой “катастрофой” (только уменьшает инкремент нарастания на конечную величину).
4. При наличии демпфирования всегда (при любых $k \ne 0$, $K$, $\alpha $ и $\beta $) существует ровно одна неустойчивая мода собственных колебаний течения, в том числе
и при превышении порогового значения 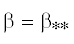 (зависящего от $K$ и $\alpha $), когда неустойчивость пропадает, если пренебрегать демпфированием.
(зависящего от $K$ и $\alpha $), когда неустойчивость пропадает, если пренебрегать демпфированием.
Список литературы
Kramer M.O. Boundary-layer stabilization by distributed damping // J. Aeronaut. Sci. 1957. V. 24. P. 458–460.
Benjamin T.B. Effects of a flexible boundary on hydrodynamic stability // J. Fluid Mech. 1960. № 9. P. 513–532.
Benjamin T.B. The threefold classification of unstable disturbances in flexible surfaces bounding inviscid flows // J. Fluid Mech. 1963. № 16. P. 436–450.
Landahl M.T. On the stability of a laminar incompressible boundary layer over a flexible surface// J. Fluid Mech. 1962. № 13. P. 609–632.
Carpenter P.W., Garrad A.D. The hydrodynamic stability of flow over Kramer-type compliant surfaces. Part 1. Tollmien-Schlichting instabilities // J. Fluid Mech. 1985. V. 155. P. 465–510.
Riley J.J., Gad-el-Hak, Metcalfe R.W. Compliant coatings// Ann. Rev. Fluid Mech. 1988. № 20. P. 393–420.
Flow Past Highly Compliant Boundaries and in Collapsible Tubes // Proc. of the IUTAM Symp., University of Warwick, UK, 26–30 March 2001. Kluwer Acad. Publ., 2003.
Gad-el-Hak M. Compliant coatings for drag reduction // Progress in Aerospace Sciences. 2002. V. 38. Iss. 1. January 2002. P. 77–99.
Carpenter P.W. Recent progress in the use of compliant walls for laminar flow control // Progress in Industrial Mathematics at ECMI 2006. Math. in Industry. 2008. № 12. P. 178.
Нейланд В.Я. К теории отрыва ламинарного пограничного слоя в сверхзвуковом потоке // Изв. АН СССР. Сер. механ. жидкости и газа. 1969. № 4. С. 53–58.
Stewartson K., Williams P.G. Self-induced separation // Proc. Roy. Soc. A. 1969. V. 312. № 1509. P. 181–206.
Messiter A.F. Boundary-layer flow near the trailing edge of a flat plate // SIAM J. Appl. Math. 1970. V. 18. № 1. P. 241–257.
Савенков И.В. Подавление роста нелинейных волновых пакетов упругостью обтекаемой поверхности // Ж. вычисл. матем. и матем. физ. 1995. Т. 35. № 1. С. 95–103.
Савенков И.В. Об абсолютной неустойчивости несжимаемого пограничного слоя на податливой поверхности // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 2. С. 281–290.
Савенков И.В. Влияние инерционности податливой поверхности на вязкую неустойчивость несжимаемого пограничного слоя// Ж. вычисл. матем. и матем. физ. 2019. Т. 59. № 4. С. 707–715.
Walker J.D.A., Fletcher A., Ruban A.I. Instabilities of a flexible surface in supersonic flow // Q. Jl Mech. Appl. Math. 2006. V. 59. № 2. P. 253–276.
Савенков И.В. Невязкая неустойчивость несжимаемого пограничного слоя на податливой поверхности // Ж. вычисл. матем. и матем. физ. 2020. Т. 60. № 7. С. 1268–1280.
Жук В.И. Волны Толлмина–Шлихтинга и солитоны. М.: Наука, 2001. 167 с.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики