1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 63, № 9, 2023

Журнал вычислительной математики и математической физики, 2023, T. 63, № 9, стр. 1446-1457

О единственности решения систем линейных алгебраических уравнений, к которым редуцируются обратные задачи гравиметрии и магнитометрии: региональный вариант

И. И. Колотов 1, Д. В. Лукьяненко 1, И. Э. Степанова 1, 2, *, А. В. Щепетилов 1, А. Г. Ягола 1

1 МГУ им. М.В. Ломоносова, физический факультет, кафедра математики
119992 Москва, Ленинские горы, 1, Россия

2 Институт физики Земли им. О.Ю. Шмидта РАН
123995 Москва, ул. Б. Грузинская, 10, стр. 1, Россия

* E-mail: tet@ifz.ru

Поступила в редакцию 06.02.2023
После доработки 06.02.2023
Принята к публикации 29.05.2023

Полный текст (PDF)

Аннотация

Рассматриваются условия однозначной разрешимости систем линейных алгебраических уравнений, к решению которых редуцируются многие обратные задачи гравимагниторазведки. Математические постановки обратных задач выполняются с учетом сферичности планеты. Библ. 11. Фиг. 5.

Ключевые слова: разрешимость, вырожденные системы, интегральные представления.

ВВЕДЕНИЕ

При решении обратных геофизических задач интерпретационного характера необходимо находить скалярные и векторные функции, описывающие плотности распределения источников поля. В общем случае указанные функции зависят от бесконечного (зачастую, несчетного) числа параметров и, согласно результатам, приведенным, например, в [1], однозначно не могут быть восстановлены. Если перейти к конечномерным аппроксимациям как наблюдаемых элементов аномальных физических полей, так и самих источников, то единственное решение условно-вариационных задач, возникающих при интерпретации данных гравиметрии и магнитометрии, можно получить при выполнении ряда условий. Мы попытаемся сформулировать условия однозначной разрешимости соответствующих систем линейных алгебраических уравнений (СЛАУ) в региональном варианте, т.е. тогда, когда необходимо учитывать сферичность Земли. Постановки такого рода появляются при исследованиях физических полей на больших полигонах, размеры которых превышают 1 градус (приблизительно 111 км для Земли) в двух направлениях.

1. ЕДИНСТВЕННОСТЬ РЕШЕНИЯ СЛАУ В РЕГИОНАЛЬНОМ ВАРИАНТЕ МЕТОДА S-АППРОКСИМАЦИЙ

Основные характеристики метода S-аппроксимаций в двух случаях (локальном и региональном) были изложены в работах первого автора (см., например, [1–5]). Этот метод хорошо зарекомендовал себя при решении самых разнообразных обратных геофизических и геодезических задач и был модифицирован с целью нахождения более адекватных реальности распределений эквивалентных по внешнему полю источников.

Напомним основные положения регионального варианта метода S-аппроксимаций.

Для нахождения производных гравитационного поля в некоторой совокупности точек ${{M}_{\nu }}$ с координатами ${{x}^{{(\nu )}}} = (x_{1}^{{(\nu )}},x_{2}^{{(\nu )}},x_{3}^{{(\nu )}})$, из внешности СE некоторой области $E \subset {{R}^{3}}$ в рамках метода линейных интегральных представлений (см. [1]) необходимо действовать следующим образом.

Пусть D – сфера, описываемая уравнением $r = {\text{const}} = R.$

По заданным плотностям ${{\rho }_{1}}({{\xi }_{1}},{{\xi }_{2}}) \in {{L}_{2}}(D)$ и ${{\rho }_{2}}({{\xi }_{1}},{{\xi }_{2}}) \in {{L}_{2}}(D)$ простого и двойного слоев мы должны найти совокупность ограниченных линейных функционалов вида

(1.1)
$\begin{gathered} {{p}_{s}} = \int\limits_D {{{\rho }_{1}}({{\xi }_{1}},{{\xi }_{2}})P_{1}^{{(s)}}({{\xi }_{1}},{{\xi }_{2}})\mu ({{\xi }_{1}},{{\xi }_{2}})d{{\xi }_{1}}} d{{\xi }_{2}} + \int\limits_D {{{\rho }_{2}}({{\xi }_{1}},{{\xi }_{2}})P_{2}^{{(s)}}} ({{\xi }_{1}},{{\xi }_{2}})\mu ({{\xi }_{1}},{{\xi }_{2}})d{{\xi }_{1}}d{{\xi }_{2}}, \\ s = 1,{\text{ }}2, \ldots ,S, \\ \end{gathered} $
где для всех s

(1.2)
$\begin{gathered} {{\left\| {P_{1}^{{(s)}}} \right\|}^{2}} = \int\limits_D {{{{(P_{1}^{{(s)}})}}^{2}}({{\xi }_{1}},{{\xi }_{2}})d\mu ({{\xi }_{1}},{{\xi }_{2}})} < + \infty , \hfill \\ {{\left\| {P_{2}^{{(s)}}} \right\|}^{2}} = \int\limits_D {{{{(P_{2}^{{(s)}})}}^{2}}({{\xi }_{1}},{{\xi }_{2}})d\mu ({{\xi }_{1}},{{\xi }_{2}})} < + \infty . \hfill \\ \end{gathered} $

В формулах (1.1) и (1.2) $\mu ({{\xi }_{1}},{{\xi }_{2}})$ – мера на поверхности D, ${{\xi }_{1}},\;{{\xi }_{2}}$ – координаты на поверхности D. В случае сферы в роли ${{\xi }_{1}},\;{{\xi }_{2}}$ выступают $\vartheta ,\;\varphi ,$ $d\mu ({{\xi }_{1}},{{\xi }_{2}}) = {{R}^{2}}\sin \vartheta d\vartheta d\varphi .$

В дальнейшем в роли области E у нас будет выступать “идеальная” Земля, а в роли внешности такой идеальной Земли – реальная Земля.

Представим себе идеализированную Землю как внутренность сферы радиуса ${{R}_{0}}$. Реальная Земля тогда может трактоваться как область трехмерного пространства, ограниченная замкнутой кусочно-непрерывной поверхностью S, незначительно отклоняющейся от сферы радиуса ${{R}_{0}}$. Предполагается, что приближенные значения функции $G(x)$, гармонической вне этой сферы, заданы в произвольном множестве точек${{x}^{{(i)}}},\;i = 1,2, \ldots N$, на поверхности S:

(1.3)
${{f}_{{i,\delta }}} = {{f}_{i}} + \delta {{f}_{i}},\quad {{f}_{i}} = G({{x}^{{(i)}}}).$

Так как G(x) гармонична при $r > {{R}_{0}}$, она имеет следующее интегральное представление:

(1.4)
$\begin{gathered} G(x) = \frac{{R_{0}^{2}}}{{4\pi }}\int\limits_0^{2\pi } {\int\limits_0^\pi {\frac{{\sigma (\tilde {\vartheta },\tilde {\varphi })\widetilde {\sin \vartheta }d\tilde {\vartheta }d\tilde {\varphi }}}{{R(\xi - x)}}} } + \frac{{R_{0}^{2}}}{{4\pi }}\int\limits_0^{2\pi } {\int\limits_0^\pi {\frac{{w(\tilde {\vartheta },\tilde {\varphi })({{R}_{0}} - r\cos \vartheta {\kern 1pt} ')\widetilde {\sin \vartheta }d\tilde {\vartheta }d\tilde {\varphi }}}{{{{R}^{3}}(\xi - x)}}} } , \\ R(\xi - x) = {{\left( {R_{0}^{2} - 2{{R}_{0}}r\cos \vartheta {\kern 1pt} '\; + {{r}^{2}}} \right)}^{{1/2}}},\quad \xi = ({{R}_{0}}\widetilde {\cos \varphi }\widetilde {\sin \vartheta },{{R}_{0}}\widetilde {\sin \varphi }\widetilde {\sin \vartheta },{{R}_{0}}\widetilde {\cos \varphi }), \\ x = (r\cos \varphi \sin \vartheta ,r\sin \varphi \sin \vartheta ,r\cos \vartheta ),\quad \cos \vartheta {\kern 1pt} ' = \sin \vartheta \widetilde {\sin \vartheta }\cos (\varphi - \tilde {\varphi }) + \cos \vartheta \widetilde {\cos \vartheta }. \\ \end{gathered} $

Функция $\sigma (\tilde {\vartheta },\tilde {\phi })$ в (1.4) – плотность простого слоя, распределенного на сфере радиуса ${{R}_{0}}$, $w(\tilde {\vartheta },\tilde {\phi })$ – плотность двойного слоя, распределенного на той же сфере; $R(\xi - x)$ – расстояние между текущей точкой сферы $\xi $ и точкой наблюдения x. Дифференцирование правой части (1.4) – по различным координатам точки наблюдения G(x), даже если эти производные (например, $\partial V{\text{/}}\partial r$ – радиальная производная гравитационного потенциала) не являются гармоническими функциями.

Формула (1.4) является одной из форм интегрального представления гармонической функции вне сферы радиуса R (см. [6]):

(1.5)
$V(x) = \frac{1}{{4\pi }}\int\limits_0^{2\pi } {\int\limits_0^\pi {\left( {\frac{1}{{R(\xi - x)}}\frac{{\partial V(\xi )}}{{\partial {\mathbf{n}}}} - V(\xi )\frac{\partial }{{\partial {\mathbf{n}}}}\left( {\frac{1}{{R(\xi - x}}} \right)} \right)\widetilde {\sin \vartheta }d\tilde {\vartheta }d\tilde {\phi },} } $
где ${\mathbf{n}}$ – внешняя нормаль к единичной сфере (мы можем написать $\partial {\text{/}}\partial r$, r – радиальная координата радиус-вектора x).

Условно-вариационная задача для $\sigma $ и w (см. [4, 7]) имеет следующее решение:

(1.6)
$\sigma (\hat {\xi }) = \sum\limits_{i = 1}^N {{{\lambda }_{i}}Q_{i}^{{(1)}}(\xi )} ,\quad w(\hat {\xi }) = \sum\limits_{i = 1}^N {{{\lambda }_{i}}Q_{i}^{{(2)}}(\xi )} ,\quad \hat {\xi } = (\tilde {\vartheta },\tilde {\varphi }),\quad \xi = (R,\tilde {\vartheta },\tilde {\varphi }),$
где $Q_{i}^{{(1)}}(\xi )$ и $Q_{i}^{{(2)}}(\xi )$представляются в виде

(1.7)
$Q_{i}^{{(1)}}(\xi ) = \frac{1}{{R(\xi - {{x}^{{(i)}}})}},\quad Q_{i}^{{(2)}}(\xi ) = \frac{{{{R}_{0}} - {{r}_{i}}\cos \vartheta _{i}^{'}}}{{{{R}^{3}}(\xi - {{x}^{{(i)}}})}}.$

Величины ${{\lambda }_{i}}$ являются компонентами N-вектора $\lambda $, дающего решение системы линейных уравнений

(1.8)
$A\lambda = {{f}_{\delta }},\quad {{f}_{\delta }} = f + \delta f,$

где ${{f}_{\delta }}$ имеет компоненты ${{f}_{{i,\delta }}}$ (см. (1.3)) и элементы матрицы $A = {{A}^{{\text{T}}}} \geqslant 0$ записываются как

(1.9)
$\begin{gathered} {{a}_{{ij}}} = \int\limits_0^{2\pi } {\int\limits_0^\pi {\left[ {Q_{i}^{{\left( 1 \right)}}\left( \xi \right)Q_{j}^{{\left( 1 \right)}}\left( \xi \right) + Q_{i}^{{\left( 2 \right)}}\left( \xi \right)Q_{j}^{{\left( 2 \right)}}\left( \xi \right)} \right]\widetilde {\sin \vartheta }d\tilde {\vartheta }d\tilde {\phi }} } = \frac{{2\pi }}{{{{{({{h}_{i}}{{h}_{j}})}}^{{1/2}}}{{r}_{i}}{{r}_{j}}}}\left( {1 + \frac{{0.25}}{{{{r}_{i}}{{r}_{j}}{{h}_{i}}{{h}_{j}}}}} \right) \times \\ \times \;F(2arctg(\sqrt {{{h}_{i}}{{h}_{j}}} ),\sqrt {0.5(1 + \cos {{\alpha }_{i}}_{j})} ) - \frac{{\pi (3{{{({{h}_{i}}{{h}_{j}})}}^{2}} - 4{{h}_{i}}{{h}_{j}}\cos {{\alpha }_{i}}_{j} + 1)}}{{{{r}_{i}}^{2}r_{j}^{2}{{h}_{i}}{{h}_{j}}{{{(\sqrt {1 - 2{{h}_{i}}{{h}_{j}}\cos {{\alpha }_{i}}_{j}) + {{{({{h}_{i}}{{h}_{j}})}}^{2}}} )}}^{3}}}}. \\ \end{gathered} $
Здесь ${{h}_{i}} = {{R}_{0}}{\text{/}}{{r}_{i}},$ ${{h}_{j}} = {{R}_{0}}{\text{/}}{{r}_{j}}$. ${{\alpha }_{{ij}}}$ – угол между векторами ${{x}_{i}}$ и ${{x}_{j}}$. Предполагаем, что вектор ${{x}_{i}}$ параллелен оси Oz, а вектор ${{x}_{j}}$ лежит в плоскости zOx (мы всегда так можем выбрать систему координат). Тогда указанные векторы будут иметь координаты
${{x}_{i}} = ({{r}_{i}},\,0,\,0)\quad {\text{и}}\quad {{x}_{j}} = ({{r}_{j}}\sin {{\alpha }_{{ij}}},\,0,\,{{r}_{j}}\cos {{\alpha }_{{ij}}}).$
Функция $F(\varphi ,k)$ – это эллиптический интеграл I рода.

В настоящей работе мы ограничимся рассмотрением представления элементов аномального гравитационного поля в региональном и глобальном масштабах в виде потенциала простого слоя. Элементы матрицы системы (1.9) принимают тогда вид

(1.10)
${{a}_{{ij}}} = \frac{{2\pi }}{{{{{({{h}_{i}}{{h}_{j}})}}^{{1/2}}}{{r}_{i}}{{r}_{j}}}}F(2\operatorname{arctg} (\sqrt {{{h}_{i}}{{h}_{j}}} ),\sqrt {0.5(1 + \cos {{\alpha }_{i}}_{j})} ).$

Покажем, что в размерности 2 СЛАУ не вырождена.

Для этого выпишем явное выражение для элементов матрицы (1.10):

(1.11)
$\begin{gathered} {{a}_{{ij}}} = \frac{{2\pi }}{{{{{({{h}_{i}}{{h}_{j}})}}^{{1/2}}}{{r}_{i}}{{r}_{j}}}}\int\limits_0^{\sqrt {{{h}_{i}}{{h}_{j}}} } {\frac{{dh}}{{\sqrt h \sqrt {1 - 2h\cos {{\alpha }_{{ij}}} + {{h}^{2}}} }}} . \hfill \\ \hfill \\ \end{gathered} $

Для того чтобы матрица системы (1.8) с элементами (1.10) или (1.11) была вырождена, достаточно, чтобы какие-либо две строки этой матрицы были пропорциональны. Пусть это будут строки с номерами i и j. Покажем, что если соответствующие этим индексам точки наблюдения различны, то пропорциональность не может иметь места. Сначала докажем следующие две леммы.

Лемма 1. Для произвольной непрерывно дифференцируемой на отрезке $[c,d],\;0 < c < d,$ функции F(y), не обращающейся в нуль на этом отрезке вместе со своей производной, строго возрастающей и логарифмически выпуклой вниз, для любых $a,b \in [c,d],$ $0 < a < b,$ выполняется неравенство

(1.12)
$F(a)F(b) \geqslant {{\left[ {F(\sqrt {ab)} } \right]}^{2}}.$

Доказательство. Введем вспомогательную переменную х и рассмотрим выражение

$\Phi (x) = F(a{\text{/}}x)F(bx).$

Будем считать, что переменная x меняется таким образом, что аргумент функции $F(a{\text{/}}x)$ или F(bx) лежит на отрезке $[c,d].$

Вычислим производную функции $\Phi (x)$ и приравняем ее нулю:

(1.13)
$\Phi {\kern 1pt} '(x) = - \frac{a}{{{{x}^{2}}}}F{\kern 1pt} '(a{\text{/}}x)F(bx) + bF(a{\text{/}}x)F{\kern 1pt} '(bx) = 0 \Rightarrow {{x}^{2}} = \frac{a}{b}\frac{{F{\kern 1pt} '(a{\text{/}}x)F(bx)}}{{F(a{\text{/}}x){{F}^{'}}(bx)}}.$

Легко видеть, что при ${{x}^{2}} = a{\text{/}}b$ аргументы функций в числителе и знаменателе (1.13) совпадают и равны $\sqrt {ab} $. При этом производная функции $\Phi (x)$ в точке $x = \sqrt {ab} $ равна нулю. Следовательно, эта функция достигает в указанной точке экстремума. Для логарифмически выпуклой вниз функции это – минимум.

В самом деле, вторая производная от логарифма такой функции положительна:

$\ln \left( {F(x)} \right){\kern 1pt} '{\kern 1pt} ' = \left( {\frac{{F{\kern 1pt} '(x)}}{{F(x)}}} \right){\kern 1pt} ' > 0.$

Если $x = \sqrt {a{\text{/}}b} ,$ $a < b,$ то x меньше единицы, а при x = 1 будем иметь $\Phi {\kern 1pt} '(1) = $ $ = - aF{\kern 1pt} '(a)F(b) + bF(a)F{\kern 1pt} '(b) > 0$ для логарифмически выпуклой вниз функции F(x) при b > a. На отрезке $\left[ {\sqrt {a{\text{/}}b} ,1} \right]$ производная функции $\Phi {\kern 1pt} '(x)$ также положительна вследствие логарифмической выпуклости функции $F(x)$.

Лемма 2. Для любой функции F(x), представляющейся на отрезке $[c,d],\;0 < c < d,$ абсолютно сходящимся степенным рядом с положительными коэффициентами, справедливо неравенство (1.12) при любых $a,b \in [c,d]$, $0 < a < b$.

Доказательство. Выпишем неравенство (1.12) для частичных сумм соответствующих степенных рядов и учтем тот факт, что произведение абсолютно сходящихся степенных рядов есть абсолютно сходящийся степенной ряд:

${{F}_{n}}(x) = \sum\limits_{i = 0}^n {{{a}_{i}}{{x}^{i}}} ,\quad F(y) = \sum\limits_{k = 0}^n {{{a}_{k}}{{y}^{k}}} ,$
$F(x)F(y) = \sum\limits_{i = 0}^n {\sum\limits_{k = 0}^n {{{a}_{i}}{{a}_{k}}} } {{x}^{i}}{{y}^{k}} \geqslant \sum\limits_{i = 0}^n {\sum\limits_{k = 0}^n {{{a}_{i}}{{a}_{k}}} } {{\left( {\sqrt {xy} } \right)}^{{i + k}}} = {{\left( {F\left( {\sqrt {xy} } \right)} \right)}^{2}},$
так как ${{a}_{i}}{{a}_{k}}({{x}^{i}}{{y}^{k}} + {{x}^{k}}{{y}^{i}}) \geqslant 2{{a}_{i}}{{a}_{k}}\left( {{{x}^{{i + k{\text{/}}2}}}{{y}^{{i + k{\text{/}}2}}}} \right)$, $i,k = 0,...,n$.

Устремим теперь $n \to \infty $ и получим требуемое утверждение при x = a и y = b.

Теперь перейдем к доказательству невырожденности системы (1.8)–(1.10). Нам нужно убедиться в том, что

(1.14)
${{a}_{{ii}}}{{a}_{{jj}}} \geqslant {{\left( {{{a}_{{ij}}}} \right)}^{2}},$
причем знак равенства имеет место лишь в случае совпадения двух точек наблюдения. Рассмотрим неравенство (1.14):

${{a}_{{ii}}}{{a}_{{jj}}} = \frac{{4{{\pi }^{2}}}}{{h_{i}^{2}h_{j}^{2}r_{i}^{2}r_{j}^{2}}}\int\limits_0^{{{h}_{i}}} {\int\limits_0^{{{h}_{j}}} {\frac{{dxdy}}{{\sqrt {xy} (1 - x)(1 - y)}}} } ,$
(1.15)
$a_{{ij}}^{2} = \frac{{4{{\pi }^{2}}}}{{h_{i}^{2}h_{j}^{2}r_{i}^{2}r_{j}^{2}}}\int\limits_0^{{{{\sqrt {{{h}_{j}}h} }}_{i}}} {\int\limits_0^{{{{\sqrt {{{h}_{j}}h} }}_{i}}} {\frac{{dxdy}}{{\sqrt {xy} \sqrt {1 - 2{{h}_{i}}\cos {{\alpha }_{{ij}}} + {{h}_{i}}^{2}} \sqrt {1 - 2{{h}_{j}}\cos {{\alpha }_{{ij}}} + {{h}_{j}}^{2}} }}} } ,$
${{a}_{{ii}}}{{a}_{{jj}}} \geqslant a_{{ij}}^{2} \Rightarrow \int\limits_0^{{{h}_{i}}} {\int\limits_0^{{{h}_{j}}} {\frac{{dxdy}}{{\sqrt {xy} (1 - x)(1 - y)}}} } \geqslant \int\limits_0^{{{{\sqrt {{{h}_{j}}h} }}_{i}}} {\int\limits_0^{{{{\sqrt {{{h}_{j}}h} }}_{i}}} {\frac{{dxdy}}{{\sqrt {xy} \sqrt {1 - 2{{h}_{i}}\cos {{\alpha }_{{ij}}} + {{h}_{i}}^{2}} \sqrt {1 - 2{{h}_{j}}\cos {{\alpha }_{{ij}}} + {{h}_{j}}^{2}} }}} } .$

Надо доказать, что строгое неравенство в формуле (1.15) выполняется всегда, если $\cos {{\alpha }_{{ij}}} \ne 1.$ Подынтегральная функция в левой части (1.15) в каждой точке по (x, y) больше подынтегральной функции в правой части, если точки наблюдения не совпадают ($\cos {{\alpha }_{{ij}}} \ne 1,$ ${{h}_{i}} \ne {{h}_{j}}$). По этой причине мы можем оценить интегралы только одной из этих функций (соответствующей произведению диагональных элементов) по двум областям. Но интеграл в левой части (1.15) вычисляется в явном виде:

$\int\limits_0^{{{h}_{i}}} {\int\limits_0^{{{h}_{j}}} {\frac{{dxdy}}{{\sqrt {xy} (1 - x)(1 - y)}}} } = \ln \left( {\frac{{1 + {{h}_{i}}}}{{1 - {{h}_{i}}}}} \right)\ln \left( {\frac{{1 + {{h}_{j}}}}{{1 - {{h}_{j}}}}} \right),$
$\int\limits_0^{\sqrt {{{h}_{i}}{{h}_{j}}} } {\int\limits_0^{\sqrt {{{h}_{i}}{{h}_{j}}} } {\frac{{dxdy}}{{\sqrt {xy} (1 - x)(1 - y)}}} } = \ln {{\left( {\frac{{1 + \sqrt {{{h}_{i}}{{h}_{j}}} }}{{1 - \sqrt {{{h}_{i}}{{h}_{j}}} }}} \right)}^{2}}.$

Положим теперь $F(x) = \ln \left( {\frac{{1 + x}}{{1 - x}}} \right)$ и применим лемму 1 или лемму 2. Получим требуемое утверждение. Таким образом, доказана следующая

Теорема 1. Система (1.8)–(1.10) не вырождена в размерности 2, если точки наблюдения различны.

Рассмотрим теперь случай двойного слоя. Элементы матрицы тогда выражаются формулой

(1.16)
${{a}_{{ij}}} = \frac{{2\pi }}{{{{{({{h}_{i}}{{h}_{j}})}}^{{1/2}}}{{r}_{i}}{{r}_{j}}}}F(2\operatorname{arctg} (\sqrt {{{h}_{i}}{{h}_{j}}} ),\sqrt {0.5(1 + \cos {{\alpha }_{i}}_{j})} ) - \frac{{\pi (3{{{({{h}_{i}}{{h}_{j}})}}^{2}} - 4{{h}_{i}}{{h}_{j}}\cos {{\alpha }_{i}}_{j} + 1)}}{{{{r}_{i}}^{2}r_{j}^{2}{{h}_{i}}{{h}_{j}}{{{(\sqrt {1 - 2{{h}_{i}}{{h}_{j}}\cos {{\alpha }_{i}}_{j}) + {{{({{h}_{i}}{{h}_{j}})}}^{2}}} )}}^{3}}}}.$

Попробуем оценить второе слагаемое в (1.16). Заметим сначала, что при выполнении условия

(1.17)
$\frac{1}{3} \leqslant {{h}_{i}}{{h}_{j}} < 1$
числитель второго слагаемого в (1.16) всегда неотрицателен.

Числитель $ - \frac{{\pi (3{{{({{h}_{i}}{{h}_{j}})}}^{2}} - 4{{h}_{i}}{{h}_{j}}\cos {{\alpha }_{i}}_{j} + 1)}}{{{{r}_{i}}^{2}r_{j}^{2}{{h}_{i}}{{h}_{j}}{{{(\sqrt {1 - 2{{h}_{i}}{{h}_{j}}\cos {{\alpha }_{i}}_{j}) + {{{({{h}_{i}}{{h}_{j}})}}^{2}}} )}}^{3}}}}$ меньше для внедиагональных элементов (когда $\cos {{\alpha }_{i}}_{j} \ne 1$ или ${{h}_{i}} \ne {{h}_{j}}$), а знаменатель – соответственно, больше, чем у диагональных: вычитается большее по модулю число. Поскольку для любых четырех положительных чисел ${{a}_{1}},\;{{a}_{2}},\;{{b}_{1}},\;{{b}_{2}}$, удовлетворяющих условиям ${{a}_{1}}{{a}_{2}} \geqslant {{a}^{2}}$, ${{b}_{1}}{{b}_{2}} \geqslant {{b}^{2}}$, где a и b – также положительные заданные числа, справедливо неравенство

(1.18)
$\left( {{{a}_{1}} + {{b}_{1}}} \right)\left( {{{a}_{2}} + {{b}_{2}}} \right) \geqslant {{\left( {a + b} \right)}^{2}},$

то верна следующая

Теорема 2. Система (1.8), (1.16) не вырождена в размерности 2, если координаты точек наблюдения не совпадают.

Замечание. Точки наблюдения могут иметь одинаковые угловые координаты, но тогда они должны находиться на разных расстояниях от начала координат. Неравенство (1.18) доказывается элементарно. В самом деле,

$\left( {{{a}_{1}} + {{b}_{1}}} \right)\left( {{{a}_{2}} + {{b}_{2}}} \right) \geqslant {{a}_{1}}{{a}_{2}} + {{b}_{1}}{{b}_{2}} + {{a}_{1}}{{b}_{2}} + {{a}_{2}}{{b}_{1}} \geqslant {{a}^{2}} + {{b}^{2}} + 2ab = {{\left( {a + b} \right)}^{2}},$
так как ${{a}_{1}}{{b}_{2}} + {{a}_{2}}{{b}_{1}} \geqslant 2\sqrt {{{a}_{1}}{{a}_{2}}{{b}_{1}}{{b}_{2}}} \geqslant 2ab$.

2. ЕДИНСТВЕННОСТЬ РЕШЕНИЯ ОБРАТНЫХ ЗАДАЧ МАГНИТОМЕТРИИ

Обратные задачи магниторазведки (особенно нелинейные, когда требуется определить не только плотность распределения источников аномального магнитного поля, но и локализовать носители масс) являются весьма сложными и требуют применения различных регуляризирующих алгоритмов (см. [8–11]). В настоящей статье мы ограничимся исследованием парамагнитных сред, когда зависимость вектора намагниченности от напряженности внешнего магнитного поля считается линейной. Для ферромагнетиков интегральные уравнения, связывающие результаты наблюдений (компоненты вектора магнитной индукции) и свойства среды, будут нелинейными, и для анализа однозначной разрешимости таких постановок требуется несколько иной математический аппарат.

Мы полагаем, что для магнитной индукции имеет место следующее интегральное представление (см. [8, 9]):

$\bar {B}({{\bar {r}}_{s}}) = \frac{{{{\mu }_{0}}}}{{4\pi }}\iiint\limits_V {K({{{\bar {r}}}_{s}}},\bar {r})M(\bar {r})dv,\quad \bar {r} = (r,\vartheta ,\phi );\quad {{\bar {r}}_{s}} = ({{r}_{s}},{{\vartheta }_{s}},{{\phi }_{s}}),$
(2.1)
$K({{\bar {r}}_{s}},\bar {r}) = \frac{1}{{{{\rho }^{5}}}}\left[ {\begin{array}{*{20}{c}} {2\rho _{r}^{2} - \rho _{\vartheta }^{2} - \rho {{{_{\phi }^{2}}}^{{}}}}&{3{{\rho }_{r}}{{\rho }_{\vartheta }}}&{3{{\rho }_{r}}{{\rho }_{\phi }}} \\ {3{{\rho }_{r}}{{\rho }_{\vartheta }}}&{2\rho _{\vartheta }^{2} - \rho _{r}^{2} - \rho _{\phi }^{2}}&{3{{\rho }_{\vartheta }}{{\rho }_{\phi }}} \\ {3{{\rho }_{r}}{{\rho }_{\phi }}}&{3{{\rho }_{\vartheta }}{{\rho }_{\phi }}}&{2\rho _{\phi }^{2} - \rho _{r}^{2} - \rho _{\vartheta }^{2}} \end{array}} \right],$
$\bar {\rho } = \bar {r} - {{\bar {r}}_{s}},\quad \rho \equiv \left| {\bar {r} - {{{\bar {r}}}_{s}}} \right|.$
Здесь ${{\bar {r}}_{s}}$ – радиус-вектор точки наблюдения ${{P}_{s}}$ в сферической системе координат, $\bar {r}$ – радиус-вектор точки внутри носителя V, $\bar {B}({{\bar {r}}_{s}})$ – магнитная индукция в системе СИ, измеренная в точке, характеризующейся радиус-вектором ${{\bar {r}}_{s}}$, ${{\mu }_{0}}$ – магнитная постоянная в системе СИ. Через $K({{\bar {r}}_{s}},\bar {r})$ обозначена матричная функция координат точки наблюдения и точки, принадлежащей носителю, $M(\bar {r})$ – вектор-функция, характеризующая намагниченность среды. В отличие от локального варианта, сферическая система координат фиксирована и связана с общеземной, в противном случае результаты наблюдений магнитного поля в разных точках планеты не были бы согласованы. Начало координат расположено в центре Земли. Необходимо также подчеркнуть, всюду в данном разделе статьи предполагается, что компоненты вектора магнитной индукции измеряются в точке наблюдения, с которой связан репер криволинейной системы координат, гладко зависящий от координат этой точки. Фактически, мы имеем дело с некоторым расслоением реперов. Поменять местами магнитные диполи и точки наблюдения нельзя, в отличие от локального случая, когда все измерения выполняются в некоторой декартовой системе координат и базисные векторы зафиксированы в пространстве.

Поле, создаваемое одним магнитным диполем, выражается формулой

(2.2)
$B({{\bar {r}}_{s}}) = \frac{{{{\mu }_{0}}}}{{4\pi }}\frac{{3\left( {\bar {m},\bar {r} - {{{\bar {r}}}_{s}}} \right)\left( {\bar {r} - {{{\bar {r}}}_{s}}} \right) - {{\rho }^{2}}\bar {m}}}{{{{\rho }^{5}}}}.$

В (2.2) приняты такие же обозначения, что и в (2.1). Через $\bar {m} = {{\left( {{{m}_{r}},{{m}_{\vartheta }},{{m}_{\varphi }}} \right)}^{{\text{T}}}}$ обозначен магнитный момент точечного диполя в указанной сферической системе координат. Как и в локальном случае, установим в точках наблюдения условные “сенсоры”. В результате дискретизации интегрального представления (2.1) мы приходим к следующей системе линейных алгебраических уравнений:

$\sum\limits_{i = 1}^M {\left( {\frac{{3\left\{ {{{m}_{{ir}}}{{\rho }_{{ki,r}}} + {{m}_{{i\vartheta }}}{{\rho }_{{ki,\vartheta }}} + {{m}_{{i\varphi }}}{{\rho }_{{ki,\varphi }}}} \right\}{{\rho }_{{ki,r}}}}}{{\rho _{{ki}}^{5}}} - \frac{{{{m}_{{ir}}}}}{{\rho _{{ki}}^{3}}}} \right)} = {{B}_{{kr}}},$
(2.3)
$\sum\limits_{i = 1}^M {\left( {\frac{{3\left\{ {{{m}_{{ir}}}{{\rho }_{{ki,r}}} + {{m}_{{i\vartheta }}}{{\rho }_{{ki,\vartheta }}} + {{m}_{{i\varphi }}}{{\rho }_{{ki,\varphi }}}} \right\}{{\rho }_{{ki,\vartheta }}}}}{{\rho _{{ki}}^{5}}} - \frac{{{{m}_{{i\vartheta }}}}}{{\rho _{{ki}}^{3}}}} \right)} = {{B}_{{k\vartheta }}},$
$\sum\limits_{i = 1}^M {\left( {\frac{{3\left\{ {{{m}_{{ir}}}{{\rho }_{{ki,r}}} + {{m}_{{i\vartheta }}}{{\rho }_{{ki,\vartheta }}} + {{m}_{{i\varphi }}}{{\rho }_{{ki,\varphi }}}} \right\}{{\rho }_{{ki,\varphi }}}}}{{\rho _{{ki}}^{5}}} - \frac{{{{m}_{{i\varphi }}}}}{{\rho _{{ki}}^{3}}}} \right)} = {{B}_{{k\varphi }}},\quad k = 1,...,N.$

В общем случае число сенсоров N не совпадает с числом неизвестных дипольных моментов M. В (2.3) через $\rho _{{ki}}^{{}}$ обозначено расстояние между k-м сенсором и i-м диполем, а через ${{{\mathbf{\bar {\rho }}}}_{{ki}}} = \left( {{{\rho }_{{ki,r}}},{{\rho }_{{ki,\vartheta }}},{{\rho }_{{ki,\varphi }}}} \right)$ – вектор, соединяющий k-й сенсор с i-м диполем с компонентами в сферической системе координат, ${{\bar {m}}_{i}} = {{\left( {{{m}_{{ir}}},{{m}_{{i\vartheta }}},{{m}_{{i\varphi }}}} \right)}^{{\text{T}}}}$ – магнитный момент i-го диполя в сферической системе координат.

Система (3) имеет блочный вид

(2.4)
$\left[ {\begin{array}{*{20}{c}} {{{K}_{{11}}}}&{{{K}_{{12}}}}&{...}&{{{K}_{{1N}}}} \\ {{{K}_{{21}}}}&{{{K}_{{22}}}}&{...}&{{{K}_{{2N}}}} \\ {...}&{...}&{...}&{...} \\ {K_{{N1}}^{{}}}&{{{K}_{{N2}}}}&{...}&{{{K}_{{NN}}}} \end{array}} \right]\left( \begin{gathered} \begin{array}{*{20}{c}} {{{{\bar {m}}}_{1}}} \\ {{{{\bar {m}}}_{2}}} \\ {...} \end{array} \hfill \\ {{{\bar {m}}}_{N}} \hfill \\ \end{gathered} \right) = \left( \begin{gathered} \begin{array}{*{20}{c}} {{{{\bar {B}}}_{1}}} \\ {{{{\bar {B}}}_{2}}} \\ {...} \end{array} \hfill \\ {{{\bar {B}}}_{N}} \hfill \\ \end{gathered} \right),\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array}$
где блок ${{K}_{{il}}}$ соответствует i-му сенсору и l-му диполю, ${{\bar {m}}_{i}}$ – вектор компонент i-го диполя, ${{\bar {B}}_{l}}$ – вектор-функция, измеренная в l-м сенсоре:

(2.5)
${{K}_{{il}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{2\rho _{{il,r}}^{2} - \rho _{{il,\vartheta }}^{2} - \rho _{{il,\varphi }}^{2}}}{{\rho _{{il}}^{5}}}}&{\frac{{3{{\rho }_{{il,r}}}{{\rho }_{{il,\vartheta }}}}}{{\rho _{{il}}^{5}}}}&{\frac{{3{{\rho }_{{il,r}}}{{\rho }_{{il,\varphi }}}}}{{\rho _{{il}}^{5}}}} \\ {\frac{{3{{\rho }_{{il,\vartheta }}}{{\rho }_{{il,r}}}}}{{\rho _{{il}}^{5}}}}&{\frac{{2\rho _{{il,\vartheta }}^{2} - \rho _{{il,r}}^{2} - \rho _{{il,\varphi }}^{2}}}{{\rho _{{il}}^{5}}}}&{\frac{{3{{\rho }_{{il,\vartheta }}}{{\rho }_{{il,\varphi }}}}}{{\rho _{{il}}^{5}}}} \\ {\frac{{3{{\rho }_{{il,\varphi }}}{{\rho }_{{il,r}}}}}{{\rho _{{il}}^{5}}}}&{\frac{{3{{\rho }_{{il,\varphi }}}{{\rho }_{{il,\vartheta }}}}}{{\rho _{{il}}^{5}}}}&{\frac{{2\rho _{{il,\varphi }}^{2} - \rho _{{il,\vartheta }}^{2} - \rho _{{il,\varphi }}^{2}}}{{\rho _{{il}}^{5}}}} \end{array}} \right],\quad {{\rho }_{{il}}} = \left| {{{{\bar {r}}}_{i}} - {{{\bar {r}}}_{l}}} \right| = {{\rho }_{{il,r}}}.$

Попытаемся выяснить, по аналогии с рассмотренными нами ранее в локальном варианте, условия однозначной разрешимости системы (2.4).

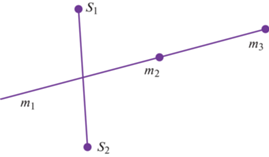
2.1 . Два диполя и N сенсоров, расположенных на одной прямой, проходящей через начало координат

Пусть и сенсоры, и диполи располагаются на одной прямой ОХ, проходящей через центр фиксированной сферической системы координат. Координаты диполей обозначим через ${{x}_{1}},{{x}_{2}}$, а координаты сенсоров – через $x_{1}^{s},x_{2}^{s}$. Предположим сначала, что диполи и сенсоры не разделяют друг друга (см. фиг. 1). В начале координат не могут находиться ни сенсоры, ни диполи ввиду неоднозначности задания координат в указанной точке.

Фиг. 1.

Расположение двух сенсоров и двух магнитных диполей. Диполи не разделяют сенсоры.

Система (2.4) принимает тогда вид

(2.6)
${{A}_{{22}}}\bar {x} = {{\bar {B}}_{2}},\;$
${{A}_{{22}}} = \left[ \begin{gathered} \begin{array}{*{20}{c}} {\frac{2}{{r_{{11}}^{3}}}}&0&0 \\ 0&{ - \frac{1}{{r_{{11}}^{3}}}}&0 \\ 0&0&{ - \frac{1}{{r_{{11}}^{3}}}} \end{array}\quad \begin{array}{*{20}{c}} {\frac{2}{{r_{{12}}^{3}}}}&0&0 \\ 0&{ - \frac{1}{{r_{{12}}^{3}}}}&0 \\ 0&0&{ - \frac{1}{{r_{{12}}^{3}}}} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\frac{2}{{r_{{21}}^{3}}}}&0&0 \\ 0&{ - \frac{1}{{r_{{21}}^{3}}}}&0 \\ 0&0&{ - \frac{1}{{r_{{12}}^{3}}}} \end{array}\quad \begin{array}{*{20}{c}} {\frac{2}{{r_{{22}}^{3}}}}&0&0 \\ 0&{ - \frac{1}{{r_{{22}}^{3}}}}&0 \\ 0&0&{ - \frac{1}{{r_{{22}}^{3}}}} \end{array} \hfill \\ \end{gathered} \right],$
(2.7)
${{r}_{{11}}} = \left| {{{x}_{1}} - {{x}_{{1s}}}} \right|,\quad {{r}_{{12}}} = \left| {{{x}_{1}} - {{x}_{{2s}}}} \right|,\quad {{r}_{{21}}} = \left| {{{x}_{2}} - {{x}_{{1s}}}} \right|,\quad {{r}_{{22}}} = \left| {{{x}_{2}} - {{x}_{{2s}}}} \right|,$
${{\bar {B}}_{2}} = \left( \begin{gathered} \begin{array}{*{20}{c}} {{{B}_{{1x}}}} \\ {{{B}_{{1y}}}} \\ {{{B}_{{1z}}}} \end{array} \hfill \\ \begin{array}{*{20}{c}} {{{B}_{{2x}}}} \\ {{{B}_{{2y}}}} \\ {{{B}_{{2z}}}} \end{array} \hfill \\ \end{gathered} \right),\quad \bar {x} = \left( \begin{gathered} \begin{array}{*{20}{c}} {{{m}_{{1x}}}} \\ {{{m}_{{1y}}}} \\ {{{m}_{{1z}}}} \end{array} \hfill \\ \begin{array}{*{20}{c}} {{{m}_{{2x}}}} \\ {{{m}_{{2y}}}} \\ {{{m}_{{2z}}}} \end{array} \hfill \\ \end{gathered} \right).$

Переобозначим элементы в матрице системы (2.7):

(2.8)
${{\tilde {A}}_{{22}}} = \left[ \begin{gathered} \begin{array}{*{20}{c}} {{{a}_{{11}}}}&0&0 \\ 0&{{{b}_{{11}}}}&0 \\ 0&0&{{{b}_{{11}}}} \end{array}\begin{array}{*{20}{c}} {{{a}_{{12}}}}&0&0 \\ 0&{{{b}_{{12}}}}&0 \\ 0&0&{{{b}_{{12}}}} \end{array} \hfill \\ \begin{array}{*{20}{c}} {{{a}_{{21}}}}&0&0 \\ 0&{{{b}_{{21}}}}&0 \\ 0&0&{{{b}_{{21}}}} \end{array}\begin{array}{*{20}{c}} {{{a}_{{22}}}}&0&0 \\ 0&{{{b}_{{22}}}}&0 \\ 0&0&{{{b}_{{22}}}} \end{array} \hfill \\ \end{gathered} \right].$

Для того чтобы детерминант матрицы (2.8) был равен нулю, необходимо и достаточно, чтобы координаты сенсоров совпадали (при различных координатах диполей):

(2.9)
$\begin{gathered} \det A = 0 \Rightarrow {{a}_{{11}}}{{a}_{{22}}} - {{a}_{{12}}}{{a}_{{21}}} = {{\left( {{{b}_{{11}}}{{b}_{{22}}} - {{b}_{{12}}}{{b}_{{21}}}} \right)}^{2}} = 0 \Rightarrow \\ \Rightarrow {{a}_{{ij}}} = - 2{{b}_{{ij}}} \Rightarrow \det A = 0 \Leftrightarrow {{b}_{{11}}}{{b}_{{22}}} - {{b}_{{12}}}{{b}_{{21}}} = 0 \Leftrightarrow \left( {{{x}_{{1s}}} - {{x}_{1}}} \right)\left( {{{x}_{{2s}}} - {{x}_{2}}} \right) = \left( {{{x}_{{1s}}} - {{x}_{2}}} \right)\left( {{{x}_{{2s}}} - {{x}_{1}}} \right) \Rightarrow \\ \Rightarrow {{x}_{{1s}}}({{x}_{1}} - {{x}_{2}}) = {{x}_{{2s}}}({{x}_{1}} - {{x}_{2}}) \Rightarrow \left( {{{x}_{{1s}}} - {{x}_{{2s}}}} \right)\left( {{{x}_{1}} - {{x}_{2}}} \right) = 0. \\ \end{gathered} $

Таким образом, нами доказана следующая

Теорема 3. Решение системы (2.4) единственно, если два сенсора и два диполя расположены в различных точках на одной и той же прямой, проходящей через начало координат фиксированной сферической системы. Диполи и сенсоры при этом не “разделяют друг друга”.

Рассмотрим теперь случай, когда в начале координат расположен первый диполь, затем идет второй сенсор, потом – второй диполь, и последний – первый сенсор (см. фиг. 2). В этом случае для равенства нулю детерминанта матрицы получаем равенство

${{x}_{{1s}}}{{x}_{{2s}}} + {{x}_{1}}{{x}_{2}} = 0.5({{x}_{2}} + {{x}_{1}})({{x}_{{1s}}} + {{x}_{{2s}}}).$
Фиг. 2.

Расположение двух сенсоров и двух магнитных диполей. Диполи разделяют сенсоры.

Если координаты диполей связаны с координатами сенсоров данным соотношением, то получим, что в таком случае система уравнений вырождена, и компоненты двух диполей определить однозначно нельзя.

Замечание. Можно, безусловно, рассмотреть сразу общий случай расположения диполей. Детерминант обращается в нуль при выполнении либо условия

$\left( {{{x}_{{1s}}} - {{x}_{1}}} \right)\left( {{{x}_{{2s}}} - {{x}_{2}}} \right) = \left( {{{x}_{{1s}}} - {{x}_{2}}} \right)\left( {{{x}_{{2s}}} - {{x}_{1}}} \right),$

что соответствует случаю “неразделенных” диполей, либо условия

$\left( {{{x}_{{1s}}} - {{x}_{1}}} \right)\left( {{{x}_{{2s}}} - {{x}_{2}}} \right) = \left( {{{x}_{{1s}}} - {{x}_{2}}} \right)\left( {{{x}_{1}} - {{x}_{{2s}}}} \right),$

и в последнем случае система уравнений может быть вырождена.

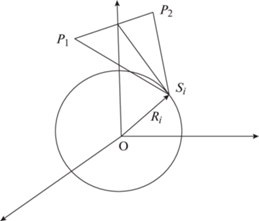
2.2. N диполей и N сенсоров, расположенных в одной вертикальной плоскости, проходящей через ось OZ

Рассмотрим теперь случай, когда у всех векторов, соединяющих диполи и сенсоры, отсутствует компонента вдоль ${{\bar {e}}_{\varphi }}$.

Пусть требуется определить компоненты N магнитных диполей ${{\bar {m}}_{1}},{{\bar {m}}_{2}},...,{{\bar {m}}_{N}}$ по измеренным в N произвольных точках некоторой вертикальной плоскости, содержащей ось OZ, трем компонентам вектора магнитной индукции (т.е. известным векторам ${{\bar {B}}_{1}},{{\bar {B}}_{2}},...,{{\bar {B}}_{N}}$). Принимая во внимание особенности сферической системы координат, здесь и далее будем предполагать, что сенсоры не размещаются вдоль оси OZ, а также что ни сенсоры, ни диполи не находятся в начале координат выбранной нами (фиксированной) сферической системы координат.

Система уравнений (21) приобретает вид

$\sum\limits_{i = 1}^N {\left( {\frac{{3\left\{ {{{m}_{{ir}}}{{\rho }_{{ki,r}}} + {{m}_{{i\vartheta }}}{{\rho }_{{ki,\vartheta }}}} \right\}{{\rho }_{{ki,r}}}}}{{\rho _{{ki}}^{5}}} - \frac{{{{m}_{{ir}}}}}{{\rho _{{ki}}^{3}}}} \right)} = {{B}_{{kr}}},$
(2.10)
$\sum\limits_{i = 1}^N {\left( {\frac{{3\left\{ {{{m}_{{ir}}}{{\rho }_{{ki,r}}} + {{m}_{{i\vartheta }}}{{\rho }_{{ki,\vartheta }}}} \right\}{{\rho }_{{ki,\vartheta }}}}}{{\rho _{{ki}}^{5}}} - \frac{{{{m}_{{i\vartheta }}}}}{{\rho _{{ki}}^{3}}}} \right)} = {{B}_{{k\vartheta }}},$
$\sum\limits_{i = 1}^N {\left( { - \frac{{{{m}_{{i\varphi }}}}}{{\rho _{{ki}}^{3}}}} \right)} = {{B}_{{k\varphi }}},\quad k = 1,...,N.$

Если для каких-либо двух индексов k и l справедливы соотношения

(2.11)
${{\rho }_{{ki}}} = {{\rho }_{{li}}},\quad i = 1,...,N,$
то две строки в (2.10) будут совпадать (в k-м и l-м блоках для соответствующих сенсоров):

(2.12)
$\left[ {\begin{array}{*{20}{c}} 0&{ - \frac{1}{{\rho _{{k1}}^{3}}};}&0&{ - \frac{1}{{\rho _{{k2}}^{3}}};}&{...;}&0&{ - \frac{1}{{\rho _{{kN}}^{3}}}}&0 \\ 0&{ - \frac{1}{{\rho _{{l1}}^{3}}};}&0&{ - \frac{1}{{\rho _{{l2}}^{3}}};}&{...;}&0&{ - \frac{1}{{\rho _{{lN}}^{3}}}}&0 \end{array}} \right].$

Такая ситуация может возникнуть в том случае, когда какие-либо два сенсора расположены симметрично относительно прямой, на которой лежат магнитные диполи (см. фиг. 3).

Фиг. 3.

Расположение сенсоров и магнитных диполей в вертикальной плоскости.

Таким образом, нами доказана аналогичная локальному варианту

Теорема 4. Если все сенсоры и диполи расположены в вертикальной плоскости, проходящей через ось OZ, все диполи лежат на одной прямой и для каких-то двух сенсоров имеет место ситуация, изображенная на фиг. 3, то решение системы (2.10) определяется неоднозначно.

2.3. Случай N диполей на оси OZ и N сенсоров, расположенных в произвольных точках

Рассмотрим постановку обратной задачи по поиску компонент N магнитных диполей, которые находятся в точках вертикальной оси OZ (за исключением начала координат), по информации от N сенсоров, расположение которых более-менее произвольно. Из изложенного в п. 2.2 настоящего раздела следует, что если для каких-либо двух сенсоров выполняются условия теоремы 4, то решение системы уравнений (2.4) определяется неоднозначно. В частности, если какие-либо два из N сенсоров лежат на окружности произвольного радиуса с центром на OZ, а сама окружность расположена в горизонтальной плоскости. Тогда радиус-векторы, соединяющие эти два сенсора с каждым из диполей, имеют нулевую компоненту вдоль ${{\bar {e}}_{\varphi }}$, и строки матрицы системы (2.4), соответствующие указанным двум сенсорам, “выглядят” так же, как в (2.12), поскольку расстояния от выделенных сенсоров до диполя с произвольным номером l одинаковы. Таким образом, для рассмотренного варианта взаимного расположения диполей и сенсоров будет справедлив аналог теоремы 4.

2.4. Случай N диполей и N сенсоров, расположенных в касательной плоскости к конусу $\vartheta = {\text{const}}$

Перейдем теперь к изучению случая, когда сенсоры располагаются вдоль образующей конуса $\vartheta = {\text{const}}.$ Диполи при этом должны лежать в касательной плоскости к конусу, содержащей указанную образующую (фиг. 4).

Фиг. 4.

Расположение сенсоров и магнитных диполей в плоскости, касательной к конусу $\vartheta = {\text{const}}$.

При таком расположении диполей и сенсоров у радиус-векторов, соединяющих диполи и сенсоры, будет отсутствовать компонента ${{\bar {e}}_{\vartheta }}.$

Система уравнений (21) принимает вид

(2.13)
$\begin{gathered} \sum\limits_{i = 1}^N {\left( {\frac{{3\left\{ {{{m}_{{ir}}}{{\rho }_{{ki,r}}} + {{m}_{{i\vartheta }}}{{\rho }_{{ki,\varphi }}}} \right\}{{\rho }_{{ki,r}}}}}{{\rho _{{ki}}^{5}}} - \frac{{{{m}_{{ir}}}}}{{\rho _{{ki}}^{3}}}} \right)} = {{B}_{{kr}}},\quad \sum\limits_{i = 1}^N {\left( { - \frac{{{{m}_{{i\vartheta }}}}}{{\rho _{{ki}}^{3}}}} \right)} = {{B}_{{k\vartheta }}}, \\ \sum\limits_{i = 1}^N {\left( {\frac{{3\left\{ {{{m}_{{ir}}}{{\rho }_{{ki,r}}} + {{m}_{{i\vartheta }}}{{\rho }_{{ki,\varphi }}}} \right\}{{\rho }_{{ki,\varphi }}}}}{{\rho _{{ki}}^{5}}} - \frac{{{{m}_{{i\varphi }}}}}{{\rho _{{ki}}^{3}}}} \right)} = {{B}_{{k\varphi }}},\quad k = 1,...,N. \\ \end{gathered} $

Если диполи лежат на серединном перпендикуляре к отрезку, соединяющему какие-то два сенсора, то опять мы оказываемся в ситуации, когда две строки матрицы системы (2.13) совпадают, поскольку имеют вид (2.12).

Следовательно, верна следующая

Теорема 5. При расположении N сенсоров и N диполей в касательной плоскости к какому-либо конусу $\vartheta = {\text{const}}$ и выполнении следующего условия: диполи лежат на серединном перпендикуляре к отрезку, соединяющему какие-либо два сенсора, решение системы (2.13) определяется неоднозначно.

2.5. Случай двух диполей и N сенсоров, произвольным образом расположенных в пространстве

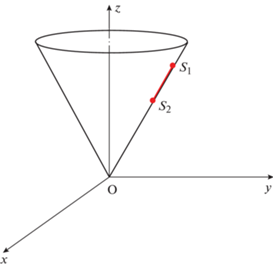
Рассмотрим, наконец, проблему интерпретации магнитометрических данных по информации от N сенсоров, расположенных в пространстве произвольным образом. В каком случае возможно вырождение системы (2.4) из-за обращения в нуль компоненты радиус-векторов ${{{\mathbf{\bar {\rho }}}}_{{ki}}} = \left( {{{\rho }_{{ki,r}}},{{\rho }_{{ki,\vartheta }}},{{\rho }_{{ki,\varphi }}}} \right)$ вдоль ${{\bar {e}}_{r}}$?

Пусть у нас два каких-либо диполя расположены в точках ${{P}_{1}},\;{{P}_{2}}$ (см. фиг. 5): на некоторой прямой, параллельной плоскости XOY, и симметрично относительно оси OZ. Предположим также, что касательная плоскость в точке сферы, на которой расположен один из сенсоров, проходит через эти два магнитных диполя (фиг. 5). В этом случае радиус-вектор сенсора ${{S}_{1}}$, как легко видеть, перпендикулярен указанной касательной плоскости, а векторы, соединяющие два диполя с этим сенсором, не имеют компоненты ${{\bar {e}}_{r}}$ и равны по модулю. Система (2.4) модифицируется и имеет следующий вид:

(2.14)
$\begin{gathered} \sum\limits_{i = 1}^2 {\left( { - \frac{{{{m}_{{ir}}}}}{{\rho _{{ki}}^{3}}}} \right)} = {{B}_{{kr}}},\quad \sum\limits_{i = 1}^2 {\left( {\frac{{3\left\{ {{{m}_{{i\vartheta }}}{{\rho }_{{ki,\vartheta }}} + {{m}_{{i\varphi }}}{{\rho }_{{ki,\varphi }}}} \right\}{{\rho }_{{ki,\vartheta }}}}}{{\rho _{{ki}}^{5}}} - \frac{{{{m}_{{i\vartheta }}}}}{{\rho _{{ki}}^{3}}}} \right)} = {{B}_{{k\vartheta }}}, \\ \sum\limits_{i = 1}^2 {\left( {\frac{{3\left\{ {{{m}_{{i\vartheta }}}{{\rho }_{{ki,\vartheta }}} + {{m}_{{i\varphi }}}{{\rho }_{{ki,\varphi }}}} \right\}{{\rho }_{{ki,\varphi }}}}}{{\rho _{{ki}}^{5}}} - \frac{{{{m}_{{i\varphi }}}}}{{\rho _{{ki}}^{3}}}} \right)} = {{B}_{{k\varphi }}},\quad k = 1,...,N. \\ \end{gathered} $
Фиг. 5.

Случай двух диполей и N сенсоров, произвольным образом расположенных в пространстве.

Если все N сенсоров расположены подобным образом по отношению к выделенным двум диполям, то мы снова оказываемся в ситуации, аналогичной описанной выше, а именно, система (31) вырождается, поскольку, по крайней мере, две ее строки пропорциональны:

(2.15)
$\left[ \begin{gathered} \begin{array}{*{20}{c}} 0&{ - \frac{1}{{\rho _{{k1}}^{3}}}}&0 \end{array};\;\begin{array}{*{20}{c}} 0&{ - \frac{1}{{\rho _{{k2}}^{3}}}}&0 \end{array} \hfill \\ \begin{array}{*{20}{c}} 0&{ - \frac{1}{{\rho _{{l1}}^{3}}}}&0 \end{array};\;\begin{array}{*{20}{c}} 0&{ - \frac{1}{{\rho _{{l2}}^{3}}}}&0 \end{array} \hfill \\ \end{gathered} \right],\quad {{\rho }_{{k1}}} = {{\rho }_{{k2}}};\quad {{\rho }_{{l1}}} = {{\rho }_{{l2}}}.$

Таким образом, нами доказана следующая

Теорема 6. Если два диполя расположены в произвольной горизонтальной плоскости симметрично относительно оси OZ и одновременно на всех касательных плоскостях к сферам, на которых находятся N сенсоров, то система (2.14) вырождена.

ЗАКЛЮЧЕНИЕ

Рассмотренные в настоящей работе примеры вырожденных и невырожденных систем линейных алгебраических уравнений, к которым редуцируются многие геофизические задачи интерпретационного характера, могут быть полезны при планировании эксперимента, выборе оптимальной сети пунктов наблюдений при проведении гравиметрической или магнитометрической съемки. Перспективным представляется подход к решению обратных геофизических и геодезических задач, при котором координаты как источников, так и точек наблюдения рассматриваются “единым блоком” – возникает необходимость исследования свойств некоторой расширенной системы нелинейных уравнений, элементы которой являются сечениями некоторого гладкого расслоения.

Метод S-аппроксимаций является весьма простым и эффективным методом решения линейных обратных задач гравиметрии и магнитометрии и может применяться также для поиска нулевого или первого приближения к решению нелинейной обратной задачи по определению геометрии и местоположения источника аномального гравитационного или магнитного поля. При решении такого типа задач необходимо применение регуляризирующих алгоритмов (см. [10, 11]). Постановки, приведенные в разд. 2 настоящей статьи, могут быть рассмотрены и в рамках метода линейных интегральных представлений: в случае магнитного поля вид линейных функционалов (1) изменится, но не кардинальным образом.

Авторы выражают глубокую благодарность А.С. Леонову за полезные рекомендации и внимание к работе.

Работа выполнена при финансовой поддержке РНФ (грант № 23-41-00002).

Список литературы

  1. Страхов В.Н. Геофизика и математика. М.: ОИФЗ РАН, 1999. 64 с.

  2. Страхов В.Н., Степанова И.Э. Метод S-аппроксимаций и его использование при решении задач гравиметрии (локальный вариант) // Физика Земли. 2002. № 2. С. 3–19.

  3. Степанова И.Э. Апробация методики S-аппроксимаций на материалах детальной гравиметрической и магнитометрических съемок // Геофиз. журнал. 2007. Т. 28. № 1. С. 97–105.

  4. Stepanova I.E. On the S-approximation of the Earth’s gravity field. Regional version // Inverse Problem. Sci. and Engineer. 2009. V 17. № 8. P. 1095–1111.

  5. Gudkova T.V., Stepanova I.E., Batov A.V. Density anomalies in subsurface layers of mars: model estimates for the site of the InSight mission seismometer // Solar System Res. 2020. V. 54. P. 15–19.

  6. Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Основные дифференциальные уравнения математической физики. М.: Физматгиз, 1962. 767 с.

  7. Лаврентьев М.А., Люстерник Л.А. Курс вариационного исчисления. М.–Л.: Гостоптехиздат, 1950.

  8. Lukyanenko D.V., Yagola A.G. Some methods for solving of 3D inverse problem of magnetometry // Eurasian J. Math. and Comp. Appl. 2016. V. 4. № 3. P. 4–14.

  9. Kolotov I.I., Lukyanenko D.V., Stepanova I.E., et al. Recovering the magnetic image of Mars from satellite observations // J. of Imaging. 2021. V. 7. № 11. P. 234.

  10. Тихонов А.Н., Гончарский А.В., Степанов В.В., Ягола А.Г. Численные методы решения некорректных задач. М.: Наука, 1990. 230 с.

  11. Ягола А.Г., Степанова И.Э., Ван Янфей, Титаренко В.Н. Обратные задачи и методы их решения. Приложения к геофизике. М.: Бином. Лаборатория знаний, 2014. 214 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал