1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 63, № 9, 2023

Журнал вычислительной математики и математической физики, 2023, T. 63, № 9, стр. 1513-1523

ЧИСЛЕННЫЙ АЛГОРИТМ ОПРЕДЕЛЕНИЯ ИСТОЧНИКА ДИФФУЗИОННО-ЛОГИСТИЧЕСКОЙ МОДЕЛИ ПО ДАННЫМ ИНТЕГРАЛЬНОГО ТИПА, ОСНОВАННЫЙ НА ТЕНЗОРНОЙ ОПТИМИЗАЦИИ

Т. А. Звонарева 1, 2, С. И. Кабанихин 2, 3, О. И. Криворотько 1, 2, 3, *

1 ИВМиМГ СО РАН
630090 Новосибирск, пр-кт Акад. Лаврентьева, 6, Россия

2 НГУ
630090 Новосибирск, ул. Пирогова, 2, Россия

3 ИМ им. С.Л. Соболева СО РАН
630090 Новосибирск, пр-кт Акад. Коптюга, 4, Россия

* E-mail: krivorotko.olya@mail.ru

Поступила в редакцию 09.12.2022
После доработки 09.12.2022
Принята к публикации 29.05.2023

Полный текст (PDF)

Аннотация

Разработан алгоритм численного решения задачи определения источника в модели распространения информации в синтетических онлайн социальных сетях, описываемой уравнениями типа “реакции–диффузии”, по дополнительной информации о процессе в фиксированные моменты времени. Исследована степень некорректности задачи определения источника в параболическом уравнении, основанная на анализе сингулярных чисел линеаризованного оператора обратной задачи. Разработанный алгоритм основан на комбинации метода тензорной оптимизации и градиентного спуска с учетом регуляризации А.Н. Тихонова. Численные расчеты демонстрируют наименьшую относительную погрешность восстановленного источника, полученную разработанным алгоритмом в сравнении с классическими подходами. Библ. 26. Фиг. 4. Табл. 2.

Ключевые слова: задача об источнике, модель “реакции–диффузии”, обратная задача, тензорная оптимизация, регуляризация, градиентные методы.

ВВЕДЕНИЕ

Оценка последствий принимаемых решений в социальных и экономических сферах опирается на создание и исследование моделей управляемых систем. В этом направлении существенную помощь могут оказать аналогии с процессами из различных предметных областей (математическая физика, механика сплошной среды, геофизика и др.) с хорошо развитым математическим аппаратом (см. [1]).

В настоящей работе рассматривается начально-краевая задача для диффузионно-логистической модели

(1)
$\begin{gathered} {{u}_{t}} = d{{u}_{{xx}}} + \left( {1 - \frac{u}{K}} \right)r(t)u,\quad {{l}_{1}} \leqslant x \leqslant {{l}_{2}},\quad t \geqslant 1, \hfill \\ u(x,1) = Q(x),\quad {{l}_{1}} \leqslant x \leqslant {{l}_{2}}, \hfill \\ {{u}_{x}}({{l}_{1}},t) = {{u}_{x}}({{l}_{2}},t) = 0,\quad t \geqslant 1, \hfill \\ \end{gathered} $
которая описывает процесс распространения информации в онлайн социальной сети (см. [2]). Здесь $u(x,t)$ – плотность пользователей, вовлеченных в процесс распространения информации, $K$ – константа, описывающая максимальную пропускную способность сети, $r(t)$ [1/час] – скорость роста числа активных пользователей, $Q(x)$ – гладкая функция источника распространения информации в социальной сети в зависимости от количества связей $x = 1,2, \ldots $, интерполированная с помощью сплайнов по дискретному набору связей, удовлетворяющая ограничениям
$0\;\leqslant \;Q(x)\;\leqslant \;{{Q}_{{\max }}},\quad Q(x) = 0\quad \forall {\kern 1pt} x < {{l}_{1}}\quad {\text{и}}\quad Q(x) = {{Q}_{{\max }}}\quad \forall {\kern 1pt} x > {{l}_{2}}\; \geqslant \;{{l}_{1}}.$
Переменная $x$ характеризует расстояние от источника, т.е. $x = 0$ соответствует источнику, $x = i$ – минимальное количество связей от источника до вовлеченного пользователя. Например, вовлеченный пользователь отреагировал на новость “друга”, который в свою очередь отреагировал (репост, реакция) на новость своего “друга”-источника. В таком случае вовлеченный пользователь находится на расстоянии $x = 2$ от источника.

Подобное уравнение “реакции–диффузии” было рассмотрено в статье А.Н. Колмогорова, И.Г. Петровского и Н.С. Пискунова [3], в которой $u(x,t)$ означала концентрацию исследуемого вида в популяции при ${{Q}_{{\max }}} = 1$, $K = 1$. В этом случае предельная скорость перемещения популяции равна $v(t) = 2\sqrt {dr(t)} $.

Если ввести функцию потока $\Psi (x,t)$, характеризующую количество вовлеченных пользователей, проходящую через точку с координатой $x$ в единицу времени в момент $t$, то закон сохранения для модели (1) примет вид

$\frac{{\partial u(x,t)}}{{\partial t}} + \frac{{\partial \Psi (x,t)}}{{\partial x}} = \left( {1 - \frac{u}{K}} \right)r(t)u.$

В случае, когда функции потока $\Psi (x,t)$ и плотности $u(x,t)$ связаны соотношением Фика

$\Psi (x,t) = - v(u)\frac{{\partial u}}{{\partial x}},$
уравнение из модели (1) примет вид
$\frac{{\partial u}}{{\partial t}} = \left( {1 - \frac{u}{K}} \right)r(t)u + \frac{\partial }{{\partial x}}\left( {v(u)\frac{{\partial u}}{{\partial x}}} \right).$
Здесь $v(u)$ – неотрицательная функция скорости потока.

Замечание. Начально-краевая задача об определении источника $\varphi (x)$ может быть записана в виде

(2)
$\begin{gathered} \frac{{\partial{ \tilde {u}}}}{{\partial t}} = \left( {1 - \frac{{\tilde {u}}}{K}} \right)r(t)\tilde {u} + d\frac{{{{\partial }^{2}}\tilde {u}}}{{\partial {{x}^{2}}}} + \varphi (x)k(x,t),\quad t \in (1,T),{\kern 1pt} x \in ({{l}_{1}},{{l}_{2}}), \hfill \\ \tilde {u}(x,1) < 0,\quad x \in ({{l}_{1}},{{l}_{2}}), \hfill \\ {{{\tilde {u}}}_{x}}({{l}_{1}},t) = {{{\tilde {u}}}_{x}}({{l}_{2}},t) = 0,\quad t \in (1,T). \hfill \\ \end{gathered} $
В случае $k(x,t) = \delta (x)\delta (t)$, где $\delta $ – дельта-функция Дирака, задача определения функции $\varphi (x)$ из (2) сводится к задаче определения функции $Q(x)$ из (1) (см. [4]).

Определение источника $\varphi (x)$ крайне важно при моделировании динамики популяции, распространения информации в социальных сетях, приложениях математической физики, так как решение $\tilde {u}(x,t)$ сильно зависит от линейной части члена, отвечающего за реакцию. В физических приложениях линейная часть часто неизвестна или известна частично, и $\varphi (x)$ нельзя измерить напрямую, поскольку он является результатом смешанного влияния нескольких факторов. Таким образом, в большинстве случаев $\tilde {u}(x,t)$ не доступны одновременно для всех $x$ и всех моментов времени $t$. В работе разработан эффективный алгоритм определения функции источника $Q(x)$ в начально-краевой задаче (1) по дополнительной информации о процессе в фиксированные моменты времени.

В Институте системного программирования РАН разрабатываются подходы анализа социальных процессов, основанные на онтологии, графовых структурах, методах машинного обучения и искусственного интеллекта (см. [5]). В настоящей работе предложен упрощенный подход описания процесса распространения информации в онлайн социальных сетях, основанный на описании процессов посредством дифференциальных уравнений.

Статья организована следующим образом. В разд. 1 сформулирована обратная задача (задача об источнике) для модели (1) в классической и вариационной постановках и исследован линеаризованный оператор обратной задачи на степень некорректности. В разд. 2 сформулирован комбинированный алгоритм численного решения задачи об источнике, основанный на методах тензорной оптимизации и градиентного типа. В разд. 3 приведены результаты и анализ численных расчетов определения функции источника распространения информации в онлайн социальных сетях по синтетическим данным о количестве вовлеченных пользователей в фиксированные моменты времени. В заключении сформулированы выводы по статье и направления дальнейших исследований.

1. ПОСТАНОВКА ОБРАТНОЙ ЗАДАЧИ

В обратной задаче, в отличие от прямой, помимо функции $u(x,t)$ неизвестной является и начальная функция плотности $Q(x)$. Рассматривается дополнительная информация следующего вида:

(3)
$\sum\limits_{i = 1}^{{{N}_{1}}} \;u({{x}_{i}},{{t}_{k}}) = {{f}_{k}},\quad k = 1, \ldots ,{{N}_{2}}.$
Таким образом, в обратной задаче (1), (3) требуется восстановить функцию $Q(x)$ модели (1) по данным ${{f}_{k}}$ вида (3). Так как данные обратной задачи не полны, такая обратная задача некорректна (см. [6]) (ее решение может быть неединственным и/или неустойчивым).

Благодаря неравенствам Карлемана, метод, введенный Бухгеймом и Клибановым (см. [7]), позволил установить важные результаты, включающие неравенства устойчивости, связывающие восстанавливаемую функцию источника с наблюдениями на части области $\omega \times (1,T)$, $\omega \subset ({{l}_{1}},{{l}_{2}})$, и наблюдения на всей области $({{l}_{1}},{{l}_{2}})$ в фиксированный момент времени $t{\kern 1pt} *$ (см. [8, 9]). В [10] был предложен подход определения функции источника по дополнительной информации о решении в фиксированный момент времени и точки пространства в одномерном случае, получены результаты единственности и устойчивости решения. В [11] В. Исаков получил теорему условной устойчивости решения задачи об источнике для модели (2) с необходимостью дополнительных граничных наблюдений. В [12] А. Хасанов использовал подход слабого решения для минимизации функционала невязки. Больше теоретических и практических результатов приведены в современных работах и ссылках в них (см. [13, 14]).

Для описания быстротекущих процессов (движения плазмы, модели теплопроводности, распространение информации в социальных сетях) в [15, 16] предложен подход регуляризации параболической системы (2) путем добавления второй производной по времени с малым параметром $\varepsilon $ в качестве коэффициента. В нашем случае

(4)
$\begin{gathered} \varepsilon {{u}_{{tt}}} + {{u}_{t}} = d{{u}_{{xx}}} + \left( {1 - \frac{u}{K}} \right)r(t)u,\quad {{l}_{1}} \leqslant x \leqslant {{l}_{2}},\quad t \geqslant 1, \hfill \\ u(x,1) = Q(x),\quad {{u}_{t}}(x,1) = 0,\quad {{l}_{1}} \leqslant x \leqslant {{l}_{2}}, \hfill \\ {{u}_{x}}({{l}_{1}},t) = {{u}_{x}}({{l}_{2}},t) = 0,\quad t \geqslant 1. \hfill \\ \end{gathered} $

Гиперболическая модель имеет заметные преимущества при использовании явных схем численного решения прямых и сопряженных задач. Особенно ярко эти преимущества по сравнению с параболической моделью (2) проявляются при использовании подробных пространственных сеток, применение которых стало возможным с появлением вычислительных систем сверхвысокой производительности. В то же время добавленный член имеет сингулярный характер. Вопрос о близости решений сингулярно возмущенных и невозмущенных уравнений впервые исследован в работах А.Н. Тихонова [17, 18]. В [16] показано, что оптимальным представляется выбор параметра $\varepsilon $ в виде:

$\varepsilon < \frac{{{{h}_{x}}}}{V},$
где ${{h}_{x}}$ – шаг по пространственной сетке, $V$ – характерная скорость диффузионного процесса. При этом, с одной стороны, обеспечивается близость решений параболической и гиперболической моделей (см. [15]), а с другой – обеспечивается заметный вычислительный эффект при использовании явных схем.

1.1. Исследование сингулярных чисел оператора линеаризованной обратной задачи

Используя дискретизацию начально-краевой задачи (1), обратную задачу определения $q = ({{q}_{0}}, \ldots ,{{q}_{5}}) = (Q(1), \ldots ,Q(6))$ по дополнительной информации вида (3) можно представить в виде системы линейных алгебраических уравнений

$Aq = f,$
где $A$ – матрица размера ${{N}_{2}} \times N$, а $q$ и $f = ({{f}_{1}}, \ldots ,{{f}_{{{{N}_{2}}}}})$ – векторы размерности $N$ и ${{N}_{2}}$ соответственно. Обратную задачу (4), (3) аналогично можно представить в виде ${{A}_{\varepsilon }}q = f$.

Зависимость решения от возмущения правой части $f$ в случае невырожденной матрицы $A$ для возмущенной задачи

$A(q + \delta q) = f + \delta f$
имеет вид $A\delta q = \delta f$, откуда $\delta q = {{A}^{{ - 1}}}\delta f$, $\left\| {\delta q} \right\| \leqslant \left\| {{{A}^{{ - 1}}}} \right\|\left\| {\delta f} \right\|$. Кроме того, $\left\| A \right\|\left\| q \right\| \geqslant \left\| f \right\|$.

Из этих соотношений мы имеем неулучшаемую оценку для относительной ошибки решения:

(5)
$\frac{{\left\| {\delta q} \right\|}}{{\left\| q \right\|}} \leqslant \left\| A \right\|\left\| {{{A}^{{ - 1}}}} \right\|\frac{{\left\| {\delta f} \right\|}}{{\left\| f \right\|}}.$
Таким образом, погрешность определяется константой ${\kern 1pt} {\text{cond}}{\kern 1pt} (A) = \left\| A \right\|\left\| {{{A}^{{ - 1}}}} \right\|$, которая называется числом обусловленности системы (матрицы). Системы с плохо обусловленными матрицами можно считать практически неустойчивыми, хотя формально задача корректна, и выполнено условие устойчивости $\left\| {{{A}^{{ - 1}}}} \right\| < \infty $.

В случае возмущения матрицы оценка (5) принимает вид

$\frac{{\left\| {\delta q} \right\|}}{{\left\| q \right\|}} \leqslant {\text{cond}}{\kern 1pt} (A)\frac{{\left\| {\delta A} \right\|}}{{\left\| A \right\|}}{\text{/}}\left( {1 - {\text{cond}}{\kern 1pt} (A)\frac{{\left\| {\delta A} \right\|}}{{\left\| A \right\|}}} \right)$
(при $\left\| {{{A}^{{ - 1}}}} \right\|\left\| {\delta A} \right\| < 1$).

Известно, что число обусловленности выражается через сингулярные числа матрицы следующим образом:

${\kern 1pt} {\text{cond}}{\kern 1pt} (A) = \frac{{{{\sigma }_{1}}(A)}}{{{{\sigma }_{p}}(A)}},$
где ${{\sigma }_{1}}(A)$ и ${{\sigma }_{p}}(A)$ – максимальное и минимальное сингулярные числа матрицы $A$, $p = \min (N,{{N}_{2}})$.

После линеаризации и дискретизации обратных задач (1), (3) (см. [19]) и (4), (3) при ${{N}_{1}} = 5$, ${{N}_{2}} = 22$ получим дискретные аналоги операторов обратных задач. В численных расчетах $K = 25$, $d = 0.01$, и функция $r(t)$ имеет вид:

$r(t) = \frac{{{{\beta }_{2}}}}{{{{\beta }_{1}}}} - {{e}^{{ - {{\beta }_{1}}(t - 1)}}}\left( {\frac{{{{\beta }_{2}}}}{{{{\beta }_{1}}}} - {{\beta }_{3}}} \right),\quad {\text{где}}\quad {{\beta }_{1}} = 1.5,\quad {{\beta }_{2}} = 0.375,\quad {{\beta }_{3}} = 1.65.$
Сингулярные числа матриц $A$ и ${{A}_{\varepsilon }}$ представлены на фиг. 1.

Фиг. 1.

Графики убывания сингулярных чисел операторов $A$ (черная линия с ромбами) и ${{A}_{\varepsilon }}$ при $\varepsilon = 0.1$ (оранжевая линия с кругами) линеаризованных обратных задач (1), (3) и (4), (3) в логарифмической шкале.

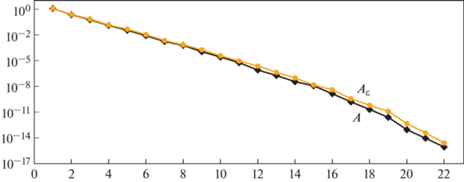
Таким образом, числа обусловленности матриц $A$ и ${{A}_{\varepsilon }}$ имеют порядок ${{10}^{{16}}}$ и ${{10}^{{15}}}$ соответственно. Это означает, что решение линеаризованной обратной задачи неустойчиво. Добавление малого параметра $\varepsilon $ со второй производной по времени не значительно уменьшает число обусловленности матрицы ${{A}_{\varepsilon }}$. В следующем разделе обратная задача сведена к задаче минимизации функционала с учетом регуляризирующего слагаемого.

1.2. Вариационная постановка обратной задачи

Пусть $u(x,t) \in {{L}^{2}}(({{l}_{1}},{{l}_{2}}) \times (1, + \infty ))$. Тогда обратную задачу можно свести к соответствующей задаче минимизации следующего целевого функционала:

(6)
$J(q) = \frac{{T - 1}}{{{{N}_{2}}}}\sum\limits_{k = 1}^{{{N}_{2}}} {{\left| {\sum\limits_{i = 1}^{{{N}_{1}}} \,u({{x}_{i}},{{t}_{k}};q) - {{f}_{k}}} \right|}^{2}},$
где $u(x,t;q)$ – решение прямой задачи для начальной функции плотности $Q(x)$, определяемой из набора параметров $q = ({{q}_{0}}, \ldots ,{{q}_{{N - 1}}})$, т.е. $Q({{x}_{i}}) = {{q}_{{i - 1}}}$, $i = 1, \ldots ,N$, $N = 6$ – число параметров.

Для данной обратной задачи также был сформулирован регуляризирующий функционал А.Н. Тихонова (см. [17, 20])

(7)
${{J}_{T}}(q) = \frac{{T - 1}}{{{{N}_{2}}}}\sum\limits_{k = 1}^{{{N}_{2}}} {{\left| {\sum\limits_{i = 1}^{{{N}_{1}}} u({{x}_{i}},{{t}_{k}};q) - {{f}_{k}}} \right|}^{2}} + \alpha \sum\limits_{j = 0}^{N - 1} {{\left| {{{q}_{j}} - q_{j}^{0}} \right|}^{2}}$
с параметром регуляризации $\alpha {{ = 10}^{{ - 2}}}$ и линейно убывающим ${{q}^{0}}$.

2. МЕТОДЫ ОПТИМИЗАЦИИ

Задача определения вектора $q \in {{R}^{6}}$ является некорректной, а именно, как показано в п. 1.1, решение неустойчиво (число обусловленности достигает порядка ${{10}^{{16}}}$). Более того, функция $Q(x)$ определяется на всем интервале $x \in [{{l}_{1}},{{l}_{2}}]$ с помощью интерполяции вектора $q$ кубическими сплайнами, что порождает неединственность решения.

Дополнительная информация (3) обратной задачи задана в дискретном виде.

В [19] были проведены расчеты для более полных данных $u({{x}_{i}},{{t}_{k}}) = {{f}_{{ik}}}$, $i = 1, \ldots ,{{N}_{1}}$, $k = 1, \ldots ,{{N}_{2}}$, с применением комбинации методов глобальной оптимизации (метод роя частиц) и градиентных подходов. Для решения поставленной обратной задачи был применен метод оптимизации тензорного поезда, который сводит функцию нескольких переменных к тензору (см. [21]) и является в сравнении с природоподобными алгоритмами эффективнее без потери точности для многомасштабных задач.

2.1. Метод тензорного разложения функционала

Метод глобальной оптимизации тензорного поезда (Tensor Train global optimization, TT) (см. [21]) заменяет исходную задачу оптимизации на эквивалентную задачу поиска максимума по модулю. Для этого исходная функция непрерывно и монотонно отображается на часть интервала $[0; + \infty )$ и после дискретизации преобразуется в тензор.

Однако число элементов в таком тензоре растет экспоненциально с ростом числа искомых параметров. Поэтому идеей метода является аппроксимация тензора методом TT-CROSS (см. [22]), который получает приближение тензора в ТТ-формате. Этот формат представляет собой разложение, в котором исходный тензор размерности $N$ сводится к $N$ тензорам размерности 3.

Для вычислительных экспериментов был адаптирован пакет программ ttpy на языке программирования Python. В данном случае исходный функционал $J(q)$ отображается с помощью функции $g(J(q) - \alpha )$ и вводится сетка с $n$ узлами по каждому из $N$ направлений, а тензор значений функции $g(q)$ обозначается через $G$. Тогда алгоритм метода имеет следующий вид:

0. Для каждого $i = 1, \ldots ,N - 1$:

• Случайным образом генерируется тензор ${{\hat {G}}_{i}}({{j}_{1}};{{j}_{2}};{{j}_{3}})$ и считается $QR$-разложение матрицы развертки ${{\hat {G}}_{i}}({{j}_{1}}{{j}_{2}};{{j}_{3}}) = {{Q}_{i}}{{R}_{i}}$.

• Процедура maxvol(${{Q}_{i}}$) находит набор номеров строк $\{ p\} $, соответствующий квадратной подматрице максимального объема (см. [23]).

• Используя значения сетки и полученный на предыдущем шаге ${{\hat {q}}_{{i - 1}}}$, генерируется массив ${{\hat {q}}_{i}}$, из которого выбираются строки с номерами из $\{ p\} $.

1. Пока число итераций меньше ${{n}_{{{\text{swp}}}}}$ (параметр функции min_func в пакете ttpy), чередуются следующие действия:

(a) Для $i = N - 1, \ldots ,1$:

– На основе ${{\hat {q}}_{i}}$ и ${{\hat {q}}_{{i + 1}}}$ генерируется множество потенциальных решений $M$ и обновляется сдвиг $\alpha $.

– Массив значений функционала $J(\tilde {q})$, $\tilde {q} \in M$, представляется в виде тензора ${{A}_{i}}({{j}_{1}};{{j}_{2}};{{j}_{3}})$ и считается сингулярное разложение матрицы развертки ${{A}_{i}}({{j}_{2}}{{j}_{3}};{{j}_{1}}) = {{U}_{i}}{{S}_{i}}({{V}_{i}}){\kern 1pt} *$.

– Процедура rect_maxvol(${{U}_{i}}$) находит набор номеров строк $\{ p\} $, соответствующий прямоугольной подматрице максимального объема (см. [24]).

– Используя значения сетки и ${{\hat {q}}_{{i + 1}}}$, генерируется массив ${{\hat {q}}_{i}}$, из которого выбираются строки с номерами из $\{ p\} $.

(б) Для $i = 0, \ldots ,N - 2$:

– На основе ${{\hat {q}}_{i}}$ и ${{\hat {q}}_{{i + 1}}}$ генерируется множество потенциальных решений $M$ и обновляется сдвиг α.

– Массив значений функционала $J(\tilde {q})$, $\tilde {q} \in M$, представляется в виде тензора ${{A}_{i}}({{j}_{1}};{{j}_{2}};{{j}_{3}})$ и считается $QR$-разложение матрицы развертки ${{A}_{i}}({{j}_{1}}{{j}_{2}};{{j}_{3}}) = {{Q}_{i}}{{R}_{i}}$.

– Процедура rect_maxvol(${{Q}_{i}}$) находит набор номеров строк $\{ p\} $, соответствующий прямоугольной подматрице максимального объема.

– Используя значения сетки и ${{\hat {q}}_{i}}$, генерируется массив ${{\hat {q}}_{{i + 1}}}$, из которого выбираются строки с номерами из $\{ p\} $.

На нечетных итерациях выполняется вариант (a), на четных итерациях – (б).

Данный метод использует только некоторые строки и столбцы изначального тензора значений функции $g(q)$, из-за чего может не найти точку глобального оптимума, а лишь обнаружить близкое к оптимальному значение. Поэтому для увеличения точности решения обратной задачи мы рассмотрели комбинированный метод.

2.2. Комбинированный метод

Данный метод состоит в последовательном применении метода глобальной оптимизации ТТ и локального многоуровневого градиентного метода (МГМ) (см. [25]). Ранее уже были проведены численные эксперименты для подобной обратной задачи, решаемой с помощью МГМ (см. [26]). Алгоритм МГМ имеет следующий вид:

${{q}^{{m + 1}}} = {{\theta }_{{m + 1}}}{{z}^{m}} + (1 - {{\theta }_{{m + 1}}}){{y}^{m}},\quad {{\theta }_{{m + 1}}} \in \arg \mathop {\min }\limits_{\theta \in [0;1]} J(\theta {{z}^{m}} + (1 - \theta ){{y}^{m}}),$
${{y}^{{m + 1}}} = {{q}^{{m + 1}}} - {{\zeta }_{{m + 1}}}J{\kern 1pt} '{\kern 1pt} ({{q}^{{m + 1}}}),\quad {{\zeta }_{{m + 1}}} \in \arg \mathop {\min }\limits_{\zeta \geqslant 0} J({{q}^{{m + 1}}} - \zeta J{\kern 1pt} '{\kern 1pt} ({{q}^{{m + 1}}})),$
${{z}^{{m + 1}}} = {{z}^{m}} - {{\eta }_{{m + 1}}}J{\kern 1pt} '{\kern 1pt} ({{q}^{{m + 1}}}),\quad {{\eta }_{{m + 1}}} = \frac{1}{{2{{L}_{{m + 1}}}}} + \sqrt {\frac{1}{{4L_{{m + 1}}^{2}}} + \eta _{m}^{2}} ,$
${{L}_{{m + 1}}} = \frac{{{{{\left\| {J{\kern 1pt} '{\kern 1pt} ({{q}^{{m + 1}}})} \right\|}}^{2}}}}{{2(J({{q}^{{m + 1}}}) - J({{y}^{{m + 1}}}))}},\quad {{\eta }_{0}} = 0.$

В качестве начального приближения для МГМ был взят результат метода ТТ. Скорость сходимости по функционалу метода МГМ имеет порядок $O\left( {{{m}^{{ - 2}}}} \right)$.

3. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ

Решение задач минимизации (6) и (7) проводилось с помощью методов ТТ, ТТ в комбинации с МГМ (ТТ + МГМ). Сравнение результатов проведено с результатом комбинации методов роя частиц и МГМ для синтетических данных обратной задачи. Вычисления проводились на вычислительном узле с двумя процессорами Intel Xeon Gold 6248R, количество ядер в каждом процессоре – 24, частота – 3 Гц, 384 Гб оперативной памяти.

3.1. Входные параметры

Прямая задача решается конечно-разностным методом на равномерной сетке в замкнутой области $\bar {D} = \{ (x,t)|{{l}_{1}} \leqslant x \leqslant {{l}_{2}},\;1 \leqslant t \leqslant T\} $:

$\bar {\omega } = \{ ({{x}_{j}},{{t}_{n}})\,{\text{|}}\,{{x}_{j}} = {{l}_{1}} + jh,\;{{t}_{n}} = 1 + n\tau ,\;j = 0, \ldots ,{{N}_{x}},\;n = 0, \ldots ,{{N}_{t}}\} ,$
где $h = \frac{{{{l}_{2}} - {{l}_{1}}}}{{{{N}_{x}}}}$ и $\tau = \frac{{T - 1}}{{{{N}_{t}}}}$.

Для применения классического непрерывного подхода функция начальной плотности $Q(x)$ определяется из вектора ${{q}_{{{\text{ex}}}}}$ (см. табл. 2) интерполяцией кубическими сплайнами (см. [26]).

Прямая задача (1) решается с помощью явной конечно-разностной схемы с порядком аппроксимации $O(\tau + {{h}^{2}})$.

Положим в численных расчетах ${{l}_{1}} = 1$, ${{l}_{2}} = 6$, $T = 24$, ${{N}_{x}} = 50$ и ${{N}_{t}} = 575$ (см. [26]). И в случае функционала А.Н. Тихонова $q_{j}^{0} \in [0,6]$ расположены равномерно, т.е. ${{q}^{0}} = (6,4.8,3.6,2.4,1.2,0)$.

В качестве синтетических данных ${{f}_{k}}$ были взяты значения решения прямой задачи в каждой десятой точке по $x$ и в каждой двадцать пятой точке по $t \geqslant 50$, т.е. ${{N}_{1}} = 6$ и ${{N}_{2}} = 22$. Значения параметров ${{q}_{{{\text{ex}}}}}$ в табл. 2 эмитируют реальные данные новостного сайта Digg.com, представленные в [2].

Относительная ошибка вычислялась по формуле

${{\delta }_{m}} = \frac{{{{{\left\| {{{q}_{{{\text{ex}}}}} - {{q}^{m}}} \right\|}}^{2}}}}{{{{{\left\| {{{q}_{{{\text{ex}}}}}} \right\|}}^{2}}}}.$
Здесь ${{q}_{{{\text{ex}}}}}$ – точные значения дискретизованной функции $Q(x)$, а ${{q}^{m}}$ – аппроксимация решения обратной задачи, которая соответствует минимуму функционала $J({{q}^{m}})$ (6).

3.1.1. Параметры ТТ. Исходный функционал отображался с помощью функции $g(q) = \pi {\text{/}}2 - \operatorname{arctg} (J(q) - \alpha )$. Для всех $N$ направлений выбирался интервал изменения параметров $[0,6]$, а максимально возможный ранг тензоров в разложении ${{r}_{{{\text{max}}}}} = 7$ и количество итераций во всех численных экспериментах ${{n}_{{{\text{swp}}}}} = 10$.

При увеличении количества узлов $n$ по каждому из направлений растет вычислительная сложность (см. п. 3.3), поэтому в расчетах было выбрано оптимальное по времени и значению целевого функционала число узлов $n = 51$.

3.1.2. Параметры МГМ. На каждой итерации параметр спуска определяется на отрезке $[0,{{\zeta }_{{{\text{max}}}}}]$ с шагом ${{\zeta }_{h}}$. А градиент вычислялся через решение сопряженной задачи (см. [26]).

3.2. Результаты численных экспериментов

Было выявлено, что при значениях $n \leqslant 50$ изменение параметров ${{r}_{{{\text{max}}}}}$ и ${{n}_{{{\text{swp}}}}}$ никак не влияет на результат работы программы, лишь увеличивая время ее работы. А минимальные значения функционала $J(q) = 6.16 \times {{10}^{0}}$ и погрешности $\delta = 2.04 \times {{10}^{{ - 2}}}$ достигались при $n = 51$, ${{r}_{{{\text{max}}}}} = 7$ и ${{n}_{{{\text{swp}}}}} = 10$. Однако решение обратной задачи еще далеко от точного, поэтому для уточнения применялся МГМ.

В табл. 1 и 2 и на фиг. 2 представлены результаты решения задачи минимизации целевого функционала методом ТТ, комбинацией ТТ + МГМ, ТТ + МГМ с регуляризацией А.Н. Тихонова и комбинацией стохастического глобального метода роя частиц (МРЧ) + МГМ. Можно заметить, что метод ТТ работает почти в 2 раза дольше комбинации МРЧ + МГМ, но находит решение лучше в смысле значений погрешности. Применение МГМ к методу ТТ приводит к уменьшению функционала, но незначительно влияет на погрешность, а применение регуляризации А.Н. Тихонова уменьшает погрешность, но увеличивает время работы программы более чем в 2 раза. Таким образом, наименьшее значение погрешности $\delta = 1.29 \times {{10}^{{ - 2}}}$ достигается при работе регуляризованного комбинированного метода ТТ + МГМ.

Таблица 1.  

Результаты, ${{t}_{{{\text{ЭВМ}}}}}$ – время работы программы

Метод Функционал $\delta $ ${{t}_{{{\text{ЭВМ}}}}}$, ч
ТТ $J(q) = 6.16 \times {{10}^{0}}$ $2.04 \times {{10}^{{ - 2}}}$ 1.09
ТТ + МГМ $J(q) = 7.43 \times {{10}^{{ - 3}}}$ $1.89 \times {{10}^{{ - 2}}}$ 1.1
ТТ + МГМ + рег. ${{J}_{T}}(q) = 1.56 \times {{10}^{{ - 1}}}$ $1.29 \times {{10}^{{ - 2}}}$ 2.55
МРЧ + МГМ $J(q) = 6.67 \times {{10}^{{ - 2}}}$ $1.03 \times {{10}^{0}}$ 0.64
Таблица 2.  

Значения точного ${{q}_{{{\text{ex}}}}}$ и найденных решений обратной задачи (1), (3)

Параметр ${{q}_{0}}$ ${{q}_{1}}$ ${{q}_{2}}$ ${{q}_{3}}$ ${{q}_{4}}$ ${{q}_{5}}$
${{q}_{{{\text{ex}}}}}$ 5.8 1.7 1.9 1 0.95 0.7
${{q}_{{{\text{ТТ}}}}}$ 5.76 1.44 2.639 0.84 0.96 0.72
${{q}_{{{\text{ТТ}} + {\text{МГМ}}}}}$ 5.758 1.316 2.556 0.813 0.965 0.801
${{q}_{{{\text{ТТ}} + {\text{МГМ}} + {\text{рег}}{\text{.}}}}}$ 5.759 1.899 1.456 0.986 1.246 0.415
${{q}_{{{\text{МРЧ}} + {\text{МГМ}}}}}$ 1.629 0.197 3.611 4.307 1.255 2.076
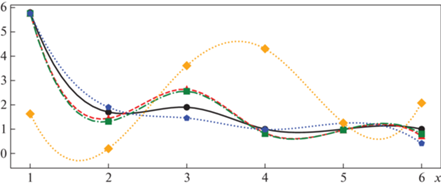
Фиг. 2.

Восстановленная начальная функция плотности активных пользователей $Q(x)$. Непрерывной черной линией с кругами изображено точное решение обратной задачи, красной штриховой линией с треугольниками – решение, полученное методом ТТ, зеленой пунктирной линией с квадратами – решение, полученное комбинацией ТТ + МГМ, синей пунктирной линией с пятиугольниками – решение, полученное с помощью комбинации ТТ + МГМ с регуляризацией А.Н. Тихонова, и оранжевой пунктирной линией с ромбами изображено решение, полученное комбинацией МРЧ + МГМ.

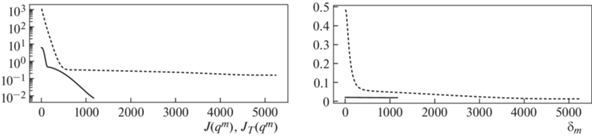
На фиг. 3 непрерывными линиями изображены кривые, полученные комбинацией ТТ + + МГМ, а пунктирной линией – кривые, полученные комбинированным методом с регуляризацией А.Н. Тихонова. Из фиг. 3 следует, что функционал (6) убывает быстрее, а функционал (7) не достигает минимального значения. Это связано с выбором ${{q}^{0}}$, что не позволяет функционалу достигнуть похожих значений. А погрешность регуляризованного комбинированного метода хоть и имеет сравнительно большие значения на первых итерациях, но достигает значения меньшего, чем в случае отсутствия регуляризации.

Фиг. 3.

Графики зависимости функционалов (в логарифмической шкале) и относительной погрешности МГМ от номера итерации $m$ с начальным приближением в виде решения, полученного методом ТТ для случаев без (непрерывная линия) и с регуляризацией А.Н. Тихонова (пунктирная линия).

3.3. Вычислительная сложность

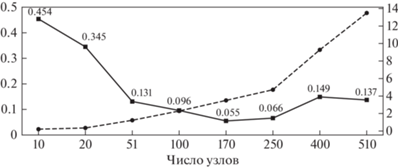
Был проведен ряд численных экспериментов для фиксированных параметров метода ТТ ${{r}_{{{\text{max}}}}} = 7$ и ${{n}_{{{\text{swp}}}}} = 10$ и набора $n = \{ 10$, 20, 51, 100, 170, 250, 400, $510\} $, который показал, что при увеличении числа узлов $n$ метода ТТ уменьшаются значения функционала и погрешности, но критически увеличивается время работы программы, что продемонстрировано на фиг. 4. В результате было выбрано значение $n = 51$ с учетом оптимального времени работы и приемлемого значения функционала.

Фиг. 4.

Непрерывная линия с квадратами демонстрирует убывание функционала с увеличением числа узлов, а штриховая линия с кругами – график возрастания времени работы программы с увеличением числа узлов.

4. ЗАКЛЮЧЕНИЕ

Математическая модель типа “реакции–диффузии”, возникающая в биологии, экологии и других приложениях, была адаптирована для описания процесса распространения информации в онлайн социальных сетях. Особенность моделирования состояла в описании социальных процессов в дискретном пространстве с неизвестным источником. В работе численно исследована и решена задача восстановления источника распространения информации по синтетическим данным интегрального типа в фиксированные моменты времени. Анализ степени убывания сингулярных чисел линеаризованного оператора показал необходимость применения методов регуляризации. Разработанный алгоритм решения обратной задачи основан на комбинации вариации метода покрытий и градиентного метода с применением регуляризации А.Н. Тихонова. Было проведено сравнение с природоподобным алгоритмом и показано преимущество использования комбинации метода тензорной оптимизации и градиентного метода с регуляризацией А.Н. Тихонова.

Список литературы

  1. Четверушкин Б.Н., Осипов В.П., Балута В.И. Подходы к моделированию последствий принятия решений в условиях противодействия // Препринт ИПМ им. М.В. Келдыша. 2018. № 43. 15 с.

  2. Wang F., Wang H., Xu K., Wu J., Jia X. Characterizing Information Diffusion in Online Social Networks with Linear Diffusive Model // Proceed. of ICDCS. 2013. P. 307–316.

  3. Колмогоров А.Н., Петровский И.Г., Пискунов Н.С. Исследование уравнения диффузии, соединенной с возрастанием вещества, и его применение к одной биологической проблеме // Бюлл. МГУ. Сер. А. Математика и механика. 1937. Т. 1. № 6. С. 1–26.

  4. Владимиров В.С. Уравнения математической физики. М.: Наука, 1981.

  5. Самохвалов Д.И. Определение аккаунтов злоумышленников в социальной сети ВКонтакте при помощи методов машинного обучения // Тр. Института системного программирования РАН. 2020. Т. 32. № 3. С. 109–117.

  6. Kabanikhin S. Definitions and examples of inverse and ill-posed problems // J. Inverse Ill-Posed Probl. 2009. V. 16. № 4. P. 317–357.

  7. Бухгейм А.Л., Клибанов М.В. Единственность в целом одного класса многомерных обратных задач // Докл. АН СССР. 1981. Т. 260. № 2. С. 269–272.

  8. Yamamoto M., Zou J. Simultaneous reconstruction of the initial temperature and heat radiative coefficient // Inverse Problems. 2001. V. 17. P. 1181.

  9. Bellassoued M., Yamamoto M. Inverse source problem for a transmission problem for a parabolic equation // J. Inverse Ill-Posed Probl. 2006. V. 14(1). P. 47–56.

  10. Cristofol M., Garnier J., Hamel F., Roques L. Uniqueness from pointwise observations in a multi-parameter inverse problem // Commun. Pure and Appl. Analys. 2012. V. 11(1). P. 173–188.

  11. Isakov V. Inverse Problems for Partial Differential Equations. New York: Springer, 2017.

  12. Hasanov A. Simultaneous determination of source terms in a linear parabolic problem from the final overdetermination: Weak solution approach // J. Math. Analys. Appl. 2007. V. 330. Iss. 2. P. 766–779.

  13. Penenko A., Mukatova Z. Inverse modeling of diffusion-reaction processes with image-type measurement data // 2018 11th Inter. Multiconference Bioinformatics of Genome Regulation and Structure/Systems Biology (BGRS/SB). 2018. P. 39–43.

  14. Kaltenbacher B., Rundell W. The inverse problem of reconstructing reaction–diffusion systems // Inverse Problems. 2020. V. 36. P. 065011.

  15. Моисеев Т.Е., Мышецкая Е.Е., Тишкин В.Ф. О близости решений невозмущенных гиперболизированных уравнений теплопроводности для разрывных начальных данных // Докл. АН. Математика. 2018. Т. 481. № 6. С. 605–609.

  16. Четверушкин Б.Н., Ольховская О.Г. Моделирование процесса лучистой теплопроводности на высокопроизводительных вычислительных системах // Докл. АН. Математика, информатика, процессы управления. 2020. Т. 491. № 1. С. 111–114.

  17. Тихонов А.Н. Об устойчивости обратных задач // Докл. АН СССР. 1943. Т. 39. № 5. С. 195–198.

  18. Тихонов А.Н. О зависимости решений дифференциальных уравнений от малого параметра // Матем. сб. 1948. Т. 22(64). № 2. С. 193–204.

  19. Krivorotko O., Zvonareva T., Zyatkov N. Numerical solution of the inverse problem for diffusion-logistic model arising in online social networks // Commun. Comput. Info. Sci. 2021. V. 1476. P. 444–459.

  20. Тихонов А.Н., Гончарский А.В., Степанов В.В., Ягола А.Г. Регуляризирующие алгоритмы и априорная информация. М.: Наука, 1983.

  21. Zheltkova V.V., Zheltkov D.A., Grossman Z., Bocharov G.A., Tyrtyshnikov E.E. Tensor based approach to the numerical treatment of the parameter estimation problems in mathematical immunology // J. Inverse Ill-Posed Probl. 2018. V. 26. № 1. P. 51–66.

  22. Oseledets I.V., Tyrtyshnikov E.E. TT-cross approximation for multidimensional arrays // Linear Algebra Appl. 2010. V. 432. № 1. P. 70–88.

  23. Goreinov S.A., Oseledets I.V., Savostyanov D.V., Tyrtyshnikov E.E., Zamarashkin N.L. How to Find a Good Submatrix // Matrix Methods: Theory, Algorithms and Appl. 2010. P. 247–256.

  24. Mikhalev A., Oseledets I. Rectangular maximum-volume submatrices and their applications // Linear Algebra Appl. 2018. V. 538. P. 187–211.

  25. Gasnikov A.V., Nesterov Y.E. Universal method for stochastic composite optimization problems // Comput. Math. Math. Phys. 2018. V. 58. № 1. P. 48–64.

  26. Звонарева Т.A., Криворотько О.И. Сравнительный анализ градиентных методов определения источника диффузионно-логистической модели // Ж. вычисл. матем. и матем. физ. 2022. Т. 62. № 4. С. 694–704.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал