Химия высоких энергий, 2022, T. 56, № 4, стр. 255-268
Статистическая термодинамика и кинетика поликонденсации. I. Ансамбли со случайно расположенными связями между мономерами
В. А. Бендерский a, *, Е. И. Кац b, И. П. Ким a
a Федеральное государственное бюджетное учреждение науки Институт проблем химической физики
Российской академии наук
142432 Московская обл., Черноголовка, просп. акад. Семенова, 1, Россия
b Институт Теоретической Физики им. Л.Д. Ландау РАН
142432 Московская обл., Черноголовка, просп. акад. Семенова, 1, Россия
* E-mail: bender@icp.ac.ru
Поступила в редакцию 11.01.2022
После доработки 04.03.2022
Принята к публикации 05.03.2022
- EDN: LWAVNM
- DOI: 10.31857/S0023119322040040
Аннотация
Поликонденсация (ПК) представлена как процесс необратимого роста во времени $t$ числа случайно расположенных связей $B(t)$ с одинаковой энергией ${{E}_{0}}$ в ансамбле из $M$ мономеров при $t = 0$. Показано, что $MB$-ансамбли изоморфны классам группы перестановок, составленным из $n$-меров, являясь их неприводимыми представлениями с фиксированными $M$ и $B{{E}_{0}}$. Представление $MB$-ансамблей, как собственных состояний, позволяет найти число элементов в них ${{S}_{M}}(B)$ = $\left( {\begin{array}{*{20}{c}} {M - 1} \\ B \end{array}} \right)$ и их ММР $n{{P}_{{MB}}}(n)$ = $\left( {\begin{array}{*{20}{c}} {M - n - 1} \\ {M - B - 2} \end{array}} \right)$, Распределения включают растущую ($B \ll M{\text{/}}2$) и падающую ($M - B \ll M{\text{/}}2$) ветви детерминированных переходов $\Delta B = 1$, разделенных областью стохастичности, вызванной перемешиванием элементов различных классов.
I. ВВЕДЕНИЕ
За 80 лет после пионерских работ Флори и Стокмайера [1–3], положивших начало теоретическому изучению полимеров, в этой области опубликовано огромное многообразие исследований, выполненных различными методами. Перечислим основные из них: 1) статистическая термодинамика [1, 2], 2) химическая кинетика, основанная как на детерминированных уравнениях Смолуховского (УС) для концентраций [3], так и стохастических уравнениях Фоккера–Планка и Ланжевена [4–8], 3) теория фракталов [9–13], 4) общая теория наноразмерных систем, в которых флуктуации одного порядка со средними [10–13], и 5) теории сетей, состоящих из перемешивающихся каналов реакций между объектами [13, 14], относящихся к общей теории разветвленных цепных процессов [15–17]. Внутри некоторых областей возникли самостоятельные направления, не связанные с первоначальным рассмотрением задачи о полимерах и скорее относящиеся к общей теории неупорядоченных конденсированных сред, в том числе наноструктур. Например, в направлении 1), благодаря компьютерным методам Монте-Карло, подробно изучены переходы золя в гель в конечных системах и условия образования “рыхлого” геля, предшествующего образованию плотного [18–23]. В направлении 2) появилась теория особых (ударно-волновых) решений УС, справедливых в пост-гелевой области (времен, бóльших гель-точки) [24–31]. Последовательное применение статистической термодинамики к полимеризующимся системам [32–36] показало, что собственными состояниями такой системы являются не индивидуальные полимеры, а их ансамбли с зависящими от степени превращения и времени молекулярно-массовым распределением. Применение теории протекания по фракталам [14, 16, 34] позволило найти соотношения самоподобия и установить справедливость универсальных размерных соотношений между концентрациями и временем в критической области золь-гель перехода.
Цели и методы этих исследований, как и их результаты, зачастую не сопоставляются друг с другом, хотя многие из исходных задач [1–3] остаются до сих пор не решенными [37, 38]. Среди них, в первую очередь, следует назвать практически важные задачи поиска полимерных материалов нового поколения с управляемой наноразмерной архитектурой [39–42]. Малоизученной остается справедливость гипотез Флори и их применимость к ансамблям с конечным числом мономеров [32–36].
Отличие открытых систем (с бесконечным начальным числом мономеров) от конечных состоит в том, что в последних масса сохраняется при всех $t$, тогда как в первых масса постоянна только в “догелевой” области $t \leqslant {{t}_{c}}$, а в конечный момент времени (в критической точке $t = {{t}_{c}}$) возникает особое решение, не зависящее от начальных условий и определяемое квазистационарным потоком (7). Это новое решение описывает рост массы геля, благодаря которому относительная масса золя уменьшается при $t > {{t}_{c}}$ [30, 31]. В конечных ансамблях начальная масса мономеров постепенно переходит в $n$-меры с растущей длиной и изменяющейся шириной распределения. Процесс заканчивается образованием М-мера, в который собираются все мономеры. Очевидно, что в открытых и достаточно больших конечных системах кинетика роста $n$-меров с промежуточной длиной приблизительно одинакова при $t \leqslant {{t}_{c}}$, различна в пост-гелевой области и вновь совпадает в термодинамическом пределе
где образуется одно и то же конечное состояние. Если в открытых системах состав золя остается приблизительно таким же, как и в гель-точке, то в конечных системах распределение $n$-меров в пост-гелевой области продолжает изменяться, благодаря бимолекулярным реакциям между партнерами с увеличивающейся длиной цепи. Гипотезы Флори относятся к открытым ансамблям и не описывают распределение $n$-меров в обеих фазах конечных систем при $t > {{t}_{c}}$. Единственная характеристика геля, рассматриваемая в [1–3], – его относительная масса, которая ничего не говорит о распределении $n$-меров, хотя именно это распределение определяет локальную структуру полимеров. Это утверждение подтверждает не только образование рыхлых гелей, как промежуточных состояний между золем и плотным гелем, но и поликонденсация кремнийорганических мономеров, приводящая к образованию продуктов, содержаших кристаллоподобные наноразмерные фрагменты, встроенные в случайно разветвленные цепи [43–48]. Один из возможных механизмов обусловлен уменьшением константы скорости бимолекулярной реакции между $n$-мерами с ростом длины цепи [47, 48], что противоречит гипотезам Флори.Цель настоящей статьи – последовательный анализ пост-гелевой области в конечных системах. В последующих разделах рассмотрены следующие вопросы. Второй раздел является кратким обзором гипотез Флори и их связи с кинетическими уравнениями в открытых ансамблях. В третьем разделе эти результаты сравниваются с решениями кинетических уравнений в конечных ансамблях. Раздел заканчивается рассмотрением конечных ансамблей в термодинамическом пределе. В четвертом разделе показано, что изоморфизм микроканонических ансамблей $n$-меров с классами групп перестановок позволяет найти простые аналитические зависимости молекулярно-массового распределения от числа мономеров и числа связей и рассмотрена промежуточная область между начальным ростом коротких цепей и переходом конечных систем к пределу (1), когда образуются $n$-меры с $n \approx M$. Выводы собраны в пятом разделе.
II. ГИПОТЕЗЫ ФЛОРИ: АНСАМБЛИ С БЕСКОНЕЧНЫМ ЧИСЛОМ МОНОМЕРОВ
Общий метод расчета равновесной функции распределения полимеров по длине цепи основан на постулатах статистической термодинамики и гипотезах Флори−Стокмайера [1–3], упрощенно описывающих поликонденсацию (ПК), как процесс образования случайно расположенных химических связей между звеньями. Гипотезы состоят в следующем.
(I) Каждый мономер содержит одно звено цепи $R$ и $f \geqslant $ 3 одинаковых функциональных групп $A$. (II) Химическая связь между двумя звеньями образуется в результате бимолекулярной реакции между функциональными группами различных мономеров
(2)
$\begin{gathered} R{{A}_{f}} + R{{A}_{{f{\kern 1pt} '}}}\xrightarrow{{{{k}_{0}}}}{{A}_{{f - 1}}}{{R}_{2}}{{A}_{{f{\kern 1pt} ' - 1}}} + AA, \\ {{R}_{2}} = R - R, \\ \end{gathered} $(III) Каждое звено способно образовать $f$‑связей, так что при $f$ = 3, 4, … образуются линейный $n$-мер (из двух концевых и $(n - 2)$ внутренних звеньев с одной и двумя связями) и разветвленные цепи с двойными и тройными узлами соответственно. (IV) Полимер ${{R}_{n}}$ из $n$-звеньеа ($n$-мер) образуется в результате последовательности ($n - 1)$ бимолекулярной реакции, совокупность которых суммирует все возможные равновероятные пути образования $n$-мера
(3)
${{R}_{{n{\kern 1pt} '}}}{{A}_{{n{\kern 1pt} '}}} + {{R}_{{n - n{\kern 1pt} '}}}{{A}_{{n - n{\kern 1pt} '}}}\xrightarrow{{{{K}_{{n - n',n'}}}}}{{R}_{n}}{{A}_{n}} + AA{\kern 1pt} '.$Согласно закону действующих масс, константа скорости роста цепи (3) ${{K}_{{n - n',n'}}}$ пропорциональна константе скорости “элементарной” реакции (2), ${{k}_{0}}$, умноженной на произведение стехиометрических коэффициентов, равных числу функциональных групп в партнерах
(4)
${{K}_{{n - n{\kern 1pt} ',n{\kern 1pt} '}}} = ((f - 2)n{\kern 1pt} ' + 2)((f - 2)(n - n{\kern 1pt} ') + 2){{k}_{0}}.$В (4) учтено, что число активных функциональных групп в реагентах равно их полному числу $fn{\kern 1pt} '$ и $f(n - n{\kern 1pt} ' - 1)$ за вычетом $2(n{\kern 1pt} ' - 1)$ и $2(n - n{\kern 1pt} ' - 1)$ групп, истраченных ранее на образование связей в них самих. Гипотеза (IV) предполагает, что элементарная константа ${{k}_{0}}$ и энергии образующихся связей $R - R{\kern 1pt} '$, ${{E}_{0}}$, не зависят от $f$и $n$.
Система кинетических уравнений Смолуховского для бесконечного ансамбля, удовлетворяющая гипотезам Флори
(5)
$\begin{gathered} d{{P}_{n}}{\text{/}}dt = 1{\text{/}}2\sum\limits_{n{\kern 1pt} ' = 1}^{n - n{\kern 1pt} '} {K(n{\kern 1pt} ',n - n'){{P}_{{n{\kern 1pt} '}}}{{P}_{{n - n{\kern 1pt} '}}}} - \\ - \,\,\sum\limits_{n{\kern 1pt} ' = 1}^\infty {K(n,n + n{\kern 1pt} '){{P}_{n}}{{P}_{{n + n{\kern 1pt} '}}}} , \\ \end{gathered} $решена Стокмайером [3], где ${{P}_{n}}(t)$ − зависящие от времени концентрации $n$-меров. Уравнение (5) описывает ПК, как последовательный рост числа связей $B(t)$. При $f \geqslant $ 3 константы скорости растут с ростом длины цепи, так что в конечный момент времени, называемый гель-точкой ${{t}_{c}}$, возникает разрыв производных в решениях УС, приводящий при $t > {{t}_{c}}$ к уменьшению массы золя (первого момента распределения ${{M}_{1}}(t)$).
В [31] УС (5) переписаны в форме уравнений непрерывности входящих и выходящих массовых потоков для всех $n$-меров
где входящий поток учитывает, что $n$-мер образуется из всех $n{\kern 1pt} '$- и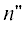 -меров, если
-меров, если 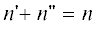 , а уходящий обусловлен рекомбинацией $n$-мера со всеми $n{\kern 1pt} '$-мерами $(n{\kern 1pt} ' \geqslant 1)$ с образованием более длинной цепи $(n + n{\kern 1pt} ')$. Уменьшение массы золя рассматривается как поток в гель, т.е. в бесконечный N-мер.
, а уходящий обусловлен рекомбинацией $n$-мера со всеми $n{\kern 1pt} '$-мерами $(n{\kern 1pt} ' \geqslant 1)$ с образованием более длинной цепи $(n + n{\kern 1pt} ')$. Уменьшение массы золя рассматривается как поток в гель, т.е. в бесконечный N-мер.
Для конечных ансамблей решение системы уравнений (5) определяется двумя граничными условиями: начальной концентрацией мономеров, которая в дальнейшем предполагается заданной, и выходящим из ансамбля потоком. В зависимости от этого потока концентрации образующихся полимеров могут быть равновесными и/или квазистационарными. Если выходящий поток равен нулю, решение кинетических уравнений определяет совокупность равновесных состояний ${{\bar {P}}_{n}}$, при которых все производные равны нулю в один и тот же момент времени $t = t{\kern 1pt} *$
(7)
${{\left. {d{{P}_{n}}{\text{/}}dt} \right|}_{{t = t*}}} = 0,\,\,\,{{P}_{n}}(t*) = {{\bar {P}}_{n}} = {{\Omega }_{n}}\bar {P}_{1}^{n},$причем в единственном начальном состоянии ${{P}_{1}}(0) = 1$ ${{\Omega }_{1}} = 1$. В равновесных состояниях все $n$-меры находятся в условиях детального баланса потоков (6). Поскольку $n$-меры ($1 < n < M$) являются промежуточными состояниями параллельно-последовательных реакций. образующих сеть ПК, все эти состояния равновесны. Таким образом, конечные ансамбли в отсутствие входящих и выходящих потоков приходят к термодинамическому равновесию (1). Для конечных равновесных ансамблей масса мономеров сохраняется в течение всего процесса роста цепи. Если потоки не равны нулю, но для всех $n$-меров равны одному и тому же постоянному значению
образуется ансамбль квазистационарных состояний, когда концентрации зависят от $J$, как единственного параметра. Следует подчеркнуть, что понятие квазистационарных состояний одинаково применимо как к обратимым реакциям при наличии фрагментации, так и к необратимым реакциям в ее отсутствие, поскольку начальное число мономеров не сохраняется, уменьшаясь выходящим потоком $J \ne 0$.
Выходящий поток включает сумму потоков из всех равновесных состояний, когда продуктом являются $n$-меры с длиной цепи $n > M$. Максимальный поток равен сумме выходящих потоков из всех состояний $1 \leqslant n \leqslant M$
(10)
${{J}_{{\max }}} = \sum\limits_{n = 1}^\infty {\sum\limits_{n' = 1}^n {{{K}_{{M - n + n',n'}}}} } {{P}_{{M - n + n'}}}{{P}_{{n'}}}.$Отметим, что определение квазистационарных состояний в теории ПК [31] отличается от традиционного для последовательности реакций в формальной химической кинетике, где условия (9) нет и производные (7) равны нулю в различные моменты времени, создавая при $J \ne 0$ волну последовательного превращения промежуточных состояний с различным распределением [47, 48]. Постоянство потока, не зависящее от времени и длины цепи, является дополнительной гипотезой Флори (V), которая определяет состав золя при образовании геля и квазистационарные концентрации $n$-меров, меньшие равновесных
(11)
${{\tilde {P}}_{n}} = {{\bar {P}}_{n}}\left( {1 - \frac{{{{J}_{n}}}}{{{{J}_{{\max }}}}}} \right).$Принципиальное отличие открытых систем от конечных состоит в том, что в последних масса сохраняется при всех $t$, тогда как в первых масса постоянна только в “догелевой” области $t \leqslant {{t}_{c}}$, а в критической точке $t = {{t}_{c}}$ возникает особое решение, не зависящее от начальных условий и определяемое потоком (6). Это новое решение описывает рост массы геля, благодаря которому масса золя уменьшается при $t > {{t}_{c}}$. В конечных ансамблях начальная масса мономеров постепенно переходит в $n$-меры с растущей длиной и изменяющейся шириной распределения. Процесс заканчивается образованием М-мера, в который собираются все мономеры. Очевидно, что в открытых и достаточно больших конечных системах кинетика роста $n$-меров с промежуточной длиной цепи приблизительно одинакова при $t \leqslant {{t}_{c}}$, различна в постгелевой области и вновь совпадает в термодинамическом пределе (1), когда образуется одно и то же конечное состояние. Если в открытых системах состав золя остается приблизительно таким же, как и в гель-точке, то в конечных системах распределение $n$-меров в постгелевой области продолжает расширяться, благодаря бимолекулярным реакциям между партнерами с увеличивающейся длиной. Таким образом, гипотезы Флори относятся к открытым ансамблям и не описывают распределение $n$-меров в обеих фазах при $t > {{t}_{c}}$. Единственная характеристика – относительная масса золя и геля, – ничего не говорит о распределении $n$-меров, хотя именно это распределение определяет локальную структуру полимеров. Это утверждение подтверждает образование рыхлого геля, как промежуточного состояния между золем и плотным гелем. Один из возможных механизмов этого явления обусловлен уменьшением константы скорости элементарной бимолекулярной реакции ${{k}_{0}}$ с ростом длины цепи, обусловленный изменением вязкости среды с ростом степени превращения [10, 39, 40].
Обобщения модели $R{{A}_{f}}$ рассматривают мономеры с несколькими сортами функциональных групп типа ${{A}_{{f1}}}R{{B}_{{f2}}}$ [24, 27, 28]. Согласно гипотезе (III), константу скорости поликонденсации для таких мономеров можно представить квадратным трехчленом
и найти распределения при различных значениях параметров. При $A = 1,\,\,B = C = 0;$ A = 0, B = 1/2, C = 0 и $A = B = 0,\,\,C = 1$ константа скорости (3) постоянна, пропорциональна числу функциональных групп в партнерах и их произведению соответственно. Как показывает анализ кинетических уравнений [29–31], этими тремя случаями исчерпываются режимы цепных процессов поликонденсации от линейных цепей с монотонным ростом их длины во времени до нелинейных (взрывных) процессов, скорость которых неограниченно возрастает в конечный момент времени, вызывая фазовый переход из золя в гель.
III. КОНЕЧНЫЕ АНСАМБЛИ
При конечном числе мономеров М, между которыми случайно расположены $B$ связей, образуется замкнутый ансамбль, состоящий из n-меров с длиной цепи от 1 до $N = M - B$ , число которых изменяется от 1 (все мономеры объединены в один “гигантский” кластер) до $M$, когда ансамбль состоит из мономеров и связи отсутствуют. В [32–36] те же самые ансамбли обозначаются $(MN)$, мы предпочитаем характеризовать их числом мономеров и числом связей, как в теории протекания.
Уравнение для сумм состояний ${{\Omega }_{n}}$ следует из того, что оно, во-первых, равно концентрации n-мера ${{P}_{n}}$, умноженной на удвоенное число связей в $n$-мере, и , во-вторых, числу всех пар $n{\kern 1pt} '$- и $(n - n{\kern 1pt} ')$-меров, из которых его можно образовать. Равенство числа n-меров, полученных двумя способами, приводит к уравнению
(13)
$\begin{gathered} 2(n - 1){{P}_{n}} = \sum\limits_{n' = 1}^{n - 1} {\left( {\begin{array}{*{20}{c}} n \\ {n{\kern 1pt} '} \end{array}} \right){{K}_{{n - n,n'}}}{{P}_{{n - n'}}}{{P}_{{n'}}}} , \\ \left( {\begin{array}{*{20}{c}} n \\ {n{\kern 1pt} '} \end{array}} \right) = \frac{{n!}}{{n{\kern 1pt} '!(n - n{\kern 1pt} ')!}}. \\ \end{gathered} $Суммируя в (13) ${{P}_{n}}$ и $n{{P}_{n}}$, находим два уравнения в неотрицательных целых чисел для нулевого и первого моментов функции распределения
(14)
${{M}_{0}} = \sum\limits_{n = 1}^N {{{P}_{n}}} = N,\,\,\,\,{{M}_{1}} = \sum\limits_{n = 1}^N {n{{P}_{n}}} = M.$Первое из уравнений (14) определяет число $n$-меров ($n = 1,..,N$) в $MB$-ансамбле, а второе – число мономеров в их составе. Разность этих уравнений пропорциональна суммарному числу связей и, согласно гипотезе (IV), равна полной энергии всех связей в $MN$-ансамбле
Таким образом, (13)–(15) определяют совокупность двухпараметрических $MB$-ансамблей с постоянным числом $n$-меров и постоянной энергией связи. Подчеркнем, что $MB$-ансамбль является не индивидуальным $n$-мером с фиксированной длиной цепи, а микроканоническим ансамблем, состоящим из $n$-меров с длиной цепи от 1 до $N$, в котором сумма состояний (8) определяется двумя уравнениями (14), а канонический ансамбль разделяется на микроканонические с фиксированными (собственными) значениями энергии.
Заменив факториалы в (13) их асимптотиками по формуле Стирлинга (${{v}_{n}}! \approx \sqrt {2\pi {{v}_{n}}} {{\left( {{{v}_{n}}{\text{/}}e} \right)}^{{{{v}_{n}}}}}$), введем множители Лагранжа
(16)
$\beta = \frac{\partial }{{\partial M}}{{\left( {\ln {\kern 1pt} {{\Omega }_{{MN}}}} \right)}_{N}},\,\,\,\gamma = \frac{\partial }{{\partial N}}{{\left( {\ln {\kern 1pt} {{\Omega }_{{MN}}}} \right)}_{M}},$максимальные значения которых
(17)
$\begin{gathered} {{F}_{{MN}}}(\left\{ {{{v}_{n}}} \right\} = \ln (\Omega ) - \gamma M - \beta M, \\ {{\left. {\frac{{\partial {{F}_{{MN}}}}}{{\partial {{v}_{n}}}}} \right|}_{{{{v}_{n}} = v_{n}^{*}}}} \approx \ln (P_{n}^{*}{\text{/}}n!) - \gamma - \beta N = 0, \\ \end{gathered} $определяют наиболее вероятные населенности состояний $MB$-ансамблей [13, 14, 32–35, 52]
Как непосредственно следует из (14) и (17), статистическая сумма для $MB$-ансамбля и ее производные пропорциональны моментам
(19)
$\begin{gathered} {{Z}_{{MN}}} = \sum\limits_{n = 1}^N {\frac{{{{v}_{n}}}}{{n!}}{{e}^{{ - \beta n}}}} = {{e}^{\gamma }}M, \\ \frac{{\partial Z_{{MN}}^{q}}}{{\partial {{\beta }^{q}}}} = {{( - 1)}^{q}}\sum\limits_{n = 1}^N {{{n}^{q}}\frac{{{{v}_{n}}}}{{n!}}{{e}^{{ - \beta n}}}} = {{( - 1)}^{q}}{{e}^{\gamma }}\sum\limits_{n = 1}^N {{{n}^{q}}v_{n}^{*}} . \\ \end{gathered} $Распределение (19) было впервые получено в [1, 2] из термодинамических соображений (13) и в [3] из кинетических уравнений. Поскольку любая конечная группа порядка $M$изоморфна подгруппе группы перестановок того же порядка ${{\pi }_{M}}$ [49], $MB$-ансамбли изоморфны классам циклических перестановок в N-циклах, связанных с нумерацией мономеров, между которыми образуются связи в элементах ${{\pi }_{M}}$. Поскольку перестановки мономеров внутри цикла создает один и тот же элемент, число элементов в классе связано с его циклической структурой. Если на перестановку группы ${{\pi }_{N}}$, содержащую циклы из (${{1}^{{{{v}_{1}}}}}{{2}^{{{{v}^{2}}}}}...{{m}^{{{{v}_{m}}}}}$) элементов, действуют все $N!$ перестановок, эта операция оставляет на месте все скобки, разделяющие циклы. Очевидно, что ${{v}_{1}}!{{v}_{2}}!...{{v}_{m}}!$ перестановок будут совпадать. Аналогичное совпадение получится для всех циклов с длиной от 1 до $M$, так что число элементов в классе равно
(20)
$G({{v}_{1}},{{v}_{2}},...{{v}_{N}};M) = v!{{\left( {\prod\limits_{k - 1}^N {{{k}^{{{{v}_{k}}}}}} } \right)}^{{ - 1}}},$Чтобы найти статистическую сумму канонического $M$-ансамбля, необходимо: (1) найти число конфигураций входящих в состав микроканонических $MB$-ансамблей и (2) найти молекулярно-массовые распределения $n$-меров в них. Поскольку микроканонический $MB$-ансамбль состоит из ${{v}_{n}}$ $n$-меров (с длиной цепи $n$, образованной $(n - 1)$-связью), составляющие вектора (21), ${{v}_{n}}$ удовлетворяют двум уравнениям (14), и канонический $M$-ансамбль состоит из такого же числа классов, что группа перестановок ${{\pi }_{M}}$.
В $MB$-ансамбль, объединяющий все конфигурации с заданным числом связей, входит несколько классов группы перестановок
(23)
$\begin{gathered} {{\Omega }_{n}} = \Omega (\left\{ {{{v}_{n}}} \right\},M,N) = \\ = \,\,\frac{{M!}}{{{{v}_{1}}!{{v}_{2}}!...{{v}_{N}}!}}{{\left( {\frac{{{{P}_{1}}}}{{1!}}} \right)}^{{{{v}_{1}}}}}{{\left( {\frac{{{{P}_{2}}}}{{2!}}} \right)}^{{{{v}_{2}}}}}...{{\left( {\frac{{{{P}_{N}}}}{{N!}}} \right)}^{{{{v}_{N}}}}}. \\ \end{gathered} $Комбинаторные тождества для биномиальных коэффициентов [50, 51]
(24)
$\begin{gathered} \sum\limits_{k = 0}^n {\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right){{x}^{k}}{{{(1 - x)}}^{k}} = 1,} \\ \sum\limits_{k = 0}^n {\frac{k}{n}\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right){{x}^{k}}{{{(1 - x)}}^{k}} = x} \\ \sum\limits_{k = 0}^n {\frac{{{{k}^{2}}}}{{{{n}^{2}}}}\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right){{x}^{k}}{{{(1 - x)}}^{k}} = (1 - {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0em} n}){{x}^{2}} + {x \mathord{\left/ {\vphantom {x n}} \right. \kern-0em} n},} \\ \sum\limits_{k = 0}^n {{{{\left( {\begin{array}{*{20}{c}} k \\ n \end{array} - x} \right)}}^{2}}\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right){{x}^{k}}{{{(1 - x)}}^{k}} = x(1 - x){\text{/}}n,} \\ \end{gathered} $позволяют найти решение уравнений (14), подставляя в два первых тождества $x = $ 1/2.
Непосредственное сравнение классов группы перестановок ${{\pi }_{M}}$ с конфигурациями$MB$-ансамблей показывает, что их число совпадает при $M = $ = 4–10. Изоморфизм при всех $M$ доказывается по индукции. Предполагая, что группы ${{\pi }_{{MB}}}$ изоморфны составляющим $MB$-ансамблей, из тех же тождеств (24) следует, что изоморфизм сохраняется и при $M + $ 1. Поскольку для неотрицательных целых значений $n$, $\Gamma (n) = (n - 1)!$, факториалы в биномиальных коэффициентах, как функции дискретной переменной $n$, можно заменить гамма-функциями непрерывной переменной $X$, такой, что в точках $X = N$ справедливо равенство
(25) имеет единственный максимум в интервале $[1,M]$
и является четной функцией отклонений от максимума
что позволяет аппроксимировать ее гауссианом в приближении Стирлинга
(28)
${{P}_{M}}(X) \approx \sigma \sqrt {2\pi } \exp \left( { - (X - {{{{X}_{m}}{{)}^{2}}} \mathord{\left/ {\vphantom {{{{X}_{m}}{{)}^{2}}} {{{\sigma }^{2}}}}} \right. \kern-0em} {{{\sigma }^{2}}}}} \right),\,\,{{X}_{m}} \gg 1.$Нормированные распределения микроканонических $MB$-ансамблей
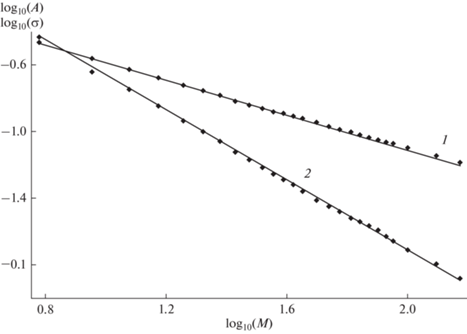
приведены на рис. 1. Параметры гауссиана (28) найдены из условия наилучшей аппроксимации в интервале [0, M]. Их зависимость от $M$ представлена на рис. 2.
Рис. 1.
Нормированное распределение по числу $n$-меров в микроканонических $MB$-ансамблях $N = M - B$ из числа мономеров $M$ = 39, 55, 80, 115, 150 (кривые 1−5 соответственно).

Рис. 2.
Параметры гауссианов ${{X}_{M}}$и $\sigma $, показанных на рис. 1, как функции числа мономеров в канонических $M$-ансамблях. Кривая 1 − средние значения длины цепи, кривая 2 – дисперсия распределения.
Классы в составе ансамблей $M$ = [3, 10] приведены в табл. 1. При $M$ = 3 образуются три ансамбля $B$ = 0, 1 и 2, состоящие из трех мономеров (31), мономера и димера (1112) и одного тримера (13) соответственно. При $M$ = 4 возникают четыре ансамбля $B$ = 0, 1, 2 и 3 состава 41, (1113 ; 22), 2112, 14, причем ансамбль ($M$ = 4, $B$ = 2) включает два класса перестановок – мономер–тример и два димера. При дальнейшем росте числа мономеров число классов в $MB$-ансамблях растет $\sim {{(B{\text{/}}2)}^{2}}$, что следует из (24). Как показано на рис. 1, максимум распределения (26) смещается с ростом порядка группы перестановок пропорционально ~(M/2). Рост числа классов в составе $MB$-ансамбля происходит вплоть до максимума (28). Последующее уменьшение числа классов при B > M/2 обусловлено уменьшением числа партнеров в конечном ансамбле. Таким образом, зависимость числа классов от $M$ состоит из трех областей: начального роста, области с максимальным числом классов в окрестности максимума гауссиана (28) и спада, когда число элементов в классах $M - B \ll M{\text{/}}2$. Максимуму (28) соответствует не только наибольшее число классов, но и число элементов в них, что иллюстрируют кинетические деревья, показанные на рис. 3. Корень дерева соответствует одной тождественной перестановке ${{M}_{1}}$. С ростом $B$ число классов в строке растет пропорционально $B$. Стрелками показаны переходы между классами перестановок, входящие в переход $(M,B) \to (M,B + 1)$.Число переходов $\Delta B = 1$, вызывающих рост цепи, увеличивается не только за счет всех переходов между $n$ и $n{\kern 1pt} '$, входящих в состав одного класса, но и за счет роста числа элементов в классах.
Таблица 1.
Классы групп перестановок ${{\pi }_{M}}$ в составе $MN$-ансамблей в обозначении (3)*
| M | N | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 3 | 13 | 1121 | 31 | |||||||
| 4 | 14 | 1113 22 |
2112 | 41 | ||||||
| 5 | 15 | 1114 1213 |
2113 1122 |
3112 | 51 | |||||
| 6 | 16 | 1115 1214 23 |
2114 111213 32 |
3113 2122 |
4112 | 61 | ||||
| 7 | 17 | 1116 1215 1314 |
2115 111214 1123 2213 |
3114 211213 1132 |
4113 3122 |
5112 | 71 | |||
| 8 | 18 | 1117 1216 1315 24 |
2116 111215 111314 1223 |
3115 2123 112213 211214 42 |
4114 311213 2132 |
5113 4122 |
6112 | 81 | ||
| 9 | 19 | 1118 1217 1316 1415 |
2117 111216 111315 1124 121314 2215 33 |
3116 211215 211314 111223 112214 3213 |
4115 311214 3123 212213 1142 |
5114 411213 3132 |
6113 5122 |
7112 | 91 | |
| 10 | 110 | 1119 1218 1317 1416 25 |
2118 111217 111316 111415 2216 1224 121315 2314 |
3117 211216 211315 2124 112215 1133 2223 3214 |
4116 311215 311314 212214 113213 52 211223 |
4115 411214 4123 312213 2142 |
6114 511313 4132 |
7113 6122 |
8112 | 101 |
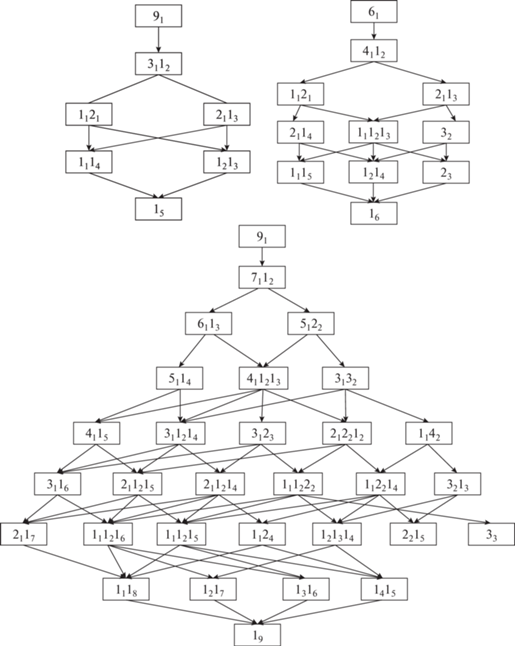
Рис. 3.
Деревья сети реакций поликонденсации в ансамблях из М = 5, 6, 9 мономеров. Прямоугольники в горизонтальных рядах обозначают классы групп перестановок. Строчные значения определяют число n-меров, подстрочные индексы равны числу мономеров в них n. Верхний ряд относится к начальному состоянию из М мономеров (число связей В = 0), нижний ряд – к М-меру (В = М − 1). Стрелки указывают переходы между классами перестановок $\Delta B$ = 1.
IV. МОЛЕКУЛЯРНО-МАССОВОЕ РАСПРЕДЕЛЕНИЕ В $MB$-АНСАМБЛЯХ
Два первых тождества (24) определяют не зависящее от $B$ общее число мономеров в $n$-мерах и число классов в $MB$-ансамбле
(30)
$\sum\limits_{v = 1}^M {\left( {\begin{array}{*{20}{c}} {M - 1} \\ v \end{array}} \right) = {{2}^{{M - 1}}}} ,\,\,\,\sum\limits_{v = 1}^M v \left( {\begin{array}{*{20}{c}} M \\ v \end{array}} \right) = N{{2}^{{M - 2}}}.$Первое тождество следует из определения суммы $v = ({{v}_{1}},...{{v}_{n}},...{{v}_{N}})$, а второе определяет составляющие полиномиального коэффициента (20)
(31)
${{v}_{{MN}}}(n) = N\left( {\begin{array}{*{20}{c}} {M - n - 1} \\ {N - 2} \end{array}} \right),$(31) показывает, что число элементов в $MB$-ансамбле (табл. 2), можно найти, не вычисляя число классов. При малом числе связей
число классов в каждом из ансамблей не зависит от $M$. При $B$ = 0 и 1 ансамбль состоит из одного класса ${{M}_{1}}$ и ${{(M - 2)}_{1}}{{1}_{2}}$, включающего только мономеры, и мономеры и один димер. Ансамбль $(M2)$ содержит два класса ${{(M - 3)}_{1}}{{1}_{3}}$ и ${{(M - 2)}_{1}}2{}_{2}$. При $M = 3$, $B = 2$ ансамбль состоит из одного класса ${{1}_{1}}{{1}_{2}}$, а при 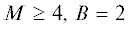 − из двух классов ${{(M - 3)}_{1}}{{1}_{3}}$ и ${{(M - 4)}_{1}}{{2}_{2}}$. При $B$ = 3 ансамбли (43) и (53) включают один и два класса, а при $M \geqslant 6$ $(M3)$ состоят из трех классов (рис. 3). При $B \to M$ число классов уменьшается. Ансамбль $M(M - 1)$ содержит только один класс ${{1}_{M}}$. В ансамбле $M(M - 2)$ число классов $[M{\text{/}}2]$, где $[x]$-целая часть $x$. В области $M - B \ll M{\text{/}}2$ число классов растет вплоть до максимума (26). Таблица 3 иллюстрирует, как формируется состав микроканонических ансамблей из классов группы
перестановок. При $N = 2$ классы в ансамбле $(M,M - 2)$, содержат по одному $n$-меру из $\left\{ {{{1}_{1}}{{{(M - 2)}}_{1}};\;{{1}_{2}}{{{(M - 3)}}_{1}};{{1}_{3}}{{{(M - 4)}}_{1}},...} \right\}$ с полиномиальными коэффициентами (21), равными 2. При $N = 3$ в ансамбль входят классы 21(M – 2)1 : : 1112(M – 3)1 : 1113(M – 4)1 : …, 21(M – 2)1 : 22(M – ‒ 4)1…; для которых полиномиальные коэффициенты равны 6,3,6,6,6,6,6,6 и 3,6 соответственно.
Как показано в двух правых столбцах табл. 3, число элементов в ансамбле равно суммам коэффициентов (30). Число элементов в ансамблях
(8$B$), приведенное в табл. 4, показывает, как его изменение связано с числом классов и числом элементов в них.
− из двух классов ${{(M - 3)}_{1}}{{1}_{3}}$ и ${{(M - 4)}_{1}}{{2}_{2}}$. При $B$ = 3 ансамбли (43) и (53) включают один и два класса, а при $M \geqslant 6$ $(M3)$ состоят из трех классов (рис. 3). При $B \to M$ число классов уменьшается. Ансамбль $M(M - 1)$ содержит только один класс ${{1}_{M}}$. В ансамбле $M(M - 2)$ число классов $[M{\text{/}}2]$, где $[x]$-целая часть $x$. В области $M - B \ll M{\text{/}}2$ число классов растет вплоть до максимума (26). Таблица 3 иллюстрирует, как формируется состав микроканонических ансамблей из классов группы
перестановок. При $N = 2$ классы в ансамбле $(M,M - 2)$, содержат по одному $n$-меру из $\left\{ {{{1}_{1}}{{{(M - 2)}}_{1}};\;{{1}_{2}}{{{(M - 3)}}_{1}};{{1}_{3}}{{{(M - 4)}}_{1}},...} \right\}$ с полиномиальными коэффициентами (21), равными 2. При $N = 3$ в ансамбль входят классы 21(M – 2)1 : : 1112(M – 3)1 : 1113(M – 4)1 : …, 21(M – 2)1 : 22(M – ‒ 4)1…; для которых полиномиальные коэффициенты равны 6,3,6,6,6,6,6,6 и 3,6 соответственно.
Как показано в двух правых столбцах табл. 3, число элементов в ансамбле равно суммам коэффициентов (30). Число элементов в ансамблях
(8$B$), приведенное в табл. 4, показывает, как его изменение связано с числом классов и числом элементов в них.
Таблица 2.
Число классов группы перестановок, входящих в состав $MB$-микроканонических ансамблей
| M | B | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
| 1 | 1 | |||||||||||||||||
| 2 | 1 | 1 | ||||||||||||||||
| 3 | 1 | 1 | 1 | |||||||||||||||
| 4 | 1 | 1 | 2 | 1 | ||||||||||||||
| 5 | 1 | 1 | 2 | 2 | 1 | |||||||||||||
| 6 | 1 | 1 | 2 | 3 | 3 | 1 | ||||||||||||
| 7 | 1 | 1 | 2 | 3 | 4 | 3 | 1 | |||||||||||
| 8 | 1 | 1 | 2 | 3 | 5 | 5 | 4 | 1 | ||||||||||
| 9 | 1 | 1 | 2 | 3 | 5 | 6 | 7 | 4 | 1 | |||||||||
| 10 | 1 | 1 | 2 | 3 | 5 | 7 | 9 | 8 | 5 | 1 | ||||||||
| 11 | 1 | 1 | 2 | 3 | 5 | 7 | 10 | 11 | 10 | 5 | 1 | |||||||
| 12 | 1 | 2 | 3 | 5 | 7 | 11 | 13 | 15 | 17 | 6 | 1 | |||||||
| 13 | 1 | 1 | 2 | 3 | 5 | 7 | 10 | 15 | 16 | 18 | 14 | 6 | 1 | |||||
| 14 | 1 | 1 | 2 | 3 | 5 | 7 | 10 | 15 | 20 | 23 | 23 | 16 | 7 | 1 | ||||
| 15 | 1 | 1 | 2 | 3 | 5 | 7 | 10 | 15 | 21 | 24 | 27 | 26 | 19 | 7 | 1 | |||
| 16 | 1 | 1 | 2 | 3 | 5 | 7 | 10 | 15 | 22 | 26 | 33 | 35 | 30 | 21 | 8 | 1 | ||
| 17 | 1 | 1 | 2 | 3 | 5 | 7 | 10 | 15 | 22 | 27 | 33 | 34 | 35 | 30 | 24 | 8 | 1 | |
| 18 | 1 | 1 | 2 | 3 | 5 | 7 | 10 | 15 | 22 | 27 | 35 | 40 | 44 | 46 | 36 | 26 | 9 | 1 |
Таблица 3.
Распределение $n$-меров по конфигурациям $MN$-ансамблей, $M$ = 8
| $N$ | $v{{\backslash }}n$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 18 | 1 | |||||||
| 2 | 1117 | 2 | 2 | ||||||
| 2 | 1216 | 2 | 2 | ||||||
| 2 | 1315 | 2 | 2 | ||||||
| 2 | 24 | 2 | |||||||
| 3 | 2116 | 6 | 3 | ||||||
| 3 | 111215 | 6 | 6 | 6 | |||||
| 3 | 111314 | 6 | 6 | 6 | |||||
| 3 | 1223 | 3 | 6 | ||||||
| 3 | 2214 | 4 | 3 | ||||||
| 4 | 3115 | 12 | 4 | ||||||
| 4 | 2123 | 12 | 12 | ||||||
| 4 | 112213 | 12 | 24 | 12 | |||||
| 4 | 211214 | 24 | 12 | 12 | |||||
| 4 | 42 | 4 | |||||||
| 5 | 4114 | 20 | 5 | ||||||
| 5 | 311213 | 60 | 20 | 20 | |||||
| 5 | 2132 | 20 | 30 | ||||||
| 6 | 5113 | 30 | 6 | ||||||
| 6 | 4122 | 60 | 30 | ||||||
| 7 | 6112 | 42 | 7 | ||||||
| 8 | 81 | 8 |
Таблица 4.
Суммарное распределение $n$-меров в $MN$-ансамблях, $M$ = 8
| N | n | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ${{S}_{{MN}}}$ | $N{{S}_{{MN}}}$ | |
| 1 | 1 | 1 | 1 | |||||||
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 7 | 14 | |
| 3 | 18 | 15 | 12 | 9 | 6 | 3 | 21 | 63 | ||
| 4 | 60 | 40 | 24 | 12 | 4 | 35 | 140 | |||
| 5 | 100 | 50 | 20 | 5 | 35 | 165 | ||||
| 6 | 90 | 30 | 6 | 21 | 126 | |||||
| 7 | 42 | 7 | 7 | 49 | ||||||
| 8 | 8 | 1 | 8е | |||||||
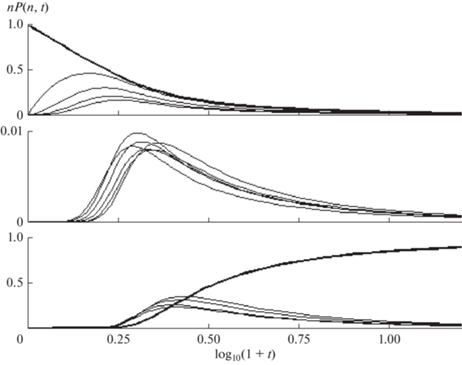
Зависящие от времени концентрации $n$-меров разделяются на три группы с различной кинетикой (рис. 4). Концентрации коротких $n$-меров (верхняя панель) максимальны в моменты времени, увеличивающиеся с ростом $n$, чему соответствует рост цепи с последовательным образованием квази-стационарных состояний. В широкой промежуточной области (средняя панель) концентрации становятся почти на порядок меньше, и их максимумы расположены в сравнительно узкой области времен. Кинетика этих состояний качественно соответствует представлению [31] о квазистационарных состояний с максимальной концентрацией в один и тот же момент времени. Когда образуются $n$-меры с длиной цепи, близкой к $M$ (нижняя панель), максимальные концентрации возрастают по мере роста длины цепи. С ростом $M$ промежуточная область расширяется, что согласуется с гипотезой Флори (V) для $M = \infty $. Критическая точка ${{t}_{c}}$ формируется из совокупности близко расположенных максимумов концентраций.
Рис. 4.
Зависящие от времени молекулярно-массовые распределения мономеров в образующихся в процессе ПК $n$‑мерах. $M$ = 32. Верхняя панель: $n = $ 1, жирная линия, $n = $ 2–5, – кривые с уменьшающимися с ростом $n$ амплитудами, умноженными на 5, 10, 15 и 20. Средняя панель: $n$ = 11, 13, 15, 18. 21, 24. Нижняя панель: $n = $ 28, 29, 30, 31, амплитуды, умножены на 20, 20, 15, 10, соответственно, $n$ = 32 , жирная линия.
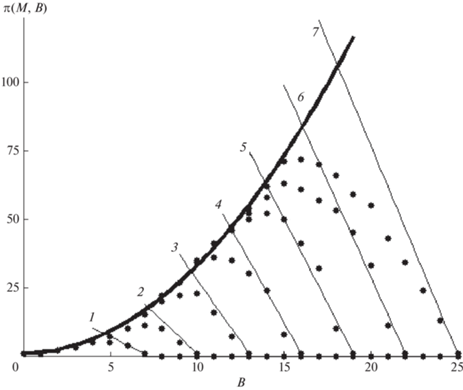
Рассмотренная картина образования $MB$-ансамблей из классов группы перестановок и превращения конечных ансамблей в бесконечный позволяет также рассмотреть механизм появления стохастичности при описании ПК детерминированными кинетическими уравнениями. Основная идея введения $MB$-ансамблей для описания сети реакций состоит в том, что эти микроканонические ансамбли являются неприводимыми представлениями группы перестановок, характеризуют собственные значения числа частиц $M$ и полной энергии $B{{E}_{0}}$, и их собственные функции взаимно ортогональны. Переходы между собственными состояниями обусловлены конечной высотой потенциального барьера, разделяющего долины реагентов и продуктов в реакциях (2) и (3) и их элементарные константы скорости не зависят от $M$ и $B$. Связь констант скорости с свойствами поверхности потенциальной энергии для этих реакций описывается теорией переходного состояния. Высота барьера минимальна в седловой точке (переходном состоянии), через которую проходят разделяющие долины сепаратрисы [53], которая сама основана на стохастических представлениях. При достаточно высоком барьере в окрестности сепаратрисы образуется стохастический слой, в котором перемешиваются преодолевающие барьер траектории. Поверхность потенциальной энергии для сети реакций состоит из множества переходных состояний и их сепаратрис, каждая из которых окружена стохастическим слоем, так что динамику ПК определяет отношение ширины этих слоев к расстоянию между седловыми точками ближайших по энергии реакций. Спектральный критерий предполагает, что стохастичность возникает, если перекрываются слои соседних седловых точек [53]. Примеры перехода от регулярной динамики к хаосу в различных квантовых системах рассмотрены в [54]. В применении к сетям реакций критерий предсказывает возникновение хаоса в промежуточной области $B\sim M{\text{/}}2$, тогда как в областях $B \to 0$ и $B \to M - 1$ процесс ПК остается регулярным. Стохастичность проявляется в том, что перекрывающиеся слои сепаратрис, принадлежащих реакциям с участием $n$-меров различных классов, перемешиваются, создавая общие области хаоса с островами устойчивости в (МВ)-плоскости. Отметим, что в конечных ансамблях динамический хаос появляется всегда, когда число мономеров достигает критического значения. Эту картину динамического хаоса иллюстрирует рис. 5, на котором показана зависимость числа классов перестановок $\pi (M,B)$ в микроканонических ансамблях с изменяющимися $M$и $B$. Растущее с ростом $B$ число классов не зависит от $M$ (жирная кривая), достигает максимума в области перемешивания классов и затем уменьшается. Как и в задачах [54], перемешивание происходит в окрестности максимума, где расположены близкие по энергии состояния, принадлежащие различным неприводимым представлениям.
Рис. 5.
Число классов группы перестановок $\pi (M,B)$ в составе $MB$-ансамблей с растущим числом мономеров $M$ = 8, 11, 14, 17, 20, 23, 26 (кривые 1–6 соответственно). Точками показаны результаты численного расчета. Жирная линия – не зависящая от $M$ зависимость $\pi (M,B)$ от числа связей $B$, относящаяся к термодинамическому пределу ($M = \infty $). Прямые 1–7 аппроксимируют область роста цепей в интервале $B$ $[M{\text{/}}2,M - 1]$.
В заключение перечислим причины, когда хаос может возникать за счет отклонений от гипотез Флори. В органических полимерах энтальпии образования связей С−С изменяются в интервале 5−8 Ккал/моль в зависимости от их валентности и окружения, что приводит к значениям ${{k}_{0}}$, отличающимся в пределах порядка. Другая причина − тримолекулярные реакции, скорости которых в концентрированных растворах сопоставимы с бимолекулярными [55]. Наконец, изменения свойств резервуара в процессе ПК (изменение вязкости, диэлктрической проницаемости и концентраций ионов) также может влиять на распределение $n$‑меров и возникновение хаоса. Перечисленные задачи можно рассмотреть, пользуясь методом, рассмотренным в этой статье.
V. ВЫВОДЫ
1. Показано, что предложенное в [32–36, 51] представление процесса поликондесации как необратимого роста во времени $t$ числа случайно расположенных связей $B(t)$ с одинаковой энергией ${{E}_{0}}$ в ансамбле из $M$ мономеров при $t = 0$, позволяет количественно описать рост длины полимерной цепи как в открытых, так и конечных ансамблях.
2. Показано, что МВ-ансамбли изоморфны классам группы перестановок, составленным из $n$-меров, являются их неприводимыми представлениями с фиксированными $M$ и $B{{E}_{0}}$.
3. Представление $MB$-ансамблей, как собственных состояний, позволяет найти число элементов в них ${{S}_{M}}(B) = \left( {\begin{array}{*{20}{c}} {M - 1} \\ B \end{array}} \right)$ и их молекулярно-массовое распределение $n{{P}_{{MB}}}(n) = \left( {\begin{array}{*{20}{c}} {M - n - 1} \\ {M - B - 2} \end{array}} \right)$.
4. Распределения включают растущую ($B \ll {M \mathord{\left/ {\vphantom {M 2}} \right. \kern-0em} 2}$) и падающую ($M - B \ll {M \mathord{\left/ {\vphantom {M 2}} \right. \kern-0em} 2}$ ветви детерминированных переходов $\Delta B = 1$, разделенных областью стохастичности, вызванной перемешиванием элементов различных классов в окрестности переходного состояния элементарных реакций роста цепи.
5. Стохастичность обусловлена перемешиванием траекторий реакций роста цепи, в которых реагентами являются $n$-меры, относящиеся к различным классам.
Список литературы
Flory P.J.J. // Am. Chem. Soc. 1941. V. 63. P. 3096.
Flory P.J. // Principles of Polymer Chemistry. 1979. Cornell Univ. Press. N.Y.
Stockmayer W.H. // J. Chem. Phys. 1943. V. 11. P. 45.
van Kampen N.G. // Adv. Chem. Phys. 1976. V. 34. P. 245.
Gillespie D.T. // Physica A. 1992. V. 188. P. 404.
Gillespie D.T. // J. Chem. Phys. 2000. V. 113. P. 207.
Gillespie D.T. // Annu. Rev. Phys. Chem. 2007. V. 58. P. 35.
Gillespie D.T. // J. Chem. Phys. 2009. V. 131. № 214107.
De Gennes P.G. // Scaling concept of polymer physics. 1979. Cornell Unuv. Pres. Ithaka, N.Y.
Zwanzig R. // Non-equilibrium Statistical Mechanics. 2001. Oxford Univ. Press. Oxford.
Stauffer D., Aharony A. // Introduction to percolation theory. 2003. Taylor-Francis. London.
Duerr H.P., Dietz K. // Mathem. Biosci. 2000. V. 165. P. 135.
Krapinsky P.L., Redner S., Ben-Naim E. // A Kinetic View of Statistical Physics. 2010. Cambridge Univ. Press. Cambridge.
Cohen R., Halvin S. // Complex Networks: Structure, Robustness and Functions. 2010. Cambridge Univ. Press. Cambridge.
Harris T.E. // The theory of branching processes. 1963. Springer. Berlin.
Chorin A.J., Hald O.H. // Stochastic Tools in Mathematics and Science. 2009. Springer. N.Y.
Lyons R., Peres Y. // Probability on Trees and Networks. 2016. Cambridge Univ. Press. N.Y.
Lifshitz I.M., Grosberg A.Y., Khochlov A.R. // Rev. Mod. Phys. 1978. V. 50. P. 683
Marcus A. // Technometrics 1968. V.10. P. 133.
Lushnikov A.A. // J. Colloid Interface Sci. 1978. V. 65. P. 276.
Buffet E., Pule J.V. // J. Stat. Phys. 1990. V. 58. P. 1042.
Lushnikov A.A. // Phys.Rev. Lett. 2004. V. 93. № 198302.
Lushnikov A.A. // J. Phys. A. 2005 V. 38. L. 35.
Ziff R.M. // J. Stat. Phys. 1980. V. 23. P. 241.
Ziff R.M., Stell G. // J. Chem. Phys. 1980. V. 73. P. 3492.
Ziff R.M., Hendricks E.M., Ernst M.B. // Phys. Rev. Lett. 1982. V. 49. P. 593.
Spouge J.L. // J. Phys. A. 1985. V.18. P. 3063.
van Roessel H.J., Shirvani M. // Physica D. 2006. V. 222. P. 29.
Aldous D.J. // Bernoulli 1999. V. 5. P. 3.
Leyfraz F. // Phys. Rep. 2003. V. 383. P. 95.
Wattis J.A.D. // Physica D. 2006. V. 222. P. 1.
Matsoukas T. // Phys. Rev. E. 2014. V. 90. N. 022113.
Matsoukas T. // Scientific Reports 2015. V.5. N. 8855
Matsoukas T. // Phys. Rev. E. 2015. V. 91. N. 052105.
Matsoukas T. // Generalized Statistical Thermodynamics of Probability Distribution and Stochastic Processes. 2019. Springer. Berlin.
Matsoukas T. // Entropy. 2019. V. 21. № 890.
Grosberg A.Y., Khochlov A.R. // Adv. Polym. Sci. 2006. V. 196. P. 189.
Everaers R., Grosberg A.Y., Rubinstein M., Rosa A. // Soft Mat. 2017. V. 13. P. 1223.
Wang W., Zheng Y., Roberts E., Duxbury C.J., Ding L., Irvine D.J., Howdle S.M. // Macromolecules. 2007. V. 40. P. 7184.
Matyjaszewski K. // Science. 2011. V. 333. P. 1104.
Lu J., Vanden-Eijnden E. // J. Chem. Phys. 2014. V. 141. N. 044109.
Chiuchiu D., Ferrare J., Pigolotti S. // Phys. Rev. E. 2019. V. 100. № 062502.
Sanchez J., McCormick A.V. // J. Non-Cryst. Solids. 1994. V. 167. P. 289.
Ng L.V., Thompson P., Sanchez J., Macosko C.W., McCormick A.V. // Macromolecules 1995. V. 28. P. 6471.
Brunet F.J. // Non-Crystal.Solids. 1998. V. 231. P. 58.
Ким И.П., Черняк А.В., Бендерский В.А. // Химмия высоких энергий. 2021. Т. 55. С. 128. (Kim I.P., Chernyak A.V., Benderskii V.A. High Energy Chem. 2021. V. 55. P. 123.)
Ким И.П., Коткин А.С., Бендерский В.А. // Химия высоких энергий. 2021. Т. 55. С. 171. (Kim I.P., Kotkin A.S., Benderskii V.A. High Energy Chem. 2021. V. 55. P. 169.)
Бендерский В.А., Кац Е.И., Ким И.П., Коткин А.С. // Химия высоких энергий. 2021. Т. 55. С. 255. (Benderskii V.A., Kats E.I., Kim I.P., Kotkin A.S. High Energy Chem. 2021. V. 55. P. 255.)
Stewart W.J. // Probability, Markov Chains, Queues and Simulation. 2009. Princeton Univ. Press. Princeton.
Abramovich M., Stegun I.A. // Handbook of Mathematical Functions. 1964. Nation. Bureau Standards. Washington.
Riordan J. // Combinatorial Identities. 1979. Krieger R. Huntington, N.Y.
Matsoukas T. // Phys. Rev. E. 2015. V. 91. № 052105.
Zaslavskii G.M. // Chaos in Dynamical Systems.1985. Harwood. N.Y.
Benderskii V.A., Kats E.I. // JETP. 2021. V. 133. P. 411.
Jiang Y., Gang H. // Phys. Rev. B. 1989. V. 39. P. 4659; V. 40. P. 661.
Дополнительные материалы отсутствуют.
Инструменты
Химия высоких энергий