Физикохимия поверхности и защита материалов, 2019, T. 55, № 2, стр. 144-152
К условиям смены типа кривой зависимости величины эффекта Ребиндера от объемной концентрации адсорбата с изотермой S-образного вида
Э. М. Подгаецкий *
Федеральное государственное бюджетное учреждение науки Институт прикладной механики
Российской академии наук
119991 Москва, Ленинский просп., 32а, Россия
* E-mail: Podgaetsky@mail.ru
Поступила в редакцию 23.08.2018
После доработки 30.08.2018
Принята к публикации 05.09.2018
Аннотация
Исследуется аналитически величина термодинамической оценки эффекта Ребиндера как функция объемной концентрации адсорбата в жидком растворе омывающем твердую поверхность в случае, когда его изотерма на недеформированной поверхности имеет S-обраную форму. В терминах построенной ранее теории равновесной адсорбции на твердой поверхности с учетом ее деформации и наличия на ней электрического заряда выводятся условия смены типа зависимости величины эффекта Ребиндера от объемной концентрации адсорбата – от куполообразной к монотонно возрастающей.
ВВЕДЕНИЕ
Открытие эффекта Ребиндера [1] – снижение, например, поверхностной твердости после адсорбции активного компонента на поверхности – и введение его в научный оборот в последующие десятилетия способствовали применению эффекта в различных видах производственной деятельности прежде всего в горном деле [2]. Широкое применение эффекта со временем столкнулось с трудностями управления в его использовании – адсорбционный эффект мог и снижать, а мог и повышать поверхностную твердость в зависимости от многих факторов – от рода поверхности, от адсорбата, его концентрации в растворе и даже от растворителя [3]. Эти трудности и отсутствие объясняющей теории приводили иногда даже к отрицанию практической пользы эффекта в горном деле [4].
Построенная в [5–8] термодинамическая теория равновесной адсорбции из жидкости на твердой поверхности с учетом электрического заряда на ней и ее деформации позволила вывести [9, 10] аналитически зависимость приращения $\Delta {{\tilde {\sigma }}_{r}}$ поверхностного натяжения ${{\tilde {\sigma }}_{r}}$ межфазного слоя вследствие адсорбции в функции объемной концентрации адсорбата $\tilde {c}$ учетом электрического потециала $\tilde {\varphi }$ твердой фазы и ее деформации. Полное выражение этого приращения в построенной теории [9, 10] содержит слагаемое – интегральный оператор, оказавшийся отрицательно определенной величиной. В [11] для случая, когда адсорбатом являлось ПАВ (поверхностно активное вещество) – ДТАБ (додецилтриметиламмония бромид), а адсорбентом кварц, гранит и микроклин, была использована аналитически простая аппроксимация исходной изотермы адсорбции из [12], имевшей выраженный S-образный вид ее формы. Выведенные благодаря этому аналитические выражения приращения $\Delta {{\tilde {\sigma }}_{r}}$смогли описать наличие у него острого максимума на оси $\tilde {c},$ полученного экспериментально при бурении в граните и кварце – рис. 1.
Рис. 1.
Изменение скорости бурения в различных породах алмазной бурильной коронкой при использовании водных растворов ДТАБ: 1 – гранит уэстерли; 2 – кварц; 3 – микроклин [3].

При этом точка максимума на оси $\tilde {c}$–${{\tilde {c}}_{{\max }}}$ – в использованной теории оказалась весьма близкой к экспериментальным значениям точки максимума эффекта Ребиндера в эксперименте для гранита и кварца.
Наличие такого острого максимума, т.е. узость по оси $\tilde {c}$ области действия эффекта Ребиндера (–$\Delta {{\tilde {\sigma }}_{r}}$ >0), называемая часто “избирательностью” активного компонента, является типичным случаем для многих ПАВ [13]. Что и послужило автору [4] поводом заключить, что в реальных условиях бурения в горном деле эффект Ребиндера мало применим.
Таким образом возникает потребность анализа теории эффекта, чтобы избежать либо значительно уменьшить остроту такой избирательности.
ИСХОДНЫЕ УРАВНЕНИЯ
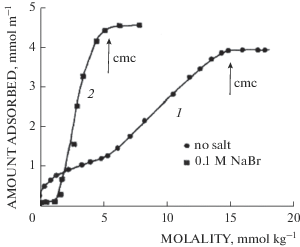
S-образная форма изотермы адсорбции поверхностно активного компонента в жидкости, омывающей твердую поверхность, например, ПАВ, делает зависимость величины эффекта Ребиндера от $\tilde {c}$ обычно остро избирательной. С другой стороны она позволяет применить, как в [11], кусочно-линейную аппроксимацию графика изотермы и получить возможность сравнительного анализа простых выражений для $\Delta {{\tilde {\sigma }}_{r}}.$ Для этого необходимо наличие двух таких однокомпонентных изотерм с одинаковым ПАВ и одинаковым адсорбентом, а их различие вызвано влиянием, например, неактивных добавок в жидком растворе. Такие две изотермы для ДТАБ в водном растворе на кремнеземе, взятые из [14] и аналогичные изотерме из [12] представлены на рис. 2 – кривые (1) и (2). Кривая (2) соответствует случаю, когда в раствор добавлен 0.1 М NaBr.
Рис. 2.
Изотерма адсорбции додецилтриметиламмония бромида в водном растворе на кремнеземе в отсутствие – (1) и с добавкой 0.1 М NaBr – (2) [14].
Воспользуемся теперь теорией [9, 10], построенной для однокомпонентной равновесной адсорбции из жидкого раствора на твердой поверхности при наличии на ней электрического заряда с поверхностной плотностью $\tilde {q}$ и с учетом ее деформации, а исходной изотермой, т.е. на недеформированной и не заряженной поверхности, является изотерма S-образного вида, подобно изотермам на рис. 2. Для применения аналитики теории [9, 10] введем безразмерные переменные
(1)
$\begin{gathered} \Gamma = \frac{{\tilde {\Gamma }}}{{\Gamma {\text{*}}}},\,\,\,\,c = \frac{{\tilde {c}}}{{c{\text{*}}}},\,\,\,\,{{\sigma }_{r}} = \frac{{{{{\tilde {\sigma }}}_{r}}}}{{RT\Gamma {\text{*}}}},\,\,\,\,q = \frac{{\tilde {q}\varphi {\text{*}}}}{{RT\Gamma {\text{*}}}}, \\ \varphi = \frac{{\tilde {\varphi }}}{{\varphi {\text{*}}}},\,\,\,\,\vartheta \equiv \frac{{S - {{S}_{0}}}}{{{{S}_{0}}}}, \\ \end{gathered} $Выпишем из [9, 10] аналитические выражения термодинамической оценки величины эффекта Ребиндера $\bar {\Delta }\sigma $
(2)
$\begin{gathered} \bar {\Delta }\sigma \equiv {{\sigma }_{r}}\left( {0,\varphi ,\vartheta } \right) - {{\sigma }_{r}}\left( {\Gamma ,\varphi ,\vartheta } \right) = \\ = \int\limits_0^\Gamma {\Gamma \frac{{A{\text{'}}}}{A}d\Gamma - z\Gamma } \equiv I - z\Gamma , \\ z \equiv - (1 + \vartheta )(g + {{k}_{0}}), \\ \end{gathered} $(3)
$\begin{gathered} Bc\left| {_{\begin{subarray}{l} \vartheta = 0 \\ \varphi = {{\varphi }_{0}} \end{subarray} }} \right. = A(\Gamma ), \hfill \\ B \equiv {\text{const}} \geqslant 0. \hfill \\ \end{gathered} $Будем полагать, что функция А(Г) в (3) удовлетворяет обычным условиям
Величина $\bar {\Delta }\sigma ,$ введенная в (2), облегчает использование терминов “положительный” ($\bar {\Delta }\sigma $ > 0) или “отрицательный” ($\bar {\Delta }\sigma $ < 0) эффект Ребиндера, впервые введенных в [8].
Выпишем также выведенное в [9, 10] уравнение адсорбции
(4)
$Bc\exp \left\{ {\int\limits_{{{\varphi }_{0}}}^\varphi {{{\varepsilon }_{1}}(\varphi )d\varphi - \frac{{\vartheta z}}{{1 + \vartheta }}} } \right\} = A(\Gamma ),$(4a)
$q \equiv \frac{{\tilde {q}\varphi {\text{*}}}}{{RT\Gamma {\text{*}}}} = {{\varepsilon }_{0}}(\varphi ,\vartheta ) + {{\varepsilon }_{1}}(\varphi )\Gamma + \Gamma \frac{{dg}}{{d\varphi }}\vartheta .$Реконструкцию функции А(Г) по кривым (1), (2) рис. 2 будем строить, предполагая , что они измерялись на недеформированной поверхности, т.е. при $\vartheta = 0,$ и считая ${{\varepsilon }_{1}} \equiv 0.$ Экспериментальные зависимости $\tilde {\Gamma }$ от $\tilde {c}$ на рис. 2, т.е. изотермы адсорбции (1), (2), фрагментарно близки к отрезкам прямых, кроме области малых значений $\tilde {c},$ в которой эти кривые имеют выраженный нелинейный вид. Граничное значение концентрации $\tilde {c}$ в этой области для кривой (1) обозначим $\tilde {c}_{{11}}^{0},$ а для кривой (2) – $\tilde {c}_{{12}}^{0}.$ Вне этих областей будем аппроксимировать зависимость $\tilde {\Gamma }\left( {\tilde {c}} \right)$ отрезками прямых аналогично способу, изложенному в [11]. Обозначим такую аппроксимацию для изотермы (1) – ${{\tilde {\Gamma }}_{{\left( 1 \right)}}},$ а для изотермы (2) – ${{\tilde {\Gamma }}_{{\left( 2 \right)}}}.$
Как видно из рис. 2 кривые (1) и (2) при больших значениях $\tilde {c}$ можно аппроксимировать константами – ${{\tilde {\Gamma }}_{{\left( 1 \right)}}} = {{\tilde {\Gamma }}_{{31}}} \equiv {\text{const}}$ для кривой (1) и ${{\tilde {\Gamma }}_{{\left( 2 \right)}}} = {{\tilde {\Gamma }}_{{32}}} \equiv {\text{const}}$ для кривой (2). Теперь проведем вручную прямую с наклоном ${{\tilde {\kappa }}_{{21}}},$ приближенную по ее наклону и положению к центральному участку кривой (1) и аналогично с наклоном ${{\tilde {\kappa }}_{{22}}}$ для кривой (2). Пересечение такой прямой с асимптотой ${{\tilde {\Gamma }}_{{\left( 1 \right)}}} = {{\tilde {\Gamma }}_{{31}}} \equiv {\text{const}}$ для кривой (1) определяет точку $\tilde {c}_{{31}}^{0},$ а для кривой (2) – точку $\tilde {c}_{{32}}^{0}.$ Далее проведем прямую линию, приближенную вручную по ее наклону ${{\tilde {\kappa }}_{{11}}}$ и положению к кривой (1), и аналогично по наклону ${{\tilde {\kappa }}_{{12}}}$ и положению к кривой (2) в выпуклой части этих кривых, предшествующих точке изгиба. Пересечение этих наклонных прямых с наклонными прямыми с коэффициентами ${{\tilde {\kappa }}_{{21}}},$ ${{\tilde {\kappa }}_{{22}}},$ построенными ранее, определяет точку $\left( {\tilde {c}_{{21}}^{0},{{{\tilde {\Gamma }}}_{{21}}}} \right),$ соответствующую изотерме (1), и точку $\left( {\tilde {c}_{{22}}^{0},{{{\tilde {\Gamma }}}_{{22}}}} \right)$ – изотерме (2). Обе эти точки являются правыми концами отрезков прямолинейной аппроксимации, соответственно, для кривой (1) и (2), в выпуклой области этих кривых. Крайние левые точки $\tilde {c}_{{11}}^{0},$ $\tilde {c}_{{12}}^{0}$ в дальнешем выбираются на этих отрезках из условия наибольшего удлинения фрагментов ($\tilde {c}_{{11}}^{0},$ $\tilde {c}_{{21}}^{0}$) и ($\tilde {c}_{{12}}^{0},$ $\tilde {c}_{{22}}^{0}$), но без скачка кривизны и используются для построения нелинейной аппроксимации функций ${{\tilde {\Gamma }}_{{(1)}}}$ и ${{\tilde {\Gamma }}_{{(2)}}}$ в области $\tilde {c} < \tilde {c}_{{11}}^{0}$ и $\tilde {c} < \tilde {c}_{{12}}^{0}$ соответственно.
Таким образом каждая из экспериментальных кривых (1), (2) из рис. 2 может быть аппроксимирована описанным образом ручной подгонки непрерывной кусочно-линейной функцией ${{\tilde {\Gamma }}_{{(1)}}}$ при $\tilde {c} > \tilde {c}_{{11}}^{0}$ для кривой (1) и функцией ${{\tilde {\Gamma }}_{{(2)}}}$ при $\tilde {c} > \tilde {c}_{{12}}^{0}$ для кривой (2). Как указывалось ранее при $\tilde {c} > \tilde {c}_{{31}}^{0}$ для кривой (1) и при $\tilde {c} > \tilde {c}_{{32}}^{0}$ для кривой (2) будем использовать, соответственно, аппроксимации ${{\tilde {\Gamma }}_{{(1)}}} \equiv {{\tilde {\Gamma }}_{{31}}}$ и ${{\tilde {\Gamma }}_{{(2)}}} \equiv {{\tilde {\Gamma }}_{{32}}}.$ Левые концы первых интервалов, т.е. точки $\tilde {c}_{{11}}^{0}$ и $\tilde {c}_{{12}}^{0},$ определяются подгонкой по указанному выше критерию.
Аналитически построенные аппроксимации ${{\tilde {\Gamma }}_{{(1)}}}$ в области $\tilde {c} > \tilde {c}_{{11}}^{0}$ и ${{\tilde {\Gamma }}_{{(2)}}}$ в области $\tilde {c} > \tilde {c}_{{12}}^{0}$ имеют вид
(5)
${{\tilde {\Gamma }}_{{(1)}}} = \left\{ \begin{gathered} {{{\tilde {\Gamma }}}_{{11}}} + {{{\tilde {k}}}_{{11}}}\left( {\tilde {c} - \tilde {c}_{{11}}^{0}} \right),\,\,\,\,\tilde {c}_{{11}}^{0} < \tilde {c} < \tilde {c}_{{21}}^{0} \hfill \\ {{{\tilde {\Gamma }}}_{{21}}} + {{{\tilde {k}}}_{{21}}}\left( {\tilde {c} - \tilde {c}_{{21}}^{0}} \right),\,\,\,\,\tilde {c}_{{21}}^{0} < \tilde {c} < \tilde {c}_{{31}}^{0} \hfill \\ {{{\tilde {\Gamma }}}_{{31}}},\,\,\,\,\tilde {c} > \tilde {c}_{{31}}^{0} \hfill \\ \end{gathered} \right.,$(6)
${{\tilde {\Gamma }}_{{(2)}}} = \left\{ \begin{gathered} {{{\tilde {\Gamma }}}_{{12}}} + {{{\tilde {k}}}_{{12}}}\left( {\tilde {c} - \tilde {c}_{{12}}^{0}} \right),\,\,\,\,\tilde {c}_{{12}}^{0} < \tilde {c} < \tilde {c}_{{22}}^{0} \hfill \\ {{{\tilde {\Gamma }}}_{{22}}} + {{{\tilde {k}}}_{{22}}}\left( {\tilde {c} - \tilde {c}_{{22}}^{0}} \right),\,\,\,\,\tilde {c}_{{22}}^{0} < \tilde {c} < \tilde {c}_{{32}}^{0} \hfill \\ {{{\tilde {\Gamma }}}_{{32}}},\,\,\,\,\tilde {c} > \tilde {c}_{{32}}^{0} \hfill \\ \end{gathered} \right..$Коэффициенты наклона прямых ${{\tilde {\kappa }}_{{11}}},$ ${{\tilde {\kappa }}_{{21}}},$ ${{\tilde {\kappa }}_{{12}}},$ ${{\tilde {\kappa }}_{{22}}}$ связаны с величинами ${{\tilde {\Gamma }}_{{ij}}},$ ${{\tilde {c}}_{{ij}}}(j = 1,2;\,\,i = 1,2,3)$ условиями
(7)
$\begin{gathered} {{{\tilde {\kappa }}}_{{11}}} = \frac{{{{{\tilde {\Gamma }}}_{{21}}} - {{{\tilde {\Gamma }}}_{{11}}}}}{{\tilde {c}_{{21}}^{0} - \tilde {c}_{{11}}^{0}}},\,\,\,\,{{{\tilde {\kappa }}}_{{21}}} = \frac{{{{{\tilde {\Gamma }}}_{{31}}} - {{{\tilde {\Gamma }}}_{{21}}}}}{{\tilde {c}_{{31}}^{0} - \tilde {c}_{{21}}^{0}}}, \hfill \\ {{{\tilde {\kappa }}}_{{12}}} = \frac{{{{{\tilde {\Gamma }}}_{{22}}} - {{{\tilde {\Gamma }}}_{{12}}}}}{{\tilde {c}_{{22}}^{0} - \tilde {c}_{{12}}^{0}}},\,\,\,\,{{{\tilde {\kappa }}}_{{22}}} = \frac{{{{{\tilde {\Gamma }}}_{{32}}} - {{{\tilde {\Gamma }}}_{{22}}}}}{{\tilde {c}_{{32}}^{0} - \tilde {c}_{{22}}^{0}}}. \hfill \\ \end{gathered} $На рис. 3 представлены графики аппроксимаций ${{\tilde {\Gamma }}_{{(1)}}}(\tilde {c})$ и ${{\tilde {\Gamma }}_{{(2)}}}(\tilde {c}),$ построенные указанным методом ручной подгонки в области их кусочно-линейной зависимости. А на рис. 4 функции ${{\tilde {\Gamma }}_{{(1)}}}$ и ${{\tilde {\Gamma }}_{{(2)}}}$ изображены иллюстративно также и в области значений $\tilde {c}$($\tilde {c} \leqslant \tilde {c}_{{11}}^{0}$ для ${{\tilde {\Gamma }}_{{(1)}}}$ и $\tilde {c} \leqslant \tilde {c}_{{12}}^{0}$ для ${{\tilde {\Gamma }}_{{(2)}}}$), где эти функции зависят от $\tilde {c}$ нелинейно.
Рис. 3.
Графики функций ${{\tilde {\Gamma }}_{{(1)}}}$ (5) и ${{\tilde {\Gamma }}_{{(2)}}}$ (6) в области их кусочно-линейной зависимости – при $\tilde {c} > \tilde {c}_{{11}}^{0}$ для ${{\tilde {\Gamma }}_{{(1)}}}$ и при $\tilde {c} > \tilde {c}_{{12}}^{0}$ для ${{\tilde {\Gamma }}_{{(2)}}}.$
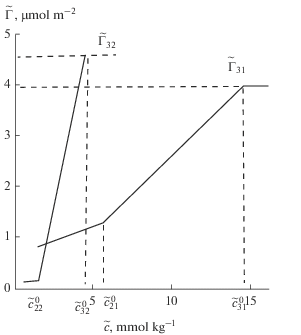
Рис. 4.
К иллюстрации положения точек ${{\tilde {\Gamma }}_{{12}}},\,\,{{\tilde {\Gamma }}_{{22}}},\,\,{{\tilde {\Gamma }}_{{11}}},\,\,{{\tilde {\Gamma }}_{{21}}}$ по оси $\tilde {\Gamma }$ и точек $\tilde {c}_{{12}}^{0},\,\,\tilde {c}_{{22}}^{0},\,\,\tilde {c}_{{11\,}}^{0},\,\,\tilde {c}_{{21}}^{0}$ по осии $\tilde {c}$ на графиках функций ${{\tilde {\Gamma }}_{{(1)}}},\,\,{{\tilde {\Gamma }}_{{(2)}}}$ в области значений $\tilde {c} \leqslant {{\tilde {c}}_{{21}}}$ и $\tilde {c} \leqslant {{\tilde {c}}_{{22}}}$ соответственно.

Чтобы провести оцифровку значений $\tilde {c}_{{ij}}^{0},$ ${{\tilde {\Gamma }}_{{ij}}},$ воспользуемся ортогональной сеткой, налагаемой на рис. 2 с построенными на нем аппроксимациями ${{\tilde {\Gamma }}_{{(1)}}},$ ${{\tilde {\Gamma }}_{{(2)}}}$ в области $\tilde {c} > \tilde {c}_{{11}}^{0}$ и $\tilde {c} > \tilde {c}_{{12}}^{0}$ соответственно. Результаты такой оцифровки в миллиметрах по горизонтальной ($\mathop {{\text{м м }}}\limits^ \to $) оси и в миллиметрах по вертикальной (${\text{м м }} \uparrow $) оси даны в табл. 1, где приведены также избранные указанным ранее способом значения $\tilde {c}_{{11}}^{0},$ $\tilde {c}_{{12}}^{0}$ и расчитанные по формулам (7) значения ${{\tilde {\kappa }}_{{ij}}}.$
Таблица 1.
Значения $\tilde {c}_{{11}}^{0},$ $\tilde {c}_{{21}}^{0},$ $\tilde {c}_{{31}}^{0},$ ${{\tilde {\Gamma }}_{{11}}},$ ${{\tilde {\Gamma }}_{{21}}},$ ${{\tilde {\Gamma }}_{{31}}},$ ${{\tilde {\kappa }}_{{11}}},$ ${{\tilde {\kappa }}_{{21}}}$
| $\tilde {c}_{{11}}^{0},$$\mathop {{\text{м м }}}\limits^ \to $ | $\tilde {c}_{{21}}^{0},$ $\mathop {{\text{м м }}}\limits^ \to $ | $\tilde {c}_{{31}}^{0},$ $\mathop {{\text{м м }}}\limits^ \to $ | ${{\tilde {k}}_{{11}}},$$\frac{{{\text{м м }} \uparrow }}{{\mathop {{\text{м м }}}\limits^ \to }}$ | ${{\tilde {k}}_{{21}}},$$\frac{{{\text{м м }} \uparrow }}{{\mathop {{\text{м м }}}\limits^ \to }}$ | ${{\tilde {\Gamma }}_{{11}}},$${\text{м м }} \uparrow $ | ${{\tilde {\Gamma }}_{{21}}},$${\text{м м }} \uparrow $ | ${{\tilde {\Gamma }}_{{31}}},$${\text{м м }} \uparrow $ |
|---|---|---|---|---|---|---|---|
| 4.0 | 17.5 | 45.5 | 0.307 | 0.964 | 8.0 | 13.0 | 40.0 |
В табл. 2 приведены значения $\tilde {c}_{{12}}^{0},$ $\tilde {c}_{{22}}^{0},$ $\tilde {c}_{{32}}^{0},$ ${{\tilde {\Gamma }}_{{12}}},$ ${{\tilde {\Gamma }}_{{22}}},$ ${{\tilde {\Gamma }}_{{32}}},$ ${{\tilde {\kappa }}_{{12}}},$ ${{\tilde {\kappa }}_{{22}}}$ для аппроксимации ${{\tilde {\Gamma }}_{{(2)}}},$ полученные аналогично.
Таблица 2.
Значения $\tilde {c}_{{12}}^{0},$ $\tilde {c}_{{22}}^{0},$ $\tilde {c}_{{32}}^{0},$ ${{\tilde {\Gamma }}_{{12}}},$ ${{\tilde {\Gamma }}_{{22}}},$ ${{\tilde {\Gamma }}_{{32}}},$ ${{\tilde {\kappa }}_{{12}}},$ ${{\tilde {\kappa }}_{{22}}}$
| $\tilde {c}_{{12}}^{0},$$\mathop {{\text{м м }}}\limits^ \to $ | $\tilde {c}_{{22}}^{0},$ $\mathop {{\text{м м }}}\limits^ \to $ | $\tilde {c}_{{32}}^{0},$ $\mathop {{\text{м м }}}\limits^ \to $ | ${{\tilde {k}}_{{12}}},$$\frac{{{\text{м м }} \uparrow }}{{\mathop {{\text{м м }}}\limits^ \to }}$ | ${{\tilde {k}}_{{22}}},$$\frac{{{\text{м м }} \uparrow }}{{\mathop {{\text{м м }}}\limits^ \to }}$ | ${{\tilde {\Gamma }}_{{12}}},$${\text{м м }} \uparrow $ | ${{\tilde {\Gamma }}_{{22}}},$${\text{м м }} \uparrow $ | ${{\tilde {\Gamma }}_{{32}}},$${\text{м м }} \uparrow $ |
|---|---|---|---|---|---|---|---|
| 2.0 | 5.0 | 15.0 | 0.166 | 4.4 | 1.5 | 2.0 | 46.0 |
Для перевода значений $\tilde {c},$ $\tilde {\Gamma },$ $\tilde {\kappa }$ в табл. 1, 2 в физические размерности $\frac{{{\text{mmol}}}}{{{\text{kg}}}},$ $\frac{{\mu {\text{mol}}}}{{{{{\text{M}}}^{2}}}},$ $\frac{{{\text{kg}}}}{{{{{\text{M}}}^{{\text{2}}}}}}$ нужно воспользоваться удельными на 1 мм вертикальной и горизонтальной оси коэффициентами миллиметровой ортогональной сетки. Наложение указанной сетки на рис. 3 позволяет найти приближенные значения
(8)
$1\,\,\mathop {{\text{м м }}}\limits^ \to = 0.313\frac{{{\text{mmol}}}}{{{\text{kg}}}},\,\,\,\,1\,\,{\text{м м }} \uparrow = 0.1\frac{{\mu {\text{mol}}}}{{{{{\text{M}}}^{{\text{2}}}}}}.$Результат пересчета значений $\tilde {c}_{{ij}}^{0},\,\,{{\tilde {\Gamma }}_{{ij}}},\,\,{{\tilde {k}}_{{ij}}}$ на физические размерности с учетом коэффициентов (8) иллюстрирует табл. 3.
Таблица 3.
Значения $\tilde {c}_{{ij}}^{0},$ ${{\tilde {\Gamma }}_{{ij}}},$ ${{\tilde {k}}_{{ij}}}$ в физических размерностях для аппроксимаций ${{\tilde {\Gamma }}_{{(1)}}},$ ${{\tilde {\Gamma }}_{{(2)}}}$
| $\tilde {c}_{{11}}^{0},$$\frac{{{\text{mmol}}}}{{{\text{kg}}}}$ | $\tilde {c}_{{21}}^{0},$$\frac{{{\text{mmol}}}}{{{\text{kg}}}}$ | $\tilde {c}_{{31}}^{0},$$\frac{{{\text{mmol}}}}{{{\text{kg}}}}$ | ${{\tilde {k}}_{{11}}},$$\frac{{{\text{kg}}}}{{{{M}^{{\text{2}}}}}}$ | ${{\tilde {k}}_{{21}}},$$\frac{{{\text{kg}}}}{{{{M}^{{\text{2}}}}}}$ | ${{\tilde {\Gamma }}_{{11}}},$$\frac{{{\mu mol}}}{{{{M}^{{\text{2}}}}}}$ | ${{\tilde {\Gamma }}_{{21}}},$$\frac{{{\mu mol}}}{{{{M}^{{\text{2}}}}}}$ | ${{\tilde {\Gamma }}_{{31}}},$$\frac{{{\mu mol}}}{{{{M}^{{\text{2}}}}}}$ |
|---|---|---|---|---|---|---|---|
| 1.25 | 5.47 | 14.22 | $0.118\,\,{{10}^{{ - 3}}}$ |
$0.308\,\,{{10}^{{ - 3}}}$ | 0.80 | 1.30 | 4.0 |
| $\tilde {c}_{{12}}^{0},$$\frac{{{\text{mmol}}}}{{{\text{kg}}}}$ | $\tilde {c}_{{22}}^{0},$$\frac{{{\text{mmol}}}}{{{\text{kg}}}}$ | $\tilde {c}_{{32}}^{0},$$\frac{{{\text{mmol}}}}{{{\text{kg}}}}$ | ${{\tilde {k}}_{{12}}},$$\frac{{{\text{kg}}}}{{{{M}^{{\text{2}}}}}}$ | ${{\tilde {k}}_{{22}}},$$\frac{{{\text{kg}}}}{{{{M}^{{\text{2}}}}}}$ | ${{\tilde {\Gamma }}_{{12}}},$$\frac{{{\mu mol}}}{{{{M}^{{\text{2}}}}}}$ | ${{\tilde {\Gamma }}_{{22}}},$$\frac{{{\mu mol}}}{{{{M}^{{\text{2}}}}}}$ | ${{\tilde {\Gamma }}_{{32}}},$$\frac{{{\mu mol}}}{{{{M}^{{\text{2}}}}}}$ |
| 0.625 | 1.56 | 4.69 | $0.533 \times {{10}^{{ - 4}}}$ | $1.408 \times {{10}^{{ - 3}}}$ | 0.15 | 0.20 | 4.60 |
Чтобы выразить величины из табл. 3 в безразмерных переменных, выберем конкретные масштабные значения $\Gamma {\text{*}}$ и $c{\text{*}}$
(9)
$\Gamma {\text{*}} \equiv {{\tilde {\Gamma }}_{{31}}},\,\,\,\,\tilde {c}{\text{*}} \equiv \tilde {c}_{{31}}^{0}$(10)
$\begin{gathered} c_{{ij}}^{0} \equiv \frac{{\tilde {c}_{{ij}}^{0}}}{{c{\text{*}}}},\,\,\,\,{{\Gamma }_{{ij}}} \equiv \frac{{{{{\tilde {\Gamma }}}_{{ij}}}}}{{\Gamma {\text{*}}}}(i = 1,2,3;j = 1,2), \\ {{k}_{{ij}}} \equiv \frac{{{{{\tilde {k}}}_{{ij}}}c{\text{*}}}}{{\Gamma {\text{*}}}},\,\,\,\,(i = 1,2;j = 1,2), \\ \end{gathered} $(11)
${{\Gamma }_{{(1)}}} = \frac{{{{{\tilde {\Gamma }}}_{{(1)}}}}}{{\Gamma {\text{*}}}},\,\,\,\,{{\Gamma }_{{(2)}}} = \frac{{{{{\tilde {\Gamma }}}_{{(2)}}}}}{{\Gamma {\text{*}}}}.$В табл. 4 приведены значения $c_{{ij}}^{0},\,\,{{\Gamma }_{{ij}}},\,\,{{k}_{{ij}}},$ расчитанные из табл. 3 с учетом (10), (11) и (8).
Таблица 4.
Безразмерные значения $c_{{ij}}^{0},$ ${{\Gamma }_{{ij}}},$ ${{k}_{{ij}}}$
| $c_{{11}}^{0}$ | $c_{{21}}^{0}$ | $c_{{31}}^{0}$ | ${{k}_{{11}}}$ | ${{k}_{{21}}}$ | ${{\Gamma }_{{11}}}$ | ${{\Gamma }_{{21}}}$ | ${{\Gamma }_{{31}}}$ |
|---|---|---|---|---|---|---|---|
| 8.79 × × ${{10}^{{ - 2}}}$ | 0.385 | 1.0 | 0.421 | 1.095 | 0.2 | 0.325 | 1.0 |
| $c_{{12}}^{0}$ | $c_{{22}}^{0}$ | $c_{{32}}^{0}$ | ${{k}_{{12}}}$ | ${{k}_{{22}}}$ | ${{\Gamma }_{{12}}}$ | ${{\Gamma }_{{22}}}$ | ${{\Gamma }_{{32}}}$ |
| 4.39 × × ${{10}^{{ - 2}}}$ | 0.110 | 0.329 | 0.19 | 5.005 | 0.0375 | 0.05 | 1.15 |
Функции ${{\Gamma }_{{(1)}}},$ ${{\Gamma }_{{(2)}}}$ с учетом (5), (6), (8), (10), (11) примут вид соответственно при $c > c_{{11}}^{0}$ и $c > c_{{21}}^{0}$
(12)
${{\Gamma }_{{(1)}}} = \left\{ \begin{gathered} {{\Gamma }_{{11}}} + {{k}_{{11}}}(c - c_{{11}}^{0}),\,\,\,\,c_{{11}}^{0} < c < c_{{21}}^{0} \hfill \\ {{\Gamma }_{{21}}} + {{k}_{{21}}}(c - c_{{21}}^{0}),\,\,\,\,c_{{21}}^{0} < c < c_{{31}}^{0} \hfill \\ {{\Gamma }_{{31}}},\,\,\,\,c > c_{{31}}^{0} \hfill \\ \end{gathered} \right.,$(13)
${{\Gamma }_{{(2)}}} = \left\{ \begin{gathered} {{\Gamma }_{{12}}} + {{k}_{{12}}}(c - c_{{12}}^{0}),\,\,\,\,c_{{12}}^{0} < c < c_{{22}}^{0} \hfill \\ {{\Gamma }_{{22}}} + {{k}_{{22}}}(c - c_{{22}}^{0}),\,\,\,\,c_{{22}}^{0} < c < c_{{32}}^{0} \hfill \\ {{\Gamma }_{{32}}},\,\,\,\,c > c_{{32}}^{0} \hfill \\ \end{gathered} \right..$Экспериментальные точки (знаки квадратов и кружков) на кривых (1) и (2) рис. 2 в области малых значений $\tilde {c},$ т.е. при $\tilde {c} \leqslant \tilde {c}_{{11}}^{0}$ для кривой (1) и $\tilde {c} \leqslant \tilde {c}_{{12}}^{0}$ для кривой (2) сильно затрудняют построение графической аппроксимации ${{\tilde {\Gamma }}_{{(1)}}}$ и ${{\tilde {\Gamma }}_{{(2)}}}$ в этих областях $\tilde {c},$ особенно для ${{\tilde {\Gamma }}_{{(2)}}}$ как это видно из рис. 2. Поэтому будем строить аппроксимации ${{\tilde {\Gamma }}_{{(1)}}}$ и ${{\tilde {\Gamma }}_{{(2)}}}$ в этих областях аналитически с использованием специального условия – существование при $\tilde {c} \ll \tilde {c}_{{11}}^{0}$ и $\tilde {c} \ll \tilde {c}_{{12}}^{0}$ участка Генри у графиков изотерм на рис. 2 соответственно условию (3в). Тогда такие участки будут и у функций ${{\Gamma }_{{(1)}}},$ ${{\Gamma }_{{(2)}}}$ в области малых c.
ПОСТРОЕНИЕ НЕЛИНЕЙНОЙ АППРОКСИМАЦИИ ФУНКЦИЙ ${{\Gamma }_{{(1)}}},$ ${{\Gamma }_{{(2)}}}$ В ОБЛАСТИ $с \leqslant с _{{11}}^{0}$ И $с \leqslant с _{{12}}^{0}$ СООТВЕТСТВЕННО
Используя теперь безразмерные переменные Г, с, рассмотрим функцию Ф(с)
(14)
$\Phi \left( c \right) \equiv {{\Gamma }_{1}} + \kappa (c - {{c}_{1}}) + {{\kappa }_{1}}{{(c - {{c}_{1}})}^{2}}.$Полагая ${{\Gamma }_{1}} > 0,$ $k > 0,$ ${{c}_{1}} > 0$ заданными величинами, найдем параметр ${{k}_{1}}$ из условия
(16)
$\Phi {\text{'}}\left| {_{{c = 0}}} \right. \equiv \frac{{d\Phi }}{{dc}}\left| {_{{c = 0}}} \right. > 0,$Подставляя Ф(с) из (14) в (15), получим
Из (18) найдем κ
Когда функция Ф(с) = Г(с), т.е. является изотермой адсорбции, то условия (15)–(17) как раз и служат математическим выражением наличия у изотермы Г(с) участка Генри при малых с. С учетом (17) и (19) аппроксимация функции Ф(с), т.е. ${{\Gamma }_{{(1)}}}$ и ${{\Gamma }_{{(2)}}},$ будет выпуклой кривой в соответствующей области с, т.к.
(20)
$\Phi {\text{''}}(c) = 2{{\kappa }_{1}} = - \frac{{{{\Gamma }_{1}} - \kappa {{c}_{1}}}}{{c_{1}^{2}}} < 0.$Подставляя в (20) ${{\Gamma }_{1}} = {{\Gamma }_{{11}}},$ $\kappa = {{\kappa }_{{11}}},$ ${{c}_{1}} = c_{{11}}^{0},$ найдем выражение ${{\Gamma }_{{(1)}}} = \Phi (c)$ при $0 \leqslant c < c_{{11}}^{0}$
(21)
$\begin{gathered} {{\Gamma }_{{(1)}}} = {{\Gamma }_{{11}}} + {{\kappa }_{{11}}}\left( {c - c_{{11}}^{0}} \right) - \\ - \,\,\frac{{{{\Gamma }_{{11}}} - {{\kappa }_{{11}}}c_{{11}}^{0}}}{{{{{\left( {c_{{11}}^{0}} \right)}}^{2}}}}{{\left( {c - c_{{11}}^{0}} \right)}^{2}},\,\,\,\,0 \leqslant c < c_{{11}}^{0}. \\ \end{gathered} $Аналогично, при $\Phi (c) = {{\Gamma }_{{(2)}}}$ подставляя в (14) ${{\Gamma }_{1}} = {{\Gamma }_{{12}}},\,\,\kappa = {{\kappa }_{{12}}},\,\,{{c}_{1}} = c_{{12}}^{0},$ получим
(22)
$\begin{gathered} {{\Gamma }_{{(2)}}} = {{\Gamma }_{{12}}} + {{\kappa }_{{12}}}\left( {c - c_{{12}}^{0}} \right) - \\ - \,\,\frac{{{{\Gamma }_{{12}}} - {{\kappa }_{{12}}}c_{{12}}^{0}}}{{{{{\left( {c_{{12}}^{0}} \right)}}^{2}}}}{{\left( {c - c_{{12}}^{0}} \right)}^{2}},\,\,\,\,0 \leqslant c < c_{{12}}^{0}. \\ \end{gathered} $Чтобы упростить аналитику определения типа функции $\bar {\Delta }\sigma (c),$ т.е. знака ее производной, рассмотрим далее случай, когда $\vartheta = 0,\,\,{{\varepsilon }_{1}} = 0.$ Это позволяет заменить функцию Г(с) функцией ${{\Gamma }_{{\left| \begin{subarray}{l} \vartheta = 0 \\ {{\varepsilon }_{1}} = 0 \end{subarray} \right.}}},$ а затем ее аппроксимацией ${{\Gamma }_{{(1)}}}$ или ${{\Gamma }_{{(2)}}}.$
Перейдем в интегральном операторе I (2a) к переменной интегрирования с
(23)
$I \equiv \int\limits_0^\Gamma {\Gamma \frac{{A{\text{'}}}}{A}d\Gamma = \int\limits_0^c {\Gamma (c)\frac{{dA}}{{d\Gamma }}\frac{{\frac{{d\Gamma }}{{dc}}}}{{A[\Gamma (c)]}}dc} .} $Согласно определению функции А в (3) при $\vartheta = 0,\,\,{{\varepsilon }_{1}} = 0$
(24)
$\begin{gathered} A \equiv Bc(\Gamma ) \hfill \\ \frac{{dA}}{{d\Gamma }} = B\frac{{dc}}{{d\Gamma }}. \hfill \\ \end{gathered} $Подставляя (24) в (23), найдем
(25)
$I = \int\limits_0^c {\Gamma (c)\frac{{B\frac{{dc}}{{d\Gamma }}}}{{Bc}}\frac{{dc}}{{\frac{{dc}}{{d\Gamma }}}} = \int\limits_0^c {\frac{{\Gamma (c)dc}}{c}} } .$Используя равенство (25) в (2), получим представление производной $\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}}$
(26)
$\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}} = \frac{{\Gamma (c)}}{c} - z\frac{{d\Gamma }}{{dc}}.$Или с учетом (26)
(27)
$c\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}} = \Gamma (c) - zc\frac{{d\Gamma }}{{dc}} \equiv f(c).$Полагая $\Gamma (c) \equiv \Phi (c),$ из (27) и (14) имеем
(28)
$\begin{gathered} f(c) = {{\Gamma }_{1}} + \kappa (c - {{c}_{1}}) - \frac{{({{\Gamma }_{1}} - \kappa {{c}_{1}})}}{{c_{1}^{2}}}{{(c - {{c}_{1}})}^{2}} - \\ - \,\,zc[\kappa - 2\frac{{{{\Gamma }_{1}} - \kappa {{c}_{1}}}}{{c_{1}^{2}}}(c - {{c}_{1}})] = \\ = {{\Gamma }_{1}} + \kappa [(1 - z)c - {{c}_{1}}] - \\ - \,\,\frac{{{{\Gamma }_{1}} - \kappa {{c}_{1}}}}{{c_{1}^{2}}}[{{(c - {{c}_{1}})}^{2}} - 2zc(c - {{c}_{1}})]. \\ \end{gathered} $Функция $f(c)$ (28) с учетом (17) удовлетворяет условиям
(29)
$\begin{gathered} f{{(c)}_{{\left| {c = 0} \right.}}} = {{\Gamma }_{1}} - \kappa {{c}_{1}} - ({{\Gamma }_{1}} - \kappa {{c}_{1}}) = 0 \\ \frac{{\partial f}}{{\partial c}} = \kappa (1 - z) - \frac{{{{\Gamma }_{1}} - \kappa {{c}_{1}}}}{{c_{1}^{2}}}\left[ {2(c - {{c}_{1}}) - } \right. \\ \left. { - \,\,2z(c - {{c}_{1}} + c)} \right] = \kappa (1 - z) - \\ - \,\,2\frac{{{{\Gamma }_{1}} - \kappa {{c}_{1}}}}{{c_{1}^{2}}}\left[ {(1 - z)(c - {{c}_{1}}) - zc} \right] > 0, \\ 0 \leqslant c < {{c}_{1}}, \\ \end{gathered} $(30)
$f(c) \equiv c\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}} > 0,\,\,\,\,0 < c < {{c}_{1}}.$(31)
$\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}} > 0,\,\,\,\,0 < c \leqslant {{c}_{1}}.$(32)
${{\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}}}_{{\left| {\Gamma = {{\Gamma }_{{(1)}}}} \right.}}} > 0,\,\,\,\,0 < c < c_{{11}}^{0},$(33)
${{\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}}}_{{\left| {\Gamma = {{\Gamma }_{{(2)}}}} \right.}}} > 0,\,\,\,\,0 < c < c_{{12}}^{0}.$При этом неравенство (17), используемое для вывода (32) и (33), при подстановке в него значений ${{c}_{1}},\,\,{{\Gamma }_{1}},\,\,\kappa $ из табл. 4, соответствующих функции ${{\Gamma }_{{(1)}}}$ или ${{\Gamma }_{{(2)}}},$ выполняется
(34)
$\begin{gathered} {{\Gamma }_{{11}}} - {{\kappa }_{{11}}}c_{{11}}^{0} = 0.163 > 0, \hfill \\ {{\Gamma }_{{12}}} - {{r}_{{12}}}c_{{12}}^{0} = 0.0292 > 0. \hfill \\ \end{gathered} $Условие (29а), налагаемое и далее, является необходимым, как показано в [11], для адекватного описания знака эффекта Ребиндера при малых концентрациях адсорбата.
Важно также отметить, что построенные в итоге аппроксимации ${{\Gamma }_{{(1)}}}$ и ${{\Gamma }_{{(2)}}}$ в (12), (13) и в (21), (22) по изотермам (1) и (2) физически также отвечают, как и сами изотермы, условиям, когда $\vartheta = 0,\,\,{{\varepsilon }_{1}} = 0.$
ОПРЕДЕЛЕНИЕ ЗНАКА ПРОИЗВОДНОЙ $\frac{{\partial \left( {\bar {\Delta }\sigma } \right)}}{{\partial c}}$ И ТОЧКИ МАКСИМУМА ВЕЛИЧИНЫ $\bar {\Delta }\sigma $ ПО ОСИ С ДЛЯ АППРОКСИМАЦИЙ ${{\Gamma }_{{(1)}}}$ И ${{\Gamma }_{{(2)}}}$
Вначале найдем условия, при которых производная $\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}}$ может изменить свой знак с положительного на отрицательный в некоторой точке на оси с, т.е. в этой точке реализуется куполообразная форма функции $\bar {\Delta }\sigma (c).$ Используя выражение величины $\bar {\Delta }\sigma $ в (2), представим производную $\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}}$ в виде
(35)
$\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}} = \frac{{\partial (\bar {\Delta }\sigma )}}{{\partial \Gamma }}\frac{{\partial \Gamma }}{{\partial c}} = \left( {\Gamma \frac{{A{\text{'}}}}{A} - z} \right)\frac{{\partial \Gamma }}{{\partial c}}.$Из уравнения изотермы (4) найдем производную $\frac{{\partial \Gamma }}{{\partial c}}$
Подставляя (36) в (35), получим
(37)
$\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}} = \left( {\Gamma \frac{{A{\text{'}}}}{A} - z} \right)\frac{{A{\text{'}}}}{{cA}}.$Из (37) и неравенства (3а) следует
(38)
$\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}} > 0,\,\,\,\,z \leqslant 0,\,\,\,\,c > 0.$Неравенство (38) означает, что куполообразная форма зависимости $\bar {\Delta }\sigma (c)$ при $z \leqslant 0$ невозможна, поэтому далее примем условие
а с учетом (29а) из (39) придем к ограничению для zИз (32) и (33) следует, что отрицательное значение производной $\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}}$ возможно только при $c > c_{{11}}^{0}$ для ${{\Gamma }_{{(1)}}}$ и при $c > c_{{12}}^{0}$ для ${{\Gamma }_{{(2)}}}.$ Для определения знака производной $\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}}$ в указанном диапазоне с воспользуемся знакоопределяющей функцией $f(c)$ (27), учитывая представление функций ${{\Gamma }_{{(1)}}},$ ${{\Gamma }_{{(2)}}}$ в (12) и (13)
$c > c_{{11}}^{0}$ для ${{\Gamma }_{{(1)}}}$ и при $c > c_{{12}}^{0}$ для ${{\Gamma }_{{(2)}}}.$ Для определения знака производной $\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}}$ в указанном диапазоне с воспользуемся знакоопределяющей функцией $f(c)$ (27), учитывая представление функций ${{\Gamma }_{{(1)}}},$ ${{\Gamma }_{{(2)}}}$ в (12) и (13)
(40)
$\begin{gathered} f{{(c)}_{{\left| {\Gamma = {{\Gamma }_{{(1)}}}} \right.}}} = {{\Gamma }_{{(1)}}} - zc\frac{{\partial {{\Gamma }_{{(1)}}}}}{{\partial c}} = \\ = \left\{ \begin{gathered} {{\Gamma }_{{11}}} + {{k}_{{11}}}\left[ {(1 - z)c - c_{{11}}^{0}} \right],\,\,\,\,c_{{11}}^{0} < c < c_{{21}}^{0} \hfill \\ {{\Gamma }_{{21}}} + {{k}_{{21}}}\left[ {(1 - z)c - c_{{21}}^{0}} \right],\,\,\,\,c_{{21}}^{0} < c < c_{{31}}^{0} \hfill \\ {{\Gamma }_{{31}}},\,\,\,\,c > c_{{31}}^{0} \hfill \\ \end{gathered} \right., \\ \end{gathered} $(41)
$\begin{gathered} f{{(c)}_{{\left| {\Gamma = {{\Gamma }_{{(2)}}}} \right.}}} = {{\Gamma }_{{(2)}}} - zc\frac{{\partial {{\Gamma }_{{(2)}}}}}{{\partial c}} = \\ = \left\{ \begin{gathered} {{\Gamma }_{{12}}} + {{k}_{{12}}}\left[ {(1 - z)c - c_{{12}}^{0}} \right],\,\,\,\,c_{{12}}^{0} < c < c_{{22}}^{0} \hfill \\ {{\Gamma }_{{22}}} + {{k}_{{22}}}\left[ {(1 - z)c - c_{{22}}^{0}} \right],\,\,\,\,c_{{22}}^{0} < c < c_{{32}}^{0} \hfill \\ {{\Gamma }_{{32}}},\,\,\,\,c > c_{{32}}^{0} \hfill \\ \end{gathered} \right.. \\ \end{gathered} $Выпишем выражения функций $f(c)\left| {_{{\Gamma = {{\Gamma }_{{(1)}}}}}} \right.$ и $f(c)\left| {_{{\Gamma = {{\Gamma }_{{(2)}}}}}} \right.$ отдельно при $c_{{11}}^{0} < c < c_{{21}}^{0}\,$ и при $c_{{12}}^{0} < c < c_{{22}}^{0}\,$ из (40) и (41) в форме
(42)
$\begin{gathered} f{{(c)}_{{\left| {\Gamma = {{\Gamma }_{{(1)}}}} \right.}}} = {{\kappa }_{{11}}}c\left( {1 - z + \frac{{{{\Gamma }_{{11}}} - {{\kappa }_{{11}}}c_{{11}}^{0}}}{{{{\kappa }_{{11}}}c}}} \right), \\ c_{{11}}^{0} < c < c_{{21}}^{0}, \\ \end{gathered} $(43)
$\begin{gathered} f{{(c)}_{{\left| {\Gamma = {{\Gamma }_{{(2)}}}} \right.}}} = {{\kappa }_{{12}}}c\left( {1 - z + \frac{{{{\Gamma }_{{12}}} - {{\kappa }_{{12}}}c_{{12}}^{0}}}{{{{\kappa }_{{12}}}c}}} \right), \\ c_{{12}}^{0} < c < c_{{22}}^{0}, \\ \end{gathered} $Учитывая неравенства (34) и (39а), из (42), (43) и (27) получим
(44)
$\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}}\left| {\Gamma = {{\Gamma }_{{(1)}}}} \right. > 0,\,\,\,\,0 < c < c_{{21}}^{0},$(45)
$\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}}\left| {\Gamma = {{\Gamma }_{{(2)}}}} \right. > 0,\,\,\,\,0 < c < c_{{22}}^{0}.$Неравенства (44), (45) означают, что с учетом (32) и (33) условие куполообразности, когда $\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}} < 0,$ для обеих аппроксимаций ${{\Gamma }_{{(1)}}},$ ${{\Gamma }_{{(2)}}}$ возможно лишь при $c_{{21}}^{0} < c < c_{{31}}^{0}$ и $c_{{22}}^{0} < c < c_{{32}}^{0}.$ Выпишем для этого соответствующие неравенства
(46)
$\begin{gathered} \frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}}\left| {\Gamma = {{\Gamma }_{{(1)}}}} \right. = {{\kappa }_{{21}}}\left( {1 - z + \frac{{{{\Gamma }_{{21}}} - {{\kappa }_{{21}}}c_{{21}}^{0}}}{{{{\kappa }_{{21}}}c}}} \right) < 0, \\ c_{{21}}^{0} < c < c_{{31}}^{0},\,\,\,\,{{\Gamma }_{{21}}} - {{\kappa }_{{21}}}c_{{21}}^{0} < 0, \\ \end{gathered} $(47)
$\begin{gathered} \frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}}\left| {\Gamma = {{\Gamma }_{{(2)}}}} \right. = {{\kappa }_{{22}}}\left( {1 - z + \frac{{{{\Gamma }_{{22}}} - {{\kappa }_{{22}}}c_{{22}}^{0}}}{{{{\kappa }_{{22}}}c}}} \right) < 0, \\ c_{{22}}^{0} < c < c_{{32}}^{0},\,\,\,\,{{\Gamma }_{{22}}} - {{\kappa }_{{22}}}c_{{22}}^{0} < 0. \\ \end{gathered} $Так как ${{\kappa }_{{21}}} > 0$ и, согласно (29а), z < 1, решением неравенства (46) относительно с является интервал
(48)
$\begin{gathered} c_{{21}}^{0} < c < \min \left( {c_{{31}}^{0},\,\,{{c}_{{{\text{м }}1}}}} \right) \\ {{c}_{{{\text{м }}1}}} \equiv \frac{{{{\kappa }_{{21}}}c_{{21}}^{0} - {{\Gamma }_{{21}}}}}{{(1 - z){{\kappa }_{{21}}}}} = \frac{{1 - {{P}_{1}}}}{{1 - z}}c_{{21}}^{0}, \\ \end{gathered} $Из неравенства (48) с необходимостью следует условие
Подставляя в (50) выражение ${{c}_{{{\text{м }}1}}}$ из (48), придем к неравенству
Используя значения ${{\Gamma }_{{21}}},\,\,{{\kappa }_{{21}}},\,\,c_{{21}}^{0}$ из табл. 4, найдем соответствующее частное значение ${{P}_{1}}$
Таким образом с учетом (51) и (29а) условие куполообразной зависимости функции $\bar {\Delta }\sigma (c)$ для аппроксимации ${{\Gamma }_{{(1)}}}$ (12) примет вид
(53)
$\begin{gathered} {{P}_{1}} < z < 1 \\ c_{{21}}^{0} < c < \min (c_{{31}}^{0},{{c}_{{{\text{м }}1}}}). \\ \end{gathered} $При этом максимальное значение величины $\bar {\Delta }\sigma $ по оси с, учитывая (44) и (46) будет в точке $c_{{\max }}^{0}$
Аналогичное условие куполообразной зависимости функции $\bar {\Delta }\sigma (c)$ для аппроксимации ${{\Gamma }_{{(2)}}}$ (13) примет вид
(55)
$\begin{gathered} {{P}_{2}} < z < 1 \\ c_{{22}}^{0} < c < \min (c_{{32}}^{0},{{c}_{{{\text{м }}2}}}), \\ \end{gathered} $(56)
$\begin{gathered} {{c}_{{{\text{м }}2}}} \equiv \frac{{1 - {{P}_{2}}}}{{1 - z}}c_{{22}}^{0} \\ {{P}_{2}} \equiv \frac{{{{\Gamma }_{{22}}}}}{{{{\kappa }_{{22\,}}}c_{{22}}^{0}}} \approx 0.091. \\ \end{gathered} $Точка максимума $c_{{\max }}^{0}$ величины $\bar {\Delta }\sigma $ для аппроксимации ${{\Gamma }_{{(2)}}}$ с учетом неравенств (45) и (47) будет равна
УСЛОВИЯ СМЕНЫ ТИПА ЗАВИСИМОСТИ $\bar {\Delta }\sigma (c)$ – ОТ КУПОЛООБРАЗНОЙ К МОНОТОННО ВОЗРАСТАЮЩЕЙ
Куполообразная форма зависимости эффекта Ребиндера от с при использовании ПАВ встречается часто в форме резкой избирательности по концентрации с, что яляется уязвимым местом в применении ПАВ в производственной деятельности [4]. Поэтому представляет интерес найти условия перехода к монотонно возрастающей зависимости по с термодинамической оценки эффекта, т.е. $\bar {\Delta }\sigma $ от с. Будем полагать для аппроксимации ${{\Gamma }_{{(2)}}}$ выполненным условие (55) – условие куполообразной формы функции $\bar {\Delta }\sigma {{(c)}_{{\left| {\Gamma = {{\Gamma }_{{(2)}}}} \right.}}}.$ Так как условие (53) приводит тоже к куполообразной форме функции $\bar {\Delta }\sigma {{(c)}_{{\left| {\Gamma = {{\Gamma }_{{(1)}}}} \right.}}},$ примем альтернативное к (53) ограничение на величину z, чтобы исключить для аппроксимации ${{\Gamma }_{{(1)}}}$ куполообразный тип функции $\bar {\Delta }\sigma (c)$
Рассмотрим в интервале $c_{{21}}^{0} < c < c_{{31}}^{0}$ с учетом (58) неравенство, вытекающее из условия монотонного роста функции $\bar {\Delta }\sigma {{(c)}_{{\left| {\Gamma = {{\Gamma }_{{(1)}}}} \right.}}}$
(59)
$\begin{gathered} {{\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}}}_{{\left| {\Gamma = {{\Gamma }_{{(1)}}}} \right.}}} = {{\kappa }_{{21}}}\left( {1 - z + \frac{{{{\Gamma }_{{21}}} - {{\kappa }_{{21}}}c_{{21}}^{0}}}{{{{\kappa }_{{21}}}c}}} \right) > 0, \\ c_{{21}}^{0} < c < c_{{31}}^{0}. \\ \end{gathered} $Запишем теперь(59) в виде
(60)
$\frac{c}{{c_{{21}}^{0}}} > \frac{{1 - {{P}_{1}}}}{{1 - z}},\,\,\,\,c_{{21}}^{0} < c < c_{{31}}^{0}.$Так как с учетом (58)
и в указанном интервале то из (59) с учетом (61) и (62) следует(63)
$\begin{gathered} {{\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}}}_{{\left| {\Gamma = {{\Gamma }_{{(1)}}}} \right.}}} = {{\kappa }_{{21}}}(1 - z)\left[ {1 - \frac{{(1 - {{P}_{1}})}}{{1 - z}}\frac{{c_{{21}}^{0}}}{c}} \right] = \\ = \,\,{{\kappa }_{{21}}}\frac{{(1 - z)c_{{21}}^{0}}}{c}\left[ {\frac{c}{{c_{{21}}^{0}}} - \frac{{1 - {{P}_{1}}}}{{1 - z}}} \right] > \\ > \,\,{{\kappa }_{{21}}}\frac{{(1 - z)c_{{21}}^{0}}}{c}\left[ {1 - \frac{{1 - {{P}_{1}}}}{{1 - z}}} \right] > 0,\,\,\,\,c_{{21}}^{0} < c < c_{{31}}^{0}. \\ \end{gathered} $Учитывая, что ${{\kappa }_{{21}}} > 0$ из (63), (61) следует
(64)
$\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}}\left| {\Gamma = {{\Gamma }_{{(1)}}}} \right. > 0,\,\,\,\,c_{{21}}^{0} < c < c_{{31}}^{0}.$Из представления функции $f{{(c)}_{{\left| {\Gamma = {{\Gamma }_{{(1)}}}} \right.}}}$ при $c > c_{{31}}^{0}$ в (41) найдем из (27)
(65)
$\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}}\left| {\Gamma = {{\Gamma }_{{(1)}}}} \right. = \frac{{{{\Gamma }_{{31}}}}}{c} > 0,\,\,\,\,c > c_{{31}}^{0}.$Из (64), (65) и (44) в итоге получим
(66)
$\frac{{\partial (\bar {\Delta }\sigma )}}{{\partial c}}\left| {\Gamma = {{\Gamma }_{{(1)}}}} \right. > 0,\,\,\,\,c > 0.$Так как $\bar {\Delta }\sigma \left| {_{{c = 0}}} \right. = 0$ неравенство (66) означает, что
т.е. эффект Ребиндера по аппроксимации ${{\Gamma }_{{(1)}}}$ имеет положительный знак при $c > 0$ и величина его термодинамической оценки $\bar {\Delta }\sigma $ монотонно растет с концентрацией с при $c > 0.$Неравенства (53) и (55) позволяют заключить, что при выполнении дополнительного условия
а также (42а) и (43а) при переходе от изотермы (2) к изотерме (1) рис. 2 происходит смена типа зависимости функции $\bar {\Delta }\sigma (c)$ – от куполообразной к монотонно растущей с концентрацией с. Нумерация изотерм в таком переходе – от 2 к 1 – не имеет обязательного значения и может быть перенумерована.При этом можно допустить, что физической причиной изменения формы изотермы адсорбата – от (1) к (2) на рис. 2 и наоборот может быть не только добавка в раствор простого электролита как в [14]. Важно, чтобы адсорбция оставалась однокомпонентной для возможности применения теории [9, 10] и для обеих изотерм сохранялась S-образная форма.
Если значения параметра z теории [9, 10], соответствующие изотерме (1) и (2) ${{z}_{1}} \ne {{z}_{2}}$ и удовлетворяют аналогичным (53) и (55) неравенствам
(68)
$\begin{gathered} {{z}_{1}} < {{P}_{1}} < 1 \hfill \\ {{P}_{2}} < {{z}_{2}} < 1, \hfill \\ \end{gathered} $Критерием выбора, например, из двух ПАВ в обоих случаях, когда ${{z}_{1}} = {{z}_{2}}$ или ${{z}_{1}} \ne {{z}_{2}},$ может служить увеличение параметра ${{P}_{1}}\,\,$или/и уменьшение параметра ${{P}_{2}},$ как это следует из (68а), (68), (67). Такой критерий выбора изотермы адсорбции достигается оптимизацией характеристик функций ${{\Gamma }_{{(1)}}}$ и ${{\Gamma }_{{(2)}}}$ с учетом определения параметров ${{P}_{1}},$ ${{P}_{2}}$ в (49) и (56).
Определение величины параметра z, который сильно облегчил бы проверку адекватности теории и ее использование, является новой, выходящей за рамки статьи, задачей. Ее решение требует разработки специальных методик в будущих исследованиях.
ЗАКЛЮЧЕНИЕ
1. На основе построенной ранее теории однокомпонентной равновесной адсорбции из жидкости на твердой поверхности исследована аналитически термодинамическая оценка эффекта Ребиндера – приращение поверхностного натяжения межфазного слоя – в функции от объемной концентрации адсорбата в жидком растворе в случае исходной изотермы – на недеформированной поверхности – S-образного вида.
2. Показано, что функция этой зависимости может иметь и куполообразную форму и монотонно растущую с концентрацией адсорбата.
3. В терминах параметров теории выведены условия, при которых происходит переход от куполообразной формы к монотонно возрастающей.
4. Такой переход от одной изотермы к другой может помочь избежать резкую концентрационную избирательность действия эффекта Ребиндера при использовании ПАВ в разрушении твердых материалов.
Список литературы
Ребиндер П.А. // VI съезд русских физиков. М.: ОГИЗ, 1928. С. 29.
Ребиндер П.А., Шрейнер Л.А., Жигач К.Д. Понизители твердости в бурении. М., Л.: АН СССР, 1944. 199 с.
Грей Дж.Р., Дарли Г.С.Г. Состав и свойства буровых агентов. М.: Изд. “Недра”, 1985. 509 с.
Евсеев В.Д. // Бурение и нефть. 2010. № 9. С. 16.
Подгаецкий Э.М. // Электрохимия. 1999. Т. 35. С. 528.
Подгаецкий Э.М. // Электрохимия. 2005. Т. 41. С. 20.
Подгаецкий Э.М. // Поверхность. Рентгеновские, синхротронные и нейтронные исследования. 2010. № 1. С. 97.
Подгаецкий Э.М. // Физикохимия поверхности и защита материалов. 2013. Т. 49. С. 155.
Подгаецкий Э.М. // Физикохимия поверхности и защита материалов. 2013. Т. 49. С. 239.
Подгаецкий Э.М. // Физикохимия поверхности и защита материалов. 2014. Т. 50. С. 339.
Подгаецкий Э.М. // Физикохимия поверхности и защита материалов. 2017. Т. 53. С. 572; 2017. Т. 53. С. 233; 2018. Т. 54. С. 435.
Bouzerda M. Ph.D. Thesis, CNRS Lab 330 Montpelier, 1991.
Латышев О.Г. Разрушение горных пород. М.: Теплотехник, 2007. 672 с.
Bouzerda M., Lindheimer M., Partyka S., Brun B. // Adsorption on New and Modified Inorganic Sorbents. 1996. V. 99. P. 611.
Дополнительные материалы отсутствуют.
Инструменты
Физикохимия поверхности и защита материалов


