Физикохимия поверхности и защита материалов, 2020, T. 56, № 2, стр. 215-224

ВВЕДЕНИЕ

Прогресс современных нанотехнологий сделал возможным получение металлических наночастиц самых разных форм и составов. Параллельно с этим происходило и развитие разнообразных математических, по большей части, численных методов, позволяющих найти спектральные характеристики как самих наночастиц, так и молекул вблизи них [1]. Тем не менее, мы полагаем, что возможности использования в наноплазмонике сферических частиц отнюдь не исчерпаны. Это связано как с относительной простотой их синтеза, так и хорошо разработанным математическим аппаратом, применяемым для описания оптических свойств [1–3]. Одним из таких свойств является наличие полей большой напряженности в непосредственной близости от поверхности наночастиц благородных металлов. Напомним, что ближним называют электромагнитное поле, возникающее вблизи (c внешней стороны на расстоянии r от центра) рассеивающей сферической частицы радиусом a или непосредственно на ее поверхности, т.е. при r = a.

Рассматриваемая оптическая система изображена на рис. 1. С формальной точки зрения рассеяние электромагнитной волны малой частицей представляет собой преобразование падающей на нее, как правило, плоской волны в сферическую. Удобным математическим приемом, упрощающим описание этого процесса, является совместное применение декартовых и сферических координат. При этом если сама рассеивающая частица имеет форму сферы, то и начало обеих координатных систем естественно расположить в ее центре.

Рис. 1.

Рассматриваемая оптическая система.

Используемая декартова система координат ориентирована так, чтобы направление распространения падающей волны совпадало с осью z, а изменяющийся по гармоническому закону E(t) = = E₀e^−iωt вектор напряженности электрического поля направлен вдоль оси x. Итак, плоская монохроматическая (с частотой ω и длиной λ в вакууме) линейно поляризованная волна, двигаясь в однородной изотропной непоглощающей среде с показателем преломления n, падает на частицу радиусом a. В сферической системе координат напряженность электрического поля рассеянной волны можно представить в виде суммы трех взаимно перпендикулярных векторов E_θ, E_φ и E_r. Отметим, что при увеличении r поперечные (E_θ и E_φ) и продольная (E_r) составляющие напряженности поля ведут себя по-разному: E_θ и E_φ уменьшаются как 1/r, а E_r как 1/r² [2, 3, 11]. Собственно говоря, это обстоятельство, пусть и качественно, но объясняет основные отличия ближнего поля от дальнего. С учетом сказанного понятно, что при достаточно малых a и r ≈ a выполняются соотношения E_r$ \gg $ E_θ и E_φ; если же r $ \gg $ a, то E_θ и E_φ$ \gg $ E_r.

Для количественной характеристики ближнего поля, существующего вблизи наночастицы, в [2] были введены две безразмерные функции Q_nf и Q_r, имеющие физический смысл эффективности [3]:

В выражениях (1), (2) I₀ = |E₀|² – интенсивность падающей волны, E_r, E_θ, E_φ – проекции вектора напряженности (E_sca) поля рассеянной волны.

Из формул (1) и (2) ясно, что интеграл, входящий в Q_nf, представляет собой вычисленный на расстоянии r от центра и усредненный по углам θ и φ квадрат модуля напряженности электрического поля рассеянной волны. При расчете Q_r усредняется только ее радиальная компонента, и поэтому понятно, что Q_nf всегда больше, чем Q_r. Кроме того, указанные выше различия в характере зависимостей поперечной и продольной составляющих E_sca от r приводят к разному асимптотическому поведению Q_nf и Q_r. С помощью численных расчетов можно показать, что при r $ \gg $ a Q_r(r) → 0, а Q_nf(r) → Q_sca, т.е. к величине эффективности дальнего поля.

Как уже упоминалось, понятие эффективности ближнего поля было предложено в работе [2]. Появление этой статьи было неслучайным. Авторы [2] сделали попытку объяснения таких интересных, обнаруженных к этому времени явлений, как гигантское (от 10⁵ до 10⁶) усиление рамановского рассеяния [4–6] и многократное увеличение флуоресценции [7, 8] вблизи поверхности хорошо проводящих (Cu, Ag, Au) металлов. На качественном уровне им это, безусловно, удалось. Дело в том, что во всех экспериментальных схемах, для которых характерно существенное увеличение интенсивности спектров неупругого рассеяния, всегда присутствуют какие-либо локальные структуры с размерами элементов от одного до ста нанометров. Это справедливо, например, для шероховатых металлических поверхностей. В [2] были получены формулы для Q_nf и Q_r, аналогичные приведенным ниже выражениям (3), (4). Затем для водных дисперсий меди, серебра и золота, в широком (200−1200 нм) диапазоне длин волн проводились расчеты численных значений Q_nf на поверхности частиц. Результаты этих вычислений, выполненных, в частности, для золотых сферических частиц с a = 22 нм, показали, что в этом случае $Q_{{nf}}^{{{\text{max}}}}$ = 71, а длина волны, при которой достигается это значение, равна 550 нм.

Из подстановки этих значений в выражение (1) следует, что если r = a, то максимальная величина входящего в него интеграла в 223 раза больше, чем I₀. Таким образом, в этом случае интенсивность ближнего поля вблизи поверхности наночастиц золота оказывается намного большей интенсивности первичной плоской волны, взаимодействующей с ними. Следовательно, можно предположить, что и в других похожих ситуациях причиной увеличения интенсивности как упругого, так и неупругого рассеяния является наличие сильных электромагнитных полей, возникающих в непосредственной близости от локальных структур, элементы которых имеют высокую проводимость и малые радиусы кривизны.

Повышенную интенсивность таких полей можно использовать, например, при получении кратеров правильной формы в образцах кремния [9] или понижении пороговых значений энергии лазера, применяемого для оптического инициирования энергетических материалов [10]. В [9, 10] использовались импульсные (фемтосекундные) лазеры с длиной волны 780 и 1064 нм соответственно. Авторы обеих работ стремились получить максимальные величины $Q_{{nf}}^{{{\text{max}}}}$ для наночастиц из золота, окруженных воздухом (n = 1.0) [9] или контактирующих с органическим соединением [10], для которого n = 1.5. При этом в обоих случаях у исследователей была возможность предварительного выбора оптимального (с точки зрения увеличения значений Q_nf) размера используемых наночастиц. Для этого они провели вычисления с помощью формулы (3) и установили, что радиус наночастиц, отвечающих наибольшим Q_nf равен 80 [9] и 125 нм [10], а сами величины $Q_{{nf}}^{{{\text{max}}}}$ равны 15 и 23 соответственно. Следует также отметить, что при формировании оптической системы, предназначенной для получения больших значений Q_nf, авторы [10] стремились к тому, чтобы соблюдались условия применимости теории Ми для ансамбля частиц. Это − однородность их размеров, а также хаотичность распределения в объеме образца. При этом расстояние между частицами должно быть намного больше длины падающей волны [11].

Мы уже упоминали, что $Q_{{nf}}^{{{\text{max}}}}$, найденное для золотых сферических частиц с a = 22 нм, помещенных в водную (n = 1.33) среду, было равно 71 и достигалось при λ = 550 нм [2]. Ясно, что это значение существенно больше, чем $Q_{{nf}}^{{{\text{max}}}}$ = 15, рассчитанное в [9], или $Q_{{nf}}^{{{\text{max}}}}$ = 23, полученное в [10]. Очевидно, что во всех этих случаях мы имеем дело с оптическими системами, у которых общим является лишь материал наночастиц, а их размер, длина волны падающего излучения и показатель преломления окружающей среды различаются. Понятно также, что, основываясь на таком небольшом массиве разнородных данных, сделать сколько-нибудь надежные обобщения, отражающие поведение функции Q_nf для других значений λ, a и n, невозможно. Таким образом, задача определения условий, при которых величины Q_nf будут максимальными, безусловно, актуальна.

Целью проведенного нами исследования было построение и изучение свойств как самой спектральной зависимости максимальной эффективности ближнего поля $Q_{{nf}}^{{{\text{max}}}}$ (λ), так и других связанных с ней функций, в широком, практически важном диапазоне длин волн. При этом выбор модельных сред, окружающих наночастицы золота, также основывался на вполне практических соображениях. В качестве таких сред были выбраны воздух (n = 1.0), вода (n = 1.33) и некое типичное органическое соединение с n = 1.5.

РАСЧЕТ ЧИСЛЕННЫХ ЗНАЧЕНИЙ Q_nf И Q_r

Прежде всего, отметим, что в дальнейшем мы будем обсуждать только ближнее поле, существующее на поверхности частиц (т.е. при r = a). Представленные ниже формулы из [12] отличаются от выражений, впервые полученных в [2], тем, что в (3), (4) используются $h_{m}^{{\left( 1 \right)}}$ (ka) − сферические функции Ханкеля первого (а не второго, как в [2]) рода порядка m. Этот способ записи Q_nf и Q_r обусловлен тем, что мы выбрали такую же, как в [3, 12] зависимость напряженности электрического поля от времени E(t) = E₀e^–iωt, тогда как в [2] E(t) = E₀e^iωt.

Итак, с учетом сделанных замечаний функции Q_nf и Q_r имеют вид:

Приводить здесь формулы для других входящих в (3), (4) величин не имеет смысла, так как выражения для коэффициентов рассеяния a_m, b_m достаточно громоздки, а функции $h_{m}^{{(1)}}(ka)$ находятся с помощью рекуррентных соотношений, запись которых также занимает довольно много места. На самом деле, все необходимое для точного вычисления этих величин можно найти в специальной программе [3]. Опираясь на уже имевшиеся к тому времени наработки, ее авторы предложили свой вариант надежного расчета Q_E и Q_sca, т.е. эффективностей экстинкции и дальнего поля. Функции Q_E и Q_sca можно найти по формулам из [2]

Выражения для Q_E и Q_sca выглядят несколько проще, чем (3), (4), поскольку они короче, и не содержат функций $h_{m}^{{(1)}}(ka)$ в явном виде. В действительности, однако, для того чтобы найти коэффициенты a_m и b_m, требуются именно $h_{m}^{{(1)}}(ka)$ [3]. Таким образом, для расчета Q_nf и Q_r мы воспользовались широко известной программой [3], дополнив ее вычислениями рядов по формулам (3) и (4).

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Расчеты, выполненные с помощью формулы (3) для сферических частиц золота, показывают, что при заданных λ и n зависимости Q_nf от a представляют собой гладкие кривые с максимумом (рис. 2). Следовательно, располагая достаточным количеством таких кривых, можно найти как сами максимальные величины эффективности ближнего поля $Q_{{nf}}^{{{\text{max}}}}$(λ), так и соответствующие им радиусы частиц a($Q_{{nf}}^{{{\text{max}}}}$). Для этих же значений a($Q_{{nf}}^{{{\text{max}}}}$) с помощью формулы (4) можно определить спектральное поведение функции Q_r(λ).

Рис. 2.

Экстремальные зависимости Q_nf от радиуса a для двух длин волн: 400 (а) и 600 нм (б) (номера 1, 2 и 3 относятся к средам с n = 1.0, 1.33, 1.5).

Вычисления проводили для трех значений n, соответствующих, как уже упоминалось, воздуху (n = 1.0), воде (n = 1.33) и органическому соединению (n = 1.5). При этом использовали оптические постоянные золота, полученные в [13]. Спектральные характеристики функций $Q_{{nf}}^{{{\text{max}}}}$(λ), Q_r(λ), a($Q_{{nf}}^{{{\text{max}}}}$(λ)) и других, связанных с ними переменных исследовали в диапазоне длин волн от 200 до 1950 нм. Закономерности поведения зависимостей $Q_{{nf}}^{{{\text{max}}}}$(λ, 1.5) и a($Q_{{nf}}^{{{\text{max}}}}$(λ, 1.5)) можно понять с помощью рис. 3. Позже мы еще вернемся к нему, а сейчас рассмотрим рис. 4а, на котором приводятся графики функций $Q_{{nf}}^{{{\text{max}}}}$(λ) для трех значений n. Нам представляется разумным разбиение каждой из этих кривых на две части.

Рис. 3.

Зависимости $Q_{{nf}}^{{{\text{max}}}}$ и a($Q_{{nf}}^{{{\text{max}}}}$) от λ при n = 1.5 во всем изученном спектральном диапазоне. Прямая 1 – базовая линия.

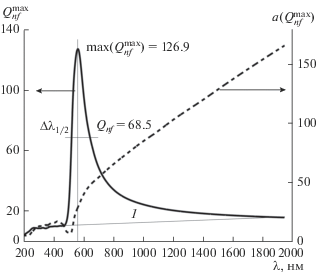
Рис. 4.

Зависимости $Q_{{nf}}^{{{\text{max}}}}$ от λ для трех разных значений n: во всем исследованном спектральном диапазоне (а) и в интервалах 200−475 нм (б), 480−530 нм (в) и 1000−1950 нм (г) (нумерация кривых та же, что и на рис. 2).

На первом участке всех трех кривых наблюдается плавный, приблизительно линейный, хотя и с разным наклоном, рост значений $Q_{{nf}}^{{{\text{max}}}}$. Начало второго участка можно отнести к величине λ ≅ 480 нм. Здесь начинается интенсивный рост кривых; все они достигают максимальных значений и затем плавно спадают. По сути дела, эти части графиков представляют собой асимметричные кривые резонансного типа. Аналогично ведут себя и функции Q_r (λ).

При более подробном рассмотрении первого участка (см. рис. 4б) видно, что все кривые $Q_{{nf}}^{{{\text{max}}}}$(λ) изменяются схожим образом, демонстрируя заметное (примерно в два раза) и при этом практически линейное возрастание величин $Q_{{nf}}^{{{\text{max}}}}$(λ) в интервале длин волн от 200 до 275 нм. Далее, при изменении λ от 275 до 475 нм рост функций $Q_{{nf}}^{{{\text{max}}}}$(λ) существенно замедляется, и их численные значения увеличиваются приблизительно на 10%. Для этого диапазона длин волн справедливы неравенства: $Q_{{nf}}^{{{\text{max}}}}$(λ, 1.0) > $Q_{{nf}}^{{{\text{max}}}}$(λ, 1.33) > $Q_{{nf}}^{{{\text{max}}}}$(λ, 1.5).

Представленные на рис. 4в графики зависимостей $Q_{{nf}}^{{{\text{max}}}}$(λ) интересны тем, что здесь происходит инверсия кривых $Q_{{nf}}^{{{\text{max}}}}$(λ) относительно показателя преломления окружающей среды. Уже при λ ≅ 504 нм, значения $Q_{{nf}}^{{{\text{max}}}}$ для n = 1.33 превышают $Q_{{nf}}^{{{\text{max}}}}$, найденные для n = 1.0 и n = 1.5. Это соотношение между величинами $Q_{{nf}}^{{{\text{max}}}}$ сохраняется вплоть до λ ≅ 519 нм. Наконец, начиная с этой точки и до конца изученного нами диапазона длин волн, значения $Q_{{nf}}^{{{\text{max}}}}$ подчиняются неравенствам: $Q_{{nf}}^{{{\text{max}}}}$(λ, 1.5) > $Q_{{nf}}^{{{\text{max}}}}$(λ, 1.33) > $Q_{{nf}}^{{{\text{max}}}}$(λ, 1.0).

Глядя на рис. 4в, можно увидеть, что кривые $Q_{{nf}}^{{{\text{max}}}}$ пересекаются только попарно, при λ примерно равных 504 и 519 нм соответственно. В то же время видно, что если λ ≅ 506 нм, то все три кривые максимально сближаются.

Вернувшись к рис. 4а, обсудим поведение представленных на нем зависимостей $Q_{{nf}}^{{{\text{max}}}}$(λ). Как уже упоминалось, при λ ≅ 480 нм начинается их интенсивный рост, причем с увеличением n положение максимума этих кривых изменяется не слишком значительно: λ^max = 540 (n = 1.0), 558 (n = 1.33) и 568 нм (n = 1.5). То же самое справедливо и в отношении полуширины Δλ_1/2 обсуждаемых кривых. Так, Δλ_1/2 =156 нм (n = 1.0), Δλ_1/2 =139 нм (n = 1.33), и Δλ_1/2 =123 нм (n = 1.5). Способ определения численных значений Δλ_1/2 можно понять с помощью рис. 3. Здесь мы использовали широко распространенный в спектроскопии прием, называемый методом базовой линии [14].

Рис. 4а также показывает, что с увеличением n сами экстремальные значения $Q_{{nf}}^{{{\text{max}}}}$ существенно возрастают: $Q_{{nf}}^{{{\text{max}}}}$ = 43.4 (n = 1.0), 83.9 (n = 1.33) и 126.9 (n = 1.5), а на последнем, убывающем участке кривых $Q_{{nf}}^{{{\text{max}}}}$(l) (см. рис. 4г) происходит их существенное сближение. Так, при λ = 1000 нм, $Q_{{nf}}^{{{\text{max}}}}$ для n = 1.5 и n = 1.0 различаются на 25%, а при λ = 1950 нм, разница между этими величинами уменьшается до 6.5%.

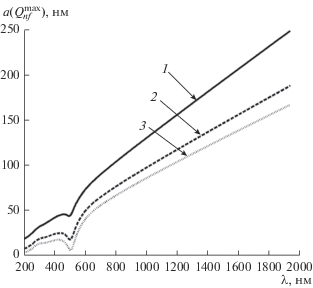
С помощью рис. 5 можно понять, как ведет себя функция a($Q_{{nf}}^{{{\text{max}}}}$) в зависимости от λ и n. Во-первых, a($Q_{{nf}}^{{{\text{max}}}}$(λ, 1.0)) > a($Q_{{nf}}^{{{\text{max}}}}$(λ, 1.33)) > a($Q_{{nf}}^{{{\text{max}}}}$(λ, 1.5)) при любых λ. Во-вторых, все кривые изменяются схожим образом; в частности, все они имеют по одному явно выраженному минимуму. Для минимальных значений этих функций выполняются следующие соотношения: a($Q_{{nf}}^{{{\text{max}}}}$(502, 1.0)) = 43 нм, a($Q_{{nf}}^{{{\text{max}}}}$(509, 1.33)) = 17 нм, a($Q_{{nf}}^{{{\text{max}}}}$(509, 1.5)) = 5 нм. В-третьих, при бóльших величинах λ во всем рассматриваемом спектральном диапазоне наблюдается устойчивый линейный рост значений a($Q_{{nf}}^{{{\text{max}}}}$(λ)). Для n = 1.5 изменение λ от 200 до 1950 нм приводит к возрастанию a($Q_{{nf}}^{{{\text{max}}}}$) от 3 до 166 нм; при n = 1.33, a($Q_{{nf}}^{{{\text{max}}}}$) увеличивается от 6 до 188 нм; если n = 1.0, эта же величина изменяется от 18 до 248 нм.

Рис. 5.

Зависимости a($Q_{{nf}}^{{{\text{max}}}}$) от λ для трех значений n во всем исследованном спектральном диапазоне (нумерация кривых та же, что и на рис. 2).

Прямая пропорциональность между a($Q_{{nf}}^{{{\text{max}}}}$(λ, n)) и λ подтверждается при построении графиков, по оси ординат которых отложены значения параметра a($Q_{{nf}}^{{{\text{max}}}}$(λ))/λ, т.е. приведенного радиуса частиц, а по оси абсцисс − длина волны. Рис. 6 показывает, что кривые a($Q_{{nf}}^{{{\text{max}}}}$(λ))/λ вновь изменяются схожим образом, а для n = 1.0 и 1.33 происходит небольшое (до λ ≅ 506 и 510 нм соответственно) смещение их минимумов в сторону бóльших λ. Кроме того, видно, что с ростом n протяженность участков кривых a($Q_{{nf}}^{{{\text{max}}}}$(λ))/λ, параллельных оси абсцисс, уменьшается. Так, для n = 1.0 этот участок можно отсчитывать от λ ≅ 820 нм, для n = 1.33 − от λ ≅ 970 нм, а для n = 1.50 − от λ ≅ 1050 нм.

Рис. 6.

Зависимости приведенного радиуса a($Q_{{nf}}^{{{\text{max}}}}$)/λ от λ для трех значений n во всем исследованном спектральном диапазоне (нумерация кривых та же, что и на рис. 2).

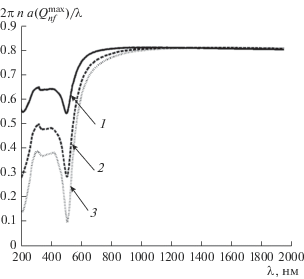
Вид этого графика подталкивает к реализации еще одного, менее очевидного, но очень полезного преобразования полученных данных. Если ось абсцисс оставить в прежнем виде, а по ординате отложить переменную na($Q_{{nf}}^{{{\text{max}}}}$(λ, n))/λ, то, начиная с λ ≅ 1000 нм, все кривые na($Q_{{nf}}^{{{\text{max}}}}$(λ))/λ сливаются в одну. На самом деле, с точки зрения удобства интерпретации и обсуждения полученных результатов по оси ординат лучше отсчитывать численные значения параметра дифракции 2πna($Q_{{nf}}^{{{\text{max}}}}$(λ))/λ.

Зависимость этой переменной от λ представлена на рис. 7. Видно, что при λ > 1000 нм для всех значений n и a($Q_{{nf}}^{{{\text{max}}}}$(λ)) величина параметра дифракции равна 0.8. Таким образом, если в этом диапазоне длин волн выполняется равенство x = = 2πna($Q_{{nf}}^{{{\text{max}}}}$(λ, n))/λ = 0.8, то значения Q_nf максимальны. Очевидно, что при любом λ, выбранном из этого интервала, можно найти лишь произведение na($Q_{{nf}}^{{{\text{max}}}}$(λ)), а не величины n и a($Q_{{nf}}^{{{\text{max}}}}$(λ)) по отдельности. Тем не менее, понятно, что для решения многих задач этого вполне достаточно. Стоит также отметить, что представленное выше эмпирическое соотношение можно, в частности, применять при работе с уже упоминавшемся фемтосекундным лазером, имеющем длину волны 1064 нм.

Рис. 7.

Зависимости параметра дифракции 2πna($Q_{{nf}}^{{{\text{max}}}}$)/λ от λ для трех значений n во всем исследованном спектральном диапазоне (нумерация кривых та же, что и на рис. 2).

Отметим некоторые характерные особенности оптических констант, использованных нами в расчетах. Прежде всего, следует подчеркнуть, что мы брали приведенные в [13] объемные значения оптических постоянных золота. Кроме того, фактически мы использовали воду как модельное соединение с n = 1.33, в то время как в изучаемом нами диапазоне длин волн ее показатель преломления изменяется от n = 1.396 (при λ = 200 нм), до n = 1.306 (при λ = 2000 нм) [15]. Ясно, что для учета таких (вызванных дисперсией) вариаций в величине n потребуется лишь минимальная модификация предложенной программы. Кроме того, понятно, что это приведет лишь к небольшим изменениям численных значений $Q_{{nf}}^{{{\text{max}}}}$(λ, n), a($Q_{{nf}}^{{{\text{max}}}}$(λ, n)), a($Q_{{nf}}^{{{\text{max}}}}$(λ, n))/λ и 2πna($Q_{{nf}}^{{{\text{max}}}}$(λ, n))/λ. Очевидно, иная ситуация возникает при попытке учесть зависимость оптических постоянных наночастиц золота от их радиуса. Хорошо известно [3], что при малых значениях a изменения оптических постоянных могут быть весьма значительными и это (для относительно небольших радиусов) может вызвать достаточно серьезные изменения в поведении обсуждаемых здесь функций. Тем не менее, мы полагаем, что использование (в качестве первого приближения) объемных величин оптических постоянных во всем диапазоне значений a, не только вполне допустимо, но даже полезно, поскольку дальнейшее сравнение найденных нами зависимостей с аналогичными результатами, учитывающими влияние размеров частицы на ее оптические постоянные, может оказаться весьма продуктивным.

Еще один этап данной работы заключался в сопоставлении полученных нами результатов с имеющимися в литературе теоретическими расчетами и экспериментальными данными. Статья [16] содержит сведения, которые мы можем использовать для подтверждения как корректности проведенных нами вычислений, так и практической ценности найденных зависимостей $Q_{{nf}}^{{{\text{max}}}}$(λ, n) и a($Q_{{nf}}^{{{\text{max}}}}$(λ, n)). В этой работе изучались оптимальные условия получения кратеров на поверхности образцов кремния. Абляция материала подложки осуществлялась с помощью линейно поляризованного излучения лазера (с длительностью импульса 100 фемтосекунд и длиной волны 820 нм), направленного на ансамбли золотых сферических наночастиц, с радиусами 20, 40 и 100 нм, хаотическим образом расположенных на ее поверхности. При формировании этого ансамбля соблюдались указанные выше условия применимости теории Ми [11], и изучалось воздействие ближнего поля на участки образца, расположенные в непосредственной близости от поверхности изолированной сферической наночастицы. С помощью проведенных экспериментов было установлено, что образование наиболее протяженных и глубоких кратеров происходило при использовании частиц с радиусами приблизительно (c разбросом на уровне 8%) равными 100 нм. Обратившись к полученной нами кривой 1, представленной на рис. 5 можно видеть, что для лазера с λ = = 820 нм, радиусы наночастиц, обеспечивающих реализацию максимальных значений Q_nf несколько превышают 100 нм. Более точные вычисления дают значение a = 105 нм. Таким образом, разница между теоретическим предсказанием и экспериментальным результатом не превышает 5%. Расчеты, выполненные нами для λ = 820 нм и a = = 105 нм, приводят к значению $Q_{{nf}}^{{{\text{max}}}}$ = 21.4. К сожалению, напрямую сравнить вычисленные и измеренные значения $Q_{{nf}}^{{{\text{max}}}}$ нельзя, поскольку таких измерений не проводилось. Тем не менее, можно сопоставить полученную нами величину $Q_{{nf}}^{{{\text{max}}}}$ с результатами вычислений, проведенных в [16]. Используя метод конечных разностей во временной области (FTDT) было рассчитано пространственное распределение электрического поля вблизи золотой наночастицы лежащей на плоской поверхности кремния. Авторы [16] нашли, что наибольшее значение напряженности поля будет наблюдаться в точке контакта частицы с подложкой, и эта величина в 26 раз превышает напряженность поля исходной плоской волны, падающей на частицу. Понятно, что с увеличением расстояния от поверхности кремния, электромагнитное поле, существующее вблизи самой частицы, будет все больше походить на ближнее поле, характерное для изолированной золотой частицы, помещенной в воздушную среду. Напомним, что Q_nf определяется с помощью усреднения “коэффициента усиления” ближнего поля по азимутальным и полярным углам, и поэтому мы полагаем, что найденная нами величина Q_nf = 21.4, хорошо коррелирует со своим максимальным значением Q = 26. Отметим также, что, строго говоря, во всех расчетах проведенных в [16], следовало бы говорить только об интенсивности ближнего поля, но поскольку при вычислениях выполненных в этой работе, для напряженности падающей на частицу исходной волны было выбрано единичное значение, все сделанные нами выводы остаются справедливыми.

Другую возможность количественного сопоставления полученных нами результатов с имеющимися в литературе экспериментальными данными дает усиленное поверхностью рамановское рассеяние (SERS). Прежде всего, следует отметить, что само это явление связано с возникновением на поверхности проводящей наночастицы ближнего (усиленного по сравнению с падающей волной) поля [17]. К сожалению, сравнить напрямую (как это сделано в предыдущем примере) полученные нами значения Q_nf с величинами коэффициента усиления интенсивности рамановского рассеяния нельзя, поскольку строгая теория этого явления разработана только для случая дипольного приближения [18, 19]. Тем не менее, имеющиеся в литературе данные дают возможность сравнения рассчитанных нами значений a($Q_{{nf}}^{{{\text{max}}}}$(λ, n)) с экспериментально определенными радиусами наночастиц, отвечающих максимальным значениям интенсивности рамановского рассеяния. В [20] была получена зависимость этой величины от радиуса золотых наночастиц, имеющих форму, близкую к сферической. В экспериментах использовались наборы частиц, имеющих высокую степень монодисперсности. с радиусами 8, 25, 40, 60, 67.5 и 80 нм. На поверхность этих наночаcтиц был адсорбирован пиридин (Py), сами частицы осаждались на стеклоуглеродный (GC) электрод, и затем из системы удалялась вода. В экспериментах измерялась интенсивность рамановской полосы, имеющей максимум при ν = 1007 см^–1. В качестве источника возбуждающего излучения использовался гелий-неоновый лазер с λ = 632.8 нм. Следовательно, применяя развитый нами подход, можно (для λ = 632.8 нм, и n = 1) найти a($Q_{{nf}}^{{{\text{max}}}}$), и сопоставить эту величину с экспериментально определенным радиусом наночастиц, обеспечивающем максимальное усиление рамановского рассеяния. Рассчитанная нами величина a($Q_{{nf}}^{{{\text{max}}}}$) = 77.2 нм. В тоже время, найденное с помощью эксперимента значение a = 67.5 нм. Таким образом, разница между этими величинами не превышает 15%. Учитывая то обстоятельство, что в сформированной на поверхности электрода тонкой пленке, частицы располагались на сравнительно небольшом расстоянии друг от друга, и, следовательно, условия применимости теории Ми не соблюдались, такое согласие между теорией и экспериментом можно считать вполне удовлетворительным.

Еще одну возможность сопоставления наших расчетов с результатами экспериментов, проводимых с использованием (для усиления рамановского рассеяния) золотых наночастиц дает работа [21]. Схема проведения эксперимента была такой же, как и в предыдущем примере. Здесь (с помощью лазера с λ = 632.8 нм) измерялась интенсивность рамановского рассеяния для двух полос (с максимумами при ν = 1078 см^–1 и ν = 1594 см^–1) 4-меркаптобензойной кислоты адсорбированной на поверхности золотых частиц с радиусами 15, 20, 25, 30, 40 и 45 нм. Эти частицы находились во взвешенном состоянии в водной среде, причем, как и в предыдущем случае, расстояние между ними было не слишком велико. Авторы [21] нашли, что для обеих упомянутых выше полос максимальные интенсивности рамановского рассеяния достигались при значениях a = 45 нм, а рассчитанное нами a($Q_{{nf}}^{{{\text{max}}}}$) = 54 нм. Таким образом, отличия в значениях a и a($Q_{{nf}}^{{{\text{max}}}}$) лежат в пределах 20%. Снова, учитывая, что здесь расстояние между частицами было относительно небольшим, согласие между измерениями, выполненными в [21], и результатами наших вычислений, можно считать удовлетворительным. Более того, близость экспериментально найденных и рассчитанных значений радиусов золотых наночастиц позволяет, на наш взгляд, использовать значения a($Q_{{nf}}^{{{\text{max}}}}$) (в качестве первого приближения) при планировании экспериментов, целью которых является максимальное усиление интенсивности рамановского рассеяния молекул, находящихся на поверхности сферических наночастиц с высокой проводимостью.

Таким образом, проведенные нами расчеты выявили ряд закономерностей, присущих поведению функций $Q_{{nf}}^{{{\text{max}}}}$(λ, n), a($Q_{{nf}}^{{{\text{max}}}}$(λ, n)), a($Q_{{nf}}^{{{\text{max}}}}$(λ, n))/λ и 2πna($Q_{{nf}}^{{{\text{max}}}}$(λ, n))/λ в достаточно широком спектральном диапазоне. Изучив спектральное поведение этих величин, мы выявили возможности их потенциального практического применения. Тем не менее, на наш взгляд, существуют и другие, не столь очевидные перспективы использования найденных зависимостей. Речь идет о том, что с их помощью можно попытаться понять некоторые конкретные особенности взаимодействия плоской электромагнитной волны с изучаемой наночастицей. Дело в том, что выражения (3), (4), с помощью которых находятся Q_nf и Q_r, достаточно сложны, и возможности их детального количественного анализа весьма ограничены. Здесь ситуация аналогична той, что существует при анализе рядов, входящих в выражения для эффективностей рассеяния и экстинкции [3]. В этих случаях проводится поиск тех значений λ, при которых знаменатели отдельных членов ряда близки к нулю и поэтому данные слагаемые вносят заметный (а зачастую и доминирующий) вклад в Q_E и Q_sca. В то же время, мы полагаем, что из вида и конкретных численных значений, полученных нами кривых $Q_{{nf}}^{{{\text{max}}}}$(λ), можно попытаться получить дополнительную информацию о механизме взаимодействия волны и частицы.

Стоит напомнить, что наибольшие величины $Q_{{nf}}^{{{\text{max}}}}$ приходятся как раз на те участки графиков $Q_{{nf}}^{{{\text{max}}}}$(λ), в которых мы увидели асимметричные кривые резонансного типа. Такие зависимости хорошо изучены и эффективно описываются с помощью небольшого числа параметров с ясным физическим смыслом [22]. Напомним также, что наиболее, на наш взгляд, интересным является поведение всех этих кривых на их восходящих участках, причем в достаточно узком (от 500 до 520 нм) интервале длин волн. Именно здесь наблюдается инверсия зависимостей $Q_{{nf}}^{{{\text{max}}}}$(λ) относительно n, а величины a($Q_{{nf}}^{{{\text{max}}}}$(λ)) достигают минимальных значений.

Следует подчеркнуть еще одно важное обстоятельство, связанное с перспективами дальнейшего использования предложенного в статье подхода. Проведенные расчеты (результаты которых здесь не приводятся) показывают, что в поведении функций Q_E и Q_sca проявляются закономерности, аналогичные обнаруженным при изучении Q_nf и Q_r. Говоря конкретнее, при заданных λ и n зависимости Q_E и Q_sca от a также представляют собой гладкие кривые с максимумом. Таким образом, как и в случае Q_nf, имея набор таких кривых, можно найти как сами максимальные величины эффективности экстинкции и рассеяния, так и соответствующие им значения радиуса частицы. Для найденных таким способом значений a можно с помощью формул (5), (6) определить спектральное поведение функций $Q_{E}^{{{\text{max}}}}$(λ) и $Q_{{sca}}^{{{\text{max}}}}$(λ) для разных n. Стоит, однако, отметить, что практическое применение этих результатов пока не вполне ясно.

Несколько иная ситуация характерна для эффективности поглощения Q_abs, численные значения которой находятся с помощью выражения

Сферические наночастицы благородных металлов достаточно давно и успешно используются для нагревания окружающей их среды [23]. Следовательно, построение спектральных зависимостей функций $Q_{{abs}}^{{{\text{max}}}}$(λ) поможет более эффективному решению проблем этой области наноплазмоники.

ЗАКЛЮЧЕНИЕ

Таким образом, проведенное исследование позволило выявить ряд закономерностей, присущих поведению функций $Q_{{nf}}^{{{\text{max}}}}$(λ, n), a($Q_{{nf}}^{{{\text{max}}}}$(λ, n)), в достаточно широком, практически значимом спектральном диапазоне. Полученные результаты представляют, по нашему мнению, существенный интерес как с точки зрения развития фундаментальных исследований в области наноплазмоники, так и при решении прикладных задач, связанных, например, с использованием лазерной абляции поверхности различных материалов [9, 16, 24, 25], или усиления интенсивности рамановского рассеяния с помощью сферических металлических наночастиц с высокой проводимостью [26].

Авторы благодарят В.М. Рудого за инициирование данной работы, плодотворное обсуждение полученных результатов и помощь при подготовке статьи к печати.