Физикохимия поверхности и защита материалов, 2020, T. 56, № 5, стр. 451-458

ВВЕДЕНИЕ

Расчет поверхностных характеристик многокомпонентных твердых растворов сплавов представляет интерес для многих физико-химических процессов [1, 2]. Среди них наибольший интерес представляет поверхностное натяжение (ПН). Это понятие было введено Гиббсом в основах термодинамики [3] и до настоящего времени является предметом многих обсуждений и трактовок [4–10]. Вопросам расчета ПН было посвящено много теоретических работ, но и до настоящего времени он остается актуальным. Во многом это связано с относительно малым числом измерений поверхностного натяжения твердых тел по сравнению с их измерениями для паро-жидкостных систем.

ПН рассматривается как для твердого тела в целом, так и для отдельных его зерен. ПН зерен чистых металлов и сплавов является важнейшей их характеристикой при рассмотрении разных процессов равновесия и при рассмотрении разнообразных кинетических процессов: зарождения новой фазы, сегрегации примесей на границах, роста и диффузии границ зерен и так далее [11–15].

Развитие моделей имеет значение в интерпретации экспериментальных данных по поверхностным свойствам твердых растворов. В работе [16] дано краткое описание состояния теории, и сделан шаг в ее развитии в связи с переходом на упорядоченные смеси. В данной работе дан конкретный пример использования подхода [16] для расчета поверхностных характеристик упорядоченных бинарных твердых растворов. В основе теории находится модель решеточного газа (МРГ), которая хорошо известна в литературе, и которая активно использовалась в расчетах поверхностного натяжения твердых и жидких растворов [17–20].

Объемная фаза. Ограничимся рассмотрением простейшей бинарной упорядоченной системы, содержащей в объемной фазе две взаимопроникающие подрешетки: простые кубические решетки (z = 6) или ОЦК решетки (z = 8) типа β-латуни (здесь z – число ближайших соседей любого узла решетки). Первую подрешетку, узлы которой заняты преимущественно компонентом А, обозначим через α, вторую подрешетку, узлы которой преимущественно заняты компонентом В, обозначим через β. Каждый узел α-подрешетки окружен узлами β-подрешетки, и наоборот. Это позволяет задать упорядоченное состояние частиц с помощью введенных в [16] функций распределений узлов разного типа: k_α= k_β= 1/2, и z_αβ= z_βα= z. В системе находится s компонентов смеси i (i = A, B и V – вакансии, обозначаемые символом число компонентов s = 3 включает вакансии). Для простоты будем считать, что энергетические параметры не зависят от типов узлов, на которых находятся компоненты смеси.

Обозначим через θ_γ (γ = α, β) вероятность заполнения узлов типа γ. Будем учитывать взаимодействия между ближайшими соседями. Уравнения [16] на локальные заполнения узлов разного типа в однородной объемной фазе (внутренние степени свободы частиц и их параметры взаимодействия не зависят от типа узла подрешетки) запишутся как

где $\theta _{{\alpha \beta }}^{{ij}}$ – вероятность нахождения пары частиц ij рядом, причем компонент i находится в ячейке α, а компонент j находится в ячейке подрешетки β. Аналогично выписывается уравнение (1) для подрешетки β. Величины $a_{\gamma }^{i}{{P}_{i}}$ фиксируют значения химических потенциалов компонентов i в ячейках подрешетки γ (γ = α, β). Величина Pⁱ – равновесное давление компонента i.

Граница раздела фаз. Переходная область между твердым раствором и паром представлена в виде многослойной области с переменной плотностью компонентов. Это означает, что внутри слоя выделяются два типа узлов, соответствующих двум типам подрешеток в одинаковой пропорции. Поэтому каждый узел решетки f будет характеризоваться двумя индексами (f = γ, q): типа подрешетки (γ = α, β) и номер слоя q (1 ≤ q ≤ κ).

Распределение компонентов смеси i (i = A, B и V – вакансии, обозначаемые символом число компонентов s = 3 включает вакансии) в слое q подрешетки γ (γ = α и β) границы раздела фаз $\theta _{{q\left( \gamma \right)}}^{i}$, 2 ≤ q ≤ κ – 1, описывается в квазихимическом приближении следующей системой уравнений

где узел $p\left( {\gamma {\kern 1pt} '} \right)$ подрешетки $\gamma {\kern 1pt} '$, $\gamma {\kern 1pt} ' \ne \gamma $, принадлежит окружению $G\left( {q\left( \gamma \right)} \right)$ узла $q\left( \gamma \right)$. Величины $a_{{q\left( \gamma \right)}}^{i}P_{{}}^{i}$ фиксируют значения химических потенциалов компонентов i в ячейках q(γ). Как и выше величина Pⁱ – равновесное давление компонента i. Для объемной фазы величина $a_{{q\left( \gamma \right)}}^{i}$, представляющая собой коэффициент удерживания частицы i узлом решеточной системой типа q или аналог парциального коэффициента Генри в адсорбции, определяется как отношение $a_{{q\left( \gamma \right)}}^{i} = F_{{q\left( \gamma \right)}}^{i}/F_{i}^{0}$ статсумм молекулы в решеточной структуре ($F_{{q\left( \gamma \right)}}^{i}$) и в объемной фазе ($F_{i}^{0}$).

Здесь ${\text{ }}\Lambda _{{q\left( \gamma \right)}}^{i}$ – функция неидеальности в квазихимическом приближении; β = (R_BT)^–1; R_B – газовая постоянная; $\theta _{{q\left( \gamma \right)p\left( {\gamma {\kern 1pt} '} \right)}}^{{ij}}$ – вероятность нахождения пары рядом, причем компонент i находится в ячейке слоя q подрешетки γ, а компонент j находится в ячейке слоя p подрешетки $\gamma {\kern 1pt} '$; $t_{{q\left( \gamma \right)p\left( {\gamma {\kern 1pt} '} \right)}}^{{ij}} = {{\theta _{{q\left( \gamma \right)p\left( {\gamma {\kern 1pt} '} \right)}}^{{ij}}} \mathord{\left/ {\vphantom {{\theta _{{q\left( \gamma \right)p\left( {\gamma {\kern 1pt} '} \right)}}^{{ij}}} {\theta _{{q\left( \gamma \right)}}^{i}}}} \right. \kern-0em} {\theta _{{q\left( \gamma \right)}}^{i}}}$ – условная вероятность нахождения молекулы сорта j в ячейке слоя p подрешетки $\gamma {\kern 1pt} '$ рядом с частицей i в ячейке слоя q подрешетки γ; ${{\varepsilon }^{{ij}}}$ – энергия взаимодействия частиц сорта i и j, описываемая потенциальной функцией Леннард–Джонса: ${{\varepsilon }^{{ij}}} = 4\varepsilon _{{ij}}^{0}\{ {{({{{{\sigma }_{{ij}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{ij}}}} r}} \right. \kern-0em} r})}^{6}}$ – ${{\left( {{{{{\sigma }_{{ij}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{ij}}}} r}} \right. \kern-0em} r}} \right)}^{{12}}}\} $, где σ_ij и $\varepsilon _{{ij}}^{0}$ – параметры, характеризующие расстояние между твердыми несжимаемыми сферами молекул сорта i и j и глубину потенциальной ямы соответственно. Для ближайших соседей ${{\varepsilon }^{{ij}}} = \varepsilon _{{ij}}^{0}$. Символ s относится к вакансиям; взаимодействия с вакансиями равны нулю ${{\varepsilon }^{{sj}}} = \varepsilon _{{ij}}^{0} = 0$.

О РЕШЕНИИ СИСТЕМ УРАВНЕНИЙ РАВНОВЕСНОГО РАСПРЕДЕЛЕНИЯ КОМПОНЕНТОВ

Решение системы (3) и (4) (аналогично системы (1) и (2)) предполагает использование нормировочных связей на унарные $\sum\nolimits_{i = 1}^s {\theta _{{q\left( \gamma \right)}}^{i}} = 1$ и парные $\sum\nolimits_{j = 1}^s {\theta _{{q\left( \gamma \right)p\left( {\gamma {\kern 1pt} '} \right)}}^{{ij}}} = \theta _{{q\left( \gamma \right)}}^{i}$ функции. Редуцирование этих систем для равновесного состояния смеси обсуждается в [16, 21]. Суть редуцирования состоит в том, что уравнения на парные функции (2) и (4) обращаются в тождество с помощью замены переменных

где новые переменные $u_{{q(\gamma )p(\gamma {\kern 1pt} ')}}^{i} = t_{{p(\gamma {\kern 1pt} ')q(\gamma )}}^{{si}}$ являются нормированными: $\sum\nolimits_{i = 1}^s {u_{{q(\gamma )p(\gamma {\kern 1pt} ')}}^{i}} = 1$. Тогда в новых переменных решается только система уравнений на функции $u_{{q(\gamma )p(\gamma {\kern 1pt} ')}}^{i}$.

Адекватность текущего приближения для искомых $u_{{q(\gamma )p(\gamma {\kern 1pt} ')}}^{i}$ в ходе итераций и полученных по ним значений унарных $\theta _{{q\left( \gamma \right)}}^{i}$ и парных $\theta _{{q\left( \gamma \right)p\left( {\gamma {\kern 1pt} '} \right)}}^{{ij}}$ функций проверяется выполнением ряда условий, вид которых зависит от поставленной задачи. В ходе анализа рассматриваются две задачи:

а) Расчет изотермической связи плотности и давления в объемной фазе (κ = 1). В этом случае ставятся следующие условия: 1) равенство соотношения давлений $P_{{}}^{i}$ компонентов соотношению заданных долей x_i (доли давлений компонентов от общего давления системы): $\frac{{{{P}_{i}}}}{{{{P}_{j}}}} = \frac{{{{x}_{i}}}}{{{{x}_{j}}}},$ $i \ne j \ne s,\,\,q = 1$. 2) равенство суммы локальных плотностей компонентов плотности брутто: $\sum\nolimits_{\gamma = \alpha ,\beta } {{{k}_{\gamma }}} \sum\nolimits_{i = 1}^{s - 1} {\theta _{q}^{i} = \theta } $.

Всего система в этой задаче состоит из 2(s – 1) числа уравнений.

б) Расчет концентрационного профиля переходной области жидкость–пар (κ > 2) – для него ставятся следующие условия: 1) равенство давления$p_{{q\left( \gamma \right)}}^{i}$, вычисленного через локальные плотности по опорным парам, равновесному давлению ${{P}_{i}}$, определенному через изотерму сосуществующих фаз:

Это условие ставится для опорных пар q(γ)p*(γ') монослоев q, 2 ≤ q ≤ (κ – 1). Для монослоев q = 1, κ оно априори выполняется из изотермы сосуществования объемных фаз. Всего условие образует 2(κ – 2)(s – 1) число независимых уравнений. 2) однозначность определения давления через различные пары:

Это условие ставится для остальных пар q(γ)p(γ') монослоев q, 1 ≤ q ≤ κ. Условие образует 2(${{N}_{{qp}}}$ – κ) · · (s – 1) независимых уравнений, ${{N}_{{qp}}}$ – число различных пар qp.

Таким образом, в общем случае решается система из 2(${{N}_{{qp}}}$ – 2) · (s – 1) числа уравнений с неизвестными $u_{{q(\gamma )p(\gamma {\kern 1pt} ')}}^{i}$, 1 ≤ i ≤ s – 1, которая решалась итерационным методом Ньютона, $N$ – число пар по монослоям и подрешеткам, с неизвестными $u_{{q\left( \gamma \right)p\left( {\gamma {\kern 1pt} '} \right)}}^{i}$, 1 ≤ i ≤ s – 1. Точность решения по плотностям не ниже 0.1–0.01%.

Найденные распределения $\theta _{{q\left( \gamma \right)}}^{i}$ используются для расчета как всех термодинамических характеристик в объемной фазе и внутри переходной области, так и структурных характеристик строения шероховатой поверхности твердого тела на границе с его паром.

ПОВЕРХНОСТНЫЕ ХАРАКТЕРИСТИКИ

По концентрационному профилю рассчитываются среднее давление π_q в монослое q и поверхностное натяжение σ [22]:

Избыточная свободная энергия поверхности F_b = U_b – TS_b, S_b – энтропия, как и внутренняя энергия U_b определяются через концентрационный профиль:

где ${{f}_{q}}$ – доля узлов монослоя q от общего числа узлов в переходной области, 2 ≤ q ≤ κ – 1, $F_{q}^{{}} = {{U}_{q}} - T{{S}_{q}}$ – локальная свободная энергия в слое q, где ${{\Delta }_{{qp}}}$ – символ Кронекера, обращающийся в единицу, если p = q, иначе равный нулю.

По концентрационному профилю рассчитываются структурные характеристики строения шероховатой поверхности твердого тела на границе с его паром.

Удельная поверхность (площадь поверхности 1 г адсорбента) рассчитывается как ${{S}_{m}}$ = $ = {{M_{{mon}}^{V}\lambda _{{}}^{2}{{N}_{{\text{A}}}}} \mathord{\left/ {\vphantom {{M_{{mon}}^{V}\lambda _{{}}^{2}{{N}_{{\text{A}}}}} {\left( {{{N}_{{ads}}}{{M}_{{\text{A}}}}} \right)}}} \right. \kern-0em} {\left( {{{N}_{{ads}}}{{M}_{{\text{A}}}}} \right)}}$, где N_A – число Авогадро, M_A – молярная масса адсорбента, λ – межмолекулярное расстояние для адсорбента, N_ads – общее число частиц адсорбента, $M_{{mon}}^{V}$ – общее число адцентров на поверхности адсорбента [23, 24]:

где ${{N}_{{tr}}}$ – общее число ячеек переходной области адсорбента; ${{\Delta }_{{0{{m}_{q}}}}}$ – символ Кронекера, обращающийся в ноль, если узел примыкает к адсорбенту (${{m}_{q}} = \sum\nolimits_p {{{m}_{{qp}}}} > 0$), иначе равный единице; $\Theta _{{q\left( \gamma \right)}}^{V}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right)$ – вероятность того, что узел принадлежит типу ($q\left( \gamma \right)$,{m_qp}), т.е. выполняются следующие события: а) узел лежит в монослое q подрешетки γ, б) узел является свободным от частиц адсорбента, вероятность чего задается локальной плотностью $\theta _{q}^{V}$, в) в каждом соседнем монослое p подрешетки $\gamma {\kern 1pt} '$ расположено заданное число частиц адсорбента m_qp, вероятность чего для отдельного монослоя p задается условной функцией ${{\left( {t_{{q\left( \gamma \right)p\left( {\gamma {\kern 1pt} '} \right)}}^{{VA}}} \right)}^{{{{m}_{{qp}}}}}}$, соответственно остальные узлы – вакансии с вероятностью ${{\left( {t_{{q\left( \gamma \right)p\left( {\gamma {\kern 1pt} '} \right)}}^{{VV}}} \right)}^{{{{z}_{{qp}}} - {{m}_{{qp}}}}}}$. В итоге, получаем вероятность того, что выбранный узел в адсорбционном объеме принадлежит типу (q$\left( \gamma \right)$,{m_qp}): где $C_{{{{z}_{{qp}}}}}^{{{{m}_{{qp}}}}}$ – число сочетаний m_qp частиц адсорбента по z_qp ячейкам монослоя p.

Если нормировать величину $M_{{mon}}^{V}$ на число ячеек в переходной области ${{N}_{{tr}}}$, то получаем число адцентров на поверхности адсорбента, приходящееся на единицу поверхности раздела фаз ${{S}_{n}} = {{M_{{mon}}^{V}} \mathord{\left/ {\vphantom {{M_{{mon}}^{V}} {{{N}_{{tr}}}}}} \right. \kern-0em} {{{N}_{{tr}}}}}$. Данная характеристика ${{S}_{n}}$ будет использоваться далее при описании шероховатой поверхности как оценка удельной поверхности.

В переходной области двухкомпонентного сплава возможна сегрегация одного из примесного компонента, которую будем оценивать в процентах. Сегрегация компонента i на подрешетке γ в среднем по переходной области:

где $\Gamma _{{q\left( \gamma \right)}}^{i}$ – сегрегация компонента i в монослое q переходной области подрешетки γ.

В переходной области на поверхности твердого тела образуются столбцы разной высоты h, 1 ≤ ≤ h ≤ κ – 2. Вероятность образования столбца высотой h в среднем по подрешеткам α и β составляет:

где $q\left( \delta \right) = q\left( \gamma \right)$, если монослой q четный, и $q\left( \delta \right) = q\left( {\gamma {\kern 1pt} '} \right)$, если монослой q нечетный. В выражении (12) первая скобка определяет вероятность, что в первом монослое переходной области q = 2, т.е. в основании столбца, есть частица А или В; следующий знак произведения дает вероятность того, что и на всех узлах выше основания столбца вплоть до q = h также находится частица А или В; следующая скобка и последующий знак произведения определяют вероятность того, что на всех уздах выше монослоя q = h располагаются вакансии.

Среднее число адцентров на столбце высотой h в переходной области шириной (κ – 2) составляет:

где второй знак суммы дает сумму вероятностей того, что на площадке из монослоя q столбика высотой h располагается вакансия, т.е. она доступна для адсорбции; единица в конце выражения (14) дает еще один адцентр на вершине столбца, вероятность свободы которого от частиц А и В задается в общей вероятности столбца высотой h, ${{P}_{h}}$.

Таким образом, далее мы будем описывать шероховатую поверхность твердого тела следующими характеристиками строения поверхности: ${{S}_{n}}$, ${{P}_{h}}$, ${{S}_{h}}$ и $\Gamma _{\gamma }^{i}$.

РЕЗУЛЬТАТЫ РАСЧЕТОВ

Рассматривается модельный равновесный бинарный раствор компонентов А и В (с парными энергетическими параметрами взаимодействия ε_АА = 1, ε_ВВ = 0.8ε_АА и ε_АВ = 4.5(ε_АА + ε_ВВ)/2). Распределения компонентов рассчитываются на вложенных друг в друга подрешетках α и β, образующих примитивную кубическую решетку. P^A : : P^В = 1 : 1. Варьируются соотношение давлений компонентов сплава P^A : P^В и приведенная температура системы τ, τ = T/T_cr, где T, T_cr – температура в системе и критическая температура расслаивания. Расчет проведен вблизи температуры кристаллизации.

На рис. 1 показаны концентрационные профили плотности в переходной области компонента А (кривые 1–3) на подрешетках α (рис. 1а, 1в) и β (рис. 1б, 1г) и компонента В (кривые 4–6) на подрешетках α (рис. 1б, 1г) и β (рис. 1а, 1в).

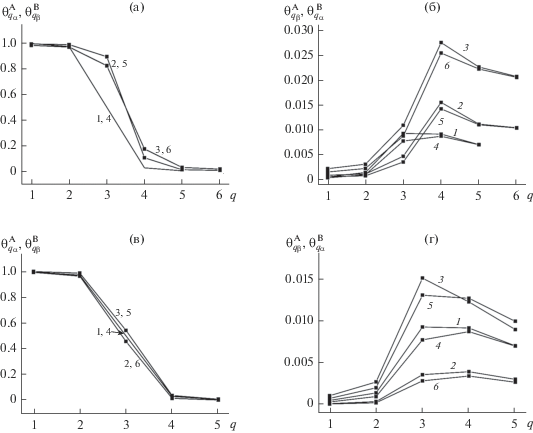
Рисунки 1а, 1б построены при парциальном давлении компонента А P^A/P = 0.5 и при вариации приведенной температуры τ = 0.45 (кривые 1 и 4), 0.49 (2 и 5) и 0.55 (3 и 6). Рисунки 1в, 1г построены при вариации парциального давлении компонента А P^A/P = 0.5 (кривые 1 и 4), 0.2 (2 и 5) и 0.8 (3 и 6) и при приведенной температуре τ = 0.45.

На рис. 1а при заданной температуре концентрационные профили компонента А на α и компонента В на β практически совпали: кривые 1 и 4, 2 и 5, 3 и 6. Это следствие того, что мы наблюдаем компоненты, преобладающие на соответствующих решетках, при P ^A : P^В = 1 : 1 и малой разнице между ε_АА и ε_ВВ по сравнению с ε_АВ, что приводит к близким концентрациям А и В в переходной области. Более ощутима разница в концентрационных профилях компонента В на α и компонента А на β на рис. 1б, где данные компоненты являются примесными на соответствующих решетках. Согласно рис. 1а, 1б увеличение температуры увеличивает ширину переходной области, а концентрация обоих компонентов в переходной области возрастает со стороны пара и убывает со стороны жидкости.

Рисунок 1в демонстрирует, что с нарушением соотношения давлений P ^A : P^В = 1, начинают различаться концентрационные профили компонента А на α и компонента В на β. Но при этом совпали профили компонента А на α при P^A/P = = 0.2 (кривая 2) и компонента В на β при P^A/P = = 0.8 (кривая 6) и профили А на α при P^A/P = 0.8 (кривая 3) и компонента В на β при P^A/P = 0.2 (кривая 5). Это также следствие близости ε_АА и ε_ВВ по сравнению с ε_АВ. Увеличение давления P^A увеличивает концентрации компонента А во всей переходной области на обеих подрешетках: на подрешетке α на рис. 1в кривая 3 при P ^A/P = 0.8 лежит выше всех, а кривая 2 P ^A/P = 0.2 ниже всех. Концентрация компонента В соответственно уменьшается при этом во всей переходной области на обеих подрешетках.

На рис. 2 показаны зависимости от высоты столбика h в переходной области вероятности его образования P_h (рис. 2а, 2в) и среднее число адцентров S_h (рис. 2б, 2г) на столбике (значения усреднены по подрешеткам α и β). Рисунки 1а, 1б построены при парциальном давлении компонента А P^A/P = 0.5 и при вариации приведенной температуры τ = 0.45 (кривая 1), 0.49 (2) и 0.55 (3). Рисунки 1в, 1г построены при вариации парциального давления компонента А P^A/P = 0.5 (кривая 1), 0.2 (2) и 0.8 (3) и при приведенной температурt τ = 0.45.

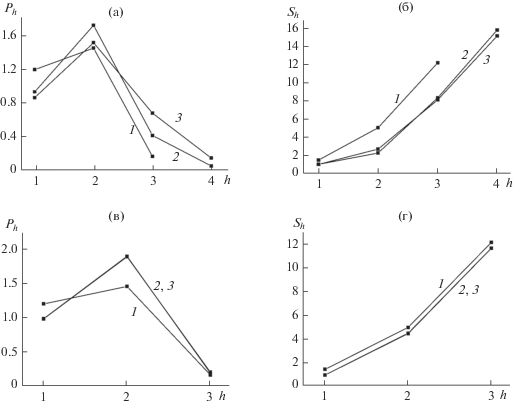
Рисунки 2а, 2в показывает, что наиболее вероятно образование столбиков средней высоты h = 2. Высота h = 1 менее вероятна, так как мала вероятность наличия вакансий в следующих монослоях. Высота h = 3 и 4 менее вероятна, так как мала вероятность наличия частиц А или В в монослоях переходной области со стороны пара.

Согласно рис. 1а увеличение температуры уменьшает вероятность образования малых столбцов высотой h = 1 и увеличивает вероятность образования больших столбцов высотой h ≥ 3, так как увеличивается концентрация компонентов со стороны пара и уменьшается со стоны жидкости. На столбцы высотой h = 2 максимальной вероятности образования изменение температуры сказывается неоднозначным образом из-за наложения двух упомянутых факторов.

Рисунки 2б, 2г демонстрируют увеличение среднего числа адцентров S_h на столбике с ростом его высоты h. Согласно рис. 2б рост температуры с уменьшением ширины переходной области сильно увеличивает S_h столбиков любой высоты h, а при постоянной ширине переходной области увеличивается S_h только у высоких столбиков, а у маленьких убывает.

Из рис. 2г следует, что равное соотношение давлений компонентов А и В (кривая 1) обеспечивает максимальные значения S_h для столбцов любой высоты h. А при P^A/P = 0.2 (кривая 2) и 0.8 (3) кривые совпали, в виду малой разницы между ε_АА и ε_ВВ по сравнению с ε_АВ при противоположности соотношений давлений.

Для рассмотренных систем с заданным парциальным давлением компонента А P ^A/P при заданной приведенной температуре τ в табл. 1 представлены данные:

– среднее число адцентров в переходной области, приходящее на единицу площади границы раздела фаз, ${{S}_{n}}$,

– сегрегация компонента i на подрешетках α и β в среднем по переходной области, ${\text{Г}}_{\alpha }^{i}$ и ${\text{Г}}_{\beta }^{i}$ ,

– безразмерная величина поверхностного натяжения на границе твердого тела, σβλ²,

– безразмерные величины избыточной свободной энергии поверхности, βF_b и внутренней энергии переходной области, βU_b.

Согласно табл. 1 среднее число адцентров в переходной области ${{S}_{n}}$, являющееся мерой удельной поверхности, убывает с уменьшением температуры T и с увеличением давления парциального давления одного из компонентов, нарушающим соотношение примерно P ^A : P^В = 1 : 1. Соотношение 1 : 1 обосновано тем, что энергии ε_АА и ε_ВВ практически совпадают друг с другом по сравнению с ε_АВ. Варьирование значений ε_АА и ε_ВВ и увеличение разницы между ними будет менять соотношение (P ^A : P^В)*, обеспечивающее максимальное значение ${{S}_{n}}$.

Для рассмотренной системы получены сегрегации компонента A на подрешетке β и компонента В на подрешетке α, так как данные компоненты образуют примеси на соответствующих подрешетках. Сегрегации обоих компонентов на соответствующих подрешетках растут с убыванием температуры. С увеличением парциального давления A, P ^A/P, величина ${\text{Г}}_{\beta }^{{\text{A}}}$ растет, а величина ${\text{Г}}_{\alpha }^{{\text{B}}}$ убывает.

Поверхностное натяжение σβλ², избыточная свободная энергия βF_b и внутренняя энергия βU_b переходной области растут с уменьшением температуры и с отклонением состава сплава от соотношения (P ^A : P^В)*, при котором наблюдалось максимальное значение ${{S}_{n}}$. Таким образом, соотношение (P ^A : P^В)* также обеспечивает минимальные значения поверхностного натяжения, избыточной свободной энергии и внутренней энергии.

ЗАКЛЮЧЕНИЕ

Разработана методика расчета равновесных поверхностных характеристик, включая поверхностную энергию и поверхностного натяжения, в системах твердое тело–пар для бинарных твердых растворов разной степени упорядоченности на базе МРГ. Предварительно необходимо найти концентрационные профили компонентов раствора вблизи плоскости разделa фаз. Найденные концентрационные профили могут быть использованы для расчета всего спектра структурных поверхностных характеристик для анализа степени шероховатости рассматриваемой границы раздела фаз. Попутно можно оценить степень поверхностной сегрегации компонентов раствора, и характер исчезновения упорядочения вблизи границы. Такая информация важна для кинетики различных поверхностных процессов.

Работа выполнена в рамках государственного задания ИОНХ РАН в области фундаментальных научных исследований.