Физикохимия поверхности и защита материалов, 2022, T. 58, № 4, стр. 339-349

1. ВВЕДЕНИЕ

Объемные свойства сегнетоэлектриков изучаются более семидесяти лет [1–7]. При понижении температуры сегнетоэлектрики переходят в состояние спонтанной поляризации, которое связано с процессами упорядочения ионов в решетках многоатомных кристаллов, состоящих из двух, трех и более сортов атомов ионов. Процессы упорядочения ионов в сегнетоэлектриках традиционно разделяются на два типа в зависимости от механизма формирования упорядоченного состояния: смещение мягких подрешеток в поле потенциала жестких подрешеток (сегнетоэлектрики смещения) и перераспределение отдельных ионов между эквивалентными положениями вблизи других подрешеток (сегнетоэлектрики порядок-беспорядок). Соответственно, при понижении температуры ниже критической Т_crit сегнетоэлектрики делятся на два типа в зависимости от типа реализуемого фазового перехода: смещения и порядок – беспорядок.

Поверхностные свойства и размерные зависимости сегнетоэлектриков изучаются порядка тридцати лет. Это изучение размерных эффектов началось с поиска критического размера толщины полимерных пленок. Было получено, что сегнетоэлектрические пленки обладают фазовым переходов до толщин порядка 1 нм. Этот переход является фазовым переходом первого рода, а также дополнительно был найден новый фазовый переход, который реализуется в поверхностных слоях пленок [8, 9].

Аналогичные фазовые переходы рассматривались в других сегнетоэлектрических наноструктурах, в частности в перовскитных (сегнетоэлектрики типа смещения) пленках [10, 11]. Много внимания уделялось проводящим монокристаллам, допированным разными добавками, гетероструктурам на основе пленок ВаТiО₃ (n-типа), проводящим композитам, и композитам на основе пористых металлических матриц с внедренными сегнетоэлектриками типа KNO₃, NaNO₂ и другими (см. например, [12–20]). Во многом эти работы обусловлены прикладной направленностью в области физической электроники и к многочисленным электрофизическим приложениям. Поэтому следует также указать на работы, в которых более конкретно рассматриваются взаимосвязи между свойствами сегнетоэлектрических материалов с поверхностными процессами [21, 22], например, влияние химического состава окружающей среды на сегнетоэлектрические свойств пленок. Так в [21], было экспериментально продемонстрировано, что сегнетоэлектрические поверхности с противоположной полярностью по-разному адсорбируют молекулы. В работе [22] наблюдался обратный эффект – химическое окружение определяет ориентацию электрической поляризации пленки сегнетоэлектрика, как это обычно наблюдается под электрическим напряжением. В этом случае в системе вместо вариации электрического поля менялась величина давления окружающего газа (кислорода в [22]).

Также для перовскитов впервые были проведены эксперименты по определению критического размера отдельных частиц [23–29]. Аналогичные данные по композитам для сегнетоэлектриков типа порядок-беспорядок в пористых матрицах имеются в меньшем количестве (см. например, [30, 31]). Для отдельных наночастиц таких данных авторы не встретили.

Как правило, все эксперименты для сегнетоэлектриков [12–16, 30, 32–38] трактуются с позиции феноменологической теории Ландау [39–44], в которой отсутствует учет эффектов корреляции взаимодействующих частиц. Однако, для сегнетоэлектриков типа порядок – беспорядок часто используются более точные методы статфизики, основанные на модели Изинга [3, 45, 46], которые традиционно применяются для других упорядоченных систем (сплавы, растворы, адсорбированные частицы и т.д.) [47–53 ]. Модель Изинга эквивалентна модели решеточного газа (МРГ) [45, 46, 54]. С помощью МРГ впервые было исследовано влияние размера ограниченного по объему домена на величину критической температуры T_crit упорядочения бинарного сплава АВ стехиометрического состава А : В = 1 : 1 [55, 56]. Согласно этой эквивалентности в работах [55, 56] эти результаты также относятся к исследованию на микроскопическом уровне влияния размера домена в сегнетоэлектриках типа порядок-беспорядок на величину критической температуры T_crit(L), где L – сторона кубического домена. Было получено, что уменьшение размера домена уменьшает критическую температуру T_crit, а также исследовано влияние внешнего поля на значения T_crit и учета эффекта непрямых корреляций. Привлечение МРГ к сегнетоэлектрикам порядок – беспорядок впервые позволило вывести анализ размерных эффектов в сегнетоэлектриках типа порядок – беспорядок с фазовым структурным переходом второго рода на уровень микроскопического анализа фазовых переходов первого рода [57].

В данной работе техника МРГ использована для расчета на микроскопическом уровне свойств межфазных границ внутри сегнетоэлектриков типа смещения и на их внешней границе с паром. Соответствующая модель сегнетоэлектрика типа смещения на основе МРГ предложена в работе [58]. Эта модель основана на концепции о двух-ямном потенциале, в котором смещаются ионы мягкой подрешетки. Эти смещения отражают процесс перераспределения ионов, приводящих к появлению спонтанной поляризации сегнетоэлектрика, в рамках простейшей “одно-ионной модели” сегнетоэлектрика смещения АВ: распределения ионов мягкой подрешетки А происходят в поле жесткой подрешетки В [6].

Традиционно межионные взаимодействия описываются с помощью эффективных парных потенциалов или потенциалов электростатического взаимодействия [1–7]. При этом часто вводят представления, уменьшающие величину энергии кулоновского потенциала: используют понятия о долях ковалентности связей в ионных кристаллах (стр. 9 [2]) или о долях энергии деполяризации [2, 59] при формировании доменов: этот путь дает уменьшение энергии деполяризации на 2–3 порядка (стр. 100 [2]). Современные представления о расчете энергий межионных взаимодействий приводят к не менее проблемным построениям, поэтому в работе [58] были использованы эффективные парные потенциалы, определяемые по известным экспериментальным данным.

Расчет межионных распределений в данной работе проводится в квазихимическом приближении (КХП), учитывающем прямые корреляции между ионами. При использовании эффективных парных потенциалов требуется их нахождение по известным экспериментальным данным о каких-либо характеристиках. Часто для этой цели привлекают величину Т_crit, что также использовано ниже. Энергетические параметры получаются при описании известной величины T_crit для объемной фазы [1, 7, 23] (раздел 2). Далее эта информация используется для расчета свойств межфазных границ (раздел 3) и для размерной зависимости Т_crit(L) в отдельных наночастицах (граница сегнетоэлектрик – паровая фаза) (раздел 4).

2. ОБЪЕМНАЯ ФАЗА

Одно-ионная модель сегнетоэлектрика соответствует стехиометрическому веществу АВ с двумя вложенными друг в друга подрешетками. Обозначим подрешетку с жесткими ионами В как подрешетку β (ее узлы располагаются в центре соответствующих одноименных ячеек β). Другая подрешетка относится к ячейкам с мобильными ионами А, которые находясь в двух-ямном потенциале, формируют две свои подрешетки α и γ, равноудаленных от центра ячейки f вдоль одной из осей системы – это ось поляризации. Подрешетка для ионов А состоит из двух подрешеток для локальных минимумов потенциала [58]. Каждый из узлов подрешеток α и γ может быть заполнен ионом А.

Реальная двухкомпонентная система дополнительно содержит вакансии. Общее число состояний занятости узлов решетки отвечает частицам i = A, B, V, где V – вакансии, а вся рассматриваемая решетка, состоящая из узлов трех подрешеток δ = α, β и γ, каждая из которых представляет собой примитивную кубическую решетку (z = 6 – число ближайших соседних узлов одной и той же подрешетки; расстояние между узлами одной подрешетки отвечает постоянной решетки). Иными словами, на ячейках происходит упорядочивание компонентов А и В, а внутри ячеек с ионами А узлы α преимущественно заполнены частицами А, а узлы γ – вакансиями V. Такое упорядочивание отвечает смещениям в двух-ямном потенциале.

На рис. 1 показана схема подрешеток α (незакрашенные круги), β (закрашенные круги) и γ (кресты) в объемной фазе. На схеме отмечены расстояния r_x и r_y между центром ячейки с узлом β и центром ячейки с узлами α и γ вдоль оси x и оси y соответственно. Также на схеме обозначено расстояние r_αγ между узлами α и γ.

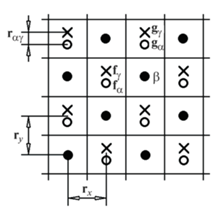
Выберем в качестве центральной ячейки ячейку f с узлами α и γ и присвоим этим узлам, принадлежащим к центральной ячейке, обозначения f_α и f_γ. Данную ячейку f окружают ячейки с единственным в них узлом β и ячейки g с узлами α и γ, которым присвоим обозначения g_α и g_γ.

Параметры взаимодействия между ионами АА и АВ на разных расстояниях между узлами подрешеток, δ = α, β, γ, задаются для каждой координационной сферы (к.с.). Будем учитывать взаимодействия в пределах постоянной решетки. Для узлов α и γ это отвечает взаимодействиям в пределах 4 к.с., 1 ≤ ρ_α, ρ_γ ≤ 4, для узлов β это взаимодействие в пределах 2 к.с., 1 ≤ ρ_β ≤ 2. Для узла α ячейки f имеется следующее окружение ближайших соседей: в 1 к.с. узел γ с ${{z}_{{{{f}_{\alpha }}{{f}_{\gamma }}}}} = 1$ внутри ячейки f, во 2 к.с. узел β с ${{z}_{{{{f}_{\alpha }}\beta }}}$ = 4, в 3 к.с. узел γ из соседней ячейки g с ${{z}_{{{{f}_{\alpha }}{{g}_{\gamma }}}}} = 8$, в 4 к.с. узел α из соседней ячейки g с ${{z}_{{{{f}_{\alpha }}{{g}_{\alpha }}}}} = 12$. Аналогичное окружение имеет узел γ в силу симметричного положения с α относительно центра ячейки f. Для узла β имеется следующее окружение ближайших соседей: в 1 к.с. узел α и γ в соседней ячейке g с ${{z}_{{\beta {{g}_{\alpha }}}}}$ = 4 и ${{z}_{{\beta {{g}_{\gamma }}}}}$ = 4 соответственно, во 2 к.с. узел β с ${{z}_{{\beta \beta }}} = 12$.

Взаимодействия между ионами BB, $\varepsilon _{{\beta \beta }}^{{BB}}$, и АВ, $\varepsilon _{{\delta \beta }}^{{AB}}$, δ = α, γ, между ячейками задаются через потенциал типа Ми или Леннард–Джонса с потенциальными минимумами ε^BB и ε^AB соответственно. Взаимодействия между ближайшими ионами АА внутри одной ячейки выполняют роль блокировки их одновременного заполнения. Они задаются как произведение $\varepsilon _{{\delta \varphi }}^{{AA}} = {{k}_{{\delta \varphi }}}{{\varepsilon }^{{АА}}}$, δ, φ = α, γ, где коэффициенты k_δφ и потенциал ε^АА представляют собой варьируемые параметры.

В исходной постановке для двухкомпонентной системы (i = A, B, V) локальная изотерма для узла δ = α, β, γ в КХП запишется как

где $\beta = {1 \mathord{\left/ {\vphantom {1 {\left( {{{R}_{{\text{B}}}}T} \right)}}} \right. \kern-0em} {\left( {{{R}_{{\text{B}}}}T} \right)}}$, ${{R}_{{\text{B}}}}$ – газовая постоянная, φ – тип узлов, соседнего к узлу δ в пределах ρ_δ к.с., $\theta _{{\delta \varphi }}^{{ij}}$ – вероятность нахождения пары частиц ij рядом, причем компонент i находится в узле δ, а компонент j находится в узле φ. Величины $a_{0}^{i}{{P}^{i}}$ фиксируют значения химических потенциалов компонентов i в объемной фазе. Величина Pⁱ – равновесное давление компонента i, смысл величин констант Генри $a_{0}^{i}$ подробно пояснен в работе [58].

В одно-ионной модели (однокомпонентной системе, i = A, V) рассматриваются только две подрешетки α и γ, смещенные относительно центров ячеек f, на которых располагаются частицы А и вакансии V. Заполнения подрешетки β в однокомпонентной системе не рассматриваются, а учитывается только влияние поля подрешетки β на состояние узлов α и γ в ячейках f [6, 58]. Взаимодействия между ионами А учитываются также в пределах постоянной решетки, и в отсутствии пар с узлами β у узлов α и γ рассматривается только 3 к.с., 1 ≤ ρ_α, ρ_γ ≤ 3, ближайших соседей. Для узла α ячейки f имеется следующее окружение ближайших соседей: в 1 к.с. узел γ с ${{z}_{{{{f}_{\alpha }}{{f}_{\gamma }}}}} = 1$ внутри ячейки f, во 2 к.с. узел γ и в 3 к.с. узел α с ${{z}_{{{{f}_{\alpha }}{{g}_{\gamma }}}}} = 8$ и ${{z}_{{{{f}_{\alpha }}{{g}_{\alpha }}}}} = 12$ соответственно между соседними ячейками f и g. Взаимодействия между одноименными компонентами А задаются как указано выше в двухкомпонентной системе (i = A, B, V) в виде $\varepsilon _{{\delta \varphi }}^{{AA}} = {{k}_{{\delta \varphi }}}{{\varepsilon }^{{АА}}}$, δ, φ = α, γ.

Локальная изотерма для узла подрешетки δ, δ = α, γ, в КХП запишется как

где ${{a}_{\delta }}$ – коэффициент Генри, ${{a}_{\delta }} = {{a}_{0}}\exp \left\{ {\beta {{\varepsilon }^{{AB}}}{{Q}_{\delta }}} \right\}$, где параметр ε^AB совпадает по величине с аналогичной величиной в двухкомпонентной системе (i = A, B, V), ${{Q}_{\delta }}$ – коэффициент потенциала поля подрешетки β в узлах δ (внешнее поле одинаково влияет на ионы А в узлах α, γ, и оно опущено). В расчетах принималось ${{Q}_{\delta }}$ = 4, что отвечает числу ближайших узлов подрешетки β для узлов ячейки f (${{z}_{{\beta f}}}$ = 4). Таким образом, основным отличием однокомпонентной системы (i = A, V) от двухкомпонентной (i = A, B, V) является то, что в двухкомпонентной системе взаимодействия между разноименными ионами А и В учитываются непосредственно через парные корреляторы $\theta _{{\delta \varphi }}^{{AB}}$, а в однокомпонентной системе – через суммарный потенциал поля подрешетки β, ${{\varepsilon }^{{AB}}}{{Q}_{\delta }}$, фигурирующий в коэффициенте Генри ${{a}_{\delta }}$ (при ${{Q}_{{{\text{ext}}}}}$).

Здесь функции $t_{{\delta \varphi }}^{{AA}}$ означают условные вероятности нахождения ионов А на узлах δ рядом с узлом φ. Они умножаются на величины $x_{{\delta \varphi }}^{{AA}} = \exp \left\{ { - \beta \varepsilon _{{\delta \varphi }}^{{AA}}} \right\} - 1$, содержащие энергии $\varepsilon _{{\delta \varphi }}^{{AA}}$ на соответствующих расстояниях. Для рассматриваемой однокомпонентной системы (i = A, V) функции $t_{{\delta \varphi }}^{{AA}}$ выражаются [53, 60] через локальные концентрации в виде

где $\delta _{{\delta \varphi }}^{{AA}} = 1 + x_{{\delta \varphi }}^{{AA}}\left( {1 - \theta _{\delta }^{A} - \theta _{\varphi }^{A}} \right)$, $b_{{\delta \varphi }}^{{AA}} = \left\{ {{{{\left[ {\delta _{{\delta \varphi }}^{{AA}}} \right]}}^{2}}} \right. + $ $ + \,\,{{\left. {4x_{{\delta \varphi }}^{{AA}}\theta _{\delta }^{A}\theta _{\varphi }^{A}} \right\}}^{{1/2}}}$.

Все условные парных функции подчиняются нормировочным соотношениям: $\sum\nolimits_{j = 1}^s {t_{{\delta \varphi }}^{{ij}}} = 1$ [60, 61]. Система уравнений вида (6) для обеих подрешеток α и γ замыкается равенством ${{\theta }_{f}} = {{\theta }_{{{{f}_{\alpha }}}}} + {{\theta }_{{{{f}_{\gamma }}}}}$. В расчетах варьировалась плотность ионов А в ячейках f или вакансий $\theta _{f}^{V} = 1 - {{\theta }_{f}}$ от $\theta _{f}^{V} = {{10}^{{ - 3}}}$ до $\theta _{f}^{V} = {{10}^{{ - 6}}}$.

На рис. 2 сравниваются кривые температурной зависимости локальных плотностей (рис. 2а) и химпотенциала компонента А (рис. 2б) при следующих параметрах: ${{k}_{{{{f}_{\alpha }}{{f}_{\gamma }}}}}$ = 20 (1, 3–6), 25 (2), ${{k}_{{{{f}_{\alpha }}{{g}_{\gamma }}}}}$ = = 3.5 (1–2, 4–5), 8.5 (3, 6) и ${{k}_{{{{f}_{\alpha }}{{g}_{\alpha }}}}}$ = 0.4 (1–3, 5–6), 0.1 (4), ε^AB = 2500 (1–4, 6), 3500 (5) кал/моль при ε^AA = –250 кал/моль. Кривая 6 построена для двумерной системы d = 2, являющейся плоским аналогом описанной выше трехмерной системы d = 3. Кривые 1–6 построены в рамках однокомпонентной системы (i = A, V).

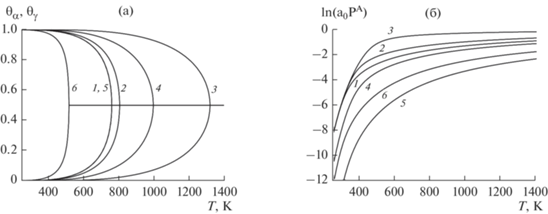
Локальные плотности компонента А не зависят от силы взаимодействия с компонентом В на решетке β и от способа учета данного взаимодействия. Поэтому кривые на рис. 2а универсальны как для однокомпонентной системы (i = A, V), так и для двухкомпонентной системы (i = A, B, V).

Согласно рис. 2а, критическая температура растет с ростом коэффициентов ${{k}_{{{{f}_{\alpha }}{{f}_{\gamma }}}}}$, ${{k}_{{{{f}_{\alpha }}{{g}_{\gamma }}}}}$, характеризующих взаимодействие между ионами А на разных узлах α и γ, и с уменьшением ${{k}_{{{{f}_{\alpha }}{{g}_{\alpha }}}}}$, характеризующим взаимодействие между ионами А на одинаковых узлах α или γ. Кривые 1 и 5 совпадают, так как критическая температура, как и диаграмма в целом, не меняются с изменением ε^AB по причинам названным выше. Критическая температура сильно уменьшается с переходом к квадратной решетке, d = 2 (6).

На рис. 2б получили, что увеличение отталкивания между ионами А на любых узлах увеличивает химпотенциал А: кривые 2 и 3 лежат выше кривой 1, и наоборот: кривая 4 лежит ниже кривой 1. Увеличение притяжения между ионами А и В, ε^AB, уменьшает А: кривые 5 и 7 лежат ниже черной кривой 1. В двумерной системе d = 2 (6) химпотенциал А ниже, чем в соответствующей трехмерной d = 3 (3).

Кривые 1–6, построенные в рамках однокомпонентной системы (i = A, V), практически в точности отвечают аналогичным кривым, получаемым в рамках двухкомпонентной системы (i = A, В, V), благодаря тому, что задаваемая величина коэффициента потенциала поля подрешетки β, ${{Q}_{\delta }}$ = 4, дает хорошую корреляцию результатов между одно- и двухкомпонентной системами.

Параметры: d = 3, ${{k}_{{{{f}_{\alpha }}{{f}_{\gamma }}}}}$ = 20, ${{k}_{{{{f}_{\alpha }}{{g}_{\gamma }}}}}$ = 3.5, ${{k}_{{{{f}_{\alpha }}{{g}_{\alpha }}}}}$ = 0.8, ε^AА = –253 кал/моль, дают критическую температуру упорядочивания типа смещения для объема, равную 763 К, что равно экспериментальному значению для системы PbTiO₃ [23]. Данные параметры использовались ниже для характеристик межфазных границ раздела и размерной зависимости Т_crit(L) в наночастицах.

3. МЕЖФАЗНЫЕ ГРАНИЦЫ РАЗДЕЛА ФАЗ

Влияние границы раздела фаз распространяется внутрь фаз на ширину κ* монослоев, что делает общую систему неоднородной. Число монослоев κ* определяется из минимума свободной энергии системы [60, 61] – это формирует концентрационный профиль между фазами 1 ≤ q ≤ κ, κ = κ* + 2, где прибавляется по два монослоя от фаз: q = 1, κ – монослои фаз. Граница фазы определяется условием разупорядочения ионов А в своих ячейках ($\theta _{\alpha }^{A} = \theta _{\gamma }^{A}$) [58].

Можно выделить пять типов границ между фазами с разной ориентацией оси поляризации. На рис. 3 показаны схемы межфазных границ. Для рассматриваемой кубической геометрии системы возможно пять типов границ в зависимости от направления осей поляризации (смещения) в соседних фазах. Схемы на рис. 3 построены для переходной области шириной κ = 6, где q = 1 и 6 – монослои фаз. В ячейках помечены узлы α (o – круги) и γ (× – кресты). Геометрическое положение границы между фазами проходит между граничными монослоями q = 3 и 4 – на рис. 3 она отмечена вертикальной тройной линией.

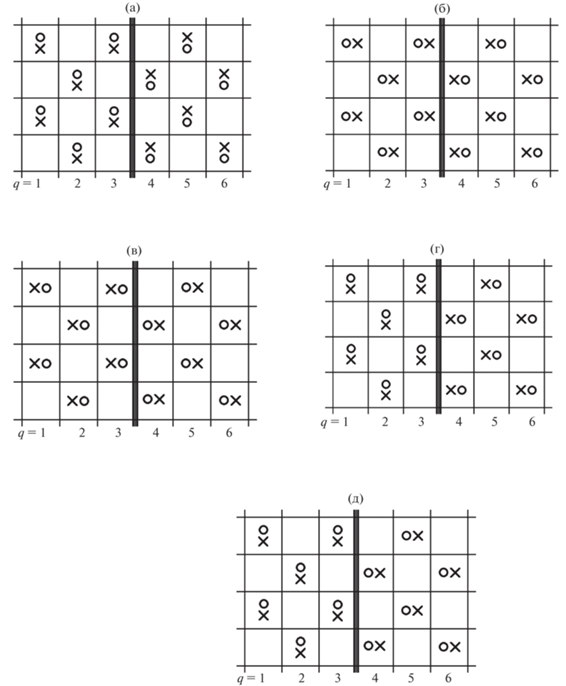
Первые три типа (рис. 3а–3в) являются симметричными по своим свойствам относительно границы раздела фаз, проходящей между q = 3 и 4, т.е. свойства переходной области по левую сторону от границы воспроизводят свойства переходной области по правую сторону от границы. Последние два типа (рис. 3г, 3д) характеризуются несимметричными свойствами переходной области относительно границы раздела фаз и являются комбинацией левой части 1-ого типа и правой части 2-ого и 3-его типов, соответственно.

Концентрационный профиль в переходной области рассчитывается по КХП уравнениям (это локальные изотермы для ионов А)

где (p, n) – номер монослоя, q – 1 ≤ p ≤ q + 1, и тип узла, n = α, γ, соответственно, соседнего к узлу (q, k); $a_{{q,k}}^{{}} = {{a}_{0}}\exp \left\{ {\beta {{\varepsilon }^{{AB}}}{{Q}_{{q,k}}}} \right\}$, как и выше ${{Q}_{{q,k}}}$ = 4 – коэффициент потенциала поля подрешетки β в узлах (q, k); данный коэффициент общий для всех узлов ячеек f.

Из решения (5) получаем профиль локальных плотностей в узлах подрешеток α и γ, по которому рассчитывается среднее давление π_q,k в узлах (q,k):

На рис. 4 приведены профили локальных плотностей (рис. 4а) и внутренних давлений (рис. 4б) в узлах подрешетки α (сплошные кривые) и γ (пунктирные кривые) в переходных областях с границей 1-ого типа (кривая 1 с символами-квадратами), 2-ого типа (кривая 2 с символами-кругами), 3-его типа (кривая 3 с символами-треугольниками), 4-ого типа (кривая 4 с символами-ромбами), 5‑ого типа (кривая 5 с символами-звездами). Профили построены для приведенной температуры τ = T/T_cr = 0.81, где T_cr – критическая температура упорядочивания по типу смещения.

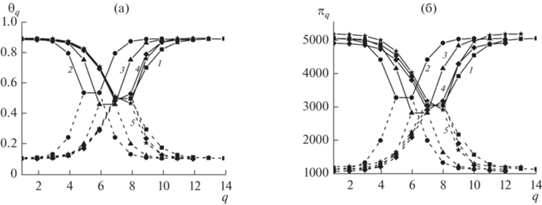
Верхние символы на сплошных кривых, выше примерно θ_q = 0.5, относятся к узлам подрешетки α, а нижние символы на пунктирных кривых – к узлам подрешетки γ. Символы по центру около θ_q = 0.5, на которых сходятся сплошные и пунктирные кривые, относятся к граничным монослоям, в которых имеет место разупорядочивание, в следствие чего плотности на подрешетках α и γ равны.

Профили кривых 1–3 на рис. 4 симметричны, так как симметрична структура решетки (см. рис. 3а–3в). Профиль 4 представляет собой комбинацию левой части профиля 1 и правой части профиля 2, подобно тому, как сама структура решетки складывается из правой и левой половин схем границ типа 1 и 2 соответственно (см. рис. 3г). Профиль 5 представляет собой комбинацию левой части профиля 1 и правой части профиля 3, подобно тому, как сама структура решетки складывается из правой и левой половин схем границ типа 1 и 3 соответственно (см. рис. 3д).

Межфазное натяжение (МН), σ, на межфазной границе рассчитывается как суммарное избыточное внутреннее давление в монослоях переходной области, π_q,k, по сравнению с внутренним давлением в фазе, π_1,k:

где A – площадь единичной поверхности (площадь ячейки).

На рис. 5 представлены температурные зависимости ширины межфазной переходной области κ в числах монослоев (рис. 4а) и МН σ в безразмерных единицах (рис. 4б) для границ 1–5 типов (кривые 1–5 соответственно).

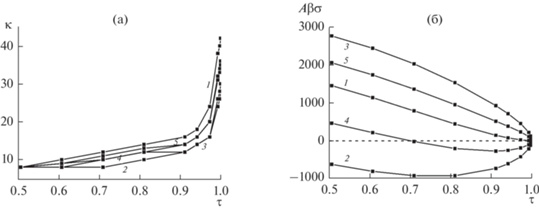
С ростом температуры ширина переходной области увеличивается для всех типов границ (рис. 5а). Согласно рис. 5а тип границ 1 (1) обладает наибольшей шириной межфазной области κ. Также согласно рис. 4б, граница типа 1 (1) единственная имеет температурную зависимость МН, подобную температурной зависимостью МН на границе системы плотная фаза – пар, т.е. зависимость монотонная с уменьшением скорости снижения МН с ростом температуры [57].

У 2-ого (2) и 3-его (3) типа границ ширина межфазной области (рис. 5а) наименьшая, а температурные зависимости МН (рис. 5б) практически симметричны друг к другу относительно кривой 1-ого типа границы (1). Кривая МН для 2-ого типа границы (2 на рис. 5б) полностью относится к отрицательным значениям (которые указывают на нестабильность данного типа границы в сформулированной схеме – смещения в соседних фазах направлены друг навстречу друг другу).

Значения ширины переходной области κ и МН σ для 4-ого типа границы (4) представляют собой среднее между соответствующими значениями для 1-ого (1) и 2-ого (2) типа границ. При этом кривая МН для 4-ого типа границы (4 на рис. 5б) уходит частично в отрицательные значения. Значения ширины переходной области и МН для 5‑ого типа границы (5) представляют собой среднее между соответствующими значениями для 1‑ого (1) и 3-его (3) типа границ.

Приведенные зависимости отражают “изолированные” свойства типов границ между конкретными упорядоченными фазами. Эти величины не отражают свойств макро-образцов. В реальных материалах важную роль играет упаковка доменов в трехмерных макро-образцах [2]. Микроскопические модели указывают на специфику границ разных соседних фаз, которая должна учитываться при обсуждении реализуемых способов упаковок доменов.

4. РАЗМЕРНЫЙ ЭФФЕКТ

Формулировка граничных условий упорядоченных фаз позволяет ввести ограничение на объем домена твердой фазы и рассмотреть зависимость термодинамических функций домена от его размера по уравнениям [60, 61], модифицированным для учета смещений ионов А в двух-ямном потенциале.

Будем рассматривать размерный эффект при условии, что на границе домена отсутствуют внешние связи, т.е. за пределами домена – вакуум. Используем для простоты приближенную модель, что все границы домена имеют вид 1-ого типа, т.е. смещение подрешеток от центра ячеек происходит вдоль границы домена. Кроме того, при описании размерного эффекта учтем усредненным способом различия в числах связей для ячеек, находящихся в “объеме”, на грани, на ребрах и в углах куба домена.

Для узлов в фазе (q, k), q = 1, k = α, γ, подсчитывается число внутренних “объемных” узлов $N_{{1,k}}^{{\left( 0 \right)}}$, число узлов, примыкающих к поверхности переходной области, т.е. “на грани куба”, $N_{{1,k}}^{{\left( 1 \right)}}$, число узлов “на ребрах” $N_{{1,k}}^{{\left( 2 \right)}}$ и число узлов в углах куба $N_{{1,k}}^{{\left( 3 \right)}}$.

Для узлов, отвечающих объему, выписывается список его возможных соседей (p, n), 1 ≤ p ≤ t_p, во всех возможных положениях в объеме: внутри объема, на грани, на ребре и в углах. Для каждого варианта положения узла q = 1 (внутри объема, на грани, на ребре и в углах) выписываются соответствующие им числа $z_{{1,k;p,n}}^{{\left( m \right)}}$, 1 ≤ p ≤ t_p, отвечающие их окружению. Затем для каждой пары (q, k; p, n), q = 1, 1 ≤ p ≤ t_p, проводится усреднение по числу пар:

Аналогично для узлов в монослоях переходной области (q, k), 2 ≤ q ≤ κ, k = α, γ, с учетом, что в них возможны только три положения: на грани, на ребре и в углах, т.е. k меняется от 1 до 3. Получаем:

Для получения концентрационного профиля в переходной области на границе домена используются уравнения (5), где коэффициент Генри имеет вид $a_{{q,k}}^{{}} = {{a}_{0}}\exp \left\{ {\beta {{\varepsilon }^{{AB}}}{{Q}_{{q,k}}}} \right\}\exp \left\{ {\beta \left| {{{\varepsilon }^{{AA}}}} \right|Q_{{q,k}}^{*}} \right\}$, где ${{Q}_{{q,k}}}$ = 4 – коэффициент потенциала поля подрешетки β в узлах (q, k), $Q_{{q,k}}^{*}$ – коэффициент потенциала внешнего поля на границе домена в узлах (q, k), здесь ${{Q}_{{{\text{ext}}}}} = \left| {{{\varepsilon }^{{AA}}}} \right|Q_{{q,k}}^{*}$, без детализации его природы (см. [58]). Результаты ниже получены при рассмотрении влияния внешнего поля на 4 монослоя переходной области у границы.

На рис. 6 показана зависимость критической температуры упорядочивания по типу смещения, T_cr, от размера частицы r в нм для вариантов (1–3) с отсутствием упорядочивания ионов А ($\theta _{\alpha }^{A} = \theta _{\gamma }^{A}$) и с их упорядочиванием ($\theta _{\alpha }^{A} \ne \theta _{\gamma }^{A}$) (4) в граничном монослое с внешним потенциалом $Q_{{q,k}}^{*}$ = 0 (1, 4), 9 (2), –9 (3). На вставке рис. 6 показана зависимость критической температуры от величины потенциала внешнего поля $Q_{{q,k}}^{*}$ при 25 нм с разупорядочиванием (1) и упорядочиванием (2) в граничном монослое. Пунктирная линия на вставке расположена на уровне 763 К, что равно значению критической температуры Т_crit(bulk) объемной фазы PbTiO₃ [7, 23]. Точками на рис. 6 представлены экспериментальные данные для системы PbTiO₃ [23].

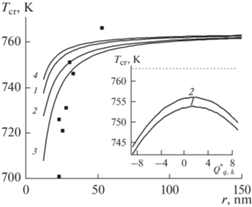
Рисунок 6 показывает, что в целом модель качественно отражает основную тенденцию экспериментальных данных: величина Т_crit(L) для изолированной наночастицы уменьшается с уменьшением размера домена L (как и в случае сегнетоэлектриков порядок – беспорядок [55, 56]). Вариант разупорядоченного граничного монослоя (1) дает лучшее согласие с экспериментом, чем вариант упорядоченного граничного монослоя (2). Также согласие с экспериментом усиливается при увеличении величины вклада потенциала внешнего поля как с сильным притяжением $Q_{{q,k}}^{*}$ = 9 (2) или с сильным отталкиванием $Q_{{q,k}}^{*}$ = –9 (3). Аналогичный результат влияния внешнего поля был получен ранее для сегнетоэлектриков порядок – беспорядок [55, 56]: как положительные, так и отрицательные значения ${{Q}_{{ext}}}$ увеличивают диапазон уменьшения Т_crit(L) с уменьшением размера домена L.

Таким образом, несмотря на упрощенный характер использованной модели (все грани куба являются границами первого типа и усредненный характер учета разных вкладов границ, ребер и вершин куба) модель позволяет выйти на качественное описание эксперимента по размерной зависимости Т_crit(L).

Здесь важно также обсуждение самой экспериментальной размерной зависимости, которая влияет на качество интерпретации экспериментальных данных. Самая верхняя точка авторов превышает объемное значение Т_crit(bulk) примерно на 3°. Это либо неточность экспериментальной методики, либо более сложный характер поведения зависимости Т_crit(L). Эксперимент указывает на очень резкое возрастание Т_crit(L) с ростом L, причем основной эффект роста проявляется при изменении размера на 10 нм.

Хотя, в целом, можно говорить о монотонном возрастании Т_crit(L) с увеличением размера образца. Однако более детальное рассмотрение указывает, что из шести точек с Т_crit(L) < Т_crit(bulk) две пары точек (или из пяти пар точек) имеют отрицательный наклон кривой. Если к этому добавить “отрицательный наклон” верхней точки Т_crit(L) по отношению к Т_crit(bulk), то это также же может указывать на недостаточную точность измерений, либо на более сложный характер обсуждаемого эффекта в зависимости от конкретных условий измерений. Часто это связано с сильной неравновесностью материала, и, в частности, с насыщенностью кислородными вакансиями [62].

Наконец, учитывая, что учет непрямых корреляций сдвигает рассчитанные кривые Т_crit(L) вправо в область больших величин L [56] (в сторону экспериментальных точек), можно сделать вывод о качественном соответствии модели, позволяющей описывать размерные эффекты сегнетоэлектриков типа смещения, и эксперимента. Здесь дополнительно следует учитывать отличия по геометрии реальных наночастиц (и их размерную неоднородность) от формы идеального куба, рассмотренного в расчетах, и возможность изменения величин энергетических параметров модели, определенных по объемной фазе. Перечисленные вопросы по самим экспериментальным данным также указывают на необходимость более целенаправленного изучения данного вопроса.

ЗАКЛЮЧЕНИЕ

Выполнен первый микроскопический расчет по новой модели для сегнетоэлектрика типа смещения на основе существования двух-ямного потенциала для мягкой подрешетки ионов А в бинарном стехиометрическом сегнетоэлектрике АВ [58]. В работе разработан алгоритм расчета микроскопических распределений ионов в кристаллической решетке и свойств сегнетоэлектриков типа смещения для простейшей одно-ионной модели на основе разработок [61]. Расчет проводится по математическим моделям МРГ. Расчет величин межфазных натяжений, и зависимости Т_crit(L) проведен в квазихимическом приближении с учетом коррелированного распределения соседних ионов.

Модель является феноменологической – она использует эффективные энергетические парные параметры, соответствующие величине критической температуры упорядочения в объемной фазе, для оценок поверхностных и размерных вкладов в поведении характеристик сегнетоэлектриков типа смещения. С ее помощью можно проводить широкий спектр численных исследований характеристик неоднородных сегнетоэлектриков типа смещения, обсуждаемых в работе [58]. Простейшие примеры расчета межфазных натяжений и Т_crit(L), приведенные в данной работе, демонстрируют ее возможности, которые недоступны существующим подходам по микроскопическому описанию свойств сегнетоэлектриков в теории феноменологической теории [39–44] и ее современных вариантах [37, 62].

Полученные результаты для локальных микроскопических систем указывают на необходимость построения более конкретной модели границ раздела упорядоченных фаз и границ твердое–пар, как и совместного включения разных факторов (неоднородности системы, деформаций решетки и т.д.) для выхода на реальный эксперимент. Однако уже приведенные примеры указывают на перспективность нового подхода.

Работа выполнена в рамках государственного задания ИОНХ РАН в области фундаментальных научных исследований (№ 44.2).