1. На главную
  2. Электронные версии
  3. Электрохимия
  4. T. 55, № 11, 2019

Электрохимия, 2019, T. 55, № 11, стр. 1337-1342

Эргодический анализ трехмерного спектра Чебышева электрохимического шума

А. Л. Клюев a, А. Д. Давыдов a, Т. Б. Кабанова a, Б. М. Графов a, *, **

a Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
119071 Москва, Ленинский просп., 31, Россия

* E-mail: boris.grafov@yandex.ru
** E-mail: bmg@elchem.ac.ru

Поступила в редакцию 29.01.2019
После доработки 20.04.2019
Принята к публикации 20.05.2019

Полный текст (PDF)

Аннотация

Изучена эргодичность электрохимического шума коррозионного процесса в отношении трехмерного спектра Чебышева. Экспериментально измерен электрохимический шум коррозионной системы “два идентичных электрода из стали Ст-3 в растворе NaCl + бензотриазол”. Использование шумовых спектров Чебышева в тесте на эргодичность электрохимического шума продиктовано тем, что интенсивность второй и более высокой спектральной линии спектра Чебышева устойчива по отношению к тренду электрохимического шума. Установлено, что в начальный период взаимодействия электрода и электролита электрохимический шум коррозионного процесса характеризуется слабой эргодичностью. Однако уже через 2.5 ч тест на эргодичность фиксирует установление стационарного состояния. Аналогичная ситуация имеет место в отношении электронного шума измерительной аппаратуры. Тест на эргодичность электронного шума с использованием второй компоненты трехмерного спектра Чебышева фиксирует достижение измерительной аппаратурой стационарного состояния спустя 30 мин после включения. Тест на эргодичность в отношении второй компоненты трехмерного спектра Чебышева может быть использован в анализе эргодических свойств случайного шума любой природы даже в условиях сильного тренда.

Ключевые слова: электрохимический шум, коррозия металла, эргодичность, спектры Чебышева, тренд электрохимического шума

ВВЕДЕНИЕ

Идея эргодичности лежит в основе современных методов анализа случайного временного ряда [1–4]. Согласно принципу эргодичности выборочное среднее значение стационарной случайной функции времени, соответствующее достаточно протяженной реализации, совпадает с теоретическим средним значением, соответствующим теоретическому ансамблю реализаций. Строго говоря, проверить соблюдение принципа эргодичности в рамках одной единственной реализации весьма затруднительно. Однако в рамках одной единственной реализации можно проверить близость двух выборочных средних значений, относящихся к двум статистически независимым частям одной достаточно протяженной реализации. Близость указанных двух выборочных средних значений означает, что выборка электрохимического шума обладает эргодическими свойствами. Если выборка обладает эргодичностью, то выборочное среднее значение близко к теоретическому значению, а электрохимическая система находится в стационарном состоянии.

Оценка эргодичности выборки электрохимического шума осложнена наличием тренда. В электрохимической литературе [5–9] описаны различные методы выделения трендового сигнала. Вычитание трендового сигнала из данных по электрохимическому шуму в ряде случаев приводит к существенному искажению электрохимического шума. Альтернативой является анализ электрохимического шума методом дискретной спектроскопии Чебышева [10, 11]. Дискретная спектроскопия Чебышева использует полиномы Чебышева дискретной переменной [12, 13]. Дискретные линии спектра Чебышева, начиная со второй спектральной линии, проявляют устойчивость к тренду даже высокого уровня [14, 15].

Цель настоящей работы состоит в том, чтобы представить алгоритм и провести оценку эргодичности электрохимического шума коррозионного процесса и эргодичности электронного шума измерительной аппаратуры в отношении трехмерного спектра Чебышева. Оценка эргодичности проводится путем сопоставления двух трехмерных спектров Чебышева. Один трехмерный спектр Чебышева соответствует реализации, прочитанной в прямом направлении. В этом случае мы можем говорить о прямом времени, о прямой реализации или о прямом спектре. Другой трехмерный спектр Чебышева соответствует той же реализации, но прочитанной в обратном направлении (обратное время, обратная реализация, обратный спектр). Трехмерный спектр Чебышева обеспечивает наибольшую глубину выборочного усреднения.

Самое значительное влияние тренд электрохимического шума оказывает на нулевую компоненту спектра Чебышева. Первая компонента спектра обладает несколько меньшей чувствительностью к действию тренда. Вторая компонента спектра Чебышева обладает высокой устойчивостью по отношению к тренду. Чтобы проследить устойчивость эргодического анализа к действию тренда, мы применили метод искусственного тренда высокого уровня в отношении первой и второй компоненты трехмерного спектра Чебышева.

Статья организована следующим образом. В начале статьи мы обсуждаем алгоритм, который мы используем для анализа эргодичности случайного временного ряда в отношении первой и второй компоненты трехмерного спектра Чебышева. Затем следует описание экспериментальной части. После этого мы обсуждаем эргодичность трехмерного спектра Чебышева электрохимического шума коррозионного процесса и электронного шума измерительной аппаратуры. Там же идет обсуждение устойчивости эргодических свойств трехмерного спектра Чебышева электрохимического и электронного шума по отношению к искусственному тренду высокого уровня.

АЛГОРИТМ ОЦЕНКИ ЭРГОДИЧНОСТИ ЭЛЕКТРОХИМИЧЕСКОГО ШУМА

Современная обработка случайных процессов [16–19] проводится в цифровой форме. Для этого случайные сигналы после аналогового усиления подвергаются дискретизации. Примем интервал между соседними отсчетами за единицу времени. Пусть длина дискретной реализации y(t) стационарной случайной функции равна D. Это значит, что дискретное время t пробегает целочисленные значения от 0 до (D – 1). Реализацию случайного шума y(t) можно прочитать как в направлении прямого времени t в виде случайной последовательности $fw(t),$ так и в направлении обратного времени τ в виде случайной последовательности bw(τ):

(1)
$fw(t) = y(t)\,\,\,\,\left( {t = 0,1,2 \ldots ,D - 1} \right),$
(2)
$bw(\tau ) = y(D - 1 - \tau )\,\,\,\,\left( {\tau = 0,1,2 \ldots ,D - 1} \right).$

Разобьем прямую и обратную реализацию ($fw(t)$ и bw(τ)) на M последовательно расположенных трехточечных сегментов. Присвоим каждому сегменту свой номер m (m = 0, 1, 2, …, M – 1). Сопоставим каждому сегменту с номером m в прямой и обратной последовательности ($fw(t)$ и bw(τ)) свой трехмерный случайный вектор $FWm3$ и $BWm3$ соответственно:

(3)
$FWm3 = \left[ {fw\left( m \right),fw\left( {m + 1} \right),fw\left( {m + 2} \right)} \right],$
(4)
$BWm3 = \left[ {bw\left( m \right),bw\left( {m + 1} \right),bw\left( {m + 2} \right)} \right].$

В квадратных скобках в (3) и (4) выписаны компоненты трехмерных векторов $FWm3$ и $BWm3.$

Первую компоненту трехмерного спектра Чебышева для прямой (FW13) и обратной (BW13) последовательности определим соотношениями (5) и (6):

(5)
$FW13 = \frac{1}{M}\sum\limits_{m = 0}^{M - 1} {{{{\left( {P13 \cdot FWm3} \right)}}^{2}}} ,$
(6)
$BW13 = \frac{1}{M}\sum\limits_{m = 0}^{M - 1} {{{{\left( {P13 \cdot BWm3} \right)}}^{2}}} ,$
где $P13$ = $\frac{{\left[ { - 1,0,1} \right]}}{{\sqrt 2 }}$ представляет собой неслучайный трехмерный вектор единичной длины, соответствующий дискретному нормированному на единицу полиному Чебышева первого порядка. Посредством точки в круглых скобках (·) обозначено скалярное произведение (dot product) трехмерных векторов.

Вторую компоненту трехмерного спектра Чебышева для прямой (FW23) и обратной (BW23) последовательности определим соотношениями (7) и (8)

(7)
$FW23 = \frac{1}{M}\sum\limits_{m = 0}^{M - 1} {{{{\left( {P23 \cdot FWm3} \right)}}^{2}}} ,$
(8)
$BW23 = \frac{1}{M}\sum\limits_{m = 0}^{M - 1} {{{{\left( {P23 \cdot BWm3} \right)}}^{2}}} ,$
где $P23$ = $\frac{{\left[ {1, - 2,1} \right]}}{{\sqrt 6 }}$ представляет собой неслучайный трехмерный вектор единичной длины, соответствующий дискретному нормированному на единицу полиному Чебышева второго порядка.

Интенсивности спектральных линий (FW13, BW13, FW23, BW23) двух трехмерных спектров Чебышева получены путем усреднения по всем сегментам (с номерами от m = 0 до m = M – 1) с применением прямоугольного окна [20]. Отметим, что интересующие нас интенсивности спектральных линий Чебышева (FW13, BW13, FW23, BW23) являются функциями глубины M выборочного усреднения.

ИСКУССТВЕННЫЙ ТРЕНД ВЫСОКОГО УРОВНЯ

Выше для оценки спектра Чебышева был использован прямой алгоритм в виде аналога периодограммы Шустера [21]. Использование непрямого алгоритма, основанного на дискретной версии теоремы Винера–Хинчина для спектра Чебышева [22], затруднено из-за влияния тренда на поведение автокорреляционной функции. Устойчивость предлагаемого теста на эргодичность мы проверяем методом искусственного тренда высокого уровня. Для этого к дискретной реализации случайного процесса y(t) прибавлен тренд TR(t) высокого уровня (уравнение (9)):

(9)
$TR(t) = 1V\sin (\pi t{\text{/}}D)\,\,\,\,\left( {t = 0,1,2 \ldots ,D - 1} \right).$

Далее на основе дискретной реализации y(t) и тренда (9) мы образуем две дискретные искусственные реализации с высоким трендом, прямую TRfw(t) и обратную TRbw(τ):

(10)
$TRfw(t) = y(t) + TR(t)\,\,\,\,\left( {t = 0,1 \ldots ,D - 1} \right),$
(11)
$\begin{gathered} TRbw(\tau ) = y(D - 1 - \tau ) + TR(D - 1 - \tau ) \\ \left( {\tau = 0,1 \ldots ,D - 1} \right). \\ \end{gathered} $

Затем выражения (10) и (11) мы используем вместо выражений (1) и (2) и получаем вместо соотношений (3)–(8) соотношения (12)–(17):

(12)
$\begin{gathered} TRFWm3 = \\ = \left[ {TRfw\left( m \right),TRfw\left( {m + 1} \right),TRfw\left( {m + 2} \right)} \right], \\ \end{gathered} $
(13)
$\begin{gathered} TRBWm3 = \\ = \left[ {TRbw\left( m \right),TRbw\left( {m + 1} \right),TRbw\left( {m + 2} \right)} \right], \\ \end{gathered} $
(14)
$TRFW13 = \frac{1}{M}\sum\limits_{m = 0}^{M - 1} {{{{\left( {P13 \cdot TRFWm3} \right)}}^{2}}} ,$
(15)
$TRBW13 = \frac{1}{M}\sum\limits_{m = 0}^{M - 1} {{{{\left( {P13 \cdot TRBWm3} \right)}}^{2}}} ,$
(16)
$TRFW23 = \frac{1}{M}\sum\limits_{m = 0}^{M - 1} {{{{\left( {P23 \cdot TRFWm3} \right)}}^{2}}} ,$
(17)
$TRBW23 = \frac{1}{M}\sum\limits_{m = 0}^{M - 1} {{{{\left( {P23 \cdot TRBWm3} \right)}}^{2}}} .$

Соотношения (14) и (16) позволяют вычислить первую (TRFW13) и вторую (TRFW23) компоненты прямого трехмерного спектра Чебышева в условиях сильного искусственного тренда. На основе соотношений (15) и (17) можно вычислить в условиях сильного искусственного тренда первую (TRBW13) и вторую (TRBW23) компоненту обратного трехмерного спектра Чебышева.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

В работе использовался электродный блок, состоящий из двух идентичных стержней из стали Ст3, залитых эпоксидной смолой так, что в контакте с коррозионной средой были торцы этих стержней диаметром 1 мм, расположенные на расстоянии 1 мм друг от друга. Коррозионной средой служил 3%-ный раствор NaCl в бидистиллате с добавкой 9.2 мМ 1,2,3-бензотриазола. Флуктуации напряжения между двумя электродами фиксировались с помощью оценочного комплекта EVAL AD7176-2SDZ фирмы “Analog Devices”, США [23]. Комплект включает в себя 24‑битный АЦП, на входе которого находится высокоомный низкошумящий усилитель, и плату контроллера, обеспечивающего связь АЦП с ЭВМ.

Запись шумовых данных начиналась сразу после погружения электродного блока в рабочий раствор, содержащий 3% NaCl и 9.2 мМ БТА в бидистилляте (реализация 1). Повторная запись шумовых данных проводилась спустя 2.5 ч после погружения (реализация 2). Предварительно записывались шумы прибора: сразу после включения (реализация 1) и через 30 мин (реализация 2). Каждая реализация содержит $D = {{2}^{{15}}}$ отсчетов, частота дискретизации ${{f}_{{\text{s}}}} = 20\,\,{\text{Hz}}.$

ТЕСТ НА ЭРГОДИЧНОСТЬ ТРЕХМЕРНОГО СПЕКТРА ЧЕБЫШЕВА ЭЛЕКТРОННОГО ШУМА ИЗМЕРИТЕЛЬНОЙ АППАРАТУРЫ

Начнем обсуждение с эргодического анализа электронного шума измерительной аппаратуры, так как в отсутствие стабильности измерительной аппаратуры нет смысла ставить вопрос об эргодическом анализе электрохимического шума.

Кривые на рис. 1 и 2 построены с использованием изложенного выше алгоритма и характеризуют шум измерительной аппаратуры при закороченном входе.

Рис. 1.

Тест на эргодичность электронного шума измерительной аппаратуры в отношении первой компоненты трехмерного спектра Чебышева. (а) Реализация 1: 1 – прямая (FW13) и 2 – обратная (BW13) последовательности. (б) Реализация 2: 1 – прямая (FW13) и 2 – обратная (BW13) последовательности. (в) Влияние тренда. Реализация 2: 1 – прямая (TRFW13) и 2 – обратная (TRBW13) последовательности.

Рис. 2.

Тест на эргодичность электронного шума измерительной аппаратуры в отношении второй компоненты трехмерного спектра Чебышева. (а) Реализация 1: 1 – прямая (FW23) и 2 – обратная (BW23) последовательности. (б) Реализация 2: 1 – прямая (FW23) и 2 – обратная (BW23) последовательности. (в) Влияние тренда. Реализация 2: 1 – прямая (TRFW23) и 2 – обратная (TRBW23) последовательности.

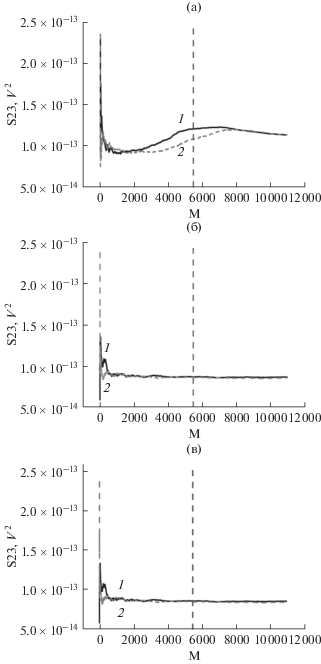
Вертикальный пунктир отмечает половину возможной глубины усреднения. Прямая fw(t) и обратная bw(τ) последовательности не имеют общих элементов при такой или меньшей глубине усреднения. Кривые рис. 1а и 2а отражают внутреннее состояние измерительной аппаратуры сразу после ее включения, а рис. 1б и 2б – спустя 30 мин после включения. Видно, что тест на эргодичность в отношении первой компоненты трехмерного спектра Чебышева (рис. 1а) однозначно свидетельствует, что измерительная аппаратура непосредственно после включения находится в релаксационном состоянии. Об этом же свидетельствует и тест на эргодичность в отношении второй компоненты трехмерного спектра Чебышева (рис. 2а). Кривые прямого и обратного времени на рис. 1а и 2а заведомо не совпадают в середине реализации. Вместе с тем, из рис. 1б и 2б четко видно, что спустя 30 мин после включения измерительная аппаратура уже находится в стационарном состоянии. Об этом свидетельствует как тест на эргодичность в отношении первой компоненты трехмерного спектра Чебышева, так и тест на эргодичность в отношении второй компоненты трехмерного спектра Чебышева.

Устойчивость эргодического анализа к тренду электронного шума была проверена методом искусственного тренда высокого уровня. Рисунок 1в показывает, что наличие тренда может исказить результаты теста на эргодичность в отношении первой компоненты трехмерного спектра Чебышева. Одновременно видно (рис. 2в), что тест на эргодичность в отношении второй компоненты трехмерного спектра Чебышева проявляет устойчивость к воздействию тренда высокого уровня. Различие между значениями интенсивностей на рис. 2в и составляет менее 0.1%.

ЭРГОДИЧНОСТЬ ТРЕХМЕРНОГО СПЕКТРА ЧЕБЫШЕВА ЭЛЕКТРОХИМИЧЕСКОГО ШУМА КОРРОЗИОННОГО ПРОЦЕССА В ПРИСУТСТВИИ ИНГИБИТОРА

Рисунок 3 демонстрирует эргодические свойства электрохимического шума коррозионного процесса в отношении трехмерного спектра Чебышева. Вертикальный пунктир отмечает половину максимальной глубины усреднения. Кривые на рис. 3 построены в соответствии с вышеизложенным алгоритмом (уравнения (7), (8) и (16), (17)).

Рис. 3.

Тест на эргодичность шума коррозионного процесса в отношении второй компоненты трехмерного спектра Чебышева. (а) Тест выполнен сразу после погружения электродной пары в электролит. Реализация 1: 1 – прямая (FW23) и 2 – обратная (BW23) последовательности. (б) Тест выполнен спустя 2.5 ч после контакта электродной пары и электролита. Реализация 2: 1 – прямая (FW23) и 2 – обратная (BW23) последовательности. (в) Тест выполнен спустя 2.5 ч после контакта пары электродов и электролита. Влияние тренда. Реализация 2: 1 – прямая (TRFW23) и 2 – обратная (TRBW23) последовательности.

Рисунок 3а построен на основании реализации электрохимического шума, которая была зафиксирована сразу после установления прямого контакта между электродной парой и электролитом. Видно, что принцип эргодичности в отношении второй компоненты трехмерного спектра Чебышева не соблюдается. Это можно объяснить тем, что идет нестационарный процесс образования защитной пленки с участием ингибитора БТА на электродах [24], который и сопровождается нестационарным электрохимическим шумом.

Рисунок 3б использует данные реализации электрохимического шума, зарегистрированной спустя 2.5 ч после введения стальных электродов в раствор с ингибитором. Ясно видно, что принцип эргодичности в отношении второй компоненты трехмерного спектра Чебышева соблюдается, начиная с глубины усреднения M = 400. Сопоставление рис. 3б и 3в показывает, что тест на эргодичность в отношении второй компоненты трехмерного спектра обладает устойчивостью к воздействию искусственного тренда высокого уровня. Различие между значениями интенсивностей на рис. 2в и 2б, начиная с М = 10, составляет менее 0.02%.

ЗАКЛЮЧЕНИЕ

Эргодичность является ключевым понятием в анализе электрохимического шума. Любой метод обработки стационарного случайного временного ряда строится на отождествлении выборочного среднего значения с его эргодическим пределом. Такое отождествление вполне оправдано в условиях достаточно протяженной реализации. При этом, для статистически независимых частей одной и той же реализации выборочные средние значения должны совпадать. Именно таким способом с использованием прямого и обратного случайного временного ряда в настоящей работе осуществлено тестирование на эргодичность выборки электрохимического шума коррозионного процесса и выборки электронного шума регистрирующей аппаратуры.

Экспериментально установлено, что существует определенный период времени, в течение которого измерительная аппаратура после включения находится в нестационарном релаксирующем состоянии. В этот период времени эргодичность электронного шума измерительной аппаратуры в отношении второй компоненты трехмерного спектра Чебышева не соблюдается. Однако, спустя 30 мин после включения измерительная аппаратура переходит в стационарное состояние, о чем свидетельствует соблюдение принципа эргодичности в отношении второй компоненты трехмерного спектра Чебышева.

Установлено, что полученные данные по эргодичности второй компоненты трехмерного спектра Чебышева устойчивы по отношению к тренду высокого уровня. В то же время, тренд исказил самым серьезным образом тест на эргодичность в отношении первой компоненты трехмерного спектра Чебышева.

Дискретная спектроскопия Чебышева является мощным инструментом анализа эргодических свойств электрохимического шума, обладающего сильным трендом.

Теория стохастического анализа [25] носит междисциплинарный характер. В условиях тренда дискретная спектроскопия Чебышева может быть применена для устойчивой оценки эргодических свойств случайного временного ряда любой природы.

Список литературы

  1. Yaglom, A.M., An Introduction to the Theory of Stationary Random Functions, Courier Corporation, 2004.

  2. Kirchgassner, G.K. and Wolters, J., Introduction to Modern Time Series Analysis, New York: Springer, 2007.

  3. Chatfield, C., The Analysis of Time Series: An Introduction, New York: CRC Press, 2016.

  4. Бендат, Дж., Пирсол, А. Измерение и анализ случайных процессов. М.: Мир, 1974. [Bendat, J.S. and Piersol, A.G., Random Data: Analysis and Measurement Procedures, New York: Wiley, 2000.]

  5. Lentka, L. and Smulko, J., Methods of trend removal in electrochemical noise data–Overview, Measurement, 2019, vol. 131, p. 569.

  6. Martinez-Luaces, V. and Ohanian, M., Data Simulation and Trend Removal Optimization Applied to Electrochemical Noise. Recent Trends in Computational Science and Engineering, Serdar Celebi, Ed., IntechOpen, 2018. https://doi.org/10.5772/intechopen.73831

  7. Astafev, E.A., Ukshe, A.E., Manzhos, R.A., Dobrovolsky, Y.A., Lakeev, S.G., and Timashev, S.F., Flicker noise spectroscopy in the analysis of electrochemical noise of hydrogen-air PEM fuel cell during its degradation, Int. J. Electrochem. Sci., 2017, vol. 12, p. 1742.

  8. Timashev, S.F. and Polyakov, Y.S., Review of flicker noise spectroscopy in electrochemistry, Fluctuation Noise Lett., 2007, vol. 7, p. R15.

  9. Bertocci, U., Huet, F., Nogueira, R.P., and Rousseau, P., Drift removal procedures in the analysis of electrochemical noise, Corrosion, 2002, vol. 58, p. 337.

  10. Астафьев, М.Г., Каневский, Л.С., Графов, Б.М. Применение дискретных полиномов Чебышева для анализа электрохимического шума. Электрохимия. 2007. Т. 43. С. 19. [Astaf’ev, M.G., Kanevskii, L.S., and Grafov, B.M., Analyzing electrochemical noise with Chebyshev’s discrete polynomials, Russ. J. Electrochem., 2007, vol. 43, p. 17.]

  11. Графов, Б.М., Добровольский, Ю.А., Давыдов, А.Д., Укше, А.Е., Клюев, А.Л., Астафьев, Е.А. Электрохимическая шумовая диагностика: Анализ алгоритма ортогональных разложений. Электрохимия. 2015. Т. 51. С. 579. [Grafov, B.M., Dobrovol’skii, Y.A., Davydov, A.D., Ukshe, A.E., Klyuev. A.L., and Astaf’ev, E.A., Electrochemical noise diagnostics: analysis of algorithm of orthogonal expansions, Russ. J. Electrochem., 2015, vol. 51, p. 503.]

  12. Gogin, N. and Hirvensalo, M., Recurrent construction of MacWilliams and Chebyshev matrices, Fundam. Inform., 2012, vol. 116, p. 93.

  13. Nikiforov, A.F., Uvarov, V.B., and Suslov S.K., Classical Orthogonal Polynomials of a Discrete Variable, Berlin: Springer, 1991.

  14. Grafov, B.M., Kluev, A.L., Kabanova, T.B., and Davydov, A.D., Chebyshev spectra resistance to trend of random noise, Fluctuation Noise Lett., 2018, vol. 18, p. 1850028.

  15. Grafov, B.M., Klyuev, A.L., Davydov, A.D., and Lukovtsev, V.P., Chebyshev’s noise spectroscopy for testing electrochemical systems, Bulgar. Chem. Comm., 2017, vol. 49, p. 102.

  16. Vaseghi, S.V., Advanced Digital Signal Processing and Noise Reduction, Chichester: Wiley, 2008.

  17. Stranneby, D., Digital Signal Processing: DSP and Applications, Oxford: Elsevier, 2001.

  18. Hayes, M.H., Statistical Digital Signal Processing and Modeling, New York: Wiley, 2009.

  19. Stoica, P. and Moses R., Spectral Analysis of Signals, Upper Saddle River: Prentice Hall, 2005.

  20. Bartlett, M.S., Smoothing periodograms for time series with continuous spectra, Nature, 1948, vol. 161, p. 686.

  21. Schuster, A., The periodogram of magnetic declinations as obtained from the records of the Greenwich Observatory during the years 1871–1895, Trans. Cambridge Philos. Soc., 1900, vol. 18, p. 107.

  22. Grafov, B.M., Klyuev, A.L., and Davydov, A.D., Discrete version of Wiener–Khinchin theorem for Chebyshev’s spectrum of electrochemical noise, J. Solid State Electrochem., 2018, vol. 22, p. 1661.

  23. http://www.analog.com/en/design-center/evaluation-hardware-and-software/evaluation-boards-kits/eval-ad 7176-2.html.

  24. Kim, Y.S. and Kim, J.G., Electrochemical and quantum chemical studies of 1, 2, 3-benzotriazole as inhibitor for copper and steel in simulated tap water, Mater. Trans., 2017, vol. 58, no. 1, p. 76.

  25. Van Kampen, N.G., Foreword: the theory of noise, Fluctuation Noise Lett., 2001, vol. 1, p. 3.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Электрохимия

Архивы выпусков Информация о журнале Отправить рукопись в журнал