1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 87, № 2, 2023

Прикладная математика и механика, 2023, T. 87, № 2, стр. 200-210

Тепловая конвекция двух несмешивающихся жидкостей в трехмерном канале с полем скоростей специального вида

В. К. Андреев 1, *, Е. Н. Лемешкова 1, **

1 Институт вычислительного моделирования СО РАН
Красноярск, Россия

* E-mail: andr@icm.krasn.ru
** E-mail: elena_cher@icm.krasn.ru

Поступила в редакцию 28.12.2022
После доработки 01.03.2023
Принята к публикации 01.03.2023

Полный текст (PDF)

Аннотация

Исследуется трехмерное стационарное течение двух несмешивающихся жидкостей в слое, ограниченном твердыми параллельными стенками. Верхняя стенка теплоизолирована, а на нижней задано квадратичное по горизонтальным координатам поле температур. Поля скоростей в жидкостях имеют специальный вид: их горизонтальные компоненты линейны по одноименным координатам. Возникающая сопряженная краевая задача в рамках модели Обербека–Буссинеска является обратной и редуцируется к системе десяти интегродифференциальных уравнений. Для малых чисел Марангони (ползущее течение) поставленная задача решена в аналитическом виде. Нелинейная задача решается тау-методом. Показано, что решение нелинейной задачи с уменьшением числа Марангони аппроксимируется решением задачи о ползущем течении. Проведен анализ влияния физических и геометрических параметров, а также поведения температуры на подложке, на структуру конвекции в слоях.

Ключевые слова: уравнения Обербека–Буссинеска, термокапиллярность, обратная задача

1. Введение. Течения типа Хименца [1] известны как двумерные течения вблизи критической точки и характеризуются наличием зон с более высокими давлением и температурой, чем в окружающей области. Такие течения можно наблюдать как в макромасшатабах (например, использование технологий гидроразрыва пласта в нефтедобывающей промышленности), так и в микромасшатабах (например, жидкостные биочипы в медицине). Изучение характеристик подобных течений необходимо для оценки технологических параметров, а также для прогнозирования динамики и эволюции жидких слоев. Точные решения определяющих уравнений – наиболее эффективный способ исследования процессов в жидкости, а также получения оценочных характеристик. В настоящее время представлены решения задач, описывающих течения типа Хименца в различной геометрии: осесимметричный [2] и трехмерный [3, 4] аналоги решения Хименца, в том числе для течений в цилиндрической геометрии [5, 6]. Краткий обзор точных решений, близких к решению Хименца, дан в [7].

Исходная идея искать точные решения уравнений Навье–Стокса с линейной зависимостью компонент скорости от двух пространственных переменных, по-видимому, впервые предложена в работе [8]. Было показано, что общая трехмерная система уравнений вязкой магнитной гидродинамики редуцируется к замкнутой системе одномерных уравнений. Аналогичный результат для уравнений газовой динамики был получен в [9]. В работе [10] изучено решение уравнений Обербека–Буссинеска, описывающее тепловую конвекцию в трехмерном слое. В зависимости от граничных условий рассмотрены следующие движения: в слое, ограниченном твердыми стенками; твердой стенкой и свободной границей; совместное движение двух и более жидкостей с общей поверхностью раздела. Задача о ползущем конвективном движении вязкой теплопроводной жидкости с плоской свободной границей подробно изучена в [11]. В работах [12, 13] рассмотрено двухслойное трехмерное течение жидкостей при малых числах Марангони, поле скоростей которых имеет специальный вид, а также учтено полное энергетическое условие.

В настоящей работе рассматривается совместная конвекция двух вязких теплопроводных жидкостей в трехмерном слое с твердыми плоскими стенками. Верхняя стенка теплоизолирована, а на нижней стенке задано нестационарное поле температур. Жидкости предполагаются несмешивающимися и на плоской границе раздела между ними заданы сложные условия сопряжения [14]. Эволюция этой системы описывается системой уравнений Обербека–Буссинеска в каждой жидкости. Решение указанной задачи ищется в классе полей скоростей, линейных по двум координатам [15], а поля температур и давлений – квадратичные функции тех же координат.

2. Постановка задачи. Рассматривается слой $ - {{l}_{1}} < z < {{l}_{2}}$, ${\text{|}}x{\text{|}} < \infty $, ${\text{|}}y{\text{|}} < \infty $, заполненный двумя вязкими несмешивающимися теплопроводными жидкостями. Первая жидкость занимает слой $ - {{l}_{1}} < z < 0$, а вторая – $0 < z < {{l}_{2}}$. Границы слоя $z = - {{l}_{1}}$, $z = {{l}_{2}}$ – суть твердые неподвижные стенки, а $z = 0$ – также неподвижная поверхность раздела между несмешивающимися жидкостями (см. рис. 1). Стационарное течение в слоях описывается уравнениями Обербека–Буссинеска [16], решения которых ищется в специальном виде (здесь и далее $j = 1,2$)

(2.1)
$\begin{gathered} {{u}_{j}} = \left( {({{f}_{j}}(z) + {{h}_{j}}(z))x,({{f}_{j}}(z) - {{h}_{j}}(z))y, - 2\int\limits_0^z {{f}_{j}}(\xi )d\xi } \right) \\ {{{\bar {p}}}_{j}} = {{{\bar {p}}}_{j}}(x,y,z),\quad {{\theta }_{j}} = {{a}_{j}}(z){{x}^{2}} + {{b}_{j}}(z){{y}^{2}} + {{q}_{j}}(z) \\ \end{gathered} $
Рис. 1.

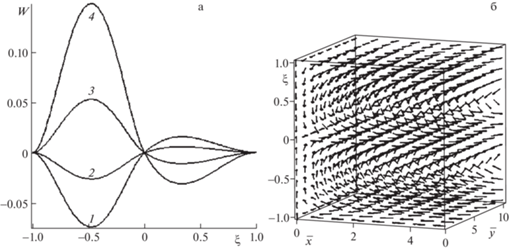
а: Безразмерная вертикальная компонента скорости $W(\xi )$ в зависимости от ${{\alpha }_{2}}$ при ${{\alpha }_{1}} = 0.5$, ${{l}_{1}} = 1$ см, ${{l}_{2}} = 1$ см: 1 – ${{\alpha }_{2}} = - 1$, 2 – ${{\alpha }_{2}} = - 0.6$, 3 – ${{\alpha }_{2}} = - 0.1$, 4 – ${{\alpha }_{2}} = 0.5$; б: поле скоростей при ${{\alpha }_{1}} = {{\alpha }_{2}} = 0.5$.

После подстановки (2.1) в систему уравнений Обербека–Буссинеска и анализ ее совместности приходим к выводу, что и ${{\bar {p}}_{j}}$ есть квадратичные функции по $x$, $y$ (ниже они выписаны в безразмерной форме). В (2.1) ${{u}_{j}}(x)$, ${{\bar {p}}_{j}}(x)$, ${{\theta }_{j}}(x)$ – вектора скорости, модифицированные давления и температуры в слоях. Более специальный случай представления поля скорости (2.1) для движения одной жидкости рассмотрен в [14, 17], причем давление зависело лишь от вертикальной координаты и времени. Температура распределена по квадратичному закону (2.1) только на свободных границах слоя $z = \pm Z(t)$ и вызывала термокапиллярный эффект. Численное решение последней задачи с учетом общего распределения температуры $\theta (z,y,z,t)$ в слое $ - Z(t) < z < Z(t)$ проведено в статье [18]. Обстоятельный обзор точных решений системы Навье–Стокса с линейной зависимостью компонент скорости от $x$ и $y$ приведен в [15].

В настоящей работе квадратичная зависимость по $x$ и $y$ температур в (2.1) является дополнительным предположением. Также предполагается, что поверхностное натяжение линейно зависит от температуры этой поверхности $\theta (x,y,0,t)$

(2.2)
$\sigma (\theta ) = {{\sigma }_{0}} - {{\unicode{230} }}\theta $
с постоянными ${{\sigma }_{0}} > 0$ и ${{\unicode{230} }} > 0$.

Для первого слоя при $j = 1$ положим

(2.3)
$\begin{array}{*{20}{c}} {\xi = \frac{z}{{{{l}_{1}}}},\quad - {\kern 1pt} 1 < \xi < 0,\quad {{f}_{1}} = \frac{{{{\chi }_{1}}}}{{l_{1}^{2}}}{\text{M}}{{F}_{1}}(\xi ),\quad {{h}_{1}} = \frac{{{{\chi }_{1}}}}{{l_{1}^{2}}}{\text{M}}{{H}_{1}}(\xi )} \\ {{{a}_{1}} = a{\kern 1pt} *{\kern 1pt} {{A}_{1}}(\xi ),\quad {{b}_{1}} = a{\kern 1pt} *{\kern 1pt} {{B}_{1}}(\xi ),\quad {{q}_{1}} = \theta {\kern 1pt} *{\kern 1pt} {{Q}_{1}}(\xi ),\quad {{s}_{j}} = \frac{{\chi _{1}^{2}}}{{l_{1}^{4}}}{\text{M}}{{S}_{j}};\quad j = 1,2} \\ {{\text{M}} = \frac{{{{\unicode{230} }}a{\kern 1pt} *{\kern 1pt} l_{1}^{3}}}{{{{\mu }_{1}}{{\chi }_{1}}}},\quad {{{\text{P}}}_{1}} = \frac{{{{\nu }_{1}}}}{{{{\chi }_{1}}}},\quad {{L}_{1}} = \frac{{{{\rho }_{1}}{{\beta }_{1}}gl_{1}^{2}}}{{{\unicode{230} }}},\quad d = \frac{{a{\kern 1pt} *{\kern 1pt} l_{1}^{2}}}{{\theta {\kern 1pt} *}},} \end{array}$
где ${\text{M}}$ – число Марангони, ${{{\text{P}}}_{1}}$ – число Прандтля, $a{\kern 1pt} *{\kern 1pt} {{l}_{1}}$ – характерный градиент температуры, а $\theta {\kern 1pt} *$ – характерная температура. Для второго слоя $j = 2$ положим

(2.4)
$\begin{array}{*{20}{c}} {\xi = \frac{z}{{{{l}_{2}}}},\quad 0 < \xi < 1,\quad {{f}_{2}} = \frac{{{{\chi }_{1}}}}{{l_{1}^{2}}}{\text{M}}{{F}_{2}}(\xi ),\quad {{h}_{2}} = \frac{{{{\chi }_{1}}}}{{l_{1}^{2}}}{\text{M}}{{H}_{2}}(\xi )} \\ {{{a}_{2}} = a{\kern 1pt} *{\kern 1pt} {{A}_{2}}(\xi ),\quad {{b}_{2}} = a{\kern 1pt} *{\kern 1pt} {{B}_{2}}(\xi ),\quad {{q}_{2}} = \theta {\kern 1pt} *{\kern 1pt} {{Q}_{2}}(\xi ),\quad {{s}_{k}} = \frac{{\chi _{1}^{2}}}{{l_{1}^{4}}}{\text{M}}{{S}_{k}};\quad k = 3,4} \\ {{{{\text{P}}}_{2}} = \frac{{{{\nu }_{2}}}}{{{{\chi }_{2}}}},\quad {{L}_{2}} = \frac{{\rho {{\rho }_{2}}{{\beta }_{2}}g{{l}_{1}}{{l}_{2}}}}{{{\unicode{230} }}},\quad \rho = \frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}},\quad \chi = \frac{{{{\chi }_{1}}}}{{{{\chi }_{2}}}},\quad l = \frac{{{{l}_{1}}}}{{{{l}_{2}}}},\quad \mu = \frac{{{{\mu }_{1}}}}{{{{\mu }_{2}}}}} \end{array}$

В (2.3), (2.4) ${{\rho }_{j}} > 0$, ${{\nu }_{j}} > 0$, ${{\mu }_{j}} > 0$, ${{\beta }_{j}} > 0$, ${{\chi }_{j}} > 0$ – постоянные плотности, кинематические вязкости, динамические вязкости, коэффициенты теплового расширения жидкости, температуропроводности; $g > 0$ – ускорение силы тяжести. Подставляя вид решения (2.1) в систему уравнений Обербека–Буссинеска, учитывая (2.3), (2.4), получим систему нелинейных интегродифференциальных уравнений на неизвестные функции ${{F}_{j}}(\xi )$, ${{H}_{j}}(\xi )$, ${{A}_{j}}(\xi )$, ${{B}_{j}}(\xi )$, ${{Q}_{j}}(\xi )$ и постоянных ${{S}_{i}}$, $i = \overline {1,4} $

${\text{M}}\left( {F_{j}^{2} + H_{j}^{2} - 2{{F}_{{j\xi }}}\int\limits_0^\xi {{F}_{j}}(\zeta )d\zeta } \right) = {{{\text{P}}}_{j}}{{\gamma }_{j}}{{F}_{{j\xi \xi }}} - {{{\text{P}}}_{1}}{{L}_{j}}\int\limits_0^\xi [{{A}_{j}}(\zeta ) + {{B}_{j}}(\zeta )]d\zeta - {{S}_{i}}$
$2{\text{M}}\left( {{{F}_{j}}{{H}_{j}} - {{H}_{{j\xi }}}\int\limits_0^\xi {{F}_{j}}(\zeta )d\zeta } \right) = {{{\text{P}}}_{j}}{{\gamma }_{j}}{{H}_{{j\xi \xi }}} - {{{\text{P}}}_{1}}{{L}_{1}}\int\limits_0^\xi \left[ {{{A}_{j}}(\zeta ) - {{B}_{j}}(\zeta )} \right]d\zeta - {{S}_{k}}$
(2.5)
$2{\text{M}}\left[ {{{A}_{j}}\left( {{{F}_{j}} + {{H}_{j}}} \right) - {{A}_{{j\xi }}}{\kern 1pt} \int\limits_0^\xi {{F}_{j}}(\zeta )d\zeta } \right] = {{\gamma }_{j}}{{A}_{{j\xi \xi }}}$
$2{\text{M}}\left[ {{{B}_{j}}({{F}_{j}} - {{H}_{j}}) - {{B}_{{j\xi }}}\int\limits_0^\xi {{F}_{j}}(\zeta )d\zeta } \right] = {{\gamma }_{j}}{{B}_{{j\xi \xi }}}$
$ - 2{\text{M}}{{Q}_{{j\xi }}}{\kern 1pt} \int\limits_0^\xi {{F}_{j}}(\zeta )d\zeta = {{\gamma }_{j}}{{Q}_{{j\xi \xi }}} + 2d\tilde {\chi }({{A}_{j}} + {{B}_{j}})$

В уравнениях (2.5) ${{\gamma }_{1}} = 1$, $\tilde {\chi } = 1$, $i = 1$, $k = 2$ для первого слоя $ - 1 < \xi < 0$ при $j = 1$ и ${{\gamma }_{2}} = {{l}^{2}}{\text{/}}\chi $, $\tilde {\chi } = {{\chi }^{{ - 1}}}$, $i = 3$, $k = 4$ для второго слоя $0 < \xi < 1$ при $j = 2$. Система (2.5) дополняется граничными условиями. На нижней твердой стенке $\xi = - 1$

(2.6)
$\begin{gathered} {{F}_{1}}( - 1) = {{H}_{1}}( - 1) = 0,\quad \int\limits_{ - 1}^0 {{F}_{1}}(\xi )d\xi = 0,\quad {{A}_{1}}( - 1) = {{\alpha }_{1}} \\ {{B}_{1}}( - 1) = {{\alpha }_{2}},\quad {{Q}_{1}}( - 1) = {{\alpha }_{3}}, \\ \end{gathered} $
т.е. выполнены условия прилипания и задана температура. В безразмерных переменных температура на нижней стенке есть
$\overline \theta (\bar {x},\bar {y}, - 1) = \frac{{\theta (x,y, - {{l}_{1}})}}{{\theta {\kern 1pt} *}} = d{{\bar {\alpha }}_{1}}{{\bar {x}}^{2}} + d{{\bar {\alpha }}_{2}}{{\bar {y}}^{2}} + {{\bar {\alpha }}_{3}},$
где, согласно замене (2.4), ${{\bar {\alpha }}_{1}} = {{\alpha }_{1}}{\text{/}}a{\kern 1pt} *$, ${{\bar {\alpha }}_{2}} = {{\alpha }_{2}}{\text{/}}a{\kern 1pt} *$, ${{\bar {\alpha }}_{3}} = {{\alpha }_{3}}{\text{/}}\theta {\kern 1pt} *$, ${{\alpha }_{k}} = \operatorname{const} $, $k = 1,2,3$, $\bar {x} = x{\text{/}}{{l}_{1}}$, $\bar {y} = y{\text{/}}{{l}_{1}}$. Поэтому ${{A}_{1}}( - 1) = d{{\bar {\alpha }}_{1}} \equiv {{\alpha }_{1}}$, ${{B}_{1}}( - 1) = d{{\bar {\alpha }}_{2}} \equiv {{\alpha }_{2}}$, ${{Q}_{1}}( - 1) = {{\bar {\alpha }}_{3}} \equiv {{\alpha }_{3}}$. Очевидно, что температурное поле на нижней твердой стенке имеет экстремум в точке $\bar {x} = 0$, $\bar {y} = 0$: при ${{\alpha }_{1}},{{\alpha }_{2}} < 0$ – максимум, а при ${{\alpha }_{1}},{{\alpha }_{2}} > 0$ – минимум.

Верхняя стенка $\xi = 1$ предполагается теплоизолированной и на ней также выполняются условия прилипания

(2.7)
$\begin{array}{*{20}{c}} {{{A}_{{2\xi }}}(1) = {{B}_{{2\xi }}}(1) = {{Q}_{{2\xi }}}(1) = 0,\quad {{F}_{2}}(1) = {{H}_{2}}(1) = 0,\quad \int\limits_0^1 {{F}_{2}}(\xi )d\xi = 0} \end{array}$

На поверхности раздела $\xi = 0$ имеем [14]

(2.8)
$\begin{array}{*{20}{c}} {{{F}_{1}}(0) = {{F}_{2}}(0),\quad {{H}_{1}}(0) = {{H}_{2}}(0)} \\ {{{A}_{1}}(0) = {{A}_{2}}(0),\quad {{B}_{1}}(0) = {{B}_{2}}(0),\quad {{Q}_{1}}(0) = {{Q}_{2}}(0)} \\ {\mu {{F}_{{1\xi }}}(0) - l{{F}_{{2\xi }}}(0) = - \mu ({{A}_{1}}(0) + {{B}_{1}}(0))} \\ {\mu {{H}_{{1\xi }}}(0) - l{{H}_{{2\xi }}}(0) = - \mu ({{A}_{1}}(0) - {{B}_{1}}(0))} \end{array}$
(2.9)
$\begin{array}{*{20}{c}} {l{{A}_{{2\xi }}}(0) - k{{A}_{{1\xi }}}(0) = 0,\quad l{{B}_{{2\xi }}}(0) - k{{B}_{{1\xi }}}(0) = 0,\quad l{{Q}_{{2\xi }}}(0) - k{{Q}_{{1\xi }}}(0) = 0} \end{array}$

Условия (2.8) являются следствиями непрерывности скорости и температуры на поверхности раздела, а также динамического условия для касательных напряжений. При выводе последних двух соотношений (2.8) учтено равенство (2.2). Условие для нормальных напряжений эквивалентно тому, что поверхность раздела остается плоской. Данное предположение может выполняться, например, при действии достаточного большого капиллярного давления [19]. Непрерывность потоков тепла влечет равенства (2.9). Для полной определенности задачи необходимо поставить еще два условия

(2.10)
$\begin{array}{*{20}{c}} {\int\limits_{ - 1}^0 {{H}_{1}}(\xi ){\kern 1pt} d\xi = 0,\quad \int\limits_0^1 {{H}_{2}}(\xi ){\kern 1pt} d\xi = 0,} \end{array}$
означающие вместе с интегральными равенствами (2.6), (2.7) замкнутость течений в слоях. Заметим, что задача для ${{Q}_{j}}(\xi )$ при известных ${{F}_{j}}(\xi )$, ${{A}_{j}}(\xi )$ и ${{B}_{j}}(\xi )$ отделяется. Их поведение не влияет на поле скоростей. Поэтому далее будет решаться задача для определения функций ${{F}_{j}}(\xi )$, ${{H}_{j}}(\xi )$, ${{A}_{j}}(\xi )$, ${{B}_{j}}(\xi )$ и постоянных ${{S}_{k}}$.

Приведем формулы для модифицированных давлений в безразмерном виде

${{\bar {p}}_{1}} = \frac{{{{\rho }_{1}}{{\nu }_{1}}{{\chi }_{1}}}}{{l_{1}^{2}}}\operatorname{M} {{\Pi }_{1}}\left( \xi \right)$
${{\Pi }_{1}}\left( \xi \right) = \left[ {2{{L}_{1}}\int\limits_0^\xi {{{A}_{1}}d\zeta } + \frac{1}{{{{\operatorname{P} }_{1}}}}\left( {{{S}_{1}} + {{S}_{2}}} \right)} \right]\frac{{{{{\bar {x}}}^{2}}}}{2} + \left[ {2{{L}_{1}}\int\limits_0^\xi {{{B}_{1}}d\zeta } + \frac{1}{{{{\operatorname{P} }_{1}}}}\left( {{{S}_{1}} - {{S}_{2}}} \right)} \right]\frac{{{{{\bar {y}}}^{2}}}}{2} - $
$ - \;2\frac{{{{F}_{1}}}}{{{{\operatorname{P} }_{1}}}} - 2\frac{\operatorname{M} }{{{{\operatorname{P} }_{1}}}}{{\left( {\int\limits_0^\xi {{{F}_{1}}d\zeta } } \right)}^{2}} + \frac{{{{L}_{1}}}}{d}\int\limits_0^\xi {{{Q}_{1}}d\zeta + {{\Pi }_{{10}}}} $
${{\bar {p}}_{2}} = \frac{{{{\rho }_{2}}{{\nu }_{2}}{{\chi }_{2}}}}{{l_{2}^{2}}}\operatorname{M} {{\Pi }_{2}}\left( \xi \right)$
${{\Pi }_{2}}\left( \xi \right) = \left[ {\frac{{2\chi \nu {{L}_{2}}}}{{{{l}^{2}}}}\int\limits_0^\xi {{{A}_{2}}d\zeta } + \frac{{{{\chi }^{2}}}}{{{{l}^{2}}{{\operatorname{P} }_{2}}}}\left( {{{S}_{3}} + {{S}_{4}}} \right)} \right]\frac{{{{{\bar {x}}}^{2}}}}{2} + \left[ {\frac{{2\chi \nu {{L}_{1}}}}{{{{l}^{2}}}}\int\limits_0^\xi {{{B}_{2}}d\zeta } + \frac{{{{\chi }^{2}}}}{{{{l}^{2}}{{\operatorname{P} }_{2}}}}\left( {{{S}_{3}} - {{S}_{4}}} \right)} \right]\frac{{{{{\bar {y}}}^{2}}}}{2} - $
$ - \;2\frac{{\chi {{F}_{2}}}}{{{{l}^{2}}}} - 2\frac{{{{\chi }^{2}}\operatorname{M} }}{{{{l}^{4}}{{\operatorname{P} }_{2}}}}{{\left( {\int\limits_0^\xi {{{F}_{2}}d\zeta } } \right)}^{2}} + \frac{{\chi \nu {{L}_{2}}}}{{d{{l}^{2}}}}\int\limits_0^\xi {{{Q}_{2}}d\zeta + {{\Pi }_{{20}}}} ,$
где ${{\Pi }_{{10}}},{{\Pi }_{{20}}}$ – произвольные постоянные.

3. Решение при малых числах Марангони. Предположим, что $\left| {\text{M}} \right| \ll 1$ и будем искать решение в виде (считаем, что ${{L}_{j}} = O(1)$ при $M \to 0$)

$\begin{array}{*{20}{c}} {{{F}_{j}} = F_{j}^{{(0)}} + {\text{M}}F_{j}^{{(1)}} + \ldots ,\quad {{H}_{j}} = H_{j}^{{(0)}} + {\text{M}}H_{j}^{{(1)}} + \ldots ,\quad {{S}_{k}} = S_{k}^{{(0)}} + {\text{M}}S_{k}^{{(1)}} + \ldots } \\ {{{A}_{j}} = A_{j}^{{(0)}} + {\text{M}}A_{j}^{{(1)}} + \ldots ,\quad {{B}_{j}} = B_{j}^{{(0)}} + {\text{M}}B_{j}^{{(1)}} + \ldots ;\quad k = \overline {1,4} } \end{array}$

В нулевом приближении получим линейную задачу вида (2.5)–(2.10), где ${\text{M}} = 0$. После некоторых преобразований решение указанной задачи найдется в виде (индекс “(0)” опущен)

${{F}_{1}}(\xi ) = \frac{{({{\alpha }_{1}} + {{\alpha }_{2}})}}{{48l}}\left( {l{{L}_{1}}\left( {1 - 8{{\xi }^{3}}} \right) - \frac{{(4\xi + 1)}}{{(l + \mu )}}\left( {{{l}^{2}}{{L}_{1}} + \nu {{L}_{2}} - 12l\mu } \right)} \right) - \frac{{{{S}_{1}}}}{{2{{{\text{P}}}_{1}}}}{{\xi }^{2}}$
${{F}_{2}}(\xi ) = \frac{{({{\alpha }_{1}} + {{\alpha }_{2}})}}{{48l}}\left( { - \frac{{4\nu {{L}_{2}}}}{l}\left( {2{{\xi }^{3}} + \xi } \right) + l{{L}_{1}}(1 - 4\xi ) + \frac{{(4\xi - 1)}}{{(l + \mu )}}\left( {{{l}^{2}}{{L}_{1}} + \nu {{L}_{2}} - 12l\mu } \right)} \right) - \frac{{\nu {{S}_{3}}}}{{2{{{\text{P}}}_{1}}{{l}^{2}}}}{{\xi }^{2}}$
(3.1)
${{S}_{1}} = \frac{{3{{{\text{P}}}_{1}}({{\alpha }_{1}} + {{\alpha }_{2}})}}{8}\left( {{{L}_{1}} + \frac{1}{{3l(l + \mu )}}\left( {{{l}^{2}}{{L}_{1}} + \nu {{L}_{2}} - 12l\mu } \right)} \right)$
${{S}_{3}} = {{{\text{P}}}_{1}}({{\alpha }_{1}} + {{\alpha }_{2}})\left( { - \frac{{{{L}_{2}}}}{2} + \frac{{6{{l}^{2}}}}{{48\nu l(l + \mu )}}\left( {{{l}^{2}}{{L}_{1}} + \nu {{L}_{2}} - 12l\mu } \right) - \frac{{6{{l}^{2}}{{L}_{1}}}}{{48\nu }}} \right)$
${{A}_{j}}(\xi ) = {{\alpha }_{1}},\quad {{B}_{j}}(\xi ) = {{\alpha }_{2}}$

Вид функций ${{H}_{1}}(\xi )$, ${{H}_{2}}(\xi )$ и постоянных ${{S}_{2}}$, ${{S}_{4}}$ будет совпадать с ${{F}_{1}}(\xi )$, ${{F}_{2}}(\xi )$ и ${{S}_{1}}$, ${{S}_{3}}$, соответственно, с заменой ${{\alpha }_{1}} + {{\alpha }_{2}}$ на ${{\alpha }_{1}} - {{\alpha }_{2}}$. Для первого слоя $j = 1$, $ - 1 < \xi < 0$ и для второго слоя $j = 2$, $0 < \xi < 1$.

Заметим, что ${{F}_{j}}(\xi )$ пропорциональны ${{\alpha }_{1}} + {{\alpha }_{2}}$, а ${{H}_{j}}(\xi )$ пропорциональны ${{\alpha }_{1}} - {{\alpha }_{2}}$. Поэтому для радиального нагрева подложки (${{\alpha }_{1}} = {{\alpha }_{2}} \equiv \alpha $) ${{H}_{j}}(\xi ) = 0$, ${{A}_{j}}(\xi ) = {{B}_{j}}(\xi )$ и ${{S}_{2}} = {{S}_{4}} = 0$, а в случае, когда ${{\alpha }_{1}} = - {{\alpha }_{2}}$ имеем ${{F}_{j}}(\xi ) = 0$ и ${{S}_{1}} = {{S}_{3}} = 0$.

В случае невесомости $({{L}_{j}} = 0)$ формулы (3.1) существенно упрощаются

(3.2)
$\begin{array}{*{20}{c}} {{{F}_{1}}(\xi ) = \frac{{\mu ({{\alpha }_{1}} + {{\alpha }_{2}})(4\xi + 1)}}{{4(l + \mu )}} - \frac{{{{S}_{1}}}}{{2{{{\text{P}}}_{1}}}}{{\xi }^{2}},\quad {{F}_{2}}(\xi ) = - \frac{{\mu ({{\alpha }_{1}} + {{\alpha }_{2}})(4\xi - 1)}}{{4(l + \mu )}} - \frac{{\nu {{S}_{3}}}}{{2{{{\text{P}}}_{1}}{{l}^{2}}}}{{\xi }^{2}}} \\ {{{S}_{1}} = - \frac{{3\mu {{{\text{P}}}_{1}}({{\alpha }_{1}} + {{\alpha }_{2}})}}{{2(l + \mu )}},\quad {{S}_{3}} = - \frac{{3{{l}^{2}}\rho {{{\text{P}}}_{1}}({{\alpha }_{1}} + {{\alpha }_{2}})}}{{2(l + \mu )}}} \end{array}$

Вид функций ${{A}_{j}}(\xi )$ и ${{B}_{j}}(\xi )$ остается прежним.

На рис. 1, 2 приведены профили безразмерной вертикальной компоненты скорости $W(\xi )$ для системы хладагент R134а (фреон) ($j = 1$)–воздух ($j = 2$) [20]. На рис. 1,а приведены профили безразмерной вертикальной компоненты скорости $W(\xi )$ в зависимости от ${{\alpha }_{2}}$. Если ${{\alpha }_{1}} + {{\alpha }_{2}} < 0$, то в первом слое возникает возвратное течение (жидкость движется в противоположном направлении оси $z$), а во втором слое течение направлено по оси $z$ ($\xi $) (кривые 1, 2), а если ${{\alpha }_{1}} + {{\alpha }_{2}} > 0$, то направление течений в слоях меняется на противоположное (кривые 3, 4). Кривая 4 соответствует радиальному нагреву, когда ${{\alpha }_{1}} = {{\alpha }_{2}} = \alpha > 0$. Видно, что во втором слое течение направлено в противоположную сторону оси $z$, а в первом слое – в направлении оси $z$, что и изображено на рис. 1,б. Аналогичная ситуация будет иметь место для любого случая. Поэтому далее будут приведены результаты расчетов только для вертикальной компоненты скорости, поскольку она дает представление о сформировавшихся течениях в слоях.

Рис. 2.

Безразмерная вертикальная компонента скорости $W(\xi )$ в зависимости от безразмерного параметра а: $l$: 1 – $l = 3 \times {{10}^{{ - 4}}}$, 2 – $l{{ = 10}^{{ - 3}}}$, 3 – $l = 0.1$ и б: ускорения силы тяжести $g$: 1 – $g = 0$ м/с2, 2 – $g = 3$ м/с2, 3 – $g = 6$ м/с2, 4 – $g = 9.8$ м/с2.

На рис. 2 приведены профили безразмерной вертикальной компоненты скорости $W(\xi )$ в зависимости от безразмерного параметра $l$ и ускорения силы тяжести $g$. При значении $l = 3 \times {{10}^{{ - 4}}}$ и меньше в каждом слое течение направлено по оси $z$. При $l{{ = 10}^{{ - 3}}}$ во втором слое течение становится двухвихревым, а с увеличением $l$ течение становится полностью возвратным. Структура течения в первом слое не изменяется. Кривая 1 на рис. 2,б соответствует случаю невесомости при радиальном нагреве (см. (3.2)). Видно, что с ростом $g$ направление течений в слоях меняется на противоположное.

4. Решение общей нелинейной задачи. Для решения общей нелинейной задачи (2.5)–(2.10) применяется тау-метод, являющийся модификацией метода Галеркина [21]. Произведем замену переменных в первом слое $\xi {\kern 1pt} ' = - \xi $. Тогда задача (2.5)–(2.10) перепишется в виде (штрихи опущены)

${{K}_{j}} \equiv {\text{M}}\left( {F_{j}^{2} + H_{j}^{2} - 2{{F}_{{j\xi }}}{\kern 1pt} \int\limits_0^\xi {\kern 1pt} {{F}_{j}}d\zeta } \right) - {{{\text{P}}}_{j}}{{\gamma }_{j}}{{F}_{{j\xi \xi }}} - {{{\text{P}}}_{1}}{{L}_{j}}{\kern 1pt} \int\limits_0^\xi {\kern 1pt} [{{A}_{j}} + {{B}_{j}}]d\zeta + {{S}_{i}} = 0$
(4.1)
$\begin{gathered} {{T}_{j}} \equiv 2{\text{M}}\left( {{{F}_{j}}{{H}_{j}} - {{H}_{{j\xi }}}{\kern 1pt} \int\limits_0^\xi {{F}_{j}}d\zeta } \right) - {{{\text{P}}}_{j}}{{\gamma }_{j}}{{H}_{{j\xi \xi }}} - {{{\text{P}}}_{1}}{{L}_{1}}\int\limits_0^\xi {\kern 1pt} \text{[}{{A}_{j}} - {{B}_{j}}]d\zeta + {{S}_{k}} = 0 \\ {{N}_{j}} \equiv 2{\text{M}}\left[ {{{A}_{j}}({{F}_{j}} + {{H}_{j}}) - {{A}_{{j\xi }}}{\kern 1pt} \int\limits_0^\xi {{F}_{j}}d\zeta } \right] - {{\gamma }_{j}}{{A}_{{j\xi \xi }}} = 0 \\ \end{gathered} $
${{D}_{j}} \equiv 2{\text{M}}\left[ {{{B}_{j}}({{F}_{j}} - {{H}_{j}}) - {{B}_{{j\xi }}}{\kern 1pt} \int\limits_0^\xi {{F}_{j}}d\zeta } \right] - {{\gamma }_{j}}{{B}_{{j\xi \xi }}} = 0$
${{F}_{j}}(1) = 0,\quad {{H}_{j}}(1) = 0,\quad {{A}_{1}}(1) = {{\alpha }_{1}},\quad {{B}_{1}}(1) = {{\alpha }_{2}},\quad {{A}_{{2\xi }}}(1) = {{B}_{{2\xi }}}(1) = 0$
${{F}_{1}}(0) = {{F}_{2}}(0),\quad {{H}_{1}}(0) = {{H}_{2}}(0),\quad {{A}_{1}}(0) = {{A}_{2}}(0),\quad {{C}_{1}}(0) = {{C}_{2}}(0)$
(4.2)
$l{{F}_{{2\xi }}}(0) + \mu {{F}_{{1\xi }}}(0) = \mu ({{A}_{1}}(0) + {{B}_{1}}(0))$
$l{{H}_{{2\xi }}}(0) + \mu {{H}_{{1\xi }}}(0) = \mu ({{A}_{1}}(0) - {{B}_{1}}(0))$
$l{{A}_{{2\xi }}}(0) + k{{A}_{{1\xi }}}(0) = 0,\quad l{{B}_{{2\xi }}}(0) + k{{B}_{{1\xi }}}(0) = 0$
(4.3)
$\int\limits_0^1 {{F}_{j}}(\xi )d\xi = \int\limits_0^1 {{H}_{j}}(\xi )d\xi = 0;\quad j = 1,2$

Приближенное решение задачи (4.1)–(4.3) ищется в виде сумм

(4.4)
$\begin{gathered} {{F}_{{jn}}}(\xi ) = \sum\limits_{k = 1}^n {\kern 1pt} F_{j}^{k}{{R}_{k}}(\xi ),\quad {{H}_{{jn}}}(\xi ) = \sum\limits_{k = 1}^n {\kern 1pt} H_{j}^{k}{{R}_{k}}(\xi ) \\ {{A}_{{jn}}}(\xi ) = \sum\limits_{k = 0}^n {\kern 1pt} A_{j}^{k}{{R}_{k}}(\xi ),\quad {{B}_{{jn}}}(\xi ) = \sum\limits_{k = 0}^n {\kern 1pt} B_{j}^{k}{{R}_{k}}(\xi ), \\ \end{gathered} $
где ${{R}_{k}}(z) = {{P}_{k}}(2z - 1)$ – смещенные полиномы Лежандра, $z \in [0,1]$, ${{P}_{k}}(z)$ – обычные полиномы Лежандра. Из интегральных условий (4.3), учитывая ортогональность полиномов Лежандра ${{R}_{k}}(z)$ на отрезке [0, 1], получим $F_{j}^{0} = H_{j}^{0} = 0$. Остальные коэффициенты $F_{j}^{k}$, $H_{j}^{k}$, $A_{j}^{k}$, $B_{j}^{k}$, и постоянные ${{S}_{{kn}}}$, $k = \overline {1,4} $ находятся из системы галеркинских приближений
(4.5)
$\begin{array}{*{20}{c}} {\int\limits_0^1 {{K}_{j}}{{R}_{m}}(\xi )d\xi = 0,\quad \int\limits_0^1 {{T}_{j}}{{R}_{m}}(\xi )d\xi = 0,\quad \int\limits_0^1 {{N}_{j}}{{R}_{m}}(\xi )d\xi = 0} \\ {\int\limits_0^1 {{D}_{j}}{{R}_{m}}(\xi )d\xi = 0;\quad m = 0,...,n - 2} \end{array}$
и преобразованных граничных условий (4.2)

$\sum\limits_{k = 1}^n {\kern 1pt} F_{j}^{k} = 0,\quad \sum\limits_{k = 1}^n {\kern 1pt} H_{j}^{k} = 0\quad \sum\limits_{k = 0}^n {\kern 1pt} A_{1}^{k} - {{\alpha }_{1}} = 0,\quad \sum\limits_{k = 0}^n {\kern 1pt} B_{1}^{k} - {{\alpha }_{2}} = 0$
$\sum\limits_{k = 0}^n {\kern 1pt} A_{2}^{k}R_{k}^{'}(1) = 0,\quad \sum\limits_{k = 0}^n {\kern 1pt} B_{2}^{k}R_{k}^{'}(1) = 0\quad \sum\limits_{k = 1}^n {\kern 1pt} {{( - 1)}^{k}}F_{1}^{k} = \sum\limits_{k = 1}^n {\kern 1pt} {{( - 1)}^{k}}F_{2}^{k},$
(4.6)
$\begin{gathered} \sum\limits_{k = 1}^n {\kern 1pt} {{( - 1)}^{k}}H_{1}^{k} = \sum\limits_{k = 1}^n {\kern 1pt} {{( - 1)}^{k}}H_{2}^{k}\quad \sum\limits_{k = 0}^n {\kern 1pt} {{( - 1)}^{k}}A_{1}^{k} = \sum\limits_{k = 0}^n {\kern 1pt} {{( - 1)}^{k}}A_{2}^{k},\quad \sum\limits_{k = 0}^n {\kern 1pt} {{( - 1)}^{k}}B_{1}^{k} = \sum\limits_{k = 0}^n {\kern 1pt} {{( - 1)}^{k}}B_{2}^{k} \\ l\sum\limits_{k = 1}^n {\kern 1pt} F_{2}^{k}R_{k}^{'}(0) + \mu \sum\limits_{k = 1}^n {\kern 1pt} F_{1}^{k}R_{k}^{'}(0) = \mu \left( {\sum\limits_{k = 0}^n {\kern 1pt} {{{( - 1)}}^{k}}A_{1}^{k} + \sum\limits_{k = 0}^n {\kern 1pt} {{{( - 1)}}^{k}}B_{1}^{k}} \right) \\ \end{gathered} $
$l{\kern 1pt} \sum\limits_{k = 1}^n {\kern 1pt} H_{2}^{k}R_{k}^{'}(0) + \mu {\kern 1pt} \sum\limits_{k = 1}^n {\kern 1pt} H_{1}^{k}R_{k}^{'}(0) = \mu \left( {\sum\limits_{k = 0}^n {\kern 1pt} {{{( - 1)}}^{k}}A_{1}^{k} - \sum\limits_{k = 0}^n {\kern 1pt} {{{( - 1)}}^{k}}B_{1}^{k}} \right)$
$l{\kern 1pt} \sum\limits_{k = 0}^n {\kern 1pt} A_{2}^{k}R_{k}^{'}(0) + k{\kern 1pt} \sum\limits_{k = 0}^n {\kern 1pt} A_{1}^{k}R_{k}^{'}(0) = 0,\quad l{\kern 1pt} \sum\limits_{k = 0}^n {\kern 1pt} B_{2}^{k}R_{k}^{'}(0) + k{\kern 1pt} \sum\limits_{k = 0}^n {\kern 1pt} B_{1}^{k}R_{k}^{'}(0) = 0$

В частности, неизвестные постоянные ${{S}_{{kn}}}$ определяются по известным ${{F}_{{jn}}}$, ${{H}_{{jn}}}$, ${{A}_{{jn}}}$ и ${{B}_{{jn}}}$ из уравнений $\int_0^1 {{{K}_{j}}{{R}_{0}}(\xi )d\xi } $ = 0, $\int_0^1 {{{T}_{j}}{{R}_{0}}(\xi )d\xi } $ = 0. При выводе системы (4.6) было учтено, что ${{R}_{k}}(1) = 1$, ${{R}_{k}}(0) = {{( - 1)}^{k}}$. Таким образом уравнения (4.5), (4.6) образуют замкнутую систему алгебраических нелинейных уравнений на коэффициенты $F_{j}^{k}$, $H_{j}^{k}$, $A_{j}^{k}$, $B_{j}^{k}$ и постоянные ${{S}_{{kn}}}$.

Для решения нелинейной системы уравнений (4.5), (4.6) применялся метод Ньютона. В качестве нулевых приближений для неизвестных коэффициентов $F_{j}^{k}$, $H_{j}^{k}$, $A_{j}^{k}$, $B_{j}^{k}$ и постоянных ${{S}_{{kn}}}$ взяты значения, удовлетворяющие уравнениям (4.5) и условиям (4.6). В результате для различных нулевых приближений было найдено единственное решение. Расчеты проводились при $n = 10$, при этом разность полученных при $n = 10$ и $n = 11$ для ${{S}_{k}}$ составляет порядка ${{10}^{{ - 15}}}$, что говорит о хорошей сходимости $\tau $-метода при решении данной краевой задачи. Профили безразмерной вертикальной компоненты скорости $W(\xi )$, соответствующие найденному решению, в зависимости от числа Марангони изображены на рис. 3а. Кривая 3 (M = 0.1) практически совпадает с кривой 3, изображенной на рис. 1а (M = 0), а именно $\mathop {\max }\limits_{\xi \in [ - 1,0]} \left| {W(\xi ,{\text{M}} = 0)} \right|$ – $\mathop {\max }\limits_{\xi \in [ - 1,0]} \left| {W(\xi ,{\text{M}} = 0.1)} \right|$ ≈ 10–5. Аналогичная ситуация будет и для случая невесомости (рис. 3,б). Кривая 3 (M = 0.1) практически совпадает с кривой 1, изображенной на рис. 2,б (M = 0), а именно $\mathop {\max }\limits_{\xi \in [ - 1,0]} \left| {W(\xi ,{\text{M}} = 0)} \right|$ – $\mathop {\max }\limits_{\xi \in [ - 1,0]} \left| {W(\xi ,{\text{M}} = 0.1)} \right|$ ≈ 10–8. То есть, с уменьшением числа Марангони решение общей нелинейной задачи стремится к решению модельной задачи о ползущем течении.

Рис. 3.

Безразмерная вертикальная компонента скорости $W(\xi )$ в зависимости от числа Марангони (M) при а: ${{\alpha }_{1}} = 0.5$, ${{\alpha }_{2}} = - 0.1$, $g = 9.8$ м/с2: 1 – M = 10, 2 – M = 1, 3 – M = 0.1; б: ${{\alpha }_{1}} = 0.5$, ${{\alpha }_{2}} = 0.5$, $g = 0$ м/с2: 1 – M = 10, 2 – M = 1, 3 – M = 0.1.

Заключение. Задача о стационарном трехмерном двухслойном движении со специальным полем скоростей сведена к сопряженной задаче для системы одномерных интегродифференциальных уравнений. Полученная задача является обратной относительно градиентов давлений вдоль горизонтальных координат. Решение линейной задачи (при малых числах Марангони) найдено в аналитическом виде. Нелинейная задача решена тау-методом. Найденное решение при уменьшении числа Марангони стремится к решению задачи о ползущем течении. Проведен анализ влияния безразмерных физических и геометрических параметров на структуру течений в слоях.

Работа поддержана Красноярским математическим центром, финансируемым Минобрнауки РФ в рамках мероприятий по созданию и развитию региональных НОМЦ (Соглашение 075-02-2021-1384).

Список литературы

  1. Hiemenz K. Die Grenzschicht an einem in den gleichförmigen Flüssigkeitsstrom eingetauchten geraden Kreiszylinder // Dinglers Poliytech. J. 1911. V. 326. P. 321–440.

  2. Howann F. Der Einfluss grosser Zahigkeit bei der Stromung um den Zylinder und um die Kugel // Zeitschrift für Angewandte Mathematik und Mechanik. 1936. V. 16. P. 153–164.

  3. Howarth L. The boundary layer in three-dimensional flow. Part II. The flow near a stagnation point // Lond. Edinb. Dubl. Phil. Mag.: Ser. 7. 1951. V. 42. № 335. P. 1433–1440.

  4. Davey A. Boundary-layer flow at a saddle point of attachment // J. Fluid Mech. 1961. V. 10. № 4. P. 593–610.

  5. Wang C.Y. Axisymmetric stagnation flow on a cylinder // Q. Appl. Math. 1974. V. 32. № 2. P. 207–213.

  6. Gorla R.S.R. Unsteady laminar axisymmetric stagnation flow over a circular cylinder // Develop. Mech. 1977. V. 9. P. 286–288.

  7. Bekezhanova V.B., Andreev V.K., Shefer I.A. Influence of heat defect on the characteristics of a two-layer flow with the Hiemenz-type velocity // Interfac. Phenom.&Heat Transfer. 2019. V. 7. I. 4. P. 345–364.

  8. Lin C.C. Note on a class of exact solutions in magnetohydrodynamics // Arch. Rational Mech. Anal. 1958. V. 1. P. 391–395.

  9. Сидоров А.Ф. О двух классах решений уравнений механики жидкости и газа и их связи с теорией бегущих волн // ПМТФ. 1989. № 2. С. 34–40.

  10. Andreev V.K. On a creeping 3D convective motion of fluids with an isothermal interface // J. Sib. Fed. Univ. Math.&Phys. 2020. V. 13. № 6. P. 661–669.

  11. Азанов А.А., Андреев В.К. Решение задачи о ползущем движении жидкости со свободной границей со специальным полем скоростей в трехмерной полосе // Некоторые актуальные проблемы современной математики и математического образования. Герценовские чтения – 2021. Матер. научн. конф. СПб.: Изд. РГПУ им. А.И. Герцена. Изд. ВВМ. 2021. С. 42–54.

  12. Andreev V.K., Lemeshkova E.N. Two-layer steady creeping thermocapillary flow in a three-dimensional channel // J. Appl. Mech. Tech. Phys. 2022. V. 63. № 1. P. 82–88.

  13. Andreev V.K. On a creeping 3D convective motion of fluids with an isothermal interface // J. Sib. Fed. Univ. Math.&Phys. 2020. V. 13 (6). P. 661–669.

  14. Andreev V.K., Gaponenko Yu.A., Goncharova O.N., Pukhnachev V.V. Mathematical Models of Convection. Berlin; Boston: De Gruyter, 2020.

  15. Аристов С.Н., Князев Д.В., Полянин А.Д. Точные решения уравнений Навье–Стокса с линейной зависимостью компонент скорости от двух пространственных переменных // Теорет. основы хим. технол. 2009. Т. 43. № 5. С. 547–566.

  16. Джозеф Д. Устойчивость движений жидкости. М.: Мир, 1981. 638 с.

  17. Pukhnachev V.V. Model of viscous layer deformation by thermocapillary forces // Eur. J. Appl. Math. 2002. V. 13. № 2. P. 205–224.

  18. Rezanova E.V. Numerical modelling of heat transfer in the layer of viscous incompressible liquid with free boundaries // EPJ Web Conf. 2017. № 159. P. 00047.

  19. Zeytounian R.Kh. The Benard–Marangoni thermocapillary instability problem // UFN. 1998. V. 168. № 3. P. 259–286.

  20. Богданов С.Н., Бурцев С.И., Иванов О.П., Куприянова А.В. Холодильная техника. Кондиционирование воздуха. Свойства веществ: Справ. / Под ред. Богданова С.Н. СПб.: СПбГАХПТ, 1999. 320 с.

  21. Fletcher C.A.J. Computational Galerkin Method. Springer, 1984.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал