Прикладная математика и механика, 2023, T. 87, № 2, стр. 186-199

Уединенныe волны в двухслойной жидкости с кусочно-экспоненциальной стратификацией

Н. И. Макаренко^1, *, Ж. Л. Мальцева^1, **, А. А. Черевко^1, ***

¹ Институт гидродинамики им. М.А. Лаврентьева СО РАН
Новосибирск, Россия

^* E-mail: makarenko@hydro.nsc.ru
^** E-mail: maltseva@hydro.nsc.ru
^*** E-mail: cherevko@hydro.nsc.ru

Поступила в редакцию 01.02.2023
После доработки 01.03.2023
Принята к публикации 01.03.2023

EDN: TZPUKQ
DOI: 10.31857/S0032823523020091

Аннотация

Рассматривается задача о внутренних стационарных волнах в двухслойной жидкости с плотностью, экспоненциально зависящей от глубины внутри слоев и имеющей скачок на поверхности раздела. Выведено нелинейное уравнение второго длинноволнового приближения и рассмотрено семейство асимптотических подмоделей, описывающих уединенные волны конечной амплитуды. Исследованы дисперсионные свойства и режимы распространения волн в зависимости от безразмерных параметров фонового кусочно-постоянного течения.

Ключевые слова: двухслойная жидкость, слабая стратификация, уединенные волны

Внутренние волны играют важную роль в процессах переноса и трансформации энергии в стратифицированных потоках в океане [1–3]. Уединенные волны являются одним из основных объектов при изучении закономерностей распространения локализованных нелинейных возмущений в диспергирующих неоднородных средах [4–6]. В работе рассматривается двумерная задача об уединенных волнах в двухслойной жидкости с плотностью, экспоненциально зависящей от глубины внутри слоев и имеющей скачок на поверхности раздела. Указанная гидродинамическая постановка является естественным обобщением модели движения расслоенной жидкости с постоянными плотностями в слоях. Математическая формулировка данной задачи сводится к решению нелинейного эллиптического уравнения Дюбрей–Жакотэн–Лонга [7, 8] для функции тока, дополненного кинематическим и динамическим граничными условиями на поверхности раздела. Методом возмущений по параметрам слабой стратификации выведено нелинейное уравнение второго длинноволнового приближения, описывающее уединенные волны конечной амплитуды. Исследованы дисперсионные свойства линеаризованной задачи, дающие условия до- и сверхкритичности невозмущенного стратифицированного потока. Рассмотрены асимптотические подмодели, описывающие некоторые предельные режимы распространения нелинейных волн [9–12].

1. Постановка задачи. Рассматривается двумерное течение двухслойной жидкости в области, ограниченной снизу горизонтальным дном $y = - {{h}_{1}}$ и сверху – непроницаемой крышкой $y = {{h}_{2}}$ (рис. 1). Течение является установившимся в системе отсчета, связанной с бегущей волной. Стационарные уравнения Эйлера невязкой неоднородной жидкости имеют вид

(1.1)

${{u}_{x}} + {{{v}}_{y}} = 0,\quad u{{\rho }_{x}} + {v}{{\rho }_{y}} = 0$

(1.2)

$\rho (u{{u}_{x}} + {v}{{u}_{y}}) + {{p}_{x}} = 0,\quad \rho (u{{{v}}_{x}} + {v}{{{v}}_{y}}) + {{p}_{y}} = - \rho g,$

где $(u,{v})$ – вектор скорости, $p$ – давление, $\rho $ – плотность жидкости, $g$ – ускорение силы тяжести. Условия непротекания на ровном дне и крышке имеют вид

(1.3)

${v} = {{\left. 0 \right|}_{{y = - {{h}_{1}},y = {{h}_{2}}}}}$

Рис. 1.

Схема движения жидкости.

На искомой поверхности раздела слоев $y = \eta (x)$ должны быть выполнены кинематическое и динамическое граничные условия

(1.4)

$u{{\eta }_{x}} - {v} = {{\left. 0 \right|}_{{y = \eta \pm 0}}},\quad [p] = {{\left. 0 \right|}_{{y = \eta }}}$

(квадратные скобки здесь означают символ скачка). В невозмущенном потоке, к которому течение должно стремиться при ${\text{|}}x{\text{|}} \to + \infty $, граница раздела совпадает с прямой $y = 0$, вектор скорости кусочно-постоянен: $(u,{v}) = ({{u}_{j}},0)$ в $j$-м слое $(j = 1,2)$, а профиль плотности задается в виде

(1.5)

${{\rho }_{0}}(y) = \left\{ \begin{gathered} {{\rho }_{1}}\exp \left( { - N_{1}^{2}y{\text{/}}g} \right),\quad - {\kern 1pt} {{h}_{1}} < y < 0 \hfill \\ {{\rho }_{2}}\exp \left( { - N_{2}^{2}y{\text{/}}g} \right),\quad 0 < y < {{h}_{2}}, \hfill \\ \end{gathered} \right.$

где ${{N}_{j}}$ – частота плавучести (частота Брента–Вяйсяля), постоянная внутри $j$-го слоя. Величины ${{\rho }_{2}} < {{\rho }_{1}}$ являются предельными значениями для плотности сверху и снизу на поверхности раздела.

С введением функции тока $\psi $ для поля скоростей $u = {{\psi }_{y}}$, ${v} = - {{\psi }_{x}}$ система уравнений Эйлера (1.1)–(1.2) эквивалентным образом сводится к уравнению Дюбрей-Жакотэн–Лонга ([7, 8], см. также [1])

$\rho (\psi )\Delta \psi + \rho _{\psi }^{'}(\psi )\left( {\frac{1}{2}{{{\left| {\nabla \psi } \right|}}^{2}} + gy} \right) = (\rho (\psi )b(\psi ))_{\psi }^{'}$

Зависимость плотности жидкости $\rho $ от функции тока $\psi $ в $j$-м слое дается формулой $\rho (\psi ) = {{\rho }_{0}}(\psi {\text{/}}{{u}_{j}})$ ($j = 1,2$), а функция Бернулли $b$ имеет вид

$b = {{b}_{j}}(\psi ) = \frac{1}{2}u_{j}^{2} + \frac{{g\psi }}{{{{u}_{j}}}} + \frac{{{{g}^{2}}}}{{N_{j}^{2}}}{\kern 1pt} \left( {1 - {{e}^{{\tfrac{{N_{j}^{2}\psi }}{{g{{u}_{j}}}}}}}} \right)$

Давление $p$ выражается через функцию $\psi $ в силу интеграла Бернулли

$\frac{1}{2}{{\left| {\nabla \psi } \right|}^{2}} + \frac{p}{{\rho (\psi )}} + gy = b(\psi )$

Таким образом, задача об уединенных волнах в двухслойной жидкости с кусочно-экспоненциальной стратификацией заключается в отыскании формы границы раздела $\eta (x)$ и функции тока $\psi = {{\psi }_{1}}(x,y)$ ($ - {{h}_{1}} < y < \eta (x)$) и $\psi = {{\psi }_{2}}(x,y)$ ($\eta (x) < y < {{h}_{2}}$), удовлетворяющей внутри каждого из слоев нелинейному уравнению

(1.6)

${{\psi }_{{jxx}}} + {{\psi }_{{jyy}}} = \frac{{N_{j}^{2}}}{{g{{u}_{j}}}}\left\{ {g\left( {y - \frac{{{{\psi }_{j}}}}{{{{u}_{j}}}}} \right) + \frac{1}{2}\left( {\psi _{{jx}}^{2} + \psi _{{jy}}^{2} - u_{j}^{2}} \right)} \right\}\quad (j = 1,2)$

условиям постоянства функции тока на дне, крышке и поверхности раздела, равносильным кинематическим условиям (1.3)–(1.4):

(1.7)

${{\psi }_{1}}(x, - {{h}_{1}}) = - {{u}_{1}}{{h}_{1}},\quad {{\psi }_{1}}(x,\eta (x)) = {{\psi }_{2}}(x,\eta (x)) = 0,\quad {{\psi }_{2}}(x,{{h}_{2}}) = {{u}_{2}}{{h}_{2}},$

динамическому условию, следующему из условия (1.4) непрерывности давления на поверхности раздела слоев $y = \eta (x)$:

(1.8)

${{\rho }_{1}}\left( {\psi _{{1x}}^{2} + \psi _{{1y}}^{2} - u_{1}^{2} + 2g\eta } \right) = {{\rho }_{2}}\left( {\psi _{{2x}}^{2} + \psi _{{2y}}^{2} - u_{2}^{2} + 2g\eta } \right),$

и условию затухания волны на бесконечности

(1.9)

${{\psi }_{j}}(x,y) \to {{u}_{j}}{\kern 1pt} y,\quad \eta (x) \to 0\quad (x \to \pm \infty )$

Задача (1.6)–(1.9) допускает первый интеграл, вытекающий из интегрального закона сохранения потока горизонтального импульса

$\int\limits_{ - {{h}_{1}}}^{{{h}_{2}}} {\left( {\rho {{u}^{2}} + p} \right)dy} = \operatorname{const} $

для стационарных уравнений Эйлера (1.1)–(1.2). В терминах функции тока данный закон сохранения имеет вид

(1.10)

${{\rho }_{1}}\int\limits_{ - {{h}_{1}}}^{\eta (x)} {{e}^{{ - \tfrac{{N_{1}^{2}{{\psi }_{1}}}}{{g{{u}_{1}}}}}}}{{\Psi }_{1}}dy + {{\rho }_{2}}\int\limits_{\eta (x)}^{{{h}_{2}}} {{e}^{{ - \tfrac{{N_{2}^{2}{{\psi }_{2}}}}{{g{{u}_{2}}}}}}}{{\Psi }_{2}}dy = C,$

где подынтегральные функции ${{\Psi }_{j}}$ даются формулой

${{\Psi }_{j}} = \psi _{{jy}}^{2} - \psi _{{jx}}^{2} + u_{j}^{2} + 2g\left( {\frac{{{{\psi }_{j}}}}{{{{u}_{j}}}} - y} \right) - \frac{{2{{g}^{2}}}}{{N_{j}^{2}}}\left( {{{e}^{{\tfrac{{N_{j}^{2}{{\psi }_{j}}}}{{g{{u}_{j}}}}}}} - 1} \right),$

а константа интегрирования $C$, зависящая от параметров основного течения, находится из условия (1.9).

2. Безразмерные переменные. Выберем в качестве масштаба для линейных величин невозмущенную глубину ${{h}_{1}}$ нижнего слоя, а для функции тока – объемные расходы жидкости в слоях:

$(x,y,\eta ) = {{h}_{1}}(\bar {x},\bar {y},\bar {\eta }),\quad {{\psi }_{j}} = {{u}_{j}}{{h}_{j}}{{\bar {\psi }}_{j}}\quad (j = 1,2)$

Тогда в нижнем слое безразмерная функция тока должна быть решением краевой задачи

(2.1)

$\begin{gathered} {{\psi }_{{1xx}}} + {{\psi }_{{1yy}}} + \lambda _{1}^{2}({{\psi }_{1}} - y) = \frac{1}{2}{{\sigma }_{1}}\left( {\psi _{{1x}}^{2} + \psi _{{1y}}^{2} - 1} \right)\quad ( - 1 < y < \eta (x)) \\ {{\psi }_{1}}(x, - 1) = - 1,\quad {{\psi }_{1}}(x,\eta (x)) = 0 \\ \end{gathered} $

(черта в обозначениях безразмерных величин здесь и далее опущена). В верхнем слое аналогичные уравнения имеют вид

(2.2)

$\begin{gathered} {{\psi }_{{2xx}}} + {{\psi }_{{2yy}}} + \lambda _{2}^{2}{{r}^{2}}({{\psi }_{2}} - ry) = \frac{1}{2}{{\sigma }_{2}}\left( {\psi _{{2x}}^{2} + \psi _{{2y}}^{2} - {{r}^{2}}} \right)\quad (\eta (x) < y < 1{\text{/}}r) \\ {{\psi }_{2}}(x,\eta (x)) = 0,\quad {{\psi }_{2}}(x,1{\text{/}}r) = 1, \\ \end{gathered} $

а динамическое граничное условие (1.8) принимает форму

(2.3)

$2\eta = F_{2}^{2}\left( {{{r}^{{ - 2}}}\psi _{{2x}}^{2} + {{r}^{{ - 2}}}\psi _{{2y}}^{2} - 1} \right) - F_{1}^{2}\left( {\psi _{{1x}}^{2} + \psi _{{1y}}^{2} - 1} \right)\quad (y = \eta (x))$

В уравнениях (2.11)–(2.13) присутствуют следующие безразмерные константы. Спектральными параметрами в рассматриваемой задаче являются плотностные (денсиметрические) числа Фруда ${{F}_{j}}$, нормирующие фазовую скорость волны относительно каждого из слоев, и числа Лонга ${{\lambda }_{j}}$, характеризующие баланс между силами плавучести и инерции [13]:

(2.4)

${{F}_{j}} = \frac{{{{u}_{j}}}}{{\sqrt {{{g}_{j}}{{h}_{j}}} }},\quad {{\lambda }_{j}} = \frac{{{{N}_{j}}{{h}_{j}}}}{{{{u}_{j}}}}\quad (j = 1,2),$

где ${{g}_{j}} = g({{\rho }_{1}} - {{\rho }_{2}}){\text{/}}{{\rho }_{j}}$ – приведенные гравитационные ускорения для каждого из слоев. Кусочно-экспоненциальная стратификация (1.5) в невозмущенном течении определяется тремя независимыми константами

${{\sigma }_{j}} = \frac{{N_{j}^{2}{{h}_{j}}}}{g}\quad (j = 1,2),\quad \mu = \frac{{{{\rho }_{1}} - {{\rho }_{2}}}}{{{{\rho }_{2}}}}$

При этом параметры Буссинеска ${{\sigma }_{j}}$ характеризуют градиенты плотности внутри каждого из слоев, а величина $\mu $ – скачок плотности между слоями (в таком качестве в литературе часто используется также число Атвуда A = $({{\rho }_{1}} - {{\rho }_{2}}){\text{/}}({{\rho }_{1}} + {{\rho }_{2}})$). Все три величины $\mu $, ${{\sigma }_{1}}$, ${{\sigma }_{2}}$ являются естественными малыми параметрами в натурных условиях слабой стратификации. В уравнениях (2.1)–(2.3) в явном виде присутствуют только ${{\sigma }_{1}}$ и ${{\sigma }_{2}}$, однако параметр $\mu $ играет важную роль, поскольку числа Лонга ${{\lambda }_{j}}$ и числа Фруда ${{F}_{j}}$, определяемые формулой (2.4), не являются независимыми параметрами – они связаны соотношениями

(2.5)

$\lambda _{1}^{2} = \frac{{{{\sigma }_{1}}(1 + \mu )}}{{\mu F_{1}^{2}}},\quad \lambda _{2}^{2} = \frac{{{{\sigma }_{2}}}}{{\mu F_{2}^{2}}}$

Кроме того, в задаче имеется геометрический параметр $r = {{h}_{1}}{\text{/}}{{h}_{2}}$ – отношение толщин невозмущенных слоев.

Уравнения (2.1)–(2.3) охватывают частные случаи, когда плотность жидкости тождественно постоянна в одном из слоев или сразу в обоих. А именно, случай ${{\sigma }_{2}} = {{\lambda }_{2}} = 0$ соответствует наличию однородного безвихревого приповерхностного слоя, а при ${{\sigma }_{1}} = {{\lambda }_{1}} = 0$ однородным является придонный слой. Однако присутствие в формуле (2.5) отношений малых параметров ${{\sigma }_{1}}{\text{/}}\mu $ и ${{\sigma }_{2}}{\text{/}}\mu $ указывает на возможную неравномерность предельного перехода ${{\sigma }_{1}} \to 0$, ${{\sigma }_{2}} \to 0$. Кроме того, наличие скачка скорости на границе раздела в фоновом течении может вести к развитию сдвиговой неустойчивости Кельвина–Гельмгольца, причем энергетически наиболее опасными для разрушения течения являются длинноволновые возмущения. Поток с постоянными скоростями и плотностями в слоях устойчив к ним при следующем ограничении на скорости, плотности и толщины слоев [4]:

(2.6)

$\left| {{{u}_{1}} - {{u}_{2}}} \right| < \sqrt {\frac{{g({{\rho }_{1}} - {{\rho }_{2}})({{\rho }_{1}}{{h}_{2}} + {{\rho }_{2}}{{h}_{1}})}}{{{{\rho }_{1}}{{\rho }_{2}}}}} $

3. Дисперсионные свойства. Рассмотрим условия, обеспечивающие свойство сверхкритичности нелинейных стационарных волн в рассматриваемой системе по отношению к фазовым скоростям линейных гармонических волн. Линеаризация уравнений (2.1)–(2.3) на невозмущенном кусочно-постоянном течении, описываемом точным решением

(3.1)

$\eta = 0,\quad {{\psi }_{1}} = y\quad ( - 1 < y < 0),\quad {{\psi }_{2}} = ry\quad \left( {0 < y < {{r}^{{ - 1}}}} \right)$

и отыскание решений в виде волновых пакетов $\eta (x)$ = $a\exp (ikx)$ и $\psi = {{\psi }_{0}}$ + $W(y)\exp (ikx)$ приводит к спектральной задаче Штурма–Лиувилля для амплитудной функции $W$ (см. [1, 2]), которая дает в случае закона стратификации (1.5) дисперсионное соотношение

(3.2)

$\Delta (k;F,\lambda ,\sigma ) = 0,$

где функция $\Delta $ имеет вид

(3.3)

$\Delta (k;F,\lambda ,\sigma ) = F_{1}^{2}\left( {{{\kappa }_{1}}\operatorname{ctg} {{\kappa }_{1}} + \frac{{{{\sigma }_{1}}}}{2}} \right) + F_{2}^{2}\left( {{{\kappa }_{2}}\operatorname{ctg} {{\kappa }_{2}} - \frac{{{{\sigma }_{2}}}}{2}} \right) - 1$

с вспомогательными волновыми числами

(3.4)

$\kappa _{j}^{2}\;\mathop = \limits^{{\text{def}}} \;\lambda _{j}^{2} - k_{j}^{2} - {{\left( {\frac{{{{\sigma }_{j}}}}{2}} \right)}^{2}}\quad (j = 1,2)$

Здесь обозначено ${{k}_{1}} = rk$ и ${{k}_{2}} = k$, и, кроме того, нужно учитывать, что числа Лонга ${{\lambda }_{j}}$ связаны с числами Фруда ${{F}_{j}}$ формулой (2.5). В силу самосопряженности рассматриваемой спектральной задачи квадрат волнового числа ${{k}^{2}}$, играющий роль собственного значения, всегда вещественный. Поэтому корни $k$ уравнения (3.2) могут быть только вещественными или мнимыми, и в силу четности дисперсионной функции $\Delta $ по $k$ они образуют симметричные пары на координатных осях комплексной $k$-плоскости, причем кратным может оказаться только корень $k = 0$. Спектр линейных гармонических волн образует точки в плоскости пар чисел Фруда $F = ({{F}_{1}},{{F}_{2}})$, для которых дисперсионное соотношение (3.2) имеет по крайне мере одну пару вещественных корней $k$. В зависимости от количества пар действительных корней весь спектр разбивается на счетное множество вложенных друг в друга подобластей, содержащих спектры отдельных волновых мод. Границы этих областей задаются ветвями кривой, определяемой уравнением $\Delta (0;F,\lambda (F),\sigma )$ = 0, или, в развернутой форме,

(3.5)

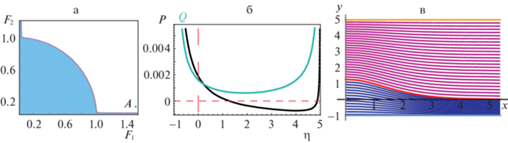
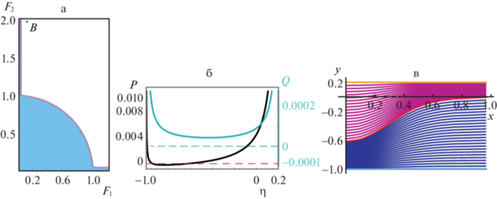
$\begin{gathered} F_{1}^{2}\left[ {\sqrt {\frac{{{{\sigma }_{1}}(1 + \mu )}}{{\mu F_{1}^{2}}} - {{{\left( {\frac{{{{\sigma }_{1}}}}{2}} \right)}}^{2}}} {\text{ctg}}\sqrt {\frac{{{{\sigma }_{1}}(1 + \mu )}}{{\mu F_{1}^{2}}} - {{{\left( {\frac{{{{\sigma }_{1}}}}{2}} \right)}}^{2}}} + \frac{{{{\sigma }_{1}}}}{2}} \right] + \\ + \;F_{2}^{2}\left[ {\sqrt {\frac{{{{\sigma }_{2}}}}{{\mu F_{2}^{2}}} - {{{\left( {\frac{{{{\sigma }_{2}}}}{2}} \right)}}^{2}}} {\text{ctg}}\sqrt {\frac{{{{\sigma }_{2}}}}{{\mu F_{2}^{2}}} - {{{\left( {\frac{{{{\sigma }_{2}}}}{2}} \right)}}^{2}}} - \frac{{{{\sigma }_{2}}}}{2}} \right] = 1 \\ \end{gathered} $

В пределе при ${{\sigma }_{1}} = {{\sigma }_{2}} = 0$ отсюда получается спектр линейных гармонических волн в двухслойной жидкости с постоянными плотностями ${{\rho }_{1}}$ и ${{\rho }_{2}}$ в слоях, который порождается волновыми числами единственной моды и совпадает с кругом $F_{1}^{2} + F_{2}^{2} \leqslant 1$. Граница спектра, задаваемая уравнением (3.5), трансформируется в единичную окружность неравномерным относительно $({{F}_{1}},{{F}_{2}})$ образом из-за присутствия в подкоренных выражениях отношений ${{\sigma }_{1}}{\text{/}}\mu $ и ${{\sigma }_{2}}{\text{/}}\mu $ малых параметров при обратных степенях чисел Фруда ${{F}_{j}}$. Указанная неравномерность проявляется в возникновении при ${{\sigma }_{j}} \to 0$ спектральных пограничных слоев [14] в окрестности координатных осей ${{F}_{1}}$ и ${{F}_{2}}$ плоскости $({{F}_{1}},{{F}_{2}})$, содержащих все спектры старших мод, начиная со второй моды (см. рис. 2а и рис. 3a). Точки $({{F}_{1}},{{F}_{2}})$, для которых отсутствуют вещественные корни $k$ дисперсионного уравнения (3.2), принадлежат сверхкритической области, лежащей вне непрерывного спектра главной моды линейных гармонических волн.

Рис. 2.

Уединенная волна возвышения главной моды для стратифицированного течения с параметрами ${{\sigma }_{1}} = {{\sigma }_{2}}$ = = 0.00007, $\mu = 0.003$, $r = 0.2$, ${{F}_{1}} = 1.5$, ${{F}_{2}} = 0.129$.

4. Длинноволновое приближение. В сверхкритической области все корни дисперсионного соотношения (3.2) чисто мнимые. Пусть $k = \pm i\varepsilon $ – наименьший из них по модулю. Величина $\varepsilon > 0$, являющаяся минимальным положительным корнем уравнения $\Delta (i\varepsilon ;F,\lambda (F),\sigma )$ = 0, дает показатель экспоненциального затухания решений типа уединенных волн: $\eta (x)\sim a{{e}^{{ - \varepsilon |x|}}}$ при $\left| x \right| \to \infty $. Этот показатель мал для точек $F = ({{F}_{1}},{{F}_{2}})$ вблизи границы спектра, поэтому при построении длинноволнового приближения его удобно связать с малыми параметрами кусочно-экспоненциальной стратификации (1.5). Учитывая, что параметры Буссинеска ${{\sigma }_{1}}$ и ${{\sigma }_{2}}$ независимы друг от друга в разных слоях, выберем в качестве основного малого параметра величину $\sigma = \sqrt {\sigma _{1}^{2} + \sigma _{2}^{2}} $ и введем полярный угол $\varphi $ в плоскости $({{\sigma }_{1}},{{\sigma }_{2}})$, полагая ${{\sigma }_{1}} = \cos \varphi $, ${{\sigma }_{2}} = sin\varphi $. Из разложения дисперсионной функции

$\Delta (0;F,\lambda ,\sigma ) - \Delta (i\varepsilon ;F,\lambda ,\sigma ) = \left( {F_{1}^{2}\frac{{2{{\lambda }_{1}} - \sin 2{{\lambda }_{1}}}}{{4{{{\sin }}^{2}}{{\lambda }_{1}}}} + F_{2}^{2}\frac{{2{{\lambda }_{2}} - \sin 2{{\lambda }_{2}}}}{{4{{{\sin }}^{2}}{{\lambda }_{2}}}}} \right){{\varepsilon }^{2}} + O({{\varepsilon }^{4}} + {{\sigma }^{2}}{{\varepsilon }^{2}})$

следует, что на семействе линий уровня вида $\Delta (0;F,\lambda (F),\sigma )$ = Mσ ($M = \operatorname{const} $ > 0), располагающемся вблизи границы спектра главной моды в плоскости $({{F}_{1}},{{F}_{2}})$ (со стороны сверхкритической области), показатель затухания $\varepsilon $ имеет порядок $\sqrt \sigma $ при $\sigma \to 0$. Учитывая это, будем искать решение зависящим от медленной переменной $\xi = \sqrt \sigma x$. При выводе длинноволнового приближения используется асимптотическое представление функций тока в виде

(4.1)

${{\psi }_{j}}(x,y) = \psi _{j}^{{(0)}}(\xi ,y) + \sigma \psi _{j}^{{(1)}}(\xi ,y) + O\left( {{{\sigma }^{2}}} \right)\quad (j = 1,2)$

Коэффициенты $\psi _{j}^{{(m)}}(\xi ,y)$ разложения (4.1) находятся в результате интегрирования получаемой из (2.1), (2.2) рекуррентной последовательности обыкновенных дифференциальных уравнений с независимой переменной $y$, в которые $\xi $ входит в качестве параметра. В частности, коэффициенты низшего порядка выражаются через функцию $\eta $ по формулам

$\psi _{1}^{{(0)}} = y - \eta \frac{{\sin {{\lambda }_{1}}(1 + y)}}{{\sin {{\lambda }_{1}}(1 + \eta )}},\quad \psi _{2}^{{(0)}} = ry - r\eta \frac{{\sin {{\lambda }_{2}}(1 - ry)}}{{\sin {{\lambda }_{2}}(1 - r\eta )}}$

Коэффициент $\psi _{1}^{{(1)}}$, дающий в нижнем слое $ - 1 < y < \eta $ дисперсионную поправку в длинноволновое приближение (4/1), имеет вид

$\begin{gathered} \psi _{1}^{{(1)}} = \frac{{sin{{\alpha }_{1}}(y)}}{{2\lambda _{1}^{2}}}{{\left( {\frac{\eta }{{sin{{\alpha }_{1}}(\eta )}}} \right)}_{{\xi \xi }}}\{ {{\alpha }_{1}}(\eta ){\text{ctg}}{{\alpha }_{1}}(\eta ) - {{\alpha }_{1}}(y){\text{ctg}}{{\alpha }_{1}}(y)\} + \\ + \;cos\varphi \left\{ {\frac{{\eta (2\eta - 3y)}}{6}\frac{{sin{{\alpha }_{1}}(y)}}{{sin{{\alpha }_{1}}(\eta )}} + \frac{{{{\eta }^{2}}}}{6}{\kern 1pt} \left( {\frac{{sin{{\lambda }_{1}}(y - \eta ) - sin{{\alpha }_{1}}(y)}}{{{{{\sin }}^{3}}{{\alpha }_{1}}(\eta )}} + \frac{{1 + {{{\sin }}^{2}}{{\alpha }_{1}}(y)}}{{{{{\sin }}^{2}}{{\alpha }_{1}}(\eta )}}} \right)} \right\}, \\ \end{gathered} $

где обозначено ${{\alpha }_{1}}(y) = {{\lambda }_{1}}(1 + y)$, ${{\alpha }_{1}}(\eta ) = {{\lambda }_{1}}(1 + \eta )$. Аналогично, в верхнем слое $\eta < y < {{r}^{{ - 1}}}$ коэффициент $\psi _{2}^{{(1)}}$ имеет вид

$\begin{gathered} \psi _{2}^{{(1)}} = \frac{{\sin {{\alpha }_{2}}(y)}}{{2r\lambda _{2}^{2}}}{{\left( {\frac{\eta }{{\sin {{\alpha }_{2}}(\eta )}}} \right)}_{{\xi \xi }}}\{ {{\alpha }_{2}}(y){\text{ctg}}{{\alpha }_{2}}(y) - {{\alpha }_{2}}(\eta ){\text{ctg}}{{\alpha }_{2}}(\eta )\} + \\ + \;\sin \varphi \left\{ {\frac{{{{r}^{2}}\eta (2\eta - 3y)}}{6}\frac{{\sin {{\alpha }_{2}}(y)}}{{\sin {{\alpha }_{2}}(\eta )}} + \frac{{{{r}^{2}}{{\eta }^{2}}}}{6}{\kern 1pt} \left( {\frac{{\sin {{\lambda }_{2}}r(\eta - y) - \sin {{\alpha }_{2}}(y)}}{{{{{\sin }}^{3}}{{\alpha }_{2}}(\eta )}} + \frac{{1 + {{{\sin }}^{2}}{{\alpha }_{2}}(y)}}{{{{{\sin }}^{2}}{{\alpha }_{2}}(\eta )}}} \right)} \right\}, \\ \end{gathered} $

где ${{\alpha }_{2}}(y) = {{\lambda }_{2}}(1 - ry)$, ${{\alpha }_{2}}(\eta ) = {{\lambda }_{2}}(1 - r\eta )$. Теперь нужно воспользоваться законом сохранения импульса (1.10), записанным в безразмерной форме

(4.2)

$\int\limits_{ - 1}^\eta {{e}^{{ - {{\sigma }_{1}}{{\psi }_{1}}}}}{{\Psi }_{1}}dy + \int\limits_\eta ^{1{\text{/}}r} {{e}^{{ - {{\sigma }_{2}}{{\psi }_{2}}}}}{{\Psi }_{2}}dy = C,$

где

${{\Psi }_{1}} = \frac{{\mu F_{1}^{2}}}{2}\left( {\psi _{{1y}}^{2} - \sigma \psi _{{1\xi }}^{2} + 1} \right) + (1 + \mu )\left( {{{\psi }_{1}} - y - \frac{{{{e}^{{{{\sigma }_{1}}{{\psi }_{1}}}}} - 1}}{{{{\sigma }_{1}}}}} \right)$

${{\Psi }_{2}} = \frac{{\mu F_{2}^{2}}}{{2{{r}^{3}}}}\left( {\psi _{{2y}}^{2} - \sigma \psi _{{2\xi }}^{2} + {{r}^{2}}} \right) + \frac{1}{r}\left( {{{\psi }_{2}} - ry - \frac{{{{e}^{{{{\sigma }_{2}}{{\psi }_{2}}}}} - 1}}{{{{\sigma }_{2}}}}} \right),$

а постоянная $C$, вычисленная на точном решении (3.1), описывающем кусочно-постоянное течение, имеет вид

$\begin{gathered} C = \mu \left( {F_{1}^{2} + {{r}^{{ - 2}}}F_{2}^{2}} \right) + (1 + \mu )\left( {{{e}^{{{{\sigma }_{1}}}}} - 1 - {{\sigma }_{1}}} \right)\left( {\frac{1}{{\lambda _{1}^{2}}} + \frac{1}{{\sigma _{1}^{2}}}} \right) + \\ + \;\frac{1}{{{{r}^{2}}}}\left( {1 - {{\sigma }_{2}} - {{e}^{{ - {{\sigma }_{2}}}}}} \right)\left( {\frac{1}{{\lambda _{2}^{2}}} + \frac{1}{{\sigma _{2}^{2}}}} \right) \\ \end{gathered} $

Подставляя ряды (4.1) в интегральное соотношение (4.2) и оставляя в нем слагаемые с точностью до величин порядка $O\left( {{{\sigma }^{2}}} \right)$, получаем искомое нелинейное дифференциальное уравнение второго приближения теории длинных волн для функции $\eta = \eta (x)$:

(4.3)

$Q(\eta ;F){{\left( {\frac{{d\eta }}{{dx}}} \right)}^{2}} = {{\eta }^{2}}P(\eta ;F)$

Здесь функции $P$ и $Q$ имеют структуру квазиполиномов

(4.4)

$P = {{p}_{0}} + {{p}_{1}}\eta + {{p}_{2}}{{\eta }^{2}},\quad Q = {{q}_{0}} + {{q}_{1}}\eta + {{q}_{2}}{{\eta }^{2}} + {{q}_{3}}{{\eta }^{3}} + {{q}_{4}}{{\eta }^{4}}$

с коэффициентами ${{p}_{j}} = {{p}_{j}}(\eta ;F)$ и ${{q}_{j}} = {{q}_{j}}(\eta ;F)$, наследующими тригонометрическую зависимость коэффициентов рядов (4.1) от переменной $\eta $. В частности, коэффициенты ${{p}_{0}}$ и ${{q}_{0}}$ даются формулами

(4.5)

${{p}_{0}}(\eta ;F) = \frac{1}{2}\mu \left\{ {F_{1}^{2}\left( {{{\lambda }_{1}}{\text{ctg}}{{\alpha }_{1}}(\eta ) + \frac{{{{\sigma }_{1}}}}{2}} \right) + F_{2}^{2}\left( {{{\lambda }_{2}}{\text{ctg}}{{\alpha }_{2}}(\eta ) - \frac{{{{\sigma }_{2}}}}{2}} \right) - 1} \right\}$

(4.6)

${{q}_{0}}(\eta ;F) = \frac{{\mu F_{1}^{2}}}{{8{{\lambda }_{1}}}}\frac{{2{{\lambda }_{1}} - \sin [2{{\alpha }_{1}}(\eta )]}}{{{{{\sin }}^{2}}{{\alpha }_{1}}(\eta )}} + \frac{{\mu F_{2}^{2}}}{{8{{r}^{2}}{{\lambda }_{2}}}}\frac{{2{{\lambda }_{2}} - \sin [2{{\alpha }_{2}}(\eta )]}}{{{{{\sin }}^{2}}{{\alpha }_{2}}(\eta )}}$

Явные формулы для остальных коэффициентов ${{p}_{j}}$ и ${{q}_{j}}$ с $j \geqslant 1$ имеют более громоздкий вид и приведены в Приложении. Решения типа уединенных волн для уравнения (4.3) описываются квадратурами

(4.7)

$x = \pm \int\limits_\eta ^a \sqrt {\frac{{Q(s;F)}}{{P(s;F)}}} \frac{{ds}}{s},$

где амплитуда волны определяется простым корнем $s = a$ функции $P(s;{\kern 1pt} F)$, ближайшим к точке $s = 0$. Параметрическая область существования уединенных волн дается той частью плоскости $F = ({{F}_{1}},{{F}_{2}})$, для которой подкоренное выражение $Q{\text{/}}P$ в (4.7) остается положительным всюду в интервале между точками $s = 0$ и $s = a$.

5. Асимптотические подмодели. Дополнительные предположения об относительных порядках параметров или малости искомой функции в базовом уравнении (4.3) порождают для него семейство приближенных субмоделей. Для малых $\eta $ уравнение (4.3), рассматриваемое для медленной независимой переменной $x = \sqrt \sigma \xi $, можно представить в форме

(5.1)

$\sigma \eta _{\xi }^{2} = {{\eta }^{2}}\left[ {{{\gamma }_{0}} + {{\gamma }_{1}}\eta + {{\gamma }_{2}}{{\eta }^{2}} + O\left( {{{\eta }^{3}}} \right)} \right],$

где ${{\gamma }_{0}}(F) = {{p}_{0}}(0;F){\text{/}}{{q}_{0}}(0;F)$ с величинами ${{p}_{0}}$ и ${{q}_{0}}$ из формул (4.5) и (4.6). Поскольку ${{\alpha }_{1}}(0) = {{\lambda }_{1}}$ и ${{\alpha }_{2}}(0) = {{\lambda }_{2}}$, имеем ${{q}_{0}}(0;F) > 0$ и, согласно определению дисперсионной функции (3.3), также

${{p}_{0}}(0;F) = \frac{\mu }{2}\Delta (0;F) + O\left( {{{\sigma }^{2}}} \right)$

Такая связь коэффициента ${{\gamma }_{0}}$ с дисперсионной функцией $\Delta $ означает, что требование положительности ${{\gamma }_{0}}$, необходимое для существования малого решения уравнения (5.1), равносильно условию сверхкритичности описываемых уединенных волн. Асимптотика решений уравнения (5.1) существенно зависит также от поведения коэффициента ${{\gamma }_{1}}(F)$. Для тех точек $F = ({{F}_{1}},{{F}_{2}})$, где ${{\gamma }_{1}}(F) \ne 0$, растяжение искомой функции $\eta = \sigma {{\eta }_{0}}$ в (5.1) дает на линиях уровня $\Delta (0;F) = M\sigma $ ($M > 0$), примыкающих к границе спектра со стороны сверхкритической области, укороченное уравнение вида $\eta _{{0\xi }}^{2}$ = $\eta _{0}^{2}({{\gamma }_{0}} + {{\gamma }_{1}}{{\eta }_{0}})$. В исходных безразмерных переменных оно порождает обычные уединенные волны типа КдВ с профилем $\eta (x) = a{\text{c}}{{{\text{h}}}^{{ - 2}}}(\kappa x{\text{/}}2))$. При этом в случае ${{\gamma }_{1}} < 0$, получаются волны возвышения, а в случае ${{\gamma }_{1}} > 0$ – уединенные волны типа впадин. Амплитуда волны $a$ в обоих случаях имеет одинаковый с $\sigma $ порядок малости, а волновое число $\kappa $ порядок $\sqrt \sigma $, что согласуется с исходными предположениями при выводе уравнения (4.3). В окрестности точек $F = ({{F}_{1}},{{F}_{2}})$, в которых достигается равенство ${{\gamma }_{1}}(F) = 0$, нелинейности третьей и четвертой степеней по $\eta $ в правой части (5.1) дают одинаковый вклад, поэтому здесь малые решения имеют другую асимптотику (см. [5] и имейющиеся там ссылки). Дополнительное растяжение переменных $\zeta = \sqrt \sigma \xi $, $\eta = \sigma {{\eta }_{0}}$ дает на линиях уровня $\Delta (0;F) = M{{\sigma }^{2}}$ ($M > 0$) уравнение вида

$\eta _{{0\zeta }}^{2} = \eta _{0}^{2}\left( {M + {{\vartheta }_{1}}{{\eta }_{0}} + {{\vartheta }_{2}}\eta _{0}^{2}} \right),$

решение которого имеет вид уединенных волн с уплощенными вершинами

${{\eta }_{0}}(\zeta ) = \frac{{{{a}_{1}}{{a}_{2}}}}{{{{a}_{2}} + ({{a}_{2}} - {{a}_{1}}){\text{s}}{{{\text{h}}}^{2}}\kappa \zeta }};\quad {{\kappa }^{2}} = {{a}_{1}}{{a}_{2}}$

В любом из рассмотренных случаев уединенные волны главной моды ответвляются от основного течения на границе непрерывного спектра линеаризованной задачи, причем ветвление происходит в сверхкритическую область. При этом асимптотическая близость точек $F$ к границе спектра нейтрализует наличие малого параметра $\sigma $ при $\eta _{\xi }^{2}$ в левой части уравнения (5.1) и обеспечивает равномерную пригодность длинноволнового приближения при $ - \infty < \xi < + \infty $. Аналогичная асимптотическая схема может быть использована и для описания ветвления уединенных волн старших мод, однако в таком случае согласно имеющейся картине спектра будет возникать нелинейный резонанс с периодическими волновыми пакетами главной моды [5]. Эта ситуация требует дополнительного анализа и не рассматривается в данной статье.

При малых числах Лонга ${{\lambda }_{j}}$ для функций $P(\eta ;F)$ и $Q(\eta ;F)$ справедливы приближенные выражения

$P = \frac{\mu }{2}\left\{ {\frac{{F_{1}^{2}}}{{1 + \eta }} + \frac{{F_{2}^{2}}}{{1 - r\eta }} - 1} \right\} + O\left( {\left| \lambda \right|} \right),\quad Q = \frac{\mu }{6}\left\{ {\frac{{F_{1}^{2}}}{{1 + \eta }} + \frac{{F_{2}^{2}}}{{{{r}^{2}}(1 - r\eta )}}} \right\} + O\left( {\left| \lambda \right|} \right)$

Поэтому в пределе ${{\lambda }_{1}},{{\lambda }_{2}} \to 0$ уравнение (4.3) принимает форму

(5.2)

${{\left( {\frac{{d\eta }}{{dx}}} \right)}^{2}} = 3{{r}^{2}}{{\eta }^{2}}\frac{{F_{1}^{2}(1 - r\eta ) + F_{2}^{2}(1 + \eta ) - (1 + \eta )(1 - r\eta )}}{{{{r}^{2}}F_{1}^{2}(1 - r\eta ) + F_{2}^{2}(1 + \eta )}}$

Уравнение (5.2) известно как уравнение второго приближения теории длинных волн для двухслойной жидкости с постоянными плотностями в слоях [3, 15, 16]. Знаменатель дроби в правой части (5.2) положителен всюду в интервале $ - 1 < \eta < 1{\text{/}}r$, поэтому положительным в окрестности значения $\eta = 0$ должен быть и числитель. А это возможно тогда и только тогда, когда числа Фруда ${{F}_{1}}$ и ${{F}_{2}}$ удовлетворяют неравенству $F_{1}^{2} + F_{2}^{2} > 1$, что является условием сверхкритичности невозмущенного двухслойного течения. При этом решения типа уединенных волн существуют в случае $\left| {{{F}_{1}}} \right| + r\left| {{{F}_{2}}} \right|$ < < $\sqrt {1 + r} $, а в качестве предельного режима при $\left| {{{F}_{1}}} \right| + r\left| {{{F}_{2}}} \right|$ = $\sqrt {1 + r} $ получаются решения типа плавного бора [3].

Для сверхкритических точек $F$, находящихся вблизи узких полос спектра, где выполнено одно из условий ${{F}_{1}} = O(\sqrt {{{\sigma }_{1}}} )$ или ${{F}_{2}} = O(\sqrt {{{\sigma }_{2}}} )$, параметры ${{\lambda }_{j}}$ не являются малыми: ${{\lambda }_{j}} = \pi + O({{\sigma }_{j}})$. В этих случаях уравнение (4.3) также сильно упрощается в пределе при $\sigma \to 0$ без предположений о малости амплитуды волны. В частности, при ${{\lambda }_{2}} \to \pi $ оно принимает предельную форму

(5.3)

$F_{1}^{2}{{\left( {\frac{{d\eta }}{{dx}}} \right)}^{2}} = 3{{\eta }^{2}}\left( {F_{1}^{2} - 1 - \eta } \right)$

Указанное уравнение по форме совпадает с известным уравнением Буссинеска–Рэлея для поверхностных уединенных волн в нижнем слое однородной жидкости с ${{F}_{1}} > 1$. В литературе такую аппроксимацию двухслойного течения иногда называют полутораслойным приближением, поскольку в этом случае влияние верхнего слоя становится опосредованным. Заметим, что данное приближение согласуется и с уравнением (5.2), которое в пределе при ${{F}_{2}} \to 0$ также дает уравнение (5.3).

Особый предельный случай возникает в ситуации, когда параметр $\mu $ имеет одинаковый порядок с параметрами Буссинеска ${{\sigma }_{1}},\;{{\sigma }_{2}}$. Физически это означает, что малый скачок плотности в слабом пикноклине сравним с суммарными перепадами плотности по всей глубине прилегающих слоев. Такая ситуация, типичная для придонных течений в океане с экстремально слабой глубоководной стратификацией, подробно рассматривалась в [17, 18], где неравенство (2.6), являющееся условием гиперболичности уравнений двухслойной мелкой воды [4], использовалось для характеристики параметрических областей устойчивости уединенных внутренних волн. Разрушение течения в результате местного усиления сдвига скорости в окрестности вершины волны наблюдалось в лабораторных экспериментах [19] и для расслоенных течений в океане, в которых цуги уединенных внутренних волн являются генераторами интенсивного перемешивания придонных потоков [20].

6. Примеры. Здесь приводятся результаты расчета уединенных волн главной моды, описываемых нелинейным дифференциальным уравнением (4.3). Рис. 2 иллюстрирует решение в виде одиночной волны возвышения в случае, когда невозмущенная глубина нижнего слоя в пять раз меньше глубины верхнего слоя. Указанный волновой режим реализуется для пары чисел Фруда $({{F}_{1}},{{F}_{2}})$ = (1.5, 0.129). Точка $A$ с этими координатами находится в сверхкритической области непосредственно над спектральным пограничным слоем вблизи оси абсцисс $O{{F}_{1}}$ (рис. 2,а). На рис. 2,б показаны графики функций $P$ и $Q$, дающих по формуле (4.7) решение уравнения (4.3). Функция $P(\eta ;F)$ имеет простой положительный корень $\eta = a = 1.28$, ближайший к точке $\eta = 0$, который дает амплитуду уединенной волны в придонном слое единичной безразмерной глубины.

Рис. 3 демонстрирует решение уравнения (4.3) в виде волны понижения, когда невозмущенная глубина верхнего слоя в пять раз меньше глубины нижнего слоя. Этот режим получается для чисел Фруда $({{F}_{1}},{{F}_{2}})$ = (0.138, 1.99), соответствующая ему точка $B$ находится справа от спектрального пограничного слоя вблизи оси ординат $O{{F}_{2}}$. График функции $P(\eta ;F)$ на рис. 3,б показывает наличие у нее двух достаточно близких отрицательных корней $\eta = - 0.62$ (он определяет амплитуду волны $a$) и $\eta = - 0.9$, благодаря чему заметна тенденция к уплощению линий тока в центре впадины. Амплитуда данной уединенной волны понижения почти в пять раз превышает невозмущенную толщину верхнего слоя.

Рис. 3.

Уединенная волна типа впадины для стратифицированного течения с параметрами ${{\sigma }_{1}} = {{\sigma }_{2}}$ = = 0.00007, $\mu = 0.003$, $r = 5$, ${{F}_{1}} = 0.138$, ${{F}_{2}} = 1.99$.

Заключение. В работе выведено уравнение второго приближения теории стационарных длинных волн для двухслойной жидкости с кусочно-экспоненциальной стратификацией. Полученное уравнение порождает иерархию асимптотических подмоделей, описывающих уединенные волны конечной амплитуды. Базовое приближенное уравнение (4.3) может использоваться в широком диапазоне параметров стратификации, включая шельфовые и глубоководные условия океана.

Работа выполнена при финансовой поддержке Российского научного фонда (код проекта 21-71-20039).

Приложение. Здесь приводятся выражения для коэффициентов в формуле (4.4) функций $P$ и $Q$ из уравнения (4.3). Для функции $P$, зависящей линейно от квадратов чисел Фруда $F_{1}^{2}$ и $F_{2}^{2}$, справедливо представление

$P(\eta ;F) = {{P}_{0}}(\eta ) + \mu F_{1}^{2}{{P}_{1}}(\eta ) + \mu F_{2}^{2}{{P}_{2}}(\eta ),$

где ${{P}_{j}}(\eta ) = {{p}_{{j0}}} + {{p}_{{j1}}}\eta + {{p}_{{j2}}}{{\eta }^{2}}$ ($j = 0,1,2$) – квазиполиномы второй степени по $\eta $ с тригонометрическими коэффициентами

${{p}_{{00}}} = - \frac{\mu }{2}$

${{p}_{{01}}} = - \frac{{{{\sigma }_{1}}(1 + \mu )}}{{48{{{\sin }}^{2}}{{\alpha }_{1}}{{{\cos }}^{2}}({{\alpha }_{1}}{\text{/2}})}}(2{{\sigma }_{1}} - 2 + (4{{\sigma }_{1}} - 1)\cos {{\alpha }_{1}} + 2\cos 2{{\alpha }_{1}} + \cos 3{{\alpha }_{1}}) - $

$ - \;\frac{{r{{\sigma }_{2}}}}{{48{{{\sin }}^{2}}{{\alpha }_{2}}{{{\cos }}^{2}}({{\alpha }_{2}}{\text{/2}})}}(2{{\sigma }_{2}} + 2 + (4{{\sigma }_{2}} + 1)\cos {{\alpha }_{2}} - 2\cos 2{{\alpha }_{2}} - \cos 3{{\alpha }_{2}})$

${{p}_{{02}}} = - \frac{{\sigma _{1}^{2}(1 + \mu )}}{{24{{{\sin }}^{2}}{{\alpha }_{1}}{{{\cos }}^{2}}({{\alpha }_{1}}{\text{/2}})}}(1 + 2\cos {{\alpha }_{1}}) + \frac{{r\sigma _{2}^{2}}}{{24{{{\sin }}^{2}}{{\alpha }_{2}}{{{\cos }}^{2}}({{\alpha }_{2}}{\kern 1pt} /{\kern 1pt} 2)}}(1 + 2\cos {{\alpha }_{2}})$

${{p}_{{10}}} = \frac{1}{4}(2{{\lambda }_{1}}{\text{ctg}}{{\alpha }_{1}} + {{\sigma }_{1}})$

${{p}_{{20}}} = \frac{1}{4}(2{{\lambda }_{2}}{\text{ctg}}{{\alpha }_{2}} + {{\sigma }_{2}})$

${{p}_{{11}}} = - \frac{{{{\lambda }_{1}}{{\sigma }_{1}}}}{{144\sin ({{\alpha }_{1}}{\kern 1pt} /{\kern 1pt} 2){{{\cos }}^{3}}({{\alpha }_{1}}{\text{/2}})}}{{(1 + 2\cos {{\alpha }_{1}})}^{2}}$

${{p}_{{21}}} = - \frac{{r{{\lambda }_{2}}{{\sigma }_{2}}}}{{144\sin ({{\alpha }_{2}}/2)\cos 3({{\alpha }_{2}}{\text{/2}})}}{{(1 + 2\cos {{\alpha }_{2}})}^{2}}$

${{p}_{{12}}} = {{p}_{{22}}} = 0$

Для функции $Q$ справедливо представление

$Q(\eta ;F) = \frac{{\mu F_{1}^{2}}}{{8{{\lambda }_{1}}}}\frac{{{{Q}_{1}}(\eta )}}{{{{{\sin }}^{5}}{{\alpha }_{1}}(\eta )}} + \frac{{\mu F_{2}^{2}}}{{8{{r}^{2}}{{\lambda }_{2}}}}\frac{{{{Q}_{2}}(\eta )}}{{{{{\sin }}^{5}}{{\alpha }_{2}}(\eta )}},$

где ${{Q}_{j}}(\eta ) = {{q}_{{j0}}} + {{q}_{{j1}}}\eta + {{q}_{{j2}}}{{\eta }^{2}} + {{q}_{{j3}}}{{\eta }^{3}} + {{q}_{{j4}}}{{\eta }^{4}}$ с коэффициентами

${{q}_{{10}}} = {{\sin }^{3}}{{\alpha }_{1}}(2{{\lambda }_{1}} - \sin 2{{\alpha }_{1}})$

${{q}_{{20}}} = {{\sin }^{3}}{{\alpha }_{2}}(2{{\lambda }_{2}} - \sin 2{{\alpha }_{2}})$

${{q}_{{11}}} = - \frac{1}{4}{{\lambda }_{1}}\sin {{\alpha }_{1}}(8\lambda _{1}^{2} - 7 + (8\lambda _{1}^{2} + 4)\cos 2{{\alpha }_{1}} + 3\cos 4{{\alpha }_{1}} + 4{{\lambda }_{1}}\sin 2{{\alpha }_{1}})$

${{q}_{{21}}} = \frac{1}{4}r{{\lambda }_{2}}\sin {{\alpha }_{2}}(8\lambda _{2}^{2} - 7 + (8\lambda _{2}^{2} + 4)\cos 2{{\alpha }_{2}} + 3\cos 4{{\alpha }_{2}} + 4{{\lambda }_{2}}\sin 2{{\alpha }_{2}})$

${{q}_{{12}}} = \frac{{\lambda _{1}^{2}}}{{16}}\left( {\left( {56\lambda _{1}^{2} - 18} \right)\cos {{\alpha }_{1}} + \left( {8\lambda _{1}^{2} + 15} \right)\cos 3{{\alpha }_{1}} + 3\cos 5{{\alpha }_{1}} - 44{{\lambda }_{1}}\sin \alpha _{1}^{{}} - 28{{\lambda }_{1}}\sin 3{{\alpha }_{1}}} \right)$

${{q}_{{22}}} = - \frac{{{{r}^{2}}\lambda _{2}^{2}}}{{16}}\left( {\left( {56\lambda _{2}^{2} - 18} \right)\cos {{\alpha }_{2}}{\kern 1pt} {\kern 1pt} + \left( {8\lambda _{2}^{2} + 15} \right)\cos 3{{\alpha }_{2}}{\kern 1pt} {\kern 1pt} + 3\cos 5{{\alpha }_{2}}{\kern 1pt} {\kern 1pt} - 44\lambda _{2}^{{}}\sin {{\alpha }_{2}}{\kern 1pt} {\kern 1pt} - 28{{\lambda }_{2}}\sin 3{{\alpha }_{2}}} \right)$

${{q}_{{13}}} = \frac{{\lambda _{1}^{3}}}{4}(28{{\lambda }_{1}}\cos {{\alpha }_{1}} + 4{{\lambda }_{1}}\cos 3{{\alpha }_{1}} - 7\sin {{\alpha }_{1}} - 3\sin 3{{\alpha }_{1}})$

${{q}_{{23}}} = - \frac{{{{r}^{3}}\lambda _{2}^{3}}}{4}(28{{\lambda }_{2}}\cos {{\alpha }_{2}} + 4{{\lambda }_{2}}\cos 3{{\alpha }_{2}} - 7\sin {{\alpha }_{2}} - 3\sin 3{{\alpha }_{2}})$

${{q}_{{14}}} = \frac{{\lambda _{1}^{4}}}{2}(7\cos {{\alpha }_{1}} + \cos 3{{\alpha }_{1}}),\quad {{q}_{{24}}} = \frac{{{{r}^{4}}\lambda _{2}^{4}}}{2}(7\cos {{\alpha }_{2}} + \cos 3{{\alpha }_{2}})$

Во всех указанных выше формулах ${{\alpha }_{1}} = {{\lambda }_{1}}(1 + \eta )$, ${{\alpha }_{2}} = {{\lambda }_{2}}(1 - r\eta )$.

Список литературы

Краусс В. Внутренние волны. Л.: Гидрометеоиздат, 1968.
Yih C.S. Stratified Flows. New York: Acad. Press, 1980.
Ле Блон П.Х., Майсек Л. Волны в океане. М.: Мир, 1981.
Овсянников Л.В. Нелинейные проблемы теории поверхностных и внутренних волн / Л.В. Овсянников, Н.И. Макаренко, В.И. Налимов и др. Новосибирск: Наука. Сиб. отд., 1985.
Ильичев А.Т. Уединенные волны в моделях гидромеханики. М.: Физматлит, 2003.
Helfrich K.R., Melville W.K. Long nonlinear internal waves // Annu. Rev. Fluid Mech. 2006. V. 38. P. 395–425.
Dubreil-Jacotin M.L. Sur les theoremes d’existence relatifs aux ondes permanentes perodiques a deux dimensions dans les liquides heterogenes // J. Math. Pure Appl. 1937. V. 16. № 9. P. 43–67.
Long R.R. Some aspects of the flow of stratified fluid. I. A theoretical investigation // Tellus. 1953. V. 5. P. 42–57.
Voronovich A.G. Strong solitary internal waves in a 2.5-layer model // J. Fluid Mech. 2003. V. 474. P. 85–94.
Goullet A., Choi W. Large amplitude internal solitary waves in a two-layer system of piecewise linear stratification // Phys. Fluids. 2008. V. 20. P. 096601. https://doi.org/10.1063/1.2978205
Макаренко Н.И., Мальцева Ж.Л. Асимптотические модели внутренних стационарных волн // ПМТФ. 2008. Т. 49. № 4. С. 151–161.
Макаренко Н.И., Мальцева Ж.Л. Уединенные волны в двухслойной слабостратифицированной жидкости // ПМТФ. 2009. Т. 50. № 2. С. 72–78.
Sutherland B.R. Internal Gravity Waves. Cambridge: Univ. Press, 2010.
Макаренко Н.И., Мальцева Ж.Л. О спектре фазовых скоростей внутренних волн в слабостратифицированной двухслойной жидкости // Изв. РАН. МЖГ. 2009. № 2. С. 125–145.
Miyata M. An internal solitary wave of large amplitude // La Mer. 1985. V. 23. № 2. P. 43–48.
Choi W., Camassa R. Fully nonlinear internal waves in a two-fluid system // J. Fluid Mech. 1999. V. 396. P. 1–36.
Makarenko N., Maltseva J., Morozov E., Tarakanov R., Ivanova K. Internal waves in marginally stable abyssal stratified flow // Nonlin. Proces. Geophys. 2018. V. 25. P. 659–669.
Макаренко Н.И., Мальцева Ж.Л., Морозов Е.Г., Тараканов Р.Ю., Иванова К.А. Внутренние стационарные волны в глубоководных стратифицированных течениях // ПМТФ. 2019. Т. 60. № 2. С. 74–83.
Carr M., Fructus D., Grue J., Jensen A., Davies P.A. Convectively induced shear instability in large amplitude internal solitary waves // Phys. Fluids. 2008. V. 20. P. 126601.
Van Haren H., Gostiaux L., Morozov E., Tarakanov R. Extremely long Kelvin – Helmholtz billow trains in the Romanche fracture zone // Geophys. Res. Lett. 2014. V. 44. P. 8445–8451.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал