Прикладная математика и механика, 2023, T. 87, № 2, стр. 265-279
Упругие волны, захваченные полубесконечной полосой с защемленными боковыми сторонами и изломанным торцом
1 Институт проблем машиноведения РАН
Санкт-Петербург, Россия
* E-mail: srgnazarov@yahoo.co.uk
Поступила в редакцию 24.12.2022
После доработки 15.02.2023
Принята к публикации 15.02.2023
- EDN: TZWXRA
- DOI: 10.31857/S0032823523020108
Аннотация
Указаны несколько геометрических условий захвата упругих волн однородной изотропной полосой с одной или двумя защемленными боковыми сторонами и достаточно произвольно искривленным торцом. Найдены формы резонатора, обеспечивающие любое заданное наперед количество линейно независимых захваченных волн.
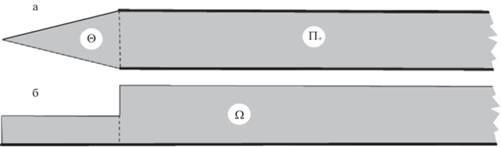
1. Постановка задачи. Пусть ${{\Pi }}$ – единичная полоса и ${{\Pi }_{ + }}$ = $\{ x = ({{x}_{1}},{{x}_{2}})$ : ${{x}_{1}} > 0$, ${{x}_{2}} \in (0,1)\} $ – ее полубесконечная часть (далее – полуполоса). Собственные колебания плоского однородного изотропного тела ${{\Omega }} \subset {{\Pi }}$, содержащего полуполосу ${{{{\Pi }}}_{ + }}~$ (рис. 1), описываются системой дифференциальных уравнений
(1.1)
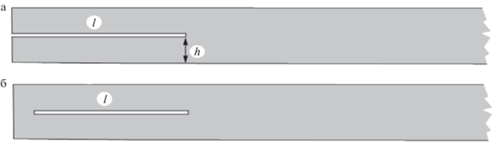
$ - {{\partial }_{1}}{{\sigma }_{{1k}}}\left( {u;x} \right) - {{\partial }_{2}}{{\sigma }_{{2k}}}\left( {u;x} \right) = \Lambda {{u}_{k}}\left( x \right);\quad x \in \Omega ,\quad k = 1,2$Рис. 1.
Упругие волноводы. Резонатор Θ отделен штрих-пунктирной линией, а защемленные участки изображены полужирными линиями.
Здесь ${{\partial }_{j}} = \partial {\text{/}}\partial {{x}_{j}}$ при j = 1, 2, ${{\sigma }_{{jk}}}$ – декартовы компоненты тензора напряжений, порожденного вектором смещений $u = \left( {{{u}_{1}},{{u}_{2}}} \right)$
Кроме того, $\lambda \geqslant 0$ и $\mu > 0$ – постоянные Ламе, ${{\delta }_{{j,k}}}$ – символ Кронекера, ${{\Lambda }} = \rho {{\omega }^{2}}$ – спектральный параметр, а $\omega > 0$ – частота гармонических во времени колебаний и $\rho > 0$ – постоянная плотность упругого тела. Граница ${{\Gamma }} = \partial {{\Omega }}$ разбита на участки ${{{{\Gamma }}}_{D}}$ и ${{{{\Gamma }}}_{N}}$, на которых поставлены условия Дирихле (жесткого защемления) и Неймана (свободного края)
При этом $n = \left( {{{n}_{1}},{{n}_{2}}} \right)$ – единичный вектор внешней нормали и ${{\sigma }^{{\left( n \right)}}}\left( u \right){\text{\;}}$ – вектор нормальных напряжений с декартовыми компонентами
Далее рассматриваем две ситуации, с которыми связываем индексы J = 1 и $J = 2$ соответственно, а именно
В первой ситуации закреплены обе $\left( {p = 0,1} \right)$ боковые стороны ${{\varpi }_{p}}$ = $\{ x:{{x}_{1}} > 0$, ${{x}_{2}} = p\} $ полуполосы ${{{{\Pi }}}_{ + }}$, но во второй – только нижняя ${{\varpi }_{0}}$, расположенная на оси абсцисс. Множество $\Theta = \Omega {{\backslash }}{{\bar {\Pi }}_{ + }}$ называем резонатором упругого волновода ${{\Omega }}$, а границу $\varpi = \partial \Theta {{\backslash }}\partial {{\Pi }_{ + }}$ – его торцом. Торец может быть полностью свободен от внешних воздействий (рис. 1,а), но допускается его частичное закрепление (рис. 1,б) вдоль отрезков на $\partial {{\Pi }}$ при $J = 1$ или только на оси абсцисс при J = 2.
Задачи вида (1.1)–(1.3) возникают при изучении явления пограничного слоя около краев листовой прокладки между параллельными фланцами или цилиндрической накладки на абсолютно жесткий профиль. Установлено [1], что решающую роль при образовании моделей пониженной размерности собственных колебаний упомянутых объектов играет наличие или отсутствие захваченных упругих волн в волноводе ${{\Omega }}$, т.е. решений задачи (1.1)–(1.3), исчезающих на бесконечности с экспоненциальной скоростью. Возникновение таких волн провоцирует эффект локализации мод собственных колебаний тонкой трехмерной пластины около ее кромки. Именно поиску захваченных волн и посвящена настоящая статья.
2. Инструментарий спектрального анализа. Вариационная постановка задачи (1.1)–(1.3) апеллирует к интегральному тождеству [2, 3]
(2.1)
$E\left( {u,\psi ;\Omega } \right) = \Lambda {{\left( {u,\psi } \right)}_{\Omega }};\quad \psi \in H_{0}^{1}\left( {\Omega ;{{\Gamma }_{D}}} \right)$При этом ${{(\,,\,)}_{{{\Omega }}}}$ – натуральное скалярное произведение в пространстве Лебега ${{L}_{2}}\left( \Omega \right)$, $H_{0}^{1}\left( {\Omega ;{{\Gamma }_{D}}} \right)$ – пространство Соболева функций, подчиненных условию Дирихле (1.2), а $E\left( {u,u;{{\Omega }}} \right)$ – удвоенная упругая энергия, запасенная телом ${{\Omega }}$
Пространства скалярных и векторных функций не различаем в обозначениях.
Поскольку левая часть формулы (2.1) – положительно определенная замкнутая в пространстве $H_{0}^{1}\left( {{{\Omega }};{{{{\Gamma }}}_{D}}} \right)$ билинейная форма, задаче (2.1) (или (1.1)–(1.3) в дифференциальной форме) ставится ([4], гл. 10 § 1) в соответствие положительно определенный самосопряженный неограниченный оператор A в пространстве $~{{L}^{2}}\left( {{\Omega }} \right)$. В работе [5] и далее в разд. 3 установлено, что непрерывным спектром ${{\wp }_{c}}~$оператора A служит луч $[{{{{\Lambda }}}^{\dag }}, + \infty )$ с точкой отсечки
Не зависящая от продольной координаты ${{x}_{1}}$ волна имеет вид
(2.3)
${{w}^{\dag }}~\left( {{{x}_{2}}} \right) = ~\sin \left( {\pi {{J}^{{~ - 1}}}{{x}_{2}}} \right){{e}_{{\left( 1 \right)}}}~$Здесь ${{e}_{{\left( k \right)}}} = \left( {{{\delta }_{{k,1}}},{{\delta }_{{k,2}}}} \right)$ – орт оси ${{x}_{k}},k = 1,2$
Нижняя грань $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\wp } ~$ всего спектра $\wp $ оператора задачи (2.1) находится согласно минимальному принципу ([4], теорема 10.2.1)
(2.4)
$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\wp } = {{\inf }_{{\psi \in H_{0}^{1}\left( {\Omega ;{{\Gamma }_{D}}} \right){{\backslash }}\left\{ 0 \right\}}}}\frac{{E\left( {\psi ,\psi ;\Omega } \right)}}{{{{{\left\| {\psi ;{{L}^{2}}\left( \Omega \right)} \right\|}}^{2}}~}}~$Если случилось, что правая часть соотношения (2.4) строго меньше ${{{{\Lambda }}}^{\dag }}$, то дискретный спектр ${{\wp }_{d}}$, точки которого порождают захваченные волны в теле ${{\Omega }}$, непустой и ${{{{\Lambda }}}_{1}} = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\wp } $ – первое (наименьшее) собственное число в нем. Наконец, при наличии в ${{\wp }_{d}}$ нескольких точек все они находятся при помощи максиминимального принципа
(2.5)
${{{{\Lambda }}}_{j}} = {{\max }_{{{{\mathcal{E}}_{j}} \subset H_{0}^{1}\left( {\Omega ;{{\Gamma }_{D}}} \right)}}}{{\inf }_{{\psi \in {{\mathcal{E}}_{j}}\backslash \left\{ 0 \right\}}}}\frac{{E\left( {\psi ,\psi ;{{\Omega }}} \right)}}{{{{{\left\| {\psi ;{{L}^{2}}\left( {{\Omega }} \right)} \right\|}}^{2}}}},~$При этом ${{\mathcal{E}}_{j}}$ – любое подпространство в $H_{0}^{1}\left( {{{\Omega }};{{{{\Gamma }}}_{D}}} \right)$ с коразмерностью j – 1; в частности, ${{\mathcal{E}}_{1}} = H_{0}^{1}\left( {{{\Omega }};{{{{\Gamma }}}_{D}}} \right)$, т.е. соотношение (2.5) при j = 1 превращается в соотношение (2.4). Более точно, теорема 10.2.2 [4] гарантирует, что в том случае, когда правая часть формулы (2.5) строго меньше ${{{{\Lambda }}}^{\dag }}$, дискретный спектр ${{\wp }_{d}}$ содержит, по крайней мере, точки ${{{{\Lambda }}}_{1}}, \ldots ,{{{{\Lambda }}}_{j}}$ и последняя из указанных принимает вид (2.5).
3. Непрерывный спектр. Проверим формулу (2.2) в ситуации $J = 2$. Теория эллиптических краевых задач в областях с цилиндрическими выходами на бесконечности (см. [6] и ([7], гл. 5), ([8], § 3)) показывает, что точкой отсечки ${{{{\Lambda }}}^{\dag }}$ непрерывного спектра ${{\wp }_{c}} = [{{\Lambda }^{\dag }},~ + \infty )$ задачи (1.1)–(1.3) при J = 2 служит наименьшее число ${{\Lambda }}$, при котором для какого-то параметра $\xi \in \mathbb{R}$ следующая краевая задача для системы обыкновенных дифференциальных уравнений имеет нетривиальное решение
(3.1)
$\begin{gathered} - \mu \left( {\partial _{z}^{2} - {{\xi }^{2}}} \right){{U}_{1}} - \left( {\lambda + \mu } \right)i\xi \left( {i\xi {{U}_{1}} + {{\partial }_{z}}{{U}_{2}}} \right) = {{\Lambda }}{{U}_{1}}\quad {\text{при}}\quad z \in \left( {0,1} \right) \\ - \mu \left( {\partial _{z}^{2} - {{\xi }^{2}}} \right){{U}_{2}} - \left( {\lambda + \mu } \right){{\partial }_{z}}\left( {i\xi {{U}_{1}} + {{\partial }_{z}}{{U}_{2}}} \right) = {{\Lambda }}{{U}_{1}}\quad {\text{при}}\quad z \in \left( {0,1} \right) \\ \end{gathered} $(3.3)
$\left( {\lambda + 2\mu } \right){{\partial }_{z}}{{U}_{2}}\left( 1 \right) + \lambda i\xi {{U}_{1}}\left( 1 \right) = 0,\quad \mu i\xi {{U}_{2}}\left( 1 \right) + \mu {{\partial }_{z}}{{U}_{1}}\left( 1 \right) = 0~$Здесь i – мнимая единица. Задача (3.1)–(3.3) получается из задачи (1.1)–(1.3) в бесконечной полосе ${{\Pi }} = \mathbb{R} \times \left( {0,1} \right)$ при ${{\Gamma }_{D}} = \left\{ {x:~{{x}_{2}} = 0} \right\}$ и ${{\Gamma }_{N}} = \left\{ {x:{{x}_{2}} = 1} \right\}$ посредством преобразования Фурье. Для ${{\Lambda }} = \mu {{\pi }^{2}}{\text{/4}}$ нужное решение имеет вид $\sin \left( {\pi z{\text{/2}}} \right)$ (ср. формулы (2.2) и (2.3)).
Убедимся в том, что при ${{\Lambda }} < \mu {{\pi }^{2}}{\text{/4}}$ и любом $\xi \in \mathbb{R}$ задача (3.1), (3.3) имеет только тривиальное решение – этот факт достаточен для справедливости равенства $\wp _{c}^{2} = \left[ {\left( {\mu {{\pi }^{2}}} \right){\text{/4}}, + \infty } \right)$, так как согласно общим результатам ([7], гл. 5) непрерывный спектр цилиндрического волновода – связное множество на положительной полуоси ${{\mathbb{R}}_{ + }}$.
Обозначим чертой комплексное сопряжение, умножим уравнения (3.1) соответственно на $\overline {{{U}_{1}}} $ и $\overline {{{U}_{2}}} $, а затем проинтегрируем по $z \in \left( {0,1} \right)$ при учете краевых условий (3.3). В результате суммирования получим равенство
(3.4)
${{\Lambda }}\mathop \smallint \limits_0^1 {{\left| U \right|}^{2}}dz = \mathop \smallint \limits_0^1 \left( {2\mu {{\xi }^{2}}{{{\left| {{{U}_{1}}} \right|}}^{2}} + 2\mu {{{\left| {{{\partial }_{z}}{{U}_{2}}} \right|}}^{2}} + \mu {{{\left| {{{\partial }_{z}}{{U}_{1}} + i\xi {{U}_{2}}} \right|}}^{2}}} \right)dz + \lambda \mathop \smallint \limits_0^1 {{\left| {i\xi {{U}_{1}} + {{\partial }_{z}}{{U}_{2}}} \right|}^{2}}dz~$Последний неотрицательный интеграл далее игнорируем ввиду ненадобности. Алгебраическая формула
(3.5)
$\mathop \smallint \limits_0^H {{\left| {{{\partial }_{z}}\mathcal{U}\left( z \right)} \right|}^{2}}dz \geqslant \frac{{{{\pi }^{2}}}}{{4{{H}^{2}}}}\mathop \smallint \limits_0^1 {{\left| {\mathcal{U}\left( z \right)} \right|}^{2}}dz\quad {\text{для}}\quad \mathcal{U} \in {{H}^{1}}\left( {0,H} \right),\quad \mathcal{U}\left( 0 \right) = 0~$Следовательно, $U = 0$ при ${{\Lambda }} < \mu {{\pi }^{2}}{\text{/4}}$.
Формула (2.2) для точки отсечки непрерывного спектра задачи (1.1)–(1.3) в ситуации J = 2 проверена. Ситуация J = 1, в которой условия Неймана (3.3) заменены условиями Дирихле ${{U}_{1}}\left( 1 \right) = 0~$ и $~{{U}_{2}}\left( 1 \right) = 0$, была разобрана в статье [5] при помощи значительно более простых выкладок.
4. Достаточное условие существования захваченной волны. В силу минимального принципа (2.4) дискретный спектр ${{\wp }_{d}}~$ непустой при условии, что нашлась пробная вектор-функция ${{\psi }^{\delta }} \in H_{0}^{1}\left( {{{\Omega }};{{{{\Gamma }}}_{D}}} \right)$, обеспечивающая неравенство
(4.1)
$E\left( {{{\psi }^{\delta }},~{{\psi }^{\delta }};{{\Omega }}} \right) - {{{{\Lambda }}}^{\dag }}{{\left\| {{{\psi }^{\delta }};{{L}^{2}}\left( {{\Omega }} \right)} \right\|}^{2}} < 0$Определим ее следующим образом
Здесь $\delta > 0$ и потому ${{\psi }^{\delta }} \in H_{0}^{1}\left( {{{\Omega }};{{{{\Gamma }}}_{D}}} \right)$ при учете условий, наложенных на форму резонатора в разд. 1. Согласно формуле (2.2) имеем
(4.2)
$ = E\left( {{{\omega }^{\dag }},{{\omega }^{\dag }};{{\Theta }}} \right) + \frac{{\mu {{\pi }^{2}}}}{{4\delta {{J}^{2}}}} + O\left( \delta \right)$В итоге при учете соотношений (2.2) и (2.3) обнаруживаем, что неравенство (4.1), превратившееся в оценку ${{\theta }^{\dag }} + C\delta < 0$, выполнено при малом $~\delta > 0$, если оказалось, что
(4.3)
${{\theta }^{\dag }} = Ew{{\left\| {{{\omega }^{\dag }};{{L}^{2}}\left( {{\Theta }} \right)} \right\|}^{2}} = \frac{{\mu {{\pi }^{2}}}}{{{{{\text{J}}}^{{~2}}}}}\mathop \smallint \limits_{{\Theta }} \cos \left( {\frac{{2\pi }}{{\text{J}}}{{x}_{2}}{\text{\;}}} \right)dx < 0$Для подынтегрального выражения справедливо соотношение
Таким образом, добиться захвата волны путем подбора формы резонатора нетрудно: достаточно поместить резонатор ${{\Theta }}$ в полуполосу
Последнему требованию удовлетворяют, например, волноводы на рис. 2,г, в случае J = 1 и на рис. 2,д, в случае J = 2.
Рис. 2.
Полуполоса со скошенным торцом (а), и “ласточкиным хвостом” (б). Прямоугольные выемка (в) и наросты, центральный (г) и боковой (д). Штрих-пунктиром изображена средняя линия.

Кроме того, в ситуации J = 1 ограничение (4.3) выполнено для волновода на рис. 1,а, а при симметричном наросте – и на рис. 2,г. В ситуации J = 2 ограничение (4.3) обеспечено наверняка для волноводов на рис. 2,а, д.
Вместе с тем в общем случае неизвестно, оказывается ли пустым дискретный спектр при условии ${{\theta }^{\dag }} > 0$. Впрочем, при помощи одномерного неравенства Фридрихса (3.5) можно убедиться в том, что для случая J = 1 волноводы на рис. 1,а, и рис. 2,д, не производят захват волны, если толщина H выступов не превосходит 1/2, а значит, при любой ширине выемки то же верно и для волновода на рис. 2,в. При J = 2 то же неравенство (3.5) обеспечивает отсутствие захваченных волн у волновода на рис. 1,б. В то же время следующие разделы предоставят захваченные волны, например, у волноводов на рис. 2,а,б,д, при определенных значениях геометрических параметров.
5. Еще одно достаточное условие. При J = 1 нетрудно проверить, что
для полуполос со скошенным торцом (рис. 1,а, или рис. 2,а) или с “ласточкиным хвостом” (рис. 2,б). В ситуации J = 2 для наростов толщиной H < 1/2 на рис. 1,а, или рис. 2,а величина ${{\theta }^{\dag }}$ соответственно положительна и отрицательна, а значит, при каком-то, обязательно нецентральном, положении нароста на рис. 1,г, равенство (5.1) становится верным. Можно привести и многие другие примеры выполнения введенного ограничения.При помощи приема [9] убедимся в том, что в случае (5.1) захват волны происходит при любой форме резонатора. На торце $\varpi $ выберем точку P, в которой косинус $\cos (\pi {{J}^{{~ - 1}}}{{x}_{2}})$ и компонента ${{n}_{1}}\left( P \right)$ вектора нормали отличны от нуля, а в качестве пробной вектор-функции в минимальном принципе (2.4) возьмем сумму
(5.2)
${{{{\Psi }}}^{\delta }}\left( x \right) = {{\psi }^{\delta }}\left( x \right) + \sqrt \delta {{e}_{{\left( 2 \right)}}}{{\Phi }}\left( x \right)$(5.3)
$\begin{gathered} {{\left\| {{{{{\Psi }}}^{\delta }};{{L}^{2}}\left( {{\Omega }} \right)} \right\|}^{2}} = {{\left\| {{{w}^{\dag }};{{L}^{2}}\left( {{\Theta }} \right)} \right\|}^{2}} + \frac{1}{{4\delta }} + O\left( \delta \right) \\ E\left( {{{{{\Psi }}}^{\delta }},{{{{\Psi }}}^{\delta }};{{\Omega }}} \right) = E\left( {{{w}^{\dag }},{{w}^{\dag }};{{\Theta }}} \right) + \frac{{\mu {{\pi }^{2}}}}{{4\delta {{J}^{2}}}} + 2\sqrt \delta E\left( {{{w}^{\dag }},{{e}_{{\left( 2 \right)}}}{{\Phi }};{{\Theta }}} \right) + O\left( \delta \right) \\ \end{gathered} $Отметим, что ${{\left( {{{w}^{\dag }},{{e}_{{\left( 2 \right)}}}\Phi } \right)}_{\Theta }} = 0$ согласно определениям (2.3) и (5.2). После подстановки соотношений (5.3) в неравенство (4.1) обнаруживаем, что в силу формул (2.2) и (5.1) члены порядков ${{\delta }^{{ - 1}}}$ и 1 взаимно уничтожаются, т.е. само неравенство принимает вид
Поскольку ${{\sigma }_{{12}}}\left( {{{w}^{\dag }};x} \right) = \pi \mu {{J}^{{~ - 1}}}\cos \left( {\pi {{J}^{{~ - 1}}}{{x}_{2}}} \right)$, выбор точки P позволяет сделать последний интеграл отрицательным при подходящей функции ${{\Phi }}$, и тем самым для достаточно малого $\delta > 0~$ обеспечить неравенство (4.1), гарантирующее существование захваченной волны.
Малое возмущение профиля торца способно нарушить равенство (5.1), причем придать выражению (4.3) любой знак. При этом достаточно малое возмущение не выводит собственное число из дискретного спектра ${{\wp }_{d}}$. Следовательно, найденное условие ${{\theta }^{\dag }} \leqslant 0$ наличия захваченной волны является только достаточным и такая волна может существовать и при ${{\theta }^{\dag }} > 0$. Подробно это наблюдение обсуждается [10] для скалярных задач. Вопрос о наглядном геометрическом условии отсутствия захваченных упругих волн остается открытым для волноводов любой природы.
Метод Фурье демонстрирует, что уравнение Гельмгольца в полуполосе ${{{{\Pi }}}_{ + }}$ с условиями Дирихле на прямом торце $\varpi $ = $\left\{ {x:{{x}_{1}} = 0,{{x}_{2}} \in \left( {0,1} \right)} \right\}$ и с условиями Дирихле или Неймана на ее боковых сторонах не имеет захваченных волн. Поскольку касательное напряжение ${{\sigma }_{{12}}}\left( {{{w}^{\dag }}} \right)~$ не вырождается на торце $~\varpi $, приведенные рассуждения обнаруживают захваченную волну в задаче (1.1)–(1.3) в полуполосе ${{{{\Pi }}}_{ + }}$. Этот результат был получен в работе [5], однако в ней не найдена полная кратность дискретного спектра – для абсолютного большинства геометрических форм этот вопрос остается открытым до сих пор. Кроме того, в отличие от скалярных задач осталось неизвестным, возникает или нет в задачах теории упругости пороговый резонанс [11–13].
6. Полуполоса с трещиной. Пусть ${{\Omega }}_{h}^{\ell } = {{{{\Pi }}}^{\ell }}{{\backslash }}T_{h}^{\ell }$ – удлиненная полуполоса ${{{{\Pi }}}^{\ell }}$ = = $\left\{ {x:{{x}_{1}} > - l,{{x}_{2}} \in \left( {0,1} \right)} \right\}$ с трещиной $T_{h}^{\ell }$ = $\left\{ {x:{{x}_{1}} \in \left( { - \ell ,0} \right],{{x}_{2}} = h} \right\}$ (рис. 3, а), где $\ell > 0$ – большой положительный параметр и $h \in \left( {{\text{1/2,1}}} \right)$ (случай $h \leqslant {\text{1/2}}$ обсуждаем в конце раздела). Исследуя спектр задачи (1.1)–(1.3) при ${{\Gamma }}_{D}^{\ell }$ = $\{ x:{{x}_{1}} > - l,{{x}_{2}} = 0,1\} $ (боковые стороны защемлены, а берега трещины и торец полуполосы свободны), рассмотрим вспомогательную задачу: систему уравнений (1.1) в длинном прямоугольнике ${{\Xi }}_{h}^{\ell }$ = = $\left( { - \ell ,0} \right) \times \left( {0,h} \right)$ с краевыми условиями
(6.1)
$\begin{gathered} {{u}^{\ell }}\left( x \right) = 0\quad {\text{при}}\quad {{x}_{1}} \in \left( { - \ell ,0} \right),~\quad {{x}_{2}} = 0\quad {\text{или}}\quad {{x}_{1}} = 0,~\quad {{x}_{2}} \in \left( {0,h} \right) \\ {{\sigma }^{{\left( n \right)}}}\left( {{{u}^{\ell }};x} \right) = 0\quad {\text{при}}\quad {{x}_{1}} \in \left( { - \ell ,0} \right),\quad {{x}_{2}} = h\quad {\text{или}}\quad {{x}_{1}} = - \ell ,\quad {{x}_{2}} \in \left( {0,h} \right) \\ \end{gathered} $Иными словами, на боковой стороне $\upsilon = \left\{ {x:{{x}_{1}} = 0,{{x}_{2}} \in \left( {0,h} \right)} \right\}$ прямоугольника ${{\Xi }}_{h}^{\ell }~$ назначены искусственные условия Дирихле, а краевые условия на остальных сторонах унаследованы от исходных условий (1.2) и (1.3). Следуя обычной процедуре (см., напр., ([14], гл. 16) и ([15], гл. 4)) асимптотику собственных пар $\{ {{{{\Lambda }}}^{\ell }},{{u}^{\ell }}\} $ задачи (1.1), (5.1) ищем в виде
(6.2)
${{{{\Lambda }}}^{\ell }} = \mu {{\pi }^{2}}{{\left( {2h} \right)}^{{ - 2}}} + {{\ell }^{{ - 2}}}M + \ldots $(6.3)
$\begin{gathered} {{u}^{\ell }}\left( x \right) = \sin \left( {\frac{\pi }{{2h}}{{x}_{2}}} \right){v}\left( \eta \right){{e}_{{\left( 1 \right)}}} + \frac{1}{\ell }{{V}_{2}}\left( {{{x}_{2}}} \right){{e}_{{\left( 2 \right)}}}~\frac{{d{v}}}{{d\eta }}\left( \eta \right) + \frac{1}{{{{\ell }^{2}}}}{{V}_{1}}\left( {\eta ,{{x}_{2}}} \right){{e}_{{\left( 1 \right)}}} + \ldots ~ \\ {\text{при}}\quad x \in {{\Xi }}_{h}^{\ell } \\ \end{gathered} $Здесь многоточие заменяет младшие асимптотические члены, не существенные для предпринимаемого анализа, $\eta = {{\ell }^{{ - 1}}}{{x}_{1}}$ – растянутая продольная координата, а остальные ингредиенты принятых представлений подлежат определению.
Подставим соотношения (6.2) и (6.3) в систему (1.1). Выполнив дифференцирование, обнаружим, что множители при ${{h}^{{ - 2}}}~$ взаимно уничтожаются, а обращение в нуль суммы множителей при ${{h}^{{ - 1}}}{{\partial }_{\eta }}v\left( \eta \right)$ дает обыкновенное дифференциальное уравнение
(6.4)
$ - \left( {\lambda + 2\mu } \right)\frac{{{{d}^{2}}{{V}_{2}}}}{{d~x_{2}^{2}}}\left( {{{x}_{2}}} \right) - \frac{{{{\pi }^{2}}\mu }}{{4~{{h}^{2}}}}{{V}_{2}}\left( {{{x}_{2}}} \right) = \left( {\lambda + \mu } \right)\frac{\pi }{{2h}}~\cos \left( {\frac{{\pi {{x}_{2}}}}{{2h}}} \right);\quad {{x}_{2}} \in \left( {0,h} \right)$Снабдив уравнение вытекающими из равенств (6.1) граничными условиями
(6.5)
${{V}_{2}}\left( 0 \right) = 0,\quad \left( {\lambda + 2\mu } \right)\frac{{d{{V}_{2}}}}{{d{{x}_{2}}}}\left( h \right) = - \lambda $При этом
На очередном шаге процедуры получим задачу
(6.6)
$\begin{gathered} - \mu \frac{{{{d}^{2}}{{V}_{1}}}}{{dx_{{2~}}^{2}}}\left( {\eta ,{{x}_{2}}} \right) - \frac{{{{\pi }^{2}}\mu }}{{4~{{h}^{2}}}}{{V}_{1}}\left( {\eta ,{{x}_{2}}} \right) = M\sin \left( {\frac{{\pi {{x}_{2}}}}{{2h}}} \right){v}\left( \eta \right) + \left( {\lambda + \mu } \right)\frac{{d{{V}_{2}}}}{{d{{x}_{2}}}}~\left( {{{x}_{2}}} \right)\frac{{{{d}^{2}}v}}{{d{{\eta }^{2}}}}\left( \eta \right) + \\ + \left( {\lambda + 2\mu } \right)\sin \left( {\frac{{\pi {{x}_{2}}}}{{2h}}} \right)\frac{{{{d}^{2}}{v}}}{{d{{\eta }^{2}}}}~\left( \eta \right);\quad {{x}_{2}} \in \left( {0,h} \right)~ \\ \end{gathered} $(6.7)
${{V}_{1}}\left( 0 \right) = 0,\quad \mu \frac{{d{{V}_{1}}}}{{d{{x}_{2}}}}\left( h \right) = - \mu ~{{V}_{2}}\left( h \right)\frac{{{{d}^{2}}~{v}}}{{d{{\eta }^{2}}}}\left( \eta \right)$Условие ее разрешимости – ортогональность правых частей собственной функции $\sin (\pi {{x}_{2}}~{\text{/}}2h)$ в смысле формулы Грина – сводится к обыкновенному дифференциальному уравнению
(6.8)
$ - B\frac{{{{d}^{2}}{v}}}{{d{{\eta }^{2}}}}\left( \eta \right) = M{v}\left( \eta \right);\quad \eta \in \left( { - 1,0} \right)$(6.9)
$\begin{gathered} B = \mu + \left( {\lambda + 2\mu } \right)\frac{4}{\pi }\alpha \left( {1 + 4{{\alpha }^{2}}} \right){{\left( {\cos \left( {\frac{\pi }{2}\alpha } \right)} \right)}^{{ - 1}}}b\left( \alpha \right) \\ b\left( \alpha \right) = \frac{{4\alpha }}{{1 + 4{{\alpha }^{2}}}} - \sin \left( {\frac{\pi }{2}\alpha } \right) > 0~\quad {\text{при}}\quad \alpha \in \left( {0,\frac{1}{{\sqrt 2 }}} \right] \\ \end{gathered} $Собственные пары этого уравнения, снабженного граничными условиями
имеют вид(6.11)
$\left\{ {{{M}_{k}};{{{v}}_{k}}\left( \eta \right)} \right\} = \left\{ {b{{\pi }^{2}}~{{k}^{2}},\sin \left( {\pi ~k\eta } \right)~} \right\};\quad k = 1,2,3, \ldots $Пусть, как упоминалось, h > 1/2 и
Тогда сумма $\mu {{\pi }^{2}}{{\left( {2~h} \right)}^{{ - 2}}} + {{\ell }^{{ - 2}}}{{M}_{k}}$ попадает на интервал $\left( {0,\mu {{\pi }^{2}}} \right)$, в котором может находиться дискретный спектр задачи (1.1)–(1.3) в ситуации J = 1. Это наблюдение дает возможность обнаружить собственные числа при помощи максиминимального принципа (2.5).
Зафиксируем натуральное число j в соотношении (2.5) и определим вектор-функции ${{U}^{1}}, \ldots ,{{U}^{j}}$ с компонентами
(6.12)
$\begin{gathered} U_{1}^{q}\left( x \right) = A\sin \left( {\frac{{\pi {{x}_{2}}}}{{2h}}} \right){{{v}}_{q}}\left( {\frac{{{{x}_{1}}}}{\ell }} \right) + \frac{1}{{{{\ell }^{2}}}}A{{X}^{\ell }}\left( {{{x}_{1}}} \right){{V}_{{1q}}}\left( {\frac{{{{x}_{1}}}}{\ell },{{x}_{2}}} \right)~ \\ U_{2}^{q}\left( x \right) = \frac{1}{\ell }A{{X}^{\ell }}\left( {{{x}_{1}}} \right){{V}_{{2q}}}\left( {{{x}_{2}}} \right)\frac{{d{{{v}}_{q}}}}{{d\eta }}~\left( {\frac{{{{x}_{1}}}}{\ell }} \right) \\ \end{gathered} $Здесь ${{{v}}_{k}}$ – собственная функция задачи (6.8), (6.10) из списка (6.11), ${{V}_{{1q}}}$ – решение задачи (6.6), (6.7), содержащей функцию ${v} = {{{v}}_{q}}$ и ставшей разрешимой по построению, а ${{X}^{\ell }}$ – срезающая функция, которая нужна для продолжения компонент (6.12) нулем с прямоугольника ${{\Xi }}_{h}^{\ell }$ на всю область ${{\Omega }}_{h}^{\ell }$
(6.13)
${{X}^{\ell }}\left( {{{x}_{1}}} \right) = 1\quad {\text{при}}\quad {{x}_{1}} \in \left( {1 - \ell , - 1} \right),\quad {{X}^{\ell }}\left( {{{x}_{1}}} \right) = 0\quad {\text{при}}\quad {{x}_{1}} > 0$Благодаря нормирующему множителю $A = 2{{\left( {\ell h} \right)}^{{ - 1/2}}}$ выполнены соотношения
Иными словами, вектор-функции ${{U}^{1}}, \ldots ,{{U}^{j}}$ “почти ортонормированы” в пространстве ${{L}^{2}}\left( {{{{{\Omega }}}^{\ell }}} \right)$ при большом размере $\ell $, а значит, любое подпространство ${{\mathcal{E}}_{j}}$ из формулы (2.5) содержит нетривиальную линейную комбинацию
Вычислим дробь Рэлея из максимального принципа (2.5). Имеем
Обозначим через $L\left( {{{\nabla }_{x}}} \right)$ и ${{B}^{0}}\left( {{{\nabla }_{2}}} \right)$, ${{B}^{h}}\left( {{{\nabla }_{2}}} \right)$ матрицы дифференциальных операторов размером 2 × 2, взятые из системы уравнений (1.1) в прямоугольнике ${{\Xi }}_{h}^{\ell }$ и краевых условий (1.3) на его основаниях $\Upsilon _{0}^{\ell }$ = $\left\{ {x:{{x}_{1}} \in \left( { - \ell ,0} \right)} \right.$, $\left. {{{x}_{2}} = 0} \right\}$, $\Upsilon _{h}^{\ell }$ = $\left\{ {x:{{x}_{1}} \in \left( { - \ell ,0} \right)} \right.$, $\left. {{{x}_{2}} = h} \right\}$. Обработаем члены представления
Рассмотрим последние два скалярных произведения (t = 0 и t = h) и заметим, что
(6.14)
$\left| {{{\Psi }^{{{{\mathcal{E}}_{j}}}}}\left( {{{x}_{1}},t} \right)B_{k}^{t}\left( {{{\nabla }_{x}}} \right){{\Psi }^{{{{\mathcal{E}}_{j}}}}}\left( {{{x}_{1}},t} \right)} \right| \leqslant c{{A}^{2}}~{{\ell }^{{ - 3}}};\quad k = 1,2$При ${{x}_{1}} \in \left( {1 - \ell , - 1} \right)$ оценка (6.14) обеспечена процедурой построения асимптотики, точнее структурой граничных условий (6.5) и (6.7), но при ${{x}_{1}} \in \left( { - \ell ,1 - \ell } \right)$ ∪ (–1, 0) нужно еще учесть дифференцирования срезки ${{X}^{\ell }}$, а также соотношение
(6.15)
$\left| {{{{v}}_{q}}\left( \eta \right)} \right| \leqslant {{c}_{q}}\min \left\{ {\left| \eta \right|,\left| {1 + \eta } \right|} \right\} \leqslant {{c}_{q}}{{\ell }^{{ - 1}}}\min \left\{ {\left| {{{x}_{1}}} \right|,\left| {\ell + {{x}_{1}}} \right|} \right\}~$Таким образом,
Аналогично, уравнения (6.4) и (6.6) обеспечивают неравенства
Как и ранее, разные мажоранты возникли из-за дифференцирования срезки (6.13). Впрочем, в силу формул (6.12) и (6.15) находим, что
Собрав полученные соотношения, получим
Таким образом, при достаточно большом ${{\ell }_{j}}$ и $\ell \geqslant {{\ell }_{j}}$ правая часть неравенства (6.16) строго меньше точки отсечки (2.2) при J = 1, т.е. согласно максиминимальному принципу кратность дискретного спектра задачи (1.1)–(1.3) в полуполосе с трещиной ${{{{\Omega }}}^{\ell }} = {{{{\Pi }}}^{\ell }}{{\backslash }}{{T}^{\ell }}$ равна или превосходит выбранное число j.
Подведем итог: удлинение асимметричной продольной трещины в полуполосе с защемленными боковыми сторонами позволяет добиться любого количества линейно независимых захваченных волн в волноводе ${{{{\Omega }}}^{\ell }}$. Асимптотический анализ показывает, что эти волны концентрируются в прямоугольнике ${{\Xi }}_{h}^{\ell }$, а именно, они затухают с экспоненциальной скоростью в целой полуполосе ${{{{\Pi }}}_{ + }}$ и приобретают малые амплитуды в верхнем прямоугольнике ${{\Xi }}_{{1 - h}}^{\ell }$ = $\left\{ {x:{{x}_{1}} \in \left( { - \ell ,0} \right)} \right.$, $\left. {{{x}_{2}} \in \left( {h,1} \right)} \right\}$ с высотой $1 - h < {\text{1/2}}$.
Аналогичные указанным конструкции в прямоугольнике ${{\Xi }}_{{1 - h}}^{\ell }$ не позволяют обнаружить точки дискретного спектра, так как $\mu {{\pi }^{2}}{{\left( {2\left( {1 - h} \right)} \right)}^{{ - 2}}}$ > $\mu {{\pi }^{2}}$ при $h > {\text{1/2}}$ и, следовательно, применить максиминимальный принцип не удается. Вместе с тем случай $h \in \left( {{\text{0,1/2}}} \right)$ по сути не отличается от рассмотренного $h \in \left( {{\text{1/2,1}}} \right)$ и требует лишь замены ${{x}_{2}} \mapsto 1 - {{x}_{2}}$ поперечной координаты. По той же причине предъявленный анализ не дает результата для симметричной ($h = {\text{1/2}}$) трещины. Впрочем, для нее выполнено требование (5.1), а значит, по крайней мере одна захваченная волна существует, однако осталось непонятным, увеличивается ли их количество при росте длины $\ell $ трещины $T_{{1/2}}^{\ell }$.
Точно так же в ситуации J = 2 при $T_{h}^{\ell } = \left\{ {x = :~{{x}_{1}} \in \left( { - \ell ,0} \right)} \right.$, $\left. {{{x}_{2}} = h} \right\}$ приведенные построения в ${{\Xi }}_{h}^{\ell }$ бесполезны при всяком $h \in \left( {0,1} \right)$. Вместе с тем любое заданное наперед количество захваченных волн появляется в задаче (1.1)–(1.3) при J = 2, если $h \in \left( {0,1} \right)$ и размер $\ell $ достаточно велик. Этот уже упомянутый в [16] результат получается при помощи максиминимального принципа, примененного к обычным приближенным конструкциям упругих полей в балке Кирхгофа ${{\Xi }}_{{1 - h}}^{\ell }$ с малой относительной толщиной ${{\ell }^{{ - 1}}}\left( {1 - h} \right)$, у которой (балки) защемлены торцы, а основания свободны от внешних воздействий (ср. конец разд. 7).
Использование срезки (6.13) означает, что форма левого конца полуполосы ${{{{\Pi }}}^{\ell }}$ и краевые условия на нем не играют никакой роли. Кроме того, результаты в целом сохраняются и для внутренней трещины большой длины на рис. 3, б.
7. Множественность точек дискретного спектра в полуполосе со скошенным торцом. В ситуации J = 1, т.е. при ${{\Gamma }_{D}} = \left\{ {x \in \partial \Omega :{{x}_{2}} = 0,1} \right\}$, рассмотрим задачу (1.1)–(1.3) в волноводе с заостренным концом (рис. 1,а). Пусть резонатор ${{{{\Theta }}}^{\ell }}$ – длинный (как и ранее, $\ell ~$ – большой положительный параметр) прямоугольный треугольник
(7.1)
${{\Theta }^{\ell }} = \left\{ {x \in \Pi {\kern 1pt} :,{{x}_{1}} < 0,{{x}_{2}} < \operatorname{tg} \theta \left( {{{x}_{1}} + \ell } \right)} \right\}$При этом угол наклона $\theta = \operatorname{arctg} {{\ell }^{{ - 1}}} \in \left( {0,\pi {\text{/2}}} \right)~$ – малый параметр. Сформируем вспомогательную задачу в треугольнике ${{\Theta }}$. На катете ${{\varpi }^{0}}~ = \left\{ {x:{{x}_{1}} = 0,{{x}_{2}} \in \left( {0,~1} \right)} \right\}$, совпадающем с торцом полуполосы ${{\Pi }_{ + }}$, назначим искусственное условие Дирихле и построим асимптотику собственных пар полученной задачи теории упругости о балке ${{{{\Theta }}}^{\ell }}$ переменной толщины $H\left( \eta \right) = 1 + \eta $, где $\eta = {{x}_{1}}{\text{/}}\ell $ – растянутая продольная координата. Воспользуемся асимптотической процедурой из работы [17], для чего укажем соотношение
(7.2)
$\frac{{{{\pi }^{2}}}}{4} - \frac{{{{\pi }^{2}}}}{{4~H\left( \eta \right)}} = \frac{{{{\pi }^{2}}}}{4}\frac{{\left( {H\left( \eta \right) - 1} \right)}}{{H\left( \eta \right)}} = \frac{{{{\pi }^{2}}}}{4}\frac{1}{\ell }\frac{{{{x}_{1}}}}{{1 + {{\ell }^{{ - 1}}}{{x}_{1}}}} = \frac{{{{\pi }^{2}}}}{4}\frac{{{{x}_{1}}}}{\ell }\left( {1 + O\left( {\frac{{\left| {{{x}_{1}}} \right|}}{\ell }} \right)} \right)$Выбор дробного показателя в формуле (7.3) обусловлен следующим наблюдением: порядок ${{\ell }^{{ - 2/3}}}$ главного члена $O\left( {{{\ell }^{{ - 1}}}\left| {{{x}_{1}}} \right|} \right)$ = $O\left( {{{\ell }^{{ - 2/3}}}\left| \xi \right|} \right)$ выражения (7.2) такой же, как у множителя в равенстве ${{\partial }^{2}}{\text{/}}\partial x_{1}^{2}$ = ${{\ell }^{{ - 2/3}}}{{\partial }^{2}}{\text{/\;}}\partial {{\xi }^{2}}$.
Примем похожие на выражения (6.2) и (6.3) асимптотические представления для собственных пар $\left\{ {{{{{\Lambda }}}^{\ell }},{{u}^{\ell }}} \right\}$ задачи теории упругости для треугольной балки ${{{{\Theta }}}^{\ell }}$, закрепленной вдоль нижнего основания
Подставив эти формулы в систему уравнений (1.1) и краевые условия (1.2) и (1.3) на длинных катете и гипотенузе треугольника ${{{{\Theta }}}^{\ell }}$, получим прежнюю, уже решенную, задачу (6.4), (6.5), однако согласно представлению (7.2) и замене координаты (7.3) в правой части уравнения (6.6) для составляющей ${{V}_{1}}$ появляется дополнительное слагаемое
Таким образом, условие разрешимости модифицированной задачи (6.6), (6.7) принимает вид уравнения
Коэффициент B имеет вид (6.9). Полученная задача Дирихле для уравнения Эйри (см., например, книгу [18]) имеет дискретный спектр, образующий строго монотонную неограниченную положительную последовательность собственных чисел
Соответствующие собственные функции ${{{v}}_{m}}$ затухают на бесконечности с экспоненциальной скоростью, а именно
Как и ранее, при большом $\ell $ сумма $\frac{{{{\pi }^{2}}}}{4} + {{\ell }^{{ - 2/3}}}{{M}_{j}}$ строго меньше точки отсечки ${{{{\Lambda }}}^{\dag }}$ непрерывного спектра задачи (1.1)–(1.3) в ситуации J = 1. Упомянутое свойство затухания собственных функций ${{{v}}_{1}}, \ldots ,{{{v}}_{j}}$ означает, что построенный предложенным в разд. 5 способом набор пробных вектор-функций ${{U}_{1}}, \ldots ,{{U}_{j}}$ при помощи максиминимального принципа (2.3) позволяет обнаружить не менее j точек дискретного спектра рассматриваемой задачи в случае $\ell > {{\ell }_{j}}$ и некотором ${{\ell }_{j}} > 0$.
Если J = 2 и ${{\Omega }^{\ell }}$ – полуполоса с “ласточкиным хвостом” (рис. 2, б), то предыдущие конструкции в треугольнике
(7.5)
${{\Theta }}_{ + }^{\ell } = \left\{ {x:{{x}_{1}} \in \left( { - \ell ,0} \right),{{x}_{2}} \in \left( {1 - H\left( {{{\ell }^{{ - 1}}}{{x}_{1}}} \right),1} \right)} \right\}$Одномерная модель такой балки имеет вид
(7.6)
$\frac{{\mu \left( {\lambda + \mu } \right)}}{{3\left( {\lambda + 2\mu } \right)}}\frac{{{{d}^{2}}}}{{d{{\eta }^{2}}~}}\left( {H{{{\left( \eta \right)}}^{3}}\frac{{{{d}^{2}}w~}}{{d{{\eta }^{2}}}}\left( \eta \right)} \right) = M~H\left( \eta \right)w\left( \eta \right);\quad \eta \in \left( { - 1,0} \right)$Коэффициенты обыкновенного дифференциального уравнения (7.6) вырождаются в точке $\eta = - 1$ и поэтому граничные условия в ней не нужны (см. ([19], § 28 и § 37) и, напр., [20]). Вместе с тем задача (7.6), (7.7) имеет полностью дискретный спектр, образующий последовательность вида (7.4). При этом для собственных чисел задачи в треугольнике (7.5) верна асимптотическая формула (см., например, ([15], гл. 7))
Здесь ${{C}_{m}}$ и ${{\ell }_{m}}$ – положительные величины, а ${\text{2/}}\ell ~$ – средняя относительная толщина балки ${{\Theta }}_{ + }^{\ell }$. Теперь по прежней схеме при помощи максиминимального принципа (2.3) проверяем, что увеличение размера $\ell $ вызывает неограниченное возрастание кратности дискретного спектра.
В полуполосе с заостренным концом (рис. 1,а), свободном от внешних воздействий, интерпретация резонатора
Список литературы
Назаров С.А. Двумерные асимптотические модели тонких цилиндрических упругих прокладок // Дифф. уравн. 2022. Т. 58. № 12. C. 1666–1682.
Ладыженская О.А. Краевые задачи математической физики. М.: Наука, 1973.
Фикера Г. Теоремы существования в теории упругости. М.: Мир, 1974.
Бирман М.Ш., Соломяк М.З. Спектральная теория самосопряженных операторов в гильбертовом пространстве. Л.: изд-во Ленингр. ун-та, 1980.
Камоцкий И.В., Назаров С.А. О собственных функциях, локализованных около кромки тонкой области // Пробл. матем. анализа. 1999. Вып. 19. С. 105–148.
Кондратьев В.А. Краевые задачи для эллиптических уравнений в областях с коническими или угловыми точками // Тр. Московск. матем. об-ва. 1963. Т. 16. С. 219–292.
Nazarov S.A., Plamenevsky B.A. Elliptic Problems in Domains with Piecewise Smooth Boundaries. Berlin, New York: Walter de Gruyter, 1994.
Назаров С.А. Полиномиальное свойство самосопряженных эллиптических краевых задач и алгебраическое описание их атрибутов // УМН. 1999. Т. 54. № 5. С. 77–142.
Камоцкий И.В., Назаров С.А. Экспоненциально затухающие решения задачи о дифракции на жесткой периодической решетке // Матем. заметки. 2003. Т. 73. № 1. С. 138–140.
Назаров С.А. Вариационный и асимптотический методы поиска собственных чисел под порогом непрерывного спектра // Сибирск. матем. ж. 2010. Т. 51. № 5. С. 1086–1101.
Molchanov S., Vainberg B. Scattering solutions in networks of thin fibers: small diameter asymptotics // Comm. Math. Phys. 2007. V. 273. № 2. P. 533—559.
Grieser D. Spectra of graph neighborhoods and scattering // Proc. London Math. Soc. 2008. V. 97. № 3. P. 718–752.
Назаров С.А. Пороговые резонансы и виртуальные уровни в спектре цилиндрических и периодических волноводов // Изв. РАН. Сер. матем. 2020. Т. 84. № 6. С. 73–130.
Mazja W.G., Nasarow S.A., Plamenewski B.A. Asymptotische Theorie elliptischer Randwertaufgaben in singulär gestörten Gebieten. 1 & 2 Berlin: Akademie, 1991.
Назаров С.А. Асимптотическая теория тонких пластин и стержней. Понижение размерности и интегральные оценки. Новосибирск: Науч. книга, 2002.
Назаров С.А. Упругие волны, захваченные однородным анизотропным полуцилиндром // Матем. сб. 2013. Т. 204. № 11. С. 99–130.
Назаров С.А. Околовершинная локализация собственных функций задачи Дирихле в тонких многогранниках // Сибирск. матем. ж. 2013. Т. 54. № 3. С. 655–672.
Бабич В.М., Булдырев В.С. Асимптотические методы в задачах дифракции коротких волн. М.: Наука, 1972.
Михлин С.Г. Вариационные методы в математической физике. М.: Наука, 1970.
Campbell A., Nazarov S.A., Sweers G.H. Spectra of two-dimensional models for thin plates with sharp edges // SIAM J. Math. Anal. 2010. V. 42. № 6. P. 3020–3044.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика