Прикладная математика и механика, 2023, T. 87, № 2, стр. 280-302

1. Введение. Конструкции из композитных материалов (КМ) широко используются в современной конструкторской практике [1–4] и в процессе эксплуатации часто испытывают воздействие интенсивных термосиловых нагрузок [5–8], при которых компоненты их композиций деформируются пластически [5–7, 9–13]. Поэтому актуальна проблема математического моделирования неизотермического упругопластического динамического поведения тонкостенных КМ-изделий, в том числе и искривленных панелей и пологих оболочек, которая на сегодняшний день находится на стадии становления [5–7, 12–17].

Физико-механические свойства многих материалов существенно зависят от температуры [10, 18, 19], кроме того, при динамическом нагружении их пластические характеристики зависят и от скорости деформирования [18, 19], поэтому в [17] была построена модель термоупруговязкопластического деформирования многонаправленно армированного материала и проведен ряд расчетов термомеханического поведения гибких пластин из таких КМ, нагруженных в поперечном направлении воздушной взрывной волной. В работе [17] продемонстрировано, что упруговязкопластический расчет металлокомпозитных пластин необходимо проводить при учете теплового отклика в них, а пластины из стеклопластика можно рассчитывать без учета возникающего при этом температурного поля (в силу пренебрежимо малого нагрева таких композитных конструкций). Однако известно, что при высокоскоростном нагружении материалов основным источником выделения тепла в них является диссипация энергии механического происхождения, которая равна полной свертке произведения тензоров напряжений и скоростей деформаций [20]. Так как частота поперечных колебаний искривленных панелей значительно больше, чем аналогичных пластин, изготовленных из тех же материалов и имеющих те же характерные размеры, то и скорости деформаций пологих КМ-оболочек при их динамическом нагружении в поперечном направлении будут существенно больше, чем у подобных им КМ-пластин. Следовательно, при таком нагружении искривленных КМ-панелей тепловыделение в них может оказаться значительно большим, чем в аналогичных КМ-пластинах, и результаты, полученные в [17], уже нельзя будет дословно переносить на пологие КМ-оболочки.

Для расчета волновых процессов в динамически изгибаемых тонкостенных элементах КМ-конструкций и для учета их слабого сопротивления поперечным сдвигам используют неклассические теории Тимошенко–Рейсснера [5, 7, 21, 22], Амбарцумяна [17, 23], Редди [24, 25] и теории изгиба более высоких порядков [5, 26, 27].

Для интегрирования физически и геометрически нелинейных задач динамики пластин и оболочек используют явные [5, 17] и неявные [6, 28] численные схемы.

Исходя из вышеизложенного, данная работа посвящена моделированию неизотермического упруговязкопластического деформирования динамически нагружаемых в поперечном направлении пологих армированных оболочек при использовании теории изгиба Амбарцумяна. Связанная нелинейная термомеханическая задача, возникающая при этом, численно интегрируется с использованием явной схемы шагов по времени.

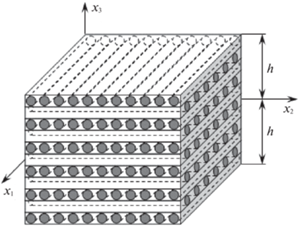
2. Формулировка задачи и метод ее решения. Рассмотрим пологую оболочку толщиной 2h, с которой свяжем ортогональную систему координат ${{x}_{i}}$ так, чтобы отсчетная поверхность ${{x}_{3}} = 0$ была срединной ($\left| {{{x}_{3}}} \right| \leqslant h$), а координатные линии ${{x}_{1}}$ и ${{x}_{2}}$ совпадали с линиями главных кривизн этой поверхности (рис. 1, на котором искривленность панели не изображена в силу ее малости). Оболочка усилена N семействами волокон (возможно и пространственно) с плотностями армирования ${{\omega }_{k}}$ ($1 \leqslant k \leqslant N$). В поперечном направлении ${{x}_{3}}$ структура армирования однородна.

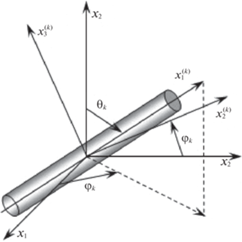
С каждым k-м семейством волокон свяжем ортогональную систему координат $x_{i}^{{(k)}}$. При этом ось $x_{1}^{{(k)}}$ направим вдоль траектории армирования, а ее ориентацию в пространстве ${{x}_{1}}{{x}_{2}}{{x}_{3}}$ зададим двумя углами сферической системы координат ${{\theta }_{k}}$ и ${{\varphi }_{k}}$ (рис. 2). Направляющие косинусы $l_{{ij}}^{{(k)}}$ оси $x_{i}^{{(k)}}$ в глобальной системе координат ${{x}_{j}}$ ($i,j = \overline {1,3} $, $1 \leqslant k \leqslant N$) определяются формулами [17]:

Внешние касательные силы на лицевых поверхностях панели традиционно не учитываем, а в случае пространственного армирования дополнительно считаем, что выполняются требования, предъявляемые к структуре армирования, приведенные в замечании в [17]. (При многонаправленном плоском армировании (см. рис. 1) указанные требования выполняются заведомо.) Тогда на основании результатов работ [17, 23] перемещения точек гибкой пологой КМ-оболочки ${{U}_{i}}$ и осредненные деформации ее композиции ${{\varepsilon }_{{ij}}}$ в рамках теории Амбарцумяна аппроксимируются так:

где w – прогиб конструкции; ${{u}_{i}}$ – перемещения точек срединной поверхности (${{x}_{3}} = 0$) в тангенциальных направлениях ${{x}_{i}}$; $\varepsilon _{{i3}}^{0}$ – деформации поперечных сдвигов в точках этой же поверхности; ${{R}_{i}}$ – радиусы главных кривизн отсчетной поверхности; ${{t}_{0}}$ – начальный момент времени t; ${{\partial }_{i}}$ – оператор частного дифференцирования по переменной ${{x}_{i}}$ ($i = 1,2$); ${{\delta }_{{ij}}}$ – символ Кронекера; $\Omega $ – область, занимаемая КМ-панелью в плане. В выражениях (2.2) и (2.3) неизвестны двумерные функции w, ${{u}_{i}}$ и $\varepsilon _{{i3}}^{0}$ ($i = 1,2$), зависящие и от времени t.

В настоящем исследовании моделируется поведение искривленной КМ-панели как гибкой тонкостенной термомеханической системы, поэтому с приемлемой для практических приложений точностью напряжение ${{\sigma }_{{33}}}\left( {t,{\mathbf{r}}} \right)$ по координате ${{x}_{3}}$ можно аппроксимировать так [17, 22]:

где $\sigma _{{33}}^{{( \pm )}}\left( {t,{\mathbf{x}}} \right) \equiv {{\sigma }_{{33}}}\left( {t,{\mathbf{x}}, \pm h} \right)$ – нормальные напряжения на верхней (+) и нижней (–) лицевых поверхностях конструкции, известные из соответствующих силовых граничных условий.

К соотношениям (2.2) и (2.3) необходимо присоединить уравнения движения гибкой пологой КМ-оболочки, которые при учете равенства (2.4) имеют вид [23]:

где ${{\rho }_{0}}$ и ${{\rho }_{k}}$ – объемные плотности материалов связующего и арматуры k-го семейства; ${{\omega }_{0}}$ – относительное объемное содержание связующей матрицы в представительном элементе композиции; ${{\gamma }_{i}}$ – традиционно вводимые для удобства новые кинематические переменные; ${{\sigma }_{{ij}}}$ – осредненные напряжения в композиции искривленной панели; ${{F}_{{ij}}}$, ${{F}_{{i3}}}$ и ${{M}_{{ij}}}$ – внутренние силовые факторы; точка – производная по времени t. Внешне массовые силы в уравнениях (2.5) не учитываются.

Как уже отмечалось, для интегрирования формулируемой нелинейной задачи предполагается использовать явную численную схему, т.е. значения неизвестных функций будем вычислять в дискретные моменты времени ${{t}_{n}}$ ($n = 0,1,2,...$). При этом считаем, что в моменты времени ${{t}_{m}}$ уже определены величины следующих функций [17]:

где $\sigma _{{ij}}^{{(k)}}$ и $\varepsilon _{{ij}}^{{(k)}}$ – тензоры напряжений и деформаций в k-м компоненте композиции ($k = 0$ – связующая матрица, $k \geqslant 1$ – волокна k-го семейства); ${{\chi }_{k}}$ – параметр Одквиста (упрочнения) того же материала; $\Theta $ – температура КМ (пологой оболочки).

Определяющие уравнения термоупруговязкопластического деформирования армированного материала, пригодные для практического использования, получим на основе следующих предположений [29]:

1. В пределах представительного элемента КМ является макроскопически квазиоднородным телом. (При достаточно равномерном и густом наполнении связующего материала тонкими волокнами это допущение справедливо.)

2. Между связующей матрицей и волокнами имеет место идеальный термомеханический контакт.

3. В пределах представительного элемента, выделенного из КМ на миниуровне, напряжения, деформации и их скорости во всех компонентах и в композиции в целом кусочно-постоянны. Эффектами более высоких порядков, характеризующих локальные изменения полей напряжений, деформаций и их скоростей на микроуровне в малых окрестностях границ контакта связующего и волокон, пренебрегаем.

4. Поля деформаций, напряжений и их скоростей усредняем по объему репрезентативной ячейки КМ (т.е., согласно допущению 3, пропорционально ${{\omega }_{k}}$, $0 \leqslant k \leqslant N$).

5. Материалы компонентов композиции являются однородными и изотропными; их пластическое течение ассоциировано с поверхностями нагружения, соответствующими условию текучести Мизеса и зависящими от параметров упрочнения, температуры и скоростей деформирования.

Повторяя на базе этих гипотез рассуждения из работы [17], получим, что в рассматриваемый дискретный момент времени ${{t}_{n}}$ связь между скоростями осредненных напряжений ${{\dot {\sigma }}_{{ij}}}$, деформаций ${{\dot {\varepsilon }}_{{ij}}}$ и температурой композиции $\Theta $ можно записать в следующей матричной форме:

где $\Delta $ – шаг по времени; I – единичная $6 \times 6$-матрица; B, ${{{\mathbf{B}}}_{k}}$, ${{{\mathbf{E}}}_{k}}$, ${{{\mathbf{C}}}_{k}}$, ${{{\mathbf{Z}}}_{k}}$, ${{{\mathbf{\bar {Z}}}}_{k}}$, ${{{\mathbf{\bar {\bar {Z}}}}}_{k}}$ и ${{{\mathbf{Y}}}_{k}}$ – $6 \times 6$-матрицы; ${\mathbf{D}}_{k}^{{ - 1}}$ и ${{{\mathbf{H}}}^{{ - 1}}}$ – матрицы, обратные $6 \times 6$-матрицам ${{{\mathbf{D}}}_{k}}$ и H; p, f, g, ${{{\mathbf{r}}}_{k}}$, ${{\varsigma }_{k}}$, ${{{\mathbf{p}}}_{k}}$ и ${{\beta }_{k}}$ – шестикомпонентные векторы-столбцы; ${{\varepsilon }_{k}}$ – шестикомпонентный вектор-столбец деформаций $\varepsilon _{{ij}}^{{(k)}}$ k-го компонента композиции, по структуре аналогичный вектору $\varepsilon $ (см. выражения (2.10)). Ненулевые элементы матриц ${{{\mathbf{C}}}_{k}} = \left( {c_{{ij}}^{{(k)}}} \right)$, ${{{\mathbf{D}}}_{k}} = \left( {d_{{ij}}^{{(k)}}} \right)$, ${{{\mathbf{\bar {Z}}}}_{k}} = \left( {\bar {z}_{{ij}}^{{(k)}}} \right)$, ${{{\mathbf{\bar {\bar {Z}}}}}_{k}} = \left( {\bar {\bar {z}}_{{ij}}^{{(k)}}} \right)$ и вектор-столбцов ${{\varsigma }_{k}} = \left( {\varsigma _{i}^{{(k)}}} \right)$, ${{\beta }_{k}} = \left( {\beta _{i}^{{(k)}}} \right)$ вычисляются так: где $e_{{ij}}^{{(k)}}$ и $p_{{ij}}^{{(k)}}$ – упругие и пластические деформации k-го материала композиции; ${{E}_{k}} = {{E}_{k}}\left( \Theta \right)$ и ${{\nu }_{k}} = {{\nu }_{k}}\left( \Theta \right)$ – модуль Юнга и коэффициент Пуассона того же компонента; ${{\alpha }_{k}} = {{\alpha }_{k}}\left( \Theta \right)$ – коэффициент линейного температурного расширения; $\tau _{s}^{{(k)}} = \tau _{s}^{{(k)}}\left( {{{\chi }_{k}},{{H}_{k}},\Theta } \right)$ – мгновенный предел текучести при чистом сдвиге, зависящий от уровня накопленной пластической деформации ${{\chi }_{k}}$ и значений интенсивности скорости деформаций ${{H}_{k}}$ и температуры $\Theta $ в текущий момент времени ${{t}_{n}}$; $p_{l}^{{(k)}}$ и $b_{{lj}}^{{(k)}}$ ($0 \leqslant k \leqslant N$) – элементы вектор-столбцов ${{{\mathbf{p}}}_{k}}$ и матриц ${{{\mathbf{B}}}_{k}}$, определенных равенствами (2.10) и (2.11); ${{\gamma }_{k}}$ – параметр переключения, определяющий при ${{\gamma }_{k}} = 0$ условия термоупругого деформирования, разгрузки или нейтрального нагружения, а при ${{\gamma }_{k}} = 1$ – активного нагружения при пластическом деформировании k-го материала композиции; индекс “т” – операция транспонирования. По повторяющимся индексам k и l в выражениях (2.14) суммирования нет. В равенствах (2.14) опущен верхний индекс n, означающий рассматриваемый дискретный момент времени $t = {{t}_{n}}$. Между вектор-столбцами $\dot {\varepsilon }$ и ${{\dot {\varepsilon }}_{k}}$ (см. соотношения (2.9)–(2.11)) существует матричная связь [17]: где матрицы H, ${{{\mathbf{E}}}_{k}}$и вектор-столбцы g, ${{{\mathbf{r}}}_{k}}$ определены выражениями (2.11). Для материалов композиции выполняются определяющие соотношения, записанные в матричной форме [17]: где ${{\dot {\sigma }}_{k}}$ – шестикомпонентный вектор-столбец скоростей напряжений $\dot {\sigma }_{{ij}}^{{(k)}}$ в k-й фазе композиции, по структуре аналогичный вектору $\sigma $ в соотношениях (2.10); матрица ${{{\mathbf{B}}}_{k}}$ и вектор ${{{\mathbf{p}}}_{k}}$ определены равенствами (2.11).

Вектор-столбец ${{\ddot {\varepsilon }}_{k}}$ в соотношениях (2.14) необходимо выразить его конечно-разностным аналогом, используя формулу трапеций [17]:

где последнее слагаемое определено в (2.11).

Не выписанные в соотношениях (2.13) элементы $6 \times 6$-матриц ${{{\mathbf{G}}}_{k}} = \left( {g_{{ij}}^{{(k)}}} \right)$ и ${{{\mathbf{Q}}}_{k}} = \left( {q_{{ij}}^{{(k)}}} \right)$ представлены в табл. (21.40) и (21.44) в [29]. Эти матрицы ${{{\mathbf{G}}}_{k}}$ и ${{{\mathbf{Q}}}_{k}}$ задают преобразования векторов-столбцов ${{\dot {\sigma }}_{k}}$ и ${{\dot {\varepsilon }}_{k}}$ (см. равенство (2.16)) при переходе от глобальной ортогональной системы координат ${{x}_{j}}$ к локальной системе $x_{i}^{{(k)}}$ (см. рис. 2). Направляющие косинусы $l_{{ij}}^{{(k)}}$ ($i,j = \overline {1,\,3} $, $1 \leqslant k \leqslant N$) между указанными осями вычисляются по формулам (2.1).

Согласно условиям соответствия (2.10), из третьего уравнения системы (2.9), линеаризованной по методу переменных параметров упругости [17, 30], выразим скорость поперечной деформации пологой КМ-оболочки:

где ${{b}_{{3i}}}$ и ${{p}_{3}}$ ($i = \overline {1,6} $) – элементы матрицы B и вектора p в равенстве (2.9); скорость ${{\dot {\sigma }}_{3}}$ получается из соотношения (2.4) дифференцированием по времени t. Производные ${{\dot {\varepsilon }}_{i}}$ в правой части равенства (2.17) определяются путем дифференцирования по t кинематических соотношений (2.3), т.е. характеризуются двумерными функциями w, $\dot {w}$, ${{\dot {u}}_{i}}$ и $\dot {\varepsilon }_{{i3}}^{0}$ ($i = 1,2$).

Как и в [17], температуру $\Theta $ аппроксимируем по толщине искривленной панели полиномом порядка L:

где ${{\Theta }^{0}} = {\text{const}}$ – температура естественного состояния конструкции; ${{\Theta }_{l}}$ – искомые двумерные функции, зависящие и от времени t.

Согласно известным экспериментальным данным [10, 18], удельную теплоемкость k-го материала композиции ${{c}_{k}}$ вполне допустимо представить полиномом второго порядка от температуры:

где $c_{l}^{{(k)}}$ ($l = \overline {0,2} $) – известные коэффициенты.

Так как метрику в пологой оболочке с приемлемой для практических приложений точностью можно отождествить с метрикой в декартовой прямоугольной системе координат [23], используя результаты работы [17], в качестве разрешающих двумерных уравнений теплофизической составляющей рассматриваемой задачи, соответствующих разложению (2.18), получим равенства

где U – удельная внутренняя энергия материала конструкции; ${{q}_{i}}$ – компоненты вектора теплового потока в КМ, связанные с $\operatorname{grad} \Theta $ законом Фурье для волокнистого материала (см. соотношения (3.1) и (3.2) в [17]); $q_{\infty }^{{( \pm )}}$ – заданные тепловые потоки через верхнюю (+) и нижнюю (–) лицевые поверхности оболочки; $\Theta _{\infty }^{{( \pm )}}$ – температуры окружающей среды со стороны тех же поверхностей; ${{\alpha }^{{( \pm )}}}$ – коэффициенты теплоотдачи на тех же поверхностях; ${{\lambda }_{{33}}}$ – коэффициент теплопроводности композиции в направлении ${{x}_{3}}$, определяемый по структурным формулам (3.2) и (3.3) из [17]; $\rho $ задано первым выражением в (2.6).

Приведенные двумерные уравнения (2.20) при учете выражений (2.23) получены из трехмерного уравнения теплового баланса методом взвешенных невязок; при этом в качестве весовых функций использовались однородные полиномы $x_{3}^{m}$. Равенства (2.21) – это тепловые граничные условия на лицевых поверхностях искривленной КМ-панели, преобразованные с учетом разложения для температуры (2.18). Уравнения (2.22) задают связь между двумерными функциями ${{U}^{{(m)}}}$ (см. формулу (2.23)) и коэффициентами представления (2.18) при учете аппроксимаций (2.19).

Для завершения постановки задачи термоупруговязкопластического деформирования искривленной КМ-панели к уравнениям (2.3), (2.5) и (2.9) необходимо присоединить общеизвестные силовые (выраженные через силовые факторы ${{F}_{{ij}}}$, ${{F}_{{i3}}}$ и ${{M}_{{ij}}}$, $i,j = 1,2$) и кинематические граничные условия, а также начальные условия для неизвестных функций w, ${{u}_{i}}$ и $\varepsilon _{{i3}}^{0}$, $i = 1,2$ (см. выражения (2.7)) [23]. Кроме того, для однозначного определения функций ${{\Theta }_{l}}$ ($0 \leqslant l \leqslant L$) в разложении (2.18) нужно использовать соответствующие теплофизические граничные условия, которые также получаются методом взвешенных невязок и при учете выражений (2.18) и (2.23) имеют вид [17]:

где ${{n}_{1}}$, ${{n}_{2}}$ – направляющие косинусы внешней нормали к контуру $\Gamma $, ограничивающему область $\Omega $; ${{\alpha }_{ * }}$, $\Theta _{\infty }^{*}$, $q_{\infty }^{*}$ имеют тот же смысл, что и аналогичные величины в соотношениях (2.21), только на торцевой поверхности конструкции.

Для интегрирования уравнений (2.20) по времени необходимо задать начальные значения для функций ${{U}^{{(m)}}}$ при $t = {{t}_{0}}$. Эти значения получаются из равенств (2.22) при подстановке в них функций ${{\Theta }_{l}}\left( {{{t}_{0}},{\mathbf{x}}} \right)$ ($0 \leqslant l \leqslant L$), полученных из разложения (2.18) заданной начальной температуры $\Theta \left( {{{t}_{0}},{\mathbf{x}}} \right)$ КМ-оболочки.

Как и в [17], заменим вторые производные по t от неизвестных функций в левых частях уравнений (2.5) их конечно-разностными аналогами на трехточечном шаблоне $\left\{ {{{t}_{{n - 1}}},{{t}_{n}},{{t}_{{n + 1}}}} \right\}$, тогда с учетом обозначений, аналогичных (2.8) получим

По формулам (2.6) при учете предположений (2.8) в текущий дискретный момент времени ${{t}_{n}}$ можно определить все внутренние силовые факторы и внешние силы $\sigma _{{33}}^{{( \pm )}}$, входящие в правые части уравнений (2.25). Следовательно, из этих равенств при учете соответствующих граничных условий [23] по явной схеме можно вычислить значения искомых функций $\mathop w\limits^{n + 1} $, $\mathop {{{u}_{i}}}\limits^{n + 1} $ и $\mathop {{{\gamma }_{i}}}\limits^{n + 1} $ в следующий момент времени ${{t}_{{n + 1}}}$. Затем, используя выражения (2.7), можно получить и значения деформаций $\mathop {\varepsilon _{{i3}}^{0}}\limits^{n + 1} $ ($i = 1,2$), определяющих совместно с $\mathop w\limits^{n + 1} $ и $\mathop {{{u}_{i}}}\limits^{n + 1} $ перемещения точек конструкции и усредненные деформации композиции (см. соотношения (2.2) и (2.3)).

Предполагаем, что помимо функций, указанных в равенствах (2.8), при $t = {{t}_{m}}$ дополнительно известны значения и таких функций [17] (см. соотношения (2.18), (2.21) и (2.23)):

Для численного интегрирования теплофизической составляющей рассматриваемой связанной задачи также используем явную схему, но на двухточечном шаблоне по времени $\left\{ {{{t}_{n}},{{t}_{{n + 1}}}} \right\}$. Заменив производные по t в левых частях равенств (2.20) их конечными разностями и учитывая обозначения, аналогичные (2.26), получим уравнения

Используя выражения (2.23) и принимая во внимание предположения (2.26), в текущий момент времени ${{t}_{n}}$ можем вычислить правые части в уравнениях (2.27). Затем, учитывая тепловые граничные (2.24) и начальные температурные условия, из равенств (2.27) по явной схеме определяем значения функций $\mathop {{{U}^{{(m)}}}}\limits^{n + 1} $ на следующем шаге по времени ${{t}_{{n + 1}}}$. После этого при $t = {{t}_{{n + 1}}}$ из уравнений (2.21) и (2.22), в которых правые части уже известны, при учете соотношений (2.23) получаем коэффициенты разложения температуры $\mathop {{{\Theta }_{l}}}\limits^{n + 1} \left( {\mathbf{x}} \right)$ (см. формулу (2.18)). В случае термочувствительных материалов фаз композиции, когда в разложении (2.19) $c_{1}^{{(k)}} \ne 0$ и/или $c_{2}^{{(k)}} \ne 0$ ($0 \leqslant k \leqslant N$), система уравнений (2.21) и (2.22) является нелинейной относительно функций ${{\Theta }_{l}}$ ($0 \leqslant l \leqslant L$). Линеаризовать уравнения (2.22) можно, используя, например, метод переменных теплофизических параметров, формально аналогичный методу переменных параметров упругости [30]. В остальном разработанный численный метод интегрирования рассматриваемой задачи термоупруговязкопластического динамического деформирования пологих КМ-оболочек при учете равенств (2.3), (2.4), (2.17) и структурных соотношений (2.9), (2.15) и (2.16) реализуется так, как подробно описано в [17], где было показано, что шаг интегрирования по времени $\Delta $ в уравнениях (2.25) и (2.27) нужно выбирать, исходя из необходимого условия устойчивости Куранта–Фридрихса–Леви [5, 31].

3. Обсуждение результатов расчетов. Исследуем термоупруговязкопластический динамический изгиб относительно тонких пологих цилиндрических КМ-оболочек ($\Omega $: $\left| {{{x}_{1}}} \right| \leqslant a$, $\left| {{{x}_{2}}} \right| \leqslant b$, $a = 3b$; $1{\text{/}}{{R}_{1}} \equiv 0$, ${{R}_{2}} \equiv R = {\text{const}}$; $2h = 2$ см, $b = 50$ см), стрела подъема которых  f  над продольными (в направлении ${{x}_{1}}$) кромками равна 10 см. При этом радиус кривизны КМ-панелей вычисляется так: $R = \left( {{{b}^{2}} + {{f}^{2}}} \right){\text{/}}\left( {2f} \right)$. В рассматриваемом случае $0 < f < 0.4b$, поэтому оболочки действительно являются пологими [23]. Кромки конструкций жестко закреплены: $w = 0$, ${{u}_{i}} = 0$ и ${{\gamma }_{i}} = 0$, ${\mathbf{x}} \in \Gamma $, $t \geqslant {{t}_{0}}$ (см. выражения (2.2) и (2.7)). До начального момента времени $t = {{t}_{0}} = 0$ искривленные КМ-панели покоятся ($w = 0$, ${{u}_{i}} = 0$ и ${{\gamma }_{i}} = 0$, ${\mathbf{x}} \in \Omega $, $t \leqslant {{t}_{0}}$, $i = 1,2$) при температуре естественного состояния $\Theta = {{\Theta }^{0}} = {\text{20}}^\circ {\text{C}}$ (${\mathbf{x}} \in \Omega $, $\left| {{{x}_{3}}} \right| \leqslant h$ и $t \leqslant {{t}_{0}}$). При $t = {{t}_{0}} = 0$ конструкции нагружаются избыточным давлением $p\left( t \right)$, которое порождается воздушной взрывной волной [28]:

где ${{t}_{{{\text{max}}}}}$ – момент времени, при котором $p\left( t \right)$ достигает наибольшего по модулю значения $\left| {{{p}_{{\max }}}} \right|$; ${{t}_{{{\text{min}}}}}$ – момент времени, при котором уже можно пренебречь $\left| {p\left( t \right)} \right|$ по сравнению с $\left| {{{p}_{{\max }}}} \right|$ (в частности, выражение (3.2) справедливо при $p\left( {{{t}_{{{\text{min}}}}}} \right)$ = $0.01{{p}_{{\max }}}$). На основании данных экспериментов [28] в расчетах примем ${{t}_{{{\text{max}}}}} = 0.1$ мс и ${{t}_{{{\text{min}}}}} = 2$ мс. Из соотношений (3.1) вытекает: при ${{p}_{{\max }}} > 0$ пологие оболочки нагружаются со стороны нижней (вогнутой) лицевой поверхности (при этом предполагается, что $\sigma _{{33}}^{{( + )}} \equiv 0$), а при ${{p}_{{\max }}} < 0$ – со стороны верхней (выпуклой) лицевой поверхности (при этом считаем, что $\sigma _{{33}}^{{( - )}} \equiv 0$).

Известно, что при нарастании внешней динамической нагрузки до максимального ее значения за время, меньшее 0.1 мкс, в КМ-конструкциях возникают откольные явления и расслоения [7]. Так как в рассматриваемом случае нагружения ${{t}_{{{\text{max}}}}}$ = 0.1 мс $ \gg $ 0.1 мкс, материал искривленных панелей остается сплошным, и вполне обоснованно применимы допущения, использованные в разд. 2.

Теплообмен КМ-панелей с окружающей средой на лицевых поверхностях происходит в условиях естественной конвекции (${{\alpha }^{{( \pm )}}} = 30$ Вт/(м² К) [32] и $q_{\infty }^{{( \pm )}} \equiv 0$) при температуре воздуха $\Theta _{\infty }^{{( \pm )}} = {{\Theta }^{0}}$ (см. равенства (2.21)). На торцевых поверхностях тонкостенных конструкций задана температура, которая поддерживается равной ${{\Theta }^{0}}$ (см. формулу (2.24) при $\alpha _{*}^{{}} \to \infty $ и $\Theta _{\infty }^{*} = {{\Theta }^{0}}$).

Оболочки выполнены из эпоксидной смолы [9] и армированы стеклянными волокнами [10] (стеклопластик) или из магниевого сплава ВТ65 [18] и усилены стальной проволокой марки У8А [10] (металлокомпозиция). Упругопластическое деформирование компонентов композиций при постоянстве температуры $\Theta $ и скорости деформаций $\dot {\varepsilon }$ определяется диаграммой с линейным упрочнением

где $\sigma $ и $\varepsilon $ – осевое напряжение и соответствующая ему деформация при растяжении–сжатии; $E_{{\text{s}}}^{{(k)}} = E_{{\text{s}}}^{{(k)}}\left( {\Theta ,\dot {\varepsilon }} \right)$ – модуль упрочнения k-го материала композиции; $\sigma _{{\text{s}}}^{{(k)}} = \sigma _{{\text{s}}}^{{(k)}}\left( {\Theta ,\dot {\varepsilon }} \right)$ – условный предел текучести того же материала. Физико-механические характеристики компонентов композиций представлены в табл. 1, где в скобках указана температура ($\Theta ,^\circ {\text{C}}$), при которой определено значение соответствующей величины. Во второй и третьей частях табл. 1 (для скоростей деформаций $\dot {\varepsilon } = {\text{0}}{\text{.417}}$ c^–1 и $\dot {\varepsilon } = {\text{104}}$ c^–1) представлены только те значения характеристик, которые отличаются от данных, приведенных в первой части (для $\dot {\varepsilon } = 5 \times 1{{{\text{0}}}^{{ - 4}}}$ c^–1). Как и в [17], предполагается: в рассматриваемом диапазоне изменения скорости деформации $\dot {\varepsilon }$ можно пренебречь зависимостью упругих и теплофизических характеристик материалов композиции от $\dot {\varepsilon }$ [18, 19]. В расчетах зависимости физико-механических характеристик от температуры $\Theta $ аппроксимировались линейно по данным, указанным в табл. 1, а аппроксимации зависимостей характеристик пластичности материалов от скорости деформирования $\dot {\varepsilon }$ принимались такими же, как в [17].

Для реализации разработанного в разд. 1 численного метода по пространственным переменным ${{x}_{1}}$ и ${{x}_{2}}$ вводилась регулярная сетка с шагами $\Delta {{x}_{1}} = \Delta {{x}_{2}} = b{\text{/}}50$ = 1 см; шаг по времени $\Delta $ задавался равным 0.25 мкс. При такой дискретизации рассматриваемых задач необходимые условия устойчивости построенной конечно-разностной схемы выполняются с запасом (см. формулы (6.3) в [17]).

Пологие оболочки усилены двумя семействами волокон ($N = 2$), уложенных в направлениях ${{x}_{1}}$ и ${{x}_{2}}$ соответственно (как изображено на рис. 1) с плотностями армирования ${{\omega }_{1}} = 0.1$ и ${{\omega }_{2}} = {\text{0}}{\text{.3}}$. Углы армирования для такой плоской структуры, согласно рис. 2, имеют значения: ${{\theta }_{1}} = {{\theta }_{2}} = \pi {\text{/}}2$, ${{\varphi }_{1}} = 0$ и ${{\varphi }_{2}} = \pi {\text{/}}2$ (см. соотношения (2.1)).

Чтобы выяснить вопрос о выборе значения L в формуле (2.18), при котором обеспечивалась бы приемлемая для практических расчетов точность определения температуры $\Theta $, исследуем зависимости от L наибольших значений ${{\Theta }_{{{\text{max}}}}}\left( L \right)$ = $\mathop {\max }\limits_{t,{\mathbf{r}}} \Theta \left( {t,{\mathbf{r}};L} \right)$ ($\left| {{{x}_{1}}} \right| \leqslant a$, $\left| {{{x}_{2}}} \right| \leqslant b$, $\left| {{{x}_{3}}} \right| \leqslant h$ и $0 \leqslant t \leqslant 50$ мс). На рис. 3 представлены эти зависимости для стеклопластиковой КМ-панели (рис. 3,а), полученные при $\left| {{{p}_{{\max }}}} \right| = 8$ МПа (см. выражения (3.1) и (3.2)), и для Mg–У8А-оболочки (рис. 3,б) при $\left| {{{p}_{{\max }}}} \right| = 30$ МПа. При указанных значениях $\left| {{{p}_{{\max }}}} \right|$ в рассматриваемых конструкциях наблюдается пластическое деформирование компонентов композиции. Значению $L = 0$ на рис. 3 соответствуют случаи, когда тепловой отклик в пологих КМ-оболочках не учитывается, поэтому условно принято ${{\Theta }_{{{\text{max}}}}}\left( 0 \right) = {{\Theta }^{0}}$ = 20°C. Сплошные кривые на рис. 3 рассчитаны при учете зависимости пластических свойств материалов композиции от скорости их деформирования (от величины ${{H}_{k}}$ в соотношениях (2.14)), а штриховые кривые, номера которых помечены штрихом, – без учета этой зависимости (термоупругопластическое деформирование). В последнем случае расчеты проводились по данным первой части табл. 1 (при значении $\dot {\varepsilon } = 5 \times {{10}^{{ - 4}}}$ с^–1). Кривые 1 и 1' получены при нагружении КМ-панелей снизу – со стороны вогнутой лицевой поверхности (${{p}_{{\max }}} > 0$), а кривые 2 и 2' – при нагружении сверху – со стороны выпуклой лицевой поверхности (${{p}_{{\max }}} < 0$).

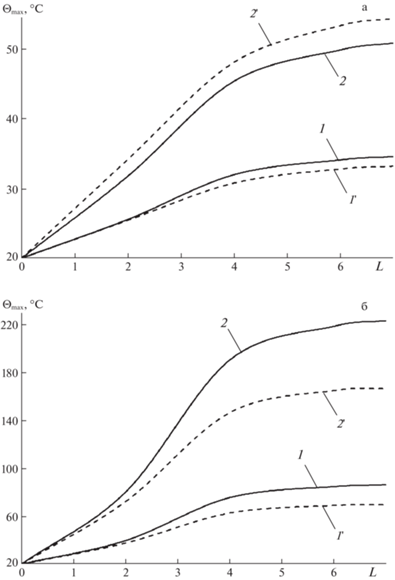
Анализ поведения кривых на рис. 3 показывает, что приращение величины ${{\Theta }_{{{\text{max}}}}}$ при переходе от $L = 6$ к $L = 7$ можно считать практически пренебрежимо малым. При $L \geqslant 8$ система линеаризованных уравнений (2.21) и (2.22), из которой при учете соотношений (2.23) в текущий момент времени вычисляются коэффициенты в представлении температуры (2.18), становится плохо обусловленной, поэтому зависимости ${{\Theta }_{{{\text{max}}}}}\left( L \right)$ при $L \geqslant 8$ являются расходящимися и на рис. 3 не изображены. (Этот результат качественно совпадает с полученным ранее для КМ-пластин разной относительной толщины [17].) Далее в расчетах принимаем $L = 7$.

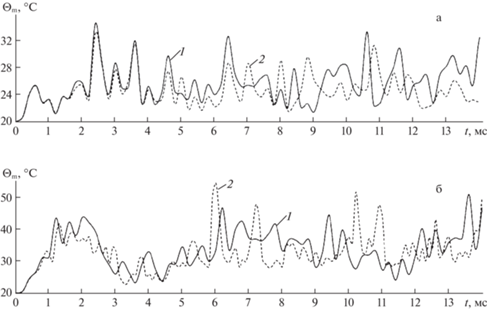
На рис. 4 изображены осцилляции наибольших значений температуры ${{\Theta }_{{\text{m}}}}\left( t \right)$ = = $\mathop {\max }\limits_{\mathbf{r}} \Theta \left( {t,{\mathbf{r}}} \right)$ ($\left| {{{x}_{1}}} \right| \leqslant a$, $\left| {{{x}_{2}}} \right| \leqslant b$ и $\left| {{{x}_{3}}} \right| \leqslant h$) в стеклопластиковой пологой оболочке, нагруженной снизу (рис. 4,а) давлением ${{p}_{{\max }}} = 8$ МПа и сверху: ${{p}_{{\max }}} = - 8$ МПа (рис. 4,б). Сплошные кривые 1 на рис. 4 рассчитаны по термоупруговязкопластической теории, а штриховые кривые 2 – термоупругопластической теории. Сравнение поведения кривых 1 и 2 на рис. 4 показывает, что расчеты, выполненные по термоупруговязкопластической (кривые 1) и по термоупругопластической (кривые 2) моделям деформирования компонентов композиции искривленных панелей при их динамическом поперечном нагружении, приводят к существенно разным температурным откликам. При этом указанные теории деформирования предсказывают разные значения достигаемого максимума температуры ${{\Theta }_{{{\text{max}}}}}$ = $\mathop {\max }\limits_{t \geqslant {{t}_{0}}} {{\Theta }_{{\text{m}}}}\left( t \right)$. Так, при нагружении стеклопластиковой панели снизу, согласно поведению кривой 1 на рис. 4,а, значение ${{\Theta }_{{{\text{max}}}}}$ = = 34.5°C при учете чувствительности фазовых материалов к скорости их деформирования и ${{\Theta }_{{{\text{max}}}}}$ = 33.2°C (см. кривую 2 на рис. 4,а) при неучете этой чувствительности. Оба указанных значения достигаются в один и тот же момент времени $t \approx 2.4$ мс и в данном случае различаются незначительно (менее, чем на 1.5°C). Однако уже в случае нагружения пологой оболочки из стеклопластика сверху (см. рис. 4,б) такое различие становится более существенным, причем значения ${{\Theta }_{{{\text{max}}}}}$, полученные по термоупруговязкопластической и термоупругопластической теориям, достигаются в разные моменты времени. А именно: согласно поведению кривой 1 на рис. 4,б, значение ${{\Theta }_{{{\text{max}}}}}$ = = 50.8°C достигается при $t \approx 13.6$ мс, а на кривой 2 глобальный максимум со значением ${{\Theta }_{{{\text{max}}}}}$ = 54.3°C реализуется при $t \approx 6$ мс. Таким образом, расчеты, выполненные без учета зависимости пластических свойств материалов композиции от скорости их деформирования, занижают расчетное значение ${{\Theta }_{{{\text{max}}}}}$ при нагружении стеклопластиковой искривленной панели снизу (см. рис. 4,а), и, наоборот, завышают это значение при нагружении такой конструкции сверху (см. рис. 4,б). Для сравнения напомним: согласно результатам работы [17], аналогичная стеклопластиковая пластина с теми же характерными размерами и с такой же структурой армирования при ${{p}_{{\max }}} = \pm 4$ МПа нагревается практически до таких же значений ${{\Theta }_{{{\text{max}}}}}$, что и пологая оболочка, нагруженная снизу (см. рис. 4,а). Однако эти значения существенно меньше тех, что достигаются при нагружении искривленной панели сверху (см. рис. 4,б).

На рис. 5 изображены аналогичные зависимости ${{\Theta }_{{\text{m}}}}\left( t \right)$, полученные для металлокомпозитной пологой оболочки, нагруженной снизу при ${{p}_{{\max }}} = 30$ МПа (рис. 5,а) и сверху при ${{p}_{{\max }}} = - 30$ МПа (рис. 5,б). Номера кривых на рис. 5 имеют тот же смысл, что и на рис. 4. Поведение кривых 1 и 2 на рис. 5 различается в еще большей степени, чем на рис. 4. Объясняется это тем, что пластические свойства связующего рассматриваемой металлокомпозиции сильно чувствительны к изменению скорости его деформирования, а компоненты стеклопластиковой композиции относительно слабо чувствительны к изменению этой скорости (см. табл. 1).

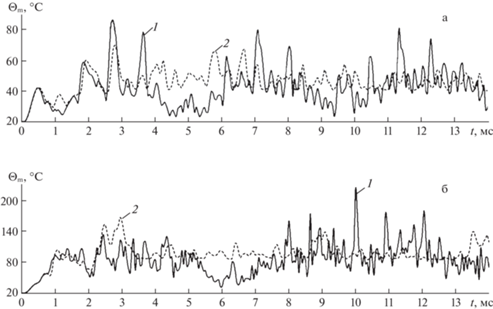
Сравнение кривых с одинаковыми номерами на рис. 4,а, 4,б и 5,а, 5,б соответственно показывает, что при практически одинаковых уровнях максимальных значений интенсивностей деформаций компонентов композиций, достигаемых в процессе поперечных осцилляций оболочек, металлокомпозитные искривленные панели (как и в случае пластин [17]) нагреваются в значительно большей степени, чем стеклопластиковые. Так, согласно поведению кривых на рис. 5,б, в отдельных точках пологой Mg–У8А-оболочки, нагруженной сверху, температура может превышать 100°C. Однако резкий интенсивный нагрев отдельных точек такой конструкции является кратковременным и длится менее 1 мс.

Согласно поведению кривой 2 на рис. 3,б (при $L = 7$) и кривой 1 на рис. 5,б, для Mg–У8А-панели, нагруженной воздушной взрывной волной сверху, пиковые значения температуры могут превышать 200°C. По оценкам же, приведенным в [33], при ударном нагружении металлических образцов в областях локализованной пластической деформации температура может достигать 1000 K и выше. Как видно из предыдущего анализа, максимальные значения температуры для металлокомпозитной пологой оболочки уже сопоставимы с этими оценками.

В [17] было показано, что динамический неупругий расчет стеклопластиковых пластин можно проводить без учета температуры в них (в силу незначительного их нагрева – не более, чем на 13°C). Расчеты же, выполненные по формулам данной работы, демонстрируют необходимость учета теплового отклика в пологих стеклопластиковых оболочках, нагружаемых воздушной взрывной волной. Так, на рис. 6 изображены поперечные колебания центральной точки искривленной панели из стеклопластика (${{w}_{0}}\left( t \right) \equiv w\left( {t,0,0} \right)$), определенные при значениях ${{p}_{{\max }}} = 8$ МПа (рис. 6,а) и ${{p}_{{\max }}}$ = = –8 МПа (рис. 6,б). Кривые 1 и 2 на рис. 6 рассчитаны при тех же условиях, что и на рис. 4, а пунктирные кривые 1' приведены для сравнения и соответствуют упруговязкопластическому расчету, при котором изменение температурного поля в КМ-панели не учитывается. Поведение кривых 1 и 1' на рис. 6 демонстрирует, что с течением времени зависимости ${{w}_{0}}\left( t \right)$, полученные с учетом и без учета теплового отклика в стеклопластиковой пологой оболочке, все более различаются, особенно при ее нагружении со стороны выпуклой лицевой поверхности (см. рис. 6,б). Аналогичное сравнение кривых 1 и 2 на рис. 6 показывает, что зависимости ${{w}_{0}}\left( t \right)$ для рассматриваемой КМ-конструкции, рассчитанные с учетом и без учета чувствительности пластических свойств компонентов ее композиции к скорости их деформирования, с течением времени также все более различаются.

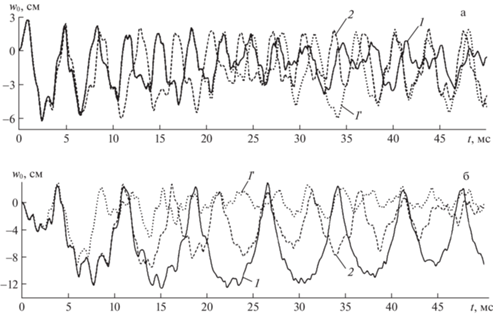
Согласно поведению кривых 1 на рис. 6,а и 6,б, максимальный по модулю прогиб искривленной стеклопластиковой панели достигается после ее прощелкивания вниз – в сторону вогнутой лицевой поверхности (вследствие динамической неустойчивости конструкции), которое наступает после прекращения действия внешней нагрузки (см. выражения (3.1) и (3.2) при $t > {{t}_{{\min }}} = 2$ мс). Так, на кривой 1 рис. 6,а наибольший по модулю прогиб ${{w}_{{\max }}}$ ≡ $\mathop {\max }\limits_{t \geqslant {{t}_{0}}} \left| {{{w}_{0}}\left( t \right)} \right|$ = 6.22 см реализуется при $t \approx 2.4$ мс, а для кривой 1 на рис. 6,б ${{w}_{{\max }}} = 12.46$ см, который достигается при $t \approx 15$ мс $ \gg $ ${{t}_{{\min }}}$. Следовательно, при нагружении искривленной панели из стеклопластика со стороны ее выпуклой лицевой поверхности наблюдается прощелкивание (причем не на первой осцилляции) вдвое большей амплитуды, чем при ее нагружении со стороны вогнутой лицевой поверхности. Это приводит к тому, что максимальные значения интенсивности деформаций фазовых материалов композиции такой оболочки в первом случае оказываются на 20–40% больше, чем во втором. Поэтому в процессе осцилляций искривленная стеклопластиковая панель, нагруженная сверху, нагревается значительно больше (см. рис. 4,б), чем при нагружении снизу (см. рис. 4,а). Расчеты показывают, что максимальные значения температуры в пологих КМ-оболочках не всегда достигаются в момент их максимального прощелкивания.

На рис. 7 изображены аналогичные зависимости ${{w}_{0}}\left( t \right)$, полученные для металлокомпозитной искривленной панели при ${{p}_{{\max }}} = 30$ МПа (рис. 7,а) и ${{p}_{{\max }}} = - 30$ МПа (рис. 7,б). Кривые на рис. 7 определены при тех же условиях, что и кривые с теми же номерами на рис. 6. Как видно из рис. 7, уже на рассматриваемом малом промежутке времени ($0 \leqslant t \leqslant 24$ мс) кривые 2 и 1' существенно отличаются от кривой 1. В еще большей степени в соответствующих расчетах различаются и осцилляции максимальных значений интенсивностей деформаций компонентов композиции Mg–У8А-оболочки (такие зависимости от времени здесь не представлены). Это замечание справедливо и для стеклопластиковых искривленных панелей, обсуждавшихся выше. Поэтому все выводы, сделанные ранее для пологих оболочек из стеклопластика, можно перенести и на металлокомпозитные конструкции с той лишь разницей, что в последних все эффекты и различия проявляются более ярко.

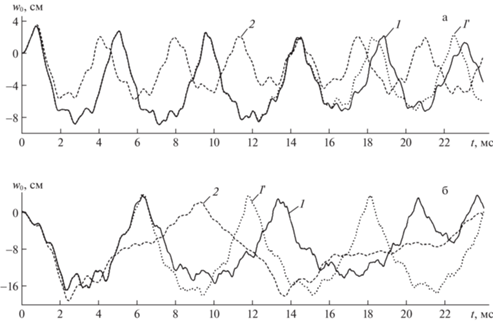
Можно предположить, что достаточно большие значения температуры, достигаемые в отдельных точках металлокомпозитной искривленной панели при ее динамических колебаниях в поперечном направлении (см. рис. 5), являются следствием того, что в проведенных расчетах использовано допущение: теплообмен тонкостенной КМ-конструкции с окружающей средой через лицевые поверхности осуществляется в условиях естественной конвекции (${{\alpha }^{{( \pm )}}} = 30$ Вт/(м² К)). Так как пологая КМ-оболочка при поперечном нагружении воздушной взрывной волной осциллирует с достаточно большой частотой (см. рис. 6 и 7), то, возможно, теплообмен через ее лицевые поверхности необходимо рассматривать как происходящий в условиях вынужденной, а не естественной конвекции. Исходя из этого допущения, были выполнены дополнительные расчеты при задании коэффициентов теплоотдачи ${{\alpha }^{{( \pm )}}} = 300$ Вт/(м² К) (см. равенства (2.21)), значения которых характерны для вынужденной конвекции газов [32]. Рассчитанные при этом величины ${{\Theta }_{{\text{m}}}}\left( t \right)$ отличаются от ранее полученных, т.е. в условиях естественной конвекции газов (см. рис. 4 и 5), только в четвертой значащей цифре. А значит, увеличение значений коэффициентов теплоотдачи на лицевых поверхностях изучаемых КМ-конструкций в 10 раз практически не оказывает влияния на результаты расчетов их термоупруговязкопластического деформирования на рассматриваемых промежутках времени ($0 \leqslant t \leqslant 50$ мс). Следовательно, на таких, достаточно малых, интервалах времени тепловые процессы, протекающие в пологих КМ-оболочках, можно считать адиабатическими, так как теплообмен кондуктивным путем в них еще пренебрежимо мал. Это обстоятельство, по-видимому, объясняет тот факт, что, как было показано выше (см. рис. 3) и в [17], для адекватного описания теплофизического состояния тонкостенной КМ-конструкции при ее динамическом нагружении в поперечном направлении температуру по толщине следует аппроксимировать полиномами 6–7 порядков, а не 1–2 порядков, как это традиционно принято делать для таких конструкций при их квазистатическом нагружении, когда доминирует именно кондуктивная составляющая теплопереноса.

Заключение. Разработанная математическая модель неизотермического упруговязкопластического деформирования гибких пологих оболочек со структурами многонаправленного армирования позволяет рассчитывать волновые процессы в них, а также учитывать слабое сопротивление таких тонкостенных элементов КМ-конструкций поперечному сдвигу и связанность механической и теплофизической составляющих рассматриваемой задачи. Разработанный метод решения позволяет численно интегрировать сформулированную нелинейную начально-краевую задачу по явной схеме при использовании численно-аналитической модели структурной механики композитов, предложенной в [17].

Проведенный сравнительный анализ термоупруговязкопластического и термоупругопластического поведения динамически нагружаемых гибких искривленных КМ-панелей показал, что в отличие от аналогичных по структуре и характерным размерам армированных пластин [17] как стеклопластиковые, так и металлокомпозитные пологие оболочки необходимо рассчитывать, учитывая наличие теплового отклика, возникающего в них при динамическом нагружении. При этом гибкие искривленные панели из стеклопластика в отдельных точках могут нагреваться дополнительно на 14…27°C (подобные же им КМ-пластины – не выше, чем на $15^\circ {\text{C}}$ [17]), а металлокомпозитные пологие оболочки – на 66…200°C (аналогичные им КМ-пластины – на 30…31°C [17]). Однако промежутки времени, на которых достигаются пиковые значения температуры кратковременны – составляют доли миллисекунды. Более интенсивный нагрев и, как следствие, большее термическое влияние наблюдается при нагружении пологих КМ-оболочек воздушной взрывной волной со стороны их выпуклых, а не вогнутых лицевых поверхностей.

При динамическом нагружении таких тонкостенных КМ-конструкций со стороны любой из лицевых поверхностей происходит их прощелкивание в сторону вогнутых лицевых поверхностей, которое наблюдается уже после прекращения действия кратковременной интенсивной нагрузки. Величины прогибов при прощелкивании в случае нагружения пологих оболочек со стороны их выпуклых лицевых поверхностей значительно превышают по модулю аналогичные величины при нагружении таких КМ-конструкций со стороны вогнутых поверхностей. Это обстоятельство и объясняет более интенсивное выделение тепла в первом случае по сравнению со вторым.

Таким образом, в отличие от армированных гибких пластин [17], аналогичные по структуре и характерным размерам пологие оболочки при динамическом нагружении нужно рассчитывать, учитывая наличие теплового отклика в них и чувствительность пластических свойств компонентов их композиций к скорости деформирования, т.е. по термоупруговязкопластической теории.

Работа выполнена в рамках государственного задания (№ госрегистрации 121030900260-6).