Журнал вычислительной математики и математической физики, 2019, T. 59, № 11, стр. 1846-1855

1. ВВЕДЕНИЕ

Во время функционирования различных механизмов или развития процессов для наблюдателя в большинстве случаев доступны не все параметры и характеристики рассматриваемого объекта. Поэтому часто возникает необходимость восстановления или реконструкции необходимой информации по данным, полученным в результате измерений. Эта проблематика широко представлена в исследованиях, связанных с математическим моделированием в информационных технологиях (восстановление изображений), экологии (загрязнение окружающей среды), медицине (вирусные заболевания и их лечение) и других областях. Существует несколько различных подходов к решению задач реконструкции неизвестного управляющего воздействия (возмущения), мы же будем использовать методику обратных задач динамики управляемых систем [1, с. 27]. Теоретическая база одного из методов, обеспечивающих в “реальном времени” динамическую реконструкцию входного воздействия на систему, заложена в работах [2]–[6]. Его суть заключается в построении специального алгоритма управления по принципу обратной связи. Согласно этому алгоритму управляющее воздействие выбирается из некоторого заданного множества по результатам неточных измерений положений системы. В большинстве работ по данной тематике решение задач динамической реконструкции основывается на методе локальной регуляризации экстремального сдвига с использованием сглаживающего функционала [1]. В данном случае возникает необходимость введения дополнительной системы – модели. Этого не происходит, если применять динамический метод невязки, который был предложен в статье [7] для систем обыкновенных дифференциальных уравнений при наличии ограничений на входное воздействие в виде выпуклого компакта и модифицирован в [8] – в случае их отсутствия (см. также [4]). Для систем с распределенными параметрами динамический метод невязки был развит в [3], [9], [10].

В настоящей работе мы модифицируем указанный метод для нелинейной системы, принадлежащей более общему классу, а именно, классу дифференциальных уравнений нецелого порядка. В последнее время исследования многих авторов посвящены различным аспектам дробного анализа (см. [11]–[14] и библиографию в них). Этот интерес вызван не только сложными теоретическими проблемами, но и прикладными задачами, построением моделей систем, имеющих самоподобную, пористую структуру, а также наследственные свойства, память. Примеры таких исследований отражены в работах [12], [15]–[17].

2. ПОСТАНОВКА ЗАДАЧИ

Для удобства чтения приведем необходимые определения из дробного анализа.

Определение 1 (см. [11, с. 42]). Интеграл дробного порядка $\gamma $ с началом в точке $\sigma $ от произвольной функции $f \in {{L}_{1}}(T,{{\mathbb{R}}^{n}})$ определяется формулой

Здесь $\Gamma ( \cdot )$ обозначает гамма-функцию Эйлера

Определение 2 (см. [11], [12]). Для функции $x \in AC(T,{{\mathbb{R}}^{n}})$ и произвольного действительного $\gamma \in (0,1)$ выражения

называются дробными производными Римана–Лиувилля и Герасимова–Капуто соответственно. Здесь $\dot {x}(t) = dx{\text{/}}dt$.

Замечание 1. Обозначения для дробных интегралов и производных используются в несколько сокращенном виде ${{I}^{\gamma }}$, ${{D}^{\gamma }}$, $^{C}{{D}^{\gamma }}$ вместо $I_{{\sigma + }}^{\gamma }$, $D_{{\sigma + }}^{\gamma }$ и $^{C}D_{{\sigma + }}^{\gamma }$ соответственно ввиду того, что на протяжении всей работы мы рассматриваем только левосторонние интегралы и производные, и начальный момент у них не меняется и всегда остается равен $\sigma $.

Перейдем к постановке задачи. Рассматривается система, описываемая нелинейным векторным дифференциальным уравнением:

где фазовый вектор системы $x \in E \subset {{\mathbb{R}}^{n}}$, $E$ – известное ограниченное множество, начальное состояние ${{x}_{\sigma }} \in {{\mathbb{R}}^{n}}$ фиксировано и задано, $B$ – постоянная $n \times m$ матрица, $g{\text{:}}\,\,T \times {{\mathbb{R}}^{n}} \to {{\mathbb{R}}^{n}}$ – дважды непрерывно дифференцируемая функция по $t$, удовлетворяющая условию Липшица с константой $L > 0$ по совокупности переменных, т.е. при любых $({{t}_{1}},{{x}_{1}})$, $({{t}_{2}},{{x}_{2}}) \in T \times {{\mathbb{R}}^{n}}$ выполняется неравенство Здесь и далее символом ${{\left| {\, \cdot \,} \right|}_{n}} = {{\left\| {\, \cdot \,} \right\|}_{n}}$ обозначается норма вектора в евклидовом пространстве. Траектория системы $x(t)$ заранее неизвестна и определяется некоторым управлением $u( \cdot )$, которое также не задано, но подчинено априорному ограничению $u(t) \in P$, $t \in T$, $P$ – заданное выпуклое ограниченное и замкнутое множество в ${{\mathbb{R}}^{m}}$.

В дискретные, достаточно частые моменты времени ${{\tau }_{i}} \in T$, ${{\tau }_{i}} < {{\tau }_{{i + 1}}}$, координаты $x({{\tau }_{i}})$ измеряются с некоторой погрешностью $h \in (0,1)$. Результаты измерения $\xi _{i}^{h} \in {{\mathbb{R}}^{n}}$ такие, что

Требуется найти управление $u( \cdot )$, порождающее $x( \cdot )$: $u( \cdot ) = u( \cdot ;x( \cdot ))$. Следует заметить, что одно и то же конкретное решение системы (1) может определяться разными управлениями. Данный факт при наличии погрешности $h$ приводит к невозможности точного восстановления $u( \cdot )$, поэтому необходимо построить алгоритм вычисления некоторого приближения $u( \cdot )$. Это приближение должно быть тем лучше, чем меньше величина погрешности измерения $x({{\tau }_{i}})$ и чем мельче сетка разбиения отрезка $T$ с узлами ${{\tau }_{i}}$.

3. АЛГОРИТМ РЕШЕНИЯ

Прежде, чем перейти к описанию алгоритма, приведем некоторые вспомогательные конструкции.

Определение 3 (см. [11, определение 2.3]). Через ${{I}^{\gamma }}({{L}_{\infty }}(T,{{\mathbb{R}}^{n}}))$ обозначим класс функций x: $T \to {{\mathbb{R}}^{n}}$, представимых дробным интегралом порядка $\gamma \in (0,1)$ от суммируемой функции: $x(t) = [{{I}^{\gamma }}\varphi ](t)$, $t \in T$, $\varphi \in {{L}_{\infty }}(T,{{\mathbb{R}}^{n}})$.

Определение 4 (см. [18]). Функцию x: $T \to {{\mathbb{R}}^{n}}$ будем называть решением задачи Коши (1), (2), если $x( \cdot ) \in \{ {{x}_{\sigma }}\} + {{I}^{\gamma }}({{L}_{\infty }}(T,{{\mathbb{R}}^{n}}))$ и равенство (1) выполнено для п.в. $t \in T$.

Будем использовать формулы приближения дробных производных прямоугольниками [13, с. 49]:

где ${{b}_{j}} = ({{(j + 1)}^{{1 - \gamma }}} - {{j}^{{1 - \gamma }}}){\text{/}}\Gamma (2 - \gamma )$, $j \in [0,i - 1]$, ${{R}_{i}} = O({{\delta }^{{2 - \gamma }}})$, символом $O(\alpha )$ обозначаются функции, допускающие оценки $O(\alpha ) \leqslant K\alpha $, K – положительное число. Если $z \in {{C}^{2}}(T,\mathbb{R})$, то из [13, теорема 3] следует оценка в которой постоянная $C$ зависит только от $\gamma $.

Введем множество всех допустимых управлений задачи (1), (2), порождающих одну и ту же траекторию $x(t)$, $t \in T$:

где ${{K}_{p}} = \{ u( \cdot ) \in {{L}_{2}}(T,{{\mathbb{R}}^{n}})u(t) \in P\;{\text{при}}\;{\text{п}}{\text{.в}}{\text{.}}\;t \in T\} $.

Замечание 2. Из свойств множества $P$ следует, что $U(x( \cdot ))$ – выпукло ограничено и замкнуто.

Алгоритм решения поставленной задачи разделяется на два этапа: подготовительный (до начала функционирования системы) и динамический (одновременно с системой). На первом этапе фиксируется равномерное разбиение $\Delta $ отрезка $T$ контрольными моментами времени ${{\tau }_{i}}$, в которые будут проводиться замеры положений системы:

Рассматривается следующее семейство множеств:

где Тогда в качестве множества приближений управляющих воздействий примем На втором этапе работа алгоритма представляет собой $\kappa - 1$ однотипный шаг. В течение $i$-го шага, выполняемого на промежутке времени $[{{\tau }_{{i - 1}}},{{\tau }_{i}})$, определяется приближение управления по формуле где $v_{i}^{h}$ – нормальный (следуя терминологии некорректных задач) элемент множества $\Omega _{i}^{h}$, который выбирается по правилу Вся процедура осуществляется до момента времени $\theta $.

Теорема 1. Пусть $\delta (h) \to 0$, $h{\text{/}}\delta (h) \to 0$ при $h \to 0$. Тогда имеет место сходимость

Чтобы установить справедливость этой теоремы, нам понадобятся некоторые вспомогательные утверждения.

Для системы (1), используя результаты [11], [12], можно показать, если $\gamma \in (1{\text{/}}2,1)$, то существует постоянная ${{M}_{0}} > 0$, при которой имеет место оценка

Лемма 1. Пусть $u( \cdot ) \in U(x( \cdot ))$. Тогда имеют место включения

Доказательство. Уравнение (1) может быть представлено в интегральном виде:

Используя выражения (14), запишем разности между значениями решения в соседних узлах разбиения Умножая последние формулы для каждого $k \in [1,i]$ на коэффициенты ${{b}_{{i - k}}}$, используемые в (5), имеем Суммируя полученные равенства по $k$, приходим к выражению Правую и левую часть последнего равенства умножив на $1/{{\delta }^{\gamma }}$ и добавив в них слагаемые $g({{\tau }_{{i - 1}}},{{\xi }_{{i - 1}}})$ и $(1{\text{/}}{{\delta }^{\gamma }})\sum\nolimits_{k = 1}^i \,{{b}_{{i - k}}}({{\xi }_{k}} - {{\xi }_{{k - 1}}})$, получим где Из условия (4) следуют неравенства используя которые, получаем оценку Принимая во внимание (5) и (6), формулу для ${{I}_{2}}$ перепишем в виде где ${{c}_{2}} = C\mathop {max}\limits_{t \in T,x \in E} {\text{|}}[{{I}^{{\gamma - 2}}}g( \cdot ,x)](t){\text{|}}$. Тогда, добавляя и вычитая выражение $g({{\tau }_{i}},x({{\tau }_{{i - 1}}}))$ под знаком нормы в (17) и учитывая условия (3) и (12), получаем Подставляя сумму неравенств (16) и (18) в (15), имеем что в сочетании с (8) приводит к формуле (13).

Лемма 2. Пусть заданы последовательности $\{ {{h}_{j}}\} _{{j = 1}}^{\infty } \subset \mathbb{R}$ и $\{ {{v}_{j}}( \cdot )\} _{{j = 1}}^{\infty } \subset {{K}_{p}}$, также выполнено условие согласования шага разбиения $\delta $ и погрешности $h$:

Если элементы последовательности $\{ {{v}_{j}}( \cdot )\} $ принадлежат ${{V}^{{{{h}_{j}}}}}$ и есть сходимостьто справедливо включение ${{v}_{0}}( \cdot ) \in U(x( \cdot ))$.

Доказательство. Будем доказывать от противного, пусть 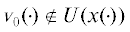, т.е., см. формулу (7), на отрезке $T$ существует ближайшее к начальному моменту времени $\sigma $ множество $[{{t}_{1}},{{t}_{2}}]$ ненулевой меры, на котором

но одновременно с этим Другими словами, существует некоторая постоянная $d > 0$, для которой имеем Зафиксируем равномерное разбиение Далее для узлов сетки будем использовать обозначение ${{\tau }_{i}} = \tau _{{i,j}}^{h}$. Пусть номера $p$ и $q$ точек разбиения ${{\Delta }^{{{{h}_{j}}}}}$ таковы, что ${{\tau }_{p}} = \tau _{{p,j}}^{h} = min\{ t \in {{\Delta }^{{{{h}_{j}}}}}\,:\;t \leqslant {{t}_{1}}\} $, ${{\tau }_{q}} = \tau _{{q,j}}^{h} = max\{ t \in {{\Delta }^{{{{h}_{j}}}}}\,:\;t \leqslant {{t}_{2}}\} $. Тогда интеграл в формуле (21) можно представить суммой Используя результаты [11], [12], получаем оценку Поскольку $P$ – выпукло ограничено и замкнуто, то ${{v}_{0}}( \cdot ) \in {{K}_{p}}$, а значит, существует постоянная ${{c}_{p}} = \mathop {sup}\limits_{{{v}_{0}} \in P} {\text{|}}{{v}_{0}}{{{\text{|}}}_{m}} < \infty $. Ввиду того, что длины отрезков $[{{t}_{1}},{{\tau }_{p}}]$ и $[{{\tau }_{q}},{{t}_{2}}]$ меньше ${{\delta }_{j}} = \delta ({{h}_{j}})$, и для подынтегральных функций выполнены неравенства (3) и (24), то первый и третий интегралы выражения (23) для всех $j$, начиная с некоторого ${{j}_{1}}$, не превосходят $d{\text{/}}2$, что приводит к оценке В последнем неравенстве под знаком нормы добавим и вычтем слагаемые в результате имеем Введем обозначения и перепишем полученное выражение в виде где В силу слабой сходимости (20) имеем В формуле (26) под интегралом добавим и вычтем выражение ${{[}^{C}}{{D}^{\gamma }}x]({{\tau }_{i}})$. Тогда для $I_{2}^{j}$ выполнено неравенство где Из определений 3 и 4 и свойств опрератора ${{I}^{\gamma }}$ [18] следует $x \in C(T,{{\mathbb{R}}^{n}})$, тогда из теоремы 2.2 [12, с. 93] получаем ${{[}^{C}}{{D}^{\gamma }}x]( \cdot ) \in C(T,{{\mathbb{R}}^{n}})$. Это дает сходимость $I_{{21}}^{j} \to 0$ при $j \to \infty $ (${{\delta }_{j}} \to 0$). Из условия (3) и оценки (12) для функции $g(s,x)$ получаем Поэтому $I_{{22}}^{j} \to 0$ при $j \to \infty $. Выражение для $I_{{23}}^{j}$ преобразуем, используя асимптотическую формулу (5), к виду Учитывая неравенства (4) и соотношение (19), получаем $I_{{23}}^{j} \to 0$ при $j \to \infty $. Следовательно, и По условию леммы ${{v}_{j}}( \cdot ) \in {{V}^{{{{h}_{j}}}}}$. Тогда имеем т.е. Поскольку выполнение (19) влечет сходимость ${{\beta }_{{{{h}_{j}}}}} \to 0$ при $j \to \infty $, то В результате сходимость последовательностей (27)–(29) дает сходимость их суммы к нулю, что противоречит (25).

Доказательство теоремы 1. Введем вспомогательную функцию

и покажем, что Для этого достаточно установить, что для произвольной последовательности $\{ {{h}_{j}}\} _{{j = 1}}^{\infty }$, ${{h}_{j}} > 0$, ${{h}_{j}} \to 0$ при $j \to \infty $, имеется сходимость Предположим противное, т.е. найдется подпоследовательность последовательности $\{ {{\tilde {v}}_{{{{h}_{j}}}}}( \cdot )\} _{{j = 1}}^{\infty }$, обозначим ее через $\{ {{u}_{j}}( \cdot )\} _{{j = 1}}^{\infty }$, со свойством Определим функцию, используя разбиение ${{\Delta }^{{{{h}_{j}}}}}$, заданное формулой (22) и управление $u$: По лемме 1 получаем ${{u}_{{ji}}} \in \Omega _{i}^{{{{h}_{j}}}}$, что приводит к включению ${{\bar {u}}_{j}}( \cdot ) \in {{V}^{{{{h}_{j}}}}}$. Принцип выбора (11) элементов $v_{i}^{{{{h}_{j}}}}$ из множества ${{V}^{{{{h}_{j}}}}}$ дает Применяя лемму 2.4 [11, с. 50], можно записать тождество Тогда, учитывая формулу (5), имеем Ввиду включения ${{[}^{C}}{{D}^{\gamma }}{{I}^{\gamma }}u]( \cdot ) \in C(T,{{\mathbb{R}}^{m}})$ [11, теорема 2.6], [20, c. 288], получаем Используя формулу (34) в неравенстве (32), находим Из свойств слабого предела следует неравенство Объединяя неравенства (35) и (36), заключаем И поскольку из леммы 2 следует включение ${{u}_{0}} \in U(x( \cdot ))$, а из замечания 2 – единственность элемента минимальной нормы, то ${{u}_{0}}( \cdot ) = u( \cdot )$. Последнее равенство противоречит (31). Таким образом, мы доказали сходимость (30). Теперь оценим интеграл находим Первое и третье слагаемые правой части последнего соотношения стремятся к нулю при $\delta \to 0$ ввиду того, что $u \in {{L}_{2}}(T,{{\mathbb{R}}^{m}})$ и ${{\left| {v_{0}^{h}} \right|}_{m}} \leqslant {{c}_{p}}$. Второе слагаемое не превосходит величины $\left\| {{{{\tilde {v}}}_{h}}( \cdot ) - u( \cdot )} \right\|_{{{{L}_{2}}(T,{{\mathbb{R}}^{m}})}}^{2}$, которая в силу сходимости (30) является бесконечно малой при $h \to 0$.

4. ОЦЕНКА СКОРОСТИ СХОДИМОСТИ АЛГОРИТМА

Установим оценку скорости сходимости алгоритма. Пусть $\omega (u,\delta )$ – модуль непрерывности функции $u$, определяемый формулой

Теорема 2. Пусть $u \in AC(T,{{\mathbb{R}}^{m}})$, $n = m$, $detB \ne 0$ и выполнены условия теоремы $1$. Тогда справедлива оценка

где ${{\beta }_{h}}$ определяется выражением (9), ${{c}_{b}} = \left\| {{{B}^{{ - 1}}}} \right\|$.

Доказательство. Учитывая формулу (10), находим

Используя определение множества (8) и выражение (33), получаем интеграл где Поскольку $u \in AC(T,\mathbb{R})$, то функция $u$ равномерно непрерывна на $T$. В таком случае, из теоремы 4.17 [19, с. 183] следует Тогда для интеграла ${{I}_{1}}$ получаем оценку Учитывая формулу (5) и лемму 1, имеем Аналогичным образом для интеграла ${{I}_{3}}$ находим Суммируя неравенства (39)–(41) по $i$ от $1$ до $\kappa $ и подставляя в (38), получаем формулу (37).