Журнал вычислительной математики и математической физики, 2019, T. 59, № 11, стр. 1856-1871

Об одной квазилинейной дифференциально-алгебраической системе уравнений в частных производных

С. В. Свинина^*

ИДСТУ СО РАН
664033 Иркутск, ул. Лермонтова 134, Россия

Поступила в редакцию 08.07.2019
После доработки 08.07.2019
Принята к публикации 08.07.2019

DOI: 10.1134/S0044466919110139

Аннотация

В работе рассмотрена смешанная задача для квазилинейной дифференциально-алгебраической системы уравнений в частных производных индекса $(1,0)$ первого порядка с двумя независимыми переменными. С помощью метода характеристик и итерационного метода доказана теорема существования решения поставленной задачи. Библ. 17.

Ключевые слова: квазилинейная дифференциально-алгебраическая система уравнений в частных производных, индекс, метод характеристик.

ВВЕДЕНИЕ

В некоторых приложениях встречаются нелинейные дифференциально-алгебраические системы уравнений в частных производных [1]–[5], которые также называют вырожденными системами, не разрешенными относительно старшей производной, системами Соболева и системами, не относящимися к типу Коши–Ковалевской. Впервые такие системы появились в работах, посвященных конкретным уравнениям гидродинамики в конце XIX и начале XX века. Интерес к ним вызвала в том числе и работа С.Л. Соболева [1]. В настоящее время наиболее хорошо исследованы линейные дифференциально-алгебраические уравнения с двумя независимыми переменными [6]–[8]. Для квазилинейных уравнений с двумя независимыми переменными пока разработаны только методы численного решения на основе сплайновой интерполяции искомой вектор-функции [9].

В настоящей работе мы рассмотрим квазилинейную дифференциально-алгебраическую систему уравнений в частных производных первого порядка с двумя независимыми переменными с матричным пучком, построенным по коэффициентам системы, специального канонического вида. Отметим, что такие системы включают в себя, как частный случай, классические гиперболические квазилинейные системы уравнений с двумя независимыми переменными, исследования которых подробно изложены в монографии [10]. Для квазилинейной дифференциально-алгебраической системы мы докажем теорему существования решения некоторой смешанной задачи, используя метод характеристик и метод последовательных приближений [11]–[14]. Каноническая структура матричного пучка системы позволит преобразовать линейные системы, полученные на каждом итерационном шаге, к расщепленным формам, состоящим из трех систем уравнений. Одна из них гиперболического типа с ненулевыми характеристиками. Две других системы параболического типа, они имеют только нулевые характеристики. С помощью хорошо известного метода характеристик, восходящего к работам Леви, мы приведем систему гиперболических уравнений в частных производных к системе обыкновенных дифференциальных уравнений. При построении характеристик, в качестве нижнего предела интегрирования, мы используем параметр, принимающий некоторые допустимые значения. Такой параметр позволит построить интегральные кривые, покрывающие искомые поверхности во всей области определения, а не в ее подобласти.

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим квазилинейную систему уравнений в частных производных:

(1)

$A(x,t,u){{\partial }_{t}}u + B(x,t,u){{\partial }_{x}}u = F(x,t,u),$

где $A(x,t,u)$ и $B(x,t,u)$ – некоторые заданные квадратные матрицы порядка $n$ тождественно вырожденные в области определения $\mathcal{U} = \{ (x,t,u):(x,t) \in U\} $, где $U = \{ (x,t):x \in {{I}_{x}} = [{{x}_{0}};X] \subset {{\mathbb{R}}^{1}},$ $t \in {{I}_{t}} = [{{t}_{0}};T] \subset {{\mathbb{R}}^{1}}\} $. При условии вырожденности матриц $A(x,t,u)$ и $B(x,t,u)$, говорят, что квазилинейная система (1) является дифференциально-алгебраической. Мы также предполагаем, что вектор-функция $F(x,t,u)$ задана в области $\mathcal{U}$.

Для системы вида (1) зададим следующие начально-краевые условия:

(2)

$u({{x}_{0}},t) = \psi (t),\quad u(x,{{t}_{0}}) = \phi (x),$

где $\psi (t)$ и $\phi (x)$ – некоторые $n$-мерные вектор-функции своих аргументов. Предположим, что в каждой точке области $\mathcal{U}$, пучок матриц $P(\lambda ,x,t,u) = A(x,t,u) + \lambda B(x,t,u)$ является регулярным. В этом случае его индекс или индекс системы (1) определяется парой чисел $(k,0)$, где $k$ – максимальная степень элементарных делителей пучка $P(\lambda ,x,t,u)$. Второй параметр индекса равен нулю, поскольку пучок $P(\lambda ,x,t,u)$, по предположению, не содержит сингулярной составляющей. Мы рассмотрим случай, когда система (1) имеет индекс $(1,0)$, то есть все элементарные делители пучка $P(\lambda ,x,t,u)$ являются простыми, при этом корни характеристического многочлена $detP(\lambda ,x,t,u)$ могут быть кратными.

Цель работы состоит в исследовании и доказательстве существования единственного решения смешанной задачи (1), (2) в области определения $U$ при определенных условиях гладкости на ее исходные данные. Под решением задачи (1), (2) мы понимаем классическое решение, т.е., решением задачи (1), (2) мы называем вектор-функцию $u(x,t)$ из пространства ${{C}^{1}}(U)$, которая в каждой точке области $U$ вместе со своими производными первого порядка ${{\partial }_{x}}u(x,t)$ и ${{\partial }_{t}}u(x,t)$ удовлетворяет уравнению (1), а на границе области $U$ удовлетворяет условиям (2).

При исследовании задачи (1), (2) нам понадобится понятие канонической формы матричного пучка $P(\lambda ,x,t,u)$. Кратко приведем некоторые сведения об $s$-гладкой эквивалентности матричного пучка $P(\lambda ,x,t,u)$ специальной канонической структуре. В работе [7] были получены достаточные условия, при выполнении которых пучок $P(\lambda ,x,t,u)$ является $s$-гладко эквивалентным следующему пучку:

$\operatorname{diag} \{ {{E}_{d}},M(x,t,u),{{E}_{p}}\} + \lambda \operatorname{diag} \{ J(x,t,u),{{E}_{l}},N(x,t,u)\} .$

Здесь предполагается, что $M(x,t,u)$ и $N(x,t,u)$ – некоторые верхние (правые) треугольные блоки с нулевой диагональю порядка $l$ и $p$ соответственно, а

$J(x,t,u) = {\text{diag}}\{ {{J}_{1}}(x,t,u),{{J}_{2}}(x,t,u),\; \ldots ,\;{{J}_{s}}(x,t,u)\} $

есть некоторая матрица порядка $d$. Здесь и далее, символом ${{E}_{d}}$ мы обозначаем единичную матрицу порядка $d$. Естественно, что должно выполняться соотношение $p = n - d - l$. При этих предположениях найдутся ненулевые ${{k}_{1}}$ и ${{k}_{2}}$, где ${{k}_{1}} = min\{ \bar {k}:M{{(x,t,u)}^{{\bar {k}}}} = 0,$ $\forall (x,t,u) \in \mathcal{U}\} $ и ${{k}_{2}} = min\{ \bar {k}:N{{(x,t,u)}^{{\bar {k}}}} = 0,$ $\forall (x,t,u) \in \mathcal{U}\} $, максимальное значение из которых определяет индекс пучка. Таким образом, пучок $P(\lambda ,x,t,u)$, для которого выполнены все условия теоремы 1 из работы [7] имеет индекс $(k,0)$, где $k = max\{ {{k}_{1}},{{k}_{2}}\} $ и мы говорим, что система (1) также имеет индекс $(k,0)$. Очевидно, что значение $k$ – это наибольшая степень элементарных делителей пучка $P(\lambda ,x,t,u)$, соответствующих нулевым и бесконечным корням характеристического многочлена $detP(\lambda ,x,t,u)$.

В настоящей работе мы предполагаем, что для системы (1) выполнены все условия теоремы 4 из работы [7] и степени элементарных делителей пучка $P(\lambda ,x,t,u)$ не превосходят единицы. В этом случае система (1) имеет индекс $(1,0)$ и в силу теоремы 4 из работы [7] для пучка $P(\lambda ,x,t,u)$ найдутся невырожденные в области определения $U$ матрицы $L(x,t,u)$ и $R(x,t,u)$, обладающие той же гладкостью, что и элементы пучка $P(\lambda ,x,t,u)$, которые выполняют следующее преобразование:

(3)

$L(x,t,u)P(\lambda ,x,t,u)R(x,t,u) = \operatorname{diag} \{ {{E}_{d}},{{\mathcal{O}}_{l}},{{E}_{p}}\} + \lambda \operatorname{diag} \{ J(x,t,u),{{E}_{l}},{{\mathcal{O}}_{p}}\} ,$

где $J(x,t,u) = {\text{diag}}\{ {{k}_{1}}(x,t,u),{{k}_{2}}(x,t,u),\; \ldots ,\;{{k}_{d}}(x,t,u)\} $, а ${{\mathcal{O}}_{l}}$ – нулевой квадратный блок порядка $l$. Правую часть в равенстве (3) мы будем называть канонической формой пучка $P(\lambda ,x,t,u)$ системы (1) индекса $(1,0)$.

Для получения необходимых оценок в пространстве ${{C}^{1}}(U)$ непрерывных в области $U$ вектор-функций мы используем нормы

(4)

${{\left\| {u(x,t)} \right\|}_{{C(U)}}} = max\{ \left\| {u(x,t)} \right\|,\;\forall (x,t) \in U\} ,\quad {\text{где}}\quad \left\| {u(x,t)} \right\| = max\{ {\text{|}}{{u}_{i}}(x,t){\text{|}},\;\forall i = 1,\; \ldots ,\;n\} ,$

(5)

${{\left\| {u(x,t)} \right\|}_{ * }} = \mathop {max}\limits_{(x,t) \in U} \{ \exp ( - {{l}_{1}}(t + x))\left\| {u(x,t)} \right\|\} ,\quad {{l}_{1}} > 0.$

Отметим, что нормы (4) и (5) эквивалентны (см. [14, c. 12], [13, с. 124]), так как выполняется неравенство

$\exp ( - {{l}_{1}}(X + T)){{\left\| {u(x,t)} \right\|}_{{C(U)}}} \leqslant \left\| {u(x,t} \right\|{{)}_{ * }} \leqslant {{\left\| {u(x,t)} \right\|}_{{C(U)}}}.$

В свою очередь, норму матрицы $A(x,t,u)$ с элементами из ${{C}^{1}}(\mathcal{U})$ мы определяем как (см. [15, c. 391])

${{\left\| {A(x,t,u)} \right\|}_{{C(\mathcal{U})}}} = \mathop {max}\limits_{(x,t,u) \in \mathcal{U}} \{ \left\| {A(x,t,u)} \right\|\} ,\quad {\text{где}}\quad \left\| {A(x,t,u)} \right\| = \mathop {max}\limits_{1 \leqslant i \leqslant n} \sum\limits_{j = 1}^n \,{\text{|}}{{a}_{{i,j}}}(x,t,u){\text{|}}\quad \forall (x,t,u) \in \mathcal{U}.$

2. ТЕОРЕМА СУЩЕСТВОВАНИЯ

В этом разделе мы доказываем основную теорему о существовании единственного решения задачи (1), (2).

Пусть выполнены следующие условия:

1) все корни характеристического многочлена $detP(\lambda ,x,t,u)$ являются вещественными и имеют постоянную кратность в области определения $\mathcal{U}$;

2) старший коэффициент многочлена $detP(\lambda ,x,t,u)$ по параметру $\lambda $ не обращается в нуль ни в одной точке области $\mathcal{U}$;

3) ранги матриц $A(x,t,u)$ и $B(x,t,u)$ являются постоянными в каждой точке области $\mathcal{U}$ и меньше размерности $n$;

4) все элементарные делители пучка $P(\lambda ,x,t,u)$ имеют первую степень;

5) все ненулевые корни характеристического многочлена $detP(\lambda ,x,t,u)$ отрицательные;

6) элементы матриц $A(x,t,u)$ и $B(x,t,u)$ принадлежат пространству ${{C}^{1}}(\mathcal{U})$; вектор-функция $\psi (t)$ принадлежит ${{C}^{1}}({{I}_{t}})$; производные ${{\partial }_{x}}A(x,t,u)$, ${{\partial }_{x}}B(x,t,u)$, ${{\partial }_{t}}A(x,t,u)$, ${{\partial }_{t}}B(x,t,u)$, ${{\partial }_{{{{u}_{j}}}}}A(x,t,u)$ и ${{\partial }_{{{{u}_{j}}}}}B(x,t,u)$, где $j = 1, \ldots ,n$, удовлетворяют условию Липшица по $u$ в области $\mathcal{U}$; вектор-функция $\phi (x)$ принадлежит пространству ${{C}^{1}}({{I}_{x}})$; вектор-функция $F(x,t,u)$ удовлетворяет условию Липшица по $u$; частные производные ${{\partial }_{{{{u}_{i}}{{u}_{j}}}}}F(x,t,u)$, ${{\partial }_{{{{u}_{j}}x}}}F(x,t,u)$ и ${{\partial }_{{{{u}_{j}}t}}}F(x,t,u)$, где $i,j = 1,\; \ldots ,\;n$, существуют, удовлетворяют условию Липшица по $u$ в области $\mathcal{U}$ и являются ограниченными в этой области;

7) частные производные ${{\partial }_{{{{u}_{j}}x}}}L(x,t,u)$, ${{\partial }_{{{{u}_{j}}t}}}L(x,t,u)$, ${{\partial }_{{{{u}_{j}}{{u}_{i}}}}}L(x,t,u)$, ${{\partial }_{{{{u}_{j}}x}}}R(x,t,u)$, ${{\partial }_{{{{u}_{j}}t}}}R(x,t,u)$, ${{\partial }_{{{{u}_{j}}{{u}_{i}}}}}R(x,t,u)$, ${{\partial }_{{xt}}}R(x,t,u)$, ${{\partial }_{{xx}}}R(x,t,u)$ и ${{\partial }_{{tt}}}R(x,t,u)$ существуют, удовлетворяют условию Липшица по $u$ в области $\mathcal{U}$ и являются ограниченными в этой области;

8) матрица $R(x,t,u)$ удовлетворяет условию Липшица по $u$ в области $\mathcal{U}$ с константой, не превосходящей некоторой постоянной $\mathcal{M}$;

9) выполнены условия согласования

$\begin{gathered} \psi ({{t}_{0}}) = \phi ({{x}_{0}}),\mathop {\left. {\quad \frac{{d\psi (t)}}{{dt}}} \right|}\nolimits_{t = {{t}_{0}}} = \mathop {\left. {\frac{{d\phi (x)}}{{dx}}} \right|}\nolimits_{x = {{x}_{0}}} , \\ A({{x}_{0}},{{t}_{0}})\mathop {\left. {\frac{{d\psi (t)}}{{dt}}} \right|}\nolimits_{t = {{t}_{0}}} + B({{x}_{0}},{{t}_{0}})\mathop {\left. {\frac{{d\phi (x)}}{{dx}}} \right|}\nolimits_{x = {{x}_{0}}} = F({{x}_{0}},{{t}_{0}},\psi ({{t}_{0}})). \\ \end{gathered} $

Тогда в области $U$ существует единственное решение $u(x,t)$ системы (1), непрерывное в $U$ вместе с частными производными первого порядка по переменным $x$ и $t$, удовлетворяющее условиям (2).

Кратко опишем доказательство теоремы. Сначала мы преобразуем систему (1) к удобной форме, используя специальное представление вектор-функции $F(x,t,u)$. К полученной системе мы применяем метод последовательных приближений. В результате на каждом шаге итерационного процесса мы получаем линейную систему дифференциально-алгебраических уравнений индекса $(1,0)$. Такие системы с помощью гладких матричных преобразований мы приводим к расщепленной форме и показываем, что их решения образуют фундаментальную последовательность, а ее предел удовлетворяет в области определения $U$ системе (1) с начально-краевыми условиями (2). Для получения необходимых оценок мы используем метод характеристик, с помощью которого записываем расщепленные дифференциальные системы в интегральной форме. Для обоснования дифференцируемости предельной функции мы строим необходимые дифференциальные следствия расщепленной системы, записанной в интегральной форме. Аналогично мы доказываем, что последовательность производных является фундаментальной, а ее предел удовлетворяет соответствующей системе, полученной в результате дифференцирования системы (1). В заключение мы показываем, что построенное решение задачи (1), (2) является единственным.

Перейдем теперь непосредственно к доказательству теоремы, разбивая его на основные пункты.

2.1. Преобразование системы и построение функциональной последовательности

В силу первого и третьего условий настоящей теоремы найдутся невырожденные в области $\mathcal{U}$ матрицы $L(x,t,u)$ и $R(x,t,u)$ с элементами из ${{C}^{1}}(\mathcal{U})$, приводящие пучок $P(\lambda ,x,t,u)$ к каноническому виду (3). Выполним преобразование системы (1), используя идею преобразования правой части квазилинейного уравнения из статьи [16]. Для этого мы представим вектор $F(x,t,u)$ следующим образом: $F(x,t,u) = {{L}^{{ - 1}}}(x,t,u)\mathcal{F}(x,t,u)$. Запишем

(6)

$\begin{array}{*{20}{c}} {\mathcal{F}(x,t,u) = \mathcal{F}(x,t,u) - \mathcal{F}(x,t,o) + \mathcal{F}(x,t,o) = \int\limits_0^1 {{\partial }_{\xi }}\mathcal{F}(x,t,\xi u)d\xi + \mathcal{F}(x,t,o) = } \\ { = \;\int\limits_0^1 {{\partial }_{u}}\mathcal{F}(x,t,\xi u)ud\xi + \mathcal{F}(x,t,o),} \end{array}$

где ${{\partial }_{u}}\mathcal{F}(x,t,\xi u) = ({{\partial }_{{{{u}_{{{{s}_{2}}}}}}}}{{\mathcal{F}}_{{{{s}_{1}}}}}(x,t,\xi u))$ – матрица Якоби, где ${{s}_{1}},{{s}_{2}} = 1,\; \ldots ,\;n$ и $o$ – нулевой вектор. Пусть

$C(x,t,u) = - \int\limits_0^1 \,{{\partial }_{u}}\mathcal{F}(x,t,\xi u)d\xi .$

Тогда вектор $F(x,t,u)$ с учетом (6) принимает следующий вид:

(7)

$F(x,t,u) = - {{L}^{{ - 1}}}(x,t,u)(C(x,t,u)u - \mathcal{F}(x,t,o)).$

Перепишем систему (1) с учетом равенства (7)

(8)

$A(x,t,u){{\partial }_{t}}u + B(x,t,u){{\partial }_{x}}u + {{L}^{{ - 1}}}(x,t,u)C(x,t,u)u = {{L}^{{ - 1}}}(x,t,u)\mathcal{F}(x,t,o)$

и применим затем к задаче (2), (8) метод последовательных приближений

(9)

$\begin{array}{*{20}{c}} {A(x,t,{{u}_{k}}){{\partial }_{t}}{{u}_{{k + 1}}} + B(x,t,{{u}_{k}}){{\partial }_{x}}{{u}_{{k + 1}}} + {{L}^{{ - 1}}}(x,t,{{u}_{k}})C(x,t,{{u}_{k}}){{u}_{{k + 1}}} = {{L}^{{ - 1}}}(x,t,{{u}_{k}})\mathcal{F}(x,t,o),} \\ {{{u}_{0}}(x,t) = \phi (x),\quad {{u}_{{k + 1}}}(x,{{t}_{0}}) = \phi (x),\quad {{u}_{{k + 1}}}({{x}_{0}},t) = \psi (t),\quad k \geqslant 0.} \end{array}$

Умножая систему в (9) слева на матрицу $L(x,t,{{u}_{k}})$ и выполняя замену переменной

(10)

${{u}_{{k + 1}}}(x,t) = R(x,t,{{u}_{k}}){{v}_{{k + 1}}}(x,t),$

в результате получаем систему

(11)

$\begin{array}{*{20}{c}} {\mathcal{A}{{\partial }_{t}}{{v}_{{k + 1}}} + \mathcal{B}(x,t,{{u}_{k}}){{\partial }_{x}}{{v}_{{k + 1}}} + \mathcal{C}(x,t,{{u}_{k}}){{v}_{{k + 1}}} = \mathcal{F}(x,t,o),} \\ {{{u}_{0}}(x,t) = \phi (x),\quad {{v}_{{k + 1}}}(x,{{t}_{0}}) = \Phi (x),\quad {{u}_{{k + 1}}}({{x}_{0}},t) = \Psi (t),\quad k \geqslant 0,} \end{array}$

где матричные коэффициенты имеют следующий вид:

$\mathcal{A} = {\text{diag}}\{ {{E}_{d}},{{\mathcal{O}}_{l}},{{E}_{p}}\} ,\quad \mathcal{B}(x,t,{{u}_{k}}) = {\text{diag}}\{ J(x,t,{{u}_{k}}),{{E}_{l}},{{\mathcal{O}}_{p}}\} ,$

$\begin{array}{*{20}{c}} {\mathcal{C}(x,t,{{u}_{k}}) = L(x,t,{{u}_{k}})A(x,t,{{u}_{k}})\left\{ {{{\partial }_{t}}R(x,t,{{u}_{k}}) + \sum\limits_{j = 1}^n \,{{\partial }_{{{{u}_{{j,k}}}}}}R(x,t,{{u}_{k}}){{\partial }_{t}}{{u}_{{j,k}}}} \right\} + } \\ { + \;L(x,t,{{u}_{k}})B(x,t,{{u}_{k}})\left\{ {{{\partial }_{x}}R(x,t,{{u}_{k}}) + \sum\limits_{j = 1}^n \,{{\partial }_{{{{u}_{{j,k}}}}}}R(x,t,{{u}_{k}}){{\partial }_{x}}{{u}_{{j,k}}}} \right\} + C(x,t,{{u}_{k}})R(x,t,{{u}_{k}})} \end{array}$

Кроме того, $\Phi (x) = {{R}^{{ - 1}}}(x,{{t}_{0}},\phi (x))\phi (x)$ и $\Psi (t) = {{R}^{{ - 1}}}({{x}_{0}},t,\psi (t))\psi (t)$. Заметим, что на каждом шаге итерации $k$ равенства (11) представляют собой начально-краевую задачу для линейной дифференциально-алгебраической системы уравнений в частных производных индекса $(1,0)$. Такие задачи хорошо исследованы. Для них получены условия существования решения в пространстве ${{C}^{1}}(U)$ [17] и разработаны эффективные методы численного решения на основе сплайновой интерполяции [6]. Отметим, что для каждого значения $k$ условия теоремы существования решения начально-краевой задачи (11) выполнены (см. [17]) при выполнении условий настоящей теоремы. Поэтому, подставляя стартовое значение ${{u}_{0}}(x,t)$ в коэффициенты системы из (11), мы получаем начально-краевую задачу (11), которая в силу теоремы из [17] имеет решение ${{v}_{1}}(x,t) \in {{C}^{1}}(U)$. С помощью равенства (10) по решению ${{v}_{1}}(x,t)$ мы восстанавливаем вектор ${{u}_{1}}(x,t) \in {{C}^{1}}(U)$. Затем подставляем ${{u}_{1}}(x,t)$ в коэффициенты системы из (11) и находим ${{v}_{2}}(x,t) \in {{C}^{1}}(U)$ и так далее. Предположим, что ${{v}_{k}}(x,t) \in {{C}^{1}}(U)$ – решение задачи (11) на $k$-м шаге. Используя равенство (10), мы находим вектор-функцию ${{u}_{k}}(x,t)$, которая также принадлежит пространству ${{C}^{1}}(U)$. Подставляя ${{u}_{k}}(x,t)$ в коэффициенты системы из (11), мы получаем граничную задачу, для которой снова выполнены все условия теоремы существования из работы [17]. Следовательно, на $(k + 1)$-м шаге существует решение граничной задачи (11) ${{v}_{{k + 1}}}(x,t) \in {{C}^{1}}(U)$. Таким образом, задачи (11) разрешимы при любом $k \geqslant 0$ и определяют бесконечную последовательность $\{ {{v}_{k}}(x,t):k \geqslant 0\} $ в пространстве ${{C}^{1}}(U)$.

Далее нам необходимо доказать, что последовательность $\{ {{v}_{k}}(x,t)\} $ является фундаментальной. Для этой цели мы запишем систему (11) в расщепленной интегральной форме.

2.2. Интегральная форма дифференциальной системы

Разобьем матрицу $\mathcal{C}(x,t,{{u}_{k}})$ на блоки ${{\mathcal{C}}^{i}}(x,t,{{u}_{k}})$, где $i = 1,2,3$ размеров $(d \times n)$, $(l \times n)$ и $(p \times n)$ и запишем систему (11) в расщепленном виде

(12)

$\begin{array}{*{20}{c}} {{{\partial }_{t}}v_{{k + 1}}^{1}(x,t) + J(x,t,{{u}_{k}}){{\partial }_{x}}v_{{k + 1}}^{1}(x,t) + {{\mathcal{C}}^{1}}(x,t,{{u}_{k}}){{v}_{{k + 1}}}(x,t) = {{\mathcal{F}}^{1}}(x,t,o),} \\ {{{\partial }_{x}}v_{{k + 1}}^{2}(x,t) + {{\mathcal{C}}^{2}}(x,t,{{u}_{k}}){{v}_{{k + 1}}}(x,t) = {{\mathcal{F}}^{2}}(x,t,o),} \\ {{{\partial }_{t}}v_{{k + 1}}^{3}(x,t) + {{\mathcal{C}}^{3}}(x,t,{{u}_{k}}){{v}_{{k + 1}}}(x,t) = {{\mathcal{F}}^{3}}(x,t,o),} \end{array}$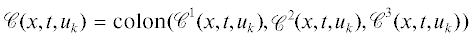

где ${{v}_{{k + 1}}}(x,t) = {{(v_{{k + 1}}^{1}(x,t),v_{{k + 1}}^{2}(x,t),v_{{k + 1}}^{3}(x,t))}^{ \top }}$, $\mathcal{F}(x,t,o) = {{({{\mathcal{F}}^{1}}(x,t,o),{{\mathcal{F}}^{2}}(x,t,o),{{\mathcal{F}}^{3}}(x,t,o))}^{ \top }}$ и

. Напомним, что матрица $J(x,t,{{u}_{k}})$ определена в (3). Рассмотрим задачи Коши

(13)

$\frac{{dx}}{{dt}} = {{k}_{i}}(x,t,{{u}_{k}}),\quad x({{t}^{0}}) = {{x}^{0}},\quad i = 1,\; \ldots ,\;d,$

где ${{k}_{i}}(x,t,{{u}_{k}}) \in {{C}^{1}}(\mathcal{U})$ – диагональные элементы матрицы $J(x,t,{{u}_{k}})$. Заметим, что

${{k}_{i}}(x,t,{{u}_{k}}) > 0\quad \forall (x,t,{{u}_{k}}) \in \mathcal{U}.$

Величины ${{x}^{0}}$ и ${{t}^{0}}$ являются параметрами, которые принимают свои значения на границе области $U$. Обозначим эту границу $\Gamma $, то есть $({{x}^{0}},{{t}^{0}}) \in \Gamma $, где $\Gamma = \{ (x,t):(x \in {{I}_{x}},t = {{t}_{0}}) \vee (x = {{x}_{0}},t \in {{I}_{t}})\} $. Таккак функции ${{k}_{i}}(x,t,{{u}_{k}})$ – определены и непрерывны в области $U$, то решение задачи Коши существует и единственно для каждого $i$ и каждого $k$ на отрезке $[{{t}^{0}},T]$. Решения задач (13) обозначим ${{x}_{i}} = {{x}_{i}}(x,t,{{x}^{0}},{{t}^{0}},{{u}_{k}})$. Это ненулевые характеристики системы (1). Через каждую граничную точку $({{x}^{0}},{{t}^{0}})$ проходит ровно $d$ ненулевых характеристик. С учетом (13) запишем систему (12) в следующем виде:

(14)

$\begin{array}{*{20}{c}} {dv_{{i,k + 1}}^{1}(x,t){\text{/}}dt + \mathcal{C}_{i}^{1}(x,t,{{u}_{k}}){{v}_{{k + 1}}}(x,t) = \mathcal{F}_{i}^{1}(x,t,o),\quad i = 1,\; \ldots ,\;d,} \\ {{{\partial }_{x}}v_{{k + 1}}^{2}(x,t) + {{\mathcal{C}}^{2}}(x,t,{{u}_{k}}){{v}_{{k + 1}}}(x,t) = {{\mathcal{F}}^{2}}(x,t,o),} \\ {{{\partial }_{t}}v_{{k + 1}}^{3}(x,t) + {{\mathcal{C}}^{3}}(x,t,{{u}_{k}}){{v}_{{k + 1}}}(x,t) = {{\mathcal{F}}^{3}}(x,t,o),} \\ {{{u}_{{k + 1}}}(x,t) = R(x,t,{{u}_{k}}){{v}_{{k + 1}}}(x,t),\quad {{u}_{0}}(x,t) = \phi (x),\quad k \geqslant 0,} \\ {{{v}_{{k + 1}}}({{x}_{0}},t) = \Psi (t),\quad {{v}_{{k + 1}}}(x,{{t}_{0}}) = \Phi (x),} \end{array}$

где $dv_{{i,k + 1}}^{1}(x,t){\text{/}}dt$ – полная производная $i$-й компоненты блока

$v_{{k + 1}}^{1}(x,t) = {{(v_{{1,k + 1}}^{1}(x,t),v_{{2,k + 1}}^{1}(x,t),\; \ldots ,\;v_{{d,k + 1}}^{1}(x,t))}^{ \top }}$

по переменной $t$ в направлении характеристики $x = {{x}_{i}}(x,t,{{u}_{k}},{{x}^{0}},{{t}^{0}})$ и

${{\mathcal{F}}^{1}}(x,t,o) = {{(\mathcal{F}_{1}^{1}(x,t,o),\mathcal{F}_{2}^{1}(x,t,o),\; \ldots ,\;\mathcal{F}_{d}^{1}(x,t,o))}^{ \top }}.$

Запишем систему (14) в интегральной форме

(15)

$\begin{array}{*{20}{c}} {v_{{i,k + 1}}^{1}(x,t) = \omega _{i}^{1}({{x}_{i}},t) - \int\limits_{{{t}^{0}}}^t \,\mathcal{C}_{i}^{1}({{x}_{i}},\tau ,{{u}_{k}}({{x}_{i}},\tau )){{v}_{{k + 1}}}({{x}_{i}},\tau )d\tau ,\quad {{t}^{0}} \in {{I}_{t}},} \\ {v_{{k + 1}}^{2}(x,t) = {{\omega }^{2}}(x,t) - \int\limits_{{{x}_{0}}}^x \,{{\mathcal{C}}^{2}}(s,t,{{u}_{k}}(s,t)){{v}_{{k + 1}}}(s,t)ds,} \\ {v_{{k + 1}}^{3}(x,t) = {{\omega }^{3}}(x,t) - \int\limits_{{{t}_{0}}}^t \,{{\mathcal{C}}^{3}}(x,\tau ,{{u}_{k}}(x,\tau )){{v}_{{k + 1}}}(x,\tau )d\tau ,} \\ {{{u}_{{k + 1}}}(x,t) = R(x,t,{{u}_{k}}){{v}_{{k + 1}}}(x,t),\quad {{u}_{0}}(x,t) = \phi (x),\quad k \geqslant 0,} \end{array}$

где

$\omega (x,t) = {{({{\omega }^{1}}(x,t),{{\omega }^{2}}(x,t),{{\omega }^{3}}(x,t))}^{ \top }},\quad {{\omega }^{1}}(x,t) = {{(\omega _{1}^{1}(x,t),\omega _{2}^{1}(x,t), \ldots ,\omega _{d}^{1}(x,t))}^{ \top }},$

$\omega _{i}^{1}({{x}_{i}},t) = v_{i}^{1}({{x}^{0}},{{t}^{0}}) + \int\limits_{{{t}^{0}}}^t \,\mathcal{F}_{i}^{1}({{x}_{i}},t,o)d\tau ,\quad {{\omega }^{2}}(x,t) = {{v}^{2}}({{x}_{0}},t) + \int\limits_{{{x}_{0}}}^x \,{{\mathcal{F}}^{2}}(s,t,o)ds,$

${{\omega }^{3}}(x,t) = {{v}^{3}}(x,{{t}_{0}}) + \int\limits_{{{t}_{0}}}^t \,{{\mathcal{F}}^{3}}(x,\tau ,o)d\tau .$

Также запишем систему (15) в операторном виде

(16)

$\begin{array}{*{20}{c}} {{{v}_{{k + 1}}}(x,t) + {{\mathcal{L}}_{k}}{{v}_{{k + 1}}}(x,t) = \omega (x,t),\quad k \geqslant 0,} \\ {{{u}_{{k + 1}}}(x,t) = R(x,t,{{u}_{k}}){{v}_{{k + 1}}}(x,t),\quad {{u}_{0}}(x,t) = \phi (x),} \end{array}$

где ${{\mathcal{L}}_{k}}$ – оператор, который действует следующим образом:

${{\mathcal{L}}_{k}}{{v}_{{k + 1}}}(x,t) = {{(\mathcal{L}_{k}^{1}{{v}_{{k + 1}}}(x,t),\mathcal{L}_{k}^{2}{{v}_{{k + 1}}}(x,t),\mathcal{L}_{k}^{3}{{v}_{{k + 1}}}(x,t))}^{ \top }},$

$\mathcal{L}_{k}^{1}{{v}_{{k + 1}}}(x,t) = \mathop {\left( {\int\limits_{{{t}^{0}}}^t {\mathcal{C}_{1}^{1}({{x}_{1}},\tau ,{{u}_{k}}({{x}_{1}},\tau )){{v}_{{k + 1}}}({{x}_{1}},\tau )d\tau } ,\; \ldots ,\;\int\limits_{{{t}^{0}}}^t {\mathcal{C}_{d}^{1}} ({{x}_{d}},\tau ,{{u}_{k}}({{x}_{d}},\tau )){{v}_{{k + 1}}}({{x}_{d}},\tau )d\tau } \right)}\nolimits^ \top ,$

$\mathcal{L}_{k}^{2}{{v}_{{k + 1}}}(x,t) = \int\limits_{{{x}_{0}}}^x {{{\mathcal{C}}^{2}}} (s,t,{{u}_{k}}(s,t)){{v}_{{k + 1}}}(s,t)ds,$

$\mathcal{L}_{k}^{3}{{v}_{{k + 1}}}(x,t) = \int\limits_{{{t}_{0}}}^t {{{\mathcal{C}}^{3}}} (x,\tau ,{{u}_{k}}(x,\tau )){{v}_{{k + 1}}}(x,\tau )d\tau .$

Теперь мы можем перейти к доказательству сходимости последовательности $\{ {{v}_{k}}(x,t)\} $ к решению задачи (1), (2).

2.3. Доказательство сходимости последовательности $\{ {{v}_{k}}(x,t)\} $

Пусть ${{v}_{{k + 1,s}}} = {{v}_{{k + s + 1}}} - {{v}_{{k + 1}}}$, тогда из (16) получаем

(17)

${{v}_{{k + 1,s}}} + {{\mathcal{L}}_{{k + s}}}{{v}_{{k + 1,s}}} + ({{\mathcal{L}}_{{k + s}}} - {{\mathcal{L}}_{k}}){{v}_{{k + 1}}} = 0.$

В свою очередь, из (17) мы получаем неравенство

(18)

${{\left\| {{{v}_{{k + 1,s}}}} \right\|}_{ * }} \leqslant {{\left\| {{{\mathcal{L}}_{{k + s}}}{{v}_{{k + 1,s}}}} \right\|}_{ * }} + {{\left\| {({{\mathcal{L}}_{{k + s}}} - {{\mathcal{L}}_{k}}){{v}_{{k + 1}}}} \right\|}_{ * }}.$

Далее $\mathcal{C}_{i}^{2}(x,t,u)$ и $\mathcal{C}_{j}^{3}(x,t,u)$, где $i = 1,\; \ldots ,\;l$ и $j = 1,\; \ldots ,\;p$, обозначают строки блоков ${{\mathcal{C}}^{2}}(x,t,u)$ и ${{\mathcal{C}}^{3}}(x,t,u)$ соответственно. Оценим по норме ${{\mathcal{L}}_{{k + s}}}{{v}_{{k + 1,s}}}$. Имеем

${{\left\| {{{\mathcal{L}}_{{k + s}}}{{v}_{{k + 1,s}}}} \right\|}_{ * }} = \mathop {max}\limits_{(x,t) \in U} \left\{ {exp( - {{l}_{1}}(t + x))\left\| {{{\mathcal{L}}_{{k + s}}}{{v}_{{k + 1,s}}}} \right\|} \right\} = $

$ = \mathop {max}\limits_{(x,t) \in U} \left\{ {exp( - {{l}_{1}}(t + x))max\left\{ {\left| {\int\limits_{{{t}^{0}}}^t {\mathcal{C}_{1}^{1}} ({{x}_{1}},\tau ,{{u}_{{k + s}}}({{x}_{1}},\tau )){{v}_{{k + 1,s}}}({{x}_{1}},\tau )d\tau } \right|, \ldots } \right.} \right.$

$ \ldots ,\left| {\int\limits_{{{t}^{0}}}^t {\mathcal{C}_{d}^{1}} ({{x}_{d}},\tau ,{{u}_{{k + s}}}({{x}_{d}},\tau )){{v}_{{k + 1,s}}}({{x}_{d}},\tau )d\tau } \right|,\;\left| {\int\limits_{{{x}^{0}}}^x {\mathcal{C}_{1}^{2}} (s,t,{{u}_{{k + s}}}(s,t)){{v}_{{k + 1,s}}}(s,t)ds} \right|,\; \ldots $

$ \ldots ,\left| {\int\limits_{{{x}^{0}}}^x {\mathcal{C}_{l}^{2}} (s,t,{{u}_{{k + s}}}(s,t)){{v}_{{k + 1,s}}}(s,t)ds} \right|,\;\left| {\int\limits_{{{t}^{0}}}^t {\mathcal{C}_{1}^{3}} (x,\tau ,{{u}_{{k + s}}}(x,\tau )){{v}_{{k + 1,s}}}(x,\tau )d\tau } \right|, \ldots $

$\left. {\left. { \ldots ,\left| {\int\limits_{{{t}^{0}}}^t {\mathcal{C}_{p}^{3}} (x,\tau ,{{u}_{{k + s}}}(x,\tau )){{v}_{{k + 1,s}}}(x,\tau )d\tau } \right|} \right\}} \right\} \leqslant $

$ \leqslant \mathop {max}\limits_{(x,t) \in U} \left\{ {\left\| {\mathcal{C}(x,t,u(x,t))} \right\| \cdot max\left\{ {\int\limits_{{{t}^{0}}}^t {exp} ({{l}_{1}}(\tau - t))exp( - {{l}_{1}}(\tau + x))\left\| {{{v}_{{k + 1,s}}}({{x}_{1}},\tau )} \right\|d\tau , \ldots } \right.} \right.$

$ \ldots \int\limits_{{{t}^{0}}}^t {exp} ({{l}_{1}}(\tau - t))exp( - {{l}_{1}}(\tau + x))\left\| {{{{v}}_{{k + 1,s}}}({{x}_{d}},\tau )} \right\|d\tau ,\;\int\limits_{{{x}^{0}}}^x {exp} ({{l}_{1}}(s - x))exp( - {{l}_{1}}(s + t))\left\| {{{v}_{{k + 1,s}}}(s,t)} \right\|ds,$

$\left. {\left. {\int\limits_{{{t}^{0}}}^t {exp} ({{l}_{1}}(\tau - t))exp( - {{l}_{1}}(\tau + x))\left\| {{{v}_{{k + 1,s}}}(x,\tau )} \right\|d\tau } \right\}} \right\} \leqslant {{\left\| {\mathcal{C}(x,t,u(x,t))} \right\|}_{{C(U)}}} \cdot {{\left\| {{{v}_{{k + 1,s}}}(x,t)} \right\|}_{ * }} \times $

$ \times \mathop {max}\limits_{(x,t) \in U} \left\{ {\int\limits_{{{t}^{0}}}^t {exp} ({{l}_{1}}(\tau - t))d\tau ,\;\int\limits_{{{x}^{0}}}^x {exp} ({{l}_{1}}(s - x))ds,\;\int\limits_{{{t}^{0}}}^t {exp} ({{l}_{1}}(\tau - t))d\tau } \right\} \leqslant $

$ \leqslant \frac{1}{{{{l}_{1}}}}{{\left\| {\mathcal{C}(x,t,u(x,t))} \right\|}_{{C(U)}}} \cdot {{\left\| {{{v}_{{k + 1,s}}}(x,t)} \right\|}_{ * }}max\left\{ {1 - exp( - {{l}_{1}}T),1 - exp( - {{l}_{1}}X)} \right\}.$

Пусть $\rho = \tfrac{1}{{{{l}_{1}}}}max\left\{ {1 - exp( - {{l}_{1}}T),1 - exp( - {{l}_{1}}X)} \right\}$ и ${{c}_{1}} = {{\left\| {C(x,t,u(x,t))} \right\|}_{{C(U)}}}$. Тогда

(19)

${{\left\| {{{\mathcal{L}}_{{k + s}}}{{v}_{{k + 1,s}}}} \right\|}_{ * }} \leqslant \rho {{c}_{1}}{{\left\| {{{v}_{{k + 1,s}}}} \right\|}_{ * }}.$

Так как для произвольной постоянной величины $\kappa $ выполняется $\mathop {lim}\limits_{{{l}_{1}} \to \infty } \left( {1 - exp( - {{l}_{1}}\kappa )} \right){\text{/}}{{l}_{1}} = 0$, то при достаточно большом значении ${{l}_{1}}$ будет $0 < \rho {{c}_{1}} < 1$. Далее, оценим по норме разность $({{\mathcal{L}}_{{k + s}}} - {{\mathcal{L}}_{k}}){{v}_{{k + s + 1}}}$. Имеем

$({{\mathcal{L}}_{{k + s}}} - {{\mathcal{L}}_{k}}){{v}_{{k + 1}}} = \left( {\int\limits_{{{t}^{0}}}^t {(\mathcal{C}_{1}^{1}({{x}_{1}},\tau ,{{u}_{{k + s}}}({{x}_{1}},\tau )) - \mathcal{C}_{1}^{1}({{x}_{1}},\tau ,{{u}_{k}}({{x}_{1}},\tau )))} {{v}_{{k + 1}}}({{x}_{1}},\tau )d\tau , \ldots } \right.$

$ \ldots ,\int\limits_{{{t}^{0}}}^t {(\mathcal{C}_{d}^{1}({{x}_{d}},\tau ,{{u}_{{k + s}}}({{x}_{d}},\tau )) - \mathcal{C}_{d}^{1}({{x}_{d}},\tau ,{{u}_{k}}({{x}_{d}},\tau )))} {{v}_{{k + 1}}}({{x}_{d}},\tau )d\tau ,$

$\int\limits_{{{t}^{0}}}^t {({{\mathcal{C}}^{2}}(s,t,{{u}_{{k + s}}}(s,t)) - {{\mathcal{C}}^{2}}(s,t,{{u}_{k}}(s,t)))} {{v}_{{k + 1}}}(s,t)ds,$

$\mathop {\left. {\int\limits_{{{t}^{0}}}^t {({{\mathcal{C}}^{3}}(x,\tau ,{{u}_{{k + s}}}(x,\tau )) - {{\mathcal{C}}^{3}}(x,\tau ,{{u}_{k}}(x,\tau )))} {{v}_{{k + 1}}}(x,\tau )d\tau } \right)}\nolimits^ \top .$

В силу шестого и седьмого условий теоремы, матрица $\mathcal{C}(x,t,u)$ удовлетворяет условию Липшица по $u$ в области $\mathcal{U}$. Следовательно, выполняется неравенство

(20)

${{\left\| {\mathcal{C}(x,t,{{u}_{2}}) - \mathcal{C}(x,t,{{u}_{1}})} \right\|}_{ * }} \leqslant {{c}_{2}}{{\left\| {{{u}_{2}} - {{u}_{1}}} \right\|}_{ * }}\quad \forall {{u}_{1}},{{u}_{2}} \in \mathcal{U},$

с некоторой постоянной ${{c}_{2}}$. (Далее у нас появляются другие постоянные ${{c}_{i}}$.) Пусть ${{u}_{{k,s}}} = {{u}_{{k + s}}} - {{u}_{k}}$, тогда с учетом (20) получаем оценку

${{\left\| {({{\mathcal{L}}_{{k + s}}} - {{\mathcal{L}}_{k}}){{v}_{{k + 1}}}} \right\|}_{ * }} \leqslant {{c}_{2}}\rho {{\left\| {{{v}_{{k + 1}}}} \right\|}_{ * }}{{\left\| {{{u}_{{k,s}}}} \right\|}_{ * }}.$

Покажем, что для любого $k$ выполняется неравенство ${{\left\| {{{v}_{k}}} \right\|}_{ * }} \leqslant {{c}_{3}}$. Система (16) эквивалентна системе (11), поэтому она однозначно разрешима при любом $k$. Из (16) находим

(21)

${{\left\| {{{v}_{{k + 1}}}(x,t)} \right\|}_{ * }} \leqslant {{c}_{3}},\quad {\text{где}}\quad {{c}_{3}} = {{\left\| {\omega (x,t)} \right\|}_{ * }}{\text{/}}(1 - \rho {{c}_{1}}).$

Из (18), (19) и (20) имеем оценку

(22)

${{\left\| {{{v}_{{k + 1,s}}}} \right\|}_{ * }} \leqslant \frac{{\rho {{c}_{2}}{{c}_{3}}}}{{1 - \rho {{c}_{1}}}}{{\left\| {{{u}_{{k,s}}}} \right\|}_{ * }}.$

Оценим по норме ${{u}_{{k,s}}}$. Из (15) находим

(23)

${{u}_{{k,s}}} = R(x,t,{{u}_{{k + s - 1}}}){{v}_{{k,s}}} + (R(x,t,{{u}_{{k + s - 1}}}) - R(x,t,{{u}_{{k - 1}}})){{v}_{k}}.$

Так как элементы матрицы $R(x,t,u)$ принадлежат ${{C}^{1}}(\mathcal{U})$, то матрица $R(x,t,u)$ является ограниченной в области $\mathcal{U}$ и удовлетворяет условию Липшица по $u$, то есть выполняются оценки

${{\left\| {R(x,t,u)} \right\|}_{{C(\mathcal{U})}}} \leqslant {{c}_{4}}\quad {\text{и}}\quad {{\left\| {R(x,t,{{u}_{2}}) - R(x,t,{{u}_{1}})} \right\|}_{ * }} \leqslant {{c}_{5}}{{\left\| {{{u}_{2}} - {{u}_{1}}} \right\|}_{ * }}\quad \forall {{u}_{1}},{{u}_{2}} \in \mathcal{U}.$

Тогда из (23) получаем

(24)

${{\left\| {{{u}_{{k,s}}}} \right\|}_{ * }} \leqslant {{c}_{4}}{{\left\| {{{v}_{{k,s}}}} \right\|}_{ * }} + {{c}_{5}}{{\left\| {{{u}_{{k - 1,s}}}} \right\|}_{ * }}{{\left\| {{{v}_{k}}} \right\|}_{ * }}.$

С учетом (22), неравенство (24) переписывается в следующем виде:

(25)

${{\left\| {{{u}_{{k + 1,s}}}} \right\|}_{ * }} \leqslant {{\kappa }_{1}}{{\left\| {{{u}_{{k,s}}}} \right\|}_{ * }},\quad {\text{где}}\quad {{\kappa }_{1}} = \frac{{\rho {{c}_{6}}}}{{1 - \rho {{c}_{1}}}} + {{c}_{5}}{{c}_{3}}.$

Если принять за $\mathcal{M}$ величину, равную $(1 - \rho {{\left\| {C(x,t,u)} \right\|}_{{C(U)}}}){\text{/}}({{\left\| {\omega (x,t)} \right\|}_{ * }})$, то в силу восьмого условия теоремы будет выполняться неравенство ${{c}_{5}}{{c}_{3}} < 1$. Поэтому увеличивая достаточно ${{l}_{1}}$, мы всегда можем добиться, чтобы выполнялось неравенство ${{\kappa }_{1}} < 1$. Из (16), для любых $k$ и $s$, имеем ${{\left\| {{{u}_{{k,s}}}} \right\|}_{ * }} \leqslant 2{{c}_{4}}{{c}_{3}}$, тогда из (25) получаем

(26)

${{\left\| {{{u}_{{k + 1,s}}}} \right\|}_{ * }} \leqslant 2{{c}_{4}}{{c}_{3}}\kappa _{1}^{k}.$

Таким образом, последовательность $\{ {{u}_{k}}\} $ является сходящейся в себе. В силу признака Коши (см. [13, c. 35]) последовательность $\{ {{u}_{k}}\} $ является сходящейся по норме ${{\left\| {{{u}_{k}}} \right\|}_{ * }}$ в пространстве $C(U)$. В силу эквивалентности двух норм ${{\left\| {{{u}_{k}}} \right\|}_{ * }}$ и ${{\left\| {{{u}_{k}}} \right\|}_{{C(U)}}}$ последовательность $\left\| {{{u}_{k}}} \right\|$ также является сходящейся по норме ${{\left\| {{{u}_{k}}} \right\|}_{{C(U)}}}$ в этом пространстве к некоторой предельной функции $u(x,t)$. Покажем, что последовательность $\{ {{v}_{k}}\} $ будет фундаментальной. Имеем

(27)

${{v}_{{k + 1}}}(x,t) = {{R}^{{ - 1}}}(x,t,{{u}_{k}}){{u}_{{k + 1}}}(x,t).$

Из (27) получаем

(28)

${{v}_{{k + 1,s}}} = {{R}^{{ - 1}}}(x,t,{{u}_{{k + s}}}){{u}_{{k + 1,s}}} + ({{R}^{{ - 1}}}(x,t,{{u}_{k}}) - {{R}^{{ - 1}}}(x,t,{{u}_{k}})){{u}_{{k + 1}}}.$

Элементы матрицы ${{R}^{{ - 1}}}(x,t,u)$ принадлежат пространству $C(\mathcal{U})$, следовательно, ${{R}^{{ - 1}}}(x,t,u)$ является ограниченной и удовлетворяет условию Липшица

(29)

${{\left\| {{{R}^{{ - 1}}}(x,t,u)} \right\|}_{{C(\mathcal{U})}}} \leqslant {{c}_{6}}\quad {\text{и}}\quad {{\left\| {{{R}^{{ - 1}}}(x,t,{{u}_{2}}) - {{R}^{{ - 1}}}(x,t,{{u}_{1}})} \right\|}_{ * }} \leqslant {{c}_{7}}{{\left\| {{{u}_{2}} - {{u}_{1}}} \right\|}_{ * }}.$

Из (28) с учетом (29) получаем неравенство

(30)

${{\left\| {{{v}_{{k + 1,s}}}} \right\|}_{ * }} \leqslant {{c}_{6}}({{\left\| {{{u}_{{k + 1,s}}}} \right\|}_{ * }} + {{\left\| {{{u}_{{k,s}}}} \right\|}_{ * }}),$

из которого имеем оценку

(31)

${{\left\| {{{v}_{{k + 1,s}}}} \right\|}_{ * }} \leqslant {{c}_{8}}\kappa _{1}^{k}.$

Из неравенства (31) следует, что последовательность $\{ {{v}_{k}}\} $ является фундаментальной. В силу признака Коши последовательность $\{ {{v}_{k}}\} $ сходится по норме ${{\{ {{v}_{k}}\} }_{ * }}$ и, следовательно, по норме ${{\left\| {{{v}_{k}}} \right\|}_{{C(U)}}}$ в пространстве $C(U)$ к некоторой предельной функции $v(x,t)$.

Покажем, что $u(x,t)$ является решением задачи (1), (2). Переходя к пределу в (15) при $k \to \infty $, получаем, что функция $u(x,t)$ удовлетворяет системе интегральных уравнений

$\begin{gathered} v_{i}^{1}(x,t) = \omega _{i}^{1}({{x}_{i}},t) - \int\limits_{{{t}^{0}}}^t \,\mathcal{C}_{i}^{1}({{x}_{i}},\tau ,u({{x}_{i}},\tau ))v({{x}_{i}},\tau )d\tau ,\quad {{t}^{0}} \in {{I}_{t}}, \\ {{v}^{2}}(x,t) = {{\omega }^{2}}(x,t) - \int\limits_{{{x}_{0}}}^x \,{{\mathcal{C}}^{2}}(s,t,u(s,t))v(s,t)ds, \\ \end{gathered} $

$\begin{gathered} {{v}^{3}}(x,t) = {{\omega }^{3}}(x,t) - \int\limits_{{{t}_{0}}}^t \,{{\mathcal{C}}^{3}}(x,\tau ,u(x,\tau ))v(x,\tau )d\tau , \\ u(x,t) = R(x,t,u)v(x,t),\quad {{u}_{0}}(x,t) = \phi (x). \\ \end{gathered} $

Следовательно, $u(x,t)$ удовлетворяет и системе дифференциальных уравнений

(32)

$\begin{gathered} {{\partial }_{t}}{{v}^{1}}(x,t) + J(x,t,u){{\partial }_{x}}{{v}^{1}}(x,t) + {{\mathcal{C}}^{1}}(x,t,u)v(x,t) = {{\mathcal{F}}^{1}}(x,t,o), \\ {{\partial }_{x}}{{v}^{2}}(x,t) + {{\mathcal{C}}^{2}}(x,t,u)v(x,t) = {{\mathcal{F}}^{2}}(x,t,o), \\ {{\partial }_{t}}{{v}^{3}}(x,t) + {{\mathcal{C}}^{3}}(x,t,u)v(x,t) = {{\mathcal{F}}^{3}}(x,t,o),\quad u(x,t) = R(x,t,u)v(x,t) \\ v({{x}_{0}},t) = {{R}^{{ - 1}}}({{x}_{0}},t,u({{x}_{0}},t))\Psi (t),\quad v(x,{{t}_{0}}) = {{R}^{{ - 1}}}(x,{{t}_{0}},u(x,{{t}_{0}}))\Phi (x). \\ \end{gathered} $

Покажем, что система (32) эквивалентна системе (1) с условием (2). Запишем систему (32) в матричном виде

(33)

$\begin{array}{*{20}{c}} {\mathcal{A}{{\partial }_{t}}v + \mathcal{B}(x,t,u){{\partial }_{x}}v + \mathcal{C}(x,t,u)v = \mathcal{F}(x,t,o),} \\ {v({{x}_{0}},t) = {{R}^{{ - 1}}}({{x}_{0}},t,u({{x}_{0}},t))\psi (t),\quad v(x,{{t}_{0}}) = {{R}^{{ - 1}}}(x,{{t}_{0}},u(x,{{t}_{0}}))\phi (x),\quad u(x,t) = R(x,t,u)v(x,t),} \end{array}$

где матричные коэффициенты имеют вид

$\begin{gathered} \mathcal{A} = {\text{diag}}\{ {{E}_{d}},{{\mathcal{O}}_{l}},{{E}_{p}}\} ,\quad \mathcal{B}(x,t,u) = {\text{diag}}\{ J(x,t,u),{{E}_{l}},{{\mathcal{O}}_{p}}\} \quad {\text{и}} \\ \mathcal{C}(x,t,u) = L(x,t,u)A(x,t,u){{\partial }_{t}}R(x,t,u) + L(x,t,u)B(x,t,u){{\partial }_{t}}R(x,t,u) + C(x,t,u)R(x,t,u). \\ \end{gathered} $

Производные ${{\partial }_{t}}R(x,t,u)$ и ${{\partial }_{x}}R(x,t,u)$ имеют следующий вид:

$\begin{gathered} {{\partial }_{t}}R(x,t,u) = {{\partial }_{t}}R(x,t,u) + \sum\limits_{j = 1}^n \,{{\partial }_{{{{u}_{j}}}}}R(x,t,u){{\partial }_{t}}{{u}_{j}}, \\ {{\partial }_{x}}R(x,t,u) = {{\partial }_{x}}R(x,t,u) + \sum\limits_{j = 1}^n \,{{\partial }_{{{{u}_{j}}}}}R(x,t,u){{\partial }_{x}}{{u}_{j}}. \\ \end{gathered} $

Умножим систему (33) слева на матрицу ${{L}^{{ - 1}}}(x,t,u)$ и вернемся в (33) к искомой функции $u(x,t)$. В результате получим

(34)

$\begin{gathered} {{L}^{{ - 1}}}(x,t,u)\mathcal{A}{{\partial }_{t}}({{R}^{{ - 1}}}(x,t,u)u) + {{L}^{{ - 1}}}(x,t,u)\mathcal{B}(x,t,u){{\partial }_{x}}({{R}^{{ - 1}}}(x,t,u)u) + \\ + \;{{L}^{{ - 1}}}(x,t,u)\mathcal{C}(x,t,u){{R}^{{ - 1}}}(x,t,u)u(x,t) = {{L}^{{ - 1}}}(x,t,u)\mathcal{F}(x,t,o), \\ u({{x}_{0}},t) = \psi (t),\quad u(x,{{t}_{0}}) = \phi (x). \\ \end{gathered} $

Преобразуем (34) к виду

$\begin{array}{*{20}{c}} {A(x,t,u){{\partial }_{t}}u + B(x,t,u){{\partial }_{x}}u + \Delta u = F(x,t,u),} \\ {u({{x}_{0}},t) = \psi (t),\quad u(x,{{t}_{0}}) = \phi (x),} \end{array}$

где

$\begin{array}{*{20}{c}} {\Delta = A(x,t,u)(R(x,t,u){{\partial }_{t}}{{R}^{{ - 1}}}(x,t,u) + {{\partial }_{t}}R(x,t,u){{R}^{{ - 1}}}(x,t,u)) + } \\ { + \;B(x,t,u)(R(x,t,u){{\partial }_{x}}{{R}^{{ - 1}}}(x,t,u) + {{\partial }_{x}}R(x,t,u){{R}^{{ - 1}}}(x,t,u)).} \end{array}$

Так как в $\Delta $ выражения в скобках представляют собой производные ${{\partial }_{t}}(R(x,t,u){{R}^{{ - 1}}}(x,t,u))$ и ${{\partial }_{x}}(R(x,t,u){{R}^{{ - 1}}}(x,t,u))$, то $\Delta \equiv 0$. Таким образом, задача (32) эквивалентна задаче (1), (2). Следовательно, функция $u(x,t)$ является решением задачи (1), (2).

Далее, мы докажем, что $u(x,t)$ непрерывно дифференцируема по переменным $x$ и $t$ в области $U$.

2.4. Доказательство непрерывной дифференцируемости решения $u(x,t)$ по переменным $x$ и $t$

Из непрерывности подынтегральных функций в (30) следует непрерывная дифференцируемость компонент $v_{i}^{1}(x,t)$ первой блочной компоненты ${{v}^{1}}(x,t)$ предельной функции $v(x,t)$ по переменной $t$ вдоль соответствующего характеристического направления $x = {{x}_{i}}(x,t,{{x}^{0}},{{t}^{0}})$. Вторая блочная компонента ${{v}^{2}}(x,t)$ предельной функции $v(x,t)$ непрерывно дифференцируема по переменной $x$ и третья блочная компонента ${{v}^{3}}(x,t)$ непрерывно дифференцируема по переменной $t$. Остается доказать, что первая блочная компонента ${{v}^{1}}(x,t)$ непрерывно дифференцируема по переменным $x$ и $t$, вторая блочная компонента ${{v}^{2}}(x,t)$ непрерывно дифференцируема по переменной $t$ и третья ${{v}^{3}}(x,t)$ по переменной $x$. Сначала докажем, что первая ${{v}^{1}}(x,t)$ и третья ${{v}^{3}}(x,t)$ компоненты предельной функции $v(x,t)$ дифференцируемы по переменной $x$.

Пусть $\mathop {\bar {v}}\nolimits_{k + 1} = {{(v_{{k + 1}}^{1},v_{{k + 1}}^{3})}^{ \top }}$, $\bar {\mathcal{L}}{{v}_{{k + 1}}}(x,t) = \mathop {(\mathcal{L}_{k}^{1}{{v}_{{k + 1}}}(x,t),\mathcal{L}_{k}^{3}{{v}_{{k + 1}}}(x,t))}\nolimits^ \top $ и $\bar {\omega }(x,t) = {{({{\omega }^{1}}(x,t),{{\omega }^{3}}(x,t))}^{ \top }}$. Первое и третье уравнения системы (15) запишем в виде операторного уравнения

(35)

${{\bar {v}}_{{k + 1}}}(x,t) + {{\bar {\mathcal{L}}}_{k}}{{v}_{{k + 1}}}(x,t) = \bar {\omega }(x,t).$

Продифференцируем уравнение (35) по переменной $x$. Получим

(36)

${{\partial }_{x}}{{\bar {v}}_{{k + 1}}}(x,t) + ({{\partial }_{x}}{{\bar {\mathcal{L}}}_{k}}){{v}_{{k + 1}}}(x,t) + {{\bar {\mathcal{L}}}_{k}}{{\partial }_{x}}{{v}_{{k + 1}}}(x,t) = {{\partial }_{x}}\bar {\omega }(x,t).$

Разобьем каждую блочную строку ${{\mathcal{C}}_{i}}(x,t,u)$, где $i = 1,2,3$, матрицы $\mathcal{C}(x,t,u)$, так, чтобы в каждом блоке содержалось по $d$, $l$ и $p$ столбцов соответственно. Получим матрицу $\mathcal{C}(x,t,u) = ({{\mathcal{C}}^{{i,j}}}(x,t,u))$, где $i,j = 1,2,3$, состоящую из блоков

$\begin{gathered} {{\mathcal{C}}^{{1,j}}}(x,t,u) = {\text{colon}}(\mathcal{C}_{{1,j}}^{1}(x,t,u),\;\mathcal{C}_{{2,j}}^{1}(x,t,u),\; \ldots ,\;\mathcal{C}_{{d,j}}^{1}(x,t,u)), \\ {{\mathcal{C}}^{{2,j}}}(x,t,u) = {\text{colon}}(\mathcal{C}_{{1,j}}^{2}(x,t,u),\;\mathcal{C}_{{2,j}}^{2}(x,t,u),\; \ldots ,\;\mathcal{C}_{{l,j}}^{2}(x,t,u)), \\ {{\mathcal{C}}^{{3,j}}}(x,t,u) = {\text{colon}}(\mathcal{C}_{{1,j}}^{3}(x,t,u),\;\mathcal{C}_{{2,j}}^{3}(x,t,u),\; \ldots ,\;\mathcal{C}_{{p,j}}^{3}(x,t,u)). \\ \end{gathered} $

Согласно этому разбиению запишем $\mathcal{L}_{k}^{i}{{v}_{{k + 1}}}(x,t) = (\mathcal{L}_{{k,1}}^{i}v_{{k + 1}}^{1}(x,t),\mathcal{L}_{{k,2}}^{i}v_{{k + 1}}^{2}(x,t),\mathcal{L}_{{k,3}}^{i}v_{{k + 1}}^{3}(x,t))$, где $i = 1,2,3$. Пусть ${{\bar {\mathcal{L}}}_{k}}{{v}_{{k + 1}}} = ({{\bar {\mathcal{L}}}_{{k,1}}}{v}_{{k + 1}}^{1},{{\bar {\mathcal{L}}}_{{k,2}}}v_{{k + 1}}^{2},{{\bar {\mathcal{L}}}_{{k,3}}}v_{{k + 1}}^{3})$, где каждый блок имеет вид ${{\bar {\mathcal{L}}}_{{k,i}}}v_{{k + 1}}^{i} = {{(\mathcal{L}_{{k,i}}^{1}v_{{k + 1}}^{i},\mathcal{L}_{{k,i}}^{3}v_{{k + 1}}^{i})}^{ \top }}$. Исключая из уравнения (35) компоненту ${{\partial }_{x}}v_{{k + 1}}^{2}(x,t)$, используя второе уравнение из (12), получаем

(37)

${{\partial }_{x}}{{\bar {v}}_{{k + 1}}} + ({{\partial }_{x}}{{\bar {\mathcal{L}}}_{k}}){{v}_{{k + 1}}} + {{\bar {\mathcal{L}}}_{{k,1}}}{{\partial }_{x}}v_{{k + 1}}^{1} + {{\bar {\mathcal{L}}}_{{k,3}}}{{\partial }_{x}}v_{{k + 1}}^{3} + {{\bar {\mathcal{L}}}_{{k,2}}}({{\mathcal{F}}^{2}}(x,t,o) - {{\mathcal{C}}^{2}}(x,t,{{u}_{k}}){{v}_{{k + 1}}}) = {{\partial }_{x}}\bar {\omega }(x,t).$

Обозначив ${{\partial }_{x}}{{\bar {v}}_{{k + 1,s}}} = {{\partial }_{x}}{{\bar {v}}_{{k + s + 1}}} - {{\partial }_{x}}{{\bar {v}}_{{k + 1}}}$, из (37) находим

(38)

$\begin{array}{*{20}{c}} {{{\partial }_{x}}{{{\bar {v}}}_{{k + 1,s}}} + ({{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{{k + s}}}){{v}_{{k + s + 1}}} - ({{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{k}}){{v}_{{k + 1}}} + {{{\bar {\mathcal{L}}}}_{{k + s,1}}}{{\partial }_{x}}v_{{k + s + 1}}^{1} - {{{\bar {\mathcal{L}}}}_{{k,1}}}{{\partial }_{x}}v_{{k + 1}}^{1} + } \\ { + \;{{{\bar {\mathcal{L}}}}_{{k + s,3}}}{{\partial }_{x}}v_{{k + s + 1}}^{3} - {{{\bar {\mathcal{L}}}}_{{k,3}}}{{\partial }_{x}}v_{{k + 1}}^{3} + {{{\bar {\mathcal{L}}}}_{{k,2}}}{{\mathcal{C}}^{2}}(x,t,{{u}_{k}}){{v}_{{k + 1}}} - {{{\bar {\mathcal{L}}}}_{{k + s,2}}}{{\mathcal{C}}^{2}}(x,t,{{u}_{{k + s}}}){{v}_{{k + s + 1}}} + } \\ { + \;\left( {{{{\bar {\mathcal{L}}}}_{{k + s,2}}} - {{{\bar {\mathcal{L}}}}_{{k,2}}}} \right){{\mathcal{F}}^{2}}(x,t,o) = 0.} \end{array}$

Слагаемые из (38) запишем в более удобной форме:

(39)

$\begin{array}{*{20}{c}} {({{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{{k + s}}}){{v}_{{k + s + 1}}} - ({{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{k}}){{v}_{{k + 1}}} = ({{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{{k + s}}} - {{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{k}}){{v}_{{k + s + 1}}} - {{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{k}}{{v}_{{k + 1,s}}},} \\ {{{{\bar {\mathcal{L}}}}_{{k + s,1}}}{{\partial }_{x}}v_{{k + s + 1}}^{1} - {{{\bar {\mathcal{L}}}}_{{k,1}}}{{\partial }_{x}}v_{{k + 1}}^{1} = ({{{\bar {\mathcal{L}}}}_{{k + s,1}}} - {{{\bar {\mathcal{L}}}}_{{k,1}}}){{\partial }_{x}}v_{{k + s + 1}}^{1} + {{{\bar {\mathcal{L}}}}_{{k,1}}}{{\partial }_{x}}{{{\bar {v}}}_{{k + 1,s}}},} \\ {{{{\bar {\mathcal{L}}}}_{{k + s,3}}}{{\partial }_{x}}v_{{k + s + 1}}^{3} - {{{\bar {\mathcal{L}}}}_{{k,3}}}{{\partial }_{x}}v_{{k + 1}}^{3} = ({{{\bar {\mathcal{L}}}}_{{k + s,1}}} - {{{\bar {\mathcal{L}}}}_{{k,3}}}){{\partial }_{x}}v_{{k + s + 1}}^{3} + {{{\bar {\mathcal{L}}}}_{{k,3}}}{{\partial }_{x}}{{{\bar {v}}}_{{k + 1,s}}},} \\ {{{{\bar {\mathcal{L}}}}_{{k + s,2}}}{{C}^{3}}(x,t,{{u}_{{k + s}}}){{v}_{{k + s + 1}}} - {{{\bar {\mathcal{L}}}}_{{k,2}}}{{\mathcal{C}}^{3}}(x,t,{{u}_{k}}){{v}_{{k + 1}}} = } \\ { = ({{{\bar {\mathcal{L}}}}_{{k + s,2}}}{{\mathcal{C}}^{3}}(x,t,{{u}_{{k + s}}}) - {{{\bar {\mathcal{L}}}}_{{k,2}}}{{\mathcal{C}}^{3}}(x,t,{{u}_{k}})){{v}_{{k + s + 1}}} + {{{\bar {\mathcal{L}}}}_{{k,2}}}{{\mathcal{C}}^{3}}(x,t,{{u}_{k}}){{v}_{{k + 1,s}}}.} \end{array}$

Перепишем равенство (38), используя выражения (39)

(40)

$\begin{array}{*{20}{c}} {{{\partial }_{x}}{{{\bar {v}}}_{{k + 1,s}}} = - ({{{\bar {\mathcal{L}}}}_{{k,1}}} + {{{\bar {\mathcal{L}}}}_{{k,3}}}){{\partial }_{x}}{{{\bar {v}}}_{{k + 1,s}}} - ({{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{{k + s}}} - {{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{k}}){{v}_{{k + s + 1}}} + ({{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{k}}){{v}_{{k + 1,s}}} - } \\ { - \;({{{\bar {\mathcal{L}}}}_{{k + s,1}}} - {{{\bar {\mathcal{L}}}}_{{k,1}}}){{\partial }_{x}}v_{{k + s + 1}}^{1} - ({{{\bar {\mathcal{L}}}}_{{k + s,3}}} - {{{\bar {\mathcal{L}}}}_{{k,3}}}){{\partial }_{x}}v_{{k + s + 1}}^{3} - ({{{\bar {\mathcal{L}}}}_{{k + s,2}}} - {{{\bar {\mathcal{L}}}}_{{k,2}}}){{\mathcal{F}}^{2}}(x,t,o) + } \\ { + \;({{{\bar {\mathcal{L}}}}_{{k + s,2}}}{{\mathcal{C}}^{3}}(x,t,{{u}_{{k + s}}}) - {{{\bar {\mathcal{L}}}}_{{k,2}}}{{\mathcal{C}}^{3}}(x,t,{{u}_{k}})){{v}_{{k + s + 1}}} + {{{\bar {\mathcal{L}}}}_{{k,2}}}{{\mathcal{C}}^{3}}(x,t,{{u}_{k}}){{v}_{{k + 1,s}}}.} \end{array}$

Получим оценку по норме вектора ${{\partial }_{x}}{{\bar {v}}_{{k + 1,s}}}$. Из (40) находим

(41)

$\begin{gathered} {{\left\| {{{\partial }_{x}}{{{{\bar {v}}}}_{{k + 1,s}}}} \right\|}_{ * }} \leqslant {{\left\| {({{{\bar {\mathcal{L}}}}_{{k,1}}} + {{{\bar {\mathcal{L}}}}_{{k,3}}}){{\partial }_{x}}{{{{\bar {v}}}}_{{k + 1,s}}}} \right\|}_{ * }} + {{\left\| {({{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{{k + s}}} - {{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{k}}){{{v}}_{{k + s + 1}}}} \right\|}_{ * }} + {{\left\| {({{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{k}}){{{v}}_{{k + 1,s}}}} \right\|}_{ * }} + \\ + \;{{\left\| {({{{\bar {\mathcal{L}}}}_{{k + s,1}}} - {{{\bar {\mathcal{L}}}}_{{k,1}}}){{\partial }_{x}}{v}_{{k + s + 1}}^{1}} \right\|}_{ * }} + {{\left\| {({{{\bar {\mathcal{L}}}}_{{k + s,3}}} - {{{\bar {\mathcal{L}}}}_{{k,3}}}){{\partial }_{x}}{v}_{{k + s + 1}}^{3}} \right\|}_{ * }} + {{\left\| {({{{\bar {\mathcal{L}}}}_{{k + s,2}}} - {{{\bar {\mathcal{L}}}}_{{k,2}}}){{\mathcal{F}}^{2}}(x,t,o)} \right\|}_{ * }} + \\ + \;{{\left\| {({{{\bar {\mathcal{L}}}}_{{k + s,2}}}{{\mathcal{C}}^{3}}(x,t,{{u}_{{k + s}}}) - {{{\bar {\mathcal{L}}}}_{{k,2}}}{{\mathcal{C}}^{3}}(x,t,{{u}_{k}})){{{v}}_{{k + s + 1}}}} \right\|}_{ * }} + {{\left\| {{{{\bar {\mathcal{L}}}}_{{k,2}}}{{\mathcal{C}}^{3}}(x,t,{{u}_{k}}){{{v}}_{{k + 1,s}}}} \right\|}_{ * }}{\kern 1pt} . \\ \end{gathered} $

Оценим отдельно каждое слагаемое из первой части неравенства (41). Аналогично оценке (19) находим

(42)

${{\left\| {\left( {{{{\bar {\mathcal{L}}}}_{{k,1}}} + {{{\bar {\mathcal{L}}}}_{{k,3}}}} \right){{\partial }_{x}}{{{\bar {v}}}_{{k + 1,s}}}} \right\|}_{ * }} \leqslant 2\rho {{c}_{1}}{{\left\| {{{\partial }_{x}}{{{\bar {v}}}_{{k + 1,s}}}} \right\|}_{ * }}.$

Далее оценим второе слагаемое из правой части (41). Имеем

$\begin{gathered} ({{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{{k + s}}} - {{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{k}}){{v}_{{k + s + 1}}} = \left( {\int\limits_{{{t}^{0}}}^t {\left( {{{\partial }_{{{{x}_{1}}}}}\mathcal{C}_{1}^{1}({{x}_{1}},\tau ,{{u}_{{k + s}}}({{x}_{1}},\tau )) + \sum\limits_{j = 1}^n \,{{\partial }_{{{{u}_{{j,k + s}}}}}}\mathcal{C}_{1}^{1}({{x}_{1}},\tau ,{{u}_{{k + s}}}({{x}_{1}},\tau )) \times } \right.} } \right. \\ \left. { \times \;{{\partial }_{{{{x}_{1}}}}}{{u}_{{j,k + s}}} - {{\partial }_{{{{x}_{1}}}}}\mathcal{C}_{1}^{1}({{x}_{1}},\tau ,{{u}_{k}}({{x}_{1}},\tau )) - \sum\limits_{j = 1}^n \,{{\partial }_{{{{u}_{{j,k}}}}}}\mathcal{C}_{1}^{1}({{x}_{1}},\tau ,{{u}_{k}}({{x}_{1}},\tau )){{\partial }_{{{{x}_{1}}}}}{{u}_{{j,k}}}} \right){{\partial }_{x}}{{x}_{1}}{{v}_{{k + s + 1}}}({{x}_{1}},\tau )d\tau ,\, \ldots \\ \end{gathered} $

$\begin{gathered} \ldots ,\int_{{{t}^{0}}}^t \left( {{{\partial }_{{{{x}_{d}}}}}\mathcal{C}_{d}^{1}({{x}_{d}},\tau ,{{u}_{{k + s}}}({{x}_{d}},\tau )) + \sum\limits_{j = 1}^n \,{{\partial }_{{{{u}_{{j,k + s}}}}}}\mathcal{C}_{d}^{1}({{x}_{d}},\tau ,{{u}_{{k + s}}}({{x}_{d}},\tau )){{\partial }_{{{{x}_{d}}}}}{{u}_{{j,k + s}}} - } \right. \\ \left. { - \;{{\partial }_{{{{x}_{d}}}}}\mathcal{C}_{d}^{1}({{x}_{d}},\tau ,{{u}_{k}}({{x}_{d}},\tau )) - \sum\limits_{j = 1}^n {{\partial }_{{{{u}_{{j,k}}}}}}\mathcal{C}_{1}^{d}({{x}_{d}},\tau ,{{u}_{k}}({{x}_{d}},\tau )){{\partial }_{{{{x}_{d}}}}}{{u}_{{j,k}}}} \right){{\partial }_{x}}{{x}_{d}}{{v}_{{k + s + 1}}}({{x}_{d}},\tau )d\tau , \\ \end{gathered} $

$\begin{gathered} \int\limits_{{{t}_{0}}}^t {\left( {{{\partial }_{x}}{{\mathcal{C}}^{3}}(x,\tau ,{{u}_{{k + s}}}(x,\tau )) + \sum\limits_{j = 1}^n \,{{\partial }_{{{{u}_{{j,k + s}}}}}}{{\mathcal{C}}^{3}}(x,\tau ,{{u}_{{k + s}}}(x,\tau )){{\partial }_{x}}{{u}_{{j,k + s}}} - {{\partial }_{x}}{{\mathcal{C}}^{3}}(x,\tau ,{{u}_{k}}(x,\tau )) - } \right.} \\ \mathop {\left. {\left. { - \;\sum\limits_{j = 1}^n \,{{\partial }_{{{{u}_{{j,k}}}}}}{{\mathcal{C}}^{3}}(x,\tau ,{{u}_{k}}(x,\tau )){{\partial }_{x}}{{u}_{{j,k}}}} \right){{v}_{{k + s + 1}}}(x,\tau )d\tau } \right)}\nolimits^ \top , \\ \end{gathered} $

где ${{\partial }_{x}}{{u}_{{j,k,s}}} = {{\partial }_{x}}{{u}_{{j,k + s}}} - {{\partial }_{x}}{{u}_{{j,k}}}$. Перепишем последнее равенство, преобразуя выражения в правой части. Получим

$\begin{gathered} ({{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{{k + s}}} - {{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{k}}){{{v}}_{{k + s + 1}}} = \left( {\int\limits_{{{t}^{0}}}^t {({{\partial }_{{{{x}_{1}}}}}\mathcal{C}_{1}^{1}({{x}_{1}},\tau ,{{u}_{{k + s}}}({{x}_{1}},\tau )) - {{\partial }_{{{{x}_{1}}}}}\mathcal{C}_{1}^{1}({{x}_{1}},\tau ,{{u}_{k}}({{x}_{1}},\tau ))} } \right. + \\ + \sum\limits_{j = 1}^n \,(({{\partial }_{{{{u}_{{j,k + s}}}}}}\mathcal{C}_{1}^{1}({{x}_{1}},\tau ,{{u}_{{k + s}}}({{x}_{1}},\tau )) - {{\partial }_{{{{u}_{{j,k}}}}}}\mathcal{C}_{1}^{1}({{x}_{1}},\tau ,{{u}_{k}}({{x}_{1}},\tau ))){{\partial }_{{{{x}_{1}}}}}{{u}_{{j,k,s}}} + \\ \end{gathered} $

$\begin{gathered} + \;{{\partial }_{{{{u}_{{j,k}}}}}}\mathcal{C}_{1}^{1}({{x}_{1}},\tau ,{{u}_{k}}({{x}_{1}},\tau )){{\partial }_{{{{x}_{1}}}}}{{u}_{{j,k,s}}} + ({{\partial }_{{{{u}_{{j,k + s}}}}}}\mathcal{C}_{1}^{1}({{x}_{1}},\tau ,{{u}_{{k + s}}}({{x}_{1}},\tau )) - \\ \left. {\mathop { - \;{{\partial }_{{{{u}_{{j,k}}}}}}\mathcal{C}_{1}^{1}({{x}_{1}},\tau ,{{u}_{k}}({{x}_{1}},\tau ))){{\partial }_{{{{x}_{1}}}}}{{u}_{{j,k}}})}\limits_{}^{} } \right){{\partial }_{x}}{{x}_{1}}{{{v}}_{{k + s + 1}}}d\tau ,\,... \\ \end{gathered} $

$\begin{gathered} \ldots ,\int\limits_{{{t}^{0}}}^t {({{\partial }_{{{{x}_{d}}}}}\mathcal{C}_{d}^{1}({{x}_{d}},\tau ,{{u}_{{k + s}}}({{x}_{d}},\tau )) - {{\partial }_{{{{x}_{d}}}}}\mathcal{C}_{d}^{1}({{x}_{d}},\tau ,{{u}_{k}}({{x}_{d}},\tau )) + } \\ + \;\sum\limits_{j = 1}^n \,(({{\partial }_{{{{u}_{{j,k + s}}}}}}\mathcal{C}_{d}^{1}({{x}_{d}},\tau ,{{u}_{{k + s}}}({{x}_{d}},\tau )) - {{\partial }_{{{{u}_{{j,k}}}}}}\mathcal{C}_{d}^{1}({{x}_{d}},\tau ,{{u}_{k}}({{x}_{d}},\tau ))){{\partial }_{{{{x}_{d}}}}}{{u}_{{j,k,s}}} + \\ \end{gathered} $

$\begin{gathered} + \;{{\partial }_{{{{u}_{{j,k}}}}}}\mathcal{C}_{d}^{1}({{x}_{d}},\tau ,{{u}_{k}}({{x}_{d}},\tau )){{\partial }_{{{{x}_{d}}}}}{{u}_{{j,k,s}}} + ({{\partial }_{{{{u}_{{j,k + s}}}}}}\mathcal{C}_{d}^{1}({{x}_{d}},\tau ,{{u}_{{k + s}}}({{x}_{d}},\tau )) - \\ - \;{{\partial }_{{{{u}_{{j,k}}}}}}\mathcal{C}_{d}^{1}({{x}_{d}},\tau ,{{u}_{k}}({{x}_{d}},\tau ))){{\partial }_{{{{x}_{d}}}}}{{u}_{{j,k}}})){{\partial }_{x}}{{x}_{d}}{{{v}}_{{k + s + 1}}}d\tau , \\ \end{gathered} $

$\begin{gathered} \int\limits_{{{t}_{0}}}^t {({{\partial }_{x}}{{\mathcal{C}}^{3}}(x,\tau ,{{u}_{{k + s}}}(x,\tau )) - {{\partial }_{x}}{{\mathcal{C}}^{3}}(x,\tau ,{{u}_{k}}(x,\tau ))} + \\ + \;\sum\limits_{j = 1}^n \,(({{\partial }_{{{{u}_{{j,k + s}}}}}}{{\mathcal{C}}^{3}}(x,\tau ,{{u}_{{k + s}}}(x,\tau )) - {{\partial }_{{{{u}_{{j,k}}}}}}{{\mathcal{C}}^{3}}(x,\tau ,{{u}_{k}}(x,\tau ))){{\partial }_{x}}{{u}_{{j,k,s}}} + \\ \end{gathered} $

$\begin{gathered} + \;{{\partial }_{{{{u}_{{j,k}}}}}}{{\mathcal{C}}^{3}}(x,\tau ,{{u}_{k}}(x,\tau )){{\partial }_{x}}{{u}_{{j,k,s}}} + ({{\partial }_{{{{u}_{{j,k + s}}}}}}{{\mathcal{C}}^{3}}(x,\tau ,{{u}_{{k + s}}}(x,\tau )) - \\ \mathop { - \;{{\partial }_{{{{u}_{{j,k}}}}}}{{\mathcal{C}}^{3}}(x,\tau ,{{u}_{k}}(x,\tau ))){{\partial }_{x}}{{u}_{{j,k}}})){{{v}}_{{k + s + 1}}}d\tau )}\nolimits^ \top . \\ \end{gathered} $

В силу шестого и седьмого условий теоремы, матрица ${{\partial }_{x}}\mathcal{C}(x,t,u)$ удовлетворяет условию Липшица по $u$

(43)

${{\left\| {{{\partial }_{x}}\mathcal{C}(x,t,{{u}_{2}}) - {{\partial }_{x}}\mathcal{C}(x,t,{{u}_{1}})} \right\|}_{ * }} \leqslant {{c}_{9}}{{\left\| {{{u}_{2}} - {{u}_{1}}} \right\|}_{ * }}\quad \forall {{u}_{1}},{{u}_{2}} \in \mathcal{U}$

и является ограниченной в области $C(\mathcal{U})$. Используя (43), находим

(44)

${{\left\| {({{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{{k + s}}} - {{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{k}}){{v}_{{k + s + 1}}}} \right\|}_{ * }} \leqslant {{c}_{{10}}}\rho {{\left\| {{{v}_{{k + s + 1}}}} \right\|}_{ * }}\left\{ {{{{\left\| {{{u}_{{k,s}}}} \right\|}}_{ * }}(1 + {{{\left\| {{{\partial }_{x}}{{u}_{{k,s}}}} \right\|}}_{ * }} + {{{\left\| {{{\partial }_{x}}{{u}_{k}}} \right\|}}_{ * }}) + {{{\left\| {{{\partial }_{x}}{{u}_{{k,s}}}} \right\|}}_{ * }}} \right\}.$

Оценим сначала ${{\left\| {{{\partial }_{x}}{{u}_{k}}} \right\|}_{ * }}$. Имеем

${{\partial }_{x}}{{u}_{{k + 1}}} = \left( {{{\partial }_{x}}R(x,t,{{u}_{k}}) + \sum\limits_{j = 1}^n \,{{\partial }_{{{{u}_{j}}}}}R(x,t,{{u}_{k}})} \right){{v}_{{k + 1}}} + R(x,t,{{u}_{k}}){{\partial }_{x}}{{v}_{{k + 1}}}.$

Тогда

(45)

${{\left\| {{{\partial }_{x}}{{u}_{{k + 1}}}} \right\|}_{ * }} \leqslant {{c}_{{11}}}{{\left\| {{{v}_{{k + 1}}}} \right\|}_{ * }} + {{c}_{{12}}}{{\left\| {{{\partial }_{x}}{{u}_{k}}} \right\|}_{ * }}.$

Из (36) и второго уравнения в (14) находим

${{\left\| {{{\partial }_{x}}{{{\bar {v}}}_{{k + 1}}}} \right\|}_{ * }} \leqslant {{c}_{{15}}},\quad {\text{и}}\quad {{\left\| {{{\partial }_{x}}v_{{k + 1}}^{2}} \right\|}_{ * }} \leqslant {{c}_{{16}}},$

где

${{c}_{{15}}} = \frac{{{{c}_{{14}}}\rho (1 + {{{\left\| {F(x,t,o)} \right\|}}_{{C(U)}}}) + {{{\left\| {{{\partial }_{x}}\bar {\omega }(x,t)} \right\|}}_{{C(U)}}}}}{{1 - {{c}_{{13}}}\rho }}\quad {\text{и}}\quad {{c}_{{16}}} = {{\left\| {{{\mathcal{F}}^{2}}(x,t,o)} \right\|}_{ * }} + {{c}_{3}}{{\left\| {{{\mathcal{C}}^{2}}(x,t,u)} \right\|}_{ * }}.$

Следовательно, ${{\left\| {{{\partial }_{x}}{{v}_{{k + 1}}}} \right\|}_{ * }} \leqslant {{c}_{{17}}}$, где ${{c}_{{17}}} = max\{ {{c}_{{15}}},{{c}_{{16}}}\} $. Подставляя в (45) полученную оценку и учитывая (21), находим

(46)

${{\left\| {{{\partial }_{x}}{{u}_{{k + 1}}}} \right\|}_{ * }} \leqslant {{c}_{{18}}},\quad {\text{где}}\quad {{c}_{{18}}} = {{c}_{3}}{{c}_{{11}}} + {{c}_{{12}}}{{c}_{{17}}}.$

Далее, продифференцируем равенство (23) по переменной $x$

(47)

$\begin{array}{*{20}{c}} {{{\partial }_{x}}{{u}_{{k,s}}} = {{\partial }_{x}}R(x,t,{{u}_{{k + s - 1}}}){{v}_{{k,s}}} + \sum\limits_{j = 1}^n \,{{\partial }_{{{{u}_{{j,k + s - 1}}}}}}R(x,t,{{u}_{{k + s - 1}}}){{\partial }_{x}}{{u}_{{k + s - 1}}}{{v}_{{k,s}}} + R(x,t,{{u}_{{k + s - 1}}}) \times } \\ { \times \;{{\partial }_{x}}{{v}_{{k,s}}} + ({{\partial }_{x}}R(x,t,{{u}_{{k + s - 1}}}) - {{\partial }_{x}}R(x,t,{{u}_{{k - 1}}})){{v}_{k}} + \sum\limits_{j = 1}^n \,({{\partial }_{{{{u}_{{j,k + s - 1}}}}}}R(x,t,{{u}_{{k + s - 1}}}){{\partial }_{x}}{{u}_{{k + s - 1}}} - } \\ { - \;{{\partial }_{{{{u}_{{j,k - 1}}}}}}R(x,t,{{u}_{{k - 1}}}){{\partial }_{x}}{{u}_{{k - 1}}}){{v}_{k}} + (R(x,t,{{u}_{{k + s - 1}}}) - R(x,t,{{u}_{{k - 1}}})){{v}_{k}}.} \end{array}$

Учитывая ограниченность матричных коэффициентов из правой части равенства (47), а также ограниченность векторов ${{v}_{k}}$, ${{\partial }_{x}}{{u}_{k}}$ и ${{v}_{{k,s}}}$ (оценки (21), (31) и (46)), из (47) получаем

${{\left\| {{{\partial }_{x}}{{u}_{{k,s}}}} \right\|}_{ * }} \leqslant {{c}_{{19}}}{{\left\| {{{\partial }_{x}}{{v}_{{k,s}}}} \right\|}_{ * }}.$

Отдельно оценим компоненту ${{\partial }_{x}}v_{{k,s}}^{2}$. Из второго уравнения в (14) получаем

(48)

${{\partial }_{x}}v_{{k,s}}^{2}(x,t) = - ({{\mathcal{C}}^{2}}(x,t,{{u}_{{k + s - 1}}}) - {{\mathcal{C}}^{2}}(x,t,{{u}_{{k - 1}}})){{v}_{{k + s}}} - {{\mathcal{C}}^{2}}(x,t,{{u}_{{k - 1}}}){{v}_{{k,s}}}.$

Из (48) находим

(49)

${{\left\| {{{\partial }_{x}}v_{{k,s}}^{2}(x,t)} \right\|}_{ * }} \leqslant {{c}_{{20}}}\kappa _{1}^{k}.$

Следовательно, из (44), используя (21), (26), (46) и (49) получаем

(50)

Перейдем к оценке следующего слагаемого $({{\partial }_{x}}{{\bar {\mathcal{L}}}_{k}}){{v}_{{k + 1,s}}}$ из (41). Имеем

${{\partial }_{x}}{{\bar {\mathcal{L}}}_{k}}{{v}_{{k + 1,s}}} = \left( {\int\limits_{{{t}^{0}}}^t {\left( {{{\partial }_{{{{x}_{1}}}}}\mathcal{C}_{1}^{1}({{x}_{1}},\tau ,{{u}_{{k + s}}}({{x}_{1}},\tau )) + \sum\limits_{j = 1}^n \,{{\partial }_{{{{u}_{{j,k + s}}}}}}\mathcal{C}_{1}^{1}({{x}_{1}},\tau ,{{u}_{{k + s}}}({{x}_{1}},\tau )){{\partial }_{{{{x}_{1}}}}}{{u}_{{j,k + s}}}} \right)} } \right.{{\partial }_{x}}{{x}_{1}}{{v}_{{k + 1,s}}}({{x}_{1}},\tau )d\tau \,, \ldots \;$

$...,\,\,\int\limits_{{{t}^{0}}}^t {\left( {{{\partial }_{{{{x}_{d}}}}}\mathcal{C}_{d}^{1}({{x}_{d}},\tau ,{{u}_{{k + s}}}({{x}_{d}},\tau )) + \sum\limits_{j = 1}^n \,{{\partial }_{{{{u}_{{j,k + s}}}}}}\mathcal{C}_{d}^{1}({{x}_{d}},\tau ,{{u}_{{k + s}}}({{x}_{d}},\tau )){{\partial }_{{{{x}_{d}}}}}{{u}_{{j,k + s}}}} \right){{\partial }_{x}}{{x}_{d}}{{v}_{{k + 1,s}}}({{x}_{d}},\tau )d\tau } ,$

$\int\limits_{{{t}_{0}}}^t {\mathop {\left. {\left( {{{\partial }_{x}}{{\mathcal{C}}^{3}}(x,\tau ,{{u}_{{k + s}}}(x,\tau )) + \sum\limits_{j = 1}^n \,{{\partial }_{{{{u}_{{j,k + s}}}}}}{{\mathcal{C}}^{3}}(x,\tau ,{{u}_{{k + s}}}(x,\tau )){{\partial }_{x}}{{u}_{{j,k + s}}}} \right){{v}_{{k + 1,s}}}(x,\tau )d\tau } \right)}\nolimits^ \top .} $

При выполнении условий 6) и 7) настоящей теоремы, матрица ${{\partial }_{x}}\mathcal{C}(x,t,u)$ является ограниченной в области $\mathcal{U}$, следовательно,

(51)

${{\left\| {({{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{k}}){{v}_{{k + 1,s}}}} \right\|}_{ * }} \leqslant {{c}_{{23}}}\rho {{\left\| {{{v}_{{k + 1,s}}}} \right\|}_{ * }}.$

Из (51) с помощью (31) получаем

(52)

${{\left\| {({{\partial }_{x}}{{{\bar {\mathcal{L}}}}_{k}}){{v}_{{k + 1,s}}}} \right\|}_{ * }} \leqslant {{c}_{{24}}}\rho \kappa _{1}^{k}.$

Далее оценим $({{\bar {\mathcal{L}}}_{{k + s,1}}} - {{\bar {\mathcal{L}}}_{{k,1}}}){{\partial }_{x}}v_{{k + s + 1}}^{1}$. Имеем

$({{\bar {\mathcal{L}}}_{{k + s,1}}} - {{\bar {\mathcal{L}}}_{{k,1}}}){{\partial }_{x}}v_{{k + s + 1}}^{1} = \left( {\int\limits_{{{t}^{0}}}^t {(\mathcal{C}_{{1,1}}^{1}({{x}_{1}},\tau ,{{u}_{{k + s}}}({{x}_{1}},\tau )) - \mathcal{C}_{{1,1}}^{1}({{x}_{1}},\tau ,{{u}_{k}}({{x}_{1}},\tau ))){{\partial }_{x}}v_{{k + s + 1}}^{1}({{x}_{1}},\tau )d\tau } ,} \right.$

$ \ldots ,\int\limits_{{{t}^{0}}}^t {(\mathcal{C}_{{d,1}}^{1}({{x}_{d}},\tau ,{{u}_{{k + s}}}({{x}_{d}},\tau )) - \mathcal{C}_{{d,1}}^{1}({{x}_{d}},\tau ,{{u}_{k}}({{x}_{d}},\tau ))){{\partial }_{x}}v_{{k + s + 1}}^{1}({{x}_{d}},\tau )d\tau } ,$

$\mathop {\left. {\int\limits_{{{t}_{0}}}^t {({{\mathcal{C}}^{{3,1}}}(x,\tau ,{{u}_{{k + s}}}(x,\tau )) - {{\mathcal{C}}^{{3,1}}}(x,\tau ,{{u}_{k}}(x,\tau ))){{\partial }_{x}}v_{{k + s + 1}}^{1}(x,\tau )d} \tau } \right)}\nolimits^ \top .$

Следовательно,

(53)

${{\left\| {({{{\bar {\mathcal{L}}}}_{{k + s,1}}} - {{{\bar {\mathcal{L}}}}_{{k,1}}}){{\partial }_{x}}v_{{k + s + 1}}^{1}} \right\|}_{ * }} \leqslant {{c}_{{25}}}\rho {{\left\| {{{u}_{{k,s}}}} \right\|}_{ * }}{{\left\| {{{\partial }_{x}}v_{{k + s + 1}}^{1}(x,t)} \right\|}_{ * }}.$

Следовательно,

(54)

${{\left\| {{{\partial }_{x}}v_{{k + s + 1}}^{1}(x,t)} \right\|}_{ * }} \leqslant {{c}_{{26}}}.$

Из (53) с учетом (54) и (26) получаем требуемую оценку

(55)

${{\left\| {({{{\bar {\mathcal{L}}}}_{{k + s,1}}} - {{{\bar {\mathcal{L}}}}_{{k,1}}}){{\partial }_{x}}v_{{k + s + 1}}^{1}} \right\|}_{ * }} \leqslant {{c}_{{27}}}\rho \kappa _{1}^{k}.$

Аналогично предыдущим рассуждениям получаем

(56)

$\begin{array}{*{20}{c}} {{{{\left\| {({{{\bar {\mathcal{L}}}}_{{k + s,3}}} - {{{\bar {\mathcal{L}}}}_{{k,3}}}){{\partial }_{x}}v_{{k + s + 1}}^{3}} \right\|}}_{ * }} \leqslant {{c}_{{28}}}\rho \kappa _{1}^{k},} \\ {{{{\left\| {({{{\bar {\mathcal{L}}}}_{{k + s,2}}} - {{{\bar {\mathcal{L}}}}_{{k,2}}}){{\mathcal{F}}^{2}}(x,t,o)} \right\|}}_{ * }} \leqslant {{c}_{{29}}}\rho \kappa _{1}^{k},} \\ {{{{\left\| {({{{\bar {\mathcal{L}}}}_{{k + s,2}}}{{\mathcal{C}}^{3}}(x,t,{{u}_{{k + s}}}) - {{{\bar {\mathcal{L}}}}_{{k,2}}}{{\mathcal{C}}^{3}}(x,t,{{u}_{k}})){{v}_{{k + s + 1}}}} \right\|}}_{ * }} \leqslant {{c}_{{30}}}\rho \kappa _{1}^{k},} \\ {{{{\left\| {{{{\bar {\mathcal{L}}}}_{{k,2}}}{{\mathcal{C}}^{3}}(x,t,{{u}_{k}}){{v}_{{k + 1,s}}}} \right\|}}_{ * }} \leqslant {{c}_{{31}}}\rho \kappa _{1}^{k}.} \end{array}$

Из (41), учитывая (42), (50), (52), (55) и (56), имеем

(57)

${{\left\| {{{\partial }_{x}}{{{\bar {v}}}_{{k + 1,s}}}} \right\|}_{ * }} \leqslant {{\kappa }_{2}}{{\left\| {{{\partial }_{x}}{{{\bar {v}}}_{{k,s}}}} \right\|}_{ * }} + {{c}_{{33}}}\kappa _{1}^{k},\quad {\text{где}}\quad {{\kappa }_{2}} = {{c}_{{22}}}\rho {\text{/}}(1 - 2{{c}_{1}}\rho ).$

При достаточно большом значении ${{l}_{1}}$ будет ${{\kappa }_{2}} < 1$. Так как для любых значений $k$ и $s$ выполняется неравенство ${{\left\| {{{\partial }_{x}}{{{\bar {v}}}_{{k,s}}}} \right\|}_{ * }} \leqslant 2{{c}_{{15}}}$, то из (57) получаем оценку

${{\left\| {{{\partial }_{x}}{{{\bar {v}}}_{{k + 1,s}}}} \right\|}_{ * }} \leqslant 2{{c}_{{15}}}\kappa _{2}^{{k + 1}} + \frac{{{{c}_{{33}}}\kappa _{1}^{k}}}{{1 - {{\kappa }_{2}}}}.$

Из неравенства (57) следует, что последовательность $\{ {{\partial }_{x}}{{\bar {v}}_{k}}\} $ является фундаментальной. В силу признака Коши последовательность $\{ {{\partial }_{x}}{{\bar {v}}_{k}}\} $ сходится по норме ${{\{ {{\partial }_{x}}{{\bar {v}}_{k}}\} }_{ * }}$ и, следовательно, по норме ${{\{ {{\partial }_{x}}{{\bar {v}}_{k}}\} }_{{C(U)}}}$ в пространстве $C(U)$ к некоторой предельной функции ${{\partial }_{x}}\bar {v}(x,t)$. Из неравенства (52) в силу условия 7) настоящей теоремы следует, что последовательность $\{ {{\partial }_{x}}{{\bar {u}}_{k}}\} $ также сходится по норме ${{\left\| {{{\partial }_{x}}{{{\bar {u}}}_{k}}} \right\|}_{{C(U)}}}$ в пространстве $C(U)$ к некоторой предельной функции ${{\partial }_{x}}\bar {u}(x,t)$. Нетрудно показать, что вектор-функция ${{\partial }_{x}}u(x,t) = {{({{\partial }_{x}}{{u}^{1}}(x,t),{{\partial }_{x}}{{u}^{2}}(x,t),{{\partial }_{x}}{{u}^{3}}(x,t))}^{ \top }}$ удовлетворяет начально-краевой задаче, полученной в результате дифференцирования задачи (1), (2) по переменной $x$. Для этого достаточно перейти к пределу при $k \to \infty $ в уравнении (36) и показать, что предельное соотношение эквивалентно системе дифференциальных уравнений, полученной в результате дифференцирования первого и третьего уравнений системы (32).

Аналогично доказывается дифференцируемость вектора $u(x,t)$ по переменной $t$.

Перейдем теперь к заключительной части доказательства и покажем, что построенное решение $u(x,t)$ является единственным.

2.5. Единственность решения задачи (1), (2)

Предположим, что задача (1), (2) имеет два различных решения ${{\tilde {u}}^{1}}(x,t)$ и ${{\tilde {u}}^{2}}(x,t)$ в области $U$. Тогда их разность удовлетворяет неравенству, аналогичному (24),

${{\left\| {{{{\tilde {u}}}^{1}}(x,t) - {{{\tilde {u}}}^{2}}(x,t)} \right\|}_{ * }} \leqslant {{k}_{1}}{{\left\| {{{{\tilde {u}}}^{1}}(x,t) - {{{\tilde {u}}}^{2}}(x,t)} \right\|}_{ * }},\quad {\text{где}}\quad 0 < {{k}_{1}} < 1.$

Очевидно, что последнее неравенство выполняется только в случае, когда ${{\tilde {u}}^{1}}(x,t) \equiv {{\tilde {u}}^{2}}(x,t)$ в области $U$.

Таким образом, теорема доказана.

Сделаем небольшие замечания по поводу условий теоремы.

Замечание 1. В случае, когда преобразующие матрицы $L(x,t,u)$ и $R(x,t,u)$ неизвестны, проверить выполнение условия 7) теоремы не представляется возможным. В этом случае нужно воспользоваться теоремой 4 из работы [7] и проверить, будут ли матрицы $A(x,t,u)$ и $B(x,t,u)$ обладать достаточной гладкостью в области $\mathcal{U}$, так как в силу теоремы 4 из работы [7] матрицы $A(x,t,u)$, $B(x,t,u)$, $L(x,t,u)$ и $R(x,t,u)$ обладают одним и тем же порядком гладкости.

Замечание 2. Из доказательства теоремы видно, что условие 8) возникло в результате следующей замены переменной ${{u}_{{k + 1}}}(x,t) = R(x,t,{{u}_{k}}(x,t)){{v}_{{k + 1}}}(x,t)$ и появления таким образом нелинейного итерационного соотношения, оператор перехода в котором должен быть оператором сжатия. Отметим, что для систем, записанных в канонической форме и для систем с правой преобразующей матрицей $R(x,t)$, не зависящей от переменной $u$, условие 8) автоматически выполняется. В общем случае для проверки условия 8) за постоянную $\mathcal{M}$ можно взять величину, меньшую ${{\mathcal{M}}_{1}}$, где ${{\mathcal{M}}_{1}} = (1 - \rho {{\left\| {C(x,t,u)} \right\|}_{{C(U)}}}){\text{/}}({{\left\| {\omega (x,t)} \right\|}_{ * }})$.

Список литературы

Соболев С.Л. Об одной новой задаче математической физики // Изв. АН СССР. Сер. матем. 1954. Т. 18. № 1. С. 3–50.
Демиденко Г.А., Успенский С.В. Уравнения и системы, не разрешенные относительно старшей производной. Новосибирск: Научн. книга, 1998.
Рущинский В.М. Пространственные линейные и нелинейные модели котлогенераторов // Вопросы идентификации и моделирования. 1968. С. 8–15.
Soto M. Selva, Tischendorf C. Numerical analysis of DAEs from coupled circuit and semiconductor simulation // Appl. Numer. Math. 2005. № 53. P. 471–488.
Lucht W. Partial differential-algebraic systems of second order with symmetric convection // Appl. Numer. Math. 2005. № 53. P. 357–371.
Гайдомак С.В. Об устойчивости неявной сплайн-коллокационной разностной схемы для линейных дифференциально-алгебраических уравнений с частными производными // Ж. вычисл. матем. и матем. физ. 2013. Т. 53. № 9. С. 1460–1479.
Гайдомак С.В. Об одной краевой задаче для линейной параболической системы первого порядка // Ж. вычисл. матем. и матем. физ. 2014. Т. 54. С. 608–618.
Гайдомак С.В. Об одном алгоритме численного решения линейной дифференциально-алгебраической системы уравнений в частных производных произвольного индекса // Ж. вычисл. матем. и матем. физ. 2015. Т. 55. № 9. С. 1530–1544.
Svinina S.V. Stability of a Spline Collocation Difference Scheme for a Quasi-Linear Differential Algebraic system of First-Order Partial Differential Equations // Computational Mathematics and Mathematical Physics. 2018. T. 58. № 11. C. 1775–1791.
Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений и их приложения к газовой динамике. М.: Наука, 1978.
Курант P., Гильберт Д. Методы математической физики. Т. 2. М.–Л.: Гостехтеориздат, 1933.
Петровский И.Г. Лекции об уравнениях с частными производными. Л.: Гос. изд. технико-теоретич. литературы, 1950.
Канторович Л.В., Акилов Г.П. Функциональный анализ. Издание второе. М.: Наука, 1977.
Красносельский М.А., Вайникко Г.М., Забрейко П.П., Рутицкий Я.Б., Стеценко В.Я. Приближенное решение операторных уравнений. М.: Наука, 1969.
Гантмахер Ф.Р. Теория матриц. М.: Физматлит, 2004.
Олейник О.А., Вентцель Т.Д. Первая краевая задача и задача Коши для квазилинейных уравнений параболического типа // Матем. сборник. 1957. Т. 41(83). № 1. С. 105–128.
Свинина С.В., Свинин А.К. Об одной начально-краевой задаче для полулинейной дифференциально-алгебраической системы уравнений в частных производных индекса (1,0) // Известия вузов. Математика. 2019. № 5. С. 70–82.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал