1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 59, № 12, 2019

Журнал вычислительной математики и математической физики, 2019, T. 59, № 12, стр. 2155-2174

О взаимодействии граничных особых точек в задаче Дирихле для эллиптического уравнения с кусочно-постоянными коэффициентами в плоской области

А. М. Боговский 1, *, В. Н. Денисов 1, **

1 МГУ, ф-т ВМК
119991 Москва, Ленинские горы, Россия

* E-mail: abogovski@gmail.com
** E-mail: vdenisov2008@yandex.ru

Поступила в редакцию 30.05.2019
После доработки 01.07.2019
Принята к публикации 08.07.2019

Полный текст (PDF)

Аннотация

Для эллиптического уравнения в дивергентной форме с разрывным скалярным кусочно-постоянным коэффициентом в неограниченной области $\Omega \subset {{\mathbb{R}}^{2}}$ с кусочно-гладкой некомпактной границей и гладкими линиями разрыва коэффициента исследуется эффект ${{L}_{p}}$-взаимодействия конечной и бесконечной особых точек слабого решения задачи Дирихле в функциональном классе с первыми производными из ${{L}_{p}}(\Omega )$ во всей шкале значений показателя $p \in (1,\infty )$. Библ. 9. Фиг. 6.

Ключевые слова: эллиптическое уравнение в дивергентной форме, разрывный кусочно-постоянный коэффициент, неограниченная область, кусочно-гладкая некомпактная граница, гладкие линии разрыва коэффициента, задача Дирихле, слабое решение с первыми производными из ${{L}_{p}}$, взаимодействие особенностей.

ВВЕДЕНИЕ

В неограниченной плоской области $\Omega \subset {{\mathbb{R}}^{2}}$ с кусочно-гладкой некомпактной границей $\partial \Omega $, имеющей один выход на бесконечность и состоящей из конечного числа гладких кривых, рассматривается краевая задача Дирихле для эллиптического уравнения в дивергентной форме с разрывным скалярным кусочно-постоянным коэффициентом $\varkappa > 0$, имеющим конечное число подобластей непрерывности в $\Omega $. Задача Дирихле рассматривается в слабой постановке, соответствующей функциональному классу решений с первыми производными из ${{L}_{p}}$ во всей шкале значений показателя $p \in (1,\infty )$.

Особые точки $\partial \Omega $, т.е. точки негладкости, предполагаются угловыми с ненулевыми углами. Линии разрыва коэффициента $\varkappa $ предполагаются гладкими и допускаются их некасательные пересечения с $\partial \Omega $, отличные от касаний. При этом допускаются случаи вхождения в граничную точку, в том числе и угловую, любого конечного числа линий разрыва. В частности, два конца одной ограниченной линии разрыва могут исходить из одной и той же граничной точки, в том числе и угловой, которая в таком случае будет угловой еще и для самой линии разрыва, если рассматривать ее как ограниченную замкнутую кусочно-гладкую кривую. Допускаются также и случаи угловых граничных точек без входящих в них линий разрыва. Конечный набор конечных особых точек слабого решения состоит из угловых точек $\partial \Omega $ и тех точек гладкости $\partial \Omega $, в которые входит одна или несколько гладких линий разрыва коэффициента $\varkappa $.

Бесконечной угловой особой точкой будем называть связную компоненту окрестности бесконечности в $\Omega $ с образующими ненулевой угол асимптотами $\partial \Omega $. Такое определение допускает области с несколькими выходами на бесконечность. Гладкие линии разрыва коэффициента $\varkappa $ могут выходить из бесконечной особой точки и возвращаться в нее.

Ради простоты пересечения и самопересечения линий разрыва не допускаются. В статье рассматриваются только модельные особые точки, допускающие локальное разделение переменных в некоторой своей окрестности, где сама граница $\partial \Omega $ и линии разрыва $\varkappa $ представлены отрезками прямых, исходящими из особой точки. Переход от модельной задачи к общему случаю производится по стандартной схеме с использованием в основном известных ${{L}_{p}}$-оценок и теоремы об устойчивости индекса при малых возмущениях в операторной норме. Известное авторам достаточно простое обоснование такого перехода представляет лишь учебно-методический интерес и публикуется отдельно.

Известно, что для области, имеющей только конечные или только бесконечные особые точки, размерность ядра носит аддитивный характер, складываясь из общей суммы размерностей нетривиальных ядер, соответствующих особым точкам по отдельности. Принципиально иная картина возникает, когда область имеет сразу оба типа особых точек: конечные и бесконечные, между которыми при определенных сочетаниях параметров задачи возникает эффект ${{L}_{p}}$-взаимодействия, обнуляющий размерность ядра, и в общем случае существенно зависящий от значения показателя $p$. В статье рассматривается простейший случай ${{L}_{p}}$-взаимодействия одной конечной и одной бесконечной особых точек с одним и тем же единственным на $(0,1)$ собственным значением $\lambda $, общим для двух, возможно различных, задач Штурма–Лиувилля. Установлено, что при любом значении показателя $p \in (1,\infty )$ слабое решение задачи единственно в классе с первыми производными из ${{L}_{p}}(\Omega )$, тогда как наличие лишь одной особой точки означает неединственность при $1 < p < 2{\text{/}}(1 + \sqrt \lambda )$ в случае конечной особой точки, или при $p > 2{\text{/}}(1 - \sqrt \lambda )$ – в случае бесконечной.

Эллиптические краевые задачи с разрывными коэффициентами лежат, например, в основе расчета критичности многокомпонентных термоизоляционных покрытий, когда наличие особой точки у решения стационарной задачи теплопроводности означает неограниченность плотности потока тепла в окрестности такой точки. Среди других известных важных приложений нельзя не упомянуть и расчет критичности ядерных реакторов (см. [1], [2]). В частности, несомненный интерес представляют необходимые и достаточные условия неограниченности плотности стационарного потока нейтронов в окрестности точек негладкости границы, разделяющей участки непрерывности кусочно-постоянной плотности коэффициента диффузии нейтронов.

Из огромного количества публикаций, посвященных исследованиям эллиптических краевых задач с разрывными коэффициентами, упомянем только следующие три, наиболее близкие как по поставленным целям исследований, так и по используемым подходам и применяемым методам. В классе сильных решений с односторонней cоболевской гладкостью $W_{2}^{2}(\Omega )$ и условиями сопряжения на гладких линиях разрыва та же краевая задача для ограниченной области $\Omega \in {{\mathbb{R}}^{2}}$ рассматривалась в [3], [4]. Слабые решения той же краевой задачи с первыми производными из ${{L}_{p}}(\Omega )$ для ограниченной области $\Omega \in {{\mathbb{R}}^{2}}$ изучались также в [5].

Статья состоит из трех разделов. В разд. 1 к классической постановке рассматриваемой задачи Дирихле добавляется ее слабая постановка в смысле интегрального тождества для класса решений с первыми производными из ${{L}_{p}}(\Omega )$, которая эквивалентна ее слабой операторной постановке с эллиптическим оператором в дивергентной форме с разрывным скалярным кусочно-постоянным коэффициентом.

Разд. 2 посвящен задаче Штурма–Лиувилля общего вида, включающей все необходимые частные случаи, возникающие при разделении переменных в локальных полярных координатах для каждого из случаев локализации в интегральном тождестве слабой постановки. Для общего оператора Штурма–Лиувилля минимизацией отношения Рэлея устанавливается существование ортогонального базиса из собственных функций в весовом пространстве ${{L}_{{2,\varkappa }}}(0,\alpha )$ с разрывным кусочно-постоянным весом $\varkappa > 0$. Особо отметим, что использование при разделении переменных весового пространства Лебега позволяет исключить появление несамосопряженных операторов Штурма–Лиувилля, что принципиально упрощает решение поставленной краевой задачи. Приведение оператора Штурма–Лиувилля к нормальному лиувиллеву виду позволяет легко установить сходимость ряда из отрицательных степеней его собственных значений. Устанавливаются также некоторые полезные свойства собственных функций и вводится качественная классификация особых точек слабого решения.

Разд. 3 целиком посвящен исследованию эффекта ${{L}_{p}}$-взаимодействия особенностей слабого решения функционального класса с первыми производными из ${{L}_{p}}(\Omega )$. Установлено, что эффект взаимодействия конечной и бесконечной особых точек возможен для большого числа типов особенностей и не требует глобального разделения переменных. До сих пор для построения подобных примеров ${{L}_{p}}$-взаимодействия особенностей решений эллиптических краевых задач еще с середины 80-х годов прошлого века использовалась очевидная возможность глобального разделения переменных для бесконечного угла на плоскости в полярных координатах.

1. ПОСТАНОВКА ЗАДАЧИ ДИРИХЛЕ

Опираясь на классическую постановку краевой задачи для эллиптического уравнения с разрывными коэффициентами в дивергентной форме, выводим определение обобщенного решения этой краевой задачи с однородными условиями Дирихле для класса решений с первыми производными из ${{L}_{p}}$ и устанавливаем корректность этого определения.

1.1. Классическая постановка

Классическая постановка задачи Дирихле приводится здесь для наглядности сравнения со слабой, и поэтому формулируется лишь для ограниченной области $\Omega \subset {{\mathbb{R}}^{2}}$, в которой выполняется эллиптическое уравнение в дивергентной форме:

(1.1)
${\text{div}}(\varkappa \nabla u) = f(x),$
с кусочно-постоянным скалярным коэффициентом $\varkappa $ и однородным краевым условием Дирихле
(1.2)
${{\left. u \right|}_{{\partial \Omega }}} = 0.$
Линии разрыва коэффициента $\varkappa $ предполагаются ${{C}^{1}}$-гладкими, тогда как граница $\partial \Omega $ является кусочно ${{C}^{1}}$-гладкой с конечным числом угловых точек, из которых могут выходить (но не обязательно) линии разрыва коэффициента $\varkappa $. При этом одни линии разрыва могут соединять разные угловые точки $\partial \Omega $, тогда как другие могут оказаться замкнутыми, т.е. выходить из угловой точки и возвращаться назад. Точка пересечения гладких линий разрыва относится к особенностям, которые в настоящей работе не рассматриваются.

Через ${\text{\{ }}{{\Gamma }_{i}}{\text{\} }}$ будем обозначать ${{C}^{1}}$-гладкие линии разрыва, а через ${\text{\{ }}{{\Omega }_{j}}{\text{\} }}$ – подобласти, на которые линии разрыва делят $\Omega $. На ${\text{\{ }}{{\Gamma }_{i}}{\text{\} }}$ выполнены условия сопряжения, т.е. условия непрерывности самого решения и его производной по конормали:

(1.3)
$\begin{gathered} \mathop {\left. u \right|}\nolimits_{\Gamma _{i}^{ - }} = \mathop {\left. u \right|}\nolimits_{\Gamma _{i}^{ + }} , \\ \varkappa \mathop {\left. {\frac{{\partial u}}{{\partial n}}{\kern 1pt} } \right|}\nolimits_{\Gamma _{i}^{ - }} = \varkappa \mathop {\left. {\frac{{\partial u}}{{\partial n}}{\kern 1pt} } \right|}\nolimits_{\Gamma _{i}^{ + }} , \\ \end{gathered} $
где знаки плюс и минус указывают на противоположные берега линий разрыва ${\text{\{ }}{{\Gamma }_{i}}{\text{\} }}$ коэффициента $\varkappa $.

Классическим решением задачи сопряжения (1.1)–(1.3) будем называть функцию , для которой

• ${{\left. u \right|}_{{{{\Omega }_{j}}}}} = {{{v}}_{j}} \in {{C}^{2}}({{\Omega }_{j}}) \cap {{C}^{1}}({{\bar {\Omega }}_{j}})\;\forall j;$

• в каждой подобласти ${{\Omega }_{j}}$ выполняется уравнение (1.1);

• в области $\Omega $ выполнены все условия сопряжения (1.3).

1.2. Слабая постановка

На пространстве Соболева $L_{p}^{1}(\Omega )$ для произвольной области $\Omega \subset {{\mathbb{R}}^{2}}$ введем норму

${{\left\| u \right\|}_{{L_{p}^{1}(\Omega )}}}\mathop = \limits^{{\text{def}}} {{\left\| {\nabla u} \right\|}_{{{{L}_{p}}(\Omega )}}} + {{\left\| u \right\|}_{{{{L}_{p}}(\omega )}}},\quad 1 < p < \infty ,$
где $\omega $ – фиксированная произвольная ограниченная подобласть $\omega \subset \Omega $. Определим пространство Соболева $ \circ {{C}^{\infty }}(\Omega )$ как замыкание в $L_{p}^{1}(\Omega )$ его подпространства финитных бесконечно дифференцируемых в $\Omega $ функций $ \circ {{C}^{\infty }}(\Omega )$, т.е.
$ \circ L_{p}^{1}(\Omega )\mathop = \limits^{{\text{def}}} {{\overline { \circ {{C}^{\infty }}(\Omega )} }^{{L_{p}^{1}(\Omega )}}}.$
На $ \circ {{C}^{\infty }}(\Omega )$ удобно ввести эквивалентную норму $\left\| u \right\| = {{\left\| {\nabla u} \right\|}_{{{{L}_{p}}(\Omega )}}}$, не зависящую от выбора подобласти $\omega \subset \Omega $. Всюду в дальнейшем пространство Соболева $ \circ L_{p}^{1}(\Omega )$ будет рассматриваться как банахово пространство с нормой

${{\left\| u \right\|}_{{L_{p}^{1}(\Omega )}}}\mathop = \limits^{{\text{def}}} {{\left\| {\nabla u} \right\|}_{{{{L}_{p}}(\Omega )}}}.$

Пространство линейных непрерывных на $ \circ L_{p}^{1}(\Omega )$ функционалов определим как двойственное к $ \circ L_{p}^{1}(\Omega )$, т.е.

$ \circ L_{p}^{{ - 1}}(\Omega )\mathop = \limits^{{\text{def}}} (L_{q}^{1}(\Omega )){\kern 1pt} {\text{*}},\quad \frac{1}{p} + \frac{1}{q} = 1.$
Понимая обобщенную дивергенцию в смысле $\mathcal{D}{\text{'}}(\Omega )$, рассмотрим дифференциальный оператор
(1.4)
$L = {\text{div}}(\varkappa \nabla \cdot ): \circ L_{p}^{1}(\Omega ) \to \circ L_{p}^{{ - 1}}(\Omega ),$
который позволяет заменить классическую форму задачи Дирихле ее операторным аналогом:

$Lu = f \in \circ L_{p}^{{ - 1}}(\Omega ).$

Операторная постановка проясняет связь размерностей $dim\;ker$ и $dim{\text{coker}}$ ядра и коядра

$\begin{gathered} kerL\mathop = \limits^{{\text{def}}} {\text{\{ }}u \in \circ L_{p}^{1}(\Omega )\,|\,Lu = 0{\text{\} }}, \\ {\text{coker}}\;L\mathop = \limits^{{\text{def}}} \circ L_{p}^{{ - 1}}(\Omega ){\text{/\{ }}Lu\,|\,u \in \circ L_{p}^{1}(\Omega ){\text{\} }} \\ \end{gathered} $
линейного оператора (1.4) в случае, когда эти размерности конечны. В свою очередь, операторная постановка эквивалентна слабой ${{L}_{p}}$-постановке той же задачи Дирихле
$\int\limits_\Omega {(\varkappa \nabla u} ,\nabla \psi )dx = - f(\psi )\quad \forall \psi \in \circ L_{p}^{1}(\Omega ),\quad \frac{1}{p} + \frac{1}{q} = 1,$
для класса слабых решений $u \in \circ L_{p}^{1}(\Omega )$. При этом, как хорошо известно, для всякого функционала $f \in \circ L_{p}^{{ - 1}}(\Omega )$ найдется векторное поле ${\mathbf{F}} \in {{{\mathbf{L}}}_{p}}(\Omega )$ такое, что $f = \operatorname{div} {\mathbf{F}}$ в смысле $\mathcal{D}{\text{'}}(\Omega )$ с оценкой

${{\left\| {\mathbf{F}} \right\|}_{{{{{\mathbf{L}}}_{p}}(\Omega )}}} \leqslant {{\left\| f \right\|}_{{ \circ L_{p}^{{ - 1}}(\Omega )}}}.$

Определение 1. Для произвольной области $\Omega \subset {{\mathbb{R}}^{2}}$ элемент $u \in \circ L_{p}^{1}(\Omega )$ называют слабым решением задачи Дирихле (1.1), (1.2), если выполняется интегральное тождество

(1.5)
$\int\limits_\Omega {\varkappa (x)(\nabla u,\nabla \psi )dx} = \int\limits_\Omega {({\mathbf{F}},\nabla \psi )} dx\quad \forall \psi \in \circ L_{q}^{1}(\Omega )$
при заданной вектор-функции ${\mathbf{F}} \in {{{\mathbf{L}}}_{p}}(\Omega )$, где $( \cdot , \cdot )$ – скалярное произведение в ${{\mathbb{R}}^{2}}$, $q = p{\text{/}}(p - 1)$ – показатель, сопряженный к $p \in (1,\infty )$.

Отметим, что в случае ограниченной области $\Omega \subset {{\mathbb{R}}^{2}}$ класс пробных функций $ \circ L_{q}^{1}(\Omega )$ может быть заменен на пространство Соболева $ \circ W_{q}^{1}(\Omega )$.

Замечание 1. При построении примеров несуществования слабых решений можно ограничиться рассмотрением правых частей $\operatorname{div} {\mathbf{F}} = f \in \circ {{C}^{\infty }}(\Omega )$. В таком случае тождество (1.5) примет более простой вид:

(1.6)
$\int\limits_\Omega \varkappa (x)(\nabla u,\nabla \psi )dx = - \int\limits_\Omega f \psi dx\quad \forall \psi \in \circ L_{q}^{1}(\Omega ).$

2. ЗАДАЧА ШТУРМА–ЛИУВИЛЛЯ

Кусочно-постоянный коэффициент $\varkappa = \varkappa (x) > 0$ с конечным числом разрывов будет использоваться в качестве весовой функции пространства Лебега ${{L}_{{2,\varkappa }}}(0,\alpha )$ со скалярным произведением

${{(u,{v})}_{\varkappa }}_{ = }\int\limits_0^\alpha \varkappa (x)u(x){v}(x)dx,$
которое порождает весовую норму

${{\left\| u \right\|}_{{2,\varkappa }}} = \mathop {\left( {\int\limits_0^\alpha \varkappa (x){{{\left| {u(x)} \right|}}^{2}}dx} \right)}\nolimits^{1/2} .$

На весовом пространстве Лебега ${{L}_{{2,\varkappa }}}(0,\alpha )$ введем операцию слабого дифференцирования

(2.1)
$L = \frac{1}{\varkappa }\left( {\varkappa u{\text{'}}} \right){\kern 1pt} {\text{'}},$
где штрих означает слабое дифференцирование на ${{L}_{{1,{\text{loc}}}}}(\mathbb{R})$ или, в более широком понимании, дифференцирование в смысле $\mathcal{D}{\text{'}}(\mathbb{R})$ с требованием регулярности обобщенной производной.

Рассматривая операцию дифференцирования (2.1) на подпространстве

${{D}_{L}}\mathop = \limits^{{\text{def}}} {\text{\{ }}u \in \circ W_{2}^{1}(0,\alpha ):\varkappa u{\text{'}} \in \circ W_{2}^{1}(0,\alpha ){\text{\} }} \subset {{L}_{{2,\varkappa }}}(0,\alpha ),$
приходим к замкнутому неограниченному дифференциальному оператору

(2.2)
$L = \frac{1}{\varkappa }\left( {\varkappa u{\text{'}}} \right){\kern 1pt} ':{{D}_{L}} \subset {{L}_{{2,\varkappa }}}(0,\alpha ) \to {{L}_{{2,\varkappa }}}(0,\alpha ).$

Справедлива следующая

Лемма 1. Дифференциальный оператор (2.2) будет самосопряженным при любом выборе кусочно-постоянной функции $\varkappa = \varkappa (x) > 0$ с конечным числом разрывов.

Доказательство. Обозначим через ${\text{\{ }}{{I}_{j}}{\text{\} }}_{{j = 1}}^{m}$ совокупность $m \geqslant 2$ интервалов ${{I}_{j}} \subset (0,\alpha )$, на которых ступенчатая функция непрерывна и принимает постоянные положительные значения ${\text{\{ }}{{\varkappa }_{j}}{\text{\} }}_{{j = 1}}^{m}$. Ввиду очевидной замкнутости оператора (2.2), для доказательства леммы достаточно убедиться в совпадении с ${{D}_{L}}$ области определения сопряженного оператора (подробности см. в главе 13 монографии [6])

(2.3)
${{D}_{{L*}}}\mathop = \limits^{{\text{def}}} \left\{ {{v} \in {{L}_{{2,\varkappa }}}(0,\alpha )\,|\,\exists f \in {{L}_{{2,\varkappa }}}(0,\alpha ):{{{(Lu,{v})}}_{\varkappa }} = {{{(u,f)}}_{{_{\varkappa }}}}\;\;\forall u \in {{D}_{L}}} \right\}.$
При этом достаточно убедиться лишь в том, что (2.3) означает принадлежность ${v} \in \circ W_{2}^{1}(0,\alpha )$, $\varkappa {v}{\kern 1pt} {\text{'}} \in W_{2}^{1}(0,\alpha )$.

Действительно, выбирая в (2.3) пробные функции $u \in \circ {{C}^{\infty }}({{I}_{j}})$, $1 \leqslant j \leqslant m$, приходим к тождествам

$(Lu,{v}) = {{\varkappa }_{j}}\int\limits_0^\alpha {u{\text{''}}} {\kern 1pt} {v}dx = {{\varkappa }_{j}}\int\limits_0^\alpha u fdx\quad \forall u \in \circ {{C}^{\infty }}({{I}_{j}}),$
из которых сразу же следует принадлежность ${v} \in W_{2}^{2}({{I}_{j}})$.

Возвращаясь теперь к определению (2.3) и выбирая в нем пробные функции $u \in {{D}_{L}} \subset \circ {{C}^{\infty }}(0,\alpha )$ так, чтобы $k$-й стык интервалов ${\text{\{ }}{{I}_{j}}{\text{\} }}$ был внутренней точкой замкнутого множества ${\text{supp}}\;u$, не пересекающегося с остальными стыками и концами отрезка $[0,\alpha ]$, получаем тождества

$\int\limits_{{{I}_{k}}} {(\varkappa u{\text{'}})} {\kern 1pt} {\text{'}}{v}dx + \int\limits_{{{I}_{{k + 1}}}} {(\varkappa u{\kern 1pt} {\text{'}}){\kern 1pt} {\text{'}}} {\kern 1pt} {v}dx = \int\limits_{{{I}_{k}}} \varkappa ufdx + \int\limits_{{{I}_{{k + 1}}}} \varkappa ufdx\quad \forall u \in \circ {{C}^{\infty }}({\text{Int}}({{\bar {I}}_{k}} \cup {{\bar {I}}_{{k + 1}}})),$
где, как уже установлено, имеем
$\begin{gathered} {v} \in W_{2}^{2}({{I}_{k}}),\quad {v}{\kern 1pt} {\text{''}} = f\quad {\text{п}}.{\text{в}}.\;{\text{на}}\quad {{I}_{k}}, \\ {v} \in W_{2}^{2}({{I}_{{k + 1}}}),\quad {v}{\kern 1pt} {\text{''}} = f\quad {\text{п}}.{\text{в}}.\;{\text{на}}\quad {{I}_{{k + 1}}}, \\ \end{gathered} $
для каждого $k$-го стыка ступенек ${{\varkappa }_{k}}$ и ${{\varkappa }_{{k + 1}}}$, $1 \leqslant k \leqslant m - 1$, $m \geqslant 2$. В силу вложений $W_{2}^{2}({{I}_{k}})$ и $W_{2}^{2}({{I}_{{k + 1}}})$ в ${{C}^{1}}({{\bar {I}}_{k}})$ и ${{C}^{1}}({{\bar {I}}_{{k + 1}}})$, соответственно, интегрированием по частям в тождестве с помощью подходящего выбора пробных функций $u \in \circ {{C}^{\infty }}({\text{Int}}({{\bar {I}}_{k}} \cup {{\bar {I}}_{{k + 1}}}))$ получаем равенства следов ${v}$ и $\varkappa {v}{\kern 1pt} {\text{'}}$ по разные стороны $k$-го стыка, означающие непрерывность ${v}$ и $\varkappa {v}{\kern 1pt} {\text{'}}$ в окрестности указанного стыка. Поскольку такая непрерывность имеет место для каждого стыка, заключаем, что функции ${v}$ и $\varkappa {v}{\kern 1pt} {\text{'}}$ непрерывны на $[0,\alpha ]$, что означает их принадлежность к пространству $W_{2}^{1}(0,\alpha )$.

Повторяя процедуру интегрирования по частям для ${v} \in W_{2}^{1}(0,\alpha )$ с условием $\varkappa {v}{\kern 1pt} {\text{'}} \in W_{2}^{1}(0,\alpha )$ с условием $\varkappa {v}{\kern 1pt} {\text{'}} \in W_{2}^{1}(0,\alpha )$ с использованием краевых условий $u(0) = u(\alpha ) = 0$, получаем краевые условия ${v}(0) = {v}(\alpha ) = 0$, означающие принадлежность ${v} \in \circ W_{2}^{1}(0,\alpha )$. Таким образом, установлено совпадение ${{D}_{{L{\text{*}}}}} = {{D}_{L}}$, означающее самосопряженность оператора (2.2), что завершает доказательство леммы.

Рассмотрим теперь вопрос о возможных постановках задачи Штурма–Лиувилля для оператора (2.2) с заданным ступенчатым коэффициентом $\varkappa $, разрывы которого заведомо исключают классическую постановку. Очевидно при этом, что для оператора (2.2) с областью определения наиболее естественной будет слабая постановка

(2.4)
$\begin{gathered} (\varkappa u{\text{'}}){\kern 1pt} {\text{'}} + \lambda \varkappa u = 0,\quad x \in (0,\alpha ), \\ u \in {{D}_{L}}\mathop = \limits^{{\text{def}}} {\text{\{ }}u \in \circ W_{2}^{1}(0,\alpha ):\varkappa u{\text{'}} \in W_{2}^{1}(0,\alpha ){\text{\} }}. \\ \end{gathered} $
Однако приведение урвнения к нормальной лиувиллевой форме превращает слабую постановку (2.4) в полуклассическую для другого отрезка с решением класса ${{C}^{1}}$, имеющим вторую кусочно-непрерывную производную с другими точками разрыва, но с теми же собственными значениями. Точнее, справедлива следующая

Лемма 2. Слабая постановка задачи Штурма–Лиувилля (2.4) со ступенчатым коэффициентом $\varkappa > 0$ эквивалентна полуклассической постановке

(2.5)
$\begin{gathered} {v}{\kern 1pt} {\text{''}} + \lambda \tilde {\varkappa }{v} = 0,\quad 0 < x < \beta , \hfill \\ {v}(0) = {v}(\beta ) = 0,\quad \beta \mathop = \limits^{{\text{def}}} \int\limits_0^\alpha {\frac{{dt}}{{\varkappa (t)}}} ; \hfill \\ \end{gathered} $
с теми же собственными значениями $\lambda $ и решением ${v} \in {{C}^{1}}[0,\beta ]$, имеющим на $(0,\beta )$ кусочно-непрерывную производную ${v}{\kern 1pt} {\text{''}}$, точки разрыва которой определены некоторым ступенчатым коэффициентом $\tilde {\varkappa } > 0$.

Доказательство. Нетрудно убедиться, что уравнение (2.4) проводится к нормальной лиувиллевой форме заменой

$u(x) = {v}\left( {\int\limits_0^x {\frac{{dt}}{{\varkappa (t)}}} } \right),\quad 0 < x < \alpha .$
Действительно, вводя новую переменную
$\xi = \int\limits_0^x {\frac{{dt}}{{\varkappa (t)}}} ,\quad \xi (x) \in [0,\beta ]\quad \forall x \in [0,\alpha ],\quad \beta \mathop = \limits^{{\text{def}}} \int\limits_0^\alpha {\frac{{dt}}{{\varkappa (t)}}} ,$
приходим к задаче Штурма–Лиувилля
$\begin{gathered} {v}{\kern 1pt} {\text{''}}(\xi ) + \lambda \tilde {\varkappa }(\xi ){v}(\xi ) = 0,\quad 0 < \xi < \beta , \\ {v}(0) = {v}(\beta ) = 0, \\ \end{gathered} $
с положительным коэффициентом $\tilde {\varkappa }(\xi )\mathop = \limits^{{\text{def}}} {{\varkappa }^{2}}(x(\xi ))$, где монотонно возрастающая непрерывная кусочно-линейная функция $x = x(\xi )$ определена как обратная к монотонно возрастающей непрерывной кусочно-линейной функции $\xi = \xi (x)$. Но функция $\varkappa = \varkappa (x)$ была определена как ступенчатая на отрезке $[0,\alpha ]$, поэтому ступенчатой будет и функция $\tilde {\varkappa } = \tilde {\varkappa }(\xi ) > 0$ на отрезке $[0,\beta ]$.

Лемма доказана.

2.1. Ортогональный базис из собственных функций

Рассмотрим теперь полуклассическую задачу Штурма–Лиувилля (2.5) в классе функций ${v} \in {{C}^{1}}[0,\beta ]$, вторые производные которых имеют конечное число линий разрывов I рода, совпадающих в точках разрыва с положительной ступенчатой функцией $\tilde {\varkappa } = \tilde {\varkappa }(\xi )$.

Теорема 1. Геометрическая кратность всех собственных значений задачи Штурма–Лиувилля в полуклассической постановке (2.5) равна единице.

Доказательство. Предположим, что уравнение $u{\text{''}} = \lambda \tilde {\varkappa }u$ имеет два линейно независимых решения ${{u}_{1}}$, ${{u}_{2}}$. Запишем производную опеределителя Вронского для этого уравнения

$\frac{{dW}}{{d\xi }} = \frac{d}{{d\xi }}\left| {\begin{array}{*{20}{c}} {{{u}_{1}}}&{{{u}_{2}}} \\ {u_{1}^{'}}&{u_{2}^{'}} \end{array}} \right| = \left| {\begin{array}{*{20}{c}} {u_{1}^{'}}&{u_{2}^{'}} \\ {u_{1}^{'}}&{u_{2}^{'}} \end{array}} \right| + \left| {\begin{array}{*{20}{c}} {{{u}_{1}}}&{{{u}_{2}}} \\ {u_{1}^{{''}}}&{u_{2}^{{''}}} \end{array}} \right| = 0 + \left| {\begin{array}{*{20}{c}} {{{u}_{1}}}&{{{u}_{2}}} \\ { - \tilde {\varkappa }u_{1}^{'} + \lambda {{u}_{1}}}&{ - \tilde {\varkappa }u_{2}^{'} + \lambda {{u}_{2}}} \end{array}} \right|.$
Вычитая первую строку, домноженную на $\lambda $ ко второй, получаем ОДУ
$\frac{{dW}}{{d\xi }} = \left| {\begin{array}{*{20}{c}} {{{u}_{1}}}&{{{u}_{2}}} \\ { - \tilde {\varkappa }u_{1}^{'}}&{ - \tilde {\varkappa }u_{2}^{'}} \end{array}} \right| = - \tilde {\varkappa }W.$
Общее решение ОДУ
$W(\xi ) = Cexp\left\{ { - \int\limits_0^\xi {\tilde {\varkappa }} (t)dt} \right\},\quad C \in \mathbb{R},\quad \xi \in (0,\beta ),$
удовлетворяет граничным условиям лишь при $W(\xi ) = 0$ $\xi \in (0,\beta )$.

Теорема доказана.

Значит, в силу эквивалентности полуклассической постановки (2.5) задачи Штурма–Лиувилля исходной (2.4) верно

Следствие 1. Геометрическая кратность всех собственных значений задачи Штурма–Лиувилля (2.4) равна единице.

Теорема 2. Существует полная в $ \circ W_{{2,\varkappa }}^{1}(0,\alpha )$ система собственных функций задачи Штурма–Лиувилля (2.4).

Доказательство. На пространстве Соболева $ \circ W_{{2,\varkappa }}^{1}(0,\alpha )$ с весовой нормой

${{\left\| u \right\|}_{{ \circ W_{{2,\varkappa }}^{1}(0,\alpha )}}}\mathop = \limits^{{\text{def}}} {{\left\| {u{\text{'}}} \right\|}_{{{{L}_{{2,}}}\varkappa (0,\alpha )}}}$
рассмотрим отношение Рэлея, т.е. функционал вида
$\Lambda (u)\mathop = \limits^{{\text{def}}} \frac{{\int\limits_0^\alpha \varkappa {{{\left| {u{\text{'}}(x)} \right|}}^{2}}dx}}{{\int\limits_0^\alpha \varkappa {{{\left| {u(x)} \right|}}^{2}}dx}},\quad u \in \circ W_{{2,\varkappa }}^{1}(0,\alpha ){\backslash \{ }0{\text{\} }}.$
Так как $\varkappa $ – кусочно-постоянная с конечным числом разрывов, то $0 < {{\varkappa }_{ * }} < \varkappa (x) < \varkappa * < \infty $. В силу весового варианта неравенства Фридрихса имеем
$\mathop {\left( {\int\limits_0^\alpha \varkappa {{{\left| u \right|}}^{2}}dx} \right)}\nolimits^2 \leqslant {{C}_{0}}\int\limits_0^\alpha \varkappa {{\left| {u{\kern 1pt} {\text{'}}} \right|}^{2}}dx\quad \forall u \in \circ W_{{2,\varkappa }}^{1}(0,\alpha )$
с наилучшей, т.е. наименьшой, положительной постоянной ${{C}_{0}}$, и получаем $\Lambda (u) \geqslant \tfrac{1}{{{{C}_{0}}}}$. Таким образом, существует точная нижняя грань
${{m}_{0}}\;\mathop = \limits^{{\text{def}}} \;inf\{ \Lambda (u):u \in \circ W_{{2,\varkappa }}^{1}(0,\alpha )\} = \frac{1}{{{{C}_{0}}}}.$
Поэтому найдется минимизирующая последовательность таких $\{ {{u}_{{1,n}}}\} _{{n = 1}}^{\infty }$ элементов ${{u}_{{1,n}}} \in \circ W_{{2,\varkappa }}^{1}(0,\alpha )$, что
$\mathop {lim}\limits_{n \to \infty } \Lambda ({{u}_{{1,n}}}) = {{m}_{1}}.$
Вводя нормировку
(2.6)
${{\tilde {u}}_{k}}\mathop = \limits^{{\text{def}}} \frac{{{{u}_{{1,n}}}}}{{{{{\left\| {{{u}_{{1,n}}}} \right\|}}_{{{{L}_{{2,}}}(0,\alpha )}}}}} \Rightarrow {{\left\| {{{{\tilde {u}}}_{k}}} \right\|}_{{{{L}_{{2,\varkappa }}}(0,\alpha )}}} = 1,$
получаем

$\Lambda ({{u}_{{1,n}}}) = \int\limits_0^\alpha {\varkappa (x)} {{\left| {{{{\tilde {u}}}_{{1,n}}}(x)} \right|}^{2}}dx \to {{m}_{0}}\quad {\text{при}}\quad n \to \infty .$

Очевидно, минимизирующая последовательность ${\text{\{ }}{{\tilde {u}}_{n}}{\text{\} }}$ ограничена в $ \circ W_{{2,\varkappa }}^{1}(0,\alpha )$, компактно вложенном в ${{L}_{{2,\varkappa }}}(0,\alpha )$. Поэтому найдется подпоследовательность ${\text{\{ }}{{\tilde {u}}_{{1,{{n}_{m}}}}}{\text{\} }}:{{\tilde {u}}_{{1,{{n}_{m}}}}} \to u$, сходящаяся слабо в $ \circ W_{2}^{1}(0,\alpha )$ и сильно в ${{L}_{{2,\varkappa }}}(0,\alpha )$. При этом слабый предел $u \in \circ W_{{2,\varkappa }}^{1}(0,\alpha )$ удовлетворяет условиям ${{\left\| u \right\|}_{{ \circ W_{{2,\varkappa }}^{1}(0,\alpha )}}} \leqslant {{m}_{0}}$ и ${{\left\| u \right\|}_{{{{L}_{{2,\varkappa }}}(0,\alpha )}}} = 1$ в силу выполнения (2.6). Однако выполнение строго неравенства ${{\left\| u \right\|}_{{ \circ W_{2}^{1}(0,\alpha )}}} < {{m}_{0}}$ невозможно в силу очевидного противоречия

$1 = \left\| u \right\|_{{{{L}_{{2,\varkappa }}}(0,\alpha )}}^{2} \leqslant {{C}_{0}}\left\| {u{\text{'}}} \right\|_{{{{L}_{{2,\varkappa }}}(0,\alpha )}}^{2} < {{C}_{0}} \cdot {{m}_{0}} = 1.$

Таким образом, имеем равенство ${{\left\| u \right\|}_{{ \circ W_{2}^{1}(0,\alpha )}}} = {{m}_{0}}$. А тогда ввиду равенства параллелограмма для гильбертовой нормы подпоследовательность ${\text{\{ }}{{\tilde {u}}_{{{{k}_{j}}}}}{\text{\} }}:{{\tilde {u}}_{{{{m}_{j}}}}} \to u$ сильно в $ \circ W_{{2,\varkappa }}^{1}(0,\alpha )$. Это означает существование ненулевого элемента ${{u}_{1}} \in \circ W_{2}^{1}(0,\alpha )$, на котором достигается нижняя грань функционала $\Lambda $. Рассмотрим функцию

$\varphi (t)\mathop = \limits^{{\text{def}}} \Lambda (u + t{v}) = \frac{{\int\limits_0^\alpha {\varkappa {{{({{u}_{1}} + t{v}{\kern 1pt} {\text{'}}{\kern 1pt} )}}^{2}}} dx}}{{\int\limits_0^\alpha {\varkappa {{{({{u}_{1}} + t{v})}}^{2}}} dx}},\quad t \in \mathbb{R},\quad {v} \in \circ W_{2}^{1}(0,\alpha ).$
Тогда функция $\varphi = \varphi (t)$ при $t = 0$ принимает свое минимальное значение при любом выборе элемента ${v} \in \circ W_{2}^{1}(0,\alpha )$. Поэтому в силу необходимого условия экстремума $\varphi {\kern 1pt} {\text{'}}(0) = 0$ $\forall {v} \in \circ W_{2}^{1}(0,\alpha )$ имеем
$\varphi {\text{'}}(0) = \frac{{2\int\limits_0^\alpha \varkappa u_{1}^{'}{v}{\kern 1pt} {\text{'}}dx}}{{\mathop {\left( {\int\limits_0^\alpha \varkappa u_{1}^{2}dx} \right)}\nolimits^2 }} - 2\frac{{\int\limits_0^\alpha \varkappa {{{(u_{1}^{'})}}^{2}}dx \cdot 2\int\limits_0^\alpha \varkappa u{v}dx}}{{\mathop {\left( {\int\limits_0^\alpha \varkappa u_{1}^{2}dx} \right)}\nolimits^2 }} = 0\quad \forall {v} \in \circ W_{2}^{1}(0,\alpha ).$
Это значит, что на ${{u}_{1}}$ достигается ${{m}_{0}}$:
$\mu _{1}^{2}\;\mathop = \limits^{{\text{def}}} \;\frac{{\int\limits_0^\alpha \varkappa u_{1}^{'}{v}{\kern 1pt} {\text{'}}dx}}{{\int\limits_0^\alpha \varkappa {{u}_{1}}{v}dx}} = {{m}_{0}} \ne 0.$
Так как, согласно следствию 1, геометрическая кратность собственных значений задачи Штурма–Лиувилля (2.4) равна единице, то, накладывая требование ${{\left\| {{{u}_{1}}} \right\|}_{{ \circ W_{{2,\varkappa }}^{1}(0,\alpha )}}} = 1$, получаем единственность собственной функции, соответствующей $\mu _{1}^{2}$.

Линейную оболочку ортонормированной системы собственных функций задачи Штурма–Лиувилля обозначим через $\mathcal{L} = \mathcal{L}({\text{\{ }}{{u}_{j}}{\text{\} }}_{{j = 1}}^{\infty })$ и заметим, что она всюду плотна в $ \circ W_{{2,\varkappa }}^{1}(0,\alpha )$. Действительно, в противном случае $ \circ W_{{2,\varkappa }}^{1}(0,\alpha ) \ominus \mathcal{L}$ будет нетривиальным замкнутым подпространством в $ \circ W_{{2,\varkappa }}^{1}(0,\alpha )$, повторяя на нем использованную выше процедуру минимизации функционала $\Lambda (u)$ и $u \bot \mathcal{L}$, являщуюся собственной функцией, приходим к противоречию.

Теорема доказана.

Поскольку $ \circ W_{2}^{1}(0,\alpha )$ является подпространством, всюду плотным в ${{L}_{2}}(0,\alpha )$, то верно

Следствие 2. Система собственных функций задачи Штурма–Лиувилля является ортогональным базисом в $ \circ W_{{2,\varkappa }}^{1}(0,\alpha )$.

Доказательство. Система полна по теореме 2 и ортогональна в теоремы 1 о единичной геометрической кратности собственных значений.

Следствие доказано.

Следствие 3. Система собственных функций задачи Штурма–Лиувилля является ортогональным базисом в ${{L}_{{2,\varkappa }}}(0,\alpha )$.

Доказательство. Поскольку $ \circ W_{2}^{1}(0,\alpha )$ является подпространством, всюду плотным в ${{L}_{2}}(0,\alpha )$, то система собственных функций полна и в ${{L}_{2}}(0,\alpha )$. Ортогональность при переходе к скалярному произведению ${{L}_{{2,\varkappa }}}$ для собственных функций сохраняется

${{({{u}_{k}},{{u}_{n}})}_{{ \circ {{W}_{{2,\varkappa }}}(0,\alpha )}}} = \int\limits_0^\alpha \varkappa u_{k}^{'}u_{n}^{'}dx = - \int\limits_0^\alpha \varkappa u_{k}^{{''}}{{u}_{n}}dx = {{\lambda }_{k}}\int\limits_0^\alpha \varkappa {{u}_{k}}{{u}_{n}}dx = {{\lambda }_{k}}{{({{u}_{k}},{{u}_{n}})}_{{{{L}_{{2,\varkappa }}}(0,\alpha )}}}.$

Следствие доказано.

Занумеруем собственные функции ${\text{\{ }}{{u}_{k}}{\text{\} }}_{{k = 1}}^{\infty }$ по возрастанию чисел ${{\mu }_{k}} > 0$, которые будем называть корнями.

2.2. Функция Грина

Рассмотрим задачу Штурма–Лиувилля в полуклассической постановке (2.5). Интегрируя уравнение, получаем

(2.7)
${v}(\xi ) + \lambda \int\limits_0^\xi {\tilde {\varkappa }} (\xi ){v}(\xi )d\eta + {{C}_{1}}\xi + {{C}_{2}} = 0,\quad 0 \leqslant \xi \leqslant \beta .$
Из краевых условий ${v}(0) = {v}(\beta ) = 0$ находим ${{C}_{1}} = 0$ и
$\beta {{C}_{1}} = - \lambda \int\limits_0^\beta {(\beta - \eta )\tilde {\varkappa }} (\eta ){v}(\eta )d\eta ,$
откуда и из (2.7) получаем
${v}(\xi ) = - \lambda \int\limits_0^\xi {(\xi - \eta )} \tilde {\varkappa }(\eta ){v}(\eta )d\eta + \lambda \frac{\xi }{\beta }\int\limits_0^\beta {(\beta - \eta )} \tilde {\varkappa }(\eta ){v}(\eta )d\eta $
для всех $\xi \in [0,\beta ]$. А тогда находим
${v}(\xi ) = \lambda \int\limits_0^\xi {\left( {1 - \frac{\xi }{\beta }} \right)} \eta \tilde {\varkappa }{v}d\eta + \lambda \int\limits_\xi ^\beta {\left( {1 - \frac{\eta }{\beta }} \right)} \xi \tilde {\varkappa }{v}d\eta ,\quad 0 \leqslant \xi \leqslant \beta ,$
${v}(\xi ) = \lambda \int\limits_0^\xi {\left( {1 - \frac{\xi }{\beta }} \right)} \eta \tilde {\varkappa }(\eta ){v}(\eta )d\eta + \lambda \int\limits_x {{{i}^{\beta }}} \left( {1 - \frac{\eta }{\beta }} \right)\xi \tilde {\varkappa }(\eta )d\eta ,\quad 0 \leqslant \xi \leqslant \beta .$
Вводя обозначение
$G(\xi ,\eta ) = \left\{ \begin{gathered} \eta \left( {1 - \tfrac{\xi }{\beta }} \right),\quad \eta < \xi , \hfill \\ \xi \left( {1 - \tfrac{\eta }{\beta }} \right),\quad \xi < \eta , \hfill \\ \end{gathered} \right.$
получаем окончательное равенство
${v}(\xi ) = \lambda \int\limits_0^\beta {G(\xi ,\eta )\tilde {\varkappa }(\eta ){v}(\eta )d\eta } ,\quad 0 \leqslant \xi \leqslant \beta ,$
где $G(\xi ,\eta )$ – функция Грина.

2.3. Сходимость рядов степеней собственных значений

Установим сходимость ряда

$\sum\limits_{k = 1}^\infty {\frac{1}{{\lambda _{k}^{2}}}} < \infty $
собственных значений ${\text{\{ }}{{\lambda }_{k}} > 0{\text{\} }}_{{k = 1}}^{\infty }$ оператора Штурма–Лиувилля
$\begin{gathered} L = \frac{1}{\varkappa }\frac{d}{{dx}}\varkappa \frac{d}{{dx}}, \\ {{D}_{L}} = {\text{\{ }}u \in \circ W_{2}^{1}(0,\alpha ):\varkappa u{\text{'}} \in W_{2}^{1}(0,\alpha ){\text{\} }}, \\ \end{gathered} $
система собственных функций которого ${\text{\{ }}{{u}_{k}}{\text{\} }}_{{k = 1}}^{\infty }$ образует ортогональный базис в $ \circ W_{{2,\varkappa }}^{1}(0,\alpha )$ (см. следствие 2).

Теорема 3. Существует зависящая только от чисел $\alpha $, ${{\varkappa }_{{{\text{min}}}}}$, ${{\varkappa }_{{{\text{max}}}}}$ постоянная $M > 0$ такая, что

$\sum\limits_{k = 1}^\infty {\frac{1}{{\lambda _{k}^{2}}}} \leqslant M.$

Доказательство. Теорему проще доказать для эквивалентной полуклассической постановки задачи Штурма–Лиувилля (2.5), собственные значения которой совпадают с собственными значениями (2.4).

Пусть ${\text{\{ }}{{{v}}_{k}}{\text{\} }}_{{k = 1}}^{\infty }$, ${\text{\{ }}{{\lambda }_{k}} > 0{\text{\} }}_{{k = 1}}^{\infty }$ – система собственных функций и собственных значений задачи Штурма–Лиувилля (2.5), т.е. задачи

$\begin{gathered} {v}{\kern 1pt} {\text{''}} + \lambda \tilde {\varkappa }(\xi ){v} = 0,\quad 0 \leqslant \xi \leqslant \beta , \\ {v}(0) = {v}(\beta ) = 0. \\ \end{gathered} $
Построенную в п. 2.2 функцию Грина оператора Штурма–Лиувилля разложим в ряд Фурье по ортогональному в ${{L}_{{2,\tilde {\varkappa }}}}(0,\beta )$ базису относительно переменной $\xi $
$G(\xi ,\eta ) = \sum\limits_{n = 1}^\infty {{{C}_{n}}} {{{v}}_{n}}(\xi )$
с коэффициентами Фурье
${{C}_{n}}(\eta ) = \frac{1}{{{{{\left\| {{{{v}}_{n}}} \right\|}}_{{L_{{2,\tilde {\varkappa }}}^{2}}}}}}\int\limits_0^\beta {G(\xi ,\eta ){{{v}}_{n}}(\xi )\tilde {\varkappa }(\xi )d\xi } ,\quad n \geqslant 1.$
Поскольку $G(\xi ,\eta )$ – функция Грина оператора Штурма–Лиувилля, то интеграл
(2.8)
$\int\limits_0^\beta G (\xi ,\eta ){{{v}}_{n}}(\xi )\tilde {\varkappa }(\xi )d\xi = \frac{1}{{{{\lambda }_{n}}}}{{{v}}_{n}}(\eta ),$
поэтому коэффициенты Фурье имеют вид
(2.9)
${{C}_{n}}(\eta ) = \frac{{{{{v}}_{n}}(\eta )}}{{{{\lambda }_{n}}\left\| {{{{v}}_{n}}} \right\|_{{{{L}_{{2,}}}\tilde {\varkappa }}}^{2}}}.$
В силу ортогональности в ${{L}_{{2,\tilde {\varkappa }}}}(0,\beta )$ системы ${\text{\{ }}{{{v}}_{n}}{\text{\} }}$ из (2.8) следует, что
$\int\limits_0^\beta {{{{\left| {G(\xi ,\eta )} \right|}}^{2}}} \tilde {\varkappa }d\xi = \sum\limits_{n = 1}^\infty {C_{n}^{2}(\eta )\left\| {{{{v}}_{n}}} \right\|_{{{{L}_{{2,}}}\tilde {\varkappa }}}^{2}} ,$
откуда и из, интегрируя по $\eta $, (2.9), находим
$\sum\limits_{n = 1}^\infty {\frac{1}{{\lambda _{n}^{2}}}} = \int\limits_0^\beta {\int\limits_0^\beta {{{{\left| {G(\xi ,\eta )} \right|}}^{2}}} } \tilde {\varkappa }(\xi )\tilde {\varkappa }(\eta )d\xi d\eta \leqslant M,$
что завершает доказательство теоремы.

2.4. Свойства собственных функций

Теорема 4. Собственная функция ${{u}_{1}}$ задачи Штурма–Лиувилля (2.4), соответствующая наименьшему корню ${{\mu }_{1}}$, не имеет нулей на $(0,\alpha )$.

Доказательство. Предположим противное, т.е. найдется точка ${{x}_{0}} \in (0,\alpha )$, в которой ${{u}_{1}}({{x}_{0}}) = 0$. Поскольку на собственной функции $u = {{u}_{1}}$ достигается минимум функционала

(2.10)
$\mathop {min}\limits_{u \in \circ W_{{2,\varkappa }}^{1}(0,\alpha )} \Lambda (u) = \frac{{\int\limits_0^\alpha \varkappa {{{\left| {u{\kern 1pt} {\text{'}}{\kern 1pt} } \right|}}^{2}}dx}}{{\int\limits_0^\alpha \varkappa {{{\left| u \right|}}^{2}}dx}} = \Lambda ({{u}_{1}}) = \mu _{1}^{2},$
то ${{u}_{1}} \in \circ W_{{2,\varkappa }}^{1}(0,\alpha )$ удовлетворяет интегральному тождеству
(2.11)
$\int\limits_0^\alpha \varkappa u_{1}^{'}{v}{\kern 1pt} {\text{'}}dx = \mu _{1}^{2}\int\limits_0^\alpha \varkappa {{u}_{1}}{v}dx,\quad {v} \in \circ W_{{2,\varkappa }}^{1}(0,\alpha ).$
Выбирая в (2.11) пробную функцию $\forall {v} \in \circ W_{{2,\varkappa }}^{1}(0,\alpha )$ вида
(2.12)
${v}(x) = {{\tilde {u}}_{1}}(x)\mathop = \limits^{{\text{def}}} \left\{ \begin{gathered} {{u}_{1}}(x),\quad 0 < x < {{x}_{0}}, \hfill \\ 0,\quad {{x}_{0}} \leqslant x < \alpha , \hfill \\ \end{gathered} \right.$
получаем равенство
$\int\limits_0^{{{x}_{0}}} \varkappa {{\left| {u{\kern 1pt} {\text{'}}{\kern 1pt} } \right|}^{2}}dx = \mu _{1}^{2}\int\limits_0^{{{x}_{0}}} \varkappa {{\left| {{{u}_{1}}} \right|}^{2}}dx,$
которое означает, что минимум (2.10) функционала $\Lambda $ достигается также и на элементе ${v}$ вида (2.12), т.е.
$\mathop {min}\limits_{ \circ W_{{2,\varkappa }}^{1}(0,\alpha )} \Lambda (u) = \mu _{1}^{2} = \Lambda ({{u}_{1}}) = \Lambda ({{\tilde {u}}_{1}}).$
Но тогда элемент ${{\tilde {u}}_{1}} \in \circ W_{{2,\varkappa }}^{1}(0,\alpha )$ должен удовлетворять интегральному тождеству
$\int\limits_0^\alpha \varkappa {{\tilde {u}}_{1}}{v}{\kern 1pt} {\text{'}}dx = \mu _{1}^{2}\int\limits_0^\alpha {\varkappa {{{\tilde {u}}}_{1}}} {v}dx,\quad {v} \in \circ W_{{2,\varkappa }}^{1}(0,\alpha ),$
из которого следует существование слабой производной
$(\varkappa {{\tilde {u}}_{1}}){\kern 1pt} {\text{'}} = - \varkappa \mu _{1}^{2}{{\tilde {u}}_{1}} \in {{L}_{2}}(0,\alpha ),$
что означает абсолютную непрерывность элемента $\varkappa \tilde {u}{{_{{}}^{'}}_{1}}$ на интервале $(0,\alpha )$ и равенство
$\varkappa {{\tilde {u}}_{1}}(x) = 0\quad \forall x \in [{{x}_{0}},\alpha ].$
Осталось заметить, что элемент ${{\tilde {u}}_{1}} \in C[0,\alpha ]$, тогда как производная $\tilde {u}_{1}^{'}$ кусочно-непрерывна на $[0,\alpha ]$ и поэтому
(2.13)
${{\tilde {u}}_{1}}(x) = 0\quad \forall x \in [{{x}_{0}},\alpha ].$
Аналогичные рассуждения с пробной функцией ${v} \in \circ W_{{2,\varkappa }}^{1}(0,\alpha )$ вида
${v} = {{\tilde {u}}_{1}}(x) = \left\{ \begin{gathered} 0,\quad 0 < x \leqslant {{x}_{0}}, \hfill \\ {{u}_{1}}(x),\quad {{x}_{0}} < x < \alpha , \hfill \\ \end{gathered} \right.$
приводят к равенству ${{\tilde {u}}_{1}}(x) = 0$ $\forall x \in [{{x}_{0}},\alpha ]$, которое в совокупности с (2.13) позволяет заключить, что ${{u}_{1}}(x) = 0$ $\forall x \in [{{x}_{0}},\alpha ]$, что невозможно для собственной функции.

Теорема доказана.

Докажем аналог теоремы сравнения [7, с. 253].

Теорема 5. Пусть имеется два уравнения:

$(\varkappa y{\text{'}}){\kern 1pt} {\text{'}}{\kern 1pt} (x) + m\varkappa (x)y(x) = 0\quad и\quad (\varkappa z{\text{'}}){\kern 1pt} {\text{'}}{\kern 1pt} (x) + M\varkappa (x)z(x) = 0$
с решениями класса $D\mathop = \limits^{{\text{def}}} {\text{\{ }}u \in W_{2}^{1}(0,\alpha ):\varkappa u{\text{'}} \in W_{2}^{1}(0,\alpha ){\text{\} }}$. Если $0 < m \leqslant M$, то между любыми двумя нулями решения $\bar {y}(x)$ первого уравнения заключен, по крайней мере, один нуль каждого решения $\bar {z}(x)$ второго уравнения.

Доказательство. Пусть ${{x}_{0}}$ и ${{x}_{1}}$ – два последовательных нуля функции $\bar {y}(x)$. Допустим, что между ними нет ни одного нуля функции $\bar {z}(x)$. Без ограничения общности можно предположить, что $\bar {y}(x) > 0$, $\bar {z}(x) > 0$ на $({{x}_{0}},{{x}_{1}})$. Тогда $\bar {y}(x)$ будет возрастать вправо от ${{x}_{0}}$ и возрастать влево ${{x}_{1}}$: следовательно, $\bar {y}{\kern 1pt} {\text{'}}({{x}_{0}}) > 0$ и $\bar {y}{\kern 1pt} {\text{'}}({{x}_{1}}) < 0$, так как $\bar {y}{\kern 1pt} {\text{'}}(x) = 0$ или $\bar {y}{\kern 1pt} {\text{'}}(x) = 0$ означало бы, что $\bar {y} \equiv 0$. Подставляем $\bar {y}(x)$ и $\bar {z}(x)$ в соответствующие уравнения. Домножая на $\bar {z}(x)$ первое уравнение, на $\bar {y}(x)$ – второе, запишем разность

$\left[ {(\varkappa \bar {y}{\kern 1pt} '){\kern 1pt} {\text{'}}{\kern 1pt} (x)\bar {z}(x) - (\varkappa \bar {z}{\kern 1pt} '){\kern 1pt} {\text{'}}{\kern 1pt} (x)\bar {y}(x)} \right] + [m\varkappa (x) - M\varkappa (x)]{\kern 1pt} \bar {y}(x)\bar {z}(x) = 0,$
откуда
$\int\limits_{{{x}_{0}}}^{{{x}_{1}}} {\bar {z}} d(\varkappa \bar {y}{\kern 1pt} {\text{'}}) - \int\limits_{{{x}_{0}}}^{{{x}_{1}}} {\bar {y}} d(\varkappa \bar {z}{\kern 1pt} ') + (m - M)\int\limits_{{{x}_{0}}}^{{{x}_{1}}} {\varkappa \bar {y}\bar {z}} dx = 0.$
Интегрируя по частям, получаем
$\left. {\bar {z}\varkappa \bar {y}{\kern 1pt} '} \right|_{{{{x}_{0}}}}^{{{{x}_{1}}}} - \left. {\bar {y}\varkappa \bar {z}{\kern 1pt} {\text{'}}} \right|_{{{{x}_{0}}}}^{{{{x}_{1}}}} = (M - m)\int\limits_{{{x}_{0}}}^{{{x}_{1}}} \varkappa \bar {y}\bar {z}dx.$
В силу условия $m \leqslant M$ интеграл в правой части не отрицателен. В левой же части – отрицательное число. Приходим к противоречию.

Теорема доказана.

Следствие 4. Если в теореме 5 выполнено строгое неравенство $m < M$, то ноль второго уравнения не попадает на нули первого.

Следствие 5. Собственные функции ${{u}_{k}}$, $k \geqslant 2$, задачи Штурма–Лиувилля (2.4) меняют знак на $(0,\alpha )$ в силу ${{\mu }_{k}} > {{\mu }_{1}}$.

Доказательство. Если решение (2.4) имеет ноль второго порядка и выше, то оно тривиально, поэтому наличие у нетривиального решения корня на $(0,\alpha )$ гарантирует смену знака на этом интервале.

Следствие доказано.

Лемма 3. Для собственных функций ${{u}_{k}}$ задачи Штурма–Лиувилля (2.4) верны неравенства

$\exists C > 0:\left| {\frac{{{{u}_{k}}(x)}}{{{{u}_{1}}(x)}}} \right| \leqslant C\mu _{k}^{2}\quad \forall k \geqslant 2.$

Доказательство. Согласно теореме 4 на $(0,\alpha )$ нет корней ${{u}_{1}}(x)$. Не ограничивая общности, будем считать, что $(0,\alpha ) = (0,1)$. Очевидно, что

$\frac{{{{u}_{k}}(x)}}{x} = \int\limits_0^1 {u_{k}^{'}} (x\tau )d\tau ,\quad x \in (0,1),$
откуда получаем оценку
$\left| {\frac{{{{u}_{k}}(x)}}{x}} \right| \leqslant {{\left\| {u_{k}^{'}} \right\|}_{{C[0,1]}}} \leqslant C{\kern 1pt} {\text{'}}{{\left\| {{{u}_{k}}} \right\|}_{{W_{2}^{2}(0,1)}}} \leqslant C{\kern 1pt} {\text{'}}{{\left\| {u_{k}^{{''}}} \right\|}_{{{{L}_{2}}(0,1)}}} = C{\kern 1pt} {\text{''}}\mu _{k}^{2}{{\left\| {{{u}_{k}}} \right\|}_{{{{L}_{2}}(0,1)}}} \leqslant C{\kern 1pt} {\text{''}}\mu _{k}^{2}\mathop {max}\limits_\Omega \varkappa .$
Запишем формулу Тейлора
${{u}_{k}}(x) = {{u}_{k}}(0) + u_{k}^{'}(0)x + \int\limits_0^x {(x - \tau )} u_{k}^{{''}}(\tau )d\tau .$
С учетом ${{u}_{1}}(0) = 0$ имеем
$\frac{{{{u}_{1}}(x)}}{x} - u_{1}^{'}(0) = \frac{1}{x}\int\limits_0^x {(x - \tau )} u_{1}^{{''}}(\tau )d\tau = x\int\limits_0^1 {(1 - \xi )} u_{1}^{{''}}(x\xi )d\xi = - \mu _{1}^{2}x\int\limits_0^1 {(1 - \xi )} {{\Phi }_{1}}(x\xi )d\xi ,$
откуда
$\left| {\frac{{{{u}_{1}}(x)}}{x} - u - 1{\kern 1pt} {\text{'}}(0)} \right| \leqslant \mu _{1}^{2}{{\left\| {1 - \xi } \right\|}_{{{{L}_{2}}(0,1)}}}\sqrt x {{\left\| {{{u}_{1}}} \right\|}_{{{{L}_{2}}(0,x)}}} = \frac{{\mu _{1}^{2}\sqrt x }}{{\sqrt 3 }}{{\left\| {{{u}_{1}}} \right\|}_{{{{L}_{2}}(0,x)}}} \leqslant \frac{{\mu _{1}^{2}\sqrt x }}{{\sqrt 3 }}\mathop {max}\limits_\Omega \varkappa .$
По неравенству треугольника
$\left| {\frac{{\left| {{{u}_{1}}(x)} \right|}}{x} - \left| {u_{1}^{'}(0)} \right|} \right| \leqslant \left| {\frac{{{{u}_{1}}(x)}}{x} - u_{1}^{'}(0)} \right|,$
выбирая для окрестности точки $x = 0$ радиус $\delta > 0:\mu _{1}^{2}\sqrt {\delta {\text{/}}3} = {\text{|}}u_{1}^{'}(0){\text{|/}}2$, получаем
$ - \frac{1}{2}\left| {u_{1}^{'}(0)} \right| \leqslant \frac{{\left| {{{u}_{1}}(0)} \right|}}{x} - \left| {u_{1}^{'}(0)} \right| \leqslant \frac{1}{2}\left| {{{u}_{1}}(0)} \right|,$
т.е.
$0 < \frac{1}{2}\left| {u_{1}^{'}(0)} \right| \leqslant \frac{{\left| {{{u}_{1}}(0)} \right|}}{x} \leqslant \frac{3}{2}\left| {u_{1}^{'}(0)} \right|.$
В $\delta $-окрестности точки $x = 1$ верны аналогичные оценки. Поэтому в силу теоремы 4 лемма доказана.

2.5. Особые точки

Рассматриваем особые точки с локально разделяющимися переменными в полярных координатах. Особыми точками задачи (1.5) будем называть следующие точки:

1) точки негладкости $\partial \Omega $,

2) точки вхождения в $\partial \Omega $ линий разрыва.

Ключевым вопросом в вычислении размерности ядра является количество значений $\mu \in (0,1)$, возникающих в особых точках. Особые точки, имеющие $\mu \in (0,1)$, будем называть сингулярными, не имеющие $\mu \in (0,1)$ – регулярными.

Пример. Рассмотрим задачу Штурма–Лиувилля:

(2.14)
$(\varkappa u{\text{'}}){\kern 1pt} {\text{'}} + \lambda \varkappa u = 0,\quad 0 < x < \alpha ,$
с разрывным коэффициентом
$\varkappa (x) = \left\{ \begin{gathered} {{\varkappa }_{1}},\quad 0 < x < \beta , \hfill \\ {{\varkappa }_{2}},\quad \beta < x < \alpha = 2\beta , \hfill \\ \end{gathered} \right.$
при заданных положительных ${{\varkappa }_{1}}$, ${{\varkappa }_{2}}$ и $\alpha \in (0,2\pi )$. Нетрудно убедиться, что в задаче (2.14) собственные значения имеют вид
${{\lambda }_{n}} = - \mu _{n}^{2},\quad {{\mu }_{n}} = \left( {n + \frac{1}{2}} \right)\frac{\pi }{\beta },\quad n \geqslant 0,$
тогда как собственные функции имеют вид
${{u}_{n}}(x) = \left\{ \begin{gathered} sin{{\mu }_{n}}x,\quad 0 \leqslant x \leqslant \beta , \hfill \\ sin{{\mu }_{n}}(\alpha - x),\quad \beta \leqslant x \leqslant \alpha = 2\beta . \hfill \\ \end{gathered} \right.$
При этом минимальным значением корней ${{\mu }_{n}}$ будет ${{\mu }_{0}} = \pi {\text{/}}(2\beta ) = \pi {\text{/}}\alpha \in (0,1)$ при $\pi < \alpha < 2\pi $.

Задача Штурма–Лиувилля (2.14) лежит в основе простейшего примера сингулярной особой точки с одним разрывом коэффициента, принимающего любые положительные значения ${{\varkappa }_{1}}$ и ${{\varkappa }_{2}}$ по обе стороны от точки разрыва.

Далее, рассмотрим отдельные виды особых точек.

2.5.1. Угловая точка границы без линий разрыва. Как известно, собственные функции и собственные значения для угла $(0,\alpha )$ легко выписываются в явном виде

${{\mu }_{k}} = \frac{\pi }{\alpha },\quad {{u}_{k}}(x) = sin{{\mu }_{k}}x,\quad k \geqslant 1,$
поэтому справедлива

Теорема 6. Задача Штурма–Лиувилля для угловой точки границы без линий разрыва коэффициента $\varkappa $ (cм. фиг. 1) имеет единственное значение корня $\mu \in (0,1)$ при $\alpha \in (\pi ,2\pi )$ и ни одного – при $\alpha \in (0,\pi ]$.

Фиг. 1.

Угловая точка границы без линий разрыва.

2.5.2. Линия разрыва, входящая в прямолинейный участок границы. В качестве второго примера рассмотрим случай, когда линия разрыва коэффициентов образует с гладкой границей угол $\beta \in (0,\pi )$. Рассматривается задача Штурма–Лиувилля (2.4) с областью определения

(2.15)
$\begin{gathered} {{D}_{L}} = \left\{ {u \in {{L}_{2}}(\pi - \beta , - \beta ):u \in W_{2}^{2}(0,\pi - \beta ),\;u \in W_{2}^{2}( - \beta ,0),} \right. \\ \left. {u( + 0) = u( - 0),\;u{\kern 1pt} {\text{'}}( + 0) = \varkappa u{\kern 1pt} {\text{'}}( - 0),\;u( - \beta ) = u(\pi - \beta ) = 0_{{\kern 1pt} }^{{\kern 1pt} }} \right\}. \\ \end{gathered} $

Следующая теорема является упрощенным и сокращенным вариантом доказанной в [5] теоремы 1.

Теорема 7. При любых заданных $\beta \in (0,\pi {\text{/}}2)$ и при любых вещественных положительных $\varkappa < 1$, а также при любых заданных $\beta \in (\pi {\text{/}}2,\pi )$ и при любых вещественных положительных $\varkappa > 1$ (см. фиг. 2) задача Штурма–Лиувилля (2.4), (2.15) имеет собственное значение с корнем $\mu \in (0,1).$

Фиг. 2.

Линия разрыва подходит к гладкой границе.

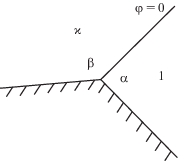
2.5.3. Линия разрыва, входящая в угловую точку границы. Теперь рассмотрим случай, когда линия разрыва коэффициентов подходит к негладкой границе. Пусть точка негладкости границы – угол с раствором $\alpha + \beta < 2\pi $, где $\alpha $, $\beta > 0$ – углы между границей $\partial \Omega $ и линией разрыва коэффициентов в точке ее пересечения с $\partial \Omega $, при этом ${{\varkappa }_{1}} = 1$ соответствует углу $\alpha $, ${{\varkappa }_{2}} = \varkappa > 0$ – углу $\beta $.

Рассматривается задача Штурма–Лиувилля (2.4) с областью определения

(2.16)
$\begin{gathered} {{D}_{L}} = \left\{ {u \in {{L}_{2}}(\beta , - \alpha ):u \in W_{2}^{2}(0,\beta ),\;u \in W_{2}^{2}( - \alpha ,0),} \right. \\ \left. {u( + 0) = u( - 0),\;u{\kern 1pt} {\text{'}}( + 0) = \varkappa u{\kern 1pt} {\text{'}}( - 0),\;u(\beta ) = u( - \alpha ) = 0_{{\kern 1pt} }^{{\kern 1pt} }} \right\}. \\ \end{gathered} $
Чтобы уйти от использования несамосопряженных операторов, введем весовое пространство $L_{2}^{{\alpha ,\beta ,\varkappa }}(\beta , - \alpha )$. Так как $\varkappa > 0$, удобно считать, что $L_{2}^{{\alpha ,\beta ,\varkappa }}$ – это вещественное гильбертово пространство со скалярным произведением
${{(u,{v})}_{\varkappa }} = \varkappa \int\limits_{ - \alpha }^0 {u{v}} dx + \int\limits_0^\beta {u{v}} dx.$
Теперь нетрудно убедиться, что оператор $L:{{D}_{L}} \subset L_{2}^{{\alpha ,\beta ,\varkappa }}(\beta , - \alpha ) \to L_{2}^{{\alpha ,\beta ,\varkappa }}(\beta , - \alpha )$ самосопряженный.

При сделанных предположениях, в силу доказанных в [5] теорем 2–5 будет справедлива

Теорема 8. Пусть $\varkappa > 0$ и $\alpha < \beta $ в случае на фиг. 3. Тогда задача Штурма–Лиувилля (2.4), (2.16) имеет собственное значение с корнем $\mu \in (0,1)$ в следующих случаях:

Фиг. 3.

Линия разрыва входит в угловую точку границы.

1) при $\pi {\text{/}}2 < \alpha < \beta $, если выполнено одно из двух условий: $1 < \beta {\text{/}}\alpha < 2$ и $\beta < \pi $, либо $\beta {\text{/}}\alpha > 2$ и $\beta > \pi $;

2) при $\alpha < \pi {\text{/}}2 < \beta $, если при $\varkappa < - {\text{tg}}\alpha {\text{/tg}}\beta $ выполнено одно из условий: $1 < \beta {\text{/}}\alpha < 2$, либо $\beta {\text{/}}\alpha > 2$ и $\pi < \beta < 3\pi {\text{/}}2$.

3. ВЗАИМОДЕЙСТВИЕ ОСОБЕННОСТЕЙ

Изучение эффекта взаимодействия особых точек начнем со случая, когда область $\Omega \subset {{\mathbb{R}}^{2}}$ имеет только две особые точки – одну конечную $x = 0$ и одну бесконечную с конечным числом входящих в них и выходящих из них гладких линий разрыва. При этом сами по себе конечные и бесконечные граничные особые точки могут быть как угловыми с углами, не равными $\pi $, так и точками гладкости с углами, равными $\pi $. В последнем случае из особой точки выходит хотя бы одна линия разрыва, тогда как некоторая окрестность вершины угла, не равного $\pi $, может не содержать ни одной линии разрыва. Предполагается также, что каждая из двух особых точек даже в случае нескольких исходяших из нее линий разрыва характеризуется всего лишь одним значением корня ${{\mu }_{1}} \in (0,1)$: конечная – значением $\mu _{1}^{0} = {{\mu }_{1}}$, а бесконечная – значением $\mu _{1}^{\infty } = {{\mu }_{1}}$.

В качестве примеров неединственности для случая только конечных или только бесконечных сингулярных особых точек сформулируем две теоремы. Начнем с ограниченной области, для которой достаточно построить всего лишь один пример неединственности с одной сингулярной особой точкой. Добавление каждой новой сингулярной особой точки автоматически увеличивает размерность ядра эллиптического оператора ввиду очевидной линейной независимости решений, соответствующих разным сингулярным особым точкам.

В качестве примера приведем простейшую теорему о размерности ядра для области с одной конечной особой точкой (см. фиг. 4).

Фиг. 4.

Пример допустимой области в теореме 9.

Теорема 9. Пусть $\Omega $ – ограниченная область следующего вида:

1) $\partial \Omega $ класса ${{C}^{1}}$ за исключение сингулярной угловой точки, из которой выходит незамкнутая линия разрыва $\Gamma $ класса ${{C}^{1}}$;

2) второй конец $\Gamma $ входит в регулярную угловую точку под прямым углом к $\partial \Omega $.

И пусть задача Штурма–Лиувилля по $\varphi $ для модельной окрестности угловой точки имеет ровно одно значение $\mu = {{\mu }_{1}} \in (0,1)$. Тогда однородная задача Дирихле (1.5) имеет нетривиальное решение u  $ \in \circ L_{p}^{1}(\Omega )$ при $1 < p < 2{\text{/}}(1 + {{\mu }_{1}})$, и размерность ядра эллиптического оператора при этом равна 1.

Теорема 9 легко доказывается построением примера нетривиального решения вида

$u = \eta (r){{r}^{{ - {{\mu }_{1}}}}}{{\Phi }_{1}}(\varphi ) + {v},$
где ${{\Phi }_{1}}$ – решение задачи Штурма–Лиувилля, соответствующее ${{\mu }_{1}}$, с гладкой срезающей функцией $\eta \in {{C}^{\infty }}(\mathbb{R})$ вида
$\eta (r) = \left\{ \begin{gathered} 1,\quad r \leqslant \delta {\text{/}}2, \hfill \\ 0,\quad \geqslant \delta , \hfill \\ \end{gathered} \right.$
и где без ограничения общности точка $r = 0$ считается вершиной угла модельной угловой точки с выходящим из нее прямолинейным отрезком, представляющим линию разрыва коэффициента $\varkappa $. Достаточно малое число $\delta > 0$ соответствует при этом размеру модельной окрестности сингулярной особой точки $r = 0$.

Невязка слабого решения $u \in \circ L_{p}^{1}(\Omega )$ определяется по теореме Рисса как слабое решение ${v} \in \circ L_{2}^{1}(\Omega )$ задачи Дирихле для уравнения

$\Delta {v} = \Delta [(1 - \eta ){{r}^{{ - {{\mu }_{1}}}}}{{\Phi }_{1}}] \in {{L}_{2}}(\Omega ).$
При этом нетривиальность решения слабого решения $u \in \circ L_{p}^{1}(\Omega )$ гарантирована условием $1 < p < 2{\text{/}}(1 + {{\mu }_{1}})$, что завершает доказательство теоремы 9.

Неограниченная область может иметь несколько бесконечных особых точек, в качестве которых обычно выступают выходы на бесконечность. Как и в случае ограниченных областей, для неограниченных достаточно построить всего лишь один пример неединственности с одной бесконечной сингулярной особой точкой. Добавление каждой новой бесконечной сингулярной особой точки будет автоматически увеличивать размерность ядра ввиду очевидной линейной независимости решений, особенности которых локализованы в разных выходах на бесконечность.

Аналогичным образом, но с заменой ${{r}^{{ - {{\mu }_{1}}}}}$ на ${{r}^{{{{\mu }_{1}}}}}$, доказывается теорема для области с бесконечной особой точкой (см. фиг. 5).

Фиг. 5.

Пример допустимой области в теореме 10.

Теорема 10. Пусть $\Omega $ – неограниченная область с границей $\partial \Omega $ класса ${{C}^{1}}$ следующего вида:

1) в модельной окрестности бесконечности $r > R$ граница $\partial \Omega $ распадается на два бесконечных не пересекающихся отрезка прямых, уходящих на бесконечность вместе с бесконечным отрезком прямой части линии разрыва $\Gamma $ между ними;

2) оставшаяся конечная часть гладкой линии разрыва $\Gamma $ упирается в границу $\partial \Omega $ под прямым углом, образуя регулярную особую точку.

И пусть задача Штурма–Лиувилля по $\varphi $ для модельной окрестности бесконечности $r > R$ имеет ровно одно значение $\mu = {{\mu }_{1}} \in (0,1)$. Тогда однородная задача Дирихле (1.5) имеет нетривиальное решение $u \in \circ L_{p}^{1}(\Omega )$ при $2{\text{/}}(1 - {{\mu }_{1}})p < \infty $, и размерность ядра эллиптического оператора при этом равна 1.

Теперь перейдем к эффекту ${{L}_{p}}$-взаимодействия особенностей слабого решения на примере простейшего случая двух особых точек – конечной и бесконечной с совпадающими корнями. Справедлива следующая

Теорема 11. Если $\mu _{1}^{0} = \mu _{1}^{\infty } = {{\mu }_{1}} \in (0,1)$, то однородная задача Дирихле (1.5) для области $\Omega $ имеет в $ \circ L_{p}^{1}(\Omega )$ при $1 < p < \infty $ только тривиальное решение.

Доказательство. Достаточно доказать, что $u \in \circ L_{p}^{1}(\Omega ) \Rightarrow u \in \circ L_{2}^{1}(\Omega )$. В окрестностях $r = 0$ и $r = \infty $ переменные $r$, $\varphi $ разделяются, а соответствущие задачи Штурма–Лиувилля характеризуются одним и тем же единственным на $(0,1)$ знчачением корня ${{\mu }_{1}}$. Собственные функции задачи Штурма–Лиувилля в окрестности нуля будем обозначать через ${{\Phi }_{k}}$, а в окрестности бесконечности – через $\mathop {\tilde {\Phi }}\nolimits_k .$ Соответственно с волной или без волны будут сопутствующие собственным функциям корни ${{\mu }_{k}}$ и числовые коэффициенты в рядах Фурье ${{A}_{k}}$, ${{B}_{k}}$.

С учетом предположения $u \in \circ L_{p}^{1}(\Omega )$ разложения решения в окрестностях нуля и бесконечности имеют вид

(3.1)
$\begin{gathered} u(r,\varphi ) = \sum\limits_{k = 1}^\infty {{{A}_{k}}} {{r}^{{{{\mu }_{k}}}}}{{\Phi }_{k}}(\varphi ) + {{B}_{1}}{{r}^{{ - {{\mu }_{1}}}}}{{\Phi }_{1}}(\varphi ),\quad 0 < r < \delta , \\ u(r,\varphi ) = {{{\tilde {A}}}_{1}}{{r}^{{{{\mu }_{1}}}}}{{{\tilde {\Phi }}}_{1}}(\varphi ) + \sum\limits_{k = 1}^\infty {{{{\tilde {B}}}_{k}}} {{r}^{{ - {{{\tilde {\mu }}}_{k}}}}}{{{\tilde {\Phi }}}_{k}}(\varphi ),\quad r > R > \delta , \\ \end{gathered} $
где ${{\tilde {\mu }}_{1}} = {{\mu }_{1}}$ и без ограничения общности считается, что коэффициент ${{\tilde {A}}_{1}} > 0$. Теперь, переписав равенство (3.1) в виде
$u(r,\varphi ) = {{\tilde {\Phi }}_{1}}(\varphi )\left[ {{{{\tilde {A}}}_{1}}{{r}^{{{{\mu }_{1}}}}} + {{{\tilde {B}}}_{1}}{{r}^{{ - {{\mu }_{1}}}}} + \sum\limits_{k = 2}^\infty {{{{\tilde {B}}}_{k}}} {{r}^{{ - {{{\tilde {\mu }}}_{k}}}}}\frac{{{{{\tilde {\Phi }}}_{k}}(\varphi )}}{{{{\Phi }_{1}}(\varphi )}}} \right],$
оценим сумму ряда. Для этого используем оценку теоремы 3, согласно которой
(3.2)
$\sum\limits_{k = 1}^\infty {\frac{1}{{\mu _{k}^{4}}}} = \sum\limits_{k = 1}^\infty {\frac{1}{{\lambda _{k}^{2}}}} \leqslant {{M}_{0}},$
оценку леммы 3, а также очевидную оценку коэффициентов Фурье
${{\tilde {B}}_{k}} = \int\limits_0^\alpha u (R,\varphi ){{\tilde {\Phi }}_{k}}(\varphi )\varkappa (\varphi )d\varphi $
по ортонормированному базису ${\text{\{ }}{{\tilde {\Phi }}_{k}}{\text{\} }}$ через норму следа рассматриваемого решения на дуге ${\text{\{ }}r = R,\;0 < \varphi < \alpha {\text{\} }}$. В силу этого и теоремы 4, а также леммы 3 имеем
$\left| {{{{\tilde {B}}}_{1}}{{r}^{{ - {{\mu }_{1}}}}} + \sum\limits_{k = 2}^\infty {{{{\tilde {B}}}_{k}}} {{r}^{{ - {{{\tilde {\mu }}}_{k}}}}}\tfrac{{{{{\tilde {\Phi }}}_{k}}}}{{\mathop {\widetilde \Phi }\nolimits_1 }}} \right| \leqslant \left| {{{{\tilde {B}}}_{1}}} \right|{{r}^{{ - {{\mu }_{1}}}}} + {{M}_{1}}\sum\limits_{k = 2}^\infty {\tilde {\mu }_{k}^{2}} {{r}^{{ - {{\mu }_{k}}/2}}} \leqslant {{M}_{0}}{{r}^{{ - {{\mu }_{1}}}}}\quad \forall r > {{R}_{0}}.$
При этом сумма ряда
$\sum\limits_{k = 2}^\infty {\tilde {\mu }_{k}^{2}} {{r}^{{ - {{\mu }_{k}}}}} = \sum\limits_{k = 2}^\infty {\tfrac{{\tilde {\mu }_{k}^{6}{{r}^{{ - {{\mu }_{k}}}}}}}{{\tilde {\mu }_{k}^{4}}}} < {{M}_{2}}$
легко оценивается с помощью (3.2) и очевидного неравенства
$\mathop {sup}\limits_{s > 1} ({{s}^{6}}{{r}^{{ - s}}}) < m(R) < \infty \quad \forall r > R$
с некоторой постоянной $m(R) > 0$. Откуда находим
$u = {{\Phi }_{1}}[{{\tilde {A}}_{1}}{{r}^{{{{\mu }_{1}}}}} + O({{r}^{{ - {{\mu }_{1}}}}})],\quad r \to \infty ,$
что гарантирует неотрицательность решения $u \geqslant 0$ на дуге ${\text{\{ }}r = R,\;0 < \varphi < \alpha {\text{\} }}$ при достаточно больших $R$.

Применяя к области ${{\Omega }_{R}}\mathop = \limits^{{\text{def}}} {\text{\{ }}x \in \Omega :\left| x \right| < R{\text{\} }}$ принцип существенного максимума (см. теорему 9.27 в [8]), заключаем, что решение $u \geqslant 0$ на ${{\Omega }_{R}}$. Покажем теперь, что это приводит к противоречию.

Поскольку ${{\tilde {A}}_{1}} \ne 0$ и $u \in \circ L_{p}^{1}(\Omega )$, имеем неравенство $p > 2{\text{/}}(1 - {{\mu }_{1}})$. Поэтому ряд Фурье в окрестности особой точки $r = 0$ имеет вид

$u(r,\varphi ) = \sum\limits_{k = 2}^\infty {{{A}_{k}}} {{r}^{{{{\mu }_{k}}}}}{{\Phi }_{k}}(\varphi ).$
Предположим, что найдется такой номер $m \geqslant 2$, что ${{A}_{m}} \ne 0$, тогда как все ${{A}_{k}} = 0$ при $k < m$. Согласно следствию 5, собственная функция ${{\Phi }_{m}}$ меняет на ${{\Omega }_{R}}$ знак, а тогда на любой дуге ${\text{\{ }}r = \delta ,\;0 < \varphi < \alpha {\text{\} }}$ с достаточно малым $\delta $ происходит смена знака рассматриваемого решения $u$. Действительно, на дуге $r = \delta $, $0 < \varphi < \alpha $ функция ${{\Phi }_{m}}$ в малой окрестности своего нуля строго монотонна и принимает значения $( - \sigma ,\sigma )$ с некоторым $\sigma > 0$. Оценивая при достаточно малых $\delta $ оставшуюся часть ряда
$\sum\limits_{k = m + 1}^\infty {{{A}_{k}}} {{r}^{{{{\mu }_{k}}}}}{{\Phi }_{k}}(\varphi ),$
получаем смену знака на дуге ${\text{\{ }}r = \delta ,\;0 < \varphi < \alpha {\text{\} }}$, что противоречит неотрицательности решения в области ${{\Omega }_{R}}$. Значит, предположение ${{A}_{m}} \ne 0$ неверно, т.е. все коэффициенты ${{A}_{k}} = 0$ при $k \geqslant 2$. Таким образом, в некоторой окрестности особой точки $r = 0$ решение тождественно равно нулю. Поскольку вне линий разрыва $\varkappa $ решение является гармонической функцией, то $u = 0$ на всей области $\Omega $. А тогда предположение ${{A}_{1}} \ne 0$ неверно, т.е. в окрестности бесконечности решение $\nabla u \in {{L}_{2}}(\Omega {\backslash }{{\Omega }_{R}})$. При этом, в чаcтности, из представления решения будет следовать, что $u \to 0$ при $r \to \infty $, что позволяет перенести принцип существенного максимума на решения класса $L_{2}^{1}({{\Omega }^{\varepsilon }})$ с неограниченной областью ${{\Omega }^{\varepsilon }} = {\text{\{ }}x \in \Omega :r > \varepsilon {\text{\} }}$ при $0 < \varepsilon < {{\varepsilon }_{0}}$, где ${{\varepsilon }_{0}}$ определяет подобласть ${\text{\{ }}x \in \Omega :\left| x \right| < {{\varepsilon }_{0}}{\text{\} }}$ особой точки $r = 0$, в которой разделяются переменные $r$, $\varphi $.

Осталось показать, что коэффициент ${{B}_{1}}$ при ${{r}^{{ - {{\mu }_{1}}}}}$ тоже равен нулю. Для этого, не ограничивая общности, предположим, что ${{B}_{1}} > 0$. Заметим, что предполагаемое нетривиальным решение $u \in \circ L_{p}^{1}(\Omega )$, т.е. показатель $p < 2{\text{/}}(1 + {{\mu }_{1}})$. При этом в силу известных локальных ${{L}_{p}}$-оценок решение задачи Дирихле для эллиптического уравнения с гладкими линиями разрыва попадает в класс $L_{2}^{1}({{\Omega }^{\varepsilon }})$ при любых $\varepsilon \in (0,{{\varepsilon }_{0}})$ (самый простой вывод таких оценок можно найти в [9]). Поэтому даже в случае $1 < p < 2{\text{/}}(1 + {{\mu }_{1}}) < 2$ к рассматриваемому решению применим принцип существенного максимума для неограниченной области ${{\Omega }^{\varepsilon }}$ при любом значении $\varepsilon \in (0,{{\varepsilon }_{0}})$. Повторяя теперь использованную выше схему доказательства, основанную на принципе существенного максимума, с учетом произвольности $\varepsilon \in (0,{{\varepsilon }_{0}})$ получаем противоречие, означающее, что ${{B}_{1}} = 0$. Таким образом, градиент решения $\nabla u \in {{{\mathbf{L}}}_{2}}(\Omega )$, т.е. $u \in \circ L_{2}^{1}(\Omega )$, откуда следует, что решение $u = 0$.

Теорема доказана.

Замечание 2. Теорема 11 не требует совпадения числа линий разрыва в конечной и бесконечной особых точках $\partial \Omega $. Так, линия разрыва может замыкаться через особую точку, т.е. начало и конец линии разрыва может совпадать с этой особой точкой. На фиг. 6 приводится пример допустимой области: показаны линии разрыва коэффициента и граница $\partial \Omega $, а пунктиром – их асимптоты в окрестности бесконечности.

Фиг. 6.

Пример допустимой области в теореме 11.

Список литературы

  1. Birkhoff G. Angular singularities of elliptic problems Collect. of Articles Dedicated to J. L. Walsh on his 75th birthday, VI. J. // Approximation Theory 6. 1972. P. 215–230.

  2. Kellogg R.B. Singularities in Interface Problem // Proc. of SYNSPADE-1970 (Numerical Solution of PDE-II). 1971. P. 351–400.

  3. Ильин Е.М. Особенности слабых решений эллиптических краевых задач с разрывными старшими коэффициентами // Записки ЛОМИ. АН СССР. 1973. Т. 38. С. 33–45.

  4. Ильин Е.М. Особенности слабых решений эллиптических уравнений с разрывными старшими коэффициентами. Угловые точки линий разрыва // Записки ЛОМИ. АН СССР. 1974. Т. 47. С. 166–169.

  5. Дудкина А.А. О размерностях ядра и коядра эллиптического оператора с разрывными коэффициентами // Вестн. РУДН. Сер. Матем. Информатика. Физ. 2008. № 4. С. 20–29.

  6. Рудин У. Функциональный анализ. М.: Мир, 1973.

  7. Степанов В.В. Курс дифференциальных уравнений. М.: Физматлит, 1958.

  8. Brezis H. Functional analysis, Sobolev spaces and partial differential equations. Universitext. New York: Springer, 2011.

  9. Дудкина А.А. К ${{L}_{p}}$-теории эллиптических краевых задач с разрывными коэффициентами: Дис. канд. физ.-матем. наук. М.: РУДН, 2010.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал