Журнал вычислительной математики и математической физики, 2019, T. 59, № 9, стр. 1554-1569

1. ВВЕДЕНИЕ

Математическое моделирование тропических циклонов давно интересует многих исследователей. В этой связи укажем нескольких авторов, предложивших различные модели этого явления (см., например, [1]–[9]). Напомним, что, как объясняется в обширной литературе (в том числе в процитированных выше работах), рост и поддержание тропического циклона обусловлены, прежде всего, восходящим движением воздуха, вызванным выделением скрытой теплоты конденсации водяного пара. Этот механизм циклона сопровождается действием силы Кориолиса, которая порождает круговое движение воздуха, а также сопровождается трением капель воды (или кусочков льдинок) о воздух, которое замедляет восходящее движение воздуха.

Целью данной работы является выявление этого механизма путем численного моделирования на основе фундаментальных уравнений механики газа (см. [10]) без учета вязкости и теплопроводности. Для этого рассматриваются уравнения в цилиндрической области с осевой симметрией (см. ниже (3)–(7)). Поскольку исследуемая модель сводится к решению системы уравнений в частных производных первого порядка, то она преобразуется в семейство уравнений на траекториях (характеристиках), что позволяет эффективно вычислять искомое решение. Идея этого моделирования частично изложена в [11].

Для численного решения выбранной модели использована разностная схема, которая частично базируется на методах, разработанных в [12] и [13]. Однако в этих работах расчет производился только для вертикального потока воздуха. В настоящей работе разработан алгоритм вычисления радиальной и тангенциальной составляющих скорости.

В рамках принятых приближений (инвариантный радиус циклона, фиксированные траектории ветра, отсутствие вязкости и теплопроводности), результат моделирования данной работы явно показывает главные аспекты эволюции тропического циклона из-за конденсации водяного пара, создающей восходящее движение воздуха, и его стабилизации из-за трения капель о воздух.

2. ПРИНЦИПЫ МОДЕЛИРОВАНИЯ И ПРЕОБРАЗОВАНИЕ УРАВНЕНИЙ

Рассмотрим движение воздуха внутри тропического циклона, принимая во внимание осевую симметрию течения в фиксированной цилиндрической области. Точнее говоря, рассмотрим течение в области

Здесь $(r,\vartheta ,z)$ – цилиндрические координаты, а ось $z$ совпадает с осью кругового движения воздуха. Область $\{ 0 < z < {{\bar {z}}_{1}},\;0 \leqslant r < {{\Lambda }_{0}}(z)\} $ будет соответствовать зоне “глаза”. Поскольку в “глазе” движение воздуха имеет несколько иные аспекты, чем в остальной части тропического циклона, то в настоящей работе мы исключаем его из нашего рассмотрения.

Если предположить, что все входящие в уравнения функции не зависят от $\vartheta $ и пренебречь вязкостью и теплопроводностью, то уравнения движения газа (воздуха) (см. [10]) в координатах $(r,z)$, примут следующий вид:

Здесь $\varrho $, $T$, ${{v}_{r}}$, ${{v}_{\vartheta }}$ и ${{v}_{z}}$ – соответственно плотность, температура, радиальная, тангенциальная и вертикальная составляющая скорости, а давление представлено как ${{R}_{1}}\varrho T$ (${{R}_{1}}$ – постоянная). Кроме того, ${{c}_{v}}$ – удельная теплоемкость воздуха, а ${{f}_{0}} = 2\left| \omega \right|sin{{\varphi }_{0}}$ – коэффициент силы Кориолиса, определяемый угловой скоростью $\omega $ вращения Земли и географической широтой центра циклона ${{\varphi }_{0}}$. Для силы Кориолиса в выбранной системе уравнений используем приближение, пренебрегающее его вертикальной составляющей и членами, связанными с вертикальной составляющей скорости. С другой стороны, эффект трения между воздухом и поверхностью моря представлен в виде $ - {{\varepsilon }_{1}}({{x}_{3}})(v - (v \cdot {{e}_{3}}){{e}_{3}})$, где ${{\varepsilon }_{1}}({{x}_{3}})$ является функцией, которая строго положительна в окрестности ${{x}_{3}} = 0$ и обращающейся в ноль при достаточно больших ${{x}_{3}}$. При этом ${{H}_{{tr}}}$ – масса водяного пара, переходящего в жидкое или твердое фазовое состояние в восходящем потоке воздуха, $\Sigma $ – количество воды в жидком или твердом фазовом состоянии (в воздухе), ${{L}_{{tr}}}$ – скрытая теплота перехода воды из газообразного в жидкое или твердое состояние.

Отметим, что поскольку

то в каждом из уравнений (3)–(7) присутствует дифференциальный оператор переноса Этот оператор определяет траектории ветра на плоскости $(r,z)$, которые могут быть рассчитаны. Для того, чтобы подчеркнуть влияние процесса конденсации, нагревания воздуха и его восходящего движения, определяющего эволюцию тропического циклона, предположим, что определенные таким образом траектории на плоскости $(r,z)$ являются гладкими и относительно устойчивыми. Выбирая соответствующим образом траектории на плоскости $(r,z)$ (в следующем разделе изложим наш выбор траекторий), преобразуем систему (3)–(7) в одно семейство уравнений на траекториях.

Предполагая, что $v_{r}^{2} + v_{z}^{2} > 0$, положим

Введем семейство функций $\gamma (s) = ({{\gamma }_{r}}(s),{{\gamma }_{z}}(s))$, определяемых соотношениями Ясно, что в предположении регулярности $({{q}_{r}}(r,z),{{q}_{z}}(r,z))$ семейство функций $\gamma $, которые проходят через каждую точку $(r,z)$ из ${{\Gamma }_{{r,z}}}$ и удовлетворяют уравнениям (9), целиком заполнит область ${{\Gamma }_{{r,z}}}$.

Предположим, что семейство функций $\{ \gamma \} $ определено и не зависит от $t$. Затем, используя соотношение

с ${{v}_{\gamma }} = \sqrt {v_{r}^{2} + v_{z}^{2}} $, уравнения (3) и (5) преобразуются к виду а используя равенство $\varrho \left( {\tfrac{{\partial {{v}_{r}}}}{{\partial r}} + \tfrac{1}{r}{{v}_{r}} + \tfrac{{\partial {{v}_{z}}}}{{\partial z}}} \right) = - {{H}_{{tr}}} - \tfrac{{\partial \varrho }}{{\partial t}} - {{v}_{\gamma }}\tfrac{{\partial \varrho }}{{\partial s}}$, которое эквивалентно (3), уравнение (7) преобразуется к виду С другой стороны, умножив уравнение (4) на ${{q}_{r}}$ и уравнение (6) на ${{q}_{z}}$ и используя равенство получим

Для численного разрешения рассмотрим приближенную задачу для этой системы уравнений, полученную путем разделения между временной эволюцией и пространственной структурой для ${{v}_{\gamma }}$, $\varrho $, $T$ (как это было сделано в [12], [13]). Точнее говоря, положим

на каждой траектории $\gamma $ (поэтому $w(t,s) = w(\gamma ;t,s)$) и предположим С другой стороны, рассмотрим ${{v}_{\vartheta }}(t,s) = {{v}_{\vartheta }}(\gamma ;t,s)$ на каждом $\gamma $ как функцию от $(t,s)$, т.е. для ${{v}_{\vartheta }}(t,s)$ не используем разделение между временной эволюцией и пространственной структурой. Действительно, ее эволюция не определяется как прямое следствие процесса конденсации пара и восходящего потока воздуха.

Для того, чтобы преобразовать уравнения (10)–(13) в приближенную задачу, используя введенное в (14)–(15) разделение между временной эволюцией и пространственной структурой, положим

Наконец, примем следующее выражение ${{H}_{{tr}}}$: где (${{[\, \cdot \,]}^{ + }}$ обозначает положительную часть), обоснование которого найдено, например, в [12]. Таким образом, предположив, что $\varrho > 0$, $w > 0$, ${{q}_{z}} \geqslant 0$, и написав $\tfrac{{dw}}{{ds}}$, $\tfrac{{d\varrho }}{{ds}}$, $\tfrac{{dT}}{{ds}}$ вместо $\tfrac{{\partial w}}{{\partial s}}$, $\tfrac{{\partial \varrho }}{{\partial s}}$, $\tfrac{{\partial T}}{{\partial s}}$, на каждой траектории $\gamma $ вместо (10)–(13) рассмотрим систему уравнений

Поскольку траектории перемещения жидкой или твердой воды отличаются от траекторий потока воздуха $\gamma $, то дадим практическое определение для вычисления массы жидкой или твердой воды на каждой траектории воздуха в разд. 4 после определения нашего выбора траекторий движения воздуха. В разд. 4 будет объяснена роль члена $D(t)$ в уравнении (22), а также граничные условия для втекания и вытекания воздуха в уравнениях (19)–(22).

3. ВЫБОР ТРАЕКТОРИЙ

Как было показано выше, если зафиксировать траектории $\gamma $, то можно свести систему уравнений (3)–(7) для неизвестных $\varrho $, $T$, ${{v}_{r}}$, ${{v}_{\vartheta }}$ и ${{v}_{z}}$ к системе четырех уравнений для четырех неизвестных $\varrho $, $T$, ${{v}_{\gamma }}$ и ${{v}_{\vartheta }}$, что позволяет эффективно выполнить необходимый расчет. Но траектории являются неизвестными, то для получения устойчивого результата моделирования тропического циклона его траектории также должны быть хорошими приближениями реальных траекторий. В этой связи напомним, что в литературе, описывающей физику тропических циклонов, принято считать, что в нижней части циклона воздух движется к центру, в области вблизи центра тайфуна он движется вверх, а в его верхней части воздух перемещается к периферии. Поэтому мы также примем эту общую схему потока воздуха.

Для того, чтобы выбор траекторий не приводил к искусственному результату, необходимо аккуратное решение вопроса о выборе траекторий. В частности, их важно выбрать так, чтобы семейство этих траекторий не нарушало закон сохранения массы. Иными словами, если $\bar {\varrho }$ представляет собой такую не зависимую от $t$ функцию, что плотность $\varrho $ должна быть близкой к $\bar {\varrho }$, а траектории определяются полем скорости $\bar {v}$ (мы будем называть $\bar {\varrho }$ основной плотностью, а $\bar {v}$ основным полем скорости), то величина $\nabla \cdot (\bar {\varrho }\bar {v})$ должна оставаться достаточно маленькой. Даже если плотность $\varrho $ неизвестна, то можно определить основную плотность $\bar {\varrho }$ по гидростатическому принципу, а основное поле скорости $\bar {v}$ можно взять в соответствии с соотношением $\nabla \cdot (\bar {\varrho }\bar {v}) \approx 0$, что согласуется со многими наблюдениями, сделанными на тропических циклонах.

При реализации численного алгоритма мы выбираем определенное число $N$ траекторий и oбозначаем их через ${{\gamma }_{j}}$, $j = 1,...,N$. Теперь полагаем, cогласно принятой схеме, что каждая траектория ${{\gamma }_{j}}$ состоит из трех компонент: нижней части $\gamma _{j}^{{[1]}}$, где воздух движется почти горизонтально к центру, восходящей части $\gamma _{j}^{{[2]}}$, и верхней части $\gamma _{j}^{{[3]}}$, где воздух движется почти горизонтально к периферии. В настоящей работе для основной скорости $\bar {v}$ в $\gamma _{j}^{{[1]}}$ и $\gamma _{j}^{{[3]}}$ примем приближение горизонтального потока, так что функция $w$ будет иметь поведение $rw(r) \approx {{a}_{{j,1}}}$ на $\gamma _{j}^{{[1]}}$ и $rw(r) \approx {{a}_{{j,3}}}$ на $\gamma _{j}^{{[3]}}$ (${{a}_{{j,1}}}$ и ${{a}_{{j,3}}}$ являются постоянными). Таким образом, потоки на компонентах $\gamma _{j}^{{[1]}}$ и $\gamma _{j}^{{[3]}}$ будут параллельны оси $r$ на плоскости $(r,z)$.

Далее положим

Из этой структуры траектории видно, что ${{\gamma }_{j}}$ имеет угол в точке $({{r}_{j}}(z_{j}^{ - }),z_{j}^{ - })$, соединяющей части $\gamma _{j}^{{[1]}}$ и $\gamma _{j}^{{[2]}}$, а также в точке $({{r}_{j}}(z_{j}^{ + }),z_{j}^{ + })$, соединяющей части $\gamma _{j}^{{[2]}}$ и $\gamma _{j}^{{[3]}}$. Наличие таких углов на траектории не является естественным. Однако в настоящей модели мы полагаем что такие углы не оказывают принципиального влияния на интегральный результат расчетов.

Для того, чтобы выбрать функции ${{r}_{j}}(z)$, которые появляются в определении $\gamma _{j}^{{[2]}}$, используем в качестве основной плотности $\bar {\varrho }$ гидростатическое распределение плотности влажного воздуха, и примем эмпирический критерий отношения между максимальным значением вертикальной составляющей ${{\bar {v}}_{z}}$ и максимальным значением радиальной составляющей ${{\bar {v}}_{r}}$ основной скорости $\bar {v}$. Примем также предположение, в соответствии с которым на величину ${{\left. {rw(r,z)} \right|}_{{(r,z) \in \gamma _{j}^{{[2]}}}}}$ не влияет $r$. Это предположение аналогично критерию, принятому выше для частей $\gamma _{j}^{{[1]}}$ и $\gamma _{j}^{{[3]}}$ траекторий.

Далее, чтобы определить использованную здесь основную плотность $\bar {\varrho }$, рассмотрим систему уравнений гидростатического распределения воздуха, который может быть влажным:

где $0 \leqslant \vartheta (z) \leqslant 1$ (для существования и единственности решения этой системы уравнений, см. [13]). Случай $\vartheta (z) = 0$ соответствует состоянию полностью сухого воздуха, а случай $\vartheta (z) = 1$ – случаю насыщенного влажного воздуха. Во втором из этих случаев температура распределена так, что происходит постоянная конденсация влаги. Выберем в качестве $\bar {\varrho }$ решение этой системы уравнений с $\vartheta (z) = 1$.

Что касается отношения максимального значения вертикальной составляющей скорости ветра к максимальному значению ее радиальной составляющей, то в моделях разных авторов эта величина различна. В нашей модели, следуя основным ее положениям [7], примем критерий

Начнем выбор траекторий с определения функции ${{\Lambda }_{0}}(z)$, которая представляет собой внешнюю границу “глаза” (см. (2)). Положим

Действительно, если в области “глаза” $\{ 0 < z < {{\bar {z}}_{1}},\;0 \leqslant r < {{\Lambda }_{0}}(z)\} $ с ${{\Lambda }_{0}}(z)$, определенной (27), воздух движется со скоростью ${{\bar {v}}_{0}}$, имеющей не зависимую от $z$ вертикальную составляющую, то справедливо $\nabla \cdot (\bar {\varrho }{{\bar {v}}_{0}}) = 0$. Это означает, что выбор ${{\Lambda }_{0}}(z)$ не будет влиять на возможное движение воздуха в “глазе” тайфуна.

Для того, чтобы определить $\gamma _{j}^{{[2]}}$ в соответствии с принятыми критериями, предположим

где ${{a}_{{j,2}}}$ – постоянная, а Поскольку $Q$ является зависимой только от $\tfrac{{{{q}_{r}}}}{{{{q}_{z}}}}$ функцией, согласно предположению (28) величина ${{\left. {rw(r,z)} \right|}_{{(r,z) \in \gamma _{j}^{{[2]}}}}}$ определяется отношением $\tfrac{{{{q}_{r}}}}{{{{q}_{z}}}}$. С другой стороны, если $({{q}_{r}},{{q}_{z}}) = (0,1)$, то $Q = \tfrac{1}{3}$, а если $({{q}_{r}},{{q}_{z}}) = (1,0)$, то $Q = 1$, в соответствии с критерием (26).

Так как согласно предположению (15) выполнено $\tfrac{{\partial \varrho }}{{\partial t}} \approx 0$, а ${{H}_{{tr}}}$ относительно небольшое, то заменяя ${{v}_{r}} = {{\alpha }_{{{{\gamma }_{j}}}}}{{q}_{r}}w$ и ${{v}_{z}} = {{\alpha }_{{{{\gamma }_{j}}}}}{{q}_{z}}w$ в (3) и считая ${{\alpha }_{{{{\gamma }_{j}}}}}$ не зависимым от $r$ и $z$ в области, представленной траекториями ${{\gamma }_{j}}$, получаем

Далее, заменяя $rw = {{a}_{{j,2}}}Q$ и $\varrho = \bar {\varrho }(z)$ в (30), получаем Так как $\tfrac{\partial }{{\partial r}}\bar {\varrho }(z) = 0$, из этого равенства следует Перепишем (31) в виде

Далее, из выражения (29) следует

Теперь заменим (33) и (34) в (32) и используем равенства которые следуют из (29); в итоге получим

Теперь построим $\gamma _{j}^{{[2]}}$, $j = 1,...,N$, последовательно определяя ${{r}_{j}}$ друг за другом (полагаем ${{r}_{0}}(z) = {{\Lambda }_{0}}(z)$). Для этого используем аппроксимацию

Если заменить $\tfrac{{\partial {{q}_{r}}}}{{\partial r}}$ выражением правой части (35) и пренебречь слагаемым $o\left( {\left| {{{r}_{j}}(z) - {{r}_{{j - 1}}}(z)} \right|} \right)$, то получим Если положить ${{q}_{z}}$ и $\tfrac{{\partial {{q}_{z}}}}{{\partial z}}$ в (37) равными их значениями на $\gamma _{{j - 1}}^{{[2]}}$, то (37) будет линейным дифференциальным уравнением для неизвестной функции ${{r}_{j}}(z)$. Таким образом, решив уравнение (37), получим ${{r}_{j}}(z)$ (и $\gamma _{j}^{{[2]}}$), $j = 1,...,N$, которые удовлетворяют принятым в модели критериям.

4. ДРУГИЕ УСЛОВИЯ И ОПРЕДЕЛЕНИЯ ДЛЯ ВЫЧИСЛИТЕЛЬНОГО МОДЕЛИРОВАНИЯ

Построив траектории ${{\gamma }_{j}} = \{ {{\gamma }_{j}}(s)\,|\,0 \leqslant s \leqslant \bar {s}_{j}^{{ - 1}}\} $, $j = 1,...,N$, мы теперь можем задать граничные условия для неизвестных функций $\varrho $, ${{v}_{\vartheta }}$, $T$, $w$ в точке входа ${{\gamma }_{j}}(0) = (\Lambda ,z_{j}^{ - })$ каждой траектории ${{\gamma }_{j}}$. Кроме того, наличие неизвестной величины $D(t)$ в уравнении (22) позволяет задать одно условие в точке выхода ${{\gamma }_{j}}(\bar {s}_{j}^{1}) = (\Lambda ,z_{j}^{ + })$ каждой траектории. Значит, мы задаем четыре условия входа

и одно условие выхода Здесь $\varrho ({{\gamma }_{j}};t,s)$ означает плотность $\varrho $ в момент времени $t$ в точке ${{\gamma }_{j}}(s)$, $0 \leqslant s \leqslant \bar {s}_{j}^{1}$. Аналогичные обозначения использованы для $T({{\gamma }_{j}};t,s)$, ${{v}_{\vartheta }}({{\gamma }_{j}};t,s)$, $w({{\gamma }_{j}};t,s)$.

Исходя из принятой физической модели, условия в точке входа ${{\gamma }_{j}}(0) = (\Lambda ,z_{j}^{ - })$ и в точке выхода ${{\gamma }_{j}}(\mathop {\overline s }\nolimits_j^1 ) = (\Lambda ,z_{j}^{ + })$ должны соответствовать условиям вне тропического циклона, поэтому предположим знание плотности ${{\varrho }_{{ex}}}(z)$ и температуры ${{T}_{{ex}}}(z)$ вне циклона, которые являются функциями от $z$, и запишем

Что касается $\bar {v}_{{\vartheta ,j}}^{0}$, то для независимости эволюции ${{v}_{\vartheta }}$, от выбора произвольного граничного значения на входе траектории, выберем достаточно малое значение $\bar {v}_{{\vartheta ,j}}^{0}$. С другой стороны, так как $w$ представляет собой нормированную скорость (см. (14)), то выберем для $\bar {w}_{j}^{0}$ не зависимую от $j$ постоянную. Таким образом, мы имеем следующие условия:

Что касается массы воды $\Sigma $ в жидком и твердом агрегатных состояниях в уравнении (22), то отметим, что она значима только в той части $\gamma _{j}^{{[2]}}$, где воздух поднимается вверх. Поэтому, учитывая, что траектории $\gamma _{j}^{{[2]}}$ наклонены и лежат одна над другой, используем следующее приближение:

где а $\varphi (\tau )$ представляет собой вероятность того, что капля (или льдинка) останется в воздухе после времени $\tau $, прошедшего с момента ее образования, и ${{\beta }_{j}}$ – коэффициент, описывающий количество жидкой или твердой воды, переносимой от траектории ${{\gamma }_{{j - 1}}}$ к траектории ${{\gamma }_{j}}$.

Для численных расчетов был использован метод конечных разностей. Обозначим через $\{ {{t}_{k}}\} $ дискретные моменты времени, а через $\{ {{s}_{{j,i}}}\} $ – координаты на траектории ${{\gamma }_{j}}$, т.е.

Здесь положения ${{s}_{j}}$ расположены в направлении течения воздуха так, что $0 = {{s}_{{j,0}}}$ и ${{s}_{{j,{{N}_{j}}}}} = \mathop {\overline s }\nolimits_j^1 $ соответствуют положениям входа и выхода потока воздуха вдоль траектории ${{\gamma }_{j}}$. Здесь примем равномерный шаг по времени ${{t}_{{k + 1}}} - {{t}_{k}} = {{\delta }_{t}}$ с постоянной ${{\delta }_{t}}$, а для положений ${{s}_{{j,i}}}$ нам удобно выбрать шаги, зависящие от $(j,i)$, т.е. ${{s}_{{j,i + 1}}} - {{s}_{{j,i}}} = {{\delta }_{s}}(j,i)$. Это позволит лучше описать структуру траекторий ${{\gamma }_{j}}$, а зависимость пространственного шага сетки от $(j,i)$ принципиально не повлияет на результаты численной схемы.

Численное решение построим с помощью явной схемы конечных разностей. Если имеется решение $(\alpha ,\varrho ,{{v}_{\vartheta }},T,w)$ для ${{t}_{0}},...,{{t}_{{k - 1}}}$ на всех траекториях, то можно вычислить $(\alpha ,\varrho ,{{v}_{\vartheta }},T,w)$ для ${{t}_{k}}$ следующим образом.

Во-первых, решим уравнение (20), написанное в следующем виде:

или и определим ${{v}_{\vartheta }}({{t}_{k}},{{s}_{{j,i}}})$ для $i = 0,...,{{N}_{j}}$ на каждой траектории ${{\gamma }_{j}}$. Действительно, условие ${{v}_{\vartheta }}({{t}_{k}},{{s}_{{j,0}}}) = \bar {v}_{\vartheta }^{0}$ (см. (39)) и уравнения (44) для $i = 1,...,{{N}_{j}}$ определят ${{v}_{\vartheta }}({{t}_{k}},{{s}_{{j,i}}})$ для $i = 0,...,{{N}_{j}}$.

Далее нам необходимо определить $(\varrho ({{t}_{k}},{{s}_{{j,i}}}),\;T({{t}_{k}},{{s}_{{j,i}}}),\;w({{t}_{k}},{{s}_{{j,i}}}))$ для $i = 0,...,{{N}_{j}}$ и $D({{t}_{k}}) = {{D}_{j}}({{t}_{k}})$ на каждой траектории ${{\gamma }_{j}}$. Если заданы $\alpha $, ${{v}_{\vartheta }}$ и $\Sigma $ и если мы используем предварительное значение ${{D}^{{(m)}}}$ для $D({{t}_{k}}) = {{D}_{j}}({{t}_{k}})$, то уравнения (19), (21), (22) на каждой траектории ${{\gamma }_{j}}$ образуют систему обыкновенных дифференциальных уравнений для неизвестных функций $\varrho $, $T$ и $w$, которые при начальных условиях (38), (40), (41), можно явно решить с помощью метода конечных разностей. Поскольку это решение зависит от предварительного значения ${{D}^{{(m)}}}$, заданного для $D({{t}_{k}}) = {{D}_{j}}({{t}_{k}})$, то значение произведения $\varrho ({{\gamma }_{j}};{{t}_{k}},\mathop {\overline s }\nolimits_j^1 )T({{\gamma }_{j}};{{t}_{k}},\mathop {\overline s }\nolimits_j^1 ) = \varrho ({{t}_{k}},{{s}_{{j,{{N}_{j}}}}})T({{t}_{k}},{{s}_{{j,{{N}_{j}}}}})$, которое мы обозначим ${{\varrho }^{{(m)}}}({{t}_{k}},\mathop {\overline s }\nolimits_j^1 ){{T}^{{(m)}}}({{t}_{k}},\mathop {\overline s }\nolimits_j^1 )$, также зависит от ${{D}^{{(m)}}}$. Однако, поскольку между ${{D}^{{(m)}}}$ и ${{\varrho }^{{(m)}}}({{t}_{k}},\mathop {\overline s }\nolimits_j^1 ){{T}^{{(m)}}}({{t}_{k}},\mathop {\overline s }\nolimits_j^1 )$ имеется сильная корреляция, физически обоснованная и подтвержденная численными вычислениями, то можно построить последовательность $\{ {{D}^{{(m)}}}\} $, которая быстро сходится к такому значению ${{D}^{{({{m}_{0}})}}}$, что ${{\varrho }^{{({{m}_{0}})}}}({{t}_{k}},\mathop {\overline s }\nolimits_j^1 ){{T}^{{({{m}_{0}})}}}({{t}_{k}},\mathop {\overline s }\nolimits_j^1 )$ удовлетворяет условию (42) с нужной точностью.

Третий и последний этап – определить $\alpha ({{t}_{k}}) = {{\alpha }_{j}}({{t}_{k}})$ из простого соотношения

Отметим здесь, что если заменить $D(t)$ производной $\tfrac{d}{{dt}}\alpha (t)$ (см. (16)), то из (14)–(15) мы получаем $\varrho wD(t) = \varrho \tfrac{{\partial {{v}_{\gamma }}}}{{\partial t}}$. Это позволяет интерпретировать член $\varrho wD(t)$ в уравнении (22), ответственным за эффект, который следует из равенства давления внутри и снаружи в точке входа $\gamma (0)$ и в точке выхода $\gamma ({{\bar {s}}_{1}})$ для линии тока воздуха с внутренним выделением скрытой теплоты конденсации водяного пара. Этот эффект аналогичен действию силы толкающей воздух вверх и, возможно, противодействующей трению водяных капель (или льдинок), которое препятствует такому подъему воздуха.

5. ВЫБОР ФИЗИЧЕСКИХ ПАРАМЕТРОВ МОДЕЛИ

Дадим пример численного решения предложенной модели эволюции тропического циклона, состоящей из уравнений (16), (19)–(22) и условий (38)–(42). Для численной реализации в соответствии с известными физическими законами (см., например, [14], [15]), необходимо прежде всего задать физические параметры:

(${{R}_{0}}$ и ${{\mu }_{a}}$ – соответственно универсальная постоянная газов и молярная масса воздуха) и определить функцию плотности насыщенного водяного пара (${{\mu }_{h}}$ – молярная масса воды), а также скрытую теплоту парообразования Так как разность плотности насыщенного пара на поверхности воды и на поверхности льда, как и скрытая теплота перехода воды из жидкого состояния в твердое, невелика, то в этой модели мы пренебрежем этими различиями и используем значения, заданные в (46), (47), которые соответствуют фазовому переходу ${{{\text{H}}}_{{\text{2}}}}{\text{O}}$ из газообразного в жидкое состояние (и обратно).

В качестве параметра силы Кориолиса выберем фиксированное значение $3 \times {{10}^{{ - 5}}}$ c^–1, которое соответствует его значению на широте 12N.

Для того, чтобы определить область $\Omega $ (или ${{\Gamma }_{{r,z}}}$), заданную в (1) (или (2)), выберем ${{\Lambda }_{1}} = 200$ км, ${{\bar {z}}_{1}} = 12$ км. Выберем также ${{\Lambda }_{0}}(0) = 10$ км и тем самым определим функцию ${{\Lambda }_{0}}(z)$ по формуле (27). Это соответствует модели тропического циклона средней мощности.

Приведем расчеты для 8 траекторий ${{\gamma }_{j}}$, $j = 1,...,8$. Разумеется, для детального расчета области ${{\Gamma }_{{r,z}}}$ и построения семейства траекторий $\{ {{\gamma }_{j}}\} $ число траекторий 8 слишком мало, но для иллюстрации поведения воздушного потока вдоль расчетных траекторий, по-нашему мнению, этого числа будет достаточно, чтобы оценить основные этапы эволюции воздушного потока и всего тропического циклона.

Для того, чтобы выбрать траектории ${{\gamma }_{j}}$, $j = 1,...,8$, предположим, что воздух, который втекает в область циклона $\Omega $, имеет влажность 50%, а воздух, который вытекает из $\Omega $, имеет влажность 100%. Тогда определим распределение плотности ${{\tilde {\varrho }}_{1}}(z)$ как решение уравнений (24)–(25) с

где ${{\bar {\zeta }}_{M}}$ выбрана так, чтобы $\{ r = {{\Lambda }_{1}},\;0 < z < {{\bar {\zeta }}_{M}}\} $ была границей втекания $({{v}_{r}} < 0)$, а $\{ r = {{\Lambda }_{1}},\;{{\bar {\zeta }}_{M}} < z < {{\bar {z}}_{1}}\} $ – границей вытекания $({{v}_{r}} > 0)$. Формальное определение ${{\bar {\zeta }}_{M}}$ не так однозначно, но его численная аппроксимация может быть построена. Используя эту функцию ${{\tilde {\varrho }}_{1}}(z)$, положим и определим $z_{j}^{ - }$ и $z_{j}^{ + }$ (см. (23)) соотношениями Определенные таким образом значения $z_{j}^{ - }$ и $z_{j}^{ + }$ приведены в табл. 1.

Траектории, построенные с помощью уравнения (36) по этим значениям $z_{j}^{ - }$ и $z_{j}^{ + }$, приведены в фиг. 1.

В условиях (38), (40), (42) мы используем значения плотности ${{\varrho }_{{ex}}}(z)$ и температуры ${{T}_{{ex}}}(z)$ вне зоны циклона. В качестве функций ${{\varrho }_{{ex}}}(z)$ и ${{T}_{{ex}}}(z)$ возьмем решение системы уравнений (24), (25) с выбором

Заметим, что условие (48) соответствует промежуточной влажности между условием (54) и полной влажностью $\vartheta (z) \equiv 1$, которая соответствует $\bar {\varrho }$.

В качестве функции ${{\varphi }_{j}}(\tau )$, использованной в выражении ${{\Sigma }_{j}}$ (см. (43)), возьмем функцию

с условием Напомним, что т.е. ${{b}_{j}}$ – средняя продолжительность времени, в котором капля (или льдинка) остается в воздухе после ее образования. С другой стороны, для коэффициентов ${{\beta }_{j}}$, использованных также в выражении ${{\Sigma }_{j}}$ (см. (43)), мы выберем условие

Для функции ${{\varepsilon }_{1}}(z)$, представляющей действие трения между воздухом и поверхностью океана, положим

6. РЕЗУЛЬТАТ ЧИСЛЕННОГО РАСЧЕТА

Приведем результат реализованного вычисления. На фиг. 2 показана эволюция коэффициентов интенсивности ${{\alpha }_{j}}(t)$ на траекториях ${{\gamma }_{j}}$, $j = 1,...,8$. Расчет был проведен шагом по времени 50 с.

Развитию скорости потока воздуха вдоль траекторий ${{\gamma }_{j}}$ сопутствует увеличение массы воды в жидком и твердом агрегатных состояниях ${{\Sigma }_{j}}(t)$, как показано на фиг. 3. Видно, что существует очень сильная корреляция между ${{\alpha }_{j}}(t)$ и ${{\Sigma }_{j}}(t)$.

Кроме того, заметим, что в этой модели развитие циклона оказывается довольно быстрым: менее чем за 24 ч он достигает своей зрелой структуры. Покажем профиль составляющей ${{v}_{\gamma }}$ скорости ветра вдоль траекторий в ее нижней части ${{\gamma }_{1}}$ и ${{\gamma }_{2}}$ через 24 ч (фиг. 4) и тангенциальной составляющей ${{v}_{\vartheta }}$ скорости ветра в нижней части траекторий ${{\gamma }_{1}}$ и ${{\gamma }_{2}}$ через 24 ч (фиг. 5). Размерность скорости дана в единицах $m{\text{/}}s$. Заметим, что тангенциальная составляющая на части ${{\gamma }_{2}}$ больше, чем на ${{\gamma }_{1}}$. Это наводит на мысль о влиянии трения на поверхности океана, тормозящего течение воздуха вблизи границы океан–атмосфера. Фиг. 6 показывает, что в верхней части тангенциальная составляющая ветра на ${{\gamma }_{2}}$ имеет то же направление, что и в нижней части, а тангенциальная составляющая ветра на ${{\gamma }_{1}}$ в периферической части тайфуна имеет противоположное направление. Это различие объясняется, по нашему мнению, тем фактом, что на траектории ${{\gamma }_{2}}$ влияние трения с поверхностью океана очень слабое и, таким образом, сила Кориолиса имеет такое же влияние в нижней части тайфуна, как и в его верхней части. С другой стороны, в нижней части ${{\gamma }_{1}}$ трение с поверхностью океана тормозит также ${{v}_{\vartheta }}$, а в верхней части этого трения нет, и таким образом в верхней части компонента ${{v}_{\vartheta }}$ на ${{\gamma }_{1}}$ благодаря силой Кориолиса выталкивается в противоположном направлении. Тот факт, что эффект трения с поверхностью океана менее очевиден в результате расчета для составляющей скорости в направлении траектории, можно интерпретировать как следствие использования при расчете фиксированных траекторий.

Что касается давления $p = {{R}_{1}}\varrho T$, то его профиль на нижней части ${{\gamma }_{1}}$ (230 м над уровнем моря) после расчета через 24 ч проведен в фиг. 7.

Фигуры 4, 5, 6, 7 показывают, что модель, предложенная в настоящей работе, разумным образом воспроизводит структуру тропического циклона.

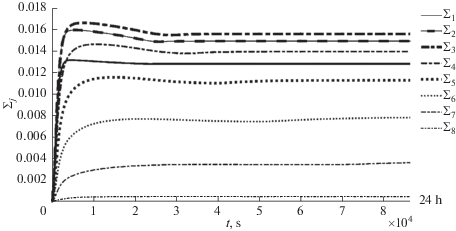
Представим также эволюцию коэффициентов интенсивности ${{\alpha }_{j}}(t)$ и массы воды в жидком или твердом состоянии ${{\Sigma }_{j}}(t)$ за 5 дней. Как видно на фиг. 8 и фиг. 9, значения ${{\alpha }_{j}}(t)$ и ${{\Sigma }_{j}}(t)$ приблизительно стабилизируются. Отметим здесь, что вдоль траекторий с большой массой воды в жидком или твердом состоянии стабилизация оказывается весьма быстрой, а вдоль траекторий с малой ${{\Sigma }_{j}}(t)$ такая стабилизация происходит медленно. На фиг. 8 и фиг. 9 не представлена эволюция ${{\alpha }_{8}}(t)$ и ${{\Sigma }_{8}}(t)$, поскольку на траектории ${{\gamma }_{8}}$ в некоторые моменты времени численные значения ${{\alpha }_{8}}(t)$ и ${{\Sigma }_{8}}(t)$ становятся отрицательными, что теряет физический смысл.

Для предложенной модели тропического циклона существует также стационарное решение. Значения коэффициентов интенсивности ${{\alpha }_{j}}$ и массы воды ${{\Sigma }_{j}}$ в жидком или твердом состоянии для стационарного решения показаны в следующей табл. 2. Видно, что, когда ${{\Sigma }_{j}}$ велико, то возникает быстрая сходимость ${{\alpha }_{j}}(t)$ и ${{\Sigma }_{j}}(t)$ к соответствующим значениям стационарного решения. Отметим также, что масса воды в жидком или твердом состоянии на ${{\gamma }_{8}}$ очень мала по сравнению с другими значениями ${{\Sigma }_{j}}$, $j = 1,...,7$. Это, по нашему мнению, вызывает относительную неустойчивость решения на ${{\gamma }_{8}}$.

7. ЗАКЛЮЧЕНИЕ И ПЕРСПЕКТИВЫ ИССЛЕДОВАНИЙ

В настоящей работе предложена система уравнений, которая в предположении осевой симметрии описывает движение воздуха вдоль семейства траекторий. Результат численного расчета выявил основные аспекты эволюции движения воздуха, вызванной конденсацией влаги с учетом скрытой теплоты парообразования, а также с учетом трения капель и льдинок, которое замедляет восходящий поток. Распределение скорости ветра и давления через 24 ч после начала расчета, полученное с помощью численного расчета, совпадает с общими характеристиками тропического циклона средней мощности. Мы интерпретируем полученную скорость роста модельного численного расчета, которая заметно превосходит данные наблюдений как следствие отличия нашей модельной постановки от реальности, в которой, помимо основного механизма тайфуна, участвуют также и другие факторы.

Использованная модель основана на описании фиксированных траекторий (на плоскости $(r,z)$), что облегчало численное решение. Однако ясно, что траектории должны сами определяться самосогласованным движением воздуха. В частности, необходимо принять во внимание следующие важные механизмы при описании циклона.

1. Эффект роста тангенциальной составляющей скорости, порождающей центробежную силу и посредством этого выталкивающей вверх воздух в нижней части траекторий.

2. Расширение зоны циклона в процессе самой эволюции циклона.

3. Эффект турбулентного движения потока воздуха.

С учетом сказанного нашей следующей задачей будет являться улучшение модели с включением вышеупомянутых факторов. Следует также учитывать перемещение самого тропического циклона. Однако моделирование этого явления в такой постановке потребует разработки нового метода.

Авторы выражают благодарность проф. О. Диаз Родригез из Института Метеорологии Гаваны (Куба) за выяснение физических аспектов тропических циклонов и доктору Д. Ремаун Бурега из Университета науки и технологии Орана (Алжир) за помощь в численном расчете. Мы благодарны также С.Л. Скороходову из ВЦ ФИЦ ИУ РАН за помощь в написании текста.