Журнал вычислительной математики и математической физики, 2020, T. 60, № 12, стр. 2122-2130

ВВЕДЕНИЕ

Оптические покрытия являются неотъемлемой частью многих современных устройств и приборов [1]. Они применяются в высококачественных зеркалах, фильтрах, поляризаторах, которые используются при изготовлении лазеров и медицинских диагностических приборов. Многослойные покрытия также позволяют практически полностью устранить отражение от линз объективов в определенном диапазоне длин волн. Это свойство используется в оптических системах, состоящих из большого числа линз, в офтальмологии, фототехнике, фотолитографии [2]. Многослойные оптические покрытия применяются в приборах современных крупных научных проектов: в рентгеновских зеркалах космических телескопов [3], в обсерваториях LIGO, где установлены интерферометры Майкельсона, дополненные высококачественными зеркалами, состоящими из многослойных покрытий [4], [5]. Основным методом получения многослойных покрытий в настоящее время является их напыление в вакуумных камерах.

Чтобы получить качественное покрытие с требуемыми оптическими характеристиками, нужно обеспечить надежный контроль процесса напыления слоев этого покрытия [6]. Наиболее широко используемые на практике методы оптического контроля являются крайне неустойчивыми к ошибкам процессов напыления и измерения контролирующего оптического сигнала. Как было ранее отмечено в работах [7]–[9], при прямом оптическом контроле без коррекции уровня сигнала остановки напыления возникают большие ошибки в толщинах слоев и наблюдается их кумулятивный рост с ростом номера напыляемого слоя. Для преодоления негативного влияния кумулятивного эффекта накопления ошибок были предложены различные подходы, позволяющие уменьшить влияние этого эффекта. Одним из таких подходов является контроль по так называемому “свингу” измеряемого сигнала, использующему зарегистрированные в ходе измерений экстремальные значения коэффициента отражения [10]. Однако и в случае контроля по свингу ошибки все равно возрастают с ростом числа напыляемых слоев. Для устранения этого эффекта в работе [11] был предложен метод контроля процесса напыления, который с теоретической точки зрения позволяет полностью устранить кумулятивный эффект накопления ошибок в напыляемых слоях, однако этот метод контроля не был реализован практически.

В данной работе мы обсуждаем видоизмененную версию предложенного в [11] метода контроля, использующую разработанный нами ранее нелокальный алгоритм анализа данных измерений [12]. Этот метод контроля напыления покрытий мы назвали “независимым”. Работа построена следующим образом. В разд. 1 детально описывается “независимый” метод контроля толщин слоев. В разд. 2 проводится сравнение численной устойчивости данного метода и других используемых на практике методов оптического контроля. В разд. 3 обсуждается вопрос о корреляции ошибок в толщинах слоев покрытий при использовании различных методов и показывается, что при использовании нового метода ошибки, допущенные в разных слоях, действительно являются некоррелированными.

1. “НЕЗАВИСИМЫЙ” МЕТОД ОПТИЧЕСКОГО КОНТРОЛЯ НАПЫЛЕНИЯ, ОСНОВАННЫЙ НА НЕЛОКАЛЬНОМ АЛГОРИТМЕ АНАЛИЗА ДАННЫХ ИЗМЕРЕНИЙ

Для того чтобы описать “независимый” метод контроля, детально рассмотрим процесс напыления многослойного оптического покрытия и введем необходимые обозначения. На подложку с показателем преломления ${{n}_{s}}$ напыляется $N$ слоев покрытия. Пусть напыляемый слой с номером $j$ имеет показатель преломления ${{n}_{j}}$ и теоретическую толщину $d_{j}^{{theor}}$, а напыление $j$-го слоя происходит со средней скоростью ${{r}_{j}}$. В процессе напыления измеряется коэффициент отражения $R_{i}^{{meas}}$ в моменты времени ${{t}_{i}}$ на длине волны ${{\lambda }_{j}}$, где ${{\lambda }_{j}}$ – выбранная длина волны мониторинга $j$-го слоя, а $i$ – сквозной по отношению к напыляемым слоям индекс, который начинается с нуля и нумерует все измерения, выполняемые в процессе напыления всего многослойного покрытия. Для целей моделирования будем считать, что коэффициент отражения $R_{i}^{{meas}}$ измеряется с нормально распределенной случайной ошибкой $\delta R$ с нулевым средним и стандартным отклонением ${{\sigma }_{R}}$. Коэффициент отражения $R_{i}^{{meas}}$ измеряется в процентах.

В момент времени ${{t}_{{{{i}_{{end,j}}}}}} = t_{j}^{{term}}$ происходит остановка процесса напыления $j$-го слоя. Разные методы контроля отличаются алгоритмами расчета времени $t_{j}^{{term}}$. Оптические методы контроля отличаются от контроля по времени тем, что $t_{j}^{{term}}$ рассчитывается из условия, что в момент остановки напыления оцениваемый коэффициент отражения $R_{i}^{{act}}(t_{j}^{{term}})$, который будет описан ниже, должен быть равен заранее оцененному уровню остановки $R_{j}^{{act,term}}$ напыления $j$-го слоя.

Функция $R_{i}^{{act}}(t)$ – это оценка зависимости значения коэффициента отражения от времени, сделанная на основе имеющихся на $i$-м шаге измерений ${\text{\{ }}({{t}_{0}},R_{0}^{{meas}}),({{t}_{1}},R_{1}^{{meas}}), \ldots ,({{t}_{i}},R_{i}^{{meas}}){\text{\} }}$, где ${{t}_{0}} = 0$, а $R_{0}^{{meas}}$ – коэффициент отражения чистой подложки. Далее в работе будет использоваться оценка $R_{i}^{{act}}(t)$, полученная с помощью нелокального алгоритма анализа данных. Детально этот алгоритм описан в работе [12], здесь приведем только его краткое описание.

В силу того, что нелокальный алгоритм анализа данных аппроксимирует измерения коэффициента отражения отдельно для каждого слоя, функция $R_{i}^{{act}}(t)$ состоит из следующих независимых фрагментов:

Нелокальный алгоритм анализа данных для построения $R_{{j,i}}^{{act}}(t)$ использует все измерения, относящиеся к напылению $j$-го слоя, т.е. ${\text{\{ }}({{t}_{{{{i}_{{beg,j}}}}}},R_{{{{i}_{{beg,j}}}}}^{{meas}}), \ldots ,({{t}_{i}},R_{i}^{{meas}}){\text{\} }}$. Число ${{i}_{{beg,j}}} = {{i}_{{end,(j - 1)}}}$ определяет индекс момента времени конца напыления $(j - 1)$-го слоя и, в то же время, начала напыления $j$-го слоя. Таким образом, ${{i}_{{beg,1}}} = 0$, а для $j > 0$ число ${{i}_{{beg,j}}} = {\text{\{ }}i:{{t}_{i}} = t_{{j - 1}}^{{term}}{\text{\} }}$. Функция $R_{i}^{{act}}(t)$ имеет индекс $i$ в связи с тем, что ее часть $R_{{j,i}}^{{act}}(t)$ пересчитывается после каждого нового измерения $({{t}_{i}},R_{i}^{{meas}})$. Заметим, что эта часть функции определена и для $t > {{t}_{i}}$, хотя аппроксимирует измерения на сегменте $[{{t}_{{{{i}_{{beg,j}}}}}},{{t}_{i}}]$. Такая экстраполяция является корректной в силу того, что в вид аппроксимирующей функции заложена модель соответствующего физического процесса, что обосновывает правильное предсказание дальнейшего процесса напыления.

На сегменте, соответствующем $j$-му слою, $R_{{j,i}}^{{act}}(t)$ определяется в виде (см. [9])

Коэффициенты ${{\alpha }_{i}}$, ${{\beta }_{i}}$, ${{\gamma }_{i}}$ вычисляются следующим образом. Поставим в соответствие каждому результату измерений $({{t}_{k}},R_{k}^{{meas}})$, $k = \overline {{{i}_{{beg,j}}},i} $, набор значений $({{x}_{k}},{{y}_{k}},{{w}_{k}})$, который вычисляется по формулам

Для определения коэффициентов ${{X}_{i}} = {{({{\alpha }_{i}},{{\beta }_{i}},{{\gamma }_{i}})}^{{\text{т}}}}$ получим систему линейных уравнений, решение которой определяется в виде где

Описанный нелокальный алгоритм позволяет получить функцию $R_{{j,i}}^{{act}}(t)$, которая используется в для определения ожидаемого уровня остановки напыления $j$-го слоя $R_{{j,i}}^{{act,term}}$.

“Независимый” метод контроля на основе вычисленных коэффициентов ${{\alpha }_{i}}$, ${{\beta }_{i}}$ и ${{\gamma }_{i}}$ определяет уровень остановки $R_{{j,i}}^{{act,term}}$ по формуле:

Формула (1), определяющая уровень остановки, естественным образом следует из физической модели, которая также использована при получении нелокального алгоритма анализа данных измерений коэффициента отражения в процессе напыления слоя [12]. Уровень остановки $R_{{j,i}}^{{act,term}}$ для $j$-го слоя соответствует коэффициенту отражения, который должен наблюдаться при достижении теоретической толщины слоя $d_{j}^{{theor}}$.

Заметим, что предложенный метод постоянно (для каждого очередного момента времени ${{t}_{i}}$) корректирует значение $R_{{j,i}}^{{act,term}}$ на основе вычисленных коэффициентов ${{\alpha }_{i}}$, ${{\beta }_{i}}$ и ${{\gamma }_{i}}$. Значение $R_{{j,i}}^{{act,term}}$ пересчитывается на каждом шаге $i$. Когда на некотором $i$-м шаге значение $R_{{j,i}}^{{act,term}}$ оказывается заключено между значениями $R_{{j,i}}^{{act}}({{t}_{i}})$ и $R_{{j,i}}^{{act}}({{t}_{i}} + \tau )$, где $\tau $ – шаг по времени, с которым ведутся измерения, то это значение и становится уровнем остановки для $j$-го слоя: $R_{j}^{{act,term}} = R_{{j,{{i}_{{end,j}}}}}^{{act,term}}$. Необходимо отметить, что так как функция $R_{{j,i}}^{{act}}(t)$ пересчитывается на каждом шаге, то, вообще говоря, нельзя гарантировать, что указанный критерий остановки будет удовлетворен. Может случиться так, что после получения новых измерений $({{t}_{i}},R_{i}^{{meas}})$ пересчитанная функция $R_{{j,i}}^{{act}}(t)$ даст оцененное значение $t_{j}^{{term}}$ меньшее, чем текущий момент времени ${{t}_{i}}$. В этом случае положим $t_{j}^{{term}}: = {{t}_{i}}$.

Далее мы сравним “независимый” метод контроля с другими методами контроля, используемыми в настоящее время на практике. Отметим, что методы оптического контроля определяются способами расчета уровня остановки $R_{j}^{{act,term}}$. Рассмотрим два основных метода контроля.

Метод контроля “без коррекции”. В этом методе остановка напыления $j$-го слоя происходит по теоретически рассчитанным значениям коэффициента отражения:

Здесь $R_{j}^{{theor,term}} = R(\vec {d}_{j}^{{theor}},{{\lambda }_{j}})$, где $R(\vec {d},\lambda )$ – функция, вычисляющая теоретическое значение коэффициента отражения на длине волны $\lambda $ в зависимости от набора толщин физических слоев $\vec {d}$, определяющих многослойное покрытие, и вектор $\vec {d}_{j}^{{theor}}$ = ${\text{\{ }}d_{1}^{{theor}},d_{2}^{{theor}}, \ldots ,d_{j}^{{theor}}{\text{\} }}$ [13]. При таком подходе все $R_{j}^{{act,term}}$ могут быть вычислены априорно еще до начала напыления.

Заметим, что в процессе напыления каждый напыленный $j$-й слой в действительности имеет физическую толщину $d_{j}^{{act}}$, вообще говоря, не равную теоретической $d_{j}^{{theor}}$. Тип контроля “без коррекции” чрезвычайно чувствителен к ошибкам в толщинах предыдущих слоев. При таком контроле ошибки очень быстро растут при росте номера слоя $j$ (кумулятивный эффект накопления ошибок, см. [7]). В связи с этим на практике часто используются другие методы контроля процесса напыления, более устойчивые к ошибкам напыления $\Delta {{d}_{k}}$.

Метод контроля по “квазисвингу”. Этот метод контроля является частным случаем наиболее широко используемого на практике контроля по “свингу” измеряемого сигнала. Контроль по “свингу” для вычисления скорректированного уровня остановки $R_{{j,i}}^{{act,term}}$ использует значения экстремумов измеряемого сигнала, достигаемых в процессе напыления $j$-го слоя. В этом случае $R_{{j,i}}^{{act,term}}$ вычисляется по формуле

где $R_{j}^{{theor,extr.last}}$ – это последнее рассчитанное теоретически экстремальное значение коэффициента отражения, т.е. это максимум $R_{j}^{{theor,max}}$, если последний наблюдаемый экстремум в течение напыления $j$-го слоя должен быть максимумом, и минимум $R_{j}^{{theor,min}}$ в противном случае. Индекс $theor$ означает, что имеются в виду экстремумы функции $R({{(d_{1}^{{theor}},d_{2}^{{theor}}, \ldots ,d_{{j - 1}}^{{theor}},d)}^{{\text{т}}}},{{\lambda }_{j}})$, зависящей от переменной $d$, где $d \geqslant 0$. Аналогичным образом определяется величина $R_{{j,i}}^{{act,extr.last}}$. $A_{j}^{{theor}}$ – теоретическая амплитуда изменения коэффициента отражения на $j$-м слое: $A_{j}^{{theor}} = R_{j}^{{theor,max}} - R_{j}^{{theor,min}}$; $A_{{j,i}}^{{act}}$ – оценка действительной амплитуды изменения коэффициента отражения на $j$-м слое, сделанная после $i$-го измерения: $A_{{j,i}}^{{act}} = R_{{j,i}}^{{act,max}} - R_{{j,i}}^{{act,min}}$.

Контроль по “квазисвингу” использует нелокальный алгоритм анализа данных, описанный выше, для вычисления этих значений: максимум и минимум $R_{{j,i}}^{{act}}(t)$ определяются в виде

Этот тип контроля назван “квазисвингом”, потому что, вообще говоря, если время напыления $j$-го слоя невелико, то экстремальные значения могут и не достигаться за время напыления $j$-го слоя, но спрогнозированные их значения будут все равно использованы при вычислении скорректированного уровня остановки, т.е. может быть использован “свинг”, который фактически не наблюдался.

Описанный тип контроля существенно более устойчив к ошибкам, допущенным при напылении предыдущих слоев, чем рассмотренный выше метод контроля без коррекции.

2. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ПО СРАВНЕНИЮ МЕТОДОВ ОПТИЧЕСКОГО КОНТРОЛЯ

Для сравнения эффективности разных методов оптического контроля нами был программно реализован симулятор напыления оптических покрытий [10], позволяющий для заданной конструкции покрытия сравнивать между собой различные методы контроля процесса напыления. Время выполнения одного вычислительного эксперимента по симуляции процесса напыления на современном персональном компьютере составляет около $0.2$ с для 20-слойного покрытия. Это позволяет анализировать ошибки напыления, полученные в результате десятков тысяч вычислительных экспериментов. Эксперименты были проведены для двух разных покрытий:

• 20-слойное четвертьволновое зеркало QWM-20. Число слоев $N = 20$, ${{n}_{s}} = 1.46$.

Для четных слоев: ${{n}_{j}} = {{n}_{L}} = 1.46$, $d_{j}^{{theor}} = {{d}_{L}} = 150{\text{/}}{{n}_{L}}$, ${{r}_{j}} = 0.25$ нм/c, ${{\sigma }_{{{{r}_{j}}}}} = 0.001$ нм/c.

Для нечетных слоев: ${{n}_{j}} = {{n}_{H}} = 2.38$, $d_{j}^{{theor}} = 150{\text{/}}{{n}_{H}}$, ${{r}_{j}} = 0.25({{n}_{H}}{\text{/}}{{n}_{L}})$ нм/c, ${{\sigma }_{{{{r}_{j}}}}} = 0.001({{n}_{H}}{\text{/}}{{n}_{L}})$ ${{\sigma }_{{{{r}_{j}}}}} = 0.001({{n}_{H}}{\text{/}}{{n}_{L}})$ нм/c.

Все ${{d}_{j}}$ измеряются в нанометрах.

Измерения проводятся для всех $j$ на длине волны ${{\lambda }_{j}} = 510$ нм.

• 28-слойный поляризатор POL-28. Число слоев $N = 28$, ${{n}_{s}} = 1.52$.

Для четных слоев ${{n}_{j}} = {{n}_{L}} = 1.46$,  ${{r}_{j}} = 0.25$ нм/c, ${{\sigma }_{{{{r}_{j}}}}} = 0.001$ нм/c.

Для нечетных слоев: ${{n}_{j}} = {{n}_{H}} = 2.05$, ${{r}_{j}} = 0.25({{n}_{H}}{\text{/}}{{n}_{L}})$ нм/c, ${{\sigma }_{{{{r}_{j}}}}} = 0.001({{n}_{H}}{\text{/}}{{n}_{L}})$ нм/c.

Вектор физических толщин в нм: ${{\vec {d}}^{{theor}}} = {\text{\{ }}128.330$, $195.813$, $119.487$, $183.328$, $115.574$, $183.111$, $118.132$, $189.457$, $122.690$, $196.483$, $126.669$, $201.566$, $128.960$, $203.485$, $129.034$, $201.793$, $126.873$, $196.878$, $122.968$, $189.891$, $118.363$, $183.304$, $115.509$, $182.830$, $118.919$, $194.655$, $129.795$, $530.535{\text{\} }}$.

Измерения проводятся для всех $j$ на длине волны ${{\lambda }_{j}} = 790$ нм.

Обозначим среднеквадратичную ошибку в толщинах слоев, допущенную при напылении покрытия, через

Для того чтобы оценить эффективность используемого метода контроля, введем усредненную ошибку по всем $S$ экспериментам с одинаковыми параметрами:

Для фиксированного стандартного отклонения ${{\sigma }_{R}}$ нормальной случайной ошибки $\delta R$ измерения коэффициента отражения $R_{i}^{{meas}}$ были проведены по $S = 100$ симуляций для каждого типа контроля и вычислены величины $\left\langle {\overline {\Delta d} } \right\rangle $. Расчеты были проведены с ${{\sigma }_{R}} = 0.01$, $0.02$, $ \ldots $, $0.10$. Таким образом, были построены графики $\left\langle {\overline {\Delta d} } \right\rangle ({{\sigma }_{R}})$, изображенные на фиг. 1.

Из результатов, представленных на фиг. 1, видно, что усредненная ошибка при реализации метода контроля “без коррекции” так быстро растет при росте ошибки измерений $R_{i}^{{meas}}$, что соответствующие кривые необходимо было представить на отдельном графике с большим масштабом, чем в случае экспериментов с двумя другими методами контроля. Рост ошибки имеет очевидно нелинейный характер. Метод контроля по “квазисвингу” при небольших ${{\sigma }_{R}}$ для покрытия POL-28 имеет ошибку $\left\langle {\overline {\Delta d} } \right\rangle $ меньше, чем у “независимого” контроля, но в остальных случаях его ошибка больше, при этом также виден нелинейный характер роста $\left\langle {\overline {\Delta d} } \right\rangle ({{\sigma }_{R}})$. В случае “независимого” метода контроля видно, что усредненная ошибка $\left\langle {\overline {\Delta d} } \right\rangle $ пропорциональна ${{\sigma }_{R}}$.

3. ИССЛЕДОВАНИЕ КОРРЕЛЯЦИИ ОШИБОК В ТОЛЩИНАХ СЛОЕВ ПРИ РАЗЛИЧНЫХ МЕТОДАХ КОНТРОЛЯ

Для исследования вопроса о корреляции ошибок в толщинах слоев при использовании описанных методов контроля были проведены по $S = {{10}^{4}}$ симуляций процесса напыления с покрытиями, описанными в предыдущем разделе, с одним фиксированным значением стандартного отклонения ${{\sigma }_{R}} = 0.01\% $. По результатам проведенных экспериментов для каждого метода контроля были составлены матрицы $A = {\text{\{ }}{{a}_{{j,s}}}{\text{\} }}$; ${{a}_{{j,s}}} = \Delta {{d}_{{j,s}}}{\text{/}}\mathop {\left\| {\Delta {{{\vec {d}}}_{s}}} \right\|}\nolimits_2 $, где вектор ошибок, соответствующий $s$-й симуляции $\Delta {{\vec {d}}_{s}} = {{(\Delta {{d}_{{1,s}}}, \ldots ,\Delta {{d}_{{N,s}}})}^{{\text{т}}}}$, индекс $j = \overline {1,N} $ соответствует номеру слоя, а индекс $s = \overline {1,S} $ – номеру симуляции. Таким образом, матрицы $A$ имеют размерность $20 \times {{10}^{4}}$ в случае покрытия QWM-20 и $28 \times {{10}^{4}}$ в случае покрытия POL-28.

При “независимом” методе контроля используются только измерения, полученные при напылении $j$-го слоя, и коррекция уровня остановки происходит таким образом, что оптическая толщина слоя контролируется полностью независимо от реально напыленных предыдущих слоев. Поэтому следует ожидать, что допущенные в разных слоях ошибки должны быть некоррелированы. Это означает, что векторы ошибок $\Delta {{\vec {d}}_{s}}$ должны быть равномерно распределены по всем направлениям в $N$-мерном пространстве. Для того чтобы убедиться, что полученные ошибки при использовании “независимого” типа контроля действительно таковы, проведем сингулярное разложение матрицы $A$.

Сингулярное разложение имеет следующее свойство. Матрица $A \in {{\mathbb{R}}^{{S \times N}}}$ представляется в виде $A = U\Sigma {{V}^{{\text{т}}}}$, где $V \in {{\mathbb{R}}^{{N \times N}}}$ есть матрица $V({{{\vec {v}}}_{1}},{{{\vec {v}}}_{1}} \ldots ,{{{\vec {v}}}_{N}})$, составленная из векторов ${{{\vec {v}}}_{j}}$, образующих ортонормированный базис в пространстве ${{\mathbb{R}}^{N}}$. Сингулярные числа ${{\sigma }_{j}}$, стоящие на диагонали в матрице $S$, есть корень квадратный из суммы квадратов проекций всех ошибок $\Delta {{\vec {d}}_{s}}$ на направление ${{{\vec {v}}}_{j}}$ в пространстве ${{\mathbb{R}}^{N}}$:

Если в пространстве ошибок нет выделенного направления, то математическое ожидание всех проекций $p$ случайного единичного вектора на ортонормированный базис должно быть одинаково $p = \sqrt {1{\text{/}}N} $. Соответственно все значения сингулярных чисел ${{\sigma }_{j}}$ для матрицы $A$, составленной из $S$ таких случайных векторов, должны находиться около значения $\sqrt {S{\text{/}}N} $. Из предположения о том, что ошибки при использовании “независимого” метода контроля равномерно распределены по всем направлениям в $N$-мерном пространстве, следует, что все сингулярные числа матрицы $A$ тоже будут примерно одинаковы и равны $\sqrt {S{\text{/}}N} $.

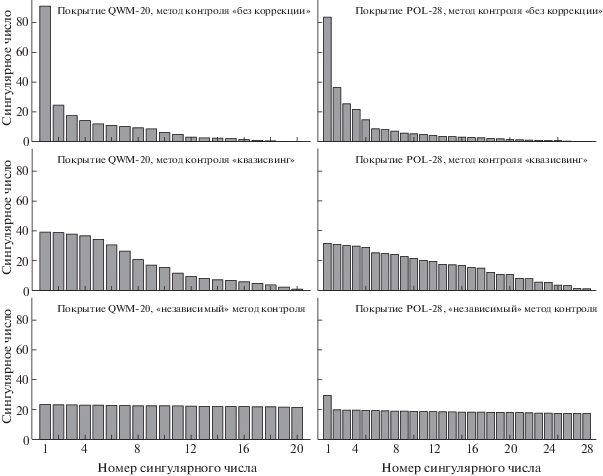
Сравним сингулярные числа разложения матрицы $A$ для всех трех рассмотренных методов контроля для покрытий QWM-20 и POL-28. Построенные диаграммы приведены на фиг. 2.

На фиг. 2 видно, что при “независимом” методе контроля сингулярные числа практически одинаковы в отличие от других методов. Одно сингулярное число матрицы $A$ для покрытия POL-28 существенно больше остальных из-за того, что это покрытие имеет толстый последний слой, который примерно в два раза толще всех остальных в этом покрытии. Поэтому в среднем ошибка, допускаемая в последнем слое, больше, чем во всех остальных слоях, и, соответственно, появляется некоторое выделенное направление в пространстве, с которым и связано данное сингулярное число.

Для дополнительной проверки отсутствия корреляции ошибок при использовании независимого метода контроля была составлена матрица RND-20 $ \in {{\mathbb{R}}^{{{{{10}}^{4}} \times 20}}}$ из случайных единичных векторов, равномерно распределенных по $20$-мерной сфере. Ожидаемое значение составило $\sqrt {{{{10}}^{4}}{\text{/}}20} \approx 22.4$. На фиг. 3 видно, что сингулярные числа матрицы $A$ для покрытия QWM-20 практически неотличимы от сингулярных чисел случайной матрицы для покрытия RND-20. Это подтверждает отсутствие выделенного направления в пространстве ${{\mathbb{R}}^{{20}}}$.

ЗАКЛЮЧЕНИЕ

В работе предложен новый метод оптического контроля. Проведены вычислительные эксперименты по напылению с использованием нового “независимого” метода контроля, а также методов контроля “без коррекции” и по “квазисвингу”. Сравнение ошибок в толщинах слоев, полученных в вычислительных экспериментах, показывает, что при использовании “независимого” метода контроля ошибки оказываются ниже, чем для других сравниваемых методов. Из анализа сингулярных чисел следует, что векторы ошибок, получаемые в экспериментах, не имеют ярко выраженного направления, что говорит о том, что ошибка в толщине каждого слоя не зависит от ошибок, допущенных в предыдущих слоях. Это свойство позволяет полностью устранить кумулятивный эффект накопления ошибок при оптическом контроле напыления покрытий.