1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 60, № 12, 2020

Журнал вычислительной математики и математической физики, 2020, T. 60, № 12, стр. 2131-2142

Модификация проекционного метода для анализа излучения радиального диполя в присутствии неоднородного тела вращения

Е. И. Семерня 1, С. П. Скобелев 1, 2, *

1 МФТИ (национальный исследовательский университет)
141701 М.о., Долгопрудный, Институтский пер., 9, Россия

2 ПАО “Радиофизика”
125363 Москва, ул. Героев Панфиловцев, 10, Россия

* E-mail: s.p.skobelev@mail.ru

Поступила в редакцию 13.08.2019
После доработки 29.06.2020
Принята к публикации 04.08.2020

Полный текст (PDF)

Аннотация

Рассмотрена задача излучения радиального электрического диполя, расположенного на оси вращения осесимметричного тела, состоящего из однородной диэлектрической сферы и внешнего неоднородного диэлектрического слоя. Новый численный алгоритм, разработанный для решения задачи, основан на проекционном методе, включающем проектирование полей на поперечные сферические функции в сочетании с применением одномерного метода конечных элементов в проекционной форме по радиальной координате. Алгоритм также обобщен на случай, когда внутренняя сфера является идеально проводящей. Приведены численные результаты, характеризующие как эффективность самого метода, так и влияние различных параметров тела на диаграмму направленности диполя. Библ. 31. Фиг. 6.

Ключевые слова: численные методы, рассеяние электромагнитных волн, диэлектрические тела вращения, неоднородные среды.

1. ВВЕДЕНИЕ

Задача рассеяния электромагнитных волн на неоднородных телах вращения представляет большой интерес в электродинамике: ее решение имеет ряд важных технических приложений в радиолокации, антенной технике, метеорологии и медицинской диагностике.

В общем случае указанная задача в строгой постановке может быть решена только численными методами. Их список включает проекционные методы (см. [1]–[8]); метод конечных элементов (см. [9], [10]); метод, основанный на замене неоднородного тела многослойным телом с однородными слоями с последующим применением метода интегральных уравнений для эквивалентных токов на поверхностях слоев (см. [11]) или метода вспомогательных источников (см. [12]); а также метод объемных интегральных уравнений (см. [13]–[15]).

Уравнения Максвелла в методах из [1], [2] и [5]–[8] проектируются на поперечные векторные сферические функции, в результате чего задача сводится к системе обыкновенных дифференциальных уравнений для коэффициентов разложений полей, зависящих только от радиальной координаты. Указанные работы содержат обоснования сходимости алгоритмов, но сами алгоритмы не доведены до численной реализации.

Проекционный метод, предложенный в [3] и реализованный в [4], предназначен для решения осесимметричных задач рассеяния на проводящих телах вращения с неоднородной диэлектрической оболочкой. Метод включает преобразование координат, сводящее геометрию задачи к неоднородному сферическому слою, поле в котором представляется в виде разложения по поперечным базисным функциям в виде диаграмм направленности кольцевых вспомогательных токов, радиусы и положения которых учитывают геометрию исходного проводящего тела. Переменные коэффициенты указанного разложения, а также постоянные коэффициенты разложения поля вне слоя по сферическим волнам, определяются путем численного решения системы обыкновенных дифференциальных уравнений, полученных в результате проектирования соответствующего уравнения в частных производных на введенные базисные функции.

Электромагнитные поля в проекционном методе из [9], [10] представляются в виде разложений по системам векторных собственных функций сферических резонаторов с электрическими и магнитными стенками. Последующее проектирование уравнений Максвелла на указанные собственные функции сводит задачу к системе линейных алгебраических уравнений. Такой подход был реализован в [10] для случая возбуждения диэлектрического тела плоской волной, распространяющейся вдоль оси вращения. Алгебраическая система в этом методе характеризуется полностью заполненной матрицей, элементы которой приходится вычислять численными методами. Результаты, приведенные в [10], показывают заметные отличия от данных, полученных строгим методом для частного случая диэлектрической сферы.

Трехмерный метод конечных элементов (см. [11], [12]) является наиболее мощным средством для численного решения задачи. Однако при его реализации требуется формировать пространственную сетку, использовать довольно сложные векторные конечные элементы, а также решать проблему сопряжения конечных элементов в ограниченной области с полем вне указанной области, для чего приходится использовать либо искусственный идеально поглощающий слой, окружающий ограниченную область, либо дополнительные поверхностные интегральные уравнения.

Методы из [13], [14] сводят задачу к алгебраическим системам с блочно-трехдиагональными матрицами, элементы которых, однако, определяются громоздкими формулами для полей кольцевых токов и требуют трудоемких численных расчетов.

Применение метода объемных интегральных уравнений (см. [15]–[17]) сводит задачу к алгебраическим системам с полностью заполненными матрицами, элементы которых также требуют трудоемких расчетов с применением численных методов.

Цель настоящей работы – исследовать возможность применения так называемого гибридного проекционного метода (ГПМ) к электродинамическому анализу неоднородных тел вращения. ГПМ ранее применялся для анализа волноводно-диэлектрических антенных решеток (см. [18], [19]), согласующих и поглощающих периодических диэлектрических структур (см. [20]–[22]), продольно неоднородных диэлектрических переходов в круглых волноводах (см. [23]–[25]) и неоднородных диэлектрических цилиндров произвольного поперечного сечения (см. [26]–[28]). Применение ГПМ представляет здесь интерес по нескольким причинам. В отличие от [11], [12], в нем используются одномерная сетка и простые треугольные конечные элементы в радиальном направлении. Кроме того, как и в [1], [2], [5]–[8], но в отличие от [3], [4], в нем используются одни те же поперечные функции для представления полей в ограниченной неоднородной области и в свободном пространстве, что обеспечивает естественный переход от одной области к другой, благодаря парциальным условиям излучения (см. [1]). Как и в [13], [14], задача здесь также сводится к уравнениям с блочно-трехдиагональными матрицами, но матричные элементы определяются простыми выражениями, не требующими трудоемких вычислений. Указанные особенности обеспечивают потенциальные преимущества ГПМ и по сравнению с проекционным методом (см. [9], [10]) и методом объемных интегральных уравнений (см. [15]–[17]).

Разработка и исследования алгоритмов, основанных на указанном подходе, здесь ограничиваются случаем осесимметричного возбуждения неоднородного тела вращения радиальным электрическим диполем, расположенным на оси вращения тела. Этот случай представляет интерес для исследования влияния осесимметричных неоднородных объектов на характеристики излучения антенн, расположенных вблизи них.

2. ПОСТАНОВКА ЗАДАЧИ И МЕТОД РЕШЕНИЯ

Продольное сечение диэлектрического тела вращения, расположенного в свободном пространстве в декартовых координатах x, y, z и сферических координатах r, θ, φ, показано на фиг. 1. Тело содержит однородную сферу радиуса a1 и относительной диэлектрической проницаемости ε1 с центром, расположенным в начале координат. Указанная сфера окружена неоднородным внешним слоем с относительной диэлектрической проницаемостью ε(r, θ). Неоднородность слоя может проявляться также и отличием его внешней поверхности от сферической поверхности. Относительная магнитная проницаемость сферы и неоднородного слоя считается равной единице.

Фиг. 1.

Геометрия задачи и продольное сечение тела вращения.

Мы предполагаем, что рассматриваемое тело возбуждается элементарным радиальным электрическим диполем, расположенным на оси вращения z вблизи тела на расстоянии r0 от начала координат (фиг. 1). Цель задачи – определить поле, излученное диполем в присутствии тела, включая диаграмму направленности (ДН) диполя, и поле внутри тела.

Электромагнитное поле, соответствующее возбуждению, указанному выше, содержит азимутальную составляющую напряженности магнитного поля Hφ, радиальную составляющую напряженности электрического поля Er и меридиональную составляющую напряженности электрического поля Eθ. Указанные составляющие должны удовлетворять уравнениям Максвелла

(1)
$\frac{1}{r}\frac{{\partial (r{{E}_{\theta }})}}{{\partial r}} - \frac{1}{r}\frac{{\partial {{E}_{r}}}}{{\partial \theta }} = i\omega {{\mu }_{0}}{{H}_{\varphi }},$
(2)
$\frac{1}{{r\sin \theta }}\frac{{\partial (\sin \theta {{H}_{\varphi }})}}{{\partial \theta }} = - i\omega {{\varepsilon }_{0}}\hat {\varepsilon }{\kern 1pt} {{E}_{r}} + j_{r}^{e},$
(3)
$ - \frac{1}{r}\frac{{\partial (r{{H}_{\varphi }})}}{{\partial r}} = - i\omega {{\varepsilon }_{0}}\hat {\varepsilon }{{E}_{\theta }},$
где ε0 и μ0 – электрическая и магнитная постоянные свободного пространства соответственно, $\hat {\varepsilon }$ – относительная диэлектрическая проницаемость соответствующей области,
(4)
$j_{r}^{e}(r,\theta ,\varphi ) = {{I}^{e}}l\frac{{\delta (r - {{r}_{0}})\delta (\theta - 0)\delta (\varphi - 0)}}{{{{r}^{2}}\sin \theta }}$
есть плотность тока диполя с дипольным моментом, определяемым электрическим током ${{I}^{e}}$ и длиной l, и ω – круговая частота в гармонической зависимости полей от времени, взятой в виде e–iωt.

Определяя Er и Eθ из (2) и (3) и подставляя их в (1), получаем уравнение

(5)
$\frac{\partial }{{\partial r}}\left[ {\frac{1}{{\hat {\varepsilon }}}{\text{ }}\frac{{\partial (r{{H}_{\varphi }})}}{{\partial r}}} \right] + \frac{1}{{{{r}^{2}}}}\frac{\partial }{{\partial \theta }}\left[ {\frac{1}{{\hat {\varepsilon }}}\frac{1}{{\sin \theta }}\frac{{\partial (r{{H}_{\varphi }}\sin \theta )}}{{\partial \theta }}} \right] + {{k}^{2}}r{{H}_{\varphi }} = \frac{\partial }{{\partial \theta }}\left( {\frac{1}{{\hat {\varepsilon }}}j_{r}^{e}} \right)$
для магнитного поля Hφ, где $k = \omega \sqrt {{{\varepsilon }_{0}}{{\mu }_{0}}} = 2\pi {\text{/}}\lambda $ – волновое число и λ – длина волны в свободном пространстве.

Введем в рассмотрение сферу радиуса a с центром, расположенным в начале координат, которая охватывает рассматриваемое тело и диполь, как показано на фиг. 1, и рассмотрим уравнение (5) в областях $r \geqslant a$, ${{a}_{1}} \leqslant r \leqslant a$ и $0 \leqslant r \leqslant {{a}_{1}}$. Уравнение (5) для первой области, где $\hat {\varepsilon } = 1$ и правая часть равна нулю, решается хорошо известным методом разделения переменных. Применяя этот метод, можно записать решение в виде суперпозиции сферических волн, расходящихся от рассеивателя

(6)
${{H}_{\varphi }}(r,\theta ) = \frac{{{{H}_{0}}}}{{kr}}\sum\limits_{q = 1}^\infty {{{R}_{q}}{{\zeta }_{q}}(kr){{T}_{q}}(\theta )} ,$
где Rq – коэффициенты, подлежащие определению, ζq(kr) – функции Риккати–Ханкеля I рода,
(7)
${{T}_{q}}(\theta ) = \sqrt {\frac{{2q + 1}}{{2q(q + 1)}}} P_{q}^{1}(\cos \theta )$
суть ортонормированные поперечные функции, определяемые присоединенными функциями Лежандра $P_{q}^{1}(\cos \theta )$, и
(8)
${{H}_{0}} = - \frac{{i{{k}^{2}}{{I}^{e}}l}}{{4\pi }}$
есть множитель, через который поле диполя в дальней зоне в отсутствиe тела можно определить формулой

(9)
${{H}_{{\varphi \infty }}}(r,\theta ) = {{H}_{0}}\frac{{{{e}^{{ikr}}}}}{{kr}}{{e}^{{ - ik{{r}_{0}}\cos \theta }}}\sin \theta .$

Решение уравнения (5) для поля в центральной сферической области, не содержащей источников и где $\hat {\varepsilon } = {{\varepsilon }_{1}}$, может быть записано в виде разложения

(10)
${{H}_{\varphi }}(r,\theta ) = \frac{{{{H}_{0}}}}{{kr}}\sum\limits_{q = 1}^\infty {{{B}_{q}}{{\psi }_{q}}({{k}_{1}}r){{T}_{q}}(\theta )} $
с неизвестными коэффициентами Bq, функциями Риккати–Бесселя ψq(k1r) и волновым числом ${{k}_{1}} = k\sqrt {{{\varepsilon }_{1}}} $.

Решение уравнения (5) для поля в области ${{a}_{1}} \leqslant r \leqslant a$, где $\hat {\varepsilon } = \varepsilon (r,\theta )$ внутри слоя и $\hat {\varepsilon } = 1$ вне слоя, будем искать в виде разложения

(11)
${{H}_{\varphi }}(r,\theta ) = {{H}_{0}}\sum\limits_{q = 1}^\infty {{{H}_{q}}(r){{T}_{q}}(\theta )} $
по поперечным функциям (7) с неизвестными коэффициентами Hq(r), зависящими от радиальной координаты r.

Магнитные поля (6), (10) и (11), а также соответствующие поперечные электрические поля, определяемые из (3), должны быть непрерывными на сферических поверхностях при $r = {{a}_{1}}$ и $r = a$. Проектирование указанных граничных условий на поперечные функции (7) с весом $\sin \theta $ дает следующие соотношения для коэффициентов разложения:

(12)
${{\psi }_{p}}({{k}_{1}}{{a}_{1}}){{B}_{p}} - k{{a}_{1}}{{H}_{p}}({{a}_{1}}) = 0,$
(13)
${{\left. {\sum\limits_{q = 1}^\infty {{{{\tilde {\varepsilon }}}_{{pq}}}({{a}_{1}})\frac{{d[r{{H}_{q}}(r)]}}{{dr}}} {\kern 1pt} } \right|}_{{r = {{a}_{1}}}}} = \frac{1}{{\sqrt {{{\varepsilon }_{1}}} }}{{B}_{p}}\psi _{p}^{'}({{k}_{1}}{{a}_{1}}),$
(14)
$ka{{H}_{p}}(a) - {{\zeta }_{p}}(ka){{R}_{p}} = 0,$
(15)
${{\left. {\sum\limits_{q = 1}^\infty {{{{\tilde {\varepsilon }}}_{{pq}}}(a)\frac{{d[r{{E}_{p}}(r)]}}{{dr}}{\kern 1pt} } } \right|}_{{r = a}}} = {{R}_{p}}\zeta _{p}^{'}(ka),$
где
(16)
${{\tilde {\varepsilon }}_{{pq}}}(r) = \int\limits_0^\pi {\frac{1}{{\hat {\varepsilon }(r,\theta )}}{{T}_{p}}(\theta ){{T}_{q}}(\theta )\sin \theta d\theta } $
и $p = 1,\;2,\; \ldots $ .

Магнитное поле (11) должно удовлетворять уравнению (5). Подставляя (11) в (5), проектируя (5) на поперечные функции (7) и учитывая свойства функций Лежандра $P_{q}^{1}(\theta ) = - d{{P}_{q}}{\text{/}}d\theta $ в (7) и

(17)
$\frac{1}{{\sin \theta }}\frac{d}{{d\theta }}\left[ {\sin \theta \frac{{d{{P}_{q}}}}{{d\theta }}} \right] = - q(q + 1){{P}_{q}}$
при интегрировании второго слагаемого в (5) по частям, мы получаем следующую систему обыкновенных дифференциальных уравнений:
(18)
$\frac{d}{{dr}}\sum\limits_{q = 1}^\infty {{{{\tilde {\varepsilon }}}_{{pq}}}(r)\frac{{d{{V}_{q}}}}{{dr}}} - \frac{{{{\alpha }_{p}}}}{{{{r}^{2}}}}\sum\limits_{q = 1}^\infty {{{{\tilde {\varepsilon }}}_{{0pq}}}(r){{\alpha }_{q}}{{V}_{q}}} + {{k}^{2}}{{V}_{p}} = - ik{{A}_{p}}\delta (r - {{r}_{0}}),$
где ${{V}_{q}}(r) = kr{{H}_{q}}(r)$,
(19)
${{\tilde {\varepsilon }}_{{0pq}}}(r) = \int\limits_0^\pi {\frac{1}{{\hat {\varepsilon }(r,\theta )}}{{{\bar {P}}}_{p}}(\theta ){{{\bar {P}}}_{q}}(\theta )\sin \theta d\theta } ,$
(20)
${{A}_{p}} = \frac{{\sqrt {2p + 1} \sqrt {2p(p + 1)} }}{{{{{(k{{r}_{0}})}}^{2}}}},$
(21)
${{\bar {P}}_{p}}(\theta ) = \sqrt {\frac{{2p + 1}}{2}} {{P}_{p}}(\cos \theta )$
суть нормированные полиномы Лежандра и ${{\alpha }_{p}} = \sqrt {p(p + 1)} $.

Решение дифференциальных уравнений (18) осуществляется с использованием одномерного метода конечных элементов в проекционной форме, как это делалось в [18]–[28]. Согласно этому подходу, решение для Vq(r) ищем в виде разложения

(22)
${{V}_{q}}(r) = \sum\limits_{n = 1}^N {{{V}_{{nq}}}{{f}_{n}}(r)} ,$
где Vnq – неизвестные, но уже постоянные, коэффициенты, N – число узлов с координатами ${{r}_{n}} = {{a}_{1}} + (n - 1)\Delta $, $\Delta = (a - {{a}_{1}}){\text{/}}(N - 1)$ и ${{f}_{n}}(r)$ – треугольные функции (см., например, [18], [19]) с вершинами, расположенными в указанных узловых точках. Следующая операция – проектирование уравнений (18) на треугольную функцию ${{f}_{{n'{\kern 1pt} }}}(r)$. Интегрирование первого слагаемого в (18) по частям и подстановка (13) и (15) в слагаемые, образующиеся вне интеграла, сводят (18) к линейным алгебраическим уравнениям
(23)
$ - \frac{1}{{\sqrt {{{\varepsilon }_{1}}} }}\psi _{p}^{'}({{k}_{1}}{{a}_{1}}){{B}_{p}}{{\delta }_{{n'1}}} + \sum\limits_{n = 1}^N {\sum\limits_{q = 1}^\infty {Z_{{n'n}}^{{pq}}{{V}_{{nq}}}} } + \zeta _{p}^{'}(ka){{R}_{p}}{{\delta }_{{n'N}}} = - i{{A}_{p}}{{f}_{{n'}}}{\kern 1pt} ({{r}_{0}}),$
где ${{\delta }_{{n'n}}}$ – символ Кронекера и
(24)
$Z_{{n'n}}^{{pq}} = I_{{n'n}}^{{(1)}}{{\delta }_{{pq}}} - {{\alpha }_{p}}{{\alpha }_{q}}I_{{n'n}}^{{(2)}} - I_{{n'n}}^{{(3)}}$
суть матричные элементы, определяемые следущими интегралами:
(25)
$I_{{n'n}}^{{(1)}} = k\int\limits_{{{a}_{1}}}^a {{{f}_{{n'}}}{{f}_{n}}dr} ,$
(26)
$I_{{n'n}}^{{(2)}} = \frac{1}{k}\int\limits_{{{a}_{1}}}^a {\frac{{{{f}_{{n'}}}{{f}_{n}}}}{{{{r}^{2}}}}{{{\tilde {\varepsilon }}}_{{0pq}}}dr} ,$
(27)
$I_{{n'n}}^{{(3)}} = \frac{1}{k}\int\limits_{{{a}_{1}}}^a {\frac{{d{{f}_{{n'}}}}}{{dr}}\frac{{d{{f}_{n}}}}{{dr}}{{{\tilde {\varepsilon }}}_{{pq}}}dr} $
для $n{\text{'}} = 1,\;2,\; \ldots ,\;N$ и $p = 1,\;2,\; \ldots $ .

Уравнение (12), где ka1Hp(a1) = V1p, уравнения (23) и уравнение (14), где kaHp(a) = VNp, образуют полную систему линейных алгебраических уравнений. Ее размер после усечения равен (N + 2)L, где L – число поперечных функций, учтенных в (6), (10) и (11). Матрица системы имеет блочно-трехдиагональную структуру, пример которой показан на фиг. 2. Решив полученную систему, мы можем рассчитать поля в центральной сфере и неоднородном слое, а также поле, излученное в свободное пространство. В частности, используя асимптотическое выражение ζq(kr) ≈ (–1)q+1eikr для функций Риккати–Ханкеля для больших kr и представление поля (6) в виде (9), мы можем рассчитать ДН диполя в присутствии тела:

(28)
$F(\theta ) = \sum\limits_{q = 1}^L {{{{( - i)}}^{{q + 1}}}{{R}_{q}}{{T}_{q}}(\theta )} ,$
как множитель, стоящий после произведения H0eikr/(kr).

Фиг. 2.

Пример структуры матрицы системы линейных алгебраических уравнений для N = 6 и L = 5.

3. МОДИФИКАЦИИ МЕТОДА

Если сфера, введенная для решения задачи, не охватывает электрический диполь, т.е. если ${{r}_{0}} > a$, то алгоритм, описанный выше, может быть модифицирован следующим образом. Полное поле в свободном пространстве вне указанной сферы при $a < r < {{r}_{0}}$ представляется в виде

(29)
${{H}_{\varphi }}(r,\theta ) = \frac{{{{H}_{0}}}}{{kr}}\sum\limits_{q = 1}^\infty {[A_{q}^{ - }{{\psi }_{q}}(kr) + {{R}_{q}}{{\zeta }_{q}}(kr)]{\kern 1pt} {{T}_{q}}(\theta )} ,$
где $A_{q}^{ - } = - {{A}_{q}}{{\zeta }_{q}}(k{{r}_{0}})$ соответствует разложению поля диполя, падающего на сферу.

Соотношения (14) и (15), следующие из граничных условий, должны быть заменены формулами

(30)
$ka{{H}_{p}}(a) - {{\zeta }_{p}}(ka){{R}_{p}} = A_{p}^{ - }{{\psi }_{p}}(ka),$
(31)
${{\left. {\sum\limits_{q = 1}^\infty {{{{\tilde {\varepsilon }}}_{{pq}}}(a)\frac{{d[r{{E}_{p}}(r)]}}{{dr}}} {\kern 1pt} } \right|}_{{r = a}}} = A_{p}^{ - }\psi _{p}^{'}(ka) + {{R}_{p}}\zeta _{p}^{'}(ka),$
правая часть в уравнении (18) должна быть равна нулю, а правые части в уравнениях (23), которые должны решаться совместно с (12) и (30), должны быть равны $ - {\kern 1pt} A_{p}^{ - }\psi _{p}^{'}(ka){{\delta }_{{n'N}}}$.

Наконец, ДН (28) должна быть модифицирована в виде

(32)
$F(\theta ) = {{e}^{{ - ik{{r}_{0}}\cos \theta }}}\sin \theta + \sum\limits_{q = 1}^L {{{{( - i)}}^{{q + 1}}}{{R}_{q}}{{T}_{q}}(\theta )} ,$
где первое слагаемое в правой части равно ДН диполя в отсутствиe тела.

Вторая модификация соответствует случаю, когда центральная сфера является не диэлектрической, а идеально проводящей. Этот случай представляет интерес не только сам по себе, но и потому, что к нему могут быть сведены задачи рассеяния на несферических проводящих телах вращения путем соответствующего преобразования координат, как это сделано в [3], [4]. Алгоритм решения, описанный в разд. 2, может быть модифицирован для этого случая следующим образом. Так как поле внутри центральной сферы теперь равно нулю, то поле (10) и соотношение (12) должны быть исключены из рассмотрения, а левая часть соотношения (13) должна быть равна нулю. Последнее условие исключает первое слагаемое из уравнения (23). В результате размер усеченной системы уравнений (23) и (14) становится равным (N + 1)L вместо (N + 2)L, имевшим место в предыдущем случае. После решения системы характеристики излучения диполя могут быть рассчитаны с использованием (6) и (28) при ${{r}_{0}} < a$ или по формулам

(33)
${{H}_{\varphi }}(r,\theta ) = \frac{{{{H}_{0}}}}{{kr}}\sum\limits_{q = 1}^\infty {(A_{q}^{ + } + {{R}_{q}}){{\zeta }_{q}}(kr){{T}_{q}}(\theta )} ,$
где $A_{q}^{ + } = - {{A}_{q}}\psi (k{{r}_{0}})$ и (32) при $r > {{r}_{0}} > a$.

4. РЕАЛИЗАЦИЯ АЛГОРИТМОВ И ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Алгоритмы, описанные выше, были реализованы в нескольких программах в среде МАТЛАБ. Интеграл (25) для различных сочетаний n и n' определяется элементарными выражениями (см. [19, с. 251]). Вычисление интегралов (26) и (27) проводилось с использованием разложения функций ${{\tilde {\varepsilon }}_{{0pq}}}(r)$ и ${{\tilde {\varepsilon }}_{{pq}}}(r)$ по треугольным функциям, как в (22), с последующим аналитическим интегрированием произведений указанных функций и их производных. Работа программ контролировалась несколькими способами, включая сравнение результатов с данными, полученными другими методами, применимыми к случаю слоя из однородного диэлектрика. Некоторые примеры и численные результаты, характеризующие возможности метода, приводятся ниже.

Первый пример соответствует однородной диэлектрической сфере радиуса a0 и относительной проницаемости ε, возбуждаемой диполем, расположенным на расстоянии h от ее поверхности. Задача в этом случае имеет строгое аналитическое решение. В частности, ДН диполя может быть рассчитана, согласно (32), где ${{r}_{0}} = {{a}_{0}} + h$ и

(34)
${{R}_{q}} = - A_{q}^{ - }\frac{{\psi _{q}^{'}(m\alpha ){{\psi }_{q}}(\alpha ) - m{{\psi }_{q}}(m\alpha )\psi _{q}^{'}(\alpha )}}{{\psi _{q}^{'}(m\alpha ){{\zeta }_{q}}(\alpha ) - m{{\psi }_{q}}(m\alpha )\zeta _{q}^{'}(\alpha )}},$
$m = \sqrt \varepsilon $ и $\alpha = k{{a}_{0}}$. Сместим теперь эту сферу вниз из начала координат на расстояние ${{z}_{0}}$, как показано на вставке фиг. 3, и применим ГПМ для решения задачи. Входные параметры задачи определяются следующим образом: ${{a}_{1}} = {{a}_{0}} - {{z}_{0}}$, $a = {{a}_{0}} + {{z}_{0}}$, ${{r}_{0}} = {{a}_{1}} + h$ и $\varepsilon (r,\theta ) = {{\varepsilon }_{1}} = \varepsilon $. Интегралы (16) и (19) в этом случае определяются формулами
(35)
${{\tilde {\varepsilon }}_{{pq}}}(r) = {{\delta }_{{pq}}} + \left( {\frac{1}{\varepsilon } - 1} \right){{N}_{{1p}}}{{N}_{{1q}}}\int\limits_{ - 1}^{{{x}_{r}}} {P_{p}^{1}(x)P_{q}^{1}(x)dx} ,$
(36)
${{\tilde {\varepsilon }}_{{0pq}}}(r) = {{\delta }_{{pq}}} + \left( {\frac{1}{\varepsilon } - 1} \right){{N}_{{0p}}}{{N}_{{0q}}}\int\limits_{ - 1}^{{{x}_{r}}} {{{P}_{p}}(x){{P}_{q}}(x)dx} ,$
где N1q и N0q – нормировочные коэффициенты, стоящие перед $P_{q}^{1}$ в (7) и перед Pq в (21), и
(37)
${{x}_{r}}(r) = \cos {{\theta }_{r}} = \frac{{a{{a}_{1}} - {{r}^{2}}}}{{(a - {{a}_{1}})r}}$
есть косинус угловой координаты точки на поверхности смещенной сферы. Интегралы от произведений присоединенных функций Лежандра в (35) и полиномов Лежандра в (36) вычислялись с использованием соотношения, которое мы вывели для неопределенных интегралов,
(38)
$F_{{pq}}^{m} = \int {P_{p}^{m}P_{q}^{m}dx} = \frac{1}{{p + q + 1}}\left[ {\frac{{(q + m)P_{{q - 1}}^{m}P_{p}^{m} - (p + m)P_{{p - 1}}^{m}P_{q}^{m}}}{{p - q}} + xP_{p}^{m}P_{q}^{m}} \right]$
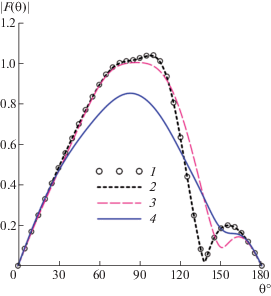
для $q \ne p$ и рекуррентного соотношения
(39)
$F_{{pp}}^{m} = \frac{1}{{p - m}}\left\{ {\frac{{2p - 1}}{{2p + 1}}[(p - m + 1)F_{{p + 1,p - 1}}^{m} + (p + m)F_{{p - 1,p - 1}}^{m}] - (p + m - 1)F_{{p,p - 2}}^{m}} \right\}$
для $p = q > m$, причем (39) вычисляется с использованием (38) и явных выражений $F_{{00}}^{0}(x) = x$ и $F_{{11}}^{1}(x) = x - {{x}^{3}}{\text{/}}3$.

Фиг. 3.

Амплитудная ДН диполя в присутствии однородной сферы радиуса 0.5λ и относительной проницаемости 3: 1 – аналитическое решение, L = 15; 2, 3 и 4 – ГПМ, L = 19, N = 5 (2), 11 (3) и 41 (4).

Результаты расчетов амплитудной ДН диполя |F(θ)| при a0 = 0.5λ, ε = 3 и h = 0.3λ приведены на фиг. 3. Кружочки 1 соответствуют ДН, рассчитанной с использованием строгой формулы (34) при учете L = 15 членов ряда (32). Указанное значение L обеспечивает стабилизацию первых четырех значащих цифр амплитудной ДН диполя. Кривые 2, 3 и 4 соответствуют применению ГПМ для сферы, смещенной вниз на расстояние z0 = 0.2λ. Результаты получены при учете L = 19 членов рядов (6), (10), (11) и (28) при различном числе треугольных функций N. Мы видим, что результаты сходятся к точному решению при увеличении N.

Амплитудные ДН диполя в задаче с геометрическими параметрами, указанными выше, но для однородной сферы с проницаемостью ε = ε1 = 0.4 + 0.2i, соответствующей плазме на частоте, превышающей плазменную частоту (см. [29]), приведены на фиг. 4. Здесь мы также наблюдаем сходимость результатов, полученных предлагаемым методом, к результатам точного решения. Расчеты, проведенные для других значений параметров сферы, показали, что с увеличением размеров и проницаемости сферы требуется учитывать большее число членов разложения по сферическим функциям L и по треугольным функциям N для достижения высокой точности, что является ожидаемым результатом. В качестве начальных значений выбирались L = [2ka] и N = = [(a – a1)/50], где [x] означает целую часть числа x. Уточнение указанных значений далее осуществлялось в ходе численного эксперимента при проверке сходимости результатов.

Фиг. 4.

Амплитудная ДН диполя в присутствии однородной сферы радиуса 0.5λ и относительной проницаемости 0.4 + 0.2i: 1 – аналитическое решение, L = 15; 2, 3 и 4 – ГПМ, L = 19, N = 5 (2), 11 (3) и 21 (4).

Второй пример соответствует электрическому диполю, расположенному над идеально проводящей сферой радиуса a1, расположенной внутри диэлектрического сфероида, один из фокусов которого совпадает с центром сферы, как показано на вставке фиг. 5. Размеры сфероида задаются его апофокусным расстоянием, совпадающим с радиусом внешней сферы a, и перифокусным расстоянием b. Указанные параметры определяют размер большой полуоси ae = (a + b)/2 и фокусное расстояние fe = (a – b)/2, через которые можно определить размер малой полуоси ${{b}_{e}} = \sqrt {a_{e}^{2} - f_{e}^{2}} = \sqrt {ab} $. Будем считать, что проницаемость сфероида зависит только от радиальной координаты и зададим эту зависимость линейной функцией

(40)
$\varepsilon (r) = \frac{{({{\varepsilon }_{a}} - {{\varepsilon }_{{a1}}})r + {{\varepsilon }_{{a1}}}a - {{\varepsilon }_{a}}{{a}_{1}}}}{{a - {{a}_{1}}}},$
где ${{\varepsilon }_{{a1}}} = \varepsilon ({{a}_{1}})$ и ${{\varepsilon }_{a}} = \varepsilon (a)$. Функции (16) и (19) в этом случае определяются формулами ${{\tilde {\varepsilon }}_{{pq}}}(r) = {{\tilde {\varepsilon }}_{{0pq}}}(r) = {{\delta }_{{pq}}}{\text{/}}\varepsilon (r)$ для ${{a}_{1}} \leqslant r \leqslant b$ и формулами (35) и (36) для $b \leqslant r \leqslant a$, где ε следует заменить на ε(r), а косинус угловой координаты точки на поверхности тела теперь определяется выражением
(41)
${{x}_{r}} = \frac{{{{p}_{e}} - r}}{{{{x}_{e}}r}},$
полученным с использованием уравнения эллипса $r(\theta ) = {{p}_{e}}{\text{/}}(1 + {{x}_{e}}\cos \theta )$, записанного в полярных координатах с полюсом в фокусе, где ${{p}_{e}} = b_{e}^{2}{\text{/}}{{a}_{e}} = 2ab{\text{/}}(a + b)$ – фокальный параметр и ${{x}_{e}} = {{f}_{e}}{\text{/}}{{a}_{e}} = (a - b){\text{/}}(a + b)$ – эксцентриситет.

Фиг. 5.

Амплитудная ДН диполя в присутствии идеально проводящей сферы, расположенной внутри диэлектрического сфероида: 1 – МВИ, ε = 3; 2, 3 и 4 – ГПМ, L = 41, N = 101, εa1 = εa = 3 (2), εa1 = 3 и εa = 1 (3) и εa1 = = 3 + 0.4i и εa = 1 (4).

Амплитудные ДН диполя, соответствующие геометрическим параметрам a1 = 0.4λ, a = 1.5λ, b = 0.5λ и r0 = 0.7λ, приведены на фиг. 5. ДН 1 и 2 получены для случая однородного сфероида с проницаемостью εa1 = εa= 3. В этом случае задача также была решена методом вспомогательных источников (см. [30]) с использованием осесимметричных кольцевых азимутальных магнитных токов. Две системы по 160 источников располагались на софокусных сфероидальных вспомогательных поверхностях с размерами больших полуосей, равных ${{a}_{e}} \pm 0.05\lambda $, и 40 источников располагались на сферической вспомогательной поверхности радиуса ${{a}_{1}} - 0.05\lambda $ внутри центральной сферы. Угловые координаты источников на сфероидах задавались параметрически (см. [31]), что обеспечило наиболее быстрое уменьшение невязки выполнения граничных условий, а на сфере – равномерное. Указанные параметры обеспечивают выполнение граничных условий на поверхности диэлектрического сфероида и на поверхности внутренней сферы с погрешностью, не превышающей 10–6. ДН диполя, соответствующая МВИ, показана кривой 1, которую мы используем в качестве эталона. ДН 2 соответствует ГПМ, примененному с использованием L = 41 поперечных функций и N = 100 треугольных функций. ДН 3, полученная ГПМ с использованием указанного количества поперечных и треугольных функций, соответствует неоднородному сфероиду без потерь с εa1 = 3 и εa = 1, а ДН 4 – сфероиду с потерями при εa1 = 3 + 0.4i и εa = 1. Мы видим, что и неоднородный диэлектрик, и наличие потерь в этом случае могут заметно влиять на форму ДН диполя.

Амплитудные ДН диполя, соответствующие геометрическим параметрам, указанным выше, но со сферой, находящейся внутри плазменного сфероида, приведены на фиг. 6. ДН 1 и 2, соответствующие однородному сфероиду с εa1 = εa = 0.4, получены с использованием МВИ и ГПМ с входными параметрами, такими же, как и в предыдущем случае. Здесь мы снова наблюдаем хорошее совпадение результатов, полученных разными методами. ДН 3, полученная с использованием ГПМ, соответствует неоднородному плазменному сфероиду без потерь при εa1 = 0.4 и εa = 1, а ДН 4 – неоднородному плазменному сфероиду с потерями при εa1 = 0.4 + 0.4i и εa = 1. Мы видим, что радиальная неоднородность сфероида и наличие потерь в нем приводят к изменениям формы ДН диполя. Однако влияние указанных факторов здесь не столь значительно по сравнению со случаем обычного диэлектрика, рассмотренного выше (фиг. 5). Это различие объясняется более слабым проникновением поля диполя внутрь сфероида в случае плазмы, и поэтому более слабыми эффектами переотражения волн между внутренними поверхностями.

Фиг. 6.

Амплитудная ДН диполя в присутствии идеально проводящей сферы, расположенной внутри плазменного сфероида: 1 – МВИ, ε = 0.4; 2, 3 и 4 – ГПМ, L = 41, N = 101, εa1 = εa = 0.4 (2), εa1 = 0.4 и εa = 1 (3) и εa1 = = 0.4 + 0.4i и εa = 1 (4).

5. ЗАКЛЮЧЕНИЕ

В статье рассмотрена задача возбуждения неоднородного диэлектрического тела вращения в виде однородной диэлектрической или идеально проводящей сферы, окруженной неоднородной диэлектрической оболочкой, радиальным электрическим диполем, расположенным на оси вращения. Для решения задачи были разработаны несколько алгоритмов, основанных на ГПМ, включающем проектирование электромагнитных полей на поперечные сферические функции и применение одномерного метода конечных элементов для решения полученной системы обыкновенных дифференциальных уравнений.

Разработанные алгоритмы реализованы в соответствующих программах на языке МАТЛАБ, работа которых была проверена несколькими способами. Проверки включали рассмотрение однородной диэлектрической сферы, задача возбуждения которой допускает строгое аналитическое решение. ГПМ в этом случае был применен для сферы с центром, смещенным из начала координат, и продемонстрирована сходимость результатов к точному решению при увеличении числа функций, учитываемых в разложении искомых полей. Вторым объектом, использованным для проверки, была идеально проводящая сфера, расположенная внутри однородного вытянутого диэлектрического сфероида. Результаты решения задачи с использованием ГПМ в этом случае сравнивались с результатами, полученными методом вспомогательных источников с контролируемой точностью выполнения граничных условий на поверхностях сферы и сфероида.

В работе также получены новые результаты для ДН диполя в присутствии проводящей сферы, окруженной неоднородной диэлектрической оболочкой в форме вытянутого сфероида с зависимостью проницаемости сфероида от радиальной координаты по линейному закону. Показано, что ДН диполя в случае оболочки из обычного диэлектрика заметно отличается от ДН диполя для случая однородной оболочки. Результаты также показывают заметное влияние потерь в оболочке на форму ДН, что объясняется проникновением поля диполя внутрь сфероида и переотражениями между поверхностью последнего и поверхностью внутренней сферы.

Аналогичные результаты были получены также для случая плазменного сфероида на частоте, превышающей плазменную частоту. В этом случае влияние неоднородности оболочки и наличие потерь в ней на форму ДН диполя оказываются слабее, чем для случая обычного диэлектрика, что объясняется более слабым проникновением поля диполя внутрь сфероида.

Список литературы

  1. Свешников А.Г. Дифракция на ограниченном теле // Докл. АН СССР. 1969. Т. 184. № 1. С. 63–65.

  2. Свешников А.Г., Ильинский А.С. Прямой метод для задач дифракции на локальном неоднородном теле // Ж. вычисл. матем. и матем. физ. 1971. Т. 11. № 4. С. 960–968.

  3. Свешников А.Г., Еремин Ю.А. Проекционные методы во внешних задачах дифракции // Докл. АН СССР. 1975. Т. 221. № 1. С. 84–86.

  4. Свешников А.Г., Еремин Ю.А. Проекционный метод исследования внешних задач дифракции с учетом геометрии рассеивателя // Вычисл. методы и программирование. Вып. 28. Изд-во МГУ, 1978. С. 14–23.

  5. Апельцин В.Ф. Обоснование проекционного метода решения аксиально-симметричных задач дифракции на локально-неоднородных телах // Ж. вычисл. матем. и матем. физ. 1979. Т. 19. № 5. С. 1188–1204.

  6. Апельцин В.Ф., Ильинский А.С., Сабитов Б.Р. Обоснование модифицированного неполного проекционного метода для задач рассеяния от гидрометеоров // Ж. вычисл. матем. и матем. физ. 1986. Т. 26. № 10. С. 1535–1551.

  7. Ильинский А.С., Кравцов В.В., Свешников А.Г. Математические модели электродинамики. М.: Высш. школа, 1991.

  8. Stout B., Neviere M., Popov E. Light diffraction by a three-dimensional object: differential theory // J. Opt. Soc. Am. A. 2005. V. 22. № 11. P. 2385–2404.

  9. Никольский В.В. Проекционный метод для незамкнутых электродинамических систем // Радиотехн. и электроника. 1971. Т. 16. № 8. С. 1342–1351.

  10. Малушков Г.Д. Рассеяние неоднородным диэлектрическим телом вращения // Изв. вузов. Радиофиз. 1975. Т. 18. № 2. С. 269–279.

  11. Morgan M.A., Mei K.K. Finite-element computation of scattering by inhomogeneous penetrable bodies of revolution // IEEE Trans. Antennas Propagat. 1979. V. AP-27. № 2. P. 202–214.

  12. Greenwood A.D., Jin J.-M. Finite-element analysis of complex axisymmetric radiating structures // IEEE Trans. Antennas Propagat. 1999. V. 47. № 8. P. 1260–1266.

  13. Васильев Е.Н., Материкова Л.Б. Возбуждение многослойного диэлектрического тела вращения произвольной формы // Изв. вузов. Радиофиз. 1973. Т. 16. № 1. С. 97–109.

  14. Kyurkchan A.G., Manenkov S.A. Application of modified method of discrete sources for solving a problem of wave diffraction on a multilayered body of revolution // J. Quantitative Spectroscopy & Radiative Transfer. 2014. V. 146. P. 295–303.

  15. Kucharski A.A. A method of moments solution for electromagnetic scattering by inhomogeneous dielectric bodies of revolution // IEEE Trans. Antennas Propagat. 2000. V. 48. № 8. P. 1202–1210.

  16. Маненков С.А. Задача дифракции электромагнитного поля на неоднородном теле с осевой симметрией // Радиотехн. и электроника. 2018. Т. 63. № 1. С. 3–13.

  17. Shcherbakov A.A. Calculation of the electromagnetic scattering by non-spherical particles based on the volume integral equation in the spherical wave function basis // J. Quantitative Spectroscopy & Radiative Transfer. 2019. V. 231. P. 102–114.

  18. Скобелев С.П., Япарова А.А. Гибридный проекционный метод анализа волноводных решеток с выступающими диэлектрическими элементами. Двумерные задачи // Радиотехн. и электроника. 2007. Т. 52. № 3. С. 311–321.

  19. Скобелев С.П. Фазированные антенные решетки с секторными парциальными диаграммами направленности. М.: Физматлит, 2010.

  20. Скобелев С.П., Смольникова О.Н. Анализ одномерно-периодических диэлектрических структур гибридным проекционным методом // Радиотехн. и электроника. 2012. Т. 57. № 10. С. 1066–1077.

  21. Skobelev S.P., Smolnikova O.N. Analysis of doubly periodic inhomogeneous dielectric structures by a hybrid projective method // IEEE Trans. Antennas Propagat. 2013. V. 61. № 10. P. 5078–5087.

  22. Скобелев С.П., Смольникова О.Н. Анализ и оптимизация согласующих двумерно-периодических диэлектрических структур с коническими углублениями // Радиотехн. и электроника. 2015. Т. 60. № 11. С. 1178–1184.

  23. Смольникова О.Н., Федотова Н.А., Скобелев С.П. Анализ продольно неоднородного диэлектрического перехода в круглом волноводе: 1. Гибридный проекционный метод // Радиотехн. 2015. № 4. С. 84–90.

  24. Смольникова О.Н., Федотова Н.А., Скобелев С.П. Анализ продольно неоднородного диэлектрического перехода в круглом волноводе: 2. Осесимметричное возбуждение и численные результаты // Радиотехн. 2015. № 10. С. 35–42.

  25. Смольникова О.Н., Федотова Н.А., Скобелев С.П. Анализ продольно неоднородного диэлектрического перехода в круглом волноводе: 3. Численные результаты при возбуждении волной ТЕ11 // Радиотехн. 2016. № 10. С. 64–69.

  26. Некрасова Е.С., Скобелев С.П. Модификация гибридного проекционного метода для электродинамического анализа неоднородного диэлектрического цилиндра произвольного поперечного сечения // Радиотехн. 2017. № 10. С. 35–43.

  27. Некрасова Е.С., Смольникова О.Н., Скобелев С.П. Рассеяние Н-поляризованной плоской волны на неоднородном диэлектрическом цилиндре произвольного поперечного сечения. Часть 1. Метод анализа // Радиотехн. 2018. № 4. С. 17–22.

  28. Некрасова Е.С., Смольникова О.Н., Скобелев С.П. Рассеяние Н-поляризованной плоской волны на неоднородном диэлектрическом цилиндре произвольного поперечного сечения. Часть 2. Модификация метода и численные результаты // Радиотехн. 2018. № 10. С. 42–53.

  29. Гинзбург В.Л. Распространение электромагнитных волн в плазме. 2-е изд. М.: Наука, 1967.

  30. Кюркчан А.Г., Маненков С.А., Негорожина Е.С. Решение задачи дифракции электромагнитного поля на телах вращения при помощи модифицированного метода дискретных источников // Радиотехн. и электроника. 2006. Т. 51. № 11. С. 1285–1293.

  31. Коробкина А.В., Скобелев С.П. Сравнение некоторых модификаций метода вспомогательных источников // Радиотехн. 2017. № 4. С. 60–65.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал