Журнал вычислительной математики и математической физики, 2020, T. 60, № 12, стр. 2098-2121

1. ВВЕДЕНИЕ

В явном аналитическом виде (через гипергеометрические функции Гаусса и Аппéля) дано решение задачи о кавитационном обтекании равнобочного клина – известной задачи плоской стационарной теории струй идеальной жидкости [1]–[5] – для ряда классических схем замыкания каверны¹¹. В настоящей, первой части работы рассмотрены схемы Гельмгольца–Кирхгофа, Жуковского–Рошко и Рябушинского. Во второй части, публикация которой планируется в ближайшее время, аналитические решения будут даны для первой и второй схемы Тулина и схемы Эфроса.

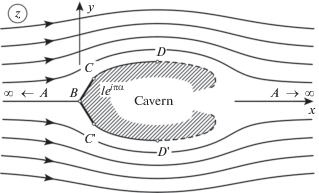
Принимается, что обтекаемый клин и течение жидкости вокруг него симметричны относительно оси $x$ (см. фиг. 1); стенки клина, наклоненные к оси $x$ под углами $ \pm \pi \alpha $, имеют длину $l$, так что основание $(CC{\kern 1pt} ')$ клина имеет размер $2lsin(\pi \alpha )$. Пусть скорость жидкости на бесконечности направлена вдоль оси $x$ и равна ${{V}_{\infty }}$. Картина распределения линий тока для такого течения на комплексной плоскости $z = x + iy$ изображена на фиг. 1; линии снабжены стрелками, указывающими направление движения жидкости²². Одна из линий выходит вместе с потоком жидкости из бесконечности – точки $A$, движется вдоль вещественной отрицательной полуоси к острию клина – точке $B$ и далее раздваивается: одна ее ветвь идет по верхней $(BC)$, а другая – по нижней стенке $(BC{\kern 1pt} ')$ клина, в концах $C$ и $C{\kern 1pt} '$ которого эти ветви от него отрываются, сохраняя гладкость, а их продолжения образуют за клином каверну – область, заполненную газом или парами жидкости. Движение жидкости, при котором возникает каверна, называют кавитационным.

Указанные продолжения $(CD)$ и $(C{\kern 1pt} {\text{'}}D{\kern 1pt} ')$ являются свободными линиями тока, их вид заранее не известен и определяется косвенным образом из условия постоянства давления на них; через $D$ и $D{\kern 1pt} {\text{'}}$ обозначены точки, в которых скорость направлена, как и в бесконечности, параллельно оси $x$. Форма последних участков $(DA)$ и $(D{\kern 1pt} {\text{'}}A)$ линий тока, по которым поток “возвращается” на бесконечность, показана на фиг. 1 лишь частично и условно (они изображены штриховыми линиями); форма этих участков зависит от некоторых предписанных на них требований, которые называют “схемой” замыкания каверны.

Для каждой из трех рассматриваемых схем замыкания каверны, перечисленных выше, найденно аналитическое решение задачи. Оно было численно реализовано, получены картины обтекания, вычислены значения коэффициента сопротивления ${{{\mathbf{C}}}_{x}}$ и найдены относительная длина $\mathfrak{L}$ и ширина $\mathfrak{W}$ каверны. Кроме того, установлен вид асимптотики коэффициента ${{{\mathbf{C}}}_{x}}(Q)$ и размеров $\mathfrak{L}$ и $\mathfrak{W}$ каверны при стремлении к нулю числа кавитации $Q$ – известной характеристики кавитационного течения (ее определение см. в п. 2.3), причем первые коэффициенты этих асимптотик выписаны явно.

2. ПОСТАНОВКА ЗАДАЧИ И РАССМАТРИВАЕМЫЕ СХЕМЫ ЗАМЫКАНИЯ КАВЕРНЫ

2.1. При формулировке задачи об обтекании препятствия, определении характеристик течения и при получении решения задачи используются известные положения и подходы плоской теории струй идеальной жидкости [1]–[6]. В этой теории вводится, как известно, комплексный потенциал течения – аналитическая на плоскости $z = x + iy$ функция

где $u(x,y)$ – вещественный потенциал, а $v(x,y)$ – функция тока, так что уравнение линии тока есть $v(x,y) = {\text{const}}$. Скорость ${\mathbf{V}}(z)$ выражается через $f(z)$ по формуле здесь $V(z) = \left| {{\mathbf{V}}(z)} \right|$ и $\theta (z) = \arg {\mathbf{V}}(z)$ – соответственно модуль и угол наклона скорости к оси $x$, $f{\kern 1pt} '$ – производная, а верхняя черта означает комплексное сопряжение.

Все другие характеристики течения выражаются через комплексный потенциал $f(z)$, поэтому для решения задачи теории струй достаточно найти эту функцию.

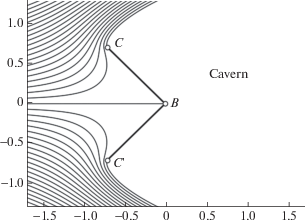
2.2. Поскольку для изучаемой задачи кавитационного обтекания клина (см. фиг. 1) течение симметрично относительно вещественной оси, то связанные с ней теоретические рассмотрения будем проводить только для верхней половины течения, которая занимает область ${{\mathcal{B}}_{z}}$, изображенную на фиг. 2а; численные же результаты будем приводить для всей области течения, включая ее нижнюю половину (как на фиг. 1).

Пусть линия тока, являющаяся границей $\partial {{\mathcal{B}}_{z}}$ области ${{\mathcal{B}}_{z}}$, соответствует значению $v = 0$ функции тока. Из принятого условия, что скорость в бесконечной точке $A$ (см. фиг. 2а) направлена вдоль оси $x$ и непрерывна в окрестности этой точки, следует, что линия $\partial {{\mathcal{B}}_{z}}$ горизонтальна как при выходе из бесконечности, так и при входе в нее. Таким образом, ограниченная ею область ${{\mathcal{B}}_{z}}$ является криволинейной полуплоскостью (в смысле [6]), а угол $\theta $ наклона касательной к этой линии непрерывен в точке $A$ и равен в ней нулю. Тогда согласно [6] комплексный потенциал $w = f(z)$ осуществляет конформное отображение области ${{\mathcal{B}}_{z}}$ на верхнюю полуплоскость $\mathbb{H}_{w}^{ + }: = \{ \operatorname{Im} w > 0\} $, т.е.

с однозначно определяющими его условиями:

Это соответствие точек между областями ${{\mathcal{B}}_{z}}$ и $\mathbb{H}_{w}^{ + }$ показано на фиг. 2а³³, фиг. 2б.

Линия $\partial {{\mathcal{B}}_{z}}$ состоит из нескольких звеньев. Очевидно, что первым звеном $\Gamma _{z}^{{(1)}} = (AB)$ является отрицательная вещественная полуось, а вторым $\Gamma _{z}^{{(2)}} = (BC)$ – стенка клина длиной $l$, наклоненная к вещественной оси под углом $\pi \alpha $ (в градусах – это 180°α), см. фиг. 1, фиг. 2а. На следующем звене $\Gamma _{z}^{{(3)}} = (CD)$, являющемся свободной линией тока, принимается, как обычно [1]–[5], условие постоянства давления $p(z)$ со стороны газов, заполняющих каверну. Из этого условия и закона Бернулли,

где $\rho $ – плотность жидкости, следует, что модуль скорости потока постоянен на этой дуге; он обозначается через ${{V}_{Q}}$, т.е. $\left| {{\mathbf{V}}(\Gamma _{z}^{{(3)}})} \right| = {{V}_{Q}}$. Таким образом, для комплексного потенциала $f(z)$ на дуге $\Gamma _{z}^{{(3)}}$ одновременно выполняются два условия: первое из которых означает, что $\Gamma _{z}^{{(3)}}$ является частью нулевой линии тока, а второе – что модуль скорости на ней равен ${{V}_{Q}}$. Из этих условий находится вид звена $\Gamma _{z}^{{(3)}}$ границы $\partial {{\mathcal{B}}_{z}}$.

Последнее звено $\Gamma _{z}^{{(4)}} = (DA)$, начало которого условно изображено на фиг. 2а штриховой линией, заранее неизвестно так же, как заранее неизвестно и звено $\Gamma _{z}^{{(3)}}$. Эти звенья находятся из решения задачи обтекания.

Таким образом, вид звеньев $\Gamma _{z}^{{(1)}}$ и $\Gamma _{z}^{{(2)}}$ не зависит от схемы замыкания каверны, а звенья $\Gamma _{z}^{{(3)}}$, $\Gamma _{z}^{{(4)}}$ определяются этой схемой и имеют свой вид для каждой из них.

2.3. Введем годограф скорости в форме Жуковского [7] с помощью равенства

которое с учетом (1) перепишем в виде: Эта аналитическая в области ${{\mathcal{B}}_{z}}$ функция $\zeta = \omega (z)$, называемая функцией годографа, с отличной от нуля производной в области течения ${{\mathcal{B}}_{z}}$ (поскольку в ней нет точек остановки), осуществляет ее конформное отображение на односвязную область ${{\mathcal{B}}_{\zeta }}$, называемую областью годографа, Неотрицательное число $Q$, определяемое по формуле называют числом кавитации. В подобных задачах часто задают ${{V}_{\infty }}$ и $Q$, тогда Обозначим через $\Gamma _{\zeta }^{{(j)}}$ образ дуги $\Gamma _{z}^{{(j)}}$ (на плоскости $\zeta $) при отображении $\zeta = \omega (z)$, Перечисленные дуги $\Gamma _{\zeta }^{{(j)}}$, $j = \overline {1,4} $, составляют границу области годографа,

Рассмотрим вопрос о том, какой вид имеет область ${{\mathcal{B}}_{\zeta }}$ для исследуемых схем замыкания каверны. Проследим за движением жидкости по нулевой линии тока (см. фиг. 2а). Жидкость, вытекая из точки $A$ со скоростью ${{V}_{\infty }}$, движется по звену $\Gamma _{z}^{{(1)}}$, постепенно замедляясь, к точке остановки $B$ – острию клина; при продолжении движения по стенке клина $\Gamma _{z}^{{(2)}}$ модуль скорости возрастает и достигает в концевой точке $C$ значения ${{V}_{Q}}$. При дальнейшем движении жидкости, теперь уже по свободной линии тока, ее скорость, оставаясь по модулю равной ${{V}_{Q}}$, становится в некоторой точке $D$ горизонтальной, т.е. $\arg {\mathbf{V}}(D) = 0$ (см. фиг. 2а). Тогда, в соответствии со сказанным, из формулы (6) получаем, что, независимо от схемы замыкания каверны, справедливы следующие утверждения:

1) координаты точек $A$, $B$, $C$ и $D$ на плоскости годографа⁴⁴ суть

2) звено $\Gamma _{\zeta }^{{(1)}}$ представляет собой часть вещественной положительной полуоси,

3) линия $\Gamma _{\zeta }^{{(2)}}$ является вещественной положительной полуосью, поднятой на $i\pi \alpha $,

4) звено $\Gamma _{\zeta }^{{(3)}}$ представляет собой, с учетом условий (5) на свободной линии тока, отрезок мнимой оси,

На фиг. 2в изображена область годографа ${{\mathcal{B}}_{\zeta }}$, граница которой состоит из найденных звеньев $\Gamma _{\zeta }^{{(1)}}$, $\Gamma _{\zeta }^{{(2)}}$, $\Gamma _{\zeta }^{{(3)}}$ и четвертого, неопределенного пока звена $\Gamma _{\zeta }^{{(4)}}$, изображенного поэтому условно штриховой линией. В следующем пункте это звено – и в целом область ${{\mathcal{B}}_{\zeta }}$ – задается своим способом для каждой из рассматриваемых схем.

Таким образом, вид звеньев $\Gamma _{\zeta }^{{(1)}}$, $\Gamma _{\zeta }^{{(2)}}$, $\Gamma _{\zeta }^{{(3)}}$ не зависит от схемы замыкания каверны (заметим, что $\Gamma _{\zeta }^{{(1)}}$ зависит от числа $Q$), а последнее звено $\Gamma _{\zeta }^{{(4)}}$ имеет предписанный вид для каждой схемы.

2.4. Изложим три рассматриваемые в работе схемы замыкания каверны.

Схема, предложенная Г. Гельмгольцем и Г. Кирхгофом [8], [9] (см. фиг. 3), соответствует случаю $Q = 0$, поэтому для нее, согласно (10), модуль скорости жидкости на каверне и на бесконечности одинаков (${{V}_{Q}} = {{V}_{\infty }}$), точки $A$ и $D$ сливаются в одну, а дуга $\Gamma _{\zeta }^{{(4)}}$ вырождается в эту точку. Тогда, согласно (11), граница⁵⁵ $\partial{ \mathcal{B}}_{\zeta }^{H}$ состоит из трех звеньев, а учитывая их вид (13)–(15), находим, что область годографа для этой схемы представляет собой полуполосу

изображенную на фиг. 3в.

Выясним теперь вид области годографа $\mathcal{B}_{\zeta }^{Z}$ для схемы, предложенной Н.Е. Жуковским и А. Рошко [7], [10] (см. фиг. 4). Здесь уже модуль скорости на каверне ${{V}_{Q}}$ отличается от этого модуля на бесконечности ${{V}_{\infty }}$, причем, согласно (10) $($см. также [2]$)$, выполняется неравенство ${{V}_{Q}} > {{V}_{\infty }}$. Для данной схемы принимается, что скорость на всем звене $\Gamma _{z}^{{(4)}}$ горизонтальна (см. фиг. 4а),

т.е. при таком способе замыкания каверны предполагается, что $\Gamma _{z}^{{(4)}}$ представляет собой (фиктивную) горизонтальную твердую стенку, на которую плавно натекает свободная линия тока $\Gamma _{z}^{{(3)}}$. Тогда, используя формулу (6), получаем, что дуга $\Gamma _{\zeta }^{{(4)}}$ есть отрезок $[0,ln\sqrt {1 + Q} ]$ вещественной оси. Учитывая вид (13)–(15) первых трех участков границы $\partial {{\mathcal{B}}_{\zeta }}$, видим, что область годографа для схемы Жуковского–Рошко является той же полуполосой, что и для схемы Гельмгольца–Кирхгофа, но с другим положением точки $A$ (см. фиг. 4в), координата которой дается первой формулой (12).

В схеме, предложенной Д.П. Рябушинским [11] (см. фиг. 5), принимается, что картина течения жидкости является зеркально-симметричной относительно вертикальной прямой ${{\mathcal{P}}_{z}}$,

соединяющей точку $D$ и бесконечно удаленную точку $A$ (см. фиг. 5а), поэтому четвертое звено $\Gamma _{z}^{{(4)}}$ является зеркальным отражением первых трех относительно прямой ${{\mathcal{P}}_{z}}$. Иначе говоря, при таком способе замыкания каверны предполагается, что свободная линия тока, продолжающаяся после точки $D$, плавно натекает на (фиктивную) твердую стенку $(C{\kern 1pt} {\text{*}}B{\kern 1pt} {\text{*}})$, являющуюся зеркальным (относительно прямой ${{\mathcal{P}}_{z}}$) образом стенки $\Gamma _{z}^{{(2)}}$, т.е.

Из указанной симметрии течения следует также, что функция $w = f(z)$, осуществляющая отображение (2), преобразует прямую ${{\mathcal{P}}_{z}}$ в прямую ${{\mathcal{P}}_{w}}: = f({{\mathcal{P}}_{z}})$, соединяющую точки $D$ и $A$ на плоскости $w$ (см. фиг. 5б),

При этом точки, симметричные относительно ${{\mathcal{P}}_{z}}$, переходят в точки, симметричные относительно ${{\mathcal{P}}_{w}}$, т.е. где $\delta $ – (вещественная) координата ${{D}_{w}}$ (см. фиг. 5б). Так как в силу той же симметрии имеем $\arg {\mathbf{V}}(z) = 0$, $z \in {{\mathcal{P}}_{z}}$, то с помощью (6) видим, что образом прямой ${{\mathcal{P}}_{z}}$ на плоскости годографа будет интервал вещественной оси (ср. фиг. 4в и 5в). Тогда, применяя принцип симметрии Римана–Шварца [6], находим, что область годографа $\mathcal{B}_{\zeta }^{R}$ для схемы Рябушинского представляет собой объединение: во-первых, полуполосы (16) из схемы Жуковского–Рошко, во-вторых, симметричной полуполосы в нижней полуплоскости и, в-третьих, соединяющего их интервала ${{\mathcal{P}}_{\zeta }}$, т.е. см. фиг. 5в.

Описанные схемы Гельмгольца–Кирхгофа, Жуковского–Рошко и Рябушинского проиллюстрированы соответственно на фиг. 3, 4, 5. Здесь для каждой из трех схем дана: во-первых, область ${{\mathcal{B}}_{z}}$ (фиг. 3а, 4а, 5а) – верхняя половина области течения; во-вторых, соответствующая ей область потенциала (фиг. 3б, 4б, 5б), являющаяся для этих схем полуплоскостью $\mathbb{H}_{w}^{ + }$; и, в-третьих, область годографа ${{\mathcal{B}}_{\zeta }}$ (фиг. 3в, 4в, 5в). При этом показано соответствие между точками на разных плоскостях. Участки границы ${{\mathcal{B}}_{z}}$, являющиеся твердыми стенками (реальными или фиктивными) и их образы на других плоскостях изображены жирными линиями.

Дана также область ${{\mathcal{B}}_{t}}$ на вспомогательной плоскости $t$, связь которой с иными плоскостями определена ниже, в п. 3.2.

Отметим, что представленная на фиг. 3а, 4а, 5а картина течения и вид области ${{\mathcal{B}}_{z}}$ для каждой схемы получены как результат решения соответствующих задач с помощью изложенного ниже, в разд. 3–7 алгоритма. Обозначив через $\Delta \tilde {v}$ шаг значений функции тока между соседними линиями тока, приведем значения параметров для указанных рисунков:

– для фиг. 3а (схема Гельмгольца–Кирхгофа) $l = 1$, $\alpha = \tfrac{1}{3}$, т.е. $\pi \alpha = 60^\circ $, ${{V}_{\infty }} = 0.5$, $\Delta \tilde {v} = 0.3$;

– для фиг. 4а (схема Жуковского–Рошко) $l = 1$, $\alpha = \tfrac{1}{3}$, т.е. $\pi \alpha = 60^\circ $, ${{V}_{\infty }} = 1$, $Q = 0.6$, $\Delta \tilde {v} = 0.3$;

– для фиг. 5а (схема Рябушинского) $l = 1$, $\alpha = 0.3$, т.е. $\pi \alpha = 54^\circ $, ${{V}_{\infty }} = 1$, $Q = 1$, $\Delta \tilde {v} = 0.6$.

Обратим внимание на точку $D$ на фиг. 2а, 3а, 4а, 5а, являющуюся “наивысшей” точкой каверны, т.е. ее точкой, наиболее удаленной от оси $x$. Это свойство связано с тем, что, согласно [2], дуга $\Gamma _{z}^{{(3)}}$, как свободная линия тока, всегда обращена выпуклостью от каверны в сторону потока, а касательная к ней в точке $D$ горизонтальна. В п. 4.2 мы используем это свойство точки $D$ для оценки размеров каверны.

3. ОБЩЕЕ РЕШЕНИЕ ЗАДАЧИ

3.1. Рассматриваемая задача о кавитационном обтекании клина заключается в том, чтобы построить комплексный потенциал течения $w = f(z)$, исходя из заданной геометрии клина (т.е. параметров $l$ и $\alpha $), заданного вида области годографа ${{\mathcal{B}}_{\zeta }}$ и вытекающего из (12) соответствия между точками $A$, $B$, $C$ на плоскостях $z$ и $\zeta $ (см. фиг. 2а, 2в). Если функция $w = f(z)$ или обратная к ней найдена, то все остальные характеристики течения могут быть выражены через нее, что и сделано для ряда важных функций и величин ниже, в разд. 4.

Введем функцию $\zeta = F(w)$ как суперпозицию функции годографа $\zeta = \omega (z)$ и функции $z = {{f}^{{ - 1}}}(w)$, обратной к комплексному потенциалу,

Из соотношений (2) и (8) вытекает, что введенная функция осуществляет конформное отображение со следующим соответствием точек $A$, $B$, $C$ на плоскостях $w$ и $\zeta $ (см. фиг. 2б, 2в): здесь $\varkappa : = f(l{{e}^{{i\pi \alpha }}})$ – координата образа концевой точки $C$ клина.

Потенцируя равенство (7), получаем выражение

подставляя в которое $z = {{f}^{{ - 1}}}(w)$ и используя тождество находим с учетом определения (23) равенство Интегрируя его, устанавливаем представление для функции, обратной к комплексному потенциалу

3.2. Чтобы привести интеграл (28) к более удобной для использования форме, введем две вспомогательные функции

и их суперпозицию отметим, что Переходя в подынтегральной функции в (28) от переменной $w$ к переменной $h$ по формуле где $w = {{F}^{{ - 1}}}(\zeta )$ – функция, обратная к (23), а $H(h)$ определяется из (30), получаем Для дифференциала $dw$ в (28) переход к переменной $h$ осуществляем с помощью замены где функция $w = \chi (t)$ определяется в виде суперпозиции а $\zeta = T(t)$ дается формулой (29). Тогда

Подставляя производную $\Theta {\kern 1pt} '(h)$ из (32), а также равенства (34) и (37) в интеграл (28), приводим его к виду

где верхний предел $h(w) = {{\Theta }^{{ - 1}}} \circ {{\chi }^{{ - 1}}}(w)$.

Отметим, что, как нетрудно показать, фигурирующая в интеграле (38) функция $\chi {\kern 1pt} '\; \circ \Theta (h)$ имеет нуль второго порядка в точке $h = 0$, поэтому интеграл (38) конечен при конечных $w$, и для него выполняется равенство ${{f}^{{ - 1}}}(0) = 0$, соответствующее первому условию (3). Заметим еще, что эта функция положительна на отрезке $h \in [0,1]$. Важно, что для рассматриваемых схем функция $w = \chi (t)$ легко строится и обращается в аналитическом виде.

Для завершения решения задачи осталось найти неизвестный заранее образ $\varkappa $ конца $C$ стенки клина на плоскости потенциала $w$. Он находится из следующего уравнения:

получаемого с помощью представления (38).

В разд. 5–7 для каждой из рассматриваемых схем конкретизируется вид фигурирующей в интеграле (38) функция $\chi {\kern 1pt} '\; \circ \Theta (h)$ и вид верхнего предела $h(w) = {{\Theta }^{{ - 1}}} \circ {{\chi }^{{ - 1}}}(w)$ интеграла (38). Это позволяет получить функцию ${{f}^{{ - 1}}}(w)$, величину $\varkappa $ и другие характеристики решения задачи в явном аналитическом виде.

4. PACЧЕТ ХАРАКТЕРИСТИК ТЕЧЕНИЯ В ОБЩЕМ СЛУЧАЕ

4.1. Обратимся к вычислению коэффициента сопротивления ${{{\mathbf{C}}}_{x}}$ – относительной величины суммарной силы, действующей на клин. Он определяется как отношение $x$-компоненты интеграла сил, действующих на клин (равный удвоенному интегралу по верхней стенке), к произведению величины $\tfrac{1}{2}\rho V_{\infty }^{2}$ на длину основания клина $2lsin(\pi \alpha )$, т.е.

где $p(z)$ и ${{p}_{Q}}$ – давление на клин соответственно со стороны потока и со стороны каверны.

Используя закон Бернулли (4), а также равенство $\theta = \pi \alpha $ для угла наклона скорости на дуге $\Gamma _{z}^{{(2)}}$ и выполняющееся на ней соотношение

переписываем формулу (40) для коэффициента сопротивления в виде Вынесем из-под знака интеграла величину $V_{Q}^{2}$ и примем во внимание равенства вытекающие соответственно из (6) и (10), а результат подставим в формулу (41) для коэффициента сопротивления; тогда получим Перейдем к переменной $w$ с помощью соотношений $z = {{f}^{{ - 1}}}(w)$, $dz = {{f}^{{ - 1}}}{\kern 1pt} '(w)dw$ и формулы (23), после чего, вынося из фигурных скобок выражение $exp[ - F(w)]$, убеждаемся с помощью (27), что его произведение с ${{f}^{{ - 1}}}{\kern 1pt} '(w)$ равно $1{\text{/}}{{V}_{Q}}$. Используя еще тождество приходим к соотношению Переходя здесь от переменной $w$ к переменной $h$ с помощью равенств (34), (37), находим окончательное интегральное представление для коэффициента сопротивления в общем случае: Для каждой из рассматриваемых схем из этой формулы ниже получено явное выражение для ${{{\mathbf{C}}}_{x}}$.

4.2. Для оценки размеров каверны будем исходить из значения координаты “наивысшей” точки $D$ каверны. Введем в связи с этим величину $\mathfrak{L}$ относительной длины и величину $\mathfrak{W}$ относительной ширины каверны как отношение соответственно условной длины ${{D}_{x}}$ каверны и ее “поперечника” $2{{D}_{y}}$ к размеру основания $2lsin(\pi \alpha )$ клина, т.е.

Для того чтобы вычислить эти величины, найдем вначале комплексную координату точки $D$, воспользовавшись тем, что согласно (12), координата ее образа на плоскости годографа есть ${{D}_{\zeta }} = 0$. Тогда из второй формулы (31) находим ${{D}_{h}} = - 1$, а используя представление (38), записываем формулу для $z$-координаты точки $D$ в общем случае: Отделяя здесь действительную и мнимую части и подставляя результат в формулу (44), получаем величину $\mathfrak{L}$ относительной длины и величину $\mathfrak{W}$ относительной ширины каверны.

Для каждой из рассматриваемых схем из формул (44) и (45) ниже получены явные выражения для $\mathfrak{L}$ и $\mathfrak{W}$.

4.3. Найдем представление для линий тока. Согласно п. 2.1, координата $z(u)$ точек линии

соответствующей значению ${\tilde {v}} = {\text{const}}$ функции тока, где $u$ – параметр, принимающий вещественные значения, записываются с помощью соотношения (38) в виде формулы: Здесь верхний предел равен $h(u + i\tilde {v}) = {{\Theta }^{{ - 1}}} \circ {{\chi }^{{ - 1}}}(u + i\tilde {v})$, где ${{\Theta }^{{ - 1}}}$ дается первой формулой (32), а о функции ${{\chi }^{{ - 1}}}(w)$ сказано в конце разд. 3.

Ниже для каждой из рассматриваемых схем эта формула приведена к замкнутой аналитической форме и численно реализована в виде картины обтекания.

5. PACЧЕТ ТЕЧЕНИЯ ПО СХЕМЕ ГЕЛЬМГОЛЬЦА–КИРХГОФА

5.1. Поскольку, согласно п. 2.4, областью годографа $\mathcal{B}_{\zeta }^{H}$ для рассматриваемой схемы является полуполоса (16), приведенная на фиг. 3в, то, используя сведения об элементарных функциях, например, из монографии [6], нетрудно убедиться, что ее образом при отображении $t = {{T}^{{ - 1}}}(\zeta )$, определяемом первой формулой (31), является полуплоскость, т.е.

с соответствием точек, изображенным на фиг. 3в, 3г. Тогда из (24) и (48) вытекает откуда очевидно, что функция $w = \chi (t)$ осуществляет дробно-линейное отображение со следующим соответствием точек $A$, $B$, $C$ на (комплексных) плоскостях $t$ и $w$: Такую функцию, обратную к ней, и ее производную для схемы Гельмгольца–Кирхгофа находим без труда:

Подставляя вторую формулу (29) и $\chi {\kern 1pt} '(t)$ из (51) в суперпозицию

а результат – в уравнение (39) для $\varkappa $, приводим его (с учетом ${{V}_{Q}} = {{V}_{\infty }}$ для данной схемы) к следующему виду: откуда получаем равенство

Заметим, что входящий сюда интеграл, а также некоторые приводимые ниже интегралы могут быть выражены через гипергеометрическую функцию Гаусса [12], [13], которая определяется в виде ряда

сходящегося в единичном круге $\mathbb{U}: = \{ {\text{|}}x{\kern 1pt} {\text{|}} < 1\} $; здесь $\Gamma (a)$ – гамма-функция. Если же $x$ выходит за его пределы, то для вычисления этой функции используются формулы аналитического продолжения [12], представляющие ее в виде экспоненциально (как и ряд (55)) сходящихся рядов, области сходимости которых покрывают в совокупности всю внешность круга $\mathbb{U}$. Для того чтобы выразить интеграл (54) через функцию Гаусса, воспользуемся интегральным представлением Эйлера [12], Применяя это представление к интегралу из (54), находим окончательное выражение для $\varkappa $ в схеме Гельмгольца–Кирхгофа:

Подставляя суперпозицию (52) в формулу (38) для $z = {{f}^{{ - 1}}}(w)$, получаем обратную к потенциалу функцию:

где верхний предел $h(w) = {{\Theta }^{{ - 1}}} \circ {{\chi }^{{ - 1}}}(w)$, вытекающий из (32) и (51), записывается в виде Преобразуя формулу (58) с помощью представления (56), получаем окончательное выражение для обратной к потенциалу функции в схеме Гельмгольца–Кирхгофа: где $h(w)$ определяется формулой (59).

Построим картину обтекания клина для рассматриваемой схемы. Для этого в соответствии с п. 4.3 подставим $w = u + i\tilde {v}$ в формулы (59), (60), где параметр $u$ пробегает вещественные значения. Тогда получим значения координат $z(u)$ точек на линии тока, соответствующей $v = \tilde {v}$, в зависимости от параметра $u$. Численная реализация описанного алгоритма построения линий тока дала их распределение для рассматриваемого обтекания при схеме Гельмгольца–Кирхгофа для следующих случаев:

– фиг. 6: $l = 1$, $\alpha = \tfrac{1}{4}$, т.е. $\pi \alpha = 45^\circ $, ${{V}_{\infty }} = 1$, $\Delta \tilde {v} = 0.2$;

– фиг. 7: $l = 1$, $\alpha = \tfrac{3}{4}$, т.е. $\pi \alpha = 135^\circ $, ${{V}_{\infty }} = 1$, $\Delta \tilde {v} = 0.03$.

Кроме того (о чем было сказано в конце п. 2.4), на фиг. 3а дана верхняя половина картины обтекания при $l = 1$, $\alpha = \tfrac{1}{3}$, т.е. $\pi \alpha = 60^\circ $, ${{V}_{\infty }} = 0.5$, $\Delta \tilde {v} = 0.3$.

5.2. Чтобы найти коэффициент сопротивления, обозначаемый через ${\mathbf{C}}_{x}^{H}$, соответствующий данной схеме, подставим суперпозицию (52) в общее представление (43) для этого коэффициента

учитывая формулу (57) для $\varkappa $ и выражая фигурирующий здесь интеграл с помощью (56) через функцию Гаусса, приходим к окончательному выражению для коэффициента сопротивления при схеме Гельмгольца–Кирхгофа для задачи обтекания клина: Мы не помещаем здесь численные результаты, получаемые по этой формуле, так как они с хорошей точностью ($ \sim {\kern 1pt} {{10}^{{ - 3}}}$) совпадают с известными результатами И.В. Мещерского [14], приведенными, например, в монографии [2]. Отметим только, что из формулы (62) легко вытекают следующие соотношения для коэффициента ${\mathbf{C}}_{x}^{H}$ как функции угла $\pi \alpha $что хорошо согласуется с результатами И.В. Мещерского и полученными здесь численными результатами.

Заметим еще, что для данной схемы размеры каверны неограничены, а исследование зависимости характеристик течения от $Q$ невозможно, поскольку схема соответствует значению $Q = 0$.

6. PACЧЕТ ТЕЧЕНИЯ ПО СХЕМЕ ЖУКОВСКОГО–РОШКО

6.1. Согласно п. 2.4, область годографа для рассматриваемой схемы, обозначаемая через $\mathcal{B}_{\zeta }^{Z}$, представляет собой ту же полуполосу, что и в схеме Гельмгольца–Кирхгофа, но с другим расположением точки $A$, а именно, ${{A}_{\zeta }} = ln\sqrt {1 + Q} $ (ср. фиг. 3в и 4в). Как и при изучении предыдущей схемы, видим, что ее образом ${{T}^{{ - 1}}}(\mathcal{B}_{\zeta }^{Z})$ согласно (48) является полуплоскость $\mathbb{H}_{t}^{ + }$ с соответствием точек $A$, $B$, $C$, изображенным на фиг. 4в, 4г. Тогда в силу (24), (36) и (48) очевидно

а значит, $\chi $ является дробно-линейным отображением с нормировкой: где $\tau $ – координата точки $A$ на плоскости $t$ – дается формулой Такая функция $w = \chi (t)$, обратная к ней, и ее производная имеют для схемы Жуковского–Рошко вид:

Подставляя $t = \Theta (h)$ из (29) и $\chi {\kern 1pt} '(t)$ из (67) в суперпозицию $\chi {\kern 1pt} '\; \circ \Theta (h)$,

а результат – в уравнение (39) для $\varkappa $, приводим его к следующему виду: Записывая входящий сюда интеграл с помощью представления (56) через комбинацию функций Гаусса, находим явное выражение для $\varkappa $ в схеме Жуковского–Рошко: Здесь через $\Phi (a,\tau )$ обозначен определенный интеграл представимый через $F(a,b;c;x)$ в виде: где введено обозначение

Подставляя суперпозицию (68) в формулу (38) для $z = {{f}^{{ - 1}}}(w)$, получаем обратную к потенциалу функцию в виде:

Применяя к обоим интегралам представление (56), получаем окончательную формулу для этой функции в схеме Жуковского–Рошко: через функцию $J(a,\tau ;h)$, являющуюся интегралом и выражаемую в терминах гипергеометрической функции $F(a,b;c;x)$: Верхний предел $h(w) = {{\Theta }^{{ - 1}}} \circ {{\chi }^{{ - 1}}}(w)$ в интегралах (74) и (76), вытекающий из (32) и второй формулы (67), записывается в виде

Построим картину обтекания клина для рассматривамой схемы. Чтобы рассчитать линию тока, соответствующую $v = \tilde {v}$, подставим в соответствии с п. 4.3 $w = u + i\tilde {v}$ в формулы (75), (77), (78), где параметр $u$ пробегает вещественные значения. Тогда получим значение координат $z(u)$ точек на линии тока, соответствующей $v = \tilde {v}$, как функцию параметра $u$. Численная реализация такого алгоритма дала картину линий тока для рассматриваемого обтекания при схеме Жуковского–Рошко для следующих случаев:

– фиг. 8: $l = 1$, $\alpha = \tfrac{1}{4}$, т.е. $\pi \alpha = 45^\circ $, ${{V}_{\infty }} = 1$, $Q = 0.6$, $\Delta \tilde {v} = 0.2$;

– фиг. 9: $l = 1$, $\alpha = \tfrac{3}{4}$, т.е. $\pi \alpha = 135^\circ $, ${{V}_{\infty }} = 1$, $Q = 0.6$, $\Delta \tilde {v} = 0.1$.

Кроме того (о чем было сказано в конце п. 2.4), на фиг. 4а дана верхняя половина картины обтекания при $l = 1$, $\alpha = \tfrac{1}{3}$, т.е. $\pi \alpha = 60^\circ $, ${{V}_{\infty }} = 0.5$, $Q = 0.6$, $\Delta \tilde {v} = 0.3$.

6.2. Обозначив через ${\mathbf{C}}_{x}^{Z}$ коэффициент сопротивления для схемы Жуковского–Рошко, подставим суперпозицию (68) в общее представление (43) для коэффициента сопротивления. Тогда получим

а учитывая формулу (70) для $\varkappa $ и записывая фигурирующий здесь интеграл с помощью представления (56), приходим к окончательному выражению для коэффициента сопротивления в схеме Жуковского–Рошко: где $\Phi (\alpha ,\tau )$ определена через функции Гаусса в (72). В результате выполненной численной реализации такого алгоритма были получены значения величины ${{{\mathbf{C}}}_{x}}$ при различных $\alpha $ и $Q$, приведенные в табл. 1.

Особый интерес представляет асимптотика коэффициента сопротивления ${\mathbf{C}}_{x}^{Z}$ как функции числа кавитации при малых $Q$. Из соотношения (66) получаем:

Подставляя это разложение в (72), (73), а результат – в формулу (80), и учитывая вид (62) коэффициента сопротивления ${\mathbf{C}}_{x}^{H}$ для схемы Гельмгольца–Кирхгофа, находим, что асимптотика коэффициента сопротивления ${\mathbf{C}}_{x}^{Z}$ для схемы Жуковского–Рошко имеет вид: где коэффициенты $E_{2}^{Z}$ и $E_{3}^{Z}$ суть

Отметим, что если в асимптотике (82) положить $Q = 0$, то мы получим, как и следовало ожидать, что ${\mathbf{C}}_{x}^{Z}(0) = {\mathbf{C}}_{x}^{H}$.

6.3. Для того чтобы найти величины ${{\mathfrak{L}}^{Z}}$ относительной длины и ${{\mathfrak{W}}^{Z}}$ относительной ширины каверны для рассматриваемой схемы, вычислим сперва координату $D_{z}^{Z}$ “наивысшей” точки $D$ каверны, подставив суперпозицию (68) в интеграл (45); в результате получим

Записывая этот интеграл через функцию $J(a,\tau ;h)$, выражаемую согласно (77) в терминах функции Гаусса, получаем окончательную формулу для координаты “наивысшей” точки $D$ каверны в схеме Жуковского–Рошко:

Выполненные по этой формуле расчеты координаты $D_{z}^{Z} = D_{x}^{Z} + iD_{y}^{Z}$ с подстановкой ее вещественной и мнимой части в выражения (44) позволили для схемы Жуковского–Рошко построить графики зависимости величины ${{\mathfrak{L}}^{Z}}$ от угла $\pi \alpha $ при различных $Q$, изображенные на фиг. 10, а также графики зависимости величины ${{\mathfrak{W}}^{Z}}$ от угла $\pi \alpha $ при различных $Q$, изображенные на фиг. 11.

Получим теперь асимптотики при $Q \to 0$ величин ${{\mathfrak{L}}^{Z}}(Q)$ и ${{\mathfrak{W}}^{Z}}(Q)$, рассматриваемых как функции числа кавитации. Подставим оценку (81) для $\tau $ в выражения (68), определяющие ${{h}_{1}}$ и ${{h}_{2}}$, а найденные соотношения – в равенство (77) для $J(a,\tau ; - 1)$ и воспользуемся в последнем формулами аналитического продолжения функции Гаусса в единицу [12]. Используя полученный результат в формуле (85), отделяя вещественную и мнимую части и подставляя их в определение (44) для величин $\mathfrak{L}$ и $\mathfrak{W}$, устанавливаем асимптотики относительной длины и относительной ширины каверны в изучаемой задаче обтекания клина для схемы Жуковского–Рошко:

Из этих формул, как нетрудно заметить, следует, что длина каверны растет быстрее, чем ее ширина, при $Q \to 0$.

7. PACЧЕТ ТЕЧЕНИЯ ПО СХЕМЕ РЯБУШИНСКОГО

7.1. Как установлено в п. 2.4, область годографа $\mathcal{B}_{\zeta }^{R}$ для схемы Рябушинского определяется формулой (22) и имеет вид, представленный на фиг. 5в. Используя симметрию этой области относительно интервала ${{\mathcal{P}}_{\zeta }}$, определяемого по формуле (21), и применяя принцип симметрии Римана–Шварца [6] к отображению $t = {{T}^{{ - 1}}}(\zeta )$, находим с учетом (48), что образом области $\mathcal{B}_{\zeta }^{R}$ при этом отображении является объединение $\mathcal{B}_{t}^{R}$ верхней $\mathbb{H}_{t}^{ + }$ и нижней $\mathbb{H}_{t}^{ - }$ полуплоскостей, соединенных интервалом ${{\mathcal{P}}_{t}}: = {{T}^{{ - 1}}}({{\mathcal{P}}_{\zeta }}) = \{ t \in (1,\tau )\} $ (см. фиг. 5г), т.е.

и, таким образом, имеем отображение с соответствием точек $A$, $B$, $C$ и $D$, изображенным на фиг. 5в, 5г, где координата ${{A}_{t}} = \tau $ определяется, как и для предыдущей схемы, формулой (66).

Обозначим (пока неизвестные) координаты $C_{w}^{R}$ и $D_{w}^{R}$ соответственно через $\varkappa $ и $\delta $ (см. фиг. 5б) и разрежем полуплоскость потенциала $\mathbb{H}_{w}^{ + }$ вертикальной прямой ${{\mathcal{P}}_{w}}$, определяемой из (19), на две части, левую из которых назовем $\mathbb{L}$. Тогда, используя принцип симметрии, видим, что функция $\chi (t) - \delta $ отображает полуплоскость $\mathbb{H}_{t}^{ + }$ на $\mathbb{L}$, а значит, ее квадрат ${{(\chi (t) - \delta )}^{2}}$ отображает $\mathbb{H}_{t}^{ + }$ на $\mathbb{H}_{w}^{ + }$ и является дробно-линейной функцией с соответствием точек $\tau \to \infty $, $\infty \to {{\delta }^{2}}$, $1 \to 0$. Отсюда находим, что функция $w = \chi (t)$, обратная к ней и ее производная имеют для схемы Рябушинского вид:

Из соотношений (23) и (36) следует равенство $\varkappa = \chi ( - 1)$. Используя его в сочетании с первой формулой (90), находим связь между неизвестными $\varkappa $ и $\delta $: Подставим теперь $t = \Theta (h)$ из (29) и $\chi {\kern 1pt} '(t)$ из (90) в суперпозицию $\chi {\kern 1pt} '\; \circ \Theta (h)$, имеющую для схемы Рябушинского вид где ${{h}_{1}}$ и ${{h}_{2}}$ определяются равенствами (68), а результат – в соотношение (39). Из него получаем для $\delta $ следующее выражение: Записывая входящий сюда интеграл через функцию Аппé ля [12], с помощью интегрального представления типа Эйлера, находим окончательную формулу для $\delta $ в схеме Рябушинского: Тогда величина $\varkappa $ вычисляется через $\delta $ по формуле (91).

Подставляя суперпозицию (92) в формулу (38) для $z = {{f}^{{ - 1}}}(w)$, получаем обратную к потенциалу функцию в виде:

Применяя к обоим интегралам представление (95), получаем окончательную формулу для этой функции в схеме Рябушинского: где вместо $h$ следует подставить зависимость вытекающую из суперпозиции $h(w) = {{\Theta }^{{ - 1}}} \circ {{\chi }^{{ - 1}}}(w)$ с использованием (32) и (90).

Построим картину обтекания клина для рассматривамой схемы Рябушинского. Аналогично другим схемам и согласно п. 4.3, для расчета координат $z(u)$ точек линии тока, соответствующей $v = \tilde {v}$, подставим $w = u + i\tilde {v}$ в формулы (98), (99), где параметр $u$ пробегает вещественные значения. Численная реализация такого алгоритма дала картину линий тока для рассматриваемого обтекания при схеме Рябушинского для следующих случаев:

– фиг. 12: $l = 1$, $\alpha = \tfrac{1}{4}$, т.е. $\pi \alpha = 45^\circ $, ${{V}_{\infty }} = 1$, $Q = 0.9$, $\Delta \tilde {v} = 0.15$;

– фиг. 13: $l = 1$, $\alpha = \tfrac{1}{2}$, т.е. $\pi \alpha = 90^\circ $, ${{V}_{\infty }} = 1$, $Q = 1.0$, $\Delta \tilde {v} = 0.15$;

– фиг. 14: $l = 1$, $\alpha = \tfrac{3}{4}$, т.е. $\pi \alpha = 135^\circ $, ${{V}_{\infty }} = 1$, $Q = 1.0$, $\Delta \tilde {v} = 0.15$.

Кроме того (о чем было сказано в конце п. 2.4), на фиг. 5а дана верхняя половина картины обтекания при $l = 1$, $\alpha = 0.3$, т.е. $\pi \alpha = 54^\circ $, ${{V}_{\infty }} = 1.0$, $Q = 1.0$, $\Delta \tilde {v} = 0.6$.

7.2. Обозначив через ${\mathbf{C}}_{x}^{R}$ коэффициент сопротивления для схемы Рябушинского и подставляя суперпозицию (92) в общее представление (43) для коэффициента сопротивления, получаем

а учитывая формулу (93) для $\delta $ и записывая фигурирующий здесь интеграл с помощью представления (95), приходим к окончательному выражению для коэффициента сопротивления в схеме Рябушинского через функции Аппеля: где (напомним) ${{h}_{1}}$ и ${{h}_{2}}$ определяются равенствами (68), а входящая в них величина $\tau $ выражается через $Q$ по формуле (66). Численная реализация такого алгоритма позволила получить значения величины ${\mathbf{C}}_{x}^{R}$ при различных $\alpha $ и $Q$, приведенные в табл. 2.

Используя упомянутые формулы (66), (68), (94), (101) и оценку (81) для $\tau $, а также учитывая вид (62) коэффициента сопротивления ${\mathbf{C}}_{x}^{H}$ для схемы Гельмгольца–Кирхгофа, получаем следующую асимптотику коэффициента сопротивления ${\mathbf{C}}_{x}^{R}$ для схемы Рябушинского:

где

Сравнение коэффициентов (103) и (82) разложений (102) и (82) для схем соответственно Рябушинского и Жуковского–Рошко показывает, что они связаны соотношениями:

7.3. Для того чтобы найти величины ${{\mathfrak{L}}^{R}}$ относительной длины и ${{\mathfrak{W}}^{R}}$ относительной ширины каверны для схемы Рябушинского, вычислим сперва координату $D_{z}^{R}$ “наивысшей” точки $D$ каверны, подставив суперпозицию (92) в интеграл (45); в результате получим выражение:

которое можно переписать с использованием представления (95) для функции Аппé ля в виде:

Выполненные по этой формуле расчеты координаты $D_{z}^{R} = D_{x}^{R} + iD_{y}^{R}$ с подстановкой ее вещественной и мнимой части в выражения (44) позволили для схемы Рябушинского построить графики зависимости величины ${{\mathfrak{L}}^{R}}$ от угла $\pi \alpha $ при различных $Q$, изображенные на фиг. 15, а также графики зависимости величины ${{\mathfrak{W}}^{R}}$ от угла $\pi \alpha $ при различных $Q$, изображенные на фиг. 16.

Получим теперь асимптотики величин ${{\mathfrak{L}}^{R}}(Q)$ и ${{\mathfrak{W}}^{R}}(Q)$, рассматриваемых как функции числа кавитации, для схемы Рябушинского при $Q \to 0$. Подставим оценку (81) для $\tau $ в выражения (68), определяющие ${{h}_{1}}$ и ${{h}_{2}}$, а найденные соотношения – в представление (106) для координаты “наивысшей” точки $D$ каверны и воспользуемся в этом представлении формулами аналитического продолжения функции Аппéля в единицу [15], [16]. Используя этот результат в формуле (106), отделяя вещественную и мнимую части и подставляя их в определение (44) для величин $\mathfrak{L}$ и $\mathfrak{W}$, устанавливаем асимптотики относительной длины и относительной ширины каверны в изучаемой задаче обтекания клина для схемы Рябушинского:

Сравнивая эти формулы с аналогичными формулами (86), (87) для схемы Жуковского–Рошко, находим, что ${{\mathfrak{L}}^{R}} \sim 2\,{{\mathfrak{L}}^{Z}}$, а ${{\mathfrak{W}}^{R}} \sim \frac{4}{\pi }\,{\kern 1pt} {{\mathfrak{W}}^{Z}}$.

Авторы выражают благодарность С.И. Безродных и С.В. Пикулину за помощь в работе, а В.Б. Заметаеву за полезные обсуждения.