Журнал вычислительной математики и математической физики, 2020, T. 60, № 12, стр. 2143-2161

2.1 Общий случай

Рассматривается стационарная трехмерная задача фильтрации вязкой жидкости в кусочно-однородной среде (фиг. 1).

Пусть $\Omega $ – область фильтрации, ограниченная снаружи замкнутой гладкой поверхностью ${{\Sigma }_{1}}$. Предположим, что в области $\Omega $ имеется основная область ${{\Omega }_{1}}$, для которой внешняя часть границы есть поверхность ${{\Sigma }_{1}}$, и области ${{\Omega }_{2}}, \ldots ,{{\Omega }_{{{{N}_{d}}}}}$ – пористые включения. Пусть границами областей ${{\Omega }_{m}}$ являются гладкие замкнутые поверхности ${{\Sigma }_{m}}$, $m = 2, \ldots ,{{N}_{d}}$. При этом $\Omega = {{\Omega }_{1}} \cup {{\bar {\Omega }}_{2}} \cup \ldots {{\bar {\Omega }}_{{Nd}}}$ и все области ${{\Omega }_{m}}$, $m = 1, \ldots ,{{N}_{d}}$, попарно не пересекаются (здесь использовано обозначение $\bar {\Omega }$ – замыкание множества $\Omega $). Пусть ${{\Sigma }^{2}} = \bigcup\nolimits_{m = 2}^{{{N}_{d}}} \,{{\Sigma }_{m}}$ – суммарная граница всех включений, и пусть ${{\Sigma }^{1}} = {{\Sigma }_{1}}$ – внешняя граница области течения. Будем предполагать, что каждая из поверхностей ${{\Sigma }_{m}}$, $m = 1, \ldots ,{{N}_{d}}$, ориентирована так, что положительной считается внешняя сторона. Пусть ${\mathbf{n}} = {\mathbf{n}}(x)$, $x \in {{\Sigma }_{m}}$, $m = 1, \ldots ,{{N}_{d}}$, – орт внешней (положительной) нормали к поверхности ${{\Sigma }_{m}}$ в точке $x$.

Каждая область ${{\Omega }_{m}}$ характеризуется коэффициентом гидравлической проводимости ${{\kappa }_{m}}$.

Предположим, что приток и вытекание жидкости в области фильтрации происходят через внешнюю поверхность ${{\Sigma }_{1}}$, а также в заданных точечных источниках. Пусть имеется ${{N}_{s}}$ источников, расположенных в точках ${{q}_{l}}$, в каждом из которых задан расход жидкости ${{Q}_{l}}$, $l = 1, \ldots ,{{N}_{s}}$ (далее точечный сток рассматривается как источник с отрицательным расходом жидкости). Будем полагать, что каждый точечный источник расположен внутри одной из областей ${{\Omega }_{m}}$, $m = 1,2, \ldots ,{{N}_{d}}$ (при этом ${{q}_{l}} \notin {{\Sigma }^{1}},$ ${{q}_{l}} \notin {{\Sigma }^{2}}$). Поток через внешнюю поверхность предполагается известным и определяется заданием нормальной компоненты скорости фильтрации жидкости на поверхности ${{\Sigma }_{1}}$.

Граничные условия и интенсивности точечных источников заданы таким образом, что выполняется закон сохранения масс – суммарный поток жидкости в источниках и через внешнюю границу равен нулю.

Предполагается, что фильтрация жидкости в каждой из областей ${{\Omega }_{m}}$ описывается законом Дарси–Бринкмана [3] для неизвестных полей скорости фильтрации жидкости ${\mathbf{v}}$ и давления жидкости $p$:

где $\mu $ – динамическая вязкость жидкости. Так же во всех областях ${{\Omega }_{m}}$, $m = 1,...,{{N}_{d}}$, требуется выполнение уравнения неразрывности На внешней границе области фильтрации ${{\Sigma }^{1}}$ ставятся граничные условия на поток жидкости и условие непроскальзывания, обусловленное наличием вязкости. На суммарной границе раздела сред ${{\Sigma }^{2}}$, состоящей из участков ${{\Sigma }_{m}}$ – границ областей ${{\Omega }_{m}}$, $m = 2,...,{{N}_{d}}$, должны выполняться условия непрерывности скорости и давления. Перечисленные граничные условия формулируются в виде системы равенств Здесь ${{f}_{0}}(x)$ – заданная функция, определяющая поток жидкости через внешнюю границу, ${{{\mathbf{v}}}^{ + }}(x)$ и ${{{\mathbf{v}}}^{ - }}(x)$ – краевые значения скорости на внешней и внутренней стороне рассматриваемой поверхности соответственно, “$ \cdot $” – скалярное произведение, “$ \times $” – векторное произведение.

Поля скоростей и давления ищутся в виде

где ${\mathbf{u}}$ и $\tilde {p}$ – неизвестные вторичные поля скоростей и давления, а ${{{\mathbf{v}}}_{0}}$ и ${{p}_{0}}$ – первичные поля скоростей и давления, создаваемые заданной системой точечных источников:

При этом уравнения (1) и (2) выполняются в областях ${{\Omega }_{m}},m = 1,...,{{N}_{d}}$, вне точек ${{q}_{l}}$, $l = 1,...,{{N}_{s}}$, а вторичные поля скоростей и давления удовлетворяют условиям ${\mathbf{u}} \in {{C}^{2}}({{\Omega }_{m}})$, $\tilde {p} \in {{C}^{1}}({{\Omega }_{m}})$, $m = 1,...,{{N}_{d}}$. На поверхностях ${{\Sigma }_{1}}$ и ${{\Sigma }_{2}}$ должны существовать краевые значения неизвестных функций, фигурирующие в граничных условиях (3).

Упомянутое выше условие о равенстве нулю суммарного потока жидкости формулируется в виде следующего соотношения:

Уравнения (1) и (2) позволяют разложить вторичное поле скоростей на потенциальную ${{{\mathbf{v}}}_{p}}$ и соленоидальную ${{{\mathbf{v}}}_{s}}$ составляющие в каждой из областей ${{\Omega }_{m}}$:

Потенциал $\varphi $ является решением уравнения Лапласа, поэтому будем строить для него интегральное представление, используя классические поверхностные потенциалы простого и двойного слоя. Введем следующие обозначения:

где $W[S,h]$ – потенциал простого слоя, размещенного на поверхности $S$ с плотностью $h$, $U[S,g]$ – потенциал двойного слоя, размещенного на поверхности $S$, с плотностью $g$.

Соленоидальная составляющая поля скоростей является решением векторного уравнения Гельмгольца в каждой из областей ${{\Omega }_{m}}$:

где ${{k}_{m}} = 1{\text{/}}\sqrt {{{\kappa }_{m}}} $. Частным решением данного уравнения в области ${{\Omega }_{m}}$ является векторный потенциал ${{R}_{m}}$ (см. [5]): где ${\mathbf{j}}$ – касательное векторное поле на поверхности $S$.

Будем искать вторичные поля скоростей и давления ${\mathbf{v}}$ и $p$ в следующем виде (подробное изложение построения интегрального представления решения изложено в [5]):

где $h$ – неизвестная плотность потенциала простого слоя, размещенного на поверхностях ${{\Sigma }^{1}}$ и ${{\Sigma }^{2}}$, $g$ – неизвестная плотность потенциала двойного слоя, размещенного на поверхности ${{\Sigma }^{2}}$, ${\mathbf{j}}$ – неизвестное касательное векторное поле, размещенное на поверхностях ${{\Sigma }^{1}}$ и ${{\Sigma }^{2}}$.

Напомним основные свойства краевых значений поверхностных потенциалов простого и двойного слоя, а также векторного потенциала $R$, размещенных на гладкой замкнутой поверхности $S$. При достаточной гладкости этой поверхности и плотностей существуют краевые значения этих потенциалов на поверхности [6, § 2.4, 2.5, с. 57–70]:

здесь знак “$ + $” соответствует краевым значениям с внешней стороны поверхности, знак “$ - $” – с внутренней, индекс $m$ в операторе ${{R}_{m}}$ указывает на значение параметра ${{\kappa }_{m}}$, используемое в данном операторе, через $\operatorname{Grad} g$ обозначен поверхностный градиент функции $g$ (см. [6, § 2.1, с. 45]). Операторы в правых частях понимаются в смысле прямого значения на поверхности. Под прямыми значениями потенциалов $W,U,R$ понимаются значения, получаемые непосредственно из формул (7) и (8) при подстановке в них рассматриваемого значения $x \in S$, а под прямыми значениями градиентов потенциалов $W$ и $U$ понимаются значения, определяемые формулами последний интеграл понимается в смысле главного значения.

Используя приведенные формулы, запишем выражения для краевых значений функций ${\mathbf{v}}$ и $p$ на граничных поверхностях.

Краевое значение скорости на поверхности ${{\Sigma }^{1}}$ имеет вид

Краевые значения скорости на поверхностях ${{\Sigma }_{m}}$, $m = 2,...,{{N}_{d}}$, выражаются формулой где мы обозначили $m + = 1$, $m - = m$. Краевые значения давления на поверхностях ${{\Sigma }_{m}}$, $m = 2,...,{{N}_{d}}$, выражаются формулой

Поля скоростей и давления, заданные формулами (9) и (11), удовлетворяют уравнениям (1), (2) автоматически. В статье [5] была записана следующая система граничных интегральных уравнений относительно неизвестных функций $h$, $g$, ${\mathbf{j}}$, возникающая из подстановки записанных формул для краевых значений скорости и давления (12)–(14) в систему граничных условий (3):

где ${{\beta }_{m}} = 2({{\kappa }_{m}} - {{\kappa }_{1}}){\text{/}}({{\kappa }_{m}} + {{\kappa }_{1}})$. В статье [5] доказано, что если функции $h$, $g$, ${\mathbf{j}}$ удовлетворяют определенным условиям гладкости и являются решением системы интегральных уравнений (15), то поле скоростей ${\mathbf{v}}$, определяемое формулой (9), и давление $p$, определяемое формулой (11), являются решением краевой задачи (1)–(3).

Отметим, что давление $p$ в рассматриваемой краевой задаче определено с точностью до постоянного слагаемого. Первое уравнение системы (15) может быть выполнено только при условии (6), а последнее уравнение этой системы служит для выделения единственного решения.

2.2. Частные случаи

Наряду с задачей (1)–(3), так же, как и в статье [5], рассмотрим два упрощенных варианта этой задачи. Первый – задача фильтрации вязкой жидкости в однородной области ${{\Omega }_{1}}$ с заданным потоком через граничную поверхность. Второй – задача сопряжения скорости и давления на одной из поверхностей ${{\Sigma }_{m}}$, $m = 2, \ldots ,{{N}_{d}}$, внешняя область ${{\Omega }_{1}}$ считается бесконечной.

Задача в области без включений. В области $\Omega = {{\Omega }_{1}}$ без включений, которая имеет границу $\Sigma = {{\Sigma }^{1}}$, ищутся полные поля скоростей ${\mathbf{v}}$ и давления $p$, представляющиеся в виде (4) и (5), где ${{{\mathbf{v}}}_{0}}$ и ${{\varphi }_{0}}$ – заданные функции, ${\mathbf{u}}$ и $\tilde {p}$ – неизвестные функции, удовлетворяющие следующим уравнениям и граничным условиям:

где ${{f}_{0}}$ – заданная функция на поверхности $\Sigma $, удовлетворяющая условию (6).

Вторичные поля скоростей и давления ищем в виде

Неизвестные функция $h$ и касательное поле ${\mathbf{j}}$ ищутся из системы интегральных уравнений

Задача сопряжения. Пусть задана замкнутая поверхность $\Sigma $. Обозначим для этой задачи внешнюю (неограниченную) область ${{\Omega }_{1}}$, а внутреннюю область ${{\Omega }_{2}}$. На границе раздела областей – поверхности $\Sigma $ – скорость и давление непрерывны. Ищутся полные поля скоростей ${\mathbf{v}}$ и давления $p$, представляющиеся в виде (4) и (5), где ${{{\mathbf{v}}}_{0}}$ и ${{\varphi }_{0}}$ – заданные функции (источники расположены в точках ${{q}_{l}} \in {{\Omega }_{1}} \cup {{\Omega }_{2}}$), ${\mathbf{u}}$ и $\tilde {p}$ – неизвестные функции, удовлетворяющие следующим уравнениям и граничным условиям:

Вторичные поля скоростей и давления ищем в виде

Неизвестные функции $h$, $g$ и касательное поле ${\mathbf{j}}$ ищутся из системы интегральных уравнений

где $\beta = 2\tfrac{{{{\kappa }_{2}} - {{\kappa }_{1}}}}{{{{\kappa }_{2}} + {{\kappa }_{1}}}},$ ${{\varphi }_{0}}$ определяется формулой (5).

3.1. Дискретизация поверхностей

Каждая из поверхностей, ограничивающих область фильтрации и области включений, аппроксимируется системой четырехугольных ячеек, все вершины которых лежат на аппроксимируемой поверхности. Пусть ${{\sigma }_{k}}$, $k = 1,...,{{N}^{1}}$, – система ячеек, аппроксимирующих внешнюю поверхность ${{\Sigma }^{1}}$, и пусть ${{\sigma }_{k}}$, $k = {{N}^{1}} + 1,...,N$, – система ячеек, аппроксимирующих суммарную границу включений ${{\Sigma }^{2}}$. Обозначим также ${{N}^{2}} = N - {{N}^{1}}$ – число ячеек, аппроксимирующих суммарную границу включений. При этом предполагается, что для каждой из замкнутых поверхностей ${{\Sigma }_{m}}$, $m = 1,...,{{N}_{d}}$, являющейся границей области фильтрации или границей одного из включений, система ячеек ${{\sigma }_{k}}$, соответствующих этой поверхности, образует некоторую замкнутую поверхность ${{\tilde {\Sigma }}_{m}}$, на которой указанные ячейки формируют конформную сетку. Предполагается, что все приближенные поверхности ${{\tilde {\Sigma }}_{m}}$ попарно не пересекаются, так же как и исходные поверхности.

Краем каждой ячейки разбиения является некоторый, вообще говоря, пространственный четырехугольный контур. При построении разбиения могут возникать также треугольные ячейки, которые рассматриваются как вырожденные четырехугольники с двумя совпадающими вершинами.

Строящаяся ниже численная схема с точки зрения учета геометрии поверхностей оперирует только с угловыми точками ячеек. При сформированных вершинах ячеек уже не требуется знание параметризации исходных поверхностей.

Для каждой ячейки с номером $k$ определим приближенный вектор внешней нормали ${{{\mathbf{n}}}_{k}}$ как единичный вектор, сонaправленный векторному произведению диагоналей ячейки (в общем случае диагонали не пересекаются) (см. фиг. 2 в центре). Построим также два вектора ${\mathbf{\tau }}_{k}^{1}$, ${\mathbf{\tau }}_{k}^{2}$, которые будем назвать касательными для ячейки ${{\sigma }_{k}}$, таким образом, чтобы тройка векторов $({{{\mathbf{n}}}_{k}},{\mathbf{\tau }}_{k}^{1},{\mathbf{\tau }}_{k}^{2}) = 1$ являлась правой ортонормированной. Для каждой ячейки вычислим приближенную площадь ${{s}_{k}}$ как половину модуля векторного произведения диагоналей. Так же для каждой ячейки построим точку коллокации ${{x}_{k}}$, как точку пересечения отрезков соединяющих середины противоположных сторон ячейки.

3.2. Дискретизация интегральных операторов

Будем аппроксимировать функции $h,\;g,\;{\mathbf{j}}$ функциями $\tilde {h},\;\tilde {g},\;{\mathbf{\tilde {j}}}$, заданными на приближенных поверхностях ${{\tilde {\Sigma }}_{m}}$, $m = 1,...,{{N}_{d}}$, и принимающими на каждой ячейке разбиения постоянное значение. Пусть

$k = 1,...,N$, для функций $h$ и ${\mathbf{\tilde {j}}}$, $k = {{N}^{1}} + 1,...,N$, для функции $\tilde {g}$.

При этом указанные равенства должны быть выполнены во внутренних точках ячеек, под внутренними точками ячейки будем понимать точки этой ячейки, не лежащие на ее краю. Значения приближенных функций на краях ячеек несущественны с точки зрения вычисления интегральных операторов. Для строгости можно положить все эти функции равными 0 на краях ячеек.

Каждый вектор ${{{\mathbf{j}}}_{k}}$ предполагается ортогональным вектору ${{{\mathbf{n}}}_{k}}$. Тогда этот вектор можно разложить по касательным векторам для рассматриваемой ячейки: ${{{\mathbf{j}}}_{k}} = j_{i}^{1}{\mathbf{\tau }}_{k}^{1} + j_{i}^{2}{\mathbf{\tau }}_{k}^{2}$.

Введенные кусочно-постоянные функции определяются наборами значений

Пусть $\Sigma $ – одна из поверхностей ${{\Sigma }_{m}}$, $m = 1,...,{{N}_{d}}$, а $\tilde {\Sigma } = {{\tilde {\Sigma }}_{m}}$ – приближающая ее поверхность. Потенциалы $W[\Sigma ,h]$, $U[\Sigma ,g]$ и $R[\Sigma ,{\mathbf{j}}]$ в уравнениях (15) будем приближать потенциалами $W[\tilde {\Sigma },\tilde {h}]$, $U[\tilde {\Sigma },\tilde {g}]$ и $R[\tilde {\Sigma },{\mathbf{\tilde {j}}}]$ соответственно, и запишем вместо интегральных уравнений (15) аналогичные уравнения на поверхностях $\mathop {\tilde {\Sigma }}\nolimits_m $, которые должны выполняться в точках коллокации ${{x}_{k}}$, $k = 1,...,N$. При этом прямые значения интегральных операторов $W[\Sigma ,h]$, $U[\Sigma ,g]$ и $R[\Sigma ,{\mathbf{j}}]$ в точках поверхности $\Sigma $ и их градиентов в этих точках, которые фигурируют в уравнениях (15), заменяются прямыми значениями операторов $W[\tilde {\Sigma },\tilde {h}]$, $U[\tilde {\Sigma },\tilde {g}]$ и $R[\tilde {\Sigma },{\mathbf{\tilde {j}}}]$ в точках коллокации, которые трактуются как точки, лежащие на поверхности $\tilde {\Sigma }$.

Аппроксимация потенциалов простого и двойного слоя и их градиентов. Прямое значение потенциала простого слоя в точке коллокации ${{x}_{i}}$ приблизим выражением

Прямое значение потенциала двойного слоя в точке ${{x}_{i}}$ приближается формулой

Для аппроксимации прямого значения градиента потенциала простого слоя в точке коллокации ${{x}_{i}}$ используем формулу

Заметим, что при $i = k$ интегралы в выражении для величин ${{W}_{{ik}}}$ являются несобственными абсолютно сходящимися, а в выражении для величин ${{{\mathbf{w}}}_{{ik}}}$ – сингулярными, понимаемыми в смысле главного значения. Способ приближенного вычисления таких интегралов по ячейкам будет описан ниже.

В уравнения (15) входит также градиент потенциала двойного слоя. При этом потенциал двойного слоя размещается на суммарной поверхности включений ${{\Sigma }^{2}}$, а в уравнения входят значения градиента этого потенциала только на внешней границе ${{\Sigma }^{1}}$. Это означает, что нам необходимо аппроксимировать значения градиента потенциала двойного слоя в точках, удаленных от этой поверхности на расстояние, большее некоторой положительной величины.

Пусть $\Sigma $ – одна из поверхностей ${{\Sigma }_{m}} \subset {{\Sigma }^{2}}$, $m = 2,...,{{N}_{d}}$. Для вычисления градиента потенциала двойного слоя в точке ${{x}_{i}} \in {{\tilde {\Sigma }}^{1}}$ используется метод вихревых рамок, развитый и аппробированный в панельных методах аэродинамики (см. [7, § 7.1, с. 175–178; .21.1, с. 434–436])). В основе этого метода лежит формула Био-Савара, связывающая градинт потенциала двойного слоя с плотностью, равной 1, размещенного на каждой ячейке разбиения, с контурным интегралом по краю этой ячейки (см., например, [8, § 12, с. 187–192], [9, формула (15)]):

где $\partial {{\sigma }_{k}}$ – край ячейки ${{\sigma }_{k}}$, ${\mathbf{\tau }}(y)$ – единичный направляющий вектор на контуре $\partial \sigma $ в точке $y \in \partial {{\sigma }_{k}}$, направление обхода контура согласовано с ориентацией поверхности ячейки так же, как в формуле Стокса. Поскольку в нашем случае край ячейки $\partial {{\sigma }_{k}}$ есть ломаная линия, величина ${{{\mathbf{u}}}_{{ik}}}$ вычисляется аналитически с помощью следующей формулы для интеграла по отрезку $[a,b] \subset {{\mathbb{R}}^{3}}$ (скорость, индуцируемая вихревым отрезком, см. [7, § 21.2, с. 436–437]):

Аппроксимация векторного потенциала. Для прямого значения оператора ${{R}_{m}}[\tilde {\Sigma },{\mathbf{\tilde {j}}}]$ в точке коллокации ${{x}_{i}}$ справедливо представление

Интегралы в выражениях для величин ${{W}_{{ik}}}$, ${{U}_{{ik}}}$, ${{{\mathbf{w}}}_{{ik}}}$, ${{{\mathbf{r}}}_{{ik,m}}}$, входящих в формулы (26)–(29), вычисляются приближенно по методу прямоугольников. При этом каждая ячейка ${{\sigma }_{k}}$ делится на более мелкие ячейки второго уровня. Построение ячеек разбиения второго уровня осуществляется путем построения на каждой стороне ячейки ${{\sigma }_{k}}$ точек, делящих сторону на четное число ${{n}_{0}}$ равных частей (см. фиг. 2, справа). Далее соответствующие точки, лежащие на противоположных сторонах рассматриваемой ячейки, соединяются отрезками. В результате ячейка разбивается на $n_{0}^{2}$ ячеек второго уровня ${{\sigma }_{{kj}}}$. В каждой ячейке ${{\sigma }_{{kj}}}$ дополнительного разбиения выбирается узел ${{y}_{{kj}}}$ как точка пересечения отрезков, соединяющих середины противоположных сторон этой вторичной ячейки. При этом в силу условия четности числа ${{n}_{0}}$ точка коллокации ${{x}_{k}}$ является угловой точкой некоторых вторичных ячеек и не совпадает ни с одним из узлов ${{y}_{{kj}}}$.

Далее, например, величина ${{W}_{{ik}}}$ заменяется конечной суммой:

где $s({{\sigma }_{{kj}}})$ – площадь вторичной ячейки ${{\sigma }_{{kj}}}$. Остальные из указанных величин вычисляются аналогично. Схема такого типа для вычисления интегралов с полярной особенностью была описана в статье [10].

Дискретизация поверхностного градиента. Для численной аппроксимации поверхностного градиента функции $g$, заданной на поверхности $\Sigma $, в точке, приближаемой точкой коллокации ${{x}_{i}} \in \tilde {\Sigma }$, используем формулы из статьи [11, формула (3.5)]. Обозначим вершины ячейки ${{\sigma }_{i}}$ как ${{x}_{{i,1}}},\;{{x}_{{i,2}}},\;{{x}_{{i,3}}},\;{{x}_{{i,4}}}$, пронумеруем стороны ячейки $l{\kern 1pt} ' = 1,...,4$, и построим векторы обхода сторон ячейки ${\mathbf{z}}_{{l'}}^{i}$: ${\mathbf{z}}_{{l'}}^{i} = {{x}_{{i,(l + 1)}}} - {{x}_{{i,l}}}$, $l = 1,2,3$, ${\mathbf{z}}_{4}^{i} = {{x}_{{i,1}}} - {{x}_{{i,4}}}$. Номер ячейки, граничащей с ячейкой ${{\sigma }_{i}}$ со стороны $l{\kern 1pt} '$, будем обозначать $j(l{\kern 1pt} ',i)$. Приближенное значение поверхностного градиента функции $g$, соответствующее точке коллокации ${{x}_{i}}$, вычисляется по формуле

где ${{g}_{j}}$ – значение функции $g$ в точке, соответствующей точке коллокации ${{x}_{j}}$.

В дискретных уравнениях поверхностный градиент проектируется на касательные направления:

3.3. Дискретизация уравнений

Приближенное решение уравнений (15) будем искать как кусочно-постоянные функции $\tilde {h}$, $\tilde {g}$ и ${\mathbf{\tilde {j}}}$ вида (24), определенные на поверхностях ${{\tilde {\Sigma }}^{1}}$, ${{\tilde {\Sigma }}^{2}}$, где каждый вектор ${{{\mathbf{j}}}_{k}}$ ортогонален вектору ${{{\mathbf{n}}}_{k}}$ – приближенному вектору нормали к ячейке ${{\sigma }_{k}}$. При этом задача сводится к нахождению векторов $\vec {h}$, $\vec {g}$, $\mathop {\vec {j}}\nolimits^1 $, $\mathop {\vec {j}}\nolimits^2 $ вида (25), содержащих значения неизвестных кусочно-постоянных функций на ячейках разбиения.

Для нахождения приближенного решения заменим в уравнениях (15) поверхности ${{\Sigma }^{1}}$ и ${{\Sigma }^{2}}$ на их приближения ${{\tilde {\Sigma }}^{1}}$ и ${{\tilde {\Sigma }}^{2}}$, подставим в них приближенные функции вида (24) и запишем уравнения во всех точках коллокации ${{x}_{i}}$, $i = 1, \ldots ,N$, используя формулы, описанные в п. 3.2. При записи каждого из этих уравнений в точке ${{x}_{i}}$ полагаем, что ${\mathbf{n}} = {{{\mathbf{n}}}_{i}}$. Заметим, что 2-е и 5-е уравнения в системе (15) векторные. Записывая эти уравнения в точке коллокации ${{x}_{i}}$, спроектируем их на касательные векторы к ячейке, на которой лежит эта точка. При записи каждого из указанных векторных уравнений в точке коллокации ${{x}_{i}}$ сначала умножим это уравнение справа векторно на вектор ${{{\mathbf{n}}}_{i}}$, а затем скалярно на векторы ${\mathbf{\tau }}_{i}^{l}$, $l = 1,2$. В результате получим следующую систему линейных алгебраических уравнений:

где ${{f}_{{0,i}}}$ – значение функции ${{f}_{0}}$, заданной на поверхности ${{\Sigma }_{1}}$, в точке, аппроксимируемой точкой коллокации ${{x}_{i}}$, ${{{\mathbf{v}}}_{{0,i}}} = {{{\mathbf{v}}}_{0}}({{x}_{i}})$, ${{\varphi }_{{0,i}}} = {{\varphi }_{0}}({{x}_{i}})$, $s({{\sigma }_{k}})$ – площадь ячейки ${{\sigma }_{k}}$, в уравнениях (35) $m = m(i)$ – номер поверхности $\mathop {\tilde {\Sigma }}\nolimits_m $, на которой лежит точка ${{x}_{i}}$, ${{W}_{{ik}}}$, ${{U}_{{ik}}}$, ${{{\mathbf{w}}}_{{ik}}}$, ${{{\mathbf{u}}}_{{ik}}}$, ${{{\mathbf{r}}}_{{ik,m}}}$ – коэффициенты квадратурных формул (26)–(29), $t_{{ik}}^{l}$ – коэффициенты, возникающие при аппроксимации поверхностного градиента ${\text{Grad}}\,g$ в соответствии с формулами (31), (32):

Поскольку первое уравнение системы (15) имеет одно условие разрешимости на правую часть, в аппроксимирующую его систему линейных уравнений (33) введена регуляризирующая переменная $\xi $, которая является дополнительной неизвестной. Такой метод регуляризации интегральных уравнений, имеющих условие разрешимости на правую часть, описан в [7, с. 475].

Решив систему уравнений (33)–(38), можно вычислить приближенные значения скорости жидкости и давления в любой точке $x \in {{\Omega }_{m}}$, $m = 1,...,{{N}_{d}}$, по формулам, аппроксимирующим формулы (9), (11):

где $e$ – функция, тождественно равная 1 на данной ячейке. Величины $\nabla W[{{\sigma }_{k}},e]$, $\nabla U[{{\sigma }_{k}},e]$, ${{R}_{m}}[{{\sigma }_{k}},{\mathbf{\tau }}_{k}^{l}]$ суть интегралов по ячейке разбиения ${{\sigma }_{k}}$, которые вычисляются делением этой ячейки на более мелкие ячейки 2-го уровня, как в формуле (30). Заметим также, что формулы такого типа применимы только для точек, отделенных от граничных поверхностей на расстояние, не малое по отношению к шагу разбиения поверхностей. В частности, мы предполагаем, что если рассматриваемая точка $x$ лежит в области ${{\Omega }_{m}}$, $m = 2,...,{{N}_{d}}$, то она одновременно лежит и в области, ограниченной приближенной поверхностью ${{\tilde {\Sigma }}_{m}}$. А если точка $x$ лежит в области ${{\Omega }_{1}}$, то она лежит внутри области, ограниченной поверхностью ${{\tilde {\Sigma }}_{1}}$ и вне замыкания областей, ограниченных поверхностями ${{\tilde {\Sigma }}_{m}}$, $m = 2,...,{{N}_{d}}$.

3.4. Численные схемы для упрощенных вариантов задачи

Для упрощенных вариантов задачи, рассмотренных в п. 2.1, возникают следующие системы уравнений.

Задача в области без включений. Задача в области без включений (16) сводится к системе интегральных уравнений (19). Аппроксимируя поверхность $\Sigma $ системой ячеек ${{\sigma }_{k}}$, $k = 1,...,N$, с выбранными на них точками коллокации ${{x}_{k}}$, $k = 1,...,N$, и применяя квадратурные формулы, описанные в п. 3.2, получим следующую систему линейных уравнений для неизвестных ${{h}_{k}}$, $k = 1,...,N$, – приближенных значений функции $h$, соответствующих ячейкам разбиения, и $j_{k}^{1}$, $j_{k}^{2}$, $k = 1,...,N$, – координат приближенных значений поверхностных токов ${{{\mathbf{j}}}_{k}}$, соответствующих ячейкам разбиения, в локальных базисах этих ячеек:

везде $i = 1,...,N$, $l = 1,2$. При этом приближенные значения скорости жидкости и давления в области течения ищутся по формулам (39), (40) без слагаемых с величинами ${{g}_{k}}$.

Задача сопряжения. Задача сопряжения (20) сводится к системе интегральных уравнений (23). Опять, аппроксимируя поверхность $\Sigma $ из этой задачи системой ячеек ${{\sigma }_{k}}$, $k = 1,...,N$, с выбранными на них точками коллокации ${{x}_{k}}$, $k = 1,...,N$, и применяя квадратурные формулы, описанные в п. 3.2, получим следующую систему линейных уравнений неизвестных ${{h}_{k}}$, ${{g}_{k}}$, $k = 1,...,N$, – приближенных значений функций $h$ и $g$, соответствующих ячейкам разбиения, и $j_{k}^{1}$, $j_{k}^{2}$, $k = 1,...,N$, – координат приближенных значений ${{{\mathbf{j}}}_{k}}$ плотности векторного потенциала ${\mathbf{j}}$, в локальных базисах ячеек:

везде $i = 1,...,{{N}_{1}}$, $l = 1,2$. При этом приближенные значения скорости жидкости и давления в области течения ищутся по формулам (39), (40).

Заметим, что матрицы систем (41) и (42) состоят из миноров матрицы системы (33)–(37) для основной рассматриваемой задачи.

4.1. Задача в однородной области

Рассмотрим упрощенную краевую задачу (16) о фильтрационном течении в области без включений, граница которой – поверхность $\Sigma $ – есть сфера радиуса $R = 1$. Задача решается в безразмерном виде при следующих значениях параметров пористой среды: $\kappa = 0.01$, $\mu = 30$.

Решались уравнения (41), позволяющие построить приближенное решение соответствующих этой задаче граничных интегральных уравнений (19). Для анализа практической сходимости метода были построены численные решения для пяти вариантов расчетных сеток, аппроксимирующих поверхность $\Sigma $, параметры которых $\left[ {\begin{array}{*{20}{c}} N&{400}&{800}&{1600}&{3200}&{6400} \\ h&{0.25}&{0.16}&{0.125}&{0.08}&{0.0625} \end{array}} \right]$ (здесь $N$ – число ячеек, $h$ – наибольший из диаметров ячеек). Пример расчетной сетки приведен на фиг. 3, слева (для $N = 800$).

Были рассмотрены два варианта задачи (см. фиг. 3, справа).

Вариант задачи № 1 – течение инициировано заданием потока через внешнюю границу при отсутствии источников и стоков внутри области течения.

Вариант задачи № 2 – течение инициировано заданными источником и стоком внутри области течения при отсутствии потока через границу.

В первом случае предполагалось, что на поверхности ${{\Sigma }^{1}}$ имеются входное ${{S}_{{{\text{in}}}}}$ и выходное ${{S}_{{{\text{out}}}}}$ отверстия с центрами в точках ${{x}_{{{\text{in}}}}} = ( - 1,0,0)$, ${{x}_{{{\text{out}}}}} = (1,0,0)$ соответственно, одинакового радиуса ${{r}_{0}} = 0.15$, через которые осуществляются втекание и вытекание жидкости со скоростью, имеющей параболический профиль. С математической точки зрения входное и выходное отверстия рассматривались как участки поверхности $\Sigma $, определяемые соотношениями ${{S}_{{{\text{in}}}}} = \left\{ {x \in \Sigma :{\text{|}}x - {{x}_{{{\text{in}}}}}{\text{|}} < {{r}_{0}}} \right\}$, ${{S}_{{{\text{out}}}}} = \left\{ {x \in \Sigma :{\text{|}}x - {{x}_{{{\text{out}}}}}{\text{|}} < {{r}_{0}}} \right\}$. Поток жидкости через эти отверстия моделировался заданием функции ${{f}_{0}}$ в задаче (16) в виде

функция ${{f}_{0}}$ полагалась равной нулю на остальной части поверхности $\Sigma $, здесь $Q = 16$ – заданный поток жидкости. При этом в системе линейных уравнений (41) мы полагали ${{f}_{{0,i}}} = {{f}_{0}}({{x}_{i}})$, где значения ${{f}_{0}}({{x}_{i}})$ вычислялись по формуле (43) c где ${{s}_{i}}$ – площадь ячейки ${{\sigma }_{i}}$. При этом функции ${{{\mathbf{v}}}_{0}}$ и ${{\varphi }_{0}}$ равны 0.

Во втором случае предполагалось, что течение инициируется первичными полями скоростей ${{{\mathbf{v}}}_{0}}$ и давления ${{\varphi }_{0}}$, определяемыми формулой (5), где ${{N}_{s}} = 2$, ${{q}_{1}} = ( - 0.5,0,0)$, ${{q}_{2}} = (0.5,0,0)$ – положения источника и стока, ${{Q}_{1}} = - {{Q}_{2}} = 1$. При этом функция ${{f}_{0}}$ в задаче (16) полагалась равной 0.

На фиг. 4 показаны поля скоростей, полученные численно для этих двух вариантов задачи в сечении $O{{x}_{1}}{{x}_{2}}$ с применением формулы (39) (данные поля скоростей получены при использовании разбиения поверхности $\Sigma $ на $N = 1600$ ячеек, расположение расчетного сечения показано на фиг. 3, справа).

Для оценки точности численного решения задачи был проведен анализ точности выполнения граничного условия на поле скоростей. Заметим, что приближенные поля скоростей и давления, получаемые по формулам (39), (40), автоматически удовлетворяют уравнениям (1), (2) в области течения. А вот граничные условия при построении этих решений проверялись только приближенно и только в точках коллокации. Заметим также, что формулы (39), (40) изначально ориентированы на вычисление скорости и давления на расстояниях от границы, не малых по сравнению с шагом сетки.

Влияние вязкости должно проявляться в том, что должно быть выполнено граничное условие ${\mathbf{n}} \times {\mathbf{v}} = 0$ на всей части границы и ${\mathbf{v}} = 0$ на той части границы, где отсутствует поток. На фиг. 4 видно, что скорость действительно затухает при приближении к точкам границы, лежащим вне входного и выходного отверстий.

Для более точного анализа мы исследовали поведение значений скорости ${\mathbf{v}}$ вблизи границы методом экстраполяции из внутренней области. Используемый алгоритм экстраполяции состоял в следующем.

Выберем параметр ${{h}_{0}} > 0$ – толщину области экстраполяции. Далее для каждой точки $x \in \Omega $, лежащей на расстоянии, меньшем ${{h}_{0}} > 0$ от поверхности $\Sigma $, построим точку ${{z}^{0}} \in \Sigma $ – основание кратчайшего перепендикуляра, опущенного на поверхность $\Sigma $. Далее построим точки ${{z}^{k}} = {{z}^{0}} + {\mathbf{n}}{\kern 1pt} '({{z}^{0}})k{{h}_{0}}$, $k = 1,2,3$, где ${\mathbf{n}}{\kern 1pt} '({{z}^{0}})$ – орт вектора нормали к поверхности $\Sigma $ в точке ${{z}^{0}}$, направленный в сторону области, из которой экстраполируется скорость.

Далее построим экстраполированное значение ${{{\mathbf{v}}}_{{\mathbf{p}}}}$ скорости жидкости в точке $x$ по формуле

коэффициенты квадратичной функции ${\mathbf{\alpha }}$, ${\mathbf{\beta }}$, ${\mathbf{\gamma }}$ выбираются так, что ${\mathbf{V}}(k * {{h}_{0}}) = {\mathbf{v}}({{z}^{k}})$, $k = 1,2,3$, ${\mathbf{v}}$ – скорость, полученная прямым вычислением по формуле (39).

На фиг. 5, слева графики изображают зависимость модуля скорости от расстояния до поверхности для точек, лежащих на отрезке $AB$, для первого варианта задачи (положение этого отрезка показано на фиг. 3, справа).

Кривая 1 соответствует значениям скорости ${\mathbf{v}}$, полученной прямым вычислением по формуле (39). В этом расчете использовалось разбиение с максимальным диаметром ячейки $h = 0.125$. Видно, что вблизи поверхности характер кривой резко меняется, это связано с погрешностью, возникающей, когда расстояние до поверхности мало по сравнению с шагом дискретизации. Кривая 2 показывает зависимость для модуля скорости ${{{\mathbf{v}}}_{{\mathbf{p}}}}$, полученной путем экстраполяции из внешней области, толщина области сглаживания была выбрана как ${{h}_{0}} = h{\text{/}}4$, исходя из анализа поведения кривой 1. На графике круглыми маркерами отмечены значения, соответствующие точкам, по которым проводилась экстраполяция. Квадратным маркером отмечено нулевое значение скорости на границе, соответствующее случаю точного выполнения граничного условия.

Заметим, что экстраполированная скорость стремится к 0 при приближении к поверхности, что соответствует граничному условию.

Для количественной оценки точности выполнения граничного условия на всей поверхности были рассчитаны краевые значения скорости во всех точках коллокации путем экстраполяции из области течения. Cреднее значение погрешности модуля скорости на границе области вычислялось по формуле

На фиг. 5, справа приведены зависимости величины $E({\mathbf{v}})$ от числа ячеек разбиения сетки, аппроксимирующей поверхность, для двух рассматриваемых вариантов задачи. При этом во всех вариантах расчета толщина области сглаживания выбиралась как ${{h}_{0}} = h{\text{/}}4$. Видно повышение точности аппроксимации скорости на границе при увеличении числа ячеек разбиения.

4.2. Задача сопряжения

Была рассмотрена краевая задача (20) о сопряжении течений в двух областях в случае, когда поверхность раздела $\Sigma $ есть сфера радиуса $R = 1$ (см. фиг. 6). Задача решалась при значениях параметров ${{\kappa }_{1}} = 0.01$, ${{\kappa }_{2}} = 0.001$, $\mu = 30$. Течение инициировалось источником и стоком, расположенными во внешней области в точках ${{q}_{1}} = ( - 1.5,0,0)$, ${{q}_{2}} = (1.5,0,0)$ соответственно. Первичные поля скорости ${{{\mathbf{v}}}_{0}}$ и давления ${{\varphi }_{0}}$ задавались формулой (5), где ${{N}_{s}} = 2$, ${{Q}_{1}} = - {{Q}_{2}} = 1$. Функция ${{f}_{0}}$ в задаче (20) полагалась равной 0.

Численно решалась система уравнений (42), аппроксимирующая граничные интегральные уравнения (23). Были получены решения на тех же поверхностных сетках, что и для предыдущей задачи, параметры сеток приведены выше.

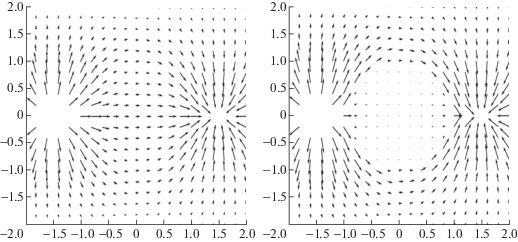
На фиг. 7, справа показано поле скоростей в сечении (положение сечения изображено на фиг. 6), полученное в этой задаче по формуле (39) в варианте расчета с разбиением сферы на $1600$ ячеек. На фиг. 6, слева для сравнения приведено первичное поле (такое поле соответствует течению, индуцируемому теми же источниками в однородной среде без включения). Сравнение этих полей скоростей показывает, что при наличии области с малой проводимостью течение перестраивается в обход этой области.

На фиг. 8 показаны распределения в этом же сечении значений потенциала $\varphi $ (слева) и давления (справа). Для расчета потенциала и давления использовались формулы (11) и (40). Здесь видны разрывность потенциала на поверхности $\Sigma $ и непрерывность давления на этой же поверхности.

На фиг. 9, слева приведены зависимости модуля скорости от величины $r = {\text{|}}x{\kern 1pt} {\text{|}}$ на отрезке $AB$, положение которого показано на фиг. 6. Здесь, как и в предыдущей задаче, кривая 1 соответствует значениям скорости, рассчитанным напрямую по формуле (39), кривая 2 соответствует значениям скорости, полученным с применением экстраполяции из области течения. При этом при $r > 1$ экстраполяция осуществлялась из области ${{\Omega }_{1}}$, а при $r < 1$ – из области ${{\Omega }_{2}}$. Этот график соглаcуется с условием непрерывности скорости на границе раздела сред.

Для количественной оценки точности выполнения граничного условия на всей поверхности раздела были рассчитаны для каждой точки коллокации ${{x}_{i}}$ краевые значения скорости ${\mathbf{v}}_{{\mathbf{i}}}^{ + }$ и ${\mathbf{v}}_{{\mathbf{i}}}^{ - }$, полученные путем экстраполяции из областей ${{a}_{1}}$ и ${{\Omega }_{2}}$ соответственно. При вычислениях опять использовалось значение параметра ${{h}_{0}} = h{\text{/}}4$, где $h$ – наибольший из диаметров ячеек разбиения.

Далее вычислялась величина $E({\mathbf{v}})$, характеризующая среднюю относительную погрешность выполнения граничного условия на скорость, по формуле

На фиг. 9, справа, приведена погрешность $E({\mathbf{v}})$ в зависимости от числа ячеек разбиения для этой задачи.

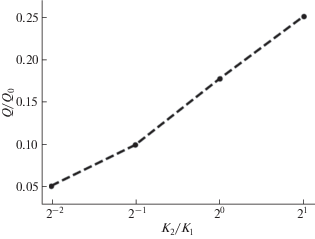
Так же на примере рассматриваемой задачи было проведено исследование влияния проводимости среды во внутренней области ${{\Omega }_{2}}$ на объем жидкости, проходящей через границу этой области. Для этого были получены решения краевой задачи (20) для той же конфигурации поверхности $\Sigma $ и для того же первичного поля, что и в рассмотренном примере, но при различных значениях проницаемости среды во внутренней области: ${{\kappa }_{2}} = \{ 0.0025,0.005,0.01,0.02\} $, и для одних и тех же значений параметров ${{\kappa }_{1}} = 0.01$, $\mu = 30$. Отметим, что случай ${{\kappa }_{2}} = {{\kappa }_{1}}$ фактически обозначает отсутствие границы разделов сред $\Sigma $.

Расчеты проводились с аппроксимацией поверхности системой из $N = 1600$ ячеек. По результатам расчетов были получены значения скорости во всех точках коллокации ${\mathbf{v}}({{x}_{i}})$ (для вычисления краевого значения скорости на поверхности $\Sigma $ здесь дискретизировалась формула (13)). Далее вычислялся поток жидкости через поверхность включения $\Sigma $ по формуле

На фиг. 10 приведены зависимость обезразмеренного потока $Q$ от отношения проводимостей внутренней и внешней сред ${{\kappa }_{2}}{\text{/}}{{\kappa }_{1}}$, обезразмеривание производилось делением потока $Q$ на сумму ${{Q}_{0}} = \left| {{{Q}_{1}}} \right| + \left| {{{Q}_{2}}} \right|$ модулей потоков в источниках поля. Видно, что поток через поверхность раздела сред растет с увеличением проводимости внутренней области.

4.3. Полная задача

Рассмотрим краевую задачу (1)–(3): пусть ${{\Sigma }^{1}}$ – зашумленная сфера радиуса ${{R}_{1}} = 1$ с центром в начале координат, ${{\Sigma }^{2}}$ – зашумленная сфера радиуса ${{R}_{2}} = 0.6$, полученная поворотом относительно начала координат и сжатием первой сферы (см. фиг. 11, слева).

Данная геометрия является упрощенным представлением лимфоузла, основанным на модели, представленной в работе [12].

Рассматривалась задача фильтрации жидкости в области ${{\Omega }_{1}}$, внешней границей которой является поверхность ${{\Sigma }_{1}}$, содержащей включение – область ${{\Omega }_{2}}$, ограниченную поверхностью ${{\Sigma }_{2}}$. Параметры среды и жидкости были выбраны как ${{\kappa }_{1}} = 0.01$, ${{\kappa }_{2}} = 0.001$, $\mu = 30$. Течение жидкости инициировалось заданными потоками жидкости с параболическим профилем на входных отверстиях с центрами в точках ${{x}_{{{\text{in}}}}} = ( - 1,0,0)$, ${{x}_{{{\text{out}}}}} = (1,0,0)$ соответственно, одинакового радиуса ${{r}_{0}} = 0.15$, при одновременном наличии источника и стока в точках ${{q}_{{{\text{in}}}}} \equiv {{q}_{1}} = ( - 0.25,0,0)$, ${{q}_{{{\text{out}}}}} \equiv {{q}_{2}} = (0.25,0,0)$ внутри области ${{\Omega }_{2}}$. При этом правая часть ${{f}_{0}}$ в граничном условии задачи (1)–(3) задавалась в виде (43), где $ - {{Q}_{{{\text{in}}}}} = {{Q}_{{{\text{out}}}}} = 16$. Первичные поля скоростей и давления задавались в виде (5) со значениями ${{Q}_{1}} = - {{Q}_{2}} = 1$.

Приближенное решение системы интегральных уравнений (15) искалось из системы линейных уравнений (33)–(38), при этом для поверхностей ${{\Sigma }^{1}}$ и ${{\Sigma }^{2}}$ использовалась аппроксимация поверхностными сетками с одинаковым числом ячеек $N = 8192$ на каждой поверхности.

На фиг. 11 приведено распределение поля скоростей, а на фиг. 12 – потенциала $\varphi $ и давления в сечении области течения плоскостью $O{{x}_{1}}{{x}_{2}}$. Видно, что течение идет, в основном, в обход труднопроходимой области. Только 8.5% потока проходит через внутреннюю область. Течение внутри области ${{\Omega }_{2}}$ обусловлено, в основном, точечными источниками, однако потенциал, создаваемый ими, много меньше потенциала входных и выходных отверстий.