Журнал вычислительной математики и математической физики, 2020, T. 60, № 9, стр. 1546-1565
Динамика упругого штампа на упругой полуплоскости при образовании трещин
Л. А. Алексеева 1, 2, *, Т. Б. Дуйшеналиев 3, **, Б. Т. Сарсенов 2, 4, ***
1 Институт математики и математического моделирования
050010 Алматы, ул. Пушкина, 125, Казахстан
2 Институт механики и машиноведения
им. У.А. Джолдасбекова
050010 Алматы, ул. Курмангазы, 29, Казахстан
3 Национальный исследовательский университет “МЭИ”
111250 Москва, ул. Красноказарменная, 14, Россия
4 Международный казахско-турецкий университет
им. Х.А. Ясави
161200 Туркестан, пр-т Саттарханова, 29, Казахстан
* E-mail: alexeeva@math.kz
** E-mail: duishenaliev@mail.ru
*** E-mail: bakytbek.sarsenov@ayu.edu.kz
Поступила в редакцию 20.11.2019
После доработки 03.02.2020
Принята к публикации 09.04.2020
Аннотация
Для исследования динамики сооружений в зоне землетрясений рассмотрена модельная краевая задача динамики упругого штампа на упругой полуплоскости при дифракции и преломлении волн, обусловленных сбросом напряжений на трещине. Для решения задачи принята явная разностная схема, построенная на основе метода бихарактеристик с привлечением идеи расщепления по пространственным координатам. Рассмотрены задачи дифракции и преломления волн в упругое включение при сбросе вертикальных и сдвиговых напряжений на горизонтальной трещине в упругой полуплоскости, моделирующие динамику сейсмических процессов при образовании тектонических трещин отрыва и сдвига. Проведены компьютерные эксперименты для сред с разными упругими параметрами и при разном расстоянии штампа от трещины, результаты которых представлены в виде осциллограмм движения дневной поверхности и штампа, а также дифракционных полей скоростей перемещений и инвариантов тензоров напряжений в среде и штампе. Библ. 9. Фиг. 22.
ВВЕДЕНИЕ
Изучение воздействия сейсмических волн при землетрясениях на состояние земной коры, ее поверхности и наземные сооружения методами математического моделирования относится к числу наиболее сложных нестационарных контактных краевых задач механики деформируемого твердого тела и практически мало разработано.
Здесь исследуется напряженно-деформированное состояние поверхностного сооружения при воздействии сейсмических волн в земной коре при землетрясениях. Для этого рассмотрена модельная краевая задача динамики упругого штампа на упругой полуплоскости при дифракции и преломлении упругих волн, обусловленных сбросом напряжений на трещине в упругой полуплоскости.
Задача рассмотрена при условии плоской деформации. Приведены определяющие гиперболические уравнения динамической теории упругости, которые описывают движение среды и штампа, краевые и контактные условия на границах и контактной поверхности. Для решения задачи принята явная разностная схема, построенная на основе метода бихарактеристик [1], [2] с привлечением идеи расщепления по пространственным координатам [3]–[5]. Дано описание точечной расчетной схемы и шаблона для изотропной упругой полуплоскости с прямоугольным упругим штампом на ее границе. Получены разрешающие разностные уравнения для внутренних, граничных, угловых, особых и контактных точек сопряжения штампа и полуплоскости.
Проведена компьютерная реализация алгоритма решения задач дифракции и преломления волн в упругое включение на упругой полуплоскости при сбросе вертикальных и сдвиговых напряжений на горизонтальной трещине в упругой полуплоскости, моделирующие динамику сейсмических процессов при образовании тектонических трещин отрыва и сдвига. Проведены компьютерные эксперименты для сред с разными упругими параметрами и при разном расстоянии штампа от трещины, результаты которых здесь представлены в виде осциллограмм движения дневной поверхности и штампа, а также дифракционных полей скоростей перемещений и инвариантов тензоров напряжений в среде и штампе.
1. ПОСТАНОВКА КОНТАКТНОЙ КРАЕВОЙ ЗАДАЧИ
Рассматривается полуплоскость ${{x}_{1}} \geqslant 0$ упругой однородной изотропной среды (первая среда ${{D}_{1}}$) с плотностью ${{\rho }^{{(1)}}}$ и упругими коэффициентами Ламе ${{\lambda }^{{(1)}}}$ и ${{\mu }^{{(1)}}}$, на поверхности которого расположено упругое тело (штамп – вторая среда ${{D}_{2}}$) высотой ${{d}_{1}}$ и шириной $2{{d}_{2}}$ с плотностью ${{\rho }^{{(2)}}}$ и коэффициентами Ламе ${{\lambda }^{{(2)}}}$, ${{\mu }^{{(2)}}}$.
До начального момента времени среды находились в статическом состоянии, которое здесь не рассматривается. Предполагается, что в начальный момент времени $t = 0$ в упругой полуплоскости на глубине $L$ возникает горизонтальная трещина $S$ (${{x}_{1}} = L$, $\left| {{{x}_{2}}} \right| \leqslant d$) (фиг. 1). При $t > 0$ динамическое состояние сред описывается векторами ${{{\mathbf{u}}}^{{(k)}}}$ ($k = 1,\;2$) (смещение $k$-й среды от статического состояния) и тензорами динамических напряжений $\sigma _{{ij}}^{{\left( k \right)}}$. Следовательно,
(1.1)
${{{\mathbf{u}}}^{{(k)}}} = 0,\quad {{{\mathbf{\dot {u}}}}^{{(k)}}} = 0\quad {\text{при}}\quad t = 0.$(1.2)
$\sigma _{{1j}}^{{\left( 1 \right)}} = 0\quad \left( {j = 1,\;2} \right),\quad {\text{при}}\quad {{x}_{1}} = 0,\quad \left| {{{x}_{2}} - {{d}_{3}}} \right| > {{d}_{2}},$(1.3)
$\sigma _{{1j}}^{{\left( 2 \right)}} = 0\quad \left( {j = 1,2} \right),\quad {\text{при}}\quad {{x}_{1}} = - {{d}_{1}},\quad \left| {{{x}_{2}} - {{d}_{3}}} \right| \leqslant {{d}_{2}},$(1.4)
$\sigma _{{2j}}^{{\left( 2 \right)}} = 0\quad \left( {j = 1,2} \right)\quad {\text{при}}\quad \left| {{{x}_{2}} - {{d}_{3}}} \right| = {{d}_{2}},\quad - {{d}_{1}} \leqslant {{x}_{1}} \leqslant 0.$(1.5)
${v}_{i}^{{\left( 1 \right)}} = {v}_{i}^{{\left( 2 \right)}},\quad \sigma _{{1j}}^{{\left( 1 \right)}} = \sigma _{{1j}}^{{\left( 2 \right)}}\quad \left( {i,j = 1,\;2} \right)\quad {\text{при}}\quad {{x}_{1}} = 0,\quad \left| {{{x}_{2}} - {{d}_{3}}} \right| \leqslant {{d}_{2}}.$2. УРАВНЕНИЯ ДВИЖЕНИЯ УПРУГИХ ПОЛУПЛОСКОСТИ И ШТАМПА
Для решения поставленной задачи наряду с начальными (1.1) и граничными условиями (1.2)–(1.5) используется система дифференциальных уравнений, состоящая из уравнений движения упругой среды и закона Гука [6]:
(2.1)
$\sigma _{{i\beta ,\beta }}^{{(k)}} + F_{i}^{{(k)}} = {{\rho }^{{(k)}}}\frac{{{{\partial }^{2}}u_{i}^{{(k)}}}}{{\partial {{t}^{2}}}}\quad (i,k = 1,2),$(2.2)
$\sigma _{{ij}}^{{(k)}} = {{\lambda }^{{(k)}}}u_{{\beta ,\beta }}^{{(k)}}{{\delta }_{{ij}}} + {{\mu }^{{(k)}}}(u_{{i,j}}^{{(k)}} + u_{{j,i}}^{{(k)}})\quad (i,j,k = 1,\;2).$Компоненты ${{F}_{i}}$ объемной силы $F$ определяются сингулярной обобщенной функцией – простым слоем на трещине $S$ [7]. Здесь они имеют следующий вид:
(2.3)
${{F}_{i}} = {{n}_{\beta }}{{[{{\sigma }_{{i\beta }}}]}_{S}}{{\delta }_{S}}(x) = {{n}_{\beta }}{{[{{\sigma }_{{i\beta }}}]}_{S}}\delta ({{x}_{1}} - L)H(d - \left| {{{x}_{2}}} \right|),\quad i = 1,\;2,$(2.4)
${{n}_{\beta }}{{[{{\sigma }_{{i\beta }}}(x)]}_{S}} = {{P}_{i}}(x,t),\quad x \in S,\quad t > 0.$Для решения поставленной задачи используется метод бихарактеристик [1]–[5], на основе которого разработаны алгоритм и пакет программ на языке Delphi, проведены его отладка, тестирование и численные эксперименты.
3. РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ МЕТОДОМ БИХАРАКТЕРИСТИК
Решение задачи удобно строить в безразмерных переменных, которые получаем после введения обозначений:
$c_{1}^{{(k) * }} = \sqrt {\tfrac{{{{\lambda }^{{(k) * }}} + 2{{\mu }^{{(k) * }}}}}{{{{\rho }^{{(k){\text{*}}}}}}}} ,\quad c_{2}^{{(k) * }} = \sqrt {\tfrac{{{{\mu }^{{(k) * }}}}}{{{{\rho }^{{(k) * }}}}}} $
суть скорости распространения продольных и поперечных волн в $k$-й среде.
После введения безразмерных величин из уравнений (2.1), (2.2) после простых преобразований имеем ($i,j,k = 1,\;2$):
(3.1)
$\begin{gathered} {{\rho }^{{(k)}}}{\dot {v}}_{i}^{{(k)}} = \sigma _{{i\beta ,\beta }}^{{(k)}} + F_{i}^{{(k)}}, \\ \mathop {\dot {\sigma }}\nolimits_{ij}^{(k)} = \gamma _{{ij}}^{{(k)}}{v}_{{i,j}}^{{(k)}} + \gamma _{{ji}}^{{(k)}}{v}_{{j,i}}^{{(k)}}(1 - {{\delta }_{{ij}}}) + \gamma _{{33}}^{{(k)}}({v}_{{\beta ,\beta }}^{{(k)}} - {v}_{{i,j}}^{{(k)}}){{\delta }_{{ij}}}. \\ \end{gathered} $(3.2)
$\begin{array}{*{20}{c}} {{{\rho }^{{(k)}}}{\dot {v}}_{i}^{{(k)}} - \sigma _{{ij,j}}^{{(k)}} = a_{{ij}}^{{(k)}} + F_{i}^{{(k)}},} \\ {\dot {\sigma }_{{ij}}^{{(k)}} - \gamma _{{ij}}^{{(k)}}{v}_{{i,j}}^{{(k)}} = b_{{ij}}^{{(k)}},} \end{array}$(3.3)
$\begin{array}{*{20}{c}} {a_{{ij}}^{{(k)}} = \sigma _{{i\beta ,\beta }}^{{(k)}} - \sigma _{{ij,j}}^{{(k)}},} \\ {b_{{ij}}^{{(k)}} = \gamma _{{ji}}^{{(k)}}{v}_{{j,i}}^{{(k)}}(1 - {{\delta }_{{ij}}}) + \gamma _{{33}}^{{(k)}}(v_{{\beta ,\beta }}^{{(k)}} - {v}_{{i,j}}^{{(k)}}){{\delta }_{{ij}}}.} \end{array}$(3.5)
$d\sigma _{{ij}}^{{(k)}} \mp {{\rho }^{{(k)}}}\lambda _{{ij}}^{{(k)}}d{v}_{i}^{{(k)}} = (b_{{ij}}^{{(k)}} \mp \lambda _{{ij}}^{{(k)}}[a_{{ij}}^{{(k)}} + F_{i}^{{(k)}}])dt.$Расчетная схема среды и штампа такова, что допускает систему координат ${{x}_{i}}$ ($i = 1,\;2$), в которой граничные поверхности являются координатными. Для построения алгоритма ${{D}_{1}}$ и ${{D}_{2}}$ разбиваются на ячейки, образуемые пересечениями координатных поверхностей ${{x}_{i}} = {\text{const}}$ ($i = 1,\;2$). Линейные размеры этих ячеек в направлении осей ${{x}_{1}}$ и ${{x}_{2}}$ считаются равномерными и равными $h$. Пересечения линий ${{x}_{i}} = {\text{const}}$ ($i = 1,\;2$) образуют узлы. В этих узловых точках отыскиваются значения искомых функций ${v}_{i}^{{\left( k \right)}}$, $\sigma _{{ij}}^{{\left( k \right)}}$ ($i,j = 1,\;2$) в различные моменты времени ${{t}_{n}} - \tau ,\;{{t}_{n}},\;{{t}_{n}} + \tau $ ($n = 1,2,\; \ldots ,\;N$) с шагом по времени $\tau $. Получившаяся сетка является трехмерной. Точечная сетка, на основе которых строится разностная схема, помимо упомянутых узловых точек, содержит точки, образованные пересечениями бихарактеристик с гиперплоскостями $t = {\text{const}}$. Использование явной разностной схемы второго порядка точности позволяет установить значения неизвестных величин в узловых точках плоскости ${{t}_{{n + 1}}}$ временного слоя по известным их значениям в узлах предыдущего слоя ${{t}_{n}}$. Принимается шаблон, состоящий из узла О и точек $E_{{ij}}^{{ \pm (k)}}$, лежащих на координатных линиях ${{x}_{j}} = {\text{const}}$ и отстоящих от точки О на расстояния $\lambda _{{ij}}^{{(k)}}\tau $. Наклонные прямые, исходящие из точки А, являются бихарактеристиками. В дальнейшем значениям функций в точке О приписывается верхний знак “О”; в точках $E_{{ij}}^{{ \pm (k)}}$ – нижний ($ij$) и верхний знак $ \pm $ (например, $\sigma _{{ij}}^{{ \pm \left( k \right)}}$), а в точке А дополнительный индекс не приписывается. Точки О и А представляют собой одну и ту же точку тела в моменты времени, отстоящие друг от друга на один шаг $\tau $ по времени.
На основании описанных точечных схем разрабатываемая ниже методика решения динамических задач позволяет определить скорости частиц ${v}_{i}^{{\left( k \right)}}$ и компоненты тензора напряжений $\sigma _{{ij}}^{{\left( k \right)}}$ в точке А на нечетном слое по времен ${{t}_{n}}$, если известны их значения на предыдущем слое ${{t}_{{n - 1}}}$ ($n = 1,\;2,\; \ldots ,\;N$) в точке О и в прилегающих к ней точках $E_{{ij}}^{{ \pm (k)}}$. Разностные схемы такого типа являются явными и удобны тем, что эти системы решаются последовательно от одного временного слоя к следующему. При этом искомые величины в каждой узловой точке, в отличие от неявной разностной схемы, вычисляются независимо от других.
3.1. Разрешающие разностные уравнения во внутренних точках
Ниже построен расчетный алгоритм второго порядка точности. Интегрирование системы уравнений (3.2) от точки O до точки A и соотношений (3.5) от точки $E_{{ij}}^{{ \pm (k)}}$ до точки А методом трапеции позволяет получить выражения следующего типа:
(3.6)
$\begin{gathered} {v}_{i}^{{(k)}} = {v}_{i}^{{0(k)}} + \frac{\tau }{{2{{\rho }^{{(k)}}}}}(\sigma _{{ij,j}}^{{0(k)}} + a_{{ij}}^{{0(k)}} + F_{i}^{{0(k)}} + \sigma _{{ij,j}}^{{(k)}} + a_{{ij}}^{{(k)}} + F_{i}^{{(k)}}), \\ \sigma _{{ij}}^{{(k)}} = \sigma _{{ij}}^{{0(k)}} + \frac{\tau }{2}(\gamma _{{ij}}^{{(k)}}{v}_{{i,j}}^{{0(k)}} + b_{{ij}}^{{0(k)}} + \gamma _{{ij}}^{{(k)}}{v}_{{i,j}}^{{(k)}} + b_{{ij}}^{{(k)}}), \\ \end{gathered} $(3.7)
$\sigma _{{\alpha j}}^{{(k)}} - \sigma _{{ij}}^{{ \pm (k)}} \mp {{\rho }^{{(k)}}}\lambda _{{ij}}^{{(k)}}({v}_{i}^{{(k)}} - {v}_{i}^{{(k)}}) = \frac{\tau }{2}(b_{{ij}}^{{(k)}} + b_{{ij}}^{{ \pm (k)}} \mp \lambda _{{ij}}^{{(k)}}[a_{{ij}}^{{(k)}} + a_{{ij}}^{{ \pm (k)}} + F_{i}^{{(k)}} + F_{i}^{{ \pm (k)}}]),$(3.8)
$\begin{gathered} a_{{ij}}^{{ \pm (k)}} = a_{{ij}}^{{0(k)}} \mp \lambda _{{ij}}^{{(k)}}\tau \frac{{\partial a_{{ij}}^{{0(k)}}}}{{\partial {{x}_{j}}}}, \\ b_{{ij}}^{{ \pm (k)}} = b_{{ij}}^{{0(k)}} \mp \lambda _{{ij}}^{{(k)}}\tau \frac{{\partial b_{{ij}}^{{0(k)}}}}{{\partial {{x}_{j}}}}, \\ \end{gathered} $(3.9)
$\begin{gathered} \sigma _{{ij}}^{{ \pm (k)}} = \sigma _{{ij}}^{{0(k)}} \mp \lambda _{{ij}}^{{(k)}}\tau \frac{{\partial \sigma _{{ij}}^{{0(k)}}}}{{\partial {{x}_{j}}}} + \frac{1}{2}{{(\lambda _{{ij}}^{{(k)}}\tau )}^{2}}\frac{{{{\partial }^{2}}\sigma _{{ij}}^{{0(k)}}}}{{\partial x_{j}^{2}}}, \\ {v}_{\alpha }^{{ \pm (k)}} = {v}_{i}^{{0(k)}} \mp \lambda _{{ij}}^{{(k)}}\tau \frac{{\partial v_{{ij}}^{{0(k)}}}}{{\partial {{x}_{j}}}} + \frac{1}{2}{{(\lambda _{{ij}}^{{(k)}}\tau )}^{2}}\frac{{{{\partial }^{2}}{v}_{i}^{{0(k)}}}}{{\partial x_{j}^{2}}}. \\ \end{gathered} $(3.10)
$\sigma _{{ij,j}}^{{(k)}} \mp {{\rho }^{{(k)}}}\lambda _{{ij}}^{{(k)}}{v}_{{i,j}}^{{(k)}} = \sigma _{{ij,j}}^{{0(k)}} + \tau [\gamma _{{ij}}^{{(k)}}{v}_{{i,jj}}^{{(k)}} + b_{{ij,j}}^{{(k)}}] \mp \lambda _{{ij}}^{{(k)}}({{\rho }^{{(k)}}}{v}_{{i,j}}^{{0(k)}} + \tau [\sigma _{{ij,jj}}^{{0(k)}} + a_{{ij,j}}^{{0(k)}}]) + F_{i}^{{ \pm (k)}} - F_{i}^{{0(k)}}.$(3.11)
$\begin{array}{*{20}{c}} {{v}_{{i,j}}^{{(k)}} = {v}_{{i,j}}^{{0(k)}} + \frac{\tau }{{{{\rho }^{{(k)}}}}}(\sigma _{{ij,jj}}^{{0(k)}} + a_{{ij,j}}^{{0(k)}}) + \frac{1}{{2{{\rho }^{{(k)}}}\lambda _{{ij}}^{{(k)}}}}(F_{i}^{{ - (k)}} - F_{i}^{{ + (k)}}),} \\ {\sigma _{{ij,j}}^{{(k)}} = \sigma _{{ij,j}}^{{0(k)}} + \tau (\gamma _{{ij}}^{{(k)}}{v}_{{i,jj}}^{{(k)}} + b_{{ij,j}}^{{(k)}}) + \frac{1}{2}(F_{i}^{{ - (k)}} + F_{i}^{{ + (k)}} - 2F_{i}^{{0(k)}}).} \end{array}$3.2. Разностные уравнения в граничных точках
На граничных линиях ${{x}_{j}} = {\text{const}}$ заданы две компоненты тензора напряжений (см. (1.2)–(1.4)). В расчетах не могут быть использованы два условия из (3.10), условия на двух характеристиках, не принадлежащих исследуемой области. Тем самым по сравнению с внутренними точками число уравнений (3.10) сокращается на два. Совокупность оставшихся уравнений (3.10), (3.6) и двух граничных условий из (1.2)–(1.4) является замкнутой линейной системой относительно тринадцати неизвестных (восьми производных и пяти функций). Точки контактных линий также рассматриваются как граничные точки только для отдельных областей ${{D}_{1}}$, ${{D}_{2}}$. В каждой из этих точек сопряжения число уравнений (3.10), (3.6) равно 22, а неизвестных 26. Замкнутая система уравнений получается, если использовать наряду с уравнениями (3.6), (3.10) четыре условия жесткого сцепления штампа и полуплоскости (1.5).
3.3. Разностные уравнения в неособых и особых угловых точках
В угловых точках, образовавшихся пересечением двух границ, все условия, заданные на двух границах, должны выполняться. Поэтому в угловых точках задаются четыре условия вместо четырех условий на четырех бихарактеристиках, не принадлежащих области ${{D}_{1}} \cap {{D}_{2}}$, которые замыкают систему линейных уравнений относительно тринадцати неизвестных.
В верхних угловых точках тела ${{D}_{2}}$ (см. фиг. 1) заданы четыре компоненты тензора напряжений. В силу закона парности касательных напряжений только три из них являются линейно независимыми. Число неизвестных производных можно сократить непосредственным дифференцированием граничных функций $\sigma _{{ij}}^{{ \pm (k)}}$ ($i \ne j$) в (1.3), (1.4). Тем самым получаем производные $\sigma _{{21,1}}^{{ \pm (k)}}$ и $\sigma _{{12,2}}^{{ \pm (k)}}$. Остальные неизвестные вычисляются при последовательном решении уравнений (3.10) и (3.6).
Разностные уравнения в особых угловых точках строятся иначе. Нижние угловые точки тела ${{D}_{2}}$ являются контактными точками неоднородной среды ${{D}_{1}} \cap {{D}_{2}}$, которые имеют особенности. Развивая идеи, впервые описанные в [5], вычисляются разностные уравнения в особых угловых точках исследуемого тела. В этих особых точках из физических соображений принимается, что компоненты напряжений $\sigma _{{12}}^{{(2)}} = 0$ и $\sigma _{{22}}^{{(2)}} = 0$ и используются условия контакта (1.5).
В этих особых точках производные ${v}_{{i,2}}^{{(1)}}$ и $\sigma _{{i,2}}^{{(2)}}$ могут терпеть разрывы. Поэтому предполагается, что область ${{D}_{1}}$ по линии продолжения боковых сторон тела ${{D}_{2}}$ мысленно разделяется на подобласти (I), (II). Тем самым около особых точек рассматриваются три подобласти (I), (II), (III) (см. фиг. 1). Для подобластей (I) и (II) принимаются условия непрерывности функций
(3.12)
${v}_{i}^{{({\text{I}})}} = {v}_{i}^{{({\text{II}})}},\quad \sigma _{{ij}}^{{({\text{I}})}} = \sigma _{{ij}}^{{({\text{II}})}}\quad \left( {i,j = 1,\;2} \right)$(3.13)
${v}_{{_{i},1}}^{{({\text{I}})}} = {v}_{{_{i},1}}^{{({\text{II}})}},\quad \sigma _{{i1,1}}^{{({\text{I}})}} = \sigma _{{i1,1}}^{{({\text{II}})}}\quad \left( {i,j = 1,\;2} \right).$Двенадцать производных для первой среды и восемь производных для второй среды вычисляются по формуле (3.11). Подставляя в уравнение (3.6) производные, найденные таким образом, для каждой подобласти и выполняя условия (1.5), (3.12) и (3.13), вычисляются неизвестные функции в этих точках, как многосвязаных узлах совокупности подобластей (I), (II), (III):
Относительно сказанного в пп. 3.1–3.3 можно заметить, что значения производных в узловых точках исследуемой области на нижнем слое по времени вычисляются с использованием центральной разности во внутренних узловых точках, а в граничных точках соответствующим аппроксимациями “вперед” и “назад”.
Проведена компьютерная реализация алгоритма, отладка программы и на ее основе выполнен ряд численных экспериментов, результаты некоторых из них приведем ниже.
4. МОДЕЛИРОВАНИЕ ДИНАМИКИ УПРУГОГО МАССИВА ПРИ ОБРАЗОВАНИИ ГОРИЗОНТАЛЬНЫХ ТРЕЩИН РАЗРЫВА
При образовании трещин разрыва происходит сброс напряжений, перпендикулярных поверхности трещины. При этом в среде в окрестности трещины формируются две ударные упругие волны объемной и сдвиговой деформации, которые распространяются со скоростями продольных и поперечных волн и дифрагируют на дневной поверхности, отражаясь от нее и порождая поверхностные волны.
Здесь моделируется горизонтальная трещина разрыва, параллельная дневной поверхности. Расчеты произведены для среды с безразмерными параметрами: $\rho = 1$, ${{c}_{1}} = \sqrt {{{\gamma }_{{11}}}} = 1$, ${{c}_{2}} = \sqrt {{{\gamma }_{{12}}}} = 0.577$ при глубине и ширине трещины соответственно $L = 1$, $d = 0.1$, на интервале времени (0, 6).
Скачок напряжений на трещине задается в виде вертикального импульса (см. фиг. 2):
В расчетах шаги по пространственной сетке ${{h}_{1}} = {{h}_{2}} = h = 0.05$, по времени – $\tau = 0.025$, a параметр дельтаобразной функции $\varepsilon = h$.4.1. Осциллограммы скоростей и напряжений на дневной поверхности
На фиг. 3 представлены графики изменения с течением времени вертикальных и горизонтальных компонент скорости движения разных точек дневной поверхности. Скорости распространения продольных и поперечных волн в безразмерных величинах составляют ${{c}_{1}} = 1$ и ${{c}_{2}} = 0.577$ соответственно. Отсюда следует, что объемные (продольные) и сдвиговые (поперечные) волны от трещин к точке О (0, 0) придут за время ${{t}_{1}} = 1$ и ${{t}_{2}}\;{\text{ = }}\;{\text{73}}$ соответственно, а в точку А(0, 1) за ${{t}_{1}} = 35$ и ${{t}_{2}} = 2.33$, в точку В(0, 2) за ${{t}_{1}} = 2.15$ и ${{t}_{2}} = 3.71$ и в точку С(0, 3) за ${{t}_{1}} = 3.07$ и ${{t}_{2}} = 5.3$. До момента прихода упругих волн среда покоится. Затем в расчетные моменты времени возникает всплеск скорости колебания и начинается естественный колебательный характер движения среды. Картина симметричная относительно эпицентра О (${{x}_{1}} = 0$, ${{x}_{2}} = 0$), так как сброс напряжений происходит симметрично и параллельно вертикальной оси. Максимальные вертикальные скорости в эпицентре, а с удалением от него они убывают.
Фиг. 3.
Осциллограммы скоростей ${{{v}}_{1}}$ (а) и скоростей ${{{v}}_{2}}$ (б) дневной поверхности при ${{x}_{1}} = 0$, ${{x}_{2}} = 0;\;1;\;2;\;3$ (трещина отрыва).

На фиг. 4 представлены осциллограммы напряжений ${{\sigma }_{{22}}}$ на поверхности ${{x}_{1}} = 0$ (фиг. 4а) и на глубине ${{x}_{1}} = 0.5$ (фиг. 4б) в точках ${{x}_{2}} = 0$; ${{x}_{2}} = 1$; ${{x}_{2}} = 2$; ${{x}_{2}} = 3$. Напряжения меняют знак: в эпицентре в основном это растягивающие напряжения. А вдали от него на дневной поверхности происходит колебательный процесс со сменой сжимающих напряжений на растягивающие и наоборот.
Фиг. 4.
Осциллограммы напряжений ${{\sigma }_{{22}}}$ на поверхности ${{x}_{1}} = 0$ (а) и на глубине ${{x}_{1}} = 0.5$ (б), при ${{x}_{2}} = 0;\;1;\;2;\;3$ (трещина отрыва).

На фиг. 5 и 6 показаны срезы скорости ${{{v}}_{1}}$ и напряжений ${{\sigma }_{{11}}}$ и ${{\sigma }_{{22}}}$ на плоскости ${{x}_{2}} = 0$ в упругой полуплоскости (в силу симметричности воздействия в данной плоскости ${{{v}}_{2}} = 0$) в момент времени $t = 1$, $t = 1.5$ и $t = 2$. Можно заметить, что в момент времени $t = 1$ волна только добегает до дневной поверхности (нет еще отраженной волны) и скорость ${{{v}}_{1}}$ так же симметрична, а напряжения ${{\sigma }_{{11}}}$ и ${{\sigma }_{{22}}}$ антисимметричны относительно оси, проходящей вдоль трещины, что соответствует данному воздействию. А также этот момент соответствует моменту когда, внешнее воздействие снято, и среда начинает свободно противодействовать. Это видно по изменению направления скорости ${{{v}}_{1}}$ и напряжениям рядом с трещиной, которые перешли из сжимающих напряжений в растягивающие и, наоборот, из растягивающих напряжений в сжимающие.
Фиг. 5.
Срез скоростей ${{{v}}_{1}}$ на плоскости ${{x}_{2}} = 0$ при $t = 1,5$ (а), $t = 2$ (б) (трещина отрыва).

Фиг. 6.
Срез напряжении ${{\sigma }_{{11}}}$ и ${{\sigma }_{{22}}}$ на плоскости ${{x}_{2}} = 0$, в моменты времени $t = 1.5$ (а), $t = 2$ (б) (трещина отрыва).

В момент времени $t = 1.5$ отраженная от дневной поверхности волна добегает до середины расстояния до трещины, а в момент $t = 2$ добегает до трещины, при этом теряется симметричность графика. Сравнивая на фигурах амплитуды колебания, можно заметить, что с течением времени амплитуда убывает. Это связано с тем, что в эти моменты нет внешнего воздействия, а среда противодействует, заставляя волну гаснуть (волна теряет энергию).
4.2. Векторные поля скоростей в среде при образовании трещины отрыва
На фиг. 7 представлены векторные поля скоростей в среде. В начальный момент на трещине возникают две ударные волны: объемная сжатия-расширения, которая движется со скоростью ${{c}_{1}}$, и сдвиговая, скорость которой ${{c}_{2}}$. Объемные волны опережают сдвиговые. На фигуре им соответствуют кольцевые зоны в окрестности трещины. На фронтах ударных волн должны выполняться условия на скачки [9]:
Фиг. 7.
Векторное поле скоростей до отражения ударных волн: $t = 0.5$ (а); $t = 1$ (б) (трещина отрыва).

В момент времени $t = 0.5$ объемная волна пробегает расстояние 0.5, а сдвиговая волна 0.29, что и видим на фиг. 7а. Можно заметить, что на концах трещины образовалось вихревое поле, что характеризует сдвиговые волны. Края трещины работают как источники цилиндрических сдвиговых волн. На фиг. 8б показан момент, когда отраженная объемная волна добежала до трещины, а сдвиговая, пройдя сквозь эту отраженную волну (с некоторыми искажениями), добежала до дневной поверхности и начался процесс отражения. Возникает сложная дифракционная картина взаимодействия падающих и отраженных ударных волн и формируется сложное напряженно-деформированное состояние среды.
4.3. Напряженное состояние породного массива
На фиг. 9 представлены изолинии первых (фиг. 9а) и вторых (фиг. 9б) инвариантов тензора напряжения в момент времени $t = 1.5$. Первый инвариант определяет давление в среде, второй – интенсивность касательных напряжений. Как видим, напряжения в верхней зоне от дифракции волн на дневной поверхности в полтора раза превышают напряжения в свободной нижней зоне рассеивания упругих волн (0.12 и 0.8 для фиг. 9а и 0.0045 и 0.0030 для фиг. 9б). При переходе к размерным величинам используем формулы:
Обычно в сейсмологии для грунтов используют следующие параметры: $\rho $ = 1600 кг/м3, ${{c}_{2}} = 200$ м/с, ${{c}_{1}} = 346.41$ м/с. Учитывая эти параметры, если взять глубину расположения трещины $L = 100$ м, расчетный безразмерный интервал времени (0, 6) окажется в реальности (0, 73c), длина трещины 2d = 20 м, то в эпицентре О(0, 0) максимальная по абсолютной величине скорость ${{{v}}_{1}} = 62.28$ м/с, а напряжение ${{\sigma }_{{22}}} = 7.66$ МН/м2.
5. ДИНАМИКА СРЕДЫ ПРИ СБРОСЕ ГОРИЗОНТАЛЬНЫХ НАПРЯЖЕНИЙ НА ТРЕЩИНЕ
При образовании сдвиговой трещины происходит сброс горизонтальных напряжений. На фиг. 10, 11 представлены осциллограммы скоростей и напряжений в эпицентре и фиксированных точках поверхности и среды. Скорости распространения продольных и поперечных волн в безразмерных величинах составляют ${{c}_{1}} = 1$ и ${{c}_{2}} = 0.577$ соответственно. Отсюда следует, что объемные (продольные) и сдвиговые (поперечные) волны от трещины к точке О(0, 0) придут за время ${{t}_{1}} = 1$ и ${{t}_{2}} = 73$ соответственно, а в точку А(0, 1) за ${{t}_{1}} = 35$ и ${{t}_{2}} = 2.33$, в точку В(0, 2) за ${{t}_{1}} = 2.15$ и ${{t}_{2}} = 3.7$ и в точку С(0, 3) за ${{t}_{1}} = 3.07$ и ${{t}_{2}} = 5.3$. В указанные моменты времени возникают колебания дневной поверхности. Характер колебаний в эпицентре на поверхности резко отличается от колебаний при образовании трещины отрыва. Преобладают горизонтальные колебания поверхности.
Фиг. 10.
Осциллограммы скоростей ${{{v}}_{1}}$ (а) и скоростей ${{{v}}_{2}}$ (б) на дневной поверхности ${{x}_{1}} = 0$, при 1) ${{x}_{2}} = 0$; 2) ${{x}_{2}} = 1$; 3) ${{x}_{2}} = 2$; 4) ${{x}_{2}} = 3$ (трещина сдвига).

Фиг. 11.
Осциллограммы напряжении ${{\sigma }_{{22}}}$ на дневной поверхности ${{x}_{1}} = 0$ (а) и на глубине ${{x}_{1}} = 0.5$ (б), при 1) ${{x}_{2}} = 1$; 2) ${{x}_{2}} = 2$; 3) ${{x}_{2}} = 3$ (трещина сдвига).

Скорость ${{{v}}_{1}} = 0$ в эпицентре О (и по всей прямой ${{x}_{2}} = 0$) объясняется типом воздействия на трещине. Так как в перпендикулярном направлении к дневной поверхности движется сдвиговая волна, то можно заметить, что чем ближе точка к эпицентру, тем выше амплитуда колебания горизонтальных скоростей точек дневной поверхности. Отрицательное направление скорости ${{{v}}_{2}}$ в точке О в промежуток времени (1; 7) объясняется взаимодействием фронтов распространяющихся волн.
На фиг. 12 представлены изолинии первого и второго инвариантов тензора напряжений в моменты времени $t = 1.5$ при образовании трещин сдвига. Они характеризуют распределение давления и интенсивности касательных напряжений в окрестности очага землетрясения.
На фиг. 13 представлено векторное поле скоростей в среде при сбросе горизонтальных напряжений на трещине:
Поскольку картина антисимметрична относительно вертикальной оси, то далее на фигурах представлена только правая половина (в левой половине направление векторов меняется на противоположное). В момент времени $t = 1$ объемная волна сжатия-расширения пробегает расстояние до поверхности, а сдвиговая волна 0.577$L$. Можно заметить вихревую зону, распространяющуюся вверх и вниз от трещины, порождаемую сдвиговыми деформациями на трещине. Ее окаймляет и опережает зона объемных расширений – сжатий, интенсивность скоростей перемещений в которой меньше, чем за фронтом сдвиговой волны.Фиг. 13.
Векторное поле скоростей при подходе ударной волны к поверхности: $t = 1$ (трещина сдвига).

Взаимодействие объемных и сдвиговых волн с дневной поверхностью и между собой (после отражения) порождают разные волны, среди них поверхностные. На фиг. 14 можно видеть, как начинает формироваться волна вдоль дневной поверхности, образуя поверхностную волну Рэлея. В данной среде она распространяется со скоростью ${{c}_{R}} = 0.918{{c}_{2}}$, т.е. близко к скорости распространения сдвиговой волны. Волны, идущие от трещины вниз, не встречая препятствий, рассеиваются с глубиной и с течением времени.
6. ДИНАМИЧЕСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ УПРУГОГО ШТАМПА ПРИ ПРЕЛОМЛЕНИИ СЕЙСМИЧЕСКИХ ВОЛН
Исследовалось напряженно-деформированное состояние штампа при преломлении сейсмических волн, при образовании трещин отрыва и сдвига. Проводился сопоставительный анализ в зависимости от расстояния штампа до эпицентра. Здесь на фиг. 15–19 представлены результаты расчетов для штампа, расположенного в эпицентре (фиг. 15а–19а) и на некотором расстоянии от него (фиг. 15б–19б), при образовании трещины разрыва в опорном массиве.
Фиг. 15.
Векторное поле скоростей точек тела ${{D}_{2}}$ в момент времени, когда преломленные волны распространились до середины штампа.

Фиг. 16.
Векторное поле скоростей точек тела ${{D}_{2}}$ до отражения преломленных волн от верхней границы.
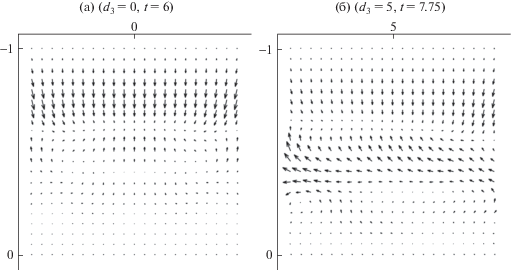
Фиг. 17.
Векторное поле скоростей точек тела ${{D}_{2}}$ в момент времени, когда преломленные волны отразились от верхнего торца.

Фиг. 18.
Изолинии первого инварианта тензора напряжений штампа в момент времени, когда преломленные волны распространились до середины.

Фиг. 19.
Изолинии второго инварианта тензора напряжений штампа в момент времени, когда преломленные волны распространились до середины.

В качестве материала для штампа взят бетон с параметрами: $\rho $ = 2500 кг/м3, ${{c}_{1}}$ = 3593 м/с, ${{c}_{2}}$ = = 2200 м/с, при следующих размерах штампа: ${{d}_{1}} = 1$, ${{d}_{2}} = 0.5$.
Здесь представлены расчеты напряженно-деформированного состояния штампа при образовании в подстилающем пространстве трещины разрыва. На фиг. 15 представлены векторные поля скоростей точек тела ${{D}_{2}}$ в момент времени, когда преломленные волны дошли до середины штампа. При ${{d}_{3}} = 0$ (фиг. 15а) распространяется только продольная волна, и можно заметить эффект взаимодействия с боковой поверхностью. А при ${{d}_{3}} = 5$ (фиг. 15б) за продольной волной следует и поперечная волна, что соответствует типу воздействия. Здесь тоже заметен эффект взаимодействия, но сильнее с правой стороной. Это объясняется тем, что штамп стоит справа от эпицентра.
На фиг. 16 представлены векторные поля скоростей точек тела ${{D}_{2}}$ в момент времени, когда преломленная волна только добежала до верхнего торца штампа. На первой фигуре можно заметить, что за продольной волной начинается образование слабых поперечных волн, а на втором видно, что отраженная с правой боковой стороны волна порождает поперечную волну, которая достигла левой стороны.
На фиг. 17 представлены векторные поля скоростей точек тела ${{D}_{2}}$ в момент времени, когда преломленные волны отразились от верхнего торца. Здесь наблюдается сложная дифракционная картина. На фиг. 17а видно, что верхние угловые точки работают как источники продольных и поперечных волн.
На фиг. 18–21 представлены изолинии первого и второго инвариантов тензора напряжений в разные моменты времени, которые характеризуют напряженное состояние тела.
Фиг. 20.
Изолинии первого инварианта напряжения тела ${{D}_{2}}$ в момент времени, когда преломленные волны отразились от верхнего торца.

Фиг. 21.
Изолинии первого инварианта напряжения тела ${{D}_{2}}$ в момент времени, когда преломленные волны отразились от верхнего торца.

Сравнивая их, видим, что тело в эпицентре подвергается обеим деформациям схожего характера, причем они симметричны оси ${{x}_{1}}$, и для тела, смещенного от эпицентра, характер объемных и сдвиговых изменений схож, но здесь волна деформации распространяется и от правой боковой стороны. А распределение давления и интенсивности касательных напряжений в первом теле сравнительно больше, чем во втором. Это связано с тем, что распространяющаяся волна возмущений теряет энергию по мере прохождения пути. Эти фигуры наглядно демонстрируют, если посмотреть на движение боковых поверхностей штампа, как деформируются здания при землетрясениях, причем сдвиговые деформации наиболее разрушительны.
На фиг. 22 представлены осциллограммы скорости движения сечения штампа на заданной высоте в его различных точках.
Аналогичные исследования для поверхностного сооружения были проведены при дифракции и преломлении сейсмических волн при образовании сдвиговых трещин.
ЗАКЛЮЧЕНИЕ
В задачах геофизики и сейсмологии исследование процессов распространения, дифракции и преломления волн на границах раздела сред и дневной поверхности тесно связано с вопросами сейсмического районирования территорий, сейсмостойким строительством как наземных, так и подземных сооружений. Наиболее экономичными и эффективными для изучения волновых процессов в средах и конструкциях являются методы математического моделирования. Их использование связано с построением математических моделей и созданием на их базе программных комплексов, которые дают возможность проводить разнообразные численные эксперименты по изучению напряженно-деформированного состояния сред и конструкций при разнообразных динамических воздействиях, которые на реальных объектах провести экспериментально часто просто невозможно.
Разработанный пакет программ позволяет определить характеристики напряженно-дефор-мированного состояния породного массива и поверхностного сооружения в любой расчетной точке области при дифракции и преломлении сейсмических волн, порождаемых источниками на трещине различного типа, варьировать геометрические параметры расчетной схемы и физико-механические параметры сооружения и породного массива.
Разработанные методы решения краевых задач можно использовать для исследования процессов распространения и дифракции волн в земной коре, а также при динамических воздействиях различной природы в наземных сооружениях для исследования их сейсмостойкости.
Список литературы
Клифтон Р.Д. Разностный метод в плоских задачах динамической упругости // Механика (сборник переводов). М., 1968. С. 103–122.
Рекер В.В. Численные решения трехмерных задач динамической теории упругости // Прикл. механ. Серия Е. 1970. № 1. С. 121–129.
Тарабрин Г.Т. Применение метода бихарактеристик для решения нестационарных задач динамики анизотропных массивов // Строительная механ. и расчет сооружений. 1980. № 4. С. 38–42.
Тарабрин Г.Т. Решение методом бихарактеристик нестационарных задач динамики анизотропных оболочек // Строительная механ. и расчет сооружений. 1980. № 6. С. 53–58.
Байтелиев Т.Б., Мардонов Б. Решение плоской динамической задачи теории упругости для полосы методом пространственных характеристик. В кн.: Проблемные вопросы механики горных пород. Алма-Ата: Наука, 1972. С. 194–209.
Новацкий В. Теория упругости. М.: Мир, 1975.
Алексеева Л.А., Дильдабаева И.Ш. Обобщенные решения уравнений динамики упругой среды с криволинейной трещиной при плоской деформации // Матем. журнал. 2007. Т. 7. № 2. С. 19–31.
Владимиров В.С. Обобщенные функции в математической физике. М.: Наука, 1986.
Петрашень Г.И. Распространение волн в анизотропных упругих средах. М.: Наука, 1980.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики









