Журнал вычислительной математики и математической физики, 2020, T. 60, № 9, стр. 1566-1575
Метод суммарной аппроксимации для уравнения, описывающего процессы дробления и замерзания капель в конвективных облаках
Б. А. Ашабоков 1, А. Х. Хибиев 2, *, М. Х. Шхануков-Лафишев 2
1 ФГБУН Институт информатики и проблем регионального управления КБНЦ РАН
360051 Нальчик, ул. И. Арманд, 37а, Россия
2 ФГБУН Институт прикладной математики и автоматизации
КБНЦ РАН
360051 Нальчик, ул. Шортанова, 89а, Россия
* E-mail: akkhibiev@gmail.com
Поступила в редакцию 11.12.2019
После доработки 03.02.2020
Принята к публикации 09.04.2020
Аннотация
Рассматривается локально-одномерная схема для уравнения параболического типа общего вида в $p$-мерном параллелепипеде. Для описания процессов дробления и замерзания капель в конвективных облаках в рассматриваемое уравнение включается нелокальный интегральный источник специального вида. Получена априорная оценка для решения локально-одномерной схемы и доказана ее сходимость. Библ. 10. Фиг. 1.
Ключевые слова: краевая задача, локально-одномерная схема, устойчивость, сходимость схемы, погрешность аппроксимации.
ВВЕДЕНИЕ
Краевые задачи для параболических уравнений общего вида с нелокальным источником возникают при изучении диффузии в турбулентной плазме, при описании функции распределения по массам капель и ледяных частиц, изменения функции рапределения капель за счет микрофизических процессов конденсации, коагуляции капель, дробления и замерзания [1]–[6]. Введем функцию $u(x,m,t)$ такую, что $u(x,m,t)dm$ дает в каждой точке $x = ({{x}_{1}},{{x}_{2}},{{x}_{3}})$ в момент времени $t$ концентрацию облачных капель, масса которых заключена в интервале от $m$ до $m + dm.$ При этом $u(x,m,t)dm$ есть вероятность того, что масса облачных капель в момент времени $t$ находится между $m$ и $m + dm$, величина $u(x,m,t)$ называется плотностью вероятности.
1. ПОСТАНОВКА ЗАДАЧИ
В цилиндре ${{Q}_{T}} = G \times (0 < t \leqslant T]$, основанием которого служит прямоугольный параллелепипед $G = {\text{\{ }}x = ({{x}_{1}},{{x}_{2}},\; \ldots ,\;{{x}_{p}}):0 < {{x}_{\alpha }} < {{l}_{\alpha }},\;\alpha = 1,\;2,\; \ldots ,\;p{\text{\} }}$ с границей $\Gamma $ рассматривается задача
где(3)
$\begin{gathered} Lu = \sum\limits_{\alpha = 1}^p {{{L}_{\alpha }}u} ,\quad {{L}_{\alpha }}u = \frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{k}_{\alpha }}(x,t)\frac{{\partial u}}{{\partial {{x}_{\alpha }}}}} \right) + {{r}_{\alpha }}\frac{{\partial u}}{{\partial {{x}_{\alpha }}}} - \frac{1}{p}q(x,m,t)u(x,m,t) + \\ + \;\frac{1}{p}\int\limits_0^{{{m}_{1}}} Q (m,m{\text{'}})P(m{\text{'}})u(x,m{\text{'}},t)dm{\text{'}}, \\ \end{gathered} $Предположим, что задача (1), (2) имеет единственное достаточно гладкое решение. При оценке порядка аппроксимации будем предполагать, что ${{k}_{\alpha }}(x,t) \in {{C}^{{3,1}}}({{\bar {Q}}_{T}})$, ${{r}_{\alpha }}(x,t)$, $q(x,m,t)$, $f(x,m,t) \in {{C}^{{2,1}}}({{\bar {Q}}_{T}})$, где ${{C}^{{{{n}_{1}},{{n}_{2}}}}}({{\bar {Q}}_{T}})$ – класс функций, непрерывных вместе со своими частными производными порядка ${{n}_{1}}$ по $x$ и ${{n}_{2}}$ по $t$ в замкнутой области ${{\bar {Q}}_{T}}$. Функции $Q(m,m{\text{'}})$, $P(m)$, $R(x,m)$ рассчитываются по следующим формулам (см. [7]):
$\begin{gathered} P(m) = 2.94 \cdot {{10}^{{ - 7}}}exp(34r(m)), \\ R(x,m) = Aexp[B({{T}_{m}}(m) - {{T}_{b}}(x))], \\ Q(m,m{\text{'}}) = \frac{{145.37}}{m}\frac{{r(m)}}{{r(m')}}exp\left( { - 7\frac{{r(m)}}{{r(m{\text{'}})}}} \right), \\ \end{gathered} $
где $A$, $B$ – параметры,
2. ЛОКАЛЬНО-ОДНОМЕРНАЯ СХЕМА (ЛОС)
На отрезке $\left[ {0,T} \right]$ введем равномерную сетку ${{\bar {\omega }}_{\tau }} = {\text{\{ }}{{t}_{j}} = j\tau ,\;j = 0,1,\; \ldots ,\;{{j}_{0}}{\text{\} }}$ с шагом $\tau = \tfrac{T}{{{{j}_{0}}}}$. Каждый интервал $({{t}_{j}},{{t}_{{j + 1}}})$ разобьем на $p$ частей точками ${{t}_{{j + \tfrac{\alpha }{p}}}} = {{t}_{j}} + \tfrac{\alpha }{p}\tau $, $\alpha = 1,2,\; \ldots ,\;p$, и обозначим через ${{\Delta }_{\alpha }} = \left( {{{t}_{{j + \tfrac{{\alpha - 1}}{p}}}},{{t}_{{j + \tfrac{\alpha }{p}}}}} \right]$. Пространственную сетку выберем равномерной по каждому направлению $O{{x}_{\alpha }}$ с шагом ${{h}_{\alpha }} = \tfrac{{{{l}_{\alpha }}}}{{{{N}_{\alpha }}}}$, $\alpha = 1,\;2,\; \ldots ,\;p$:
$\mathop {\bar {\omega }}\nolimits_h = \prod\limits_{\alpha = 1}^p {{{{\bar {\omega }}}_{{{{h}_{\alpha }}}}}} ,\quad {{\bar {\omega }}_{{{{h}_{\alpha }}}}} = \left\{ {x_{\alpha }^{{(i\alpha )}} = {{i}_{\alpha }}{{h}_{\alpha }}:{{i}_{\alpha }} = 0,\;1,\; \ldots ,\;{{N}_{\alpha }},\;\alpha = 1,\;2,\; \ldots ,\;p} \right\}.$
Уравнение (1) перепишем в виде
или
(5)
$\sum\limits_{\alpha = 1}^p {{{\Re }_{\alpha }}} u = 0,\quad {{\Re }_{\alpha }}u = \frac{1}{p}\frac{{\partial u}}{{\partial t}} - {{L}_{\alpha }}u - {{f}_{\alpha }},\quad \sum\limits_{\alpha = 1}^p {{{f}_{\alpha }}} = f,$(6)
${{\Re }_{\alpha }}{{{v}}_{{(\alpha )}}} = \frac{1}{p}\frac{{\partial {{{v}}_{{(\alpha )}}}}}{{\partial t}} - {{L}_{\alpha }}{{{v}}_{{(\alpha )}}} - {{f}_{\alpha }} = 0,\quad x \in G,\quad t \in {{\Delta }_{\alpha }},$
$\begin{gathered} {{{v}}_{{(\alpha )}}} = 0,\quad {{x}_{\alpha }} = 0, \hfill \\ {{{v}}_{{(\alpha )}}} = 0,\quad {{x}_{\alpha }} = {{l}_{\alpha }}, \hfill \\ \end{gathered} $
полагая при этом [8, с. 522]
${{{v}}_{{(1)}}}(x,m,0) = {{u}_{0}}(x,m),\quad {{{v}}_{{(1)}}}(x,m,{{t}_{j}}) = {{{v}}_{{(p)}}}(x,m,{{t}_{j}}),\quad j = 1,\;2,\; \ldots ,$
${{{v}}_{{(\alpha )}}}\left( {x,m,{{t}_{{j + \tfrac{{\alpha - 1}}{p}}}}} \right) = {{{v}}_{{(\alpha - 1)}}}\left( {x,m,{{t}_{{j + \tfrac{{\alpha - 1}}{p}}}}} \right),\quad j = 2,\;3,\; \ldots ,\;p.$
Аппроксимируем каждое уравнение (6) номера $\alpha $ двухслойной схемой на полуинтервале ${{\Delta }_{\alpha }}$, тогда получаем цепочку $p$ одномерных разностных уравнений:
(7)
$\frac{{{{y}^{{j + \tfrac{\alpha }{p}}}} - {{y}^{{j + \tfrac{{\alpha - 1}}{p}}}}}}{\tau } = {{\Lambda }_{\alpha }}{{y}^{{j + \tfrac{\alpha }{p}}}} + \varphi _{\alpha }^{{j + \tfrac{\alpha }{p}}},\quad \alpha = 1,\;2,\; \ldots ,\;p,$(8)
${{\Lambda }_{\alpha }}{{y}^{{j + \tfrac{\alpha }{p}}}} = {{\varkappa }_{\alpha }}{{\left( {{{a}_{\alpha }}y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{j + \tfrac{\alpha }{p}}}} \right)}_{{{{x}_{\alpha }}}}} + b_{\alpha }^{ + }a_{\alpha }^{{( + 1\alpha )}}y_{{{{x}_{\alpha }}}}^{{j + \tfrac{\alpha }{p}}} + b_{\alpha }^{ - }{{a}_{\alpha }}y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{j + \tfrac{\alpha }{p}}} - \frac{1}{p}d{{y}^{{j + \tfrac{\alpha }{p}}}} + \frac{1}{p}\sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} Q (m,{{m}_{{{{i}_{m}}}}})P({{m}_{{{{i}_{m}}}}}){{y}^{{(\alpha )}}}(x,{{m}_{{{{i}_{m}}}}},t){{\hbar }_{m}},$(9)
${{\left. {{{y}^{{j + \tfrac{\alpha }{p}}}}} \right|}_{{{{\gamma }_{{h,\alpha }}}}}} = 0,\quad y(x,m,0) = {{u}_{0}}(x,m),\quad \alpha = 1,\;2,\; \ldots ,\;p,$
$\begin{gathered} {{\gamma }_{{h,\alpha }}} - {\text{множество}}\;{\text{граничных}}\;{\text{узлов}}\;{\text{по}}\;{\text{направлению}}\;{{x}_{\alpha }}, \\ {{a}_{\alpha }} = {{k}_{\alpha }}\left( {{{x}^{{( - 0.5{{h}_{\alpha }})}}},\bar {t}} \right),\quad {{x}^{{( - 0.5{{h}_{\alpha }})}}} = ({{x}_{1}},{{x}_{2}},\; \ldots ,\;{{x}_{{\alpha - 1}}},{{x}_{\alpha }} - 0.5{{h}_{\alpha }},{{x}_{{\alpha + 1}}},\; \ldots ,\;{{x}_{p}}), \\ \bar {t} = {{t}^{{j + \tfrac{1}{2}}}},\quad \varkappa = \frac{1}{{1 + {{R}_{\alpha }}}},\quad {{R}_{\alpha }} = \frac{{0.5{{h}_{\alpha }}\left| {{{r}_{\alpha }}} \right|}}{{{{k}_{\alpha }}}} - {\text{разностное}}\;{\text{число}}\;{\text{Рейнольдса}}, \\ r_{\alpha }^{ + } = 0.5({{r}_{\alpha }} + \left| {{{r}_{\alpha }}} \right|) \geqslant 0,\quad r_{\alpha }^{ - } = 0.5({{r}_{\alpha }} - \left| {{{r}_{\alpha }}} \right|) \leqslant 0,\quad {{r}_{\alpha }} = r_{\alpha }^{ + } + r_{\alpha }^{ - }, \\ b_{\alpha }^{ + } = \frac{{r_{\alpha }^{ + }}}{{{{k}_{\alpha }}}},\quad b_{\alpha }^{ - } = \frac{{r_{\alpha }^{ - }}}{{{{k}_{\alpha }}}},\quad {{a}_{i}} = {{k}_{{i - \tfrac{1}{2}}}}(\bar {t}),\quad \varphi _{\alpha }^{{j + \tfrac{\alpha }{p}}} = {{f}_{\alpha }}(x,m,{{t}_{{j + 0.5}}}),\quad d = q, \\ \end{gathered} $
3. ПОГРЕШНОСТЬ АППРОКСИМАЦИИ ЛОС
Характеристикой точности решения локально-одномерной схемы является разность ${{z}^{{i + \tfrac{\alpha }{p}}}} = {{y}^{{i + \tfrac{\alpha }{p}}}} - {{u}^{{i + \tfrac{\alpha }{p}}}}$, где ${{u}^{{i + \tfrac{\alpha }{p}}}}$ – решение исходной задачи (1), (2). Подставляя ${{y}^{{i + \tfrac{\alpha }{p}}}} = {{z}^{{i + \tfrac{\alpha }{p}}}} + {{u}^{{i + \tfrac{\alpha }{p}}}}$ в разностное уравнение (7), получаем для погрешности уравнение
(10)
$\frac{{{{z}^{{j + \tfrac{\alpha }{p}}}} - {{z}^{{j + \tfrac{{\alpha - 1}}{p}}}}}}{\tau } = {{\Lambda }_{\alpha }}{{z}^{{j + \tfrac{\alpha }{p}}}} + \Psi _{\alpha }^{{j + \tfrac{\alpha }{p}}},$(11)
${{z}^{{j + \tfrac{\alpha }{p}}}} = 0\quad {\text{при}}\quad x = {{\gamma }_{{h,\alpha }}},\quad z(x,m,0) = 0.$
, если $\sum\limits_{\alpha = 1}^p {{{f}_{\alpha }}} = f$, представим погрешность в виде суммы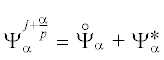 
:
Очевидно, что $\Psi _{\alpha }^{ * } = O\left( {{{{\left| h \right|}}^{2}} + \tau } \right)$, 
, ${{\left| h \right|}^{2}} = h_{1}^{2} + h_{2}^{2} + \; \cdots \; + h_{p}^{2}$, т.е. ЛОС обладает суммарной аппроксимацией $O\left( {{{{\left| h \right|}}^{2}} + \tau } \right)$.
4. УСТОЙЧИВОСТЬ ЛОС
Умножим уравнение (7) скалярно на ${{y}^{{(\alpha )}}} = {{y}^{{j + \tfrac{\alpha }{p}}}}$:
${{\left( {y_{{\bar {t}}}^{{(\alpha )}},{{y}^{{(\alpha )}}}} \right)}_{\alpha }} = {{\left( {{{\Lambda }_{\alpha }}{{y}^{{(\alpha )}}},{{y}^{{(\alpha )}}}} \right)}_{\alpha }} + {{\left( {{{\varphi }^{{(\alpha )}}},{{y}^{{(\alpha )}}}} \right)}_{\alpha }},$
(12)
${{(u,{v})}_{\alpha }} = \sum\limits_{{{i}_{\alpha }} = 1}^{{{N}_{\alpha }} - 1} {{{u}_{{{{i}_{\alpha }}}}}} {{{v}}_{{{{i}_{\alpha }}}}}{{h}_{\alpha }},\quad {{\left( {u,{v}} \right]}_{\alpha }} = \sum\limits_{{{i}_{\alpha }} = 1}^{{{N}_{\alpha }}} {{{u}_{{{{i}_{\alpha }}}}}} {{{v}}_{{{{i}_{\alpha }}}}}{{h}_{\alpha }},$
$(u,{v}) = \sum\limits_{x \in {{\omega }_{h}}} u {v}H,\quad H = \prod\limits_{\alpha = 1}^p {{{h}_{\alpha }}} .$
Преобразуем каждое слагаемое тождества (12):
$\left( {y_{{\bar {t}}}^{{(\alpha )}},{{y}^{{(\alpha )}}}} \right) = \tfrac{1}{2}{{\left( {\left\| {{{y}^{{(\alpha )}}}} \right\|_{{{{L}_{2}}(\alpha )}}^{2}} \right)}_{{\bar {t}}}} + \tfrac{\tau }{2}\left\| {{{y}_{{\bar {t}}}}} \right\|_{{{{L}_{2}}(\alpha )}}^{2},$
$\begin{gathered} {{\left( {{{\Lambda }_{\alpha }}{{y}^{{(\alpha )}}},{{y}^{{(\alpha )}}}} \right)}_{\alpha }} = {{\left( {{{\varkappa }_{\alpha }}{{{({{a}_{\alpha }}y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{(\alpha )}})}}_{{{{x}_{\alpha }}}}},{{y}^{{(\alpha )}}}} \right)}_{\alpha }} + {{\left( {b_{\alpha }^{ + }a_{\alpha }^{{( + 1\alpha )}}y_{{{{x}_{\alpha }}}}^{{(\alpha )}},{{y}^{{(\alpha )}}}} \right)}_{\alpha }} + {{\left( {b_{\alpha }^{ - }{{a}_{\alpha }}y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{(\alpha )}},{{y}^{{(\alpha )}}}} \right)}_{\alpha }} - \\ - \;\frac{1}{p}{{\left( {d{{y}^{{j + \tfrac{\alpha }{p}}}},{{y}^{{(\alpha )}}}} \right)}_{\alpha }} + \frac{1}{p}{{\left( {\sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} Q (m,{{m}_{{{{i}_{m}}}}})P({{m}_{{{{i}_{m}}}}}){{y}^{{(\alpha )}}}(x,{{m}_{{{{i}_{m}}}}},t){{\hbar }_{m}},{{y}^{{(\alpha )}}}} \right)}_{\alpha }}, \\ \end{gathered} $
где ${{\varkappa }_{\alpha }} = \tfrac{1}{{1 + {{R}_{\alpha }}}}$, ${{R}_{\alpha }} = \tfrac{{0.5{{h}_{\alpha }}\left| {{{r}_{\alpha }}} \right|}}{{{{k}_{\alpha }}}}$. Так как $\varkappa = 1 - \tfrac{{0.5{{h}_{\alpha }}\left| {{{r}_{\alpha }}} \right|}}{{{{k}_{\alpha }}}} + O(h_{\alpha }^{2})$, то $\varkappa $ заменим на $1 - \tfrac{{0.5{{h}_{\alpha }}\left| {{{r}_{\alpha }}} \right|}}{{{{k}_{\alpha }}}}$. Тогда последнее выражение перепишем в виде
$\begin{gathered} {{\left( {{{\Lambda }_{\alpha }}{{y}^{{(\alpha )}}},{{y}^{{(\alpha )}}}} \right)}_{\alpha }} = - {{\left( {{{a}_{\alpha }},y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{2}} \right]}_{\alpha }} + {{\left( {b_{\alpha }^{ + }a_{\alpha }^{{( + 1\alpha )}}{{y}_{{{{x}_{\alpha }}}}},{{y}^{{(\alpha )}}}} \right)}_{\alpha }} + {{\left( {b_{\alpha }^{ - }{{a}_{\alpha }}y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{(\alpha )}},{{y}^{{(\alpha )}}}} \right)}_{\alpha }} - \\ - \;\frac{1}{p}\left( {d{{y}^{{(\alpha )}}},{{y}^{{(\alpha )}}}} \right) + 0.5{{h}_{\alpha }}{{\left( {{{a}_{\alpha }}{{{\left( {\frac{{\left| {{{r}_{\alpha }}} \right|}}{{{{k}_{\alpha }}}}} \right)}}_{{\mathop {\bar {x}}\nolimits_\alpha }}},y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{(\alpha )}}{{y}^{{(\alpha )}}}} \right]}_{\alpha }} + 0.5{{h}_{\alpha }}{{\left( {{{a}_{\alpha }}{{{\left( {\frac{{\left| {{{r}_{\alpha }}} \right|}}{{{{k}_{\alpha }}}}} \right)}}_{{{{i}_{\alpha }} - 1}}},y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{2}} \right]}_{\alpha }} + \\ + \;\frac{1}{p}{{\left( {\sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} Q (m,{{m}_{{{{i}_{m}}}}})P({{m}_{{{{i}_{m}}}}}){{y}^{{(\alpha )}}}(x,{{m}_{{{{i}_{m}}}}},t){{\hbar }_{m}},{{y}^{{(\alpha )}}}} \right)}_{\alpha }}. \\ \end{gathered} $
С помощью леммы 1 из [9] находим
$\begin{gathered} {{\left( {b_{\alpha }^{ + }a_{\alpha }^{{( + 1\alpha )}}{{y}_{{{{x}_{\alpha }}}}},{{y}^{{(\alpha )}}}} \right)}_{\alpha }} + {{\left( {b_{\alpha }^{ - }{{a}_{\alpha }}y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{(\alpha )}},{{y}^{{(\alpha )}}}} \right)}_{\alpha }} \leqslant 2\frac{{{{c}_{1}}{{c}_{2}}}}{{{{c}_{0}}}}\left( {\varepsilon \left| {\left| {\left. {y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{(\alpha )}}} \right]} \right|} \right._{{{{L}_{2}}(\alpha )}}^{2} + c(\varepsilon )\mathop {\left\| {{{y}^{{(\alpha )}}}} \right\|}\nolimits_{{{L}_{2}}(\alpha )}^2 } \right), \\ \frac{1}{p}\left( {d{{y}^{{(\alpha )}}},{{y}^{{(\alpha )}}}} \right) \leqslant \frac{1}{p}{{c}_{2}}\mathop {\left\| {{{y}^{{(\alpha )}}}} \right\|}\nolimits_{{{L}_{2}}(\alpha )}^2 , \\ \end{gathered} $
$\begin{gathered} 0.5{{h}_{\alpha }}{{\left( {{{a}_{\alpha }}{{{\left( {\frac{{\left| {{{r}_{\alpha }}} \right|}}{{{{k}_{\alpha }}}}} \right)}}_{{\mathop {\bar {x}}\nolimits_\alpha }}},y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{(\alpha )}}{{y}^{{(\alpha )}}}} \right]}_{\alpha }} \leqslant 0.5{{h}_{\alpha }}{{c}_{4}}{{\left( {{{y}^{{(\alpha )}}},y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{(\alpha )}}} \right]}_{\alpha }} \leqslant 0.5{{h}_{\alpha }}{{c}_{4}}{{\left| {\left. {\left| {y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{(\alpha )}}} \right.} \right]} \right|}_{{{{L}_{2}}(\alpha )}}}{{\left\| {{{y}^{{(\alpha )}}}} \right\|}_{{{{L}_{2}}(\alpha )}}} \leqslant \\ \leqslant \;0.5{{h}_{\alpha }}{{c}_{4}}\left( {\varepsilon \left| {\left. {\left| {y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{(\alpha )}}} \right.} \right]} \right|_{{{{L}_{2}}(\alpha )}}^{2} + c(\varepsilon )\left\| {{{y}^{{(\alpha )}}}} \right\|_{{{{L}_{2}}(\alpha )}}^{2}} \right),\quad {\text{где}}\quad \left| {{{a}_{\alpha }}{{{\left( {\frac{{\left| {{{r}_{\alpha }}} \right|}}{{{{k}_{\alpha }}}}} \right)}}_{{\mathop {\bar {x}}\nolimits_\alpha }}}} \right| \leqslant {{c}_{4}}, \\ 0.5{{\hbar }_{\alpha }}{{\left( {{{a}_{\alpha }}{{{\left( {\frac{{\left| {{{r}_{\alpha }}} \right|}}{{{{k}_{\alpha }}}}} \right)}}_{{{{i}_{\alpha }} - 1}}},y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{(\alpha )}}} \right]}_{\alpha }} \leqslant 0.5{{h}_{\alpha }}{{c}_{5}}\left| {\left. {\left| {y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{(\alpha )}}} \right.} \right]} \right|_{{{{L}_{2}}(\alpha )}}^{2},\quad \left| {{{a}_{\alpha }}{{{\left( {\frac{{\left| {{{r}_{\alpha }}} \right|}}{{{{k}_{\alpha }}}}} \right)}}_{{{{i}_{\alpha }} - 1}}}} \right| \leqslant {{c}_{5}}, \\ \end{gathered} $
$\begin{gathered} \frac{1}{p}{{\left( {\sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} Q (m,{{m}_{{{{i}_{m}}}}})P({{m}_{{{{i}_{m}}}}}){{y}^{{(\alpha )}}}(x,{{m}_{{{{i}_{m}}}}},t){{\hbar }_{m}},{{y}^{{(\alpha )}}}} \right)}_{\alpha }} \leqslant \frac{1}{p}{{\left\| {\sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} Q (m,{{m}_{{{{i}_{m}}}}})P({{m}_{{{{i}_{m}}}}}){{y}^{{(\alpha )}}}(x,{{m}_{{{{i}_{m}}}}},t){{\hbar }_{m}}} \right\|}_{{{{L}_{2}}(\alpha )}}}{{\left\| {{{y}^{{(\alpha )}}}} \right\|}_{{{{L}_{2}}(\alpha )}}} \leqslant \\ \leqslant \;\varepsilon \frac{1}{p}\left\| {\sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {{{y}^{{(\alpha )}}}} (x,{{m}_{{{{i}_{m}}}}},t){{\hbar }_{m}}} \right\|_{{{{L}_{2}}(\alpha )}}^{2} + \frac{1}{{4\varepsilon p}}\left\| {{{y}^{{(\alpha )}}}} \right\|_{{{{L}_{2}}(\alpha )}}^{2} = \varepsilon \frac{1}{p}\sum\limits_{{{i}_{\alpha }} = 1}^{{{N}_{\alpha }} - 1} {{{{\left( {\sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {{{y}^{{(\alpha )}}}} (x,{{m}_{{{{i}_{m}}}}},t){{\hbar }_{m}}} \right)}}^{2}}} {{h}_{\alpha }} + \frac{1}{{4\varepsilon p}}\left\| {{{y}^{{(\alpha )}}}} \right\|_{{{{L}_{2}}(\alpha )}}^{2} = \\ = \;\varepsilon \frac{{{{m}_{1}}}}{p}\left\| {{{y}^{{(\alpha )}}}} \right\|_{{{{L}_{\alpha }}(\alpha ,m)}}^{2} + \frac{1}{{4\varepsilon p}}\left\| {{{y}^{{(\alpha )}}}} \right\|_{{{{L}_{2}}(\alpha )}}^{2}. \\ \end{gathered} $
Подставляя полученные оценки в тождество (12), находим
(13)
$\begin{gathered} \frac{1}{2}{{\left( {\left\| {{{y}^{{j + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}(\alpha )}}^{2}} \right)}_{{\bar {t}}}} + {{\left( {\left( {1 - 0.5{{h}_{\alpha }}\frac{{\left| {{{r}_{\alpha }}} \right|}}{{{{k}_{\alpha }}}}} \right){{a}_{\alpha }},y_{{{{x}_{\alpha }}}}^{2}} \right]}_{\alpha }} \leqslant \frac{1}{2}\left\| {{{\varphi }^{{j + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}(\alpha )}}^{2} + \\ + \;c(\varepsilon )\left\| {{{y}^{{(\alpha )}}}} \right\|_{{{{L}_{2}}(\alpha )}}^{2} + \varepsilon \left( {{{c}_{4}} + \frac{{2{{c}_{1}}{{c}_{2}}}}{{{{c}_{0}}}}} \right)\left| {\left. {\left| {y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{(\alpha )}}} \right.} \right]} \right|_{{{{L}_{2}}(\alpha )}}^{2} + \varepsilon \frac{{{{m}_{1}}}}{p}\left\| {{{y}^{{(\alpha )}}}} \right\|_{{{{L}_{\alpha }}(\alpha ,m)}}^{2}. \\ \end{gathered} $(14)
$\frac{1}{2}\left\| {{{y}^{{j + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}(\alpha )}}^{2} + \frac{{{{c}_{0}}}}{2}\tau \left| {\left. {\left| {{{y}_{{\mathop {\bar {x}}\nolimits_\alpha }}}} \right.} \right]} \right|_{{{{L}_{2}}(\alpha )}}^{2} \leqslant \frac{\tau }{2}\left\| {{{\varphi }^{{j + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}(\alpha )}}^{2} + c(\varepsilon )\tau \left\| {{{y}^{{j + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}(\alpha )}}^{2} + \varepsilon \frac{{l_{\alpha }^{2}{{m}_{1}}}}{{4p}}\tau \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left| {\left. {\left| {y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{j + \tfrac{\alpha }{p}}}} \right.} \right]} \right|_{{{{L}_{2}}(\alpha )}}^{2}} {{\hbar }_{m}} + \frac{1}{2}\left\| {{{y}^{{j + \tfrac{{\alpha - 1}}{p}}}}} \right\|_{{{{L}_{2}}(\alpha )}}^{2}.$(15)
$\left\| {{{y}^{{j + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2} + {{c}_{0}}\tau \left| {\left. {\left| {{{y}_{{\mathop {\bar {x}}\nolimits_\alpha }}}} \right.} \right]} \right|_{{{{L}_{2}}({{\omega }_{h}})}}^{2} \leqslant \tau \left\| {{{\varphi }^{{j + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2} + c(\varepsilon )\tau \left\| {{{y}^{{j + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2} + \varepsilon \frac{{l_{\alpha }^{2}{{m}_{1}}}}{{2p}}\tau \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left| {\left. {\left| {y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{j + \tfrac{\alpha }{p}}}} \right.} \right]} \right|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}} + \left\| {{{y}^{{j + \tfrac{{\alpha - 1}}{p}}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}.$(16)
$\begin{gathered} \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{y}^{{j + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}} + {{c}_{0}}\tau \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left| {\left| {\left. {{{y}_{{\mathop {\bar {x}}\nolimits_\alpha }}}} \right]} \right.} \right|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}} \leqslant \tau \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{\varphi }^{{j + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}} + \\ + \;c(\varepsilon )\tau \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{y}^{{j + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}} + \varepsilon \frac{{l_{\alpha }^{2}m_{1}^{2}}}{{2p}}\tau \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left| {\left. {\left| {{{y}_{{\mathop {\bar {x}}\nolimits_\alpha }}}} \right.} \right]} \right|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}} + \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{y}^{{j + \tfrac{{\alpha - 1}}{p}}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}}. \\ \end{gathered} $(17)
$\begin{gathered} \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{y}^{{j + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}} + \frac{{{{c}_{0}}}}{2}\tau \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left| {\left. {\left| {y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{(\alpha )}}} \right.} \right]} \right|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}} \leqslant \tau \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{\varphi }^{{j + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}} + \\ + \;c(\varepsilon )\tau \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{y}^{{j + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}} + \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{y}^{{j + \tfrac{{\alpha - 1}}{p}}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}}. \\ \end{gathered} $Просуммируем (17) сначала по $\alpha = 1,\;2,\; \ldots ,\;p$:
$\begin{gathered} \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{y}^{{j + 1}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}} + \frac{{{{c}_{0}}}}{2}\sum\limits_{\alpha = 1}^p \tau \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left| {\left| {\left. {{{y}_{{\mathop {\bar {x}}\nolimits_\alpha }}}} \right]} \right.} \right|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}} \leqslant \sum\limits_{\alpha = 1}^p \tau \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{\varphi }^{{j + \tfrac{\alpha }{p}}}}} \right\|} _{{{{L}_{2}}({{\omega }_{h}})}}^{2}{{\hbar }_{m}} + \\ + \;c(\varepsilon )\sum\limits_{\alpha = 1}^p \tau \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{y}^{{j + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}} + \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{y}^{j}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}}, \\ \end{gathered} $
затем по $j{\text{'}}$ от $0$ до $j$:
(18)
$\begin{gathered} \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{y}^{{j + 1}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}} + \frac{{{{c}_{0}}}}{2}\sum\limits_{j' = 0}^j \tau \sum\limits_{\alpha = 1}^p {\sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left| {\left. {\left| {y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{j' + \tfrac{\alpha }{p}}}} \right.} \right]} \right|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} } {{\hbar }_{m}} \leqslant \sum\limits_{j' = 0}^j \tau \sum\limits_{\alpha = 1}^p {\sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{\varphi }^{{j' + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} } {{\hbar }_{m}} + \\ + \;c(\varepsilon )\sum\limits_{j' = 0}^j \tau \sum\limits_{\alpha = 1}^p {\sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{y}^{{j' + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}}} + \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{y}^{0}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}}. \\ \end{gathered} $(19)
$\sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{y}^{{j + 1}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}} \leqslant c(\varepsilon )\sum\limits_{j' = 0}^j \tau \sum\limits_{\alpha = 1}^p {\sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{y}^{{j' + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} } {{\hbar }_{m}} + {{F}^{j}},$
${{F}^{j}} = \sum\limits_{j' = 0}^j \tau \sum\limits_{\alpha = 1}^p {\sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{\varphi }^{{j + \tfrac{\alpha }{p}}}}} \right\|} _{{{{L}_{2}}({{\omega }_{h}})}}^{2}{{\hbar }_{m}}} + \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{y}^{0}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}},$
С помощью неравенства (19) на основании леммы 4 (см. [10, с. 171]) из неравенства (18) получаем априорную оценку
(20)
$\sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{y}^{{j + 1}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}}\, + \,\sum\limits_{j' = 0}^j \tau \sum\limits_{\alpha = 1}^p {\sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left| {\left. {\left| {y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{j' + \tfrac{\alpha }{p}}}} \right.} \right]} \right|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} } {{\hbar }_{m}}\, \leqslant \,M(t)\left[ {\sum\limits_{j' = 0}^j \tau \sum\limits_{\alpha = 1}^p {\sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{\varphi }^{{j' + \tfrac{\alpha }{p}}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} } {{\hbar }_{m}}\, + \,\sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{y}^{0}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}}} \right].$Теорема 1. Локально-одномерная схема (7)–(9) устойчива по начальным данным и правой части так, что для решения задачи (7)–(9) при любых $h$ и $\tau \leqslant {{\tau }_{0}}$ справедлива оценка (20).
5. СХОДИМОСТЬ ЛОКАЛЬНО-ОДНОМЕРНОЙ СХЕМЫ
По аналогии с [8, с. 528] представим решение задачи (10), (11) в виде суммы ${{z}_{{(\alpha )}}} = {{{v}}_{{(\alpha )}}} + {{\eta }_{{(\alpha )}}},{{z}_{{(\alpha )}}} = {{z}^{{j + \tfrac{\alpha }{p}}}},$ где ${{\eta }_{{(\alpha )}}}$ определяется условиями
Из (21) следует
Для 
Функция ${{{v}}_{{(\alpha )}}}$ определяется условиями
Решение задачи (22) оценим с помощью теоремы 1. Так как ${{\eta }^{j}} = 0$, ${{\eta }_{\alpha }} = O(\tau )$, $\left\| {{{z}^{j}}} \right\| \leqslant \left\| {{{{v}}^{j}}} \right\|$, то из оценки (20) следует
Теорема 2. Пусть задача (1), (2) имеет единственное непрерывное в $\mathop {\bar {Q}}\nolimits_T $ решение $u(x,m,t)$ и существуют непрерывные в $\mathop {\bar {Q}}\nolimits_T $ производные
$\frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}},\frac{{{{\partial }^{4}}u}}{{\partial x_{\alpha }^{2}\partial x_{\beta }^{2}}},\frac{{{{\partial }^{3}}u}}{{\partial x_{\alpha }^{2}\partial t}},\frac{{{{\partial }^{2}}f}}{{\partial x_{\alpha }^{2}}},\quad \alpha = 1,\;2,\; \ldots ,\;p,\quad \alpha \ne \beta ,$
тогда локально-одномерная схема (7)–(9)
сходится со скоростью $O({{\left| h \right|}^{2}} + \tau )$ так, что
${{\left\| {{{y}^{{j + 1}}} - {{u}^{{j + 1}}}} \right\|}_{1}} \leqslant M\left( {{{{\left| h \right|}}^{2}} + \tau } \right),\quad {{\left| h \right|}^{2}} = h_{1}^{2} + h_{2}^{2} + \; \ldots \; + h_{p}^{2}.$
$\left\| {{{y}^{{j + 1}}}} \right\|_{1}^{2} = \sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left\| {{{y}^{{j + 1}}}} \right\|_{{{{L}_{2}}({{\omega }_{h}})}}^{2}} {{\hbar }_{m}} + \sum\limits_{j' = 0}^j \tau \sum\limits_{\alpha = 1}^p {\sum\limits_{{{i}_{m}} = 0}^{N({{m}_{1}})} {\left| {\left. {\left| {y_{{\mathop {\bar {x}}\nolimits_\alpha }}^{{j' + \tfrac{\alpha }{p}}}} \right.} \right]} \right|} } _{{{{L}_{2}}({{\omega }_{h}})}}^{2}{{\hbar }_{m}}.$
6. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ
Тестовый пример. В цилиндре ${{\bar {Q}}_{T}} = \bar {G} \times [0,T]$, основанием которого является прямоугольник $\bar {G} = \left\{ {x = ({{x}_{1}},{{x}_{2}}):0 \leqslant {{x}_{\alpha }} \leqslant {{l}_{\alpha }},\;\alpha = 1,\;2} \right\}$ с границей $\Gamma $, $\bar {G} = G \cup \Gamma ,$ рассмотрим первую краевую задачу
(23)
$\begin{gathered} \frac{{\partial u}}{{dt}} = \frac{\partial }{{\partial {{x}_{1}}}}\left( {{{k}_{1}}({{x}_{1}},{{x}_{2}},t)\frac{{\partial u}}{{\partial {{x}_{1}}}}} \right) + \frac{\partial }{{\partial {{x}_{2}}}}\left( {{{k}_{2}}({{x}_{1}},{{x}_{2}},t)\frac{{\partial u}}{{\partial {{x}_{2}}}}} \right) + {{r}_{1}}({{x}_{1}},{{x}_{2}},t)\frac{{\partial u}}{{\partial {{x}_{1}}}} + \\ + \;{{r}_{2}}({{x}_{1}},{{x}_{2}},t)\frac{{\partial u}}{{\partial {{x}_{2}}}} - \frac{1}{2}{{q}_{1}}({{x}_{1}},{{x}_{2}},m,t)u({{x}_{1}},{{x}_{2}},m,t) - \frac{1}{2}{{q}_{2}}({{x}_{1}},{{x}_{2}},m,t)u({{x}_{1}},{{x}_{2}},m,t) + \\ + \;\int\limits_0^{{{m}_{1}}} Q (m,m{\text{'}})P(m{\text{'}})u(x,m{\text{'}},t)dm{\text{'}} + f({{x}_{1}},{{x}_{2}},m,t), \\ 0 < {{x}_{1}} < {{l}_{1}},\quad 0 < {{x}_{2}} < {{l}_{2}},\quad 0 < t \leqslant T, \\ \end{gathered} $
$\begin{gathered} {{k}_{1}}({{x}_{1}},{{x}_{2}},t) = {{k}_{2}}({{x}_{1}},{{x}_{2}},t) = {{e}^{{{{x}_{1}} + {{x}_{2}} + t}}}, \\ {{r}_{1}}({{x}_{1}},{{x}_{2}},t) = {{r}_{2}}({{x}_{1}},{{x}_{2}},t) = ({{x}_{1}}{{x}_{2}} - 0.5)cos({{x}_{1}}{{x}_{2}} + t), \\ {{q}_{1}}({{x}_{1}},{{x}_{2}},m,t) = {{q}_{2}}({{x}_{1}},{{x}_{2}},m,t) = {{e}^{{t + m}}}cos({{x}_{1}}{{x}_{2}}), \\ \end{gathered} $
$\begin{gathered} Q(m,m{\text{'}}) = {{e}^{{2m{\text{'}} + m}}},\quad P(m{\text{'}}) = {{e}^{{ - m{\text{'}}}}}, \\ f({{x}_{1}},{{x}_{2}},m,t) = 3{{t}^{2}}{{e}^{m}}(x_{1}^{3} - {{l}_{1}}x_{1}^{2})(x_{2}^{3} - {{l}_{2}}x_{2}^{2}) - \\ - \;{{e}^{{{{x}_{1}} + {{x}_{2}} + t}}}{{t}^{3}}{{e}^{m}}(x_{2}^{3} - {{l}_{2}}x_{2}^{2})(3x_{1}^{2} - 2{{l}_{1}}{{x}_{1}} + 6{{x}_{1}} - 2{{l}_{1}}) - \\ \end{gathered} $
$\begin{gathered} - \;{{e}^{{{{x}_{1}} + {{x}_{2}} + t}}}{{t}^{3}}{{e}^{m}}(x_{1}^{3} - {{l}_{1}}x_{1}^{2})(3x_{2}^{2} - 2{{l}_{2}}{{x}_{2}} + 6{{x}_{2}} - 2{{l}_{2}}) - \\ - \;({{x}_{1}}{{x}_{2}} - 0.5)cos({{x}_{1}}{{x}_{2}} + t){{t}^{3}}{{e}^{m}}(x_{2}^{3} - {{l}_{2}}x_{2}^{2})(3x_{1}^{2} - 2{{l}_{1}}{{x}_{1}}) - \\ - \;({{x}_{1}}{{x}_{2}} - 0.5)cos({{x}_{1}}{{x}_{2}} + t){{t}^{3}}{{e}^{m}}(x_{1}^{3} - {{l}_{1}}x_{1}^{2})(3x_{2}^{2} - 2{{l}_{2}}{{x}_{2}}) + \\ \end{gathered} $
$\begin{gathered} + \;{{e}^{{t + 2m}}}cos({{x}_{1}}{{x}_{2}}){{t}^{3}}(x_{1}^{3} - {{l}_{1}}x_{1}^{2})(x_{2}^{3} - {{l}_{2}}x_{2}^{2}) - \\ - {{t}^{3}}{{e}^{m}}(x_{1}^{3} - {{l}_{1}}x_{1}^{2})(x_{2}^{3} - {{l}_{2}}x_{2}^{2})({{e}^{{2{{m}_{1}}}}} - 1), \\ 0 < m \leqslant {{m}_{1}},\quad {{m}_{1}} = 1,\quad {{l}_{1}} = {{l}_{2}} = 1,\quad T = 1. \\ \end{gathered} $
Точное решение задачи (23), (24): u(x, m, t) = ${{t}^{3}}{{e}^{m}}(x_{1}^{3} - {{l}_{1}}x_{1}^{2})(x_{2}^{3} - {{l}_{2}}x_{2}^{2})$.
Численные расчеты для функции распределения по массам капель с учетом микрофизических процессов дробления и замерзания представлены (см. фиг. 1) для следующей задачи:
$\begin{gathered} \frac{{\partial {{f}_{1}}}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {K\frac{{\partial {{f}_{1}}}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {K\frac{{\partial {{f}_{1}}}}{{\partial y}}} \right) + u\frac{{\partial {{f}_{1}}}}{{\partial x}} + (w - {{V}_{1}})\frac{{\partial {{f}_{1}}}}{{\partial y}} - R(x,y,m){{f}_{1}} - P(m){{f}_{1}} + \\ + \;\int\limits_0^{{{m}_{1}}} Q (m,m{\text{'}})P(m{\text{'}}){{f}_{1}}(x,y,m{\text{'}},t)dm{\text{'}} + {{I}_{1}}, \\ 0 < x < 15,\quad 0 < y < 30,\quad 0 < t \leqslant T,\quad {{\left. {{{f}_{1}}} \right|}_{\Gamma }} = 0,\quad {{f}_{1}}(x,y,m,0) = 0, \\ \end{gathered} $
где ${{f}_{1}}(x,y,m,t)$ – функция распределения по массам капель. Образование новых капель на ядрах конденсации
учитывает слагаемое ${{I}_{1}}(x,y,m,t)$. Этот процесс описывается формулой [2]:
${{I}_{1}}(x,y,m,t) = \frac{{\alpha ({{q}_{p}}(x,y) - {{q}_{s}}(x,y))f_{1}^{0}(x,y,m)}}{{\omega (f_{1}^{0})}},$
где ${{q}_{p}}$ – влажность воздуха в точке $(x,y)$, ${{q}_{s}}$ – влажность насыщенного водяного пара в той же точке, $\alpha $ – численный коэффициент, $f_{1}^{0}$ – заданное распределение капель в той же точке, $\omega (f_{1}^{0})$ – водность заданного распределения капель, $u$ и $w$ – горизонтальная и вертикальная составляющие скоростей воздушных потоков, ${{V}_{1}}$ – скорость падения капель.
Фиг. 1.
Функция распределения по массам капель: без учета дробления и замерзания (сплошная линия), с учетом дробления и замерзания (штриховая линия).
Коэффициент турбулентной диффузии вычисляется по формуле:
$K = C{{L}^{2}}\mathop {\left[ {\mathop {\left( {\frac{{\partial u}}{{\partial x}}} \right)}\nolimits^2 + \mathop {\left( {\frac{{\partial u}}{{\partial y}}} \right)}\nolimits^2 + \mathop {\left( {\frac{{\partial w}}{{\partial x}}} \right)}\nolimits^2 + \mathop {\left( {\frac{{\partial w}}{{\partial y}}} \right)}\nolimits^2 } \right]}\nolimits^{1/2} .$
Таблица 1.
Изменение погрешности при уменьшении размеров сетки
| ${{h}_{1}} = {{h}_{2}}$ | $m$ | $\tau $ | Максимальная погрешность |
|---|---|---|---|
| 1/10 | 1/10 | 1/100 | 0.0501006 |
| 1/20 | 1/20 | 1/400 | 0.0232227 |
| 1/40 | 1/40 | 1/1600 | 0.0079458 |
Таблица 2.
Значения масс $m$, радиусов $r$ и скоростей падения ${{V}_{1}}$ капель
| № | $m$ (г) | $r$ (см) | ${{V}_{1}}$ (м/c) |
|---|---|---|---|
| 1 | 2.5000e–10 | 0.00039080 | 0.001817 |
| 2 | 3.5360e–10 | 0.00043865 | 0.002290 |
| 3 | 5.0000e–10 | 0.00049237 | 0.002885 |
| 4 | 7.0710e–10 | 0.00055267 | 0.003635 |
| 5 | 1.0000e–9 | 0.00062035 | 0.004580 |
| 6 | 1.4142e–9 | 0.00069632 | 0.005770 |
| 7 | 2.0000e–9 | 0.00078159 | 0.007270 |
| 8 | 2.8284e–9 | 0.00087731 | 0.009159 |
| 9 | 4.0000e–9 | 0.00098475 | 0.011540 |
| 10 | 5.6569e–9 | 0.00110534 | 0.014539 |
| 11 | 8.0000e–9 | 0.00124070 | 0.018318 |
| 12 | 1.1314e–8 | 0.00139264 | 0.023079 |
| 13 | 1.6000e–8 | 0.00156319 | 0.029078 |
| 14 | 2.2627e–8 | 0.00175462 | 0.036636 |
| 15 | 3.2000e–8 | 0.00196949 | 0.046159 |
| 16 | 4.5255e–8 | 0.00221068 | 0.058156 |
| 17 | 6.4000e–8 | 0.00248140 | 0.073273 |
| 18 | 9.05100e–8 | 0.00278528 | 0.092318 |
| 19 | 1.2800e–7 | 0.00312637 | 0.116313 |
| 20 | 1.8102e–7 | 0.00350923 | 0.146545 |
| 21 | 2.5600e–7 | 0.00393898 | 0.184635 |
| 22 | 3.6204e–7 | 0.00442136 | 0.353708 |
| 23 | 5.1200e–7 | 0.00496280 | 0.397024 |
| 24 | 7.2408e–7 | 0.00557056 | 0.445645 |
| 25 | 1.0240e–6 | 0.00625274 | 0.500219 |
| 26 | 1.4482e–6 | 0.00701846 | 0.561477 |
| 27 | 2.0480e–6 | 0.00787796 | 0.630237 |
| 28 | 2.8963e–6 | 0.00884271 | 0.707417 |
| 29 | 4.0960e–6 | 0.00992561 | 0.794049 |
| 30 | 5.7926e–6 | 0.01114112 | 0.891289 |
| 31 | 8.1920e–6 | 0.01250548 | 1.000439 |
| 32 | 1.1585e–5 | 0.01403693 | 1.122954 |
| 33 | 1.6384e–5 | 0.01575592 | 1.260474 |
| 34 | 2.3170e–5 | 0.01768542 | 1.414834 |
| 35 | 3.2768e–5 | 0.01985122 | 1.588097 |
| 36 | 4.6340e–5 | 0.02228224 | 1.782579 |
| 37 | 6.5536e–5 | 0.02501096 | 2.000877 |
| 38 | 9.2682e–5 | 0.02807386 | 2.245909 |
| 39 | 1.3107e–4 | 0.03151184 | 2.520947 |
Список литературы
Ашабоков Б.А., Шаповалов А.В. Конвективные облака: численные модели и результаты моделировaния в естественных условиях и при активном воздействии. Нальчик: Изд-во КБНЦ РАН, 2008. 252 с.
Коган Е.Л., Мазин И.П., Сергеев Б.Н., Хворостиков В.Н. Численное моделирование облаков. М.: Гидрометеоиздат, 1984. 178 с.
Berry E.X. Cloud droplet growth by collection // J. Atmos. Sci. 1967. V. 24. P. 688–701.
Berry E.X., Reinharolt R.L. An analysis of cloud drop growth by collection: part 2. Single initial distributions // J. Atmos. Sci. 1974. V. 31. P. 1825–1837.
Чудновский Л.Ф. Теплофизика почвы. М.: Наука, 1976. 353 с.
Кожанов А.И. Об одной нелокальной краевой задаче с переменными коэффициентами для уравнений теплопроводности и Аллера // Дифференц. ур-ния. 2004. Т. 10. № 6. С. 763–774.
Tzivion S., Feingold G., Levin Z. An efficient numerical solution to the stochastic collection equation // J. Atmos. Sci. 1987. V. 44. P. 3139–3149.
Самарский А.А. Теория разностных схем. М.: Наука, 1977. 656 с.
Андреев В.Б. О сходимости разностных схем, аппроксимирующих вторую и третью краевые задачи для эллиптических уравнений // Ж. вычисл. матем. и матем. физ. 1968. Т. 8.
Самарский А.А., Гулин А.В. Устойчивость разностных схем. М.: Наука, 1973. 480 с.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики
Пн.-пт.: 10.00-19.00