1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 60, № 9, 2020

Журнал вычислительной математики и математической физики, 2020, T. 60, № 9, стр. 1587-1603

Граничные условия для моделирования воздействия колес на железнодорожный путь

А. А. Кожемяченко 1, *, И. Б. Петров 1, 2, А. В. Фаворская 1, 2, 3, Н. И. Хохлов 1, 2

1 МФТИ
141701 М.о., Долгопрудный, Институтский пер., 9, Россия

2 НИИСИ РАН
117218 Москва, Нахимовский пр-т, 36, к. 1, Россия

3 НИЦ “Курчатовский институт”
123182 Москва, пл. Акад. Курчатова, 1, Россия

* E-mail: anton-kozhemyachenko@yandex.ru

Поступила в редакцию 04.10.2019
После доработки 12.12.2019
Принята к публикации 09.04.2020

Полный текст (PDF)

Аннотация

Работа посвящена численному моделированию распределения динамической нагрузки по железнодорожному пути при движении тяжеловесных железнодорожных составов. Железнодорожный путь представлен как многослойная линейно-упругая среда. Решается полная система уравнений, описывающая состояние линейно-упругого тела, и система уравнений механики сплошной среды. Используется сеточно-характеристический метод, позволяющий корректно описывать контактные и граничные условия. Получены аналитические выражения, учитывающие влияние на рельсы со стороны поврежденных колес, соответствующие граничные условия и выполнена их программная реализация. Библ. 60. Фиг. 15.

Ключевые слова: сеточно-характеристический метод, численное моделирование, система “колесо–рельс”.

1. ВВЕДЕНИЕ

Проблемами выявления дефектов элементов системы “рельс–колесо”, в том числе с применением компьютерного моделирования, занимаются многие научные группы в разных странах мира. Существуют разные подходы к моделированию воздействия ползунов на железнодорожные пути. Дадим краткую историю развития данного направления научных исследований в последние годы. Ползуны возникают из-за скольжения колес во время торможения в условиях плохого сцепления с проходимым участком железнодорожного пути. На круговой поверхности катания появляется плоское место, вызванное сильным торможением, при котором колеса заклиниваются, т.е. перестают вращаться и ползут по рельсам. В [1] использованы пространственно-временные модели взаимодействия колесо–вагон для предсказания ударных сил, обусловленных ползунами, представлены результаты экспериментов с неисправным основанием внутри направляющей рельс, показана обратная зависимость размера ползуна и заданного диаметра колеса. Аналогичный подход к моделированию был использован в [2]. В [3] проведено сравнение результатов измерений с результатами расчетов при помощи метода конечных элементов системы “колесо–рельс”, которое выявило достаточно хорошее соответствие для скоростей до 120 км/ч. Численные методы для задач контактной механики, такие как транспонирование матриц и вариационные методы, могут быть использованы для негерцианских задач [4]. Эти методы были адаптированы в [5] для приложения к реальным системам “рельс–колесо”. Однако все они базируются на предположении, что упругое поведение контактирующих тел может быть аппроксимировано упругим полупространством [4]. В предлагаемом методе рассматривается гетерогенная линейно-упругая среда, состоящая из рельсов, шпал, воздушного пространства между шпалами, насыпи и геологической среды под насыпью, в которой проводится полноволновое моделирование. В [6] рассмотрен эффект изменения окружности колеса, в том числе и ползунов, показано, что необходим более точный критерий замены дефектных колес, основанный на ударных нагрузках. В [7] контакт “колесо–рельс” был изучен с помощью метода конечных элементов (FEM) и теории Герца. В [8] был предложен гибридный метод, в котором контактная сила определялась в интегральной области с помощью простой модели системы “рельс–колесо”. Для того чтобы учесть значительные поверхностные дефекты, такие как ползуны, требуется более детализированная модель контакта. В [9] была использована численная негерцианская модель контакта с помощью табличного метода с целью изучения ударов от ползунов. Трудность применения предложенного подхода связана с тем, что требуемый диапазон варьирования огромен, а точность табличных данных нужна очень высокая. В [10] и [11] проанализировано влияние геометрии ползуна на ударную силу, предложено использовать минимум кривизны колеса как более подходящий параметр для классификации ползунов, чем длина и глубина плоского участка. В [11] рассмотрены разные этапы роста ползуна на колесе, и в том числе соответствующие траектории центра колеса и изменение их частот. В [12] показано, что неровность имеет незначительное влияние на очевидное распределение контактного давления для железнодорожного транспорта при типичных нагрузках. В [13] минимум радиуса кривизны двух контактирующих поверхностей очень близок к большей полуоси контактного участка, при этом модель контакта, основанная на полупространстве, находится в хорошем соответствии с конечно-элементной моделью. В [14] задача динамического контакта между колесом и рельсами была промоделирована с помощью 3D конечно-элементной модели. Данная модель сравнивалась с моделью Герца и моделью контакта [15] для квазистатических случаев. В большинстве работ колесо чаще всего упрощается до негибкого жесткого тела, улучшенные модели колесных пар предполагались для расчета ударной силы плоского участка колеса [16]. Влияние модели гибкой колесной пары было обнаружено в основном на временные силы после удара по причине наличия ползуна. Гибкость колесной пары, как было обнаружено в [17], также влияет на поведение транспортного средства при движении. В [18] предложена эффективная пространственно-временная модель взаимодействия колесо-вагон. В [19] пространственно-временная модель взаимодействия системы “колесо–рельс” вместе с численной негерцианской моделью контакта используются для предсказания вибраций и шумов от ударов ползунов. В [20] с использованием уравнений Уфлянда–Миндлина для ортотропной пластинки, имеющей цилиндрическую анизотропию, произведен расчет поведения рельса под динамической нагрузкой, вызванной движением колеса (без дефектов). В [21] проведен аналитический расчет процесса воздействия колеса с множественными ползунами на путь на основе оценки частотной характеристики динамической системы и с учетом случайной природы процесса. В работе [22] исследованы динамические воздействия, которые испытывает конструкция верхнего строения железнодорожного пути при наличии дефектов в колесных парах. На основе модели контакта колесо – рельс определены наибольшие напряжения, возникающие в рельсе при наличии дефектов колеса (ползун, навар), а также величины критических трещин в зависимости от размеров дефекта колеса. Использовались аналитические соотношения, выведенные на основе теории Герца–Беляева. Колесо и рельс находятся в контакте на площади по причине локальных изгибов под нормальной нагрузкой. Для плоскостей контакта, которые могут быть определены в соответствии с гиперболической формой, может быть применена теория Герца для задач нормального контакта с нелинейной жесткостью, которая зависит от радиусов кривизны двух плоскостей [23]. Ползуны слишком крупные, чтобы рассматривать их как незначительные неровности, и это делает контакт негерцианским, что учтено в аналитических выражениях, полученных авторами, и в предложенном гибридном подходе к моделированию дальнейшего распространения волновых процессов в ж/д пути. В [24] рассмотрены различные типы дефектов, вызывающие вибрации, а железнодорожный путь моделируется приближенной моделью с сосредоточенной массой, lumped mass model (CLM), а для моделирования волновых процессов в грунте используется метод конечных элементов. В настоящей работе авторами предложено рассматривать всю гетерогенную структуру железнодорожного пути как упругое тело и рассчитывать все сопутствующие волновые процессы.

В последние годы исследования также ведутся в следующих направлениях. В [25] с помощью метода конечных элементов проводилась оценка остаточных напряжений в рельсовом колесе, вызванных полем напряжений от процесса термообработки железнодорожного колеса. В [26] был проведен набор тестов на основе контактных дисков, измеряющих коэффициент трения, который фокусируется на влиянии условий окружающей среды (относительной влажности и температуры). Кроме того, изучалось влияние оксидов железа, листьев и смесей гликоля/воды на коэффициент трения. Когда можно предсказать распространение трещин и скорость износа, оптимизация обслуживания может быть модернизирована, и могут быть разработаны экономически эффективные меры. В [27] предложено развитие модели распространения трещины, которая может применяться как для железнодорожных колес, так и для рельсов. Два неизвестных параметра материала в модели были откалиброваны по измерениям трещины на голландских железных дорогах в течение 5 лет. Метод расчета системы “рельс–колесо”, предложенный автором, предполагает возможность реализации различных моделей распространения трещин и от импульсных нагрузок, и от циклических. В [28] исследование изменения напряженного состояния железнодорожного колеса в процессе эксплуатации было проведено при помощи метода конечных элементов в ПО NX NASTRAN. В последние годы исследования ведутся по разным направлениям. В первую очередь, это физическое моделирование [29], моделирование качения колеса [30], а также разнообразные аналитические подходы [31], [32]. В [33] предложена трехмерная модель колеса с учетом длины, ширины и глубины ползуна, разработана динамическая модель высокоскоростного рельсового соединения для исследования влияния колеса на динамику системы “рельс–колесо”. Предложенный подход представлен и для 2D, и для 3D моделей ползунов и позволяет провести аналогичные исследования. В [34] исследования повреждений колес проводились на модельных роликах и предложена методика пересчета повреждений модельных роликов на железнодорожные колесные пары.

Авторами были предложены аналитические выражения для расчета пространственно-временного распределения давления неповрежденных колес на рельс, и колес с повреждениями различной степени. Железнодорожный путь при этом рассматривается как гетерогенная линейно-упругая среда, что позволяет более детально учитывать контактное взаимодействие ж/д пути с поврежденными и неповрежденными колесами поезда. Для расчета волновых процессов в ж/д пути применен сеточно-характеристический метод, ранее применявшийся в [35]–[39]. Ранее данный численный метод успешно применялся для решения задач сейсмики [40], сейсмической разведки [41]–[45], разрушения объектов под динамическими нагрузками [46]–[50] и неразрушающего контроля [51]–[53]. Сеточно-характеристический метод позволяет проводить высокоточное полноволновое моделирование всего динамического процесса движения подвижного состава с дефектами колес (ползун). Было разработано специальное граничное условие, учитывающее три стадии взаимодействия поврежденного колеса с ж/д путями. Для решения данного типа задач сеточно-характеристический метод используется впервые. Следует отметить, что для решения этого класса задач с применением разработанного авторами граничного условия могут быть использованы также другие методы, позволяющие моделировать волновые процессы во временной области. Например, разрывный метод Галеркина [54], метод спектральных элементов [55], псевдоспектральный метод [56], различные вариации конечно-разностных методов во временной области (FDTD, finite-difference method in the time domain) [57], [58] и конечно-разностный метод на сдвинутых сетках (SDFD, staggered-grid finite differences) [59], явные и неявные безматричные алгоритмы метода конечных элементов на основе сопряженных градиентов с учетом контактных взаимодействий [60].

2. ПОСТАНОВКА ЗАДАЧИ

В работе решается следующая система уравений для моделирования распространения упругих волн:

(2.1)
${\rho }\frac{{\partial {\mathbf{V}}}}{{\partial t}} = {{\left( {\nabla \cdot {\mathbf{\sigma }}} \right)}^{{\text{т}}}},$
(2.2)
$\frac{{\partial {\mathbf{\sigma }}}}{{\partial t}} = \frac{{\nu }}{{1 - 2{\nu }}}\frac{E}{{1 + {\nu }}}\left( {\nabla \cdot {\mathbf{V}}} \right){\mathbf{I}} + \frac{1}{2}\frac{E}{{1 + {\nu }}}\left( {\nabla \otimes {\mathbf{V}} + {{{\left( {\nabla \otimes {\mathbf{V}}} \right)}}^{{\text{т}}}}} \right),$
где ${\rho }$ − плотность материала, ${\mathbf{V}}$ − скорость бесконечно-малого элемента материала, ${\mathbf{\sigma }}$ − тензор напряжений Коши, $E$ − модуль Юнга, ${\nu }$ − коэффициент Пуассона.

Скорость распространения продольных P-волн и поперечных S-волн в материале определяется выражениями:

(2.3)
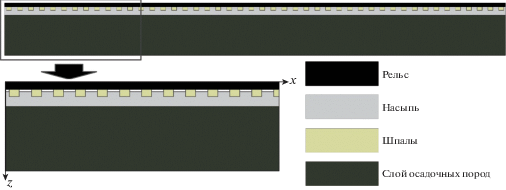
${{c}_{{\text{P}}}} = \sqrt {\frac{{1 - {\nu }}}{{1 - 2{\nu }}}\frac{E}{{1 + {\nu }}}\frac{1}{{\rho }}} ,$
(2.4)
${{c}_{{\text{S}}}} = \sqrt {\frac{1}{2}\frac{E}{{1 + {\nu }}}\frac{1}{{\rho }}} .$

Модель железнодорожного пути и области интегрирования изображены на фиг. 1. Упругие характеристики материалов приведены в табл. 1. Части железнодорожного пути, состоящие из разных материалов, помечены разными цветами: черный цвет (рельсы, сталь), светло-серый цвет (ж/д насыпь, гравий), бежевый цвет (ж/д шпалы, дерево) и темно-зеленый цвет (слой осадочных пород, геологическая порода под ж/д насыпью). Белый цвет соответствует воздуху.

Фиг. 1.

Железнодорожный путь.

Таблица 1.  

Параметры упругости сред в составе железнодорожного пути

Часть ж/д пути Материал Скорость распространения P-волн, м/с Скорость распространения S-волн, м/с Плотность, кг/м3
Рельсы Сталь 5740 3092 7800
Ж/д насыпь Гравий 1000 500 400
Шпалы Дерево 800 400 2000
Слой осадочных пород Геологическая порода 2000 1000 2000

В данной постановке была аналитически рассчитана в соответствии с формулами, приведенными ниже, пространственная динамическая нагрузка на железнодорожный путь со стороны колес без дефектов и со стороны колес с ползунами. Применяется сеточно-характеристический метод на структурированных сетках. Использовались следующие параметры дискретизации: шаг по времени $\tau = 8.5 \times {{10}^{{ - 7}}}$ c, координатный шаг по вертикали ${{h}_{y}} = 0.005$ м, координатный шаг вдоль направления движения поезда ${{h}_{x}} = 0.01$ м.

3. СЕТОЧНО-ХАРАКТЕРИСТИЧЕСКИЙ МЕТОД

Для численного решения систем уравнений (2.1), (2.2) применяется сеточно-характеристический метод. С его помощью можно строить корректные численные алгоритмы для расчета граничных точек и точек контактирующих сред, имеющих разные параметры Ламе и/или плотности. Систему в двумерном случае можно представить в виде

(3.1)
${{{\mathbf{q}}}_{t}} + {{{\mathbf{A}}}_{1}}{{{\mathbf{q}}}_{x}} + {{{\mathbf{A}}}_{2}}{{{\mathbf{q}}}_{y}} = 0.$

Далее производится расщепление по двум направлениям и получается выражение вида

(3.2)
${{{\mathbf{q}}}_{t}} + {{{\mathbf{A}}}_{1}}{{{\mathbf{q}}}_{x}} = 0,$
для которого справедливо точное выражение
(3.3)
${\mathbf{q}}\left( {x,y,t + \tau } \right) = \sum\limits_{j = 1}^J {{\mathbf{X}}_{j}^{1}{\mathbf{q}}(x - c_{j}^{1}\tau ,y,t)} ,$
(3.4)
$\sum\limits_{j = 1}^J {{\mathbf{X}}_{j}^{1}} = {\mathbf{I}},$
где ${\mathbf{X}}_{j}^{1}$ – некие матрицы, выражающиеся через компоненты матрицы ${{{\mathbf{A}}}_{1}}$, $c_{j}^{1}$ – собственные значения матрицы ${{{\mathbf{A}}}_{1}}$, $\tau $ – шаг интегрирования по времени, $J$ – количество собственных значений матрицы ${{{\mathbf{A}}}_{1}}$. Если у матрицы ${{{\mathbf{A}}}_{1}}$ существуют множества отрицательных, нулевых и положительных собственных значений ${{J}^{ - }}$, ${{J}^{0}}$, ${{J}^{ + }}$ соответственно и выполнено (3.4), то, выражая ${\mathbf{X}}_{j}^{1}$, соответствующие нулевым собственным значениям, получаем
(3.5)
$\sum\limits_{j \in {{J}^{0}}}^{} {{\mathbf{X}}_{j}^{1} = {\mathbf{I}} - \sum\limits_{j \in {{J}^{ - }}}^{} {{\mathbf{X}}_{j}^{1} - } } \sum\limits_{j \in {{J}^{ + }}}^{} {{\mathbf{X}}_{j}^{1}} .$
Как следствие этого получаем для (3.3) эквивалентное представление:

(3.6)
${\mathbf{q}}\left( {x,y,t + \tau } \right) = {\mathbf{q}}\left( {x,y,t} \right) + \sum\limits_{j \in {{J}^{ + }} \cup {{J}^{ - }}} {{\mathbf{X}}_{j}^{1}({\mathbf{q}}(x - c_{j}^{1}\tau ,y,t) - {\mathbf{q}}(x,y,t))} .$

Матрица ${{{\mathbf{A}}}_{1}}$ гиперболическая, у нее существует набор собственных векторов, и она представима в виде

(3.7)
${{{\mathbf{A}}}_{1}} = {{{\mathbf{\Omega }}}^{1}}{{{\mathbf{\Lambda }}}^{1}}{{({{{\mathbf{\Omega }}}^{1}})}^{{ - 1}}},$
где матрица ${{{\mathbf{\Omega }}}^{1}}$ составлена из собственных векторов, а собственные значения матрицы ${{{\mathbf{A}}}_{1}}$ есть элементы диагональной матрицы ${{{\mathbf{\Lambda }}}^{1}}$. Теперь уравнение (3.2) запишем в виде:

(3.8)
${{{\mathbf{q}}}_{t}} + {{{\mathbf{\Omega }}}^{1}}{{{\mathbf{\Lambda }}}^{1}}{{({{{\mathbf{\Omega }}}^{1}})}^{{ - 1}}}{{{\mathbf{q}}}_{x}} = 0.$

Вычисления, проводящиеся в соответствии с формулой (3.6), разбиваются на три стадии. На первой стадии проводится умножение всех векторов $\vec {q}\left( {x,y,t} \right)$ на матрицу ${{{\mathbf{\Omega }}}^{1}}$, на второй стадии находится выражение в двумерном случае, а на третьей стадии делается обратная замена:

(3.9)
$\vec {\omega }\left( {x,y,t} \right) = {{({{{\mathbf{\Omega }}}^{1}})}^{{ - 1}}}{\mathbf{q}}\left( {x,y,t} \right),$
(3.10)
$\vec {\omega }\left( {x,y,t + \tau } \right) = \vec {\omega }\left( {x,y,t} \right) + \sum\limits_{j \in {{J}^{ + }} \cup {{J}^{ - }}} {\vec {\omega }(x - c_{j}^{1}\tau ,y,t) - \vec {\omega }\left( {x,y,t} \right)} ,$
(3.11)
$\vec {q}\left( {x,y,t} \right) = {{{\mathbf{\Omega }}}^{1}}\vec {\omega }\left( {x,y,t} \right).$

4. ИЗОТРОПНЫЕ ЛИНЕЙНО-УПРУГИЕ СРЕДЫ

Рассмотрим для определенности направление $x$. Пусть вектор $\vec {n}$ направлен вдоль выбранного направления, а вектор ${{\vec {n}}_{1}}$ образует с ним декартову систему координат. Введем симметричные тензоры второго ранга

(4.1)
${{{\mathbf{N}}}_{{ij}}} = \frac{1}{2}\left( {{{n}_{i}} \otimes {{n}_{j}} + {{n}_{j}} \otimes {{n}_{i}}} \right),$
где индексы варьируются от 0 до 1, а под ${{\vec {n}}_{0}}$ понимается вектор $\vec {n}$.

Действие матрицы ${{{\mathbf{A}}}_{1}}$ на вектор неизвестных, задаваемых соотношением

(4.2)
$\vec {q} = \left[ {\begin{array}{*{20}{c}} {{\vec {v}}} \\ {\mathbf{\sigma }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{{v}}_{1}}} \\ {{{{v}}_{2}}} \\ {{{\sigma }_{{11}}}} \\ {{{\sigma }_{{22}}}} \\ {{{\sigma }_{{12}}}} \end{array}} \right],$
записывается в виде

(4.3)
${{{\mathbf{A}}}_{1}}\left[ {\begin{array}{*{20}{c}} {{\vec {v}}} \\ {\mathbf{\sigma }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{1}{\rho }\left( {{\mathbf{\sigma }} \cdot \vec {n}} \right)} \\ {\lambda \left( {\vec {n} \cdot {\vec {v}}} \right){\mathbf{I}} + \mu \left( {\vec {n} \otimes {\vec {v}} + {\vec {v}} \otimes \vec {n}} \right)} \end{array}} \right].$

Матрицы ${{{\mathbf{A}}}_{1}}$ и ${{{\mathbf{A}}}_{2}}$ имеют набор собственных значений

(4.4)
$\left\{ {{{с}_{p}}, - {{c}_{p}},{{c}_{s}}, - {{c}_{s}},0} \right\}.$

Действие матрицы ${{({{{\mathbf{\Omega }}}^{1}})}^{{ - 1}}}$ на вектор неизвестных (4.2) можно представить в виде

(4.5)
${{\omega }_{{1,2}}} = {{\left( {{{{\left( {{{{\mathbf{\Omega }}}^{1}}} \right)}}^{{ - 1}}}\left[ {\begin{array}{*{20}{c}} {{\vec {v}}} \\ {\mathbf{\sigma }} \end{array}} \right]} \right)}_{{1,2}}} = \vec {n} \cdot {\vec {v}} \mp \frac{1}{{{{c}_{p}}\rho }}{{{\mathbf{N}}}_{{00}}} \div {\mathbf{\sigma }},$
(4.6)
${{\omega }_{{3,4}}} = \vec {n} \cdot {\vec {v}} \mp \frac{1}{{{{c}_{s}}\rho }} \cdot {{{\mathbf{N}}}_{{01}}} \div {\mathbf{\sigma }},$
(4.7)
${{\omega }_{5}} = \left( {{{{\mathbf{N}}}_{{11}}} - \frac{\lambda }{{\lambda + 2\mu }}{{{\mathbf{N}}}_{{00}}}} \right) \div {\mathbf{\sigma }}.$

Действие матрицы ${{{\mathbf{\Omega }}}^{1}}$ из (3.11) следующее:

(4.8)
$\left[ {\begin{array}{*{20}{c}} {{\vec {v}}} \\ {\mathbf{\sigma }} \end{array}} \right] = {{{\mathbf{\Omega }}}^{1}}\vec {\omega } = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {({{\omega }_{1}} + {{\omega }_{2}})\vec {n} + \left( {{{\omega }_{3}} + {{\omega }_{4}}} \right){{{\vec {n}}}_{1}}} \\ {\left( {{{\omega }_{2}} - {{\omega }_{1}}} \right)\left( {\rho \left( {{{c}_{p}} - {{c}_{3}}} \right){{{\mathbf{N}}}_{{00}}} + \rho {{c}_{3}}{\mathbf{I}}} \right) + 2\rho {{c}_{s}}\left( {{{\omega }_{4}} - {{\omega }_{3}}} \right){{{\mathbf{N}}}_{{01}}} + 2{{\omega }_{5}}\left( {{\mathbf{I}} - {{{\mathbf{N}}}_{{00}}}} \right)} \end{array}} \right],$
где через ${{c}_{3}}$ обозначена величина

(4.9)
${{с}_{3}} = \frac{\lambda }{{\lambda + 2\mu }}{{c}_{p}}.$

5. АНАЛИТИЧЕСКИЕ ВЫРАЖЕНИЯ ДЛЯ МОДЕЛИРОВАНИЯ ДИНАМИЧЕСКОЙ НАГРУЗКИ ЖЕЛЕЗНОДОРОЖНОГО СОСТАВА НА РЕЛЬСЫ

Для моделирования динамической нагрузки движущегося ж/д состава на рельсы используются граничные условия заданной плотности внешних сил на головку рельса в соответствии со следующими формулами:

(5.1)
${\mathbf{\sigma }} \cdot {\mathbf{n}} = {\mathbf{f}}\left( {x,t} \right),$
(5.2)
${{x}_{{{\text{TRAIN}}}}}\left( {x,t} \right) = x - {{x}_{0}} - {{V}_{{{\text{TRA}}{\text{IN}}}}}\left( {t - {{t}_{{{\text{SMOOTH}}}}}} \right),$
(5.3)
${{d}_{1}}\left( {x,t} \right) = {{x}_{{{\text{TRAIN}}}}}\left( {x,t} \right) - \frac{{{{L}_{{{\text{TRAIN}}}}}}}{2} - \frac{{{{H}_{{{\text{TRAIN}}}}}}}{2},$
(5.4)
${{d}_{2}}\left( {x,t} \right) = {{x}_{{{\text{TRAIN}}}}}\left( {x,t} \right) - \frac{{{{L}_{{{\text{TRAIN}}}}}}}{2} + \frac{{{{H}_{{{\text{TRAIN}}}}}}}{2},$
(5.5)
${{d}_{3}}\left( {x,t} \right) = {{x}_{{{\text{TRAIN}}}}}\left( {x,t} \right) + \frac{{{{L}_{{{\text{TRAIN}}}}}}}{2} - \frac{{{{H}_{{{\text{TRAIN}}}}}}}{2},$
(5.6)
${{d}_{4}}\left( {x,t} \right) = {{x}_{{{\text{TRAIN}}}}}\left( {x,t} \right) + \frac{{{{L}_{{{\text{TRAIN}}}}}}}{2} + \frac{{{{H}_{{{\text{TRAIN}}}}}}}{2},$
(5.7)
${\mathbf{f}}\left( {x,t} \right) = {{f}_{0}}\left( {\frac{1}{2} + \frac{{{{d}_{I}}\left( {x,t} \right)}}{{{{N}_{{{\text{STEPS}}}}}h}},t} \right){\mathbf{n}},\quad \left| {{{d}_{I}}\left( {x,t} \right)} \right| \leqslant \frac{{{{N}_{{{\text{STEPS}}}}}h}}{2},\quad I = 1,\;2,\;3,\;4,$
(5.8)
${{f}_{0}}\left( {x,t} \right) = - {{k}_{{{\text{SMOOTH}}}}}\left( t \right){{k}_{{{\text{GRID}}}}}\left( x \right){{P}_{0}},$
(5.9)
${{k}_{{{\text{SMOOTH}}}}}\left( t \right) = \left\{ \begin{gathered} 0,\quad t < 0, \hfill \\ \frac{t}{{{{T}_{{{\text{SMOOTH}}}}}}},\quad t \in \left[ {0,{{T}_{{{\text{SMOOTH}}}}}} \right] \hfill \\ 1,\quad t > {{T}_{{{\text{SMOOTH}}}}}, \hfill \\ \end{gathered} \right.,$
(5.10)
${{k}_{{{\text{GRID}}}}}\left( x \right) = \left\{ \begin{gathered} 0,\quad x < 0, \hfill \\ \frac{x}{h},\quad x \in \left[ {0,h} \right], \hfill \\ 1,\quad x \in \left[ {h,\left( {{{N}_{{{\text{STEPS}}}}} - 1} \right)h} \right], \hfill \\ {{N}_{{{\text{STEPS}}}}} - \frac{x}{h},\quad x \in \left[ {\left( {{{N}_{{{\text{STEPS}}}}} - 1} \right)h,{{N}_{{{\text{STEPS}}}}}h} \right], \hfill \\ 0,\quad x > {{N}_{{{\text{STEPS}}}}}h, \hfill \\ \end{gathered} \right.$
(5.11)
${{P}_{0}} = {{k}_{{{\text{RADIUS}}}}}\sqrt[3]{{\frac{{{{k}_{{{\text{VIBR}}}}}{{m}_{{{\text{TRAIN}}}}}{{E}^{2}}}}{{{{N}_{{{\text{WHEEL}}}}}R_{{{\text{WHEEL}}}}^{2}}}}}.$

В выражениях (5.1)−(5.9) величина ${\mathbf{n}}$ − внешняя к границе нормаль, ${\mathbf{f}}$ − поверхностная плотность внешних сил, ${{d}_{I}}$, $I = 1,\;2,\;3,\;4$, − номер узла расчетной сетки в рельсе, на которую оказывает давление колесная пара с номером I, ${{V}_{{{\text{TRA}}{\text{IN}}}}}$ − скорость поезда в м/с, ${{x}_{0}}$ − начальное положение центра вагона или локомотива, ${{L}_{{{\text{TRAIN}}}}}$, ${{H}_{{{\text{TRAIN}}}}}$ − геометрические параметры поезда, приведенные на фиг. 2, ${{x}_{{{\text{TRAIN}}}}}$ − положение центра вагона или локомотива в момент времени t, ${{N}_{{{\text{STEPS}}}}}$ − число узлов по пространственной координате в расчетной сетке, в которых колесо давит на рельс, $h$ − шаг по координате, x – координата вдоль направления движения поезда.

Фиг. 2.

Вагон или локомотив.

Коэффициенты ${{k}_{{{\text{SMOOTH}}}}}$ и ${{T}_{{{\text{SMOOTH}}}}}$ используются для моделирования медленного возрастания давления поезда на рельсы от нуля до финального значения. Если не использовать коэффициент ${{k}_{{{\text{SMOOTH}}}}}$, то вычисления будут произведены для поезда, рывком установленного на рельсы за время ${\tau }$. Предполагается ${{T}_{{{\text{SMOOTH}}}}} = 40\,000 \cdot {\tau = 0}{\text{.34}}$ c, ${\tau }$ − шаг по времени. Движение поезда начинается в момент ${{T}_{{{\text{SMOOTH}}}}}$.

В выражениях (5.8), (5.11) ${{P}_{0}}$ − давление одного неповрежденного колеса, ${{k}_{{{\text{VIBR}}}}}$ − коэффициент, характеризующий систему амортизации, ${{m}_{{{\text{TRAIN}}}}}$ − масса вагона или локомотива, $E$ − модуль, ${{N}_{{{\text{WHEEL}}}}}$ − число колес вагона или локомотива, ${{R}_{{{\text{WHEEL}}}}}$ − радиус колес. Давление ${{P}_{0}}$ рассчитывается в соответствии с методом, предложенным в [32], с ${{k}_{{{\text{RADIUS}}}}} = 5\;860$. Можно использовать другие приближения для оценки давления неповрежденного колеса.

Варьируя данные параметры, можно учитывать разные типы вагонов и локомотивов. Для  иллюстраций ниже, масса вагона бралась равной 90 т, ${{L}_{{{\text{TRAIN}}}}} = 10$ м, ${{H}_{{{\text{TRAIN}}}}} = 1.85$ м, ${{R}_{{{\text{WHEEL}}}}} = 0.475$ м, ${{P}_{0}} = 188$ МПа, ${{N}_{{{\text{STEPS}}}}} = 5$ и $V{}_{{{\text{TRA}}{\text{IN}}}}$, равной 120 и 15 км/ч.

6. АНАЛИТИЧЕСКИЕ ВЫРАЖЕНИЯ ДЛЯ РАСЧЕТА ВЛИЯНИЯ ПОВРЕЖДЕННОГО КОЛЕСА НА РЕЛЬСЫ

Для моделирования влияния поврежденного колеса с ползуном на рельсы используются граничные условия с заданной плотностью внешних сил. Можно найти плотность внешних сил колесной пары поезда с ползуном и номером ${{I}_{{FLAT\_SPOT}}}$, используя следующие аналитические выражения:

(6.1)
${\mathbf{f}}\left( {x,t} \right) = {{f}_{{{\text{FLAT\_SPOT}}}}}\left( {\frac{1}{2} + \frac{{{{d}_{I}}\left( {x,t} \right)}}{{{{L}_{{{\text{CONTACT}}}}}\left( t \right)}},t} \right){\mathbf{n}},\quad \left| {{{d}_{I}}\left( {x,t} \right)} \right| \leqslant \frac{{{{L}_{{{\text{CONTACT}}}}}\left( t \right)}}{2},\quad I = {{I}_{{FLAT\_SPOT}}},$
(6.2)
${{f}_{{{\text{FLAT\_SPOT}}}}}\left( {x,t} \right) = - {{k}_{{{\text{SMOOTH}}}}}\left( t \right){{k}_{{{\text{GRID\_FLAT\_SPOT}}}}}\left( x \right)\left( {{{P}_{0}} + {{P}_{{{\text{FLAT\_SPOT}}}}}\left( {x,t} \right)} \right),$
(6.3)
${{k}_{{{\text{GRID\_FLAT\_SPOT}}}}}\left( x \right) = \left\{ \begin{gathered} 0,\quad x < 0, \hfill \\ \frac{x}{h},\quad x \in \left[ {0,h} \right], \hfill \\ 1,\quad x \in \left[ {h,{{L}_{{{\text{CONTACT}}}}}\left( t \right) - h} \right], \hfill \\ \frac{{{{L}_{{{\text{CONTACT}}}}}\left( t \right) - x}}{h},\quad x \in \left[ {{{L}_{{{\text{CONTACT}}}}}\left( t \right) - h,{{L}_{{{\text{CONTACT}}}}}\left( t \right)} \right], \hfill \\ 0,\quad x > {{L}_{{{\text{CONTACT}}}}}\left( t \right), \hfill \\ \end{gathered} \right.$
(6.4)
${{L}_{{{\text{CONTACT}}}}}\left( t \right) = {\text{MAX}}\left\{ {{{L}_{{{\text{CONTACT\_FLAT\_SPOT}}}}}\left( t \right),{{N}_{{{\text{STEPS}}}}}h} \right\},$
(6.5)
${{L}_{{{\text{CONTACT\_FLAT\_SPOT}}}}}\left( t \right) = \left\{ \begin{gathered} 0,\quad t < {{t}_{0}}, \hfill \\ L_{{{\text{CONTACT\_FLAT\_SPOT}}}}^{0}\left( t \right),\quad t \in \left[ {{{t}_{0}},{{t}_{2}}} \right] \hfill \\ 0,\quad t > {{t}_{2}}, \hfill \\ \end{gathered} \right.,$
(6.6)
$L_{{{\text{CONTACT\_FLAT\_SPOT}}}}^{0}\left( t \right){\text{ = }}\left\{ \begin{gathered} {{L}_{{{\text{FLAT\_SPOT}}}}},\quad {\alpha }\left( t \right) \leqslant {{{\alpha }}_{{{\text{CR}}}}}, \hfill \\ \frac{{\varepsilon }}{{\tan \left( {{\alpha }\left( t \right)} \right)}},\quad {\alpha }\left( t \right) > {{{\alpha }}_{{{\text{CR}}}}}, \hfill \\ \end{gathered} \right.$
(6.7)
${{L}_{{{\text{FLAT\_SPOT}}}}} = 2{{R}_{{{\text{WHEEL}}}}}\sin {{{\alpha }}_{0}},$
(6.8)
${{{\alpha }}_{{{\text{CR}}}}} = \arctan \left( {\frac{{\varepsilon }}{{{{L}_{{{\text{FLAT\_SPOT}}}}}}}} \right),$
(6.9)
${{P}_{{{\text{FLAT\_SPOT}}}}}\left( {x,t} \right) = \left\{ \begin{gathered} 0,\quad t < {{t}_{0}}, \hfill \\ P_{{{\text{FLAT\_SPOT}}}}^{0}\left( {L_{{{\text{CONTACT\_FLAT\_SPOT}}}}^{0}\left( t \right),t} \right),\quad t \in \left[ {{{t}_{0}},{{t}_{1}}} \right], \hfill \\ {{k}_{{{\text{SMOOTH\_IMPACT}}}}}\left( t \right)P_{{{\text{FLAT\_SPOT}}}}^{0}\left( {{{L}_{{{\text{FLAT\_SPOT}}}}},{{t}_{1}}} \right),\quad t > {{t}_{1}} \hfill \\ \end{gathered} \right.$
(6.10)
$P_{{{\text{FLAT\_SPOT}}}}^{0}\left( {L,t} \right) = {{c}_{{{\text{P,RAIL}}}}}{{{\rho }}_{{{\text{RAIL}}}}}{{V}_{{{\text{IMPACT}}}}}\left( {L,t} \right),$
(6.11)
${{V}_{{{\text{IMPACT}}}}}\left( {L,t} \right) = L\left( {{\omega } + \frac{{{\beta }{{{\left( {t - {{t}_{0}}} \right)}}^{2}}}}{2}} \right),\quad t \in \left[ {{{t}_{0}},{{t}_{1}}} \right],$
(6.12)
${{k}_{{{\text{SMOOTH\_IMPACT}}}}}\left( t \right) = \left\{ \begin{gathered} 1 - \frac{{t - {{t}_{1}}}}{{{{t}_{{{\text{SMOOTH\_IMPACT}}}}}}},\quad t \in \left[ {{{t}_{1}},{{t}_{1}} + {{t}_{{{\text{SMOOTH\_IMPACT}}}}}} \right], \hfill \\ 0,\quad t > {{t}_{1}} + {{t}_{{{\text{SMOOTH\_IMPACT}}}}}, \hfill \\ \end{gathered} \right.$
(6.13)
${{t}_{{{\text{SMOOTH\_IMPACT}}}}} = \frac{{2{{H}_{{{\text{RAIL}}}}}}}{{{{c}_{{{\text{P,RAIL}}}}}}},$
(6.14)
${{{\alpha }}_{0}} = \arccos \left( {1 - \frac{{{{H}_{{{\text{FLAT\_SPOT}}}}}}}{{{{R}_{{{\text{WHEEL}}}}}}}} \right),$
(6.15)
${\omega } = \frac{{V{}_{{{\text{TRAIN}}}}}}{{{{R}_{{{\text{WHEEL}}}}}}},$
(6.16)
${\beta } = \frac{{V{}_{{{\text{TRA}}{\text{IN}}}}}}{{{{J}_{{{\text{WHEEL}}}}}}}\frac{{{{k}_{{{\text{VIBR}}}}}{{m}_{{{\text{TRAIN}}}}}g}}{{{{N}_{{{\text{WHEEL}}}}}}},$
(6.17)
${\alpha }\left( t \right) = \left\{ \begin{gathered} {{{\alpha }}_{0}} - {\omega }\left( {t - {{t}_{0}}} \right) - \frac{{{\beta }{{{\left( {t - {{t}_{0}}} \right)}}^{3}}}}{6},\quad t \in \left[ {{{t}_{0}},{{t}_{1}}} \right], \hfill \\ {{{\alpha }}_{0}} + {\omega }\left( {t - {{t}_{2}}} \right),\quad t \in \left[ {{{t}_{1}},{{t}_{2}}} \right], \hfill \\ \end{gathered} \right.$
(6.18)
${{{\alpha }}_{0}} = {\omega }\Delta {{t}_{1}} + \frac{{{\beta }{{{\left( {\Delta {{t}_{1}}} \right)}}^{3}}}}{6},$
(6.19)
${{t}_{0}} = {{T}_{{{\text{SMOOTH}}}}} + \frac{{{{x}_{{{\text{FLAT\_SPOT}}}}}}}{{V{}_{{{\text{TRAIN}}}}}} + \frac{{2{\pi }}}{{\omega }}t,\quad {{x}_{{{\text{FLAT\_SPOT}}}}} \in \left[ {0,\;2\pi {{R}_{{{\text{WHEEL}}}}}} \right],$
(6.20)
${{t}_{1}} = {{t}_{0}} + \Delta {{t}_{1}},$
(6.21)
${{t}_{2}} = {{t}_{1}} + \frac{{{{{\alpha }}_{0}}}}{{\omega }}.$

В выражениях (6.6), (6.8) ε − малая длина, при которой колесо и рельсы считаются соприкасающимися; она бралась равной 1 мм. В выражениях (6.7), (6.14) ${{H}_{{{\text{FLAT\_SPOT}}}}}$ − глубина ползуна. В приведенных ниже расчетах ${{H}_{{{\text{FLAT\_SPOT}}}}} = 2$ мм, ${{L}_{{{\text{FLAT\_SPOT}}}}}$ − длина ползуна. Фото колесной пары с ползуном изображено на фиг. 3.

Фиг. 3.

Колесная пара с ползуном.

В выражениях (6.12), (6.13) ${{t}_{{{\text{SMOOTH\_IMPACT}}}}}$ − время возрастания давления, ${{H}_{{{\text{RAIL}}}}}$ − высота рельса, ${{c}_{{{\text{P,RAIL}}}}}$ − скорость Р-волн в материале рельса, ${{{\rho }}_{{{\text{RAIL}}}}}$ − плотность материала. В выражении (6.16) $g$ − ускорение свободного падения Земли, ${{J}_{{{\text{WHEEL}}}}}$ − момент инерции колесной пары, в данной работе предполагается ${{J}_{{{\text{WHEEL}}}}} = 553.55$ кг⋅м2. В выражении (6.19) ${{x}_{{{\text{FLAT\_SPOT}}}}}$ − координата на ободе колеса, соответствующая началу ползуна, ${{x}_{{{\text{FLAT\_SPOT}}}}}$= 0 мм. Значение $\Delta {{t}_{1}}$ задается выражением (6.18). Варьируя данные параметры, можно моделировать различные ситуации, например, местоположения ползунов на колесной паре, а также учитывать разные типы вагонов и локомотивов.

7. ОСОБЕННОСТИ РАСЧЕТА ДАВЛЕНИЯ КОЛЕС ПОДВИЖНОГО СОСТАВА НА РЕЛЬС

В данном разделе дается обоснование выражения (5.10). Для этого рассмотрим дискретизацию участка рельса, приведенную на фиг. 4а. Пусть колесо уже взаимодействует с ячейкой 1 и еще не взаимодействует с ячейкой 2. На фиг. 4б колесо взаимодействует с ячейкой 2 и уже не взаимодействует с ячейкой 1. Тогда для фиг. 4а давление на ячейку 1 равняется P0, а давление на ячейку 2 равняется нулю. Для фиг. 4б давление на ячейку 2 равняется P0, а давление на ячейку 1 равняется 0. Распределения давлений в ячейках приведены на графиках в нижней части фигур, координата x направлена вдоль рельса.

Фиг. 4.

Дискретизация участка рельса, испытывающего давление колеса (сверху) и распределения давления (снизу) в разные моменты времени.

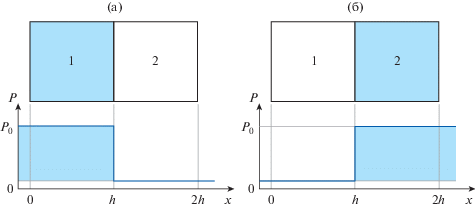
Рассмотрим переход колеса из положения на фиг. 4а в положение на фиг. 4б, т.е. ситуацию на фиг. 5а, на котором колесо давит на часть ячейки 2 с давлением P0, а на всю ячейку 2 – с давлением $\frac{a}{h}{{P}_{0}}$. Таким образом, для равномерной расчетной сетки получим зависимость давления от времени в каждой ячейке, приведенную на фиг. 5б и соответствующую выражению (34).

Фиг. 5.

Дискретизация перекатывания колеса с одного участка рельса на другой: а – распределение давления; б – итоговое распределение давления в каждой точке от времени.

8. РАСЧЕТ ПРОЦЕССА УДАРА КОЛЕСА С ПОЛЗУНОМ О РЕЛЬС

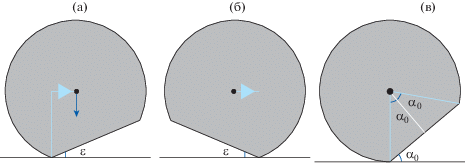
В данном разделе дается обоснование выражениям из разд. 6. Для их получения рассматриваются три этапа удара колеса с ползуном о рельс: поворот колеса вокруг точки начала ползуна, удар и поворот колеса вокруг точки окончания ползуна, приведенные на фиг. 6а и 6б соответственно. В выражениях из разд. 6 данные этапы соответствуют диапазонам $\left[ {{{t}_{0}},{{t}_{1}}} \right]$, $\left[ {{{t}_{1}},{{t}_{1}} + {{t}_{{{\text{SMOOTH\_IMPACT}}}}}} \right]$, $\left[ {{{t}_{1}},{{t}_{2}}} \right]$ соответственно. Можно выделить еще четвертый этап – этап проскальзывания. Он будет рассмотрен в данном разделе.

Фиг. 6.

Модель воздействия поврежденного колеса на рельс: а – первый этап удара колеса с ползуном о рельс; б – третий этап удара; в – простейшая геометрия ползуна.

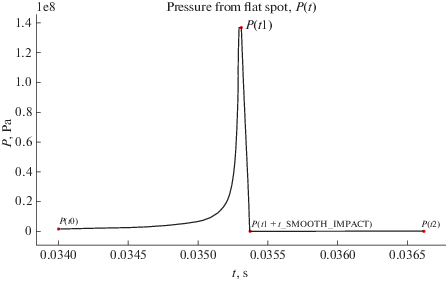
На фиг. 7 показана зависимость от времени дополнительного давления (6.9) из-за присутствия в колесе ползуна, где красными точками отмечены соответствующие величины в моменты времени ${{t}_{0}}$, ${{t}_{1}}$, ${{t}_{1}} + {{t}_{{{\text{SMOOTH\_IMPACT}}}}}$, ${{t}_{2}}$.

Фиг. 7.

Дополнительное давление вследствие дефекта в колесе.

При повороте колеса вокруг точки начала ползуна точка давления поезда постепенно смещается со скоростью движения поезда, формируя вращательный момент. При этом угловая скорость вращения колесной пары с ползуном будет удовлетворять следующему выражению:

(8.1)
${{J}_{{{\text{WHEEL}}}}}\frac{{\partial \omega }}{{\partial t}} = V{}_{{{\text{TRAIN}}}}\left( {t - {{t}_{0}}} \right)\frac{{{{k}_{{{\text{VIBR}}}}}{{m}_{{{\text{TRAIN}}}}}g}}{{{{N}_{{{\text{WHEEL}}}}}}}.$

Решением данного уравнения будет служить функция, заданная выражением, которое фигурирует в соотношениях (6.11), (6.17) (при $t \in \left[ {{{t}_{0}},{{t}_{1}}} \right]$) и (6.18):

(8.2)
$\omega \left( t \right) = \frac{{V{}_{{{\text{TRAIN}}}}}}{{{{J}_{{{\text{WHEEL}}}}}}}\frac{{{{k}_{{{\text{VIBR}}}}}{{m}_{{{\text{TRAIN}}}}}g}}{{{{N}_{{{\text{WHEEL}}}}}}}\frac{{{{{\left( {t - {{t}_{0}}} \right)}}^{2}}}}{2} + C.$

На основе выражения (8.2) находим величину ${\beta }$ в соответствии с соотношением (6.16).

Сила удара при этом рассчитывается в соответствии с выражением (6.10) с помощью инварианта Римана для волнового уравнения; оно приведено ниже. В последующих выражениях представлена эквивалентная запись, из которой ясно, что давление, подобранное в соответствии с формулой (6.10), вызовет такое же изменение инварианта Римана, что и скорость колеса при ударе:

(8.3)
${\text{I}}_{{{\text{RIEMANN}}}}^{1} = {{{v}}_{y}} - \frac{1}{{{{c}_{{{\text{P,RAIL}}}}}{{{\rho }}_{{{\text{RAIL}}}}}}}{{\sigma }_{{yy}}},$
(8.4)
${\text{I}}_{{{\text{RIEMANN}}}}^{1} = \frac{1}{{{{c}_{{{\text{P,RAIL}}}}}{{{\rho }}_{{{\text{RAIL}}}}}}}P_{{{\text{FLAT\_SPOT}}}}^{0}\left( {L,t} \right),$
(8.5)
${\text{I}}_{{{\text{RIEMANN}}}}^{1} = {{V}_{{{\text{IMPACT}}}}}\left( {L,t} \right).$
В выражении (8.3) координата у направлена вертикально вверх.

Длительность этого удара вычисляется в соответствии с выражением (6.13) и представляет собой время, необходимое волновому фронту, чтобы отразиться от подошвы рельса и вернуться к точке взаимодействия.

При повороте колеса вокруг точки окончания ползуна движение колеса обусловлено общим движением состава и происходит линейно в соответствии с выражением (6.17) при $t \in \left[ {{{t}_{1}},{{t}_{2}}} \right]$. Для моделирования эффекта проскальзывания достаточно видоизменить выражение (6.17) следующим образом:

(8.6)
${\alpha }\left( t \right) = \left\{ \begin{gathered} {{{\alpha }}_{0}} - {\omega }\left( {t - {{t}_{0}}} \right) - \frac{{{\beta }{{{\left( {t - {{t}_{0}}} \right)}}^{3}}}}{6},\quad t \in \left[ {{{t}_{0}},{{t}_{1}}} \right], \hfill \\ 0,\quad t \in \left[ {{{t}_{1}},{{t}_{1}} + \Delta {{t}_{{{\text{SLIP}}}}}} \right], \hfill \\ {{{\alpha }}_{0}} + {\omega }\left( {t - {{t}_{2}} - \Delta {{t}_{{{\text{SLIP}}}}}} \right),\quad t \in \left[ {{{t}_{1}} + \Delta {{t}_{{{\text{SLIP}}}}},{{t}_{2}} + \Delta {{t}_{{{\text{SLIP}}}}}} \right]. \hfill \\ \end{gathered} \right.$
Здесь $\Delta {{t}_{{{\text{SLIP}}}}}$ – время, в течение которого длится проскальзывание колесной пары с ползуном.

При повороте колеса увеличение площадки контакта происходит при условии, что расстояние между колесом и ж/д рельсом меньше ${\varepsilon }$ в соответствии с фиг. 6. Этим обусловлены выражения (6.6) и (6.8).

Соотношения (6.7), (6.14) становятся очевидными из фиг. 6в и обуслoвливаются использованной геометрической моделью ползуна. Заметим, что в рамках предложенной модели воздействия поврежденного колеса на рельс можно использовать и более сложные геометрические модели ползуна, чем представленная на фиг. 6в. Также можно учитывать динамическое углубление ползуна, добавив в соответствующие выражения зависимость от времени. В целом следует отметить, что предложенная модель воздействия поврежденного колеса на рельсы и ж/д путь является достаточно гибкой и может быть расширена для учета более сложных физических эффектов.

Фиг. 8.

Главная вертикальная компонента тензора напряжений Коши, ${{{\sigma }}_{{zz}}}$. Глубина ползуна 2 мм. Скорость поезда 120 км/ч.

Фиг. 9.

Главная вертикальная компонента тензора напряжений Коши, ${{{\sigma }}_{{zz}}}$. Без повреждений. Скорость поезда 120 км/ч.

Фиг. 10.

Главная вертикальная компонента тензора напряжений Коши, ${{{\sigma }}_{{zz}}}$. Глубина ползуна 2 мм. Скорость поезда 15 км/ч.

Фиг. 11.

Сдвиговая компонента тензора напряжений Коши, ${{{\sigma }}_{{xz}}}$. Глубина ползуна 2 мм. Скорость поезда 120 км/ч.

Фиг. 12.

Сдвиговая компонента тензора напряжений Коши, ${{{\sigma }}_{{xz}}}$. Без повреждений. Скорость поезда 120 км/ч.

Фиг. 13.

Сдвиговая компонента тензора напряжений Коши, ${{{\sigma }}_{{xz}}}$. Глубина ползуна 2 мм. Скорость поезда 15 км/ч.

9. РАСЧЕТ ВОЛНОВЫХ ЯВЛЕНИЙ В РЕЛЬСЕ И Ж/Д ПУТИ

На фиг. 8–13 представлены различные компоненты вычисленного тензора напряжений Коши ${\mathbf{\sigma }}$. Оранжевый цвет соответствует положительным величинам этого тензора, бирюзовый – отрицательным, темно-серый – нулевым, при этом представлено одно и то же положение колесной пары вагона. В вычислениях предполагается, что ползун располагается только на первой колесной паре.

Можно видеть влияние колеса с ползуном на рельс. Также на приведенных иллюстрациях видно, что из-за того, что на малых скоростях составу требуется большее время, чтобы колесные пары оказались бы в одном и том же положении, волновой фронт, вызванный влиянием поврежденного колеса на рельсы, распространился дальше для фиг. 8, 11, чем для фиг. 10, 13.

10. МОДЕЛИРОВАНИЕ ПОЯВЛЕНИЯ ТРЕЩИН

Для расчета поврежденных областей рельса используется модель формирования трещин. Данный метод основан на анализе компонент тензора напряжений Коши. Трещина появляется впервые, когда одно из главных напряжений достигает значения ${{\sigma }_{{{\text{MAX}}}}}$ (характеристика материала). Плоскость трещины перпендикулярна к направлению главного напряжения. В каждом узле трещины нормальные и тангенциальные (с учетом направления трещины) компоненты тензора напряжений Коши зануляются. Изменение значений ${{{\sigma }}_{{{\text{MAX}}}}}$ позволяет учитывать разные типы ж/д путей и различные погодные условия. В данном разделе предполагается ${{{\sigma }}_{{{\text{MAX}}}}} = 780$ МПа.

Процесс формирования трещин на разных стадиях взаимодействия “ж/д путь – колесная пара” (скорость поезда 120 км/ч) представлен на фиг. 14, 15. Направление роста трещины указано стрелками.

Фиг. 14.

Разрушения в рельсах, вызванные колесной парой с ползуном. Глубина ползуна 2 мм. Первая трещина. Скорость поезда 120 км/ч.

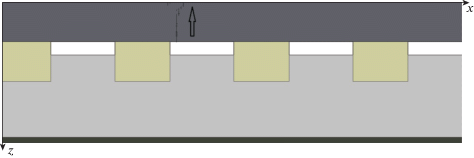
Фиг. 15.

Разрушения в рельсах, вызванные колесной парой с ползуном. Глубина ползуна 2 мм. Финальное разрушение. Скорость поезда 120 км/ч.

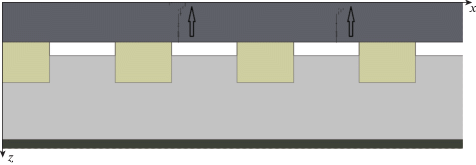
Было высказано предположение, что задание пониженной ${{\sigma }_{{{\text{MAX}}}}}$ в окрестности начального разрушения поверхности рельса позволит получить модель формирования трещин, вызванных долговременной эксплуатацией, и усталостных трещин. Также отметим, что возникает дополнительная вторая трещина (фиг. 15), вызванная волновыми процессами в рельсе. Если данная гипотеза верна, то образование этих дополнительных повреждений зависит от характеристик железнодорожного пути.

Расчеты показали, что трещины отсутствуют у подвижных составов, движущихся со скоростью 15 км/ч. Таким образом, результаты, полученные в процессе моделирования, находятся в соответствии с нормами транспортировки составов с поврежденными колесными парами на ремонтные станции.

11. ЗАКЛЮЧЕНИЕ

Был рассмотрен метод расчета влияния на рельсы поврежденного колеса с ползуном. Было предложено вычислять давление колесной пары на рельсы, используя аналитические выражения для граничных условий на верхней границе рельса, а затем вычислять решение полной системы уравнений, описывающих состояние сплошной линейно-упругой среды в рельсах, шпалах, насыпи и слое осадочных пород с возможностью изменения скоростей упругих волн, плотности и геометрии. Также были разработаны аналитические выражения, учитывающие влияние на рельсы со стороны поврежденных колес, соответствующие граничные условия и выполнена их программная реализация. Предложено использовать модель формирования повреждений ж/д пути, основанную на максимальном значении главного напряжения. Изменение разных параметров вычислений позволяет учитывать разные степени повреждения колесной пары, различные типы вагонов и локомотивов, рельсов, расстояния между шпалами, погодные условия и характеристики геологических сред.

Предложенные граничные условия, моделирующие удар ползуна о рельс, позволяют учитывать динамический контакт между рельсом и колесом, в том числе поврежденным. Учитываются четыре стадии взаимодействия колеса и рельса.

Полученные результаты моделирования показывают, что в окрестности первоначальной трещины существуют дополнительные трещины в случаях со значительными повреждениями рельсов. Данный эффект вызывается волновыми явлениями в ж/д пути, вызванными ударом ползуна и движением остальных колесных пар. Кроме того, предложено изменять параметры прочности стали, чтобы иметь возможность учитывать в модели разрывы, вызванные долговременной эксплуатацией.

Предложенный метод моделирования влияния поврежденной колесной пары на железнодорожные пути может быть использован для улучшения показателей надежности и уменьшения убытков от транспортировки вагонов и локомотивов с поврежденными колесными парами на ремонтные станции, а также для оценки и уменьшения совокупных убытков от различных методов замены колесных пар в разных условиях.

Список литературы

  1. Newton S.G., Clark R.A. An investigation into the dynamic effects on the track of wheel flats on railway vehicles // J. Mech. Engng Science. 1979. V. 21. № 4. P. 287–297.

  2. Nielsen J.C.O., Igeland A. Vertical dynamic interaction between train and track influence of wheel and track imperfections // J. Sound and Vibration. 1995. V. 187. № 5. P. 825–839.

  3. Dong R.G., Sankar S., Dukkipati R.V. A finite element model of railway track and its application to the wheel flat problem. Proceedings of the Institution of Mechanical Engineers, Part F // J. Rail and Rapid Transit. 1994. V. 208. № 16. P. 61–72.

  4. Johnson K.L. Contact Mechanics. Cambridge: Cambridge University Press, 1987.

  5. Remington P., Webb J. Estimation of wheel/rail interaction forces in the contact area due to roughness // J. Sound and Vibration. 1996. V. 193. № 1. P. 83–102.

  6. Nielsen J.C.O., Johansson A. Out-of-round railway wheels – a literature survey. Proceedings of the Institution of Mechanical Engineers, Part F // J. Rail and Rapid Transit. 2000. V. 214. № 2. P. 79–91.

  7. Yan W., Fischer F.D. Applicability of the Hertz contact theory to rail-wheel contact problems // Archive Appl. Mech. 2000. V. 70. № 4. P. 255–268.

  8. Wu T.X., Thompson D.J. A hybrid model for the noise generation due to railway wheel flats // J. Sound and Vibration. 2002. V. 251. № 1. P. 115–139.

  9. Baeza L., Roda A., Carballeira J., Giner E. Railway train-track dynamics for wheelflats with improved contact models // Non-linear Dynamics. 2006. V. 45. № 3. P. 385–397.

  10. Steenbergen M.J.M.M. The role of the contact geometry in wheel–rail impact due to wheel flats // Vehicle System Dynamics. 2007. V. 45. № 12. P. 1097–1116.

  11. Steenbergen M.J.M.M. The role of the contact geometry in wheel–rail impact due to wheel flats: part II // Vehicle System Dynamics. 2008. V. 46. № 8. P. 713–737.

  12. Alonso A., Gimenez J.G. Wheel–rail contact: roughness, heat generation and conforming contact influence // Tribology Internat. 2008. V. 41. № 8. P. 755–768.

  13. Wiest M., Kassa E., Daves W., Nielsen J.C.O., Ossberger H. Assessment of methods for calculating contact pressure in wheel–rail/switch contact // Wear. 2008. V. 265. № (9–10). P. 1439–1445.

  14. Zhao X., Li Z. The solution of frictional wheel–rail rolling contact with a 3D transient finite element model: validation and error analysis // Wear. 2011. V. 271. P. 444–452.

  15. Kalker J.J. Three-Dimensional Elastic Bodies in Rolling Contact. Kluwer Academic Publishers, 1990.

  16. Martinez-Casas J., Mazzola L., Baeza L., Bruni S. Numerical estimation of stresses in railway axles using a train–track interaction model // International Journal of Fatigue. 2013. V. 47. P. 18–30.

  17. Kaiser I. Refining the modelling of vehicle–track interaction // Vehicle System Dynamics. 2012. V. 50. Suppl. 1. P. 229–243.

  18. Pieringer A., Kropp W., Nielsen J.C. The influence of contact modelling on simulated wheel/rail interaction due to wheel flats // Wear. 2014. V. 314. № (1–2). P. 273–281.

  19. Yang J., Thompson D.J. Time-domain prediction of impact noise from wheel flats based on measured profiles // J. Sound and Vibration. 2014. V. 333. № 17. P. 3981–3995.

  20. Loktev A.A., Sycheva A.V., Vershinin V.V. Modelling of Work of a Railway Track at the Dynamic Effects of a Wheel Pair // Proc. of the 2014 Internat. Conf. on Theor. Mech. and Appl.Mech., Venice, Italy, March 15–17, 2014. P. 16–19.

  21. Коган А.Я. Воздействие на путь поездов, имеющих в своем составе вагоны с ползунами на колесных парах // Вестн. ВНИИЖТ. 2014. № 3. С. 3–8.

  22. Мазов Ю.Н., Локтев А.А., Сычев В.П. Оценка влияния дефектов колес подвижного состава на состояние железнодорожного пути // Инженерные изыскания и обследование зданий. Специальное строительство. 2015. С. 61–72.

  23. Thompson D.J. Railway Noise and Vibration: Mechanisms, Modelling and Means of Control. Oxford: Elsevier Science, 2008.

  24. Kouroussis G., Alexandrou G., Connolly D.P., Vogiatzis K., Verlinden O. Railway-induced ground vibrations in the presence of local track irregularities and wheel flats // Proc. of the 5th Internat. Conf. on Comput. Meth. in Structural Dynamics and Earthquake Engng. National Technical University of Athens. 2015. P. 26–37.

  25. Nejad R.M. Using three-dimensional finite element analysis for simulation of residual stresses in railway wheels // Engng Failure Analys. 2014. V. 45. P. 449–455.

  26. Zhu Y., Lyu Y., Olofsson U. Mapping the friction between railway wheels and rails focusing on environmental conditions // Wear. 2015. V. 324. P. 122–128.

  27. Dirks B., Enblom R., Ekberg A., Berg M. The development of a crack propagation model for railway wheels and rails // Fatigue & Fracture of Engng. Materials & Structures. 2015. V. 38. № 12. P. 1478–1491.

  28. Буйносов А.П., Денисов Д.С. Исследование изменения напряженного состояния железнодорожного колеса в процессе эксплуатации // Приоритетные научные исследования и разработки. Сб. статей Международной научно-практической конференции. 2016. С. 20–26.

  29. Huang Y.B., Shi L.B., Zhao X.J., Cai Z.B., Liu Q.Y., Wang W.J. On the formation and damage mechanism of rolling contact fatigue surface cracks of wheel/rail under the dry condition // Wear. 2018. V. 400–401. P. 62–73.

  30. Yang Z., Boogaard A., Chen R., Dollevoet R., Li Z. Numerical and experimental study of wheel-rail impact vibration and noise generated at an insulated rail joint // Int. J. Impact Engng. 2018. V. 113. P. 29–39.

  31. Bogdevicius M., Zygiene R., Bureika G., Dailydka S. An analytical mathematical method for calculation of the dynamic wheel–rail impact force caused by wheel flat // Vehicle System Dynamics. 2016. V. 54. № 5. P. 689–705.

  32. Loktev A.A., Sychev V.P., Buchkin V.A., Bykov Y.A., Andreichicov A.V., Stepanov R.N. Determination of the pressure between the wheel of the moving railcar and rails subject to the defects // Proceedings of the 2017 International Conference “Quality Management, Transport and Information Security, Information Technologies”, IT and QM and IS. 2017. № 8085934. P. 748–751.

  33. Zunsong R. An investigation on wheel/rail impact dynamics with a three-dimensional flat model // Vehicle System Dynamics. 2018. P. 1–21.

  34. Воробьев А.А., Федоров И.В., Иванов И.А., Конограй О.А. Методика расчета размера контактно-усталостных повреждений железнодорожного колеса по результатам, полученным на модельных роликах // Бюллетень результатов научных исследований. 2018. № 1.

  35. Khokhlov N.I., Golubev V.I. On the class of compact grid-characteristic schemes // Smart Innovation, Systems and Technologies. 2019. V. 133. P. 64–77.

  36. Petrov I.B., Favorskaya A.V., Khokhlov N.I. Grid-characteristic method on embedded hierarchical grids and its application in the study of seismic waves // Comput. Math. and Math. Phys. 2017. V. 57. № 11. P. 1771–1777.

  37. Favorskaya A.V., Zhdanov M.S., Khokhlov N.I., Petrov I.B. Modelling the wave phenomena in acoustic and elastic media with sharp variations of physical properties using the grid-characteristic method // Geophysical Prospecting. 2018. V. 66. № 8. P. 1485–1502.

  38. Petrov I.B., Favorskaya A.V., Muratov M.V., Biryukov V.A., Sannikov A.V. Grid-characteristic method on unstructured tetrahedral grids // Doklady Mathematics. 2014. V. 90. № 3. P. 781–783.

  39. Favorskaya A.V., Petrov I.B. Grid-characteristic method // Smart Innovation, Systems and Technologies. 2018. V. 90. P. 117–160.

  40. Favorskaya A.V., Petrov I.B. Numerical modeling of wave processes in rocks by the grid-characteristic method // Math. Models and Comput. Simulat. 2018. V. 10 № 5. P. 639–647.

  41. Favorskaya A., Petrov I., Khokhlov N. Numerical modeling of wave processes during shelf seismic exploration // Proc. Comput. Scie. 2016. V. 96. P. 920–929.

  42. Stognii P.V., Khokhlov N.I. 2D seismic prospecting of gas pockets // Smart Innovation, Systems and Technologies. 2019. V. 133. P. 156–166.

  43. Favorskaya A.V., Petrov I.B. The use of full-wave numerical simulation for the investigation of fractured zones // Math. Models and Comput. Simulat. 2019. V. 11. № 4. P. 518–530.

  44. Golubev V.I. The usage of grid-characteristic method in seismic migration problems // Smart Innovation, Systems and Technologies. 2019. V. 133. P. 143–155.

  45. Favorskaya A.V., Khokhlov N.I., Golubev V.I., Ekimenko A.V., Pavlovskiy Y.V., Khromova I.Y., Petrov I.B. Wave processes modelling in geophysics // Smart Innovation, Systems and Technologies. 2018. V. 90. P. 187–218.

  46. Favorskaya A.V., Breus A.V., Galitskii B.V. Application of the grid-characteristic method to the seismic isolation model // Smart Innovation, Systems and Technologies. 2019. V. 133. P. 167–181.

  47. Favorskaya A.V., Petrov I.B. Study of seismic isolation by full-wave numerical modeling // Doklady Earth Sci. 2018. V. 481. № 2. P. 1070–1072.

  48. Golubev V., Khokhlov N., Grigorievyh D., Favorskaya A. Numerical simulation of destruction processes by the grid-characteristic method // Proc. Comput. Scie. 2018. V. 126. P. 1281–1288.

  49. Favorskaya A., Golubev V., Grigorievyh D. Explanation the difference in destructed areas simulated using various failure criteria by the wave dynamics analysis // Proc. Comput. Sci. 2018. V. 126. P. 1091–1099.

  50. Breus A., Favorskaya A., Golubev V., Kozhemyachenko A., Petrov I. Investigation of seismic stability of high-rising buildings using grid-characteristic method // Proc. Comput. Sci. 2019. V. 154. P. 305–310.

  51. Petrov I.B., Favorskaya A.V., Khokhlov N.I., Miryakha V.A., Sannikov A.V., Golubev V.I. Monitoring the state of the moving train by use of high performance systems and modern computation methods // Math. Models and Comput. Simulat. 2015. V. 7. № 1. P. 51–61.

  52. Favorskaya A.V. Investigation the material properties of a plate by laser ultrasound using the analysis of multiple waves // Comput. Research and Model. 2019. V. 11. № 4. P. 653–673.

  53. Favorskaya A.V., Kabisov S.V., Petrov I.B. Modeling of ultrasonic waves in fractured rails with an explicit approach // Doklady Mathematics. 2018. V. 98. № 1. P. 401–404.

  54. Dumbser M., Kaser M. An arbitrary high-order discontinuous Galerkin method for elastic waves on unstructured meshes – II. The three-dimensional isotropic case // Geophysical J. Int. 2006. V. 167. № 6. P. 319–336.

  55. Komatitsch D., Vilotte J.P., Vai R., Castillo-Covarrubias J.M., Sanchez-Sesma F.J. The spectral element method for elastic wave equations-application to 2-D and 3-D seismic problems // Int. J. Numerical Methods in Engng. 1999. V. 45. № 9. P. 1139–1164.

  56. Faccioli E., Maggio F., Paolucci R, Quarteroni A. 2D and 3D elastic wave propagation by a pseudo-spectral domain decomposition method // J. Seismology. 1997. V. 1. № 3. P. 237–251.

  57. Moczo P., Robertsson J.O.A., Eisner L. The finite-difference time-domain method for modeling of seismic wave propagation // Advances in Geophysics. 2007. V. 48. P. 421–516.

  58. Wang T., Tang X. Finite-difference modeling of elastic wave propagation: A nonsplitting perfectly matched layer approach // Geophysics. 2003. V. 68. № 5. P. 1749–1755.

  59. Graves R.W. Simulating seismic wave propagation in 3D elastic media using staggered-grid finite differences // Bulletin of the Seismological Society of America. 1996. V. 86. № 4. P. 1091–1106.

  60. Burago N.G., Nikitin I.S. Algorithms of through calculation for damage processes // Comput. Research and Model. 2018. V. 10. № 5. P. 645–666.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал