Журнал вычислительной математики и математической физики, 2020, T. 60, № 9, стр. 1513-1532

О периодическом внутреннем слое в задаче реакция-диффузия с источником модульно-кубичного типа

Н. Н. Нефедов^1, *, Е. И. Никулин^1, **, А. О. Орлов^1, ***

¹ МГУ, физ. факультет
119991 Москва, Ленинские горы, Россия

^* E-mail: nefedov@phys.msu.ru
^** E-mail: nikulin@physics.msu.ru
^*** E-mail: orlov.andrey@physics.msu.ru

Поступила в редакцию 11.11.2019
После доработки 10.01.2020
Принята к публикации 09.04.2020

DOI: 10.31857/S0044466920090136

Аннотация

Исследована сингулярно возмущенная периодическая задача для параболического уравнения реакция-диффузия в случае разрывного источника – нелинейности, описывающей реакцию (взаимодействие). Рассмотрен случай существования внутреннего переходного слоя в условиях несбалансированной и сбалансированной реакции. Построено асимптотическое приближение и исследована асимптотическая устойчивость по Ляпунову периодических решений в каждом из рассмотренных случаев. Для доказательства существования решения и его асимптотической устойчивости используется асимптотический метод дифференциальных неравенств. Приведен пример и проведены численные расчеты, иллюстрирующие теоретический результат. Библ. 21. Фиг. 4.

Ключевые слова: сингулярно возмущенные параболические задачи, периодические задачи, уравнения реакция-диффузия, двумерные контрастные структуры, сбалансированная нелинейность, внутренние слои, фронты, асимптотические методы, дифференциальные неравенства, асимптотическая устойчивость по Ляпунову, разрывная реакция.

1. ПОСТАНОВКА ЗАДАЧИ

Рассматривается сингулярно возмущенное уравнение реакция-диффузия, естественно возникающее в математических моделях с быстрой реакцией:

(1)

$\begin{gathered} {{N}_{\varepsilon }}(u): = {{\varepsilon }^{2}}\left( {\Delta u - \frac{{\partial u}}{{\partial t}}} \right) - f(u,x,y,t,\varepsilon ) = 0, \\ (x,y,t) \in {{D}_{t}}: = \{ (x,y,t) \in {{R}^{3}}:x,y) \in D,\;t \in R\} , \\ \frac{{\partial u}}{{\partial {{n}_{\Gamma }}}}(x,y,t,\varepsilon ) = 0,\quad (x,y) \in \Gamma ,\quad t \in R, \\ u(x,y,t,\varepsilon ) = u(x,y,t + T,\varepsilon ),\quad (x,y) \in \bar {D},\quad t \in R, \\ \end{gathered} $

где $\Delta = \tfrac{{{{\partial }^{2}}}}{{\mathop {\partial x}\nolimits^2 }} + \tfrac{{{{\partial }^{2}}}}{{\mathop {\partial y}\nolimits^2 }}$, производная $\tfrac{\partial }{{\partial {{n}_{\Gamma }}}}$ берется по внутренней нормали к гладкой границе $\Gamma $ заданной двумерной односвязной области $D$, а $\varepsilon > 0$ – малый параметр.

Интерес к различным классам периодических задач связан как с различными приложениями, так и новыми математическими задачами, возникающими при их рассмотрении (см., например, [1], [2]). Настоящая работа развивает асимптотический метод дифференциальных неравенств на новый класс задач (см. [3] и ссылки в этой работе).

Исследуется новый класс сингулярно возмущенных периодических задач в случае разрывного источника – нелинейности, описывающей реакцию (взаимодействие). Рассмотрение таких задач инициировано работами по изучению внутренних слоев в задачах, где коэффициенты адвекции или реакции претерпевают разрывы и их называют нелинейностями модульного типа (см. [4]–[7] и ссылки в этих работах). Ряд приложений такого типа уравнений можно найти в [8].

Задача (1) рассматривается при условии, что функция $f(u,x,y,t,\varepsilon )$ имеет вид:

$f\left( {u,x,y,t,\varepsilon } \right) = \left\{ \begin{gathered} {{f}^{{( + )}}}\left( {u,x,y,t,\varepsilon } \right),\quad {\text{если}}\quad u \geqslant {{\varphi }_{2}}(x,y,t)\quad \left( {x,y} \right) \in \bar {D},\quad t \in R; \hfill \\ {{f}^{{( - )}}}\left( {u,x,y,t,\varepsilon } \right),\quad {\text{если}}\quad u < {{\varphi }_{2}}(x,y,t)\quad \left( {x,y} \right) \in \bar {D},\quad t \in R, \hfill \\ \end{gathered} \right.$

где ${{f}^{{( - )}}}\left( {u,x,y,t,\varepsilon } \right)$, ${{f}^{{( + )}}}\left( {u,x,y,t,\varepsilon } \right)$ – достаточно гладкие функции. Очевидно, что замена $z = u(x,y,t,\varepsilon ) - {{\varphi }_{2}}(x,y,t,\varepsilon )$ приводит к задаче с правой частью, разрывной при $z = 0$. Поэтому, не ограничивая общности, будем предполагать выполненными следующие условия:

(A1) Пусть функция $f(u,x,y,t,\varepsilon )$ имеет вид:

$f\left( {u,x,y,t,\varepsilon } \right) = \left\{ \begin{gathered} {{f}^{{( + )}}}\left( {u,x,y,t,\varepsilon } \right),\quad {\text{если}}\quad u \geqslant 0,\quad \left( {x,y} \right) \in \bar {D},\quad t \in R, \hfill \\ {{f}^{{( - )}}}\left( {u,x,y,t,\varepsilon } \right),\quad {\text{если}}\quad u < 0,\quad \left( {x,y} \right) \in \bar {D},\quad t \in R. \hfill \\ \end{gathered} \right.$

Здесь ${{f}^{{( - )}}}\left( {u,x,y,t,\varepsilon } \right)$, ${{f}^{{( + )}}}\left( {u,x,y,t,\varepsilon } \right)$ – достаточно гладкие T-периодические функции. Такие разрывные нелинейности принято называть нелинейностями модульного типа. Предположим также следующее.

(A2) Пусть уравнение ${{f}^{{( + )}}}\left( {u,x,y,t,0} \right) = 0$ имеет единственное $T$-периодическое решение $u = {{\varphi }^{{( + )}}}(x,y,t)$, а уравнение ${{f}^{{( - )}}}\left( {u,x,y,t,0} \right) = 0$ имеет единственное $T$-периодическое решение $u = {{\varphi }^{{( - )}}}(x,y,t)$, причем выполнены неравенства

${{\varphi }^{{( - )}}}(x,y,t) < 0 < {{\varphi }^{{( + )}}}(x,y,t),\quad (x,y) \in \bar {D},\quad t \in R.$

Для этих корней выполняются неравенства

(A3) $f_{u}^{{( + )}}({{\varphi }^{{( + )}}},x,y,t,0) > 0$, $f_{u}^{{( - )}}({{\varphi }^{{( - )}}},x,y,t,0) > 0$, $(x,y) \in \bar {D}$, $t \in R$.

Поскольку решение задачи (1) при выполнении условий (A1)–(A3) в значительной мере аналогично решению в случае нелинейностей (источников) кубического типа (см. [9] и ссылки в этой работе), то мы называем рассматриваемую в работе нелинейность источником модульно-кубического типа. Отметим, что настоящая работа развивает результаты работы [10].

Будем исследовать вопрос о существовании задачи (1) гладкого периодического решения, которое для любого момента времени $t$ при $\varepsilon \to 0$ внутри области, ограниченной некоторой гладкой замкнутой кривой $C(t,\varepsilon ) \subset D$, стремится к корню ${{\varphi }^{{( + )}}}(x,y,t)$, а снаружи – к другому корню ${{\varphi }^{{( - )}}}(x,y,t)$, и резко изменяется от ${{\varphi }^{{( - )}}}(x,y,t)$ до ${{\varphi }^{{( + )}}}(x,y,t)$ в окрестности кривой $C(t,\varepsilon )$. Кривую $C(t,\varepsilon )$ называют кривой переходного слоя. Отметим, что положение этой кривой заранее не известно и определяется в процессе построения асимптотики решения. Это отличает рассматриваемую задачу от задач с разрывом источника в некоторой точке или на гиперповерхности, в окрестности которых локализован внутренний слой (такие задачи рассматривались в [11], [12]).

Нам понадобятся и другие предположения, которые мы сформулируем ниже.

Определим положение кривой переходного слоя из условия равенства нулю решения задачи (1) на этой кривой: $C(t,\varepsilon ) = \{ (x,y) \in D:u(x,y,t,\varepsilon ) = 0\} .$ Кривая $C(t,\varepsilon )$ разделяет область $D$ на подобласти ${{D}^{{( - )}}}$ и ${{D}^{{( + )}}}$ – соответственно внешнюю и внутреннюю относительно этой кривой.

Решение задачи (1) определяется следующим образом.

Определение. $T$-периодическая по $t$ функция $u(x,y,t,\varepsilon ) \in {{C}^{{1,1,1}}}(D) \cap {{C}^{{2,2,1}}}({{D}^{{( - )}}} \cup {{D}^{{( + )}}})$ называется решением задачи (1), если она удовлетворяет уравнению (1) в каждой из областей ${{D}^{{( \mp )}}},$ а также граничному условию.

2. ПОСТРОЕНИЕ АСИМПТОТИКИ

2.1. Асимптотическое разложение решения

Для построения формальной асимптотики используется схема асимптотической теории контрастных структур, достаточно подробно описанная в [13]. Для этого задача (1) разбивается на две. В области ${{D}^{{( + )}}}$ рассматривается задача

$\begin{gathered} {{\varepsilon }^{2}}\left( {\vartriangle u - \frac{{\partial u}}{{\partial t}}} \right) - {{f}^{{( + )}}}(u,x,y,t,\varepsilon ) = 0, \\ (x,y,t) \in D_{t}^{{( + )}}: = \{ (x,y,t) \in {{R}^{3}}:(x,y) \in {{D}^{{( + )}}},\;t \in R\} , \\ u(x,y,t,\varepsilon ) = 0,\quad (x,y) \in C(t,\varepsilon ),\quad t \in R, \\ u(x,y,t,\varepsilon ) = u(x,y,t + T,\varepsilon ),\quad (x,y) \in {{D}^{{( + )}}},\quad t \in R, \\ \end{gathered} $

а в области ${{D}^{{( - )}}}$ рассматривается задача

$\begin{gathered} {{\varepsilon }^{2}}\left( {\vartriangle u - \frac{{\partial u}}{{\partial t}}} \right) - {{f}^{{( - )}}}(u,x,y,t,\varepsilon ) = 0, \\ (x,y,t) \in D_{t}^{{( - )}}: = \{ (x,y,t) \in {{R}^{3}}:(x,y) \in {{D}^{{( - )}}},\;t \in R\} , \\ u(x,y,t,\varepsilon ) = 0,\quad (x,y) \in C(t,\varepsilon ),\quad t \in R, \\ \frac{{\partial u}}{{\partial {{n}_{\Gamma }}}}(x,y,t,\varepsilon ) = 0,\quad (x,y) \in \Gamma ,\quad t \in R, \\ u(x,y,t,\varepsilon ) = u(x,y,t + T,\varepsilon ),\quad (x,y) \in {{{\bar {D}}}^{{( - )}}},\quad t \in R. \\ \end{gathered} $

Для описания внутреннего переходного слоя (аналогично [14]) рассмотрим однопараметрическое семейство кривых $\{ \bar {C}(t)\} : = \{ \bar {C}(t) \subset D:\bar {C}(t)$ – достаточно гладкая простая замкнутая кривая; $\bar {C}(t) = \bar {C}(t + T),\;\left. {t \in R} \right\}$. Для каждой кривой $C(t)$ определим $\delta $-окрестность ${{\bar {C}}^{\delta }}(t): = \{ P \in D:{\text{dist}}(P,\bar {C}(t)) < \delta \} $, $\delta = {\text{const}} > 0$. Далее, стандартным образом введем в $\delta $-окрестности кривой $\bar {C}(t) \in \{ \bar {C}(t)\} $ локальную систему координат $(r,\theta )$, где $\theta \in [0,\bar {\Theta }(\bar {C}(t))]$ – это координата точки $M \in \bar {C}(t)$, ${\text{dist}}\{ (x,y),\bar {C}\} = {\text{dist}}\{ (x,y),M\} $; $r = \pm {\text{dist}}\{ (x,y),\bar {C}\} $, $(x,y) \in {{D}^{ \pm }}$, где ${{D}^{ + }},\;{{D}^{ - }}$ – соответственно внутренняя и внешняя области, на которые разбивает область $D$ кривая $\bar {C}(t)$. Пусть при каждом фиксированном $t$ кривая $\bar {C}(t)$ определена в параметрической форме: $x = X(\theta ,t)$, $y = Y(\theta ,t)$, a ${\mathbf{n}}(\theta ,t) = ({{n}_{1}}(\theta ,t),{{n}_{2}}(\theta ,t))$ – внутренняя нормаль ($({{n}_{1}}(\theta ,t)$ и ${{n}_{2}}(\theta ,t))$ – направляющие косинусы нормали) к кривой $\bar {C}(t)$ в точке $(0,\theta )$. При достаточно малом $\delta $ в $\delta $-окрестности кривой $\bar {C}(t)$ существует взаимно однозначное соответствие между координатами $(x,y)$ и $(r,\theta )$:

$x = X(\theta ,t) + r{{n}_{1}}(\theta ,t),\quad y = Y(\theta ,t) + r{{n}_{2}}(\theta ,t).$

Аналогично для описания пограничного слоя в достаточно малой окрестности кривой $\Gamma $ вводятся локальные координаты $({{r}_{\Gamma }},{{\theta }_{\Gamma }})$.

Пусть нам известна кривая ${{C}_{0}}(t) \in \{ \bar {C}(t)\} $, являющаяся нулевым приближением для кривой $C(t,\varepsilon )$, и в ее окрестности введена локальная система координат $(r,\theta )$. Уравнение для кривой переходного слоя $C(t,\varepsilon )$ будем искать в следующем виде:

(2)

$r = \lambda {\text{*}}(\theta ,t,\varepsilon ) = \varepsilon \lambda _{1}^{*}(\theta ,t,\varepsilon ) = \varepsilon ({{\lambda }_{1}}(\theta ,t) + \varepsilon {{\lambda }_{2}}(\theta ,t) + {{\varepsilon }^{2}}{{\lambda }_{3}}(\theta ,t) + ...),$

где правая часть представляется в виде ряда по степеням $\varepsilon $ с неизвестными коэффициентами ${{\lambda }_{i}}(\theta ,t),\;i = 1,2,...$. Ниже мы покажем, как найти ${{C}_{0}}(t)$.

Далее для функций асимптотики в области ${{D}^{{( - )}}}$ используем обозначение $( - )$, в области ${{D}^{{( + )}}}$ – $( + )$. Построим асимптотику в виде ряда по степеням $\varepsilon $, не раскладывая в такой ряд функцию $\lambda {\text{*}}(\theta ,t,\varepsilon )$:

(3)

${{U}^{{( \pm )}}}(x,y,t,\varepsilon ) = {{\bar {u}}^{{( \pm )}}}(x,y,t,\varepsilon ) + {{Q}^{{( \pm )}}}(\xi ,\theta ,t,\varepsilon ) + \Pi (\tau ,{{\theta }_{\Gamma }},t,\varepsilon ),$

где регулярная часть имеет вид:

${{\bar {u}}^{{( \pm )}}}(x,y,t,\varepsilon ) = \bar {u}_{0}^{{( \pm )}}(x,y,t) + \varepsilon \bar {u}_{1}^{{( \pm )}}(x,y,t) + \ldots + {{\varepsilon }^{n}}\bar {u}_{n}^{{( \pm )}}(x,y,t) + \ldots - $

есть регулярная часть асимптотики,

$\Pi (\tau ,{{\theta }_{\Gamma }},t,\varepsilon ) = {{\Pi }_{0}}(\tau ,{{\theta }_{\Gamma }},t) + \varepsilon {{\Pi }_{1}}(\tau ,{{\theta }_{\Gamma }},t) + \ldots + {{\varepsilon }^{n}}{{\Pi }_{n}}(\tau ,{{\theta }_{\Gamma }},t) + \ldots ,\quad \tau = \frac{{{{r}_{\Gamma }}}}{\varepsilon } - $

погранслойная часть асимптотики, служащая для приближения решения вблизи границы $\Gamma $,

${{Q}^{{( \pm )}}}(\xi ,\theta ,t,\varepsilon ) = Q_{0}^{{( \pm )}}(\xi ,\theta ,t,\varepsilon ) + \varepsilon Q_{1}^{{( \pm )}}(\xi ,\theta ,t,\varepsilon ) + \ldots + {{\varepsilon }^{n}}Q_{n}^{{( \pm )}}(\xi ,\theta ,t,\varepsilon ) + \ldots - $

есть часть асимптотики, служащая для приближения внутреннего переходного слоя в окрестности $C(t,\varepsilon )$ ($\xi = (r - \lambda {\text{*}}(\theta ,t,\varepsilon )){\text{/}}\varepsilon $), члены которой, как будет показано ниже, определяются из уравнений, в которые входят функция $\lambda {\text{*}}(\theta ,t,\varepsilon )$ и ее частные производные, этим и объясняется зависимость функций ${{Q}_{i}}$ от аргумента $\varepsilon $. Если включить $\lambda {\text{*}}(\theta ,t,\varepsilon )$ и ее частные производные в аргументы функций ${{Q}_{i}}$, то при действии на них оператор ${{\varepsilon }^{2}}\left( {\Delta - \tfrac{\partial }{{\partial t}}} \right)$ будет выглядеть уже иным образом.

Метод пограничных функций (см. [9], [15]) с учетом особенностей параболического оператора (см. [9], [10]) приводит к последовательности задач для определения коэффициентов асимптотических рядов (3), из которых, в частности, получим $\bar {u}_{0}^{{( - )}}(x,y,t) = {{\varphi }^{{( - )}}}(x,y,t)$, $\bar {u}_{0}^{{( + )}}(x,y,t) = {{\varphi }^{{( + )}}}(x,y,t)$. Функции $u_{i}^{{( \pm )}}(x,y,t),\;i = 1,2,3, \ldots $, а также пограничные функции ${{\Pi }_{i}}(\tau ,{{\theta }_{\Gamma }},t)$ строятся стандартным образом, и мы это построение в работе рассматривать не будем.

В дальнейшем, eсли указана конкретная кривая $\bar {C}(t) \in \{ \bar {C}(t)\} $, будем пользоваться обоими наборами аргументов $(x,y,t)$ и $(r,\theta ,t)$, сохраняя при этом обозначение функций, которые от них зависят, например: ${{\varphi }^{{( + )}}}(x,y,t) = {{i}^{{( + )}}}(r,\theta ,t)$.

Остановимся подробнее на построении функций внутреннего переходного слоя. Оператор Лапласа в локальных координатах $(r,\theta )$ имеет вид (см. [15]):

$\Delta = \frac{{{{\partial }^{2}}}}{{\mathop {\partial r}\nolimits^2 }} + \Delta r\frac{\partial }{{\partial r}} + {{\left| {\nabla \theta } \right|}^{2}}\frac{{{{\partial }^{2}}}}{{\mathop {\partial \theta }\nolimits^2 }} + \Delta \theta \frac{\partial }{{\partial \theta }},$

где $\Delta r,\;\nabla \theta ,\;\Delta \theta $ – известные функции $r$ и $\theta $ ($\Delta r = \tfrac{{{{\partial }^{2}}r}}{{\partial {{x}^{2}}}} + \tfrac{{{{\partial }^{2}}r}}{{\partial {{y}^{2}}}}$, аналогично определяются $\nabla \theta $ и $\Delta \theta $). Тогда, при действии на часть асимптотики для внутреннего переходного слоя, дифференциальный оператор ${{D}_{\varepsilon }}: = {{\varepsilon }^{2}}\left( {\Delta - \tfrac{\partial }{{\partial t}}} \right)$ в переменных $(\xi ,\theta ,t)$ приобретает вид:

${{D}_{\varepsilon }} = \frac{{{{\partial }^{2}}}}{{\mathop {\partial \xi }\nolimits^2 }} + \varepsilon s(\varepsilon \xi + \lambda {\text{*}},\theta ,t)\frac{\partial }{{\partial \xi }} + {{\varepsilon }^{2}}{{L}_{2}},$

где $s(r,\theta ,t): = \Delta r(r,\theta ,t) - \mathop {\left. {\tfrac{{\partial r}}{{\partial t}}(r,\theta ,t)} \right|}\nolimits_{x,y = {\text{const}}} $,

$\begin{gathered} {{L}_{2}}: = {{\left| {\nabla \theta } \right|}^{2}}\left( {\mathop {\left( {\frac{{\partial \lambda _{1}^{*}}}{{\partial \theta }}} \right)}\nolimits^2 \frac{{{{\partial }^{2}}}}{{\mathop {\partial \xi }\nolimits^2 }} - 2\frac{{\partial \lambda _{1}^{*}}}{{\partial \theta }}\frac{{{{\partial }^{2}}}}{{\partial \xi \partial \theta }} - \frac{{{{\partial }^{2}}\lambda _{1}^{*}}}{{\mathop {\partial \theta }\nolimits^2 }}\frac{\partial }{{\partial \xi }} + \frac{{{{\partial }^{2}}}}{{\mathop {\partial \theta }\nolimits^2 }}} \right) + \\ + \;\Delta \theta \left( { - \frac{{\partial \lambda _{1}^{*}}}{{\partial \theta }}\frac{\partial }{{\partial \xi }} + \frac{\partial }{{\partial \theta }}} \right) - \frac{{\partial \theta }}{{\partial t}}\frac{\partial }{{\partial \theta }} - \frac{\partial }{{\partial t}} + \left( {\frac{{\partial \lambda _{1}^{*}}}{{\partial \theta }}\mathop {\left. {\frac{{\partial \theta }}{{\partial t}}{\kern 1pt} } \right|}\nolimits_{x,y = {\text{const}}} + \frac{{\partial \lambda _{1}^{*}}}{{\partial t}}} \right)\frac{\partial }{{\partial \xi }}. \\ \end{gathered} $

Пусть ${{{\mathbf{R}}}_{0}}(\theta ,{\mathbf{t}}) = \{ X(\theta ,t),Y(\theta ,t)\} $ – радиус-вектор точки кривой ${{C}_{0}}$ с координатами $\theta ,t$. Нетрудно показать, что

$\mathop {\left. {\frac{{\partial r}}{{\partial t}}(r,\theta ,t)} \right|}\nolimits_{x,y = {\text{const}}} = \mp \left( {\frac{{\partial {{{\mathbf{R}}}_{0}}(\theta ,{\mathbf{t}})}}{{\partial t}},{\mathbf{n}}(\theta ,t)} \right),$

что представляет собой нормальную компоненту скорости $\tfrac{{\partial {{{\mathbf{R}}}_{0}}(\theta ,{\mathbf{t}})}}{{\partial t}}$ точки $y(\theta ,t)$ кривой ${{C}_{0}}(t)$. Также известно (см. [14]), что $\Delta r(r,\theta ,t)$ – кривизна кривой ${{\Gamma }_{r}}(t): = \{ (x(\theta ,t),\;y(\theta ,t)) \in D:\{ x,y\} = $ $ = {{{\mathbf{R}}}_{0}}(\theta ,t) + r{\mathbf{n}}(\theta ,t),\;y \in {{C}_{0}}(t)\} $ в точке $(x(\theta ,t),y(\theta ,t))$.

Действуя по схеме алгоритма А.Б. Васильевой, определим функции $Q_{i}^{{( \pm )}}$.

Члены $Q_{0}^{{( \pm )}}(\xi ,\theta ,t,\varepsilon )$ определяются из следующих задач:

(4)

$\begin{gathered} \frac{{{{\partial }^{2}}Q_{0}^{{( \pm )}}(\xi ,\theta ,t,\varepsilon )}}{{\mathop {\partial \xi }\nolimits^2 }} = {{f}^{{( \pm )}}}({{\varphi }^{{( \pm )}}}(\lambda {\text{*}},\theta ,t) + Q_{0}^{{( \pm )}}(\xi ,\theta ,t,\varepsilon ),\lambda {\text{*}},\theta ,t,0), \\ Q_{0}^{{( \pm )}}(0,\theta ,t,\varepsilon ) + \bar {u}_{0}^{{( \pm )}}(\lambda {\text{*}},\theta ,t) = 0,\quad Q_{0}^{{( \pm )}}( \pm \infty ,\theta ,t,\varepsilon ) = 0. \\ \end{gathered} $

Известно (см., например, [13]), что задача (4) имеет единственное, монотонное по $\xi $ решение, причем имеют место следующие оценки:

(5)

$\frac{{\partial Q_{0}^{{( \pm )}}(\xi ,\theta ,t,\varepsilon )}}{{\partial \xi }} \geqslant {{C}_{0}}{{e}^{{ - {{k}_{0}}|\xi |}}},\quad \left| {Q_{0}^{{( \pm )}}(\tau ,\theta ,t,\varepsilon )} \right| \leqslant C_{0}^{'}{{e}^{{ - k_{0}^{'}|\xi |}}},$

где ${{C}_{0}},\;C_{0}^{'},\;{{k}_{0}},\;k_{0}^{'}$ – некоторые положительные константы.

Функции $Q_{1}^{{( \pm )}}$ определяются из следующих задач:

(6)

$\begin{gathered} \frac{{{{\partial }^{2}}Q_{1}^{{( \pm )}}}}{{\mathop {\partial \xi }\nolimits^2 }} - \frac{{\partial{ \tilde {f}}_{*}^{{( \pm )}}}}{{\partial u}}Q_{1}^{{( \pm )}} = r_{1}^{{( \pm )}}, \\ Q_{1}^{{( \pm )}}(0,\theta ,t,\varepsilon ) + \bar {u}_{1}^{{( \pm )}}(\lambda {\text{*}},\theta ,t) = 0,\quad Q_{1}^{{( \pm )}}( \pm \infty ,\theta ,t,\varepsilon ) = 0, \\ r_{1}^{{( \pm )}}(\xi ,\theta ,t,\varepsilon ): = - \frac{{\partial Q_{0}^{{( \pm )}}}}{{\partial \xi }}(\xi ,\theta ,t,\varepsilon )s(\lambda {\text{*}},\theta ,t) + \xi \left( {\frac{{\partial{ \tilde {f}}_{*}^{{( \pm )}}}}{{\partial u}}\frac{{\partial{ \bar {u}}_{0}^{{( \pm )}}}}{{\partial r}}(\lambda {\text{*}},\theta ,t) + \frac{{\partial{ \tilde {f}}_{*}^{{( \pm )}}}}{{\partial r}}} \right) + {{{\bar {u}}}_{1}}(\lambda {\text{*}},\theta ,t)\frac{{\partial{ \tilde {f}}_{*}^{{( \pm )}}}}{{\partial u}} + \frac{{\partial{ \tilde {f}}_{*}^{{( \pm )}}}}{{\partial \varepsilon }}, \\ \end{gathered} $

где символы “$ \sim $”, “$ * $” над и справа от функции означают, что ее значение берется при аргументе $(Q_{0}^{{( \pm )}}(\xi ,\theta ,t,\varepsilon ) + \bar {u}_{0}^{{( \pm )}}(\lambda {\text{*}},\theta ,t),\lambda {\text{*}},\theta ,t,0)$.

Решение задач (6) представляется в явном виде (см., например, [13]):

(7)

$Q_{1}^{{( \pm )}}(\xi ,\theta ,t,\varepsilon ) = - \bar {u}_{1}^{{( \pm )}}(\lambda {\text{*}},\theta ,t)\frac{{{{{\tilde {v}}}^{{( \pm )}}}(\xi ,\theta ,t,\varepsilon )}}{{{{{\tilde {v}}}^{{( \pm )}}}(0,\theta ,t,\varepsilon )}} + {{\tilde {v}}^{{( \pm )}}}(\xi ,\theta ,t,\varepsilon )\int\limits_0^\xi \,\mathop {({{{\tilde {v}}}^{{( \pm )}}}(s,\theta ,t,\varepsilon ))}\nolimits^{ - 2} \int\limits_{ \pm \infty }^s \,{{\tilde {v}}^{{( \pm )}}}(\eta ,\theta ,t,\varepsilon )r_{1}^{{( \pm )}}(\eta ,\theta ,t,\varepsilon )d\eta ds,$

где

${{\tilde {v}}^{{( \pm )}}}(\xi ,\theta ,t,\varepsilon ) = \frac{{\partial Q_{0}^{{( \pm )}}(\xi ,\theta ,t,\varepsilon )}}{{\partial \xi }},$

причем ${{\tilde {v}}^{{( \pm )}}}(\xi ,\theta ,t,\varepsilon ) > 0$ в рассматриваемой области. Для $Q_{1}^{{( \pm )}}$ справедлива оценка

(8)

${\text{|}}Q_{1}^{{( \pm )}}(\xi ,\theta ,t,\varepsilon ){\text{|}} < {{C}_{1}}{{e}^{{ - {{k}_{1}}|\xi |}}},$

где ${{C}_{1}},\;{{k}_{1}}$ – некоторые положительные константы.

Функции внутреннего переходного слоя более высоких порядков находятся из задач, аналогичных задачам для функций $Q_{1}^{{( \pm )}}$:

(9)

$\begin{gathered} \frac{{{{\partial }^{2}}Q_{i}^{{( \pm )}}}}{{\mathop {\partial \xi }\nolimits^2 }} - \frac{{\partial{ \tilde {f}}_{*}^{{( \pm )}}}}{{\partial u}}Q_{i}^{{( \pm )}} = r_{i}^{{( \pm )}}(\xi ,\theta ,t,\varepsilon ),\quad i = 2,3,4,..., \\ Q_{i}^{{( \pm )}}(0,\theta ,t,\varepsilon ) + \bar {u}_{i}^{{( \pm )}}(\lambda {\text{*}},\theta ,t) = 0,\quad Q_{i}^{{( \pm )}}( \pm \infty ,\theta ,t,\varepsilon ) = 0, \\ \end{gathered} $

где $r_{i}^{{( \pm )}}(\xi ,\theta ,t,\varepsilon )$ – известные функции. В частности, для $i = 2$ имеем

(10)

$\begin{gathered} r_{2}^{{( \pm )}}(\xi ,\theta ,t,\varepsilon ): = - {{s}_{r}}(\lambda {\text{*}},\theta ,t){{{\tilde {v}}}^{{( \pm )}}}\xi - s(\lambda {\text{*}},\theta ,t)\frac{{\partial Q_{1}^{{( \pm )}}}}{{\partial \xi }} - \\ - \;{{\left| {\nabla \theta (\lambda {\text{*}},\theta ,t)} \right|}^{2}}\left[ {\mathop {\left( {\frac{{\partial \lambda _{1}^{*}}}{{\partial \theta }}} \right)}\nolimits^2 \frac{{\partial {{{\tilde {v}}}^{{( \pm )}}}}}{{\partial \xi }} - 2\frac{{\partial \lambda _{1}^{*}}}{{\partial \theta }}\frac{{\partial {{{\tilde {v}}}^{{( \pm )}}}}}{{\partial \theta }} - \frac{{{{\partial }^{2}}\lambda _{1}^{*}}}{{\mathop {\partial \theta }\nolimits^2 }}{{{\tilde {v}}}^{{( \pm )}}} + \frac{{{{\partial }^{2}}Q_{0}^{{( \pm )}}}}{{\mathop {\partial \theta }\nolimits^2 }}} \right] - \Delta \theta (\lambda {\text{*}},\theta ,t)\left( { - {{{\tilde {v}}}^{{( \pm )}}}\frac{{\partial \lambda _{1}^{*}}}{{\partial \theta }} + \frac{{\partial Q_{0}^{{( \pm )}}}}{{\partial \theta }}} \right) + \\ \, + \frac{{\partial \theta }}{{\partial t}}\frac{{\partial Q_{0}^{{( \pm )}}}}{{\partial \theta }} + \frac{{\partial Q_{0}^{{( \pm )}}}}{{\partial t}} - \left( {\frac{{\partial \lambda _{1}^{*}}}{{\partial \theta }}\frac{{\partial \theta }}{{\partial t}} + \frac{{\partial \lambda _{1}^{*}}}{{\partial t}}} \right){{{\tilde {v}}}^{{( \pm )}}} + g_{2}^{{( \pm )}}(\xi ,\theta ,t,\varepsilon ). \\ \end{gathered} $

Здесь $g_{2}^{{( \pm )}}(\xi ,\theta ,t,\varepsilon )$ – коэффициент при ${{\varepsilon }^{2}}$, стоящий в разложении выражения

${{f}^{{( \pm )}}}({{\bar {u}}^{{( \pm )}}}(\lambda {\text{*}} + \varepsilon \xi ,\theta ,t,\varepsilon ) + {{Q}^{{( \pm )}}}(\xi ,\theta ,t,\varepsilon ),\lambda {\text{*}} + \varepsilon \xi ,\theta ,t,\varepsilon ) - {{f}^{{( \pm )}}}({{\bar {u}}^{{( \pm )}}}(\lambda {\text{*}} + \varepsilon \xi ,\theta ,t,\varepsilon ),\lambda {\text{*}} + \varepsilon i,\theta ,t,\varepsilon )$

по степеням $\varepsilon $.

Замечание 1. Заметим, что из вида уравнения (4) следует, что в функциях $Q_{0}^{{( \pm )}}(\xi ,\theta ,t,\varepsilon )$, ${{\tilde {v}}^{{( \pm )}}}(\xi ,\theta ,t,\varepsilon )$, считая $\theta ,\;t,\;\lambda {\text{*}}$ параметрами, мы можем перейти к другому набору аргументов $(\xi ,\theta ,t,\lambda {\text{*}})$. В дальнейшем мы будем пользоваться обоими наборами аргументов, для каждого конкретного случая выбирая наиболее удобный.

Заметим, что формально $Q$-функции определены для $\tau \in R$, однако фактически они имеют смысл только при ${\text{|}}\tau {\kern 1pt} {\text{|}} \leqslant \tfrac{\delta }{\varepsilon }$. Для их гладкого продолжения на всю область $D$ применяется стандартный прием использования срезающих функций (см., например, [15]).

Таким образом, формальное построение асимптотики решения с внутренним переходным слоем для задачи завершено. Перейдем к определению локализации внутреннего переходного слоя.

2.2. Асимптотическое разложение для кривой переходного слоя

Важнейшая проблема построения асимптотики – это нахождение разложения по малым $\varepsilon $ для кривой перехода $C(t,\varepsilon )$. Нулевой порядок задается кривой ${{C}_{0}}(t)$, а следующие порядки – функциями ${{\lambda }_{i}}(t,\theta )$ в уравнении (2). Для их нахождения используется условие ${{C}^{1}}$-сшивания. Непрерывность асимптотики $U$ на кривой выполняется за счет согласованности асимптотик ${{U}^{{( - )}}}$ и ${{U}^{{( + )}}}$. Потребуем также непрерывности первых производных асимптотики на этой кривой (условие ${{C}^{1}}$-сшивания):

(11)

$\mathop {\left. {\varepsilon \frac{{\partial {{U}^{{( + )}}}}}{{\partial r}}} \right|}\nolimits_{r = \lambda {\text{*}}(\theta ,t,\varepsilon )} - \mathop {\left. {\varepsilon \frac{{\partial {{U}^{{( - )}}}}}{{\partial r}}} \right|}\nolimits_{r = \lambda {\text{*}}(\theta ,t,\varepsilon )} = 0.$

Подставляя асимптотическое разложение (3) в условие (11), получаем

(12)

$\begin{gathered} \frac{{\partial Q_{0}^{{( + )}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }} - \frac{{\partial Q_{0}^{{( - )}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }} + \\ \, + \varepsilon \left( {\frac{{\partial{ \bar {u}}_{0}^{{( + )}}(\lambda {\text{*}},\theta ,t)}}{{\partial r}} + \frac{{\partial Q_{1}^{{( + )}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }} - \left( {\frac{{\partial{ \bar {u}}_{0}^{{( - )}}(\lambda {\text{*}},\theta ,t)}}{{\partial r}} + \frac{{\partial Q_{1}^{{( - )}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }}} \right)} \right) + \\ \, + {{\varepsilon }^{2}}\left( {\frac{{\partial{ \bar {u}}_{1}^{{( + )}}(\lambda {\text{*}},\theta ,t)}}{{\partial r}} + \frac{{\partial Q_{2}^{{( + )}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }} - \left( {\frac{{\partial{ \bar {u}}_{1}^{{( - )}}(\lambda {\text{*}},\theta ,t)}}{{\partial r}} + \frac{{\partial Q_{2}^{{( - )}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }}} \right)} \right) + ... = 0. \\ \end{gathered} $

Рассмотрим выражение при ${{\varepsilon }^{0}}$:

$H(\lambda {\text{*}},\theta ,t): = \frac{{\partial Q_{0}^{{( + )}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }} - \frac{{\partial Q_{0}^{{( - )}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }}.$

Введем функции

${{\tilde {u}}^{{( \pm )}}}(\xi ,\theta ,t,\lambda {\text{*}}): = \bar {u}_{0}^{{( \pm )}}(\lambda {\text{*}},\theta ,t) + Q_{0}^{{( \pm )}}(\xi ,\theta ,t,\lambda {\text{*}}),$

которые, согласно (4) , являются решениями задач

(13)

$\begin{gathered} \frac{{{{\partial }^{2}}{{u}^{{( \pm )}}}}}{{\mathop {\partial \xi }\nolimits^2 }} = \tilde {f}_{*}^{{( \pm )}}, \\ {{{\tilde {u}}}^{{( \pm )}}}(0,\theta ,t,\lambda {\text{*}}) = 0,\quad {{{\tilde {u}}}^{{( \pm )}}}( \pm \infty ,\theta ,t,\lambda {\text{*}}) = {{\varphi }^{{( \pm )}}}(\lambda {\text{*}},\theta ,t), \\ \end{gathered} $

где символы “$ \sim $”, “$ * $” над и справа от функции означают, что ее значение берется при аргументе $(Q_{0}^{{( \pm )}}(\xi ,\theta ,t,\lambda {\text{*}}) + \bar {u}_{0}^{{( \pm )}}(\lambda {\text{*}},\theta ,t),\lambda {\text{*}},\theta ,t,0)$.

Функция $H$ в обозначениях ${{\tilde {u}}^{{( \pm )}}}$ имеет вид:

(14)

$H(\lambda {\text{*}},\theta ,t) = \frac{{\partial {{{\tilde {u}}}^{{( + )}}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }} - \frac{{\partial {{{\tilde {u}}}^{{( - )}}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }}.$

Пусть

${{G}_{1}}(\lambda {\text{*}},\theta ,t): = \frac{{\partial{ \bar {u}}_{0}^{{( + )}}(\lambda {\text{*}},\theta ,t)}}{{\partial r}} + \frac{{\partial Q_{1}^{{( + )}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }} - \left( {\frac{{\partial{ \bar {u}}_{0}^{{( - )}}(\lambda {\text{*}},\theta ,t)}}{{\partial r}} + \frac{{\partial Q_{1}^{{( - )}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }}} \right),$

${{G}_{i}}(\varepsilon ,\theta ,t): = \frac{{\partial{ \bar {u}}_{{i - 1}}^{{( + )}}(\lambda {\text{*}},\theta ,t)}}{{\partial r}} + \frac{{\partial Q_{i}^{{( + )}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }} - \left( {\frac{{\partial{ \bar {u}}_{{i - 1}}^{{( - )}}(\lambda {\text{*}},\theta ,t)}}{{\partial r}} + \frac{{\partial Q_{i}^{{( - )}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }}} \right),\quad i = 2,3,...,$

разложим теперь (11) в ряд по степеням $\varepsilon $, используя (2):

(15)

$\begin{gathered} H(0,\theta ,t) + \varepsilon \left( {\mathop {\left. {\frac{{\partial H}}{{\partial \lambda {\text{*}}}}{\kern 1pt} } \right|}\nolimits_{\lambda {\text{*}} = 0} {{\lambda }_{1}}(\theta ,t) + \mathop {\left. {{{G}_{1}}} \right|}\nolimits_{\varepsilon = 0} } \right) + \\ + \;{{\varepsilon }^{2}}\left( {\frac{{\lambda _{1}^{2}(\theta ,t)}}{2}\mathop {\left. {\frac{{{{\partial }^{2}}H}}{{\mathop {\partial \lambda {\text{*}}}\nolimits^2 }}{\kern 1pt} } \right|}\nolimits_{\lambda {\text{*}} = 0} + {{\lambda }_{2}}(\theta ,t)\mathop {\left. {\frac{{\partial H}}{{\partial \lambda {\text{*}}}}{\kern 1pt} } \right|}\nolimits_{\lambda * = 0} + {{\lambda }_{1}}(\theta ,t)\mathop {\left. {\frac{{\partial {{G}_{1}}}}{{\partial \lambda {\text{*}}}}{\kern 1pt} } \right|}\nolimits_{\lambda {\text{*}} = 0} + \mathop {\left. {{{G}_{2}}} \right|}\nolimits_{\varepsilon = 0} } \right) + ... = 0. \\ \end{gathered} $

Стандартным образом понижая порядок в уравнении (13), можно получить следующие выражения:

(16)

$\begin{gathered} {{({{{\tilde {v}}}^{{( + )}}}(\xi ,\theta ,t,\lambda {\text{*}}))}^{2}} = 2\int\limits_{{{\varphi }^{{( + )}}}(\lambda {\text{*}},\theta ,t)}^0 \,{{f}^{{( + )}}}(u,\lambda {\text{*}},\theta ,t,0){\kern 1pt} du, \\ {{({{{\tilde {v}}}^{{( - )}}}(\xi ,\theta ,t,\lambda {\text{*}}))}^{2}} = 2\int\limits_{{{\varphi }^{{( - )}}}(\lambda {\text{*}},\theta ,t)}^0 \,{{f}^{{( - )}}}(u,\lambda {\text{*}},\theta ,t,0){\kern 1pt} du. \\ \end{gathered} $

Можно показать, используя (13), что справедливо следующее представление для $H$:

(17)

$\begin{gathered} H(\lambda {\text{*}},\theta ,t) = \\ = - \frac{2}{{\tfrac{{\partial Q_{0}^{{( + )}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }} + \tfrac{{\partial Q_{0}^{{( - )}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }}}}\left( {\int\limits_{{{\varphi }^{{( - )}}}(\lambda {\text{*}},\theta ,t)}^0 \,{{f}^{{( - )}}}(u,\lambda {\text{*}},\theta ,t,0)du + \int\limits_0^{{{\varphi }^{{( + )}}}(\lambda {\text{*}},\theta ,t)} \,{{f}^{{( + )}}}(u,\lambda {\text{*}},\theta ,t,0)du} \right) = \\ = - \frac{2}{{\tfrac{{\partial Q_{0}^{{( + )}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }} + \tfrac{{\partial Q_{0}^{{( - )}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }}}}\int\limits_{{{\varphi }^{{( - )}}}(\lambda {\text{*}},\theta ,t)}^{{{\varphi }^{{( + )}}}(\lambda {\text{*}},\theta ,t)} \,f(u,\lambda {\text{*}},\theta ,t,0)du. \\ \end{gathered} $

Введем функцию

(18)

$I(x,y,t): = \int\limits_{{{\varphi }^{{( - )}}}(x,y,t)}^{{{\varphi }^{{( + )}}}(x,y,t)} \,f(u,x,y,t,0)du.$

Оказывается, что построение асимптотики для кривой перехода зависит существенным образом от свойств функции $I(x,y,t)$. В данной работе рассматриваются случаи баланса и отсутствия баланса реакции. О том, какие требования предъявляются при этом для функции$I$, будет сказано ниже. Отметим, что построение асимптотики для решения одинаково для этих обоих случаев.

2.3. Случай несбалансированной реакции

Рассмотрим вначале так называемый случай несбалансированной реакции. Ему отвечает следующее требование:

(A4) Пусть существует кривая ${{C}_{0}}(t) \in \{ \bar {C}\} $ такая, что $\mathop {\left. {I(r,\theta ,t)} \right|}\nolimits_{r = 0} = 0,\theta \in [0,{{\theta }_{0}}]$, $t \in R$, где $[0,{{\theta }_{0}}]$ – это область изменения координаты $\theta $.

В дальнейшем нам также понадобится условие, накладывающее ограничение на выбор кривой ${{C}_{0}}(t)$.

(A5) Пусть для кривой ${{C}_{0}}(t)$ имеет место неравенство

$\mathop {\left. {\frac{{\partial I(r,\theta ,t)}}{{\partial r}}{\kern 1pt} } \right|}\nolimits_{r = 0} < 0,\quad \theta \in [0,{{\theta }_{0}}],\quad t \in R.$

Таким образом, кривая ${{C}_{0}}(t)$ определена. В силу условия (А4) имеем

(19)

${{\tilde {v}}^{{( - )}}}(0,\theta ,t,0) = {{\tilde {v}}^{{( + )}}}(0,\theta ,t,0),$

т.е. $\tilde {v}(\xi ,\theta ,t,0)$ – непрерывная по $\xi $ функция в рассматриваемой области. Поэтому здесь и далее индекс $( \pm )$ в выражениях для $\tilde {v}(\xi ,\theta ,t,0)$ можно опустить.

Определим член ${{\lambda }_{1}}(\theta ,t)$ в разложении (2). При ${{\varepsilon }^{1}}$ равенство (15) дает

(20)

$\frac{{\partial{ \hat {H}}}}{{\partial \lambda {\text{*}}}}{{\lambda }_{1}}(\theta ,t) + {{\hat {G}}_{1}} = 0,$

где символ “$ \wedge $” над функцией означает, что ее значение берется при аргументе $(0,\theta ,t)$.

Преобразуем выражение при $\varepsilon $ в (12):

(21)

$\begin{gathered} {{G}_{1}}(\lambda {\text{*}},\theta ,t) = \frac{{\partial {{\varphi }^{{( + )}}}}}{{\partial r}}(\lambda {\text{*}}\theta ,t) - \frac{{\partial {{\varphi }^{{( - )}}}}}{{\partial r}}(\lambda {\text{*}},\theta ,t) + \left[ { - \bar {u}_{1}^{{( \pm )}}(\lambda {\text{*}},\theta ,t)\frac{{\tilde {v}_{\xi }^{{( \pm )}}(0,\theta ,t,\varepsilon )}}{{{{{\tilde {v}}}^{{( \pm )}}}(0,\theta ,t,\varepsilon )}}} \right]_{ - }^{ + } + \\ \, + \left[ {\frac{{s(\lambda {\text{*}},\theta ,t)}}{{{{{\tilde {v}}}^{{( \pm )}}}(0,\theta ,t,\lambda {\text{*}})}}\int\limits_0^{ \pm \infty } \,{{{({{{\tilde {v}}}^{{( \pm )}}}(\eta ,\theta ,t,\lambda {\text{*}}))}}^{2}}d\eta } \right]_{ - }^{ + } + \left[ { - \frac{{\tfrac{{\partial {{\varphi }^{{( \pm )}}}}}{{\partial r}}(\lambda {\text{*}},\theta ,t)}}{{{{{\tilde {v}}}^{{( \pm )}}}(0,\theta ,t,\lambda {\text{*}})}}\int\limits_0^{ \pm \infty } \,{{{\tilde {v}}}^{{( \pm )}}}(\eta ,\theta ,t,\lambda {\text{*}})\eta \frac{{\partial{ \tilde {f}}_{*}^{{( \pm )}}}}{{\partial u}}d\eta } \right]_{ - }^{ + } + \\ + \;\left[ { - \frac{1}{{{{{\tilde {v}}}^{{( \pm )}}}(0,\theta ,t,\lambda {\text{*}})}}\int\limits_0^{ \pm \infty } \,{{{\tilde {v}}}^{{( \pm )}}}(\eta ,\theta ,t,\lambda {\text{*}})\left( {\eta \frac{{\partial{ \tilde {f}}_{*}^{{( \pm )}}}}{{\partial r}} + \frac{{\partial{ \tilde {f}}_{*}^{{( \pm )}}}}{{\partial \varepsilon }}} \right)d\eta } \right]_{ - }^{ + } + \left[ { - \frac{{{{{\bar {u}}}_{1}}(\lambda {\text{*}},\theta ,t)}}{{{{{\tilde {v}}}^{{( \pm )}}}(0,\theta ,t,\lambda {\text{*}})}}\int\limits_0^{ \pm \infty } \,{{{\tilde {v}}}^{{( \pm )}}}(\eta ,\theta ,t,\lambda {\text{*}})\frac{{\partial{ \tilde {f}}_{*}^{{( \pm )}}}}{{\partial u}}d\eta } \right]_{ - }^{ + }. \\ \end{gathered} $

Здесь и далее выражение, заключенное в скобки вида $[\;]_{ - }^{ + }$, представляет собой разность функции, стоящей внутри скобок, взятой с индексом $( + )$ и той же функции, но взятой с индексом $( - )$. Нетрудно показать, что

$\int\limits_0^{ \pm \infty } \,{{\tilde {v}}^{{( \pm )}}}(\eta ,\theta ,t,\lambda {\text{*}})\frac{{\partial{ \tilde {f}}_{*}^{{( \pm )}}}}{{\partial u}}d\eta = - {{f}^{{( \pm )}}}(0,\lambda {\text{*}},\theta ,t,0),$

$\int\limits_0^{ \pm \infty } \,{{\tilde {v}}^{{( \pm )}}}(\eta ,\theta ,t,\lambda {\text{*}})\eta \frac{{\partial{ \tilde {f}}_{*}^{{( \pm )}}}}{{\partial u}}d\eta = {{\tilde {v}}^{{( \pm )}}}(0,\theta ,t,\lambda {\text{*}}),$

а также

$\tilde {v}_{\xi }^{{( \pm )}}(0,\theta ,t,\varepsilon ) = {{f}^{{( \pm )}}}(0,\lambda {\text{*}},\theta ,t,0).$

Таким образом, выражение для ${{G}_{1}}(\lambda {\text{*}},\theta ,t)$ принимает вид

$\begin{gathered} {{G}_{1}}(\lambda {\text{*}},\theta ,t) = \left[ {\frac{{s(\lambda {\text{*}},\theta ,t)}}{{{{{\tilde {v}}}^{{( \pm )}}}(0,\theta ,t,\lambda {\text{*}})}}\int\limits_0^{ \pm \infty } \,{{{({{{\tilde {v}}}^{{( \pm )}}}(\eta ,\theta ,t,\lambda {\text{*}}))}}^{2}}d\eta } \right]_{ - }^{ + } + \\ \, + \left[ { - \frac{1}{{{{{\tilde {v}}}^{{( \pm )}}}(0,\theta ,t,\lambda {\text{*}})}}\int\limits_0^{ \pm \infty } \,{{{\tilde {v}}}^{{( \pm )}}}(\eta ,\theta ,t,\lambda {\text{*}})\left( {\eta \frac{{\partial{ \tilde {f}}_{*}^{{( \pm )}}}}{{\partial r}} + \frac{{\partial{ \tilde {f}}_{*}^{{( \pm )}}}}{{\partial \varepsilon }}} \right)d\eta } \right]_{ - }^{ + }. \\ \end{gathered} $

Подставляя это равенствo в (20), с учетом (7) получаем уравнение для нахождения ${{\lambda }_{1}}(\theta ,t)$:

(22)

$\frac{{\partial{ \hat {I}}}}{{\partial r}}{{\lambda }_{1}} + \int\limits_{ - \infty }^{ + \infty } \,\left( { - \tilde {v}(\tau ,\theta ,t,0)\hat {s} + \frac{{\partial{ \tilde {f}}}}{{\partial r}}\tau + \frac{{\partial{ \tilde {f}}}}{{\partial \varepsilon }}} \right)\tilde {v}(\tau ,\theta ,t,0)d\tau = 0,$

где символ “$ \sim $” над функцией означает, что ее значение берется при аргументе $({{\tilde {u}}^{{( \pm )}}}(\tau ,\theta ,t,0),0,\theta ,t,0)$.

Уравнение (22) разрешимо в силу условия (A5), таким образом, коэффициент 1-го порядка в разложении (2) определен.

Выписывая уравнения, определяющие $Q_{i}^{{( \pm )}}$, и следующие приближения в соотношении (15), по стандартной схеме получаем алгебраические задачи для ${{\lambda }_{i}}(\theta ,t)$:

(23)

$\frac{{\partial{ \hat {I}}}}{{\partial r}}{{\lambda }_{i}} + {{f}_{i}} = 0,\quad i \geqslant 1,$

где ${{f}_{i}}(\theta ,t)$ – известные на $i$-м шаге функции.

Таким образом, указан способ определения всех неизвестных функций ${{\lambda }_{i}}(\theta ,t)$ для некритического случая.

2.4. Случай баланса реакции

Случай баланса реакции имеет место, если выполнено следующее требование тождественного равенства нулю функции $I$:

(A'4) Пусть $I \equiv 0$, $(x,y,t) \in {{D}_{t}}$.

Это условие коренным образом отличает сбалансированный, или критический, случай от несбалансированного, поскольку, как будет видно далее, оно изменяет алгоритм построения асимптотики и несколько усложняет доказательство существования решения с построенной асимптотикой.

В отличие от некритического случая, в рассматриваемом критическом случае найти кривую ${{C}_{0}}$, зная лишь $Q_{0}^{{( \pm )}}$, не удается. Действительно, в силу условия (А'4) получаем, что

(24)

${{\tilde {v}}^{{( + )}}}(0,\theta ,t,r) - {{\tilde {v}}^{{( - )}}}(0,\theta ,t,r) \equiv 0.$

Следовательно, уравнения для определения положения кривой переходного слоя будут следовать из равенства нулю коэффициентов при степенях $\varepsilon $ следующих порядков. Из (24) следует, что ${{\tilde {v}}^{{( - )}}}(0,\theta ,t,r) = {{\tilde {v}}^{{( + )}}}(0,\theta ,t,r)$, т.е. $\tilde {v}(\xi ,\theta ,t,r)$ – непрерывная по $\xi $ функция в рассматриваемой области. Поэтому здесь и далее индекс $( \pm )$ в выражениях для $\tilde {v}(\xi ,\theta ,r)$ можно опустить.

Преобразуем выражение при ${{\varepsilon }^{2}}$ в (12), используя (10):

$\begin{gathered} {{G}_{2}}(\varepsilon ,\theta ,t): = \frac{{\partial{ \bar {u}}_{1}^{{( + )}}(\lambda {\text{*}},\theta ,t)}}{{\partial r}} + \frac{{\partial Q_{2}^{{( + )}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }} - \left( {\frac{{\partial{ \bar {u}}_{1}^{{( - )}}(\lambda {\text{*}},\theta ,t)}}{{\partial r}} + \frac{{\partial Q_{2}^{{( - )}}(0,\theta ,t,\lambda {\text{*}})}}{{\partial \xi }}} \right) = \\ \, = \frac{{\partial{ \bar {u}}_{1}^{{( + )}}}}{{\partial r}}(\lambda {\text{*}},\theta ,t) - \frac{{\partial{ \bar {u}}_{1}^{{( - )}}}}{{\partial r}}(\lambda {\text{*}},\theta ,t) + \left[ { - \bar {u}_{1}^{{( \pm )}}(\lambda {\text{*}},\theta ,t)\frac{{\tilde {v}_{\xi }^{{( \pm )}}(0,\theta ,t,\varepsilon )}}{{{{{\tilde {v}}}^{{( \pm )}}}(0,\theta ,t,\varepsilon )}}} \right]_{ - }^{ + } + \\ \end{gathered} $

(25)

$\begin{gathered} \, + \left[ { - \frac{1}{{{{{\tilde {v}}}^{{( \pm )}}}(0,\theta ,t,\lambda {\text{*}})}}\int\limits_0^{ \pm \infty } \,{{{\tilde {v}}}^{{( \pm )}}}(\eta ,\theta ,t,\lambda {\text{*}})r_{2}^{{( \pm )}}(\eta ,\theta ,t,\lambda {\text{*}})d\eta } \right]_{ - }^{ + } = \\ = \left[ { - \frac{1}{{{{{\tilde {v}}}^{{( \pm )}}}(0,\theta ,t,\lambda {\text{*}})}}\left( {\frac{{{{\partial }^{2}}\lambda _{1}^{*}}}{{\mathop {\partial \theta }\nolimits^2 }}{{{\left| {\nabla \theta } \right|}}^{2}}\int\limits_0^{ \pm \infty } \,{{{\tilde {v}}}^{2}}d\xi } \right.} \right. + \frac{{\partial \lambda _{1}^{*}}}{{\partial \theta }}\int\limits_0^{ \pm \infty } \,\tilde {v}\left( {2{{{\left| {\nabla \theta } \right|}}^{2}}\frac{{\partial{ \tilde {v}}}}{{\partial \theta }} + \Delta \theta \tilde {v} - \frac{{\partial \theta }}{{\partial t}}\tilde {v}} \right)d\xi - \\ \end{gathered} $

$\begin{gathered} \, - \left. {\left. {\frac{{\partial \lambda _{1}^{*}}}{{\partial t}}\int\limits_0^{ \pm \infty } \,{{{\tilde {v}}}^{2}}d\xi + \int\limits_0^{ \pm \infty } \,\tilde {v}{{h}_{2}}d\xi } \right)} \right]_{ - }^{ + } = - \frac{1}{{{{{\tilde {v}}}^{{( \pm )}}}(0,\theta ,t,\lambda {\text{*)}}}}\left[ {\frac{{{{\partial }^{2}}\lambda _{1}^{*}}}{{\mathop {\partial \theta }\nolimits^2 }}{{{\left| {\nabla \theta (\lambda {\text{*}},\theta ,t)} \right|}}^{2}}\int\limits_{ - \infty }^\infty \,{{{\tilde {v}}}^{2}}d\xi } \right. + \\ + \;\frac{{\partial \lambda _{1}^{*}}}{{\partial \theta }}\int\limits_{ - \infty }^\infty \,\tilde {v}\left( {2{{{\left| {\nabla \theta } \right|}}^{2}}\frac{{\partial{ \tilde {v}}}}{{\partial \theta }} + \Delta \theta (\lambda {\text{*}},\theta ,t)\tilde {v} - \mathop {\left. {\frac{{\partial \theta (\lambda {\text{*}},\theta ,t)}}{{\partial t}}} \right|}\nolimits_{x,y = {\text{const}}} \tilde {v}} \right)d\xi - \left. {\frac{{\partial \lambda _{1}^{*}}}{{\partial t}}\int\limits_{ - \infty }^\infty \,{{{\tilde {v}}}^{2}}d\xi + \int\limits_{ - \infty }^\infty \,\tilde {v}{{h}_{2}}d\xi } \right], \\ \end{gathered} $

где ${{h}_{2}}(\lambda {\text{*}},\xi ,\theta ,t)$ – известная функция.

Разложим теперь (11) в ряд по степеням $\varepsilon $, используя (2) и учитывая (24):

(26)

$\begin{gathered} {{\left. {\varepsilon {{G}_{1}}} \right|}_{{\varepsilon = 0}}} + {{\varepsilon }^{2}}\left[ {{{\lambda }_{1}}(\theta ,t)\mathop {\left. {\frac{{\partial {{G}_{1}}}}{{\partial \lambda {\text{*}}}}{\kern 1pt} } \right|}\nolimits_{\varepsilon = 0} + {{{\left. {{{G}_{2}}} \right|}}_{{\varepsilon = 0}}}} \right] + \\ + \;{{\varepsilon }^{3}}\left[ {{{\lambda }_{2}}(\theta ,t)\mathop {\left. {\frac{{\partial {{G}_{1}}}}{{\partial \lambda {\text{*}}}}{\kern 1pt} } \right|}\nolimits_{\varepsilon = 0} + \frac{1}{2}\lambda _{1}^{2}(\theta ,t)\mathop {\left. {\frac{{{{\partial }^{2}}{{G}_{1}}}}{{\mathop {\partial \lambda {\text{*}}}\nolimits^2 }}{\kern 1pt} } \right|}\nolimits_{\varepsilon = 0} + \mathop {\left. {\frac{{\partial {{G}_{2}}}}{{\partial \varepsilon }}{\kern 1pt} } \right|}\nolimits_{\varepsilon = 0} + {{{\left. {{{G}_{3}}} \right|}}_{{\varepsilon = 0}}}} \right]... = 0. \\ \end{gathered} $

Теперь приравнивая к нулю коэффициент при $\varepsilon $ в разложении (26), с учетом (21), получаем

(27)

$ - \left( {\Delta \hat {r} - \mathop {\left. {\frac{{\partial{ \hat {r}}}}{{\partial t}}{\kern 1pt} } \right|}\nolimits_{x,y = {\text{const}}} } \right)\int\limits_{ - \infty }^{ + \infty } \,{{\tilde {v}}^{2}}(\xi ,\theta ,t,0){\kern 1pt} d\xi + \int\limits_{ - \infty }^{ + \infty } \,\left( {\frac{{\partial{ \tilde {f}}}}{{\partial r}}\xi + \frac{{\partial{ \tilde {f}}}}{{\partial \varepsilon }}} \right)\tilde {v}(\xi ,\theta ,t,0)d\xi = 0,$

где символ “$ \wedge $” над функцией означает, что ее значение берется при аргументе $(0,\theta ,t)$.

Потребуем выполнение условия

(A'5) Пусть существует кривая ${{C}_{0}}(t) \in \{ \bar {C}(t)\} $, удовлетворяющая уравнению (27).

Таким образом, уравнение для нахождения кривой переходного слоя в нулевом приближении получено. Теперь определим коэффициент ${{\lambda }_{1}}$. Для этого приравняем к нулю член при $\varepsilon $ в разложении (26). Используя (25), получаем уравнение для нахождения ${{\lambda }_{1}}(\theta ,t)$:

(28)

$ - \frac{{\partial {{\lambda }_{1}}}}{{\partial t}}m(\theta ,t) + \frac{{{{\partial }^{2}}{{\lambda }_{1}}}}{{\mathop {\partial \theta }\nolimits^2 }}a(\theta ,t) + \frac{{\partial {{\lambda }_{1}}}}{{\partial \theta }}b(\theta ,t) + {{\lambda }_{1}}c(\theta ,t) = {{g}_{1}}(\theta ,t),$

где

$\begin{gathered} m(\theta ,t): = \int\limits_{ - \infty }^{ + \infty } \,{{{\tilde {v}}}^{2}}(\xi ,\theta ,t,0),\quad a(\theta ,t): = {{\left| {\nabla \hat {\theta }} \right|}^{2}}m(\theta ,t), \\ b(\theta ,t): = \int\limits_{ - \infty }^\infty \,\tilde {v}\left( {2{{{\left| {\nabla \theta } \right|}}^{2}}\tfrac{{\partial{ \tilde {v}}}}{{\partial \theta }} + \Delta \theta (\lambda {\text{*}},\theta ,t)\tilde {v} - \mathop {\left. {\tfrac{{\partial \theta (\lambda {\text{*}},\theta ,t)}}{{\partial t}}} \right|}\nolimits_{x,y = {\text{const}}} \tilde {v}} \right)d\xi {\kern 1pt} , \\ \end{gathered} $$c(\theta ,t): = \mathop {\left. {\tfrac{{\partial \left[ { - \left( {\Delta r - \mathop {\left. {\tfrac{{\partial r}}{{\partial t}}{\kern 1pt} } \right|}\nolimits_{x,y = {\text{const}}} } \right)\int\limits_{ - \infty }^{ + \infty } {{{{\tilde {v}}}^{2}}d\xi } + \int\limits_{ - \infty }^{ + \infty } {\left( {\tfrac{{\partial{ \tilde {f}}}}{{\partial r}}\xi + \tfrac{{\partial{ \tilde {f}}}}{{\partial \varepsilon }}} \right)\tilde {v}d\xi } } \right]}}{{\partial \lambda {\text{*}}}}} \right|}\nolimits_{\lambda {\text{*}} = 0} ,\quad {{g}_{1}}(\theta ,t): = - \int\limits_{ - \infty }^{ + \infty } {\tilde {v}{{h}_{2}}d\xi } .$

Разделив уравнение для ${{\lambda }_{1}}$ (28) на коэффициент при производной по времени $m(\theta ,t) > 0$, получим

(29)

$ - \frac{{\partial {{\lambda }_{1}}}}{{\partial t}} + \frac{{{{\partial }^{2}}{{\lambda }_{1}}}}{{\mathop {\partial \theta }\nolimits^2 }}\tilde {a}(\theta ,t) + \frac{{\partial {{\lambda }_{1}}}}{{\partial \theta }}\tilde {b}(\theta ,t) + {{\lambda }_{1}}\tilde {c}(\theta ,t) = {{\tilde {g}}_{1}}(\theta ,t),$

где $\tilde {a}(\theta ,t) = \tfrac{{a(\theta ,t)}}{{m(\theta ,t)}}$ и т.д.

Пусть функции $\tilde {\beta }(t)$ и $\tilde {\alpha }(t)$ определяются из уравнений

(30)

$\frac{{d\tilde {\beta }}}{{dt}} - \bar {c}(t)\tilde {\beta } = p,\quad \frac{{d\tilde {\alpha }}}{{dt}} - \bar {c}(t)\tilde {\alpha } = - p,$

где $\bar {c}(t) = \mathop {max}\limits_{\theta \in [0,2\pi )} \,\tilde {c}(\theta ,t)$, $p$ – некоторая константа, значение которой будет определено далее.

Пусть выполнены дополнительные условия: $\tilde {\beta }(t) = \tilde {\beta }(t + T)$, $\tilde {\alpha }(t) = \tilde {\alpha }(t + T)$.

Введем в рассмотрение оператор

$L: = - \frac{\partial }{{\partial t}} + \tilde {a}(\theta ,t)\frac{{{{\partial }^{2}}}}{{\mathop {\partial \theta }\nolimits^2 }} + \tilde {b}(\theta ,t)\frac{\partial }{{\partial \theta }} + \tilde {c}(\theta ,t) - {{\tilde {g}}_{1}}(\theta ,t).$

Тогда

$\begin{gathered} L[\tilde {\beta }] = - \frac{{\partial{ \tilde {\beta }}}}{{\partial t}} + \tilde {\beta }\tilde {c}(\theta ,t) - {{{\tilde {g}}}_{1}}(\theta ,t) = - p + \left( {\tilde {c}(\theta ,t) - \bar {c}(t)} \right)\tilde {\beta } - {{{\tilde {g}}}_{1}}(\theta ,t), \\ L[\tilde {\alpha }] = - \frac{{\partial{ \tilde {\alpha }}}}{{\partial t}} + \tilde {\alpha }\tilde {c}(\theta ,t) - {{{\tilde {g}}}_{1}}(\theta ,t) = p + \left( {\tilde {c}(\theta ,t) - \bar {c}(t)} \right)\tilde {\alpha } - {{{\tilde {g}}}_{1}}(\theta ,t). \\ \end{gathered} $

Функции $\tilde {\beta }(t)$ и $\tilde {\alpha }(t)$ могут быть найдены в явном виде:

(31)

$\tilde {\beta }(t) = \Phi (t){{\tilde {\beta }}_{0}} + \Phi (t)\int\limits_0^t \,{{\Phi }^{{ - 1}}}(s)pds,\quad \tilde {\alpha }(t) = \Phi (t){{\tilde {\alpha }}_{0}} - \Phi (t)\int\limits_0^t \,{{\Phi }^{{ - 1}}}(s)pds,$

где

$\mathop {\tilde {\beta }}\nolimits_0 = \frac{{\Phi (T)}}{{1 - \Phi (T)}}\int\limits_0^T \,{{\Phi }^{{ - 1}}}(s)pds,\quad \mathop {\tilde {\alpha }}\nolimits_0 = - \frac{{\Phi (T)}}{{1 - \Phi (T)}}\int\limits_0^T \,{{\Phi }^{{ - 1}}}(s)pds,\quad \Phi (t) = exp\left( {\int\limits_0^t \,\bar {c}(\tau )d\tau } \right).$

Нам потребуется условие

(A'6) Пусть $\int_0^T {\bar {c}(\tau )d\tau < 0} $ для $t \in R$.

Для постановки задачи для нахождения ${{\lambda }_{1}}(\theta ,t)$ нам не хватает следующих периодических граничных условий:

(32)

$\begin{gathered} {{\lambda }_{1}}(\theta ,t) = {{\lambda }_{1}}(\theta ,t + T),\quad {{\lambda }_{1}}(\theta ,t) = {{\lambda }_{1}}(\theta + {{\Theta }_{0}},t), \\ \frac{{\partial {{\lambda }_{1}}(\theta ,t)}}{{\partial \theta }} = \frac{{\partial {{\lambda }_{1}}(\theta + {{\Theta }_{0}},t)}}{{\partial \theta }},\quad t \in R,\quad \theta \in R. \\ \end{gathered} $

Уравнение (28) с граничными условиями (32) имеет единственное решение в силу условия (A'6). В этом легко убедиться, взяв в качестве верхнего решения функцию $\tilde {\beta }(t)$, а в качестве нижнего решения $\tilde {\alpha }(t)$. Действительно, в силу условия (A'6) имеем $\tilde {\beta }(t) > 0$, $\tilde {\alpha }(t) < 0$, $\tilde {c}(\theta ,t) - \bar {c}(t) \leqslant 0$ для $t \in R$. Выберем константу

$p > \mathop {max}\limits_{\theta \in [0,2\pi )t \in R} \left| {{{{\tilde {g}}}_{1}}(\theta ,t)} \right|.$

В итоге получаем, что $L[\beta (t)] < 0$, $L[\alpha (t)] > 0$, $t \in R$, а упорядоченность верхнего и нижнего решения выполнена автоматически. Таким образом, коэффициент ${{\lambda }_{1}}$ в разложении (2) определен.

Выписывая уравнения, определяющие $Q_{i}^{{( \pm )}}$, и следующие приближения в соотношении (26), получаем задачи для ${{\lambda }_{i}}(\theta ,t)$:

(33)

$ - \frac{{\partial {{\lambda }_{i}}}}{{\partial t}}m(\theta ,t) + \frac{{{{\partial }^{2}}{{\lambda }_{i}}}}{{\mathop {\partial \theta }\nolimits^2 }}a(\theta ,t) + \frac{{\partial {{\lambda }_{i}}}}{{\partial \theta }}b(\theta ,t) + {{\lambda }_{i}}c(\theta ,t) = {{g}_{i}}(\theta ,t),$

где ${{g}_{i}}(\theta ,t)$-известные на $i$-м шаге Т-периодические функции $t$. Эти задачи с соответствующими граничными условиями также однозначно разрешимы в силу условия (A'6).

Таким образом, формальная асимптотика для кривой перехода в критическом случае полностью построена.

Замечание 2. В отличие от случая нелинейности кубического типа (см., например, [10]), в рассматриваемом случае разрывной реакции на фазовой плоскости $(\tilde {u},\tilde {v})$ сепаратриса, соединяющая точки покоя типа седло ${{\varphi }^{{( - )}}}$ и ${{\varphi }^{{( + )}}}$, оказывается негладкой кривой. Действительно,

$\mathop {\left. {\frac{{d{{{\tilde {v}}}^{{( + )}}}}}{{d{{{\tilde {u}}}^{{( + )}}}}}} \right|}\nolimits_{\xi = 0} - \mathop {\left. {\frac{{d{{{\tilde {v}}}^{{( - )}}}}}{{d{{{\tilde {u}}}^{{( - )}}}}}} \right|}\nolimits_{\xi = 0} = \mathop {\left. {\frac{{\tilde {f}_{*}^{{( + )}}}}{{{{{\tilde {v}}}^{{( + )}}}}}} \right|}\nolimits_{\xi = 0} - \mathop {\left. {\frac{{\tilde {f}_{*}^{{( - )}}}}{{{{{\tilde {v}}}^{{( - )}}}}}} \right|}\nolimits_{\xi = 0} = \frac{{f(0 + 0,0,\theta ,t,0) - f(0 - 0,0,\theta ,t,0)}}{{\tilde {v}}} < 0.$

(См. далее пример в п. 6.2 и иллюстрацию к нему на фиг. 3б.)

3. ОБОСНОВАНИЕ ПОСТРОЕННОЙ АСИМПТОТИКИ

Обозначим через $U_{n}^{{( \pm )}}(x,y,t,\varepsilon )$ частичные суммы порядка $n$ построенных асимптотических рядов, в которых аргумент $\xi $ у $Q$-функций заменен на

${{\xi }_{{n + 1}}} = \left( {r - \sum\limits_{i = 1}^{n + 1} \,{{\varepsilon }^{i}}{{\lambda }_{i}}(\theta ,t)} \right){\text{/}}\varepsilon ,$

а $\lambda {\text{*}}$ на

$\lambda _{{n + 1}}^{*} = \sum\limits_{i = 1}^{n + 1} \,{{\varepsilon }^{i}}{{\lambda }_{i}}(\theta ,t),$

найденные по алгоритму, изложенному в п. 2.3 для некритического и п. 2.4 для критического случаев. В подобластях $\bar {D}_{n}^{{( - )}}$ и $\bar {D}_{n}^{{( + )}}$, на которые область $\bar {D}$ разделяется кривой $r = \lambda _{{n + 1}}^{*}$, при построении $U_{n}^{{( \pm )}}(x,y,t,\varepsilon )$ используются функции ${{Q}^{{( - )}}}$ и ${{Q}^{{( + )}}}$ соответственно.

В этом пункте проводится доказательство существования решения задачи (1), близкого к построенной асимптотике $U_{n}^{{( \pm )}}(x,y,t,\varepsilon )$. Отметим, что для достижения близости порядка $O({{\varepsilon }^{{n + 1}}})$ в двух рассматриваемых случаях требуется строить верхние и нижние барьеры различных порядков (см. далее). Но, поскольку они в обоих случаях отвечают асимптотике $U_{n}^{{( \pm )}}(x,y,t,\varepsilon )$, за ними условимся сохранять индекс $n$.

Сформулируем и докажем соответствующие теоремы для каждого случая.

3.1. Несбалансированный случай

Теорема 1. Если выполнены условия (А1)–(А5), то при достаточно малых $\varepsilon $ существует решение $u(x,y,t,\varepsilon )$ задачи (1), причем имеет место оценка

$\left| {{{U}_{n}}(x,y,t,\varepsilon ,\varepsilon ) - u(x,y,t,\varepsilon )} \right| < C{{\varepsilon }^{{n + 1}}},\quad (x,y) \in \bar {D},\quad t \in R.$

Доказательство. Для доказательства этого утверждения воспользуемся асимптотическим методом дифференциальных неравенств. Заметим, что функция $f$ в силу наложенных на нее условий (A1)–(A3) имеет в точке $u = 0$ скачок определенного знака: $f(0 + 0,x,y,t,\varepsilon ) - $ $ - \;f(0 - 0,x,y,t,\varepsilon ) \leqslant 0$. Эта функция, очевидно, является каратеодориевой и для нее справедлив результат работ [16], [17] и их развития на случай разрывного источника в [18]. Верхнее и нижнее решения задачи (1) будем строить путем модификации членов асимптотического ряда аналогично тому, как это делалось в [10]:

(34)

$\begin{gathered} {{\beta }_{n}}(x,y,t,\varepsilon ) = \bar {u}_{0}^{{( \pm )}}(x,y,t) + \varepsilon \bar {u}_{1}^{{( \pm )}}(x,y,t) + \ldots + {{\varepsilon }^{{n + 2}}}\bar {u}_{{n + 2}}^{{( \pm )}}(x,y,t) + Q_{0}^{{( \pm )}}({{\xi }_{\beta }},\theta ,t,{{\lambda }_{{n\beta }}}) + \\ + \;\varepsilon Q_{1}^{{( \pm )}}({{\xi }_{\beta }},\theta ,t,\varepsilon ) + \ldots + {{\varepsilon }^{{n + 2}}}{{q}^{{( \pm )}}}({{\xi }_{\beta }},\theta ,t,\varepsilon ) + {{\Pi }_{\beta }}(\tau ,{{\theta }_{\Gamma }},t,\varepsilon ) + {{\varepsilon }^{{n + 2}}}(\gamma + Q_{{n + 2}}^{{( \pm )}}({{\xi }_{\beta }},\theta ,t,\varepsilon )), \\ \end{gathered} $

где ${{\lambda }_{{n\beta }}}(\theta ,t,\varepsilon ) = \lambda _{{n + 1}}^{*}(\theta ,t,\varepsilon ) + {{\varepsilon }^{{n + 2}}}({{\lambda }_{{n + 2}}}(\theta ,t,\varepsilon ) - {{\delta }_{0}})$, ${{\xi }_{\beta }} = (x - {{\lambda }_{{n\beta }}}(\theta ,t,\varepsilon )){\text{/}}\varepsilon $,$\gamma > 0$ – постоянная, обеспечивающая выполнение необходимого дифференциального неравенства, ${{\delta }_{0}} > 0$ – константа, обеспечивающая неравенства для скачка производных на кривой переходного слоя. Функции $Q_{i}^{{( \pm )}}({{\xi }_{\beta }},\theta ,t,\varepsilon )$ определяются из задач (9), где $\lambda {\text{*}}$ заменена на ${{\lambda }_{{n\beta }}}$. Функции $q_{\beta }^{{( \pm )}}$ необходимы для компенсации изменений, вносимой постоянной $\gamma $, и определяются из задач

(35)

$\begin{gathered} \frac{{{{\partial }^{2}}q_{\beta }^{{( \pm )}}(\xi ,\theta ,t,\varepsilon )}}{{\mathop {\partial \xi }\nolimits^2 }} - \frac{{\partial f}}{{\partial u}}(u_{\beta }^{{( \pm )}},{{\lambda }_{{n\beta }}},\theta ,t,0)q_{\beta }^{{( \pm )}}(\xi ,\theta ,t,\varepsilon ) = {{r}_{\beta }}(\xi ,\theta ,t,\varepsilon ), \\ q_{\beta }^{{( \pm )}}(0,\theta ,t,\varepsilon ) + \gamma = 0,\quad q_{\beta }^{{( \pm )}}( \pm \infty ,\theta ,t,\varepsilon ) = 0, \\ \end{gathered} $

где

(36)

$\tilde {u}_{\beta }^{{( \pm )}} = {{\tilde {u}}^{{( \pm )}}}(\xi ,\theta ,t,{{\lambda }_{\beta }}),\quad {{r}_{\beta }}(\xi ,t,\varepsilon ) = \gamma \left( {\frac{{\partial f}}{{\partial u}}(\tilde {u}_{\beta }^{{( \pm )}},{{\lambda }_{{n\beta }}},t,0) - \frac{{\partial f}}{{\partial u}}({{\varphi }^{{( \pm )}}},{{\lambda }_{{n\beta }}},t,0)} \right).$

Функции ${{\Pi }_{\beta }}$ обеспечивают выполнение необходимых дифференциальных неравенств вблизи границы $\Gamma $ (их построение рассматривается, например, в [13]). Здесь для функций асимптотики во внутренней относительно кривой ${{C}_{\beta }}(t,\varepsilon ):\{ r = {{\lambda }_{\beta }}(t,\theta ,\varepsilon )\} $ области используем обозначение $( + )$, а во внешней – $( - )$. Нижнее решение ${{\alpha }_{n}}(x,y,t,\varepsilon )$ имеет аналогичную структуру.

Необходимые дифференциальные неравенства проверяются прямым вычислением, аналогично работе [19]. Для верхнего решения имеем

${{N}_{\varepsilon }}{{\beta }_{n}} = {{\varepsilon }^{2}}\left( {\Delta - \frac{\partial }{{\partial t}}} \right){{\beta }_{n}} - f({{\beta }_{n}},x,y,t,\varepsilon ) = - {{\varepsilon }^{{n + 2}}}\frac{{\partial{ \bar {f}}}}{{\partial u}}\gamma + O({{\varepsilon }^{{n + 3}}}),$

где черта над функцией означает, что ее значение берется при аргументе $({{u}_{0}},0,\theta ,t,0)$. В силу условия (А3) при достаточно малом $\varepsilon $ при любом $\gamma > 0$ имеем ${{N}_{\varepsilon }}{{\beta }_{n}} < 0$.

Аналогичные неравенства вблизи границы выполняются за счет модификации погранслойных функций (см., например, [13]) и их проверка в данной работе не рассматривается.

Доказательство упорядоченности верхнего и нижнего решений, т.е. неравенства ${{\beta }_{n}}(x,y,t,\varepsilon ) \geqslant {{\alpha }_{n}}(x,y,t,\varepsilon )$, а также неравенства для скачка производной:

$\begin{gathered} {{\left. {\left( {\frac{{\partial \beta _{n}^{ + }}}{{\partial r}} - \frac{{\partial \beta _{n}^{ - }}}{{\partial r}}} \right)} \right|}_{r}} = {{\varepsilon }^{{n + 2}}}\frac{1}{{\tilde {v}(0,\theta ,t,0)}}\left( {\frac{{\partial I(0,\theta ,t)}}{{\partial r}}{{\delta }_{0}} - \gamma B(\theta ,t)} \right) < 0, \\ B(\theta ,t): = \int\limits_{ - \infty }^{ + \infty } {({{{\tilde {f}}}_{u}} - {{{\bar {f}}}_{u}})\tilde {v}(\xi ,\theta ,t,0)d\xi } \\ \end{gathered} $

(и аналогичного неравенства для ${{\alpha }_{n}}$) проводится так же, как в работе [19], причем для последнего существенно условие (А5).

Из известных теорем сравнения следует существование решения задачи (1), удовлетворяющего неравенству ${{\alpha }_{n}}(x,y,t,\varepsilon ) \leqslant u(x,y,t,\varepsilon ) \leqslant {{\beta }_{n}}(x,y,t,\varepsilon )$, причем, как следует из построения, ${{\alpha }_{n}}(x,y,t,\varepsilon ) - {{\beta }_{n}}(x,y,t,\varepsilon ) = O({{\varepsilon }^{{n + 1}}})$, откуда и получаем утверждение теоремы.

3.2. Критический случай

Теорема 2. Если выполнены условия (А1)–(А3), (А'4)–(A'6), то при достаточно малых $\varepsilon $ существует решение $u(x,y,t,\varepsilon )$ задачи (1), причем имеет место оценка

$\left| {{{U}_{n}}(x,y,t,\varepsilon ) - u(x,y,t,\varepsilon )} \right| < C{{\varepsilon }^{{n + 1}}},\quad (x,y) \in \bar {D},\quad t \in R.$

Доказательство. Как и в предыдущем пункте, асимптотический метод дифференциальных неравенств позволяет обосновать построенную асимптотику. Верхнее и нижнее решения задачи (1) будем строить путем модификации членов асимптотического ряда в виде

$\begin{gathered} {{\mathfrak{B}}_{n}}(x,y,t,\varepsilon ) = \bar {u}_{0}^{{( \pm )}}(x,y,t) + \varepsilon \bar {u}_{1}^{{( \pm )}}(x,y,t) + \ldots + {{\varepsilon }^{{n + 3}}}\bar {u}_{{n + 3}}^{{( \pm )}}(x,y,t) + Q_{0}^{{( \pm )}}({{\xi }_{\beta }},\theta ,t,{{\lambda }_{{n\beta }}}) + \\ + \;\varepsilon Q_{1}^{{( \pm )}}({{\xi }_{\beta }},\theta ,t,\varepsilon ) + \ldots + {{\varepsilon }^{{n + 3}}}Q_{{n + 3}}^{{( \pm )}}({{\xi }_{\beta }},\theta ,t,\varepsilon ) + {{\Pi }_{\mathfrak{B}}}(\tau ,{{\theta }_{\Gamma }},t,\varepsilon ) + {{\varepsilon }^{{n + 3}}}(\gamma + q_{\mathfrak{B}}^{{( \pm )}}({{\xi }_{\beta }},\theta ,t,\varepsilon )), \\ \end{gathered} $

где ${{\lambda }_{{n\mathfrak{B}}}}(\theta ,t,\varepsilon ) = \lambda _{n}^{*}(\theta ,t,\varepsilon ) + {{\varepsilon }^{{n + 2}}}({{\lambda }_{{n + 2}}}(\theta ,t) - \nu )$, ${{\xi }_{\mathfrak{B}}} = (x - {{\lambda }_{{n\mathfrak{B}}}}(\theta ,t,\varepsilon )){\text{/}}\varepsilon $,$\gamma > 0$ – некоторая постоянная, обеспечивающая выполнение необходимого дифференциального неравенства, $\nu (x,y,t) > 0$ – функция, обеспечивающая неравенства для скачка производных на кривой переходного слоя, которая будет уточнена ниже. Функции $q_{\mathfrak{B}}^{{( \pm )}}$ необходимы для компенсации изменений, вносимой постоянной $\gamma $ и определяются из задач (35), в которых ${{\lambda }_{{n\beta }}}$ заменена на ${{\lambda }_{{n\mathfrak{B}}}}$. Функции ${{\Pi }_{\mathfrak{B}}}$ обеспечивают выполнение необходимых дифференциальных неравенств вблизи границы $\Gamma $, они такие же, как и в представлении (34). Здесь для функций асимптотики во внутренней относительно замкнутой кривой ${{C}_{\mathfrak{B}}}(t,\varepsilon ){\kern 1pt} :\;r = {{\lambda }_{{n\mathfrak{B}}}}(t,\theta ,\varepsilon )$ области используем обозначение $( + )$, а во внешней – $( - )$. Нижнее решение ${{\mathfrak{A}}_{n}}(x,y,t,\varepsilon )$ имеет аналогичную структуру.

Необходимые дифференциальные неравенства проверяются прямым вычислением:

${{N}_{\varepsilon }}{{\mathfrak{B}}_{n}} = {{\varepsilon }^{2}}\left( {\Delta - \frac{\partial }{{\partial t}}} \right){{\mathfrak{B}}_{n}} - f({{\mathfrak{B}}_{n}},x,y,t,\varepsilon ) = - {{\varepsilon }^{{n + 3}}}\frac{{\partial{ \bar {f}}}}{{\partial u}}\gamma + O({{\varepsilon }^{{n + 4}}}).$

В силу условия (А3) при достаточно малом $\varepsilon $ при любом $\gamma > 0$ имеем ${{N}_{\varepsilon }}{{\mathfrak{B}}_{n}} < 0$.

Доказательство упорядоченности выполняется совершенно аналогично тому, как это было сделано в работе [20].

Для доказательства теоремы остается проверить условие для скачка производной.

Обозначим через

$\frac{{\partial{ \mathfrak{B}}_{n}^{{( - )}}({{\lambda }_{{n\mathfrak{B}}}}(t,\theta ,\varepsilon ),\theta ,t,\varepsilon )}}{{\partial r}},\quad \frac{{\partial{ \mathfrak{B}}_{n}^{{( + )}}({{\lambda }_{{n\beta }}}(t,\theta ,\varepsilon ),\theta ,t,\varepsilon )}}{{\partial r}}$

предельные значения производных по разные стороны от кривой $r = {{\lambda }_{{n\mathfrak{B}}}}(t,\theta ,\varepsilon )$. Тогда получим

(37)

$\begin{gathered} \varepsilon \left( {\frac{{\partial{ \mathfrak{B}}_{n}^{{( + )}}({{\lambda }_{{n\mathfrak{B}}}}(t,\theta ,\varepsilon ),\theta ,t,\varepsilon )}}{{\partial r}} - \frac{{\partial{ \mathfrak{B}}_{n}^{{( - )}}({{\lambda }_{{n\mathfrak{B}}}}(t,\theta ,\varepsilon ),\theta ,t,\varepsilon )}}{{\partial r}}} \right) = \\ = \frac{{{{\varepsilon }^{{n + 3}}}}}{{\tilde {v}(0,\theta ,t,0)}}\left( { - \frac{{d\nu }}{{dt}}m(t) + a(\theta ,t)\frac{{{{\partial }^{2}}\nu }}{{\mathop {\partial \theta }\nolimits^2 }} + b(\theta ,t)\frac{{\partial \nu }}{{\partial \theta }} + c(t)\nu - \gamma B(\theta ,t)} \right) + O({{\varepsilon }^{{n + 4}}}). \\ \end{gathered} $

Пусть $\nu (x,y,t) = \tilde {\beta }(t) > 0$ (функция $\tilde {\beta }(t)$ определена в (30)). Очевидно, что условие (А'6) обеспечивает отрицательный знак скачка производной в (37).

Все соответствующие неравенства для нижнего решения ${{\mathfrak{A}}_{n}}(x,t,\varepsilon )$ проверяются аналогично.

Таким образом, все необходимые условия известных теорем о дифференциальных неравенствах выполнены, а значит, существует решение задачи (1), удовлетворяющее неравенству ${{\mathfrak{A}}_{n}}(x,y,t,\varepsilon ) \leqslant u(x,t,\varepsilon ) \leqslant {{\mathfrak{B}}_{n}}(x,y,t,\varepsilon )$, причем, как следует из построения, ${{\mathfrak{A}}_{n}}(x,y,t,\varepsilon ) - $ $ - \;{{\mathfrak{B}}_{n}}(x,y,t,\varepsilon ) = O({{\varepsilon }^{{n + 1}}})$, что и влечет за собой утверждение теоремы.

4. АСИМПТОТИЧЕСКАЯ УСТОЙЧИВОСТЬ РЕШЕНИЯ

Периодические решения задачи (1) можно рассматривать как решения соответствующей начально-краевой задачи на полубесконечном промежутке времени:

(38)

$\begin{gathered} {{N}_{\varepsilon }}(v): = {{\varepsilon }^{2}}\left( {\Delta v - \frac{{\partial v}}{{\partial t}}} \right) - f(v,x,y,t,\varepsilon ) = 0, \\ (x,y,t) \in {{D}_{{t + }}}: = \{ (x,y,t) \in {{R}^{3}}:(x,y) \in D,\;0 < t < \infty \} , \\ \frac{{\partial u}}{{\partial {{n}_{\Gamma }}}}(x,y,t,\varepsilon ) = 0,\quad (x,y) \in \Gamma ,\quad 0 < t < \infty , \\ v(x,y,0,\varepsilon ) = {{v}^{0}}(x,y,\varepsilon ),\quad (x,y) \in D. \\ \end{gathered} $

Очевидно, что если ${{v}^{0}}(x,y,\varepsilon ) = u(x,y,0,\varepsilon )$, где $u(x,y,t,\varepsilon )$ – решение периодической задачи (1), то и задача (38) имеет решение $v(x,y,t,\varepsilon ) = u(x,y,t,\varepsilon )$. Исследование его устойчивости основано на асимптотическом методе дифференциальных неравенств. Будем искать верхнее и нижнее решения задачи (38) в виде $\alpha (x,y,t,\varepsilon ) = u(x,y,t,\varepsilon ) + {{e}^{{ - \Lambda (\varepsilon )t}}}({{\alpha }_{n}}(x,y,t,\varepsilon ) - u(x,y,t,\varepsilon ))$, $\beta (x,y,t,\varepsilon ) = $ $ = u(x,y,t,\varepsilon ) + {{e}^{{ - \Lambda (\varepsilon )t}}}({{\beta }_{n}}(x,y,t,\varepsilon ) - u(x,y,t,\varepsilon ))$, где $\Lambda (\varepsilon ) > 0$ будет указана ниже. Очевидно, что $\alpha < \beta $, и для проверки классических теорем о дифференциальных неравенствах для параболических систем из [21] достаточно показать, что ${{N}_{\varepsilon }}\beta < 0$, ${{N}_{\varepsilon }}\alpha > 0$. Подставляя указанные выше выражения для функций $\alpha $ и $\beta $ и учитывая, что $u$ является решением уравнения (1), нетрудно получить требуемые неравенства как для некритического, так и для критического случаев. Например, выражение для ${{N}_{\varepsilon }}\beta $ преобразуется к такому виду (для краткости в следующих формулах все аргументы у функций $f,\;{{f}_{u}}$ опущены, кроме первого):

$\begin{gathered} {{N}_{\varepsilon }}\beta = {{e}^{{ - \Lambda t}}}\left\{ {\,\left[ {{{\varepsilon }^{2}}\left( { - \frac{{\partial {{\beta }_{n}}}}{{\partial t}} + \Delta {{\beta }_{n}}} \right) - f({{\beta }_{n}})} \right] + \left[ {{{\varepsilon }^{2}}\left( { - \frac{{\partial u}}{{\partial t}} + \Delta u} \right) - f(u)} \right]} \right. + \\ \, + \left. {[f({{\beta }_{n}}) - f(u) - f_{u}^{*}({{\beta }_{n}} - u)] + {{\varepsilon }^{2}}\Lambda ({{\beta }_{n}} - u)} \right\}. \\ \end{gathered} $

Здесь символ “$ * $” справа от функции означает, что ее значение берется при аргументе $u(x,y,t,\varepsilon ) + \theta {{e}^{{ - \Lambda (\varepsilon )t}}}({{\alpha }_{n}}(x,y,t,\varepsilon ) - u(x,y,t,\varepsilon ))$, $0 < \theta < 1$.

Проведем оценки для каждого случая.

В несбалансированном случае воспользуемся тем, что

${{\varepsilon }^{2}}\left( { - \frac{{\partial {{\beta }_{n}}}}{{\partial t}} + \Delta {{\beta }_{n}}} \right) - f({{\beta }_{n}}) = - \gamma {{f}_{u}}{{\varepsilon }^{{n + 2}}} + O({{\varepsilon }^{{n + 3}}}),$

где $\gamma > 0$, ${{\beta }_{n}} - u = O({{\varepsilon }^{{n + 1}}})$, $f({{\beta }_{n}}) - F(u) - f_{u}^{*}({{\beta }_{n}} - u) = O({{\varepsilon }^{{2n + 2}}})$ и выбирая $\Lambda (\varepsilon ) = {{\Lambda }_{0}}$, а $\gamma $ достаточно большим, получаем

${{N}_{\varepsilon }}\beta = {{e}^{{ - {{\Lambda }_{0}}t}}}( - \gamma {{f}_{u}}{{\varepsilon }^{{n + 2}}} + O({{\varepsilon }^{{2n + 2}}}) + {{\Lambda }_{0}}O({{\varepsilon }^{{n + 3}}})) < 0$

при $n \geqslant 0$. Аналогично проверяется неравенство ${{N}_{\varepsilon }}\alpha > 0$. Таким образом, в некритическом случае построенное выше периодическое решение устойчиво с областью влияния, по крайней мере, $[{{\alpha }_{0}}(x,y,0,\varepsilon ),\;{{\beta }_{0}}(x,y,0,\varepsilon )]$, ширина этой области составляет величину порядка $O({{\varepsilon }^{1}}).$

В критическом случае проведем аналогичные оценки:

${{\varepsilon }^{2}}\left( { - \frac{{\partial {{\mathfrak{B}}_{n}}}}{{\partial t}} + \Delta {{\mathfrak{B}}_{n}}} \right) - f({{\mathfrak{B}}_{n}}) = - \gamma {{\bar {f}}_{u}}{{\varepsilon }^{{n + 3}}} + O({{\varepsilon }^{{n + 4}}}),$

где $\gamma > 0$, ${{\mathfrak{B}}_{n}} - u = O({{\varepsilon }^{{n + 1}}})$, $f({{\mathfrak{B}}_{n}}) - f(u) - f_{u}^{*}({{\mathfrak{B}}_{n}} - u) = O({{\varepsilon }^{{2n + 2}}})$. Выбирая $\Lambda (\varepsilon ) = {{\Lambda }_{0}}$ достаточно малым, а $\gamma $ достаточно большим, получаем

${{N}_{\varepsilon }}\mathfrak{B} = {{e}^{{ - {{\Lambda }_{0}}t}}}( - \gamma {{\bar {f}}_{u}}{{\varepsilon }^{{n + 3}}} + O({{\varepsilon }^{{2n + 2}}}) + {{\Lambda }_{0}}O({{\varepsilon }^{{n + 3}}})) < 0$

при $n \geqslant 1$. Аналогично проверяется неравенство ${{N}_{\varepsilon }}\mathfrak{A} > 0$. Итак, построенное выше периодическое решение устойчиво с областью влияния, по крайней мере, $[{{\mathfrak{A}}_{1}}(x,y,0,\varepsilon ),{{\mathfrak{B}}_{1}}(x,y,0,\varepsilon )]$, ширина этой области – величина порядка $O({{\varepsilon }^{2}}).$

Таким образом, справедливы следующие теоремы.

Теорема 3. Пусть выполнены условия (А1)–(А5). Тогда решение $u(x,y,t,\varepsilon )$ задачи (1) асимптотически устойчиво по Ляпунову с областью устойчивости, по крайней мере, $[{{\alpha }_{0}}(x,y,0,\varepsilon ),{{\beta }_{0}}(x,y,0,\varepsilon )]$, и, следовательно, $u(x,y,t,\varepsilon )$ – единственное решение задачи (1) в этой области.

Теорема 4. Пусть выполнены условия (А1)–(А3), (А'4)–(А'6). Тогда решение $u(x,y,t,\varepsilon )$ задачи (1) асимптотически устойчиво по Ляпунову с областью устойчивости, по крайней мере, $[{{\mathfrak{A}}_{1}}(x,y,0,\varepsilon ),{{\mathfrak{B}}_{1}}(x,y,0,\varepsilon )]$, и, следовательно, $u(x,y,t,\varepsilon )$ – единственное решение задачи (1) в этой области.

5. ПРИМЕР ПЕРИОДИЧЕСКОЙ КОНТРАСТНОЙ СТРУКТУРЫ ТИПА СТУПЕНЬКИ

5.1. Несбалансированный случай

Рассмотрим задачу:

(39)

$\begin{gathered} {{N}_{\varepsilon }}(u): = {{\varepsilon }^{2}}\left( {\Delta u - \frac{{\partial u}}{{\partial t}}} \right) - f(u,x,y,t) = 0,\quad D = \{ (x,y):{{x}^{2}} + {{y}^{2}} < 100\} , \\ (x,y,t) \in {{D}_{t}}: = \{ (x,y,t) \in {{R}^{3}}:(x,y) \in D,\;t \in R\} , \\ \frac{{\partial u}}{{\partial {{n}_{\Gamma }}}}(x,y,t,\varepsilon ) = 0,\quad (x,y) \in \Gamma ,\quad t \in R, \\ u(x,y,t,\varepsilon ) = u(x,y,t + T,\varepsilon ),\quad (x,y) \in D,\quad t \in R, \\ \end{gathered} $

где

$f\left( {u,x,y,t} \right) = \left\{ \begin{gathered} {{f}^{{( + )}}}\left( {u,x,y,t} \right) = u - {{d}^{2}}(t),\quad {\text{если}}\quad u \geqslant 0\left( {x,y} \right) \in \bar {D},\quad t \in R; \hfill \\ {{f}^{{( - )}}}\left( {u,x,y,t} \right) = u + {{x}^{2}} + {{y}^{2}},\quad {\text{если}}\quad u < 0\left( {x,y} \right) \in \bar {D},\quad t \in R, \hfill \\ \end{gathered} \right.$

$d(t) > 0$ – некоторая T – периодическая функция.

Для задачи (39) получаем, что ${{\varphi }^{{( - )}}}(x,y,t) = - ({{x}^{2}} + {{y}^{2}})$, ${{\varphi }^{{( + )}}}(x,y,t) = {{d}^{2}}(t)$, тогда

$f\left( {u,x,y,t} \right) = \left\{ \begin{gathered} {{f}^{{( + )}}}\left( {u,x,y,t} \right) = u - {{\varphi }^{{( + )}}}(x,y,t),\quad {\text{если}}\quad u \geqslant 0\left( {x,y} \right) \in \bar {D},\quad t \in R; \hfill \\ {{f}^{{( - )}}}\left( {u,x,y,t} \right) = u - {{\varphi }^{{( - )}}}(x,y,t),\quad {\text{если}}\quad u < 0\left( {x,y} \right) \in \bar {D},\quad t \in R. \hfill \\ \end{gathered} \right.$

В этом случае кривая ${{C}_{0}}(t)$ – это окружность, описываемая уравнением ${{x}^{2}} + {{y}^{2}} = {{d}^{2}}(t)$, где $d(t)$ – ее радиус. В самом деле, в локальной системе координат $(r,\theta )$ для кривой ${{C}_{0}}$, где $\theta \in [0,2\pi )$ – угол между вектором $\{ x,y\} $ и осью $x$, имеем ${{\varphi }^{{( - )}}} = - {{(r - d)}^{2}}$,

(40)

$\begin{gathered} I(r,\theta ,t) = \int\limits_{{{\varphi }^{{( - )}}}(r,\theta ,t)}^{{{\varphi }^{{( + )}}}(r,\theta ,t)} \,f(u,r,\theta ,t,0)du = \int\limits_{{{\varphi }^{{( - )}}}(r,\theta ,t)}^0 \,(u - {{\varphi }^{{( - )}}}(r,\theta ,t))du + \int\limits_0^{{{\varphi }^{{( + )}}}(r,\theta ,t)} \,(u - {{\varphi }^{{( + )}}}(r,\theta ,t))du = \\ = - \frac{1}{2}[{{({{\varphi }^{{( + )}}}(r,\theta ,t))}^{2}} - {{({{\varphi }^{{( - )}}}(r,\theta ,t))}^{2}}] = - \frac{1}{2}[{{(d(t))}^{4}} - \mathop {\left( {r - d(t)} \right)}\nolimits^4 ]\,, \\ \end{gathered} $

откуда следует, что $I(0,\theta ,t) = 0$, т.е. условие (А4) выполнено и ${{C}_{0}}$ – действительно кривая переходного слоя. Далее, в выбранной локальной системе координат имеем

(41)

$\mathop {\left. {\frac{{\partial I(r,\theta ,t)}}{{\partial r}}{\kern 1pt} } \right|}\nolimits_{r = 0} = \frac{1}{2}\mathop {\left. {\frac{{\partial {{{({{\varphi }^{{( - )}}}(r,\theta ,t))}}^{2}}}}{{\partial r}}{\kern 1pt} } \right|}\nolimits_{r = 0} = - 2{{(d(t))}^{3}} < 0,$

т.е. условие (А5) также выполнено. Задачи (13) для определения ${{\tilde {u}}^{{( \pm )}}}$ примут вид

(42)

$\begin{gathered} \frac{{{{\partial }^{2}}{{{\tilde {u}}}^{{( \pm )}}}}}{{\mathop {\partial \xi }\nolimits^2 }} = u - {{\varphi }^{{( \pm )}}}(\lambda {\text{*}},\theta ,t), \\ {{{\tilde {u}}}^{{( \pm )}}}(0,\theta ,t,\lambda {\text{*}}) = 0,\quad {{{\tilde {u}}}^{{( \pm )}}}( \pm \infty ,\theta ,t,\lambda {\text{*}}) = {{\varphi }^{{( \pm )}}}(\lambda {\text{*}},\theta ,t) \\ \end{gathered} $

и имеют, как нетрудно убедиться, решения ${{\tilde {u}}^{{( \pm )}}} = {{\varphi }^{{( \pm )}}}(\lambda {\text{*}},\theta ,t)(1 - exp( \mp \xi ))$. Тогда для функций $\tilde {v}$ получим выражения ${{\tilde {v}}^{{( \pm )}}} = \pm {{\varphi }^{{( \pm )}}}(\lambda {\text{*}},\theta ,t)exp( \mp \xi )$.

Тогда для асимптотики решения в нулевом порядке имеем выражение (пограничный слой в нулевом приближении отсутствует):

$U_{0}^{{( \pm )}}(x,y,t,\varepsilon ) = {{\varphi }^{{( \pm )}}}(x,y,t)(1 - exp( \mp {{\xi }_{0}})),$

где ${{\xi }_{0}} = \tfrac{{\left( {d(t) - \sqrt {{{x}^{2}} + {{y}^{2}}} } \right)}}{\varepsilon }$. Согласно теоремам 1 и 3, существует асимптотически устойчивое по Ляпунову решение $u(x,y,t,\varepsilon )$ задачи (39) в виде контрастной структуры типа ступенька, для которого справедлива оценка $\left| {U_{0}^{{( \pm )}}(x,y,t,\varepsilon ) - u(x,y,t,\varepsilon )} \right| = O(\varepsilon )$.

На фиг. 1, 2 и 3 изображены результаты численного эксперимента, проведенного с помощью программы “Wolfram Mathematica” при $\varepsilon = 0.1$, $T = 0.25$ и $d(t) = 2 + sin(8\pi t)$. На фиг. 3а видно, что решение соответствующей начально-краевой задачи быстро выходит на периодическое решение.

Фиг. 1.

Численное решение задачи (39) при $t = 0$.

Фиг. 2.

Асимптотика нулевого порядка (сплошная кривая) и численное решение (штриховая кривая) для задачи (39) в сечении плоскостью $y = 0$ в моменты времени а) $t = 0$, б) $t = T{\text{/}}4 = 1{\text{/}}16$. Корни вырожденного уравнения ${{\varphi }^{{( + )}}}$ и ${{\varphi }^{{( - )}}}$ изображены штрихпунктирными линиями.

Фиг. 3.

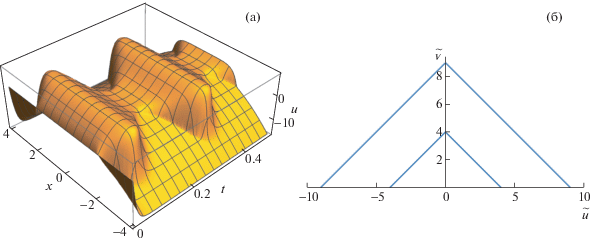
(a) Численное решение начально-краевой задачи, соответствующей задаче (39), в сечении плоскостью $y = 0$. Начальное условие выбрано в виде функции ${{v}^{0}}(x,y,t) \equiv 1$. (б) Соединительная сепаратриса на фазовой плоскости $(\tilde {u},\tilde {v})$, соответствующей задаче (39) в моменты времени $t = 0$ (нижний график) и $t = T{\text{/}}4 = 1{\text{/}}16$ (верхний график).

5.2. Случай баланса разрывной реакции

Рассмотрим задачу

(43)

$\begin{gathered} {{N}_{\varepsilon }}(u): = {{\varepsilon }^{2}}\left( {\Delta u - \frac{{\partial u}}{{\partial t}}} \right) - f(u,x,y,t,\varepsilon ) = 0,\quad D = \{ (x,y):{{x}^{2}} + {{y}^{2}} < 100\} , \\ (x,y,t) \in {{D}_{t}}: = \{ (x,y,t) \in {{R}^{3}}:(x,y) \in D,\;t \in R\} , \\ \frac{{\partial u}}{{\partial {{n}_{\Gamma }}}}(x,y,t,\varepsilon ) = 0,\quad (x,y) \in \Gamma ,\quad t \in R, \\ u(x,y,t,\varepsilon ) = u(x,y,t + T,\varepsilon ),\quad (x,y) \in \bar {D},\quad t \in R, \\ \end{gathered} $

где

$f\left( {u,x,y,t,\varepsilon } \right) = \left\{ \begin{gathered} {{f}^{{( + )}}}\left( {u,x,y,t,\varepsilon } \right) = u - A + \varepsilon w(x,y,t),\quad {\text{если}}\quad u \geqslant 0\left( {x,y} \right) \in \bar {D},\quad t \in R; \hfill \\ {{f}^{{( - )}}}\left( {u,x,y,t} \right) = u + A,\quad \quad \quad \quad \quad \;{\text{если}}\quad u < 0\left( {x,y} \right) \in \bar {D},\quad t \in R, \hfill \\ \end{gathered} \right.$

A – положительная константа, а функция

(44)

$w(t) = - \left( {\tfrac{1}{{d(t)}} + \dot {d}(t)} \right)A,$

где $d(t)$ – некоторая T – периодическая функция, например, $d(t) = 5 + \sin \left( {\tfrac{{2\pi }}{T}t} \right)$. Для задачи (43) получаем, что ${{\varphi }^{{( - )}}}(x,y,t) = - A$, ${{\varphi }^{{( + )}}}(x,y,t) = A$, тогда

$f\left( {u,x,y,t,\varepsilon } \right) = \left\{ \begin{gathered} {{f}^{{( + )}}}\left( {u,x,y,t,\varepsilon } \right) = u - {{\varphi }^{{( + )}}} + \varepsilon w(x,y,t),\quad {\text{если}}\quad u \geqslant 0\left( {x,y} \right) \in \bar {D},\quad t \in R; \hfill \\ {{f}^{{( - )}}}\left( {u,x,y,t} \right) = u - {{\varphi }^{{( - )}}},\quad \quad \quad \quad \quad \;\,{\text{если}}\quad u < 0\left( {x,y} \right) \in \bar {D},\quad t \in R. \hfill \\ \end{gathered} \right.$

(45)

$I(r,\theta ,t) = \int\limits_{{{\varphi }^{{( - )}}}(r,\theta ,t)}^{{{\varphi }^{{( + )}}}(r,\theta ,t)} \,f(u,r,\theta ,t,0)du = - \frac{1}{2}[{{({{\varphi }^{{( + )}}}(r,\theta ,t))}^{2}} - {{({{\varphi }^{{( - )}}}(r,\theta ,t))}^{2}}] \equiv 0,$

т.е. условие (А'4) выполнено.

Нетрудно убедиться, что ${{\tilde {u}}^{{( \pm )}}} = \pm A(1 - exp( \mp \xi ))$. Тогда для функций $\tilde {v}$ получим выражения ${{\tilde {v}}^{{( \pm )}}} = Aexp( \mp \xi )$.

Далее, переходя к полярным координатам $R = \sqrt {{{x}^{2}} + {{y}^{2}}} $ и $\theta $ и учитывая, что $r = d(t) - R$, получаем

$\Delta r(r,\theta ,t) = \frac{1}{R}\frac{\partial }{{\partial R}}\left( {R\frac{\partial }{{\partial R}}(d(t) - R)} \right) = - 1{\text{/}}R = \frac{1}{{r - d(t)}},$

$\mathop {\left. {\frac{{\partial r}}{{\partial t}}{\kern 1pt} } \right|}\nolimits_{x,y = {\text{const}}} = \frac{\partial }{{\partial t}}\left( {d(t) - \sqrt {{{x}^{2}} + {{y}^{2}}} } \right) = \dot {d}(t).$

Далее, имеем

$m = \int\limits_{ - \infty }^{ + \infty } \,{{\tilde {v}}^{2}}(\xi ,\theta ,t,0)d\xi = {{A}^{2}},\quad \frac{{\partial{ \tilde {f}}}}{{\partial r}} \equiv 0,\quad \int\limits_{ - \infty }^{ + \infty } \,\frac{{\partial f}}{{\partial \varepsilon }}\tilde {v}(\xi ,\theta ,t,0)d\xi = Aw(t),$

откуда получаем равенство (27):

(46)

$ - \left( {\frac{1}{{ - d(t)}} - \dot {d}(t)} \right){{A}^{2}} + Aw(t) = 0,$

которое является верным в силу задания функции $w(t)$ по формуле (44), т.е. условие (A'5) выполнено.

Далее, сосчитаем коэффициент $\tilde {c}(\theta ,t)$:

$\tilde {c}(\theta ,t): = \frac{1}{{{{A}^{2}}}}\mathop {\left. {\frac{{\partial \left[ {\left( {\tfrac{1}{{r - d(t)}} - \dot {d}(t)} \right){{A}^{2}} + Aw(t)} \right]}}{{\partial r}}{\kern 1pt} } \right|}\nolimits_{r = 0} = - 1{\text{/}}\mathop {\left( {d(t)} \right)}\nolimits^2 < 0.$

Таким образом, условие (А'6) выполнено.

$U_{0}^{{( \pm )}}(x,y,t,\varepsilon ) = \pm A(1 - exp( \mp {{\xi }_{0}})),$

где ${{\xi }_{0}} = \tfrac{{\left( {d(t) - \sqrt {{{x}^{2}} + {{y}^{2}}} } \right)}}{\varepsilon }$.

Согласно теоремам 2 и 4, существует асимптотически устойчивое по Ляпунову решение $u(x,y,t,\varepsilon )$ задачи (39) в виде контрастной структуры типа ступенька, для которого справедлива оценка $\left| {U_{0}^{{( \pm )}}(x,y,t,\varepsilon ) - u(x,y,t,\varepsilon )} \right| = O(\varepsilon )$.

На фиг. 4б изображены результаты численного эксперимента, проведенного с помощью программы “Wolfram Mathematica” при $\varepsilon = 0.1,\;T = 2\pi $ и $d(t) = 2 + sin(t)$.

Фиг. 4.

На графиках для момента времени $t = \pi {\text{/}}20$ представлены (а) асимптотика нулевого порядка и (б) асимптотика нулевого порядка (сплошная кривая) и численное решение (штриховая кривая) для задачи (43) в сечении плоскостью $y = 0$ (корни вырожденного уравнения ${{\varphi }^{{( + )}}}$ и ${{\varphi }^{{( - )}}}$ изображены штрихпунктирными линиями).

Авторы благодарны В.Ф. Бутузову за ценные замечания при обсуждении данной работы.

Список литературы

Alikakos N.D., Bates P.W., Chen X. Periodic traveling waves and locating oscillating patterns in multidimensional domains // Trans. AMS. 1999. V. 351. № 7. P. 2777–2805.
Dancer E.N., Hess P. Behaviour of a semi-linear periodic-parabolic problem when a parameter is small // Lecture Notes in Math. 1990. V. 1450. P. 12–19.
Nefedov N.N. Comparison Principle for Reaction-Diffusion-Advection Problems with Boundary and Internal Layers // Lecture notes in Computer Science. V. 8236. P. 62–72.
Руденко О.В. Линеаризуемое уравнение для волн в диссипативных средах с модульной, квадратичной и квадратично-кубичной нелинейностями // Докл. АН. 2016. Т. 471. № 1. С. 23–27.
Руденко О.В. Модульные солитоны // Докл. АН. 2016. Т. 471. № 6. С. 451–454.
Нефедов Н.Н., Руденко О.В. О движении фронта в уравнении типа Бюргерса с квадратичной и модульной нелинейностью при нелинейном усилении // Докл. АН. 2018. Т. 478. № 3. С. 274–279.
Hedberg C.M., Rudenko O.V. Collisions, mutual losses and annihilation of pulses in a modular nonlinear medium // Nonlinear Dyn. 2017. V. 90. P. 2083–2091.
Амбарцумян С.А. Разномодульная теория упругости. М.: Наука, 1982. 318 с.
Васильева А.Б., Бутузов В.Ф., Нефедов Н.Н. Сингулярно возмущенные задачи с пограничными и внутренними слоями // Труды Математического института им. В.А. Стеклова РАН. 2010. № 268. С. 268–283.
Nefedov N.N., Nikulin E.I. Existence and asymptotic stability of periodic solutions of the reaction–diffusion equations in the case of a rapid reaction // Russian Journal of Mathematical Physics. 2018. V. 25. № 1. P. 88–101.
Орлов А.О., Нефедов Н.Н., Левашова Н.Т. Решение вида контрастной структуры параболической задачи реакция-диффузия в среде с разрывными характеристиками // Дифференц. ур-ния. 2018. Т. 54. № 5. С. 673–690.
Левашова Н.Т., Нефедов Н.Н., Орлов А.О. Асимптотическая устойчивость стационарного решения многомерного уравнения реакция-диффузия с разрывным источником // Ж. вычисл. матем. и матем. физ. 2019. Т. 59. № 4. С. 611–620.
Бутузов В.Ф., Васильева А.Б., Нефедов Н.Н. Асимптотическая теория контрастных структур // Автоматика и телемехан. 1997. № 7. С. 4–32.
Nefedov N.N., Sakamoto K. Multi-dimensional stationary internal layers for spatially inhomogeneous reaction-diffusion equations with balanced nonlinearity // Hiroshima Mathematical Journal. 2003. V. 33. № 3. P. 391–432.
Васильева А.Б., Бутузов В.Ф. Асимптотические методы в теории сингулярных возмущений. М.: Высшая школа, 1990. 208 с.
Kannan R., Lakshmikantham V. Existence of periodic solutions of semilinear parabolic equations and the method of upper and lower solutions // J. Math. Anal. Appl. 1983. V. 97. № 1. P. 291–299.
Hess P. Periodic-Parabolic Boundary Value Problems and Positivity. New York: Pitman Resaerch Notes in Math. Series, 1991. 139 p.
Павленко В.Н. Сильные решения периодических параболических задач с разрывными нелинейностями // Дифференц. ур-ния. 2016. Т. 52. № 4. С. 528–539.
Nefedov N.N., Nikulin E.I. Existence and stability of periodic contrast structures in the reaction-advection-diffusion problem // Russian Journal of Mathematical Physics. 2015. V. 22. № 2. P. 215–226.
Нефедов Н.Н., Никулин Е.И. Существование и устойчивость периодических контрастных структур в задаче реакция-адвекция-диффузия в случае сбалансированной нелинейности // Дифференц. ур-ния. 2017. Т. 53. № 4. С. 524–537.
Pao C.V. Nonlinear Parabolic and Elliptic Equations. Springer Science Business Media, 1993. 777 p.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал