Журнал вычислительной математики и математической физики, 2021, T. 61, № 1, стр. 150-161

Численное решение задачи о гашении колебаний движущегося полотна

И. Е. Михайлов^1, *, И. А. Суворов^2, **

¹ ФИЦ ИУ РАН
119333 Москва, ул. Вавилова, 44/2, Россия

² МАИ НИУ
125993 Москва, Волоколамское ш., 4, Россия

^* E-mail: mikh_igor@mail.ru
^** E-mail: ivan.a.suv@gmail.com

Поступила в редакцию 06.12.2019
После доработки 13.06.2020
Принята к публикации 18.09.2020

DOI: 10.31857/S004446692012011X

Полный текст (PDF)

Аннотация

Моделируются механические процессы, происходящие при производстве бумаги. В бумагоделательной машине бумага перемещается в виде тонкого листа. Характерная толщина листа варьируется от 0.1 мм (офисная бумага) до 1 мм (картон). Все бумагоделательные машины содержат открытые участки полотна, где бумажное полотно проходит без механической поддержки во время движения от одного опорного ролика к другому. В это время оно может потерять стабильность, начать совершать поперечные колебания и в итоге порваться. Рассматривается возможность уменьшить эти колебания с помощью различных управляющих актьюаторов. Поперечные колебания движущегося полотна с ненулевой изгибной жесткостью моделируются с помощью неоднородного дифференциального уравнения в частных производных четвертого порядка. Воздействие управляющих актьюаторов моделируется функцией в правой части уравнения. Предполагается, что амплитуда колебаний одинакова в поперечном сечении движущегося полотна. Задача гашения колебаний сводится к минимизации некоторой функции многих переменных. Решение задачи разбивается на два этапа: решение начально-краевой задачи с заданным управлением и минимизация некоторой функции многих переменных. Для решения начально-краевой задачи предлагается численный метод. Дифференциальное уравнение четвертого порядка сводится к системе двух дифференциальных уравнений второго порядка. Далее делается замена искомых функций, позволяющая упростить эти уравнения. Получившиеся уравнения аппроксимируются конечно-разностной схемой, для которой показана ее абсолютная устойчивость. Эта разностная схема решается с помощью матричной прогонки. Для минимизации функции многих переменных используется метод Хука–Дживса. Приводятся примеры расчетов для трех типов актьюаторов: точечного, действующего на участке полотна и действующего на всем протяжении полотна. Библ. 5. Фиг. 12.

Ключевые слова: движущееся полотно, гашение колебаний, актьюаторы, метод оптимизации Хука–Дживса.

1. ПОСТАНОВКА ЗАДАЧИ

Целью данной работы является разработка численных методов решения задачи гашения вынужденных поперечных колебаний u(t, x) движущегося с постоянной скоростью V₀ полотна толщиной H с помощью различных видов актьюаторов (фиг. 1). Предполагается, что амплитуда этих колебаний одинакова в направлении ширины полотна. Поперечные колебания движущегося полотна с заданной изгибной жесткостью под действием внешнего управления g(t, x) описываются уравнением (см. [1], [2])

(1)

${{u}_{{tt}}} + 2~{{V}_{0}}{{u}_{{tx}}} + (V_{0}^{2} - {{c}^{2}}){{u}_{{xx}}} + D{{u}_{{xxxx}}} = g(t,x),\quad (t,x) \in \Pi = \left\{ {0 \leqslant x \leqslant l,\;0 \leqslant t \leqslant T} \right\},$

где с – скорость распространения возмущений вдоль полотна. Время t и линейный размер x отнесены к характерным величинам t* и x*.Член Du_xxxx представляет собой силу реакции, возникающую из-за сопротивления изгибу. Константа D называется изгибной жесткостью и равна

$D = \frac{{E{{H}^{3}}}}{{12(1 - {{{v}}^{2}})}},$

где E – модуль Юнга, ${v}$ – коэффициент Пуассона.

Фиг. 1.

Движущееся между роликами бумажное полотно.

Начальные отклонение и скорость поперечного перемещения полотна

(2)

$\begin{gathered} ~u(0,x) = \varphi (x), \\ {{u}_{t}}(0,x) = \psi (x) \\ \end{gathered} $

мы будем рассматривать как заданные начальные возмущения.

В качестве граничных условий при x = 0 и x = l возьмем условия шарнирного закрепления

(3)

$\begin{gathered} u(t,~0) = u(t,~l) = 0, \\ {{u}_{{xx}}}(t,~0) = {{u}_{{xx}}}(t,~l) = 0. \\ \end{gathered} $

Ставится следующая задача гашения: найти функцию g(t, x) и время Т такие, чтобы

$\begin{gathered} u(T,x) = 0, \\ {{u}_{t}}(T,x) = 0. \\ \end{gathered} $

Отметим, что эти условия эквивалентны условию

(4)

$J(T) = \mathop \smallint \limits_0^l \,({{u}^{2}}(T,x) + u_{t}^{2}(T,x))dx = 0.$

2. ГАШЕНИЕ КОЛЕБАНИЙ И МОДЕЛИ АКТЬЮАТОРОВ

Для гашения колебаний мы будем использовать модели актьюаторов различных видов, при этом функция g(t, x) будет определяться видом актьюатора.

1. Модель точечного актьюатора:

(5)

$g(t,x) = s(t)\delta (x - {{x}_{0}}),$

где x₀ – точка приложения актьюатора, s(t) – управляющая функция, δ – дельта-функция Дирака, определенная в [3].

2. Модель актьюатора конечной ширины $[{{x}_{0}},{{x}_{1}}] \subset [0,l]$:

(6)

$g(t,x) = s(t)\left\{ \begin{gathered} 1,\quad x \in [{{x}_{0}},{{x}_{1}}], \hfill \\ 0,\quad x \notin [{{x}_{0}},{{x}_{1}}]. \hfill \\ \end{gathered} \right.$

3. Модель актьюатора, действующего одинаково по всей длине полотна:

(7)

$g(t,x) = s(t).$

Во всех трех моделях на управляющую функцию $s\left( t \right)$ могут быть наложены ограничения ${{s}_{{{\text{min}}}}} \leqslant s(t) \leqslant {{s}_{{{\text{max}}}}},~$ где s_min, s_max – заданные константы.

3. ЧИСЛЕННЫЙ МЕТОД РЕШЕНИЯ НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ (1)–(3)

Введем новую вспомогательную функцию ${v}(t,~x)~$ такую, чтобы уравнение (1) можно было представить в виде двух уравнений второго порядка:

(8)

$\begin{gathered} {{u}_{t}} = {{{v}}_{{xx}}} - 2{{V}_{0}}{{u}_{x}}, \hfill \\ {{{v}}_{t}} = - D{{u}_{{xx}}} - (V_{0}^{2} - {{c}^{2}})u + f(t,x). \hfill \\ \end{gathered} $

Найдем вид функции f(t, x), при которой система (8) была бы эквивалентна (1) при достаточной гладкости функций $u(t,~x)$ и ${v}(t,~x).~$Продифференцируем первое уравнение по t, а второе дважды по x$:$

(9)

$\begin{array}{*{20}{l}} {{{u}_{{tt}}} = {{{v}}_{{txx}}} - 2{{V}_{0}}{{u}_{{tx}}},} \\ {{{{v}}_{{txx}}} = - D{{u}_{{xxxx}}} - (V_{0}^{2} - {{c}^{2}}){{u}_{{xx}}} + {{f}_{{xx}}}(t,~x),} \end{array}$

откуда

${{u}_{{tt}}} + 2{{V}_{0}}{{u}_{{tx}}} + (V_{0}^{2} - {{c}^{2}}){{u}_{{xx}}} + D{{u}_{{xxxx}}} = {{f}_{{xx}}}(t,~x).$

Сравнивая это равенство с (1), получаем

${{f}_{{xx}}}(t,~x) = g(t,~x).$

Дважды проинтегрировав левую и правую части равенства по $x$, найдем выражение для f(t, x):

$f(t,~x) = \mathop \smallint \limits_0^x \left[ {\mathop \smallint \limits_0^\eta \,g(t,~\xi )d\xi } \right]d\eta + {{k}_{1}}(t)x + {{k}_{2}}(t),$

где ${{k}_{1}}(t)$ и ${{k}_{2}}(t)$ – произвольные функции.

Получим начальные условия для системы (8). Подставив второе начальное условие ${{u}_{t}}(0,x) = \psi (x)$ из (2) в первое уравнение (8), получим

${{u}_{t}}(0,x) = {{\left. {({{{v}}_{{xx}}} - 2{{V}_{0}}{{u}_{x}})} \right|}_{{(0,~x)}}} = \psi (x).$

Откуда выражение для ${{{v}}_{{xx}}}$ примет вид

${{{v}}_{{xx}}}(0,x) = 2{{V}_{0}}{{u}_{x}}(0,x) + \psi (x).$

Дважды проинтегрируем это выражение по $x$ и получим выражение для ${v}(0,x)$:

${v}(0,x) = \Phi (x) + {{c}_{1}}x + {{c}_{2}}.$

Здесь c₁, c₂ – произвольные константы интегрирования, а функция $\Phi (x)$:

$\Phi (x) = 2{{V}_{0}}\mathop \smallint \limits_0^x \,\varphi (x){\kern 1pt} dx + \mathop \smallint \limits_0^x \left[ {\mathop \smallint \limits_0^\eta \psi (\xi )d\xi } \right]d\eta {\kern 1pt} .$

В итоге начальные условия для системы (8) примут следующий вид:

$\begin{gathered} u(0,x) = {\varphi }(x), \\ {v}(0,x) = {\Phi }(x) + {{c}_{1}}x + {{c}_{2}}. \\ \end{gathered} $

Найдем новые граничные условия для системы (8).

Граничные условия для u(t, x) будут такими

$u(t,~0) = u(t,~l) = 0.$

Найдем ${v}(t,~0)$. Приняв во внимание, что $u(t,0) = 0$ и ${{u}_{{xx}}}(t,0) = 0$ из (3), и подставив эти значения во второе уравнение системы (8), получим

${{u}_{{xx}}}(t,0) = {{\left. {\frac{1}{D}[ - {{{v}}_{t}}--(V_{0}^{2} - {{c}^{2}})u + ~f]{\kern 1pt} } \right|}_{{(t,0)}}}~ = {{\left. {\frac{1}{D}\left[ {f - {{{v}}_{t}}} \right]{\kern 1pt} } \right|}_{{(t,0)}}} = 0.$

Откуда

${{{v}}_{t}}(t,0) = f(t,0) = {{k}_{2}}(t),$

${v}(t,0) = \mathop \smallint \limits_0^t \,{{k}_{2}}(t)dt + {{c}_{3}},~$

где c₃ – произвольная константа интегрирования. Сравнивая начальное условие и левое граничное условие для функции ${v}$ в точке (0, 0), получаем ${{c}_{2}} = {{c}_{3}}.$

Найдем теперь ${v}(t,~l)$. Подставим во второе уравнение системы (8) значения $u(t,l)$ и ${{u}_{{xx}}}(t,l)$ из (3), имеем:

${{u}_{{xx}}}(t,l) = \frac{1}{D}{{[ - {{{v}}_{t}} - (V_{0}^{2} - {{c}^{2}})u + f]}_{{\{ t,l\} }}} = \frac{1}{D}{{[f - {{{v}}_{t}}]}_{{(t,l)}}} = 0,$

${{{v}}_{t}}(t,l) = f(t,l) = \mathop \smallint \limits_0^l \left[ {\mathop \smallint \limits_0^x \,g(t,~\xi )d\xi } \right]dx + {{k}_{1}}(t)l + {{k}_{2}}(t),$

${v}(t,l) = \mathop \smallint \limits_0^t \left[ {\mathop \smallint \limits_0^l \left[ {\mathop \smallint \limits_0^x \,g(t,~\xi )d\xi } \right]dx} \right]dt + l\mathop \smallint \limits_0^t \,{{k}_{1}}(t)dt + \mathop \smallint \limits_0^t \,{{k}_{2}}(t)dt + {{c}_{4}},$

где c₄ – произвольная константа интегрирования. Сравнивая начальное условие и правое граничное условие для функции ${v}$ в точке $(0,l)$, получаем ${{c}_{4}} = \Phi \left( l \right) + {{c}_{1}}l$.

Подберем теперь произвольные функции ${{k}_{1}}(t)$, ${{k}_{2}}(t)$ и константы c₁, c₂ так, чтобы для любого $t \in [0,T]$ граничные условия для функции ${v}(t,x)$ имели бы наиболее простой вид, а именно, равнялись нулю:

${v}(t,~0) = {v}(t,~l) \equiv 0.$

Положим ${{k}_{2}}(t) \equiv 0$, ${{c}_{2}} = {{c}_{3}} = 0$, тогда ${v}(t,~0) \equiv 0$ для всех $t \geqslant 0$.

Положим теперь

${{k}_{1}}(t) = - \frac{1}{l}\int_0^l {\left[ {\int_0^x {g(t,\xi )d\xi } } \right]dx} ,\quad {{c}_{1}} = - \frac{1}{l}\Phi (l),$

тогда ${v}(t,l) \equiv 0$ для всех $t \geqslant 0$.

Тогда выражение для $f(t,~x)$ примет вид

$f(t,~x) = \mathop \smallint \limits_0^x \left[ {\mathop {\smallint \,}\limits_0^\eta g(t,~\xi )d\xi } \right]d\eta - \frac{x}{l}\mathop \smallint \limits_0^l \left[ {\mathop \smallint \limits_0^\eta \,g(t,~\xi )d\xi } \right]d\eta {\kern 1pt} .$

Начальные условия для системы (8) перепишутся в виде

(10)

$\begin{gathered} u(0,{\text{\;}}x) = {\varphi }(x), \\ {v}(0,{\text{\;}}x) = {\Phi }(x) - \frac{x}{l}\Phi \left( l \right). \\ \end{gathered} $

Граничные условия имеют следующий вид:

(11)

$u(t,0) = 0,\quad u(t,l) = 0,\quad {v}(t,0) = 0,\quad {v}(t,l) = 0.$

Запишем систему (8) в матричном виде

${{\left( {\begin{array}{*{20}{c}} u \\ {v} \end{array}} \right)}_{t}} = \left( {\begin{array}{*{20}{c}} 0&1 \\ { - D}&0 \end{array}} \right){{\left( {\begin{array}{*{20}{c}} u \\ {v} \end{array}} \right)}_{{xx}}} + \left( {\begin{array}{*{20}{c}} { - 2{{V}_{0}}}&0 \\ 0&0 \end{array}} \right){{\left( {\begin{array}{*{20}{c}} u \\ {v} \end{array}} \right)}_{x}} + \left( {\begin{array}{*{20}{c}} 0&0 \\ {{{c}^{2}} - V_{0}^{2}}&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} u \\ {v} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0 \\ f \end{array}} \right)$

или

(12)

${{W}_{t}} = A{{W}_{{xx}}} + B{{W}_{x}} + C + F,$

где

$W = \left( {\begin{array}{*{20}{c}} u \\ {v} \end{array}} \right),\quad A = \left( {\begin{array}{*{20}{c}} 0&1 \\ { - D}&0 \end{array}} \right),\quad B = \left( {\begin{array}{*{20}{c}} { - 2{{V}_{0}}}&0 \\ 0&0 \end{array}} \right),\quad C = \left( {\begin{array}{*{20}{c}} 0&0 \\ {{{c}^{2}} - V_{0}^{2}}&0 \end{array}} \right),\quad F = \left( {\begin{array}{*{20}{c}} 0 \\ f \end{array}} \right).$

Сделаем замену исходной функции $~W = \mathcal{A}\hat {W}$, где $\mathcal{A} = \left( {\begin{array}{*{20}{c}} 1&0 \\ {\alpha (t,x)}&1 \end{array}} \right)$, $\alpha (t,x) = {{V}_{0}}x + ({{c}^{2}} - V_{0}^{2})t$, а $\hat {W} = \left( {\begin{array}{*{20}{c}} {\hat {u}} \\ {{\hat {v}}} \end{array}} \right)$ – новая искомая вектор-функция.

В итоге, уравнение (12) для новой вектор-функции $\hat {W}$ примет вид:

(13)

${{\hat {W}}_{t}} = \left( {\begin{array}{*{20}{c}} \alpha &1 \\ { - D - {{\alpha }^{2}}}&{ - \alpha } \end{array}} \right){{\hat {W}}_{{xx}}} + \left( {\begin{array}{*{20}{c}} 0 \\ f \end{array}} \right).$

Теперь для новой вектор-функции $\hat {W}$ запишем начальные условия

(14)

$\begin{gathered} \hat {u}(0,x) = \varphi (x), \\ {\hat {v}}(0,x) = \Phi (x) - \frac{x}{l}\Phi (l) - {{V}_{0}}x\varphi (x). \\ \end{gathered} $

Граничные условия примут вид

(15)

$\hat {u}(t,0) = 0,\quad \hat {u}(t,l) = 0,\quad {\hat {v}}(t,0) = 0,\quad {\hat {v}}(t,l) = 0.$

Построим разностную схему для численного решения (13). Зададим натуральные числа $M,\;N$ и разобьем рассматриваемую область $\{ 0 \leqslant t \leqslant T,\;~0 \leqslant x \leqslant l\} $ на прямоугольные ячейки параллельными прямыми ${{x}_{m}} = mh$, $m = 0,1, \ldots ,M$, ${{t}_{n}} = n\tau $, $n = 0,1, \ldots ,N$, где $h = \frac{l}{M}$, $\tau = \frac{T}{N}$.

Рассмотрим шаблон, на котором уравнение (13) аппроксимируем конечно-разностной схемой

(16)

$\frac{{\hat {W}_{m}^{{n + 1}} - \hat {W}_{m}^{n}}}{\tau } = \left( {\begin{array}{*{20}{c}} \alpha &1 \\ { - D - {{\alpha }^{2}}}&{ - \alpha } \end{array}} \right)\frac{{\hat {W}_{{m + 1}}^{{n + 1}} - 2\hat {W}_{m}^{{n + 1}} + \hat {W}_{{m - 1}}^{{n + 1}}}}{{{{h}^{2}}}} + \left( {\begin{array}{*{20}{c}} 0 \\ f \end{array}} \right).$

Покажем, что эта разностная схема абсолютно устойчива по Нейману. Будем искать решение однородного уравнения в виде

$\hat {W}_{m}^{n} = {{\lambda }^{n}}{{e}^{{ipm}}}{{W}_{0}},$$~$

где ${{W}_{0}} \ne 0$, p – действительное число, i – мнимая единица.

Тогда имеем

$\frac{{\lambda - 1}}{\tau }{{W}_{0}} = \left( {\begin{array}{*{20}{c}} \alpha &1 \\ { - D - {{\alpha }^{2}}}&{ - \alpha } \end{array}} \right)\frac{{{{e}^{{ip}}} - 2 + {{e}^{{ - ip}}}}}{{{{h}^{2}}}}\lambda {{W}_{0}},$

или

$\left( {(\lambda - 1)E - S\left( {\begin{array}{*{20}{c}} \alpha &1 \\ { - D - {{\alpha }^{2}}}&{ - \alpha } \end{array}} \right)\left( { - 4\lambda {{{\left( {\sin \frac{p}{2}} \right)}}^{2}}} \right)} \right){{W}_{0}} = 0,$

где $S = \frac{\tau }{{{{h}^{2}}}}$.

Эта система имеет нетривиальное решение, если

$\begin{gathered} \left| {\begin{array}{*{20}{c}} {\lambda - 1 + 4\alpha S\lambda {{{\left( {\sin \frac{p}{2}} \right)}}^{2}}}&{4S\lambda {{{\left( {\sin \frac{p}{2}} \right)}}^{2}}} \\ { - 4S\lambda ( - D - {{\alpha }^{2}}){{{\left( {\sin \frac{p}{2}} \right)}}^{2}}}&{\lambda - 1 - 4\alpha S\lambda {{{\left( {\sin \frac{p}{2}} \right)}}^{2}}} \end{array}} \right| = \\ = {{(\lambda - 1)}^{2}} - 16{{\alpha }^{2}}{{S}^{2}}{{\lambda }^{2}}{{\left( {\sin \frac{p}{2}} \right)}^{4}} + 16{{S}^{2}}{{\lambda }^{2}}(D + {{\alpha }^{2}}){{\left( {\sin \frac{p}{2}} \right)}^{4}} = 0, \\ \end{gathered} $

${{(\lambda - 1)}^{2}} + 16{{S}^{2}}{{\lambda }^{2}}D{{\left( {\sin \frac{p}{2}} \right)}^{4}} = 0.$

Пусть

${{\beta }^{2}} = 16{{S}^{2}}D{{\left( {\sin \frac{p}{2}} \right)}^{4}},\quad {{(\lambda - 1)}^{2}} + {{\beta }^{2}}{{\lambda }^{2}} = 0,\quad \lambda = \pm \beta \lambda i + 1,\quad \lambda \left( {1 \mp \beta i} \right) = 1,$

$\lambda = \frac{1}{{1 \mp \beta i}} = \frac{{1 \pm \beta i}}{{1 + {{\beta }^{2}}}} = \frac{1}{{1 + {{\beta }^{2}}}} \pm \frac{\beta }{{1 + {{\beta }^{2}}}}i,\quad \left| \lambda \right| = \sqrt {\frac{1}{{{{{(1 + {{\beta }^{2}})}}^{2}}}} + \frac{{{{\beta }^{2}}}}{{{{{(1 + {{\beta }^{2}})}}^{2}}}}} = \sqrt {\frac{1}{{1 + {{\beta }^{2}}}}} \leqslant 1,$

т.е. схема абсолютно устойчива при любых β. Будем ее решать с помощью матричной прогонки.

Сравним аналитическое решение задачи (1)–(3) с численным решением задачи (18)–(20). При

$g(t,x) = - 2{{V}_{0}}\frac{\pi }{l}\omega \sin (\omega t)\cos \frac{{\pi x}}{l},$

где

$\omega = \frac{\pi }{l}\sqrt {({{c}^{2}} - V_{0}^{2}) + D\frac{{{{\pi }^{2}}}}{{{{l}^{2}}}}} ,\quad \varphi (x) = \sin \frac{{\pi x}}{l},\quad \psi (x) = 0$

и условиях (3) аналитическим решением задачи (1)–(3) является функция $u(t,x) = \cos (\omega t)\sin \frac{{\pi x}}{l}$.

В табл. 1 при ${{V}_{0}} = 1$, $c = 2$, $D = 0.005$, l = 1 приведены аналитическое решение и расчетные решения задачи (18)–(20) в точке x = 0.5 при различных T и шагах сетки M × N. При этом число узловых точек по времени N = 2МТ.

Таблица 1

T	Аналитическое решение	Численные решения
T	Аналитическое решение	M = 10	M = 20	M = 40	M = 80
1	0.67277	0.6754	0.6717	0.6728	0.6731
2	–0.094749	–0.09466	–0.09384	–0.09499	–0.09483
5	–0.52113	–0.5219	–0.5240	–0.5218	–0.5217
10	–0.45686	–0.4594	–0.4539	–0.4561	–0.4567

Таким образом, мы видим сходимость предложенного метода с уменьшением шагов сетки и хорошее совпадение с аналитическим решением.

4. ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ ГАШЕНИЯ КОЛЕБАНИЙ

Отметим, что из условия (4) следует условие

(17)

$J(T) = \mathop \smallint \limits_0^l \,({{\hat {u}}^{2}}(T,x) + \hat {u}_{t}^{2}(T,x))dx = 0.$

Для рассматриваемых моделей актьюаторов (5)–(7) функция $f(t,x)~$ записывается в следующих видах.

1. Модель точечного актьюатора (5):

$f(t,x) = s(t)\left\{ \begin{gathered} - \frac{x}{l}(l - {{x}_{0}}),\quad x < {{x}_{0}}, \hfill \\ (x - {{x}_{0}}) - \frac{x}{l}(l - {{x}_{0}}),\quad x \geqslant {{x}_{0}}. \hfill \\ \end{gathered} \right.$

2. Модель актьюатора конечной ширины $[{{x}_{0}},{{x}_{1}}]$ (6):

$f(t,x) = s(t)\left\{ \begin{gathered} - \frac{x}{l}({{x}_{1}} - {{x}_{0}})\left( {l - \frac{{{{x}_{0}} + {{x}_{1}}}}{2}} \right),\quad x < {{x}_{0}}, \hfill \\ \frac{{{{{(x - {{x}_{0}})}}^{2}}}}{2} - \frac{x}{l}({{x}_{1}} - {{x}_{0}})\left( {l - \frac{{{{x}_{0}} + {{x}_{1}}}}{2}} \right),\quad {{x}_{0}} \leqslant x \leqslant {{x}_{1}}, \hfill \\ \left( {\frac{x}{l} - 1} \right)\frac{{x_{1}^{2} - x_{0}^{2}}}{2},\quad {{x}_{1}} < x. \hfill \\ \end{gathered} \right.$

3. Модель актьюатора, действующего одинаково вдоль всего полотна (7):

$f(t,x) = s(t)\frac{{x(x - l)}}{2}.$

Функцию $s(t)$ на отрезке $[0,T]$ аппроксимируем ломаной, соединяющей соседние точки $({{t}_{n}},{{s}_{n}})$, $({{t}_{{n + 1}}},{{s}_{{n + 1}}})$, $n = 0,1, \ldots ,N - 1$, прямыми, где ${{s}_{0}}, \ldots ,{{s}_{N}}$ – неизвестные пока постоянные.

Константы ${{s}_{0}}, \ldots ,{{s}_{N}}$ будем искать, минимизируя функцию многих переменных:

(18)

$J({{s}_{0}}, \ldots ,{{s}_{N}}) = h\mathop \sum \limits_{m = 1}^{M - 1} \left[ {{{{(\hat {u}_{m}^{N})}}^{2}} + {{{\left( {\frac{{\hat {u}_{m}^{N} - \hat {u}_{m}^{{N - 1}}}}{\tau }} \right)}}^{2}}} \right],$

представляющую собой квадратурную формулу трапеций для интеграла (17) с учетом граничных условий (15). Для минимизации будем использовать метод Хука–Дживса (см. [4]).

Фиг. 2.

5. ПРИМЕРЫ

Во всех описанных ниже примерах время Т будем выбирать так, чтобы гарантировать выполнение условия $J({{s}_{0}}, \ldots ,{{s}_{N}}) < \varepsilon $, где ε полагалось равным 0.001.

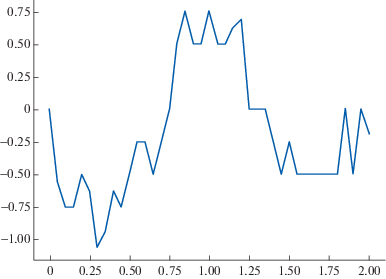
Пример 1. Рассмотрим свободные колебания движущегося полотна $(g(t,x) = 0)$ с начальными условиями $\varphi (x) = \sin (\pi x)$, $\psi (x) = 0$. Значения входных данных: ${{V}_{0}} = 1,$ $c = 2,$ $D = 0.005,$ $l = 1,$ $T = 8,$ $M = 20,$ $N = 160$.

На фиг. 3 видно, что максимальная амплитуда колебаний полотна с течением времени возрастает.

Фиг. 3.

Пример 2. Рассмотрим теперь задачу гашения колебаний с использованием точечного актьюатора (5), помещенного в точку ${{x}_{0}} = 0.5.$ Начальные условия и значения входных данных совпадают со значениями из примера 1, T = 2. На фиг. 4 показан процесс гашения колебаний с помощью управляющей функции s(t), изображенной на фиг. 5.

Фиг. 4.

Фиг. 5.

Пример 3. Погасим начальные колебания $\varphi (x) = \sin (\pi x)~$, $\psi (x) = 0$ с помощью узкого актьюатора (6) c ${{x}_{0}} = 0.3$, ${{x}_{1}} = 0.6$. Значения входных данных совпадают со значениями из примера 1, T = 2. На фиг. 6 показан процесс гашения колебаний с помощью управляющей функции s(t), изображенной на фиг. 7.

Фиг. 6.

Фиг. 7.

Пример 4. Погасим колебания с помощью актьюатора (7), действующего на протяжении всего полотна. Значения всех параметров совпадают со значениями из примера 1, T = 2. На фиг. 8 показан процесс гашения колебаний с помощью управляющей функции s(t), изображенной на фиг. 9.

Фиг. 8.

Фиг. 9.

Пример 5. Будем использовать актьюатор (7) и установим ограничения на управляющую функцию ${{s}_{{{\text{min}}}}} = - 0.6$, ${{s}_{{{\text{max}}}}} = 0.6,$ $T = 2$. На фиг. 10 и 11 изображены процесс гашения $u(t,x)$ и управляющая функция s(t) соответственно.

Фиг. 10.

Фиг. 11.

В [5] с использованием принципа максимума Понтрягина было показано, что при гашении с помощью актьюатора (7) с ограничениями ${{s}_{{{\text{min}}}}} \leqslant s(t) \leqslant {{s}_{{{\text{max}}}}}$ значение управляющей функции может частично совпадать с граничными значениями ${{s}_{{{\text{min}}}}}$, ${{s}_{{{\text{max}}}}}$. Фиг. 11 подтверждает этот вывод.

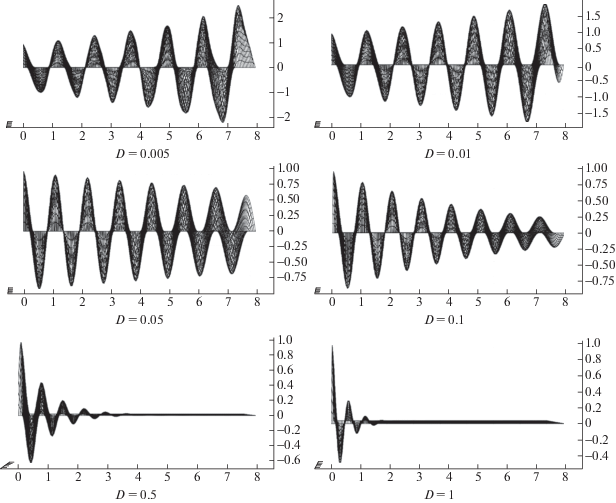
Пример 6. Рассмотрим влияние параметра D на свободные колебания $u(t,x)$ ($g(t,x) = 0$) (фиг. 12). Все входные данные взяты из примера 1.

Фиг. 12.

Как мы видим, при малых $D$ свободные колебания возрастают с течением времени, а при увеличении $D$, начиная с некоторого значения, затухают сами собой.

Список литературы

Jeronen J. On the Mechanical Stability and Out-of-Plane Dynamics of a Travelling Panel Submerged in Axially Flowing Ideal Fluid. Univer. Jyväskylä, 2011. 243 p.
Banichuk N., Barsuk A., Jeronen J., Tuovinen T., Neittaanmäki P. Stability of Axially Moving Materials. Solid Mechanics and Its Applications. V. 259. Springer, Cham, 2020. 642 p.
Владимиров В.С., Жаринов В.В. Уравнения математической физики. М.: ФИЗМАТЛИТ, 2004. 400 с.
Hooke R., Jeeves T.A. Direct Search Solution of Numerical and Statistical Problems // J. of the ACM (JACM). 1961. V. 8. Issue 2. P. 212–229.
Banichuk N., Petrov V., Sinitsyn A., Neittaanmdki P., Tuovinen T. On the Optimality Conditions for Suppression of Vibration of Axially Moving Materials.: Rep. Depart. Math. Inform. Technolgy. Ser. B. Sci. Comp. No. B 13120L6. P. 1–19. Univer. Jyvaskyla, 2016.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал