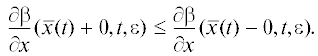Журнал вычислительной математики и математической физики, 2021, T. 61, № 12, стр. 2074-2094
Развитие методов асимптотического анализа переходных слоев в уравнениях реакции–диффузии–адвекции: теория и применение
Н. Н. Нефедов *
МГУ, физ. факультет
119991 Москва, Ленинские горы, Россия
* E-mail: nefedov@phys.msu.ru
Поступила в редакцию 25.03.2021
После доработки 25.03.2021
Принята к публикации 04.08.2021
Аннотация
Работа посвящена обзору и анализу современных асимптотических методов исследования сингулярно возмущенных задач с внутренними и пограничными слоями. Центральной частью работы является обзор работ автора, его коллег и учеников. В рассмотрении выделены краевые и начально-краевые задачи для нелинейных уравнений в частных производных эллиптического и параболического типов, а также периодические параболические задачи, которые широко используются в приложениях и носят название уравнений реакции–диффузии и реакции–диффузии–адвекции. Эти задачи могут быть интерпретированы как модели в химической кинетике, синергетике, астрофизике, биологии и других областях. Решения этих задач часто имеют как узкие пограничные области быстрого изменения, так и внутренние слои различных типов (контрастные структуры, движущиеся внутренние слои – фронты), что приводит к необходимости развивать новые асимптотические методы, чтобы исследовать их как формально, так и строго. Представлена и проиллюстрирована на актуальных задачах общая схема строгого исследования контрастных структур в сингулярно возмущенных задачах для уравнений в частных производных, основанная на применении асимптотического метода дифференциальных неравенств. Отражены основные достижения этого направления исследований дифференциальных уравнений в частных производных и выделены ключевые направления его развития. Библ. 89.
1. ВВЕДЕНИЕ
Одной из актуальных задач теории сингулярных возмущений в настоящее время является исследование нелинейных сингулярно возмущенных уравнений в частных производных, решения которых имеют пограничные и внутренние слои. Такие уравнения представляют большой интерес как в качественной теории дифференциальных уравнений, так и во многих прикладных задачах. В частности, такие уравнения возникают в математических моделях процессов типа реакция–диффузия и реакция–диффузия–адвекция в химической кинетике, синергетике, астрофизике, биологии и других областях, где исследуемые процессы характеризуются узкими пограничными областями быстрого изменения параметров процессов либо резкими внутренними слоями различных типов (контрастные структуры) – стационарными или движущимися (фронтами). Для адекватного математического описания таких процессов нужно развивать новые асимптотические методы исследования нелинейных сингулярно возмущенных задач, исследование которых (начальных задач с малыми параметрами при старших производных) начато достаточно давно. Направление исследований, представленное в данной работе, является развитием глубоких идей работ А.Н. Тихонова (см. [1]–[3]), заложивших основы современной теории сингулярных возмущений. Эти работы, объединившие теорию сингулярных возмущений с качественной теорией дифференциальных уравнений и теорией устойчивости Ляпунова, продолженные и развитые в работах А.Б. Васильевой, В.Ф. Бутузова и их учеников и последователей (см. монографию А.Б. Васильевой и В.Ф. Бутузова [4]), и по сей день формируют язык теории сингулярных возмущений, несмотря на значительно усложнившиеся рассматриваемые задачи.
Различные направления теории нелинейных сингулярно возмущенных задач интенсивно разрабатываются как у нас в стране, так и за рубежом. Об этом свидетельствует ряд международных конференций, состоявшихся в последние годы и посвященных теории сингулярных возмущений, а также конференции, посвященные внутренним слоям. У нас в стране этими исследованиями занимаются в школе В.П. Маслова и С.Ю. Доброхотова, ученики С.А. Ломова, С.А. Кащенко, С.Д. Глызин и многие другие. Эти работы активно велись и ведутся в США, eвропейских странах, Японии, Китае (P. Fife, B. McLeod P. Bates, N. Alikakos, Danielle Hilhorst, B. Fidler, L. Recke, K. Scheider, P. Szmolyan, H. Motano, Н. Morita K. Sakamoto, Vimura, Nishiura и др). Результаты этих и других специалистов представлены в трудах конференции “Patterns of Dynamics 2016”, проведенной в Берлине, и в специальном выпуске журнала “Discrete and continuous dynamical systems” V. 37, № 2, February 2017 (см. [5]), посвященном памяти Поля Файфа.
Современное состояние асимптотического анализа сингулярно возмущенных задач с пограничными и внутренними слоями можно узнать из обзора [6]. Ряд интересных результатов, развивавающих исследование задач с внутренними и пограничными слоями, получен в [7]–[9]. В настоящее время наблюдается значительный рост интереса к сингулярно возмущенным уравнениям с запаздыванием, что связано с рассмотрением более сложных моделей, важных для приложений (см., например, [10], [11] и ссылки в этих работах). Одним из важнейших приложений асимптотического анализа сингулярно возмущенных задач является разработка теории численных методов для задач с переходными слоями. Значительный вклад в развитие этого направления внесли работы А.М. Ильина, Н.С. Бахвалова, Г.И. Шишкина, Н.В. Коптевой а также ирландских математиков М. Стайнза (M. Stynes), Е. О’Риордана (E. O’Riordan) и других. С этими работами можно познакомиться в обзоре [12]. Ряд интересных результатов в области теории и их применения для численного решения сингулярно возмущенных задач переходными слоями получен в [13]–[18]. Отметим, что это активно развивающееся направление основывается на результатах асимптотического анализа работ, представленных в данном обзоре.
В настоящей работе представлено развитие хорошо известного метода пограничных функций для построения асимптотик решений различных классов задач с внутренними слоями. Основные идеи продемонстрированы на новых классах исследуемых сингулярно возмущенных задач, включающие задачи о движении фронтов, исследования устойчивых стационарных или периодических внутренних слоев в многомерных задачах. Эти результаты являются дальнейшим развитием наших исследований контрастных структур, которые были опубликованы в обзорных статьях [19]–[22].
Контрастными структурами принято называть решения с внутренними слоями нелинейных сингулярно возмущенных уравнений. Такие решения изучаются достаточно давно. Первые результаты в этом направлении были получены А.Б. Васильевой еще в начале 70-х годов прошлого века для двухточечной краевой задачи вида
(1)
$\begin{gathered} {{\varepsilon }^{2}}\frac{{{{d}^{2}}u}}{{d{{x}^{2}}}} - f(u,x) = 0,\quad x \in (0,\;1), \\ u(0,\varepsilon ) = {{u}^{{(0)}}},\quad u(1,\varepsilon ) = {{u}^{{(1)}}}. \\ \end{gathered} $Если рассмотреть двумерный аналог задачи (1)
(2)
$\begin{gathered} {{\varepsilon }^{2}}\Delta u = f(u,x,\varepsilon ),\quad x \in \mathcal{D} \subset {{R}^{2}}, \\ u(x,\varepsilon ) = g(x),\quad x \in \partial{ \mathcal{D}}, \\ \end{gathered} $Контрастная структура типа ступеньки – это решение $u(x,\varepsilon )$ задачи (2), которое близко к двум различным решениям вырожденного уравнения $f(u,x,0) = 0$ по разные стороны от некоторой замкнутой кривой $\Gamma $ (положение кривой $\Gamma $ не известно заранее, а определяется в ходе построения асимптотики). В окрестности кривой $\Gamma $ возникает область быстрого изменения решения – решение в этой области называется внутренним переходным слоем. В [25], [26] был предложен новый метод доказательства существования решений сингулярно возмущенных уравнений в частных производных, получивший название асимптотический метод дифференциальных неравенств. Этот метод оказался эффективным, и получила развитие как общая схема этого метода (см., например, [27]–[29]), так и ее применение для других классов сингулярно возмущенных задач – начально-краевых задач для параболических уравнений при описании решений с движущимися внутренними слоями (фронтами), периодических параболических краевых задач, краевых и начально-краевых задач для некоторых классов интегро-дифференциальных уравнений и некоторых классов систем.
Другой класс сингулярно возмущенных задач, который обсуждается в данной работе, представляют задачи с разрывными нелинейностями (источниками или адвективными коэффициентами), моделирующими переходные слои в области контакта различных сред, а также межфазовые переходы. В работе представлены новые результаты, касающиеся существования решений этого класса задач, их асимптотик и устойчивости.
Исследование рассмотренных задач базируется на асимптотическом методе дифференциальных неравенств. Основная идея этого подхода – построение нижних и верхних решений задачи с помощью формальной асимптотики. Для всех рассмотренных задач доказывается существование решений, оценивается точность асимптотики и исследуется их устойчивость.
Представленные в работе результаты формируют основу для дальнейшего развития и разработки методов асимптотического исследования новых классов нелинейных сингулярно возмущенных задач для уравнений в частных производных, которые широко используются в качестве математических моделей во многих важных приложениях. Развитие асимптотических методов исследования сложных нелинейных математических моделей с резкими переходными слоями позволит, наряду с решением важных математических вопросов существования, устойчивости и асимптотического приближения решений, развивать эффективные численные методы решения этих классов задач, а также новые концепции решения обратных задач на основе асимптотического анализа, исследования условий разрушения и обострения решений, а также применения полученных результатов в ряде приложений: моделировании контрастных структур в исследовании задач биофизики, экологии, генетики, нелинейной теории волн и других приложений.
Следует отметить, что данный обзор не претендует на полноту. В работе выделено то направление, в котором работает научная школа, которой принадлежит автор, и тот метод, к развитию которого он имеет непосредственное отношение.
2. ОСНОВНЫЕ ИДЕИ АСИМПТОТИЧЕСКОГО МЕТОДА ДИФФЕРЕНЦИАЛЬНЫХ НЕРАВЕНСТВ
В наших работах была разработана общая схема строгого исследования контрастных структур в сингулярно возмущенных задачах для уравнений в частных производных, основанная на применении асимптотического метода дифференциальных неравенств. Ниже для простоты изложения мы поясним эту схему на примере задачи (2), не конкретизируя требования, при которых ее реализация возможна. Как отмечалось во Введении, эта схема состоит из трех основных этапов: построения формальной асимптотики контрастной структуры, модификации асимптотики для построения верхнего и нижнего решений задачи, использования построенных нижних и верхних решений для доказательства асимптотической устойчивости по Ляпунову стационарных или периодических решений в соответствующих классах задач. Эти этапы будут кратко изложены далее в этом разделе.
2.1. Построение формальной асимптотики
Контрастные структуры типа ступеньки в задаче (2) и других аналогичных задачах изучаются в предположении, что нелинейность $f$ является бистабильной, т.е. имеет два устойчивых корня ${{\varphi }^{{( \pm )}}}(x)$ и неустойчивый корень ${{\varphi }^{{(0)}}}(x)$, причем ${{\varphi }^{{( - )}}}(x) < {{\varphi }^{{(0)}}}(x) < {{\varphi }^{{( + )}}}(x)$ при $x \in \bar {\mathcal{D}}$. Положение кривой перехода ${{\Gamma }_{\varepsilon }}$ между корнями ${{\varphi }^{{( - )}}}$ и ${{\varphi }^{{( + )}}}$ обычно определяется условием
(т.е. ${{\Gamma }_{\varepsilon }}$ определяется как проекция кривой пересечения поверхностей решения $u(x,\varepsilon )$ и корня ${{\varphi }^{{(0)}}}(x)$ на область $\mathcal{D}$).Пусть ${{\Gamma }_{0}}$ – некоторая замкнутая достаточно гладкая кривая, лежащая в $\mathcal{D}$. Введем в окрестности ${{\Gamma }_{0}}$ локальные координаты $r$, $y$, где $r$ – расстояние от точки из окрестности до кривой ${{\Gamma }_{0}}$ вдоль нормали к кривой, взятое со знаком “+” , если точка лежит внутри кривой, и со знаком “$ - $”, если точка лежит во внешней по отношению к кривой области, $y$ – координата той точки на кривой, из которой выходит указанная нормаль. Уравнение кривой ${{\Gamma }_{\varepsilon }}$ ищем в виде
(3)
$r = R(y,\varepsilon ) = \varepsilon {{R}_{1}}(y) + {{\varepsilon }^{2}}{{R}_{2}}(y) + \; \ldots \;.$Кривая ${{\Gamma }_{\varepsilon }}$ делит $\bar {\mathcal{D}}$ на внутреннюю ${{\bar {\mathcal{D}}}^{{( + )}}}$ и внешнюю ${{\bar {\mathcal{D}}}^{{( - )}}}$ по отношению к ней области.
В области ${{\bar {\mathcal{D}}}^{{( + )}}}$ рассматриваем задачу
(4)
$\begin{gathered} {{L}_{\varepsilon }}u \equiv {{\varepsilon }^{2}}\Delta u - f(u,x,\varepsilon ) = 0,\quad x \in {{{\bar {\mathcal{D}}}}^{{( + )}}}, \\ u(x,\varepsilon ) = {{\varphi }^{{(0)}}}(x),\quad x \in {{\Gamma }_{\varepsilon }}. \\ \end{gathered} $(5)
${{U}^{{( + )}}} = \sum\limits_{i = 0}^{n + 1} {{{\varepsilon }^{i}}} (\bar {u}_{i}^{{( + )}} + Q_{i}^{{( + )}}),$В области ${{\bar {\mathcal{D}}}^{{( - )}}}$ рассматриваем задачу
(6)
$\begin{gathered} {{L}_{\varepsilon }}u \equiv {{\varepsilon }^{2}}\Delta u - f(u,x,\varepsilon ) = 0,\quad x \in {{{\bar {\mathcal{D}}}}^{{( - )}}}, \\ u(x) = g(x),\quad x \in \partial D,\quad u(x,\varepsilon ) = {{\varphi }^{{(0)}}}(x),\quad x \in {{\Gamma }_{\varepsilon }}. \\ \end{gathered} $(7)
${{U}^{{( - )}}} = \sum\limits_{i = 0}^{n + 1} {{{\varepsilon }^{i}}} (u_{i}^{{( - )}} + Q_{i}^{{( - )}} + {{\Pi }_{i}}),$По самому построению (см. [4], [20]) асимптотики (5) и (7) удовлетворяют задачам (4) и (6) по невязке с точностью $O({{\varepsilon }^{{n + 2}}})$, в частности,
(8)
$\begin{gathered} {{L}_{\varepsilon }}{{U}^{{( + )}}} = {{L}_{{0R}}}\bar {u}_{0}^{{( + )}} + {{L}_{{0IL}}}Q_{0}^{{( + )}} + \\ + \;\sum\limits_{i = 1}^{n + 1} {{{\varepsilon }^{i}}} ((L_{R}^{{( + )}}\bar {u}_{i}^{{( + )}} + \bar {f}_{i}^{{( + )}}) + (L_{{IL}}^{{( + )}}Q_{i}^{{( + )}} + q_{i}^{{( + )}})) + O({{\varepsilon }^{{n + 2}}}) = O({{\varepsilon }^{{n + 2}}}), \\ \end{gathered} $(9)
$\begin{gathered} {{L}_{\varepsilon }}{{U}^{{( - )}}}) = {{L}_{{0R}}}\bar {u}_{0}^{{( - )}} + {{L}_{{0IL}}}Q_{0}^{{( - )}} + {{L}_{{0BL}}}{{\Pi }_{0}} + \\ + \;\sum\limits_{i = 1}^{n + 1} {{{\varepsilon }^{i}}} ((L_{R}^{{( - )}}\bar {u}_{i}^{{( - )}} + \bar {f}_{i}^{{( - )}}) + (L_{{IL}}^{{( - )}}Q_{i}^{{( + )}} + q_{i}^{{( - )}}) + ({{L}_{{BL}}}{{\Pi }_{i}} - {{\pi }_{i}})) + \\ + \;O({{\varepsilon }^{{n + 2}}}) = O({{\varepsilon }^{{n + 2}}}). \\ \end{gathered} $В силу граничных условий на кривой ${{\Gamma }_{\varepsilon }}$ в задачах (4) и (6) асимптотики ${{\bar {U}}^{{( + )}}}$ и ${{\bar {U}}^{{( - )}}}$ являются сшитыми до непрерывности (выполнено условие $C$-сшивания) на кривой ${{\Gamma }_{\varepsilon }}$. Эта кривая (т.е. кривая ${{\Gamma }_{0}}$) и коэффициенты ${{R}_{i}}$ в разложении (3) определяются из условия ${{C}^{1}}$-сшивания асимптотик ${{\bar {U}}^{{( + )}}}$ и ${{\bar {U}}^{{( - )}}}$ на ${{\Gamma }_{\varepsilon }}$:
(10)
$\varepsilon \frac{{\partial {{{\bar {U}}}^{{( - )}}}}}{{\partial r}} = \varepsilon \frac{{\partial {{{\bar {U}}}^{{( + )}}}}}{{\partial r}},\quad x \in {{\Gamma }_{\varepsilon }},$Более подробно этот алгоритм будет продемонстрирован на примерах в следующих разделах.
2.2. Асимптотический метод дифференциальных неравенств
Асимптотический метод дифференциальных неравенств развит нами для тех классов сингулярно возмущенных задач, где работает принцип сравнения эллиптических краевых задач, параболических начально-краевых задач и периодических по времени параболических краевых задач, а также задач для интегро-дифференциальных уравнений. Базовые теоремы сравнения для нелинейных уравнений, основанные на принципе максимума или монотонности линеаризованных операторов, берут начало от известных теорем сравнения С.А. Чаплыгина для начально-краевых задач, теорем Нагумо для краевых задач и являются одним из важнейших инструментов исследования нелинейных уравнений в частных производных. Эти теоремы можно найти в ряде статей и монографий (см., например, [30] и ссылки в этой монографии). Значительный вклад в развитие принципа сравнения внесли М.А. Красносельский, М.Г. Крейн, С.И. Похожаев, H. Amann, P. Hess, D.J. Sattinger (см. [31]–[37]). Эти идеи получили дальнейшее развитие в работах для специальных случаев (см. [38]–[44]).
Основной идеей асимптотического метода дифференциальных неравенств является использование модификации формальной асимптотики для построения функций сравнения: нижних и верхних решений, при этом основным требованием к реализации этого подхода является монотонность линеаризованных на асимптотике нулевого порядка операторов, порождающих асимптотику. Этот подход был предложен в [25], [26], определив стратегию доказательства существования и оценки точности построенной асимптотики. В [27] этот метод распространен на периодические параболические краевые задачи. В этой работе был предложен достаточно эффективный метод доказательства асимптотической устойчивости периодических решений, который затем перенесен на исследование асимптотической устойчивости стационарных решений начально-краевых задач для параболических уравнений типа реакция–диффузия, а затем обобщен и на некоторые более сложные классы квазилинейных уравнений типа реакция–диффузия–адвекция (см. [29], [45]). В последние годы этот подход распространен и на задачи реакции–диффузии–адвекции с разрывными нелинейностями и источниками (см. [46] и ссылки в этой работе). Существенным развитием метода явились результаты по асимптотическому анализу пограничных и внутренних слоев в различных задачах для интегродифференциальных уравнений (см. [28], а также [47] и ссылки в этой работе).
Для удобства изложения напомним известные понятия и факты применительно к задаче (2).
Определение. Функции $\alpha (x,\varepsilon )$ и $\beta (x,\varepsilon )$ называются нижним и верхним решениями задачи (2), если они удовлетворяют следующим условиям
(12)
$\begin{gathered} {{L}_{\varepsilon }}{{\alpha }_{{n + 1}}}(x,\varepsilon ) = {{\varepsilon }^{{n + 1}}}q(x,\varepsilon ),{{L}_{\varepsilon }}{{\beta }_{{n + 1}}}(x,\varepsilon ) = - {{\varepsilon }^{{n + 1}}}q(x,\varepsilon ),\quad x \in \mathcal{D}, \\ {{\alpha }_{{n + 1}}}(x,\varepsilon ) \leqslant g(x) \leqslant {{\beta }_{{n + 1}}}(x,\varepsilon ),\quad x \in \partial{ \mathcal{D}}, \\ \end{gathered} $(14)
${{\alpha }_{{n + 1}}}(x,\varepsilon ) \leqslant u(x,\varepsilon ) \leqslant {{\beta }_{{n + 1}}}(x,\varepsilon ).$2.3. Асимптотический метод дифференциальных неравенств в исследовании асимптотической устойчивости по Ляпунову стационарных и периодических решений
Как отмечалось выше, в [27] был предложен достаточно простой метод доказательства асимптотической устойчивости по Ляпунову периодических решений периодических параболических задач, а также определения локальной области устойчивости и единственности решений с построенной асимптотикой. Этот метод применим и для исследования асимптотической устойчивости стационарных решений с пограничными и внутренними слоями начально-краевых задач для уравнений реакции–диффузии и реакции–диффузии–адвекции. Отметим, что стандартные методы исследования устойчивости, основанные на рассмотрении соответствующих спектральных задач для линеаризованных на решении уравнений, достаточно сложны и не получили существенного развития. Основная сложность такого подхода – это наличие так называемого критического спектра – собственных значений, стремящихся к нулю при стремлении к нулю малого параметра. Такой подход для уравнений в частных производных, называемый методом сингулярного предела задачи на собственные значения, был впервые реализован в [48]. Отметим также, что эта работа сыграла важную роль и в развитии методов построения асимптотик в так называемых задачах со сбалансированной нелинейностью, а также в задачах с адвекцией, где многомерность играет существенную роль в структуре и свойствах устойчивости решения.
Проиллюстрируем схему подхода метода дифференциальных неравенств на задаче (2). Решение задачи (2) можно рассматривать как стационарное решение начально-краевой задачи
(16)
$\begin{gathered} \frac{{\partial u}}{{\partial t}} = {{\varepsilon }^{2}}\Delta u - f(u,x,\varepsilon ),\quad x \in \mathcal{D},\quad t > 0, \\ u(x,t,\varepsilon ) = g(x),\quad x \in \partial{ \mathcal{D}},\quad t > 0, \\ u(x,0,\varepsilon ) = {{u}^{0}}(x,\varepsilon ). \\ \end{gathered} $(17)
$\begin{gathered} \hat {\beta }(x,t,\varepsilon ) = u(x,\varepsilon ) + \left( {{{\beta }_{n}}(x,\varepsilon ) - u(x,\varepsilon )} \right){{e}^{{ - \lambda t}}}, \\ \hat {\alpha }(x,t,\varepsilon ) = u(x,\varepsilon ) + \left( {{{\alpha }_{n}}(x,\varepsilon ) - u(x,\varepsilon )} \right){{e}^{{ - \lambda t}}}, \\ \end{gathered} $3. НЕКОТОРЫЕ АКТУАЛЬНЫЕ ЗАДАЧИ С ПОГРАНИЧНЫМИ И ВНУТРЕННИМИ СЛОЯМИ
В этом разделе рассмотрен ряд актуальных задач, представляющих интерес как для теории сингулярных возмущений, так и для приложений. При рассмотрении этих задач проиллюстрированы основные идеи и направления развития. Одним из активно развиваемых направлений является исследование существования и устойчивость стационарных гладких решений в одномерной и многомерной задачах реакции–диффузии с разрывными источниками и адвективными членами. Эти задачи моделируют переходные слои на границе контакта двух сред с различными характеристиками. Рассмотрены задачи для стационарного уравнения реакции–диффузии на отрезке и в двумерной области. Особенностью этих задач является разрыв (первого рода) реактивного слагаемого в одномерном случае в некоторой внутренней точке, а в двумерном – на некоторой гладкой замкнутой кривой. Это новый неизученный ранее класс задач. Разработаны методы построения асимптотических приближений решений, доказано существование гладких стационарных решений уравнений реакции–диффузии с внутренним переходным слоем в окрестности разрывов в одномерном и двумерном случаях, а также получены условия, при которых эти решения являются локально единственными и асимптотически устойчивыми по Ляпунову. Кроме того, указана локальная область притяжения стационарных решений. Эти исследования представлены в [46], [49], [50] (см. также ссылки в этих работах).
Другим важным направлением исследований являются новые классы задач – задачи с модульными нелинейностями. Это новые классы математических задач с разрывными коэффициентами адвекции или(и) разрывными нелинейными источниками. Основной особенностью этих задач является то, что разрывы возникают при некоторых значениях искомой функции. Эти задачи моделируют межфазовые переходы и инициированы исследованиями в нелинейной теории волн (см. [51]–[53]). В [54], [55] проведены исследования начально-краевых задач для уравнений типа уравнения Бюргерса. Доказано существование новых классов решений с движущимся внутренним слоем (фронтом), сформулированы условия нового эффекта в этом классе задач – разрушения (обострения) фронта, и получена оценка времени движения фронта от точки начального положения до точки разрушения. Эти работы продолжили изучение задач для уравнений типа реакция–диффузия и реакция–диффузия–адвекция с движущимися внутренними слоями (фронтами). В [47], [56] было получено асимптотическое приближение фронтов в одномерной параболической и интегро-параболической задачах типа реакция–диффузия. Эти результаты затем были перенесены на квазилинейные уравнения типа реакция–диффузия–адвекция с нелинейным коэффициентом адвекции в [57]–[59]. Отметим, что рассмотрение движущихся внутренних слоев (фронтов) в ограниченных объемах с учетом пространственно-временной неоднородности существенно отличается от широко представленных в литературе исследований решений типа бегущих волн и автомодельных решений (см., например, [60]–[62] и ссылки в этих работах). Аналогичные результаты были получены в исследовании периодических фронтов в параболических периодических краевых задачах, включающих уравнения типа уравнения Бюргерса. Различные задачи этого класса представлены в [63]–[68]. В этих работах рассмотрены многомерные по пространственной переменной периодические задачи с внутренним переходным слоем и выделены классы новых задач, в которых многомерность приводит к новым ранее не изученным условиям существования и устойчивости решения с внутренним переходным слоем. Это задачи с балансом нелинейности, в которых результаты, полученные ранее для задачи реакции–диффузии обобщаются на задачи для уравнения реакции–диффузии–адвекции. Выявлены соотношения между адвекцией и реакцией, при которых адвекция играет существенную роль в устойчивости внутренних переходных слоев.
В [69]–[71] был исследован новый класс нелинейных сингулярно возмущенных задач с сингулярно возмущенными граничными условиями второго рода и третьего рода. Доказано существование стационарных и периодических по времени решений погранслойного типа, построено асимптотическое приближение по малому параметру таких решений. Исследовано множество граничных условий, при которых такие решения существуют, и установлены локальная единственность и асимптотическая устойчивость по Ляпунову таких решений. Показано, что, в отличие от аналогичной задачи Дирихле, где такое решение единственно, в рассматриваемой задаче таких решений может быть несколько, при этом каждое из них обладает своей областью устойчивости и локальной единственности.
Среди активно развиваемых направлений выделим исследование существования и условий устойчивости по Ляпунову стационарных решений начально-краевых задач и периодических решений систем параболических уравнений с быстрыми источниками разной скорости. Построена асимптотика решения, исследована асимптотическая устойчивость периодического решения. Проведено исследование систем уравнений с быстрыми источниками разной скорости в случае различной квазимонотонности правых частей (источников). В [72], [73] рассматриваются сингулярно возмущенные системы параболических уравнений в одномерной и двумерной пространственных областях с периодическими условиями по времени. Исследуется вопрос существования у системы решения типа периодического фронта. Приведен алгоритм построения асимптотического приближения решения, доказана теорема существования решения типа периодического фронта, его локальная единственность и асимптотическая устойчивость. Решение такого вида может описывать резкое изменение физических характеристик некоторой пространственно-неоднородной среды. Системы подобного типа применяются для моделирования переходных процессов в экологии, биофизике, химической кинетике, физике полупроводников и других областях. Отмеченные выше работы основаны на развитии классических методов построения асимптотик, предложенного в работах А.Б. Васильевой, В.Ф. Бутузовы и их учениками. В последние годы в работах В.Ф. Бутузова был разработан новый метод построения асимптотических приближений решения сингулярно возмущенных уравнений с кратными корнями вырожденных уравнений (см. [74]–[83] и ссылки в этих работах). В данных работах было показано, что в этом случае пограничные и внутренние слои многозонные. Структура переходных слоев, в отличиe от случаев простого слоя, существенно зависит от типа граничных условий. Исследование существования решений и их устойчивости было проведено на основе развития асимптотического метода дифференциальных неравенств на этот класс задач.
Среди важных приложений асимптотических методов выделим разработку концепции асимптотического решения обратных задач для нелинейных сингулярно возмущенных уравнений типа реакция–диффузия–адвекция. Особенностью математических моделей указанного типа является наличие в их решениях стационарных или движущихся узких внутренних переходных слоев, что приводит к неустойчивости при численном решении прямых задач и существенным образом усложняет дальнейшее исследование соответствующих обратных задач. Основная идея концепции асимптотического решения обратных задач состоит в том, что асимптотический анализ позволяет свести исходную нелинейную сингулярно возмущенную задачу к набору более простых задач, которые не содержат малых параметров и имеют меньшую пространственную размерность или содержат не дифференциальные, а алгебраические уравнения. Таким образом, применение асимптотического анализа дает возможность установить более простые связи между наблюдаемыми параметрами решения и параметрами обратной задачи, которые необходимо определить (коэффициенты в уравнении, граничные и начальные условия и т.п.), что позволяет принципиально изменить подход к решению обратных задач. Наличие малого параметра в исходной модели обеспечивает при этом достаточно точное качественное и количественное описание решения. За последнее время получены результаты по решению обратных задач для нового класса нелинейных сингулярно возмущенных уравнений типа Бюргерса с модульной и квадратичной адвекциями с периодическими по времени коэффициентами, а также некоторые классы начально-краевых задач. Показано, что в рассматриваемых моделях при определенных условиях асимптотический подход позволяет свести коэффициентные обратные задачи к линейным алгебраическим уравнениям, связывающим с заданной точностью наблюдаемое положение движущегося фронта с входными данными модели (коэффициентами в уравнении и граничными условиями). Таким образом, если имеется возможность наблюдения траектории движения фронта на некотором временном интервале, то вопрос об определении неизвестного коэффициента уравнения или граничного режима сводится к набору простых алгебраических операций. Предложено асимптотическое решение задачи восстановления функции источника в уравнении Бюргерса с модульной адвекцией по известной (точно или приближенно) информации о траектории движения фронта на заданном временном интервале (периоде). Аналогичным образом было получено асимптотическое решение задачи граничного управления, т.е. определения граничных условий, при которых фронт движется по заданному закону. Развиваемый подход продемонстрирован при решении обратной коэффициентной задачи коэффициента линейного усиления на основании асимптотического анализа и эффективных численных методов в случае, когда коэффициент линейного усиления получается на основании решения некорректно поставленной задачи дифференцирования наблюдаемой информации. Продемонстрирована высокая эффективность предлагаемого подхода по сравнению с ранее развитыми для таких классов задач (см. [84]–[87]).
В ряде работ создан новый подход аналитико-численного исследования движущихся фронтов в сингулярно возмущенных моделях типа реакция–диффузия–адвекция. Предложен метод генерации динамически адаптированной сетки для эффективного численного решения задач данного класса. Метод основан на априорной информации о движении и свойствах фронта, полученной в результате строгого асимптотического анализа сингулярно возмущенной параболической задачи. В частности, существенными параметрами, которые учитываются при построении сетки, являются оценки местоположения переходного слоя, его ширина и структура. Предлагаемый аналитико-численный подход позволяет значительно сэкономить вычислительные ресурсы, сократить время счета и повысить стабильность работы вычислительного процесса по сравнению с классическими подходами. Рассмотрены примеры, демонстрирующие основные идеи и методику применения предлагаемого подхода (см., например, [88] и ссылки в этой работе).
Продемонстрированы возможности методов асимптотического анализа в разрешении вопроса о диагностикe разрушения решения по времени и пространству уравнения Бюргерса с квадратичной и модульной нелинейностями и кубическим усилением (см. [54]). Результат, полученный методами асимптотического анализа был уточнен с помощью методики численной диагностики разрушения точного решения, которая основана на вычислении апостериорной асимптотически точной оценки погрешности, получаемой при вычислении приближенного решения на последовательности сгущающихся сеток. Численные эксперименты демонстрируют, что асимптотический результат дает хорощую оценку времени разрушения решения и его локализацию по пространству для достаточно широкого диапазона малых параметров. Таким образом, можно утверждать, что создан и развивается новый метод аналитического исследования явлений разрушения решений, областью применения которого является класс сингулярно возмущенных задач (например, задачи для уравнения типа Бюргерса). Важным отличием этого метода от используемых другими исследователями является то, что он позволяет установить факт разрушения решения не только по времени (а также получить асимптотическое приближение времени разрушения), но и определить пространственную локализацию этого явления, что является важным результатом при решении многих прикладных задач. Ниже идеи асимптотического метода дифференциальных неравенств продемонстрированы в двух классах актуальных задач. Эти разделы сейчас активно развиваются и переносятся в новые классы задач, представляющих как теоретический, так и прикладной интерес.
3.1. Многомерные внутренние слои в задаче со сбалансированной нелинейностью
В этом разделе мы проиллюстрируем общую схему применения асимптотического метода дифференциальных неравенств на примере задачи о многомерной стационарной контрастной структуре. Эта задача возникает при математическом моделировании различных процессов с межфазовыми переходами.
Рассмотрим пространственно неоднородное уравнение реакции–диффузии с граничными условиями Дирихле
(18)
$\begin{gathered} \frac{{\partial u}}{{\partial t}} = {{\epsilon }^{2}}\Delta u - f(u,x,\epsilon ),\quad x \in \mathcal{D} \subset {{R}^{N}},\quad t > 0, \\ u(x) = g(x),\quad x \in \partial{ \mathcal{D}},\quad t > 0, \\ u(x,0,\varepsilon ) = {{u}^{0}}(x,\varepsilon ) \\ \end{gathered} $(A1) Вырожденное уравнение $f(u,x,0) = 0$ имеет ровно три корня $u = {{\varphi }^{{( \pm )}}}(x)$, ${{\varphi }^{{(0)}}}(x)$ таких, что
(A2) $I(x) \equiv 0$, $x \in \bar {\mathcal{D}}$.
При выполнении условия (A2) уравнение в задаче (18) называют уравнением со сбалансированной нелинейностью.
(A3) Пусть граничное условие принадлежит области влияния корня $u = {{\varphi }^{{( - )}}}(x)$, т.е. выполнено условие
для всех $x \in \partial{ \mathcal{D}}$.Введем множество $\mathcal{S}$ гиперповерхностей
Определим функцию ${{V}_{1}}(x,\Gamma )$ для поверхностей $\Gamma \in \mathcal{S}$ следующим соотношением:
где $\kappa (x,\Gamma )$ – средняя кривизна поверхности $\Gamma $,Условие ${{C}^{1}}$-сшивания (10) выполняется в первом приближении, если наложить требование (отметим, что в случае сбалансированной нелинейности условие (10) в нулевом приближении выполняется для любой поверхности $\Gamma $):
(A4) Существует поверхность ${{\Gamma }_{0}} \in \mathcal{S}$ такая, что
Как отмечалось в предыдущем разделе, условие ${{C}^{1}}$-сшивания (10) в следующих приближениях приводит к линейным уравнениям для определения коэффициентов ${{R}_{i}}$ в асимптотическом представлении (3) для поверхности перехода ${{\Gamma }_{\varepsilon }}$: где оператор ${{A}^{\Gamma }}$ выражается через исходные данные следующим образом:(A5) Главное (наибольшее) собственное значение ${{\lambda }_{0}}$ оператора ${{A}^{\Gamma }}$ удовлетворяет условию ${{\lambda }_{0}} < 0$.
Оно обеспечивает однозначную разрешимость задач для определения ${{R}_{i}}$, а также выполнение условия существования положительного решения у неравенства ${{A}^{\Gamma }}R < 0$, которое, как отмечалось в п. 2.2, позволяет построить нижнее и верхнее решения, упорядоченные в зоне переходного слоя. Таким образом, применяя асимптотический метод дифференциальных неравенств, для задачи (18) мы получаем следующий результат.
Теорема 1. Пусть выполнены условия $(A1)$–$(A5)$. Тогда для достаточно малых $\varepsilon $ существует стационарное решение $u(x,\varepsilon )$ задачи (18) такое, что вне любых сколь угодно малых, но фиксированных окрестностей ${{\Gamma }_{\delta }}$ поверхности ${{\Gamma }_{0}}$ и $\partial {{\mathcal{D}}_{\delta }}$ границы $\partial{ \mathcal{D}}$ имеет место равномерный предельный переход
3.2. Периодические фронты в задаче с модульной адвекцией
Проиллюстрируем развитие важного направления исследований задач с разрывными коэффициентами и источниками следующей задачей:
(19)
$\begin{gathered} {{N}_{\varepsilon }}(u): = \varepsilon \frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} - \frac{{\partial u}}{{\partial t}} + \frac{{\partial \left| u \right|}}{{\partial x}} - B(u,x,t) = 0, \\ (x,t) \in \mathcal{D}: = \{ (x,t) \in {{R}^{2}}: - 1 < x < 1,\;t \in R\} , \\ u( - 1,t,\varepsilon ) = {{u}^{{( - )}}}(t),\quad u(1,t,\varepsilon ) = {{u}^{{( + )}}}(t),\quad t \in R, \\ u(x,t,\varepsilon ) = u(x,t + T,\varepsilon ),\quad t \in R,\quad - {\kern 1pt} 1 \leqslant x \leqslant 1, \\ \end{gathered} $Определим области: $\mathcal{D}: = (x,t) \in (0;1) \times (0,T]$, $\mathcal{D}_{T}^{{( - )}}: = (x,t) \in (0;x*) \times (0,T]$, ${{\mathcal{D}}^{{( + )}}}: = (x,t) \in (x*;1) \times (0,T]$ ${{\mathcal{D}}^{{( + )}}}: = (x,t) \in (x*;1) \times (0,T]$, и дадим следующее определение решения.
Определение. Функция $u(x,t,\varepsilon ) \in C(\bar {\mathcal{D}}) \cap {{C}^{1}}\mathcal{D} \cap {{C}^{{1,2}}}({{\mathcal{D}}^{{( - )}}} \cup {{\mathcal{D}}^{{( + )}}})$ называется решением задачи (19), если она удовлетворяет уравнению в (19) в каждой $D_{T}^{{( \mp )}}$, а также граничным условиям.
$({{A}_{0}})$ Предположим, что $B$, ${{u}^{{( - )}}}$ и ${{u}^{{( + )}}}$ – достаточно гладкие и $T$-периодические по $t$ функции. Пусть ${{u}^{{( - )}}}(t) < 0$, ${{u}^{{( + )}}}(t) > 0$ при $t \in R$.
При $\varepsilon = 0$ в (19) получаем так называемое вырожденное уравнение
(20)
$\frac{{\partial \left| u \right|}}{{\partial x}} - \frac{{\partial u}}{{\partial t}} - B(u,x,t) = 0.$$({{A}_{1}})$ Задачи (20), (21) и (20), (22) имеют решения $u = {{\varphi }^{{( - )}}}(x,t)$ и $u = {{\varphi }^{{( + )}}}(x,t)$, определенные при $(x,t) \in \bar {\mathcal{D}}$, $T$-периодические по $t$ и удовлетворяющие условию
Для формулировки следующих условий введем функцию $I(x,t)$:
и потребуем выполнения условий$({{A}_{2}})$ Задача
$({{A}_{3}})$ Функция
Положение внутреннего переходного слоя ${{x}_{ * }}(t,\varepsilon )$ в каждый момент времени $t$ определим как точку пересечения решения задачи (19) с прямой $u = 0$. Асимптотическое приближение функции ${{x}_{ * }}(t,\varepsilon )$ ищем в виде ряда
где ${{x}_{k}}(t)$, $k = 1,\;2,\; \ldots $, – $T$-периодические функции, которые определяются из условия ${{C}^{1}}$-сшивания асимптотик задач $D_{T}^{{( - )}}$ и $D_{T}^{{( - )}}$ (эти задачи используют дополнительные условия в точке ${{x}_{ * }}(t,\varepsilon )$ – $u({{x}_{ * }}(t,\varepsilon ),t) = 0$). Формальную асимптотику ${{U}^{{( \mp )}}}(x,t,\varepsilon )$ решения каждой из этих задач:(23)
$\begin{gathered} \varepsilon \left( {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} - \frac{{\partial u}}{{\partial t}}} \right) + \frac{{\partial \left| u \right|}}{{\partial x}} - B(u,x,t) = 0\quad {\text{при}}\quad (x,t) \in {{\mathcal{D}}^{{( \mp )}}}, \hfill \\ u( \mp 1,t,\varepsilon ) = {{u}^{{( \mp )}}}(t),\quad u({{x}_{ * }}(t,\varepsilon ),t,\varepsilon ) = 0\quad {\text{при}}\quad t \in R, \hfill \\ u(x,t,\varepsilon ) = u(x,t + T,\varepsilon )\quad {\text{при}}\quad (x,t) \in {{{\bar {\mathcal{D}}}}^{{( \mp )}}}, \hfill \\ \end{gathered} $(24)
${{U}^{{( \mp )}}}(x,t,\varepsilon ) = {{U}^{{( \mp )}}}(x,t,\varepsilon ) + {{Q}^{{( \mp )}}}(\xi ,t,\varepsilon ) = \sum\limits_{i = 0}^\infty {{{\varepsilon }^{i}}} (\bar {U}_{i}^{{( \mp )}}(x,t) + Q_{i}^{{( \mp )}}(\xi ,t)),$Для определения функций ${{x}_{i}}(t)$ используются условия ${{C}^{1}}$-сшивания
(25)
$\varepsilon \frac{{\partial {{U}^{{( - )}}}}}{{\partial x}}({{x}_{ * }}(t,\varepsilon ),t,\varepsilon ) = \varepsilon \frac{{\partial {{U}^{{( + )}}}}}{{\partial x}}({{x}_{ * }}(t,\varepsilon ),t,\varepsilon ),\quad t \in R,$Для построения погранслойной части асимптотики (24) используется растянутая переменная $\xi = (x - {{x}_{ * }}(t,\varepsilon )){\text{/}}\varepsilon $, представление А.Б. Васильевой для нелинейности $B$, а также представление дифференциального оператора
(26)
$\begin{gathered} \frac{1}{\varepsilon }\frac{{{{\partial }^{2}}{{Q}^{{( \pm )}}}}}{{\partial {{\xi }^{2}}}} + \frac{1}{\varepsilon }\frac{{\partial {{x}_{ * }}(t,\varepsilon )}}{{\partial t}}\frac{{\partial {{Q}^{{( \pm )}}}}}{{\partial \xi }} - \frac{{\partial {{Q}^{{( \pm )}}}}}{{\partial t}} = \frac{1}{\varepsilon }\left[ { \mp \frac{\partial }{{\partial \xi }}({{Q}^{{( \pm )}}})} \right] + \\ + \;[B({{{\bar {U}}}^{{( \pm )}}}({{x}_{ * }}(t,\varepsilon ) + \varepsilon \xi ,t,\varepsilon ) + {{Q}^{{( \pm )}}},{{x}_{ * }}(t,\varepsilon ) + \varepsilon \xi ,t) - \\ - \;B({{{\bar {U}}}^{{( \pm )}}}({{x}_{ * }}(t,\varepsilon ) + \varepsilon \xi ,t,\varepsilon ),{{x}_{ * }}(t,\varepsilon ) + \varepsilon \xi ,t)], \\ {{Q}^{{( \pm )}}}(0,t,\varepsilon ) + {{{\bar {U}}}^{{( \pm )}}}({{x}_{ * }}(t,\varepsilon ),t,\varepsilon ) = 0. \\ \end{gathered} $(27)
$\frac{{{{\partial }^{2}}Q_{0}^{{( - )}}}}{{\partial {{\xi }^{2}}}} = (1 - x_{*}^{'}(t))\frac{{\partial Q_{0}^{{( - )}}}}{{\partial \xi }}\quad {\text{при}}\quad \xi < 0,\quad t \in R,$(28)
$Q_{0}^{{( - )}}( - \infty ,t) = 0,\quad Q_{0}^{{( - )}}(0,t) = - {{\varphi }^{{( - )}}}({{x}_{ * }}(t),t),\quad t \in R,$(29)
$\frac{{{{\partial }^{2}}Q_{0}^{{( + )}}}}{{\partial {{\xi }^{2}}}} = ( - 1 - x_{*}^{'}(t))\frac{{\partial Q_{0}^{{( + )}}}}{{\partial \xi }},\quad \xi > 0,\quad t \in R,$(30)
$Q_{0}^{{( + )}}(\infty ,t) = 0,\quad Q_{0}^{{( + )}}(0,t) = - {{\varphi }^{{( + )}}}({{x}_{ * }}(t),t),\quad t \in R.$Из представления (26) можно получить задачи для $Q_{1}^{{( \pm )}}$ и $Q_{k}^{{( \pm )}}$ следующих порядков, решение которых выписывается в явном виде. Условие ${{C}^{1}}$-сшивания (25) в первом порядке по $\varepsilon $ достаточно просто приводится к задаче отыскания периодического решения уравнения
где Φ1(t) выражаются через известные функции асимптотики первого порядка. Решение этой задачи гарантировано условием $({{A}_{2}})$. Функции ${{x}_{k}}$ следующих порядков определяются из аналогичных задач, а условие $({{A}_{3}})$ является условием однозначной разрешимости и монотонности оператора, порождающего асимптотику положения внутреннего переходного слоя.Определим $\mathcal{D}_{n}^{{( - )}}$ и $\mathcal{D}_{n}^{{( + )}}$:
Определение. Функции $\alpha $ и $\beta $ называются упорядоченными нижним и верхним решениями задачи (19) при $\varepsilon \in {{I}_{{{{\varepsilon }_{0}}}}}$, если они удовлетворяют следующим условиям:
Замечание. Известно (см., например, [33]), что из существования упорядоченных нижнего и верхнего решений следует существование решения $u(x,t,\varepsilon )$ задачи (19), удовлетворяющее неравенствам
Имеет место следующая теорема существования решения задачи (19), его локальной единственности и его асимптотической устойчивости как периодического решения начально-краевой задачи (31):
Теорема 2. Пусть выполнены условия $({{A}_{0}})$–$({{A}_{3}})$ . Тогда при достаточно малых $\varepsilon $ существует решение задачи $($19) u(x,t,$\varepsilon )$ с переходным слоем в окрестности ${{x}_{0}}(t)$, удовлетворяющее предельным соотношениям
Для доказательства существования решения и оценки точности асимптотического приближения решения задачи (19) используются нижнее и верхнее решения ${{\alpha }_{n}}(x,t,\varepsilon )$ и ${{\beta }_{n}}(x,t,\varepsilon )$, построенные по схеме п. 2.2. При этом модификация асимптотики положения переходного слоя ${{x}_{ * }}(t,\varepsilon )$ имеет вид
Аналогичная схема доказательства применяется и в других периодических задачах, процитированных выше.
4. ЗАКЛЮЧЕНИЕ
В данной обзорной статье отражено развитие методов асимптотического анализа новых классов нелинейных сингулярно возмущенных задач для параболических и эллиптических уравнений, включающих так называемые уравнения реакции–диффузии–адвекции с пограничными и внутренними переходными слоями. Эти исследования включают в себя как разработку методов построения формальных асимптотических приближений (удовлетворяющих задаче по невязке), так и строгое обоснование – доказательство существования решения, оценку точности построенного асимптотического приближения, исследование устойчивости решений по Ляпунову. Новизна каждого класса задач может быть определена новыми дифференциальными операторами, производящими асимптотику. В основе строгих математических результатов, представленных в статье, лежит использование асимптотического метода дифференциальных неравенств. Суть этого метода состоит в использовании асимптотики для построения функций сравнения – нижних и верхних решений. При этом выясняются свойства операторов, производящих асимптотику: обратимость, монотонность. Этот метод определяет стратегию исследования. Переход к новым классам задач, в том числе обобщение ряда результатов на многомерный случай, а также на некоторые важные для приложений классы систем, требует развития как методов построения асимптотики и исследования обратимости новых классов операторов, порождающих асимптотику, так и исследования их монотонности. В ряде случаев это потребовало также привлечение и модификацию базовых теорем сравнения, устанавливающих условия существования соответствующих классов решений.
Полученные результаты асимптотического анализа широко используются и составляют основу как для развития теории численных методов, так и для создания эффективных численных алгоритмов для исследования задач с переходными слоями. В ходе работ в этом направлении создан и развивается новый метод аналитического исследования явлений разрушения решений, областью применения которого является класс сингулярно возмущенных задач (например, задачи для уравнения типа Бюргерса).
Известно, что динамика решений начально-краевых задач для параболических уравнений зависит от множества неустойчивых стационарных решений. Представляет интерес развитие методов доказательства существования и установления условий неустойчивости в классах задач, представленных выше. Продвижения в этом направлении представлены в [89].
Среди важных приложений отметим разработку концепции асимптотического решения обратных задач для нелинейных сингулярно возмущенных уравнений типа реакция–диффузия–адвекция. Известно, что наличие в их решениях стационарных или движущихся узких внутренних переходных слоев приводит к неустойчивости при численном решении прямых задач и существенным образом усложняет дальнейшее исследование соответствующих обратных задач. Основная идея концепции асимптотического решения обратных задач состоит в том, что асимптотический анализ позволяет свести исходную нелинейную сингулярно возмущенную задачу к набору более простых задач, которые не содержат малых параметров и имеют меньшую пространственную размерность или содержат не дифференциальные, а алгебраические уравнения. Таким образом, применение асимптотического анализа дает возможность установить более простые связи между наблюдаемыми параметрами решения и параметрами обратной задачи, которые необходимо определить (коэффициенты в уравнении, граничные и начальные условия и т.п.), что позволяет принципиально изменить подход к решению обратных задач.
Полученные результаты асимптотического анализа, развитие численных методов и методов решения обратных задач применены для конкретных математических моделей нелинейной теории волн, биологии, магнитной гидродинамики и урбо-экологическим моделям. Среди важных достижений отметим создание модели развития урбоэкосистем, согласно которой городскую экосистему можно рассматривать как активную среду с взаимодействующими природными и антропогенными подсистемами.
Основная часть работы посвящена идеям и результатам автора, его учеников и коллег, работающих на кафедре математики физического факультета МГУ им. М.В. Ломоносова. Автор считает своим приятным долгом выразить им глубокую благодарность. Полученные результаты создают несколько новых направлений в нелинейных задачах с внутренними и переходными слоями и, как нам представляется, определяют мировое лидерство в этой области исследований школы А.Н. Тихонова по теории сингулярных возмущений. Особенную благодарность автор выражает В.Ф. Бутузову за тесное научное взаимодействие в течение многих лет.
Список литературы
Тихонов А.Н. О зависимости решений дифференциальных уравнений от малого параметра // Матем. сб. 1948. Т. 22 (64). № 2. С. 193–204.
Тихонов А.Н. О системах дифференциальных уравнений, содержащих параметры // Матем. сб. 1950. Т. 27 (69). № 1. С. 147–156.
Тихонов А.Н. Системы дифференциальных уравнений, содержащие малые параметры при производных // Матем. сб. 1952. Т. 31 (73). № 3. С. 575–586.
Васильева А.Б., Бутузов В.Ф. Асимптотические методы в теории сингулярных возмущений. М.: Высшая школа, 1990. 208 с.
Bates P., Hilhorst D., Matano H., Morita Y. Discrete and continuous dynamical systems. 2017. V. 37. № 2. P. i–iii.
Kumar M., Singh A.K. Singular perturbation problems in nonlinear elliptic partial differential equations: a survey // Inter. J. of Nonliner Sci. 2014. V. 17. № 3. P. 195–2014.
Sakamoto K. Infinitely many fine modes bifurcating from radially symmetric internal layers // Asymptot. Anal. 2005. V. 42. P. 55–104.
Magnus R. The implicit function theorem and multi-bump solutions of periodic partial differential equations // Proc. Roy. Soc. Edinburgh Sect. 2006. V. 136. P. 559–583.
del Pino M., Kowalczyk M., Wei J. Resonance and interior layers in an inhomogeneous phase transition model // SIAM J. Math. Anal. 2007. V. 38. P. 1542–564.
Кащенко С.А. Динамика логистического уравнения с двумя запаздываниями // Дифференц. ур-ния. 2016. Т. 52. № 5. С. 561–571.
Глызин С.Д., Колесов А.Ю., Розов Н.Х. Релаксационные автоколебания в сетях Хопфилда с запаздыванием // Изв. РАН. Сер. матем. 2013. Т. 77. № 2. С. 53–96.
Kopteva N., O’Riordan E. Shishkin meshes in the numerical solution of singularly perturbed differential equations // Inter. J. of Numer. Anal. and Model. 2004. V. 1. № 1. P. 1–18.
Kopteva N., Stynes M. Stabilised approximation of interior-layer solutions of a singularly perturbed semilinear reaction diffusion problem // Numerische Mathematik. 2011. V. 119. № 2. P. 787–810.
O’Riordan E., Quinn J. Numerical method for a nonlinear singularly perturbed interior layer problem // Lectures Notes in Comput. Sci. and Eng. 2011. V. 81. P. 187–195.
Quinn J. A numerical method for a nonlinear singularly perturbed interior layer problem using an approximate layer location // Comput. and Appl. Math. 2015. V. 290. № 15. P. 500–515.
Franz S., Roos H.-G. The capriciousness of numerical methods for singular perturbations // SIAM Rev. 2011. V. 53. P. 157–173.
Fran S., Kopteva N. Green’s function estimates for a singularly perturbed convection-diffusion problem // J. Diff. Eq. 2012. V. 252. P. 1521–1545.
Kopteva N. Numerical analysis of a 2d singularly perturbed semilinear reaction-diffusion problem // Lecture Notes in Comput. Sci. 2009. V. 5434. P. 80–91.
Бутузов В.Ф., Васильева А.Б., Нефедов Н.Н. Асимптотическая теория контрастных структур // Автоматика и телемехан. 1997. № 7. С. 4–32.
Васильева А.Б., Бутузов В.Ф., Нефедов Н.Н. Контрастные структуры в сингулярно возмущенных задачах // Фундамент. и приклад. матем. 1998. Т. 4. № 3. С. 799–851.
Butuzov V.F., Nefedov N.N., Schneider K.R. Singularly Perturbed Problems in Case of Exchange of Stabilities // J. of Math. Sci. 2004. V. 121. № 1. P. 1973–2079.
Васильева А.Б., Бутузов В.Ф., Нефедов Н.Н. Сингулярно возмущенные задачи с пограничными и внутренними слоями // Тр. Матем. института им. В.А. Стеклова РАН. 2010. № 268. С. 268–283.
Fife P.C. Semilinear elliptic boundary value problems with small parameters // Arch. Rational Mech. Anal. 1973. V. 52. P. 205–232.
Файф П., Гринли У.M. Внутренние переходные слои для эллиптических краевых задач с малым параметром // Успехи матем. наук. 1974. Т. 29. № 4 (178) С. 103–130. (Russian Math. Surveys, 29:4 (1974), 103–131.)
Нефедов Н.Н. Метод дифференциальных неравенств для некоторых классов сингулярно возмущенных уравнений в частных производных // Дифференц. ур-ния. 1995. Т. 31. № 4. С. 719–723.
Нефедов Н.Н. Метод дифференциальных неравенств для некоторых классов нелинейных сингулярно возмущенных задач с внутренними слоями // Дифференц. ур-ния. 1995. Т. 31. № 7. С. 1142–1149.
Нефедов Н.Н. Асимптотический метод дифференциальных неравенств в исследовании периодических контрастных структур: существование, асимптотика, устойчивость // Дифференц. ур-ния. 2000. Т. 36. № 2. С. 262–269.
Нефедов Н.Н., Никитин А.Г. Асимптотический метод дифференциальных неравенств для сингулярно возмущенных интегро-дифферециальных уравнений // Дифференц. ур-ния. 2000. Т. 36. № 10. С. 1398–1404.
Nefedov N.N. Comparison principle for reaction-diffusion-advection problems with boundary and internal layers // Lecture Notes in Computer Sci. V. 8236. P. 62–72.
Pao C.V. Nonlinear parabolic and elliptic equations. Springer Science Business Media, 1993. 777 p.
Крейн М.Г., Рутман М.А. Линейные операторы, оставляющие инвариантным конус в пространстве Банаха // Успехи матем. наук. 1948. V. 3. № 1 (23). P. 3–95.
Dancer E.N., Hess P. Behaviour of a semi-linear periodic-parabolic problem when a parameter is small // Lecture Notes in Math. 1990. V. 1450. P. 12–19.
Hess P. Periodic-parabolic boundary value problems and positivity. New York: Pitman Res. Notes in Math. Ser., 1991. 139 p.
Забрейко П.П., Кошелев А.И., Красносельский М.А. и др. Интегральные уравнения // Итоги науки. Сер. матем. Мат. анал. 1967. 448 с.
Amman H. On the existence of positive solutions of nonlinear elliptic boundary value problems // Indiana Univ. Math. J. 1971. V. 21. P. 125–146.
Sattinger D.H. Monotone methods in nonlinear elliptic and parabolic boundary value problems // Indiana Univ. Math. J. 1972. V. 21. № 11. P. 979–1001.
Похожаев С.И. Об уравнениях вида $\Delta u = \left( {x,u,Du} \right)$ // Матем. сб. 1980. V. 113. № 2. С. 324–338.
Павленко В.Н., Ульянова О.В. Метод верхних и нижних решений для уравнений эллиптического типа с разрывными нелинейностями // Изв. вузов. Матем. 1998. № 11. С. 69–76.
Levashova N.T., Nefedov N.N., Nikolaeva O.A., Orlov A.O., Panin A.A. The solution with internal transition layer of the reaction-diffusion equation in case of discontinuous reactive and diffusive terms // Math. Meth. Appl. Sci. 2018. V. 5134. P. 1–15.
Павленко В.Н., Ульянова О.В. Метод верхних и нижних решений для уравнений параболического типа с разрывными нелинейностями // Дифференц. ур-ния. 2002. V. 38. № 4. С. 499–504.
De Coster C., Obersnel F., Omari P.A. A qualitative analysis via lower and upper solutions of first order periodic evolutionary equations with lack of uniqueness // Handbook of differential equations: ordinary differential equations. 2006. V. 3. C. 203–339.
Павленко В.Н. Сильные решения периодических параболических задач с разрывными нелинейностями // Дифференц. ур-ния. 2016. Т. 52. № 4. С. 528–539.
Kannan R., Lakshmikantham V. Existence of periodic solutions of semilinear parabolic equations and the method of upper and lower solutions // J. Math. Anal. Appl. 1983. V. 97. № 1. P. 291–299.
Fife P., Tang M. Comparison principles for reaction–diffusion systems: irregular comparison functions and applications to question of stability and speed propagation of disturbances // J. Differential Equations. 1981. V. 40. № 11. P. 168–185.
Nefedov N.N., Recke L., Schnieder K.R. Existence and asymptotic stability of periodic solutions with an interior layer of reaction-advection-diffusion equations // J. of Math. Anal. and Appl. 2013. V. 405. P. 90–103.
Левашова Н.Т., Нефедов Н.Н., Орлов А.О. Асимптотическая устойчивость стационарного решения многомерного уравнения реакция-диффузия с разрывным источником // Ж. вычисл. матем. и матем. физ. 2019. Т. 59. № 4. С. 611–620.
Нефедов Н.Н., Никитин А.Г., Петрова М.А., Рекке Л. Движущиеся фронты в интегро-параболических уравнениях реакция–адвекция–диффузия // Дифференц. ур-ния. 2011. Т. 47. № 9. С. 1305–1319.
Nefedov N.N., Sakamoto K. Multi-dimensional stationary internal layers for spatially inhomogeneous reaction-diffusion equations with balanced nonlinearity // Hiroshima Math. J. 2003. V. 33. № 3. P. 391–432.
Орлов А.О., Нефедов Н.Н., Левашова Н.Т. Решение вида контрастной структуры параболической задачи реакция–диффузия в среде с разрывными характеристиками // Дифференц. ур-ния. 2018. Т. 54. № 5. С. 673–690.
Левашова Н.Т., Нефедов Н.Н., Николаева О.А. Решение с внутренним переходным слоем двумерной краевой задачи реакция–диффузия–адвекция с разрывными реактивным и адвективным слагаемыми // Теор. и матем. физ. 2021. Т. 207. № 2. С. 293–309.
Руденко О.В. Линеаризуемое уравнение для волн в диссипативных средах с модульной, квадратичной и квадратично-кубичной нелинейностями // Докл. РАН. 2016. Т. 471. № 1. С. 23–27.
Руденко О.В. Модульные солитоны // Докл. РАН. 2016. Т. 471. № 6. С. 451–454.
Hedberg C.M., Rudenko O.V. Collisions, mutual losses and annihilation of pulses in a modular nonlinear medium // Nonlinear Dyn. 2017. V. 90, P. 2083–2091.
Нефедов Н.Н., Руденко О.В. О движении фронта в уравнении типа Бюргерса с квадратичной и модульной нелинейностью при нелинейном усилении. // Докл. РАН. 2018. Т. 478. № 3. С. 274–279.
Нефедов Н.Н., Руденко О.В. О движении, усилении и разрушении фронтов в уравнениях типа бюргерса с квадратичной модульной нелинейностью // Докл РАН. 2020. Т. 493. № 1. С. 26–31.
Божевольнов Ю.В., Нефедов Н.Н. Движение фронта в параболической задаче реакция—диффузия // Ж. вычисл. матем. и матем. физ. 2010. Т. 50. № 2. С. 276–285.
Антипов Е.А., Левашова Н.Т., Нефедов Н.Н. Асимптотика движения фронта в задаче реакция–диффузия–адвекция // Ж. вычисл. матем. и матем. физ. 2014. Т. 54. № 10. С. 35–49.
Nefedov N.N. Asymptotic analysis of reaction–diffusion–advection problems: Fronts with periodic motion and blow-up // J. of Physics: Conf. Ser. 2017. V. 811. P. 012008.
Левашова Н.Т., Нефедов Н.Н., Ягремцев А.В. Существование решения в виде движущегося фронта у задачи типа реакция–диффузия–адвекция в случае сбалансированной адвекции // Изв. РАН. Сер. матем. 2018. Т. 82. № 5. С. 131–152.
Alikakos N.D., Bates P.W., Chen X. Periodic traveling waves and locating oscillating patterns in multidimensional domains // Trans. AMS. 1999. V. 351. № 7. P. 2777–2805.
Volpert A.I., Volpert V.A. Traveling Wave Solutions of Parabolic Systems. Translatio ed. Providence, Rhode Island: Am. Math. Soc. 1994. V. 140. P. 448.
Samarskii A.A., Galaktionov V.A., Kurdyumov S.P., Mikhailov A.P. Blow-up in quasilinear parabolic equations. Berlin: Walter de Gruyter, 1995.
Nefedov N.N., Nikulin E.I. Existence and stability of periodic contrast structures in the reaction–advection–diffusion problem // Rus. J. of Math. Phys. 2015. V. 22. № 2. P. 215–226.
Нефедов Н.Н., Никулин Е.И. Существование и устойчивость периодических контрастных структур в задаче реакция–адвекция–диффузия в случае сбалансированной нелинейности // Дифференц. ур-ния. 2017. Т. 53. № 4. С. 524–537.
Nefedov N.N., Nikulin E.I. Existence and asymptotic stability of periodic solutions of the reaction–diffusion equations in the case of a rapid reaction // Rus. J. of Math. Phys. 2018. V. 25. № 1. P. 88–101.
Нефедов Н.Н., Никулин Е.И. Существование и асимптотическая устойчивость периодических двумерных контрастных структур в задаче со слабой линейной адвекцией // Матем. заметки. 2019. Т. 106. № 5. С. 708–722.
Nefedov N.N., Nikulin E.I., Recke L. On the existence and asymptotic stability of periodic contrast structures in quasilinear reaction-advection-diffusion equations // Rus. J. of Math. Phys. 2019. V. 26. № 1. P. 55–69.
Nefedov N.N. The existence and asymptotic stability of periodic solutions with an interior layer of burgers type equations with modular advection // Math. Model. of Natural Phenomena. 2019. V. 4. № 4. P. 1–14.
Butuzov V.F., Nefedov N.N., Recke L., Schneider K.R. Periodic solutions with a boundary layer of reaction–diffusion equations with singularly perturbed neumann boundary conditions // Inter. J. of Bifurcation and Chaos. 2014. V. 24. № 8. P. 1440019-1–1440019-8.
Нефедов Н.Н., Никулин Е.И. О периодических решениях с пограничным слоем в задаче реакция–диффузия с сингулярно возмущенными граничными условиями третьего рода // Дифференц. ур-ния. 2020. Т. 56. № 12. С. 1641–1650.
Нефедов Н.Н., Дерюгина Н.Н. Существование стационарного погранслойного решения в уравнении реакция–диффузия с сингулярным граничным условием Неймана // Вестник Московского университета. Сер. 3: Физика, астрономия. 2020. № 5. С. 30–34.
Мельникова А.А. Существование и устойчивость периодического решения типа фронта в двухкомпонентной системе параболических уравнений // Ж. вычисл. матем. и матем. физ. 2019. Т. 59. № 7. С. 1184–1200.
Мельникова А.А., Дерюгина Н.Н. Существование периодического решения в виде двумерного фронта в системе параболических уравнений // Дифференц. ур-ния. 2020. Т. 56. № 4. С. 475–489.
Бутузов В.Ф., Бычков А.И. Асимптотика решения начально-краевой задачи для сингулярно возмущенного параболического уравнения в случае двукратного корня вырожденного уравнения // Дифференц. ур-ния. 2013. Т. 49. № 10. С. 1295–1307.
Butuzov V.F., Nefedov N.N., Recke L., Schnieder K.R. On a singularly perturbed initial value problem in the case of a double root of the degenerate equation // Nonlinear Anal. Theory, Meth. and Appl. 2013. V. 83. P. 1–11.
Butuzov V.F. Asymptotics of the solution of a system of singularly perturbed equations in the case of a multiple root of the degenerate equation // Differential Equations. 2014. № 2. P. 177–188.
Бутузов В.Ф. Асимптотика решения сингулярно возмущенной частично диссимативной системы с кратным корнем вырожденного уравнения // Матем. сборник. 2016. Т. 207. № 8. С. 73–100.
Бутузов В.Ф. Асимптотика и устойчивость решения сингулярно возмущенной эллиптической задачи с трехкратным корнем вырожденного уравнения // Изв. РАН. Сер. матем. 2017. Т. 81. № 3. С. 21–44.
Бутузов В.Ф. Об асимптотике решения сингулярно возмущенной параболической задачи с многозонным внутренним переходным слоем // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 6. С. 961–987.
Бутузов В.Ф. Асимптотика решения частично диссипативной системы уравнений с многозонным пограничным слоем // Ж. вычисл. матем. и матем. физ. 2019. Т. 59. № 10. С. 91–112.
Бутузов В.Ф. Асимптотика погранслойного решения стационарной частично диссипативной системы с кратным корнем вырожденного уравнения // Матем. сборник. 2019. Т. 210. № 11. С. 76–102.
Бутузов В.Ф. О сингулярно возмущенных системах ОДУ с кратным корнем вырожденного уравнения // Изв. РАН. Сер. матем. 2020. Т. 84. № 2. С. 60–89.
Бутузов В.Ф. Асимптотика контрастной структуры типа ступеньки в стационарной частично диссипативной системе уравнений // Ж. вычисл. матем. и матем. физ. 2021. Т. 61. № 1. С. 57–84.
Лукьяненко Д.В., Волков В.Т., Нефедов Н.Н., Ягола А.Г. Применение асимптотического анализа для решения обратной задачи определения коэффициента линейного усиления в уравнении типа Бюргерса // Вестник Московского университета. Сер. 3: Физика, астрономия. 2019. № 2. С. 38–43.
Lukyanenko D.V., Shishlenin M.A., Volkov V.T. Asymptotic analysis of solving an inverse boundary value problem for a nonlinear singularly perturbed time-periodic reaction–diffusion–advection equation // J. of Inverse and Ill-Posed Problems. 2019. V. 27. № 5. P. 745–758.
Волков В.Т., Нефедов Н.Н. Асимптотическое решение коэффициентных обратных задач для уравнений типа Бюргерса // Ж. вычисл. матем. и матем. физ. 2020. Т. 60. № 6. С. 975–984.
Nefedov N.N., Volkov V.T. Asymptotic solution of the inverse problem for restoring the modular type source in burgers’ equation with modular advection // J. of Inverse and Ill-Posed Problems. 2020. V. 28. № 5. P. 633–639.
Волков В.Т., Лукьяненко Д.В., Нефедов Н.Н. Аналитико-численный подход для описания периодических по времени движущихся фронтов в сингулярно возмущенных моделях реакция–диффузия–адвекция // Ж. вычисл. матем. и матем. физ. 2019. Т. 59. № 1. С. 50–62.
Omel’chenko O.E., Recke L., Butuzov V.F., Nefedov N.N. Time-periodic boundary layer solutions to singularly perturbed parabolic problems // J. of Differential Equations. 2017. V. 262. № 9. P. 4823–4862.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики