1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 61, № 12, 2021

Журнал вычислительной математики и математической физики, 2021, T. 61, № 12, стр. 2060-2073

ВЫЧИСЛИТЕЛЬНАЯ РЕАЛИЗАЦИЯ МОДЕЛИ СМЕШАННОЙ РАЗМЕРНОСТИ ТЕПЛОПЕРЕНОСА В СИСТЕМЕ ГРУНТ–ТРУБА В КРИОЛИТОЗОНЕ

В. И. Васильев 1, М. В. Васильева 1, Д. Я. Никифоров 1, Н. И. Сидняев 2, С. П. Степанов 1, *, А. Н. Цеева 3

1 СВФУ
677000 Якутск, ул. Белинского, 58, Россия

2 МГТУ
105005 Москва, 2-я Бауманская ул., 5, стр. 1, Россия

3 ОАО ЯкутПНИИС
677000 Якутск, ул. Дзержинского, 20, Россия

* E-mail: cepe2a@inbox.ru

Поступила в редакцию 10.01.2020
После доработки 16.07.2021
Принята к публикации 04.08.2021

Полный текст (PDF)

Аннотация

В работе построена и численно реализована математическая модель связанного процесса теплообмена многолетнемерзлого основания здания с системой замораживающих труб и атмосферным воздухом. В качестве математической модели теплопереноса в основании здания взята многомерная задача Стефана в энтальпийной постановке со сглаженными коэффициентами и размазанным источником по температуре. В системе труб теплоперенос описывается одномерным уравнением конвекции-кондукции. Численные результаты на модельных задачах показали, что предложенный численный метод позволяет существенно снижать вычислительную трудоемкость задачи. Библ. 39. Фиг. 6. Табл. 5.

Ключевые слова: криолитозона, тепломассоперенос, задача Стефана, метод конечных элементов, вычислительный алгоритм.

1. ВВЕДЕНИЕ

В работе рассмотрим связанную модель тепломассопереноса в системе грунт–труба, описываемую системой уравнений параболического типа в двумерной или трехмерной области $\Omega $, где тепломассоперенос в сети труб изучается в одномерной постановке, поскольку диаметр трубы существенно меньше размеров расчетной области $\Omega $ и температура по ее сечению практически постоянна. Дискретизация подобных задач при полноразмерном учете толщины труб приводит к задачам большой размерности вследствие необходимости сгущения расчетной сетки в окрестности труб.

Система грунт–труба широко используется в инженерных приложениях. Например, такими системами описывается тепловое взаимодействие многолетнемерзлых грунтов с проложенными в них трубопроводными системами, заполненными теплоносителями. Они могут существенно влиять на температурное состояние вмещающих грунтов и, следовательно, на их термомеханические характеристики [1], [2]. Подобные системы получаются и при моделировании системы сезонно-охлаждающих устройств (СОУ), которые устанавливаются с целью формирования массива мерзлых грунтов под фундаментами зданий и инженерных сооружений для предотвращения их размораживания в летне-осенний период. Кроме того, есть и другой класс трубопроводных систем, получивших широкое распространение – тепловые насосы. Они используются для выкачивания тепла из грунта для обогрева зданий (геотермальный тепловой насос) с возможностью переключения с режима отопления зимой на режим конденсирования летом, их математические модели также описываются системами грунт–труба [3]. Такие системы используют разницу температур грунта и пролегающих труб, для обогрева и охлаждения оснований зданий.

Подобные задачи встречаются и при решении других прикладных задач. Например, при моделировании фильтрации в трещиновато-пористой среде учет трещин требует специального рассмотрения, поскольку фильтрация в таких средах обладает специфическими свойствами. Трещины отличаются большей проницаемостью и оказывают существенное влияние на течение в пористой среде. Традиционно для связанной системы трещин используют модели двойной пористости [4], [5]. Основной идеей, на которой базируются такие модели, является раздельный расчет течения жидкостей в пористой среде и в трещинах с заданием перетока между ними. Математическая модель двойной пористости записывается следующим образом:

$\begin{gathered} {{c}_{m}}\frac{{\partial {{p}_{m}}}}{{\partial t}} - {\text{div}}({{k}_{m}}{\text{grad}}{{p}_{m}}) - {{\alpha }_{{mf}}}({{p}_{m}} - {{p}_{f}}) = {{q}_{m}},\quad x \in \Omega ,\quad t \in (0,{{t}_{{{\text{max}}}}}], \hfill \\ {{c}_{f}}\frac{{\partial {{p}_{f}}}}{{\partial t}} - {\text{div}}({{k}_{f}}{\text{grad}}{{p}_{f}}) + {{\alpha }_{{mf}}}({{p}_{m}} - {{p}_{f}}) = {{q}_{f}},\quad x \in \Omega ,\quad t \in (0,{{t}_{{{\text{max}}}}}], \hfill \\ \end{gathered} $
где ${{p}_{m}}$ и ${{p}_{f}}$ – давление в пористой среде и в трещинах. Взаимодействие континуумов задается введением функции перетока ${{\alpha }_{{mf}}}$, обеспечивающей массообмен между пористой средой и трещинами. Отметим, что в настоящее время существуют много модификаций данной модели, в которых течение в трещинах рассматривается на размерность ниже [6]–[9].

В медицине подобные математические модели встречаются при исследовании течения крови в сосудах и мелких капиллярах с учетом перетока между ними [10]. При этом сеть мелких капилляров рассматривается как однородная среда. В некоторых случаях артерии рассматриваются как сеть сосудов, имеющая довольно сложную геометрическую структуру и рассмотрение полных трехмерных уравнений Навье–Стокса для описания кровотока в них становится затруднительным. Математические модели со смешанной размерностью позволяют учитывать сложные многомасштабные процессы, происходящие в подобных прикладных задачах, которые описываются системой уравнений:

$\begin{gathered} - {\text{div}}({{k}_{t}}{\text{grad}}{{p}_{t}}) + \beta ({{p}_{t}} - {{p}_{{v}}}){{\delta }_{\gamma }} = 0,\quad x \in \Omega ,\quad t \in (0,{{t}_{{{\text{max}}}}}], \\ - \frac{\partial }{{\partial \tau }}\left( {{{k}_{{v}}}\frac{{\partial {{p}_{{v}}}}}{{\partial \tau }}} \right) + \beta ({{p}_{{v}}} - {{p}_{t}}) = 0,\quad x \in \gamma ,\quad t \in (0,{{t}_{{{\text{max}}}}}], \\ \end{gathered} $
где $\gamma $ – одномерная область сети сосудов, ${{p}_{t}}$ и ${{p}_{{v}}}$ – давление в среде и в сети сосудов, через ${{\delta }_{\gamma }}$ обозначим меру Дирака на одномерной области $\gamma $ (трещина). Этот термин меры выражает сохранение скорости кровотока (кровь, которая теряется в сосуде, поступает в ткань).

Представленные модели имеют много общего, их отличительной особенностью является использование связанной системы уравнений для вмещающей породы и сети трещин связанных посредством наличия перетока между ними.

Задачи из указанного класса называются задачами со смешанной размерностью. При численной аппроксимации таких задач используются конформные и неконформные расчетные сетки. Под конформными сетками подразумеваются сетки, в которых элементы сетки удовлетворяют условию: если два элемента сетки пересекаются (труба и грунт), то область их пересечения представляет собой их общую грань (или ребро), т.е. соединяются по принципу “узел в узел” [11], [12]. На конформных расчетных сетках можно использовать методы как прямой аппроксимации задач с различными размерностями, так и методы прямого учета, подобные методу дискретной модели трещин (discrete fracture model, DFM), используемого при численном решении задач фильтрации [13]–[17]. В методе конечных элементов для неконформных расчетных сеток используется метод XFEM, что приводит к построению (обогащению) пространства базисных функций [18]. Еще одним методом, в котором используются неконформные сетки – встроенная модель дискретных трещин (embedded discrete fracture model, EDFM). Она базируется на концепции двойной пористости и явно учитывает влияние каждой трещины. В ней используется структурированная сетка для представления матрицы и вводятся дополнительные перетоки путем учета пересечения трещин с матричной сеткой. Таким образом, отпадают проблемы, связанные с необходимостью согласования неструктурированной сетки [19].

Математическая модель теплопереноса в грунте описывается уравнением теплопроводности и учитывает фазовый переход поровой влаги в лед и обратно. Для таких моделей существует два подхода учета фазового перехода: первый, это когда на поверхности (границе) фазового температура постоянна, а второй подход основан на использовании двухфазной модели. В двухфазной модели нет четкой границы раздела мерзлой и талой зон. Фазовый переход поровой влаги в лед проходит в протяженной области (переходной зоне) – области размазывания в предположении, что фазовый переход проходит в заданном интервале температур [20]–[22].

При построении вычислительной реализации необходимо строить геометрические области и расчетные сетки, в которых геометрическая область труб разрешается сеточно. Расчетные сетки для таких областей имеют области локального сгущения в окрестности труб и приводят при дискретизации исходной задачи к очень большим системам уравнений. Альтернативный подход, используемый в данной работе, основывается на понижении размерности модели на трубе и сведении ее к одномерной гидравлической модели, и далее, в предположении непрерывности поля температур ее аппроксимации с помощью методов, которые аналогичны методам, используемым при моделировании трещин в нефтегазоносных пластах [23], [24]. Полученная таким образом дискретная задача приводит на каждом временном слое к замкнутой системе алгебраических уравнений. Систему уравнений для нахождения распределения температуры можно расширить, добавив учет конвективного переноса тепла (тепломассопереноса). Для расчета скорости фильтрации в грунте используются закон Дарси и уравнение сохранения массы [25], [26]. Математическая модель учитывает наличие фазового перехода поровой влаги, т.е. возникновение зоны мерзлого грунта в области вокруг замораживающих труб и поверхности грунта, обусловленной знакопеременной температурой окружающей среды. Для численного решения задачи фильтрации поровой воды в грунте используется метод фиктивных областей в мерзлом грунте, который был ранее рассмотрен и описан авторами в работе [27].

Основной целью данной работы является построение эффективного вычислительного алгоритма для решения дискретного аналога рассматриваемой задачи в системе грунт–сеть труб [27]–[29].

Работа состоит из введения и семи разделов. В разд. 2 работы описывается энтальпийная математическая модель теплопереноса в промерзающем/протаивающем основании здания со сглаживанием разрывных коэффициентов в грунте с учетом фазового перехода и размазыванием функции источника по температуре. В разд. 3 выводится математическая модель пониженной размерности для описания распределения температуры в трубе. Разд. 4 посвящен построению связанной модели тепло- и массопереноса для системы грунт–труба. В разд. 5 представлена конечно-элементная аппроксимация модели по пространственным переменным и неявная дискретизация по времени. В шестом и в седьмом разделах приводятся расчеты модельной задачи распределения температуры для теплонасосов в двумерной и в трехмерной постановках соответственно.

2. ТЕПЛОПЕРЕНОС В ГРУНТЕ

Рассмотрим математическую модель, описывающую динамику распределения температуры системы грунт-труба с учетом фазовых переходов воды в лед и обратно, при заданной температуре фазового перехода T* в области $\Omega = {{\Omega }^{ - }} \cup {{\Omega }^{ + }}$ (см. [30], [31]). Здесь ${{\Omega }^{ + }}(t)$ – область, занятая талым грунтом, где температура превышает температуру фазового перехода и ${{\Omega }^{ - }}(t)$ – область, занятая мерзлым грунтом:

${{\Omega }^{ + }}(t) = {\text{\{ }}x|x \in \Omega ,\quad T(x,t) > T{\text{*\} }}\quad {{\Omega }^{ - }}(t) = {\text{\{ }}x|x \in \Omega ,\quad T(x,t) < T{\text{*\} }}.$

Фазовый переход происходит на поверхности раздела областей, занятых талым и мерзлым грунтами $S = S(t)$.

Для моделирования процессов теплопереноса с фазовыми переходами используется классическая модель Стефана [32], [33], описывающая тепловые процессы, сопровождающиеся фазовыми превращениями среды с поглощением или выделением скрытой теплоты на поверхности раздела талого и мерзлого грунтов

(2.1)
$(\alpha (\phi ) + {{\rho }^{ + }}L\delta (T - T{\text{*}}))\frac{{\partial T}}{{\partial t}} - {\text{div}}\left( {\lambda (\phi ){\text{grad}}T} \right) = f,$
где L – удельная теплота фазового перехода, $\delta (T - T{\text{*}})$ – дельта-функция Дирака. Для коэффициентов уравнения имеем следующие соотношения:
$\alpha (\phi ) = {{\rho }^{ - }}{{c}^{ - }} + \phi ({{\rho }^{ + }}{{c}^{ + }} - {{\rho }^{ - }}{{c}^{ - }}),\quad \lambda (\phi ) = {{\lambda }^{ - }} + \phi ({{\lambda }^{ + }} - {{\lambda }^{ - }}),$
$\phi = \left\{ {\begin{array}{*{20}{c}} 0&{T < T{\text{*}},} \\ 1&{T > T{\text{*}},} \end{array}} \right.\quad \delta (T - T{\text{*}}) = \frac{{d\phi }}{{dT}},$
где ${{\rho }^{ + }},{{c}^{ + }}$ и ${{\rho }^{ - }},{{c}^{ - }}$ – плотность и удельная теплоемкость талой и мерзлой зон, соответственно.

Поскольку рассматривается процесс распространения тепла в насыщенной пористой среде, то для коэффициентов объемной теплоемкости в мерзлом и талом грунтах соответственно имеем

${{c}^{ - }}{{\rho }^{ - }} = (1 - m){{c}_{{sc}}}{{\rho }_{{sc}}} + m{{c}_{i}}{{\rho }_{i}},\quad {{c}^{ + }}{{\rho }^{ + }} = (1 - m){{c}_{{sc}}}{{\rho }_{{sc}}} + m{{c}_{w}}{{\rho }_{w}},$
где m – пористость. Индексы $sc,w,i$ обозначают соответственно скелет пористой среды, воду и лед. Для коэффициентов теплопроводности в талой и мерзлой зоне имеем аналогичные соотношения:

${{\lambda }^{ - }} = (1 - m){{\lambda }_{{sc}}} + m{{\lambda }_{i}},\quad {{\lambda }^{ + }} = (1 - m){{\lambda }_{{sc}}} + m{{\lambda }_{w}}.$

На практике фазовые превращения не проходят мгновенно и могут проходить в малом интервале температуры $[T{\text{*}} - \Delta ,T{\text{*}} + \Delta ]$. В качестве функции ϕ и $\delta (T - T{\text{*}})$ возьмем достаточно гладкие функции ϕΔ и ${{\delta }_{\Delta }}(T - T{\text{*}})$ [34], зависящие от температуры:

${{\phi }_{\Delta }} = \frac{1}{2}\left( {1 + {\text{erf}}\left( {\frac{{T - T{\text{*}}}}{{\sqrt 2 \Delta }}} \right)} \right),\quad {{\delta }_{\Delta }}(T - T{\text{*}}) = \frac{1}{{\sqrt {2\pi } \Delta }}{\text{exp}}\left( { - \frac{{{{{(T - T{\text{*}})}}^{2}}}}{{2{{\Delta }^{2}}}}} \right).$

Тогда получим следующее уравнение для температуры в области $\Omega $:

(2.2)
$c{{\rho }_{\Delta }}(T)\frac{{\partial T}}{{\partial t}} - {\text{div}}\left( {{{\lambda }_{\Delta }}(T){\text{grad}}T} \right) = f,$
где $c{{\rho }_{\Delta }}(T) = \alpha ({{\varphi }_{\Delta }}) + {{\rho }^{ + }}L{{\delta }_{\Delta }}(T - T{\text{*}}),{{\lambda }_{\Delta }}(T) = \lambda ({{\varphi }_{\Delta }})$. Полученное уравнение (2.2) является стандартным квазилинейным параболическим уравнением.

3. ТЕПЛОМАССОПЕРЕНОС В ТРУБЕ

Для расчета теплового режима системы труб будем использовать модель пониженной размерности – теплогидравлическую модель (см. фиг. 1). В данной модели мы предполагаем, что в трубе циркулирует хладоноситель (фреон) с достаточно высокой температурой кипения, и поэтому в данной модели мы не будем учитывать фазовый переход хладоносителя в системе труб. Запишем уравнение теплопроводности, описывающее тепловой режим движущегося по трубе хладоносителя в цилиндрической системе координат:

(3.1)
${{c}_{p}}{{\rho }_{p}}\left( {\frac{{\partial T}}{{\partial t}} + {{{v}}_{r}}\frac{{\partial T}}{{\partial r}} + {{{v}}_{\xi }}\frac{{\partial T}}{{\partial \xi }}} \right) - \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{{\lambda }_{p}}\frac{{\partial T}}{{\partial r}}} \right) - \frac{\partial }{{\partial \xi }}\left( {{{\lambda }_{p}}\frac{{\partial T}}{{\partial \xi }}} \right) = 0,\quad {\mathbf{x}} \in \gamma ,\quad t \in (0,{{t}_{{{\text{max}}}}}],$
где ${{c}_{p}},{{\rho }_{p}}$ и ${{\lambda }_{p}}$ – удельная теплоемкость, плотность и теплопроводность теплоносителя, $T$ – температура хладоносителя в трубе, ${{{v}}_{r}}$ – скорость движения хладоносителя в радиальном направлении и ${{{v}}_{\xi }}$ – скорость движения хладоносителя в направлении движения потока.

Фиг. 1.

Иллюстрация расчетной области для системы грунт–труба. (а) $\Omega \in {{\mathcal{R}}^{d}}$ ($d = 2,3$), $\gamma \in {{\mathcal{R}}^{1}}$ и $\gamma \in \Omega $. (б) усредненная по радиусу модель для сети труб, $r \in [0,R]$ и $R$ – радиус трубы.

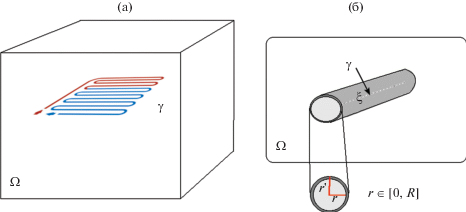
При описании теплообмена хладоносителя в трубе с вмещающим грунтом необходимо учитывать теплопередачу через тонкую цилиндрическую стенку. Для математического описания данного процесса запишем линейный тепловой поток следующим образом:

(3.2)
${{q}_{c}} = - \alpha \pi (T - {{T}_{p}}),\quad r = R,$
где ${{q}_{c}}$ – тепловой поток через цилиндрическую стенку, $T$ – температура грунта, ${{T}_{p}}$ – температура хладоносителя в трубе.

Здесь для вычисления коэффициентов $\alpha $ и $\beta $ использованы формулы из работы [35]

(3.3)
$\alpha = \frac{1}{\beta },\quad \beta = \frac{1}{{r{{\alpha }_{p}}}} + \frac{1}{{2{{\lambda }_{c}}}}ln\frac{{r{\kern 1pt} '}}{r} + \frac{1}{{r{\kern 1pt} '{{\alpha }_{g}}}},$
где $\beta $ – термическое сопротивление стенки, ${{\lambda }_{c}}$ – коэффициент теплопроводности стенки трубы, ${{\alpha }_{p}}$ и ${{\alpha }_{g}}$ – коэффициенты теплоотдачи от хладоносителя к стенке и от стенки к грунту, $r$ и $r{\kern 1pt} '$ – внутренний и наружный радиусы трубы (см. фиг. 1, где наружный радиус подразумевает учет толщины стенки трубы).

Поскольку для течения в трубах характерны значительные скорости движения хладоносителя в продольном направлении, то целесообразно пренебречь радиальной скоростью течения, ${{{v}}_{r}} = 0$. Далее уравнение (3.1) умножим на радиус r и проинтегрируем полученное уравнение вдоль оси $r \in [0,R]$

(3.4)
$\int\limits_0^R {{{c}_{p}}{{\rho }_{p}}r\frac{{\partial T}}{{\partial t}}dr + \,} \int\limits_0^R {{{c}_{p}}{{\rho }_{p}}r{{{v}}_{\xi }}\frac{{\partial T}}{{\partial \xi }}dr - \,} \int\limits_0^R {r\frac{\partial }{{\partial \xi }}\left( {{{\lambda }_{p}}\frac{{\partial T}}{{\partial \xi }}} \right)dr + {{\lambda }_{p}}R\frac{{\partial T}}{{\partial r}} = 0.} $

Определим среднюю температуру хладоносителя в трубе:

${{T}_{p}} = \frac{2}{{{{R}^{2}}}}\int\limits_0^R {rTdr} $
и с учетом контакта трубы с грунтом (3.2)
${{\lambda }_{p}}R\frac{{\partial {{T}_{p}}}}{{\partial r}} = R\alpha \pi (T - {{T}_{p}})$
получим следующее уравнение:
(3.5)
$\pi {{R}^{2}}{{c}_{p}}{{\rho }_{p}}\left( {\frac{{\partial {{T}_{p}}}}{{\partial t}} + {{{v}}_{\xi }}\frac{{\partial {{T}_{p}}}}{{\partial \xi }}} \right) - \pi {{R}^{2}}\frac{\partial }{{\partial \xi }}\left( {{{\lambda }_{p}}\frac{{\partial {{T}_{p}}}}{{\partial \xi }}} \right) + 2R\alpha \pi (T - {{T}_{p}}) = 0,\quad {\mathbf{x}} \in \gamma ,\quad t \in (0,{{t}_{{{\text{max}}}}}],$
описывающее модель пониженной размерности в трубе (теплогидравлическая модель).

4. РАСЧЕТНАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Рассмотрим систему теплового насоса, которая используется для выкачивания тепла из грунта для обогрева зданий с возможностью переключения с режима отопления зимой на режим конденсирования летом. Математическая модель описывается системой грунт–труба, которая использует разницу температур грунта и пролегающих труб. Данная модель описывает тепловое взаимодействие грунтов с трубопроводными системами, заполненными теплоносителями.

Для данной модели, когда стенки трубы сделаны из высокотеплопроводного материала, можно предположить непрерывность температуры на границе контакта трубы и грунта. В данном случае воспользуемся дельта-функцией Дирака и зададим теплоперенос в виде внутренних стоков (источников) тепла в уравнении (2.2):

(4.1)
$f = q{{\delta }_{\gamma }},$
где $q$ – мощность стока тепла и ${{\delta }_{\gamma }}$ – дельта-функция Дирака, определяющая положение трубы в грунтовом массиве
(4.2)
${{\delta }_{\gamma }}(x) = \left\{ \begin{gathered} 1{\text{/}}S,\quad x \in \gamma , \hfill \\ 0,\quad x \notin \gamma , \hfill \\ \end{gathered} \right.$
где S – площадь сечения трубы.

Далее введем индекс $m$ для грунта и $p$ для трубы. Предполагая идеальный тепловой контакт между наружной поверхностью труб и окружающего массива грунтов, мощность стоков тепла запишем в виде:

(4.3)
$q = 2\pi R{{\alpha }_{p}}({{T}_{m}} - {{T}_{p}}),$
где αp – коэффициент теплообмена между поверхностью трубы и теплоносителем, циркулирующим в грунтовом теплообменнике, ${{T}_{m}}$ – температура грунта, ${{T}_{p}}$ – температура теплоносителя и $R$ – радиус трубы. Связанную систему уравнений для температуры грунта (2.1), (4.3) и для температуры системы труб (3.5) запишем в следующем обобщенном виде:
(4.4)
$\begin{gathered} c{{\rho }_{\Delta }}({{T}_{m}})\frac{{\partial {{T}_{m}}}}{{\partial t}} - {\text{div}}({{\lambda }_{\Delta }}({{T}_{m}}){\text{grad}}{{T}_{m}}) + \kappa ({{T}_{m}} - {{T}_{p}}){{\delta }_{\gamma }}(x) = 0,\quad x \in \Omega , \\ {{b}_{p}}\left( {\frac{{\partial {{T}_{p}}}}{{\partial t}} + {{{v}}_{\xi }}\frac{{\partial {{T}_{p}}}}{{\partial \xi }}} \right) - S\frac{\partial }{{\partial \xi }}\left( {{{\lambda }_{p}}\frac{{\partial {{T}_{p}}}}{{\partial \xi }}} \right) - \kappa ({{T}_{m}} - {{T}_{p}}) = 0,\quad x \in \gamma , \\ \end{gathered} $
где ${{b}_{p}} = S{{c}_{p}}{{\rho }_{p}}$, $S = \pi {{R}^{2}}$, $\kappa = 2\pi R{{\alpha }_{p}}$, $\gamma $ – кривая, описывающая расположение системы труб.

Систему уравнений дополним начальным условием

(4.5)
${{T}_{m}}(x) = {{T}_{p}}(x) = {{T}_{0}},\quad x \in \Omega ,\quad t = 0,$
и граничным условием Неймана для грунта:
(4.6)
$ - {{\lambda }_{\Delta }}({{T}_{m}})\frac{{\partial {{T}_{m}}}}{{\partial n}} = 0,\quad x \in \partial \Omega ,$
а на концах трубы зададим различные граничные условия Дирихле и Неймана:

(4.7)
$\begin{gathered} {{T}_{p}} = {{T}_{d}},\quad \xi \in {{\xi }_{D}}, \\ - {{\lambda }_{p}}\frac{{\partial {{T}_{p}}}}{{\partial n}} = 0,\quad \xi \in {{\xi }_{N}}. \\ \end{gathered} $

Рассмотрим также и полноразмерную математическую модель без понижения порядка по пространственным переменным для уравнения в трубе

(4.8)
$\begin{gathered} c{{\rho }_{\Delta }}({{T}_{m}})\frac{{\partial {{T}_{m}}}}{{\partial t}} - {\text{div}}({{\lambda }_{\Delta }}({{T}_{m}}){\text{grad}}{{T}_{m}}) + {{\alpha }_{p}}({{T}_{m}} - {{T}_{p}}) = 0,\quad x \in {{\Omega }_{m}}, \\ {{c}_{p}}{{\rho }_{p}}\left( {\frac{{\partial {{T}_{p}}}}{{\partial t}} + {{{v}}_{\xi }} \cdot {\text{grad}}{{T}_{p}}} \right) - {\text{div}}({{\lambda }_{p}}{\text{grad}}{{T}_{p}}) - {{\alpha }_{p}}({{T}_{m}} - {{T}_{p}}) = 0,\quad x \in {{\Omega }_{p}}, \\ \end{gathered} $
где ${{\Omega }_{p}}$ – двумерная подобласть трубы (см. фиг. 2).

Фиг. 2.

Двумерная область.

Данная система параболических уравнений (4.8) замыкаются начальным и граничными условиями для грунта (4.6) и (4.7), а для области трубы зададим фиксированную температуру ${{T}_{p}} = {{T}_{d}}$ на границе $x \in {{\Gamma }_{D}}$, а на выходе – однородное граничное условие Неймана $ - {{\lambda }_{p}}\frac{{\partial {{T}_{p}}}}{{\partial n}} = 0$ при $x \in {{\Gamma }_{N}}$.

5. КОНЕЧНО-ЭЛЕМЕНТНАЯ АППРОКСИМАЦИЯ РАСЧЕТНОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

Для аппроксимации рассматриваемой математической модели изучаемого процесса (10)–(13) будем использовать неконформные сетки и метод конечных элементов [9], [36]. Определим триангуляцию $T_{m}^{h}$ расчетной области $\Omega $, где $h$ – некоторый параметр, характеризующий пространственную сетку и конечно-элементное разбиение $T_{p}^{h}$ расчетной области γ. Определим пространства

$\begin{gathered} {{V}_{m}} = {{{\hat {V}}}_{m}} = {{H}^{1}}(\Omega ),\quad {{V}_{p}} = {\text{\{ }}{v} \in {{H}^{1}}(\gamma ):{v} = {{T}_{d}},x \in {{\xi }_{D}}{\text{\} }}, \\ {{{\hat {V}}}_{p}} = {\text{\{ }}{v} \in {{H}^{1}}(\gamma ):{v} = 0,x \in {{\xi }_{D}}{\text{\} }}, \\ \end{gathered} $
и введем конечномерные пространства $V_{m}^{h},\hat {V}_{m}^{h} \subset {{V}_{m}}$, $V_{p}^{h},\hat {V}_{p}^{h} \subset {{V}_{p}}$. Далее определим в них следующую вариационную постановку задачи: найти $({{T}_{m}},{{T}_{p}}) \in (V_{m}^{h},V_{p}^{h})$ такие, что
(5.1)
$\begin{gathered} \int\limits_\Omega ^{} {c{{\rho }_{\Delta }}(\tilde {T}_{m}^{{n + 1}})\frac{{T_{m}^{{n + 1}} - T_{m}^{n}}}{\tau }{{{v}}_{m}}dx + \int\limits_\Omega ^{} {{{\lambda }_{\Delta }}(\tilde {T}_{m}^{{n + 1}}){\text{grad}}T_{m}^{{n + 1}} \cdot {\text{grad}}{{{v}}_{m}}dx + } } \,\int\limits_\gamma ^{} {\kappa (T_{m}^{{n + 1}} - T_{p}^{{n + 1}}){{{v}}_{m}}d\xi = 0,} \\ \int\limits_\gamma ^{} {{{b}_{p}}} \left( {\frac{{T_{p}^{{n + 1}} - T_{p}^{n}}}{\tau } + {{{v}}_{\xi }} \cdot {\text{gra}}{{{\text{d}}}_{\xi }}T_{p}^{{n + 1}}} \right){{{v}}_{p}}d\xi + S\int\limits_\gamma ^{} {{{\lambda }_{p}}{\text{gra}}{{{\text{d}}}_{\xi }}T_{p}^{{n + 1}} \cdot {\text{gra}}{{{\text{d}}}_{\xi }}{{{v}}_{p}}d\xi - } \\ - \,\int\limits_\gamma ^{} {\kappa (T_{m}^{{n + 1}} - T_{p}^{{n + 1}}){{{v}}_{p}}d\xi = 0,} \\ \end{gathered} $
где ${{{v}}_{m}} \in \hat {V}_{m}^{h}$ и ${{{v}}_{p}} \in \hat {V}_{p}^{h}$. Для аппроксимации по времени используем устойчивую неявную дискретизацию c шагом по времени $\tau $, где $T_{m}^{n}$ и $T_{p}^{n}$ – значения температуры с предыдущего временного слоя.

Будем использовать одну из схем, предложенных в работе [28], где вместо нелинейных коэффициентов будем использовать линеаризованные коэффициенты со значениями температуры $\tilde {T}_{m}^{{n + 1}}$, которые являются решениями аналогичной системы:

(5.2)
$\begin{gathered} \int\limits_\Omega ^{} {c{{\rho }_{\Delta }}(T_{m}^{n})\frac{{\tilde {T}_{m}^{{n + 1}} - T_{m}^{n}}}{\tau }{{{v}}_{m}}dx + \int\limits_\Omega ^{} {{{\lambda }_{\Delta }}(T_{m}^{n}){\text{grad}}\tilde {T}_{m}^{{n + 1}} \cdot {\text{grad}}{{{v}}_{m}}dx + } } \,\int\limits_\gamma ^{} {\kappa (\tilde {T}_{m}^{{n + 1}} - T_{p}^{{n + 1}}){{{v}}_{m}}d\xi = 0,} \\ \int\limits_\gamma ^{} {{{b}_{p}}\left( {\frac{{T_{p}^{{n + 1}} - T_{p}^{n}}}{\tau } + {{{v}}_{\xi }} \cdot {\text{gra}}{{{\text{d}}}_{\xi }}T_{p}^{{n + 1}}} \right){{{v}}_{p}}d\xi + S} \int\limits_\gamma ^{} {{{\lambda }_{p}}} {\text{gra}}{{{\text{d}}}_{\xi }}T_{p}^{{n + 1}} \cdot {\text{gra}}{{{\text{d}}}_{\xi }}{{{v}}_{p}}d\xi - \\ - \,\int\limits_\gamma ^{} {\kappa (\tilde {T}_{m}^{{n + 1}} - T_{p}^{{n + 1}}){{{v}}_{p}}d\xi = 0.} \\ \end{gathered} $

Далее, аппроксимацию по пространству покажем только для системы (5.1), для системы (5.2) дискретный аналог строится аналогично.

Поясним проблемы вычислительной реализации в следующем виде:

${{T}_{m}} = \sum\limits_i^{{{N}_{m}}} T_{m}^{i}{{\phi }^{i}},\quad {{T}_{p}} = \sum\limits_i^{{{N}_{p}}} T_{p}^{i}{{\psi }^{i}},\quad w = \sum\limits_i^{{{N}_{m}}} {{\phi }^{i}},\quad {{w}_{p}} = \sum\limits_i^{{{N}_{m}}} {{\psi }^{i}},$
где $T_{m}^{i}$ и $T_{p}^{i}$ – неизвестные значения, ϕi – конечно-элементные базисы при триангуляции $\mathcal{T}_{m}^{h}$, ${{\psi }^{i}}$ – базисные функции разбиения $\mathcal{T}_{p}^{h}$, ${{N}_{m}}$ – число элементов базиса $\mathcal{T}_{m}^{h}$, ${{N}_{p}}$ – число элементов базиса $\mathcal{T}_{p}^{h}$. Таким образом, после дискретизации системы (5.1) получим следующую систему алгебраических уравнений:
$\left( {\begin{array}{*{20}{c}} {{{A}_{m}}}&{ - {{A}_{{mp}}}} \\ { - {{A}_{{pm}}}}&{{{A}_{p}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{T}_{m}}} \\ {{{T}_{p}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{f}_{m}}} \\ {{{f}_{p}}} \end{array}} \right),$
где подматрицы и правая часть вычисляются по следующим формулам:
(5.3)
$\begin{gathered} {{A}_{m}} = \left\{ {a_{{ij}}^{m} = \int\limits_\Omega ^{} {\frac{{c{{\rho }_{\Delta }}(\tilde {T}_{m}^{{n + 1}})}}{\tau }{{\phi }^{j}}{{\phi }^{i}}dx + \,} \int\limits_\Omega ^{} {{{\lambda }_{\Delta }}(\tilde {T}_{m}^{{n + 1}}){\text{grad}}{{\phi }^{j}} \cdot {\text{grad}}{{\phi }^{i}}dx + \int\limits_\gamma ^{} {\kappa {{\phi }^{j}}{{\phi }^{i}}d\xi } } } \right\}, \\ {{A}_{p}} = \left\{ {a_{{ij}}^{p} = \int\limits_\gamma ^{} {{{b}_{p}}\left( {\frac{{{{\psi }^{j}}}}{\tau } + {{{v}}_{\xi }} \cdot {\text{gra}}{{{\text{d}}}_{\xi }}{{\psi }^{j}}} \right){{\psi }^{i}}d\xi + \,} S\int\limits_\gamma ^{} {{{\lambda }_{p}}{\text{gra}}{{{\text{d}}}_{\xi }}{{\psi }^{j}} \cdot {\text{gra}}{{{\text{d}}}_{\xi }}{{\psi }^{i}}d\xi + \int\limits_\gamma ^{} {\kappa {{\psi }^{j}}{{\psi }^{i}}d\xi } } } \right\}, \\ {{A}_{{mp}}} = \left\{ {a_{{ij}}^{{mp}} = \int\limits_\gamma ^{} {\kappa {{\psi }^{j}}{{\phi }^{i}}d\xi } } \right\}, \\ {{A}_{{pm}}} = \left\{ {a_{{ij}}^{{pm}} = \int\limits_\gamma ^{} {\kappa {{\phi }^{j}}{{\psi }^{i}}d\xi } } \right\}, \\ {{f}_{m}} = \left\{ {f_{i}^{m} = \int\limits_\Omega ^{} {\frac{{c{{\rho }_{\Delta }}(\tilde {T}_{m}^{{n + 1}})}}{\tau }T_{m}^{n}{{\phi }^{i}}dx} } \right\}, \\ {{f}_{p}} = \left\{ {f_{i}^{p} = \int\limits_\gamma ^{} {\frac{{{{b}_{p}}}}{\tau }T_{p}^{n}{{\psi }^{i}}d\xi } } \right\}, \\ \end{gathered} $
а также ${{T}_{m}}$ и ${{T}_{p}}$ – векторы решения. Отметим, что ${{A}_{{mp}}} = A_{{pm}}^{T}$.

Ввиду того, что мы рассматриваем связанную задачу, описывающую быстро- и медленнопротекающие процессы, очевидно, что для данной задачи хорошо подойдут схемы расщепления. Пусть $y = {{({{T}_{m}},{{T}_{p}})}^{T}}$, тогда дискретную систему можно представить в виде Ay = b, где

(5.4)
$A = \left( {\begin{array}{*{20}{c}} {{{A}_{m}}}&{ - {{A}_{{mp}}}} \\ { - A_{{mp}}^{T}}&{{{A}_{p}}} \end{array}} \right),\quad b = \left( {\begin{array}{*{20}{c}} {{{b}_{m}}} \\ {{{b}_{p}}} \end{array}} \right).$

Представим матрицу A в виде суммы матриц $A = {{A}_{1}} + {{A}_{2}}$, тогда получим явно-неявную схему ${{A}_{1}}{{y}^{{n + 1}}} + {{A}_{2}}{{y}^{n}} = b$. В зависимости от A1 и A2 получаются различные схемы расщепления [37]. В этом случае на каждом временном слое сначала вычисляется уравнение для быстрого процесса. Только потом рассчитывается медленный процесс [38]. В нашем случае это приводит к системе уравнений с верхне-треугольной матрицей:

(5.5)
${{A}_{1}} = \left( {\begin{array}{*{20}{c}} {{{A}_{m}}}&{ - {{A}_{{mp}}}} \\ 0&{{{A}_{p}}} \end{array}} \right),\quad {{A}_{2}} = \left( {\begin{array}{*{20}{c}} 0&0 \\ { - A_{{mp}}^{T}}&0 \end{array}} \right).$

В данной схеме сначала решается уравнение для трубы, температура грунта берется с предыдущего временного слоя. Затем найденная температура в трубе используется для вычисления температуры в грунте [37].

Аналогично, для второй задачи (4.8), (4.5) и (4.6) определим вариационную постановку: найти $({{T}_{m}},{{T}_{p}}) \in ({{V}_{m}},{{V}_{p}})$ такие, что

(5.6)
$\begin{gathered} \int\limits_\Omega ^{} c {{\rho }_{\Delta }}(\tilde {T}_{m}^{{n + 1}})\frac{{T_{m}^{{n + 1}} - T_{m}^{n}}}{\tau }{{{v}}_{m}}dx - \int\limits_\Omega ^{} {{{\lambda }_{\Delta }}(\tilde {T}_{m}^{{n + 1}}){\text{grad}}T_{m}^{{n + 1}} \cdot {\text{grad}}{{{v}}_{m}}dx + } \,\int\limits_\Omega ^{} {{{\alpha }_{p}}(T_{m}^{{n + 1}} - T_{p}^{{n + 1}}){{{v}}_{m}}dx = 0,} \\ \int\limits_{{{\Omega }_{p}}}^{} {{{c}_{p}}{{\rho }_{p}}\left( {\frac{{T_{p}^{{n + 1}} - T_{p}^{n}}}{\tau } + {{{v}}_{\xi }} \cdot {\text{grad}}T_{p}^{{n + 1}}} \right){{{v}}_{p}}dx - \int\limits_{{{\Omega }_{p}}}^{} {{{\lambda }_{p}}{\text{grad}}T_{p}^{{n + 1}} \cdot {\text{grad}}{{{v}}_{p}}dx - } } \\ - \int\limits_{{{\Omega }_{p}}}^{} {{{\alpha }_{p}}(T_{m}^{{n + 1}} - T_{p}^{{n + 1}}){{{v}}_{p}}dx = 0,} \\ \end{gathered} $
где ${{V}_{m}} = {{\hat {V}}_{m}} = {{H}^{1}}(\Omega ),{{V}_{p}} = {\text{\{ }}{v} \in {{H}^{1}}({{\Omega }_{p}}):{v} = {{T}_{d}},x \in {{\Gamma }_{D}}{\text{\} }}$, ${{\hat {V}}_{p}} = {\text{\{ }}{v} \in {{H}^{1}}({{\Omega }_{p}}):{v} = 0,x \in {{\Gamma }_{D}}{\text{\} }}.$

6. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ В ДВУМЕРНОЙ ПОСТАНОВКЕ

Проведем численное моделирование рассматриваемой задачи в двумерной постановке при следующих значениях входных данных: для талой зоны ${{\rho }^{ + }}{{c}^{ + }} = 2.5 \times {{10}^{6}}$ [Дж/(м3 ⋅ °K)], ${{k}^{ + }}$ = = 1.5 [Вт/(м ⋅ °K], для мерзлой зоны ${{\rho }^{ - }}{{c}^{ - }} = 2.0 \times {{10}^{6}}$ [Дж/(м3 ⋅ °K)], ${{k}^{ - }} = 2.0$ [Вт/(м ⋅ °K)], и для фазового перехода ${{\rho }^{ + }}L = 60 \times {{10}^{6}}$ [Дж/м]. В качестве расчетных параметров системы труб используем следующие параметры: ${{{v}}_{\xi }} = 0.5$ [м/с], ${{\rho }_{p}}{{c}_{p}} = {{10}^{6}}$ [Дж/(м3 ⋅ °K)], $R = 0.05$ [м], ${{\alpha }_{p}} = 80$ [Вт/(м ⋅ °K)] и температура хладоносителя на входе ${{T}_{d}} = - 20^\circ {\text{C}}$. Коэффициент кондуктивной теплопроводности равен ${{k}_{p}} = 0.09$ [Вт/(м ⋅ °K)]. Грунт и труба имеют начальную температуру 2.0°C. Численное моделирование проводится для квадратной области по $X = 20$ м и $Y = 20$ м. Все расчеты проводятся на 30 сут.

Апробацию предложенной модели и численного метода начнем с проверки сходимости численного решения на последовательности сгущающихся сеток по пространственным переменным. Для этого построим три последовательно измельчающиеся грубые сетки (см. табл. 1) для задачи (4.4)–(4.7) и эталонную сетку для задачи (4.8), (4.5), (4.6) без понижения порядка для системы труб (фиг. 3). Зафиксируем шаг по времени $\tau = 24$ ч. Для сравнения температуры в грунте используем следующую формулу относительной ${{L}_{2}}$ погрешности в процентах:

(6.1)
${{e}_{{{{L}_{2}}}}} = 100 \cdot \frac{{{\text{||}}{{T}_{1}} - {{T}_{2}}{\text{|}}{{{\text{|}}}_{{{{L}_{2}}}}}}}{{{\text{||}}{{T}_{1}}{\text{|}}{{{\text{|}}}_{{{{L}_{2}}}}}}},$
где ${{T}_{1}}$ – температура в грунте на эталонной сетке и ${{T}_{2}}$ – температура в грунте на грубых сетках.

Taблица 1.

Количество неизвестных для сеток, где $N = {{N}_{m}} + {{N}_{p}}$

Сетка Nm Np N
Эталонная сетка 501 309 51 719 553 028
Сетка 1 22 801 3619 26 420
Сетка 2 44 521 5039 495 60
Сетка 3 73 441 6527 79 968
Фиг. 3.

Сетка 1 (а) и эталонная сетка (б).

Результаты решения задачи теплопереноса представлены на фиг. 4. Распределение температуры представлено для нескольких временных слоев и иллюстрирует динамику движения хладоносителя в трубе и начало замораживания окружающего грунта. Сравнение предлагаемой модели с полноразмерной моделью отображено на табл. 2. Для проверки сходимости по временной сетке сравним решения с тремя шагами по времени (${{\tau }_{1}} = 48$ ч, ${{\tau }_{2}} = 24$ ч и ${{\tau }_{3}} = 12$ ч) с решением с шагом по времени $\tau = 2$ ч (табл. 3) на пространственной сетке 2. Для проверки схемы расщепления (5.5), для трех шагов по времени будем сравнивать решение без расщепления с решением с расщеплением. На табл. 4 представлен результат использования схемы расщепления. Представленные результаты иллюстрируют эффективность предложенной новой математической модели для системы труба–грунт в условиях криолитозоны.

Фиг. 4.

Распределение температуры на различные моменты времени $t = 1,5$ и 30 сут (слева направо) с ${{\tau }_{1}}$. Верхние графики – решение на эталонной сетке, нижние – решение на сетке 1. Белая линия – граница раздела талой и мерзлой грунтов.

Taблица 2.

Относительная погрешность (%) в зависимости от размера сетки при $\tau = 24$ ч

Сетка без расщепления с расщеплением
Сетка 1 0.4 0.41
Сетка 2 0.23 0.24
Сетка 3 0.19 0.21
Taблица 3.

Относительная погрешность (%) в зависимости от шага по времени $\tau $ на сетке 2. Сравнение с мелким шагом по времени $\tau = 2$ ч

Шаг по времени ${{\tau }_{1}}$ ${{\tau }_{2}}$ ${{\tau }_{3}}$
Погрешность 4.32 2.92 1.96
Taблица 4.

Относительная погрешность в % в зависимости от шага по времени $\tau $ на сетке 2. Сравнение со схемой расщепления

Шаг по времени ${{\tau }_{1}}$ ${{\tau }_{2}}$ ${{\tau }_{3}}$
Погрешность 0.051 0.024 0.013

На табл. 5 представлено время численной реализации предложенного численного метода за весь период решения задачи в зависимости от сетки и шага по времени. Из представленных данных следует, что предложенный метод значительно ускоряет вычисления за счет понижения размера СЛАУ. Использование схемы расщепления ускорило вычисления более чем в 2 раза. Все вычисления проводились мультифронтальным прямым методом (MUMPS), который представляет собой вариант метода Гаусса для больших разреженных систем уравнений, возникающих при использовании метода конечных элементов [39].

Taблица 5.

Время счета на эталонной мелкой сетке, на сетках 1–3 и при использовании схемы расщепления (в секундах) за весь период решения задачи в зависимости от пространственной сетки и от шага по времени

Сетка\Шаг по времени ${{\tau }_{1}}$ ${{\tau }_{2}}$ ${{\tau }_{3}}$
Эталонная сетка 1582.3 3171.8 6305.4
Сетка 1 4.1 8.4 16.5
Сетка 1 с расщеплением 1.51 2.9 5.9
Сетка 2 9.4 18.7 36.6
Сетка 2 с расщеплением 4.1 8 16.1
Сетка 3 18.5 36.1 69.3
Сетка 3 с расщеплением 8.1 16.1 31.8

7. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ В ТРЕХМЕРНОЙ ПОСТАНОВКЕ

Теперь рассмотрим задачу (4.4)–(4.7) в трехмерной области (фиг. 5) за исключением других граничных условий для грунта. Трехмерную задачу решаем с использованием схемы расщепления, где ${{N}_{m}} = 1390861$ и ${{N}_{p}} = 3619$. Как и в двумерной задаче, имеем систему СОУ, расположенную на глубине 1.5 м. Область в плане имеет такие же размеры по 20 м и высоту 8 м. Расчеты проводились за один год с шагом по времени $\tau = 24$ ч. Температура хладоносителя на входе также равна ${{T}_{d}} = - 20$°C. Грунт и труба имеют начальную температуру –2.0°C.

Фиг. 5.

Трехмерная область и пространственная сетка.

На поверхности грунта по центру на квадратной области с размером [12 м] × [12 м] зададим граничное условие Дирихле с постоянной температурой, равной 10°C, которое будет моделировать температуру сооружения. На остальной части поверхности грунта задается граничное условие Робина с учетом многолетнего гармонического колебания температуры воздуха, имеющего региональный характер, который в условиях города Якутска варьируется от ${{T}_{w}} = - 35.7^\circ {\text{C}}$ зимой до ${{T}_{s}} = 17.3^\circ {\text{C}}$ летом:

$\begin{gathered} {{T}_{m}} = 10^\circ {\text{C}},\quad x \in {{\Gamma }_{D}}, \\ - {{\lambda }_{\Delta }}({{T}_{m}})\frac{{\partial {{T}_{m}}}}{{\partial n}} = 0,\quad x \in {{\Gamma }_{N}}, \\ - {{\lambda }_{\Delta }}({{T}_{m}})\frac{{\partial {{T}_{m}}}}{{\partial n}} = \alpha (T - {{T}_{{{\text{air}}}}}),\quad x \in {{\Gamma }_{R}}, \\ {{T}_{{{\text{air}}}}} = \frac{{{{T}_{w}} - {{T}_{s}}}}{2}sin\left( {\frac{{\pi (30(M - 1) + \bar {t} + 75)}}{{180 \cdot 30 \cdot 86\,400}}} \right) + \frac{{{{T}_{w}} + {{T}_{s}}}}{2}, \\ \end{gathered} $
где $\alpha = 14$, $\bar {t} = t{\text{/}}86\,400$ – время в сутках, $M = 5$ – начальный месяц.

На фиг. 6 показано распределение температуры в грунте в различные моменты времени. Рисунки показаны со срезом некоторой части области для более детального просмотра динамики изменения температуры, где расположена труба. Представленные графики иллюстрируют, что система СОУ позволяет основанию здания находиться в мерзлом состоянии в течениe года.

Фиг. 6.

Распределение температуры в различные моменты времени года. Белая линия – изотерма нуля градусов.

Список литературы

  1. Материалы Международной научно- практической конференции по инженерному мерзлотоведению, посвященной 20-летию создания ООО НПО “Фундаментстройаркос”. Тюмень: Сити-пресс, 2011.

  2. Васильев В.И., Сидняев Н.И., Федотов А.А. и др. Моделирование распределения нестационарных температурных полей в криолитозоне при проектировании геотехнических сооружений. М.: Курс, 2017.

  3. Крылов В.А., Черноозерский В.А., Никитин А.А. и др. Учет неравномерности температурного поля в геотермальной скважине теплового насоса // Вестн. Международной академии холода. 2015. № 1. С. 75–79.

  4. Баренблатт Г.И., Желтов Ю.П., Кочина И.Н. Об основных представлениях теории фильтрации однородных жидкостей в трещиноватых породах // Прикл. матем. и механ. 1960. Т. 24. № 5. С. 852–864.

  5. Arbogast T., Douglas J., Hornung U. Derivation of the double porosity model of single phase flow via homogenization theory // SIAM Journal on Mathematical Analysis. 1990. V. 21. № 4. P. 823–836.

  6. Martin V., Jaffre J., Roberts J.E. Modeling fractures and barriers as interfaces for flow in porous media // SIAM Journal on Scientific Computing. 2005. V. 26. № 5. P. 1667–1691.

  7. Kalinkin A.A., Laevsky Yu.M. Mathematical model of water-oil displacement in fractured porous medium // Sib. Elektron. Mat. Izv. 2015. V. 12. P. 743–751.

  8. Formaggia L., Fumagalli A., Scotti A., et al. A reduced model for darcy’s problem in networks of fractures // ESAIM: Mathematical Modelling and Numerical Analysis. 2014. V. 48. № 4. P. 1089–1116.

  9. D’Angelo C., Scotti A. A mixed finite element method for darcy flow in fractured porous media with non-matching grids // ESAIM: Mathematical Modelling and Numerical Analysis. 2012. V. 46. № 2. P. 465–489.

  10. D’Angelo C., Quarteroni A. On the coupling of 1d and 3d diffusion-reaction equations: application to tissue perfusion problems // Mathematical Models and Methods in Applied Sciences. 2008. V. 18. № 8. P. 1481–1504.

  11. Panfili P., Cominelli A., Scotti A. Using embedded discrete fracture models (edfms) to simulate realistic fluid flow problems / In Second EAGE workshop on naturally fractured reservoirs. 2013. cp-371-00022.

  12. Fumagalli A., Scotti A. An efficient xfem approximation of darcy flows in arbitrarily fractured porous media // Oil & Gas Science and Technology–Revue d’IFP Energies nouvelles. 2014. V. 69. № 4. P. 555–564.

  13. Kim J., Deo M.D. Finite element, discrete-fracture model for multiphase flow in porous media // AIChE Journal. 2000. V. 46. № 6. P. 1120–1130.

  14. Karimi-Fard M., Durlofsky L.J., Aziz K., et al. An efficient discrete fracture model applicable for general purpose reservoir simulators / In SPE Reservoir Simulation Symposium. Society of Petroleum Engineers. 2003. SPE 79699. P. 1–11.

  15. Karimi-Fard M., Firoozabadi A., et al. Numerical simulation of water injection in 2d fractured media using discrete-fracture model / In SPE annual technical conference and exhibition. Society of Petroleum Engineers. 2001. SPE 71615. P. 1–16.

  16. Vasil’eva M.V., Vasiliev V.I., Krasnikov A.A., Nikiforov D.Y. Numerical simulation of single-phase fluid flow in fractured porous media // Uchenye Zapiski Kazanskogo Universiteta. Seriya Fiziko-Matematicheskie Nauki. 2017. T. 159. № 1. P. 100–115.

  17. Vasil’ev V.I., Vasil’eva M.V., Gladkikh V.S., et al. Numerical Solution of a Fluid Filtration Problem in a Fractured Medium by Using the Domain Decomposition Method // J. of Applied and Industrial Mathematics. 2018. V. 12. № 4. C. 785–796.

  18. Fries T.P., Belytschko T. The extended/generalized finite element method: an overview of the method and its applications // Internat. Journal for Numerical Methods in Eng-ng. 2010. V. 84. № 3. P. 253–304.

  19. Nikiforov D.Y., Stepanov S.P. Numerical simulation of the embedded discrete fractures by the finite element method // J. of Physics: Conference Series. 2019. IOP Publishing. Vol. 1158. N 3. Paper 032038.

  20. Олейник О.А. Об одном методе решения общей задачи Стефана // Докл. АН. 1960. Т. 135. № 5. С. 1054–1057.

  21. Каменомостская С.Л. О задаче Стефана // Матем. сборник. 1961. Т. 53. № 4. С. 489–514.

  22. Самарский А.А., Моисеенко Б.Д. Экономичная схема сквозного счета для многомерной задачи Стефана // Ж. вычисл. матем. и матем. физ. 1965. Т. 5. № 5. С. 816–827.

  23. Akkutlu I.Y., Efendiev Y., Vasilyeva M., et al. Multiscale model reduction for shale gas transport in a coupled discrete fracture and dual-continuum porous media // J. of Natural Gas Science and Eng-ng. 2017. V. 48. P. 65–76.

  24. Chung E.T., Efendiev Y., Leung T., Vasilyeva M. Coupling of multiscale and multicontinuum approaches // GEM–Internat. Journal on Geomathematics. 2017. V. 8. № 1. P. 9–41.

  25. Chung E.T., Efendiev Y., Li G., Vasilyeva M. Generalized multiscale finite element method for problems in perforated heterogeneous domains // Applicable Analysis. 2016. V. 95. № 10. P. 2254–2279.

  26. Chung E.T., Efendiev Y., Lee Ch. Mixed generalized multiscale finite element methods and applications // Multiscale Modeling & Simulation. 2015. V. 13. № 1. P. 338–366.

  27. Вабищевич П.H., Варламов С.П., Васильев В.И. и др. Численное моделирование температурного поля многолетнемерзлого грунтового основания железной дороги // Матем. моделирование. 2016. Т. 28. № 10. С. 110–124.

  28. Самарский А.А., Вабищевич П.Н. Вычислительная теплопередача. M.: ЛИБРОКОМ, 2009.

  29. Vasilyeva M., Vasil’ev V., Stepanov S. Generalized multiscale discontinuous Galerkin method for solving the heat problem with phase change // J. of Computational and Applied Mathematics. 2018. V. 340. P. 645–652.

  30. Pavlova N.V., Vabishchevich P.N., Vasilyeva M.V. Mathematical modeling of thermal stabilization of vertical wells on high performance computing systems / In International Conference on Large-Scale Scientific Computing. Springer. 2013. P. 636–643.

  31. Степанов С.П., Сирдитов И.К., Васильева М.В. и др. Разработка программного средства для численного моделирования теплового режима грунтов в условиях криолитозоны // Вестник Северо-Восточного федерального университета им. М.К. Аммосова. 2015. № 47(3). С. 115–125.

  32. Васильев В.И., Максимов А.М., Петров Е.Е. и др. Тепломассоперенос в промерзающих и протаивающих грунтах. M.: Физматлит, 1996.

  33. Цыпкин Г.Г. Течения с фазовыми переходами в пористых средах. М.: Физматлит, 2009.

  34. Vasil’ev V., Vasilyeva M. An Accurate Approximation of the Two-Phase Stefan Problem with Coefficient Smoothing // Mathematics. 2020. V. 8. № 11. Paper 1924.

  35. Михеев М.А., Михеева И.М. Основы теплопередачи. М.: Энергия, 1977.

  36. Brenner S., Scott L. The Mathematical Theory of Finite Element Methods. New York: Springer-Verlag, 2007.

  37. Kolesov A.E., Vabishchevich P.N., Vasilyeva M.V. Splitting schemes for poroelasticity and thermoelasticity problems // Computers & Mathematics with Applications. 2014. V. 67. № 12. P. 2185–2198.

  38. Вабищевич П.Н., Захаров П.Е. Численное решение нестационарных задач с различными масштабами времени // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 10. С. 1604–1615.

  39. Amestoy P.R., Duff I.-F., L’Excellent J.Y. et al. A fully asynchronous multifrontal solver using distributed dynamic scheduling // SIAM Journal on Matrix Analysis and Applications. 2001. V. 23. № 1. P. 15–41.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал