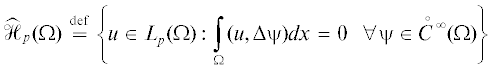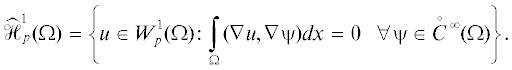Журнал вычислительной математики и математической физики, 2021, T. 61, № 2, стр. 217-223

1. ВВЕДЕНИЕ

Ф. Браудером в [1], [2] было установлено, что если $\mathcal{A}$ – линейный эллиптический дифференциальный оператор, то решение уравнения

в области $\Omega \in {{\mathbb{R}}^{n}}$, $n \geqslant 2$, может быть аппроксимировано в норме пространства Соболева $W_{p}^{l}(\Omega )$ решениями того же уравнения для какой-либо подходящей области $\widetilde \Omega \supset \overline \Omega $, содержащей замыкание $\overline \Omega $ области $\Omega $, если решения для $\widetilde \Omega $ образуют аппроксимативный базис в $W_{p}^{l}(\widetilde \Omega )$.

В настоящей работе рассматривается вопрос об аппроксимации гармоническими многочленами слабых решений уравнения Лапласа в пространствах Лебега ${{L}_{p}}(\Omega )$ и Соболева $W_{p}^{1}(\Omega )$ для ограниченной области $\Omega \in {{\mathbb{R}}^{n}}$, $n \geqslant 2$, со связной липшицевой границей при $p \in (1,\infty )$.

Необходимо отметить, что подход Ф. Браудера к аппроксимации решений эллиптических уравнений в норме $W_{p}^{l}$ принципиально опирается на двойственность пространства $\mathop W\limits^ \circ {\kern 1pt} _{p}^{l}$ и пространства функционалов $\mathop W\limits^ \circ {\kern 1pt} _{{p{\kern 1pt} '}}^{{ - l}}$ с сопряженным показателем $p{\kern 1pt} ' = p{\text{/}}(p - 1)$. Существенным недостатком такого подхода является чрезмерная сложность неизбежно возникающих при этом вспомогательных задач для оператора $\mathcal{A}$, когда $\mathcal{A}$ уже не является простейшим оператором Лапласа. Этого недостатка лишен представленный в настоящей статье новый подход к задачам аппроксимации решений.

2. АППРОКСИМАЦИЯ СЛАБЫХ РЕШЕНИЙ УРАВНЕНИЯ ЛАПЛАСА

В этом разделе рассматриваются вопросы аппроксимации гармоническими многочленами слабых решений уравнения Лапласа $\Delta u = 0$ в нормах ${{L}_{p}}(\Omega )$ и $W_{p}^{1}(\Omega )$ для области $\Omega $, т.е. для открытого связного множества $\Omega \subset {{\mathbb{R}}^{n}}$, $n \geqslant 2$. Существенно, что на замкнутых подпространствах слабых решений классов ${{L}_{p}}(\Omega )$ и $W_{p}^{1}(\Omega )$ устанавливается аппроксимативная базисность системы однородных гармонических многочленов, ортогональных на сфере ${{S}_{R}}$ в ${{\mathbb{R}}^{n}}$ какого-либо радиуса $R > 0$, выбранного и зафиксированного так, чтобы сфера ${{S}_{R}}$ содержала замыкание $\overline \Omega $ рассматриваемой области $\Omega $. Отметим, что аппроксимативная базисность здесь понимается в строгом смысле определения 9.1 в [3, с. 275].

Как с более простого, начнем со случая аппроксимации в норме ${{L}_{p}}(\Omega )$. При этом функцию $u \in {{L}_{p}}(\Omega )$ будем называть слабым решением уравнения Лапласа в $\Omega \subset {{\mathbb{R}}^{n}}$, если выполнено тождество

где символом обозначено пространство всех бесконечно дифференцируемых в $\Omega $ функций с носителем, компактным в $\Omega $. Справедлива следующая

Теорема 1. Пусть $\Omega \subset {{\mathbb{R}}^{n}}$ – ограниченная область с липшицевой связной границей, $n \geqslant 2$, $1 < p < \infty $. Для всякого слабого решения уравнения Лапласа $u \in {{L}_{p}}(\Omega )$ найдется последовательность гармонических многочленов $\{ {{h}_{m}}\} _{{m = 1}}^{\infty }$ такая, что

Доказательство. Через ${{\mathcal{H}}_{p}}(\Omega )$ обозначим замыкание в ${{L}_{p}}(\Omega )$ подпространства всех гармонических многочленов. И пусть

есть подпространство слабых решений уравнения Лапласа в области $\Omega $. Очевидно, что . Теорема будет доказана, если установить обратное включение . Для этого введем обозначение где пространство Соболева $\mathop W\limits^ \circ {\kern 1pt} _{p}^{2}(\Omega )$ определено как замыкание в $W_{p}^{2}(\Omega )$ его подпространства $\mathop C\limits^ \circ {{{\kern 1pt} }^{\infty }}(\Omega )$, что для ограниченной области $\Omega $ обеспечивает замкнутость в ${{L}_{p}}(\Omega )$ подпространства , определенного в (2.1) как область значений оператора Лапласа $\Delta {\kern 1pt} {\kern 1pt} :\;\mathop W\limits^ \circ {\kern 1pt} _{p}^{2}(\Omega ) \to {{L}_{p}}(\Omega )$.

Нетрудно убедиться, что при $1 < p < \infty $ подпространство замкнуто в ${{L}_{p}}(\Omega )$. Кроме того, имеем

где символом ${{X}^{ \bot }}$ обозначен аннулятор подпространства $X \subset {{L}_{p}}(\Omega )$. Отметим (см. [4, разд. 4.5–6)], что при $1 < p < \infty $ аннулятор подпространства $X \subset {{L}_{p}}(\Omega )$ будет сильно замкнутым подпространством в ${{L}_{{p{\kern 1pt} '}}}(\Omega )$ с сопряженным показателем $p{\kern 1pt} ' = p{\text{/}}(p - 1)$.

По определению ограниченный сферой ${{S}_{R}}$ открытый шар ${{B}_{R}}\;\mathop = \limits^{{\text{def}}} \;\{ x \in {{\mathbb{R}}^{n}}{\kern 1pt} :\;{\text{|}}x{\kern 1pt} {\text{|}} < R\} $ содержит замыкание $\overline \Omega $ области $\Omega $. С помощью растяжений и усреднений легко проверить, что совпадает с замыканием в ${{L}_{p}}({{B}_{R}})$ его подпространства

Используя ортогональное разложение гармонических функций в ${{L}_{2}}({{B}_{R}})$ по сферическим гармоникам (см. [5], [6]), легко убедиться, что любой элемент подпространства ${{\mathcal{H}}^{\infty }}({{\bar {B}}_{R}})$ аппроксимируется гармоническими многочленами в норме пространства Соболева $W_{2}^{l}({{B}_{R}})$ для любого $l \geqslant n{\text{/}}2$, а значит, и в норме ${{L}_{p}}({{B}_{R}})$ при $p \in (1,\infty )$ в силу вложения $W_{2}^{l}({{B}_{R}})$ в $C({{\bar {B}}_{R}})$. Это означает совпадение подпространств при любом $p \in (1,\infty )$.

Теорема будет доказана, если убедиться, что замыкание в ${{L}_{p}}(\Omega )$ подпространства сужений на $\Omega $ функций из ${{\mathcal{H}}^{\infty }}({{\bar {B}}_{R}})$ совпадает с при любом значении $p \in (1,\infty )$. Предположим противное. Тогда для некоторого $p \in (1,\infty )$ в силу теоремы Рисса об общем виде линейного непрерывного функционала на ${{L}_{p}}(\Omega )$ найдутся ненулевые элементы $f \in {{L}_{{p{\kern 1pt} '}}}(\Omega )$ и , удовлетворяющие условиям

Доопределяя $f = f(x)$ нулем в точках $x \in {{B}_{R}}{\backslash }\Omega $, получаем функцию $f \in {{L}_{{p{\kern 1pt} '}}}({{B}_{R}})$, удовлетворяющую условию

которое означает, что и найдется такая функция $w \in \mathop W\limits^ \circ {\kern 1pt} _{{p{\kern 1pt} '}}^{2}({{B}_{R}})$, что $f(x) = \Delta w(x)$ почти всюду в ${{B}_{R}}$. При этом для области ${{B}_{R}}{\backslash }\overline \Omega $ функция $w$ оказывается решением однородной задачи Коши где ${{\partial }_{r}}$ – производная по нормали к $\partial {{B}_{R}}$. А ввиду связности открытого множества ${{B}_{R}}{\backslash }\overline \Omega ,$, единственное решение однородной задачи Коши для оператора Лапласа может быть только нулевым на ${{B}_{R}}{\backslash }\overline \Omega $, т.е. функция $w \in \mathop W\limits^ \circ {\kern 1pt} _{{p{\kern 1pt} '}}^{2}({{B}_{R}})$ будет тождественным нулем $w = 0$ на ${{B}_{R}}{\backslash }\overline \Omega .$. Последнее означает, что $w \in \mathop W\limits^ \circ {\kern 1pt} _{{p{\kern 1pt} '}}^{2}(\Omega )$, так как граница $\partial \Omega $ липшицева (подробности см. в [7]). Но тогда , что противоречит левому из двух равенств (2.2), так как . Полученное противоречие завершает доказательство теоремы 1.

Функцию $u \in W_{p}^{1}(\Omega )$ будем называть слабым решением уравнения Лапласа в области $\Omega $, если

где точка означает скалярное произведение векторов в ${{\mathbb{R}}^{n}}$. Для таких функций справедлива следующая теорема об аппроксимации гармоническими многочленами в норме пространства Соболева $W_{p}^{1}(\Omega )$.

Теорема 2. Пусть $\Omega \subset {{\mathbb{R}}^{n}}$ – ограниченная область с липшицевой связной границей, $n \geqslant 2$, $1 < p < \infty $. Если $u \in W_{p}^{1}(\Omega )$ – слабое решение уравнения Лапласа в $\Omega $, то найдется последовательность гармонических многочленов $\{ {{h}_{m}}\} _{{m = 1}}^{\infty }$ такая, что

Доказательство  теоремы  существенно облегчила бы формальная отсылка к известному ${{{\mathbf{L}}}_{p}}$-разложению Гельмгольца–Вейля–Соболева. Но в рассматриваемом общем случае связной липшицевой границы $\partial \Omega $ это разложение известно только для достаточно малой окрестности значений показателя $p = 2$, расширение которой требует, вообще говоря, значительных дополнительных ограничений на $\partial \Omega $, заведомо лишних для доказываемой теоремы. Избежать лишних ограничений на связную липшицеву $\partial \Omega $ позволит использование лишь двух из трех компонент, участвующих в ${{{\mathbf{L}}}_{p}}$-разложении Гельмгольца–Вейля–Соболева, что потребует введения дополнительных обозначений.

Сначала введем вспомогательную ограниченную область $\Omega \in {{\mathbb{R}}^{n}}$ с липшицевой связной границей. Через ${{{\mathbf{L}}}_{p}}(\Omega )$ обозначим пространство Лебега векторных полей ${\mathbf{v}}\,:\;\Omega \to {{\mathbb{R}}^{n}}$, и пусть $\mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }^{\infty }}(\Omega )$ и $\mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }^{\infty }}(\Omega )$ – подпространства бесконечно дифференцируемых и финитных в $\Omega $ потенциальных и соленоидальных векторных полей соответственно, т.е.

Замыкания подпространств $\mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }^{\infty }}(\Omega )$ и $\mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }^{\infty }}(\Omega )$ в пространстве Лебега ${{{\mathbf{L}}}_{p}}(\Omega )$ обозначим через $\mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ и $\mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ соответственно. При этом для ограниченной области $\Omega $ с липшицевой связной границей $\partial \Omega $ имеем эквивалентное определение

где пространство Соболева $W_{p}^{1}(\Omega )$ определено как замыкание в $W_{p}^{1}(\Omega )$ его подпространства $\mathop C\limits^ \circ {{{\kern 1pt} }^{\infty }}(\Omega )$. В общем случае обычно вводится еще одно, не всегда эквивалентное, определение подпространства $\mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ (см. [8]), но в рассматриваемом здесь простейшем случае ограниченной области $\Omega \in {{\mathbb{R}}^{n}}$ со связной липшицевой границей в этом нет необходимости.

Вышеупомянутая пара компонент ${{{\mathbf{L}}}_{p}}$-разложения Гельмгольца–Вейля–Соболева – это замкнутые в ${{{\mathbf{L}}}_{p}}(\Omega )$ подпространства $\mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ и $\mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$. Сразу же заметим, что их алгебраическая сумма $\mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega ) + \mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ будет прямой, т.е. их пересечение тривиально: $\mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega ) \cap \mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega ) = \{ 0\} $, что в случае ограниченной $\Omega $ почти очевидно, так как открытое множество $\Omega {\kern 1pt} '\;\mathop = \limits^{{\text{def}}} \;{{\mathbb{R}}^{n}}{\backslash }\overline \Omega $ не пусто, а всякое ${\mathbf{v}} \in \mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega ) \cap \mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ представимо в виде ${\mathbf{v}} = \nabla u$ с некоторой $u \in \mathop W\limits^ \circ {\kern 1pt} _{p}^{1}(\Omega )$.

Доопределяя $u \in \mathop W\limits^ \circ {\kern 1pt} _{p}^{1}(\Omega )$ нулем на все ${{\mathbb{R}}^{n}}$ с сохранением класса $W_{p}^{1}$ и не меняя обозначений, будем без ограничения общности считать, что $u \in W_{p}^{1}({{\mathbb{R}}^{n}})$, где $u \subset \overline \Omega $. Принадлежность ${\mathbf{v}} \in \mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ означает интегральное тождество

в силу которого гармоническая в ${{\mathbb{R}}^{n}}$ функция $u \in {{С}^{\infty }}({{\mathbb{R}}^{n}})$, тождественно равняясь нулю вне $\Omega $, может быть только тождественным нулем в ${{\mathbb{R}}^{n}}$. Таким образом, ${\mathbf{v}} \equiv 0$ и пересечение подпространств $\mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ и $\mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ тривиально при любом значении показателя $p \in (1,\infty )$.

Проверим теперь, что прямая алгебраическая сумма $\mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega ) + \mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ замкнутых подпространств $\mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ и $\mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ будет замкнутым подпространством в ${{{\mathbf{L}}}_{p}}(\Omega )$. Для этого достаточно установить существование такой постоянной $C > 0$, что

С этой целью, полагая ${\mathbf{f}}\;\mathop = \limits^{{\text{def}}} \;\nabla u + {\mathbf{v}}$ и сохраняя прежние обозначения, доопределим $u \in \mathop W\limits^ \circ {\kern 1pt} _{p}^{1}(\Omega )$, ${\mathbf{v}} \in (\Omega )$ и ${\mathbf{f}} \in {{{\mathbf{L}}}_{p}}(\Omega )$ нулем вне ограниченной области $\Omega $. При этом получим $\nabla u \in \mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }_{p}}({{\mathbb{R}}^{n}})$ и ${\mathbf{v}} \in \mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }_{p}}({{\mathbb{R}}^{n}})$ в силу определения $\mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ и $\mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ как замыканий в ${{{\mathbf{L}}}_{p}}(\Omega )$ подпространств $\mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }^{\infty }}(\Omega )$ и $\mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }^{\infty }}(\Omega )$, тогда как носители элементов $u$, ${\mathbf{v}}$, ${\mathbf{f}}$ окажутся подмножествами замыкания $\overline \Omega $. В таком случае почти всюду в ${{\mathbb{R}}^{n}}$ будет выполняться равенство $\nabla u(x) + {\mathbf{v}}(x) = {\mathbf{f}}$, преобразование Фурье которого с учетом принадлежности ${\mathbf{v}} \in \mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }_{p}}({{\mathbb{R}}^{n}})$ приводит к равенствам где крышечка означает преобразование Фурье, т.е. При этом компактность носителей элементов $u$, ${\mathbf{v}}$, ${\mathbf{f}}$ означает непрерывность на всем ${{\mathbb{R}}^{n}}$ их образов Фурье $\hat {u}$, ${\mathbf{\hat {v}}}$, ${\mathbf{\hat {f}}}$. Из (2.5) легко находим где ${\mathbf{\hat {f}}} = ({{\hat {f}}_{1}}, \ldots ,{{\hat {f}}_{n}})$, откуда следует представление слагаемых $\nabla u$ и ${\mathbf{v}}$ через их сумму ${\mathbf{f}}$ с помощью вектор-оператора компонентами которого ${{R}_{j}}\,:\;{{L}_{p}}({{\mathbb{R}}^{n}}) \to {{L}_{p}}({{\mathbb{R}}^{n}})$ служат ограниченные на ${{L}_{p}}({{\mathbb{R}}^{n}})$ преобразования Рисса подробно описанные в [9]. Из представления (2.6) и ограниченности вектор-оператора ${\mathbf{R}}\,:\;{{L}_{p}}({{\mathbb{R}}^{n}}) \to {{{\mathbf{L}}}_{p}}({{\mathbb{R}}^{n}})$ при $1 < p < \infty $ вытекает справедливость неравенства (2.4) с некоторой постоянной $C > 0$, зависящей только от $n$ и $p$. А тогда алгебраическая сумма $\mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega ) + \mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ будет еще и прямой топологической суммой $\mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega ) \oplus \mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ замкнутых подпространств $\mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ и $\mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$.

Подпространство градиентов слабо гармонических функций в пространстве Лебега ${{{\mathbf{L}}}_{p}}(\Omega )$ обозначим через ${{{\mathbf{I}}}_{p}}(\Omega )$. Поскольку ограниченная область $\Omega $ имеет липшицеву границу, можно без ограничения общности полагать, что

Очевидно, определенное таким образом подпространство ${{{\mathbf{I}}}_{p}}(\Omega )$ будет замкнуто в пространстве Лебега ${{{\mathbf{L}}}_{p}}(\Omega )$.

Для завершения доказательства теоремы нам понадобятся еще два замкнутых в ${{{\mathbf{L}}}_{p}}(\Omega )$ подпространства потенциальных и соленоидальных векторных полей

которые служат аннуляторами подпространств $\mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ и $\mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$, т.е. где верхний индекс $ \bot $ в обозначении сильно замкнутого подпространства в рефлексивном ${{{\mathbf{L}}}_{p}}(\Omega )$ превращает это подпространство в его сильно замкнутый в ${{{\mathbf{L}}}_{{p'}}}(\Omega )$ аннулятор (см. [4, с. 108, 109]).

Отметим, что первое из двух равенств (2.9) вытекает непосредственно из теоремы Рисса об общем виде линейного непрерывного функционала на ${{{\mathbf{L}}}_{p}}(\Omega )$ и определения $\mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$, тогда как второе принято считать очевидным следствием теоремы двойственности де Рама без каких бы то ни было требований к области $\Omega \subset {{\mathbb{R}}^{n}}$. Однако для ограниченной области с липшицевой границей фундаментальная и необобщаемая теорема двойственности де Рама эквивалентна паре равенств, установленных в статье [8], а именно, следствию из теоремы 1 на c. 153 в совокупности с равенством (25) на с. 157.

Отметим также, что пересечение подпространств (2.7) легко вычисляется

так как принадлежность ${\mathbf{v}} \in {{{\mathbf{G}}}_{p}}(\Omega )$ означает, что ${\mathbf{v}} = \nabla u$ с некоторым $u \in W_{p}^{1}(\Omega )$, а принадлежность того же ${\mathbf{v}} \in {{{\mathbf{J}}}_{p}}(\Omega )$ означает выполнение условия откуда сразу же следует принадлежность ${\mathbf{v}} \in {{{\mathbf{I}}}_{p}}(\Omega )$, т.е. ${{{\mathbf{G}}}_{p}}(\Omega ) \cap {{{\mathbf{J}}}_{p}}(\Omega ) \subset {{{\mathbf{I}}}_{p}}(\Omega )$. Обратное включение следует из определения ${{{\mathbf{I}}}_{p}}(\Omega )$ как подпространства градиентов всех слабых решений уравнения Лапласа класса $W_{p}^{1}(\Omega )$.

Вычислим теперь аннулятор подпространства ${{{\mathbf{I}}}_{p}}(\Omega )$. Для этого заметим сначала, что в силу (2.8) и (2.9) аннулятор алгебраической суммы

откуда ввиду уже установленной при всех значениях показателя $p \in (1,\infty )$ замкнутости в ${{{\mathbf{L}}}_{p}}(\Omega )$ его подпространства $\mathop {\mathbf{G}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega ) + \mathop {\mathbf{J}}\limits^ \circ {{{\kern 1pt} }_{p}}(\Omega )$ находим с сопряженным показателем $p{\kern 1pt} ' = p{\text{/}}(p - 1) \in (1,\infty )$.

Наконец все готово для завершения доказательства теоремы. Через $\mathcal{H}_{p}^{1}(\Omega )$ обозначим замыкание в $W_{p}^{1}(\Omega )$ подпространства гармонических многочленов, а через 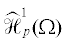– подпространство слабых решений уравнения Лапласа в области $\Omega $ класса $W_{p}^{1}(\Omega )$, т.е.

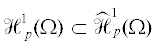Очевидно, что . Осталось доказать обратное включение, т.е. .

Для рассматриваемой ограниченной области $\Omega \subset {{\mathbb{R}}^{n}}$ с липшицевой связной границей выберем и зафиксируем радиус $R > 0$ так, чтобы открытый шар ${{B}_{R}} = \{ x \in {{\mathbb{R}}^{n}}\,:\;{\text{|}}x{\kern 1pt} {\text{|}} < R\} $ содержал замыкание $\overline \Omega $. С помощью растяжений и усреднений легко проверить, что 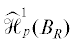совпадает с замыканием в $W_{p}^{1}({{B}_{R}})$ его подпространства гармонических функций ${{\mathcal{H}}^{\infty }}({{\bar {B}}_{R}})$. А используя ортогональное разложение элементов ${{\mathcal{H}}^{\infty }}({{\bar {B}}_{R}})$ по сферическим гармоникам (см. [5], [6]), заключаем, что любой элемент подпространства ${{\mathcal{H}}^{\infty }}({{\bar {B}}_{R}})$ аппроксимируется гармоническими многочленами в норме пространства Соболева $W_{2}^{l}({{B}_{R}})$ для любого $l \geqslant 1$. Поэтому в силу вложения $W_{2}^{l}({{B}_{R}})$ в $W_{p}^{1}({{B}_{R}})$ при значениях $l \geqslant 1 + n{\text{/}}2$ любой элемент подпространства ${{\mathcal{H}}^{\infty }}({{\bar {B}}_{R}})$ аппроксимируется гармоническими многочленами в норме $W_{p}^{1}({{B}_{R}})$ с любым показателем $p \in (1,\infty )$. Последнее означает совпадение подпространств при любом $p \in (1,\infty )$.

Таким образом, для доказательства теоремы достаточно убедиться, что замыкание в $W_{p}^{1}(\Omega )$ подпространства сужений на $\Omega $ функций из ${{\mathcal{H}}^{\infty }}({{\bar {B}}_{R}})$ совпадает с при любом $p \in (1,\infty )$, что эквивалентно совпадению замыкания в ${{{\mathbf{L}}}_{p}}(\Omega )$ подпространства градиентов гармонических функций как элементов ${{{\mathbf{I}}}_{p}}({{B}_{R}})$ c подпространством ${{{\mathbf{I}}}_{p}}(\Omega )$. Предположим противное. Тогда для некоторого $p \in (1,\infty )$ по теореме Рисса об общем виде линейного непрерывного функционала на ${{{\mathbf{L}}}_{p}}(\Omega )$ найдутся ненулевые элементы ${\mathbf{f}} \in {{{\mathbf{L}}}_{{p{\kern 1pt} '}}}(\Omega )$ и ${\mathbf{v}} \in {{{\mathbf{I}}}_{p}}(\Omega )$, удовлетворяющие условиям

Доопределяя ${\mathbf{f}}$ нулем на ${{B}_{R}}{\backslash }\Omega $, получаем вектор-функцию ${\mathbf{f}} \in {{{\mathbf{L}}}_{{p{\kern 1pt} '}}}(\Omega )$, удовлетворяющую условию

которое означает принадлежность А тогда доопределенная нулем вне $\Omega $ вектор-функция ${\mathbf{f}}$ должна иметь вид при условии ${\mathbf{f}} = 0$ на ${{B}_{R}}{\backslash }\Omega $, которое означает выполнение равенств $U = 0$ и ${\mathbf{V}} = 0$ вне области $\Omega $.

Поскольку граница $\partial \Omega $ липшицева и $U \in \mathop W\limits^ \circ {\kern 1pt} _{{p{\kern 1pt} '}}^{l}({{B}_{R}})$, условие $U = 0$ вне $\Omega $ с липшицевой границей означает, что $U \in \mathop W\limits^ \circ {\kern 1pt} _{{p{\kern 1pt} '}}^{l}(\Omega )$ (см. [7]). В свою очередь, выполнение условия ${\mathbf{V}} = 0$ вне ограниченной области $\Omega $ с липшицевой границей для вектор-функции ${\mathbf{V}} \in \mathop {\mathbf{J}}\limits^ \circ {\kern 1pt} _{{p{\kern 1pt} '}}^{{}}({{B}_{R}})$ означает, что ${\mathbf{V}} \in \mathop {\mathbf{J}}\limits^ \circ {\kern 1pt} _{{p{\kern 1pt} '}}^{{}}(\Omega )$ (см. [8]). Таким образом, имеем

что означает равенство нулю первого из двух интегралов (2.11), тогда как он равен единице. Полученное противоречие завершает доказательство теоремы.

Замечание. В доказательствах теорем 1 и 2 шар ${{B}_{R}}$ можно заменить любой ограниченной областью $\widetilde \Omega \subset {{\mathbb{R}}^{n}}$ с кусочно-гладкой связной границей такой, что $\overline \Omega \subset \widetilde \Omega $, например параллелeпипедом. При этом гармонические в $\widetilde \Omega $ функции могут дополнительно удовлетворять любым локально корректным краевым условиям (Дирихле, Неймана или третьему краевому) на одной или нескольких частях границы $\partial \widetilde \Omega $, но не на всей $\partial \widetilde \Omega $. Такой подход принципиально упрощает технику построения в явном виде, возможно, более подходящего для заданной области $\Omega $ аппроксимативного базиса из гармонических функций (не обязательно многочленов), который, учитывая форму области $\Omega $, обеспечит более эффективную реализацию аналитико-численных методов решения корректно поставленных краевых задач для уравнения Лапласа в заданной области $\Omega $.