Журнал вычислительной математики и математической физики, 2021, T. 61, № 3, стр. 373-381

Разностные схемы на основе преобразования Лагерра

А. Ф. Мастрюков^*

Институт вычисл. матем. и матем. геофизики СО РАН
630090 Новосибирск, пр-т Aкад. Лаврентьева, 6, Россия

Поступила в редакцию 30.01.2020
После доработки 30.07.2020
Принята к публикации 18.11.2020

DOI: 10.31857/S0044466921030145

Аннотация

В работе рассматриваются оптимальные разностные схемы для решения волнового уравнения с использованием преобразования Лагерра. В разностную схему уравнений для гармоник вводятся дополнительные параметры. Численные значения этих параметров получаются минимизацией погрешности разностной аппроксимации уравнения Гельмгольца. Полученные таким образом оптимальные значения параметров используются при построении разностных схем – оптимальных разностных схем. Рассмотрены оптимальные разностные схемы 2-го порядка и 4-го порядка аппроксимации. Приведены оптимальные параметры разностных схем. Значения этих параметров зависят только от отношения пространственных шагов разностной сетки. Показано, что использование оптимальных разностных схем ведет к повышению точности решения уравнений. Простая модернизация разностной схемы дает повышение эффективности алгоритма. Библ. 18. Фиг. 2. Табл. 3.

Ключевые слова: конечно-разностный метод, оптимальный, точность, электромагнитные волны, метод Лагерра.

1. ВВЕДЕНИЕ

При численном решении дифференциальных уравнений широко используются спектральные методы. Спектральные методы позволяют более эффективно решать задачи со сложной зависимостью параметров уравнений от времени. Например, в случае с релаксацией диэлектрической проницаемости, выраженной в интегральной форме [1], [2].

Конечно-разностный метод прост в программной реализации и экономичен [3], [4]. Но есть задачи, такие как частотное зондирование, в электроразведке [5], где предпочтительнее использовать спектральные методы.

В ряде задач спектральный метод, основанный на преобразовании Лагерра, по эффективности в несколько раз превосходит метод Фурье. Эффективность обусловлена видом уравнений для гармоник Лагерра [7], [8]. Левая часть этих уравнений не зависит от номера гармоники, а меняется только правая часть этой системы. Кроме того, система уравнений для гармоник всегда содержит только действительные переменные.

Важным показателем качества численного алгоритма является точность получаемого решения уравнений [9]. Существуют различные способы повышения точности решения, например, использование разностных схем более высокого порядка аппроксимации или построение разностных схем минимизирующих погрешность дисперсионного соотношения (dispersion-relation-preserving) [9]. Ко второму типу схем относятся так называемые оптимальные разностные схемы.

В работе оптимальными называются разностные схемы, параметры которых определяются минимизацией некого функционала. В данном случае параметры определяются минимизацией погрешности разностной аппроксимации уравнения Гельмгольца.

В работе [11] была предложена оптимальная разностная схема для решения волнового уравнения в спектральной области. В разностное уравнение 2-го порядка аппроксимации для заданной гармоники Фурье вводятся 3 дополнительных параметра. Значения этих параметров определяются минимизацией погрешности численного решения на точном аналитическом решении. Алгоритм рассматривается при равных пространственных шагах разностной сетки. Обобщение для неравных шагов было предложено в работе [12] введением средних значений в пространственные производные. В этом случае оптимизация проводилась по 4 параметрам.

В работах [13], [14] была рассмотрена оптимальная разностная схема 2 -го порядка аппроксимации для решения уравнений Максвелла и для решения волнового уравнения, основанная на разложении Лагерра по временной переменной. Здесь оптимизация проводилась по 4 параметрам.

В настоящей работе рассматриваются оптимальные разностные схемы 2 -го порядка и 4-го порядка аппроксимации для решения двумерного волнового уравнения на основе преобразования Лагерра, использующие различное число параметров.

Предлагаемые оптимальные схемы являются модернизацией обычных разностных схем, но они обладают более высокой точностью и более высокой эффективностью.

В работе приведены параметры оптимальных разностных схем и результаты тестовых расчетов с использованием этих схем.

2. ПОСТАНОВКА ЗАДАЧИ

Будем рассматривать волновое уравнение вида

(1)

$\frac{1}{{{{{v}}^{2}}}}\frac{{{{\partial }^{2}}E}}{{\partial {{t}^{2}}}} + \gamma \frac{{\partial E}}{{\partial t}} = \frac{{{{\partial }^{2}}E}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}E}}{{\partial {{z}^{2}}}} + S(t,x,z)$

в прямоугольной пространственной области при нулевых граничных и начальных условиях

$E(t = 0,x,z) = 0,\quad \frac{{\partial E(t = 0,x,z)}}{{\partial t}} = 0.$

Здесь $S(t,x,z)$ – источник волн, ${v}$ – скорость волны, $\gamma $ – коэффициент поглощения. Величины ${v}$, $\gamma $ являются функциями координат $x$, $z$.

Такое уравнение описывает как распространение упругих волн, так и распространение электромагнитных волн. В первом случае $E$ – это давление и ${v}$ – это скорость упругих волн, во втором случае $E$ – это напряженность электрического поля и ${v}$ – это скорость электромагнитных волн.

К такому же уравнению можно свести систему двумерных уравнений Максвелла. Уравнения Максвелла для электромагнитного поля в двумерном случае имеют вид [5], [15]

(2)

$\frac{{\partial {{H}_{x}}}}{{\partial z}} - \frac{{\partial {{H}_{z}}}}{{\partial x}} = \varepsilon \frac{{\partial {{E}_{y}}}}{{\partial t}} + \sigma {{E}_{y}} + {{J}_{y}},$

(3)

$\frac{{\partial {{E}_{y}}}}{{\partial z}} = \mu \frac{{\partial {{H}_{x}}}}{{\partial t}},$

(4)

$\frac{{\partial {{E}_{y}}}}{{\partial x}} = - \mu \frac{{\partial {{H}_{z}}}}{{\partial t}},$

где ${\mathbf{H}} = ({{H}_{x}},{{H}_{y}},{{H}_{z}})$ – напряженность магнитного поля, ${\mathbf{E}} = ({{E}_{x}},{{E}_{y}},{{E}_{z}})$ – напряженность электрического поля, ${\mathbf{J}} = ({{J}_{x}},{{J}_{y}},{{J}_{z}})$ – ток внешнего источника, $\varepsilon $ – диэлектрическая проницаемость, $\mu $ – магнитная проницаемость.

Продифференцировав по времени уравнение (2) и подставив в него выражения из уравнений (3), (4), при $\mu = {\text{const}}$ получим для электрического поля ${{E}_{y}}$ уравнение вида (1), где источник имеет вид

$S(t,x,z) = - \mu \frac{{\partial {{J}_{y}}}}{{\partial t}}.$

Систему уравнений (2)–(4) будем использовать для оценки точности решения волнового уравнения (1).

Проведем преобразование Лагерра [16] по времени уравнения (1)

(5)

${{E}_{n}} = \int\limits_0^\infty E (t){{(ht)}^{{ - \alpha /2}}}l_{n}^{\alpha }(ht)d(ht),$

(6)

$E(t) = {{(ht)}^{{\alpha /2}}}\sum\limits_{n = 0}^\infty {\frac{{n!}}{{(n + \alpha )!}}} {{E}_{n}}l_{n}^{\alpha }(ht),$

где $l_{n}^{\alpha }(ht)$ – ортогональная функция Лагерра [16] степени $n$, $\alpha $ – целая константа, $h$ – параметр преобразования Лагерра.

В результате получим уравнение для $n$-й гармоники Лагерра ${{E}_{n}}$:

(7)

$\frac{{{{\partial }^{2}}{{E}_{n}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{E}_{n}}}}{{\partial {{z}^{2}}}} + {{S}_{n}} = \frac{{{{h}^{2}}}}{{{{{v}}^{2}}}}\left( {\frac{1}{4}{{E}_{n}} + \sum\limits_{k = 0}^{n - 1} {{{E}_{k}}} + \sum\limits_{k = 0}^{n - 1} {(n - 1 - k){{E}_{k}}} } \right) + \gamma h\left( {\frac{1}{2}{{E}_{n}} + \sum\limits_{k = 0}^{n - 1} {{{E}_{k}}} } \right).$

Рассмотрим разностную аппроксимацию этого уравнения.

3. АППРОКСИМАЦИЯ УРАВНЕНИЯ

Определим ${{E}_{n}}$ и ${{S}_{n}}$ в целых $i$, $j$ узлах разностной сетки. Производные заменим конечными разностями второго порядка аппроксимации. Запишем уравнение (7) в разностном виде, используя средние значения гармоник Лагерра:

(8)

$\begin{gathered} ({{{\bar {E}}}_{{i,j + 1}}} - 2{{{\bar {E}}}_{{i,j}}} + {{{\bar {E}}}_{{i,j - 1}}}){\text{/}}(\Delta {{x}^{2}} + ({{{\bar {E}}}_{{i + 1,j}}} - 2{{{\bar {E}}}_{{i,j}}} + {{{\bar {E}}}_{{i - 1,j}}}){\text{/}}\Delta {{z}^{2}} + {{S}_{{n,i,j}}} = \\ = \frac{{{{h}^{2}}}}{{{{{v}}^{2}}}}\left( {\frac{1}{4}\left\langle {{{E}_{n}}} \right\rangle + \sum\limits_{k = 0}^{n - 1} {\left\langle {{{E}_{k}}} \right\rangle } + \sum\limits_{k = 0}^{n - 1} {(n - 1 - k)} \left\langle {{{E}_{k}}} \right\rangle } \right) + \gamma h\left( {\frac{1}{2}\left\langle {{{E}_{n}}} \right\rangle + \sum\limits_{k = 0}^{n - 1} {\left\langle {{{E}_{k}}} \right\rangle } } \right). \\ \end{gathered} $

Здесь в правой части уравнения гармоники поля заменены средними значениями по 9 точкам [12]:

(9)

$\begin{gathered} \left\langle {{{E}_{k}}} \right\rangle = c{{E}_{{k,i,j}}} + d({{E}_{{k,i,j + 1}}} + {{E}_{{k,i,j - 1}}}) + g({{E}_{{k,i + 1,j}}} + {{E}_{{k,i - 1,j}}}) + \\ + \;e({{E}_{{k,i + 1,j + 1}}} + {{E}_{{k,i + 1,j - 1}}} + {{E}_{{k,i - 1,j + 1}}} + {{E}_{{k,i - 1,j - 1}}}), \\ \end{gathered} $

где $c$, $d$, $g$, $e$ – весовые множители, удовлетворяющие уравнению

$c + 2d + 2g + 4e = 1\quad {\text{или}}\quad e = (1 - c - 2d - 2g){\text{/}}4.$

В разностных производных по $z$ использованы средние значения [12] для поля вида

(10)

${{\bar {E}}_{{i,j}}} = \frac{{1 - \beta }}{2}{{E}_{{n,i,j + 1}}} + \beta {{E}_{{n,i,j}}} + \frac{{1 - \beta }}{2}{{E}_{{n,i,j - 1}}},$

и в разностных производных по $x$ использованы средние значения вида

(11)

${{\bar {E}}_{{i,j}}} = \frac{{1 - \alpha }}{2}{{E}_{{n,i + 1,j}}} + \alpha {{E}_{{n,i,j}}} + \frac{{1 - \alpha }}{2}{{E}_{{n,i - 1,j}}}.$

Разностное уравнение (8), содержащее дополнительные параметры $\alpha $, $\beta $, $c$, $d$, $g$, $e$, аппроксимирует уравнение (7) со вторым порядком.

Подберем введенные параметры $\alpha $, $\beta $, $c$, $d$, $g$, $e$ таким образом, чтобы точность аппроксимации уравнения была наиболее высокой.

4. ВЫБОР ОПТИМАЛЬНЫХ ПАРАМЕТРОВ

Для нулевой гармоники поля $E = {{E}_{{0y}}}$, уравнение (7) можно представить в виде уравнения Гельмгольца. Без учета источников уравнение (7) принимает простой вид:

(12)

$\frac{{{{\partial }^{2}}E}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}E}}{{\partial {{z}^{2}}}} = k_{0}^{2}E,\quad k_{0}^{2} = \frac{h}{2}\left( {\frac{h}{{2{{\nu }^{2}}}} + \gamma } \right).$

В случае электромагнитных волн

$k_{0}^{2} = \mu \frac{h}{2}\left( {\varepsilon \frac{h}{2} + \sigma } \right).$

Это уравнение на разностной сетке можно записать, применяя средние значения поля, приведенные в предыдущем разделе

$\begin{gathered} \frac{{{{{\bar {E}}}_{{i + 1,j}}} - 2{{{\bar {E}}}_{{i,j}}} + {{{\bar {E}}}_{{i - 1,j}}}}}{{\Delta {{z}^{2}}}} + \frac{{{{{\bar {E}}}_{{i,j + 1}}} - 2{{{\bar {E}}}_{{i,j}}} + {{{\bar {E}}}_{{i,j - 1}}}}}{{\Delta {{x}^{2}}}} = k_{0}^{2}(c{{E}_{{n,i,j}}} + d({{E}_{{n,i,j + 1}}} + {{E}_{{n,i,j - 1}}}) + \\ + \;g({{E}_{{n,i + 1,j}}} + {{E}_{{n,i - 1,j}}}) + e({{E}_{{n,i + 1,j + 1}}} + {{E}_{{n,i + 1,j - 1}}}) + {{E}_{{n,i - 1,j - 1}}}). \\ \end{gathered} $

Уравнение (12) имеет точное решение:

$E = {{E}_{0}}ch({{k}_{x}}x)ch({{k}_{z}}z),\quad k_{x}^{2} + k_{z}^{2} = k_{0}^{2},\quad {{k}_{x}} = {{k}_{0}}\sin \theta ,\quad {{k}_{z}} = {{k}_{0}}\cos \theta .$

Подставим это решение в приведенное разностное уравнение. После простых преобразований получим уравнение

${{V}^{2}}(\theta ,k) = 1,$

где

(13)

$\begin{gathered} {{V}^{2}}(\theta ,k) = \left( {\left( {(1 - \alpha )ch\left( {\frac{{k\cos \theta }}{r}} \right) + \alpha } \right)(ch(k\sin \theta ) - 1) + } \right. \\ + \;\left. {{{r}^{2}}((1 - \beta )ch(k\sin \theta ) + \beta )\left( {ch\left( {\frac{{k\cos \theta }}{r}} \right) - 1} \right)} \right){\text{/}}\left( {{{k}^{2}}\left( {c{\text{/}}2 + d\left( {ch\left( {\frac{{k\cos \theta }}{r}} \right)} \right)} \right.} \right. + \\ \left. { + \;g\left( {ch(k\sin \theta ) + 2e(ch(k\sin \theta ))ch\left( {\frac{{k\cos \theta }}{r}} \right)} \right)} \right) \\ \end{gathered} $

и $r = \Delta x{\text{/}}\Delta z$, $k = {{k}_{0}}\Delta x$.

Будем искать параметры $\alpha $, $\beta $, $c$, $d$, $g$, $e$, требуя максимально точного выполнения равенства ${{V}^{2}}(\theta ,k) = 1$ в пределах допустимых значений $\theta $, $k$.

Для этого определим функционал

(14)

$F(u) = F(\alpha ,\beta ,c,d,g,e) = \int {\int {{{{(1 - V(\theta ,k))}}^{2}}d\theta dk} } ,$

где $u = (\alpha ,\beta ,c,d,g,e)$ – вещественный вектор искомых параметров.

Пределы интегрирования по углу $\theta = [0,\pi {\text{/}}2]$. Пределы интегрирования по второй переменной от $k = 0$ до $k = K$. Величина $k$ определяет отношение шага разностной сетки $\Delta x$ к характерному размеру $1{\text{/}}{{k}_{0}}$ изменения решения. Поэтому брать величину верхнего предела интегрирования $K$ значительно больше единицы не имеет смысла по причине очевидной потери точности.

Будем искать точку минимума функционала (14) при заданных значениях $r$, $K$ по параметрам $\alpha $, $\beta $, $c$, $d$, $g$, $e$.

Для минимизации функционала будем использовать итерационный метод Ньютона [17]. Этот метод требует вычисления первой и второй производных функционала $F(u)$. Производные $F(u)$ по параметрам $\alpha $, $\beta $, $c$, $d$, $g$, $e$ легко вычисляются, так как выражение под интегралом и функция $V(\theta ,k)$ имеют явный вид.

Минимальное значение функционала $F(u)$ при заданных значениях $r$, $K$ обозначим $I(r,K) = \min \,F(u)$. Значения параметров $\alpha $, $\beta $, $c$, $d$, $g$ в точке минимума функционала $F(u)$ будем называть оптимальными параметрами.

В табл. 1 приведены оптимальные значения параметров $\alpha $, $\beta $, $c$, $d$, $g$ и интеграла $I(r,K)$, полученные при $e = 0$, $c = 1 - 2d - 2g$, т.е. при минимизации по 5 параметрам. Учет $e \ne 0$ дает незначительное (около 20%) уменьшение значения интеграла $I(r,K)$.

Таблица 1

α	β	c	d	g	$I(r,K)$	r	K
0.8465	0.8465	0.6782	0.08044	0.08044	5.88e–05	1	1
0.8613	0.8613	0.6916	0.07708	0.07708	2.61e–04	1	1.5
0.8981	0.8981	0.7283	0.06790	0.06790	1.35e–03	1	2.5
0.4985	0.9966	0.6752	0.08187	0.08051	5.96e–05	1.5	1
0.5046	1.0105	0.6852	0.08013	0.07722	2.64e–04	1.5	1.5
0.5207	1.0467	0.7133	0.07511	0.06820	1.37e–03	1.5	2.5
0.3184	0.9735	0.6744	0.08227	0.08052	7.10e–05	2	1
0.3215	0.9860	0.6834	0.08102	0.07725	3.14e–04	2	1.5
0.3296	1.018	0.7083	0.07757	0.06827	1.60e–03	2	2.5

При заданном $r = \Delta x{\text{/}}\Delta z$, с ростом верхнего предела $K$, минимальное значение $I(r,K)$ в промежутке от $K = 0$ до $K \approx 0.3$ падает от единицы до $I \approx {{10}^{{ - 5}}}$, в промежутке от $K \approx 0.3$ до $K \approx 2.5$ растет в 30–40 раз. Малые $K$ соответствуют слабо меняющимся решениям уравнения (12).

При заданном верхнем пределе $K$ с ростом $r$ минимальное значение $I(r,K)$ растет менее, чем на 30% в промежутке $r = [1,\;3]$. Зависимость от $r$ значения $I(r,K)$ и определяемых параметров $\alpha $, $\beta $, $c$, $d$, $g$ носит монотонный характер.

Приводимые здесь разностные аппроксимации уравнения Гельмгольца используют различное число точек сетки. Шаблон разностной схемы без оптимальных параметров является 5-точечным, а шаблон разностной схемы с оптимальными параметрами является 9-точечным. Увеличение числа точек ведет к увеличению числа вычислительных операций.

Если положить $\alpha = 1$, $\beta = 1$, и искать минимум интеграла по трем параметрам, то шаблон такой оптимальной схемы остается 5-точечным, как и обычная схема 2 -го порядка. Такая простая модернизация обычной схемы 2 -го порядка не меняет структуры матрицы системы разностных уравнений (8).

В табл. 2 приведены оптимальные значения параметров $c$, $d$, $g$ для разных значений величины $r = \Delta x{\text{/}}\Delta z$ и при разных верхних пределах интегрирования по $k$ в формуле (14). Указаны также значения интеграла $I(r,K)$, полученные при этих значениях параметров. Эти значения интеграла, как и ранее, нормированы на величину интеграла для неоптимальной схемы.

Таблица 2

C	d	g	$I(r,K)$	r	K
0.7554	0.06114	0.06114	4.65e–02	1	1
0.7621	0.05946	0.05946	4.01e–02	1	1.5
0.7825	0.05435	0.05435	2.62e–02	1	2.5
0.7673	0.05005	0.06625	4.25e–02	1.5	1
0.7710	0.05062	0.06384	3.78e–02	1.5	1.5
0.7828	0.05151	0.05707	2.73e–02	1.5	2.5
0.7974	0.03316	0.06811	3.68e–02	2	1
0.7983	0.03531	0.06551	3.30e–02	2	1.5
0.8022	0.04061	0.05826	2.46e–02	2	2.5

Зависимость интеграла $I(r,K)$ от $r$, $K$ существенно отличается от случая, приведенного в табл. 1. При заданном $r$, с ростом верхнего предела $K$, минимальное значение $I(r,K)$ падает от единицы до $I \approx 2 \times {{10}^{{ - 2}}}$, в промежутке $K = [0,\;2.5]$. При заданном верхнем пределе $K$, с ростом $r$ минимальное значение $I(r,K)$ меняется менее, чем на 30% в промежутке $r = [1,\;3]$.

Значения интеграла $I(r,K)$ при $K = 2.5$ примерно на порядок больше, чем в случае минимизации по 5 параметрам, приведенным в предыдущей таблице. При уменьшении $K$ эта разница возрастет до трех порядков, т.е. схема с 5 параметрами позволяет достичь более глубокой минимизации $I(r,K)$, чем схема с 3 параметрами, но с ростом $K$ разница быстро уменьшается.

Как и для разностной схемы 2 -го порядка для разностных схем 4 -го порядка можно также построить оптимальную разностную схему. Рассмотрим разностную аппроксимацию четвертого порядка уравнения (12) вида

(15)

$\begin{gathered} \frac{{16({{E}_{{i + 1,j}}} + {{E}_{{i - 1,j}}}) - ({{E}_{{i + 2,j}}} + {{E}_{{i - 2,j}}}) - 30{{E}_{{i,j}}}}}{{12\Delta {{z}^{2}}}} - \frac{{16({{E}_{{i,j + 1}}} + {{E}_{{i,j - 1}}}) - ({{E}_{{i,j + 1}}} + {{E}_{{i,j - 1}}}) - 30{{E}_{{i,j}}}}}{{12\Delta {{x}^{2}}}} = \\ = \;k_{0}^{2}\left( {c{{E}_{{i,j}}} + d(4({{E}_{{i,j + 1}}} + {{E}_{{i,j - 1}}}){\text{/}}6 - ({{E}_{{i,j + 2}}} + {{E}_{{i,j - 2}}}){\text{/}}6} \right) + g\left( {4({{E}_{{i + 1,j}}} + {{E}_{{i - 1,j}}}){\text{/}}6 - ({{E}_{{i + 2,j}}} + {{E}_{{i - 2,j}}}){\text{/}}6} \right). \\ \end{gathered} $

Шаблон этой схемы является 9-точечным. Введение трех параметров $c$, $d$, $g$ при $\,c = 1 - d - \,g$ не увеличивает числа точек схемы. Выписав для этого случая уравнения (13), (14) и проведя минимизацию по этим трем параметрам, получим оптимальные параметры, которые приведены в табл. 3.

Таблица 3

C	d	g	$I(r,K)$	r	K
0.8897	0.05513	0.05513	2.48e–02	1	1
0.8961	0.05191	0.05191	2.13e–02	1	1.5
0.9043	0.04781	0.04781	1.84e–02	1	2
0.8952	0.04812	0.05667	1.85e–02	1.5	1
0.8993	0.04747	0.05313	1.60e–02	1.5	1.5
0.9049	0.04638	0.04864	1.38e–02	1.5	2
0.9184	0.02465	0.05693	1.58e–02	2	1
0.9208	0.02584	0.05334	1.37e–02	2	1.5
0.9245	0.02671	0.04878	1.19e–02	2	2

При заданном $r$, с ростом верхнего предела $K$, минимальное значение $I(r,K)$ падает от единицы до $I \approx {{10}^{{ - 2}}}$, в промежутке $K = [0,\;2]$. При заданном верхнем пределе $K$, с ростом $r$ минимальное значение $I(r,K)$ падает в 2.5 раза в промежутке $r = [1,\;3]$. При $K > 2.1$ точка минимума $I(r,K)$ не определяется.

5. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

Решение уравнения (1) спектральным методом Лагерра, полученное с использованием оптимальных параметров, будем сравнивать с решением системы уравнений (2)–(4) высокоточным [18] конечно-разностным методом (7-го порядка аппроксимации по времени и 6-го порядка аппроксимации по пространству).

Источник тока брался в виде

$\begin{gathered} {{J}_{y}} = f(t)\delta (z - {{z}_{s}}), \\ f(t) = {{J}_{0}}exp\left( { - \frac{{{{{(2\pi {{f}_{0}}(t - {{t}_{0}}))}}^{2}}}}{{{{\gamma }^{2}}}}} \right)\sin {\text{(}}2\pi {{f}_{0}}(t - {{t}_{0}})), \\ \end{gathered} $

где ${{f}_{0}}$ – несущая частота источника, ${{t}_{0}}$ – момент центра импульса источника, ${{z}_{s}}$ – точка расположения источника.

В преобразовании Лагерра использовались 310 гармоник Лагерра, параметры $\alpha = 1$, $h = 100$.

Точность решения оценивалaсь по величине относительной погрешности решения $D$, которая определялась выражением

(17)

$D(t) = \frac{{\int\limits_0^\infty {\left| {{{E}_{y}}(z,t) - {{E}_{{0y}}}(z,t)} \right|} dz}}{{\int\limits_0^\infty {\left| {{{E}_{{0y}}}(z,t)} \right|} dz}},$

здесь ${{E}_{y}} = E$ – решение уравнения (1), полученное с использованием разложения Лагерра, ${{E}_{{0y}}}$ – решение уравнений (2)–(4), полученное с использованием конечно-разностной схемы. На графиках, приведенных ниже, решение этой конечно-разностной схемой показано сплошной линией.

На фиг. 1 показано прохождение электромагнитной волны от точечного источника (${{E}_{y}}$ – компоненты поля) через слой, расположенный в однородной среде. Шаг разностной схемы $\Delta x = 0.05$. Точками показано расположение слоя в среде. Сплошная линия соответствует решению уравнений (2)–(4).

Фиг. 1.

Решение уравнения неоптимальной (а) и оптимальной (б) разностными схемами 2 -го порядка аппроксимации.

На фиг. 1а штрихованная линия соответствует решению обычной, неоптимальной разностной схемой 2 -го порядка. Указана величина погрешности $D$ для этого решения.

На фиг. 1б штриховая линия соответствует решению оптимальной разностной схемой 2 -го порядка с тремя оптимальными параметрами, приведенными в табл. 2, при $r = 1.5$, $K = 2.5$. Здесь величина погрешности $D$ примерно в два раза меньше, чем в случае использования неоптимальной схемы фиг. 1а.

Видно, что оптимальная разностная схема с тремя оптимальными параметрами дает более точное решение. Простая модернизация разностной схемы ведет также и к повышению эффективности алгоритма. В данном случае это дает сокращение времени счета на несколько первых процентов.

На этой же фигуре приведено решение оптимальной разностной схемой 2 -го порядка аппроксимации с 5 оптимальными параметрами, приведенными в табл. 1, и решение разностной схемой 4 -го порядка аппроксимации без оптимальных параметров. Для сравнения приведены погрешности $D2$ и $D4$ для этих алгоритмов. Эти решения графически совпадает с решением уравнений (2)–(4).

На фиг. 2 показано прохождение электромагнитной волны от точечного источника (${{E}_{y}}$ – компоненты поля) через слой, расположенный в однородной среде. Шаг разностной схемы $\Delta x = 0.07$. Точками показано расположение слоя в среде.

Фиг. 2.

Решение уравнения неоптимальной (штриховая линия) и оптимальной (сплошная линия) разностными схемами 4 -го порядка аппроксимации.

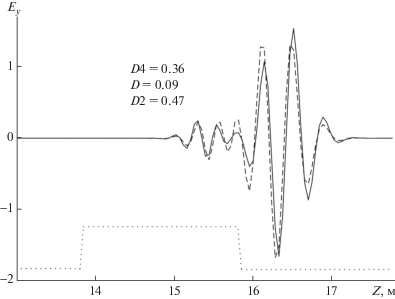
Сплошная линия соответствует решению уравнений (2)–(4), штриховая линия соответствует решению разностной схемой 4 -го порядка без оптимальных параметров. Указана величина погрешности для этого решения $D4$, ниже указана величина погрешности $D$ для решения оптимальной схемой с тремя оптимальными параметрами, приведенными в табл. 3 при $r = 1.5$, $K = 2.0$. Погрешности $D$ в четыре раза меньше погрешности $D4$.

Решение разностной схемой с тремя оптимальными параметрами, графически неотличимо от решения уравнений (2)–(4). Как и в случае, показанном на фиг. 1, здесь оптимальная разностная схема дает сокращение времени счета на несколько первых процентов.

Для сравнения, эта задача решалась с использованием оптимальной разностной схемы 2 -го порядка с 5 оптимальными параметрами из табл. 1, при $r = 1.5$, $K = 2.5$. На этой фигуре приведена только погрешность $D2$ этого решения. Разница величин $D2$ и $D4$ менее 30%, но схема 2 -го порядка в этом варианте оказывается на 20–25% экономичнее схемы 4 -го порядка.

6. ЗАКЛЮЧЕНИЕ

Использование оптимальных разностных схем позволяет повысить точность решения уравнения в сравнении с обычными схемами 2 -го порядка аппроксимации. Это верно и для разностных схем 4 -го порядка аппроксимации. Оптимальные схемы с 5 оптимальными параметрами дают более точное решение, чем оптимальные схемы с 3 оптимальными параметрами. Оптимальные схемы с 3 оптимальными параметрами требуют простой модернизации обычных неоптимальных разностных схем, но повышают точность решения задачи и сокращают время счета задачи. Значения оптимальных параметров зависят только от отношения пространственных шагов разностной схемы.

Список литературы

Luebbers R., Hansberger F.P. FDTD for Nth-order dispersive media // IEEE Trans. Ant Propog. 1992. V. 40. P. 1297–1301.
Turner G., Siggins A.F. Constant Q attenuation of subsurface radar pulses // Geophysics. 1994. V. 59. P. 1192–1200.
Bergmann T., Johan O.A. Robertsson, Klaus Holliger. Finite difference modeling of electromagnetic wave in dispersive and attenuating media // Geophysics. 1998. V. 63. P. 856–867.
Bergmann T., Joakim O. Blanch, Johan O.A. Robertsson, Klaus Holliger. A simplified Lax-Wendroff correction for staggered-grid FDTD modeling of electromagnetic wave in frequency-dependent media // Geophysics. 1999. V. 64. P. 1369–1377.
Электроразведка. Справочник геофизика / Под ред. А.Г. Тархова. М.: Недра, 1980. С. 518.
Конюх Г.В., Михайленко Б.Г. Применение интегрального преобразования Лагерра при решении динамических задач сейсмики // Труды ИВМ и МГ. Матем. моделирование в геофизике. Новосибирск. 1998. № 5. С. 107–112.
Мастрюков А.Ф., Михайленко Б.Г. Численное моделирование распространения электромагнитных волн в неоднородных средах с затуханием на основе спектрального преобразования Лагерра // Геология и геофиз. 2003. Т. 44. № 10. С. 1060–1069.
Мастрюков А.Ф., Михайленко Б.Г. Моделирование распространения электромагнитных волн в релаксационных средах на основе спектрального преобразования Лагерра // Геология и геофиз. 2006. Т. 47. № 3. С. 397–407.
Голуб Дж., Ван Лоун Ч. Матричные вычисления. М.: Мир, 1999. С. 548.
Tam C.K., Webb J.C. Dispersion-relation-preserving finite difference schemes for computational acoustics // J. Comput. Phys. 1993. V. 107. № 2. P. 262–281.
Jo C.H., Shin C., Suh H.S. An optimal 9-point, finite-difference, frequency-space, 2-d scalar wave extrapolator // Geophys. 1996. V. 61. P. 529–537.
Chen J.B. An average derivative optimal scheme for frequency-domain scalar wave equation // Geophys. 2012. V. 77. P. T201–T210.
Мастрюков А.Ф., Михайленко Б.Г. Оптимальные разностные схемы для уравнений Максвелла при решении прямых задач электромагнитных зондирований // Геология и геофиз. 2015. Т. 56. № 9. С. 1713–1722.
Мастрюков А.Ф. Оптимальные разностные схемы для волнового уравнения // Сиб. Ж. вычисл. матем. 2016. № 5. С. 107–112.
Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Наука, 1982. С. 620.
Справочник по специальным функциям / Под ред. М. Абрамовица и И. Стиган. М.: Наука, 1979. С. 832.
Васильев Ф.П. Численные методы решения экстремальных задач. М.: Наука, 1980. С. 518.
Ghris M., Fornberg B., Driscoll T.A. Staggered time integrator for wave equations // SIAM J. Numer. Analys. 2000. V. 38. P. 718–741.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал