Журнал вычислительной математики и математической физики, 2021, T. 61, № 6, стр. 951-965

1. ВВЕДЕНИЕ

Пусть $\Omega \subset {{\mathbb{R}}^{n}}$ – неограниченная область с границей $\partial \Omega \in {{C}^{2}}$, $\Omega = {{\mathbb{R}}^{n}}{{\backslash }}\bar {G}$, где $G$ – ограниченная односвязная область (или объединение конечного числа таких областей) в ${{\mathbb{R}}^{n}}$, $n \geqslant 2$, $\Omega \cup \partial \Omega = \bar {\Omega }$ – замыкание $\Omega $, $x = ({{x}_{1}},\; \ldots ,\;{{x}_{n}})$, $\left| x \right| = \sqrt {x_{1}^{2} + \cdots + x_{n}^{2}} $.

В $\Omega $ рассматривается задача для бигармонического уравнения

с условиями Дирихле на ${{\Gamma }_{1}}$ и условиями типа Стеклова на ${{\Gamma }_{2}}$где ${{\bar {\Gamma }}_{1}} \cup {{\bar {\Gamma }}_{2}} = \partial \Omega $, ${{\Gamma }_{1}} \cap {{\Gamma }_{2}} = \not {0}$, ${{\operatorname{mes} }_{{n - 1}}}{{\Gamma }_{1}} \ne 0$, $\nu = ({{\nu }_{1}},\; \ldots ,\;{{\nu }_{n}})$ – единичный вектор внешней нормали к $\partial \Omega $, $\tau \in C(\partial \Omega )$, $\tau \geqslant 0$, , 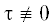и $\tau > 0$ на множестве $\partial \Omega $ положительной $(n - 1)$-мерной меры.

Эллиптические задачи с параметрами в граничных условиях называются задачами Стеклова или типа Стеклова с момента их первого появления в [1]. Для бигармонического оператора эти условия были впервые рассмотрены в [2], [3] и [4] при изучении изопериметрических свойств первого собственного значения.

Отметим, что стандартные результаты эллиптической регулярности доступны в [5]. Монография посвящена линейным и нелинейным эллиптическим краевым задачам более высокого порядка, в основном с бигармоническим или полигармоническим оператором в качестве главной части. Что касается линейных задач, то после краткого изложения теории существования и оценок L^p и Шаудера, акцент делается на положительности. Требуемые оценки ядра также представлены подробно.

В [6] и [5] изучаются спектральные и сохраняющие положительность свойства для инверсии бигармонического оператора при граничных условиях Стеклова и типа Стеклова. Они связаны с первым собственным значением задачи Стеклова. Показано, что свойство сохранения положительности весьма чувствительно к параметру, входящему в граничное условие.

Как известно, в случае, когда $\Omega $ – неограниченная область, следует дополнительно охарактеризовать поведение решения на бесконечности. Как правило, для этой цели служит либо условие конечности интеграла Дирихле (энергии), либо условие на характер убывания модуля решения при $\left| x \right| \to \infty $ (см., например, [7]–[10]). Вопросы о поведении при $\left| x \right| \to \infty $ решений задачи Дирихле для бигармонического уравнения (1) рассматривались в [11], [12], в которых при определенных условиях геометрического характера на границу области получены также оценки, характеризующие поведение $\left| {u(x)} \right|$ и $\left| {\nabla u(x)} \right|$ при $\left| x \right| \to \infty $.

В данной статье таким условием является ограниченность интеграла Дирихле с весом:

В [13] изучается слабое решение смешанной краевой задачи для бигармонического уравнения на плоскости. При решении, используя формулу Грина, задача превращается в систему интегральных уравнений Фредгольма для неизвестных данных на другой части границы. В соответствующих пространствах Соболева установлены существование и единственность решений системы граничных интегральных уравнений. В [9] с условием конечности интеграла Дирихле на поведение решения на бесконечности изучены вопросы единственности решений задачи Дирихле для эллиптических систем высокого порядка в неограниченных областях.

Отметим также работы [14]–[16], в которых изучены основные краевые задачи и задачи со смешанными краевыми условиями для бигармонического (полигармонического) уравнения. В частности, установлены существование и единственность решений в шаре, а также получены необходимые и достаточные условия разрешимости краевых задач для бигармонического (полигармонического) уравнения, в том числе с полиномиальной правой частью.

В разных классах неограниченных областей с конечным весовым интегралом энергии (Дирихле) в [17]–[32] изучены вопросы единственности, а также найдены размерности пространств решений краевых задач для системы теории упругости и бигармонического (полигармонического) уравнения. Развивая подход, основанный на использовании неравенств типа Харди (см. [7]–[9]), в настоящей работе удалось получить критерий единственности (неединственности) решений бигармонической задачи с граничными условиями Дирихле и типа Стеклова. Для построения решения используется вариационный метод, т.е. минимизируется соответствующий функционал в классе допустимых функций.

Данная работа содержит полные доказательства результатов, анонсированных в [30].

Введем обозначения: $C_{0}^{\infty }(\Omega )$ – пространство бесконечно дифференцируемых функций в области $\Omega $ и имеющих компактный носитель в $\Omega $; ${{H}^{2}}(\Omega ,\Gamma )$, $\Gamma \subset \bar {\Omega }$, – пространство, полученное пополнением множества функций из ${{C}^{\infty }}(\bar {\Omega })$, равных нулю в окрестности $\Gamma $, по норме

где ${{\partial }^{\alpha }} \equiv {{\partial }^{{|\alpha |}}}{\text{/}}\partial x_{1}^{{{{\alpha }_{1}}}},\; \ldots ,\;\partial x_{n}^{{{{\alpha }_{n}}}}$, $\alpha = ({{\alpha }_{1}},\; \ldots ,\;{{\alpha }_{n}})$ – мультииндекс, ${{\alpha }_{j}} \geqslant 0$ – целые числа, $\left| \alpha \right| = {{\alpha }_{1}} + \; \ldots \; + {{\alpha }_{n}}$; если $\Gamma = \not {0}$, то пространство ${{H}^{2}}(\Omega ,\Gamma )$ будем обозначать ${{H}^{2}}(\Omega )$;

${{\mathop H\limits^ \circ }^{2}}(\Omega )$ – пространство функций в $\Omega $, полученное пополнением множества функций из $C_{0}^{\infty }(\Omega )$ по норме пространства Соболева ${{H}^{2}}(\Omega )$;

– пространство функций в $\Omega $, полученное пополнением множества функций из $C_{0}^{\infty }(\Omega )$ в системе полунорм $\left\| {u;{{H}^{2}}({{G}_{0}})} \right\|$, где ${{G}_{0}} \subset \bar {\Omega }$ – произвольный компакт.

Обозначим

Под конусом $K$ в ${{\mathbb{R}}^{n}}$ с вершиной в начале координат будем понимать такую область, что если $x \in K$, то $\lambda x \in K$ при всех $\lambda > 0$. Будем считать, что начало координат ${{x}_{0}} = 0$ находится вне $\bar {\Omega }$.

Пусть $\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right)$ – биномиальный коэффициент $(n,k)$, $\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right)$ = 0 при $k > n$.

2. ОПРЕДЕЛЕНИЯ И ВСПОМОГАТЕЛЬНЫЕ УТВЕРЖДЕНИЯ

Определение 1. Решением однородного бигармонического уравнения (1) в $\Omega $ будем называть функцию $u \in H_{{{\text{loc}}}}^{2}(\Omega )$ такую, что для всякой функции $\varphi \in C_{0}^{\infty }(\Omega )$ выполнено интегральное тождество

Лемма. Пусть $u$ – решение уравнения (1) в $\Omega $, удовлетворяющее условию ${{D}_{a}}(u,\Omega ) < \infty $. Тогда

где $P(x)$ – многочлен, $\operatorname{ord} P(x) < {{m}_{0}} = max{\text{\{ }}2,\;2 - n{\text{/}}2 - a{\text{/}}2{\text{\} }}$, ${{\beta }_{0}} = 2 - n{\text{/}}2 + a{\text{/}}2$, $\Gamma (x)$ – фундаментальное решение уравнения (1), ${{C}_{\alpha }} = {\text{const}}$, $\beta \geqslant 0$ – целое число, а для функции ${{u}^{\beta }}(x)$ справедлива оценкадля любого мультииндекса $\gamma $.

Замечание. Для фундаментального решения $\Gamma (x)$ бигармонического уравнения известно [33], что

Доказательство леммы. Рассмотрим функцию ${v}(x) = {{\theta }_{N}}(x)u(x)$, где ${{\theta }_{N}}(x) = \theta \left( {\left| x \right|{\text{/}}N} \right)$, $\theta \in {{C}^{\infty }}({{\mathbb{R}}^{n}})$, $0 \leqslant \theta \leqslant 1$, $\theta (s) = 0$ при $s \leqslant 1$, $\theta (s) = 1$ при $s \geqslant 2$, причем $N \gg 1$ и $G \subset \left\{ {x:\left| x \right| < N} \right\}$. Продолжим функцию ${v}$ на ${{\mathbb{R}}^{n}}$, полагая $v = 0$ на $G = {{\mathbb{R}}^{n}}{{\backslash }}\bar {\Omega }$.

Тогда функция ${v} \in {{C}^{\infty }}({{\mathbb{R}}^{n}})$ и удовлетворяет уравнению

где $f \in C_{0}^{\infty }({{\mathbb{R}}^{n}})$ и ${\text{supp}}\,f \subset \left\{ {x:\left| x \right| < 2N} \right\}$. Легко видеть, что ${{D}_{a}}({v},{{\mathbb{R}}^{n}}) < \infty $.

Теперь мы можем использовать теорему 1 из [34], поскольку она основывается на лемме 2 из [34], в которой никаких ограничений на знак $\sigma $ нет. Следовательно, разложение

справедливо для любого $a$, где $P(x)$ – многочлен, $\operatorname{ord} P(x) < {{m}_{0}} = {\text{max\{ }}2,\;2 - n{\text{/}}2 - a{\text{/}}2{\text{\} }}$, ${{\beta }_{0}} = 2 - n{\text{/}}2 + a{\text{/}}2$, ${{C}_{\alpha }} = {\text{const}}$ и Отсюда и из определения функции $v$ следует равенство (3). Лемма доказана.

Определение 2. Решением бигармонической задачи с граничными условиями Дирихле и типа Стеклова (1), (2) будем называть функцию $u \in \circ H_{{{\text{loc}}}}^{2}(\Omega ,{{\Gamma }_{1}}) \cap \circ H_{{{\text{loc}}}}^{1}(\Omega )$, $\partial u{\text{/}}\partial \nu = 0$ на ${{\Gamma }_{2}}$, такую, что для всякой функции $\varphi \in \circ H_{{{\text{loc}}}}^{2}(\Omega ,{{\Gamma }_{1}}) \cap C_{0}^{\infty }({{\mathbb{R}}^{n}})$, $\partial \varphi {\text{/}}\partial \nu = 0$ на ${{\Gamma }_{2}}$, выполнено интегральное тождество

Обозначим через ${{\operatorname{Ker} }_{0}}({{\Delta }^{2}})$ пространство обобщенных решений бигармонической задачи с граничными условиями Дирихле и типа Стеклова (1), (2), имеющих конечный интеграл Дирихле, т.е.

Положим по определению Через $\dim {\text{Ke}}{{{\text{r}}}_{0}}({{\Delta }^{2}})$ и $\dim {\text{Ke}}{{{\text{r}}}_{a}}({{\Delta }^{2}})$ обозначим размерности пространств ${\text{Ke}}{{{\text{r}}}_{0}}({{\Delta }^{2}})$ и ${\text{Ke}}{{{\text{r}}}_{a}}({{\Delta }^{2}})$ соответственно. В зависимости от значения параметра $a$ будем вычислять $\dim {\text{Ke}}{{{\text{r}}}_{a}}({{\Delta }^{2}})$.

3. ОСНОВНЫЕ РЕЗУЛЬТАТЫ

Теорема 1. Бигармоническая задача (1), (2) с условием $D(u,\Omega ) < \infty $ имеет $n + 1$ линейно независимых решений, т.е. $\dim {\text{Ke}}{{{\text{r}}}_{0}}({{\Delta }^{2}}) = n + 1.$

Доказательство. Доказательство теоремы 4 приведено в [30].

Теорема 2. Если $ - n \leqslant a < n - 4,n > 4$, то ${\text{dim Ke}}{{{\text{r}}}_{a}}({{\Delta }^{2}}) = n + 1.$

Доказательство. Сначала рассмотрим случай $0 \leqslant a < n - 4$, $n > 4$.

Очевидно, что ${\text{Ke}}{{{\text{r}}}_{a}}({{\Delta }^{2}}) \subset {\text{Ke}}{{{\text{r}}}_{0}}({{\Delta }^{2}})$, если $a \geqslant 0$.

Докажем, что ${\text{Ke}}{{{\text{r}}}_{0}}({{\Delta }^{2}}) \subset {\text{Ke}}{{{\text{r}}}_{a}}({{\Delta }^{2}})$.

Пусть $u \in {\text{Ke}}{{{\text{r}}}_{0}}({{\Delta }^{2}})$. Тогда, согласно лемме 2, решение $u$ имеет вид (3), т.е.

где $P(x)$ – многочлен, $\operatorname{ord} P(x) \leqslant 1$,

Легко заметить, что ${{D}_{a}}(P(x),\Omega ) = 0$ и ${{D}_{a}}(R(x),\Omega ) < \infty $ при $a < n - 4$. Следовательно, ${{D}_{a}}(u,\Omega ) < \infty $, т.е. $u \in {\text{Ke}}{{{\text{r}}}_{a}}({{\Delta }^{2}})$.

Итак, ${\text{Ke}}{{{\text{r}}}_{a}}({{\Delta }^{2}}) = {\text{Ke}}{{{\text{r}}}_{0}}({{\Delta }^{2}})$ и ${\text{dim Ke}}{{{\text{r}}}_{a}}({{\Delta }^{2}}) = {\text{dim Ke}}{{{\text{r}}}_{0}}({{\Delta }^{2}})$. Согласно теореме 4,

Теперь рассмотрим случай $ - n \leqslant a < 0$, $n > 4$.

Пусть $u \in {\text{Ke}}{{{\text{r}}}_{a}}({{\Delta }^{2}})$, где  $ - n \leqslant a < 0$. Согласно лемме 2, решение уравнения (1) в  $\Omega $ имеет вид (3).

Так как ${\text{ord}}P(x) \leqslant 1$, то $D(P(x),\Omega ) < \infty $. Легко проверить, что $D(R(x),\Omega ) < \infty $ при $n > 4$. Следовательно, $D(u,\Omega ) < \infty $, т.е. $u \in {\text{Ke}}{{{\text{r}}}_{0}}({{\Delta }^{2}})$.

С другой стороны, очевидно, что ${\text{Ke}}{{{\text{r}}}_{0}}({{\Delta }^{2}}) \subset {\text{Ke}}{{{\text{r}}}_{a}}({{\Delta }^{2}})$, если $a < 0$.

Таким образом, ${\text{Ke}}{{{\text{r}}}_{a}}({{\Delta }^{2}}) = {\text{Ke}}{{{\text{r}}}_{0}}({{\Delta }^{2}})$ и ${\text{dim Ke}}{{{\text{r}}}_{a}}({{\Delta }^{2}}) = {\text{dim Ke}}{{{\text{r}}}_{0}}({{\Delta }^{2}})$. В силу теоремы 4, имеем

Теорема доказана.

Теорема 3. Если $n - 4 \leqslant a < n - 2$, $n > 4$, то ${\text{dim Ke}}{{{\text{r}}}_{a}}({{\Delta }^{2}}) = n$.

Доказательство.

Шаг 1. Для произвольного числа $e \ne 0$ построим обобщенное решение уравнения (1) с граничными условиями

и с условием Такое решение можно построить вариационным методом, минимизируя функционал в классе ${\text{\{ }}{v}:{v} \in {{H}^{2}}(\Omega ),\;{{\left. {v} \right|}_{{{{\Gamma }_{1}}}}} = e,\mathop {\;\left. {\tfrac{{\partial {v}}}{{\partial \nu }}} \right|}\nolimits_{{{\Gamma }_{1}}} = 0,$ ${v}$ имеет компактный носитель в $\bar {\Omega }{\text{\} }}$ допустимых функций.

Справедливость условия (6), как следствие неравенства Харди, следует из результатов работ [7]–[9]. Согласно лемме 2, решение ${{u}_{e}}$ имеет вид

где ${{P}_{e}}(x)$ – многочлен, ${\text{ord}}{{P}_{e}}(x) \leqslant 1$, Из условия (6) следует, что ${{P}_{e}}(x) \equiv 0$.

Покажем, что $C_{0}^{'} \ne 0$. Предположим, что $C_{0}^{'} = 0$. Умножив уравнение (1) на единицу и проинтегрировав по ${{\Omega }_{R}}$, получим

Покажем сначала, что Так как $C_{0}^{'} = 0$, то Следовательно, принимая во внимание граничные условия на ${{\Gamma }_{2}}$, получаем Теперь докажем, что Умножив уравнение (1) на ${{u}_{e}}$ и проинтегрировав по ${{\Omega }_{R}}$ с учетом граничных условий (5), получим где Покажем, что ${{J}_{1}}({{u}_{e}}) \to 0$, ${{J}_{2}}({{u}_{e}}) \to 0$ при $R \to \infty $. Так как то при $R \to \infty $, $n > 4$ имеем Переходя к пределу в равенстве (9) при $R \to \infty $, получаем требуемое равенство (8), так как ${{\left. {{{u}_{e}}} \right|}_{{{{\Gamma }_{1}}}}} = e$. Из равенств (7) и (8) следует, что С помощью интегрального тождества получаем, что ${{u}_{e}}$ является решением однородной задачи (1), (2), и ${{u}_{e}} = 0$, так как $e \ne 0$. Значит, $\Delta {{u}_{e}} = 0$ в $\Omega $. Отсюда и из граничных условий (5) следует (см. [35, Гл. 2.4]), что ${{u}_{e}} \equiv e \ne 0$. Полученное соотношение противоречит условию (6). Таким образом, $C_{0}^{'} \ne 0$.

Положим $s = e{\text{/}}C_{0}^{'}$.

Шаг 2. Рассмотрим теперь уравнение (1) с граничными условиями

где $A$ – ненулевой вектор из ${{\mathbb{R}}^{n}}$, $Ax$ обозначает стандартное скалярное произведение $A$ и $x$.

Для любого ненулевого вектора $A$ построим обобщенное решение бигармонического уравнения (1) с граничными условиями (10) и с условием

Решение задачи (1), (10) строится вариационным методом, минимизируя соответствующий функционал в классе допустимых функций ${\text{\{ }}{v}:{v} \in {{H}^{2}}(\Omega ),\;{{\left. {{v}(x)} \right|}_{{{{\Gamma }_{1}}}}} = {{\left. {(Ax)} \right|}_{{{{\Gamma }_{1}}}}},$ $\mathop {\left. {\tfrac{{\partial {v}(x)}}{{\partial \nu }}} \right|}\nolimits_{{{\Gamma }_{1}}} = \mathop {\left. {\tfrac{{\partial (Ax)}}{{\partial \nu }}} \right|}\nolimits_{{{\Gamma }_{1}}} ,$ ${v}$ имеет компактный носитель в $\bar {\Omega }{\text{\} }}$.

Условия (11), как следствие неравенства Харди, следует из результатов [7]–[9]. Согласно лемме 2, имеет место равенство

где ${{P}_{A}}(x)$ – многочлен, ${\text{ord}}\,{{P}_{A}}(x) \leqslant 1$, Из условия (11) следует, что ${{P}_{A}}(x) \equiv 0$.

Шаг 3. Рассмотрим функцию

где $e = s{{C}_{0}}$, число $s$ определено выше. Очевидно, что ${v}$ – решение задачи (1), (2).

Докажем, что ${{D}_{a}}({v},\Omega ) < \infty $ при $a < n - 2$. Имеем

причем $С_{0}^{'} = e{\text{/}}s = s{{C}_{0}}{\text{/}}s = {{C}_{0}}$. Следовательно, где $C_{\alpha }^{{''}} = {{C}_{\alpha }} - C_{\alpha }^{'}$, $u_{0}^{\beta }(x) = u_{A}^{\beta }(x) - u_{e}^{\beta }(x)$.

Нетрудно проверить, что ${{D}_{a}}({{\partial }^{\alpha }}\Gamma (x)C_{\alpha }^{'},\Omega ) < \infty $, ${{D}_{a}}(u_{0}^{\beta },\Omega ) < \infty $ при $a < n - 2$. Отсюда следует, что ${{D}_{a}}({{u}_{A}} - {{u}_{e}},\Omega ) < \infty $ и ${{D}_{a}}({v},\Omega ) < \infty $. Легко заметить, что .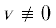

Таким образом, каждому ненулевому вектору $A$ из ${{\mathbb{R}}^{n}}$ отвечает ненулевое решение ${{{v}}_{A}}$ задачи (1), (2) с условием ${{D}_{a}}({{{v}}_{A}},\Omega ) < \infty $, причем

Пусть ${{A}_{1}},\; \ldots ,\;{{A}_{n}}$ – базис в ${{\mathbb{R}}^{n}}$. Докажем, что соответствующие решения ${{{v}}_{{{{A}_{1}}}}},\; \ldots ,\;{{{v}}_{{{{A}_{n}}}}}$ – линейно независимы.

Пусть $\sum\nolimits_{i = 1}^n {{{c}_{i}}} {{{v}}_{{{{A}_{i}}}}} \equiv 0$, где ${{c}_{i}} = {\text{const}}$. Положим ${{W}_{1}} \equiv \sum\nolimits_{i = 1}^n {{{c}_{i}}} {{A}_{i}}x$. Тогда

Покажем, что ${{W}_{1}} \equiv \sum\nolimits_{i = 1}^n {{{c}_{i}}} {{A}_{i}}x \equiv 0$. Пусть $T = \sum\nolimits_{i = 1}^n {{{c}_{i}}} {{A}_{i}} = ({{t}_{1}},\; \ldots ,\;{{t}_{n}})$. Тогда если $T \ne 0$. Следовательно, $T = \sum\nolimits_{i = 1}^n {{{c}_{i}}} {{A}_{i}} = 0$, откуда в силу линейной независимости векторов ${{A}_{1}},\; \ldots ,\;{{A}_{n}}$ получим, что ${{c}_{i}} = 0$, $i = 1,\;2,\; \ldots ,\;n$.

Таким образом, задача (1), (2) с условием ${{D}_{a}}(u,\Omega ) < \infty $ имеет по крайней мере $n$ линейно независимых решений.

Шаг 4. Докажем, что любое решение $u$ задачи (1), (2) с условием ${{D}_{a}}(u,\Omega ) < \infty $ представляется в виде линейной комбинации функций ${{{v}}_{{{{A}_{1}}}}},\; \ldots ,\;{{{v}}_{{{{A}_{n}}}}}$, т.е.

Согласно лемме 2, решение уравнения (1) в $\Omega $ имеет вид где $A$ – постоянный вектор, $B$ – некоторое число.

Так как ${{A}_{1}},\; \ldots ,\;{{A}_{n}}$ – базис в ${{\mathbb{R}}^{n}}$, то существуют константы ${{C}_{1}},\; \ldots ,\;{{C}_{n}}$ такие, что

Положим Очевидно, что функция ${{u}_{1}}$ является решением задачи (1), (2) и ${{D}_{a}}({{u}_{1}},\Omega ) < \infty $.

Докажем, что ${{u}_{1}} \equiv 0$ в $\Omega $. Имеем

где $b = B - \sum\nolimits_{i = 1}^n {{{C}_{i}}} {{e}_{i}}$, т.е. $z = {{u}_{1}} - b$ и Легко заметить, что $\chi (z,\Omega ) < \infty $. Таким образом, $z$ является решением задачи $({{z}_{b}})$: Кроме того, ${{D}_{a}}(z,\Omega ) < \infty $.

Докажем, что если $e \ne 0$, то ${{D}_{a}}({{u}_{e}},\Omega ) = \infty $, где ${{u}_{e}}$ – построенное выше решение задачи $(e)$:

Имеем ${{u}_{e}}(x) = C_{0}^{'}\Gamma (x) + {{R}_{1}}(x)$, причем $C_{0}^{'} \ne 0$, если $e \ne 0$, и Легко проверить, что ${{D}_{a}}({{R}_{1}}(x),\Omega ) < \infty $.

Так как $\Gamma (x) = C{{\left| x \right|}^{{4 - n}}}$, то внутри некоторого конуса $K$ справедливо неравенство

Поэтому если $C_{0}^{'} \ne 0$ и $a \geqslant n - 4$. Отсюда следует, что ${{D}_{a}}({{u}_{e}},\Omega ) = \infty $ при $e \ne 0$.

Теперь докажем единственность решения ${{u}_{e}}$ задачи (e). Пусть существуют два решения ${{{v}}_{1}}$ и ${{{v}}_{2}}$ такие, что

Тогда функция ${{{v}}_{e}} = {{{v}}_{1}} - {{{v}}_{2}}$ удовлетворяет условиям

Покажем, что ${{{v}}_{e}} \equiv 0$, $x \in \Omega $. Для этого в интегральном тождестве (4) для функции ${{{v}}_{e}}$, подставляя функцию $\varphi = {{{v}}_{e}}{{\theta }_{N}}(x)$, где ${{\theta }_{N}}(x) = \theta \left( {\left| x \right|{\text{/}}N} \right)$, $\theta \in {{C}^{\infty }}(\mathbb{R})$, $0 \leqslant \theta \leqslant 1$, $\theta (s) = 0$ при $s \geqslant 2$, $\theta (s) = 1$ при $s \leqslant 1$, получаем

где Применяя неравенство Коши–Буняковского с учетом условия $\chi ({{{v}}_{e}},\Omega ) < \infty $ легко показать, что ${{J}_{1}}({{{v}}_{e}}) \to 0$ и ${{J}_{2}}({{{v}}_{e}}) \to 0$ при $N \to \infty $. Следовательно, переходя к пределу в (14) при $N \to \infty $, получаем С помощью интегрального тождества получаем, что если ${{{v}}_{e}}$ является решением однородной задачи (1), (2), то $\Delta {{{v}}_{e}} = 0$, $x \in \Omega $.

Таким образом,

Из того что имеем ${{{v}}_{e}} \equiv 0$ на множестве ${{\Gamma }_{1}} \cup {{\Gamma }_{2}}$ положительной меры. Отсюда следует [35, Гл. 2.4], что ${{{v}}_{e}} \equiv 0$ в $\Omega $. Тем самым решение ${{u}_{e}}$ задачи (e) единственно. Следовательно, $z = {{u}_{e}}$ при $e = - b$ и ${{D}_{a}}(z,\Omega ) = \infty $ при $b \ne 0$.

С другой стороны, ${{D}_{a}}(z,\Omega ) < \infty $, где $z = {{u}_{1}} - b$, откуда $b = 0$. Таким образом, ${{u}_{1}} = z$ является решением следующей задачи $({{z}_{0}})$:

В силу единственности решения задачи (е) ${{u}_{1}} \equiv 0$ в $\Omega $. Теорема доказана.

Теорема 4. Если $n - 2 \leqslant a < \infty $, $n > 4$, то ${\text{dim Ke}}{{{\text{r}}}_{a}}({{\Delta }^{2}}) = 0.$

Доказательство. Пусть $a = n - 2$, $u \in {\text{Ke}}{{{\text{r}}}_{a}}({{\Delta }^{2}})$ и .

Так как ${\text{Ke}}{{{\text{r}}}_{{n - 2}}}({{\Delta }^{2}}) \subset {\text{Ke}}{{{\text{r}}}_{{n - 4}}}({{\Delta }^{2}})$, то в силу теоремы 4 решение $u$ имеет вид

где $e = s{{C}_{0}}$, а ${{C}_{0}}$ определяется из формулы (12).

Подставляя формулы (12) и (13) в (15), получаем

где ${{P}_{0}}(x) = - Ax + e$, ${{\tilde {С}}_{\alpha }} = {{C}_{\alpha }} - С_{\alpha }^{'}$, $u_{0}^{\beta }(x) = u_{A}^{\beta }(x) - u_{e}^{\beta }(x)$.

Так как $C_{0}^{'} = {{C}_{0}}$, то ${{C}_{0}} - C_{0}^{'} = 0$. Следовательно,

Докажем, что ${{\tilde {С}}_{1}} \ne 0$ в (16). Пусть ${{\tilde {C}}_{1}} = 0$, тогда Умножив уравнение (1) на $u$ и проинтегрировав по ${{\Omega }_{R}}$, учитывая граничные условия (2), получим Из (16) следует, что Поэтому Переходя к пределу при $R \to \infty $ в равенстве (17), получаем Из того что имеем $u \equiv 0$ на множестве ${{\Gamma }_{1}} \cup {{\Gamma }_{2}}$ положительной меры, и, значит, $\Delta u = 0$ в $\Omega $. Отсюда и из граничных условий (2) следует [35, Гл. 2.4], что $u \equiv 0$ в $\Omega $. Полученное противоречие показывает, что ${{\tilde {C}}_{1}} \ne 0$ в (16).

Так как $u \in {\text{Ke}}{{{\text{r}}}_{a}}({{\Delta }^{2}})$, то ${{D}_{a}}(u,\Omega ) < \infty $. Легко проверить, что ${{D}_{a}}({{P}_{0}}(x),\Omega ) = 0$ и ${{D}_{a}}({{R}_{2}}(x),\Omega ) < \infty ,$ где

Тогда в силу (16) и неравенства треугольника получим ${{D}_{a}}(({{\tilde {C}}_{1}} \times \nabla )\Gamma (x),\Omega ) < \infty .$

С другой стороны, $\Gamma (x) = C{{\left| x \right|}^{{4 - n}}}$. Тогда внутри некоторого конуса $K$ имеет место неравенство

Следовательно, Полученное противоречие означает, что $u \equiv 0$. Теорема доказана.

Теорема 5. Бигармоническая задача (1), (2) с условием ${{D}_{a}}(u,\Omega ) < \infty $ имеет $k(r,n)$ линейно независимых решений при $ - 2r + 2 - n \leqslant a < - 2r + 4 - n$, $n > 4$, $r > 1$, где

Доказательство. Для доказательства теоремы нужно определить число линейно независимых решений бигармонического уравнения (1), степени которых не превосходят заданного числа.

Известно, что размерность всех многочленов в ${{\mathbb{R}}^{n}}$ степени не выше $r$ равна $\left( {\begin{array}{*{20}{c}} {r + n} \\ n \end{array}} \right)$ (см. [36]). Тогда размерность всех бигармонических многочленов в ${{\mathbb{R}}^{n}}$ степени не выше $r$ равна

так как бигармоническое уравнение представляет собой равенство нулю некоторого многочлена степени $(r - 4)$ в ${{\mathbb{R}}^{n}}$.

Если через $k(r,n)$ обозначим число линейно независимых полиномиальных решений уравнения (1), степени которых не превосходят $r$, а через $l(r,n)$ – число линейно независимых однородных многочленов степени $r$, являющихся решениями уравнения (1), то

где

Докажем сначала, что задача (1), (2) с условием ${{D}_{a}}(u,\Omega ) < \infty $ при $ - 2r + 2 - n \leqslant a < - 2r + 4 - n$ имеет $k(r,n)$ линейно независимых решений.

Пусть ${{w}_{1}},\; \ldots ,\;{{w}_{k}}$ – базис в пространстве полиномиальных решений уравнения (1), степени которых не превосходят $r$. Так как ${\text{ord}}\,{{w}_{i}} \leqslant r$, то ${{D}_{a}}({{w}_{i}},\Omega ) < \infty $ при $ - 2r + 2 - n \leqslant a < - 2r + 4 - n$.

По каждому ${{w}_{i}}$, $i = 1,\;2,\; \ldots ,\;k$, построим решение ${{{v}}_{i}}$ уравнения (1) такое, что

Такое решение можно построить вариационным методом, минимизируя функционал в классе допустимых функций ${\text{\{ }}{v}:{v} \in {{H}^{2}}(\Omega ),\;{{\left. {v} \right|}_{{{{\Gamma }_{1}}}}} = w,\;\mathop {\left. {\tfrac{{\partial {v}}}{{\partial \nu }}} \right|}\nolimits_{{{\Gamma }_{1}}} = \mathop {\left. {\tfrac{{\partial w}}{{\partial \nu }}} \right|}\nolimits_{{{\Gamma }_{1}}} ,\;{v}$ имеет компактный носитель в $\bar {\Omega }{\text{\} }}$.

Рассмотрим разность ${{q}_{i}} = {{w}_{i}} - {{{v}}_{i}}$. Имеем

Докажем, что ${{q}_{i}}$, $i = 1,\;2,\; \ldots ,\;k$, линейно независимы. Действительно, если

то т.е. следовательно, ${{\left| W \right|}^{2}} = {{\left| V \right|}^{2}}$, ${{\left| {\nabla W} \right|}^{2}} = {{\left| {\nabla V} \right|}^{2}}$, ${{\left| {\nabla \nabla W} \right|}^{2}} = {{\left| {\nabla \nabla V} \right|}^{2}}$, и Согласно лемме 2, решение $V$ уравнения (1) в $\Omega $ имеет вид где $P(x)$ – многочлен,

Легко проверить, что $D(R(x),\Omega ) < \infty ,$

В силу неравенства треугольника, $D(P(x),\Omega ) < \infty $, Докажем, что $P(x) = 0$. Пусть $\operatorname{ord} P(x) = {{r}_{1}}$. Тогда внутри некоторого конуса $K$ выполняется неравенство Следовательно, Так как $n > 4$, то полученный интеграл сходится только при ${{r}_{1}} < 0$.

Таким образом, $P(x) \equiv 0$ и $V(x) = R(x)$, где $R(x) \to 0$ при $\left| x \right| \to \infty $. Отсюда следует, что

Так как $W$ – многочлен, то Отсюда ${{c}_{i}} = 0$, $i = 1,\;2,\; \ldots ,\;k$, в силу того, что ${{w}_{i}}$, $i = 1,\;2,\; \ldots ,\;k$, – базис в пространстве полиномиальных решений.

Таким образом, бигармоническая задача (1), (2) с условием ${{D}_{a}}(u,\Omega ) < \infty $ имеет по крайней мере $k(r,n)$ линейно независимых решений.

Докажем теперь, что всякое решение $u$ задачи (1), (2) с условием ${{D}_{a}}(u,\Omega ) < \infty $ можно представить в виде линейной комбинации построенных решений ${{q}_{i}}$, $i = 1,\;2,\; \ldots ,\;k$, ${{q}_{i}} = {{w}_{i}} - {{{v}}_{i}}$.

Согласно лемме 2, решение уравнения (1) в $\Omega $ можно представить в виде

где $P(x)$ – многочлен, ${\text{ord}}P(x) < {{m}_{0}} = [2 - n{\text{/}}2 - a{\text{/}}2]$, Так как $ - 2r + 2 - n \leqslant a < - 2r + 4 - n$, то $1 - n{\text{/}}2 - a{\text{/}}2 \leqslant r < 2 - n{\text{/}}2 - a{\text{/}}2$, следовательно, $r = [2 - n{\text{/}}2 - a{\text{/}}2] = {{m}_{0}}$ $r = [2 - n{\text{/}}2 - a{\text{/}}2] = {{m}_{0}}$. Таким образом, ${\text{ord}}P(x) \leqslant r$.

Покажем, что $P(x)$ – решение уравнения (1). Имеем

причем ${{\Delta }^{2}}R(x) \to 0$ при $\left| x \right| \to \infty $. Так как ${{\Delta }^{2}}P(x)$ – многочлен и то ${{\Delta }^{2}}P(x) \equiv 0$, т.е. $P(x)$ – полиномиальное решение бигармонического уравнения (1). Следовательно, оно представляется линейной комбинацией функций ${{w}_{i}}$, $i = 1,\;2,\; \ldots ,\;k$: Докажем, что $u = \sum\nolimits_{i = 1}^k {{{c}_{i}}} {{q}_{i}}$. Положим Тогда имеем По построению решения ${{{v}}_{i}}$ имеем $D({{{v}}_{i}},\Omega ) < \infty $, Кроме того, легко проверить, что $D(R(x),\Omega ) < \infty ,$Отсюда следует, что $D({{u}_{2}},\Omega ) < \infty $, Таким образом, ${{u}_{2}}$ является решением следующей задачи $({{u}_{2}})$: Покажем, что ${{u}_{2}} \equiv 0$, $x \in \Omega $. Для любой функции $\varphi \in H_{{{\text{loc}}}}^{2}(\Omega )$, справедливо интегральное тождество (4) Подставим $\varphi = {{u}_{2}}{{\theta }_{N}}(x)$, где ${{\theta }_{N}}(x) = \theta \left( {\left| x \right|{\text{/}}N} \right)$, $\theta \in {{C}^{\infty }}(\mathbb{R})$, $0 \leqslant \theta \leqslant 1$, $\theta (s) = 0$ при $s \geqslant 2$, $\theta (s) = 1$ при $s \leqslant 1$, получим где Применяя неравенство Коши–Буняковского и учитывая условия задачи (${{u}_{2}}$), легко показать, что ${{J}_{1}}({{u}_{2}}) \to 0$ и ${{J}_{2}}({{u}_{2}}) \to 0$ при $N \to \infty $. Следовательно, переходя к пределу в (18) при $N \to \infty $, получаем Из того что имеем ${{u}_{2}} \equiv 0$ на множестве ${{\Gamma }_{1}} \cup {{\Gamma }_{2}}$ положительной меры, и, значит, $\Delta {{u}_{2}} = 0$ в $\Omega $. Таким образом, Отсюда следует [35, Гл. 2.4], что ${{u}_{2}} \equiv 0$ в $\Omega $. Теорема доказана.