Журнал вычислительной математики и математической физики, 2021, T. 61, № 9, стр. 1492-1507

1. ВВЕДЕНИЕ

В работах [1], [2] М.М. Лаврентьев предложил подход к решению нелинейных коэффициентных обратных задач для широкого класса уравнений в частных производных, позволяющий редуцировать такие задачи к линейным интегральным уравнениям. Подход использует преобразование Лапласа исследуемого уравнения по времени. Поясним схему действий применительно к обратной задаче для волнового уравнения в ${{\mathbb{R}}^{3}}$. Рассмотрим обратную задачу акустического зондирования ограниченной неоднородности набором точечных источников, расположенных вне этой неоднородности (см. [3]). Акустическое поле $u(x,t) = u(x,t;q)$, возбуждаемое источником, находящимся в точке $q$, определяется решением задачи Коши

Здесь $c(x) > 0$ – скорость звука в точке $x \in {{\mathbb{R}}^{3}}$ и предполагается, что $c(x) \equiv {{c}_{0}}$ вне априори заданной ограниченной замкнутой области $D \subset {{\mathbb{R}}^{3}}$ с известной постоянной ${{c}_{0}}$, а значения $c(x)$ при $x \in D$ неизвестны. Для определенности функцию $c = c(x)$ считаем непрерывной на ${{\mathbb{R}}^{3}}$. Непрерывная функция $g$ удовлетворяет условиям Для отыскания $c(x)$ при $x \in D$ рассеянное поле $u = u(x,t;q)$ измеряется при $t > 0$ в точках $x \in X$, где $X \subset {{\mathbb{R}}^{3}}$ – множество детекторов, $X \cap D = \not {0}$. Будем считать, что в эксперименте зондирования используется множество источников $q \in Y$, $Y \cap D = \not {0}$. Множества $X$ и $Y$ далее считаем замкнутыми областями, расположенными на многообразиях в ${{\mathbb{R}}^{3}}$, вид которых будет уточнен далее. Для суммируемой функции $f = f(t)$, $t \geqslant 0$, определим преобразование Лапласа $\tilde {f}(p) = \int_0^\infty {{{e}^{{ - pt}}}f(t)dt} $. Будем считать, что все функции $u(x,t;q)$, $q \in Y$, и их производные по $t$ до второго порядка включительно достаточно быстро убывают при $t \to + \infty $, когда $x \in X$, так что их преобразования Лапласа существуют. Кроме того, предполагаем, что $u(x,t;q) \to 0$ при ${\text{|}}x{\kern 1pt} {\text{|}} \to \infty $ равномерно по $q \in Y$ и $t > 0$. Условия на функцию $c(x)$, обеспечивающие эти требования, обсуждаются в [4], [5]. Обозначим и перепишем уравнение (1.1) в виде Функция $c$, очевидно, однозначно определяется по $\xi $, поэтому далее ограничимся отысканием $\xi (x)$ при $x \in D$. Применяя к обеим частям последнего равенства преобразование Лапласа по времени, получаем В силу сделанных предположений, $\tilde {u}(x,p;q) \to 0$ при ${\text{|}}x{\kern 1pt} {\text{|}} \to \infty $ равномерно по $q \in Y$, $p \geqslant 0$. Нам потребуется фундаментальное решение (функция Грина) уравнения с условием на бесконечности $u(x) \to 0$, ${\text{|}}x{\kern 1pt} {\text{|}} \to \infty $. Эта функция имеет вид Из (1.4) с учетом (1.5) следует равенство Обозначим для краткости Двукратное дифференцирование равенства (1.6) по $p$ с учетом (1.7) дает Полагая в (1.6) и (1.8) $p = 0$, получаем Отсюда и из (1.5) следует, что для определения функции $\xi (x)$ имеем линейное интегральное уравнение где Заметим, что $\tilde {g}(0) \ne 0$ в силу первого условия в (1.2), функция $H_{{pp}}^{0}(x,q;0)$ определяется из (1.7). Таким образом, входными данными для определения $\xi $ служит величина рассеянного поля $u(x,t;q)$, усредненная по времени с весом ${{t}^{2}}$, для различных $(x,q) \in X \times Y$.

К уравнению (1.9), называемому в работе уравнением М.М. Лаврентьева, сводятся также обратные задачи зондирования неоднородности точечными гармоническими по времени источниками с частотой $\omega \in (0,{{\omega }_{0}}]$ (см. подробнее в [6, с. 223], [7, § 3.1], [8]). К аналогичному уравнению с заменой (1.5) функцией Грина в ограниченной области $G$ сводится обратная задача зондирования неоднородного включения $D \subset G$ (см. [9]).

Начиная с [2], значительное число работ было посвящено условиям, при которых уравнение (1.9) для любой правой части имеет не более одного решения (см. [3], [7, § 3.1], [8], [10]–[12]). Это свойство имеет место, например, если $X$, $Y$ – замкнутые области на плоскости, не пересекающей $D$, либо ограниченные поверхности, содержащие множество $D$ внутри. В качестве $X$, $Y$ можно выбрать также замкнутые области на аналитических поверхностях, например, сферах, содержащих $D$ внутри. В этих случаях размерность пространственного носителя данных $X \times Y$ в (1.9) равна четырем, в то время как искомая функция $\xi $ зависит от трех переменных. Тем самым обратная задача оказывается переопределенной. Отметим в этой связи следующий недавний результат.

Теорема 1 (см. [11], [12]). Пусть $\Pi $, $\mathcal{L}$ – плоскость и прямая в ${{\mathbb{R}}^{3}}$, не пересекающие $\bar {D}$, одно из $X$ и $Y$ – замкнутая область в $\Pi $, другое – замкнутый отрезок в $\mathcal{L}$. Тогда для любой правой части ${{f}_{0}}$ уравнение (1.9) имеет не более одного решения.

В условиях теоремы 1 размерность носителя данных $X \times Y$ оказывается равной трем, как и размерность носителя $D$ искомой функции. Несмотря на достаточно продолжительную предысторию теоретического исследования уравнения М.М. Лаврентьева, вопросы численного решения этого уравнения ранее практически не изучались. Альтернативный способ редукции описанной обратной задачи к линейному интегральному уравнению развивается в [13].

Дальнейшее содержание работы следующее. Во-первых, с целью более адекватного моделирования реальных процессов зондирования в (1.1) вместо обобщенной функции $\delta (x - q)$, сосредоточенной в точке $x = q$, мы рассматриваем распределенный источник, описываемый непрерывной функцией $\varphi (\left| {x - q} \right|)$, где $\varphi (r) = 0$ при $r \geqslant \varepsilon > 0$. Таким образом, неоднородность зондируется сигналами одной и той же пространственной формы, сосредоточенными в $\varepsilon $-окрестностях точек $q \in Y$. Переход к описанию зондирующих сигналов обычными, а не обобщенными функциями, в определенной степени упрощает теоретический анализ соответствующих волновых уравнений, к которым теперь применим классический инструментарий исследования гиперболических уравнений (см., например, [14], [15]). Наряду с этим рассматриваются уравнения более общего вида, в том числе уравнение третьего порядка, с двумя подлежащими определению коэффициентами. Устанавливается, что при наличии данных об усреднении рассеянного поля с весами ${{t}^{m}}$, $m = 2,3$, определение указанных коэффициентов сводится к уравнениям вида (1.9). Эти результаты излагаются ниже в разд. 2 и 3. В то же время использование в гиперболическом уравнении в качестве входных данных усреднений с весами ${{t}^{m}}$, $m = 3,4$, приводит к новым типам интегральных уравнений. Их мы называем уравнениями типа уравнения М.М. Лаврентьева. При подходящем выборе многообразий источников и детекторов $X$, $Y$ мы устанавливаем, что эти уравнения также имеют единственное решение. В начале разд. 4 исследуется случай $m = 3$. Получаемое интегральное уравнение оказывается линейным, но его оператор отличается от оператора в (1.9). Завершающая часть разд. 4 посвящена случаю $m = 4$. В этой ситуации соответствующее уравнение оказывается уже нелинейным, однако доказывается, что оно имеет единственное решение. Раздел 5 посвящен описанию и результатам численного эксперимента по решению уравнения вида (1.9).

2. ГИПЕРБОЛИЧЕСКОЕ УРАВНЕНИЕ ВТОРОГО ПОРЯДКА, ОПРЕДЕЛЕНИЕ ДВУХ КОЭФФИЦИЕНТОВ

Рассмотрим задачу Коши для гиперболического уравнения

Относительно функции $u(x,t) = u(x,t;q)$ считаем выполненными сделанные ранее предположения. В рассматриваемой обратной задаче по измеренным усредненным по времени значениям $u(x,t;q)$, $(x,q) \in X \times Y$, подлежат определению кусочно-непрерывные коэффициенты $b(x)$, $c(x)$, $x \in D$. Считаем, что $c(x) \equiv {{c}_{0}}$ и $b(x) = 0$ при $x \in {{\mathbb{R}}^{3}}{{\backslash }}D$, функция $g(t)$ удовлетворяет условию (1.2). Пусть $\varphi = \varphi (r)$, $r \geqslant 0$ – непрерывная функция и выполняются условия Обозначим ${{O}_{\varepsilon }}(q) = \{ x \in {{\mathbb{R}}^{3}}:\left| {x - q} \right| \leqslant \varepsilon \} $. Будем предполагать, что

Как и выше, будем интерпретировать точки $q \in Y$ как координаты зондирующих источников, описываемых слагаемым $\varphi (\left| {x - q} \right|)g(t)$ в (2.1). Указанные источники сосредоточены в $\varepsilon $-окрестности точек $q$. Согласно (2.3), эти окрестности не пересекаются с носителем неоднородности $D$. Усреднение по $t$ волнового поля $u(x,t;q)$ происходит в точках $x \in X$, где $X$ – множество детекторов. Выполняя в (2.1) преобразование Лапласа по $t$ и пользуясь обозначением (1.3), получаем подобное (1.6) равенство

где Дифференцируя обе части (2.4) по $p$, находим

Далее нам потребуется следующая лемма.

Лемма 1. Для $x \in {{\mathbb{R}}^{3}}{{\backslash }}{{O}_{\varepsilon }}(q)$ справедливо равенство

Доказательство сводится к непосредственному интегрированию. Имеем

Проводя при необходимости в последнем интеграле ортогональное преобразование $y{\kern 1pt} ' = Uz{\kern 1pt} '$, без ограничения общности можем считать, что направление вектора $x - q$ совпадает с направлением оси $y_{3}^{'}$ в координатах $(y_{1}^{'},y_{2}^{'},y_{3}^{'})$, т.е. $x - q = (0,0,{\text{|}}x - q{\kern 1pt} {\text{|}})$. Переходя к сферическим координатам и выполняя интегрирование по $\chi $, получаем По условию леммы $\left| {x - q} \right| > \varepsilon \geqslant r$, поэтому выражение в квадратных скобках есть $(r + \left| {x - q} \right|) - (\left| {x - q} \right| - r) = 2r$. Требуемое утверждение непосредственно следует отсюда.

Полагая $p = 0$ в (2.4) и используя (2.5) и лемму 1, получаем

Заметим, что условие леммы выполняется в силу (2.3). Полагая теперь $p = 0$ в (2.6) и пользуясь (2.7), находим Таким образом, для определения коэффициента $b(x)$ имеем аналогичное (1.9) интегральное уравнение

Перейдем к определению коэффициента $c(x)$ или, эквивалентно, функции $\xi (x)$. Дифференцируя (2.6) по $p$ и полагая в полученном равенстве $p = 0$, находим

Поскольку функция $b(x)$ уже определена, функция ${{\tilde {u}}_{p}}(x,0;q)$ также известна в силу (2.8). В свою очередь, функция $\tilde {u}(x,0;q)$ определена в (2.7). Таким образом, из (2.10) получаем уравнение для определения функции $\xi $: где Видим, что для определения двух коэффициентов в уравнении (2.1) достаточно иметь усредненные значения рассеянного поля При этом обе искомые функции $b(x)$, $c(x)$ определяются из интегральных уравнений (2.9), (2.11) с одним и тем же ядром. Однозначность восстановления указанных функций следует из теоремы 1.

Следующая теорема подытоживает проведенные рассуждения.

Теорема 2. Пусть выполняются условия (1.2), (2.2), (2.3), множества $X$, $Y$ выбраны как в теореме 1. Тогда данные (2.12) позволяют однозначно определить функции $b(x)$, $c(x)$ в уравнении (2.1). Именно, они находятся из уравнений (2.9) и (2.11), имеющих единственные решения.

В следующем разделе обратимся к задаче реконструкции двух коэффициентов в уравнении третьего порядка.

3. УРАВНЕНИЕ ТРЕТЬЕГО ПОРЯДКА, ОПРЕДЕЛЕНИЕ ДВУХ КОЭФФИЦИЕНТОВ

Рассмотрим уравнение

Уравнение (3.1) описывает акустические процессы в вязкой теплопроводной среде, параметр $b(x)$ определяется коэффициентами вязкости среды (см. [16]). Как и выше, требуется реконструировать кусочно-непрерывные коэффициенты $c(x)$ и $b(x)$, $x \in D$, причем $c(x) \equiv {{c}_{0}}$, $b(x) = 0$ при $x \in {{\mathbb{R}}^{3}}{{\backslash }}D$. Считаем выполненными условия (1.2), (2.2), (2.3). При прежних предположениях относительно функции $u(x,t) = u(x,t;q)$ преобразование Лапласа уравнения (3.1) дает Поскольку $b(x) = 0$ вне $D$, с учетом (2.3) получаем Обозначим тогда из (3.2) вытекает Следовательно, Поэтому для $\tilde {u}(x,0;q)$ выполняется равенство (2.7). Дифференцируя тождество (3.4) дважды по $p$ и полагая $p = 0$, с учетом равенства $\eta (x,0) = \xi (x)$ (см. (1.3), (3.3)), получаем Из (1.5), (2.7) следует, что для определения функции $\xi (x)$ и вместе с ней $c(x)$ имеем уравнение

Покажем, что и коэффициент $b(x)$ определяется из интегрального уравнения с тем же ядром, что и в (3.5). С этой целью продифференцируем равенство (3.4) трижды по $p$ и в итоговом равенстве положим $p = 0$. Имеем

Из (3.4) следует ${{\tilde {u}}_{p}}(x,p;q) = {{H}_{p}}(x,q;p) + O(p)$ при $p \to 0$. Поэтому ${{\tilde {u}}_{p}}(x,0;q) = {{H}_{p}}(x,q;0)$ есть известная функция. Кроме того, согласно (3.3), По построению функция $c(x)$ уже известна. Поэтому (3.6) приводит к интегральному уравнению для функции $v(x) = {{c}^{{ - 2}}}(x)b(x)$: где Тем самым доказана следующая теорема.

Теорема 3. Пусть выполняются условия (1.2), (2.2), (2.3), множества $X$, $Y$ выбраны как в теореме . Тогда данные

позволяют однозначно определить функции $b(x)$, $c(x)$ в уравнении (3.1). Именно, они находятся из уравнений (3.5) и (3.7), при этом $b(x) = {{c}^{2}}(x){v}(x)$. Уравнения (3.5), (3.7) имеют единственные решения.

В рассмотренных выше примерах реконструкция неизвестных коэффициентов уравнений сводилась к интегральному уравнению М.М. Лаврентьева с различными правыми частями. Наличие результатов типа теоремы 1 избавляет от необходимости отдельного анализа единственности решения каждого возникающего уравнения. Ниже покажем, что описанная ранее схема редукции коэффициентных обратных задач к интегральным уравнениям при использовании альтернативных схем усреднения сигнала может приводить к интегральным уравнениям новых типов. Вопросы единственности решений таких уравнений нуждаются в отдельном исследовании.

4. ОПРЕДЕЛЕНИЕ СКОРОСТИ ЗВУКА В ВОЛНОВОМ УРАВНЕНИИ ПРИ РАЗЛИЧНЫХ СХЕМАХ УСРЕДНЕНИЯ РАССЕЯННОГО ПОЛЯ

Обратимся к задаче реконструкции скорости распространения сигнала $c(x)$ в уравнении

Здесь в отличие от (1.1) при каждом $q \in Y$ зондирующий источник распределен в шаре ${{O}_{\varepsilon }}(q)$. Считаем выполненными условия разд. 2. Дополнительно предположим, что Без ограничения общности можем считать функцию $\varphi $ в (4.1) нормированной условием

В данном случае вместо (2.4) имеем уравнение

с функцией $H$, определенной в (2.5). Выясним возможность однозначной реконструкции коэффициента $c(x)$ по усредненным данным $\int_0^\infty {{{t}^{3}}u(x,t;q)dt} $ для $(x,q) \in X \times Y$.

Дифференцируя (4.4) по $p$ трижды и полагая $p = 0$, для $(x,q) \in X \times Y$ получаем равенство

Используя (4.4) и (2.7), находим Кроме того, из (4.4) и (2.5) следует, что при $p \to 0$ выполняется Поэтому, ввиду (1.5), (4.3) и леммы 1, Объединяя равенства (4.5)–(4.7), для $(x,q) \in X \times Y$ получаем Поэтому для нахождения функции $\xi (x)$ имеем интегральное уравнение Заметим, что, согласно (4.2), в этих формулах $\tilde {g}{\kern 1pt} '(0) \ne 0$.

Следующая теорема устанавливает единственность решения уравнения (4.8), которое мы называем уравнением типа М.М. Лаврентьева.

Теорема 4. Пусть выполняются условия (1.2), (2.2), (2.3), (4.2), (4.3), множества $X$, $Y$ выбраны как в теореме 1. Тогда данные

позволяют однозначно определить функцию $c(x)$. Уравнение (4.8) с любой правой частью имеет в классе кусочно-непрерывных функций не более одного решения.

Доказательство. Пусть для определенности $X$ и $Y$ – замкнутая область плоскости $\Pi $ и отрезок прямой $\mathcal{L}$ соответственно, $\Pi \cap D = \mathcal{L} \cap D = \not {0}$. Достаточно убедиться, что соответствующее однородное уравнение

имеет в указанном классе лишь нулевое решение. Заметим, что функция $\psi (x,q)$, определенная интегралом в левой части (4.9), вещественно аналитична по $x \in \Pi $ и $q \in \mathcal{L}$. Поэтому равенство (4.9) продолжается по аналитичности на все $(x,q) \in \Pi \times Y$. Зафиксируем произвольно точку $x \in \Pi $ и перейдем в (4.9) к пределу при $q \in \mathcal{L}$, удаляющейся в бесконечность. Аналогично зафиксируем $q \in Y$ и перейдем к пределу при $x \in \Pi $, удаляющейся в бесконечность. В результате получаем для всех $x \in X$ и $q \in Y$ соответственно. Поэтому из (4.9) следует Ссылка на теорему 1 дает $\zeta \equiv 0$, что и завершает доказательство.

Замечание 1. Аналогично устанавливается инъективность для более широкого класса вполне непрерывных интегральных операторов

где $a(x{\kern 1pt} ',x)$, $b(x{\kern 1pt} ',q)$ – фиксированные ограниченные суммируемые функции. Оператор ${{L}_{{a,b}}}$ доставляет пример нелокального (при больших ${{\left\| a \right\|}_{{{{L}_{\infty }}}}}$, ${{\left\| b \right\|}_{{{{L}_{\infty }}}}}$) возмущения вполне непрерывного оператора М.М. Лаврентьева ${{L}_{{0,0}}}$ с сохранением свойства инъективности последнего.

Всюду выше в качестве входных данных для определения искомых коэффициентов обратных задач использовались результаты усреднения по времени рассеянного поля с весами ${{t}^{m}}$, $m = 2,3$. При этом нелинейные обратные задачи сводились к линейному интегральному уравнению I рода (2.9), (2.11), (3.5), (3.7), (4.8). Сейчас покажем, что переход по той же схеме к усреднению с весом ${{t}^{4}}$ существенно меняет картину и приводит уже к нелинейному интегральному уравнению. Тем не менее при подходящем выборе областей локализации источников $X$ и детекторов $Y$ оператор этого уравнения все же остается инъективным. Этим обеспечивается единственность решения соответствующей обратной задачи волнового зондирования. Далее считаем выполненными условия (1.2), (2.2), (2.3), (4.3).

Дифференцируя равенство (4.4) по $p$ четырежды и полагая $p = 0$, для $(x,q) \in X \times Y$ получаем

Кроме того, из (4.4) следует, что при $p \to 0$ выполняется равенство где Из (4.6) и (4.11) следует Используя (4.6), (4.7), (4.12), из (4.10) для функции $\xi (x)$ получаем нелинейное интегральное уравнение В (4.13) функция определяется усредненными значениями рассеянного поля c весом ${{t}^{4}}$.

Покажем, что при определенных требованиях к выбору $X$, $Y$, сохраняющих равенство ${\text{dim}}(X \times Y) = 3$, уравнение (4.13) имеет единственное решение. Указанное равенство имеет место, если одно из многообразий $X$, $Y$ – двумерное, а второе – одномерное. Выше было достаточно одно из них выбрать в виде замкнутой области на плоскости, а второе – в виде отрезка прямой. Для обеспечения единственности решения уравнения (4.13) конструкцию двумерного многообразия необходимо несколько усложнить. Пусть $\Sigma $ – объединение двух различных сфер с произвольными центрами и радиусами в ${{\mathbb{R}}^{3}}$, расположенных так, что шары, ограниченные этими сферами, не имеют общих точек с $D$. Нам потребуется следующее известное утверждение о том, что $\Sigma $ является множеством единственности для бигармонических функций в области, содержащей $\Sigma $.

Лемма 2 (см. [17]). Пусть функция $w = w(x)$ удовлетворяет условиям

Тогда $w$ тождественно равна нулю в ${{\mathbb{R}}^{3}}{{\backslash }}D$.

Пусть теперь одно из $X$, $Y$ совпадает с $\Sigma $, а второе, как в теореме 1, есть отрезок прямой $\mathcal{L}$. Примем для определенности $X = \Sigma $. Предположим, что уравнение (4.13) имеет два кусочно-непрерывных решения ${{\xi }_{1}}$, ${{\xi }_{2}}$ и обозначим $\zeta = {{\xi }_{1}} - {{\xi }_{2}}$. Тогда из (4.13) следует

Заметим, что при $x \ne y$ выполняются равенства где через ${{\Delta }_{x}}$ обозначен оператор Лапласа по переменной $x \in {{\mathbb{R}}^{3}}$. Поэтому функция $\psi (x,q)$, стоящая в левой части (4.14), является бигармонической по $x$ вне $D$. Используя лемму 2, заключаем, что равенство (4.14) распространяется на все точки $x \in {{\mathbb{R}}^{3}}{{\backslash }}D$. Из (1.2), (2.2) следует $\tilde {g}(0)A(\varphi ,\varepsilon ) \ne 0$. Применяя оператор ${{\Delta }_{x}}$ к обеим частям (4.14) для $x \in {{\mathbb{R}}^{3}}{{\backslash }}D$ и используя тождества (4.15), получаем Ссылка на теорему 1 дает теперь следующий результат.

Теорема 5. Пусть выполняются условия (1.2), (2.2), (2.3), (4.3) и одно из множеств $X$, $Y$ совпадает с $\Sigma $, а второе есть отрезок прямой $\mathcal{L}$. Тогда данные

позволяют однозначно определить функцию $c(x)$ в уравнении (4.1). Уравнение (4.13) с любой правой частью имеет не более одного решения.

Замечание 2. Оператор левой части (4.13) описывает широкий класс нелокальных нелинейных возмущений оператора М.М. Лаврентьева ${{L}_{{0,0}}}$, сохраняющих инъективность ${{L}_{{0,0}}}$.

В следующем разделе приведем некоторые результаты численных экспериментов по решению уравнения М.М. Лаврентьева.

5. ЧИСЛЕННЫЙ ЭКСПЕРИМЕНТ

Выше показано, что решение различных коэффициентных обратных задач для уравнений волнового типа сводится к решению интегральных уравнений вида (1.9) с одним и тем же оператором в левой части и различными правыми частями. Эти уравнения имеют вид

с соответствующей функцией $f(x,q)$. В прикладных задачах зачастую искомая функция $\xi $ описывает одну или несколько локализованных неоднородностей типа всплесков на плавно меняющемся фоне, которую удобно моделировать постоянной, равной нулю. В дальнейшем для определенности считаем, что $X$ – прямоугольник, $Y$ – отрезок, параллельные одной и той же координатной плоскости, зондируемая область $D = {{[0,1]}^{3}}$. Согласно теореме 1, уравнение (5.1) с фиксированной правой частью имеет не более одного решения. Целью численного эксперимента является изучение возможности определения местоположения локализованных возмущений в $D$ с использованием при дискретизации сеток умеренных размеров. На $D$, $X$, $Y$ вводятся равномерные сетки $\left\{ {{{{\bar {x}}}_{{ijk}}}} \right\}$, $\left\{ {{{{\bar {x}}}_{{pq}}}} \right\}$, $\left\{ {{{{\bar {y}}}_{r}}} \right\}$, $0 \leqslant i,j,k$; $p,q,r \leqslant N$. Дискретизация интегрального уравнения (5.1) с использованием схемы прямоугольников приводит к линейной системе Здесь ${{\xi }_{{ijk}}}$ есть искомая аппроксимация для $\xi ({{\bar {x}}_{{ijk}}})$, $0 \leqslant i,j,$ $k \leqslant N - 1$, Регуляризация задачи (5.2) по схеме Тихонова приводит к линейной системе Здесь $A = ({{a}_{{pqr,ijk}}}) \in {{\mathbb{R}}^{{{{N}^{3}} \times {{N}^{3}}}}}$, $f = ({{f}_{{pqr}}}) \in {{\mathbb{R}}^{{{{N}^{3}}}}}$, ${{\xi }^{0}}$ – начальная оценка искомого вектора $({{\xi }_{{ijk}}}) \in {{\mathbb{R}}^{{{{N}^{3}}}}}$, $\alpha > 0$ – параметр регуляризации. В расчетах полагаем $N = 32$, $\alpha = {{10}^{{ - 11}}}$, вектор ${{\xi }^{0}}$ выбираем нулевым.

Тест 1. В этом тесте решаются два примера по реконструкции неоднородностей, находящихся на разных высотах в $D$. В примере 1 модельное решение выбрано в виде

Функция $\xi {\kern 1pt} *$ описывает две неоднородности одинаковой геометрии, расположенные на высотах ${{x}^{{(3)}}} = 0.4$, 0.5 с центрами в точках ${{Z}_{1}} = (0.5,0.7,0.4)$ и ${{Z}_{2}} = (0.5,0.4,0.5)$. Множества детекторов и источников имеют вид $X = \{ ({{x}^{{(1)}}},{{x}^{{(2)}}}, - 0.0001):0 \leqslant {{x}^{{(1)}}},{{x}^{{(2)}}} \leqslant 1\} $ и $Y = \{ (0.5,{{x}^{{(2)}}},1.0001):0 \leqslant {{x}^{{(2)}}} \leqslant 1\} $. После дискретизации указанные множества принимают соответственно вид X_N = ${{X}_{N}} = \{ (rh,sh, - 0.0001):0 \leqslant r,\;s \leqslant N\} $, ${{Y}_{N}} = \left\{ {(0.5,ph,1.0001):0 \leqslant p \leqslant N} \right\}$. В примере 2 тестовое решение описывает две неоднородности разных размеров, локализованные в окрестности точек ${{Z}_{1}}$, ${{Z}_{2}}$. В этом примере множество источников $Y$ выбрано как в примере 1, а множество детекторов взято более протяженным: $X = \{ ({{x}^{{(1)}}},{{x}^{{(2)}}}, - 0.0001): - 0.5 \leqslant {{x}^{{(1)}}} \leqslant 1.5,0 \leqslant {{x}^{{(2)}}} \leqslant 1\} $. После дискретизации получаем ${{X}_{N}} = \left\{ {( - 0.5 + r{{h}_{x}},sh, - 0.0001):0 \leqslant r,\;s \leqslant N} \right\}$, где ${{h}_{x}} = 0.0625$.

Тест 2. В примерах этого теста неоднородности располагаются на одной высоте. В примере 3 неоднородности сосредоточены в окрестности точек $(0.5,0.4,0.5)$ и $(0.5,0.7,0.5)$ и имеют различный размер,

Множества источников и детекторов здесь выбираются как в Примере 2. В Примере 4 неоднородности одинаковы по размеру и сосредоточены в окрестности точек $(0.5,0.4,0.5)$ и $(0.5,0.8,0.5)$, Вид и расположение множеств $X$ и $Y$ относительно $D$ в этом примере изменены, $X = \{ ({{x}^{{(1)}}},{{x}^{{(2)}}}, - 0.0001): - 1 \leqslant {{x}^{{(1)}}} \leqslant 10,\;0 \leqslant {{x}^{{(2)}}} \leqslant 1\} $, $Y = \{ (0.1,{{x}^{{(2)}}},1.1):0 \leqslant {{x}^{{(2)}}} \leqslant 1\} $. При этом ${{X}_{N}} = \{ ( - 1 + r{{h}_{x}},sh, - 0.0001):0 \leqslant r,\;s \leqslant N\} $, ${{h}_{x}} = 0.3438$; ${{Y}_{N}} = \{ (0.1,ph,1.1):0 \leqslant p \leqslant N\} $.

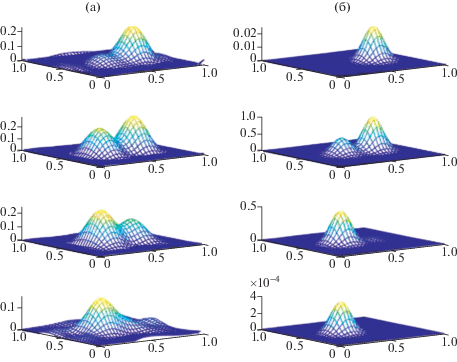
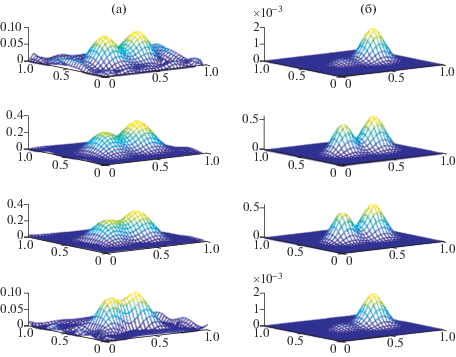
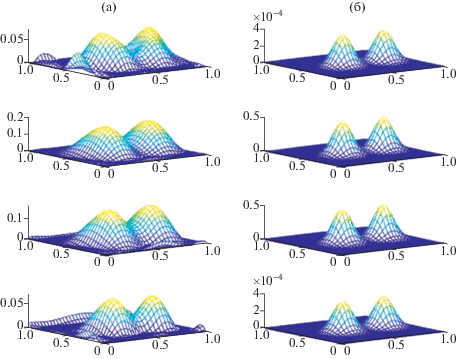
Результаты численной реконструкции модельных неоднородностей $\xi {\kern 1pt} *$ показаны на фиг. 1–4. Результат каждого примера представлен двумя колонками графиков. В правой колонке приведены изображения точного решения $\xi {\kern 1pt} *$, в левой колонке – соответствующие изображения приближенных решений ${{\xi }_{\alpha }}$. На фигурах сверху вниз представлены графики точных и приближенных функций $\xi ( \cdot , \cdot ,{{x}^{{(3)}}})$ при ${{x}^{{(3)}}} = 0.1875$, 0.4062, 0.5937, 0.8125 соответственно. Видно, что в большинстве случаев приближенное решение достаточно точно восстанавливает место расположения искомых неоднородностей и их относительные амплитуды. Заметное отклонение в относительных размерах всплесков в точном и приближенном решении наблюдается на фиг. 2, 3 в плоскостях ${{x}^{{(3)}}} = 0.1875$, 0.8125 (см. крайние верхние и нижние пары графиков). Это расхождение можно объяснить расположением источников и детекторов относительно реконструируемых неоднородностей в соответствующих примерах. На фиг. 1–4 также показано, что абсолютные значения амплитуд неоднородностей аппроксимируются более грубо по сравнению с местом локализации неоднородностей.

Альтернативный подход к численному решению интегрального уравнения (5.1) развивается в [18].