Журнал вычислительной математики и математической физики, 2021, T. 61, № 9, стр. 1465-1491
Об использовании теории тонких оболочек при анализе линейной устойчивости течения жидкости в трубе с податливой стенкой
К. В. Демьянко *
Институт вычислительной математики им. Г.И. Марчука РАН
119333 Москва, ул. Губкина, 8, Россия
* E-mail: k.demyanko@inm.ras.ru
Поступила в редакцию 29.10.2020
После доработки 25.01.2021
Принята к публикации 09.04.2021
Аннотация
Численно исследована линейная устойчивость течения Пуазейля в трубе круглого сечения с податливой стенкой с использованием двух различных моделей стенки на основе теории тонких оболочек. В рамках первой модели малые колебания стенки описываются уравнениями Лява общего вида, а в рамках второй – упрощенными уравнениями Лява, полученными с помощью известного приближения Доннела–Муштари–Власова. В частности, показано, что использование упрощенных уравнений Лява вместо общих качественно не меняет зависимость характеристик устойчивости основного течения от жесткости и демпфирования стенки, однако при некоторых значениях параметров задачи может приводить к появлению слабо нарастающих возмущений, которые не наблюдаются при использовании уравнений Лява общего вида и существенно подавляются при увеличении жесткости или демпфирования стенки. Библ. 36. Фиг. 14. Табл. 2.
1. ВВЕДЕНИЕ
Линейная устойчивость течений над податливыми поверхностями исследуется с середины XX века, когда в экспериментальной работе [1] впервые была продемонстрирована возможность задержки ламинарно-турбулентного перехода за счет нанесения на твердую обтекаемую поверхность специально подобранного податливого покрытия. Позже было установлено теоретически (см. [2], [3]), что податливость обтекаемой поверхности приводит к новым конкурирующим между собой видам неустойчивости, по-разному зависящим от вязкоупругих характеристик поверхности. Поэтому актуальны разработка критериев возникновения таких неустойчивостей и создание на основе этих критериев новых податливых покрытий, которые можно эффективно использовать для пассивного управления ламинарно-турбулентным переходом.
С этой целью наиболее подробно изучено влияние податливости обтекаемой поверхности на устойчивость различных погранслойных течений (см. обзор [4]), которые актуальны для приложений, связанных, например, с движением различных тел в жидкости. Помимо этого, исследовалась устойчивость течений в трубах круглого сечения с податливыми стенками (см. [5]). Такие течения актуальны для приложений, связанных, например, с производством медицинского оборудования, где интерес может представлять, как стабилизация потока для сокращения потерь на трение, так и его турбулизация для увеличения перемешивания и теплообмена. В ряде работ рассматривались течения в трубах, характерные для физиологических потоков в дыхательных путях или кровеносных сосудах, и делались общие выводы об их устойчивости (см. [6]–[9]). Также исследовалась устойчивость течений в каналах с податливыми стенками (см., например, [10]), в том числе, немодовая (см. [11]).
Для описания малых колебаний податливых стенок используются различные модели. Их разделяют на так называемые поверхностные и объемные (см. [4]). В поверхностных моделях, в частности, предполагается, что толщина стенки существенно меньше ее размеров в других направлениях, что позволяет сократить пространственную размерность модели. В рамках объемных моделей ограничений на толщину стенки не накладывается, и ее колебания описываются на основе трехмерных уравнений Навье (см. [12]). Объемные модели более востребованы в конкретных приложениях, однако поверхностные – проще и существенно экономичнее с точки зрения вычислительных затрат и воспроизводят основные динамические характеристики податливых поверхностей: инерцию, упругость и демпфирование. Поэтому их широко применяют во многих фундаментально-научных исследованиях (см. [4]).
Популярной поверхностной моделью является модель (см. [13]), в которой податливая стенка рассматривается, как тонкая эластичная пластина, закрепленная к твердой поверхности с помощью пружин и отклоняющаяся по нормали к поверхности. Более реалистичной альтернативой данной модели являются поверхностные модели на основе двумерной теории тонких оболочек (см. [14], [15]), допускающие смещения стенки не только в нормальном, но и в касательных направлениях. Среди них есть модели, в основе которых лежат различные упрощающие гипотезы о характере нагрузок, действующих на стенку (оболочку). Эти упрощенные модели успешно применяются во многих приложениях (см. [14], [15]), однако автору не известны работы, в которых на примере задач гидродинамической устойчивости выполнялось бы подробное сравнение различных вариантов моделей на основе теории оболочек и обсуждался бы эффект допущенных упрощений на характеристики устойчивости течения. Такое сравнение, в частности, позволило бы глубже изучить механизмы, определяющие возникновение различных неустойчивостей в потоке над податливой поверхностью.
В настоящей работе предложена новая численная модель для исследования линейной устойчивости течения вязкой несжимаемой жидкости в трубе круглого сечения с податливой стенкой. Стенка трубы рассматривается как тонкая, однородная и изотропная оболочка, которая может быть окружена основанием из однородного материала. Колебания оболочки описываются уравнениями Лява (см. [14], [15]), которые определяют ее смещения под действием сил давления любой природы. Основание рассматривается как равномерно распределенный набор пружин и демпферов (см. [15]). Такая модель основания является значительным упрощением, однако не накладывает ограничений на его толщину и позволяет рассматривать достаточно толстые двухслойные стенки, хотя и неоднородные. В уравнениях Лява основание учитывается как дополнительная нагрузка, действующая на оболочку и возникающая вследствие действия внешних сил.
В рамках численной модели уравнения Лява используются как динамические граничные условия на стенке для линеаризованных относительно основного стационарного течения уравнений движения вязкой несжимаемой жидкости. Помимо этих динамических условий, которые в работе для краткости названы полными, рассмотрены и упрощенные, на основе уравнений Лява, записанных в приближении Доннела–Муштари–Власова (см. [14], [15]). В этом приближении предполагается, что оболочка нагружается и смещается в основном по нормали к поверхности. В частности, это подразумевает пренебрежение касательными компонентами вязкого тензора напряжений в жидкости на стенке. Поскольку учет нормальной компоненты вязкого тензора напряжений в жидкости на стенке слабо влияет на устойчивость потока (см. [16], [17]), то в упрощенных условиях она также была исключена.
Целью данной работы являются численное исследование линейной устойчивости течения Пуазейля в трубе с податливой стенкой и сравнение характеристик его устойчивости, полученных с использованием полных и упрощенных динамических граничных условий. Работа организована следующим образом. В разд. 2 приводятся уравнения эволюции малых возмущений. В разд. 3 описывается модель податливой стенки и дается вид кинематических, а также полных и упрощенных динамических граничных условий. В разд. 4 полученные уравнения приводятся к безразмерному виду. В разд. 5 формулируется задача временной устойчивости (см. [18]–[20]), в рамках которой предполагается, что возмущение основного течения и соответствующее отклонение стенки заданы в начальный момент времени, гармоничны в продольном и азимутальном направлениях, и исследуется их эволюция во времени. Описывается проблема собственных значений, к численному решению которой сводится расчет характеристик устойчивости основного течения (например, критических чисел Рейнольдса, скоростей нарастания возмущений). В разд. 6 выводится модифицированное уравнение Рейнольдса–Орра (см. [18]–[20]), описывающее баланс кинетической энергии возмущения основного течения. В разд. 7 описывается пространственная аппроксимация упомянутой проблемы собственных значений, в результате которой получается обобщенная алгебраическая проблема собственных значений. Эта проблема сводится к обыкновенной проблеме примерно вдвое меньшей алгебраической размерности с помощью алгебраической редукции, предложенной и обоснованной в [21], [22]. В разд. 8 обсуждаются результаты численных экспериментов с предложенной моделью. В разд. 9 делаются выводы по результатам работы.
2. ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ ЭВОЛЮЦИИ ВОЗМУЩЕНИЙ
В декартовой системе координат рассмотрим течение вязкой несжимаемой жидкости в трехмерной бесконечной в продольном направлении трубе
(2.1)
$\left\{ {(x,y,z)\,: - \infty < x < \infty ,\;{{y}^{2}} + {{z}^{2}} < r_{{\text{b}}}^{2}} \right\}$Перейдем в цилиндрическую систему координат ($x$, $\theta $, $r$), в которой $\theta $ и $r$ связаны с $y$ и $z$ следующим образом:
где $ - \pi \leqslant \theta < \pi $, $0 \leqslant r \leqslant {{r}_{{\text{b}}}}$, кроме того,Нас будет интересовать линейная устойчивость (см. [18]–[20]) основного течения во временной постановке. Линеаризованные относительно основного течения уравнения движения вязкой несжимаемой жидкости, которые будем называть уравнениями эволюции возмущений, в координатах ($x$, $\theta $, $r$) имеют вид
(2.2)
$\begin{gathered} \frac{{\partial u}}{{\partial t}} + U\frac{{\partial u}}{{\partial x}} + {{U}_{r}}w + \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} = \nu \Delta u, \\ \frac{{\partial {v}}}{{\partial t}} + U\frac{{\partial {v}}}{{\partial x}} + \frac{1}{{\rho r}}\frac{{\partial p}}{{\partial \theta }} = \nu \left[ {\left( {\Delta - \frac{1}{{{{r}^{2}}}}} \right){v} + \frac{2}{{{{r}^{2}}}}\frac{{\partial w}}{{\partial \theta }}} \right], \\ \frac{{\partial w}}{{\partial t}} + U\frac{{\partial w}}{{\partial x}} + \frac{1}{\rho }\frac{{\partial p}}{{\partial r}} = \nu \left[ {\left( {\Delta - \frac{1}{{{{r}^{2}}}}} \right)w - \frac{2}{{{{r}^{2}}}}\frac{{\partial v}}{{\partial \theta }}} \right], \\ \frac{{\partial u}}{{\partial x}} + \frac{1}{r}\frac{{\partial {v}}}{{\partial \theta }} + \left( {\frac{1}{r} + \frac{\partial }{{\partial r}}} \right)w = 0, \\ \end{gathered} $Как правило, систему (2.2) рассматривают в области
(2.3)
$\left\{ {(x,\theta ,r)\,: - \infty < x < \infty ,\; - {\kern 1pt} \pi \leqslant \theta < \pi ,\; - {\kern 1pt} {{r}_{b}} < r < {{r}_{{\text{b}}}}} \right\}.$(2.4)
$\begin{gathered} u(x,\theta \pm \pi , - r,t) = u(x,\theta ,r,t),\quad - {\kern 1pt} {v}(x,\theta \pm \pi , - r,t) = {v}(x,\theta ,r,t), \\ - w(x,\theta \pm \pi , - r,t) = w(x,\theta ,r,t),\quad p(x,\theta \pm \pi , - r,t) = p(x,\theta ,r,t), \\ \end{gathered} $Таким образом, система (2.2) рассматривается в области (2.3) с периодическими граничными условиями для компонент скорости и их первых производных по $\theta $. Если стенка трубы твердая, то на границе $r = {{r}_{{\text{b}}}}$ накладываются условия прилипания (равенство нулю компонент скорости), если же стенка податливая, то накладываются соответствующие кинематические и динамические граничные условия. Первые выражают непрерывность компонент скорости на границе, а вторые – баланс сил (см. [28]).
Кинематические граничные условия можно записать в виде
(2.5)
$\frac{{\partial {{{\mathbf{\xi }}}_{{\text{b}}}}}}{{\partial t}}({{{\mathbf{q}}}_{{\text{b}}}},t) = {\mathbf{\hat {U}}}({{{\mathbf{q}}}_{{\text{b}}}} + {{{\mathbf{\xi }}}_{{\text{b}}}}({{{\mathbf{q}}}_{{\text{b}}}},t),t).$(2.6)
$\frac{{\partial {{\xi }_{{\text{b}}}}}}{{\partial t}} = {{u}_{{\text{b}}}} - 2\frac{{{{U}_{0}}}}{{{{r}_{b}}}}{{\zeta }_{{\text{b}}}},\quad \frac{{\partial {{\eta }_{{\text{b}}}}}}{{\partial t}} = {{{v}}_{{\text{b}}}},\quad \frac{{\partial {{\zeta }_{{\text{b}}}}}}{{\partial t}} = {{w}_{{\text{b}}}},$3. МОДЕЛЬ ПОДАТЛИВОЙ СТЕНКИ ТРУБЫ
В настоящей работе стенка трубы (2.1) рассматривается как тонкая, однородная и изотропная оболочка постоянной толщины ${{h}_{{\text{s}}}}$ с плотностью ${{\rho }_{{\text{s}}}}$, модулем Юнга ${{E}_{{\text{s}}}}$ и коэффициентом Пуассона ${{\mu }_{{\text{s}}}}$. Оболочку характеризуют срединной поверхностью, которая равноудалена от лицевых поверхностей оболочки (см. [14], [15]). Как правило, тонкой считается оболочка, для которой отношение ${{h}_{{\text{s}}}}{\text{/}}R$ ее толщины к минимальному радиусу кривизны (либо характерному линейному размеру) ее срединной поверхности не превышает 1/20. Далее будем предполагать, что это условие выполнено, хотя в некоторых случаях использование теории тонких оболочек дает приемлемые результаты даже при отношении порядка единицы (см. [14]).
Положение точки на срединной поверхности можно описать либо декартовыми координатами $x$, $y$ и $z$, либо локальными ортогональными криволинейными координатами, заданными на этой поверхности. Для цилиндрической оболочки в качестве таких координат выберем определенные выше координаты $x$ и $\theta $. Для такой оболочки $R = {{r}_{{\text{b}}}}$ с точностью до членов порядка ${{h}_{{\text{s}}}}{\text{/}}R \ll 1$.
Согласно геометрической гипотезе Кирхгофа (см. [14], [15]), лежащей в основе теории тонких оболочек, перпендикуляр, опущенный из произвольной точки оболочки на срединную поверхность, после деформации оболочки останется перпендикулярным к срединной поверхности и сохранит свою длину. Используя данную гипотезу, можно показать, что смещения оболочки в касательных направлениях меняются линейно по толщине оболочки, а нормальное смещение не зависит от расстояния до срединной поверхности. Таким образом, для рассматриваемой цилиндрической оболочки
где ${{\xi }_{h}}$, ${{\eta }_{h}}$, ${{\zeta }_{h}}$ и $\xi $, $\eta $, $\zeta $ – компоненты векторов ${{{\mathbf{\xi }}}_{h}} = {{\xi }_{h}}{{{\mathbf{e}}}_{x}} + {{\eta }_{h}}{{{\mathbf{e}}}_{\theta }} + {{\zeta }_{h}}{{{\mathbf{e}}}_{r}}$ и ${\mathbf{\xi }} = \xi {{{\mathbf{e}}}_{x}} + \eta {{{\mathbf{e}}}_{\theta }} + \zeta {{{\mathbf{e}}}_{r}}$ смещения оболочки и ее срединной поверхности соответственно, а $ - {{h}_{{\text{s}}}}{\text{/}}2 \leqslant h \leqslant {{h}_{{{\text{s/}}}}}2$ – координата по нормали ${{{\mathbf{e}}}_{r}}$ с основанием в точке $(x,\theta )$ на срединной поверхности. Кроме того,Малые колебания тонкой оболочки описываются на основе уравнений Лява (см. [15]), которые определяют смещения ее срединной поверхности под действием сил давления любой природы. Эти уравнения также позволяют описывать ситуации, когда силы, возвращающие оболочку к состоянию равновесия, вызваны внутренними напряжениями, изначально присутствующими в оболочке и не зависящими от ее смещения. В настоящей работе предполагается, что оболочка предварительно не нагружена, т.е. эти напряжения отсутствуют. Тогда колебания срединной поверхности цилиндрической оболочки описываются следующими уравнениями (см. [15]):
(3.8)
$\begin{gathered} {{\rho }_{{\text{s}}}}{{h}_{{\text{s}}}}\frac{{{{\partial }^{2}}\xi }}{{\partial {{t}^{2}}}} - \frac{{\partial {{N}_{{xx}}}}}{{\partial x}} - \frac{1}{{{{r}_{{\text{b}}}}}}\frac{{\partial {{N}_{{\theta x}}}}}{{\partial \theta }} = \mathop {\hat {q}}\nolimits_x , \\ {{\rho }_{{\text{s}}}}{{h}_{{\text{s}}}}\frac{{{{\partial }^{2}}\eta }}{{\partial {{t}^{2}}}} - \frac{{\partial {{N}_{{x\theta }}}}}{{\partial x}} - \frac{1}{{{{r}_{{\text{b}}}}}}\frac{{\partial {{N}_{{\theta \theta }}}}}{{\partial \theta }} - \frac{{{{Q}_{{\theta r}}}}}{{{{r}_{{\text{b}}}}}} = \mathop {\hat {q}}\nolimits_\theta , \\ {{\rho }_{{\text{s}}}}{{h}_{{\text{s}}}}\frac{{{{\partial }^{2}}\zeta }}{{\partial {{t}^{2}}}} - \frac{{\partial {{Q}_{{xr}}}}}{{\partial x}} - \frac{1}{{{{r}_{{\text{b}}}}}}\frac{{\partial {{Q}_{{\theta r}}}}}{{\partial \theta }} + \frac{{{{N}_{{\theta \theta }}}}}{{{{r}_{{\text{b}}}}}} = \mathop {\hat {q}}\nolimits_r , \\ \end{gathered} $В настоящей работе также будет рассматриваться двухслойная стенка: тонкая оболочка, окруженная вязкоупругим основанием толщины ${{h}_{{\text{f}}}}$ из однородного материала с плотностью ${{\rho }_{f}}$, модулем Юнга ${{E}_{{\text{f}}}}$ и коэффициентом Пуассона ${{\mu }_{{\text{f}}}}$. Основание может (см. [15]) рассматриваться в ряде случаев (см., например, [10]) как набор действующих на срединную поверхность оболочки равномерно распределенных пружин и демпферов с коэффициентами упругости ${{k}_{x}}$, ${{k}_{\theta }}$, ${{k}_{r}}$ и демпфирования ${{d}_{x}}$, ${{d}_{\theta }}$, ${{d}_{r}}$ соответственно по направлениям $x$, $\theta $, $r$. Коэффициенты упругости можно оценить (см. [15]) по формулам
Рассмотренная модель вязкоупругого основания справедлива, если модули Юнга материалов оболочки и основания существенно различные. В данной работе будем предполагать, что это условие выполняется. В противном случае основание нужно моделировать в виде вязкоупругой сплошной среды на основе уравнений Навье, как это сделано, например, в [29].
Отметим, что в теории оболочек широко применяется приближение Доннела–Муштари–Власова (см. [14], [15]), в рамках которого предполагается, что оболочка нагружается и смещается в основном по нормали к поверхности, т.е. $\mathop {\hat {q}}\nolimits_x = \mathop {\hat {q}}\nolimits_\theta = 0$. В таком случае делается пренебрежение касательными смещениями $\xi $ и $\eta $ в выражениях для изгибающих деформаций, т.е.
(3.9)
$\begin{gathered} \frac{{\partial {{N}_{{xx}}}}}{{\partial x}} + \frac{1}{{{{r}_{{\text{b}}}}}}\frac{{\partial {{N}_{{\theta x}}}}}{{\partial \theta }} = 0, \\ \frac{{\partial {{N}_{{x\theta }}}}}{{\partial x}} + \frac{1}{{{{r}_{{\text{b}}}}}}\frac{{\partial {{N}_{{\theta \theta }}}}}{{\partial \theta }} = 0, \\ {{\rho }_{{\text{s}}}}{{h}_{{\text{s}}}}\frac{{{{\partial }^{2}}\zeta }}{{\partial {{t}^{2}}}} - \frac{{\partial {{Q}_{{xr}}}}}{{\partial x}} - \frac{1}{{{{r}_{{\text{b}}}}}}\frac{{\partial {{Q}_{{\theta r}}}}}{{\partial \theta }} + \frac{{{{N}_{{\theta \theta }}}}}{{{{r}_{{\text{b}}}}}} = \mathop {\hat {q}}\nolimits_r . \\ \end{gathered} $4. ПРИВЕДЕНИЕ К БЕЗРАЗМЕРНОМУ ВИДУ
Определим число Рейнольдса следующим образом: $Re = {{U}_{0}}{{r}_{{\text{b}}}}{\text{/}}\nu $. Поделим $x$, $r$, $\xi $, $\eta $, $\zeta $ на ${{r}_{{\text{b}}}}$, скорости $u$, ${v}$ и $w$ – на ${{U}_{0}}$, время – на ${{r}_{{\text{b}}}}{\text{/}}{{U}_{0}}$, давление $p$ – на $\rho U_{0}^{2}$. Обезразмеренные уравнения (2.2) эволюции трехмерных возмущений имеют вид
(4.10)
$\begin{gathered} \frac{{\partial u}}{{\partial t}} + U\frac{{\partial u}}{{\partial x}} + {{U}_{r}}w + \frac{{\partial p}}{{\partial x}} = \frac{1}{{{\text{Re}}}}\Delta u, \\ \frac{{\partial {v}}}{{\partial t}} + U\frac{{\partial {v}}}{{\partial x}} + \frac{1}{r}\frac{{\partial p}}{{\partial \theta }} = \frac{1}{{{\text{Re}}}}\left[ {\left( {\Delta - \frac{1}{{{{r}^{2}}}}} \right){v} + \frac{2}{{{{r}^{2}}}}\frac{{\partial w}}{{\partial \theta }}} \right], \\ \frac{{\partial w}}{{\partial t}} + U\frac{{\partial w}}{{\partial x}} + \frac{{\partial p}}{{\partial r}} = \frac{1}{{{\text{Re}}}}\left[ {\left( {\Delta - \frac{1}{{{{r}^{2}}}}} \right)w - \frac{2}{{{{r}^{2}}}}\frac{{\partial {v}}}{{\partial \theta }}} \right], \\ \frac{{\partial u}}{{\partial x}} + \frac{1}{r}\frac{{\partial {v}}}{{\partial \theta }} + \left( {\frac{1}{r} + \frac{\partial }{{\partial r}}} \right)w = 0 \\ \end{gathered} $Обезразмеривание вязкоупругих параметров стенки выполним так, чтобы они не изменялись при изменении числа Рейнольдса. Для этого будем предполагать, что изменение ${\text{Re}}$ обусловлено только изменением ${{U}_{0}}$, а параметры ${{r}_{{\text{b}}}}$, $\rho $ и $\nu $ – фиксированные. Тогда поделим мембранную $K$ и изгибную $D$ жесткости оболочки на $\rho {{\nu }^{2}}{\text{/}}{{r}_{{\text{b}}}}$ и ${{r}_{{\text{b}}}}\rho {{\nu }^{2}}$ соответственно, а коэффициенты упругости ${{k}_{x}}$, ${{k}_{\theta }}$, ${{k}_{r}}$ и демпфирования ${{d}_{x}}$, ${{d}_{\theta }}$, ${{d}_{r}}$ основания – на $\rho {{\nu }^{2}}{\text{/}}r_{{\text{b}}}^{3}$ и $\rho \nu {\text{/}}{{r}_{{\text{b}}}}$ соответственно, кроме того, введем обозначение
(4.11)
$\,\,\,\,\,\,\,\,\,\frac{{\partial \eta }}{{\partial t}} - {{{v}}_{{\text{b}}}} + \frac{{{{h}_{{\text{s}}}}}}{{2{{r}_{{\text{b}}}}}}\frac{{\partial {{w}_{{\text{b}}}}}}{{\partial \theta }} = 0,$(4.12)
$\begin{gathered} \gamma \frac{{{{\partial }^{2}}\eta }}{{\partial {{t}^{2}}}} + \frac{{{{d}_{\theta }}}}{{{\text{Re}}}}\frac{{\partial \eta }}{{\partial t}} - \frac{{K(1 + \mu )}}{{2{{{\operatorname{Re} }}^{2}}}}\frac{{{{\partial }^{2}}\xi }}{{\partial x\partial \theta }} - \frac{1}{{{{{\operatorname{Re} }}^{2}}}}\left[ {\frac{{(K + D)(1 - \mu )}}{2}\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + } \right.\left. {(K + D)\frac{{{{\partial }^{2}}}}{{\partial {{\theta }^{2}}}} - {{k}_{\theta }}} \right]\eta + \\ + \;\frac{1}{{{{{\operatorname{Re} }}^{2}}}}\left( { - K\frac{\partial }{{\partial \theta }} + D\frac{{{{\partial }^{3}}}}{{\partial {{x}^{2}}\partial \theta }} + D\frac{{{{\partial }^{3}}}}{{\partial {{\theta }^{3}}}}} \right)\zeta + \frac{1}{{{\text{Re}}}}{{\left. {\left( {\frac{1}{r}\frac{{\partial w}}{{\partial \theta }} + \frac{{\partial {v}}}{{\partial r}} - \frac{{v}}{r}} \right)} \right|}_{{r = 1}}} = 0, \\ \end{gathered} $5. ЗАДАЧА ВРЕМЕННОЙ УСТОЙЧИВОСТИ
В случае анализа временной устойчивости предполагают (см. [18]–[20]), что возмущение основного течения и соответствующее смещение стенки заданы при $t = 0$ во всей трубе и являются гармоническими по $x$ и $\theta $:
(5.13)
$\,\,\,\,\,\,\,\,\,\,\,\,\,p(x,\theta ,r,t) = \tilde {p}(r){{e}^{{{\text{i}}(\alpha x + n\theta - \omega t)}}},$(5.14)
$\begin{gathered} - {\text{i}}\omega \tilde {u} + {\text{i}}\alpha U\tilde {u} - 2r\tilde {w} + {\text{i}}\alpha \tilde {p} - \frac{1}{{{\text{Re}}}}{{\Delta }_{r}}\tilde {u} = 0, \\ - {\text{i}}\omega {\tilde {v}} + {\text{i}}\alpha U{\tilde {v}} + \frac{{{\text{i}}n}}{r}\tilde {p} - \frac{1}{{{\text{Re}}}}\left[ {\left( {{{\Delta }_{r}} - \frac{1}{{{{r}^{2}}}}} \right){\tilde {v}} + \frac{{2{\text{i}}n}}{{{{r}^{2}}}}\tilde {w}} \right] = 0, \\ - {\text{i}}\omega \tilde {w} + {\text{i}}\alpha U\tilde {w} + \frac{{d\tilde {p}}}{{dr}} - \frac{1}{{{\text{Re}}}}\left[ {\left( {{{\Delta }_{r}} - \frac{1}{{{{r}^{2}}}}} \right)\tilde {w} - \frac{{2{\text{i}}n}}{{{{r}^{2}}}}{\tilde {v}}} \right] = 0, \\ {\text{i}}\alpha \tilde {u} + \frac{{{\text{i}}n}}{r}{\tilde {v}} + \left( {\frac{1}{r} + \frac{d}{{dr}}} \right)\tilde {w} = 0, \\ \end{gathered} $(5.15)
$\,\,\,\,\,\,\,\, - {\text{i}}\omega \tilde {\eta } - {{{\tilde {v}}}_{{\text{b}}}} + {\text{i}}n\frac{{{{h}_{{\text{s}}}}}}{{2{{r}_{{\text{b}}}}}}{{\tilde {w}}_{{\text{b}}}} = 0,$(5.16)
$\begin{gathered} - \;{\text{i}}\omega \left( {{{{{\tilde {v}}}}_{{\text{b}}}} - {\text{i}}n\frac{{{{h}_{{\text{s}}}}}}{{2{{r}_{{\text{b}}}}}}{{{\tilde {w}}}_{{\text{b}}}}} \right) + \alpha n\frac{{K(1 + \mu )}}{{2\gamma {{{\operatorname{Re} }}^{2}}}}\tilde {\xi } + \frac{1}{{\gamma {{{\operatorname{Re} }}^{2}}}}\left[ {\left( {{{\alpha }^{2}}\frac{{1 - \mu }}{2} + {{n}^{2}}} \right)(K + D) + {{k}_{\theta }}} \right]\tilde {\eta } - \\ - \;\frac{{{\text{i}}n}}{{\gamma {{{\operatorname{Re} }}^{2}}}}[K + ({{\alpha }^{2}} + {{n}^{2}})D]\tilde {\zeta } + \frac{1}{{\gamma {\text{Re}}}}\left[ {({{d}_{\theta }} - 1){{{{\tilde {v}}}}_{{\text{b}}}} + {\tilde {v}}_{{\text{b}}}^{{(1)}} + {\text{i}}n\left( {1 - \frac{{{{h}_{s}}{{d}_{\theta }}}}{{2{{r}_{b}}}}} \right){{{\tilde {w}}}_{{\text{b}}}}} \right] = 0, \\ \end{gathered} $(5.16')
$\begin{gathered} \text{[}2{{\alpha }^{2}} + {{n}^{2}}(1 - \mu )]\tilde {\xi } + \alpha n(1 + \mu )\tilde {\eta } - 2{\text{i}}\alpha \mu \tilde {\zeta } = 0, \\ \alpha n(1 + \mu )\tilde {\xi } + [{{\alpha }^{2}}(1 - \mu ) + 2{{n}^{2}}]\tilde {\eta } - 2{\text{i}}n\tilde {\zeta } = 0, \\ - {\text{i}}\omega {{{\tilde {w}}}_{{\text{b}}}} + \frac{K}{{\gamma {{{\operatorname{Re} }}^{2}}}}({\text{i}}\alpha \mu \tilde {\xi } + {\text{i}}n\tilde {\eta }) + \frac{1}{{\gamma {{{\operatorname{Re} }}^{2}}}}[K + {{({{\alpha }^{2}} + {{n}^{2}})}^{2}}D + {{k}_{r}}]\tilde {\zeta } + \tfrac{{{{d}_{r}}}}{\begin{gathered} \gamma {\text{Re}} \hfill \\ \end{gathered} }{{{\tilde {w}}}_{{\text{b}}}} - \tfrac{1}{\gamma }{{{\tilde {p}}}_{{\text{b}}}} = 0. \\ \end{gathered} $Система (5.14), (5.15), (5.16) является проблемой собственных значений относительно спектрального параметра $\omega $ и собственной функции
Среди ее решений ищутся только те, что удовлетворяют условиям симметрии:(5.17)
$\begin{gathered} {{( - 1)}^{n}}\tilde {u}( - r) = \tilde {u}(r),\quad {{( - 1)}^{{n + 1}}}{\tilde {v}}( - r) = {\tilde {v}}(r), \\ {{( - 1)}^{{n + 1}}}\tilde {w}( - r) = \tilde {w}(r),\quad {{( - 1)}^{n}}\tilde {p}( - r) = \tilde {p}(r). \\ \end{gathered} $Для заданных значений $\alpha $, $n$ и вязкоупругих параметров стенки трубы линейное критическое число Рейнольдса ${{\operatorname{Re} }_{{\text{c}}}}(\alpha ,n)$ будем определять как границу устойчивости нулевого решения системы (4.10), (4.11), (4.12), (2.4) ко всем возмущениям вида (5.13). Поскольку возмущение вида (5.13) нарастает со временем, если ${{\omega }_{{\text{i}}}} > 0$, и затухает, если ${{\omega }_{{\text{i}}}} < 0$, то
(5.18)
${{\operatorname{Re} }_{{\text{c}}}}(\alpha ,n) = inf\left\{ {{\text{Re}}:max\operatorname{Imag} \Lambda ({\text{Re}},\alpha ,n) = 0,{\text{Re}} > 0} \right\},$6. УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ВОЗМУЩЕНИЯ
Величину
(6.19)
$\mathcal{E}({\mathbf{u}}) = \frac{1}{2}\int\limits_{ - 1}^1 {\overline {{{u}_{i}}u_{i}^{ * }} } \frac{{\left| r \right|}}{2}dr = \frac{1}{2}\int\limits_{ - 1}^1 {\mathop {\tilde {u}}\nolimits_i \mathop {\tilde {u}}\nolimits_i^ * } \frac{{\left| r \right|}}{2}dr{\kern 1pt} {{e}^{{2{{\omega }_{i}}t}}} = \mathcal{E}({\mathbf{\tilde {u}}}){{e}^{{2{{\omega }_{i}}t}}}$Скалярно умножая первые три уравнения в (4.10) на $u{\text{*}}$, ${v}{\text{*}}$ и $w{\text{*}}$ соответственно и беря действительную часть, получим следующее уравнение:
(6.20)
$\begin{gathered} \left[ {\frac{\partial }{{\partial t}} + U\frac{\partial }{{\partial x}}} \right]\frac{1}{2}{{u}_{i}}u_{i}^{ * } = {\text{Real}}\left\{ { - {{U}_{r}}wu{\kern 1pt} {\text{*}} - \frac{{\partial pu{\kern 1pt} {\text{*}}}}{{\partial x}} - \frac{1}{r}\frac{{\partial p{v}{\kern 1pt} {\text{*}}}}{{\partial \theta }} - \left( {\frac{1}{r} + \frac{\partial }{{\partial r}}} \right)pw{\kern 1pt} {\text{*}} + } \right. \\ \left. { + \;\frac{1}{{{\text{Re}}}}\left[ {\Delta {{u}_{i}}u_{i}^{ * } - \frac{1}{{{{r}^{2}}}}({vv}{\text{*}} + ww{\kern 1pt} {\text{*}}) + \frac{2}{{{{r}^{2}}}}\left( {{v}{\kern 1pt} {\text{*}}\frac{{\partial w}}{{\partial \theta }} - w{\kern 1pt} {\text{*}}\frac{{\partial {v}}}{{\partial \theta }}} \right)} \right]} \right\}, \\ \end{gathered} $(6.21)
$\begin{gathered} \frac{{\partial{ \mathcal{E}}({\mathbf{u}})}}{{\partial t}} = - {\text{Real}}\left\{ {\int\limits_{ - 1}^1 {{{U}_{r}}} \overline {wu{\kern 1pt} {\text{*}}} \frac{{|r|}}{2}dr} \right\} - \frac{1}{{{\text{Re}}}}\int\limits_{ - 1}^1 {\left[ {\overline {\frac{{\partial {{u}_{i}}}}{{\partial x}}\frac{{\partial u_{i}^{ * }}}{{\partial x}}} + \frac{1}{{{{r}^{2}}}}\overline {\frac{{\partial {{u}_{i}}}}{{\partial \theta }}\frac{{\partial u_{i}^{ * }}}{{\partial \theta }}} + } \right.} \\ \left. { + \;\overline {\frac{{\partial {{u}_{i}}}}{{\partial r}}\frac{{\partial u_{i}^{ * }}}{{\partial r}}} + \frac{1}{{{{r}^{2}}}}\left( {\overline {{{{\left| {v} \right|}}^{2}}} + \overline {{{{\left| w \right|}}^{2}}} } \right) - \frac{2}{{{{r}^{2}}}}\left( {\overline {{v}{\kern 1pt} {\text{*}}\frac{{\partial w}}{{\partial \theta }}} - \overline {w{\kern 1pt} {\text{*}}\frac{{\partial {v}}}{{\partial \theta }}} } \right)} \right]\frac{{\left| r \right|}}{2}dr - \\ - \;{\text{Real}}\left\{ {\frac{1}{2}\left. {\overline {pw{\kern 1pt} {\text{*}}} } \right|_{{ - 1}}^{1}} \right\} + {\text{Real}}\left\{ {\frac{1}{{2{\text{Re}}}}\left. {\overline {u_{i}^{ * }\frac{{\partial {{u}_{i}}}}{{\partial r}}} } \right|_{{ - 1}}^{1}} \right\}. \\ \end{gathered} $Учитывая (5.13), уравнение (6.22) можно записать в виде
(6.22)
$\begin{gathered} 2{{\omega }_{i}}\mathcal{E}({\mathbf{\tilde {u}}}) = - {\text{Real}}\left\{ {\int\limits_{ - 1}^1 {{{U}_{r}}} \tilde {w}\tilde {u}{\text{*}}\frac{{\left| r \right|}}{2}dr} \right\} - \frac{1}{{{\text{Re}}}}\int\limits_{ - 1}^1 {\left( {{{\alpha }^{2}}{{{\tilde {u}}}_{i}}\tilde {u}_{i}^{ * } + + \frac{{{{n}^{2}}}}{{{{r}^{2}}}}{{{\tilde {u}}}_{i}}\tilde {u}_{i}^{ * }} \right.} + \\ \left. { + \;\frac{{\partial {{{\tilde {u}}}_{i}}}}{{\partial r}}\frac{{\partial u_{i}^{*}}}{{\partial r}} + \frac{1}{{{{r}^{2}}}}\left( {{{{\left| {{\tilde {v}}} \right|}}^{2}} + {{{\left| {\tilde {w}} \right|}}^{2}}} \right) - \frac{{2{\text{i}}n}}{{{{r}^{2}}}}\left( {{\tilde {v}}{\kern 1pt} {\text{*}}\tilde {w} - {\tilde {v}}\tilde {w}{\text{*}}} \right)} \right)\frac{{\left| r \right|}}{2}dr - \\ - \;{\text{Real}}\left\{ {\frac{1}{2}\tilde {p}\left. {\tilde {w}{\text{*}}} \right|_{{ - 1}}^{1}} \right\} + {\text{Real}}\left\{ {\frac{1}{{2{\text{Re}}}}\mathop {\tilde {u}}\nolimits_i^ * \left. {\frac{{\partial {{{\tilde {u}}}_{i}}}}{{\partial r}}} \right|_{{ - 1}}^{1}} \right\}. \\ \end{gathered} $7. АППРОКСИМАЦИЯ И ПРЕДВАРИТЕЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
Пространственную аппроксимацию проблемы (5.14), (5.15), (5.16), (5.17) по $r$ выполним спектральным методом коллокаций (см. [32]). В качестве узлов интерполяции давления выберем корни ${{r}_{1}},\; \ldots ,\;{{r}_{{2{{n}_{r}}}}}$ производной многочлена Лежандра ${{L}_{{2{{n}_{r}} + 1}}}$ степени $2{{n}_{r}} + 1$, а для аппроксимации компонент скорости – те же узлы и граничные точки ${{r}_{0}} = - 1$ и ${{r}_{{2{{n}_{r}} + 1}}} = 1$ (узлы Гаусса–Лобатто). Узлы ${{r}_{i}}$ не лежат на оси трубы и расположены неравномерно: расстояние между узлами вблизи оси составляет $\mathcal{O}(1{\text{/}}{{n}_{r}})$, а вблизи стенки – $\mathcal{O}(1{\text{/}}n_{r}^{2})$. В качестве базисных функций для давления используем элементарные интерполяционные многочлены Лагранжа степени $2{{n}_{r}} - 1$, которые можно представить в виде
Учитывая условия симметрии (5.17), аппроксимацию проблемы (5.14), (5.15), (5.16), (5.17) можно выполнить в узлах ${{r}_{i}}$, $i = {{n}_{r}} + 1,\; \ldots ,\;2{{n}_{r}} + 1$. В результате получим следующую линейную обобщенную алгебраическую проблему собственных значений:
(7.23)
$\begin{gathered} {\text{i}}\omega B{\mathbf{v}} = J{\mathbf{v}} + G{\mathbf{p}}, \\ 0 = F{\mathbf{v}}, \\ \end{gathered} $При $\alpha > 0$ матрицы $G$ и $F$ в проблеме (7.23), полученной описанным методом коллокаций, хотя и не являются взаимно сопряженными, но имеют полные ранги, т.е. ядра матриц $F$ и $G{\text{*}}$ имеют одинаковую размерность ${{n}_{{\text{v}}}} - {{n}_{{\text{p}}}}$, матрица $B$ является нижней треугольной с единичной диагональю, а матрица $F{{B}^{{ - 1}}}G$ не вырождена. Тогда с помощью алгебраической редукции, которая предложена и обоснована в [21], [22], можно свести обобщенную алгебраическую проблему (7.23) собственных значений к обыкновенной, имеющей в качестве спектра множество конечных собственных значений исходной проблемы (7.23). Отметим, что проблема (7.23) имеет бесконечное собственное значение кратности $2{{n}_{{\text{p}}}}$.
Для выполнения алгебраической редукции нам потребуются унитарные прямоугольные матрицы ${{Q}_{F}}$ и ${{Q}_{G}}$, столбцы которых образуют ортонормированные базисы в ядрах матриц $F$ и $G{\kern 1pt} {\text{*}}$ соответственно, и которые можно вычислить на основе QR-разложения (см. [36]) матриц $F{\kern 1pt} {\text{*}}$ и $G$ соответственно. Поскольку $B$ и $F{{B}^{{ - 1}}}G$ невырожденные, то матрица $Q_{G}^{ * }B{{Q}_{F}}$ является невырожденной (см. [21]). Произвольный вектор ${\mathbf{v}}$, удовлетворяющий второму уравнению в (7.23), однозначно представим в виде ${\mathbf{v}} = {{Q}_{F}}{\mathbf{u}}$, где ${\mathbf{u}} = Q_{F}^{ * }{\mathbf{v}}$. Подставим это представление в первое уравнение в (7.23) и умножим полученное уравнение слева на $Q_{G}^{ * }$. Учитывая, что $Q_{G}^{ * }G = 0$, получим уравнение
разделив которое слева на матрицу $Q_{G}^{ * }B{{Q}_{F}}$, придем к обыкновенной проблеме собственных значений где матрица $H = {{(Q_{G}^{ * }B{{Q}_{F}})}^{{ - 1}}}(Q_{G}^{ * }J{{Q}_{F}})$ имеет порядок ${{n}_{{\text{v}}}} - {{n}_{{\text{p}}}} = 2{{n}_{r}} + 6$, примерно вдвое меньший, чем алгебраическая размерность исходной проблемы (7.23). Отметим, что при использовании приближения Доннела–Муштари–Власова после аппроксимации мы получим проблему вида (7.23) с единичной матрицей $B$. В случае твердой стенки аппроксимация проблемы (5.14), (5.17) с условиями прилипания на стенке также приводит к проблеме вида (7.23) c единичной матрицей $B$ и ${\mathbf{v}} = {{[{{{\mathbf{u}}}^{{\text{т}}}},{{{\mathbf{v}}}^{{\text{т}}}},{{{\mathbf{w}}}^{{\text{т}}}}]}^{{\text{т}}}}$, ${{n}_{{\text{v}}}} = 3{{n}_{r}}$, ${{n}_{{\text{p}}}} = {{n}_{r}}$. В обоих случаях матрица $FG$ оказывается невырожденной и, следовательно, полученную проблему вида (7.23) можно свести с помощью редукции к проблеме вида (7.24).Для расчета приближенных ведущих собственных значений и отвечающих им собственных функций исходной проблемы (5.14), (5.17) с соответствующими граничными условиями на стенке решались полные проблемы собственных значений вида (7.24) с помощью QR-алгоритма (см. [36]). Кроме того, для приближенного вычисления интегралов в уравнении (6.22) использовалась квадратурная формула с узлами и весами Гаусса–Лобатто (см. [32]), точная для многочленов степени не выше $4{{n}_{r}} + 1$.
8. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ
Валидация предложенной численной модели была выполнена на примере течения Пуазейля в трубе с твердой стенкой. В табл. 1 даны десять ведущих собственных значений проблемы (5.14), (5.17) с условиями прилипания, аппроксимированной на сетке с ${{n}_{r}} = 60$. Эти значения хорошо согласуются с собственными значениями, представленными в [30], где, в частности, для системы (2.2) задавались граничные условия на оси трубы.
Таблица 1.
Десять ведущих собственных значений проблемы (5.14), (5.17) для течения Пуазейля в трубе с твердой стенкой при ${\text{Re}} = 3000$, $\alpha = 1.0$ и различных $n$, вычисленные на сетке ${{n}_{r}} = 60$ (указаны значащие цифры, для которых получена сходимость по шагу сетки для ${{n}_{r}} = 60$ и $120$)
| $n = 0$ | $n = 1$ | ||
|---|---|---|---|
| ${{\omega }_{r}}$ | ${{\omega }_{i}}$ | ${{\omega }_{r}}$ | ${{\omega }_{i}}$ |
| 0.94836022205056 | –0.0519731112827 | 0.911465567622 | –0.0412756446937 |
| 0.94836019848 | –0.051973123205 | 0.3709350926967 | –0.061619018004 |
| 0.89671920086 | –0.103612364 | 0.9582055429888 | –0.0883460251884 |
| 0.8967204441005 | –0.10361288922775 | 0.854788817407 | –0.088870156644 |
| 0.412396334209 | –0.112217160388 | 0.21680386299742 | –0.116877153587 |
| 0.2184358147279 | –0.121310028246 | 0.799699469658 | –0.137490337036 |
| 0.845071799712 | –0.15522016529 | 0.9100373095479 | –0.1443461448649 |
| 0.845080668126 | –0.155252667198 | 0.7453043578 | –0.1864329862 |
| 0.3762423600256 | –0.2004630477668 | 0.54931158266 | –0.19583946656 |
| 0.793784129832 | –0.206476811414 | 0.860749463473 | –0.198646109021 |
| $n = 2$ | $n = 3$ | ||
| ${{\omega }_{r}}$ | ${{\omega }_{i}}$ | ${{\omega }_{r}}$ | ${{\omega }_{i}}$ |
| 0.8882976587541 | –0.0602856895581 | 0.8643639210456 | –0.0832539769463 |
| 0.352554927086 | –0.087898980374 | 0.346401953385 | –0.1057084073627 |
| 0.832893360873 | –0.1088383407 | 0.2149198697618 | –0.1168779213441 |
| 0.93949721953134 | –0.11200161615314 | 0.809746802303 | –0.132392433171 |
| 0.2154918165293 | –0.115514380221 | 0.916719174685 | –0.1360354595293 |
| 0.778584988054 | –0.15810861034 | 0.75587931562 | –0.18203637298 |
| 0.89061857263 | –0.16729404594995 | 0.86741365559 | –0.190639836897 |
| 0.7250771394 | –0.2075914662 | 0.371236498275 | –0.212779412106 |
| 0.3750265375 | –0.209314329982 | 0.7030072226 | –0.231817870313 |
| 0.840975374942 | –0.221474731306 | 0.5517316318 | –0.2441112418 |
Далее рассматривалось течение Пуазейля с плотностью $\rho = {{10}^{3}}$ кг/м3 и коэффициентом кинематической вязкости $\nu = 3.5 \times {{10}^{{ - 6}}}$ м2/с в трубе радиуса ${{r}_{{\text{b}}}} = 10$ мм с податливой стенкой и сравнивались характеристики устойчивости основного течения, вычисленные для проблемы (5.14), (5.15), (5.17) с динамическими условиями (5.16), с характеристиками, рассчитанными для той же проблемы, но с упрощенными условиями (5.16'). Выбранные значения $\rho $, $\nu $ и ${{r}_{{\text{b}}}}$ близки к использовавшимся в работе [9] и характерны для медицинских приложений. Расчеты проводились как для однослойных стенок, состоящих из тонкой оболочки, так и для двухслойных, состоящих из оболочки, окруженной значительно более толстым и мягким основанием. Исследовалось влияние жесткости и демпфирования стенки на устойчивость основного течения. Причем демпфирование учитывалось только в основании, а оболочка была эластичной. Значения модуля Юнга оболочки ${{E}_{{\text{s}}}}$ и основания ${{E}_{{\text{f}}}}$ выбирались в диапазонах от $2 \times {{10}^{5}}$ до $8 \times {{10}^{5}}$ и от $1 \times {{10}^{3}}$ до $2 \times {{10}^{3}}$ $\Pi {\text{a}}$ соответственно. Выбранные значения ${{E}_{{\text{s}}}}$ близки к тем, что рассматривались в работе [13], а ${{E}_{{\text{f}}}}$ – в работе [29], и характерны для латекса и кремнийорганической резины соответственно. Коэффициенты демпфирования по направлениям полагались одинаковыми: ${{d}_{x}} = {{d}_{\theta }} = {{d}_{r}} = d$, и после нормировки их значения выбирались в диапазоне от $0$ до $100$. Остальные парамеры стенки были фиксированы: толщины оболочки ${{h}_{{\text{s}}}}$ и основания ${{h}_{{\text{f}}}}$ полагались равными ${{r}_{{\text{b}}}}{\text{/}}50 = 0.2$ мм и $2{{r}_{{\text{b}}}} = 20$ мм соответственно, их плотности ${{\rho }_{{\text{s}}}}$ и ${{\rho }_{{\text{f}}}}$, следуя работе [29], полагались равными плотности жидкости $\rho $. Коэффициенты Пуассона ${{\mu }_{{\text{s}}}}$ и ${{\mu }_{{\text{f}}}}$ в [29] равны $0.5$ и $0.49$ соответственно, однако в данной работе использовалось одно значение ${{\mu }_{{\text{s}}}} = {{\mu }_{{\text{f}}}} = 0.49$, поскольку изменение коэффициента Пуассона относительно слабо влияет на характеристики устойчивости потока (см. [6]).
8.1. Постоянные в азимутальном направлении возмущения
Сначала была проанализирована устойчивость основного течения к постоянным в азимутальном направлении возмущениям ($n = 0$). Здесь и далее рассматривались следующие диапазоны значений числа Рейнольдса и продольного волнового числа: $1 \leqslant {\text{Re}} \leqslant 20\,000$ и $0.1 \leqslant \alpha \leqslant 15$. В случае трубы с однослойной стенкой для рассматриваемого диапазона значений модуля Юнга ${{E}_{{\text{s}}}}$ оболочки основное течение оказалось неустойчивым только при использовании упрощенных динамических условий (5.16').
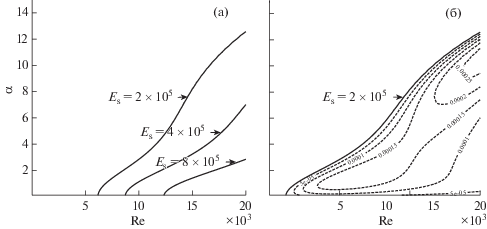
На фиг. 1 показаны нейтральные кривые и линии уровня скоростей нарастания возмущений, рассчитанные для проблемы (5.14), (5.15), (5.16'), (5.17) при различных значениях ${{E}_{{\text{s}}}}$. Нейтральные кривые отделяют области значений параметров Re и $\alpha $, при которых течение устойчиво (в данном случае слева от кривых), от значений, при которых течение неустойчиво. С ростом жесткости оболочки нейтральные кривые смещаются вправо, т.е. течение стабилизируется. Это согласуется с тем, что в трубе круглого сечения с твердой стенкой течение Пуазейля линейно устойчиво (см. [18]–[20]). При этом скорости роста нарастающих возмущений оказываются довольно малыми (${{\omega }_{{\text{i}}}} < 3 \times {{10}^{{ - 4}}}$ для ${{E}_{{\text{s}}}} = 2 \times {{10}^{5}}$ Пa).
Фиг. 1.
(а) – Нейтральные кривые $\operatorname{Re} _{{\text{c}}}^{'}(\alpha ,0)$ при различных значениях модуля Юнга ${{E}_{{\text{s}}}}$ [Па] оболочки. (б) – Нейтральная кривая $\operatorname{Re} _{{\text{c}}}^{'}(\alpha ,0)$ (сплошная линия) и линии уровня скоростей нарастания ${{\omega }_{i}}$ возмущений (пунктир) для ${{E}_{{\text{s}}}} = 2 \times {{10}^{5}}$ $\Pi {\text{a}}$, $n = 0$. Однослойная стенка.
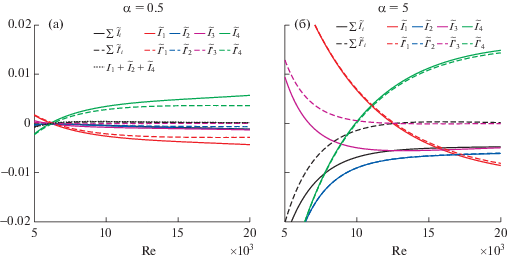
Для исследования причин такого отличия характеристик устойчивости, полученных на основе динамических условий (5.16) и (5.16'), был проанализирован вклад каждого слагаемого в уравнении (6.22) в изменение кинетической энергии возмущения основного течения в зависимости от используемых динамических условий. Для этого в узлах некоторой достаточно подробной по Re и $\alpha $ сетки вычислялась приближенная собственная функция проблемы (5.14), (5.15), (5.17) с условиями (5.16), либо (5.16'), отвечающая ее ведущему собственному значению, для которой затем рассчитывались соответствующие значения ${{\tilde {I}}_{i}}$, либо $\tilde {I}_{i}^{'}$, $i = 1,\; \ldots ,\;4$. На фиг. 2 представлены линии уровня величины $(\tilde {I}_{i}^{'} - \tilde {I}_{i}^{{}}) \times {{10}^{2}}$ в области неустойчивости. Видно, что в зависимости от используемых динамических условий при достаточно больших $\alpha $ (дополнительные расчеты показали, что при $\alpha \gtrsim 1$) наиболее сильно разнятся значения, которые принимает третье слагаемое, при этом значения остальных слагаемых отличаются гораздо слабее. Причем разница $\tilde {I}_{3}^{'} - {{\tilde {I}}_{3}}$ увеличивается с ростом $\alpha $. На фиг. 3 видно, что третье слагаемое, которое отвечает за обмен энергией между возмущением основного течения и стенкой, при рассмотренных на фиг. 2 параметрах является отрицательным, как при использовании условий (5.16), так и (5.16'), что говорит об отводе кинетической энергии возмущения к стенке. Однако в случае упрощенных условий (5.16) отвод энергии оказывается значительно меньше, чем в случае условий (5.16), при всех рассмотренных $\alpha $. Это также видно на фиг. 4, где представлены зависимости ${{\tilde {I}}_{i}}$ и $\tilde {I}_{i}^{'}$ от Re для $\alpha = 0.5$ и $5$. Интерес представляет их поведение при ${\text{Re}} \geqslant \operatorname{Re} _{{\text{c}}}^{'}(\alpha ,0)$, где, учитывая (5.18) и (6.22), $\operatorname{Re} _{{\text{c}}}^{'}(\alpha ,0)$ – это ${\text{Re}}$, при котором сумма $\tilde {I}_{i}^{'}$ равна нулю. При достаточно малом продольном волновом числе, например, $\alpha = 0.5$, выбор динамических условий, главным образом, влияет на первое, третье и четвертое слагаемые в (6.22). В то же время, если рассмотреть сумму $\mathop {\tilde {I}}\nolimits_1 + \mathop {\tilde {I}}\nolimits_2 + \mathop {\tilde {I}}\nolimits_4 $, т.е. исключить отвод кинетической энергии возмущения к стенке, то она окажется близка к сумме всех слагаемых $\tilde {I}_{i}^{'}$ при ${\text{Re}} \geqslant \operatorname{Re} _{{\text{c}}}^{'}(0.5,\;0)$ (см. фиг. 4а). Это позволяет предположить, что для $n = 0$ и рассмотренных на фиг. 2 параметров стенки, главной причиной неустойчивости основного течения при использовании упрощенных динамических условий (5.16') является малый, по сравнению со случаем использования условий (5.16), отток кинетической энергии возмущения основного течения к стенке.
Фиг. 2.
Нейтральная кривая $\operatorname{Re} _{{\text{c}}}^{'}(\alpha ,0)$ (сплошная линия) и линии уровня величины $(\tilde {I}_{i}^{'} - {{\tilde {I}}_{i}}) \times {{10}^{2}}$, $i = 1,\; \ldots ,\;4$ (пунктир), $n = 0$. Однослойная стенка, ${{E}_{{\text{s}}}} = 2 \times {{10}^{5}}$ Па.

Фиг. 3.
Нейтральная кривая $\operatorname{Re} _{{\text{c}}}^{{\text{'}}}(\alpha ,0)$ (сплошная линия) и линии уровня величин ${{\tilde {I}}_{3}} \times {{10}^{2}}$ и $\tilde {I}_{3}^{'} \times {{10}^{2}}$ (пунктир), $n = 0$. Однослойная стенка, ${{E}_{{\text{s}}}} = 2 \times {{10}^{5}}$ Па.

Фиг. 4.
Зависимость от Re величин ${{\tilde {I}}_{i}}$ и $\tilde {I}_{i}^{'}$, $i = 1,\; \ldots ,\;4$, вычисленных при использовании условий (5.16) и (5.16') соответственно, $n = 0$. Однослойная стенка, ${{E}_{{\text{s}}}} = 2 \times {{10}^{5}}$ Па.
В случае двухслойной стенки без демпфирования неустойчивость основного течения также наблюдается только при использовании упрощенных условий (5.16'). На фиг. 5 сравниваются нейтральные кривые $\operatorname{Re} _{{\text{c}}}^{'}(\alpha ,0)$ и соответствующие линии уровня скоростей нарастания возмущений. Видно, что при выбранных параметрах наличие второго слоя заметно подавляет нарастающие возмущения, хотя при достаточно больших $\alpha $ нарастание возмущений в рассматриваемом основном течении наблюдается при меньших числах Рейнольдса, чем в случае однослойной стенки. Скорости роста возмущений оказываются еще меньше, чем в случае однослойной стенки. Рост модуля Юнга основания так же, как и рост модуля Юнга оболочки, подавляет нарастающие возмущения.
Фиг. 5.
Нейтральные кривые $\operatorname{Re} _{{\text{c}}}^{'}(\alpha ,0)$ (сплошная линия) и линии уровня скоростей нарастания ${{\omega }_{i}}$ возмущений (пунктир), $n = 0$. Двухслойная стенка без демпфирования с модулем Юнга оболочки ${{E}_{{\text{s}}}} = 2 \times {{10}^{5}}$ Па при различных значениях модуля Юнга ${{E}_{{\text{f}}}}$ [Па] основания.
В случае двухслойной стенки с демпфированием ($d = 10,\;100$) в рассмотренном диапазоне значений ${\text{Re}}$ и $\alpha $ не было обнаружено нарастающих возмущений с $n = 0$ ни при использовании условий (5.16), ни при использовании упрощенных условий (5.16').
8.2. Гармонические в азимутальном направлении возмущения
Далее была проанализирована устойчивость основного течения по отношению к гармоническим в азимутальном направлении возмущениям. На фиг. 6 для трубы с однослойной стенкой представлены кривые нейтральной устойчивости ${{\operatorname{Re} }_{{\text{c}}}}(\alpha ,n)$ и $\operatorname{Re} _{{\text{c}}}^{'}(\alpha ,n)$ при различных значениях модуля Юнга ${{E}_{{\text{s}}}}$ оболочки. Видно, что при изменении ${{E}_{{\text{s}}}}$ качественное поведение кривых совпадает при всех рассмотренных $n$ и согласуется с тем, что с ростом жесткости стенки течение должно стабилизироваться. Для $n = 1$ и $2$ кривые ${{\operatorname{Re} }_{{\text{c}}}}(\alpha ,n)$ и $\operatorname{Re} _{{\text{c}}}^{'}(\alpha ,n)$ близки друг к другу при $1.5 \lesssim \alpha \lesssim 5$, а при остальных рассмотренных $\alpha $ заметно отличаются, хотя при $\alpha \gtrsim 5$ различие между ними значительно сокращается с ростом жесткости стенки. При $n = 3,\; \ldots ,\;6$ нейтральные кривые отличаются, главным образом, при достаточно больших $\alpha $, но это отличие также существенно уменьшается с ростом жесткости стенки.
Фиг. 6.
Нейтральные кривые $\operatorname{Re} _{{\text{c}}}^{{}}(\alpha ,n)$ (красный) и $\operatorname{Re} _{{\text{c}}}^{'}(\alpha ,n)$ (черный) для различных значений $n$ и модуля Юнга ${{E}_{{\text{s}}}}$ [Па] оболочки. Однослойная стенка.
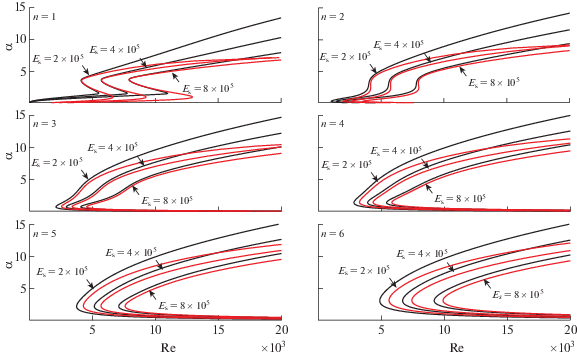
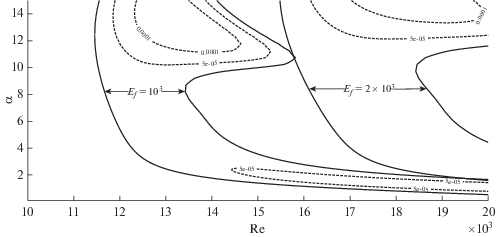
Далее мы ограничимся рассмотрением случая $n = 1$, где наблюдаются наибольшие отличия нейтральных кривых для рассмотренных параметров стенки. На фиг. 7 сравниваются нейтральные кривые $\operatorname{Re} _{{\text{c}}}^{{}}(\alpha ,1)$ и $\operatorname{Re} _{{\text{c}}}^{'}(\alpha ,1)$ и соответствующие линии уровня скоростей нарастания возмущений. Видно, что существенно отличаются только линии уровня, отвечающие ${{\omega }_{{\text{i}}}} < 0.01$, в то время как линии уровня, отвечающие ${{\omega }_{i}} \geqslant 0.01$, хорошо согласуются. Таким образом, при $n = 1$, как и при $n = 0$, использование упрощенных условий (5.16') по сравнению с условиями (5.16) приводит к появлению дополнительных областей значений ${\text{Re}}$ и $\alpha $, для которых существуют сравнительно слабо нарастающие возмущения.
Фиг. 7.
Нейтральные кривые ${{\operatorname{Re} }_{{\text{c}}}}(\alpha ,1)$ (сплошная красная линия), $\operatorname{Re} _{{\text{c}}}^{'}(\alpha ,1)$ (сплошная черная линия) и соответствующие линии уровня скоростей нарастания (пунктир), $n = 1$. Однослойная стенка, ${{E}_{{\text{s}}}} = 2 \times {{10}^{5}}$ Па.

Анализ слагаемых уравнения (6.22) показал (см. фиг. 8 и 9), что при $n = 1$ и достаточно больших $\alpha $ появление таких возмущений, как и при $n = 0$, главным образом, обусловлено существенно меньшим отводом кинетической энергии возмущения основного течения к стенке при использовании упрощенных динамических условий (5.16'), чем при использовании условий (5.16). При достаточно малых значениях $\alpha $ расчеты показали, что нельзя выделить какое-то одно слагаемое в (6.22), которое значительно сильнее других менялось бы в зависимости от выбранных динамических условий, и тем самым определить единственный механизм роста или убыли кинетической энергии возмущения, вызывающий в конечном счете отличия нейтральных кривых $\operatorname{Re} _{{\text{c}}}^{{}}(\alpha ,1)$ и $\operatorname{Re} _{{\text{c}}}^{'}(\alpha ,1)$. Например, для $\alpha = 0.3$ (см. фиг. 10) можно отметить следующее:
Фиг. 8.
Нейтральные кривые ${{\operatorname{Re} }_{{\text{c}}}}(\alpha ,1)$ (красная сплошная линия), с $\operatorname{Re} _{{\text{c}}}^{'}(\alpha ,1)$ (черная сплошная линия) и линии уровня величины $(\tilde {I}_{i}^{'} - \tilde {I}_{i}^{{}}) \times {{10}^{2}}$, $i = 1,\; \ldots ,\;4$ (пунктир), $n = 1$. Однослойная стенка, ${{E}_{{\text{s}}}} = 2 \times {{10}^{5}}$ Па.

Фиг. 9.
Нейтральные кривые ${{\operatorname{Re} }_{{\text{c}}}}(\alpha ,1)$ (красная сплошная линия), $\operatorname{Re} _{{\text{c}}}^{'}(\alpha ,1)$ (черная сплошная линия) и линии уровня величин ${{\tilde {I}}_{3}} \times {{10}^{2}}$ и $\tilde {I}_{3}^{'} \times {{10}^{2}}$ (пунктир), $n = 1$. Однослойная стенка, ${{E}_{{\text{s}}}} = 2 \times {{10}^{5}}$ Па.

Фиг. 10.
Зависимость от ${\text{Re}}$ величин ${{\tilde {I}}_{i}}$ и $\tilde {I}_{i}^{'}$, $i = 1,\; \ldots ,\;4$, вычисленных при использовании условий (5.16) и (5.16') соответственно, $\alpha = 0.3$, $n = 1$. Однослойная стенка, ${{E}_{{\text{s}}}} = 2 \times {{10}^{5}}$ Па.

– при $\operatorname{Re} _{{\text{c}}}^{'}(0.3,1) \lesssim {\text{Re}} \lesssim 565$ все слагаемые в (6.22) чувствительны к выбору динамических условий, хотя второе, отвечающее за рассеяние энергии возмущения из-за вязкости, – в меньшей степени, чем остальные;
– при $565 \lesssim {\text{Re}} \leqslant {{\operatorname{Re} }_{{\text{c}}}}(0.3,1)$ чувствительны, главным образом, первое и третье слагаемые, причем с ростом ${\text{Re}}$ третье слагаемое все слабее зависит от выбора динамических условий. Второе (за исключением узкого диапазона $3400 \lesssim {\text{Re}} \leqslant {{\operatorname{Re} }_{{\text{c}}}}(0.3,1)$) и четвертое слагаемые, напротив, принимают практически одинаковые значения, как при использовании условий (5.16), так и условий (5.16');
– при ${\text{Re}} \gtrsim {{\operatorname{Re} }_{{\text{c}}}}(0.3,1)$ все слагаемые принимают достаточно близкие значения, как при использовании условий (5.16), так и условий (5.16'). Как следствие, соответствующие линии уровня ${{\omega }_{i}}$ на фиг. 7 хорошо согласуются. Видно, что в этом случае нарастание возмущения, главным образом, обеспечивается за счет передачи ему энергии от основного течения.
Скачкообразное изменение значений ${{\tilde {I}}_{i}}$ вблизи ${\text{Re}} = 565$ при $\alpha = 0.3$ связано со сменой ведущего собственного значения и отвечающей ему собственной функции проблемы (5.14), (5.15), (5.16), (5.17). На фиг. 11 даны нормированные на $\sqrt {{{\alpha }^{2}} + {{n}^{2}}} $ главные части спектров проблемы (5.14), (5.15), (5.17) с условиями (5.16) и (5.16') в случае трубы с однослойной податливой стенкой с ${{E}_{{\text{s}}}} = 2 \times {{10}^{5}}$ Па, а также проблемы (5.14), (5.17) с условиями прилипания на твердой стенке. Видно, что почти все собственные значения, отвечающие податливой стенке, близки к собственным значениям, отвечающим твердой стенке, и, как показали расчеты, сходятся к последним с увеличением жесткости оболочки. Однако два ведущих собственных значения сильно отличаются от ведущих собственных значений для твердой стенки и не сходятся к ним при увеличении жесткости стенки (хотя и перестают быть ведущими). Одному отвечает возмущение с отрицательной фазовой скоростью ${{c}_{r}}$, а второму – с положительной. В рассматриваемом диапазоне значений Re расчеты для $\alpha = 0.3$ и ${{E}_{{\text{s}}}} = 2 \times {{10}^{5}}$ Па показали, что при ${\text{Re}} \leqslant 565$ ведущим является собственное значение с ${{c}_{r}} < 0$ в случае условий (5.16) и с ${{c}_{r}} > 0$ в случае условий (5.16'), а при ${\text{Re}} \geqslant 570$ ведущим всегда является собственное значение с ${{c}_{r}} > 0$ (см. также табл. 2). На фиг. 12 для $\alpha = 0.3$ показаны модули амплитуд $\tilde {u}$, ${\tilde {v}}$, $\tilde {w}$ компонент возмущения скорости, отвечающего ведущему собственному значению при условиях (5.16) и (5.16'). Видно, что в случае условий (5.16) модули этих амплитуд при Re = 565 и Re = 57$0$ заметно отличаются, чем и обусловлен скачок значений ${{\tilde {I}}_{i}}$ на фиг. 10. Отметим, что при Re = 57$0$ амплитуды $\left| {\tilde {u}} \right|$, $\left| {{\tilde {v}}} \right|$, $\left| {\tilde {w}} \right|$, рассчитанные при условиях (5.16), гораздо слабее отличаются от соответствующих амплитуд, вычисленных при условиях (5.16').
Фиг. 11.
Нормированная на $\sqrt {{{\alpha }^{2}} + {{n}^{2}}} $ главная часть спектра проблемы (5.14), (5.15), (5.17) с динамическими условиями (5.16) ($\bigcirc $) и (5.16') ($ \times $) в случае однослойной податливой стенки с ${{E}_{{\text{s}}}} = 2 \times {{10}^{5}}$ Па, а также проблемы (5.14), (5.17) с условиями прилипания на твердой стенке ($\square $), ${\text{Re}} = 565$, $\alpha = 0.3$, $n = 1$.
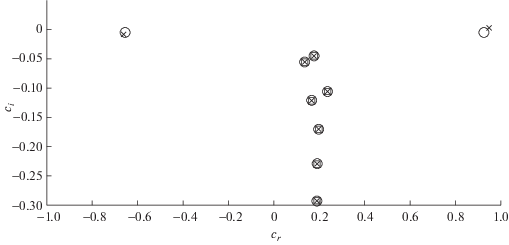
Таблица 2.
Первые два ведущих собственных значения проблемы (5.14), (5.15), (5.17) с динамическими условиями (5.16) и (5.16'), нормированные на $\sqrt {{{\alpha }^{2}} + {{n}^{2}}} $, $\alpha = 0.3$, $n = 1$. Однослойная стенка, ${{E}_{{\text{s}}}} = 2 \times {{10}^{5}}$ Па
| ${{c}_{r}} \times 10$ | ${{c}_{i}} \times {{10}^{3}}$ | ${{c}_{r}} \times 10$ | ${{c}_{i}} \times {{10}^{3}}$ | |
|---|---|---|---|---|
| ${\text{Re}} = 565$ | ||||
| (5.16) | –6.5505 | –4.8592 | 9.2550 | –4.8639 |
| (5.16') | 9.4815 | 2.8885 | –6.6181 | –8.0466 |
| ${\text{Re}} = 570$ | ||||
| (5.16) | 9.1859 | –4.8458 | –6.4816 | –4.8480 |
| (5.16') | 9.4113 | 2.8904 | –6.5481 | –8.0508 |
Фиг. 12.
Нормированные на $\mathcal{E}{{({\mathbf{\tilde {u}}})}^{{1/2}}}$ модули амплитуд компонент возмущения скорости, отвечающего ведущему собственному значению проблемы (5.14), (5.15), (5.17) с динамическими условиями (5.16) (красный) и (5.16') (черный), ${\text{Re}} = 565$ (верхний ряд), ${\text{Re}} = 570$ (нижний ряд), $\alpha = 0.3$, $n = 1$. Однослойная стенка, ${{E}_{{\text{s}}}} = 2 \times {{10}^{5}}$ Па.

Расчеты показали, что с ростом $\alpha $ упомянутые скачки значений ${{\tilde {I}}_{i}}$ наблюдаются при все меньших значениях числа Рейнольдса и, например, при $\alpha = 1$ отличия ${{\operatorname{Re} }_{{\text{c}}}}(1,1)$ и $\operatorname{Re} _{{\text{c}}}^{'}(1,1)$ обусловлены, главным образом, отличием значений, которые принимают первое и третье слагаемые в (6.22) (фиг. 13).
Фиг. 13.
Зависимость от ${\text{Re}}$ величин ${{\tilde {I}}_{i}}$ и $\tilde {I}_{i}^{'}$, $i = 1,\; \ldots ,\;4$, вычисленных при использовании условий (5.16) и (5.16') соответственно, $\alpha = 1$, $n = 1$. Однослойная стенка, ${{E}_{{\text{s}}}} = 2 \times {{10}^{5}}$ Па.

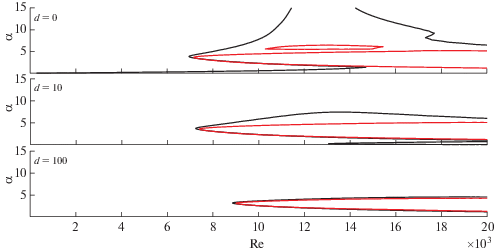
В заключение было выполнено сравнение нейтральных кривых ${{\operatorname{Re} }_{{\text{c}}}}(\alpha ,1)$ и $\operatorname{Re} _{{\text{c}}}^{'}(\alpha ,1)$ в случае двухслойной стенки (фиг. 14). Видно, что наличие второго слоя заметно подавляет нарастающие возмущения, как при использовании условий (5.16), так и (5.16'). При этом в случае условий (5.16) выделяется отдельная область неустойчивости при $5.5 \lesssim \alpha \lesssim 6.5$, а в случае упрощенных условий (5.16') появляются коротковолновые возмущения, которые нарастают при меньших числах Рейнольдса, чем в случае однослойной стенки, что также наблюдалось и при $n = 0$. Демпфирование сильно подавляет нарастающие возмущения. С его ростом разница между кривыми ${{\operatorname{Re} }_{{\text{c}}}}(\alpha ,1)$ и $\operatorname{Re} _{{\text{c}}}^{'}(\alpha ,1)$ уменьшается и уже при $d = 100$ они согласуются очень хорошо.
9. ЗАКЛЮЧЕНИЕ
В работе предложена новая численная модель для исследования линейной устойчивости течения Пуазейля в круглой трубе с податливой стенкой. Стенка рассматривается как тонкая однородная и изотропная оболочка, которая может быть окружена вязкоупругим основанием из однородного материала. Колебания стенки описываются уравнениями Лява общего вида. В рамках модели эти уравнения используются как динамические граничные условия для линеаризованных относительно основного стационарного течения уравнений движения вязкой несжимаемой жидкости. Кроме таких, полных, динамических условий, рассмотрены упрощенные, полученные с помощью приближения Доннела–Муштари–Власова. В рамках этого приближения предполагается, что оболочка нагружается и смещается в основном по нормали к срединной поверхности. Это, в частности, подразумевает пренебрежение касательными компонентами вязкого тензора напряжений в жидкости на стенке. Однако, учитывая уже известные результаты, при выводе упрощенных условий мы пренебрегли всеми компонентами вязкого тензора. Анализ характеристик устойчивости (нейтральных кривых, линий уровня скоростей нарастания возмущений) течения Пуазейля для широкого диапазона значений числа Рейнольдса, продольного и поперечного волновых чисел, жесткости и демпфирования стенки, позволил сделать следующие основные выводы:
• использование упрощенных динамических условий вместо полных качественно не меняет зависимость характеристик устойчивости основного течения от жесткости и демпфирования стенки;
• использование упрощенных динамических условий, по сравнению с полными, приводит к появлению дополнительных областей значений ${\text{Re}}$ и $\alpha $, при которых существуют слабо нарастающие возмущения;
• рост жесткости и/или демпфирования стенки значительно подавляет эти слабо нарастающие возмущения и, тем самым, сокращает отличия характеристик устойчивости основного течения, полученных при упрощенных динамических условиях, от характеристик, полученных при полных динамических условиях.
Для рассмотренных значений параметров задачи в зависимости от выбранных динамических условий сильнее всего отличаются характеристики устойчивости, отвечающие постоянным в азимутальном направлении возмущениям ($n = 0$) и стенке без демпфирования. В этом случае при использовании полных условий нарастающих возмущений обнаружено не было, в то время как при использовании упрощенных условий были найдены слабо нарастающие возмущения. Показано, что их наличие, главным образом, обусловлено значительно меньшим отводом кинетической энергии возмущения к стенке, чем при использовании полных динамических условий. При наличии демпфирования нарастающих возмущений с $n = 0$ найдено не было ни при полных, ни при упрощенных динамических условиях.
Кроме того, расчеты показали, что для рассмотренных значений $\alpha $ и параметров стенки устойчивость течения определяют гармонические в азимутальном направлении возмущения. Для $n = 1,\; \ldots ,\;6$ наибольшие отличия нейтральных кривых в зависимости от выбранных динамических условий наблюдаются при $n = 1$ для стенки без демпфирования с минимальным из рассмотренных значением модуля Юнга оболочки. В этом случае кривые, главным образом, отличаются при $\alpha \lesssim 1.5$ и $\alpha \gtrsim 5$ из-за слабо нарастающих возмущений, появляющихся при использовании упрощенных динамических условий. Анализ уравнения кинетической энергии возмущений показал, что при $\alpha \lesssim 1.5$ нельзя выделить единственный механизм изменения кинетической энергии возмущения, который определял бы в конечном счете наблюдаемые отличия характеристик устойчивости. При $\alpha \gtrsim 5$, напротив, появление слабо нарастающих возмущений при использовании упрощенных динамических условий, как и при $n = 0$, вызвано, главным образом, значительно меньшим, чем при использовании полных динамических условий, отводом кинетической энергии возмущения к стенке.
Полученные результаты об устойчивости течения Пуазейля в трубе с податливой стенкой, моделируемой на основе теории тонких оболочек, позволяют заключить, что для качественного изучения влияния вязкоупругих характеристик стенки на устойчивость основного течения при значениях параметров задачи, характерных для медицинских приложений, колебания стенки можно описывать упрощенными уравнениями Лява, полученными в приближении Доннела–Муштари–Власова. При этом важно анализировать не только нейтральные кривые, но и скорости роста возмущений. Их величина позволит судить о том, как изменятся нейтральные кривые при учете касательных напряжений, возникающих на податливой стенке.
Автор выражает благодарность А.В. Бойко (ИТПМ СО РАН) за плодотворные обсуждения результатов работы и рецензенту данной работы за важные замечания и предложения.
Список литературы
Kramer M.O. Boundary layer stabilization by distributed damping // J. Aeron. Sci. 1957. V. 24. P. 459–460.
Benjamin T. Effects of a flexible boundary on hydrodynamic stability // J. Fluid Mech. 1960. V. 9. P. 513–532.
Landahl M.T. On the stability of a laminar incompressible boundary layer over a flexible surface // J. Fluid Mech. 1962. V. 13. P. 609–632.
Gad-el-Hak M. Compliant coatings for drug reduction // Progr. Aerosp. Sci. 2002. V. 38. P. 77–99.
Kumaran V. Hydrodynamic stability of flow through compliant channels and tubes. In: Carpenter P., Pedley T. ed. Flow Past Highly Compliant Boundaries and in Collapsible Tubes: Proceed. of the IUTAM Symp. held at the Univer. of Warwick, United Kingdom, 26–30 March 2001. Springer, 2003. P. 91–118.
Evrensel C.A., Khan M.R., Elli S., Krumpe P.E. Viscous airflow through rigid tube with a compliant lining: a simple model for the air-mucus interaction in pulmonary airways // J. Biomech. Eng. 1993. V. 115. P. 262–270.
Hamadiche M., Kizilova N. Temporal and spatial instabilities of the flow in the blood vessels as multi-layered compliant tubes // Inter. J. Dyn. Fluids. 2005. V. 1. P. 1–25.
Hamadiche M., Kizilova N., Gad-el-Hak M. Suppression of absolute instabilities in the flow inside a compliant tube // Commun. Numer. Meth. Engng. 2009. V. 25. P. 505–531.
Boiko A.V. On modelling the stability of fluid flows in compliant pipes applied to hemodynamic problems // Siber. J. Phys. 2015. V. 10. P. 29–42. (In Russian)
Guaus A., Bottaro A. Instabilities of the flow in a curved channel with compliant walls // Proc. R. Soc. A Math. Phys. Eng. Sci. 2007. V. 463. № 2085. P. 2201–2222.
Hœpffner J., Bottaro A., Favier J. Mechanisms of non-modal energy amplification in channel flow between compliant walls // J. Fluid Mech. 2010. V. 642. P. 489–507.
Hahn H.G. Theory of Elasticity: Fundamentals of linear theory and its applications. Moscow: Mir, 1988. 344 p. (in Russian).
Carpenter P.W., Garrad A.D. The hydrodynamic stability of flow over Kramer-type compliant surfaces. Part 1. Tollmien–Schlichting instabilities // J. Fluid Mech. 1985. V. 155. P. 465–510.
Novozhilov V.V., Chernykh K.F., Mikhailovsky E.I. Linear theory of thin shells. Leningrad: Polytekhnika, 1991. 656 p. (in Russian).
Soedel W. Vibrations of shells and plates. 3rd ed.: Marcel Dekker, 2004. xxiv, 553 p.
Domaradzki J.A., Metcalfe R.W. Stabilization of laminar boundary layers by compliant membranes // Phys. Fluids 1986. V. 30. P. 695–705.
Nagata M., Cole T.R. On the stability of plane Poiseuille flow between compliant boundaries // WIT Trans. Model. Sim. 1999. V. 21. P. 231–240.
Schmid P.J., Henningson D.S. Stability and transition in shear flows. Berlin: Springer-Verlag, 2000. 556 p.
Drazin P.G., Reid W.H. Hydrodynamic stability, 2nd ed. Cambridge: Cambridge Univer. Press, 2004. 258 p.
Boiko A.V., Dovgal A.V., Grek G.R., Kozlov V.V. Physics of transitional shear flows. Berlin: Springer, 2012. 272 p.
Boiko A.V., Nechepurenko Yu.M. Numerical spectral analysis of temporal stability of laminar duct flows with constant cross sections // J. Comput. Math. Math. Phys. 2008. V. 48. № 10. P. 1–17.
Nechepurenko Yu.M. On the dimension reduction of linear differential-algebraic control systems // Doklady Mathematics. 2012. V. 86. P. 457–459.
Boyd J.P. Chebyshev and Fourier Spectral Methods, 2nd ed. DOVER Publ., Inc., New York, 2000. 594 p.
Meseguer Á., Trefethen L.N. A spectral Petrov–Galerkin formulation for pipe flow I: linear stability and transient growth. Rep. 00/18, Numerical Analysis Group, Oxford Univer., Computing Lab., 2000.
Fornberg B. A pseudospectral approach for polar and spherical geometries // SIAM J. Sci. Comp. 1995. V. 16. P. 1071–1081.
Trefethen L.N. Spectral Methods in MATLAB. Philadelphia: SIAM, 2000. 160 p.
Demyanko K.V. Numerical model for the investigation of hydrodynamic stability of shear flows in pipes of elliptic cross-section // Russ. J. Numer. Anal. Math. Modell. 2019. V. 34. P. 301–316.
Landau L.D., Lifshitz E.M. Fluid mechanics, 2nd ed. Oxford: Pergamont Press, 1987. 539 p.
Lucey A.D., Carpenter P.W. Boundary layer instability over compliant walls: Comparison between theory and experiment // Phys. Fluids. 1995. V. 7. P. 2355–2363.
Schmid P.J., Henningson D.S. Optimal energy density growth in Hagen-Poiseuille flow // J. Fluid Mech. 1994. V. 227. P. 197–225.
Davies C., Carpenter P.W. Numerical simulation of the evolution of Tollmien-Schlichting waves over finite compliant panels // J. Fluid Mech. 1997. V. 335. P. 361–392.
Canuto C., Hussaini M.Y., Quarteroni A., Zang T.A. Spectral methods. Fundamentals in single domains. Springer, Berlin, 2006. 563 p.
Weideman J.A.C., Reddy S.C. A MATLAB differentiation matrix suite // ACM Trans. Math. Software. 2000. V. 26. № 4. P. 465–519.
Berrut J.P., Trefethen L.N. Barycentric Lagrange interpolation // SIAM Rev. 2004. V. 46. № 3. P. 501–517.
Temam R. Navier–Stokes Equations: Theory and Numerical Analysis. NorthHolland, Amsterdam, 1977. 500 p.
Golub G.H., van Loan C.F. Matrix computations. Third ed. London: The John Hopkins Univer. Press, 1996. 694 p.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики