Журнал вычислительной математики и математической физики, 2022, T. 62, № 11, стр. 1868-1882

Интерполяционная балансно-характеристическая схема с улучшенными дисперсионными свойствами для задач вычислительной гидродинамики

Н. А. Афанасьев^1, *, Н. Э. Шагиров^1, **, В. М. Головизнин^1, ***

¹ 119991 Москва, Ленинские горы, МГУ имени М.В. Ломоносова
Москва, Россия

^* E-mail: vmnaf@cs.msu.ru
^** E-mail: nikkey.shagirov@yandex.ru
^*** E-mail: gol@ibrae.ac.ru

Поступила в редакцию 09.04.2022
После доработки 09.04.2022
Принята к публикации 07.07.2022

EDN: VZNQOV
DOI: 10.31857/S0044466922110023

Аннотация

Балансно-характеристические схемы для численного решения систем гиперболических уравнений объединяют достоинства консервативных методов улавливания скачка и метода характеристик. Они оперируют двумя типами переменных – консервативными и потоковыми. Консервативные переменные имеют смысл средних величин, относятся к серединам ячеек и вычисляются на основе метода конечного объема. Потоковые переменные определяют потоки на гранях расчетных ячеек и рассчитываются с использованием характеристической формы уравнений и локальных инвариантов Римана. Эта часть алгоритма допускает различные реализации, от которых зависят диссипативные и дисперсионные свойства алгоритмов. Так, в схеме КАБАРЕ потоковые величины вычисляются линейной экстраполяцией локальных инвариантов, но существуют и схемы с интерполяцией инвариантов и последующим переносом их по характеристикам (схемы с активными потоками). В последнем случае также возможны различные варианты. Результатам исследования одного из возможных вариантов балансно-характеристических схем интерполяционного типа для систем уравнений гиперболического типа и посвящена эта статья. Библ. 15. Табл. 1. Фиг. 13.

Ключевые слова: вычислительная гидродинамика, балансно-характеристические методы, гиперболические уравнения, инварианты Римана.

1. ВВЕДЕНИЕ

Вычислительная гидродинамика, как правило, имеет дело с системами законов сохранения гиперболического типа с возмущенной правой частью [1], [2]. К таким системам, в частности, относятся уравнения динамики стратифицированной жидкости со свободной границей, описывающие циркуляцию морей и океанов [3]. Сложная природа таких задач требует разработки численных методов высокого порядка точности, обладающих минимальным вычислительным шаблоном, применимых на сетках с произвольной топологией ячеек и эффективных с точки зрения параллелизации.

Одним из активно развивающихся подходов к решению систем уравнений гиперболического типа являются балансно-характеристические методы [4]. Такие методы позволяют учитывать не только дивергентную, но и характеристическую природу уравнений, реконструируя потоки с использованием локальных инвариантов Римана. Для балансно-характеристической схемы К-АБАРЕ [5] был проведен полный цикл исследований, начиная от решения одномерного линейного уравнения переноса [6] и заканчивая решением многомерных задач газовой динамики [5] и вычислительной океанологии [7], [8].

Недостатком схемы КАБАРЕ является ограниченность сферы ее применения расчетными сетками с четырехугольными и гексагональными ячейками. Известные обобщения схемы К-АБАРЕ на треугольные двумерные сетки [9], [10] обладают рядом недостатков, затрудняющих их применение для решения прикладных задач. Разработка балансно-характеристических схем с хорошими диссипативными и дисперсионными свойствами на расчетных сетках с более общей структурой ячеек является, таким образом, достаточно актуальной задачей.

В работе [2] был предложен балансно-характеристический метод решения систем гиперболического типа, основанный на параболической реконструкции инвариантов Римана внутри ячейки и последующим их переносом на новый временной слой. Метод был сформулирован для одномерных задач, а для многомерного случая были сформулированы основные идеи его обобщения. В ходе экспериментов выяснилось, что используемые в данном методе процедуры монотонизации на основе принципа максимума [11] неэффективны. Дальнейшее развитие предложенного метода оказалось нецелесообразным.

В настоящей статье предлагается балансно-характеристический метод второго порядка аппроксимации, также основанный на параболической реконструкции инвариантов Римана, но учитывающий интегральный смысл консервативных переменных метода. Для нового метода приводятся дисперсионные и диссипативные поверхности, анализируются его свойства в применении к линейному уравнению переноса. Метод тестируется на одномерных уравнениях переноса, Хопфа и мелкой воды.

Текст организован следующим образом. В разд. 2 приведены метод [2] и новый метод для линейного уравнения переноса, проанализированы их свойства. В разд. 3 описывается новый балансно-характеристический метод для одномерных систем законов сохранения гиперболического типа, обсуждаются его особенности. Тестовые расчеты для уравнений переноса, Хопфа и мелкой воды приводятся в разд. 4. Статья завершается разд. 5 с заключительными замечаниями.

2. ОПИСАНИЕ МЕТОДА ДЛЯ УРАВНЕНИЯ ПЕРЕНОСА

Рассмотрим простейшее одномерное линейное однородное уравнение переноса

(1)

$\frac{{\partial u}}{{\partial t}} + c\frac{{\partial u}}{{\partial x}} = 0,\quad c = {\text{const}} > 0.$

Здесь $x$ – пространственная координата, $t$ – время. Для определенности будем считать, что $(x,\;t) \in \Omega = [a,\;b] \times [0,\;T]$ и дополним наше уравнение начальным условием

(2)

$u(x,0) = f(x),\quad a \leqslant x \leqslant b,$

и некоторым граничным условием (например, условием периодичности).

Введем пространственно-временную сетку $\omega = {{\omega }_{h}} \times {{\omega }_{\tau }}$, где ${{\omega }_{h}} = \{ {{x}_{j}}\,|\,a = {{x}_{0}} < {{x}_{1}} < ... < {{x}_{N}} = b;$ ${{x}_{{j + 1}}} - {{x}_{j}} = h,\;j = \overline {0,N - 1} \} $ – сетка по пространству, ${{\omega }_{\tau }} = \{ {{t}_{n}}\,|\,0 = {{t}_{0}} < {{t}_{1}} < ... < {{t}_{K}} = T;\;{{t}_{{n + 1}}} - {{t}_{n}} = \tau ,$ $n = \overline {0,K - 1} \} $ – сетка по времени. Определим в центрах пространственных ячеек так называемые консервативные переменные: $U_{{j + 1/2}}^{n}$ – на целых слоях по времени, $U_{{j + 1/2}}^{{n + 1/2}}$ – на полуцелых слоях по времени. В узлах сетки $\omega $ определим так называемые потоковые переменные: $u_{j}^{n}$.

2.1. Метод ICCh-1 для линейного уравнения переноса

Ранее в работе [2] был предложен новый балансно-характеристический метод интерполяционного типа для решения уравнения (1):

(3)

$\frac{{U_{{j + 1/2}}^{{n + 1/2}} - U_{{j + 1/2}}^{n}}}{{\tau {\text{/}}2}} + c\frac{{u_{{j + 1}}^{n} - u_{j}^{n}}}{h} = 0,$

(4)

$u_{{j + 1}}^{{n + 1}} = (1 - 3r + 2{{r}^{2}})u_{{j + 1}}^{n} + 4r(1 - r)U_{{j + 1/2}}^{n} + 2r(r - 0.5)u_{j}^{n},$

(5)

$\frac{{U_{{j + 1/2}}^{{n + 1}} - U_{{j + 1/2}}^{{n + 1/2}}}}{{\tau {\text{/}}2}} + c\frac{{u_{{j + 1}}^{{n + 1}} - u_{j}^{{n + 1}}}}{h} = 0,$

где $r = c\tau {\text{/}}h$ – число Куранта–Фридрихса–Леви. Уравнения (3) и (5) (консервативные фазы) есть консервативные аппроксимации (1) по методу конечного объема в ячейке $[{{x}_{j}},{{x}_{{j + 1}}}]$ на слоях $n$ и $n + 1$ соответственно. Уравнение (4) (характеристическая фаза) представляет собой перенос инварианта Римана $u$ по характеристике $x - ct = {\text{const}}$, опущенной из точки $({{x}_{{j + 1}}},{{t}_{{n + 1}}})$ на слой по времени $n$ (см. фиг. 1). При этом переносимое значение $u$ восполняется по параболе ${{P}_{2}}(x)$, построенной по 3 значениям на нижнем слое: $u_{{j + 1}}^{{n + 1}} = {{P}_{2}}({{x}_{{j + 1}}} - c\tau )$,

(6)

${{P}_{2}}({{x}_{{j + 1}}}) = u_{{j + 1}}^{n},$

(7)

$\begin{gathered} {{P}_{2}}({{x}_{j}}) = u_{j}^{n}, \\ {{P}_{2}}({{x}_{{j + 1/2}}}) = U_{{j + 1/2}}^{n}. \\ \end{gathered} $

Фиг. 1.

Шаблон характеристической фазы алгоритма.

Метод ICCh-1 (interpolatory conservative-characteristic 1) (3)–(5) является устойчивым при числах Куранта $r \in [0,1]$ и обладает вторым порядком аппроксимации, но, в отличие от балансно-характеристической схемы КАБАРЕ [5], не является обратимым по времени. Для получения монотонного решения метод также дополняется процедурой нелинейной коррекции потоков на основе принципа максимума [11] после характеристической фазы (4):

(8)

$u_{{j + 1}}^{{n + 1}} = \left( {\begin{array}{*{20}{l}} {\tilde {u}_{{j + 1}}^{{n + 1}},\quad {\text{если}}\quad [\min u]_{{j + 1/2}}^{n} \leqslant \tilde {u}_{{j + 1}}^{{n + 1}} \leqslant [\max u]_{{j + 1/2}}^{n},} \\ {[\min u]_{{j + 1/2}}^{n},\quad {\text{если}}\quad \tilde {u}_{{j + 1}}^{{n + 1}} < [\min u]_{{j + 1/2}}^{n},} \\ {[\max u]_{{j + 1/2}}^{n},\quad {\text{если}}\quad \tilde {u}_{{j + 1}}^{{n + 1}} > [\max u]_{{j + 1/2}}^{n},} \end{array}} \right.$

где $\tilde {u}_{{j + 1}}^{{n + 1}}$ – потоковое значение, полученное в результате характеристической фазы (4), и

$[\min u]_{{j + 1/2}}^{n} = \min \{ u_{j}^{n},U_{{j + 1/2}}^{n},u_{{j + 1}}^{n}\} ,$

$[\max u]_{{j + 1/2}}^{n} = \max \{ u_{j}^{n},U_{{j + 1/2}}^{n},u_{{j + 1}}^{n}\} .$

Метод ICCh-1 разрабатывался в первую очередь для того, чтобы распространить его на двумерные треугольные и трехмерные тетраэдральные сетки, на которых применение схемы КА-БАРЕ достаточно проблематично [9], [10]. Но данный метод обладает нормальной дисперсией (т.е. бегущие волны всех гармоник запаздывают по отношению к аналитическому решению) при малых числах Куранта, что отражено на его дисперсионной поверхности (см. фиг. 3). Экспериментальные расчеты показывают, что нормальная дисперсия метода делает процедуру монотонизации (8) неэффективной, и затрудняет использование метода даже на простейших нелинейных уравнениях гиперболического типа. Актуальной становится разработка интерполяционного балансно-характеристического метода, обладающего схожим с методом ICCh-1 вычислительным шаблоном и хотя бы частично аномальной дисперсией при малых числах Куранта.

2.2. Метод ICCh-2 для линейного уравнения переноса

Для построения модифицированного балансно-характеристического метода интерполяционного типа изменим характеристическую фазу метода ICCh-1 (4), а консервативные фазы (3) и (5) оставим прежними. Как и ранее, потоковое значение $u_{{j + 1}}^{{n + 1}}$ мы будем переносить по характеристике $x - ct = {\text{const}}$, опущенной из точки $({{x}_{{j + 1}}},{{t}_{{n + 1}}})$ на слой по времени $n$ (см. фиг. 1), но функцию $u(x)$ на нижнем слое восполним с помощью другой параболы ${{\tilde {P}}_{2}}(x)$.

Так как консервативные фазы (3), (5) есть аппроксимации закона сохранения (1), то консервативные переменные $U_{{j + 1/2}}^{n}$ приближают средние значения $u(x,{{t}_{n}})$ по ячейкам $[{{x}_{j}},{{x}_{{j + 1}}}]$:

$U_{{j + 1/2}}^{n} \approx \frac{1}{h}\int\limits_{{{x}_{j}}}^{{{x}_{{j + 1}}}} {\kern 1pt} u(x,{{t}_{n}})dx.$

Воспользуемся этим свойством и построим на нижнем слое параболу ${{\tilde {P}}_{2}}(x)$, удовлетворяющую условиям (6), (7) и интегральному условию:

$\frac{1}{h}\int\limits_{{{x}_{j}}}^{{{x}_{{j + 1}}}} {\kern 1pt} {{\tilde {P}}_{2}}(x)dx = U_{{j + 1/2}}^{n}.$

Тогда перенос потокового значения по характеристике $u_{{j + 1}}^{{n + 1}} = {{\tilde {P}}_{2}}({{x}_{{j + 1}}} - c\tau )$ приведет к отличной от (4) характеристической фазе:

(9)

$u_{{j + 1}}^{{n + 1}} = (1 - 4r + 3{{r}^{2}})u_{{j + 1}}^{n} + 6r(1 - r)U_{{j + 1/2}}^{n} + r(3r - 2)u_{j}^{n}.$

Отметим, что способ параболической реконструкции инварианта Римана (9) также используется в V-схеме Ван Лира [12] и методе Active Flux третьего порядка [13]. Схему (3), (9), (5) назовем ICCh-2-методом (interpolatory conservative-characteristic 2).

2.3. Свойства метода ICCh-2

Для анализа диссипативных и дисперсионных свойств полученной разностной схемы подставим в уравнения (3), (9), (5) частное решение в виде бегущей волны:

$u_{j}^{n} = A\exp \{ i(\omega n\tau - kjh)\} = A{{q}^{n}}\exp \{ - i(kjh)\} ,\quad q = {{e}^{{i\omega \tau }}},$

$U_{{j + 1/2}}^{n} = B\exp \{ i(\omega n\tau - k(j + 0.5)h)\} = B{{q}^{n}}\exp \{ - i[k(j + 0.5)h]\} .$

Таким образом, получим следующее квадратное уравнение для определения $q$:

${{q}^{2}} + q[4r - 3{{r}^{3}} - 2 + {{e}^{{ikh}}}(3{{r}^{3}} - 6{{r}^{2}} + 2r)] + 1 - 4r + 6{{r}^{2}} - 3{{r}^{3}} + {{e}^{{ikh}}}(3{{r}^{3}} - 2r) = 0.$

Данное уравнение имеет два корня: ${{q}_{1}} = {{q}_{1}}(r,kh),$ ${{q}_{2}} = {{q}_{2}}(r,kh)$, которые зависят от приведенного волнового числа $kh \in [ - \pi ,\pi ]$, а также от числа Куранта $r$. Модули этих корней определяют область устойчивости схемы: схема устойчива, если ${\text{|}}{{q}_{1}}{\text{|}} \leqslant 1$ и ${\text{|}}{{q}_{2}}{\text{|}} \leqslant 1$. Относительная дисперсия разностной схемы задается величиной

$\gamma (r,kh) = \frac{\omega }{{kc}} = - \frac{i}{{rkh}}\ln [q(r,kh)]$

и определяет степень отклонения фазовой скорости бегущей волны относительно аналитического решения уравнения (1). Дисперсия называется нормальной, если ${\text{|}}\gamma (r,kh){\kern 1pt} {\text{|}} < 1$ (т.е. бегущая волна отстает от аналитического решения), и аномальной, если ${\text{|}}\gamma (r,kh){\kern 1pt} {\text{|}} > 1$ (т.е. бегущая волна опережает аналитическое решение). Отметим, что один из двух корней (обозначим его как ${{q}_{2}}$) всегда является паразитным, и не несет в себе никакой полезной информации о свойствах схемы (кроме разве что определения области неустойчивости схемы при ${\text{|}}{{q}_{2}}{\text{|}} > 1$).

На фиг. 2 приведены диссипативные поверхности первых корней $z = {\text{|}}{{q}_{1}}(r,kh){\kern 1pt} {\text{|}}$ методов ICCh-1 (а) и IССh-2 (б) для чисел Куранта $r \in [0,1]$, на фиг. 3 – дисперсионные поверхности первых корней $z = {\text{|}}{{\gamma }_{1}}(r,kh){\kern 1pt} {\text{|}}$ методов ICCh-1 (а) и ICCh-2 (б). На фиг. 4 также дополнительно приведены диссипативная (а) и дисперсионная (б) поверхности второго корня метода IСCh-2. Поверхности для чисел Куранта $r \in (1, + \infty )$ не приводятся, так как в этой области оба метода являются неустойчивыми (${\text{|}}{{q}_{1}}{\text{|}} > 1$).

Фиг. 2.

Диссипативные поверхности первых корней $z = {\text{|}}{{q}_{1}}(r,kh){\kern 1pt} {\text{|}}$ методов ICCh-1 (a) и ICCh-2 (б).

Фиг. 3.

Дисперсионные поверхности первых корней $z = {\text{|}}{{\gamma }_{1}}(r,kh){\kern 1pt} {\text{|}}$ методов ICCh-1 (a) и ICCh-2 (б).

Фиг. 4.

Диссипативная поверхность $z = {\text{|}}{{q}_{2}}(r,kh){\kern 1pt} {\text{|}}$ и дисперсионная поверхность $z = {\text{|}}{{\gamma }_{2}}(r,kh){\kern 1pt} {\text{|}}$ второго (паразитного) корня метода IССh-2.

Как видно из диссипативных поверхностей на фиг. 2, метод ICCh-2, как и метод ICCh-1, устойчив при $0 \leqslant r \leqslant 1$ и необратим по времени, но при этом обладает меньшей диссипацией. Дисперсионные поверхности на фиг. 3 показывают, что метод ICCh-2 обладает аномальной дисперсией при малых числах Куранта, но только для высоких гармоник. Метод ICCh-1 при этом обладает только нормальной дисперсией в области малых чисел Куранта. Именно наличие области аномальной дисперсии позволяет частично монотонизировать метод ICCh-2, что будет показано на тестовых расчетах.

В работе [2] было показано, что метод ICCh-1 обладает вторым порядком аппроксимации как по времени, так и по пространству. Покажем, что и для метода ICCh-2 это выполняется. Для этого просуммируем уравнения (3), (5) и подставим вместо потоковых значений $u_{j}^{{n + 1}}$ и $u_{{j + 1}}^{{n + 1}}$ выражения, задаваемые (9):

(10)

$\begin{gathered} \frac{{U_{{j + 1/2}}^{{n + 1}} - U_{{j + 1/2}}^{n}}}{\tau } + \frac{c}{2}\frac{{u_{{j + 1}}^{n} - u_{j}^{n}}}{h} + \frac{c}{2}\left[ {(1 - 4r + 3{{r}^{2}})\frac{{u_{{j + 1}}^{n} - u_{j}^{n}}}{h}} \right. + \\ \, + \left. {6r(1 - r)\frac{{U_{{j + 1/2}}^{n} - U_{{j - 1/2}}^{n}}}{h} + r(3r - 2)\frac{{u_{j}^{n} - u_{{j - 1}}^{n}}}{h}} \right] = 0. \\ \end{gathered} $

Заменяя в (10) значения сеточных функций на значения аналитического решения $u(x,t)$ в соответствующих точках и раскладывая $u(x,t)$ в ряд Тейлора в окрестности точки $({{x}_{{j + 1/2}}},{{t}_{n}})$, можно получить:

(11)

$\begin{gathered} {{u}_{t}}({{x}_{{j + 1/2}}},{{t}_{n}}) + c{{u}_{x}}({{x}_{{j + 1/2}}},{{t}_{n}}) - \frac{{{{c}^{2}}\tau }}{2}{{u}_{{xx}}}({{x}_{{j + 1/2}}},{{t}_{n}}) + \frac{\tau }{2}{{u}_{{tt}}}({{x}_{{j + 1/2}}},{{t}_{n}}) + \\ \, + \left( {\frac{{c{{h}^{2}}}}{{24}} - \frac{{{{c}^{2}}\tau h}}{8} + \frac{{5{{c}^{3}}{{\tau }^{2}}}}{{24}}} \right){{u}_{{xxx}}}({{x}_{{j + 1/2}}},{{t}_{n}}) + ... = 0. \\ \end{gathered} $

Воспользовавшись в (11) тем, что ${{u}_{t}} + c{{u}_{x}} = 0$ и ${{u}_{{tt}}} = {{c}^{2}}{{u}_{{xx}}}$ (что получается дифференцированием (1) по времени), получим следующий вид для погрешности аппроксимации в точке $({{x}_{{j + 1/2}}},{{t}_{n}})$:

(12)

$\psi _{{j + 1/2}}^{n} = \left( {\frac{{c{{h}^{2}}}}{{24}} - \frac{{{{c}^{2}}\tau h}}{8} + \frac{{5{{c}^{3}}{{\tau }^{2}}}}{{24}}} \right){{u}_{{xxx}}}({{x}_{{j + 1/2}}},{{t}_{n}}) + ...\;.$

Учитывая, что при решении уравнений гиперболического типа явными методами $\tau $ и $h$ есть величины одного порядка, (12) позволяет заключить, что метод ICCh-2 обладает вторым порядком аппроксимации. Как и метод ICCh-1, для получения монотонного решения метод ICCh-2 надо дополнять процедурой монотонизации (8).

3. ОПИСАНИЕ МЕТОДА ДЛЯ СИСТЕМ УРАВНЕНИЙ ГИПЕРБОЛИЧЕСКОГО ТИПА

Рассмотрим систему одномерных квазилинейных законов сохранения:

(13)

$\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \frac{{\partial {\mathbf{F}}({\mathbf{u}})}}{{\partial x}} = {\mathbf{Q}}(x,t,{\mathbf{u}}),$

где ${\mathbf{u}}$ – вектор неизвестных, ${\mathbf{F}}({\mathbf{u}})$ – векторная функция потоков, ${\mathbf{Q}}(x,t,{\mathbf{u}})$ – векторная функция источников и стоков. Систему (13) будем называть консервативной формой уравнений. Раскрывая в (13) производную по $x$, получим так называемую простую форму уравнений:

(14)

$\frac{{\partial {\mathbf{u}}}}{{\partial t}} + A({\mathbf{u}})\frac{{\partial {\mathbf{u}}}}{{\partial x}} = {\mathbf{Q}}(x,t,{\mathbf{u}}),$

где $A({\mathbf{u}})$ – матрица Якоби ${\mathbf{F}}({\mathbf{u}})$. Предполагая, что система (14) является гиперболической (т.е. все собственные значения $A({\mathbf{u}})$ действительны и имеется полный базис из собственных векторов) и что все аналитические выражения для инвариантов Римана известны (что выполняется для уравнения Хопфа и уравнений мелкой воды), получаем характеристическую форму уравнений:

$\frac{{\partial {\mathbf{I}}}}{{\partial t}} + \Lambda ({\mathbf{u}})\frac{{\partial {\mathbf{I}}}}{{\partial x}} = \widehat {\mathbf{Q}}(x,t,{\mathbf{I}}),$

где ${\mathbf{I}} = {\mathbf{I}}({\mathbf{u}}) = \{ {{I}_{k}}\} $ – вектор инвариантов Римана, $\Lambda ({\mathbf{u}}) = {\text{diag}}\{ {{\lambda }_{k}}\} $ – диагональная матрица собственных значений матрицы $A({\mathbf{u}})$, $\widehat {\mathbf{Q}}(x,t,{\mathbf{I}})$ – некоторая правая часть (точный вид которой нам неважен).

Метод ICCh-2 для системы законов сохранения (13) на неравномерной пространственно-временной сетке с шагами ${{\tau }_{n}} = {{t}_{{n + 1}}} - {{t}_{n}}$ и ${{h}_{{j + 1/2}}} = {{x}_{{j + 1}}} - {{x}_{j}}$ состоит из 3 фаз.

Фаза 1 (консервативная). Явное вычисление консервативных переменных на полуцелом слое ${\mathbf{U}}_{{j + 1/2}}^{{n + 1/2}}$ с помощью аппроксимации консервативных уравнений (13):

$\frac{{{\mathbf{U}}_{{j + 1/2}}^{{n + 1/2}} - {\mathbf{U}}_{{j + 1/2}}^{n}}}{{{{\tau }_{n}}{\text{/}}2}} + \frac{{{\mathbf{F}}({\mathbf{u}}_{{j + 1}}^{n}) - {\mathbf{F}}({\mathbf{u}}_{j}^{n})}}{{{{h}_{{j + 1/2}}}}} = {\mathbf{Q}}_{{j + 1/2}}^{n}.$

После вычисления консервативных переменных на промежуточном слое находятся собственные значения $({{\lambda }_{k}})_{{j + 1/2}}^{{n + 1/2}}$, которые будут определять направление переноса инвариантов Римана в характеристической фазе алгоритма.

Фаза 2 (характеристическая). Явное вычисление потоковых значений инвариантов Римана на новом временном слое ${\mathbf{I}}_{j}^{{n + 1}}$ с помощью переноса по соответствующим характеристикам (см. обозначения на фиг. 5):

$({{\tilde {I}}_{k}})_{j}^{{n + 1}} = \left( {\begin{array}{*{20}{l}} {\varphi [({{I}_{k}})_{j}^{n},({{I}_{k}})_{{cL}}^{n},({{I}_{k}})_{L}^{n},{{r}_{L}}] + {{\tau }_{n}}({{{\hat {Q}}}_{k}})_{{cL}}^{n},\quad {\text{если}}\quad ({{\lambda }_{k}})_{{cL}}^{{n + 1/2}} > 0\quad {\text{и}}\quad ({{\lambda }_{k}})_{{cR}}^{{n + 1/2}} > 0,} \\ {\varphi [({{I}_{k}})_{j}^{n},({{I}_{k}})_{{cR}}^{n},({{I}_{k}})_{R}^{n},{{r}_{R}}] + {{\tau }_{n}}({{{\hat {Q}}}_{k}})_{{cR}}^{n},\quad {\text{если}}\quad ({{\lambda }_{k}})_{{cL}}^{{n + 1/2}} < 0\quad {\text{и}}\quad ({{\lambda }_{k}})_{{cR}}^{{n + 1/2}} < 0,} \\ {0.5[({{I}_{k}})_{{cL}}^{{n + 1/2}} + ({{I}_{k}})_{{cR}}^{{n + 1/2}}] + 0.5{{\tau }_{n}}[({{{\hat {Q}}}_{k}})_{{cL}}^{n} + ({{{\hat {Q}}}_{k}})_{{cR}}^{n}]\quad {\text{иначе}},} \end{array}} \right.$

(15)

${{r}_{L}} = ({{\lambda }_{k}})_{{cL}}^{{n + 1/2}}\frac{{{{\tau }_{n}}}}{{{{h}_{{j - 1/2}}}}},{\kern 1pt} \quad {{r}_{R}} = \left| {({{\lambda }_{k}})_{{cR}}^{{n + 1/2}}} \right|\frac{{{{\tau }_{n}}}}{{{{h}_{{j + 1/2}}}}},$

$\begin{gathered} \varphi [\alpha ,\beta ,\gamma ,r] = (1 - 4r + 3{{r}^{2}})\alpha + 6r(1 - r)\beta + r(3r - 2)\gamma , \\ ({{{\hat {Q}}}_{k}})_{{j + 1/2}}^{n} = \frac{{({{I}_{k}})_{{j + 1/2}}^{{n + 1/2}} - ({{I}_{k}})_{{j + 1/2}}^{n}}}{{{{\tau }_{n}}/2}} + ({{\lambda }_{k}})_{{j + 1/2}}^{{n + 1/2}}\frac{{({{I}_{k}})_{{j + 1}}^{n} - ({{I}_{k}})_{j}^{n}}}{{{{h}_{{j + 1/2}}}}}. \\ \end{gathered} $

Требуемые значения инвариантов Римана на слоях $n$ и $n + 1{\text{/}}2$ при этом вычисляются по известным аналитическим формулам ${\mathbf{I}} = {\mathbf{I}}({\mathbf{u}})$. После переноса (15) инварианты Римана корректируются с помощью процедуры монотонизации на основе принципа максимума:

$({{I}_{k}})_{j}^{{n + 1}} = \left( {\begin{array}{*{20}{l}} {\operatorname{Max} \operatorname{Min} {{{[({{{\tilde {I}}}_{k}})_{j}^{{n + 1}}]}}_{{j - 1/2}}},\quad {\text{если}}\quad ({{\lambda }_{k}})_{{j - 1/2}}^{{n + 1/2}} > 0\quad {\text{и}}\quad ({{\lambda }_{k}})_{{j + 1/2}}^{{n + 1/2}} > 0,} \\ {\operatorname{Max} \operatorname{Min} {{{[({{{\tilde {I}}}_{k}})_{j}^{{n + 1}}]}}_{{j + 1/2}}},\quad {\text{если}}\quad ({{\lambda }_{k}})_{{j - 1/2}}^{{n + 1/2}} < 0\quad {\text{и}}\quad ({{\lambda }_{k}})_{{j + 1/2}}^{{n + 1/2}} < 0,} \\ {({{{\tilde {I}}}_{k}})_{j}^{{n + 1}}\quad {\text{иначе}},} \end{array}} \right.$

(16)

$\operatorname{Max} \operatorname{Min} {{[({{\tilde {I}}_{k}})_{j}^{{n + 1}}]}_{{j + 1/2}}} = \left( {\begin{array}{*{20}{l}} {({{{\tilde {I}}}_{k}})_{j}^{{n + 1}},\quad {\text{если}}\quad \min ({{I}_{k}})_{{j + 1/2}}^{n} \leqslant ({{{\tilde {I}}}_{k}})_{j}^{{n + 1}} \leqslant \max ({{I}_{k}})_{{j + 1/2}}^{n},} \\ {\max ({{I}_{k}})_{{j + 1/2}}^{n},\quad {\text{если}}\quad ({{{\tilde {I}}}_{k}})_{j}^{{n + 1}} > \max ({{I}_{k}})_{{j + 1/2}}^{n},} \\ {\min ({{I}_{k}})_{{j + 1/2}}^{n},\quad {\text{если}}\quad ({{{\tilde {I}}}_{k}})_{j}^{{n + 1}} < \min ({{I}_{k}})_{{j + 1/2}}^{n},} \end{array}} \right.$

$\begin{gathered} \min ({{I}_{k}})_{{j + 1/2}}^{n} = \min \{ ({{I}_{k}})_{j}^{n},({{I}_{k}})_{{j + 1/2}}^{n},({{I}_{k}})_{{j + 1}}^{n}\} + {{\tau }_{n}}({{{\hat {Q}}}_{k}})_{{j + 1/2}}^{n}, \\ \max ({{I}_{k}})_{{j + 1/2}}^{n} = \max \{ ({{I}_{k}})_{j}^{n},({{I}_{k}})_{{j + 1/2}}^{n},({{I}_{k}})_{{j + 1}}^{n}\} + {{\tau }_{n}}({{{\hat {Q}}}_{k}})_{{j + 1/2}}^{n}. \\ \end{gathered} $

После нахождения полного набора инвариантов Римана на следующем слое по времени $n + 1$ по известным аналитическим формулам вычисляются потоковые значения исходных неизвестных ${\mathbf{u}}_{j}^{{n + 1}} = {\mathbf{u}}({\mathbf{I}}_{j}^{{n + 1}})$.

Фиг. 5.

Шаблон переноса (15) инварианта Римана $({{I}_{k}})_{j}^{{n + 1}}$ слева (красный) и справа (синий).

Отметим, что в процессе проведения расчетов могут возникать так называемые звуковые точки, когда в один пространственно-временной узел приходят либо 0 ($({{\lambda }_{k}})_{{j - 1/2}}^{{n + 1/2}} < 0$ и $({{\lambda }_{k}})_{{j + 1/2}}^{{n + 1/2}} > 0$), либо 2 инварианта Римана ($({{\lambda }_{k}})_{{j - 1/2}}^{{n + 1/2}} > 0$ и $({{\lambda }_{k}})_{{j + 1/2}}^{{n + 1/2}} < 0$). В таких случаях требуется отдельный алгоритм обработки звуковых точек. В алгоритме (15) представлен самый простой способ такой обработки, когда на звуковых точках инвариант осредняется по значениям из центров левой и правой пространственно-временных ячеек. Более сложные алгоритмы обработки звуковых точек представлены в [14], [15].

Фаза 3 (консервативная). Вычисление консервативных переменных на следующем слое $U_{{j + 1/2}}^{{n + 1}}$ с помощью аппроксимации консервативных уравнений (13):

(17)

$\frac{{{\mathbf{U}}_{{j + 1/2}}^{{n + 1}} - {\mathbf{U}}_{{j + 1/2}}^{{n + 1/2}}}}{{{{\tau }_{n}}{\text{/}}2}} + \frac{{{\mathbf{F}}({\mathbf{u}}_{{j + 1}}^{{n + 1}}) - {\mathbf{F}}({\mathbf{u}}_{j}^{{n + 1}})}}{{{{h}_{{j + 1/2}}}}} = {\mathbf{Q}}_{{j + 1/2}}^{{n + 1}}.$

Схема (17) является, вообще говоря, неявной в силу наличия в правой части члена ${\mathbf{Q}}_{{j + 1/2}}^{{n + 1}}$, зависящего от еще не известной консервативной переменной ${\mathbf{U}}_{{j + 1/2}}^{{n + 1}}$. Тем не менее данное уравнение удается разрешить явно при линейной зависимости ${\mathbf{Q}}(x,t,{\mathbf{u}})$ от ${\mathbf{u}}$.

В конце третьей фазы с помощью собственных значений на новом слое $({{\lambda }_{k}})_{{j + 1/2}}^{{n + 1}}$ по заданному числу Куранта $CFL \in (0,1]$ вычисляется величина следующего шага по времени:

${{\tau }_{{n + 1}}} = CFL \cdot \mathop {\min }\limits_k \mathop {\min }\limits_j \left[ {\frac{{{{h}_{{j + 1/2}}}}}{{|{\kern 1pt} ({{\lambda }_{k}})_{{j + 1/2}}^{{n + 1}}{\kern 1pt} |}}} \right].$

4. ТЕСТОВЫЕ РАСЧЕТЫ

В данном разделе представлены результаты применения предложенного метода ICCh-2 к решению некоторых уравнений и систем уравнений в частных производных гиперболического типа. Рассматривались начально-краевые задачи для линейного уравнения переноса, уравнения Хопфа, а также для системы уравнений мелкой воды над плоским дном. Для сравнения приводятся результаты расчетов по схеме КАБАРЕ и методу ICCh-1.

4.1. Линейное уравнение переноса

Предложенный метод ICCh-2 был протестирован на задаче (1), (2) с периодическими граничными условиями на отрезке $x \in [0,\;1]$ при двух видах начальных условий – достаточно гладком и разрывном. В качестве гладкого начального условия был взят “одиночный гауссиан”

(18)

$f(x) = \exp [ - {{(x - {{x}_{0}})}^{2}}{\text{/}}{{\Delta }^{2}}];\quad {{x}_{0}} = 0.5,\quad \Delta = 0.1,$

в качестве разрывного – прямоугольник:

(19)

$f(x) = \left( {\begin{array}{*{20}{l}} {1,\quad 0.3 \leqslant x \leqslant 0.5,} \\ {0\quad {\text{иначе}}{\text{.}}} \end{array}} \right.$

Скорость переноса $c$ принималась равной единице.

Начальная инициализация потоковых и консервативных переменных проводилась следующим образом. В качестве начальных значений потоковых переменных использовались значения начального профиля в соответствующих узлах сетки ${{\omega }_{h}}$, значения консервативных переменных принимались равными полусуммам значений соседних потоковых переменных:

(20)

$u_{j}^{0} = f({{x}_{j}}),\quad j = \overline {0,N} ,$

(21)

$U_{{j + 1/2}}^{0} = 0.5(u_{j}^{0} + u_{{j + 1}}^{0}),\quad j = \overline {0,N - 1} {\kern 1pt} {\kern 1pt} .$

Сравнивались результаты, полученные по методам ICCh-2 и ICCh-1, а также по схеме КА-БАРЕ [4]. На фиг. 6 представлены результаты расчетов переноса начальных профилей (18), (19) на равномерной сетке из $N = 100$ ячеек при числе Куранта $CFL = 0.3$. Картинка (а) соответствует результату переноса начального профиля (18) и приводится на момент времени $t = 7.0$, что соответствует 7 проходам профиля по отрезку $[0,1]$. Картинка (б) соответствует результату переноса начального профиля (19) и приводится на момент времени $t = 1.0$, что соответствует 1 проходу профиля по отрезку $[0,1]$. Результаты на фиг. 6 показывают, что в случае переноса гладкого профиля при включенных процедурах монотонизации (8) метод ICCh-2 обладает меньшей численной дисперсией и диссипацией, чем методы КАБАРЕ и ICCh-1. При переносе разрывного профиля как у метода ICCh-1, так и у метода ICCh-2 возникают немонотонности, которые не удается сгладить процедурой монотоназиции. Тем не менее, так как метод ICCh-2 при $CFL = 0.3$ обладает частичной аномальной дисперсией, возникающие при его использовании немонотонности минимальны.

Фиг. 6.

Перенос начальных профилей (18), (19) для уравнения переноса (1) на $100$ ячейках, $CFL = 0.3$. (a) – результат переноса начального профиля (18) на момент времени $t = 7.0$; (б) – результат переноса начального профиля (19) на момент времени $t = 1.0$. 1 – решение, полученное по схеме КАБАРЕ, 2 – решение, полученное методом ICCh-1, 3 – решение, полученное методом ICCh-2, 4 – аналитическое решение.

В табл. 1 также приведены результаты численных исследований сходимости метода ICCh-2 на переносе гладкого профиля (18) при отключенной процедуре монотонизации (8). В табл. 1 указаны ошибки по $C$-норме ${{\left\| u \right\|}_{c}} = \mathop {\max }\limits_j {\text{|}}{{u}_{{j + 1/2}}}{\kern 1pt} {\text{|}}$ и порядки сходимости (OOC – order of convergence) на момент времени $t = 1.0$ на разных сетках. Результаты в табл. 1 позволяют заключить, что метод ICCh-2 обладает вторым порядком сходимости.

Таблица 1.

Ошибки по $C$-норме и порядки сходимости (OOC) для переноса гладкого профиля (18) по методу ICCh-2

Ячейки	C-ошибка $CFL = 0.3$	OOC$CFL = 0.3$	C -ошибка $CFL = 0.6$	OOC$CFL = 0.6$	C -ошибка $CFL = 0.9$	OOC$CFL = 0.9$
100	$4.57 \times {{10}^{{ - 3}}}$	–	$1.25 \times {{10}^{{ - 2}}}$	–	$2.5 \times {{10}^{{ - 2}}}$	–
200	$1.11 \times {{10}^{{ - 3}}}$	2.04	$3.17 \times {{10}^{{ - 3}}}$	1.98	$6.69 \times {{10}^{{ - 3}}}$	1.90
400	$2.71 \times {{10}^{{ - 4}}}$	2.03	$7.94 \times {{10}^{{ - 4}}}$	2.00	$1.7 \times {{10}^{{ - 3}}}$	1.98
800	$6.7 \times {{10}^{{ - 5}}}$	2.02	$1.99 \times {{10}^{{ - 4}}}$	2.00	$4.26 \times {{10}^{{ - 4}}}$	2.00
1600	$1.7 \times {{10}^{{ - 5}}}$	1.98	$5 \times {{10}^{{ - 5}}}$	1.99	$1.07 \times {{10}^{{ - 4}}}$	1.99

4.2. Уравнение Хопфа

Уравнение Хопфа имеет следующий вид:

(22)

$\frac{{\partial u}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {\frac{{{{u}^{2}}}}{2}} \right) = 0.$

Единственный инвариант Римана уравнения (22) и скорость его переноса совпадают с неизвестной функцией $u$.

Рассмотрим уравнение (22) в области $\Omega = [0,\;1] \times [0,\;T]$ с периодическими граничными условиями и начальным условием в виде прямоугольника:

(23)

${{u}_{0}}(x) = \left( {\begin{array}{*{20}{l}} {{{u}_{2}},\quad 0.1 \leqslant x \leqslant 0.3,} \\ {{{u}_{1}}\quad {\text{иначе}}{\text{.}}} \end{array}} \right.$

На фиг. 7 представлены результаты расчетов переноса начального профиля (23) при ${{u}_{1}} = 1,\;{{u}_{2}} = 2$ на момент времени $t = 0.4$ (a) и при ${{u}_{1}} = 0,\;{{u}_{2}} = 1$ на момент времени $t = 0.5$ (б) на равномерной сетке из $N = 100$ ячеек при числе Куранта $CFL = 0.3$. Начальные значения потоковых и консервативных переменных задавались аналогично (20), (21). В обоих расчетах у метода ICCh-2 возникают некоторые немонотонности слева от негладких участков решения. При этом для расчета задачи (б) это приводит к тому, что решение опускается ниже $0$ и возникает звуковая точка, алгоритм обработки которой (15) не приводит к аварийному останову. Отметим, что схема КАБАРЕ не обладает данным недостатком, так как процедура монотонизации (16) не дает решению уйти ниже $0$.

Фиг. 7.

Перенос начального профиля (23) для уравнения Хопфа (22) на $100$ ячейках при $CFL = 0.3$: (а) – ${{u}_{1}} = 1,\;{{u}_{2}} = 2$, профиль при $t = 0.4$; (б) – ${{u}_{1}} = 0,\;{{u}_{2}} = 1$, профиль при $t = 0.5$. 1 – решение, полученное по схеме КАБАРЕ, 2 – решение, полученное методом ICCh-2, 3 – аналитическое решение.

4.3. Уравнения мелкой воды

Рассмотрим систему одномерных уравнений мелкой воды над ровным дном:

(24)

$\frac{{\partial H}}{{\partial t}} + \frac{{\partial Hu}}{{\partial x}} = 0,\quad \frac{{\partial Hu}}{{\partial t}} + \frac{{\partial H{{u}^{2}}}}{{\partial x}} + \frac{g}{2}\frac{{\partial {{H}^{2}}}}{{\partial x}} = 0.$

Здесь $H(x,t)$ – глубина жидкости, $u(x,t)$ – горизонтальная скорость столба жидкости, $g$ – ускорение свободного падения. Система (24) обладает следующими инвариантами Римана ${{I}_{k}}$ и соответствующими им собственными значениями ${{\lambda }_{k}}$:

$\begin{gathered} {{I}_{1}} = u + 2\sqrt {gH} ,\quad {{\lambda }_{1}} = u + \sqrt {gH} , \\ {{I}_{2}} = u - 2\sqrt {gH} ,\quad {{\lambda }_{2}} = u - \sqrt {gH} . \\ \end{gathered} $

Тестирование метода ICCh-2 проводилось для различных задач Римана для дозвуковых, трансзвуковых и сверхзвуковых течений:

(25)

${{H}_{0}}(x) = \left( {\begin{array}{*{20}{c}} {{{H}_{L}},\quad a \leqslant x \leqslant x{\kern 1pt} *,} \\ {{{H}_{R}},\quad x{\kern 1pt} * < x \leqslant b,} \end{array}} \right.\quad {{u}_{0}}(x) = \left( {\begin{array}{*{20}{c}} {{{u}_{L}},\quad a \leqslant x \leqslant x{\kern 1pt} *,} \\ {{{u}_{R}},\quad x{\kern 1pt} * < x \leqslant b.} \end{array}} \right.$

Граничные условия мы не приводим, так как все расчеты для следующих тестовых задач останавливаются до того, как какие-либо волны разрежения или ударные волны достигнут границ рассматриваемой области.

4.3.1. Дозвуковые течения. Ниже представлены результаты по методу ICCh-2 и схеме КАБАРЕ для строго дозвуковых течений (${\text{|}}u{\text{|}} < \sqrt {gH} $). Были рассмотрены следующие задачи Римана (25) на сегменте $x \in [0,\;1]$:

1) волна разрежения слева, ударная волна справа

(26)

${{H}_{L}} = 2,\quad {{H}_{R}} = 1,\quad {{u}_{L}} = {{u}_{R}} = 0,\quad x{\kern 1pt} * = 0.5;$

2) две волны разрежения

(27)

${{H}_{L}} = {{H}_{R}} = 1,\quad {{u}_{L}} = - 1,\quad {{u}_{R}} = 1,\quad x{\kern 1pt} * = 0.5;$

3) сталкивающиеся ударные волны

(28)

${{H}_{L}} = {{H}_{R}} = 1,\quad {{u}_{L}} = 1,\quad {{u}_{R}} = - 1,\quad x{\kern 1pt} * = 0.5.$

На фиг. 8–10 приведены результаты расчетов задач Римана (26), (27) и (28), соответственно, по методу ICCh-2 и схеме КАБАРЕ для $CFL = 0.3$. Отметим основные свойства решений, полученных по методу ICCh-2: разрывы, как и в схеме КАБАРЕ, занимают 2–4 расчетные ячейки; в областях негладкости решений в силу частично аномальной дисперсии схемы возникают некритичные немонотонности; волны разрежения передаются достаточно точно и без артефактов. Отметим, что схема КАБАРЕ позволяет сохранить “острые” участки решения в верхних частях волн разрежения [15]. Метод ICCh-2 таким свойством не обладает и сглаживает все области негладкости решения.

Фиг. 8.

Профили глубины (а) и скорости (б) для задачи Римана (26) на сегменте $[0,\;1]$ на момент времени $t = 0.1$. 1 – решение, полученное по схеме КАБАРЕ, 2 – решение, полученное методом ICCh-2, 3 – аналитическое решение.

Фиг. 9.

Профили глубины (а) и скорости (б) для задачи Римана (27) на сегменте $[0,\;1]$ на момент времени $t = 0.1$. 1 – решение, полученное по схеме КАБАРЕ, 2 – решение, полученное методом ICCh-2, 3 – аналитическое решение.

Фиг. 10.

Профили глубины (а) и скорости (б) для задачи Римана (28) на сегменте $[0,\;1]$ на момент времени $t = 0.1$. 1 – решение, полученное по схеме КАБАРЕ, 2 – решение, полученное методом ICCh-2, 3 – аналитическое решение.

4.3.2. Сверхзвуковое течение. Здесь представлен пример расчета по методу ICCh-2 и схеме К-АБАРЕ для случая строго сверхзвукового течения (${\text{|}}u{\kern 1pt} {\text{|}} > \sqrt {gH} $). Рассматривалась следующая задача Римана (25) на сегменте $x \in [0,\;50]$:

(29)

${{H}_{L}} = 1,\quad {{H}_{R}} = 0.1,\quad {{u}_{L}} = 5,\quad {{u}_{R}} = 2.5,\quad x{\kern 1pt} * = 10.0.$

На фиг. 11 представлен результат расчета задачи (29) на равномерной сетке из $N = 101$ ячеек на момент времени $t = 5.0$. В случае строго сверхзвукового течения метод ICCh-2 дает такой же удовлетворительный результат, как и для строго дозвуковых течений, и для него справедливы те же замечания.

Фиг. 11.

Профили глубины (а) и скорости (б) для задачи Римана (29) на момент времени $t = 5.0$ на $N = 101$ ячейке. 1 – решение, полученное по схеме КАБАРЕ, 2 – решение, полученное методом ICCh-2, 3 – аналитическое решение.

4.3.3 Трансзвуковые течения. Ниже представлены результаты расчетов нескольких задач Римана о трансзвуковом течении, для которых требуется применение алгоритма обработки звуковых точек. Все балансно-характеристические методы нуждаются в подобных алгоритмах при расчете трансзвуковых задач, и для каждой системы уравнений нужен, вообще говоря, отдельный алгоритм. В случае схемы КАБАРЕ для уравнений мелкой воды наилучший алгоритм обработки звуковых точек был представлен в [15]. В случае метода ICCh-2 наиболее удовлетворительные результаты показал простейший алгоритм, представленный в (15), результаты расчетов для которого и приводятся в данном разделе.

Рассмотрим следующую трансзвуковую задачу Римана (25) на сегменте $x \in [0,\;50]$ (так называемый первый тест Торо):

(30)

${{H}_{L}} = 1.0,\quad {{H}_{R}} = 0.1,\quad {{u}_{L}} = 2.5,\quad {{u}_{R}} = 0.0,\quad x{\kern 1pt} * = 10.0.$

На фиг. 12 представлен результат расчета задачи (30) на равномерной сетке из $N = 101$ ячеек на момент времени $t = 7.0$, число Куранта $CFL = 0.3$. В областях дозвукового и сверхзвукового течения метод ICCh-2, как и прежде, показывает хорошие результаты. Но в окрестности звуковой точки у решения возникает артефакт в виде немонотонностей. Ширина такого артефакта фиксирована (4–6 ячеек), а амплитуда зависит от величины разрывов в задаче Римана.

Фиг. 12.

Профили глубины (а) и скорости (б) для задачи Римана (30) на сегменте $[0,\;50]$ на $N = 101$ ячейках в момент времени $t = 7.0$. 1 – решение, полученное по схеме КАБАРЕ, 2 – решение, полученное методом ICCh-2, 3 – аналитическое решение.

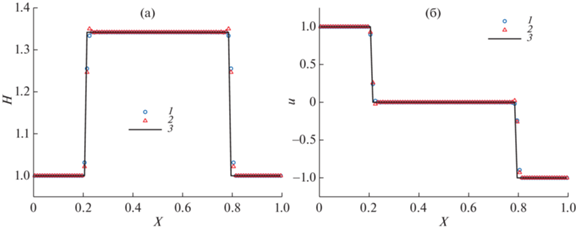
Для более подробной демонстрации вышеупомянутого артефакта рассмотрим другую трансзвуковую задачу Римана на сегменте $x \in [0,\;1]$:

(31)

${{H}_{L}} = 100,\quad {{H}_{R}} = 1,\quad {{u}_{L}} = {{u}_{R}} = 0,\quad x{\kern 1pt} * = 0.5.$

На фиг. 13 представлен результат расчета задачи (31) на равномерной сетке из $N = 101$ ячеек в момент времени $t = 0.012$, число Куранта $CFL = 0.3$. Артефакт метода ICCh-2 находится в окрестности звуковой точки $x{\kern 1pt} * = 0.5$ и занимает около 6 расчетных ячеек. По-видимому, наличие немонотонностей вызвано лишь частично аномальной дисперсией метода и неполностью работающей процедурой монотонизации (16), что говорит о том, что способ монотонизации схемы требует доработки.

Фиг. 13.

Профили глубины (а) и скорости (б) для задачи Римана (31) на сегменте $[0,\;1]$ на $N = 101$ ячейках на момент времени $t = 0.012$. 1 – решение, полученное по схеме КАБАРЕ, 2 – решение, полученное методом ICCh-2, 3 – аналитическое решение.

5. ЗАКЛЮЧЕНИЕ

В работе представлен новый явный балансно-характеристический метод решения систем нелинейных дифференциальных уравнений в частных производных гиперболического типа второго порядка аппроксимации. Характеристическая фаза метода основана на параболической реконструкции инвариантов Римана, учитывающей интегральную природу консервативных переменных, заданных в центрах ячеек. Построенная схема обладает частично аномальной дисперсией при малых числах Куранта, что позволяет избавиться от высокочастотных немонотонностей в решении. Метод был протестирован на некоторых задачах для уравнений переноса, Хопфа и мелкой воды. В случае гладких профилей решение, полученное по методу ICCh-2, обладает меньшей численной диссипацией и дисперсией по сравнению с методом ICCh-1 и схемой КАБАРЕ при включенной процедуре монотонизации. В случае разрывных решений метод также позволяет получить качественное решение, обладающее лишь незначительными немонотонностями в областях негладкостей и звуковых точек.

В качестве дальнейшей работы предложенный метод следует обобщить на случай двумерных и трехмерных систем гиперболического типа на треугольных и тетраэдральных расчетных сетках. Основные идеи такого обобщения уже были заложены в работе [2]. Особый интерес может представлять сравнение метода с существующими обобщениями схемы КАБАРЕ на треугольные сетки [9], [10].

Список литературы

Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений. М.: Физматлит, 2001. 607 с.
Головизнин В.М., Четверушкин Б.Н. Алгоритмы нового поколения в вычислительной гидродинамике // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 8. С. 20–29.
Guerrero Fernandez E., Castro-Diaz M.J., Morales de Luna T. A second-order well-balanced finite volume scheme for the multilayer shallow water model with variable density // Mathematics. 2020. V. 8. №. 5. P. 848.
Головизнин В.М., Зайцев М.А., Карабасов С.А., Короткин И.А. Новые алгоритмы вычислительной гидродинамики для многопроцессорных вычислительных комплексов. М.: Изд-во МГУ, 2013. 467 с.
Karabasov S.A., Goloviznin V.M. Compact accurately boundary-adjusting high-resolution technique for fluid dynamics // J. Comput. Phys. 2009. V. 228. № 19. P. 7426–7451.
Головизнин В.М., Самарский А.А. Разностная аппроксимация конвективного переноса с пространственным расщеплением временной производной // Матем. моделирование. 1998. Т. 10. № 1. С. 86–100.
Goloviznin V.M., Mayorov P.A., Mayorov P.A. Hyperbolic decomposition for hydrostatic approximation of free surface flow problems // J. of Physics: Conference Series. 2019. V. 1392. № 012035.
Головизнин В.М., Майоров П.А., Соловьев А.В. Новый численный алгоритм для уравнений многослойной мелкой воды на основе гиперболической декомпозиции и схемы КАБАРЕ // Морской гидрофизический ж. 2019. Т. 35. № 6. С. 600–620.
Яковлев П.Г., Карабасов С.А., Головизнин В.М. Прямое моделирование взаимодействия вихревых пар. // Матем. моделирование. 2011. Т. 23. № 11. С. 21–32.
Gorbachev D.Y., Goloviznin V.M. The Balance-Characteristic Numerical Method on Triangle Grids // J. of Physics: Conference Series. 2019. V. 1392. № 012036.
Головизнин В.М., Карабасов С.А. Нелинейная коррекция схемы Кабаре // Матем. моделирование. 1998. Т. 10. № 12. С. 107–123.
Van Leer B. Towards the Ultimate Conservative Difference Scheme. IV. A New Approach to Numerical Convection // J. Comput. Phys. 1977. V. 23. № 3. P. 276–299.
Eymann T.A., Roe P.L. Active Flux Schemes // 49th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. 2011. https://doi.org/10.2514/6.2011-382
Головизнин В.М., Исаков В.А. Применение балансно-характеристической схемы для решения уравнений мелкой воды над неровным дном // Ж. вычисл. матем. и матем. физ. 2017. Т. 57. № 7. С. 1142–1160.
Afanasiev N.A., Goloviznin V.M. A locally implicit time-reversible sonic point processing algorithm for one-dimensional shallow-water equations // J. Comput. Phys. 2021. V. 434. № 110220.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал