1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 62, № 11, 2022

Журнал вычислительной математики и математической физики, 2022, T. 62, № 11, стр. 1883-1894

Эффективный метод решения уравнения Больцмана на однородной сетке

А. Д. Беклемишев 1, 2, *, Э. А. Федоренков 1, 2, **

1 ИЯФ СО РАН
630090 Новосибирск, пр-т Акад. Лаврентьева, 11, Россия

2 НГУ
630090 Новосибирск, ул. Пирогова, 1, Россия

* E-mail: bekl@bk.ru
** E-mail: e.fedorenkov.nsu@yandex.ru

Поступила в редакцию 05.02.2022
После доработки 06.06.2022
Принята к публикации 07.07.2022

Полный текст (PDF)

Аннотация

Предложен новый численный метод решения уравнения Больцмана на однородной сетке в пространстве скоростей. Асимптотическая сложность метода $O({{N}^{3}})$, где $N$ – полное число узлов на трехмерной сетке. Алгоритм эффективен на небольших сетках за счет простоты операций и легкого распараллеливания. Метод сохраняет важнейшие свойства решения: неотрицательность, сохранение полной энергии, импульса и числа частиц. Библ. 30. Фиг. 7.

Ключевые слова: кинетическое уравнение, уравнение Больцмана, модели дискретных скоростей, 0D3V кинетический код.

1. ВВЕДЕНИЕ

Взаимодействие холодного газа с горячей плазмой играет важную роль в физике удержания высокотемпературной плазмы. Например, в открытых магнитных ловушках сложилось качественное представление о том, что нейтральный газ на торцах установки может приводить к ухудшению продольного удержания горячей плазмы. Грубые оценки показывают, что допустимая концентрация нейтрального газа для стационарного удержания не должна превышать 1012 частиц в кубическом сантиметре [1]. Это накладывает очень жесткие требования на вакуумную систему открытых ловушек. В экспериментах [2] влияние газа не столь сильно. Это может объясняться перераспределением остаточного газа в объеме установки при его взаимодействии с горячей плазмой и холодными стенками так, что его концентрация в плазме на порядки ниже, чем вблизи стенок. При этом длина свободного пробега в газе также меняется на порядки – от размера системы (в центре) до малых долей радиуса (у стенки). В таком переходном режиме можно ожидать сильного отклонения локальной функции распределения от максвелловской, что требует кинетических расчетов. Для более детального понимания роли нейтрального газа в физике удержания плазмы в открытых магнитных ловушках нами разрабатывается кинетический код. Он позволит учитывать различные элементарные процессы, происходящие при проникновении нейтрального газа в плазму. В статье мы продемонстрируем наш способ учета упругих столкновений.

Упругие столкновения газа описываются уравнением Больцмана. Его решение является серьезной численной задачей из-за нелинейности и многомерной структуры интеграла. Существуют два основных подхода к решению кинетических уравнений: стохастические численные методы, такие как метод прямого моделирования Монте-Карло (DSMC) [3]–[7], и детерминированные методы.

Прямой метод Монте-Карло заключается в моделировании движения пробных частиц, рассеивающихся на фоновом газе. Обычно детерминированные методы имеют более высокий порядок точности, однако не могут конкурировать со стохастическими методами в скорости вычислений. Для нашей задачи больший интерес представляют детерминированные методы, поскольку распределение фонового газа неизвестно. Это серьезно усложняет вычисления методом Монте-Карло из-за необходимости итераций.

Детерминированные методы, в свою очередь, делятся на два основных подхода: разложение функции распределения по гладким функциям и сеточные методы.

В первом подходе используют специальные наборы ортогональных полиномов или фурье-гармоники. В нелинейном случае этот метод получил развитие в работах Бернетта [8] и Града [9]. В качестве набора функций обычно используют полиномы Эрмита или Сонина. Такие методы хорошо подходят, когда распределения слабо отличаются от равновесного. Для более общих случаев используют спектральные методы (разложение по фурье-гармоникам). Быстрое преобразование Фурье позволяет эффективно использовать спектральные методы на практике. Первыми спектральный метод предложили независимо Л. Парески и Б. Пертхам [10] и А. Бобылев с С. Рясанов [11]. Метод получил развитие в большом числе других работ [12]–[15]. В том числе были разработаны быстрые спектральные алгоритмы [16]. Благодаря этому сложность решения уравнения Больцмана уменьшилась с $O({{N}^{{2 + \varepsilon }}})$ ($\varepsilon \sim 1{\text{/}}3$ для трехмерного пространства скоростей) до $O(N\log (N))$, где $N$ – число узлов на сетке скоростей, что сделало спектральный метод сравнимым по сложности с линейными методами Монте-Карло.

Основной недостаток разложения по фурье-гармоникам или специальным полиномам в том, что не обеспечена неотрицательность функции распределения, возникающая из-за необходимости обрезать сумму по базисным функциям. В нашей задаче необходимо добавить различные элементарные процессы (ионизация электронным ударом, перезарядка, возбуждение и т.д.). Наличие отрицательных значений может привести к некорректной обработке при учете многих элементарных процессов вместе.

Во втором подходе предполагается, что пространство скоростей дискретно ${\mathbf{v}} = \Delta v{\mathbf{n}}$, где ${\mathbf{n}} \in {{\mathbb{Z}}^{3}}$. С таким допущением интеграл столкновений Больцмана представим в виде бесконечной суммы

(1)
$St(f,f)({{v}_{i}}) \simeq \sum\limits_j {\kern 1pt} \sum\limits_{k,l} \,\Gamma _{{ij}}^{{kl}}({{f}_{k}}{{f}_{l}} - {{f}_{i}}{{f}_{j}}),$
где ${{f}_{i}} = f({{v}_{i}})$, индексы $i$, $j$, $k$, $l \in {{\mathbb{Z}}^{3}}$ – целочисленные векторы, нумерующие значения скоростей ${{v}_{i}}$, ${{w}_{j}}$, $v_{k}^{'}$, $w_{l}^{'}$ из уравнения (2) на дискретной сетке. Суммирование по $j$ заменяет интегрирование по ${\mathbf{w}}$, а сумма по $k$, $l$ заменяет интегрирование по углам рассеяния ${\mathbf{n}}$. Тензор $\Gamma _{{ij}}^{{kl}}$ обладает симметриями, отражающими физические свойства интеграла столкновений Больцмана, такие как обратимость процесса и неизменность от перестановок частиц до и после столкновения
$\Gamma _{{ij}}^{{kl}} = \Gamma _{{kl}}^{{ij}} = \Gamma _{{ji}}^{{kl}} = \Gamma _{{ij}}^{{lk}}.$
Тензор $\Gamma _{{ij}}^{{kl}}$ должен сохранять импульс и энергию в каждом элементарном акте столкновений, однако задача их сохранения на дискретной ограниченной сетке является очень нетривиальной.

Метод впервые предложил Аристов в 1985 г., и более детально его можно изучить в [17]. В дальнейшем теоретически были показаны сходимость (1) к интегралу Больцмана [18], и сходимость решения в модели дискретных скоростей к решению уравнения Больцмана [19]. Метод получил развитие в следующих работах [20], [21]. В том числе были разработаны различные способы ускорения вычислений [22], [23]. Следует отметить, что без использования различных ускорительных процедур сложность алгоритма ведет себя как $O({{N}^{{2 + \varepsilon }}})$, где $N$ – полное число узлов сетки скоростей. Это сильно увеличивает время вычислений на трехмерной сетке. А также требуется большой объем памяти для хранения вычисленных заранее коэффициентов $\Gamma _{{ij}}^{{kl}}$ даже с учетом их симметрии. Позднее был разработан новый консервативный метод дискретных скоростей, в котором количество коэффициентов, вычисленных заранее, удалось сократить до ${{N}^{2}}$ [24]. Из последних работ также следует отметить [25]. В работе предложен алгоритм со сложностью вычисления интеграла столкновений $O({{N}^{{8/3}}})$.

В этой работе будет продемонстрирован новый сеточный метод аппроксимации интеграла столкновений. Метод быстрый и консервативный, а также не требующий большого количества памяти для хранения коэффициентов.

Статья организована следующим образом. В разд. 2 кратко представим уравнение Больцмана и опишем основные свойства этого уравнения. В разд. 3 и 4 мы расскажем наш новый метод решения уравнения Больцмана. В разд. 5 мы продемонстрируем работу нашего метода на численных тестах. В разд. 6 обсудим результаты и сделаем выводы.

2. УРАВНЕНИЕ БОЛЬЦМАНА

Уравнение Больцмана (2) описывает эволюцию функции распределения газа по скоростям, вызванную парными столкновениями:

(2)
$\frac{{\partial f}}{{\partial t}} + {\mathbf{v}} \cdot \frac{{\partial f}}{{\partial {\mathbf{r}}}} + {\mathbf{a}} \cdot \frac{{\partial f}}{{\partial {\mathbf{v}}}} = St(f,f),$
где $f \equiv f({\mathbf{v}},{\mathbf{r}},t)$ – функция распределения, зависящая от скорости частицы ${\mathbf{v}} \in {{\mathbb{R}}^{3}}$, ее положения в пространстве ${\mathbf{r}} \in {{\mathbb{R}}^{3}}$ и от времени $t \in \mathbb{R}$; ${\mathbf{a}}$ – ускорение частицы, возникающее при наличии внешних сил; $St(f,f)$ – интеграл столкновений:
(3)
$St(f,f) = \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {\kern 1pt} \int\limits_{\mathbb{S}(0,1)} {\kern 1pt} B(u,{\mathbf{n}})(f({\mathbf{v}}{\kern 1pt} ')f({\mathbf{w}}{\kern 1pt} ') - f({\mathbf{v}})f({\mathbf{w}})){{d}^{2}}n{{d}^{3}}w,$
где ${\mathbf{n}}$ – направление рассеяния, ${\mathbf{u}}$ – относительная скорость сталкивающихся частиц, ${\mathbf{v}}$, ${\mathbf{w}}$ – скорости частиц до столкновения, ${\mathbf{v}}{\kern 1pt} '$, ${\mathbf{w}}{\kern 1pt} '$ – скорости частиц после столкновения. $B(u,{\mathbf{n}})$ – ядро интеграла:
$B(u,{\mathbf{n}}) = u\frac{{d\sigma }}{{d\Omega }}(u,{\mathbf{n}}),$
где $\frac{{d\sigma }}{{d\Omega }}(u,{\mathbf{n}})$ – дифференциальное сечение рассеяния, зависящее от относительной скорости и направления рассеяния. Интегрирование в (3) проводится по всем возможным направлениям рассеяния ${\mathbf{n}} \in \mathbb{S}(0,1)$ ($\mathbb{S}(0,1)$ – единичная сфера с центром в начале координат), и по всем возможным скоростям второй частицы до столкновения ${\mathbf{w}} \in {{\mathbb{R}}^{3}}$.

Скорости частиц до и после столкновения связаны законами сохранения импульса и энергии:

${\mathbf{v}} + {\mathbf{w}} = {\mathbf{v}}{\kern 1pt} '\; + {\mathbf{w}}{\kern 1pt} ',\quad {{v}^{2}} + {{w}^{2}} = v{\kern 1pt} {{'}^{2}}\; + w{\kern 1pt} {{'}^{2}},$
и могут быть выражены друг через друга следующим образом:
${\mathbf{v}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ' = \frac{1}{2}({\mathbf{v}} + {\mathbf{w}}) \pm \frac{1}{2}u{\mathbf{n}}.$
Хорошо известно, что интеграл столкновений (2) удовлетворяет законам сохранения числа частиц, импульса, энергии, а также приводит к не убыванию энтропии (H-теорема Больцмана):
(4)
$\int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} St(f,f)\left( {\begin{array}{*{20}{c}} 1 \\ {\vec {v}} \\ {{{v}^{2}}} \end{array}} \right){{d}^{3}}v = 0,\quad \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} St(f,f)\ln (f){{d}^{3}}v\;\leqslant \;0.$
Стационарное и не зависящее от пространственных координат решение уравнения (2) имеет вид максвелловской функции распределения:
(5)
${{f}_{M}} = \frac{n}{{{{\pi }^{{3/2}}}v_{T}^{3}}}\exp \left( { - \frac{{|{\kern 1pt} \vec {v} - \vec {V}{\kern 1pt} {{|}^{2}}}}{{v_{T}^{2}}}} \right),\quad {{v}_{T}} = \sqrt {\frac{{2T}}{m}} ,$
где $n$ – плотность, $T$ – температура, $\vec {V}$ – гидродинамическая скорость и $m$ – масса молекулы газа.

Условия (4) и (5) являются важными физическими свойствами. Более детально познакомиться с другими физическими и математическими аспектами уравнения Больцмана можно в [26]. В этой статье мы будем рассматривать пространственно однородное уравнение Больцмана без внешних сил:

(6)
$\frac{{\partial f}}{{\partial t}} = St(f,f).$
Учесть пространственную неоднородность и внешние силы можно стандартным методом разделения бесстолкновительного транспорта и локальных столкновений на два последовательно чередующихся шага. Более подробно этот метод освещен в [27].

Уравнение (6) в общем случае не имеет известных аналитических решений. Далее мы представим наш численный метод решения этого уравнения.

3. ОБЩЕЕ ОПИСАНИЕ МЕТОДА

3.1. Локальные упругие столкновения

Пусть в области $\Omega \subset {{\mathbb{R}}^{3}}$ пространства скоростей задана однородная сетка $\mathbb{V}$ с шагом $\Delta v$.

$\mathbb{V} = \left\{ {{{v}_{{\mathbf{i}}}} \in {{\mathbb{R}}^{3}}\,{\text{|}}\,{{v}_{{\mathbf{i}}}} = \Delta v{\mathbf{i}}{\text{,}}\;{\text{где}}\;{\mathbf{i}} \in {{\mathbb{Z}}^{3}}} \right\}.$
Обозначим через ${{f}_{{\mathbf{i}}}}$ значения функции распределения на сетке $\mathbb{V}$. Будем считать, что функция распределения между узлами сетки представима в виде линейной комбинации значений ${{f}_{{\mathbf{i}}}}$:
(7)
$f({\mathbf{v}}) = \sum\limits_{{\mathbf{k}} \in {{\mathbb{Z}}^{3}}} \,{{\alpha }_{{\mathbf{k}}}}({\mathbf{v}}){{f}_{{\mathbf{k}}}},$
коэффициенты ${{\alpha }_{{\mathbf{k}}}}({\mathbf{v}})$ зависят от скорости. Запись (7) охватывает случаи кусочно-постоянной функции распределения и трилинейной интерполяции набора ${{f}_{{\mathbf{i}}}}$. В первом случае реальное значение скорости ${\mathbf{v}}$ заменяется на ближайший узел сетки скоростей
(8)
${{\alpha }_{{\mathbf{k}}}}({\mathbf{v}}) = \delta ({\mathbf{v}} - {{v}_{{\mathbf{k}}}}),\quad {\mathbf{k}}:{\text{|}}{\mathbf{v}} - {{v}_{{\mathbf{k}}}}{\text{|}} \to \min .$
Во втором случае значение скорости ${\mathbf{v}}$ заменяется на восемь ближайших узлов кубической сетки с весами, определяемыми трилинейной интерполяцией набора ${{f}_{{\mathbf{i}}}}$:
(9)
${{\alpha }_{{\mathbf{k}}}}({\mathbf{v}}) = \sum\limits_{i = 1}^8 \frac{{{\text{|}}{{v}_{x}} - {{v}_{{{{k}_{{{{x}_{{_{i}}}}}}}}}}{\text{||}}{{v}_{y}} - {{v}_{{{{k}_{{{{y}_{{_{i}}}}}}}}}}{\text{||}}{{v}_{z}} - {{v}_{{{{k}_{{{{z}_{i}}}}}}}}{\text{|}}}}{{\Delta {{{v}}^{3}}}},\quad {{k}_{{{{j}_{i}}}}}:{\text{|}}{{v}_{j}} - {{v}_{{{{k}_{{{{j}_{i}}}}}}}}{\text{|}} < \Delta {v}.$
Подставим функцию распределения (7) в интеграл столкновений из уравнения (2)
(10)
$St(f,f)({{v}_{{\mathbf{i}}}}) \simeq \int \int {\kern 1pt} B(u,{\mathbf{n}})\left( {{{\alpha }_{{\mathbf{k}}}}({\mathbf{v}}{\kern 1pt} '){{\alpha }_{{\mathbf{l}}}}({\mathbf{w}}{\kern 1pt} ') - {{\alpha }_{{\mathbf{k}}}}({\mathbf{v}}){{\alpha }_{{\mathbf{l}}}}({\mathbf{w}})} \right){{d}^{2}}n{{d}^{3}}w{{f}_{{\mathbf{k}}}}{{f}_{{\mathbf{l}}}}.$
Вычислив пятимерный интеграл (10), мы получим значение интеграла столкновений в $i$-м узле в виде свертки
(11)
$St(f,f)({{{v}}_{{\mathbf{i}}}}) \simeq {{G}^{{{\mathbf{kl}}}}}({{{v}}_{{\mathbf{i}}}}){{f}_{{\mathbf{k}}}}{{f}_{{\mathbf{l}}}} \equiv G_{{\mathbf{i}}}^{{{\mathbf{kl}}}}{{f}_{{\mathbf{k}}}}{{f}_{{\mathbf{l}}}}{\kern 1pt} {\kern 1pt} .$
Тензор $G_{{\mathbf{i}}}^{{{\mathbf{kl}}}}$, очевидно, обладает симметрией по двум верхним индексам. Однако, даже с учетом этого, на грубой сетке размера $10 \times 10 \times 10$ нужно хранить порядка $5 \times {{10}^{8}}$ элементов. Занимаемый объем памяти коэффициентами $G_{{\mathbf{i}}}^{{{\mathbf{kl}}}}$ меньше, чем коэффициентами $\Gamma _{{{\mathbf{ij}}}}^{{{\mathbf{kl}}}}$, однако, по-прежнему очень большой для хранения их в оперативной памяти. По сути, аппроксимация интеграла столкновений (11) пока отличается от (1) только избавлением от суммирования по индексу ${\mathbf{j}}$. Коэффициенты $G_{{\mathbf{i}}}^{{{\mathbf{kl}}}}$ можно получить из $\Gamma _{{{\mathbf{ij}}}}^{{{\mathbf{kl}}}}$ следующим образом:
(12)
$G_{{\mathbf{i}}}^{{{\mathbf{kl}}}} = \sum\limits_{{\mathbf{j}} \in {{\mathbb{Z}}^{3}}} \,\Gamma _{{{\mathbf{ij}}}}^{{{\mathbf{kl}}}} - \sum\limits_{{\mathbf{n}},{\mathbf{m}} \in {{\mathbb{Z}}^{3}}} {\kern 1pt} \Gamma _{{{\mathbf{ik}}}}^{{{\mathbf{nm}}}}{{\delta }_{{{\mathbf{il}}}}}.$
Для дальнейшего упрощения метода мы воспользуемся еще одной симметрией тензора $G_{{\mathbf{i}}}^{{{\mathbf{kl}}}}$.

3.2. Трансляционная симметрия тензоров $\Gamma _{{{\mathbf{ij}}}}^{{{\mathbf{kl}}}}$ и $G_{{\mathbf{i}}}^{{{\mathbf{kl}}}}$

Если область $\Omega $, в которой задана однородная сетка скоростей, совпадает с ${{\mathbb{R}}^{3}}$, то тензор $\Gamma _{{{\mathbf{ij}}}}^{{{\mathbf{kl}}}}$ из (1) обладает трансляционной симметрией:

(13)
$\Gamma _{{{\mathbf{i}} + {\mathbf{a}},{\mathbf{j}} + {\mathbf{a}}}}^{{{\mathbf{k}} + {\mathbf{a}},{\mathbf{l}} + {\mathbf{a}}}} = \Gamma _{{{\mathbf{ij}}}}^{{{\mathbf{kl}}}}\quad \forall {\mathbf{a}} \in {{\mathbb{Z}}^{3}}.$
Это свойство можно понять, рассмотрев сферу рассеяния с диаметрально противоположными точками ${\mathbf{i}}$ и ${\mathbf{j}}$, которые в результате упругого столкновения перейдут в диаметрально противоположные точки ${\mathbf{k}}$ и ${\mathbf{l}}$ (фиг. 1). Законы сохранения энергии и импульса не позволяют находиться точкам ${\mathbf{k}}$ и ${\mathbf{l}}$ вне сферы рассеяния. Сферу рассеяния можно сдвинуть на любой вектор $\Delta v \cdot {\mathbf{a}}$, где ${\mathbf{a}} \in {{\mathbb{Z}}^{3}}$. Поскольку сетка однородна и бесконечна, то узлы с координатами ${\mathbf{i}}$, ${\mathbf{j}}$, ${\mathbf{k}}$, ${\mathbf{l}}$ перейдут в узлы с координатами ${\mathbf{i}} + {\mathbf{a}}$, ${\mathbf{j}} + {\mathbf{a}}$, ${\mathbf{k}} + {\mathbf{a}}$, ${\mathbf{l}} + {\mathbf{a}}$, лежащими на смещенной сфере рассеяния. Рассеяние $({\mathbf{i}},{\mathbf{j}}) \to ({\mathbf{k}},{\mathbf{l}})$ происходит на тот же угол и с той же относительной скоростью, что и рассеяние $({\mathbf{i}} + {\mathbf{a}},{\mathbf{j}} + {\mathbf{a}}) \to ({\mathbf{k}} + {\mathbf{a}},{\mathbf{l}} + {\mathbf{a}})$. Следовательно, имеет место равенство (13). Учитывая связи коэффициентов $G_{{\mathbf{i}}}^{{{\mathbf{kl}}}}$ и $\Gamma _{{{\mathbf{ij}}}}^{{{\mathbf{kl}}}}$ (12), тензор $G_{{\mathbf{i}}}^{{{\mathbf{kl}}}}$ тоже обладает трансляционной симметрией на бесконечной однородной сетке:
$G_{{{\mathbf{i}} + {\mathbf{a}}}}^{{{\mathbf{k}} + {\mathbf{a}},{\mathbf{l}} + {\mathbf{a}}}} = G_{{\mathbf{i}}}^{{{\mathbf{kl}}}}\quad \forall {\mathbf{a}} \in {{\mathbb{Z}}^{3}}.$
Это свойство позволяет вычислять интеграл столкновений с меньшим количеством коэффициентов. Достаточно вычислить только матрицу $G_{0}^{{{\mathbf{kl}}}}$:
(14)
$St(f,f)({{v}_{{\mathbf{i}}}}) \simeq \sum\limits_{{\mathbf{k}},{\mathbf{l}}} \,G_{0}^{{{\mathbf{k}} - {\mathbf{i}},{\mathbf{l}} - {\mathbf{i}}}}{{f}_{{\mathbf{k}}}}{{f}_{{\mathbf{l}}}} \equiv \sum\limits_{{\mathbf{k}},{\mathbf{l}}} \,G_{0}^{{{\mathbf{kl}}}}{{f}_{{{\mathbf{k}} + {\mathbf{i}}}}}{{f}_{{{\mathbf{l}} + {\mathbf{i}}}}}{\kern 1pt} {\kern 1pt} .$
Трансляционная симметрия интеграла в пространстве скоростей прямо связана с (дискретизированным) законом сохранения импульса (теорема Нетер). В любой ограниченной области законы сохранения корректно выполняться не могут. Их выполнения можно добиться внесением специальных искажений интеграла столкновений, зависящих от реализации сетки.

Фиг. 1.

Иллюстрация трансляционной симметрии коэффициентов $\Gamma _{{{\mathbf{ij}}}}^{{{\mathbf{kl}}}}$ на бесконечной однородной сетке. ${\mathbf{i}}$, ${\mathbf{j}}$, ${\mathbf{k}}$, ${\mathbf{l}}$ – узлы сетки на сфере столкновений, a – вектор смещений по однородной сетке.

3.3. Корректировка законов сохранения

Сконструируем добавку к интегралу столкновений, зависящую от пяти параметров, которые определяются из законов сохранения числа частиц, импульса и энергии. Помимо этого, добавка не должна нарушать неотрицательность функции распределения. Этого можно добиться, сделав добавку к интегралу столкновений пропорциональной функции распределения. Это гарантирует малое изменение функции распределения в той части фазового пространства, где она сама мала. Вышесказанное можно реализовать, в частности, при внесении в интеграл столкновений добавки вида

(15)
$\hat {S}t({\mathbf{v}}) = St({\mathbf{v}}) + (a + {\mathbf{b}} \cdot {\mathbf{v}} + c{{v}^{2}})f({\mathbf{v}}).$
Коэффициенты $a$, ${\mathbf{b}}$, $c$ определяются из следующих уравнений:
$\int {\kern 1pt} \hat {S}t({\mathbf{v}}){{d}^{3}}v = 0;\quad \int {\kern 1pt} {\kern 1pt} {\mathbf{v}}\hat {S}t({\mathbf{v}}){{d}^{3}}v = 0;\quad \int {\kern 1pt} {\kern 1pt} {{v}^{2}}\hat {S}t({\mathbf{v}}){{d}^{3}}v = 0.$
На сетке при известном $St({\mathbf{v}})$ эти уравнения являются линейной системой на искомые коэффициенты $a$, ${\mathbf{b}}$, $c$, что позволяет легко и быстро их находить.

На ограниченной сетке отличие суммы (15) от истинного значения состоит из двух частей: ошибка дискретизации, зависящая от размера ячейки сетки, и ошибка, связанная с положением границы счетной области, принимая во внимание, что значения функции распределения вне этой области не учитываются.

3.4. Алгоритм решения столкновительного шага

Учитывая все выше перечисленное, наш алгоритм решения уравнения (6) состоит из следующих шагов.

Шаг 1. Выделяем границы области счета и задаем в ней однородную сетку скоростей. Используя данные о сечении и заданную сетку, вычисляем матрицу $G_{0}^{{{\mathbf{kl}}}}$. Как именно это сделать, будет показано в разд. 4.

Шаг 2. В цикле по времени вычисляем по функции распределения $f({{t}_{n}}) \equiv {{f}^{n}}$ в момент времени ${{t}_{n}}$ интеграл столкновений $St({{f}^{n}},{{f}^{n}})({{v}_{i}})$ согласно формуле (14).

Шаг 3. Корректируем интеграл столкновений $St({{f}^{n}},{{f}^{n}})({{v}_{i}})$ согласно (15).

Шаг 4. Получаем функцию распределения $f({{t}_{n}} + \Delta t)$ в момент времени ${{t}_{{n + 1}}}$, как численное решение уравнения (6) по схеме Рунге–Кутты второго порядка точности.

4. АЛГОРИТМЫ ВЫЧИСЛЕНИЯ МАТРИЦЫ $G_{0}^{{{\mathbf{kl}}}}$

Пусть имеется трехмерная однородная сетка скоростей размера $N \times N \times N$ в кубе ${{[ - V,V]}^{3}}$. Далее мы продемонстрируем наш алгоритм вычисления матрицы $G_{0}^{{{\mathbf{kl}}}}$ в такой области. От способа вычисления матрицы $G_{0}^{{{\mathbf{kl}}}}$ зависит порядок точности вычисления интеграла столкновений. Здесь мы приведем метод первого порядка точности.

4.1. Алгоритм первого порядка точности вычисления интеграла столкновений

Воспользуемся представлением функции распределения (7) с коэффициентами разложения (8). Одна из частиц до столкновения будет всегда находиться в центре сетки со скоростью ${{{\mathbf{v}}}_{i}} = (0,0,0)$. Вторая частица до столкновения пробегает все возможные ${{N}^{3}}$ значений скорости ${{{\mathbf{v}}}_{j}}$. Фиксированные значения ${{{\mathbf{v}}}_{i}}$ и ${{{\mathbf{v}}}_{j}}$ задают сферу столкновений. Согласно законам сохранения энергии и импульса, скорости частиц после столкновения, ${{{\mathbf{v}}}_{k}}$ и ${{{\mathbf{v}}}_{l}}$, должны лежать на этой сфере.

Для численного интегрирования по сфере рассеяния необходимо создать равномерный набор точек на сфере. Для этого мы использовали spiral-based sampling метод [28], который создает квазиравномерный набор точек на сфере. В этом алгоритме по заданному количеству точек $M$ подбираются параметры спирали, которая лежит на сфере, соединяя два ее полюса. После чего набор из $M$ точек укладывается на спираль. С ростом $M$ заполнение сферы становится более равномерным. В качестве полюсов мы выбираем узлы ${{{\mathbf{v}}}_{i}}$ и ${{{\mathbf{v}}}_{j}}$. Набор точек на сфере задает набор направлений рассеяния ${{{\mathbf{n}}}_{{ij}}}$. Фиксируя направление, мы определяем пару скоростей частиц после столкновения $({{{\mathbf{v}}}_{k}},{{{\mathbf{v}}}_{l}})$ на сфере рассеяния. Если ни одна из скоростей не вышла за пределы сетки, то мы, согласно модели (8), находим ближайшие к этим скоростям узлы сетки (фиг. 2). Обозначим индексы этих узлов через ${\mathbf{k}}$ и ${\mathbf{l}}$, и добавим в соответствующий элемент матрицы $G_{0}^{{{\mathbf{kl}}}}$ значение

$G_{0}^{{{\mathbf{kl}}}} = \sum\limits_j \,B({\kern 1pt} {\text{|}}{{{\mathbf{v}}}_{j}}{\text{|}},{{{\mathbf{n}}}_{{ij}}})(\Delta v{{)}^{3}}\frac{{4\pi }}{M},$
где $B$ – ядро интеграла Больцмана, $\Delta v$ – шаг сетки, ${{(\Delta v)}^{3}}$ – элемент объема сетки скоростей, $M$ – число точек на сфере рассеяния, $4\pi {\text{/}}M$ – элемент телесного угла. Если хоть одна из скоростей ${{{\mathbf{v}}}_{k}},\;{{{\mathbf{v}}}_{l}}$ вышла за пределы сетки, то такой процесс учтен не будет.

Фиг. 2.

Иллюстрация столкновений учитывающихся при вычислении матрицы $G_{0}^{{{\mathbf{kl}}}}$, и процессов, приводящих к вылету частиц за область вычислений, которые не учитываются.

В итоге алгоритм первого порядка точности состоит из следующих шагов.

Шаг 1. Для каждого узла сетки скоростей ${{v}_{j}}$ создается набор возможных направлений рассеяния ${{{\mathbf{n}}}_{{ij}}}$.

Шаг 2. Для каждого направления из множества ${{{\mathbf{n}}}_{{ij}}}$ определяется пара скоростей после рассеяния $({{{\mathbf{v}}}_{k}},{{{\mathbf{v}}}_{l}})$.

Шаг 3. Проверка попадания скоростей $({{{\mathbf{v}}}_{k}},{{{\mathbf{v}}}_{l}})$ в область расчетов. Если хоть одна из скоростей вышла за пределы сетки, такой процесс не учитывается.

Шаг 4. Если скорости $({{{\mathbf{v}}}_{k}},{{{\mathbf{v}}}_{l}})$ лежат в области счета, то находим ближайшие к ним узлы сетки. Обозначим их через ${\mathbf{k}}$ и ${\mathbf{l}}$.

Шаг 5. В элемент матрицы $G_{0}^{{{\mathbf{kl}}}}$ добавляем значение $B({\kern 1pt} {\text{|}}{{{\mathbf{v}}}_{j}}{\kern 1pt} {\text{|}},{{{\mathbf{n}}}_{{ij}}})(\Delta {v}{{)}^{3}}4\pi {\text{/}}M$.

Таким образом, сложность алгоритма вычисления матрицы $G_{0}^{{{\mathbf{kl}}}}$ можно оценить как $O(M{{N}^{3}})$. В вычислении интеграла столкновений есть два источника ошибок: ошибка, связанная с ограниченностью области счета, ошибка метода интегрирования в области счета. Используя представление функции распределения (7) с коэффициентами разложения (9), в принципе можно добиться повышения точности вычисления интеграла столкновений. При условии, что ошибки, связанные с границей счетной области, не являются доминирующими.

5. ЧИСЛЕННЫЕ ТЕСТЫ

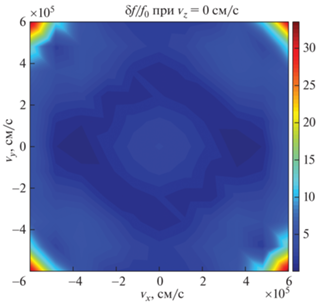
Здесь мы приведем два теста кинетического кода, основанного на описанном выше алгоритме, и продемонстрируем результаты решения уравнения Больцмана. Вычисления выполнены на процессоре Intel Core i5-11600K (12 МБ кэш-память, до 4.9 ГГц). Вычисление матрицы $G_{0}^{{kl}}$ выполняется примерно за 700 мс. Вычисление интеграла столкновений на одном шаге по времени занимает примерно 200 мс. Оба теста выполнены на сетке размера 11 × 11 × 11. Время выполнения составляет 63.5 и 99.8 с, соответственно.

5.1. Тест 1: сравнение численного решения с точным решением уравнения Больцмана

Уравнение Больцмана имеет единственное известное аналитическое решение, найденное Бобылевым [29] и затем независимо Круком и Ву [30]. Решение получено для дифференциального сечения, имеющего специальный вид:

(16)
$\frac{{d\sigma }}{{d\Omega }} = \frac{\alpha }{u},$
где $\alpha $ – постоянная величина, $u$ – относительная скорость сталкивающихся частиц. Решение уравнения Больцмана c дифференциальным сечением (16) в безразмерных переменных имеет следующий вид:
(17)
${{f}_{{BKW}}}(t,{v}) = \frac{1}{{2K{{{(2\pi K)}}^{{3/2}}}}}\left[ {5K - 3 + \frac{{1 - K}}{K}{{v}^{2}}} \right]\exp \left( { - \frac{{{{v}^{2}}}}{{2K}}} \right),$
где
$K = 1 - \exp \left( { - \frac{t}{6}} \right),$
а время и скорость обезразмерены следующим образом:
$t \to 4\pi \alpha nt,\quad v \to v\sqrt {\frac{m}{T}} .$
В вычислениях мы приняли $n = 1$, $\sqrt {m{\text{/}}T} = 1$, $\alpha = 1{\text{/}}4\pi $, а в качестве начального условия:
$f(0,v) = {{f}_{{BKW}}}(t = 6\ln (2.5),v) = \frac{{25\sqrt 5 }}{{9{{{(6\pi )}}^{{3/2}}}}}{{v}^{2}}\exp \left( { - {{v}^{2}}\frac{5}{6}} \right).$
Результаты теста в виде сравнения численного и точного решения (17) показаны на фиг. 3. При этом средняя относительная ошибка не превышает $14\% $, и локализована на краях сетки (фиг. 4).

Фиг. 3.

Точное и численное решение уравнения Больцмана в зависимости от времени. Время отсчитывается от $t = 6\ln (2.5)$.

Фиг. 4.

Среднее по сетке отклонение численного решения от точного в процентах. Время отсчитывается от $t = 6\ln (2.5)$.

5.2. Тест 2: релаксация к равновесию газа упругих шаров

В этом тесте пронаблюдаем релаксацию к максвелловскому распределению газа упругих шаров, $d\sigma {\text{/}}d\Omega = {\text{const}}$. В качестве начального условия было выбрано распределение

${{f}_{0}} = \frac{{{{n}_{0}}}}{{{{\pi }^{{3/2}}}v_{{{{T}_{0}}}}^{3}}}{{\left( {\frac{{{{v}_{y}}}}{{{{v}_{{{{T}_{0}}}}}}}} \right)}^{2}}\exp \left( { - \frac{{{{v}^{2}}}}{{v_{{{{T}_{0}}}}^{2}}}} \right).$
С учетом законов сохранения это распределение релаксирует к максвелловскому с плотностью и температурой:
$n = \frac{{{{n}_{0}}}}{2}{\text{,}}\quad T = \frac{5}{3}{{T}_{0}}$
за характерное время $\tau \sim 1{\text{/}}(\sigma n{{v}_{T}})$. Моделирование проведено со следующими параметрами:
$\begin{gathered} {{n}_{0}} = 4 \times {{10}^{{15}}}\;{\text{с}}{{{\text{м}}}^{{ - 3}}}{\text{,}}\quad {{T}_{0}} = 0.026\;{\text{эВ}}, \\ \sigma \simeq 1.3 \times {{10}^{{ - 15}}}\;{\text{с}}{{{\text{м}}}^{2}}{\text{,}}\quad \tau \sim 1.4\;{\text{мкс}}. \\ \end{gathered} $
Результат численного решения представлен на фиг. 5. Из него видно, что для данного начального распределения равновесие устанавливается за время порядка $4\tau $. Распределение остается стационарным при дальнейшем вычислении. Относительное отклонение от максвелловской функции распределения представлено на фиг. 6. Из графика следует, что самая большая ошибка в углах области счета и она составляет порядка $30\% $. Далеко от границ области расчетов ошибка порядка 5–10%. Сходимость к равновесному распределению можно пронаблюдать на фиг. 7. Здесь показано среднее по всей сетке отклонение от максвелловского распределения в зависимости от времени.

Фиг. 5.

Релаксация газа упругих шаров к равновесному распределению.

Фиг. 6.

Относительное отклонение численного решения от равновесной функции распределения в конце расчетов.

Фиг. 7.

Эволюция среднего по сетке отклонения от максвелловского распределения.

6. ЗАКЛЮЧЕНИЕ

Разработан довольно быстрый и точный метод интегрирования уравнения Больцмана на грубой равномерной сетке, работающий даже на персональном компьютере. Эффективность метода достаточна для решения одномерной задачи для газа в расширителе. Алгоритм допускает обобщение на неупругие процессы с разными сортами частиц и легко распараллеливается, что позволяет надеяться на успешное совершенствование модели.

Список литературы

  1. Soldatkina E.I. et al. Axial plasma confinement in gas dynamic trap // Plasma and Fusion Research. 2019. T. 14. C. 2402006–2402006.

  2. Soldatkina E.I. et al. Measurements of axial energy loss from magnetic mirror trap // Nuclear Fusion. 2020. T. 60. № 8. C. 086009.

  3. Ivanov M.S., Rogasinsky S.V. Analysis of numerical techniques of the direct simulation Monte Carlo method in the rarefied gas dynamics. 1988.

  4. Babovsky H., Neunzert H. On a simulation scheme for the Boltzmann equation // Math. Methods in the Applied Sciences. 1986. T. 8. № 1. C. 223–233.

  5. Bird G.A. Direct simulation and the Boltzmann equation // The Physics of Fluids. 1970. T. 13. № 11. C. 2676–2681.

  6. Nanbu K. Direct simulation scheme derived from the Boltzmann equation. I. Monocomponent gases // J. of the Physical Society of Japan. 1980. T. 49. № 5. C. 2042–2049.

  7. Bird G.A. Molecular gas dynamics and the direct simulation of gas flows. Oxford: Clarendon press, 1994. T. 5.

  8. Burnett D. The distribution of velocities in a slightly non‐uniform gas // Proc. of the London Math. Society. 1935. V. 2. № 1. C. 385–430.

  9. Grad H. On the kinetic theory of rarefied gases // Commun. on Pure and Applied Math. 1949. T. 2. № 4. C. 331–407.

  10. Pareschi L., Perthame B. A Fourier spectral method for homogeneous Boltzmann equations // Transport Theory and Statistical Physics. 1996. T. 25. № 3–5. C. 369–382.

  11. Bobylev A., Rjasanow S. Difference scheme for the Boltzmann equation based on the Fast Fourier Transform // European journal of mechanics. B, Fluids. 1997. T. 16. № 2. C. 293–306.

  12. Pareschi L., Russo G. Numerical solution of the Boltzmann equation I: Spectrally accurate approximation of the collision operator // SIAM Journal on Numerical Analysis. 2000. T. 37. № 4. C. 1217–1245.

  13. Gamba I.M., Haack J.R. A conservative spectral method for the Boltzmann equation with anisotropic scattering and the grazing collisions limit // J. of Computational Physics. 2014. T. 270. C. 40–57.

  14. Wu L. et al. Deterministic numerical solutions of the Boltzmann equation using the fast spectral method // J. of Comput. Physics. 2013. T. 250. C. 27–52.

  15. Wu L. et al. A fast spectral method for the Boltzmann equation for monatomic gas mixtures // J. of Comput. Physics. 2015. T. 298. C. 602–621.

  16. Filbet F., Mouhot C., Pareschi L. Solving the Boltzmann equation in N log2 N // SIAM J. on Scientific Computing. 2006. T. 28. № 3. C. 1029–1053.

  17. Aristov V.V. Solving the Boltzmann equation for discrete velocities // Akademiia Nauk SSSR Doklady. 1985. T. 283. C. 831–834.

  18. Schneider J. Une méthode déterministe pour la résolution de l’équation de Boltzmann : Doctoral dissertation, Paris 6, 1993.

  19. Palczewski A., Schneider J. Existence, stability, and convergence of solutions of discrete velocity models to the Boltzmann equation // J. of Statistical Physics. 1998. V. 91. № 1–2. C. 307–326.

  20. Vasiljevitch Bobylev A., Palczewski A., Schneider J. On approximation of the Boltzmann equation by discrete velocity models // Comptes rendus de l’Académie des sciences. Série 1, Mathématique. 1995. V. 320. № 5. C. 639–644.

  21. Palczewski A., Schneider J., Bobylev A.V. A consistency result for a discrete-velocity model of the Boltzmann equation // SIAM Journal on Numerical Analysis. 1997. T. 34. № 5. C. 1865–1883.

  22. Buet C. A discrete-velocity scheme for the Boltzmann operator of rarefied gas dynamics // Transport Theory and Statistical Physics. 1996. T. 25. № 1. C. 33–60.

  23. Płatkowski T., Waluś W. An acceleration procedure for discrete velocity approximation of the Boltzmann collision operator // Computers and Math. with Applicat. 2000. V. 39. № 5–6. C. 151–163.

  24. Panferov V.A., Heintz A.G. A new consistent discrete-velocity model for the Boltzmann equation // Math. Methods in the Applied Sciences. 2002. T. 25. № 7. C. 571–593.

  25. Alekseenko A., Josyula E. Deterministic solution of the spatially homogeneous Boltzmann equation using discontinuous Galerkin discretizations in the velocity space // J. of Comput. Physics. 2014. T. 272. C. 170–188.

  26. Cercignani C., Illner R., Pulvirenti M. The mathematical theory of dilute gases. London: Springer Science and Business Media, 2013. T. 106.

  27. Narayan A., Klöckner A. Deterministic Numerical Schemes for the Boltzmann Equation // arXiv. 2009. C. ar-Xiv: 0911.3589.

  28. Hardin D.P., Michaels T.J., Saff E.B. A Comparison of Popular Point Configurations on ${{\mathbb{S}}^{2}}$ // arXiv preprint arXiv:1607.04590. 2016.

  29. Bobylev A.V. Exact solutions of the Boltzmann equation // Akademiia Nauk SSSR Doklady. 1975. V. 225. C. 1296–1299.

  30. Krook M., Wu T.T. Exact solutions of the Boltzmann equation // The Physics of Fluids. 1977. T. 20. № 10. C. 1589–1595.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал