Журнал вычислительной математики и математической физики, 2022, T. 62, № 11, стр. 1895-1911

Нестационарный изгиб ортотропной консольно-закрепленной балки Тимошенко с учетом релаксации диффузионных потоков

А. В. Земсков^1, 2, *, Д. В. Тарлаковский^2, 1, **

¹ МАИ
125993 Москва, Волоколамское ш. 4, Россия

² НИИ механ. МГУ
119192 Москва, Мичуринский пр-т, 1, Россия

^* E-mail: azemskov1975@mail.ru
^** E-mail: tdvhome@mail.ru

Поступила в редакцию 17.03.2022
После доработки 25.06.2022
Принята к публикации 07.07.2022

EDN: JMPEIF
DOI: 10.31857/S004446692211014X

Полный текст (PDF)

Аннотация

Рассматривается нестационарная задача об изгибе консольно-закрепленной упругодиффузионной ортотропной балки Тимошенко под действием нагрузки, приложенной к свободному концу балки. Модель учитывает конечную скорость распространения диффузионных возмущений вследствие релаксации диффузионных потоков. Физико-механические процессы описываются связанной системой уравнений изгиба балки Тимошенко с учетом диффузии. Решение задачи ищется с помощью метода эквивалентных граничных условий. Для этого рассматривается вспомогательная задача, решение которой получается с помощью интегрального преобразования Лапласа по времени и разложения в тригонометрические ряды Фурье. Далее строятся соотношения, связывающие правые части граничных условий исходной и вспомогательной задачи. Эти соотношения представляют собой систему интегральных уравнений Вольтерра I рода. Решение этой системы осуществляется численно с помощью квадратурных формул. На примере трехкомпонентного материала выполнено численное исследование взаимодействия нестационарных механического и диффузионного полей в ортотропной балке. В заключение приведены основные выводы о влиянии связанности полей на напряженно-деформированное состояние и массоперенос в стержне. Библ. 31. Фиг. 8.

Ключевые слова: нестационарная механодиффузия, балка Тимошенко, изгиб консоли, нестационарные задачи, преобразование Лапласа, метод эквивалентных граничных условий.

ВВЕДЕНИЕ

В работе исследуются нестационарные упругодиффузионные колебания балки Тимошенко. Эта модель является уточнением классической модели балки Бернулли–Эйлера, за счет учета деформаций сдвига и влияния инерционных сил при повороте нормали относительно срединной поверхности.

Классическая модель балки Бернулли–Эйлера является наиболее простой из всех балочных моделей и в ряде случаев обеспечивает удовлетворительную точность решения инженерных задач, связанных с расчетом конструкций на прочность. Однако учет деформаций сдвига, которых нет в модели Бернулли–Эйлера, может оказаться существенным, для расчетов стержней, изготовленных из анизотропного материала, у которых модуль сдвига много меньше модуля Юнга. Так же важное значение имеет учет деформаций сдвига в задачах устойчивости трехслойных стержней и пластин, где два несущих слоя выполнены из тонкого высокопрочного жесткого материала, между ними легкий и менее прочный заполнитель.

Балки, пластины и оболочки являются основой любой конструкции, поэтому их моделям посвящено очень большое количество научных работ. Среди наиболее современных работ можно отметить [1]–[6], где изложены общие принципы построения уравнений теории пластин и оболочек, основанные на вариационных принципах и асимптотических методах моделирования. Здесь же изложены методы решения задач об изгибе пластин и оболочек при различных способах закрепления и различных видов механического нагружения.

Следует отметить, что расчет тонкостенных конструкций существенно усложняется в том случае, когда приходится учитывать взаимодействие полей различной физической природы: механических, диффузионных, температурных и пр. Поэтому чаще всего ограничиваются исследованием взаимодействия стационарных физических полей в сплошных средах и технических системах.

Анализу механодиффузионных процессов и оценке их влияния на несущую способность стержней, пластин и оболочек посвящены работы [7]–[14]. В работах [7], [8] исследуется влияние диффузионных процессов на несущую способность пологой трансверсально-изотропной оболочки. Контактное нестационарное взаимодействие стержня с упругим полупространством рассматривается в работах [9], [10]. Публикации [11]–[13] посвящены исследованию механодиффузионных процессов в пластинах. Расчет сферических оболочек с учетом диффузии рассмотрен в [14].

Моделирование нестационарных процессов как в тонкостенных элементах конструкций, так и в сплошных средах представляет собой достаточно сложную математическую задачу, связанную с обращением преобразования Лапласа, которое применяется при аналитических методах решения нестационарных начально-краевых задач. В большинстве случаев эта проблема решается с помощью специальных квадратурных формул, позволяющих приближенно вычислить интеграл Меллина. В качестве наиболее известных алгоритмов используются: метод Дурбина [15], [16], “Gaver-Stehfast algorithm” [17], “Zakian’s algorithm” [18], методы основанные на использовании ортогональных полиномов Лежандра [14] и пр. Подробное описание методов обращения преобразования Лапласа можно найти также в монографии [19]. Данные методы хорошо зарекомендовали себя при вычислении оригиналов в определенном классе функций. Однако для нахождения функций Грина эти алгоритмы не пригодны, так как функции Грина принадлежат к классу обобщенных функций, что затрудняет использование методов численного интегрирования.

В настоящей работе рассматривается задача о нестационарных колебаниях консольно-закрепленной балки с учетом диффузии. Уравнения упругодиффузионных колебаний балки получены из классической модели механодиффузии для сплошных сред с помощью вариационного принципа Даламбера [20], [21]. Основная сложность в решении данной задачи заключается в том, что краевые условия, соответствующие консольному закреплению, не позволяют воспользоваться методом Фурье разделения переменных. Это существенно осложняет обращение преобразования Лапласа, о котором говорилось ранее. Например, для свободно опертых балок [20], [21] применение метода Фурье и преобразования Лапласа позволяет свести проблему обращения преобразования Лапласа к проблеме нахождения оригиналов от рациональной функции. Такая задача решается аналитически с помощью вычетов и таблиц операционного исчисления.

Таким образом, задача об изгибе консольно-закрепленной балки с учетом диффузии намного сложнее аналогичной задачи для свободно опертой балки. Для ее решения предлагается использовать метод эквивалентных граничных условий, который заключается в том, что вместо исходной задачи рассматривается вспомогательная задача того же вида, но с граничными условиями, допускающими представление решений в виде рядов Фурье. Далее строятся соотношения, связывающие правые части граничных условий обеих задач. Эти соотношения записываются в виде системы интегральных уравнений Вольтерра I рода. Затем полученная система уравнений решается численно с помощью квадратурных формул. Предложенный метод был апробирован при решении аналогичной задачи для консольно-закрепленной балки Бернулли–Эйлера [22].

1. ПОСТАНОВКА ЗАДАЧИ

В работе рассматривается задача о нестационарном упругодиффузионном изгибе консольно-закрепленной ортотропной балки Тимошенко (фиг. 1).

Фиг. 1.

Иллюстрация к постановке задачи.

Математическая постановка представляет собой замкнутую систему уравнений поперечных колебаний балки с учетом диффузии, которая получена из общей модели упругой диффузии для сплошных сред с помощью вариационного принципа Даламбера [20], [21]:

(1)

$\begin{gathered} \ddot {v} - {{C}_{{66}}}{{k}^{2}}\left( {v{\kern 1pt} '{\kern 1pt} '\; - \chi {\kern 1pt} '} \right) - \frac{Q}{F} = 0,\quad a = \frac{F}{{{{J}_{3}}}},\quad q = \overline {1,N} , \\ \ddot {\chi } - \chi {\kern 1pt} '{\kern 1pt} '\; - a{{C}_{{66}}}{{k}^{2}}\left( {v{\kern 1pt} ' - \chi } \right) - \sum\limits_{j = 1}^N \,\alpha _{1}^{{\left( j \right)}}H_{j}^{'} - \frac{M}{{{{J}_{3}}}} = 0, \\ \sum\limits_{k = 0}^K \frac{{\tau _{q}^{k}}}{{k!}}\frac{{{{\partial }^{k}}{{{\dot {H}}}_{q}}}}{{\partial {{\tau }^{k}}}} - D_{1}^{{\left( q \right)}}H_{q}^{{''}} - \Lambda _{{11}}^{{\left( q \right)}}\chi {\kern 1pt} '''\; - \frac{{{{z}^{{\left( q \right)}}}}}{{{{J}_{3}}}} = 0,\quad {{H}_{{N + 1}}} = - \sum\limits_{j = 1}^N \,{{H}_{j}}. \\ \end{gathered} $

Здесь точки обозначают производную по времени, штрихи – производную по координате ${{x}_{1}}$. Все величины в (1) являются безразмерными. Для них приняты следующие обозначения:

$\begin{gathered} {{x}_{i}} = \frac{{x_{i}^{*}}}{l},\quad v = \frac{{v{\kern 1pt} *}}{l},\quad \tau = \frac{{Ct}}{l},\quad {{C}^{2}} = \frac{{C_{{11}}^{*}}}{\rho },\quad {{C}_{{ij}}} = \frac{{C_{{ij}}^{*}}}{{C_{{11}}^{*}}},\quad M = \frac{{lM{\kern 1pt} *}}{{C_{{11}}^{*}}},\quad Q = \frac{{lQ{\kern 1pt} *}}{{C_{{11}}^{*}}}, \\ D_{\alpha }^{{\left( q \right)}} = \frac{{D_{{\alpha \alpha }}^{{\left( q \right)}}}}{{Cl}},\quad \alpha _{\beta }^{{\left( q \right)}} = \frac{{\alpha _{{\beta \beta }}^{{\left( q \right)}}}}{{C_{{11}}^{*}}},\quad \Lambda _{{\alpha \beta }}^{{\left( q \right)}} = \frac{{{{m}^{{\left( q \right)}}}D_{{\alpha \alpha }}^{{\left( q \right)}}\alpha _{{\beta \beta }}^{{\left( q \right)}}n_{0}^{{\left( q \right)}}}}{{\rho R{{T}_{0}}Cl}},\quad {{\tau }_{q}} = \frac{{C{{\tau }^{{\left( q \right)}}}}}{l}, \\ \end{gathered} $

где $t$ – время; $x_{i}^{*}$ – прямоугольные декартовы координаты; $v{\kern 1pt} *$ – поперечный прогиб балки; $\chi $ – угол поворота сечения; $l$ – длина балки; $k$ – коэффициент сдвига Тимошенко, который зависит от формы балки (для прямоугольного сечения балки ${{k}^{2}} = 5{\text{/}}6$); ${{H}_{q}}$ – линейная плотность приращения концентрации $q$-й компоненты вещества в составе многокомпонентной среды; $n_{0}^{{(q)}}$ – начальная концентрация $q$-го вещества; $C_{{ij}}^{*}$ – упругие постоянные; $\rho $ – плотность; $\alpha _{{ij}}^{{\left( q \right)}}$ – коэффициенты, характеризующие объемное изменение среды за счет диффузии; $D_{{ij}}^{{\left( q \right)}}$ – коэффициенты диффузии; $R$ – универсальная газовая постоянная; ${{T}_{0}}$ – температура среды; ${{m}^{{(q)}}}$ – молярная масса $q$-го вещества; $F{\kern 1pt} *$ – площадь сечения; $J_{3}^{*}$ – момент инерции сечения балки относительно оси $O{{x}_{3}}$; ${{\tau }^{{\left( q \right)}}}$ – время релаксации диффузионных потоков; $Q{\kern 1pt} *$ – распределенная поперечная нагрузка; $M{\kern 1pt} *$ – распределенный изгибающий момент.

Компоненты тензора напряжений определяются с помощью равенств [20], [21]:

$\begin{array}{*{20}{c}} {{{\sigma }_{{11}}} = - {{x}_{2}}\left( {\chi {\kern 1pt} '\; + \sum\limits_{j = 1}^N \,\alpha _{1}^{{\left( j \right)}}{{H}_{j}}} \right),\quad {{\sigma }_{{22}}} = - {{x}_{2}}\left( {{{C}_{{12}}}\chi {\kern 1pt} '\; + \sum\limits_{j = 1}^N \,\alpha _{2}^{{\left( j \right)}}{{H}_{j}}} \right),\quad {{\sigma }_{{12}}} = {{C}_{{66}}}\left( {v{\kern 1pt} '\; - \chi } \right).} \end{array}$

Описываемая здесь модель учитывает конечную скорость распространения диффузионных возмущений, что обусловлено релаксацией диффузионных потоков. Инерционность в уравнения теплопереноса первым ввел Максвелл, а в 1948 году Каттанео был предложен вариант закона Фурье с релаксационным членом. Предложенная идея была распространена на модели, описывающие диффузионные процессы. В настоящее время существуют различные обобщения законов Фурье и Фика, с которыми можно ознакомиться в работах [23]–[27]. Используемая в данной работе модель массопереноса основана на теории Грина–Нагди [23], [27], согласно которой компоненты вектора диффузионного потока должны удовлетворять соотношениям:

(2)

$\sum\limits_{k = 0}^K \frac{{\tau _{q}^{k}}}{{k!}}\frac{{{{\partial }^{k}}J_{1}^{{\left( q \right)}}}}{{\partial {{\tau }^{k}}}} = - {{x}_{2}}\left( {D_{1}^{{\left( q \right)}}{{{H'}}_{q}} + \Lambda _{{11}}^{{\left( q \right)}}\chi {\kern 1pt} '{\kern 1pt} '} \right),\quad \sum\limits_{k = 0}^K \frac{{\tau _{q}^{k}}}{{k!}}\frac{{{{\partial }^{k}}J_{2}^{{\left( q \right)}}}}{{\partial {{\tau }^{k}}}} = - D_{2}^{{\left( q \right)}}{{H}_{q}} - \Lambda _{{21}}^{{\left( q \right)}}\chi {\kern 1pt} '\quad {\kern 1pt} \left( {q = \overline {1,N} } \right).$

Верхний предел суммирования $K$ в уравнениях (1) и формулах (2) определяется на основе заданной точности вычислений. Однако, как показывают расчеты [27], практически всегда можно ограничиться значением $K = 2$, а в большинстве случаев приемлемая точность обеспечивается даже при $K = 1$ (модель Каттанео). Случай $K = 0$ соответствует классической модели массопереноса с бесконечной скоростью распространения диффузионных возмущений.

Выражения для изгибающих моментов ${{M}_{0}}$ и перерезывающих сил ${{Q}_{0}}$, заданных на свободном конце стержня, также получены в работах [20], [21]

${{M}_{0}} = \left( {\chi {\kern 1pt} '\; + \sum\limits_{q = 1}^N \,\alpha _{1}^{{\left( q \right)}}{{H}_{q}}} \right){{J}_{3}},\quad {{Q}_{0}} = \left( {v{\kern 1pt} '\; - \chi } \right){{C}_{{66}}}F.$

Начальные условия полагаем нулевыми. Граничные условия в соответствии с моделью изгиба консоли имеют вид $(x = {{x}_{1}})$:

(3)

$\begin{gathered} {{\left. v \right|}_{{x = 0}}} = 0,\quad {{\left. \chi \right|}_{{x = 0}}} = 0,\quad {{\left. {{{H}_{q}}} \right|}_{{x = 0}}} = 0,\quad {{\left. {\left( {v{\kern 1pt} '\; - \chi } \right)} \right|}_{{x = 1}}} = {{f}_{{12}}}, \\ {{\left. {\left( {\chi {\kern 1pt} '\; + \sum\limits_{q = 1}^N \,\alpha _{1}^{{\left( q \right)}}{{H}_{q}}} \right)} \right|}_{{x = 1}}} = 0,\quad {{\left. {\left( {\Lambda _{{11}}^{{\left( q \right)}}\chi {\kern 1pt} '{\kern 1pt} '\; + D_{1}^{{\left( q \right)}}H_{q}^{'}} \right)} \right|}_{{x = 1}}} = 0. \\ \end{gathered} $

2. МЕТОД РЕШЕНИЯ

Как было отмечено во введении, основная проблема в решении поставленной задачи заключается в невозможности использования метода разделения переменных. Это не так важно, когда речь идет о статическом или стационарном изгибе балки. В данном случае указанное обстоятельство существенно осложняет обращение преобразования Лапласа, которое используется при решении этой задачи. Для преодоления указанной проблемы предлагается использовать метод эквивалентных граничных условий, который был успешно применен для решения аналогичной задачи для балки Бернулли–Эйлера [22].

Суть алгоритма заключается в том, что на начальном этапе вместо исходной задачи рассматривается вспомогательная задача со следующими граничными условиями:

(4)

$\begin{gathered} {{\left. v \right|}_{{x = 0}}} = 0,\quad {{\left. {\left( {\chi {\kern 1pt} '\; + \sum\limits_{q = 1}^N \,\alpha _{1}^{{\left( q \right)}}{{H}_{q}}} \right)} \right|}_{{x = 0}}}\quad = f_{{21}}^{*},\quad {{\left. {{{H}_{q}}} \right|}_{{x = 0}}} = 0, \\ {{\left. {\left( {v{\kern 1pt} '\; - \chi } \right)} \right|}_{{x = 1}}} = {{f}_{{12}}},\quad {{\left. \chi \right|}_{{x = 1}}} = f_{{22}}^{*},\quad {{\left. {\left( {\Lambda _{{11}}^{{\left( q \right)}}\chi {\kern 1pt} '{\kern 1pt} '\; + D_{1}^{{\left( q \right)}}H_{q}^{'}} \right)} \right|}_{{x = 1}}}\quad = 0, \\ \end{gathered} $

где функции $f_{{21}}^{*}\left( \tau \right)$, $f_{{22}}^{*}\left( \tau \right)$ подлежат определению.

Ее решение в интегральной форме записывается в виде

(5)

$\begin{array}{*{20}{c}} {v\left( {x,\tau } \right) = \sum\limits_{l = 1}^2 {\kern 1pt} \int\limits_0^\tau \,{{G}_{{12l}}}\left( {x,\tau - t} \right)f_{{2l}}^{*}\left( t \right)dt + \int\limits_0^\tau \,{{G}_{{112}}}\left( {x,\tau - t} \right){{f}_{{12}}}\left( t \right)dt,} \\ {\chi \left( {x,\tau } \right) = \sum\limits_{l = 1}^2 {\kern 1pt} \int\limits_0^\tau \,{{G}_{{22l}}}\left( {x,\tau - t} \right)f_{{2l}}^{*}\left( t \right)dt + \int\limits_0^\tau \,{{G}_{{212}}}\left( {x,\tau - t} \right){{f}_{{12}}}\left( t \right)dt,} \\ {{{H}_{q}}\left( {x,\tau } \right) = \sum\limits_{l = 1}^2 {\kern 1pt} \int\limits_0^\tau \,{{G}_{{q + 2,2l}}}\left( {x,\tau - t} \right)f_{{2l}}^{*}\left( t \right)dt + \int\limits_0^\tau \,{{G}_{{q + 2,12}}}\left( {x,\tau - t} \right){{f}_{{12}}}\left( t \right)dt.} \end{array}$

Здесь ${{G}_{{mkl}}}$ – функции Грина задачи (1), (4), которые являются решениями следующих задач:

(6)

$\begin{array}{*{20}{c}} {{{{\ddot {G}}}_{{1kl}}} - {{C}_{{66}}}{{k}^{2}}(G_{{1kl}}^{{''}} - G_{{2kl}}^{'}) = 0,} \\ {{{{\ddot {G}}}_{{2kl}}} - G_{{2kl}}^{{''}} - a{{C}_{{66}}}{{k}^{2}}(G_{{1kl}}^{'} - {{G}_{{2kl}}}) - \sum\limits_{q = 1}^N \,\alpha _{1}^{{\left( q \right)}}G_{{q + 2,kl}}^{'} = 0,} \\ {\sum\limits_{k = 0}^K \frac{{\tau _{q}^{k}}}{{k!}}\frac{{{{\partial }^{k}}{{{\dot {G}}}_{{q + 2,kl}}}}}{{\partial {{\tau }^{k}}}} - \sum\limits_{r = 1}^N \,D_{1}^{{\left( {qr} \right)}}G_{{r + 2,kl}}^{{''}} - \Lambda _{{11}}^{{\left( q \right)}}G_{{2kl}}^{{'''}} = 0;} \end{array}$

(7)

$\begin{gathered} {{\left. {{{G}_{{1kl}}}} \right|}_{{x = 0}}} = {{\delta }_{{1k}}}{{\delta }_{{1l}}}\delta \left( \tau \right),\quad {{\left. {\left( {G_{{2kl}}^{'} + \sum\limits_{q = 1}^N \,\alpha _{1}^{{\left( q \right)}}{{H}_{q}}} \right)} \right|}_{{x = 0}}} = {{\delta }_{{2k}}}{{\delta }_{{1l}}}\delta \left( \tau \right), \\ {{\left. {{{G}_{{q + 2,kl}}}} \right|}_{{x = 0}}} = {{\delta }_{{q + 2,k}}}{{\delta }_{{1l}}}\delta \left( \tau \right),\quad {{\left. {\left( {G_{{1kl}}^{'} - {{G}_{{2kl}}}} \right)} \right|}_{{x = 1}}} = {{\delta }_{{1k}}}{{\delta }_{{2l}}}\delta \left( \tau \right),\quad {{\left. {{{G}_{{2kl}}}} \right|}_{{x = 1}}} = {{\delta }_{{2k}}}{{\delta }_{{2l}}}\delta \left( \tau \right), \\ {{\left. {\left( {\Lambda _{{11}}^{{\left( q \right)}}G_{{2kl}}^{{''}} + {{D}_{q}}G_{{q + 2,kl}}^{'}} \right)} \right|}_{{x = 1}}} = {{\delta }_{{q + 2,k}}}{{\delta }_{{2l}}}\delta \left( \tau \right). \\ \end{gathered} $

Для нахождения функций ${{G}_{{mkl}}}$ используются преобразование Лапласа по времени и разложение в ряды Фурье. Применяя указанные действия к вспомогательной задаче (6), (7), получаем следующую систему линейных алгебраических уравнений ($s$ – параметр преобразования Лапласа, верхний индекс $L$ обозначает трансформанту Лапласа):

(8)

$\begin{array}{*{20}{c}} {{{k}_{{1n}}}\left( s \right)G_{{1kln}}^{L}\left( s \right) - {{C}_{{66}}}{{k}^{2}}{{\lambda }_{n}}G_{{2kln}}^{L}\left( s \right) = {{F}_{{1kln}}},} \\ { - a\mu {{k}^{2}}{{\lambda }_{n}}G_{{1kln}}^{L}\left( s \right) + {{k}_{{2n}}}\left( s \right)G_{{2kln}}^{L}\left( s \right) - {{\lambda }_{n}}\sum\limits_{j = 1}^N \,\alpha _{1}^{{\left( j \right)}}G_{{j + 2,kln}}^{L}\left( s \right) = {{F}_{{2kln}}},} \\ { - \Lambda _{{11}}^{{\left( q \right)}}\lambda _{n}^{3}G_{{2kln}}^{L}\left( s \right) + {{k}_{{q + 2,n}}}\left( s \right)G_{{q + 2,kln}}^{L}\left( s \right) = {{F}_{{q + 2,kln}}};} \end{array}$

(9)

$\begin{gathered} \left\{ {\begin{array}{*{20}{c}} {G_{{mkl}}^{L}\left( {x,s} \right)} \\ {G_{{q + 2,kl}}^{L}\left( {x,s} \right)} \end{array}} \right\} = \sum\limits_{n = 1}^\infty \left\{ {\begin{array}{*{20}{c}} {G_{{mkln}}^{L}\left( s \right)} \\ {G_{{q + 2,kln}}^{L}\left( s \right)} \end{array}} \right\}\sin {{\lambda }_{n}}x,\quad G_{{2kl}}^{L}\left( {x,s} \right) = \sum\limits_{n = 1}^\infty G_{{2kln}}^{L}\left( s \right)\sin {{\lambda }_{n}}x,\quad {{\lambda }_{n}} = \pi \left( {n - \frac{1}{2}} \right), \\ \left\{ {\begin{array}{*{20}{c}} {G_{{mkln}}^{L}\left( s \right)} \\ {G_{{q + 2,kln}}^{L}\left( s \right)} \end{array}} \right\} = 2\int\limits_0^1 \left\{ {\begin{array}{*{20}{c}} {G_{{mkl}}^{L}\left( {x,s} \right)} \\ {G_{{q + 2,kl}}^{L}\left( {x,s} \right)} \end{array}} \right\}\sin {{\lambda }_{n}}xdx,\quad G_{{2kln}}^{L}\left( s \right) = 2\int\limits_0^1 \,G_{{2kl}}^{L}\left( {x,s} \right)\cos {{\lambda }_{n}}xdx. \\ \end{gathered} $

Коэффициенты ${{k}_{{1n}}}\left( s \right)$ и правые части ${{F}_{{1kln}}}$ системы (8) приведены в Приложении (форму-лы (25)).

Решение системы (8) имеет вид $\left( {q,p = \overline {1,N} ,\;k = \overline {1,N + 1} } \right)$

(10)

$\begin{array}{*{20}{c}} {G_{{1kln}}^{L}\left( s \right) = \frac{{{{P}_{{1kln}}}\left( s \right)}}{{{{P}_{n}}\left( s \right)}},\quad G_{{2kln}}^{L}\left( s \right) = \frac{{{{P}_{{2kln}}}\left( s \right)}}{{{{P}_{n}}\left( s \right)}},\quad G_{{q + 2,1ln}}^{L}\left( s \right) = \frac{{{{P}_{{q + 2,1ln}}}\left( s \right)}}{{{{P}_{n}}\left( s \right)}},} \\ {G_{{q + 2,2ln}}^{L}\left( s \right) = \frac{{2\Lambda _{{11}}^{{\left( q \right)}}{{\lambda }_{n}}\left( {{{\delta }_{{1l}}} - {{{\left( { - 1} \right)}}^{{n + 1}}}{{\lambda }_{n}}{{\delta }_{{2l}}}} \right)}}{{{{k}_{{q + 2,n}}}\left( s \right)}} + \frac{{{{P}_{{q + 2,2ln}}}\left( s \right)}}{{{{Q}_{{qn}}}\left( s \right)}},} \\ {G_{{q + 2,p + 2,ln}}^{L}\left( s \right) = \frac{{{{P}_{{q + 2,p + 2,ln}}}\left( s \right)}}{{{{Q}_{{qn}}}\left( s \right)}} + \frac{{2{{\lambda }_{n}}\left( {D_{1}^{{\left( q \right)}}{{\delta }_{{pq}}} - \Lambda _{{11}}^{{\left( q \right)}}\alpha _{1}^{{\left( p \right)}}} \right){{\delta }_{{1l}}} + 2{{{\left( { - 1} \right)}}^{{n + 1}}}{{\delta }_{{pq}}}{{\delta }_{{2l}}}}}{{{{k}_{{q + 2,n}}}\left( s \right)}},} \end{array}$

где ${{P}_{n}}\left( s \right)$, ${{Q}_{{qn}}}\left( s \right)$ и ${{P}_{{jkln}}}\left( s \right)$ – многочлены от $s$, приведенные в Приложении (формулы (26) и (27)).

Оригиналы в (10) находятся с помощью вычетов и таблиц операционного исчисления [28]

$\begin{array}{*{20}{c}} {{{G}_{{ikln}}}\left( \tau \right) = \sum\limits_{j = 1}^\Sigma \,A_{{ikln}}^{{\left( j \right)}}{{e}^{{{{s}_{{jn}}}\tau }}},\quad A_{{ikln}}^{{\left( j \right)}} = \frac{{{{P}_{{ikln}}}\left( {{{s}_{{jn}}}} \right)}}{{P_{n}^{'}\left( {{{s}_{{jn}}}} \right)}}\quad \left( {i = 1,2,\quad \Sigma = \left( {K + 1} \right)N + 4} \right),} \\ {G_{{q + 2,1ln}}^{s}\left( \tau \right) = \sum\limits_{j = 1}^\Sigma \,A_{{q + 2,1ln}}^{{\left( j \right)}}{{e}^{{{{s}_{{jn}}}\tau }}},\quad A_{{q + 2,1ln}}^{{\left( j \right)}} = \frac{{{{P}_{{q + 2,1ln}}}\left( {{{s}_{{jn}}}} \right)}}{{{{{P'}}_{n}}\left( {{{s}_{{jn}}}} \right)}},} \end{array}$

(11)

$\begin{gathered} {{G}_{{q + 2,2ln}}}\left( \tau \right) = 2\Lambda _{{11}}^{{\left( q \right)}}{{\lambda }_{n}}\left( {{{\delta }_{{1l}}} - {{{\left( { - 1} \right)}}^{{n + 1}}}{{\lambda }_{n}}{{\delta }_{{2l}}}} \right)\sum\limits_{r = 1}^{K + 1} \frac{{{{e}^{{{{\xi }_{{rqn}}}\tau }}}}}{{{{{k'}}_{{q + 1,n}}}\left( {{{\xi }_{{rqn}}}} \right)}} + \sum\limits_{j = 1}^{\Sigma + K + 1} A_{{q + 1,2ln}}^{{\left( j \right)}}{{e}^{{{{s}_{{jn}}}\tau }}}, \\ {{G}_{{q + 2,p + 2,ln}}}\left( \tau \right) = \sum\limits_{j = 1}^{\Sigma + K + 1} A_{{q + 1,p + 2,ln}}^{{\left( j \right)}}{{e}^{{{{s}_{{jn}}}\tau }}} + \\ \end{gathered} $

$\begin{gathered} \, + 2\left[ {{{\lambda }_{n}}\left( {D_{1}^{{\left( q \right)}}{{\delta }_{{pq}}} - \Lambda _{{11}}^{{\left( q \right)}}\alpha _{1}^{{\left( p \right)}}} \right){{\delta }_{{1l}}} + {{{\left( { - 1} \right)}}^{{n + 1}}}{{\delta }_{{pq}}}{{\delta }_{{2l}}}} \right]\sum\limits_{r = 1}^{K + 1} \frac{{{{e}^{{{{\xi }_{{rqn}}}\tau }}}}}{{k_{{q + 1,n}}^{'}\left( {{{\xi }_{{rqn}}}} \right)}}, \\ A_{{q + 2,kln}}^{{\left( j \right)}} = \frac{{{{P}_{{q + 2,kl}}}\left( {{{s}_{{jn}}}} \right)}}{{Q_{{qn}}^{'}\left( {{{s}_{{jn}}}} \right)}}\quad \left( {k \geqslant 2} \right). \\ \end{gathered} $

Здесь ${{s}_{{jn}}}$ $\left( {j = \overline {1,\Sigma } } \right)$ – нули многочлена ${{P}_{n}}\left( s \right)$, ${{\xi }_{{rqn}}}$ – нули многочлена ${{k}_{{q + 2,n}}}\left( s \right)$. При $K = 1$ они имеют вид:

$\begin{array}{*{20}{c}} {{{\xi }_{{1qn}}}\left( {{{\lambda }_{n}}} \right) = \frac{{ - 1 - \sqrt {1 - 4{{\tau }_{q}}D_{1}^{{\left( q \right)}}\lambda _{n}^{2}} }}{{2{{\tau }_{q}}}},\quad {{\xi }_{{2qn}}}\left( {{{\lambda }_{n}}} \right) = \frac{{ - 1 + \sqrt {1 - 4{{\tau }_{q}}D_{1}^{{\left( q \right)}}\lambda _{n}^{2}} }}{{2{{\tau }_{q}}}}.} \end{array}$

На следующем этапе алгоритма строятся соотношения, связывающие правые части граничных условий обеих задач. Так как решение вспомогательной задачи должно удовлетворять граничным условиям (3), то с учетом представлений (5) указанные соотношения записываются в виде системы интегральных уравнений Вольтерра I рода, которая имеет вид [22]

(12)

$\sum\limits_{j = 1}^2 {\kern 1pt} \int\limits_0^\tau \,{{a}_{{ij}}}\left( {\tau - t} \right)f_{{2j}}^{*}\left( t \right)dt = {{\varphi }_{i}}\left( \tau \right),$

где

$\begin{gathered} {{a}_{{11}}}\left( \tau \right) = {{G}_{{221}}}\left( {0,\tau } \right),\quad {{a}_{{12}}}\left( \tau \right) = {{G}_{{222}}}\left( {0,\tau } \right), \\ {{a}_{{21}}}\left( \tau \right) = G_{{221}}^{'}\left( {1,\tau } \right) + \sum\limits_{j = 1}^N \,\alpha _{1}^{{\left( j \right)}}{{G}_{{j + 2,21}}}\left( {1,\tau } \right),\quad {{a}_{{22}}}\left( \tau \right) = G_{{222}}^{'}\left( {1,\tau } \right) + \sum\limits_{j = 1}^N \,\alpha _{1}^{{\left( j \right)}}{{G}_{{j + 2,22}}}\left( {1,\tau } \right), \\ \end{gathered} $

$\begin{array}{*{20}{c}} {{{\varphi }_{1}}\left( \tau \right) = - \int\limits_0^\tau \,{{G}_{{212}}}\left( {0,\tau - t} \right){{f}_{{12}}}\left( t \right)dt,} \\ {{{\varphi }_{2}}\left( \tau \right) = - \int\limits_0^\tau \left[ {G_{{212}}^{'}\left( {1,t - \tau } \right) + \sum\limits_{j = 1}^N \,\alpha _{1}^{{\left( j \right)}}{{G}_{{j + 2,12}}}\left( {1,\tau - t} \right)} \right]{{f}_{{12}}}\left( t \right)dt.} \end{array}$

Как известно, функции Грина принадлежат к классу обобщенных функций. Поэтому ряды (9), коэффициенты которых определяются равенствами (10), (11), сходятся только в обобщенном смысле. Это затрудняет применение численных алгоритмов для решения системы (12). Для преодоления указанной трудности проинтегрируем по частям интегралы в (12). Получим систему уравнений относительно производных $\partial f_{{2j}}^{*}\left( \tau \right){\text{/}}\partial \tau $

(13)

$\begin{array}{*{20}{c}} {\sum\limits_{j = 1}^2 {\kern 1pt} \int\limits_0^\tau \,{{A}_{{ij}}}\left( {\tau - t} \right)\frac{{\partial f_{{2j}}^{*}\left( t \right)}}{{\partial t}}dt = {{F}_{i}}\left( \tau \right),\quad {{F}_{i}}\left( \tau \right) = {{\varphi }_{i}}\left( \tau \right) - \sum\limits_{j = 1}^2 \,{{A}_{{ij}}}\left( \tau \right)f_{{2j}}^{*}\left( 0 \right),} \\ {{{A}_{{ij}}}\left( \tau \right) = \int\limits_0^\tau \,{{a}_{{ij}}}\left( t \right)dt,\quad {{A}_{{ij}}}\left( {\tau - t} \right) = \int\limits_0^{\tau - t} \,{{a}_{{ij}}}\left( \varepsilon \right)d\varepsilon .} \end{array}$

Решение системы (13) будет зависеть от значений $f_{{2j}}^{*}\left( 0 \right)$ $\left( {j = 1,2} \right)$, которые определим исходя из условия сопряжения начальных и граничных условий в угловых точках пространственно-временной области рассматриваемых задач. С учетом нулевых начальных условий будем далее полагать, что $f_{{2j}}^{*}\left( 0 \right) = 0$. В случае часто встречающихся в вычислительной практике разрывных решений функции $f_{{2j}}^{*}\left( \tau \right)$ в точке $\tau = 0$, вообще говоря, не определены и могут принимать любые значения. Поэтому здесь, исходя из вышеизложенного, также полагаем $f_{{2j}}^{*}\left( 0 \right) = 0$.

Полученная система уравнений (13) решается численно с помощью квадратурных формул. Для этого разбиваем область $\left[ {0,T} \right]$ изменения времени $\tau $ на ${{N}_{\tau }}$ отрезков точками ${{\tau }_{m}} = mh{\kern 1pt} {\kern 1pt} \left( {m = \overline {0,{{N}_{\tau }}} } \right)$ с равномерным шагом $h = T{\text{/}}{{N}_{\tau }}$ и вводим сеточные функции $y_{m}^{j} = \partial f_{{2j}}^{*}\left( {{{\tau }_{m}}} \right){\text{/}}\partial \tau $, $A_{m}^{{ij}} = {{A}_{{ij}}}\left( {{{\tau }_{m}}} \right)$.

Каждый из интегралов в (13) при $\tau = {{\tau }_{m}}$ приближенно заменяем суммой, соответствующей формуле средних прямоугольников:

$\int\limits_0^\tau \,{{A}_{{ij}}}\left( {\tau - t} \right)\frac{{\partial f_{{2j}}^{*}\left( t \right)}}{{\partial t}}dt \approx hS_{{m - 1/2}}^{{ij}} + hA_{{1/2}}^{{ij}}y_{{m - 1/2}}^{j},\quad S_{{m - 1/2}}^{{ij}} = \sum\limits_{l = 1}^{m - 1} \,A_{{m - l + 1/2}}^{{ij}}y_{{l - 1/2}}^{j}\quad \left( {i,j = \overline {1,N + 2} } \right),$

${{\tau }_{{m - 1/2}}} = \frac{{{{\tau }_{{m - 1}}} + {{\tau }_{m}}}}{2} = h\left( {m - \frac{1}{2}} \right),\quad {{\tau }_{{m - l + 1/2}}} = {{\tau }_{m}} - {{\tau }_{{l - 1/2}}} = h\left( {m - l + \frac{1}{2}} \right)\quad \left( {m = \overline {1,{{N}_{\tau }}} } \right).$

В результате приходим к рекуррентной последовательности систем линейных алгебраических уравнений $\left( {m \geqslant 1} \right):$

(14)

${\mathbf{A}}{{{\mathbf{y}}}_{{m - 1/2}}} = {{{\mathbf{b}}}_{{m - 1/2}}},$

где ${{{\mathbf{y}}}_{{m - 1/2}}} = {{\left( {y_{{m - 1/2}}^{i}} \right)}_{{2 \times 1}}}$ – столбец неизвестных, а остальные величины определяются так

$\begin{array}{*{20}{c}} {{\mathbf{A}} = {{{\left( {A_{{1/2}}^{{ij}}} \right)}}_{{2 \times 2}}},\quad {{{\mathbf{b}}}_{{m - 1/2}}} = {{{\left( {b_{{m - 1/2}}^{i}} \right)}}_{{2 \times 1}}},\quad b_{{m - 1/2}}^{i} = \frac{{{{F}_{i}}\left( {{{\tau }_{m}}} \right)}}{h} - \sum\limits_{j = 1}^2 \,S_{{m - 1/2}}^{{ij}}.} \end{array}$

Ее решение находится по формулам Крамера и имеет следующий вид:

(15)

$\begin{array}{*{20}{c}} {y_{{m - 1/2}}^{1} = \frac{{b_{{m - 1/2}}^{1}A_{{1/2}}^{{22}} - b_{{m - 1/2}}^{2}A_{{1/2}}^{{12}}}}{{A_{{1/2}}^{{11}}A_{{1/2}}^{{22}} - A_{{1/2}}^{{12}}A_{{1/2}}^{{21}}}},\quad y_{{m - 1/2}}^{2} = \frac{{b_{{m - 1/2}}^{2}A_{{1/2}}^{{11}} - b_{{m - 1/2}}^{1}A_{{1/2}}^{{21}}}}{{A_{{1/2}}^{{11}}A_{{1/2}}^{{22}} - A_{{1/2}}^{{12}}A_{{1/2}}^{{21}}}}.} \end{array}$

Таким образом, решение исходной задачи (1), (3) получается путем численного вычисления сверток функций Грина вспомогательной задачи (1), (4) с сеточными функциями (15), полученными в результате численного решения системы уравнений (14). При этом с учетом преобразования (13) свертки (5) запишутся так:

(16)

$\begin{gathered} v\left( {x,{{\tau }_{i}}} \right) = h\sum\limits_{l = 1}^2 {\kern 1pt} \sum\limits_{j = 1}^i \,{{{\tilde {G}}}_{{12l}}}\left( {x,{{\tau }_{{i - j + 1/2}}}} \right)y_{{j - 1/2}}^{l} + \int\limits_0^{{{\tau }_{i}}} \,{{G}_{{112}}}\left( {x,{{\tau }_{i}} - t} \right){{f}_{{12}}}\left( t \right)dt, \\ \chi \left( {x,{{\tau }_{i}}} \right) = h\sum\limits_{l = 1}^2 {\kern 1pt} \sum\limits_{j = 1}^i \,{{{\tilde {G}}}_{{22l}}}\left( {x,{{\tau }_{{i - j + 1/2}}}} \right)y_{{j - 1/2}}^{l} + \int\limits_0^{{{\tau }_{i}}} \,{{G}_{{212}}}\left( {x,{{\tau }_{i}} - t} \right){{f}_{{12}}}\left( t \right)dt, \\ {{H}_{q}}\left( {x,{{\tau }_{i}}} \right) = h\sum\limits_{l = 1}^2 {\kern 1pt} \sum\limits_{j = 1}^i \,{{{\tilde {G}}}_{{q + 2,2l}}}\left( {x,{{\tau }_{{i - j + 1/2}}}} \right)y_{{j - 1/2}}^{l} + \int\limits_0^{{{\tau }_{i}}} \,{{G}_{{q + 2,12}}}\left( {x,{{\tau }_{i}} - t} \right){{f}_{{12}}}\left( t \right)dt,\quad {{{\tilde {G}}}_{{mkl}}}\left( {x,\tau } \right) = \int\limits_0^\tau \,{{G}_{{mkl}}}\left( {x,t} \right)dt. \\ \end{gathered} $

3. ПРЕДЕЛЬНЫЕ ПЕРЕХОДЫ

Полагая в (1) и (4) $\alpha _{1}^{{\left( q \right)}} = 0$, $D_{1}^{{\left( q \right)}} = 0$, из соотношений (11) получаем функции Грина $G_{{ij}}^{v}\left( {x,\tau } \right) = {{\lim }_{{\alpha _{1}^{{\left( q \right)}} \to 0}}}{{G}_{{1ij}}}\left( {x,\tau } \right)$ и $G_{{ij}}^{\chi }\left( {x,\tau } \right) = {{\lim }_{{\alpha _{1}^{{\left( q \right)}} \to 0}}}{{G}_{{2ij}}}\left( {x,\tau } \right)$ упругой задачи

$\begin{gathered} G_{{11}}^{v}\left( {x,\tau } \right) = 2{{C}_{{66}}}{{k}^{2}}{\kern 1pt} \sum\limits_{n = 1}^\infty {\kern 1pt} \sum\limits_{j = 1}^2 \frac{{{{\lambda }_{n}}\left( {\lambda _{n}^{2} - \gamma _{{jn}}^{2}} \right)\sin {{\gamma }_{{jn}}}\tau \sin {{\lambda }_{n}}x}}{{{{\gamma }_{{jn}}}\left( {{{\nu }_{n}} - 2\gamma _{{jn}}^{2}} \right)}}, \\ G_{{21}}^{v}\left( {x,\tau } \right) = - 2{{C}_{{66}}}{{k}^{2}}{\kern 1pt} \sum\limits_{n = 1}^\infty {\kern 1pt} \sum\limits_{j = 1}^2 \frac{{{{\lambda }_{n}}\sin {{\gamma }_{{jn}}}\tau \sin {{\lambda }_{n}}x}}{{{{\gamma }_{{jn}}}\left( {{{\nu }_{n}} - 2\gamma _{{jn}}^{2}} \right)}}, \\ \end{gathered} $

$\begin{gathered} G_{{12}}^{v}\left( {x,\tau } \right) = 2{{C}_{{66}}}{{k}^{2}}{\kern 1pt} \sum\limits_{n = 1}^\infty {\kern 1pt} \sum\limits_{j = 1}^2 \frac{{{{{\left( { - 1} \right)}}^{{n + 1}}}\left( {\lambda _{n}^{2} - \gamma _{{jn}}^{2} + a{{C}_{{66}}}{{k}^{2}}} \right)\sin {{\gamma }_{{jn}}}\tau \sin {{\lambda }_{n}}x}}{{{{\gamma }_{{jn}}}\left( {{{\nu }_{n}} - 2\gamma _{{jn}}^{2}} \right)}}, \\ G_{{22}}^{v}\left( {x,\tau } \right) = - 2{{C}_{{66}}}{{k}^{2}}{\kern 1pt} \sum\limits_{n = 1}^\infty {\kern 1pt} \sum\limits_{j = 1}^2 \frac{{{{{\left( { - 1} \right)}}^{{n + 1}}}\lambda _{n}^{2}\sin {{\gamma }_{{jn}}}\tau \sin {{\lambda }_{n}}x}}{{{{\gamma }_{{jn}}}\left( {{{\nu }_{n}} - 2\gamma _{{jn}}^{2}} \right)}}, \\ \end{gathered} $

$\begin{gathered} G_{{11}}^{\chi }\left( {x,\tau } \right) = 2{{C}_{{66}}}{{k}^{2}}a\sum\limits_{n = 1}^\infty {\kern 1pt} \sum\limits_{j = 1}^2 \frac{{{{\gamma }_{{jn}}}\sin {{\gamma }_{{jn}}}\tau \cos {{\lambda }_{n}}x}}{{{{\nu }_{n}} - 2\gamma _{{jn}}^{2}}}, \\ G_{{21}}^{\chi }\left( {x,\tau } \right) = - 2\sum\limits_{n = 1}^\infty {\kern 1pt} \sum\limits_{j = 1}^2 \frac{{\left( {{{C}_{{66}}}{{k}^{2}}\lambda _{n}^{2} - \gamma _{{jn}}^{2}} \right)\sin {{\gamma }_{{jn}}}\tau \cos {{\lambda }_{n}}x}}{{{{\gamma }_{{jn}}}\left( {{{\nu }_{n}} - 2\gamma _{{jn}}^{2}} \right)}}, \\ \end{gathered} $

$\begin{gathered} G_{{12}}^{\chi }\left( {x,\tau } \right) = 2{{a}^{2}}C_{{66}}^{2}{{k}^{4}}\sum\limits_{n = 1}^\infty {\kern 1pt} \sum\limits_{j = 1}^2 \frac{{{{{\left( { - 1} \right)}}^{{n + 1}}}{{\lambda }_{n}}\sin {{\gamma }_{{jn}}}\tau \cos {{\lambda }_{n}}x}}{{{{\gamma }_{{jn}}}\left( {{{\nu }_{n}} - 2\gamma _{{jn}}^{2}} \right)}}, \\ G_{{22}}^{\chi }\left( {x,\tau } \right) = 2\sum\limits_{n = 1}^\infty {\kern 1pt} \sum\limits_{j = 1}^2 \frac{{{{{\left( { - 1} \right)}}^{{n + 1}}}{{\lambda }_{n}}\left( {{{C}_{{66}}}{{k}^{2}}\lambda _{n}^{2} - \gamma _{{jn}}^{2}} \right)\sin {{\gamma }_{{jn}}}\tau \cos {{\lambda }_{n}}x}}{{{{\gamma }_{{jn}}}\left( {{{\nu }_{n}} - 2\gamma _{{jn}}^{2}} \right)}}. \\ \end{gathered} $

Здесь нули многочлена ${{P}_{n}}\left( s \right)$ при $\alpha _{1}^{{\left( q \right)}} = 0$ и $D_{1}^{{\left( q \right)}} = 0$ представлены в виде

$\begin{array}{*{20}{c}} {{{s}_{{1n}}} = i{{\gamma }_{{1n}}},\quad {{s}_{{2n}}} = i{{\gamma }_{{2n}}},\quad {{s}_{{3n}}} = - {{s}_{{1n}}},\quad {{s}_{{4n}}} = - {{s}_{{2n}}},} \\ {{{\gamma }_{{1n}}} = \sqrt {\frac{{{{\nu }_{n}} + \sqrt {\nu _{n}^{2} - 4{{C}_{{66}}}{{k}^{2}}\lambda _{n}^{4}} }}{2}} ,\quad {{\gamma }_{{2n}}} = \sqrt {\frac{{{{\nu }_{n}} - \sqrt {\nu _{n}^{2} - 4{{C}_{{66}}}{{k}^{2}}\lambda _{n}^{4}} }}{2}} ,} \\ {{{\nu }_{n}} = \lambda _{n}^{2} + {{C}_{{66}}}{{k}^{2}}\lambda _{n}^{2} + a{{C}_{{66}}}{{k}^{2}}.} \end{array}$

Полагая в граничных условиях (3), (4)

$f_{{km}}^{*}\left( \tau \right) = \tilde {f}_{{km}}^{*}H\left( \tau \right),\quad {{f}_{{km}}}\left( \tau \right) = {{\tilde {f}}_{{km}}}H\left( \tau \right),$

и переходя к пределу при $\tau \to \infty $ можно получить решение задачи об изгибе консольно-закрепленной балки под действием статической нагрузки, приложенной к свободному концу. Здесь $H\left( \tau \right)$ – функция Хевисайда.

Функции Грина статической задачи $G_{{mk}}^{{st}}\left( x \right)$ выражаются через функции Грина ${{G}_{{mk}}}\left( {x,\tau } \right)$ динамической задачи с помощью соотношений [28]

(17)

$G_{{mk}}^{{st}}\left( x \right) = \mathop {\lim }\limits_{\tau \to \infty } \left[ {{{G}_{{mk}}}\left( {x,\tau } \right){\kern 1pt} *{\kern 1pt} H\left( \tau \right)} \right] = \mathop {\lim }\limits_{s \to 0} \left[ {sG_{{mk}}^{L}\left( {x,s} \right)\frac{1}{s}} \right] = \mathop {\lim }\limits_{s \to 0} G_{{mk}}^{L}\left( {x,s} \right).$

Преобразуя свертки (5) с помощью (17), получаем решение статической задачи

(18)

$\begin{array}{*{20}{c}} {{{v}^{{\left( {st} \right)}}}\left( x \right) = G_{{121}}^{{\left( {st} \right)}}\left( x \right)\tilde {f}_{{21}}^{*} + G_{{122}}^{{\left( {st} \right)}}\left( x \right)\tilde {f}_{{22}}^{*} + G_{{112}}^{{\left( {st} \right)}}\left( x \right){{{\tilde {f}}}_{{12}}},} \\ {{{\chi }^{{\left( {st} \right)}}}\left( x \right) = G_{{221}}^{{\left( {st} \right)}}\left( x \right)\tilde {f}_{{21}}^{*} + G_{{222}}^{{\left( {st} \right)}}\left( x \right)\tilde {f}_{{22}}^{*} + G_{{212}}^{{\left( {st} \right)}}\left( x \right){{{\tilde {f}}}_{{12}}},} \\ {H_{q}^{{\left( {st} \right)}}\left( x \right) = G_{{q + 2,21}}^{{\left( {st} \right)}}\left( x \right)\tilde {f}_{{21}}^{*} + G_{{q + 2,22}}^{{\left( {st} \right)}}\left( x \right)\tilde {f}_{{22}}^{*} + G_{{q + 2,12}}^{{\left( {st} \right)}}\left( x \right){{{\tilde {f}}}_{{12}}}.} \end{array}$

Вычисляя предел (17), получаем следующие выражения для функций $G_{{r21}}^{{\left( {st} \right)}}\left( x \right)$, $G_{{r12}}^{{\left( {st} \right)}}\left( x \right)$, $G_{{r22}}^{{\left( {st} \right)}}\left( x \right)$ ($r = \overline {1,N + 2} $, суммы рядов найдены с помощью таблиц [29])

$\begin{gathered} G_{{121}}^{{\left( {st} \right)}}\left( x \right) = \sum\limits_{n = 1}^\infty \frac{{{{P}_{{121n}}}\left( 0 \right)}}{{{{P}_{n}}\left( 0 \right)}}\sin {{\lambda }_{n}}x = - 2\sum\limits_{n = 1}^\infty \frac{{\sin {{\lambda }_{n}}x}}{{\lambda _{n}^{3}}} = \frac{{{{x}^{2}}}}{2} - x, \\ G_{{112}}^{{\left( {st} \right)}}\left( x \right) = \sum\limits_{n = 1}^\infty \frac{{{{P}_{{112n}}}\left( 0 \right)}}{{{{P}_{n}}\left( 0 \right)}}\sin {{\lambda }_{n}}x = 2\sum\limits_{n = 1}^\infty \frac{{{{{\left( { - 1} \right)}}^{{n + 1}}}}}{{\lambda _{n}^{2}}}\sin {{\lambda }_{n}}x + \\ \, + 2a{{C}_{{66}}}{{k}^{2}}\Phi \sum\limits_{n = 1}^\infty \frac{{{{{\left( { - 1} \right)}}^{{n + 1}}}}}{{\lambda _{n}^{4}}}\sin {{\lambda }_{n}}x = x - a{{C}_{{66}}}{{k}^{2}}\frac{\Phi }{2}\left( {\frac{{{{x}^{3}}}}{3} - x} \right), \\ \end{gathered} $

$\begin{gathered} G_{{122}}^{{\left( {st} \right)}}\left( x \right) = \sum\limits_{n = 1}^\infty \frac{{{{P}_{{122n}}}\left( 0 \right)}}{{{{P}_{n}}\left( 0 \right)}}\sin {{\lambda }_{n}}x = 2\sum\limits_{n = 1}^\infty \frac{{{{{\left( { - 1} \right)}}^{{n + 1}}}}}{{\lambda _{n}^{2}}}\sin {{\lambda }_{n}}x = x, \\ G_{{221}}^{{\left( {st} \right)}}\left( x \right) = \sum\limits_{n = 1}^\infty \frac{{{{P}_{{221n}}}\left( 0 \right)}}{{{{P}_{n}}\left( 0 \right)}}\cos {{\lambda }_{n}}x = - 2\sum\limits_{n = 1}^\infty \frac{{\cos {{\lambda }_{n}}x}}{{\lambda _{n}^{2}}} = x - 1, \\ G_{{212}}^{{\left( {st} \right)}}\left( x \right) = \sum\limits_{n = 1}^\infty \frac{{{{P}_{{212n}}}\left( 0 \right)}}{{{{P}_{n}}\left( 0 \right)}}\cos {{\lambda }_{n}}x = 2{{a}^{2}}{{C}_{{66}}}{{k}^{2}}\Phi \sum\limits_{n = 1}^\infty \frac{{{{{\left( { - 1} \right)}}^{{n + 1}}}}}{{\lambda _{n}^{3}}}\cos {{\lambda }_{n}}x = - {{a}^{2}}{{C}_{{66}}}{{k}^{2}}\Phi \left( {\frac{{{{x}^{2}}}}{2} - \frac{1}{2}} \right), \\ \end{gathered} $

(19)

$\begin{array}{*{20}{c}} {G_{{222}}^{{\left( {st} \right)}}\left( x \right) = \sum\limits_{n = 1}^\infty \frac{{{{P}_{{222n}}}\left( 0 \right)}}{{{{P}_{n}}\left( 0 \right)}}\cos {{\lambda }_{n}}x = 2\sum\limits_{n = 1}^\infty \frac{{{{{\left( { - 1} \right)}}^{{n + 1}}}}}{{{{\lambda }_{n}}}}\cos {{\lambda }_{n}}x = 1,} \end{array}$

$\begin{gathered} G_{{q + 2,21}}^{{\left( {st} \right)}}\left( x \right) = \frac{{2\Lambda _{{11}}^{{\left( q \right)}}}}{{D_{1}^{{\left( q \right)}}}}\sum\limits_{n = 1}^\infty \frac{{\sin {{\lambda }_{n}}x}}{{{{\lambda }_{n}}}} + \sum\limits_{n = 1}^\infty \frac{{{{P}_{{q + 1,21n}}}\left( 0 \right)}}{{{{Q}_{{qn}}}\left( 0 \right)}}\sin {{\lambda }_{n}}x = \\ \, = \frac{{2\Lambda _{{11}}^{{\left( q \right)}}}}{{D_{1}^{{\left( q \right)}}}}\sum\limits_{n = 1}^\infty \frac{{\sin {{\lambda }_{n}}x}}{{{{\lambda }_{n}}}} + \frac{{ - 2\Lambda _{{11}}^{{\left( q \right)}}}}{{D_{1}^{{\left( q \right)}}}}\sum\limits_{n = 1}^\infty \frac{{\sin {{\lambda }_{n}}x}}{{{{\lambda }_{n}}}} = 0, \\ G_{{q + 2,12}}^{{\left( {st} \right)}}\left( x \right) = \sum\limits_{n = 1}^\infty \frac{{{{P}_{{q + 1,12n}}}\left( 0 \right)}}{{{{Q}_{{qn}}}\left( 0 \right)}}\sin {{\lambda }_{n}}x = \\ \end{gathered} $

$\begin{gathered} \, = 2{{a}^{2}}{{C}_{{66}}}{{k}^{2}}\Lambda _{{11}}^{{\left( q \right)}}{{\Phi }_{q}}\sum\limits_{n = 1}^\infty \frac{{{{{\left( { - 1} \right)}}^{{n + 1}}}}}{{\lambda _{n}^{2}}}\sin {{\lambda }_{n}}x = {{a}^{2}}{{C}_{{66}}}{{k}^{2}}\Lambda _{{11}}^{{\left( q \right)}}{{\Phi }_{q}}x, \\ G_{{q + 2,22}}^{{\left( {st} \right)}}\left( x \right) = - \frac{{2\Lambda _{{11}}^{{\left( q \right)}}}}{{D_{1}^{{\left( q \right)}}}}\sum\limits_{n = 1}^\infty {{\left( { - 1} \right)}^{{n + 1}}}\sin {{\lambda }_{n}}x + \sum\limits_{n = 1}^\infty \frac{{{{P}_{{q + 1,22n}}}\left( 0 \right)}}{{{{Q}_{{qn}}}\left( 0 \right)}}\sin {{\lambda }_{n}}x = \\ \, = - \frac{{2\Lambda _{{11}}^{{\left( q \right)}}}}{{D_{1}^{{\left( q \right)}}}}\sum\limits_{n = 1}^\infty {{\left( { - 1} \right)}^{{n + 1}}}\sin {{\lambda }_{n}}x + \frac{{2\Lambda _{{11}}^{{\left( q \right)}}}}{{D_{1}^{{\left( q \right)}}}}\sum\limits_{n = 1}^\infty {{\left( { - 1} \right)}^{{n + 1}}}\sin {{\lambda }_{n}}x = 0. \\ \end{gathered} $

Здесь введены следующие обозначения:

(20)

$\begin{array}{*{20}{c}} {\Phi = \frac{{\prod\limits_{j = 1}^N \,D_{1}^{{\left( j \right)}}}}{{\prod\limits_{j = 1}^N \,D_{1}^{{\left( j \right)}} - \sum\limits_{j = 1}^N \,\alpha _{1}^{{\left( j \right)}}\Lambda _{{11}}^{{\left( j \right)}}\prod\limits_{r = 1,r \ne j}^N {\kern 1pt} D_{1}^{{\left( r \right)}}}},\quad {{\Phi }_{q}} = \frac{{\prod\limits_{r = 1,r \ne q}^N {\kern 1pt} D_{1}^{{\left( r \right)}}}}{{\prod\limits_{j = 1}^N \,D_{1}^{{\left( j \right)}} - \sum\limits_{j = 1}^N \,\alpha _{1}^{{\left( j \right)}}\Lambda _{{11}}^{{\left( j \right)}}\prod\limits_{r = 1,r \ne j}^N {\kern 1pt} D_{1}^{{\left( r \right)}}}}.} \end{array}$

С учетом предельного перехода (17) система уравнений (12) запишется в виде

(21)

$\sum\limits_{j = 1}^2 \,{{\tilde {a}}_{{ij}}}\tilde {f}_{{1j}}^{*} = {{\tilde {\varphi }}_{i}},$

где с учетом формул (19), (20)

(22)

Решение системы (21) находится по формулам (15). При этом используются следующие соответствия:

$y_{{m - 1/2}}^{i} \leftrightarrow \tilde {f}_{{2j}}^{*},\quad A_{{1/2}}^{{ij}} \leftrightarrow {{\tilde {a}}_{{ij}}},\quad b_{{m - 1/2}}^{i} \leftrightarrow {{\tilde {\varphi }}_{i}}.$

Используя равенства (22), получаем

$\tilde {f}_{{21}}^{*} = {{a}^{2}}{{C}_{{66}}}{{k}^{2}}{{\tilde {f}}_{{12}}},\quad \tilde {f}_{{22}}^{*} = {{a}^{2}}{{C}_{{66}}}{{k}^{2}}\left( {1 - \frac{\Phi }{2}} \right){{\tilde {f}}_{{12}}}.$

В результате решение статической задачи на основании равенств (18) записывается так

(23)

$\begin{array}{*{20}{c}} {{{v}^{{\left( {st} \right)}}}\left( x \right) = \frac{{{{a}^{2}}{{C}_{{66}}}{{k}^{2}}}}{2}\left( {{{x}^{2}} - \Phi \frac{{{{x}^{3}}}}{3}} \right){{{\tilde {f}}}_{{12}}} + x{{{\tilde {f}}}_{{12}}},} \\ {{{\chi }^{{\left( {st} \right)}}}\left( x \right) = {{a}^{2}}{{C}_{{66}}}{{k}^{2}}{{{\tilde {f}}}_{{12}}}\left( {x - \Phi \frac{{{{x}^{2}}}}{2}} \right),\quad H_{q}^{{\left( {st} \right)}}\left( x \right) = {{a}^{2}}{{C}_{{66}}}{{k}^{2}}\Lambda _{{11}}^{{\left( q \right)}}{{\Phi }_{q}}{{{\tilde {f}}}_{{12}}}x.} \end{array}$

Для несвязанной задачи при $\alpha _{1}^{{\left( q \right)}} = 0$ (в этом случае $\Lambda _{{11}}^{{\left( j \right)}} = 0$) из соотношений (20) получаем, что $\Phi = 1$, ${{\Phi }_{q}} = 1{\text{/}}D_{1}^{{\left( q \right)}}$ и равенства (23) принимают вид

(24)

${{v}^{{\left( {st} \right)}}}\left( x \right) = \frac{{{{a}^{2}}{{C}_{{66}}}{{k}^{2}}}}{2}\left( {{{x}^{2}} - \frac{{{{x}^{3}}}}{3}} \right){{\tilde {f}}_{{12}}} + x{{\tilde {f}}_{{12}}},\quad {{\chi }^{{\left( {st} \right)}}}\left( x \right) = {{a}^{2}}{{C}_{{66}}}{{k}^{2}}{{\tilde {f}}_{{12}}}\left( {x - \frac{{{{x}^{2}}}}{2}} \right),\quad H_{q}^{{\left( {st} \right)}}\left( x \right) = 0.$

Заметим, что функции прогиба ${{v}^{{\left( {st} \right)}}}\left( x \right)$ и угла поворота сечений ${{\chi }^{{\left( {st} \right)}}}\left( x \right)$, полученные с помощью предельного перехода (17), совпадают с классическим решением статической задачи об изгибе консольно-закрепленной балки Тимошенко [30].

4. РАСЧЕТНЫЙ ПРИМЕР

Для расчета рассмотрим стержень длиной $l = 1$ см, прямоугольного сечения $h \times b = 0.05l \times 0.05l$ из трехкомпонентного материала (цинк, медь, алюминий), где в качестве независимых компонент выступают цинк (компонент 1) и медь (компонент 2) [31]:

$\begin{gathered} C_{{12}}^{*} = 6.93 \times {{10}^{{10}}}\;\frac{{\text{Н}}}{{{{{\text{м}}}^{2}}}},\quad C_{{66}}^{*} = 2.56 \times {{10}^{{10}}}\;\frac{{\text{Н}}}{{{{{\text{м}}}^{2}}}},\quad {{T}_{0}} = 700\;{\text{К}},\quad \rho = 2780\;\frac{{{\text{кг}}}}{{{{{\text{м}}}^{3}}}}, \\ C_{{11}}^{*} = C_{{12}}^{*} + 2C_{{66}}^{*},\quad l = 0.01\;{\text{м}},\quad n_{0}^{{(1)}} = 0.01,\quad n_{0}^{{(2)}} = 0.045, \\ \end{gathered} $

$\begin{gathered} D_{{11}}^{{*\left( 1 \right)}} = 2.62 \times {{0}^{{ - 12}}}\;\frac{{{{{\text{м}}}^{2}}}}{{\text{с}}},\quad D_{{11}}^{{*\left( 2 \right)}} = 6.67 \times {{10}^{{ - 14}}}\;\frac{{{{{\text{м}}}^{2}}}}{{\text{с}}},\quad {{m}^{{(1)}}} = 0.065\;\frac{{{\text{кг}}}}{{{\text{моль}}}}, \\ \alpha _{{11}}^{{*\left( 1 \right)}} = 6.55 \times {{10}^{7}}\;\frac{{{\text{Дж}}}}{{{\text{кг}}}},\quad \alpha _{{11}}^{{*\left( 2 \right)}} = 6.14 \times {{10}^{7}}\;\frac{{{\text{Дж}}}}{{{\text{кг}}}},\quad {{m}^{{(2)}}} = 0.064\;\frac{{{\text{кг}}}}{{{\text{моль}}}}. \\ \end{gathered} $

Для того, чтобы сравнить полученные здесь результаты с результатами в работе [22], поперечную нагрузку на конце стержня $x = 1$ зададим в виде

${{f}_{{12}}}\left( \tau \right) = - \frac{{{{J}_{3}}}}{{{{C}_{{66}}}F}}H\left( \tau \right).$

Решая численно систему (13) и подставляя найденные оттуда функции в свертки (16), получаем прогибы балки и повороты сечений, представленные на фиг. 2 и 3 . Здесь для численного решения системы уравнений Вольтерра (13) использовалось ${{N}_{\tau }} = 40$ точек разбиения. Дальнейшее увеличение этого количества уже не приводит к какому-либо видимому изменению результатов.

Фиг. 2.

Прогибы балки $v(x,\tau )$. Сплошная линия соответствует $\tau = 3.3$, пунктирная линия – $\tau = 5.0$, штриховая линия – $\tau = 6.6$, штрихпунктирная линия – $\tau = 10.0$.

Фиг. 3.

Повороты сечений $\chi \left( {x,\tau } \right)$. Сплошная линия соответствует $\tau = 3.3$, пунктирная линия – $\tau = 5.0$, штриховая линия – $\tau = 6.6$, штрихпунктирная линия – $\tau = 10.0$.

Полученные результаты соответствуют классическим представлениям об изгибе консольно-закрепленных балок. На фиг. 4 можно видеть, как различаются прогибы балки, полученные с помощью модели Тимошенко и модели Бернулли–Эйлера. Решение аналогичной задачи для балки Бернулли–Эйлера было получено в работе [22].

Фиг. 4.

Прогибы балки $v(x,\tau )$. Решение для балки Тимошенко: сплошная линия соответствует $\tau = 3.3$, штрих-пунктирная линия – $\tau = 10.0$. Решение для балки Бернулли–Эйлера: пунктирная линия – $\tau = 3.3$, штриховая линия – $\tau = 10.0$.

Прогибы и повороты сечений, соответствующие статическому режиму нагружения, получены по формулам (23) и представлены на фиг. 5 и 6 . Видно, что при статических нагрузках массоперенос не влияет на поле перемещений.

Фиг. 5.

Прогибы балки ${{v}^{{\left( {st} \right)}}}\left( x \right)$ при статической нагрузке. Сплошная линия соответствует решению упругодиффузионной задачи; пунктирная соответствует решению упругой задачи при $\alpha _{1}^{{\left( q \right)}} = 0$.

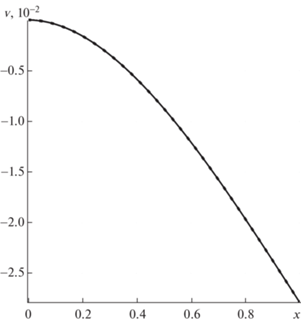
Фиг. 6.

Повороты сечений $\chi \left( x \right)$ при статической нагрузке. Сплошная линия соответствует решению упругодиффузионной задачи, пунктирная соответствует решению упругой задачи при $\alpha _{1}^{{\left( q \right)}} = 0$.

Наконец, на фиг. 7 и 8 показано, как изменяется концентрация первого и второго компонентов в результате нестационарного изгиба консольно-закрепленного стержня. На фиг. 7 видно, что на рассматриваемом промежутке времени ($\tau = 8.3 \times {{10}^{{12}}} \approx 5{\kern 1pt} $ мес) приращение концентрации первого компонента (цинк) практически достигло предельного значения (сплошная линия), которое соответствует статическому режиму нагружения балки. Диффузия второго компонента (медь) происходит медленнее. На фиг. 8 видно, что приращение концентрации за время $\tau = 8.3 \times {{10}^{{13}}} \approx 4.2{\kern 1pt} $ года еще очень далеко от предельного значения (сплошная линия). На этих рисунках предельные значения приращений концентрации цинка и меди (сплошные линии) определяются по формуле (23).

Фиг. 7.

Линейная плотность приращения концентрации ${{H}_{1}}\left( {x,\tau } \right)$. Пунктирная линия соответствует $\tau = 1.5 \times {{10}^{{12}}}$, штриховая линия – $\tau = 3.0 \times {{10}^{{12}}}$, штрихпунктирная линия – $\tau = 8.3 \times {{10}^{{12}}}$, сплошная линия соответствует решению статической задачи.

Фиг. 8.

Линейная плотность приращения концентрации ${{H}_{2}}\left( {x,\tau } \right)$. Пунктирная линия соответствует $\tau = 1.5 \times {{10}^{{13}}}$, штриховая линия – $\tau = 3.0 \times {{10}^{{13}}}$, штрихпунктиная линия – $\tau = 8.3 \times {{10}^{{13}}}$, сплошная линия соответствует решению статической задачи.

ЗАКЛЮЧЕНИЕ

Предложен алгоритм, который позволяет найти решение нестационарной задачи механодиффузии для консольно-закрепленной балки Тимошенко.

На примере трехкомпонентной балки показано, что нестационарный изгиб консоли инициирует диффузионные потоки каждой из компонент. При этом массоперенос различных компонент осуществляется с различной интенсивностью. Также возникают вертикальные диффузионные потоки цинка и меди, которые компенсируются потоком третьей компоненты. Величина диффузионного потока увеличивается от закрепленного конца стержня к свободному концу.

Для верификации предложенного алгоритма проанализированы предельные переходы к классическим задачам теории упругости для консольно-закрепленных балок, а также сделано сравнение полученных здесь результатов с результатами аналогичной задачи для балки Бернулли–Эйлера, решение которой получено в работе [22]. Исследован предельный переход к статическим режимам. Выполнено сравнение полученного статического решения с известным классическим решением для консольно-закрепленной балки Тимошенко [30].

Список литературы

Le K.C. Vibrations of shells and rods. Berlin: Springer Verlag, 1999. 419 p.
Le K.C., Yi J.H. An asymptotically exact theory of smart sandwich shells // Int. J. Engng. Sci. 2016. V. 106. P. 179–198.
Михайлова Е.Ю., Тарлаковский Д.В., Федотенков Г.В. Общая теория упругих оболочек. М.: МАИ, 2018. 112 с.
Mindlin R.D., Yang J. An Introduction to the Mathematical Theory of Vibrations of Elastic Plates. World Sc-ientific Publishing, 2006. 212 p.
Плескачевский Ю.М., Старовойтов Э.И., Леоненко Д.В. Механика трехслойных стержней и пластин, связанных с упругим основанием. М.: Физматлит, 2011. 560 с.
Mansfield E.H. The Bending and Stretching of Plates. Cambridge University Press, 2005. 244 p.
Швец Р.Н., Флячок В.М. Уравнения механодиффузии анизотропных оболочек с учетом поперечных деформаций // Матем. методы и физико-механ. поля. 1984. № 20. С. 54–61.
Швец Р.Н., Флячок В.М. Вариационный подход к решению динамических задач механотермодиффузии анизотропных оболочек // Матем. физ. и нелинейн. механ. 1991. № 16. С. 39–43.
Aouadi M., Copetti M.I.M. Analytical and numerical results for a dynamic contact problem with two stops in thermoelastic diffusion theory // ZAMM Z. Angew. Math. Mech. 2015. V. 2015. https://doi.org/10.1002/zamm.201400285
Copetti M., Aouadi M. A quasi-static contact problem in thermoviscoelastic diffusion theory // Applied Numerical Mathematics. 2016. V. 109. P. 157–183. https://doi.org/10.1051/m2an/201603
Aouadi M., Miranville A. Smooth attractor for a nonlinear thermoelastic diffusion thin plate based on Gurtin-Pipkin’s model // Asymptotic Analysis. 2015. V. 95. P. 129–160.
Aouadi M. On thermoelastic diffusion thin plate theory // Appl. Math. Mech. Engl. Ed. 2015. V. 36. № 5. P. 619–632.
Aouadi M., Miranville A. Quasi-stability and global attractor in nonlinear thermoelastic diffusion plate with memory // Evolution Equations and Control Theory. 2015. V. 4. № 3. P. 241–263.
Bhattacharya D., Kanoria M. The influence of two temperature generalized thermoelastic diffusion inside a spherical shell // Internat. Journal of Eng. and Technical Research (IJETR). 2014. V. 2. № 5. P. 151–159.
Aouadi M. A generalized thermoelastic diffusion problem for an infinitely long solid cylinder // Intern. J. Mathem. and Mathem. Sci. 2006. V. 6. P. 1–16. https://doi.org/10.1155/IJMMS/2006/25976
Elhagary M.A. Generalized thermoelastic diffusion problem for an infinitely long hollow cylinder for short times // Acta Mech. 2011. V. 218. P. 5–15.
Tripathi J.J., Kedar G.D., Deshmukh K.C. Generalized thermoelastic diffusion in a thick circular plate including heat source // Alexandria Eng. Journal. 2016. V. 55. № 3. P. 2241–2249.
Zakian V. Numerical inversions of Laplace transforms // Electron. Lett. 1969. V. 5. P. 120–121.
Крылов В.И., Скобля Н.С. Методы приближенного преобразования Фурье и обращения преобразования Лапласа. М.: ФИЗМАТЛИТ, 1974. 224 с.
Zemskov A.V., Tarlakovskii D.V. Modelling of unsteady elastic diffusion oscillations of a Timoshenko beam // Nonlinear Wave Dynamics of Materials and Structures. Advanced Structured Materials, V. 122. Springer Nature Switzerland AG 2020. P. 447–461.
Вестяк А.В., Земсков А.В. Модель нестационарных упругодиффузионных колебаний шарнирно закрепленной балки Тимошенко // Известия Pоссийской академии наук. Механика твердого тела. 2020. № 5. С. 107–119. https://doi.org/10.31857/S0572329920030174
Земсков А.В., Тарлаковский Д.В., Файкин Г.М. Нестационарный изгиб консольно-закрепленной балки Бернулли–Эйлера с учетом диффузии // Вычисл. механ. сплошных сред. 2021. Т. 14. № 1. С. 40–50.
Zenkour A.M. Thermoelastic diffusion problem for a half-space due to a refined dual-phase-lag Green-Naghdi model // Journal of Ocean Engineering and Science. 2020. V. 5. № 3. P. 214–222. https://doi.org/10.1016/j.joes.2019.12.001
Ailawaliar P., Budhiraja S. Dynamic Problem in Thermoelastic Solid Using Dual-Phase-Lag Model with Internal Heat Source // J. of Math. Sci. and App. 2014. V. 2. № 1. P. 10–16.
Формалев В.Ф. Теплоперенос в анизотропных твердых телах. Численные методы, тепловые волны, обратные задачи. М.: ФИЗМАТЛИТ, 2015. 280 с.
Abbas A.I. The effect of thermal source with mass diffusion in a transversely isotropic thermoelastic infinite medium // J. of Measurements in Engng. 2014. V. 2. № 4. P. 175–184.
Davydov S.A., Zemskov A.V. Thermoelastic Diffusion Phase-Lag Model for a Layer with Internal Heat and Mass Sources // Internat. Journal of Heat and Mass Transfer. 2022. V. 183. Part C. 122213. https://doi.org/10.1016/j.ijheatmasstransfer.2021.122213
Диткин В.А., Прудников А.П. Справочник по операционному исчислению. М.: Высшая школа, 1965. 568 с.
Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. Том 1. Элементарные функции. М.: Наука, 1981. 797 с.
Тимошенко С.П. Сопротивление материалов. Часть 1. Элементарная теория и задачи. М.: Наука. Главная редакция физико-математической литературы. 1965. 364 с.
Физические величины: Справочник Бабичев А.П., Бабушкина Н.А., Братковский А.М., и др. Под общей редакцией Григорьева И.С., Мейлихова И.З. М.: Энергоатомиздат, 1991. 1232 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал