Журнал вычислительной математики и математической физики, 2022, T. 62, № 11, стр. 1912-1926

Обтекание прямоугольного цилиндра дозвуковым потоком разреженного газа

О. И. Ровенская^1, *

¹ ВЦ ФИЦ ИУ РАН
119333 Москва, ул. Вавилова, 40, Россия

Поступила в редакцию 23.12.2020
После доработки 12.12.2021
Принята к публикации 07.06.2022

EDN: DYYLSB
DOI: 10.31857/S0044466922110102

Аннотация

Исследуется обтекание дозвуковым потоком разреженного газа прямоугольного цилиндра бесконечного размаха, используя численный метод, основанный на решении S-модельного кинетического уравнения. Изучается влияние числа Рейнольдса Re_∞ в диапазоне от 10 до 200 на возникающее вокруг прямоугольного цилиндра поле течения. При Re_∞ = 200 исследуется влияние геометрии цилиндра на поле течения, изменяя соотношение между высотой цилиндра и его длиной AR от 1 до 8. Полученные результаты представлены в виде коэффициентов сопротивления, подъемной силы, давления и числа Струхаля. Картины течения в области за цилиндром демонстрируют возникновение рециркуляционной зоны за цилиндром, размер и форма которой зависят как от числа Рейнольдса Re_∞, так и от соотношения AR. Обнаружено, что при стационарном течении коэффициенты, характеризующие течение, сильно зависят от числа Рейнольдса. В то же время данная зависимость становится слабее, когда течение становится нестационарным. С увеличением соотношения AR зона рециркуляции за цилиндром сужается, что приводит к уменьшению коэффициента сопротивления. Кроме того, оценивается надежность используемого подхода для решения подобного класса задач путем сравнения полученных результатов с данными, приведенными в литературе. Библ. 23. Фиг. 15. Табл. 3.

Ключевые слова: прямоугольный цилиндр, внешнее течение, кинетические уравнения.

1. ВВЕДЕНИЕ

Течение газа вокруг различных элементов конструкций является неотъемлемой частью приложений в авиастроении, ветроэнергетике, электротехнике (охлаждение). Картина течения вокруг таких тел зависит от числа Рейнольдса, соотношения между его сторонами и его ориентации по отношению к набегающему потоку (см. [1]–[15]).

Картина течения около прямоугольного цилиндра близка к картине, формирующейся при обтекании кругового цилиндра (см. [16]). Однако механизм отрыва потока и возникающая зависимость подъемной силы, сопротивления и числа Струхаля от числа Рейнольдса существенно отличаются для потока, обтекающего прямоугольный цилиндр. Для прямоугольного цилиндра точки отрыва потока возникают либо на его передней кромке, либо на задней кромке, в зависимости от значения числа Рейнольдса. Кроме того, область рециркуляции за прямоугольным цилиндром значительно шире и длиннее по сравнению с круговым (см. [9], [16], [17]).

В зависимости от значения числа Рейнольдса течение около прямоугольного цилиндра демонстрирует несколько основных картин: (1) – ползущее ламинарное устойчивое течение без отрыва; (2) – устойчивое течение с отрывом, возникающим на задней кромке цилиндра (при этом за цилиндром образуются присоединенные вихри); (3) – нестационарный срыв потока c задней кромки цилиндра с вихреобразованием; (4) – отрыв потока на передней кромке цилиндра и его присоединение к боковым граням цилиндра; (5) – отрыв потока на передней кромке без присоединения к граням цилиндра. В данной работе рассматриваются (1)–(3) режимы течения.

В настоящее время работы, посвященные исследованию обтекания тел плохо обтекаемой формы, особенно течений, около круговых цилиндров широко представлены в литературе (см., например, [16]). Меньшее внимание уделяется обтеканию прямоугольного цилиндра, хотя такие течения представляют большой интерес, как с практической, так и с академической точек зрения. Поэтому изучение поведения потока около прямоугольного цилиндра и аккуратное предсказание его свойств являются актуальной проблемой.

Экспериментальные работы для определения аэродинамических нагрузок на цилиндры различного поперечного сечения и частоты формирования вихрей в следе за цилиндром проводились в аэродинамических трубах или водных каналах. В некоторых работах измерения сочетаются с визуализацией потока, обеспечивающей феноменологическое понимание движения потока в окрестности тела (см. [1]–[3]).

Несмотря на геометрическую простоту задачи, численное моделирование такого течения не является тривиальной задачей, что обусловлено рядом факторов: наличием неблагоприятных градиентов давления, зон отрыва и присоединения потока, рециркуляционных областей, сильно изогнутых линий течения и вихревых взаимодействий. Следует отметить, что в большей части работ, посвященных моделированию обтекания прямоугольного цилиндра, применяются сжимаемые и несжимаемые уравнения Навье–Стокса или метод моделирования больших вихрей (LES) с использованием классической подсеточной модели Смагоринского (см., например, [4]–[15]).

В [4] для чисел Рейнольдса Re ≥ 300 и соотношении сторон цилиндра от 1 до 10 с помощью метода моделирования больших вихрей (LES) были исследованы картины течения и периодические особенности следа, возникающие за прямоугольным цилиндром. Изучены важные физические механизмы, определяющие частоту возникновения вихрей. Несжимаемые уравнения Навье–Стокса применялись для численного исследования двумерного течения около квадратного цилиндра для стационарного и нестационарного режимов течения в [5]. Анализ влияния числа Рейнольдса и угла атаки на силы, воздействующие на квадратный цилиндр, выполнен в [6] также с использованием несжимаемых уравнений Навье–Стокса.

В настоящей работе представлены результаты численного исследования нестационарного течения вокруг прямоугольного цилиндра с соотношением сторон от 1 до 8 и числе Рейнольдса в диапазоне от 10 до 200, используя S-модельное кинетическое уравнение (см. [18]). Прямой численный метод решения S-модельного уравнения был оптимизирован с помощью MPI (Message Passing Interface) для расчетов на кластере МВС-100K (см. [19]). Изучены закономерности течения и важные физические механизмы, определяющие частоту вихреобразования. При проектировании конструкций в виде прямоугольного цилиндра необходимо учитывать силы, вызванные возникающими вихревыми структурами, поэтому в работе рассчитаны и проанализированы коэффициенты сопротивления, подъема, давления и число Струхаля.

Следует отметить, что используемый численный метод уже эффективно применялся для моделирования как дозвуковых, так и сверхзвуковых течений разреженного газа в [20] и [21]. Однако для оценки надежности, используемого подхода для решения рассматриваемой задачи, выполнено также сравнение полученных результатов с данными, приведенными в литературе.

2. ПОСТАНОВКА ЗАДАЧИ

Рассматривается обтекание прямоугольного цилиндра длины A и высоты B с соотношением сторон AR = A/B равномерным дозвуковым потоком моноатомного газа со скоростью u_∞ для значений числа Рейнольдса Re_∞ в диапазоне от 10 до 200. Расчетная область вокруг цилиндра, схематично показанная на фиг. 1, представляет собой прямоугольник размера L × H. Размер расчетной области вверх по потоку до цилиндра L_u задается равной 30B, за цилиндром вниз по потоку L_d = 50B. Полный продольный размер области равен L = L_u + L_d = 80B, а поперечный размер – H = 60B. Размер расчетной области был выбран таким образом, чтобы минимизировать влияние граничных условий на течение вокруг цилиндра (см. п. 3.1).

Фиг. 1.

Геометрия расчетной области.

В качестве основных количественных характеристик, позволяющих оценить степень воздействия потока на прямоугольный цилиндр, были выбраны коэффициенты сопротивления, подъемной силы и давления:

(1)

${{C}_{D}} = \frac{{{{F}_{D}}}}{{0.5{{\rho }}u_{\infty }^{2}B}},\quad {{C}_{L}} = \frac{{{{F}_{L}}}}{{0.5{{\rho }}u_{\infty }^{2}B}},\quad {{C}_{P}} = \frac{{p - {{p}_{\infty }}}}{{0.5{{\rho }}u_{\infty }^{2}}},$

где F_D и F_l – сила сопротивления и подъемная сила, действующие на цилиндр, p – давление на поверхности цилиндра, p_∞ и u_∞ – давление и скорость набегающего потока.

Одной из важных характеристик нестационарного течения является частота срыва вихрей, в общем случае характеризующаяся безразмерным параметром – числом Струхаля (St = fB/u_∞). Для вычисления числа Струхаля использовалось быстрое преобразование Фурье временного ряда для коэффициента подъемной силы C_L.

Численный метод основан на решении S-модельного кинетического уравнения (см. [18]), которое можно записать как

(2)

$\frac{{\partial f}}{{\partial t}} + {\mathbf{\xi }}\frac{{\partial f}}{{\partial {\mathbf{x}}}} = {{J}_{S}}(f,f),$

(3)

${{J}_{S}}(f,f) = \frac{p}{{{\mu }}}\left( {M\left( {1 + \frac{{2{{m}^{2}}{\mathbf{qc}}}}{{15{{\rho }}{{{(kT)}}^{2}}}}\left( {\frac{{m{{{\mathbf{c}}}^{2}}}}{{2kT}} - \frac{5}{2}} \right)} \right) - f} \right) = \frac{p}{{{\mu }}}(S - f),$

(4)

$M({{\rho }},{\mathbf{V}},T) = \frac{{{\rho }}}{{{{{(2{{\pi }}RT)}}^{{3/2}}}}}\exp \left( { - \frac{{{{{\mathbf{c}}}^{2}}}}{{2RT}}} \right).$

Здесь f = f(t, x, ξ) – функция распределения молекул по скоростям, т.е. вероятность обнаружить частицу со скоростью ξ = (ξ_x, ξ_y, ξ_z) ∈ R³ в точке двумерного пространства x = (x, y) в момент времени t. S(ρ, c, T) и M(ρ, c, T) – стандартные локальные функции распределения Шахова и Максвелла, c = ξ – V – собственная скорость молекул газа массы m, ${\mathbf{V}} = (u,{v})$ – массовая скорость газа, q – вектор теплового потока, ρ, p и μ – плотность, давление и вязкость газа при температуре T, R = k/m – универсальная газовая постоянная, k – постоянная Больцмана.

В кинетическом подходе макровеличины, такие как плотность ρ, импульс ρV, температура T и вектор теплового потока q вычисляются интегрированием по всему скоростному пространству R³ ∈ [–∞; ∞] в момент времени t:

${{\rho (}}{\mathbf{x}}{\text{)}} = \int {f({\mathbf{x}},{\mathbf{\xi }})d{\mathbf{\xi }}} {\text{,}}$

(5)

$\begin{gathered} {{\rho (}}{\mathbf{x}}{\text{)}}{{(u({\mathbf{x}}),v({\mathbf{x}}))}^{T}} = \int {{{{{\text{(}}{{{{\xi }}}_{x}},{{{{\xi }}}_{y}})}}^{T}}f({\mathbf{x}},{\mathbf{\xi }})d{\mathbf{\xi }}} {\text{,}} \\ T({\mathbf{x}}) = \frac{m}{{3{{\rho (}}{\mathbf{x}}{\text{)}}k}}\int {{{{\mathbf{c}}}^{2}}f({\mathbf{x}},{\mathbf{\xi }})d{\mathbf{\xi }}} {\text{,}} \\ \end{gathered} $

${{({{q}_{x}}({\mathbf{x}}),{{q}_{y}}({\mathbf{x}}))}^{T}} = \frac{m}{2}\int {{{{({{c}_{x}},{{c}_{y}})}}^{T}}{{{\mathbf{c}}}^{2}}f({\mathbf{x}},{\mathbf{\xi }})d{\mathbf{\xi }}} .$

Начальное состояние потока одноатомного газа описывается функцией распределения Максвелла M(ρ, c, T) с плотностью ρ = ρ_∞, температурой T = T_∞, компонентами скорости u = u_∞ и ${v}$ = 0, где u_∞ – скорость набегающего потока.

На достаточно удаленном от цилиндра контуре Г (фиг. 1) для молекул, скорости которых направлены внутрь области (к цилиндру), задается функция распределения Максвелла M(ρ_∞, u_∞, T_∞), соответствующая однородному набегающему потоку со скоростью u_∞. На поверхности цилиндра задается диффузное отражение молекул с полной тепловой и импульсной аккомодацией:

(6)

${{f}_{w}}({\mathbf{x}},{\mathbf{\xi }}) = \kappa ({\mathbf{x}})M(1,{{u}_{w}},{{T}_{w}}),$

где u_w и T_w – скорость и температура цилиндра, здесь u_w = 0, T_w = T_∞. Плотность частиц, отраженных от поверхности цилиндра κ(x), вычисляется из условия равенства падающего и отраженного от поверхности потоков (см. [22], [23]):

(7)

$\kappa ({\mathbf{x}}) = - \frac{{\int\limits_{\xi \cdot \vartheta ({\mathbf{x}}) < 0} {f(t,{\mathbf{x}},\xi )\xi \cdot \vartheta ({\mathbf{x}})d\xi } }}{{\int\limits_{\xi \cdot \vartheta ({\mathbf{x}}) > 0} {M(1,{{u}_{w}},{{T}_{w}})\xi \cdot \vartheta ({\mathbf{x}})d\xi } }}.$

Уравнение (2) обезразмеривается с помощью параметров однородного набегающего потока газа: ρ_∞ и T_∞ и высоты цилиндра B. В работе используется модель твердых шаров, в этом случае безразмерная вязкость вычисляется как μ = T^0.5.

Так как рассматриваемое течение является двумерным, можно аналитически исключить z-составляющую молекулярной скорости ξ_z. Для получения численного решения сначала решается уравнение переноса (левая часть уравнения (2)), а затем уравнение релаксации (столкновения) (правая часть уравнения (2)). Уравнение переноса аппроксимируется схемой второго порядка точности с использованием стандартного метода TVD с функцией ограничения потока minmod (см. [20]). Однородный этап столкновений между частицами аппроксимируется явно-неявным подходом (см. [20]).

Для повышения эффективности расчетов программный код был распараллелен с помощью MPI (message passing protocol) (см. [19]). Каждому процессору присваивался свой собственный набор точек сетки в физическом пространстве. Этап релаксации (столкновения между молекулами) выполнялся независимо на различных процессорах. Перед этапом переноса процессоры обменивались данными между соседними сеточными узлами. Расчеты были выполнены на кластере MVS-100K.

3. ПАРАМЕТРЫ МОДЕЛИРОВАНИЯ

Численное моделирование обтекания прямоугольного цилиндра под нулевым углом атаки дозвуковым потоком моноатомного газа проводилось для числа Маха Ma_∞ = 0.2, что соответствует скорости набегающего потока u_∞ = 0.18257, и изменении числа Рейнольдса Re_∞ от 10 до 200, т.е. изменении числа Кнудсена Kn_∞ в диапазоне от 0.033 до 0.00165. Также изучалось влияние геометрии прямоугольного цилиндра на поле течения, увеличивая соотношение его сторон AR от 1 до 8 при фиксированном значении числа Рейнольдса Re_∞ = 200.

Для расчетов в физическом пространстве используется неоднородная, структурированная, криволинейная сетка с локальным измельчением в окрестности цилиндра. Типичная сетка, используемая в расчетах, а также ее увеличенное изображение в окрестности цилиндра показаны на фиг. 2. В табл. 1 приведены соотношение сторон цилиндра AR, соответствующий размер расчетной сетки (число узлов сетки, заданные в направлении по потоку и в поперечном направлении), число узлов сетки N_x вдоль длины цилиндра A и число узлов N_y вдоль его высоты B. Минимальный шаг сетки вдоль поверхности цилиндра составляет порядка 0.025 В и является компромиссом между требуемым разрешением течения и желаемой скоростью вычисления.

Фиг. 2.

Сетка размера 344 × 248, используемая в расчетах: (а) – полный вид, (б) – ее увеличенное изображение в окрестности цилиндра.

Таблица 1.

Геометрия цилиндра и размерность сетки

AR	Сетка	N_x	N_y
1	360 × 192	40	40
2	360 × 192	48	40
4	392 × 192	80	40
6	448 × 192	128	40
8	512 × 192	192	40

В пространстве скоростей задается однородная двумерная сетка. Размер скоростной сетки удовлетворяет условию ${{{v}}_{{\max }}} \geqslant \max ({\kern 1pt} {\text{|}}u{\kern 1pt} {\text{|,|}}{v}{\kern 1pt} {\text{|}}{\kern 1pt} ){\text{ }} + {\text{ }}3.5T_{{\max }}^{{0.5}}$. Для большинства расчетов число узлов по каждому направлению скорости выбирается равным 24, а размер скоростного пространства ограничивается максимальным значением скорости ${{{v}}_{{\max }}}$ = 5. Оптимальное число узлов в скоростном пространстве выбиралось таким образом, что удваивание их числа не изменяет значения основных характеристик течения (коэффициентов С_D, C_L и St) более чем на 1%.

Шаг по времени Δt удовлетворяет условию устойчивости Куранта–Фридрихса–Леви (CFL), где CFL = 0.4:

(8)

$\Delta t = CFL{\text{/}}{{\max }_{{ij}}}\left( {{{{{v}_{{\max }}}} \mathord{\left/ {\vphantom {{{{v}_{{\max }}}} {\Delta x}}} \right. \kern-0em} {\Delta x}} + {{{{v}_{{\max }}}} \mathord{\left/ {\vphantom {{{{v}_{{\max }}}} {\Delta y}}} \right. \kern-0em} {\Delta y}}} \right).$

3.1. Влияние размера расчетной области

В задачах с нестационарным следом и конвективными вихрями существенное влияние на точность расчетов оказывает размер расчетной области, в частности длина расчетной области за цилиндром L_d. Недостаточный размер области вниз по потоку может привести к искажению крупномасштабных структур из-за наличия конвективных вихрей.

Влияние размера расчетной области на поле течения оценивалось с помощью сравнения усредненного по времени коэффициента сопротивления С_D av, среднеквадратичного коэффициента подъемной силы C_Lrms и значения числа Струхаля St, полученных для четырех последовательно увеличивающихся размеров расчетной области L × H: 40 × 30, 60 × 45, 80 × 60 и 107 × 80, в которой расположен квадратный цилиндр (AR = 1). Число Рейнольдса Re_∞ фиксировано и равно 100. Полученные результаты приведены в табл. 2. В скобках указано изменение значений коэффициентов С_D av, C_Lrms и числа Струхаля St в процентах.

Таблица 2.

Влияние размера расчетной области для Re_∞ = 100

L × H	С_D av	C_Lrms	St
40 × 30 (L_u = 15, L_d = 25)	1.425	0.123	0.142
60 × 45 (L_u = 22.5, L_d = 37.5)	1.439 (0.94)	0.149 (21)	0.149 (5)
80 × 60 (L_u = 30, L_d = 50)	1.45 (0.76)	0.154 (3.3)	0.1515 (1.68)
107 × 80 (L_u = 40, L_d = 67)	1.455 (0.34)	0.155 (0.65)	0.1527 (0.8)

Как следует из табл. 2, вариация значений коэффициентов С_D av, C_Lrms и числа Струхаля St уменьшается с увеличением размера расчетной области. При переходе от размера 80 × 60 к размеру 107 × 80, расхождение между значениями коэффициентов становится меньше 1%.

Таким образом, для последующих расчетов использовалась область размера L × H = 80 × 60, в этом случае размер области до цилиндра L_u = 30 и за цилиндром – L_d = 50. Заметим, что вариация значений коэффициента С_D av оставалась незначительной при изменении размера расчетной области.

3.2. Влияние измельчения сетки на поле течения

Степень измельчения сетки также может оказывать влияние на результаты расчетов. Оценка влияния измельчения сетки проводилась для случая квадратного цилиндра (AR = 1) и фиксированного числа Рейнольдса Re_∞ = 100. Для этого сравнивались значения усредненного по времени коэффициента сопротивления С_D av, среднеквадратичного коэффициента подъемной силы C_Lrms и значения числа Струхаля St, полученные на трех последовательно измельченных сетках следующего размера: 172 × 124, 344 × 248 и 516 × 372. При этом число узлов сетки, равномерно распределенных вдоль стороны цилиндра, было равно 20, 40 и 70 соответственно. Полученные на разных сетках значения коэффициентов С_D av, C_Lrms и числа Струхаля St суммируются в табл. 3. Изменение значений коэффициентов при изменении степени измельчения сетки указано в процентах внутри скобок.

Таблица 3.

Влияние параметров сетки для расчетной области L × H = 80 × 60 (L_u = 30, L_d = 50) и Re_∞ = 100

Сетка	С_D av	C_Lrms	St
172 × 124	1.41	0.15	0.1480
344 × 248	1.45 (2.8)	0.154 (2.6)	0.1515 (2.4)
516 × 372	1.46 (0.69)	0.155 (0.65)	0.1522 (0.46)

Как видно из табл. 3, вариация значений коэффициентов С_D av, C_Lrms и числа Струхаля St не превышает 3% при переходе от самой грубой сетки к промежуточному уровню измельчения. При дальнейшем уточнении сетки расхождение между значениями коэффициентов уменьшается и становится меньше 1%. Таким образом, для последующих расчетов использовалась сетка размера 344 × 248.

4. АНАЛИЗ ЧИСЛЕННЫХ РЕЗУЛЬТАТОВ

4.1. Квадратный цилиндр, AR = 1: Re_∞ ≤ 40

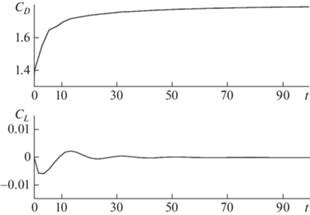
Картина течения около квадратного цилиндра сильно зависит от значения числа Рейнольдса Re_∞. При малых Re_∞ течение является стационарным и в следе за цилиндром образуется устойчивая картина течения, состоящая из двух симметричных вихрей. На фиг. 3 при Re_∞ = 20 отчетливо видна пара вращающихся против часовой стрелки вихрей, присоединенных к задней грани цилиндра и мешающих потоку газа за цилиндром. Эволюция соответствующих коэффициентов сопротивления С_D и подъемной силы C_L показана на фиг. 4.

Фиг. 3.

Мгновенные линии тока для Re_∞ = 20.

Фиг. 4.

Изменение коэффициентов сопротивления и подъемной силы С_D и C_L во времени.

На фиг. 5 показана полученная зависимость размера зоны рециркуляции за цилиндром L_r от значения числа Рейнольдса Re_∞ в сравнении с результатами [5] и [6]. Размер зоны рециркуляции за цилиндром L_r определялся как продольное расстояние от задней грани цилиндра до точки присоединения потока вдоль осевой линии следа. В [3] для стационарного течения, Re_∞ ≤ 40, около квадратного цилиндра предложена эмпирическая зависимость размера зоны рециркуляции L_r от числа Рейнольдса Re:

(9)

${{L}_{r}} = 0.0672\operatorname{Re} {\text{.}}$

Как видно на фиг. 5, размер вихрей, образующихся за цилиндром, растет вместе с увеличением числа Рейнольдса Re_∞, хотя течение в следе остается устойчивым. В то же время (фиг. 4) коэффициенты сопротивления С_D и подъемной силы C_L стремятся к постоянным значениям. Кроме того, полученная зависимость размера зоны рециркуляции L_r от Re хорошо согласуется с результатами [5], [6] и эмпирической зависимостью (9).

Фиг. 5.

Зависимость размера зоны рециркуляции L_r от числа Рейнольдса Re_∞ для устойчивого течения: 1 – результаты настоящей работы, 2 – результаты из [5], 3 – из [6].

Несмотря на то что в [5] и [6] для исследования течения около квадратного цилиндра применялись несжимаемые уравнения Навье–Стокса, в [5] и [6] использовались разные численные методы для их решения. Поэтому наблюдаемое отклонение полученных значений размера зоны L_r от данных [6] может быть связано с выбранным в [6] численным методом решения.

Полное сопротивление, которое испытывает цилиндр, включает в себя сопротивления, вызванные давлением и вязкими эффектами. Вязкое сопротивление создается трением между жидкостью и поверхностью, вдоль которой она течет. В то время как сопротивление давления возникает вследствие несимметричного распределения давления на верхней и нижней гранях цилиндра. Таким образом, коэффициент полного сопротивления может быть записан как

(10)

${{C}_{D}} = {{C}_{{Dv}}} + {{C}_{{DP}}},$

где C_Dv – коэффициент вязкостного сопротивления ${{C}_{{Dv}}} = {{F}_{{Dv}}}{\text{/}}0.5{{\rho }}u_{\infty }^{2}B$, С_DP – коэффициент сопротивления давления ${{C}_{{DP}}} = {{F}_{{DP}}}{\text{/}}0.5{{\rho }}u_{\infty }^{2}B$, F_Dv и F_DP – сила вязкого сопротивления и сила сопротивления давления, полученные интегрированием касательных и нормальных напряжений вдоль поверхности цилиндра соответственно.

На фиг. 6 видно, что усредненные по времени коэффициенты полного сопротивления С_D av и сопротивления давления С_DP av сильно зависят от числа Рейнольдса Re_∞ и уменьшаются с ростом Re_∞. При этом влияние на цилиндр вязкого сопротивления (коэффициент сопротивления C_Dv) значительно меньше, чем сопротивление давления (коэффициент С_DP) и уменьшается с увеличением Re_∞, однако, остается существенным в рассматриваемом диапазоне чисел Рейнольдса. Кроме того, полученные зависимости коэффициентов полного сопротивления С_D av и сопротивления давления С_DP av от числа Рейнольдса хорошо согласуются с результатами из [5]–[7].

Фиг. 6.

Зависимость усредненного коэффициента полного сопротивления С_D av (справа) и усредненного коэффициента сопротивления давления С_DP av от числа Рейнольдса Re_∞: 1 – результаты настоящей работы, 2 – результаты из [5], 3 – из [6], 4 – из [7].

Рассмотрим более детально распределение усредненного по времени коэффициента давления C_P av вдоль поверхности цилиндра в случае стационарного течения (фиг. 7). Вблизи точки торможения потока, расположенной на передней кромке цилиндра A–B, коэффициент давления C_P av падает с увеличением Re_∞, в то время как на задней кромке C–D (вблизи критической точки) коэффициент C_P av растет с увеличением Re_∞.

Фиг. 7.

Распределение усредненного по времени коэффициента давления вдоль поверхности цилиндра C_P av при Re_∞ = 5, 10, 20, 30 и 40.

В окрестности точки торможения поток разделяется вокруг прямоугольного цилиндра, что приводит к возникновению области высокого поверхностного давления на передней кромке цилиндра и низкого поверхностного давления на его задней кромке и, таким образом, к появлению значительного сопротивления давления. Поэтому коэффициент сопротивления С_D av, показанный на фиг. 6, уменьшается с увеличением Re_∞ в стационарном режиме.

4.2. Квадратный цилиндр, AR = 1: 50 ≤ Re_∞ < 200

При дальнейшем увеличении числа Рейнольдса, Re_∞ ≥ 50, течение в следе за цилиндром становится неустойчивым и возникает процесс вихреобразования, приводящий к формированию вихревой дорожки, состоящей из последовательности вихрей, уносимых потоком от тела (дорожка Кармана). Мгновенные линии тока, демонстрирующие типичный процесс срыва вихрей для одного периода вихреобразования T, показаны на фиг. 8 для Re_∞ = 100. На фиг. 8 можно наблюдать чередование основных вихрей, вращающихся в противоположном направлении. Два основных вращающихся в противоположных направлениях вихря, соответствующих 1/4 и 3/4 периодам вихреобразования T, показаны на фиг. 8a и 8в.

Фиг. 8.

Мгновенные линии тока и изменение коэффициента подъемной силы для Re_∞ = 100: (а) – 1/4T, (б) – 2/4T, (в) – 3/4T, (г) – T, где T – период вихреобразования.

Коэффициент подъемной силы C_L, показанный на фиг. 8 справа, изменяется по синусоидальному закону. В нестационарном режиме течения гармоническое колебание подъемной силы является результатом срыва вихря из-за движения вихря от нижней грани цилиндра к его верхней грани и обратно. Периодический срыв вихрей с поверхности цилиндра вызывает периодическое изменение давления на цилиндре и в следе за цилиндром образуется дорожка вихрей (дорожка Кармана).

Распределение усредненного по времени коэффициента давления C_P av на поверхности цилиндра для нестационарного режима течения показано на фиг. 9. В случае нестационарного режима течения коэффициент давления C_P av, усредненный за период вихреобразования T, монотонно уменьшается с увеличением Re_∞ вдоль всей поверхности цилиндра. Падение коэффициента давления C_P av на B–C–D или на C–D менее глубокое, чем в стационарном случае, что приводит к более слабому изменению значений коэффициента сопротивления С_D av с увеличением Re_∞ (фиг. 10).

Фиг. 9.

Распределение усредненного по времени коэффициента давления C_P av вдоль поверхности цилиндра при Re_∞ = 50, 100, 150 и 200.

Фиг. 10.

Зависимость усредненного по времени коэффициента полного сопротивления С_D av от числа Рейнольдса Re_∞: 1 – результаты настоящей работы, 2 – результаты из [5], 3 – из [6], 4 – из [7].

Среднеквадратичный коэффициент подъемной силы C_Lrms позволяет оценить амплитуду колебаний в следе за цилиндром. Фигура 11 демонстрирует монотонный рост коэффициента C_Lrms с увеличением числа Рейнольдса Re_∞.

Кроме того, как видно из фиг. 10 и 11 , полученные значения коэффициентов полного сопротивления С_D av и подъемной силы C_Lrms достаточно хорошо воспроизводят поведение этих коэффициентов, представленное в литературе из [5]–[8].

Фиг. 11.

Зависимость коэффициента подъемной силы C_Lrms от числа Рейнольдса Re_∞: 1 – результаты настоящей работы, 2 – результаты из [5], 3 – из [6], 4 – из [8].

Зависимость размера зоны рециркуляции за цилиндром, полученной по усредненному по времени полю течения, от числа Рейнольдса Re_∞ показана на фиг. 12. Видно, что размер зоны рециркуляции монотонно убывает с ростом Re_∞ что согласуется с результатами, полученными в [5] и [9].

Фиг. 12.

Зависимость размера зоны рециркуляции L_r от числа Рейнольдса Re_∞ для устойчивого течения: 1 –результаты настоящей работы, 2 – результаты из [5], 3 – из [9].

Чтобы оценить частоту вихреобразования, вычисляется число Струхаля St с помощью быстрого преобразования Фурье временного ряда для коэффициента подъемной силы C_L.

На фиг. 13 показано полученное число Струхаля St, а также соответствующие численные результаты из [5], [9] и экспериментальные данные из [8]. Можно видеть, что зависимость числа Струхаля St от числа Рейнольдса Re_∞, полученная в настоящей работе, хорошо воспроизводит тренд, показанный в [5], [9] и [8].

Фиг. 13.

Зависимость числа Струхаля от числа Рейнольдса Re_∞: 1 – результаты настоящей работы, 2 – результаты из [5], 3 – из [8], 4 – из [9], 5 – из [17].

Кроме того, на фиг. 13 показано изменение числа Струхаля для кругового цилиндра (см. [17]). В отличие от поведения числа Струхаля для квадратного цилиндра, для кругового цилиндра число Струхаля монотонно возрастает. Различие между поведением числа Струхаля для кругового цилиндра и квадратного цилиндра может быть объяснено различной природой потоков, возникающих вокруг них. Квадратный цилиндр – менее обтекаемое тело, чем круговой цилиндр вследствие того, что передняя грань квадратного цилиндра более тупая, а также наличия острых передних кромок. Отрыв потока и появление областей рециркуляции сверху/снизу цилиндра приводят к увеличению эффективной ширины квадратного цилиндра. Следовательно, средний поток вверх по течению фактически обтекает тело с эффективным диаметром, большим, чем физический диаметр квадратного цилиндра. Поскольку число Струхаля прямо пропорционально характерному размеру тела (высоте квадратного цилиндра B), использование эффективной высоты тела вместо высоты B приведет к увеличению числа Струхаля.

4.3. Влияние геометрии цилиндра

Геометрия цилиндра может оказывать существенное влияние на поле течения вокруг цилиндра. Для оценки данного эффекта в работе проведено исследование течения около прямоугольных цилиндров с соотношением сторон AR от 2 до 8 и фиксированном числе Рейнольдса Re_∞ = 200.

На фиг. 14 показаны мгновенные линии тока около прямоугольного цилиндра с соотношениями сторон AR = 2, 4 и 8. Как и ожидалось, с задней кромки прямоугольного цилиндра возникает срыв потока. При этом увеличение AR приводит к сужению области вихревого следа и, следовательно, к уменьшению усредненного по времени коэффициента полного сопротивления С_D av (фиг. 15), что согласуется с результатами из [12]–[14]. Некоторое отклонение значений полученного коэффициента С_D av от данных [12]–[14] связано с тем, что в этих работах течение моделируется при существенно больших значениях числа Рейнольдса – порядка 10³–10⁴.

Фиг. 14.

Мгновенные линии тока при Re_∞ = 200 для соотношений сторон цилиндра: (a) – AR = 2, (б) – AR = 4, (в) – AR = 8.

Фиг. 15.

Зависимость усредненного по времени коэффициента полного сопротивления С_D av от соотношения сторон цилиндра AR: 1 – результаты настоящей работы, 2 – результаты из [12], 3 – из [13], 4 – из [14].

ВЫВОДЫ

В данной работе численно исследовалось обтекание дозвуковым потоком разреженного газа прямоугольного цилиндра бесконечного размаха, используя S-модельное кинетическое уравнение. Для обеспечения достоверности численных результатов проведен анализ влияния размера расчетной области и параметров сетки на получаемое поле течения.

В стационарном режиме течения Re_∞ ≤ 40 наблюдалась сильная зависимость коэффициентов сопротивления и давления от значения числа Рейнольдса Re_∞, что согласуется с данными, представленными в литературе. Для нестационарного режима, Re_∞ ≥ 50, эта зависимость становилась слабее. С увеличением Re_∞ размер зоны рециркуляции увеличивался для стационарного режима, тогда как для нестационарного периодического режима размер зоны монотонно уменьшался. Геометрия цилиндра также влияла на картину течения: увеличение соотношения сторон цилиндра AR приводило к сужению зоны рециркуляции и к уменьшению коэффициента полного сопротивления.

Кроме того, сравнение с данными, приведенными в литературе, показало надежность используемого подхода, основанного на численном решении S-модельного уравнения, для задачи обтекания прямоугольного цилиндра дозвуковым потоком разреженного газа.

Список литературы

Okajima A. Strouhal numbers of rectangular cylinders // J. Fluid Mech. 1982. № 123. P. 379–398.
Lindquist C.M.Sc. Thesis, Universida de Estadual Paulista – UNESP, IlhaSolteira, Brazil, 2000.
Zdravkovich M.M. Smoke Observation of the Formation of a Karman Vortex Street // J. Fluid Mech. 1969. V. 37. P. 491–496.
Almeida O., Mansur S.S., Silveira-Neto A. On the flow past rectangular cylinders: physical aspects and numerical simulation // Therm. Eng. 2008. Iss. 7. P. 55–64.
Sharma A., Eswaran V. Heat and fluid flow across a square cylinder in the two-dimensional laminar flow regime // Numer. Heat Transfer. Part A. 2004. Iss. 45. P. 247.
Yoon D.H., Yang K.-S., Choi C.-B. Flow past a square cylinder with an angle of incidence// Phys. Fluids. 2010. Iss. 22. P. 043603.
Okajima A., Yi D., Sakuda A., Nakano T. Numerical study of blockage effects on aerodynamic characteristics of an oscillating rectangular cylinder // J. Wind Eng. Ind. Aerodyn. 1997. V. 67–68. P. 91–102.
Sohankar A., Norberg C., Davidson L. Low-Reynolds number flow around a square cylinder at incidence: study of blockage, onset of vortex shedding and outlet boundary condition // Inter. J. Numer. Methods Fluids. 1998. Iss. 26. P. 39.
Robichaux J., Balachandar S., Vanka S.P. Two-dimensional floquet instability of the wake of square cylinder// Phys. Fluids. 1999. V. 11. P. 560–578.
Olawore A.S. 2D Flow around a rectangular cylinder: A computational study // Inter. J. Sci. Technol. 2013. V. 2. Iss. 1. P. 1–26.
Okajima A., Ueno H., Sakay H. Numerical simulation of laminar and turbulent flows around rectangular cylinders// Inter. J. Num. Meth. Fluids. 1992. Iss. 15. P. 999–1012.
Ying X., Xu F. Zhang Z. Numerical simulation and visualization of flow around rectangular bluff bodies // Proc. of the 7th Inter. Colloquium on Bluff Body Aerodynamics and Applications (BBAA7) Shanghai, China, September 2–6, 2012, P. 272–281.
Okajima A. Numerical simulation of flow around rectangular cylinders // J. Wind Eng. Ind. Aerodyn. 1990. V. 33. P. 171–180.
Yu D., Kareen A. Parametric study of flow around rectangular prisms using LES // J. Ind. Aerodyn. 1998. V. 77–78. P. 653–662.
Nakamura Y., Ohya Y., Ozono S., Nakayama R. Reproducibility of flow past two-dimensional rectangular cylinders in a homogeneus turbulent flow by LES // J. Wind Eng. and Ind. Aerodyn. 1996. Iss. 65. P. 301–308.
Zdravkovich M.M. Flow Around circular cylinders. UK: Oxford Univ. Press Inc., 1997.
Williamson C.H.K. The existence of two stages in the transition to three-dimensionality of a cylinder wake // Phys. Fluids A. 1988. Iss. 31. P. 3165.
Шахов Е.М. Метод исследования движения разреженного газа. М.: Наука, 1974.
Snir M., Dongarra J., Kowalik J.S., Huss-Lederman S., Otto S.W., Walker D.W. MPI – The complete references. UK: Cambridge MIT Press, 2000.
Aristov V.V., Rovenskaya O.I. Kinetic description of the turbulence in the supersonic compressible flow over a backward/forward-facing step // Comput. Fluids. 2015. V. 111. P. 150–158.
Rovenskaya O.I., Aristov V.V. Kinetic simulation of a supersonic compressible flow over different geometry bodies // Eur. J. Mech. B Fluids. 2017. V. 64. P. 2017.
Cercignani C. Rarefied gas dynamics from basic concepts to actual calculations. UK: Cambridge Univ. Press; 1 ed., 2000.
Rovenskaya O.I. Numerical investigation of gas-surface scattering dynamics on the rarefied gas flow through a planar channel caused by a tangential temperature gradient // Inter. J. Heat and Mass Trans. 2015. V. 89. P. 1024–1033.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал