Журнал вычислительной математики и математической физики, 2022, T. 62, № 11, стр. 1927-1939

ВВЕДЕНИЕ

Изучение движения жидких субстанций в пористых средах актуально для решения технических, технологических и экологических задач. Знания о течениях нефти, воды, газа и их смесей через горные породы востребованы с точки зрения эффективного и рационального природопользования. Построение математических моделей для описания фильтрационных течений и развитие методов решения базовых уравнений составляют приоритетное направление исследований.

Наиболее часто используется представление гетерогенной многофазной среды как системы взаимодействующих взаимопроникающих континуумов [1], на базе которого развиваются гидродинамические модели разной степени сложности [2]–[4]. Описываются течения многокомпонентных реагирующих жидкостей и газов с фазовыми переходами в изотропных и анизотропных пористых средах с учетом инерционных эффектов, гидродинамической дисперсии и т.д. Решение сложных задач осуществляется численными методами с использованием коммерческих программных комплексов. Например, комплекс ANSYS FLUENT применялся для моделирования инфильтрации рассола из хранилища в окружающую пористую среду [5]. Имеются также отечественные некоммерческие комплексы программ, в частности MUFITS, с помощью которого изучалось вытеснение нефти водой и углеродным газом в подземных пористых пластах [6].

Настоящая работа посвящена исследованию фильтрационных течений подземных жидкостей с неоднородностями плотности под действием силы тяжести, которые с хорошей точностью описываются уравнением Дарси [2]–[4]. Благодаря тому что скорость таких течений невысока и число Рейнольдса, построенное по характерному размеру элемента твердой матрицы, много меньше единицы, инерционные члены отбрасываются; производной по времени также можно пренебречь в силу довольно больших временных масштабов происходящих процессов. Численное решение задач о конвективных фильтрационных течениях, особенно в классических постановках, часто осуществляется с помощью оригинальных авторских кодов, отличающихся простотой, экономичностью и возможностью получать на выходе разнообразные характеристики процесса [7]–[11].

Рассматривается жидкость с растворенной примесью (например, вода с солями). Распространение примеси описывается нестационарным уравнением конвекции-диффузии (уравнение второго порядка, параболическое) и совместно с уравнениями неразрывности и Дарси (уравнения первого порядка) образует базовую систему уравнений. Для получения численных решений используется авторский двумерный вычислительный код, основанный на конечно-разностном методе. Код, предыдущие версии которого описаны в [12], [13] применялся для решения различных задач о концентрационной конвекции [14]–[17].

Принципы построения конечно-разностных аналогов уравнения конвекции-диффузии и их решения широко обсуждаются в литературе [18]–[20]. Примеры конкретных разностных схем, включая анализ их устойчивости и сходимости, можно найти в [8], [21]–[24]. В данной работе применяется аппроксимация конвективного члена по схеме Quadratic Upstream Interpolation for Convective Kinematics (QUICK) [25], которая является условно-устойчивой и имеет третий порядок точности на равномерной сетке. Схема сохраняет монотонность при значениях сеточного числа Пекле вплоть до нескольких десятков, что позволяет увеличить шаг пространственной сетки по сравнению с центрально-разностной схемой. Диффузионный член аппроксимируется центральными разностями. В результате дискретизации получается пятидиагональная линейная система уравнений. В предыдущей версии вычислительного кода [13] интегрирование по времени осуществлялось по двухслойной явной схеме, которая имеет первый порядок точности. На современном этапе код усовершенствован – интегрирование по времени проводится по двухшаговой схеме Рунге–Кутты, которая имеет второй порядок точности.

Решается задача о концентрационно-конвективном движении, развивающемся вследствие неустойчивости Рэлея–Тейлора. Данный вид неустойчивости возникает между контактирующими жидкостями разной плотности с границей раздела, перпендикулярной силе тяжести; более тяжелая жидкость находится сверху. Следует отметить, что задача о неустойчивости Рэлея–Тейлора является одной из классических в гидродинамике [26], поэтому используется для тестирования гидродинамических моделей и численных кодов [27]. Численное моделирование конвекции Рэлея–Тейлора в пористой среде проводилось в [28]–[30]. В настоящей работе, продолжая исследование [17], учитывается изменение вязкости раствора с количеством растворенной примеси. Анализируется влияние контраста вязкости (начального отношения коэффициентов вязкости слоев) на конвективное движение и перемешивание, которые оцениваются по различным характеристикам. Рассматриваются системы с контрастом вязкости в несколько единиц, что соответствует воде и водным растворам солей. Рассматривается также система с контрастом вязкости, равным 30, что ассоциируется с парой “нефть–вода”.

При моделировании конвекции Рэлея–Тейлора в пористой среде обнаружен новый эффект [30]: если отношение коэффициентов вязкости слоев больше 20, то конвективное течение теряет симметрию движения в направлении “верх–низ”. Считалось, что вязкость раствора возрастает с добавлением примеси, поэтому верхний слой был более тяжелым и вязким. Получено, что конвективные “пальцы” быстрее движутся вниз, чем вверх. Новизна настоящего исследования заключается в том, что рассматривается другая зависимость вязкости от количества примеси: коэффициент вязкости убывает с добавлением примеси, – поэтому верхний слой оказывается более тяжелым, но менее вязким. В статье будет показано, что в такой постановке при контрасте вязкости, равном 30, конвективные “пальцы” быстрее движутся вверх. Сравнение найденной в статье и описанной в [30] закономерностей позволяет сделать однозначный вывод о направлении асимметрии движения. Стоит заметить, что численное решение в [30] получено с помощью сложного гибридного метода, включающего псевдоспектральный и конечно-разностный методы. Применялись, соответственно, преобразование Хартли и конечно-разностные аппроксимации 4-го и 6-го порядков точности; интегрирование по времени производилось по одной из разновидностей полунеявного метода Адамса 3-го порядка. Новизной настоящей работы является также и то, что в ней показано: асимметричную конвекцию Рэлея–Тейлора можно моделировать с помощью относительно простого и экономичного конечно-разностного метода.

1. ПОСТАНОВКА ЗАДАЧИ И МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Имеется прямоугольная двумерная пористая область, заполненная двухслойной жидкостью: сверху однокомпонентной жидкости, имеющей плотность ${{\rho }_{0}}$ и вязкость ${{\mu }_{0}}$, помещена двухкомпонентная жидкость с примесью, имеющая плотность ${{\rho }_{b}}$ и вязкость ${{\mu }_{b}}$; ${{\rho }_{b}} > {{\rho }_{0}}$. В начальный момент система неподвижна и находится в состоянии гидростатического равновесия; граница между слоями горизонтальна (см. фиг. 1). На границах области для скорости задается условие проскальзывания, для давления сохраняются начальные значения, жидкость через границы не проникает. Примесь диффундирует из верхней части области в нижнюю, переходная зона между слоями увеличивается. На вертикальных границах задается диффузионное распределение примеси. В силу неустойчивого состояния равновесия такой системы в поле силы тяжести (неустойчивости Рэлея–Тейлора) со временем развивается естественное концентрационно-конвективное движение. Чтобы инициировать развитие конвекции, в начальный момент задаются флуктуации плотности на границе между слоями.

Описание гидродинамических процессов производится с помощью уравнений неразрывности несжимаемой жидкости, Дарси и переноса примеси [4]. Пористость $\phi $ и проницаемость твердого скелета $k$, а также коэффициент диффузии примеси $D$ считаются постоянными; вязкость раствора $\mu $ – переменная. Исходную систему уравнений можно привести к следующему безразмерному виду [13]:

Безразмерные переменные – это скорость фильтрации ${\mathbf{u}} = ({{u}_{x}},{{u}_{y}})$, давление Π = $ = (P - {{P}_{0}}){\text{/}}(({{\rho }_{b}} - {{\rho }_{0}})gH)$, плотность $S = (\rho - {{\rho }_{0}}){\text{/}}({{\rho }_{b}} - {{\rho }_{0}})$. В качестве давления и плотности рассматриваются отклонения текущих значений $P$ и $\rho $ от значений ${{P}_{0}}$ и ${{\rho }_{0}}$ в жидкости, образующей нижний слой. Величина ${{P}_{0}}$ – гидростатическое распределение давления – линейно уменьшается с высотой. Характерными масштабами являются геометрический размер $H$, скорость $D{\text{/}}H$, время ${{H}^{2}}{\text{/}}D$, плотность $({{\rho }_{b}} - {{\rho }_{0}})$, давление $({{\rho }_{b}} - {{\rho }_{0}})gH$. Здесь $g$ – ускорение свободного падения. В уравнении (1.2) содержится число Рэлея–Дарси и безразмерная вязкость ${{f}_{\mu }} = \mu {\text{/}}{{\mu }_{0}}$.

Плотность раствора $\rho $ линейно растет с плотностью растворенной примеси ${{\rho }_{c}}$, что описывается уравнением состояния $\rho = {{\rho }_{0}} + \alpha {{\rho }_{c}}$ , используя которое можно получить другое выражение безразмерной переменной $S$, а именно: $S = \alpha {{\rho }_{c}}{\text{/}}({{\rho }_{b}} - {{\rho }_{0}})$. Видно, что $S$ – это нормированная плотность примеси. Считается, что вязкость раствора увеличивается в зависимости от $S$ экспоненциально:

Константа $\Gamma $ определяет диапазон изменения вязкости.

Расчетная область $\Omega $ в безразмерном виде задается следующим образом:

Начальные условия имеют следующий вид: На границе между слоями выполняется: Здесь $\Delta s$ – флуктуации плотности (малая величина); их определение в численном решении дано в (2.4). Распределение начального давления ${{\Pi }^{{in}}}$ следует из условия гидростатического равновесия:

На вертикальных границах изменение плотности примеси $S$ соответствует аналитическому решению уравнения диффузии [31]. Граничные условия задаются следующими выражениями:

Вязкость ${{f}_{\mu }}$ рассчитывается по полю плотности $S$ в соответствии с (1.4). Исходно выполняются следующие условия: Здесь ${{F}_{\mu }} = {{\mu }_{b}}{\text{/}}{{\mu }_{0}}$ – начальное отношение коэффициентов вязкости верхнего и нижнего слоев, которое следует из (1.4) при $S = 1$. Контрастом вязкости обычно называют отношение большего коэффициента вязкости к меньшему. Контраст вязкости совпадает с ${{F}_{\mu }}$, если ${{\mu }_{b}} > {{\mu }_{0}}$ и равен $1{\text{/}}{{F}_{\mu }}$, если ${{\mu }_{b}} < {{\mu }_{0}}$.

2. МЕТОД ЧИСЛЕННОГО РЕШЕНИЯ

Уравнения (1.1)–(1.3), записанные в плоской декартовой системе координат, заменяются конечно-разностными аналогами на разнесенной неравномерной пространственной сетке. Сначала определяются значения скорости и давления по дискретным уравнениям Дарси и неразрывности с использованием алгоритма типа SIMPLE [32]; полученные трехдиагональные системы уравнений для сеточных значений приращения давления решаются методом прогонки. Затем по дискретному уравнению конвекции-диффузии находятся значения плотности. После этого производится совместная корректировка скорости, давления и плотности итерационным методом Якоби. Когда плотность определена, по ней рассчитываются сеточные значения вязкости. Более подробно численный метод описан в [12], [13].

Формируется основная пространственная сетка

Вводятся дополнительные узлы и формируются смещенные сетки. В узлах смещенной по $x$ сетки определяется вертикальная компонента скорости ${{u}_{y}}$. В узлах смещенной по $y$ сетки определяется горизонтальная компонента скорости ${{u}_{x}}$. В узлах смещенной по $x$ и $y$ сетки определяются все скалярные переменные. Узлы сетки ${{\Omega }_{{hxy}}}$ являются центрами ячеек сетки ${{\Omega }_{h}}$.

Остановимся на методе интегрирования уравнения конвекции-диффузии, который на данном этапе изменен. Запишем пространственные производные уравнения (1.3) в конечно-разностном виде, используя схему QUICK [13], [25]. Полученное уравнение в каком-либо ($i + 1{\text{/}}2,j + 1{\text{/}}2$)-м узле можно представить следующим образом:

Здесь $L$ – линейный сеточный оператор, шаблон этого оператора включает пять узлов сетки по каждому направлению. При попытке неявно проинтегрировать (2.1) по времени приходим к пятидиагональной системе уравнений, в которых в пяти узлах сеточные значения ${{S}_{{i + 1/2,j + 1/2}}}$ взяты с верхнего временного слоя. При решении такой системы, например, прогонками возникают определенные трудности при разрешении граничных условий. Поэтому рациональным выбором оказываются явные схемы. Использование простейшей двухслойной схемы (как это сделано в [13]) дает лишь первый порядок точности по времени. Чтобы повысить точность численного интегрирования, в текущей версии вычислительного кода применяется один из методов Рунге–Кутты [19], часто используемых для решения начально-краевых задач. Суть схемы поясняется на фиг. 2. Для простоты нижние индексы у ${{S}_{{i + 1/2,j + 1/2}}}$ опускаются. Обозначим шаг интегрирования по времени через $\tau $. Сначала выполняется интегрирование на полушаге – определяется предварительное значение переменной ${{S}^{{n + 1/2}}}$. Затем вычисляется окончательное значение ${{S}^{{n + 1}}}$ с использованием найденных промежуточных значений ${{S}^{{n + 1/2}}}$: Таким образом, по ${{S}^{{n + 1/2}}}$ определяется производная ${{(dS{\text{/}}dt)}^{{n + 1/2}}}$ в точке ${{t}^{{n + 1/2}}}$, а по этой производной находится ${{S}^{{n + 1}}}$.

Можно оценить точность данной схемы. Считается, что на нижнем временном слое сеточное значение ${{S}^{n}}$ совпадает с точным значением $S({{t}^{n}})$. Вычислим погрешность $\psi $ на шаге $\tau $ как разность между точным $S({{t}^{{n + 1}}})$ и сеточным ${{S}^{{n + 1}}}$ значениями на верхнем временном слое. Будем использовать схему (2.2) и разложения $S({{t}^{{n + 1}}})$ и $S({{t}^{n}})$ в ряд Тейлора около точки ${{t}^{{n + 1/2}}}$:

Для $\psi $ можно записать следующее: В силу равенства (2.1) первое и второе слагаемые справа в (2.3) равны друг другу, поэтому окончательно получаем $\psi = O({{\tau }^{3}})$, что свидетельствует о втором порядке точности.

Чтобы инициировать развитие конвекции, в начальный момент задаются флуктуации плотности на границе раздела жидкостей, которая проходит через узлы основной сетки при $j = (m + 1){\text{/}}2$ ($m$ – нечетное число). Плотность определяется в узлах смещенной сетки, около границы раздела задаются условия:

Здесь $\sigma $ – амплитуда флуктуаций ($\sigma \ll 1$), ${{R}_{{i + 1/2}}}$ – ряд случайных чисел: ${{R}_{{i + 1/2}}} \in [0,1]$. Распределение плотности в узлах основной сетки получается интерполяцией: ${{S}_{{i + 1/2,(m + 1)/2}}} = 0.5({{S}_{{i + 1/2,m/2}}} + $ $ + \;{{S}_{{i + 1/2,m/2 + 1}}})$. Легко найти, что Здесь $\Delta {{s}_{{i + 1/2}}}$ – сеточная функция флуктуаций плотности. Известно, что время начала конвекции зависит от амплитуды флуктуаций [17], [33], поэтому во всех вариантах берется одинаковое значение $\sigma = 0.01$. Если флуктуации физических переменных не заданы, то источником малых возмущений являются погрешности численного метода и округления при вычислениях.

При проведении счета на каждом временном слое по найденным значениям переменных определяются различные величины, характеризующие движение и массоперенос. Вычисляется высота зоны перемешивания слоев ${{h}_{c}}$. Для этого сначала рассчитывается средняя масса приме-си Q на высоте ${{y}_{{j + 1/2}}}$, $j = 1,2,...m - 1$:

Если перемешивания нет, то в нижней половине области должно быть $Q = 0$, а в верхней – $Q = 1$. Определяем нижнюю координату зоны перемешивания ${{y}_{*}}$ как уровень, на котором $Q = 0.01$, т.е. ${{y}_{*}} = {{y}_{{j + 1/2}}}$, если $Q({{y}_{{j + 1/2}}}) = 0.01$. Верхняя координата $y{\kern 1pt} *$ находится из условия: $y{\kern 1pt} * = {{y}_{{j + 1/2}}}$, если $Q({{y}_{{j + 1/2}}}) = 0.99$. Окончательно вычисляем ${{h}_{c}} = y{\kern 1pt} * - {{y}_{*}}$. Определяется также высота зоны диффузионного перемешивания ${{h}_{d}}$ по аналитическому решению уравнения диффузии, записанному в (1.5); ${{h}_{d}}$ характеризует чисто диффузионный перенос примеси в отсутствие конвекции.

Рассчитывается кинетическая энергия движения примеси, приходящаяся на единицу длины области,

Компоненты скорости ${{u}_{x}}_{{i + 1/2,j + 1/2}}$ и ${{u}_{y}}_{{i + 1/2,j + 1/2}}$ находятся линейной интерполяцией соответствующих значений из соседних узлов сеток ${{\Omega }_{h}}_{y}$ и ${{\Omega }_{h}}_{x}$. В (2.5), (2.6) входят $\Delta {{x}_{{i + 1/2}}} = {{x}_{{i + 1}}} - {{x}_{i}}$, $\Delta {{y}_{{j + 1/2}}} = {{y}_{{j + 1}}} - {{y}_{j}}$ – шаги сетки ${{\Omega }_{h}}$ по $x$ и $y$.

Рассматривается завихренность скорости, которая по определению представляет собой вектор $\omega = \nabla \times {\mathbf{v}}$, где ${\mathbf{v}} = {\mathbf{u}}{\text{/}}\phi $ – скорость движения жидкости в порах; ${\mathbf{v}} = ({{v}_{x}},{{v}_{y}})$. В двумерной системе координат вектор $\omega $ имеет одну компоненту $\omega $ вдоль оси, перпендикулярной плоскости течения:

Сеточное значение ${{\omega }_{{i,j}}}$ находится в узле основной сетки ${{\Omega }_{h}}$: Здесь $\Delta {{x}_{i}} = {{x}_{{i + 1/2}}} - {{x}_{{i - 1/2}}}$, $\Delta {{y}_{j}} = {{y}_{{j + 1/2}}} - {{y}_{{j - 1/2}}}$, – шаги сетки ${{\Omega }_{{hxy}}}$ по $x$ и $y$; около горизонтальных границ задаются полушаги $\Delta {{y}_{1}} = {{y}_{{3/2}}} - {{y}_{1}}$, $\Delta {{y}_{m}} = {{y}_{m}} - {{y}_{{m - 1/2}}}$. Затем определяется суммарный модуль завихренности ${{\Sigma }_{\omega }}$, приходящийся на единицу длины области:

Вычисляется также параметр неоднородности распределения примеси $G$ вдоль линии начального положения границы между слоями жидкости, т.е. при ${{y}_{{(m + 1)/2}}}$. Полагается, что $G$ – это разность между максимальным ${{S}_{{\max }}}$ и минимальным ${{S}_{{\min }}}$ значениями плотности на этом уровне:

Чтобы обеспечить устойчивость и сходимость численного метода, численные параметры должны удовлетворять ряду критериев. Анализ устойчивости приводит к ограничению диффузионного числа Nd [34] и числа Куранта Co [19], а требование монотонности – к ограничению сеточного числа Пекле Pe [35]. В случае равномерной сетки критерии имеют вид

Здесь ${{v}_{{x\,\max }}}$ и ${{{v}}_{{y\,\max }}}$ – максимальные значения компонент скорости движения жидкости ${{v}_{x}}$ и ${{v}_{y}}$. При аппроксимации конвективного члена по центрально-разностной схеме следует использовать условие ${\text{Pe}} < 2$; применение схемы QUICK позволило увеличить значение ${\text{Pe}}$.

3. МОДЕЛИРОВАНИЕ КОНВЕКЦИИ ПРИ НЕБОЛЬШОМ КОНТРАСТЕ ВЯЗКОСТИ

Проведено моделирование конвекции Рэлея–Тейлора при значении числа Рэлея–Дарси ${\text{Ra}} = {{10}^{3}}$, которое соответствует, например, водному раствору солей в пористой среде с физическими параметрами: ${{\rho }_{0}} = {{10}^{3}}$ кг/м³, ${{\rho }_{b}} = 1.2 \times {{10}^{3}}$ кг/м³, ${{\mu }_{0}} = {{10}^{{ - 3}}}$ Па c, $D = 1.57 \times {{10}^{{ - 9}}}$ м²/c, $\alpha = 0.815$, $\phi = 0.2$, $k = 1.6 \times {{10}^{{ - 14}}}$ м². Масштаб длины $H = 10$ м. Вязкость верхнего слоя больше, чем нижнего. Контраст вязкости, равный ${{F}_{\mu }}$, варьируется. Рассмотрены четыре варианта, в которых взята константа $\Gamma = 0$; 0.405; 0.810; 1.216 и получены, соответственно, величины ${{F}_{\mu }} = 1.00$; 1.50; 2.25; 3.38. В [17] показано, что экспериментальные данные для водных растворов хлорида натрия с хорошей точностью описываются зависимостью (1.4) с константой $\Gamma = 1.0$; в настоящем исследовании взят диапазон $\Gamma $ около этого значения.

Рассматривается область $6 \times 4$, покрытая равномерной сеткой $2401 \times 1601$. Шаг интегрирования по времени $\tau $ менялся, однако, во всех вариантах $\tau \leqslant {{10}^{{ - 7}}}$. В расчетах ниже найдено для скорости движения жидкости: ${{v}_{{x\,\max }}},{{v}_{{y\,\max }}}{{ < 10}^{3}}$. Оценки показывают, что условия (2.7) соблюдаются.

Точность численного решения контролировалась по выполнению баланса массы примеси в расчетной области. На каждом временном слое вычислялась разность $\Delta M = {{M}^{n}} - {{M}^{0}}$, где ${{M}^{n}}$ и ${{M}^{0}}$ – суммарная масса примеси в текущий ${{t}^{n}}$ и начальный ${{t}^{0}}$ моменты времени. В силу того что на вертикальных границах $x = 0,{{h}_{x}}$ поддерживается определенное распределение плотности $S$ (1.5), здесь могут возникать незначительные диффузионные потоки. Рассчитывается суммарный диффузионный поток массы ${{M}_{J}}$ с начала процесса до текущего момента ${{t}^{n}}$. В точном решении выполняется $\Delta M = {{M}_{J}}$. В численном решении появляется невязка массы $\delta M$, которая определяется по выражению:

Получено, что во всех расчетах невязка $\delta M$ не превышает нескольких долей процента, что свидетельствует о высокой точности численного решения.

Можно выделить три стадии процесса, начиная с нулевого момента времени [17], [28]. На первой стадии происходит диффузионный перенос примеси из верхней части области в нижнюю. При этом переходная зона между слоями расширяется, но остается горизонтальной; конвективное движение жидкости еще не появилось. Слабые неупорядоченные перемещения частей жидкости в переходной зоне, которые порождаются флуктуациями плотности, со временем перестраиваются, усиливаются и формируется согласованное движение. На второй стадии наблюдается периодическое конвективное движение, становится заметным волнообразное искривление переходной зоны. Со временем конвективные “пальцы” удлиняются, искривляются, начинают сливаться друг с другом и процесс переходит в третью стадию, которая отличается наличием интенсивной стохастической конвекции.

Все стадии успешно воспроизводятся в численном моделировании. Учет увеличения вязкости раствора, как показано в [17], приводит к более позднему и медленному развитию конвективного течения. На фиг. 3 дано поле плотности примеси в момент времени, который соответствует третьей стадии процесса. Переход от светлого тона к темному означает увеличение плотности. Сравниваются варианты с постоянной (${{F}_{\mu }} = 1.0$) и переменной (${{F}_{\mu }} = 3.38$) вязкостью. Видно, что во втором случае зона конвективного перемешивания оказывается меньше, что объясняется замедленным развитием конвекции с увеличением вязкости и соответствует предыдущим результатам. На фиг. 4а показано, как растет высота ${{h}_{c}}$ при разных ${{F}_{\mu }}$. На первой стадии, когда конвекции нет, кривые ${{h}_{c}}$ совпадают с ${{h}_{d}}$. По отрыву ${{h}_{c}}$ от ${{h}_{d}}$ можно судить о начале конвекции, которое при увеличении ${{F}_{\mu }}$ происходит позже.

В настоящей работе анализируются характеристики, которые ранее не рассматривались. На фиг. 4б, в представлены временные зависимости кинетической энергии $K$ и модуля завихренности ${{\Sigma }_{\omega }}$. Величина $K$ ассоциируется, главным образом, с поступательным подъемно-опускным движением примеси, в то время как ${{\Sigma }_{\omega }}$ свидетельствует о перемешивании, поскольку локальная завихренность скорости – это удвоенная угловая скорость вращения [36]. По рисункам видно, что с началом конвекции $K$ и ${{\Sigma }_{\omega }}$ растут почти линейно, затем кривые претерпевают изгиб, что связано с перестройкой периодического движения в стохастическое. Возрастание ${{F}_{\mu }}$ ведет к уменьшению $K$ и ${{\Sigma }_{\omega }}$. Полученные данные о параметре неоднородности распределения примеси $G$ на фиг. 4г показывают, что неоднородность плотности при увеличении ${{F}_{\mu }}$ нарастает медленнее. Однако все кривые $G$ со временем выходят примерно на один уровень и в стадии развитой конвекции колеблются около значения $G \approx 0.85$. Предельная величина $G = 1$ не достигается из‑за диффузионного рассеяния.

4. МОДЕЛИРОВАНИЕ КОНВЕКЦИИ ПРИ БОЛЬШОМ КОНТРАСТЕ ВЯЗКОСТИ

Исследуется конвекция Рэлея–Тейлора с контрастом вязкости слоев жидкости, равным 30, что ассоциируется с парой “нефть–вода”. В этом случае верхний слой (вода), более плотный, но менее вязкий, чем нижний слой (нефть), что задается с помощью отрицательного значения $\Gamma $ в (1.4). Берется $\Gamma = - 3.40$, получается ${{F}_{\mu }} = 0.0334$ и, следовательно, контраст вязкости $1{\text{/}}{{F}_{\mu }} = 30$. Для сравнения моделируется конвекция в среде постоянной вязкости, равной вязкости воды, т.е. при ${{F}_{\mu }} = 1$. В обоих вариантах число Рэлея–Дарси, построенное по коэффициенту вязкости воды, имеет значение ${\text{Ra}} = 3 \times {{10}^{3}}$. Нефть и вода представляют собой несмешивающиеся жидкости, разделенные резкой границей. Тем не менее модель с диффузией массы между слоями, принятая в настоящем исследовании, позволяет получить качественные результаты для несмешивающихся жидкостей на стадии развитой конвекции, когда конвективный перенос оказывается существенно больше, чем диффузионный перенос.

Численное решение получено в области $10 \times 6$ на равномерной сетке $4001 \times 2001$. Шаг интегрирования по времени составляет $\tau = 0.5 \times {{10}^{{ - 7}}}$; $0.125 \times {{10}^{{ - 7}}}$ при ${{F}_{\mu }} = 0.0334;\;1$ соответственно. Компоненты максимальной скорости движения ${{v}_{{x\,\max }}},\;{{v}_{{y\,\max }}}$ не превосходят значений $6 \times {{10}^{2}}$ в первом и $2.2 \times {{10}^{3}}$ во втором случаях, так что критерии (2.7) удовлетворяются.

На фиг. 5, 6 приведены поля плотности примеси в различные моменты времени в среде с переменной и постоянной вязкостью. Поскольку значения коэффициентов вязкости отличаются очень сильно, то процессы развиваются в существенно разных временных масштабах. Чтобы провести сравнение, были выбраны такие моменты, когда высота зоны перемешивания ${{h}_{c}}$ на фрагментах (а) или (б), или (в) имеет одинаковое значение: ${{h}_{c}} = 0.5$ (а); $1.0$ (б); $2.0$ (в). Видны отличия: толщина конвективных “пальцев” на фиг. 5 заметно больше, чем на фиг. 6 в силу высокой вязкости нижнего слоя. На фиг. 5а структура течения еще близка к регулярной, в то время как на фиг. 6а уже преобразовалась в стохастическую.

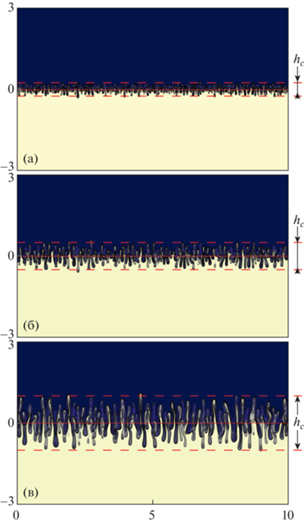
На фиг. 5 можно заметить, что движение конвективных “пальцев” происходит несимметрично относительно начального положения границы раздела между слоями, т.е. уровня $y = 0$, выделенного сплошной красной линией. “Пальцы” более вязкой жидкости поднимаются вверх с большей скоростью, чем опускаются вниз “пальцы” менее вязкой жидкости. Как следствие, зона конвективного перемешивания смещена вверх. Отношение верхней координаты зоны перемешивания $y{\kern 1pt} *$ к нижней координате ${{y}_{*}}$ (взятое по модулю, так как ${{y}_{*}} < 0$) имеет значение ${\text{|}}y{\kern 1pt} *{\kern 1pt} {\text{/}}{{y}_{*}}{\kern 1pt} {\text{|}} = 1.35$ (а); $1.74$ (б); $1.63$ (в). Однако, как показано на фиг. 6, в жидкой системе постоянной вязкости конвекция распространяется вверх и вниз одинаково; здесь ${\text{|}}y{\kern 1pt} *{\kern 1pt} {\text{/}}{{y}_{*}}{\kern 1pt} {\text{|}} = 1.0 \pm 0.03$ для всех фрагментов (а)–(в). Из сравнения фиг. 5 и 6 можно заключить, что несимметричное расширение зоны конвекции обуславливается разницей в значениях коэффициента вязкости слоев жидкости. Похожий эффект недавно описан в [30], где также проводилось численное моделирование конвекции Рэлея–Тейлора в пористой среде с экспоненциальным изменением вязкости раствора в зависимости от плотности примеси. В отличие от настоящего исследования, в [30] повышенную вязкость имеет верхний слой и преобладающее продвижение конвективных “пальцев” происходит вниз; эффект становится заметным при контрасте вязкости больше 20. В настоящей работе при тестировании вычислительного кода эффект, обнаруженный в [30], при аналогичной постановке задачи воспроизведен. Сравнивая новый результат о преобладающем распространении конвекции вверх, если вязкость раствора уменьшается при добавлении примеси, с результатом [30] можно установить следующую общую закономерность: быстрее движутся “пальцы” высоковязкой жидкости в зону жидкости низкой вязкости.

ЗАКЛЮЧЕНИЕ

Продемонстрирована эффективность авторского вычислительного кода при моделировании развития неустойчивости Рэлея–Тейлора в пористой среде на стадиях диффузионного переноса, периодической и стохастической конвекции. Легкий слой образован однокомпонентной жидкостью, тяжелый слой состоит из жидкости и растворенной примеси; вязкость раствора считается переменной. В текущей версии кода интегрирование по времени уравнения конвекции-диффузии производится по схеме Рунге–Кутты со вторым порядком точности.

Рассмотрен случай, когда верхний слой более вязкий, а контраст вязкости лежит в диапазоне от 1 до 3.38. Показано, что с увеличением контраста вязкости начало конвекции наступает позже, течение развивается медленнее, суммарная кинетическая энергия движения примеси и суммарный модуль завихренности скорости оказываются меньше. Однако параметр неоднородности распределения примеси, представляющий собой разность между максимальным и минимальным значениями плотности на линии начального положения границы между слоями, в стадии развитой конвекции выходит на один и тот же уровень независимо от контраста вязкости.

Рассмотрен случай, когда более вязким оказывается нижний слой, а контраст вязкости равен 30. Обнаружено, что распространение конвекции вверх-вниз происходит несимметрично, “пальцы” высоковязкой жидкости движутся вверх быстрее, чем опускаются “пальцы” менее вязкой жидкости. Полученный результат согласуется с описанным в литературе новым эффектом несимметричного развития конвекции при отношении коэффициентов вязкости слоев больше 20. Сравнивая полученную закономерность с приведенной в литературе, можно однозначно заключить, что асимметрия движения определяется только направлением изменения коэффициента вязкости – преимущественное распространение происходит в сторону его уменьшения. Результат работы имеет практическое применение для анализа системы, в которой слой воды располагается над слоем нефти. Хотя вода и нефть не смешиваются, но в стадии развитой конвекции поведение смешивающихся и несмешивающихся жидкостей качественно подобно. Контраст вязкости колеблется от нескольких единиц до примерно 200, поэтому можно предвидеть, что “пальцы” высоковязкой нефти будут подниматься в воде существенно быстрее, чем “пальцы” воды опускаться в нефти.

Автор благодарит Г.Г. Цыпкина за полезные обсуждения.