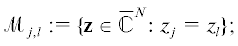Журнал вычислительной математики и математической физики, 2022, T. 62, № 12, стр. 2054-2076
Формулы для вычисления функции Лауричеллы в ситуации кроудинга переменных
1 ФИЦ ИУ РАН
119333 Москва, ул. Вавилова, 40, Россия
* E-mail: sbezrodnykh@mail.ru
Поступила в редакцию 20.05.2022
После доработки 23.06.2022
Принята к публикации 12.07.2022
- EDN: VAPUUQ
- DOI: 10.31857/S0044466922120043
Аннотация
Для функции Лауричеллы $F_{D}^{{(N)}}$, представляющей собой гипергеометрическую функцию многих комплексных переменных ${{z}_{1}}, \ldots ,{{z}_{N}}$, построены формулы аналитического продолжения, соответствующие пересечению произвольного числа сингулярных гиперплоскостей, имеющих вид $\{ {{z}_{j}} = {{z}_{l}}\} $, $j,l = \overline {1,N} $, $j\not { = }l$. Такие формулы дают выражение для рассматриваемой функции в виде линейных комбинаций гипергеометрических рядов Горна $N$ переменных, удовлетворяющих той же системе уравнений с частными производными, что и исходный ряд, с помощью которого $F_{D}^{{(N)}}$ определяется в единичном поликруге. Найденные формулы позволяют эффективно (с помощью экспоненциально сходящихся рядов) вычислять функцию $F_{D}^{{(N)}}$ и выражаемые через нее интегралы типа Эйлера во всем комплексном пространстве ${{\mathbb{C}}^{N}}$ в том числе в сложных случаях, когда переменные образуют одну или несколько групп “очень близких” величин. Такую ситуацию будем называть “кроудингом”, заимствуя этот термин из работ, посвященных практике конформных отображений. Библ. 37.
1. ВВЕДЕНИЕ
1.2. Функция Лауричеллы $F_{D}^{{(N)}}$
Рассматриваемая в работе гипергеометрическая функция Лауричеллы $F_{D}^{{(N)}}({\mathbf{a}};b,c;{\mathbf{z}})$ возникает при конструктивном решении многих актуальных задач прикладной математики (см., например, [1]–[12]). Эта функция, зависящая от $N$ комплексных переменных $({{z}_{1}}, \ldots ,{{z}_{N}}) = :{\mathbf{z}} \in {{\mathbb{C}}^{N}}$ и комплексных параметов $({{a}_{1}}, \ldots ,{{a}_{N}}) = :{\mathbf{a}} \in {{\mathbb{C}}^{N}}$, $b,c \in \mathbb{C}$, определяется в виде следующего $N$-кратного ряда (см. [13] и, например, [1], [3]):
(1.1)
$F_{D}^{{(N)}}{\kern 1pt} ({\mathbf{a}};b,{\kern 1pt} c;{\kern 1pt} {\mathbf{z}}{\kern 1pt} ){\kern 1pt} : = {\kern 1pt} \sum\limits_{|{\mathbf{k}}| = 0}^\infty {\kern 1pt} \frac{{{{{(b)}}_{{|{\mathbf{k}}|}}}{{{({\mathbf{a}})}}_{{\mathbf{k}}}}}}{{{{{(c)}}_{{|{\mathbf{k}}|}}}{\mathbf{k}}!}}{{{\mathbf{z}}}^{{\mathbf{k}}}},$(1.2)
${{\mathbb{U}}^{N}}: = \{ {\kern 1pt} {\mathbf{z}} \in {{\mathbb{C}}^{N}}{\kern 1pt} :\;{\text{|}}{{z}_{j}}{\kern 1pt} {\text{|}} < 1,\;j = \overline {1,N} {\kern 1pt} \} .$(1.3)
${\mathbf{k}}!: = {{k}_{1}}! \cdots {{k}_{N}}!,\quad {{({\mathbf{a}})}_{{\mathbf{k}}}}: = ({{a}_{1}}{{)}_{{{{k}_{1}}}}} \cdots {{({{a}_{N}})}_{{{{k}_{N}}}}}{\kern 1pt} ,\quad {{{\mathbf{z}}}^{{\mathbf{k}}}}: = z_{1}^{{{{k}_{1}}}} \cdots z_{N}^{{{{k}_{N}}}}.$(1.5)
${{(a)}_{0}} = 1,\quad {{(a)}_{m}} = \left\{ \begin{gathered} {{(a)}_{m}} = a{\kern 1pt} (a + 1) \cdots (a + m - 1),\quad m = 1,2, \ldots {\kern 1pt} , \hfill \\ {{( - 1)}^{m}}{{[(1 - a)(2 - a) \cdots ((1 - a) - m - 1)]}^{{ - 1}}},\quad m = - 1, - 2, \ldots . \hfill \\ \end{gathered} \right.$Если векторный аргумент ${\mathbf{z}}$ лежит вне единичного поликруга (1.2), то под функцией Лауричеллы понимается аналитическое продолжение (1.1), для которого естественно сохранить прежнее обозначение $F_{D}^{{(N)}}{\kern 1pt} ({\mathbf{a}};b,{\kern 1pt} c;{\kern 1pt} {\mathbf{z}})$. Такое продолжение в область
(1.6)
${{\mathbb{L}}^{N}}: = \{ {\mathbf{z}} \in {{\mathbb{C}}^{N}}\,:{\text{|arg}}(1 - {{z}_{j}}){\kern 1pt} {\text{|}} < \pi ,\;j = \overline {1,N} {\kern 1pt} \} $(1.7)
$F_{D}^{{(N)}}{\kern 1pt} ({\mathbf{a}};b,c;{\mathbf{z}}) = \frac{{\Gamma (c)}}{{\Gamma (b){\kern 1pt} \Gamma (c - b)}}\int\limits_0^1 \frac{{{{t}^{{b - 1}}}{{{(1 - t)}}^{{c - b - 1}}}}}{{\prod\limits_{j = 1}^N {\kern 1pt} {{{(1 - t{{z}_{j}})}}^{{{{a}_{j}}}}}}}dt,$Функция Лауричеллы, введенная в [13] как формальное обобщение функции Гаусса $F(a,b;c;z)$ на случай $N$ переменных, оказалась одним из наиболее востребованных представителей семейства гипергеометрических функций многих переменных (см. об этом [8]). В связи с этим вопрос об эффективном вычислении этой функции, т.е. интеграла (1.7), во всем пространстве ${{\mathbb{C}}^{N}}$ является весьма актуальной задачей.
В единичном поликруге для вычисления интеграла (1.7) можно использовать непосредственое суммирование ряда (1.1). Однако вне этого поликруга ряд (1.1) расходится и вычисление интеграла (1.7) является трудной задачей. Возникает естественный вопрос о том, можно ли представить аналитически продолженную функцию $F_{D}^{{(N)}}$ в виде обобщенных гипергеометрических рядов, экспоненциально сходящихся в соответствующих подобластях ${{\mathbb{C}}^{N}}{{\backslash }}{{\mathbb{U}}^{N}}$? Такие представления, в частности, позволили бы эффективно вычислять интегралы типа Эйлера (2.1). Ответ на этот вопрос может быть получен в рамках изучения системы дифференциальных уравнений для ряда (1.1), к рассмотрению которой переходим в следующем п. 1.2.
1.2. Проблема аналитического продолжения
Гипергеометрический ряд (1.1), рассматриваемый как функция переменных ${{z}_{1}}, \ldots ,{{z}_{N}}$, удовлетворяет следующей системе из $N$ линейных уравнений второго порядка с частными производными по переменным ${{z}_{j}}$ (см. [13], [1], [3], [4]):
(1.8)
$\left( {c + \sum\limits_{m = 1}^N {{{\theta }_{m}}} } \right)(1 + {{\theta }_{j}})(z_{j}^{{ - 1}}u({\mathbf{z}})) = \left( {b + \sum\limits_{m = 1}^N {{{\theta }_{m}}} } \right)({{a}_{j}} + {{\theta }_{j}})u({\mathbf{z}}),\quad j = \overline {1,N} ,$При дальнейшем рассмотрении будут играть важную роль точки особого множества $\mathcal{M}$, лежащие на пересечении двух или большего числа гиперплоскостей (1.9), (1.10). Будем использовать обозначение
(1.11)
${\mathbf{z}}_{{\nu ,\mu }}^{{(1,\infty ,0)}}: = (\underbrace {1, \ldots ,1}_\nu ,\underbrace {\infty , \ldots ,\infty }_\mu ,\underbrace {0, \ldots ,0}_{N - \nu - \mu })$(1.12)
${\mathbf{z}}_{\nu }^{{(1,\infty )}}: = (\underbrace {1, \ldots ,1}_\nu {\kern 1pt} ,\underbrace {\infty , \ldots ,\infty }_{N - \nu }{\kern 1pt} ).$Одним из центральных вопросов в теории функции Лауричеллы $F_{D}^{{(N)}}$ является проблема аналитического продолжения, заключающаяся в нахождении формул следующего вида:
где набор функций $\{ {{u}_{j}}({\mathbf{a}};b,c;{\mathbf{z}})\} _{{j = 0}}^{N}$, представимых в терминах гипергеометрических рядов $N$ переменных, образует базис пространства решений системы (1.8), а ${{\lambda }_{j}} \in \mathbb{C}$ – некоторые коэффициенты, зависящие от параметров ${{a}_{1}}, \ldots ,{{a}_{N}}$, $b$, $c$. Предполагается, что область $\Omega $, где ряды ${{u}_{j}}$ одновременно сходятся, имеет непустое пересечение с дополнением к единичному поликругу ${{\mathbb{U}}^{N}}$, т.е. справедливо соотношение $\Omega \cap ({{\mathbb{C}}^{N}}{{\backslash }}{{\mathbb{U}}^{N}})\not { = }\emptyset $. Представления вида (1.13) называют формулами аналитического продолжения.Отметим, что представления вида (1.13) являются обобщением классических формул аналитического продолжения функции Гаусса одного переменного на случай $N$ переменных, а фигурирующие в (1.13) функции ${{u}_{j}}({\mathbf{z}})$ играют для систем (1.8) ту же роль, что и канонические решения Куммера (см. [1], [14], [15]) для гипергеометрического уравнения, которому удовлетворяет функция Гаусса. В [8], [16] при произвольном $N$ был построен набор формул аналитического продолжения (1.13) функции Лауричеллы $F_{D}^{{(N)}}$, области сходимости которых в совокупности покрывают ${{\mathbb{C}}^{N}}$ за исключением гиперплоскостей ${{\mathcal{M}}_{{j,l}}}$, определенных равенством (1.10). Граница области сходимости каждой из таких формул содержит часть одной или нескольких гиперплоскостей ${{\mathcal{M}}_{{j,l}}}$, поэтому указанный набор формул адекватно представляет функцию $F_{D}^{{(N)}}$ и позволяет ее вычислять, когда аргумент ${\mathbf{z}}$ лежит достаточно далеко от ${{\mathcal{M}}_{{j,l}}}$.
В [17], [18] при произвольном $N$ предложен способ построения формул аналитического продолжения нового типа, позволяющий для любого пересечения $\mathcal{S}$ гиперплоскостей ${{\mathcal{M}}_{{j,l}}}$ указать представление вида (1.13), область сходимости которого имеет непустое пересечение с $\mathcal{S}$. При этом в отмеченных работах в явном виде были построены формулы для случаев, когда все переменные одновременно или близки к единице, или велики по модулю, т.е. рассмотрено продолжение $F_{D}^{{(N)}}$ в окрестности точек ${{{\mathbf{z}}}^{{(1)}}}$ и ${{{\mathbf{z}}}^{{(\infty )}}}$.
1.3. Полученные результаты об аналитическом продолжении
В настоящей работе, продолжающей исследования [17], [18], для функции Лауричеллы $F_{D}^{{(N)}}$ построен набор формул аналитического продолжения, позволяющих в окрестностях ${{\mathcal{O}}_{{\nu ,\mu }}}$ точек $z_{{\nu ,\mu }}^{{(1,\infty ,0)}}$ адекватно представить эту функцию вблизи множества ${{\mathcal{S}}_{{\nu ,\mu }}} = {{\mathcal{S}}_{1}} \cap {{\mathcal{S}}_{2}}$, где ${{\mathcal{S}}_{1}}$ – пересечение гиперплоскостей ${{\mathcal{M}}_{{j,{\kern 1pt} l}}}$ с номерами $j,l = \overline {1,\nu } $, а ${{\mathcal{S}}_{2}}$ – пересечение гиперплоскостей ${{\mathcal{M}}_{{s,{\kern 1pt} k}}}$ с номерами $s,k = \overline {\nu + 1,\nu + \mu } $. Точнее, для любого ${{\mathcal{S}}_{{\nu ,\mu }}}$ указанного вида найдена формула продолжения с областью сходимости $\Omega $, удовлетворяющей соотношению $\Omega \cap {{\mathcal{S}}_{{\nu ,\mu }}} \cap {{\mathcal{O}}_{{\nu ,\mu }}}\not { = }\emptyset $.
Такой результат устанавливает теорема 2 (см. п. 2.4). В этой теореме рассмотрен случай произвольного числа $N$ переменных функции Лауричеллы и продолжения в окрестность точек (1.11), с любыми $\nu ,\mu \geqslant 0$, $\nu + \mu \leqslant N$, и произвольным множеством ${{\mathcal{S}}_{{\nu ,\mu }}}$. В разд. 3, 4 даны примеры применения этой теоремы к построению аналитического продолжения в случае трех и четырех переменных. Утверждение теоремы 2 получено с помощью разложений интеграла типа Эйлера (1.7) в подходящие степенны́е ряды и применения приведенной в п. 2.1 теоремы 1 (см. также [8, теорема 5]).
Таким образом, построенные в работе формулы адекватно представляют функцию $F_{D}^{{(N)}}$ для случаев, когда ее переменные ${{z}_{1}}, \ldots ,{{z}_{N}}$ делятся на группы близких величин. Такую ситуацию будем называть “кроудингом” (от английского слова “to crowd” – толпиться, сбиваться в кучу). Термин “кроудинг” употребляется в работах, посвященных практике построения конформного отображения прямолинейных многоугольников на основе интеграла Кристоффеля–Шварца (см. [19]–[26]), и применяется к ситуации резко неравномерного распределения значений параметров этого интеграла. Полученная в разд. 2 теорема 2 рассматривает случай, когда переменные “толпятся” вблизи сингулярных гиперплоскостей ${{\mathcal{M}}_{{s,{\kern 1pt} k}}}$ и их пересечений ${{\mathcal{S}}_{{\nu ,\mu }}}$. Отметим также, что применение формул аналитического продолжения функции Лауричеллы позволяет добиться существенного прогресса в решении вычислительных проблем, связанных с решением проблемы параметров интеграла Кристоффеля–Шварца и вычислением конформного отображения многоугольников (см. [8]).
Ниже во Введении приведена иллюстрация применения теорем 1 и 2 для аналитического продолжения функции $F_{D}^{{(3)}}$ в окрестность точки $(1,\infty ,\infty )$, показывающая важное значение каждой из этих теорем для получения адекватных представлений функции Лауричеллы. Предположим, что переменная ${{z}_{1}}$ близка к единице, а ${{z}_{2}}$ и ${{z}_{3}}$ принимают большие по модулю значения. Применяя теорему 1 (см. п. 2.1 и [8]) для случая $N = 3$, $\nu = 1$ получаем, что аналитическое продолжение функции $F_{D}^{{(3)}}$ в область
(1.14)
${{\mathbb{V}}^{{3,1}}}: = \{ 0 < {\text{|}}1 - {{z}_{1}}{\kern 1pt} {\text{|}} < 1,\;{\text{|}}{{z}_{2}}{\kern 1pt} {\text{|}} > {\text{|}}{{z}_{3}}{\text{|}} > 1\; + \;{\text{|}}1 - {{z}_{1}}{\kern 1pt} {\text{|}},\;{\text{|}}\arg (1 - {{z}_{1}}){\kern 1pt} {\text{|}} < \pi ,\;{\text{|}}\arg ( - {{z}_{j}}){\kern 1pt} {\text{|}} < \pi ,\;j = 2,3\} $(1.15)
$F_{D}^{{(3)}}({{a}_{1}},{{a}_{2}},{{a}_{3}};b,c;{{z}_{1}},{{z}_{2}},{{z}_{3}}) = \sum\limits_{j = 0}^3 {{{A}_{j}}{{u}_{j}}({{z}_{1}},{{z}_{2}},{{z}_{3}})} ,$(1.16)
$\begin{gathered} {{u}_{0}}({{z}_{1}},{{z}_{2}},{{z}_{3}}) = ( - {{z}_{2}}{{)}^{{ - {{a}_{2}}}}}{{( - {{z}_{3}})}^{{ - {{a}_{3}}}}}\sum\limits_{{{k}_{1}},{{k}_{2}},{{k}_{3}} = 0}^\infty {{\Lambda }_{0}}({\mathbf{k}})({{z}_{1}} - {{1)}^{{{{k}_{1}}}}}z_{2}^{{ - {{k}_{2}}}}z_{3}^{{ - {{k}_{3}}}}, \\ {{u}_{1}}({{z}_{1}},{{z}_{2}},{{z}_{3}}) = {{(1 - {{z}_{1}})}^{{c - {{a}_{1}} - b}}}{{( - {{z}_{2}})}^{{ - {{a}_{2}}}}}{{( - {{z}_{3}})}^{{ - {{a}_{3}}}}}\sum\limits_{{{k}_{1}},{{k}_{2}},{{k}_{3}} = 0}^\infty {{\Lambda }_{1}}({\mathbf{k}})(1 - {{z}_{1}}{{)}^{{{{k}_{1}}}}}z_{2}^{{ - {{k}_{2}}}}z_{3}^{{ - {{k}_{3}}}}, \\ \end{gathered} $(1.17)
$\begin{gathered} {{u}_{2}}({{z}_{1}},{{z}_{2}},{{z}_{3}}) = ( - {{z}_{2}}{{)}^{{ - b}}}\sum\limits_{{{k}_{1}},{{k}_{2}},{{k}_{3}} = 0}^\infty {{\Lambda }_{2}}({\mathbf{k}}){{\left( {\frac{{{{z}_{1}} - 1}}{{{{z}_{2}}}}} \right)}^{{{{k}_{1}}}}}z_{2}^{{ - {{k}_{2}}}}{{\left( {\frac{{{{z}_{3}}}}{{{{z}_{2}}}}} \right)}^{{{{k}_{3}}}}}, \\ {{u}_{3}}({{z}_{1}},{{z}_{2}},{{z}_{3}}) = ( - {{z}_{2}}{{)}^{{ - {{a}_{2}}}}}{{( - {{z}_{3}})}^{{{{a}_{2}} - b}}}\sum\limits_{{{k}_{1}},{{k}_{2}},{{k}_{3}} = 0}^\infty {{\Lambda }_{3}}({\mathbf{k}}){{\left( {\frac{{{{z}_{1}} - 1}}{{{{z}_{3}}}}} \right)}^{{{{k}_{1}}}}}{{\left( {\frac{{{{z}_{3}}}}{{{{z}_{2}}}}} \right)}^{{{{k}_{2}}}}}z_{3}^{{ - {{k}_{3}}}}, \\ \end{gathered} $(1.18)
$\begin{gathered} {{\Lambda }_{1}}({\mathbf{k}}): = \frac{{{{{(c - b)}}_{{{{k}_{1}}}}}{{{(1 + {{a}_{1}} + {{a}_{2}} + {{a}_{3}} - c)}}_{{{{k}_{2}} + {{k}_{3}}}}}{{{({{a}_{2}})}}_{{{{k}_{2}}}}}{{{({{a}_{3}})}}_{{{{k}_{3}}}}}}}{{{{{(1 + c - {{a}_{1}} - b)}}_{{{{k}_{1}}}}}{{{(1 + {{a}_{1}} + {{a}_{2}} + {{a}_{3}} - c)}}_{{{{k}_{2}} + {{k}_{3}} - {{k}_{1}}}}}{{k}_{1}}!{{k}_{2}}!{{k}_{3}}!}}, \\ {{\Lambda }_{2}}({\mathbf{k}}): = \frac{{{{{(b)}}_{{{{k}_{1}} + {{k}_{2}} + {{k}_{3}}}}}{{{(1 - c + {{a}_{1}} + b)}}_{{{{k}_{1}} + {{k}_{2}}}}}{{{({{a}_{1}})}}_{{{{k}_{1}}}}}{{{({{a}_{3}})}}_{{{{k}_{3}}}}}}}{{{{{(1 + b - {{a}_{2}})}}_{{{{k}_{1}} + {{k}_{2}} + {{k}_{3}}}}}{{{(1 - c + {{a}_{1}} + b)}}_{{{{k}_{1}}}}}{{k}_{1}}!{{k}_{2}}!{{k}_{3}}!}}, \\ \end{gathered} $(1.19)
$\begin{gathered} {{A}_{0}} = \frac{{\Gamma (c)\Gamma (c - {{a}_{1}} - b)\Gamma (b - {{a}_{2}} - {{a}_{3}})}}{{\Gamma (b)\Gamma (c - {{a}_{1}} - {{a}_{2}} - {{a}_{3}})\Gamma (c - b)}},\quad {{A}_{1}} = \frac{{\Gamma (c)\Gamma ({{a}_{1}} + b - c)}}{{\Gamma ({{a}_{1}})\Gamma (b)}}, \\ {{A}_{2}} = \frac{{\Gamma (c)\Gamma ({{a}_{2}} - b)}}{{\Gamma ({{a}_{2}})\Gamma (c - b)}},\quad {{A}_{3}} = \frac{{\Gamma (c)\Gamma (b - {{a}_{2}})\Gamma ({{a}_{2}} + {{a}_{3}} - b)}}{{\Gamma ({{a}_{3}})\Gamma (b)\Gamma (c - b)}}. \\ \end{gathered} $ , симметричную по отношению к (1.14), дается формулой, получаемой заменами $({{z}_{1}},{{z}_{2}},{{z}_{3}}) \to ({{z}_{1}},{{z}_{3}},{{z}_{2}})$ и $({{a}_{1}},{{a}_{2}},{{a}_{3}}) \to $ $ \to ({{a}_{1}},{{a}_{3}},{{a}_{2}})$ в правой части (1.15)–(1.19).
, симметричную по отношению к (1.14), дается формулой, получаемой заменами $({{z}_{1}},{{z}_{2}},{{z}_{3}}) \to ({{z}_{1}},{{z}_{3}},{{z}_{2}})$ и $({{a}_{1}},{{a}_{2}},{{a}_{3}}) \to $ $ \to ({{a}_{1}},{{a}_{3}},{{a}_{2}})$ в правой части (1.15)–(1.19).
Обратим внимание на то, что множество
 .) Поэтому в окрестности $(1,\infty ,\infty )$ одного представления (1.15) недостаточно и необходимо получить такое представление,
которое было бы адекватно особой гиперплоскости ${{\mathcal{M}}_{{2,3}}}$, в том смысле, что соответствующие ряды в точках множества ${{\mathcal{M}}^{{(1,\infty )}}}$ сходились бы экспоненциально.
.) Поэтому в окрестности $(1,\infty ,\infty )$ одного представления (1.15) недостаточно и необходимо получить такое представление,
которое было бы адекватно особой гиперплоскости ${{\mathcal{M}}_{{2,3}}}$, в том смысле, что соответствующие ряды в точках множества ${{\mathcal{M}}^{{(1,\infty )}}}$ сходились бы экспоненциально.
Указанным свойством обладает следующее представление для $F_{D}^{{(3)}}$, которое вытекает из теоремы 2 (см. разд. 2) при $N = 3$, $\nu = 1$, $q = 2$:
(1.20)
$F_{D}^{{(3)}}({{a}_{1}},{{a}_{2}},{{a}_{3}};b,c;{{z}_{1}},{{z}_{2}},{{z}_{3}}) = \sum\limits_{j = 0}^2 {{{B}_{j}}{{v}_{j}}({{z}_{1}},{{z}_{2}},{{z}_{3}})} ,$(1.21)
$\begin{gathered} {{v}_{0}}({{z}_{1}},{{z}_{2}},{{z}_{3}}) = ( - {{z}_{2}}{{)}^{{ - {{a}_{2}} - {{a}_{3}}}}}\sum\limits_{{{k}_{1}},{{k}_{2}},{{k}_{3}} = 0}^\infty {{\Xi }_{0}}({\mathbf{k}})({{z}_{1}} - {{1)}^{{{{k}_{1}}}}}z_{2}^{{ - {{k}_{2}}}}{{\left( {\frac{{{{z}_{2}} - {{z}_{3}}}}{{{{z}_{2}}}}} \right)}^{{{{k}_{3}}}}}, \\ {{v}_{1}}({{z}_{1}},{{z}_{2}},{{z}_{3}}) = (1 - {{z}_{1}}{{)}^{{c - {{a}_{1}} - b}}}{{( - {{z}_{2}})}^{{ - {{a}_{2}} - {{a}_{3}}}}}\sum\limits_{{{k}_{1}},{{k}_{2}},{{k}_{3}} = 0}^\infty {{\Xi }_{1}}({\mathbf{k}})(1 - {{z}_{1}}{{)}^{{{{k}_{1}}}}}z_{2}^{{ - {{k}_{2}}}}{{\left( {\frac{{{{z}_{2}} - {{z}_{3}}}}{{{{z}_{2}}}}} \right)}^{{{{k}_{3}}}}}, \\ {{v}_{2}}({{z}_{1}},{{z}_{2}},{{z}_{3}}) = ( - {{z}_{2}}{{)}^{{ - b}}}\sum\limits_{{{k}_{1}},{{k}_{2}},{{k}_{3}} = 0}^\infty {{\Xi }_{2}}({\mathbf{k}}){{\left( {\frac{{{{z}_{1}} - 1}}{{{{z}_{2}}}}} \right)}^{{{{k}_{1}}}}}z_{2}^{{ - {{k}_{2}}}}{{\left( {\frac{{{{z}_{2}} - {{z}_{3}}}}{{{{z}_{2}}}}} \right)}^{{{{k}_{3}}}}}, \\ \end{gathered} $(1.22)
$\begin{gathered} {{\Xi }_{0}}({\mathbf{k}}) = \frac{{{{{(1 - c + {{a}_{1}} + {{a}_{2}} + {{a}_{3}})}}_{{{{k}_{2}}}}}{{{({{a}_{1}})}}_{{{{k}_{1}}}}}{{{({{a}_{2}} + {{a}_{3}})}}_{{{{k}_{2}} + {{k}_{3}}}}}{{{({{a}_{3}})}}_{{{{k}_{3}}}}}}}{{{{{(1 + {{a}_{1}} + b - c)}}_{{{{k}_{1}}}}}{{{(1 - b + {{a}_{2}} + {{a}_{3}})}}_{{{{k}_{2}} - {{k}_{1}}}}}{{k}_{1}}!({{a}_{2}} + {{a}_{3}}{{)}_{{{{k}_{3}}}}}{{k}_{2}}!{{k}_{3}}!}}, \\ {{\Xi }_{1}}({\mathbf{k}}) = \frac{{{{{(c - b)}}_{{{{k}_{1}}}}}{{{(1 + {{a}_{1}} + {{a}_{2}} + {{a}_{3}} - c)}}_{{{{k}_{2}}}}}{{{({{a}_{2}} + {{a}_{3}})}}_{{{{k}_{2}} + {{k}_{3}}}}}{{{({{a}_{3}})}}_{{{{k}_{3}}}}}}}{{{{{(1 + c - {{a}_{1}} - b)}}_{{{{k}_{1}}}}}{{{(1 + {{a}_{1}} + {{a}_{2}} + {{a}_{3}} - c)}}_{{{{k}_{2}} - {{k}_{1}}}}}{{{({{a}_{2}} + {{a}_{3}})}}_{{{{k}_{3}}}}}{{k}_{1}}!{{k}_{2}}!{{k}_{3}}!}}, \\ {{\Xi }_{2}}({\mathbf{k}}) = \frac{{{{{(b)}}_{{{{k}_{1}} + {{k}_{2}} + {{k}_{3}}}}}{{{(1 - c + {{a}_{1}} + b)}}_{{{{k}_{1}} + {{k}_{2}}}}}{{{({{a}_{1}})}}_{{{{k}_{1}}}}}{{{({{a}_{3}})}}_{{{{k}_{3}}}}}}}{{{{{(1 + b - {{a}_{2}} - {{a}_{3}})}}_{{{{k}_{1}} + {{k}_{2}}}}}{{{({{a}_{2}} + {{a}_{3}})}}_{{{{k}_{3}}}}}{{{(1 - c + {{a}_{1}} + b)}}_{{{{k}_{1}}}}}{{k}_{1}}!{{k}_{2}}!{{k}_{3}}!}}, \\ \end{gathered} $(1.23)
$\begin{array}{*{20}{l}} {{{B}_{0}} = \frac{{\Gamma (c)\Gamma (c - {{a}_{1}} - b)\Gamma (b - {{a}_{2}} - {{a}_{3}})}}{{\Gamma (b)\Gamma (c - {{a}_{1}} - {{a}_{2}} - {{a}_{3}})\Gamma (c - b)}},\quad {{B}_{1}} = \frac{{\Gamma (c)\Gamma ({{a}_{1}} + b - c)}}{{\Gamma ({{a}_{1}})\Gamma (b)}},{\kern 1pt} \quad {{B}_{2}} = \frac{{\Gamma (c)\Gamma ({{a}_{2}} + {{a}_{3}} - b)}}{{\Gamma ({{a}_{2}} + {{a}_{3}})\Gamma (c - b)}}.} \end{array}$(1.24)
$\{ {\text{|}}1 - {{z}_{1}}{\kern 1pt} {\text{|}} < 1,\;{\text{|}}{{z}_{2}}{\kern 1pt} {\text{|}} > 1\; + \;{\text{|}}1 - {{z}_{1}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}{{z}_{2}} - {{z}_{{3{\kern 1pt} }}}{\text{|}};\;{\text{|}}\arg (1 - {{z}_{1}}){\kern 1pt} {\text{|}} < \pi ,\;{\text{|}}\arg ( - {{z}_{2}}){\kern 1pt} {\text{|}} < \pi \} .$Возвращаясь к случаю произвольного числа переменных, подчеркнем, что при всех $N \geqslant 2$ теоремы 1 и 2 дополняют друг друга и позволяют адекватно представить функцию Лауричеллы $F_{D}^{{(N)}}$ в окрестностях точек ${{{\mathbf{z}}}^{{(1,\infty ,0)}}}$ аналогично тому, как это было продемонстрировано выше на примере трех переменных.
1.4. Функции Горна
Рассматриваемый круг вопросов является вкладом в решение проблемы аналитического продолжения и вычисления гипергеометрических рядов Горна $N$ переменных. Степеннóй $\sum\nolimits_{{\mathbf{k}} \in {{\mathbb{Z}}^{N}}} \,\Lambda ({\mathbf{k}}){{{\mathbf{z}}}^{{\mathbf{k}}}}$ называют гипергеометрическим рядом Горна (см. [2]), [27], если отношению любых двух соседних коэффициентов $\Lambda ({\mathbf{k}}) = \Lambda ({{k}_{1}}, \ldots ,{{k}_{N}})$ представляет собой рациональную функцию аргументов ${{k}_{1}}, \ldots ,{{k}_{N}}$, другими словами, справедливы соотношения
(1.25)
$\frac{{\Lambda ({\mathbf{k}} + {{{\mathbf{e}}}_{r}})}}{{\Lambda ({\mathbf{k}})}} = \frac{{{{P}_{r}}({\mathbf{k}})}}{{{{Q}_{r}}({\mathbf{k}})}},\quad r = \overline {1,N} ,$2. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ В ОКРЕСТНОСТИ ОСОБЫХ ГИПЕРПЛОСКОСТЕЙ $\{ {{z}_{j}} = {{z}_{m}}\} $ ВБЛИЗИ ТОЧЕК ${\mathbf{z}}_{{\nu ,\mu }}^{{(1,\infty ,0)}}$
2.1. Формулы продолжения в окрестность ${\mathbf{z}}_{\nu }^{{(1,\infty )}}$
Приведем результаты, вытекающие из [8], теорема 5. Определим область ${{\mathbb{V}}^{{N,\nu }}}$ с помощью следующего равенства:
(2.1)
$\begin{gathered} {{\mathbb{V}}^{{N,{\kern 1pt} \nu }}}: = \{ {\mathbf{z}} \in {{\mathbb{C}}^{N}}:0 < {\text{|}}1 - {{z}_{1}}{\text{|}} < \cdots < {\text{|}}1 - {{z}_{\nu }}{\text{|}} < 1,\;{\text{|}}\arg (1 - {{z}_{j}}){\kern 1pt} {\text{|}} < \pi ,\;j = \overline {1,\nu } , \\ {\text{|}}{{z}_{{\nu + 1}}}{\kern 1pt} {\text{|}} > \cdots > {\text{|}}{{z}_{N}}{\text{|}} > 1,\;{\text{|}}\arg ( - {{z}_{s}}){\kern 1pt} {\text{|}} < \pi ,\;s = \overline {\nu + 1,N} ,1\; + \;{\text{|}}1 - {{z}_{j}}{\kern 1pt} {\text{|}} < {\text{|}}{{z}_{s}}{\kern 1pt} {\text{|}},\;j = \overline {1,\nu } ,\;s = \overline {\nu + 1,N} \} . \\ \end{gathered} $(2.2)
${{\mathbb{V}}^{N}}: = {{\mathbb{V}}^{{N,{\kern 1pt} 0}}}: = \{ {\mathbf{z}} \in {{\mathbb{C}}^{N}}:{\text{|}}{{z}_{1}}{\kern 1pt} {\text{|}} > \cdots > {\text{|}}{{z}_{N}}{\text{|}} > 1,\;{\text{|}}\arg ( - {{z}_{s}}){\kern 1pt} {\text{|}} < \pi ,\;s = \overline {1,N} \} ,$(2.3)
${{\mathbb{V}}^{N}}: = {{\mathbb{V}}^{{N,{\kern 1pt} N}}}: = \{ {\mathbf{z}} \in {{\mathbb{C}}^{N}}:0 < {\text{|}}1 - {{z}_{1}}{\kern 1pt} {\text{|}} < \cdots < {\text{|}}1 - {{z}_{N}}{\text{|}} < 1,\;{\text{|}}\arg (1 - {{z}_{s}}){\kern 1pt} {\text{|}} < \pi ,\;s = \overline {1,N} \} .$(2.4)
$\mathbb{V}_{\sigma }^{{N,{\kern 1pt} \nu }}: = \{ {\mathbf{z}} \in {{\mathbb{C}}^{N}}:\sigma ({\mathbf{z}}) \in {{\mathbb{V}}^{{N,{\kern 1pt} \nu }}}\} .$(2.5)
${\text{|}}{{{\mathbf{a}}}_{{s,l}}}{\text{|}}: = \sum\limits_{k = s}^l {{{a}_{k}}} ,\quad {\text{|}}{\mathbf{a}}{\kern 1pt} {\text{|}}: = {\text{|}}{{{\mathbf{a}}}_{{1,N}}}{\text{|}},\quad {\text{|}}{{{\mathbf{k}}}_{{s,l}}}{\kern 1pt} {\text{|}}: = \sum\limits_{n = s}^l {{\kern 1pt} {{k}_{n}}} ,\quad {\text{|}}{\mathbf{k}}{\kern 1pt} {\text{|}}: = {\text{|}}{{{\mathbf{k}}}_{{1,N}}}{\text{|}}.$Теорема 1. Если ни одно из чисел
(2.6)
$\left( {b - \sum\limits_{s = \nu + 1}^j {{{a}_{s}}} } \right),\quad j = \overline {\nu + 1,N} ,\quad \left( {c - b - \sum\limits_{s = 1}^j {{{a}_{s}}} } \right),\quad j = \overline {1,\nu } ,$(2.7)
$\begin{array}{*{20}{l}} {F_{D}^{{(N)}}({\mathbf{a}};b,c;{\mathbf{z}}) = \sum\limits_{j = 0}^N {{{A}_{j}}\mathcal{U}_{j}^{{(1,\infty )}}} ({\mathbf{a}};b,c;{\mathbf{z}}),} \end{array}$(2.8)
$\begin{array}{*{20}{l}} {\mathcal{U}_{0}^{{(1,\infty )}}({\mathbf{a}};b,c;{\mathbf{z}}) = \left( {\prod\limits_{l = \nu + 1}^N {\kern 1pt} {{{( - {{z}_{l}})}}^{{ - {{a}_{l}}}}}} \right)\sum\limits_{|{\mathbf{k}}| = 0}^\infty \,{{\Lambda }_{0}}({\mathbf{a}};b,c;{\mathbf{k}}){\mathbf{Z}}_{0}^{{\mathbf{k}}},} \end{array}$(2.9)
$\mathcal{U}_{j}^{{(1,\infty )}}({\mathbf{a}};b,c;{\mathbf{z}}) = (1 - {{z}_{j}}{{)}^{{c - |{{{\mathbf{a}}}_{{1,j}}}| - b}}}\left( {\prod\limits_{l = j + 1}^\nu {\kern 1pt} {{{(1 - {{z}_{l}})}}^{{ - {{a}_{l}}}}}} \right)\left( {\prod\limits_{l = \nu + 1}^N {\kern 1pt} {{{( - {{z}_{l}})}}^{{ - {{a}_{l}}}}}} \right)\sum\limits_{|{\mathbf{k}}| = 0}^\infty \,{{\Lambda }_{j}}({\mathbf{a}};b,c;{\mathbf{k}}){\mathbf{Z}}_{j}^{{\mathbf{k}}},\quad j = \overline {1,\nu } ,$(2.10)
$\mathcal{U}_{j}^{{(1,\infty )}}({\mathbf{a}};b,c;{\kern 1pt} {\mathbf{z}}) = ( - {{z}_{j}}{{)}^{{|{{{\mathbf{a}}}_{{\nu + 1,j - 1}}}| - b}}}\left( {\prod\limits_{l = \nu + 1}^{j - 1} {\kern 1pt} {{{( - {{z}_{l}})}}^{{ - {{a}_{l}}}}}} \right)\sum\limits_{|{\mathbf{k}}| = 0}^\infty \,{{\Lambda }_{j}}({\mathbf{a}};b,c;{\mathbf{k}}){\mathbf{Z}}_{j}^{{\mathbf{k}}},\quad j = \overline {\nu + 1,N} ;$(2.11)
${{\Lambda }_{0}}({\mathbf{a}};b,c;{\mathbf{k}}): = \frac{{(1\; + \;{\text{|}}{\mathbf{a}}{\kern 1pt} {\text{|}} - c,{\text{|}}{{{\mathbf{k}}}_{{\nu + 1,N}}}{\text{|}}{\kern 1pt} )}}{{(1\; + \;{\text{|}}{{{\mathbf{a}}}_{{1,\nu }}}{\kern 1pt} {\text{|}} + b - c,{\text{|}}{{{\mathbf{k}}}_{{1,\nu }}}{\kern 1pt} {\text{|}}{\kern 1pt} )(1\; + \;{\text{|}}{{{\mathbf{a}}}_{{\nu + 1,N}}}{\text{|}} - b,{\text{|}}{{{\mathbf{k}}}_{{\nu + 1,N}}}{\text{|}}\; - \;{\text{|}}{{{\mathbf{k}}}_{{1,\nu }}}{\kern 1pt} {\kern 1pt} {\text{|}})}}\prod\limits_{s = 1}^N \frac{{({{a}_{s}},{{k}_{s}})}}{{{{k}_{s}}!}},$(2.12)
${{\Lambda }_{j}}({\mathbf{a}};b,c;{\mathbf{k}}): = \frac{{(c\; - \;{\text{|}}{{{\mathbf{a}}}_{{1,j - 1}}}{\kern 1pt} {\text{|}} - b,{\text{|}}{{{\mathbf{k}}}_{{j,\nu }}}{\kern 1pt} {\text{|}}\; - \;{\text{|}}{{{\mathbf{k}}}_{{1,j - 1}}}{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{(1 + c\; - \;{\text{|}}{{{\mathbf{a}}}_{{1,j}}}{\kern 1pt} {\text{|}} - b,{\text{|}}{{{\mathbf{k}}}_{{j,\nu }}}{\kern 1pt} {\text{|}}\; - \;{\text{|}}{{{\mathbf{k}}}_{{1,j - 1}}}{\kern 1pt} {\text{|}}{\kern 1pt} )}}\frac{{(1\; + \;{\text{|}}{\mathbf{a}}{\kern 1pt} {\text{|}} - c,{\text{|}}{{{\mathbf{k}}}_{{\nu + 1,N}}}{\text{|}}{\kern 1pt} )}}{{(1\; + \;{\text{|}}{\mathbf{a}}{\kern 1pt} {\text{|}} - c,{\text{|}}{{{\mathbf{k}}}_{{\nu + 1,N}}}{\text{|}} - {{k}_{j}}){{k}_{j}}!}}\prod\limits_{\begin{gathered} s = 1s\not { = }j \\ \end{gathered} }^N \frac{{({{a}_{s}},{{k}_{s}})}}{{{{k}_{s}}!}},\quad j = \overline {1,\nu } ,$(2.13)
$\begin{gathered} {{\Lambda }_{j}}({\mathbf{a}};b,c;{\mathbf{k}}): = \frac{{(b\; - {\text{|}}{{{\mathbf{a}}}_{{\nu + 1,j - 1}}}{\kern 1pt} {\text{|}},{\text{|}}{{{\mathbf{k}}}_{{1,\nu }}}{\kern 1pt} {\text{|}}\; - \;{\text{|}}{{{\mathbf{k}}}_{{\nu + 1,j - 1}}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}{{{\mathbf{k}}}_{{j,N}}}{\text{|}}{\kern 1pt} )}}{{(1 + b\; - \;{\text{|}}{{{\mathbf{a}}}_{{\nu + 1,j}}}{\kern 1pt} {\text{|}},{\text{|}}{{{\mathbf{k}}}_{{1,\nu }}}{\kern 1pt} {\text{|}}\; - \;{\text{|}}{{{\mathbf{k}}}_{{\nu + 1,j - 1}}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}{{{\mathbf{k}}}_{{j,N}}}{\text{|}}{\kern 1pt} )}} \times \\ \, \times \frac{{(1 - c\; + \;{\text{|}}{{{\mathbf{a}}}_{{1,\nu }}}{\kern 1pt} {\text{|}} + b,{\text{|}}{{{\mathbf{k}}}_{{1,\nu }}}{\kern 1pt} {\text{|}} + {{k}_{j}})}}{{(1 - c\; + \;{\text{|}}{{{\mathbf{a}}}_{{1,\nu }}}{\kern 1pt} {\text{|}} + b,{\text{|}}{{{\mathbf{k}}}_{{1,\nu }}}{\kern 1pt} {\text{|}}{\kern 1pt} ){{k}_{j}}!}}\prod\limits_{\begin{gathered} s = 1s\not { = }j \\ \end{gathered} }^N \frac{{({{a}_{s}},{{k}_{s}})}}{{{{k}_{s}}!}},\quad j = \overline {\nu + 1,N} . \\ \end{gathered} $(2.14)
$\begin{array}{*{20}{l}} {{{\mathcal{Z}}_{0}}: = \left( {{{z}_{1}} - 1, \ldots ,{{z}_{\nu }} - 1,\frac{1}{{{{z}_{{\nu + 1}}}}}, \ldots ,\frac{1}{{{{z}_{N}}}}} \right),} \end{array}$(2.15)
$\begin{array}{*{20}{l}} {{{\mathcal{Z}}_{j}}: = \left( {\frac{{1 - {{z}_{1}}}}{{1 - {{z}_{j}}}}, \ldots ,\frac{{1 - {{z}_{{j - 1}}}}}{{1 - {{z}_{j}}}},1 - {{z}_{j}},\frac{{1 - {{z}_{j}}}}{{1 - {{z}_{{j + 1}}}}}, \ldots ,\frac{{1 - {{z}_{j}}}}{{1 - {{z}_{\nu }}}},\frac{1}{{{{z}_{{\nu + 1}}}}}, \ldots ,\frac{1}{{{{z}_{N}}}}} \right),\quad j = \overline {1,\nu } ,} \end{array}$(2.16)
$\begin{array}{*{20}{l}} {{{\mathcal{Z}}_{j}}: = \left( {\frac{{{{z}_{1}} - 1}}{{{{z}_{j}}}}, \ldots ,\frac{{{{z}_{\nu }} - 1}}{{{{z}_{j}}}},\frac{{{{z}_{j}}}}{{{{z}_{{\nu + 1}}}}}, \ldots ,\frac{{{{z}_{j}}}}{{{{z}_{{j - 1}}}}},\frac{1}{{{{z}_{j}}}},\frac{{{{z}_{{j + 1}}}}}{{{{z}_{j}}}}, \ldots ,\frac{{{{z}_{N}}}}{{{{z}_{j}}}}} \right),\quad j = \overline {\nu + 1,N} .} \end{array}$(2.17)
$\begin{gathered} {{A}_{0}} = \frac{{\Gamma (c)\Gamma (c\; - \;{\text{|}}{{{\mathbf{a}}}_{{1,\nu }}}{\kern 1pt} {\text{|}} - b)\Gamma (b\; - \;{\text{|}}{{{\mathbf{a}}}_{{\nu + 1,N}}}{\text{|}}{\kern 1pt} )}}{{\Gamma (b){\kern 1pt} \Gamma (c\; - \;{\text{|}}{\mathbf{a}}{\kern 1pt} {\kern 1pt} {\text{|}})\Gamma (c - b)}}, \\ {{A}_{j}} = \frac{{\Gamma (c)\Gamma (c\; - \;{\text{|}}{{{\mathbf{a}}}_{{1,j - 1}}}{\kern 1pt} {\text{|}} - b)\Gamma ({\kern 1pt} {\text{|}}{{{\mathbf{a}}}_{{1,j}}}{\text{|}} + b - c)}}{{\Gamma ({{a}_{j}})\Gamma (b){\kern 1pt} \Gamma (c - b)}},\quad j = \overline {1,\nu } , \\ {{A}_{j}} = \frac{{\Gamma (c)\Gamma (b\; - \;{\text{|}}{{{\mathbf{a}}}_{{\nu + 1,j - 1}}}{\kern 1pt} {\text{|}}{\kern 1pt} )\Gamma ({\kern 1pt} {\text{|}}{{{\mathbf{a}}}_{{\nu + 1,j}}}{\kern 1pt} {\text{|}} - b)}}{{\Gamma ({{a}_{j}})\Gamma (b){\kern 1pt} \Gamma (c - b)}},\quad j = \overline {\nu + 1,N} . \\ \end{gathered} $Из теоремы 1 с помощью несложных рассуждений могут быть найдены формулы аналитического продолжения функции Лауричеллы в области $\mathbb{V}_{\sigma }^{{N,\nu }}$, определяемые равенством (2.12), для всех $\nu = \overline {0,N} $ и $\sigma \in {{S}_{N}}$, где, напомним, ${{S}_{N}}$ – группа перестановок множества из $N$ элементов. Действительно, учитывая равенство
(2.18)
$F_{D}^{{(N)}}({\mathbf{a}};b,c;{\mathbf{z}}) = F_{D}^{{(N)}}(\sigma ({\mathbf{a}});b,c;\sigma ({\mathbf{z}})),$2.2. Используемые обозначения
Полученные далее в п. 2.4 формулы аналитического продолжения соответствуют случаю, когда расстояния между некоторыми переменными достаточно малы (например, по сравнению с их модулями или с расстояниями до единицы). В связи с этим нам будет удобно модифицировать обозначения для переменных и параметров функции Лауричеллы.
Представим векторный аргумент ${\mathbf{z}} = ({{z}_{1}}, \ldots ,{{z}_{N}})$ функции $F_{D}^{{(N)}}$ в виде объединения $q + 1 \leqslant N$ наборов ${{{\mathbf{z}}}^{{(s)}}}$, $s = \overline {1,q + 1} $:
(2.19)
${\mathbf{z}} = ({{{\mathbf{z}}}^{{(1)}}}, \ldots ,{{{\mathbf{z}}}^{{(q + 1)}}}),\quad {{{\mathbf{z}}}^{{(s)}}}: = (z_{1}^{{(s)}}, \ldots ,z_{{{{p}_{s}}}}^{{(s)}}),\quad s = \overline {1,q + 1} ,$Будем считать, что компоненты вектора ${{{\mathbf{z}}}^{{(s)}}}$, т.е. переменные $z_{j}^{{(s)}}$ с одинаковым верхним индексом, являются “достаточно близкими” в смысле, который будет уточнен ниже в теореме 2 об аналитическом продолжении. Далее для определенности будем предполагать, что векторы ${{{\mathbf{z}}}^{{(s)}}}$ с номерами $s = \overline {1,\nu } $ содержат переменные, близкие к единице, векторы ${{{\mathbf{z}}}^{{(s)}}}$ с номерами $s = \overline {\nu + 1,q} $ составлены из больших по модулю переменных, а вектор переменные, образующие ${{{\mathbf{z}}}^{{(q + 1)}}}$, по модулю меньше единицы, т.е. ${{{\mathbf{z}}}^{{(q + 1)}}} \in \{ {\kern 1pt} {\text{|}}z_{l}^{{(q + 1)}}{\kern 1pt} {\text{|}} < 1,\;l = \overline {1,{{p}_{{q + 1}}}} \} $.
Компоненты векторного параметра ${\mathbf{a}}$ функции Лауричеллы и компоненты мультииндекса ${\mathbf{k}}$ в формуле (1.1) переобозначим соответствующим образом:
(2.21)
$\begin{gathered} {\mathbf{a}} = ({{{\mathbf{a}}}^{{(1)}}}, \ldots ,{{{\mathbf{a}}}^{{(q + 1)}}}),\quad {{{\mathbf{a}}}^{{(s)}}}: = (a_{1}^{{(s)}}, \ldots ,a_{{{{p}_{s}}}}^{{(s)}}), \\ {\mathbf{k}} = ({{{\mathbf{k}}}^{{(1)}}}, \ldots ,{{{\mathbf{k}}}^{{(q + 1)}}}),\quad {{{\mathbf{k}}}^{{(s)}}}: = (k_{1}^{{(s)}}, \ldots ,k_{{{{p}_{s}}}}^{{(s)}}), \\ \end{gathered} $(2.22)
$a_{j}^{{(s)}} = {{a}_{m}},\quad k_{j}^{{(s)}} = {{k}_{m}},\quad m = \sum\limits_{l = 1}^{s - 1} {{{p}_{s}} + j} .$Из формул (2.5) и (2.21) вытекают, например, соотношения
(2.23)
${\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}} = \sum\limits_{l = 1}^{{{p}_{s}}} {a_{l}^{{(s)}}} ,\quad {\text{|}}{\mathbf{k}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}} = \sum\limits_{l = 1}^{{{p}_{s}}} {k_{l}^{{(s)}}} ,\quad \sum\limits_{s = 1}^q {{\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\text{|}}{\kern 1pt} } = {\text{|}}{\mathbf{a}}{\kern 1pt} {\text{|}},\quad \sum\limits_{s = 1}^q {{\text{|}}{\mathbf{k}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}}} = {\text{|}}{\mathbf{k}}{\kern 1pt} {\text{|}},$В данном разделе построены формулы аналитического продолжения функции Лауричеллы $F_{D}^{{(N)}}$ в окрестность гиперплоскостей, определяемых по формуле (1.10), а также их пересечений, точнее, в новых обозначениях (2.19), формулы, справедливые вблизи множества
(2.24)
$\bigcap\limits_{s = 1}^q {{{\mathcal{M}}_{s}}} ,\quad {{\mathcal{M}}_{s}}: = \{ z_{1}^{{(s)}} = \cdots = z_{{{{p}_{s}}}}^{{(s)}}\} ,\quad s = \overline {1,q} ;$2.3. Вспомогательное разложение функции $F_{D}^{{(N)}}$
Используя введенные обозначения (2.19)–(2.23) перепишем представление типа Эйлера (1.7) в следующем виде:
(2.25)
$F_{D}^{{(N)}}{\kern 1pt} ({\mathbf{a}};b,c;{\mathbf{z}}) = \frac{{\Gamma (c)}}{{\Gamma (b)\Gamma (c - b)}}\int\limits_0^1 \frac{{{{t}^{{b - 1}}}{\kern 1pt} {{{(1 - t)}}^{{c - b - 1}}}}}{{\prod\limits_{s = 1}^{q + 1} {\kern 1pt} \prod\limits_{j = 1}^{{{p}_{s}}} \,{{{(1 - tz_{j}^{{(s)}})}}^{{a_{j}^{{(s)}}}}}}}dt.$(2.26)
$z_{j}^{{(s)}} = z_{1}^{{(s)}} + \varepsilon _{j}^{{(s)}},\quad s = \overline {1,q} ,\quad j = \overline {2,{{p}_{s}}} ,$(2.27)
${{(1 - t{\kern 1pt} z_{j}^{{(s)}})}^{{ - a_{j}^{{(s)}}}}} = (1 - t{\kern 1pt} (z_{1}^{{(s)}} + \varepsilon _{j}^{{(s)}}{{))}^{{ - a_{j}^{{(s)}}}}} = (1 - t{\kern 1pt} z_{1}^{{(s)}}{{)}^{{ - a_{j}^{{(s)}}}}}{{\left( {1 - t\frac{{\varepsilon _{j}^{{(s)}}}}{{1 - t{\kern 1pt} z_{1}^{{(s)}}}}} \right)}^{{ - a_{j}^{{(s)}}}}},\quad s = \overline {1,q} ,$(2.28)
${{(1 - t{\kern 1pt} z_{j}^{{(s)}})}^{{ - a_{j}^{{(s)}}}}} = (1 - t{\kern 1pt} z_{1}^{{(s)}}{{)}^{{ - a_{j}^{{(s)}}}}}\sum\limits_{k_{j}^{{(s)}} = 0}^\infty \frac{{(a_{j}^{{(s)}},k_{j}^{{(s)}})}}{{k_{j}^{{(s)}}{\kern 1pt} !}}{{\left( {\frac{t}{{1 - t{\kern 1pt} z_{1}^{{(s)}}}}} \right)}^{{k_{j}^{{(s)}}}}}{{(\varepsilon _{j}^{{(s)}})}^{{k_{j}^{{(s)}}}}},\quad s = \overline {1,q} ,\quad j = \overline {1,{{p}_{s}}} .$(2.29)
${{(1 - t{\kern 1pt} z_{j}^{{(q + 1)}})}^{{ - a_{j}^{{(q + 1)}}}}} = \sum\limits_{k_{j}^{{(q + 1)}} = 0}^\infty \frac{{(a_{j}^{{(q + 1)}},k_{j}^{{(q + 1)}})}}{{k_{j}^{{(q + 1)}}!}}{{(t{\kern 1pt} z_{j}^{{(q + 1)}})}^{{k_{j}^{{(q + 1)}}}}},\quad j = \overline {1,{{p}_{{q + 1}}}} .$(2.30)
$\begin{gathered} \prod\limits_{s = 1}^{q + 1} {\kern 1pt} \prod\limits_{j = 1}^{{{p}_{s}}} \,{{(1 - t{\kern 1pt} z_{j}^{{(s)}})}^{{ - a_{j}^{{(s)}}}}} = \prod\limits_{s = 1}^q \,{{(1 - tz_{1}^{{(s)}})}^{{ - |{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}|}}}\sum\limits_{s = 1}^q \sum\limits_{k_{2}^{{(s)}}, \ldots ,k_{{{{p}_{s}}}}^{{(s)}} = 0}^\infty \sum\limits_{k_{1}^{{(q + 1)}}, \ldots ,k_{{q + 1}}^{{(q + 1)}} = 0}^\infty \left[ {\left( {\prod\limits_{r = 1}^q \prod\limits_{l = 2}^{{{p}_{r}}} \frac{{(a_{l}^{{(r)}},k_{l}^{{(r)}})}}{{k_{l}^{{(r)}}!}}{{{(z_{l}^{{(r)}} - z_{1}^{{(r)}})}}^{{k_{l}^{{(r)}}}}}} \right)} \right. \times \\ \, \times \left. {\left( {\prod\limits_{l = 1}^{{{p}_{{q + 1}}}} \frac{{(a_{l}^{{(q + 1)}},k_{l}^{{(q + 1)}})}}{{k_{l}^{{(q + 1)}}!}}{{{(z_{l}^{{(q + 1)}})}}^{{k_{l}^{{(q + 1)}}}}}} \right)\left( {\prod\limits_{r = 1}^q \,{{{(1 - t{{z}_{r}})}}^{{ - |{\mathbf{k}}_{{2,{{p}_{r}}}}^{{(r)}}|}}}} \right){{t}^{{\sum\nolimits_{r = 1}^q {|{\mathbf{k}}_{{2,{{p}_{r}}}}^{{(r)}}| + |{\mathbf{k}}_{{1,{{p}_{{q + 1}}}}}^{{(q + 1)}}|} }}}} \right]; \\ \end{gathered} $(2.31)
$\begin{gathered} F_{D}^{{(N)}}{\kern 1pt} ({\mathbf{a}};b,c;{\mathbf{z}}) = \sum\limits_{s = 1}^q \,\sum\limits_{k_{2}^{{(s)}}, \ldots ,k_{{{{p}_{s}}}}^{{(s)}} = 0}^\infty \,\sum\limits_{k_{1}^{{(q + 1)}}, \ldots ,k_{{q + 1}}^{{(q + 1)}} = 0}^\infty \left[ {\frac{{\left( {b,\sum\limits_{s = 1}^q \,{\text{|}}{\mathbf{k}}_{{2,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}{\mathbf{k}}_{{1,{{p}_{{q + 1}}}}}^{{(q + 1)}}{\kern 1pt} {\text{|}}} \right)}}{{\left( {c,\sum\limits_{s = 1}^q \,{\text{|}}{\mathbf{k}}_{{2,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}{\mathbf{k}}_{{1,{{p}_{{q + 1}}}}}^{{(q + 1)}}{\kern 1pt} {\text{|}}} \right)}}} \right.\left( {\prod\limits_{r = 1}^q {\kern 1pt} \prod\limits_{l = 2}^{{{p}_{r}}} \frac{{(a_{l}^{{(r)}},k_{l}^{{(r)}})}}{{k_{l}^{{(r)}}!}}{{{(z_{l}^{{(r)}} - z_{1}^{{(r)}})}}^{{k_{l}^{{(r)}}}}}} \right) \times \\ \, \times \left( {\prod\limits_{l = 1}^{{{p}_{{q + 1}}}} \frac{{(a_{l}^{{(q + 1)}},k_{l}^{{(q + 1)}})}}{{k_{l}^{{(q + 1)}}!}}{{{(z_{l}^{{(q + 1)}})}}^{{k_{l}^{{(q + 1)}}}}}} \right)F_{D}^{{(q)}}\left( {\mathop {{\text{|}}{\mathbf{a}}_{{1,{{p}_{1}}}}^{{(1)}}{\text{|}}\; + \;{\text{|}}{\mathbf{k}}_{{2,{{p}_{1}}}}^{{(1)}}{\kern 1pt} {\text{|}}, \ldots ,{\text{|}}{\mathbf{a}}_{{1,{{p}_{q}}}}^{{(q)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}{\mathbf{k}}_{{2,{{p}_{q}}}}^{{(q)}}{\kern 1pt} {\text{|}}{\kern 1pt} ;}\limits_{_{{_{{}}}}} } \right. \\ \left. {\mathop {\left. {b + \sum\limits_{s = 1}^q \,{\text{|}}{\mathbf{k}}_{{2,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}{\mathbf{k}}_{{1,{{p}_{{q + 1}}}}}^{{(q + 1)}}{\kern 1pt} {\text{|}},c + \sum\limits_{s = 1}^q \,{\text{|}}{\mathbf{k}}_{{2,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}{\mathbf{k}}_{{1,{{p}_{{q + 1}}}}}^{{(q + 1)}}{\kern 1pt} {\text{|}}{\kern 1pt} ;\;z_{1}^{{(1)}}, \ldots ,z_{1}^{{(q)}}} \right)}\limits_{_{{_{{_{{_{{_{{}}}}}}}}}}}^{} } \right]; \\ \end{gathered} $(2.32)
${\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}} = \sum\limits_{l = 1}^{{{p}_{s}}} {a_{l}^{{(s)}}} ,\quad {\text{|}}{\mathbf{k}}_{{2,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}} = \sum\limits_{l = 2}^{{{p}_{s}}} {k_{l}^{{(s)}}} ,\quad s = \overline {1,q} ,\quad {\text{|}}{\mathbf{k}}_{{1,{{p}_{{q + 1}}}}}^{{(q + 1)}}{\kern 1pt} {\text{|}} = \sum\limits_{l = 1}^{{{p}_{{q + 1}}}} {k_{l}^{{(q + 1)}}} ,$Для построения формул аналитического продолжения функции $F_{D}^{{(N)}}$ продолжим фигурирующие в представлении (2.31) функции $F_{D}^{{(q)}}$ по переменным $z_{1}^{{(1)}}, \ldots ,z_{1}^{{(q)}}$, применяя теорему 1 (см. п. 2.1).
2.4. Формулы продолжения в окрестность точки ${\mathbf{z}}_{{\nu ,\mu }}^{{(1,\infty ,0)}}$
Введем область ${{\mathbb{O}}^{{N,\nu }}} = {{\mathbb{O}}^{{N,\nu }}}({{p}_{1}}, \ldots ,{{p}_{{q + 1}}})$ как пересечение:
где области $\mathbb{O}_{j}^{{N,\nu }} = \mathbb{O}_{j}^{{N,\nu }}\;({{p}_{1}}, \ldots ,{{p}_{{q + 1}}})$ для $j = \overline {1,\nu } $ определяются по следующим формулам:(2.34)
$\begin{gathered} \mathbb{O}_{j}^{{N,\nu }}: = \{ {\mathbf{z}} \in {{\mathbb{C}}^{N}}:{\text{|}}1 - z_{1}^{{(m)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}z_{1}^{{(m)}} - z_{n}^{{(m)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}z_{l}^{{(s)}} - z_{1}^{{(s)}}{\kern 1pt} {\text{|}} < {\text{|}}1 - z_{1}^{{(s)}}{\kern 1pt} {\text{|}},\;s = \overline {j,\nu } ,\;l = \overline {1,{{p}_{s}}} ;\;m = \overline {1,j - 1} , \\ n = \overline {2,{{p}_{m}}} ;\;{\text{|}}1 - z_{1}^{{(j)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}z_{1}^{{(j)}} - z_{l}^{{(j)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}z_{n}^{{(q + 1)}}{\kern 1pt} {\text{|}} < 1,{\text{|}}{\kern 1pt} l = \overline {1,{{p}_{j}}} ,\;n = \overline {2,{{p}_{{q + 1}}}} ;\;{\text{|}}z_{1}^{{(s)}}{\text{|}} > {\text{|}}z_{1}^{{(s)}} - z_{l}^{{(s)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}z_{n}^{{(q + 1)}}{\kern 1pt} {\text{|}}, \\ l = \overline {1,{{p}_{s}}} ,\;n = \overline {2,{{p}_{{q + 1}}}} ;\;{\text{|arg}}( - z_{1}^{{(s)}}){\kern 1pt} {\text{|}} < \pi ,s = \overline {\nu + 1,q} \} ; \\ \end{gathered} $(2.35)
$\begin{gathered} \mathbb{O}_{j}^{{N,\nu }}: = \{ {\mathbf{z}} \in {{\mathbb{C}}^{N}}:{\text{|}}z_{1}^{{(j)}}{\kern 1pt} {\text{|}} > 1\; + \;{\text{|}}z_{1}^{{(s)}} - 1{\kern 1pt} {\text{|}}\; + \;{\text{|}}z_{l}^{{(s)}} - z_{1}^{{(s)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}z_{1}^{{(j)}} - z_{n}^{{(j)}}{\kern 1pt} {\text{|}},\;s = \overline {1,\nu } ,\;l = \overline {1,{{p}_{s}}} ,\;n = \overline {2,{{p}_{m}}} ; \\ {\text{|}}z_{1}^{{(s)}}{\kern 1pt} {\text{|}} > {\text{|}}z_{1}^{{(j)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}z_{1}^{{(j)}} - z_{n}^{{(j)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}z_{1}^{{(s)}} - z_{l}^{{(s)}}{\kern 1pt} {\text{|}},\;s = \overline {\nu + 1,j - 1} ,\;l = \overline {1,{{p}_{s}}} ,\;n = \overline {2,{{p}_{j}}} ; \\ {\text{|}}z_{1}^{{(j)}}{\kern 1pt} {\text{|}} > {\text{|}}z_{1}^{{(s)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}z_{1}^{{(s)}} - z_{l}^{{(s)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}z_{1}^{{(j)}} - z_{n}^{{(j)}}{\kern 1pt} {\text{|}},\;s = \overline {j + 1,q} ,\;l = \overline {2,{{p}_{s}}} ,\;n = \overline {2,{{p}_{j}}} ;\;{\text{|arg}}( - z_{1}^{{(s)}}){\kern 1pt} {\text{|}} < \pi ,\;s = \overline {\nu + 1,q} \} , \\ \end{gathered} $(2.36)
$\begin{gathered} \mathbb{O}_{0}^{{N,\nu }}: = \{ {\mathbf{z}} \in {{\mathbb{C}}^{N}}:{\text{|}}z_{1}^{{(s)}}{\kern 1pt} {\text{|}} > {\text{|}}z_{1}^{{(s)}} - z_{l}^{{(s)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}z_{n}^{{(q + 1)}}{\kern 1pt} {\text{|}},\;s = \overline {\nu + 1,q} ,\;l = \overline {1,{{p}_{n}}} ,\;n = \overline {1,{{p}_{{q + 1}}}} ; \\ {\text{|}}z_{1}^{{(s)}} - 1{\kern 1pt} {\text{|}}\; + \;{\text{|}}z_{l}^{{(s)}} - z_{1}^{{(s)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}z_{n}^{{(q + 1)}}{\kern 1pt} {\text{|}} < 1,\;s = \overline {1,\nu } ,\;l = \overline {1,{{p}_{s}}} ,\;n = \overline {1,{{p}_{{q + 1}}}} ; \\ {\text{|}}z_{n}^{{(q + 1)}}{\kern 1pt} {\text{|}} < 1,\;n = \overline {1,{{p}_{{q + 1}}}} ;\;{\text{|arg}}( - z_{1}^{{(s)}}){\kern 1pt} {\text{|}} < \pi ,s = \overline {\nu + 1,q} \} . \\ \end{gathered} $Применяя результат теоремы 1 к функциям
(2.37)
$F_{D}^{{(q)}}\left( {\mathop {{\text{|}}{\mathbf{a}}_{{1,{{p}_{1}}}}^{{(1)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}{\mathbf{k}}_{{2,{{p}_{1}}}}^{{(1)}}{\kern 1pt} {\text{|}}, \ldots ,{\text{|}}{\mathbf{a}}_{{1,{{p}_{q}}}}^{{(q)}}{\text{|}}{\kern 1pt} \; + \;{\text{|}}{\mathbf{k}}_{{2,{{p}_{q}}}}^{{(q)}}{\kern 1pt} {\text{|}}{\kern 1pt} ;}\limits_{}^{} } \right.\;\left. {b + \sum\limits_{s = 1}^q \,{\text{|}}{\mathbf{k}}_{{2,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}{\mathbf{k}}_{{1,{{p}_{{q + 1}}}}}^{{(q + 1)}}{\kern 1pt} {\text{|}},\;c + \sum\limits_{s = 1}^q \,{\text{|}}{\mathbf{k}}_{{2,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}{\mathbf{k}}_{{1,{{p}_{{q + 1}}}}}^{{(q + 1)}}{\kern 1pt} {\text{|}};\;z_{1}^{{(1)}}, \ldots ,z_{1}^{{(q)}}} \right),$Теорема 2. Если ни одно из чисел
(2.38)
$\left( {b - \sum\limits_{s = \nu + 1}^j {{\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\text{|}}{\kern 1pt} } } \right),\quad j = \overline {\nu + 1,q} ,\quad \left( {c - b - \sum\limits_{s = 1}^j {{\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}}} } \right),\quad j = \overline {1,\nu } ,$(2.39)
$\begin{array}{*{20}{l}} {F_{D}^{{(N)}}({\mathbf{a}};b,c;{\mathbf{z}}) = \sum\limits_{j = 0}^q {{{B}_{j}}\mathcal{U}_{j}^{{(1,\infty ,0)}}({\mathbf{a}};b,c;{\mathbf{z}})} ,} \end{array}$(2.40)
$\begin{array}{*{20}{l}} {\mathcal{U}_{0}^{{(1,\infty ,0)}}({\mathbf{a}};b,c;{\mathbf{z}}) = \left( {\prod\limits_{s = \nu + 1}^q {\kern 1pt} {{{( - z_{1}^{{(s)}})}}^{{ - |{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}|}}}} \right)\sum\limits_{|{\mathbf{k}}| = 0}^\infty \,{{\Xi }_{0}}({\mathbf{a}};b,c;{\mathbf{k}}){\mathbf{Z}}_{0}^{{\mathbf{k}}},} \end{array}$(2.41)
$\begin{gathered} \mathcal{U}_{j}^{{(1,\infty ,0)}}({\mathbf{a}};b,c;{\mathbf{z}}) = (1 - z_{1}^{{(j)}}{{)}^{{c - \sum\nolimits_{s = 1}^j {|{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}|} - b}}}\left( {\prod\limits_{s = j + 1}^\nu {\kern 1pt} {{{(1 - z_{1}^{{(s)}})}}^{{ - |{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}|}}}} \right)\left( {\prod\limits_{s = \nu + 1}^q {\kern 1pt} {{{( - z_{1}^{{(s)}})}}^{{ - |{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}|}}}} \right) \times \\ \, \times \sum\limits_{|{\mathbf{k}}| = 0}^\infty \,{{\Xi }_{j}}({\mathbf{a}};b,c;{\mathbf{k}}){\mathbf{Z}}_{j}^{{\mathbf{k}}},\quad j = \overline {1,\nu } , \\ \end{gathered} $(2.42)
$\mathcal{U}_{j}^{{(1,\infty ,0)}}({\mathbf{a}};b,c;{\mathbf{z}}) = ( - z_{1}^{{(j)}}{{)}^{{\sum\nolimits_{s = \nu + 1}^{j - 1} {|{{{\mathbf{a}}}_{{1,{{p}_{s}}}}}|} - b}}}\left( {\prod\limits_{s = \nu + 1}^{j - 1} {\kern 1pt} {{{( - z_{1}^{{(s)}})}}^{{ - |{\kern 1pt} {\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}|}}}} \right)\sum\limits_{|{\mathbf{k}}| = 0}^\infty \,{{\Xi }_{j}}({\mathbf{a}};b,c;{\mathbf{k}}){\mathbf{Z}}_{j}^{{\mathbf{k}}},\quad j = \overline {\nu + 1,\;q} ;$(2.43)
$\begin{gathered} {{\Xi }_{0}}({\mathbf{a}};b,c;{\mathbf{k}}): = \frac{{\left( {1 - c + \sum\limits_{s = 1}^q \,{\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}},\sum\limits_{s = \nu + 1}^q {\kern 1pt} k_{1}^{{(s)}}\; - \;{\text{|}}{\mathbf{k}}_{{1,{{p}_{{q + 1}}}}}^{{(q + 1)}}{\kern 1pt} {\text{|}}} \right)}}{{\left( {1 + \sum\limits_{s = 1}^\nu \,{\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}} + b - c,\sum\limits_{s = 1}^\nu \,{\text{|}}{\mathbf{k}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}}} \right)\left( {1 - b + \sum\limits_{s = \nu + 1}^q {\kern 1pt} {\kern 1pt} {\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}},\sum\limits_{s = \nu + 1}^q \,k_{1}^{{(s)}} - \sum\limits_{s = 1}^\nu \,{\text{|}}{\mathbf{k}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}}\; - \;{\text{|}}{\mathbf{k}}_{{1,{{p}_{{q + 1}}}}}^{{(q + 1)}}{\kern 1pt} {\text{|}}} \right)}} \times \\ \, \times \left( {\prod\limits_{s = 1}^q \frac{{({\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}},{\text{|}}{\mathbf{k}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{({\kern 1pt} {\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}},{\text{|}}{\mathbf{k}}_{{2,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}}{\kern 1pt} )k_{1}^{{(s)}}!}}} \right)\left( {\prod\limits_{s = 1}^q {\kern 1pt} \prod\limits_{l = 2}^{{{p}_{s}}} \frac{{(a_{l}^{{(s)}},k_{l}^{{(s)}})}}{{k_{l}^{{(s)}}!}}} \right)\left( {\prod\limits_{l = 1}^{{{p}_{{q + 1}}}} \frac{{(a_{l}^{{(q + 1)}},k_{l}^{{(q + 1)}})}}{{k_{l}^{{(q + 1)}}!}}} \right), \\ \end{gathered} $(2.44)
$\begin{gathered} {{\Xi }_{j}}({\mathbf{a}};b,c;{\mathbf{k}}): = \frac{{\left( {c - \sum\limits_{s = 1}^{j - 1} \,{\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\text{|}} - b,\sum\limits_{s = j}^\nu \,k_{1}^{{(s)}} - \sum\limits_{s = 1}^{j - 1} \,k_{1}^{{(s)}} - \sum\limits_{s = 1}^{j - 1} \,{\text{|}}{\mathbf{k}}_{{2,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}}} \right)}}{{\left( {1 + c - \sum\limits_{s = 1}^j \,{\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}} - b,\sum\limits_{s = j}^\nu \,k_{1}^{{(s)}} - \sum\limits_{s = 1}^{j - 1} \,k_{1}^{{(s)}} - \sum\limits_{s = 1}^j \,{\text{|}}{\mathbf{k}}_{{2,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}}} \right)({\text{|}}{\mathbf{a}}_{{1,{{p}_{j}}}}^{{(j)}}{\kern 1pt} {\text{|}},{\text{|}}{\mathbf{k}}_{{2,{{p}_{j}}}}^{{(j)}}{\kern 1pt} {\text{|}})}} \times \\ \, \times \frac{{\left( {1 + \sum\limits_{s = 1}^q \,{\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}} - c,\sum\limits_{s = \nu + 1}^q k_{1}^{{(s)}}\; - \;{\text{|}}{\mathbf{k}}_{{1,{{p}_{{q + 1}}}}}^{{(q + 1)}}{\kern 1pt} {\text{|}}} \right)}}{{\left( {1 + \sum\limits_{s = 1}^q \,{\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\text{|}} - c,\sum\limits_{s = \nu + 1}^q {\kern 1pt} k_{1}^{{(s)}}\; - \;{\text{|}}{\mathbf{k}}_{{1,{{p}_{{q + 1}}}}}^{{(q + 1)}}{\kern 1pt} {\text{|}} - k_{1}^{{(j)}}} \right)k_{1}^{{(j)}}!}}\prod\limits_{\begin{gathered} s = 1s\not { = }j \\ \end{gathered} }^q \frac{{({\kern 1pt} {\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}},{\text{|}}{\mathbf{k}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{({\kern 1pt} {\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}},{\text{|}}{\mathbf{k}}_{{2,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\kern 1pt} {\text{|}})k_{1}^{{(s)}}!}} \times \\ \, \times \left( {\prod\limits_{s = 1}^q {\kern 1pt} \prod\limits_{l = 2}^{{{p}_{s}}} \frac{{(a_{l}^{{(s)}},k_{l}^{{(s)}})}}{{k_{l}^{{(s)}}!}}} \right)\left( {\prod\limits_{l = 1}^{{{p}_{{q + 1}}}} \frac{{(a_{l}^{{(q + 1)}},k_{l}^{{(q + 1)}})}}{{k_{l}^{{(q + 1)}}!}}} \right),\quad j = \overline {1,\nu } , \\ \end{gathered} $(2.45)
$\begin{gathered} {{\Xi }_{j}}({\mathbf{a}};b,c;{\mathbf{k}}): = \frac{{\left( {b - \sum\limits_{s = \nu + 1}^{j - 1} {\kern 1pt} {\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}},\sum\limits_{s = 1}^\nu \,{\text{|}}{\mathbf{k}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}} + \sum\limits_{s = j}^q \,{\text{|}}{\mathbf{k}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}} - \sum\limits_{s = \nu + 1}^{j - 1} {\kern 1pt} k_{1}^{{(s)}}\; + \;{\text{|}}{\mathbf{k}}_{{1,{{p}_{{q + 1}}}}}^{{(q + 1)}}{\kern 1pt} {\text{|}}} \right)}}{{\left( {1 + b - \sum\limits_{s = \nu + 1}^j {\kern 1pt} {\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}},\sum\limits_{s = 1}^\nu \,{\text{|}}{\mathbf{k}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}} + \sum\limits_{s = j + 1}^q {\kern 1pt} {\text{|}}{\mathbf{k}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}} - \sum\limits_{s = \nu + 1}^{j - 1} {\kern 1pt} k_{1}^{{(s)}} + k_{1}^{{(j)}}\; + \;{\text{|}}{\mathbf{k}}_{{1,{{p}_{{q + 1}}}}}^{{(q + 1)}}{\kern 1pt} {\text{|}}} \right)({\kern 1pt} {\text{|}}{\mathbf{a}}_{{1,{{p}_{j}}}}^{{(j)}}{\kern 1pt} {\text{|}},{\text{|}}{\mathbf{k}}_{{2,{{p}_{j}}{\kern 1pt} }}^{{(j)}}{\text{|}}{\kern 1pt} )}} \times \\ \, \times \frac{{(1 - c + \sum\limits_{s = 1}^\nu \,{\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\kern 1pt} {\text{|}} + b,\sum\limits_{s = 1}^\nu \,{\text{|}}{\mathbf{k}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\kern 1pt} {\text{|}} + k_{1}^{{(j)}})}}{{\left( {1 - c + \sum\limits_{s = 1}^\nu \,{\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}} + b,\sum\limits_{s = 1}^\nu \,{\text{|}}{\mathbf{k}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}}} \right)k_{1}^{{(j)}}!}}\prod\limits_{\begin{gathered} s = 1s\not { = }j \\ \end{gathered} }^q \frac{{({\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}},{\text{|}}{\mathbf{k}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{({\kern 1pt} {\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}},{\text{|}}{\mathbf{k}}_{{2,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}}{\kern 1pt} )k_{1}^{{(s)}}!}} \times \\ \, \times \left( {\prod\limits_{s = 1}^q {\kern 1pt} \prod\limits_{l = 2}^{{{p}_{s}}} \frac{{(a_{l}^{{(s)}},k_{l}^{{(s)}})}}{{k_{l}^{{(s)}}!}}} \right)\left( {\prod\limits_{l = 1}^{{{p}_{{q + 1}}}} \frac{{(a_{l}^{{(q + 1)}},k_{l}^{{(q + 1)}})}}{{k_{l}^{{(q + 1)}}!}}} \right),\quad j = \overline {\nu + 1,q} . \\ \end{gathered} $(2.46)
$\begin{gathered} \mathcal{Z}_{0}^{{(s)}}: = (z_{1}^{{(s)}} - 1,z_{2}^{{(s)}} - z_{1}^{{(s)}}, \ldots ,z_{{{{p}_{s}}}}^{{(s)}} - z_{1}^{{(s)}}),\quad s = \overline {1,\nu } , \\ \mathcal{Z}_{0}^{{(s)}}: = \left( {\frac{1}{{z_{1}^{{(s)}}}},\frac{{z_{1}^{{(s)}} - z_{2}^{{(s)}}}}{{z_{1}^{{(s)}}}}, \ldots ,\frac{{z_{1}^{{(s)}} - z_{{{{p}_{s}}}}^{{(s)}}}}{{z_{1}^{{(s)}}}}} \right),\quad s = \overline {\nu + 1,q} , \\ \mathcal{Z}_{0}^{{(q + 1)}}: = (z_{1}^{{(q + 1)}}, \ldots ,z_{{{{p}_{{q + 1}}}}}^{{(q + 1)}}), \\ \end{gathered} $(2.47)
$\begin{gathered} \mathcal{Z}_{j}^{{(j)}}: = \left( {1 - z_{1}^{{(j)}},\frac{{z_{1}^{{(j)}} - z_{2}^{{(j)}}}}{{1 - z_{1}^{{(j)}}}}, \ldots ,\frac{{z_{1}^{{(j)}} - z_{{{{p}_{j}}}}^{{(j)}}}}{{1 - z_{1}^{{(j)}}}}} \right), \\ \mathcal{Z}_{j}^{{(s)}}: = \left( {\frac{{1 - z_{1}^{{(j)}}}}{{1 - z_{1}^{{(s)}}}},\frac{{z_{2}^{{(s)}} - z_{1}^{{(s)}}}}{{1 - z_{1}^{{(s)}}}}, \ldots ,\frac{{z_{{{{p}_{s}}}}^{{(s)}} - z_{1}^{{(s)}}}}{{1 - z_{1}^{{(s)}}}}} \right),\quad s = \overline {j + 1,\nu } , \\ \end{gathered} $(2.48)
$\mathcal{Z}_{j}^{{(j)}}: = \left( {\frac{1}{{z_{1}^{{(j)}}}},\frac{{z_{1}^{{(j)}} - z_{2}^{{(j)}}}}{{z_{1}^{{(j)}}}}, \ldots ,\frac{{z_{1}^{{(j)}} - z_{{{{p}_{j}}}}^{{(j)}}}}{{z_{1}^{{(j)}}}}} \right),$(2.49)
${{B}_{j}} = \frac{{\Gamma (c)\Gamma (c - \sum\limits_{s = 1}^{j - 1} \,{\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}} - b)\Gamma \left( {\sum\limits_{s = 1}^j \,{\text{|}}{\mathbf{a}}_{{1,{{p}_{s}}}}^{{(s)}}{\kern 1pt} {\text{|}} + b - c} \right)}}{{\Gamma ({\kern 1pt} {\text{|}}{\mathbf{a}}_{{1,{{p}_{j}}}}^{{(j)}}{\kern 1pt} {\text{|}}{\kern 1pt} )\Gamma (b){\kern 1pt} \Gamma (c - b)}},\quad j = \overline {1,\nu } ,$Области сходимости представлений вида (2.39) для функции Лауричеллы установлены с помощью подхода [1]. В том, что функции $\mathcal{U}_{j}^{{(1,\infty ,0)}}$, $j = \overline {0,q} $, являются решениями системы (1.8), можно убедиться непосредственной подстановкой (2.40)–(2.42) в (1.8). Используя соотношение симметрии (2.18), несложно получить формулы аналитического продолжения в области, получаемые из (2.33) с помощью соответствующих симметрий.
Представления функции Лауричеллы в виде экспоненциально сходящихся рядов, которые устанавливают теоремы 1, 2, позволяют качественно исследовать и эффективно вычислять интегралы типа Эйлера (1.8) во всем пространстве ${{\mathbb{C}}^{N}}$, в том числе в сложных случаях “кроудинга” переменных, т.е. вблизи произвольных пересечений гиперплоскостей (2.24). Отметим еще, что возникающие в теоремах 1, 2 ряды (2.8)–(2.10) и (2.40)–(2.42), через которые выражаются решения системы (1.8), принадлежат классу Горна, поскольку, как нетрудно увидеть, соответствующие коэффициенты удовлетворяют свойству (1.25).
3. ПРИМЕРЫ ПРИМЕНЕНИЯ ТЕОРЕМЫ 2 ДЛЯ СЛУЧАЯ ТРЕХ ПЕРЕМЕННЫХ
В данном разделе продемонстрировано применение теоремы 2 к функции $F_{D}^{{(3)}}$, определяемой в поликруге ${{\mathbb{U}}^{3}} = \{ {\kern 1pt} {\text{|}}{{z}_{j}}{\kern 1pt} {\text{|}} < 1,j = 1,2,3\} $ с помощью гипергеометрического ряда
(3.1)
$F_{D}^{{(3)}}({{a}_{1}},{{a}_{2}},{{a}_{3}};b,{\kern 1pt} c;{{z}_{1}},{{z}_{2}},{{z}_{3}}) = \sum\limits_{{{k}_{1}},{{k}_{2}},{{k}_{3}} = 0}^\infty \frac{{{{{(b)}}_{{{{k}_{1}} + {{k}_{2}} + {{k}_{3}}}}}{{{({{a}_{1}})}}_{{{{k}_{1}}}}}{{{({{a}_{2}})}}_{{{{k}_{2}}}}}{{{({{a}_{3}})}}_{{{{k}_{3}}}}}}}{{{{{(c)}}_{{{{k}_{1}} + {{k}_{2}} + {{k}_{3}}}}}{{k}_{1}}!{{k}_{2}}!{{k}_{3}}!}}z_{1}^{{{{k}_{1}}}}z_{2}^{{{{k}_{2}}}}z_{3}^{{{{k}_{3}}}}$(3.2)
$F_{D}^{{(3)}}({{a}_{1}},{{a}_{2}},{{a}_{3}};b,c;{{z}_{1}},{{z}_{2}},{{z}_{3}}) = \frac{{\Gamma (c)}}{{\Gamma (b){\kern 1pt} \Gamma (c - b)}}\int\limits_0^1 \,{{t}^{{b - 1}}}{\kern 1pt} {{(1 - t)}^{{c - b - 1}}}{{(1 - t{{z}_{1}})}^{{ - {{a}_{1}}}}}{{(1 - t{{z}_{2}})}^{{ - {{a}_{2}}}}}{{(1 - t{{z}_{3}})}^{{ - {{a}_{3}}}}}dt.$Напомним, что формулы аналитического продолжения в окрестность точки $(1,\infty ,\infty )$ были представлены во Введении. Далее в пп. 3.1, 3.2 будут построены формулы аналитического продолжения в окрестность точек $(1,1,\infty )$, $(\infty ,\infty ,0)$ и $(1,1,0)$, адекватно представляющие функцию (3.1) и позволяющие эффективно вычислять интеграл (3.2) вблизи гиперплоскостей вида $\{ {{z}_{k}} = {{z}_{l}}\} $ и их пересечений.
3.1. Продолжение функции $F_{D}^{{(3)}}$ в окрестность точки $(1,1,\infty )$, соответствующее ${{z}_{1}} = {{z}_{2}}$
Предположим, что переменные ${{z}_{1}},\;{{z}_{2}},\;{{z}_{3}}$ функции Лауричеллы $F_{D}^{{(3)}}$ образуют две группы, в первую из которых входят ${{z}_{1}}$ и ${{z}_{2}}$, а во вторую – только ${{z}_{3}}$. Тогда согласно (2.19), (2.20) используемые в теореме 0 числа $q$, ${{p}_{s}}$, а также параметры и переменные функции Лауричеллы (3.1), (3.2) определяются следующими соотношениями:
(3.3)
$\begin{gathered} q = 2,\quad \nu = 1,\quad {{p}_{1}} = 2,\quad {{p}_{2}} = 1,\quad {{p}_{3}} = 0,\quad z_{1}^{{(1)}} = {{z}_{1}},\quad z_{2}^{{(1)}} = {{z}_{2}},\quad z_{1}^{{(2)}} = {{z}_{3}}, \\ a_{1}^{{(1)}} = {{a}_{1}},\quad a_{2}^{{(1)}} = {{a}_{2}},\quad a_{1}^{{(2)}} = {{a}_{3}},\quad k_{1}^{{(1)}} = {{k}_{1}},\quad k_{2}^{{(1)}} = {{k}_{2}},\quad k_{1}^{{(2)}} = {{k}_{3}}. \\ \end{gathered} $Применяя теорему 2, построим формулу продолжения функции $F_{D}^{{(3)}}$ в окрестность гиперплоскости
для случая переменных ${{z}_{1}},\;{{z}_{2}}$, близких к единице, и больших по модулю переменных ${{z}_{3}}$. Подставляя (3.3) в (2.43)–(2.45), находим выражения для коэффициентов рядов (2.40)–(2.42):(3.5)
${{\Xi }_{0}}({\mathbf{a}};b,c;{\mathbf{k}}) = \frac{{{{{(1 - c + {{a}_{1}} + {{a}_{2}} + {{a}_{3}})}}_{{{{k}_{3}}}}}{{{({{a}_{1}} + {{a}_{2}})}}_{{{{k}_{1}} + {{k}_{2}}}}}{{{({{a}_{2}})}}_{{{{k}_{2}}}}}{{{({{a}_{3}})}}_{{{{k}_{3}}}}}}}{{{{{(1 + {{a}_{1}} + {{a}_{2}} + b - c)}}_{{{{k}_{1}} + {{k}_{2}}}}}{{{(1 - b + {{a}_{3}})}}_{{{{k}_{3}} - {{k}_{1}} - {{k}_{2}}}}}{{{({{a}_{1}} + {{a}_{2}})}}_{{{{k}_{2}}}}}{{k}_{1}}!{{k}_{2}}!{{k}_{3}}!}},$(3.6)
${{\Xi }_{1}}({\mathbf{a}};b,c;{\mathbf{k}}) = \frac{{{{{(c - b)}}_{{{{k}_{1}}}}}{{{(1 + {{a}_{1}} + {{a}_{2}} + {{a}_{3}} - c)}}_{{{{k}_{3}}}}}{{{({{a}_{2}})}}_{{{{k}_{2}}}}}{{{({{a}_{3}})}}_{{{{k}_{3}}}}}}}{{{{{(1 + c - {{a}_{1}} - {{a}_{2}} - b)}}_{{{{k}_{1}} - {{k}_{2}}}}}{{{({{a}_{1}} + {{a}_{2}})}}_{{{{k}_{2}}}}}{{{(1 + {{a}_{1}} + {{a}_{2}} + {{a}_{3}} - c)}}_{{{{k}_{3}} - {{k}_{1}}}}}{{k}_{1}}!{{k}_{2}}!{{k}_{3}}!}}.$(3.7)
${{\Xi }_{2}}({\mathbf{a}};b,c;{\mathbf{k}}) = \frac{{{{{(b)}}_{{{{k}_{1}} + {{k}_{2}} + {{k}_{3}}}}}{{{(1 - c + {{a}_{1}} + {{a}_{2}} + b)}}_{{{{k}_{1}} + {{k}_{2}} + {{k}_{3}}}}}{{{({{a}_{1}} + {{a}_{2}})}}_{{{{k}_{1}} + {{k}_{2}}}}}{{{({{a}_{2}})}}_{{{{k}_{2}}}}}}}{{{{{(1 + b - {{a}_{3}})}}_{{{{k}_{1}} + {{k}_{2}} + {{k}_{3}}}}}{{{(1 - c + {{a}_{1}} + {{a}_{2}} + b)}}_{{{{k}_{1}} + {{k}_{2}}}}}{{{({{a}_{1}} + {{a}_{2}})}}_{{{{k}_{2}}}}}{{k}_{1}}!{{k}_{2}}!{{k}_{3}}!}}.$(3.8)
$\begin{gathered} Z_{0}^{{(1)}} = ({{z}_{1}} - 1,{{z}_{2}} - {{z}_{1}}),\quad Z_{0}^{{(2)}} = \left( {\frac{1}{{{{z}_{3}}}}} \right),\quad Z_{1}^{{(1)}} = \left( {1 - {{z}_{1}},\frac{{{{z}_{1}} - {{z}_{2}}}}{{1 - {{z}_{1}}}}} \right),\quad Z_{1}^{{(2)}} = \left( {\frac{1}{{{{z}_{3}}}}} \right), \\ Z_{2}^{{(1)}} = \left( {\frac{{{{z}_{1}} - 1}}{{{{z}_{3}}}},\frac{{{{z}_{2}} - {{z}_{1}}}}{{{{z}_{3}}}}} \right),\quad Z_{2}^{{(2)}} = \left( {\frac{1}{{{{z}_{3}}}}} \right), \\ \end{gathered} $(3.9)
${{B}_{0}} = \frac{{\Gamma (c)\Gamma (c - b - {{a}_{1}} - {{a}_{2}})\Gamma (b - {{a}_{3}})}}{{\Gamma (b)\Gamma (c - {{a}_{1}} - {{a}_{2}} - {{a}_{3}})\Gamma (c - b)}},\quad {{B}_{1}} = \frac{{\Gamma (c)\Gamma ({{a}_{1}} + {{a}_{2}} + b - c)}}{{\Gamma ({{a}_{1}} + {{a}_{2}})\Gamma (b)}},\quad {{B}_{2}} = \frac{{\Gamma (c)\Gamma ({{a}_{3}} - b)}}{{\Gamma ({{a}_{1}} + {{a}_{2}})\Gamma (c - b)}}.$Далее, учитывая соотношения (3.5)–(3.9), из теоремы 2 получаем следующее утверждение, позволяющее аналитически продолжить функцию Лауричеллы $F_{D}^{{(3)}}$ в окрестность особой гиперплоскости (3.4), т.е. в ситуации кроудинга переменных ${{z}_{1}},\;{{z}_{2}}$ для случая, когда они близки к единице, а ${\text{|}}{{z}_{3}}{\text{|}}$ – достаточно большая величина.
Теорема 3. Если ни одно из чисел $c - b - {{a}_{1}} - {{a}_{2}}$ и $b - {{a}_{3}}$ не является целым, то в области
(3.10)
$\{ ({{z}_{1}},{{z}_{2}},{{z}_{3}}) \in {{\mathbb{C}}^{3}}:{\text{|}}{{z}_{1}} - {{z}_{2}}{\kern 1pt} {\text{|}} < {\text{|}}1 - {{z}_{1}}{\kern 1pt} {\text{|}} < 1,\;{\text{|}}{{z}_{3}}{\kern 1pt} {\text{|}} > 1\; + \;{\text{|}}1 - {{z}_{1}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}{{z}_{1}} - {{z}_{2}}{\kern 1pt} {\text{|}}{\kern 1pt} ;\;{\text{|arg}}(1 - {{z}_{1}}){\kern 1pt} {\text{|}} < \pi ,\;{\text{|arg}}( - {{z}_{3}}){\kern 1pt} {\text{|}} < \pi \} $3.2. Продолжение функции $F_{D}^{{(3)}}$ в окрестность точек $(\infty ,\infty ,0)$ и $(1,1,0)$, соответствующее ${{z}_{1}} = {{z}_{2}}$
Рассмотрим продолжение в окрестность точки $(\infty ,\infty ,0)$ и предположим, что расстояние между переменными ${{z}_{1}},\;{{z}_{2}}$ функции Лауричеллы $F_{D}^{{(3)}}$ мало по сравнению с величинами ${\text{|}}{{z}_{1}}{\text{|}}$ и ${\text{|}}{{z}_{2}}{\text{|}}$. Тогда согласно (2.19), (2.20) используемые в теореме 2 числа $q$, $\nu $, ${{p}_{s}}$, а также параметры и переменные функции Лауричеллы (3.1), (3.2) определяются равенствами
(3.11)
$\begin{gathered} q = 1,\quad \nu = 0,\quad {{p}_{1}} = 2,\quad {{p}_{2}} = 1,\quad z_{1}^{{(1)}} = {{z}_{1}},\quad z_{2}^{{(1)}} = {{z}_{2}},\quad z_{1}^{{(2)}} = {{z}_{3}}, \\ a_{1}^{{(1)}} = {{a}_{1}},\quad a_{2}^{{(1)}} = {{a}_{2}},\quad a_{1}^{{(2)}} = {{a}_{3}},\quad k_{1}^{{(1)}} = {{k}_{1}},\quad k_{2}^{{(1)}} = {{k}_{2}},\quad k_{1}^{{(2)}} = {{k}_{3}}. \\ \end{gathered} $Теорема 4. Если числo ${{a}_{1}} + {{a}_{2}} - b$ не является целым, то аналитическое продолжение ряда (3.1), определяющего функцию Лауричеллы $F_{D}^{{(3)}}$, в область
(3.12)
$\{ ({{z}_{1}},{{z}_{2}},{{z}_{3}}) \in {{\mathbb{C}}^{3}}:{\text{|}}{{z}_{1}}{\text{|}} > 1\; + \;{\text{|}}{{z}_{1}} - {{z}_{2}}{\kern 1pt} {\text{|}},\;{\text{|}}{{z}_{3}}{\kern 1pt} {\text{|}} < 1,\;{\text{|arg}}( - {{z}_{1}}){\kern 1pt} {\text{|}} < \pi \} $Построим формулу продолжения в окрестность точки $(1,1,0)$ в предположении, что расстояние между переменными ${{z}_{1}},\;{{z}_{2}}$ функции Лауричеллы $F_{D}^{{(3)}}$ достаточно мало. Cогласно (2.19), (2.20) используемые в теореме 2 числа $q$, $\nu $, ${{p}_{s}}$, а также параметры и переменные функции Лауричеллы (3.1), (3.2) определяются равенствами
(3.13)
$\begin{gathered} q = 1,\quad \nu = 1,\quad {{p}_{1}} = 2,\quad {{p}_{2}} = 1,\quad z_{1}^{{(1)}} = {{z}_{1}},\quad z_{2}^{{(1)}} = {{z}_{2}},\quad z_{1}^{{(2)}} = {{z}_{3}}, \\ a_{1}^{{(1)}} = {{a}_{1}},\quad a_{2}^{{(1)}} = {{a}_{2}},\quad a_{1}^{{(2)}} = {{a}_{3}},\quad k_{1}^{{(1)}} = {{k}_{1}},\quad k_{2}^{{(1)}} = {{k}_{2}},\quad k_{1}^{{(2)}} = {{k}_{3}}. \\ \end{gathered} $Теорема 5. Если числo $c - {{a}_{1}} - {{a}_{2}} - b$ не является целым, то аналитическое продолжение ряда (3.1), определяющего функцию Лауричеллы $F_{D}^{{(3)}}$, в область
(3.14)
$\{ ({{z}_{1}},{{z}_{2}},{{z}_{3}}) \in {{\mathbb{C}}^{3}}:{\text{|}}{{z}_{1}} - {{z}_{2}}{\kern 1pt} {\text{|}} < {\text{|}}1 - {{z}_{1}}{\kern 1pt} {\text{|}},\;{\text{|}}1 - {{z}_{1}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}{{z}_{1}} - {{z}_{2}}{\kern 1pt} {\text{|}}\; + \;{\text{|}}{{z}_{3}}{\kern 1pt} {\text{|}} < 1,\;{\text{|arg}}(1 - {{z}_{1}}){\kern 1pt} {\text{|}} < \pi \} $Представленные в теоремах 3–5 формулы позволяют аналитически продолжить ряд (3.1) соответственно в области (3.10), (3.12), (3.14) и дают эффективный алгоритм для вычисления интеграла (3.2), когда аргумент $({{z}_{1}},{{z}_{2}},{{z}_{3}})$ принимает значения в этих областях.
4. ПРИМЕРЫ ПРИМЕНЕНИЯ ТЕОРЕМЫ 2 ДЛЯ СЛУЧАЯ ЧЕТЫРЕХ ПЕРЕМЕННЫХ
В данном разделе продемонстрировано применение теоремы 2 к функции $F_{D}^{{(4)}}$, определяемой в поликруге ${{\mathbb{U}}^{4}} = \{ {\text{|}}{{z}_{j}}{\text{|}} < 1,j = \overline {1,4} \} $ с помощью гипергеометрического ряда
(4.1)
$F_{D}^{{(4)}}({{a}_{1}}, \ldots ,{{a}_{4}};b,c;{{z}_{1}}, \ldots ,{{z}_{4}}) = \sum\limits_{{{k}_{1}},{{k}_{2}},{{k}_{3}} = 0}^\infty \frac{{{{{(b)}}_{{{{k}_{1}} + \cdots + {{k}_{4}}}}}{{{({{a}_{1}})}}_{{{{k}_{1}}}}}{{{({{a}_{2}})}}_{{{{k}_{2}}}}}{{{({{a}_{3}})}}_{{{{k}_{3}}}}}{{{({{a}_{4}})}}_{{{{k}_{4}}}}}}}{{{{{(c)}}_{{{{k}_{1}} + \cdots + {{k}_{4}}}}}{{k}_{1}}!{{k}_{2}}!{{k}_{3}}!{{k}_{4}}!}}z_{1}^{{{{k}_{1}}}}z_{2}^{{{{k}_{2}}}}z_{3}^{{{{k}_{3}}}}z_{4}^{{{{k}_{4}}}},$(4.2)
$F_{D}^{{(4)}}({{a}_{1}}, \ldots ,{{a}_{4}};b,c;{{z}_{1}}, \ldots ,{{z}_{4}}) = \frac{{\Gamma (c)}}{{\Gamma (b)\Gamma (c - b)}}\int\limits_0^1 \,{{t}^{{b - 1}}}{\kern 1pt} {{(1 - t)}^{{c - b - 1}}}{\kern 1pt} \prod\limits_{j = 1}^4 {{{{(1 - t{{z}_{j}})}}^{{ - {{a}_{j}}}}}dt} .$4.1. Продолжение функции $F_{D}^{{(4)}}$ в окрестность точки $(1,1,\infty ,\infty )$, соответствующее ${{z}_{1}} = {{z}_{2}}$ и ${{z}_{3}} = {{z}_{4}}$
Предположим, что переменные ${{z}_{1}},\;{{z}_{2}},\;{{z}_{3}},\;{{z}_{4}}$ функции Лауричеллы $F_{D}^{{(4)}}$ образуют две группы, в первую из которых входят ${{z}_{1}}$ и ${{z}_{2}}$, а во вторую – ${{z}_{3}}$ и ${{z}_{4}}$. Тогда согласно (2.19), (2.20) используемые в теореме 2 числа $q$, ${{p}_{s}}$, а также параметры и переменные функции Лауричеллы (3.1), (3.2) определяются следующими соотношениями:
(4.3)
$\begin{gathered} q = 2,\quad \nu = 1,\quad {{p}_{1}} = {{p}_{2}} = 2,\quad {{p}_{3}} = 0,\quad z_{1}^{{(1)}} = {{z}_{1}},\quad z_{2}^{{(1)}} = {{z}_{2}},\quad z_{1}^{{(2)}} = {{z}_{3}},\quad z_{2}^{{(2)}} = {{z}_{4}}, \\ a_{1}^{{(1)}} = {{a}_{1}},\quad a_{2}^{{(1)}} = {{a}_{2}},\quad a_{1}^{{(2)}} = {{a}_{3}},\quad a_{2}^{{(2)}} = {{a}_{4}},\quad k_{1}^{{(1)}} = {{k}_{1}},\quad k_{2}^{{(1)}} = {{k}_{2}},\quad k_{1}^{{(2)}} = {{k}_{3}},\quad k_{2}^{{(2)}} = {{k}_{4}}. \\ \end{gathered} $Применяя теорему 2, построим формулу продолжения функции $F_{D}^{{(3)}}$, справедливую вблизи гиперплоскостей
(4.4)
${{\mathcal{M}}_{{1,2}}}: = \{ {{z}_{1}} = {{z}_{2}}\} ,\quad {{\mathcal{M}}_{{3,4}}}: = \{ {{z}_{3}} = {{z}_{4}}\} ,$(4.5)
${{\Xi }_{0}}({\mathbf{a}};b,c;{\mathbf{k}}) = \frac{{{{{\left( {1 - c + \sum\limits_{s = 1}^4 \,{{a}_{s}}} \right)}}_{{{{k}_{3}}}}}{{{({{a}_{1}} + {{a}_{2}})}}_{{{{k}_{1}} + {{k}_{2}}}}}{{{({{a}_{3}} + {{a}_{4}})}}_{{{{k}_{3}} + {{k}_{4}}}}}{{{({{a}_{2}})}}_{{{{k}_{2}}}}}{{{({{a}_{4}})}}_{{{{k}_{4}}}}}}}{{{{{(1 + {{a}_{1}} + {{a}_{2}} + b - c)}}_{{{{k}_{1}} + {{k}_{2}}}}}{{{(1 - b + {{a}_{3}} + {{a}_{4}})}}_{{{{k}_{3}} - {{k}_{1}} - {{k}_{2}}}}}{{{({{a}_{1}} + {{a}_{2}})}}_{{{{k}_{2}}}}}{{{({{a}_{3}} + {{a}_{4}})}}_{{{{k}_{4}}}}}{{k}_{1}}!{{k}_{2}}!{{k}_{3}}!{{k}_{4}}!}},$(4.6)
${{\Xi }_{1}}({\mathbf{a}};b,c;{\mathbf{k}}) = \frac{{{{{(c - b)}}_{{{{k}_{1}}}}}{{{(1 + \sum\limits_{s = 1}^4 {{{a}_{s}} - c} )}}_{{{{k}_{3}}}}}{{{({{a}_{3}} + {{a}_{4}})}}_{{{{k}_{3}} + {{k}_{4}}}}}{{{({{a}_{2}})}}_{{{{k}_{2}}}}}{{{({{a}_{4}})}}_{{{{k}_{4}}}}}}}{{{{{(1 + c - {{a}_{1}} - {{a}_{2}} - b)}}_{{{{k}_{1}} - {{k}_{2}}}}}{{{({{a}_{1}} + {{a}_{2}})}}_{{{{k}_{2}}}}}{{{\left( {1 + \sum\limits_{s = 1}^4 \,{{a}_{s}} - c} \right)}}_{{{{k}_{3}} - {{k}_{1}}}}}{{k}_{1}}!{{k}_{2}}!{{k}_{3}}!{{k}_{4}}!}},$(4.7)
${{\Xi }_{2}}({\mathbf{a}};b,c;{\mathbf{k}}) = \frac{{{{{(b)}}_{{\sum\nolimits_{s = 1}^4 {{{k}_{s}}} }}}{{{(1 - c + {{a}_{1}} + {{a}_{2}} + b)}}_{{{{k}_{1}} + {{k}_{2}} + {{k}_{3}}}}}{{{({{a}_{1}} + {{a}_{2}})}}_{{{{k}_{1}} + {{k}_{2}}}}}{{{({{a}_{2}})}}_{{{{k}_{2}}}}}{{{({{a}_{4}})}}_{{{{k}_{4}}}}}}}{{{{{(1 + b - {{a}_{3}} - {{a}_{4}})}}_{{{{k}_{1}} + {{k}_{2}} + {{k}_{3}}}}}{{{({{a}_{3}} + {{a}_{4}})}}_{{{{k}_{4}}}}}{{{(1 - c + {{a}_{1}} + {{a}_{2}} + b)}}_{{{{k}_{1}} + {{k}_{2}}}}}{{{({{a}_{1}} + {{a}_{2}})}}_{{{{k}_{2}}}}}{{k}_{1}}!{{k}_{2}}!{{k}_{3}}!{{k}_{4}}!}}.$(4.8)
$\begin{gathered} Z_{0}^{{(1)}} = ({{z}_{1}} - 1,{{z}_{2}} - {{z}_{1}}),\quad Z_{0}^{{(2)}} = \left( {\frac{1}{{{{z}_{3}}}},\frac{{{{z}_{3}} - {{z}_{4}}}}{{{{z}_{3}}}}} \right),\quad Z_{1}^{{(1)}} = \left( {1 - {{z}_{1}},\frac{{{{z}_{1}} - {{z}_{2}}}}{{1 - {{z}_{1}}}}} \right), \\ Z_{1}^{{(2)}} = \left( {\frac{1}{{{{z}_{3}}}},\frac{{{{z}_{3}} - {{z}_{4}}}}{{{{z}_{3}}}}} \right),\quad Z_{2}^{{(1)}} = \left( {\frac{{{{z}_{1}} - 1}}{{{{z}_{3}}}},\frac{{{{z}_{2}} - {{z}_{1}}}}{{{{z}_{3}}}}} \right),\quad Z_{2}^{{(2)}} = \left( {\frac{1}{{{{z}_{3}}}},\frac{{{{z}_{3}} - {{z}_{4}}}}{{{{z}_{3}}}}} \right), \\ \end{gathered} $(4.9)
$\begin{gathered} {{B}_{0}} = \frac{{\Gamma (c)\Gamma (c - b - {{a}_{1}} - {{a}_{2}})\Gamma (b - {{a}_{3}} - {{a}_{4}})}}{{\Gamma (b)\Gamma (c - \sum\limits_{s = 1}^4 {{a}_{s}})\Gamma (c - b)}}, \\ {{B}_{1}} = \frac{{\Gamma (c)\Gamma ({{a}_{1}} + {{a}_{2}} + b - c)}}{{\Gamma ({{a}_{1}} + {{a}_{2}})\Gamma (b)}},\quad {{B}_{2}} = \frac{{\Gamma (c)\Gamma ({{a}_{3}} + {{a}_{4}} - b)}}{{\Gamma ({{a}_{3}} + {{a}_{4}})\Gamma (c - b)}}. \\ \end{gathered} $Далее, учитывая соотношения (4.3)–(4.9), из теоремы 2 получаем следующее утверждение, позволяющее аналитически продолжить функцию Лауричеллы $F_{D}^{{(3)}}$ в окрестность пересечения особых гиперплоскостей (4.4), т.е. в ситуации кроудинга пар переменных ${{z}_{1}},\;{{z}_{2}}$ и ${{z}_{3}},\;{{z}_{4}}$, для случая близких к единице ${{z}_{1}}$, ${{z}_{2}}$ и больших по модулю ${{z}_{3}}$, ${{z}_{4}}$.
Теорема 6. Если ни одно из чисел $c - b - {{a}_{1}} - {{a}_{2}}$ и $b - {{a}_{3}} - {{a}_{4}}$ не является целым, то в области
4.2. Продолжение функции $F_{D}^{{(4)}}$ в окрестность точки $(1,\infty ,\infty ,\infty )$, соответствующее ${{z}_{2}} = {{z}_{3}} = {{z}_{4}}$
Предположим, что переменные ${{z}_{1}},\;{{z}_{2}},\;{{z}_{3}},\;{{z}_{4}}$ функции Лауричеллы $F_{D}^{{(4)}}$ образуют две группы, в первую из которых входит только ${{z}_{1}}$, а во вторую – ${{z}_{2}}$, ${{z}_{3}}$ и ${{z}_{4}}$. Тогда согласно (2.19), (2.20) используемые в теореме 2 числа $q$, ${{p}_{s}}$, а также параметры и переменные функции Лауричеллы (3.1), (3.2) определяются следующими соотношениями:
(4.10)
$\begin{gathered} q = 2,\quad \nu = 1,\quad {{p}_{1}} = 1,\quad {{p}_{2}} = 3,\quad {{p}_{3}} = 0,\quad z_{1}^{{(1)}} = {{z}_{1}},\quad z_{1}^{{(2)}} = {{z}_{2}},\quad z_{2}^{{(2)}} = {{z}_{3}},\quad z_{3}^{{(2)}} = {{z}_{4}}, \\ a_{1}^{{(1)}} = {{a}_{1}},\quad a_{1}^{{(2)}} = {{a}_{2}},\quad a_{2}^{{(2)}} = {{a}_{3}},\quad a_{3}^{{(2)}} = {{a}_{4}},\quad k_{1}^{{(1)}} = {{k}_{1}},\quad k_{1}^{{(2)}} = {{k}_{2}},\quad k_{2}^{{(2)}} = {{k}_{3}},\quad k_{3}^{{(2)}} = {{k}_{4}}. \\ \end{gathered} $Применяя теорему 2, построим формулу продолжения функции $F_{D}^{{(4)}}$, справедливую вблизи пересечения гиперплоскостей
(4.11)
${{\mathcal{M}}_{{2,3}}}: = \{ {{z}_{2}} = {{z}_{3}}\} ,\quad {{\mathcal{M}}_{{3,4}}}: = \{ {{z}_{3}} = {{z}_{4}}\} ,$(4.12)
${{\Xi }_{0}}({\mathbf{a}};b,c;{\mathbf{k}}) = \frac{{{{{\left( {1 - c + \sum\limits_{s = 1}^4 \,{{a}_{s}}} \right)}}_{{{{k}_{2}}}}}{{{({{a}_{1}})}}_{{{{k}_{1}}}}}{{{({{a}_{2}} + {{a}_{3}} + {{a}_{4}})}}_{{{{k}_{2}} + {{k}_{3}} + {{k}_{4}}}}}{{{({{a}_{3}})}}_{{{{k}_{3}}}}}{{{({{a}_{4}})}}_{{{{k}_{4}}}}}}}{{{{{(1 + {{a}_{1}} + b - c)}}_{{{{k}_{1}}}}}{{{(1 - b + {{a}_{2}} + {{a}_{3}} + {{a}_{4}})}}_{{{{k}_{2}} - {{k}_{1}}}}}{{{({{a}_{2}} + {{a}_{3}} + {{a}_{4}})}}_{{{{k}_{3}} + {{k}_{4}}}}}{{k}_{1}}!{{k}_{2}}!{{k}_{3}}!{{k}_{4}}!}},$(4.13)
${{\Xi }_{1}}({\mathbf{a}};b,c;{\mathbf{k}}) = \frac{{{{{(c - b)}}_{{{{k}_{1}}}}}{{{\left( {1 + \sum\limits_{s = 1}^4 \,{{a}_{s}} - c} \right)}}_{{{{k}_{2}}}}}{{{({{a}_{2}} + {{a}_{3}} + {{a}_{4}})}}_{{{{k}_{2}} + {{k}_{3}} + {{k}_{4}}}}}{{{({{a}_{3}})}}_{{{{k}_{2}}}}}{{{({{a}_{4}})}}_{{{{k}_{4}}}}}}}{{{{{(1 + c - {{a}_{1}} - b)}}_{{{{k}_{1}}}}}{{{\left( {1 + \sum\limits_{s = 1}^4 \,{{a}_{s}} - c} \right)}}_{{{{k}_{2}} - {{k}_{1}}}}}{{{({{a}_{2}} + {{a}_{3}} + {{a}_{4}})}}_{{{{k}_{3}} + {{k}_{4}}}}}{{k}_{1}}!{{k}_{2}}!{{k}_{3}}!{{k}_{4}}!}},$(4.14)
${{\Xi }_{2}}({\mathbf{a}};b,c;{\mathbf{k}}) = \frac{{{{{(b)}}_{{|{\mathbf{k}}|}}}{{{(1 - c + {{a}_{1}} + b)}}_{{{{k}_{1}} + {{k}_{2}}}}}{{{({{a}_{1}})}}_{{{{k}_{1}}}}}{{{({{a}_{3}})}}_{{{{k}_{3}}}}}{{{({{a}_{4}})}}_{{{{k}_{4}}}}}}}{{{{{(1 + b - {{a}_{2}} - {{a}_{3}} - {{a}_{4}})}}_{{{{k}_{1}} + {{k}_{2}}}}}{{{({{a}_{2}} + {{a}_{3}} + {{a}_{4}})}}_{{{{k}_{3}} + {{k}_{4}}}}}{{{(1 - c + {{a}_{1}} + b)}}_{{{{k}_{1}}}}}{{k}_{1}}!{{k}_{2}}!{{k}_{3}}!{{k}_{4}}!}}.$(4.15)
$\begin{gathered} Z_{0}^{{(1)}} = ({{z}_{1}} - 1),\quad Z_{0}^{{(2)}} = \left( {\frac{1}{{{{z}_{2}}}},\frac{{{{z}_{2}} - {{z}_{3}}}}{{{{z}_{2}}}},\frac{{{{z}_{2}} - {{z}_{4}}}}{{{{z}_{2}}}}} \right),\quad Z_{1}^{{(1)}} = (1 - {{z}_{1}}),\quad Z_{1}^{{(2)}} = \left( {\frac{1}{{{{z}_{2}}}},\frac{{{{z}_{2}} - {{z}_{3}}}}{{{{z}_{2}}}},\frac{{{{z}_{2}} - {{z}_{4}}}}{{{{z}_{2}}}}} \right), \\ Z_{2}^{{(1)}} = \left( {\frac{{{{z}_{1}} - 1}}{{{{z}_{2}}}}} \right),\quad Z_{2}^{{(2)}} = \left( {\frac{1}{{{{z}_{2}}}},\frac{{{{z}_{2}} - {{z}_{3}}}}{{{{z}_{2}}}},\frac{{{{z}_{2}} - {{z}_{4}}}}{{{{z}_{2}}}}} \right), \\ \end{gathered} $(4.16)
$\begin{gathered} {{B}_{0}} = \frac{{\Gamma (c)\Gamma (c - b - {{a}_{1}})\Gamma (b - {{a}_{2}} - {{a}_{3}} - {{a}_{4}})}}{{\Gamma (b)\Gamma \left( {c - \sum\limits_{s = 1}^4 \,{{a}_{s}}} \right)\Gamma (c - b)}}, \\ {{B}_{1}} = \frac{{\Gamma (c)\Gamma ({{a}_{1}} + b - c)}}{{\Gamma ({{a}_{1}})\Gamma (b)}},\quad {{B}_{2}} = \frac{{\Gamma (c)\Gamma ({{a}_{2}} + {{a}_{3}} + {{a}_{4}} - b)}}{{\Gamma ({{a}_{2}} + {{a}_{3}} + {{a}_{4}})\Gamma (c - b)}}. \\ \end{gathered} $Далее, учитывая соотношения (4.3)–(4.9), из теоремы 2 получаем следующее утверждение, позволяющее аналитически продолжить функцию Лауричеллы $F_{D}^{{(4)}}$ в окрестность пересечения особых гиперплоскостей (4.11), т.е. в ситуации кроудинга переменных ${{z}_{2}},\;{{z}_{3}}$ и ${{z}_{4}}$, для случая близких к единице переменных ${{z}_{1}}$ и больших по модулю ${{z}_{2}}$, ${{z}_{3}}$, ${{z}_{4}}$.
Теорема 7. Если ни одно из чисел $c - b - {{a}_{1}}$ и $b - {{a}_{2}} - {{a}_{3}} - {{a}_{4}}$ не является целым, то в области
4.3. Продолжение функции $F_{D}^{{(4)}}$ в окрестность точки $(1,1,1,\infty )$, соответствующее ${{z}_{1}} = {{z}_{2}} = {{z}_{3}}$
Предположим, что переменные ${{z}_{1}},\;{{z}_{2}},\;{{z}_{3}},\;{{z}_{4}}$ функции Лауричеллы $F_{D}^{{(4)}}$ образуют две группы, в первую из которых входят ${{z}_{1}}$, ${{z}_{2}}$ и ${{z}_{3}}$, а во вторую – только ${{z}_{4}}$. Тогда согласно (2.19), (2.20) используемые в теореме 2 числа $q$, ${{p}_{s}}$, а также параметры и переменные функции Лауричеллы (3.1), (3.2) определяются следующими соотношениями:
(4.17)
$\begin{gathered} q = 2,\quad \nu = 1,\quad {{p}_{1}} = 3,\quad {{p}_{2}} = 1,\quad {{p}_{3}} = 0,\quad z_{1}^{{(1)}} = {{z}_{1}},\quad z_{2}^{{(1)}} = {{z}_{2}},\quad z_{3}^{{(1)}} = {{z}_{3}},\quad z_{1}^{{(2)}} = {{z}_{4}}, \\ a_{1}^{{(1)}} = {{a}_{1}},\quad a_{2}^{{(1)}} = {{a}_{2}},\quad a_{3}^{{(1)}} = {{a}_{3}},\quad a_{1}^{{(2)}} = {{a}_{4}},\quad k_{1}^{{(1)}} = {{k}_{1}},\quad k_{2}^{{(1)}} = {{k}_{2}},\quad k_{3}^{{(1)}} = {{k}_{3}},\quad k_{1}^{{(2)}} = {{k}_{4}}. \\ \end{gathered} $Применяя теорему 2, построим формулу продолжения функции $F_{D}^{{(4)}}$, справедливую вблизи пересечения гиперплоскостей
(4.18)
${{\mathcal{M}}_{{1,2}}}: = \{ {{z}_{1}} = {{z}_{2}}\} ,\quad {{\mathcal{M}}_{{2,3}}}: = \{ {{z}_{2}} = {{z}_{3}}\} ,$(4.19)
${{\Xi }_{0}}({\mathbf{a}};b,c;{\mathbf{k}}) = \frac{{{{{\left( {1 - c + \sum\limits_{s = 1}^4 \,{{a}_{s}}} \right)}}_{{{{k}_{4}}}}}{{{({{a}_{1}} + {{a}_{2}} + {{a}_{3}})}}_{{{{k}_{1}} + {{k}_{2}} + {{k}_{3}}}}}{{{({{a}_{2}})}}_{{{{k}_{2}}}}}{{{({{a}_{3}})}}_{{{{k}_{3}}}}}{{{({{a}_{4}})}}_{{{{k}_{4}}}}}}}{{{{{(1 + {{a}_{1}} + {{a}_{2}} + {{a}_{3}} + b - c)}}_{{{{k}_{1}} + {{k}_{2}} + {{k}_{3}}}}}{{{(1 - b + {{a}_{4}})}}_{{{{k}_{4}} - {{k}_{1}} - {{k}_{2}} - {{k}_{3}}}}}{{{({{a}_{1}} + {{a}_{2}} + {{a}_{3}})}}_{{{{k}_{2}} + {{k}_{3}}}}}{{k}_{1}}!{{k}_{2}}!{{k}_{3}}!{{k}_{4}}!}},$(4.20)
${{\Xi }_{1}}({\mathbf{a}};b,c;{\mathbf{k}}) = \frac{{{{{(c - b)}}_{{{{k}_{1}}}}}{{{\left( {1 + \sum\limits_{s = 1}^4 \,{{a}_{s}} - c} \right)}}_{{{{k}_{4}}}}}{{{({{a}_{2}})}}_{{{{k}_{2}}}}}{{{({{a}_{3}})}}_{{{{k}_{3}}}}}{{{({{a}_{4}})}}_{{{{k}_{4}}}}}}}{{{{{(1 + c - {{a}_{1}} - {{a}_{2}} - {{a}_{3}} - b)}}_{{{{k}_{1}} - {{k}_{2}} - {{k}_{3}}}}}{{{({{a}_{2}} + {{a}_{3}} + {{a}_{4}})}}_{{{{k}_{2}} + {{k}_{3}}}}}{{{\left( {1 + \sum\limits_{s = 1}^4 \,{{a}_{s}} - c} \right)}}_{{{{k}_{4}} - {{k}_{1}}}}}{{k}_{1}}!{{k}_{2}}!{{k}_{3}}!{{k}_{4}}!}},$(4.21)
${{\Xi }_{2}}({\mathbf{a}};b,c;{\mathbf{k}}) = \frac{{{{{(b)}}_{{|{\mathbf{k}}|}}}{{{(1 - c + {{a}_{1}} + {{a}_{2}} + {{a}_{3}} + b)}}_{{|{\mathbf{k}}|}}}{{{({{a}_{1}} + {{a}_{2}} + {{a}_{3}})}}_{{{{k}_{1}} + {{k}_{2}} + {{k}_{3}}}}}{{{({{a}_{2}})}}_{{{{k}_{2}}}}}{{{({{a}_{3}})}}_{{{{k}_{3}}}}}}}{{{{{(1 + b - {{a}_{4}})}}_{{|{\mathbf{k}}|}}}{{{(1 - c + {{a}_{1}} + {{a}_{2}} + {{a}_{3}} + b)}}_{{{{k}_{1}} + {{k}_{2}} + {{k}_{3}}}}}{{{({{a}_{1}} + {{a}_{2}} + {{a}_{3}})}}_{{{{k}_{2}} + {{k}_{3}}}}}{{k}_{1}}!{{k}_{2}}!{{k}_{3}}!{{k}_{4}}!}}.$(4.22)
$\begin{gathered} Z_{0}^{{(1)}} = ({{z}_{1}} - 1,{{z}_{2}} - {{z}_{1}},{{z}_{3}} - {{z}_{1}}),\quad Z_{0}^{{(2)}} = \left( {\frac{1}{{{{z}_{4}}}}} \right),\quad Z_{1}^{{(1)}} = \left( {1 - {{z}_{1}},\frac{{{{z}_{1}} - {{z}_{2}}}}{{1 - {{z}_{1}}}},\frac{{{{z}_{1}} - {{z}_{3}}}}{{1 - {{z}_{1}}}}} \right),\quad Z_{1}^{{(2)}} = \left( {\frac{1}{{{{z}_{4}}}}} \right), \\ Z_{2}^{{(1)}} = \left( {\frac{{1 - {{z}_{1}}}}{{{{z}_{4}}}},\frac{{{{z}_{2}} - {{z}_{1}}}}{{{{z}_{4}}}},\frac{{{{z}_{3}} - {{z}_{1}}}}{{{{z}_{4}}}}} \right),\quad Z_{2}^{{(2)}} = \left( {\frac{1}{{{{z}_{4}}}}} \right), \\ \end{gathered} $(4.23)
$\begin{gathered} {{B}_{0}} = \frac{{\Gamma (c)\Gamma (c - b - {{a}_{1}} - {{a}_{2}} - {{a}_{3}})\Gamma (b - {{a}_{4}})}}{{\Gamma (b)\Gamma \left( {c - \sum\limits_{s = 1}^4 \,{{a}_{s}}} \right)\Gamma (c - b)}}, \\ {{B}_{1}} = \frac{{\Gamma (c)\Gamma ({{a}_{1}} + {{a}_{2}} + {{a}_{3}} + b - c)}}{{\Gamma ({{a}_{1}} + {{a}_{2}} + {{a}_{3}})\Gamma (b)}},\quad {{B}_{2}} = \frac{{\Gamma (c)\Gamma ({{a}_{4}} - b)}}{{\Gamma ({{a}_{4}})\Gamma (c - b)}}. \\ \end{gathered} $Далее, учитывая соотношения (4.19)–(4.23), из теоремы 2 получаем следующее утверждение, позволяющее аналитически продолжить функцию Лауричеллы $F_{D}^{{(4)}}$ в окрестность пересечения особых гиперплоскостей (4.18), т.е. в ситуации кроудинга переменных ${{z}_{1}},\;{{z}_{2}}$ и ${{z}_{3}}$, для случая, когда они близки к единице, а переменное ${{z}_{4}}$ имеет большой модуль.
Теорема 8. Если ни одно из чисел $c - b - {{a}_{1}} - {{a}_{2}} - {{a}_{3}}$ и $b - {{a}_{4}}$ не является целым, то в области
Представления функций $F_{D}^{{(3)}}$ и $F_{D}^{{(4)}}$, найденные в теоремах 3–8, демонстрируют, что тео-ремы 1, 2 дают эффективный алгоритм для построения формул аналитического продолжения функции Лауричеллы (1.1). Полученные в результате применения теорем 1, 2 формулы дают эффективный алгоритм для вычисления интегралов типа Эйлера (1.7) вне области сходимости степенного ряда (1.1), которым она исходно определена. Таким образом, результаты настоящей работы могут быть востребованы при решении прикладных проблем, где возникают ряды вида (1.1), интегралы (1.7) или системы уравнений с частными производными (1.8). Одним из перспективных приложений, полученных в теоремах 2–8 представлений для функции Лауричеллы, является проблема “кроудинга” параметров интеграла Кристоффеля–Шварца, возникающая при построении конформного отображения многоугольников.
Список литературы
Exton H. Multiple hypergeometric functions and application. New York: John Willey & Sons, Inc, 1976.
Гельфанд И.М., Граев М.И., Ретах В.С. Общие гипергеометрические системы уравнений и ряды гипергеометрического типа // Успехи матем. наук. 1992. Т. 47. Вып. 4(286). С. 3–82.
Iwasaki K., Kimura H., Shimomura Sh., Yoshida M. From Gauss to Painlevé: a modern theory of special functions. Aspects of Mathematics. Vol. E16. Braunschweig: Friedrich Vieweg & Sohn, 1991.
Aomoto K., Kita M. Theory of Hypergeometric Functions. Springer monographs in mathematics. Tokyo, Dordrecht, Heidelberg: Springer, 2011.
Akerblom N., Flohr M. Explicit formulas for the scalar modes in Seiberg–Witten theory with an application to the Argyres–Douglas point. J. High Energy Phys. 2005. V. 2. № 057. P. 24.
Holzapfel R.-P., Uludag A.M., Yoshida M. Arithmetic and geometry around hypergeometric functions. Progr. Math. V. 260. Basel: Birkhäuser Verlag, 2007.
Тарасов О.В. Применение функциональных уравнений для вычисления фейнмановских интегралов // Теор. и матем. физ. 2019. Т. 200. № 2. С. 324–342.
Безродных С.И. Гипергеометрическая функция Лауричеллы $F_{D}^{{(N)}}$, задача Римана–Гильберта и некоторые приложения // Успехи матем. наук. 2018. Т. 73. № 6 (444). С. 3–94.
Brychkov Yu.A., Savischenko N.V. Application of hypergeometric functions of two variables in wireless communication theory // Lobachevskii J. of Math. 2019. V. 40. № 7. P. 938–953.
Berge J., Massey R., Baghi Q., Touboul P. Exponential shapelets: basis functions for data analysis of isolated feature // Month. Not. Royal Astron. Soc. 2019. V. 486. № 1. P. 544–559.
Bezrodnykh S.I., Vlasov V.I. Asymptotics of the Riemann–Hilbert problem for the Somov model of magnetic reconnection of long shock waves // Math. Not. 2021. V. 110. Iss. 6. P. 853–871.
Власов В.И., Скороходов С.Л. Аналитическое решение задачи о кавитационном обтекании клина. II // Ж. вычисл. мат. и матем. физ. 2021. Т. 61. № 11. С. 1873–1893.
Lauricella G. Sulle funzioni ipergeometriche a piu variabili // Rendiconti Circ. Math. Palermo. 1893. V. 7. P. 111–158.
Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Гипергеометрическая функция. Функции Лежандра. М.: Наука, 1973.
Уиттекер Э.Т., Ватсон Дж.Н. Курс современного анализа. Т. 2. М.: Эдиториал УРСС, 2002.
Bezrodnykh S.I. Analytic continuation of the Lauricella function $F_{D}^{{(N)}}$ with arbitrary number of variables. Integral Transforms and Special Functions. 2018. V. 29. № 1. P. 21–42.
Bezrodnykh S.I. Analytic continuation of Lauricella’s function $F_{D}^{{(N)}}$ for large in modulo variables near hyperplanes $\{ {{z}_{j}} = {{z}_{l}}\} $ // Integral Transforms and Special Functions. 2021. Publ. online. https://doi.org/10.1080/10652469.2021.192920610.1080/10652469.2021.1929206
Bezrodnykh S.I. Analytic continuation of Lauricella’s function $F_{D}^{{(N)}}$ for variables close to unit near hyperplanes $\{ {{z}_{j}} = {{z}_{l}}\} $ // Integral Transforms and Special Functions. 2021. Publ. online. https://doi.org/10.1080/10652469.2021.193932910.1080/10652469.2021.1939329
Henrici P. Applied and Computational Complex Analysis. Vol. 1–3. New York: John Wiley and Sons, 1991.
Trefethen L.N. Numerical construction of comformal maps Appendix to: E.B. Saff, A.D. Snider, “Fundamentals of Complex Analysis for Mathematics, Science, and Engineering”. New York, Prentice Hall, 1993.
Kythe P.K. Computational conformal mapping. Birkhäuser, 1998.
Власов В.И., Скороходов С.Л. Метод мультиполей для задачи Дирихле в двусвязных областях сложной формы. I. Общее описание метода // Ж. вычислит. матем. и матем. физ. 2000. Т. 40. № 11. С. 1633–1647.
Безродных С.И., Власов В.И. Задача Римана–Гильберта в сложной области для модели магнитного пересоединения в плазме // Ж. вычислит. матем. и матем. физ. 2002. Т. 42. № 3. С. 277–312.
Trefethen L.N., Driscoll T.A. Schwarz–Christoffel transformation. Campridge: Cambridge Univer. Press, 2005.
Banjai L. Revisiting the crowding phenomenon in Schwarz–Christoffel mapping // SIAM J. Sci. Comput. 2008. V. 30. № 2. P. 618–636.
Papamichael N., Stylianopoulos N. Numerical conformal mapping. Domain decomposition and the mapping of quadrilaterals. Hackensack, NJ World Sci. Publ. Co. Pte. Ltd. 2010, xiio pp.
Садыков Т.М., Цих А.К. Гипергеометрические и алгебраические функции многих переменных. М.: Наука, 2014.
Bezrodnykh S.I. Analytic continuation of the Horn hypergeometric series with an arbitrary number of variables // Integral Transforms and Spec Functions. 2020. V. 31. № 10. P. 788–803.
Fox F. The asymtotic expansion of hypergeometric functions // Proc. London Math. Soc. 1928. V. 27. № 2. P. 389–400.
Wright E.M. The asymtotic expansion of hypergeometric functions // Proc. London Math. Soc. 1935. V. 10. № 4. P. 286–293.
Bezrodnykh S.I. Analytic continuation of the Kampé de Fériet function and the general double Horn series // Integral Transforms and Special Functions. 2022. https://doi.org/10.1080/10652469.2022.2056601
Безродных С.И. Формулы аналитического продолжения функций Горна двух переменных // Ж. вычисл. матем. и матем. физ. 2022. Т. 62. № 6. С. 912–932.
Brychkov Yu.A., Savischenko N.V. On some formulas for the Horn functions ${{H}_{5}}(a,b;c;w,z)$ and $H_{5}^{c}(a;c;w,z)$ // Integral Transforms and Special Functions. 2021. Publ. online. https://doi.org/10.1080/10652469.2021.193802610.1080/10652469.2021.1938026
Brychkov Yu.A., Savischenko N.V. On some formulas for the Horn functions ${{H}_{6}}(a,b,b{\kern 1pt} ',w,z)$ and $H_{8}^{{(c)}}(a,b;w,z)$ // Integral Transforms and Special Functions. 2021. Publ. online. https://doi.org/10.1080/10652469.2021.201742710.1080/10652469.2021.2017427
Ananthanarayan B., Beraay S., Friot S., Marichev O., Pathak T. On the evaluation of the Appell ${{F}_{2}}$ double hypergeometric function. 2021; arXiv:2111.05798v1
Brychkov Yu.A., Savischenko N.V. On some formulas for the Horn function ${{H}_{7}}(a,b,b{\kern 1pt} ';c;w,z)$ // Integral Transforms and Special Functions. 2021. Publ. online. https://doi.org/10.1080/10652469.2022.205660010.1080/10652469.2022.2056600
Kalmykov M., Bytev V., Kniehl B., Moch S.-O., Ward B., Yost S. Hypergeometric functions and Feynman diagrams. In: Blümlein J., Schneider C. (eds) Anti-Differentiation and the Calculation of Feynman Amplitudes. Texts & Monographs in Symbolic Computation (A Series of the Research Institute for Symbolic Computation, Johannes Kepler University, Linz, Austria). Springer, Cham, 2021.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики